Do hospitals respond to decreasing prices by supplying more services?

Abstract

Regulated prices are common in markets for medical care. We estimate the effect of changes in regulated reimbursement prices on volume of hospital care based on a reform of hospital financing in Germany. Uniquely, this reform changed the overall level of reimbursement—with increasing prices for some hospitals and decreasing prices for others—without directly affecting the relative prices for different groups of patients or types of treatment. Based on administrative data, we find that hospitals react to increasing prices by decreasing the service supply and to decreasing prices by increasing the service supply. Moreover, we find some evidence that volume changes for hospitals with different price changes are nonlinear. We interpret our findings as evidence for a negative income effect of prices on volume of care.

1. INTRODUCTION

In many important markets, prices are set not by the interaction of demand and supply but by public or semi‐public agencies. Regulated prices are especially common in markets for medical care, for example, for the reimbursement of hospital services in Germany and for Medicare patients in the United States. This makes it an interesting and policy relevant question to examine how providers of medical care respond to changes in regulated prices. In this study, we examine the effect of changes in reimbursement prices on the volume of hospital care in Germany.

The direction of this effect is not a priori clear, neither based on economic theory nor based on previous empirical evidence. In a seminal study, McGuire and Pauly (1991) develop a theoretical framework for how medical providers respond to changes in regulated prices. They show that the effect of changes in regulated prices on volume of care is a combination of two effects: (a) the response to a change in relative prices between different types of services or groups of patients and (b) the response to a change in the overall price level. The second effect is typically referred to as “income effect” in the literature (McGuire, 2000). Although an increase in relative prices for a type of service is predicted to lead to an increase in the supply of this service, alternative economic models make different predictions about the sign of the income effect. According to the standard economic theory, higher prices lead to more supply of services. In contrast, models of supplier‐induced demand (Evans, 1974; Gruber & Owings, 1996) or of providers aiming at target incomes (Rizzo & Zeckhauser, 2003) predict that higher prices can lead to the supply of fewer services and lower prices can lead to the supply of more services. The underlying intuition is that providers compensate for the effect of lower prices on income by providing more services, and they exert less effort to achieve a high volume of services if prices are increasing. In line with this reasoning, the Federal budgeting process in the United States assumes that a 1% decrease in Medicare reimbursement prices increases treatment volumes by around 0.3–0.5% (Congressional Budget Office, 2007).

The empirical evidence on the effect of lower reimbursement prices on volume of care is mixed. Among the recent studies, some find that lower prices decrease volumes of care (Clemens & Gottlieb, 2014; He & Mellor, 2012; Januleviciute, Askildsen, Kaarboe, Siciliani, & Sutton, 2016), whereas other studies find that lower prices increase volumes of care (Heaton & Helland, 2009; Shigeoka & Fushimi, 2014). Most previous studies examine price changes that affect only a subset of patients or medical treatments, such as Medicare beneficiaries (Clemens & Gottlieb, 2014; He & Mellor, 2012; Rice, 1983; Yip, 1998), automobile accident victims (Heaton & Helland, 2009), at‐risk newborns (Shigeoka & Fushimi, 2014), or patients with specific diagnoses (Januleviciute et al., 2016), while leaving prices for other patients and treatments unaffected. In these settings, the effect of price changes is then a combination of the effect of a change in relative prices and an income effect, and it is very difficult to ascertain which part of the overall effect can be attributed to either of them.

In our study, we exploit a setting that makes it possible to estimate the income effect directly. Specifically, we look at changes in hospital‐specific base rates (Basisfallwerte) in Germany between the years 2004 and 2009. Changes in base rates shift the overall level of reimbursement prices in hospitals without directly affecting the relative prices for different groups of patients or types of services. In the year 2004, base rates varied widely between hospitals based on historical costs. Between 2004 and 2009, base rates gradually converged toward the average base rate at the state level. Thus, base rates increased for some hospitals and decreased for others.

In our empirical analysis, we exploit this variation in reimbursement prices. We estimate the effect of changes in base rates between 2004 and 2009 on corresponding changes in volumes of care. We use a differences‐in‐differences estimation approach with the change in prices as continuous treatment variable.

On the basis of the administrative data for a 70% random sample of all German hospitals, we find, for alternative model specifications, an elasticity of prices on the number of hospital admissions of between −0.14 and −0.2 over a 5‐year period. Thus, hospitals respond to increasing prices by decreasing service supply and to decreasing prices by increasing service supply. We interpret our findings as evidence for a negative income effect. Moreover, although we find that hospital volume increases more for hospitals with declining base rates than for hospitals with increasing base rates, this effect is nonlinear. For example, the increase in the number of admissions between the years 2004 and 2009 is smaller for hospitals with strongly increasing prices than for hospitals with weakly increasing prices.

2. INSTITUTIONAL SETTING

Hospital financing in Germany comes from several sources. By far, the most important sources are public and private health insurers, which cover around 88.5% of all hospital expenditures (Simon, 2010). Funding from these sources is largely used to cover hospitals' operating costs, including payments for physicians' services. The remaining hospital revenues are derived mainly from state governments, which are responsible for long‐term infrastructure investments. Patient co‐payments in Germany are small relative to hospital costs. Patients have to pay a fixed charge of €10 per night of their hospital stay as a contribution toward room and board, and there are surcharges for additional services such as a single room or treatment by the hospital director (for details of hospital financing in Germany, see Quentin, Geissler, Schneller‐Kreinsen, & Busse, 2010 and Simon, 2010).

Before 2004, hospital payment for operating costs was based on a mixed payment system (see description by Busse & Riesberg, 2004). Seventy‐five percent of cases were reimbursed by per diem charges. Hospitals with higher expenditures in relation to the number of hospital beds received higher per diem charges. The remaining 25% were already reimbursed according to patients' diagnosis‐related groups (DRGs). In 2004, payment based on DRGs was expanded to almost all diagnoses. The aim of this reform was to make hospital payment more transparent and to promote efficiency and competition. The German DRG payment system is similar to hospital payment systems in other countries that have introduced DRG‐type systems, starting from the early 1980s. A particular aspect of the German reform that sets it apart from DRG payment introduction in other countries is that payment changes were introduced gradually. During a first “budget‐neutral phase” in 2004, hospitals were reimbursed according to DRGs, but prices were adjusted with hospital‐specific base rates in such a way that hospitals could still achieve their historical budgets. During the “convergence phase,” which lasted from 2005 to 2009, hospital‐specific prices gradually converged toward average prices at the state level.

Under the German DRG system, a payment for a hospital admission is based on the following formula:

$${\mathit{\text{payment}}}_{i,j,t}={\mathit{drg}}_{j,t}*\mathit{\text{base}}{\mathit{\text{rate}}}_{i,t}.$$ (1)

Payment is the product of two factors: drg_j,t is the cost weight factor for DRG j in year t, and base rate_i,t refers to a hospital‐specific base rate for hospital i in year t. All discharged hospital patients are assigned to a DRG. This assignment is based mainly on diagnoses, but in some instances, it is also based on procedures and patient characteristics such as age, sex, and birthweight (for newborns). DRG cost weight factors are the same for all hospitals. They are set at the national level jointly by representatives of health insurers and hospitals, and they are adjusted annually based on detailed patient‐level cost data from a sample of hospitals. The cost weight factors are normalized such that the average cost weight factor is set to one. Cost weight factors are much higher than one for cost‐intensive DRGs such as a liver transplant, and they are lower than one for less cost‐intensive DRGs such as an ordinary hand fracture. The average cost weight factor for hospital i in year t is referred to as case‐mix index: ${\mathit{cmi}}_{i,t}=\frac{1}{N_{i,t}}\sum _j\left(N_{i,j,t}*{\mathit{drg}}_{j,t}\right)$, where N_i,t is the total number of patients admitted to hospital i in year t and N_i,j,t is the number of patients with DRG j admitted to hospital i in year t.

Hospital‐specific base rates reflect historical budgets before the introduction of DRG payment. During the budget‐neutral phase of the reform, hospital‐specific base rates were computed by dividing the pre‐reform budgets by the sum of cost weight factors. The sum of the cost weight factors was computed based on the treatments that hospitals provided before the reform. Using hospital‐specific base rates ensured that hospitals could still achieve their historical budgets under DRG payments in the early stage of the reform as long as they continued to provide the same volume and type of services.

During the 2005–2009 convergence phase, hospital‐specific base rates gradually converged toward state averages. Base rates gradually decreased for hospitals with above‐average base rates, and they increased for hospitals with below‐average base rates. A schematic illustration of the convergence process is provided in Figure 1. From 2009, hospitals in the same state received the same base rate.

Figure 1.

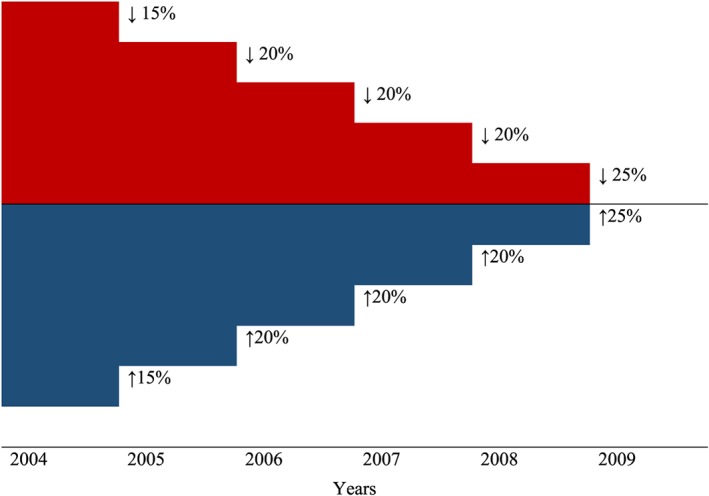
Convergence of base rates (schematic illustration). Note: This figure shows a schematic illustration for the reduction of initial differences in base rates during the convergence period [Colour figure can be viewed at http://wileyonlinelibrary.com]

The initial variation in base rates was substantial (see Figure S1). In 2004, the difference between the 10th and 90th percentiles of base rates was around 36%. The convergence of base rates implied substantial increases in across‐the‐board reimbursement prices for some hospitals and substantial reductions for others. Base rates at the 10th percentile are increased by 15.4% in real terms between 2004 and 2009, whereas those at the 90th percentile are decreased by 11.8%. ^,

Existing theoretical models show that, under some conditions, medical providers respond to decreasing prices by providing more services. McGuire and Pauly (1991) show that the income effect is negative if the coefficient of relative risk aversion, a measure of curvature of the income utility schedule, is above a given threshold. In this case, medical providers are very risk averse with respect to declining revenues, and subsequently, decision makers in hospitals reduce their efforts to generate revenues in response to higher prices, and they increase their efforts in response to lower prices. Hospitals with declining base rate factors faced substantial financial pressure. They had little room to expand the services that were not affected by changes in base rates. Specifically, price changes for hospital care apply to both publicly and privately insured patients. Moreover, hospitals and physicians who work at hospitals are largely banned from providing outpatient services. They cannot easily respond to reduced prices for inpatient care by providing more outpatient services. At the same time, a high share of costs for hospitals in Germany is fixed—at least in the short and medium term. The overwhelming part of hospital costs is personnel expenditures. Hospital physicians are mostly salaried employees, and wages for both physicians and other staff are set in wage negotiations at the federal level. Layoffs are costly. Because a high share of costs is fixed, the marginal cost of admitting an additional patient can be low. Low marginal costs make it attractive for hospitals to increase volume of care in response to lower prices.

This leads to the question of how German hospitals can increase the demand for their services. One of the most important driving factors behind patients' hospital choices are recommendations from outpatient physicians (Salfeld, Hehner, & Wichels, 2009). Thus, it is important for hospitals to cultivate good relationships with outpatient physicians who are able to refer patients to the hospital. For example, hospital directors can visit outpatient physicians and inform them about new treatment techniques available at the hospital. Reportedly, many hospitals also pay outpatient physicians for patient referrals (GKV‐Spitzenverband, 2012). In addition to increasing the number of patient admissions, hospitals can also aim to increase payments per patient admitted. There can also be substitution between these two strategies, depending on the relative costs and the benefits of increasing the number of admissions and increasing the average payment per patient admitted.

The German DRG rules make provisions to protect against induced demand. Hospitals may keep only 35% of additional revenues if they exceed the number of target admissions. Additional revenues that are generated by upcoding, that is, charging a more expensive DRG for the same treatment, are meant to be reclaimed fully by health insurers (Tuschen, Braun, & Rau, 2005). However, these provisions are not applied consistently in practice. Hospitals routinely delay the budget negotiations until late in the year, and they then negotiate target numbers of admissions that are close to the actual number of admissions (Kumar & Schönstein, 2013). Furthermore, increases in the case‐mix index can be reimbursed if the hospital can provide good medical reasons for more intensive treatment.

3. EMPIRICAL APPROACH

In our empirical strategy, we examine how treatment volumes respond to changes in base rates. We use a differences‐in‐differences regression approach. However, instead of looking at a binary treatment variable, we examine the effect of a change in prices, which is a continuous treatment variable. Thus, we compare not just two groups with different treatments, that is, one treatment group and one control group, but we look at a continuous range of treatments and compare different treatments with each other. We estimate the linear regression models with two periods and hospital‐specific fixed effects:

$$q_{i,t}=d_{2009}\mathrm{\Delta }\mathit{\text{base}}{\mathit{\text{rate}}}_{i,2004-2009}\beta +d_{2009}\gamma +x_{r\left(i\right),t}\prime \delta +{\alpha }_i+{\epsilon }_{i,t},$$ (2)

where q_i,t is the treatment volume for hospital i ∈ (1 …,  N) in year t ∈ (2004,2009), which is measured by the number of admissions (q_i,t = N_i,t) in the baseline specification. d ₂₀₀₉ is a binary indicator for the year 2009; Δbase rate_{i,2004 − 2009} is the change in the base rate of hospital i between the years 2004 and 2009; x_r(i),t includes regional demographic and economic characteristics for region r where hospital i is situated ; α_i are unobserved hospital fixed effects; and ε_i,t represents unobserved time‐varying hospital characteristics. β and γ are parameters, and δ is a vector of parameters. β is the parameter of interest, and it represents the effect of changes in reimbursement prices on changes in hospital volumes.

Our treatment variable is the change in base rates between the years 2004 and 2009. For the intermediate years 2005–2008, base rates did not always follow the adjustment schedule shown in Figure 1, but they were negotiated annually between sickness funds and hospitals. Thus, hospitals could have been able to influence base rates in those years. This concern does not apply to the year 2009, when base rates were equalized at the state level.

Regression Equation (2) provides a consistent estimator of β if the exogeneity assumption below holds:

$$E\left[{\epsilon }_{i,t}|\mathrm{\Delta }\mathit{\text{base}}{\mathit{\text{rate}}}_{i,2004-2009},x_{r\left(i\right),t},d_{2009}\right]=0.$$ (3)

Note that the equation above does not contain any assumptions about time‐invariant unobserved characteristics α_i. Hospitals with different values of Δbase rate_{i,2004 − 2009} can differ in their observed and unobserved characteristics. This does not violate the exogeneity assumption as long as changes in base rates are not correlated with changes in time‐varying unobserved hospital characteristics ε_i,t.

The exogeneity assumption in Equation (3) is akin to the common trend assumption in a differences‐in‐differences estimation framework. This assumption requires that in the absence of price changes, the number of admissions for hospitals with different values of Δbase rate_{i,2004 − 2009} should follow the same time trend. We discuss potential violations of the exogeneity assumption, including the effects of changing cost weight factors, in Section 5.

4. DATA

Our main source of data is hospital statistics from the German Statistical Office for the period 2000–2009. These hospital statistics combine information about hospital characteristics such as ownership type and size with patient‐level information on admissions, such as the main diagnosis and county of residence for each patient. These data are merged with county‐level regional indicators from the German Statistical Office and with information on base rates provided by Allgemeine Ortskrankenkasse, a group of health insurers.

Our study is based on a 70% random sample of all German hospitals. Our data include 1,159 hospitals with information on the number of admissions and base rates in the year 2004. Of those, 165 were excluded from the sample because they are not open year round or they are day clinics or psychiatric hospitals that did not adopt the DRG system. A further 193 hospitals were excluded because they could not be tracked up to 2009. Although hospital closures were very rare during our study period, mergers were quite common. Our baseline estimation sample consists of 801 hospitals.

Outcome variable in the baseline specification is the natural logarithm of the total number of annual hospital admissions. In alternative specifications, outcome variables are the natural logarithm of total revenues from the DRG system (the sum of all cost weights of hospital i in year t) and the case‐mix index, respectively. The main explanatory variable of interest is the percentage change in the base rate (Basisfallwert) of a hospital between the years 2004 and 2009.

We compute a variable for the change in average base rates for competing hospitals that attract patients from the same geographical area. This calculation consists of two steps: (a) We first compute the average base rate for competing hospitals in each county. This calculation is based on hospital market shares for residents of each county. (b) We then compute the average base rates for competing hospitals for each hospital. This calculation is based on the county shares of patients for each hospital, for example, what share of a hospital's patients resides in a specific county. ^,

We further compute variables on demographic and economic indicators for hospital catchment areas. For this calculation, we weight county‐level indicators for the average age of men, average age of women, population density, and unemployment rate based on the county shares of patients in each hospital.

Summary statistics for hospitals in our data set are shown in Panel A of Table 1. For example, the average number of admissions per hospital increased from 10,940 to 11,878 between 2004 and 2009. ^, The case‐mix index stayed on average constant around 1. The share of private hospitals increased from 14.1% to 16.7%, whereas the shares of public hospitals and not‐for‐profit hospitals decreased. The average age of the population, the Herfindahl index, and population density increased, whereas the unemployment rate decreased. The distribution of our main explanatory variable, the changes in base rates between the years 2004 and 2009, is shown in Figure 2. Changes varied from substantial decreases to substantial increases in prices. Panel B of Table 1 shows sample means for increasing and decreasing base rates. For hospitals with increasing base rates, the mean increase is 10.9%, and for hospitals with decreasing base rates, the mean decrease is −9.2%, both in real terms.

Table 1.

Descriptive statistics

Panel A: Descriptive statistics for variables for years 2004 and 2009
	Year 2004		Year 2009
	M	SD	M	SD
Number of admissions	10,940.590	10,452.560	11,878.680	11,289.700
CMI	1.001	0.264	1.012	0.407
Public hospitals	0.408	0.492	0.391	0.488
Not‐for‐profit hospitals	0.451	0.498	0.442	0.497
Private hospitals	0.141	0.348	0.167	0.373
HHI	0.189	0.131	0.198	0.139
Unemployment rate	9.935	4.144	7.726	3.007
Average age men	36.950	1.006	37.889	0.889
Average age women	40.093	1.433	40.628	1.298
Population density	0.678	0.722	0.681	0.735
Number of hospitals	801		801

Panel B: Mean of real base rate changes between 2004 and 2009
Base rate	All hospitals	Hospitals with increasing real base rates	Hospitals with decreasing real base rates
Δbase rate (2004–2009)	0.020	0.109	−0.092
N (hospitals)	801	445	356

Note. Descriptive statistics in Panel A refer to sample in baseline specification (Table 2, column 1). The variable for case‐mix index is available for 788 hospitals. Δbase rate (2004–2009) is defined as log(base rate 2009) − log(base rate 2004). Base rates in 2009 are deflated with the harmonized consumer price index to base rates in 2004.

Abbreviations: CMI, case‐mix index; HHI, Herfindahl index.

Figure 2.

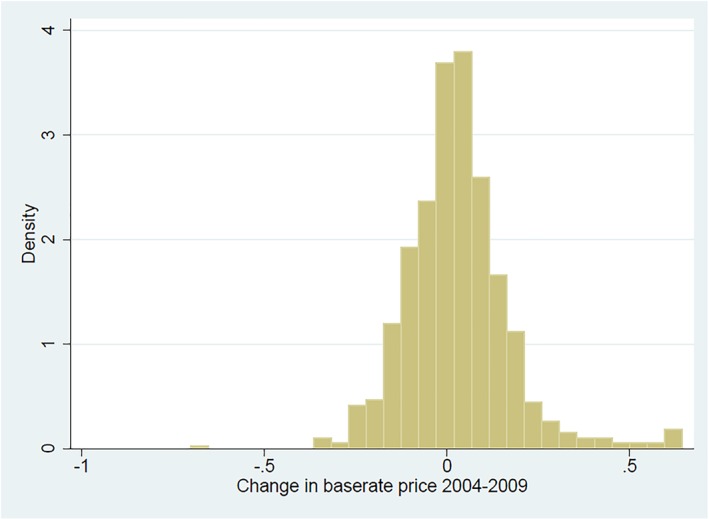
Distribution of base rate changes between 2004 and 2009. Note: This figure shows the distribution of Δbase rate (2004–2009). Δbase rate (2004–2009) is defined as log(base rate 2009) − log(base rate 2004). The sample consists of N = 801 hospitals [Colour figure can be viewed at http://wileyonlinelibrary.com]

5. RESULTS

5.1. Baseline specification

Table 2 shows estimation results for the effect of changes in base rates on the number of admissions. Our estimate of β in the baseline specification (Equation 2) in column 1 is −0.14. This coefficient is significantly different from 0 at 5% level. This implies that a 1% increase in prices causes a decrease in the number of hospital admissions by 0.14%. Correspondingly, a 1% decrease in prices causes the number of admissions to increase by 0.14%. ^,

Table 2.

Effects of base rate changes on number of admissions

	Log number of admissions
	Baseline	With additional trends	Without Hesse and Bavaria	No change of owner type	Without covariates	Without price competitors
	(1)	(2)	(3)	(4)	(5)	(6)
Δbase rate (2004–2009)	−0.136**	−0.138**	−0.155***	−0.132**	−0.133**	−0.132**
	(0.055)	(0.057)	(0.060)	(0.058)	(0.055)	(0.055)
Year effects	Yes	Yes	Yes	Yes	Yes	Yes
Regional characteristics	Yes	Yes	Yes	Yes	No	Yes
Average price of competitors	Yes	Yes	Yes	Yes	No	No
Trends by regional and hosp. charact.	No	Yes	No	No	No	No
Hospital fixed effects	Yes	Yes	Yes	Yes	Yes	Yes
N (hospitals)	801	801	689	755	801	801

Note. The table shows estimation coefficients of a fixed effects linear regression model. The sample includes observations for the years 2004 and 2009. Δbase rate (2004–2009) is defined as log(base rate 2009) − log(base rate 2004). Regional indicators include average age of men, average age of women, population density, and unemployment rate. All regional characteristics are measured for a hospital's catchment area. Trends by regional and hospital characteristics are captured by interaction terms of an indicator for the year 2009 and the following regional and hospital characteristics (measured in the year 2004): average age of men, average age of women, population density, unemployment rate, large number of beds, a high Herfindahl index, public ownership, and not‐for‐profit ownership. The Herfindahl index refers to the year 2003. Parentheses show robust standard errors clustered at the hospital level.

^* Significant at 10%.

^** Significant at 5%.

^*** Significant at 1%.

5.2. Changing cost weights

We now discuss a number of potential violations of the exogeneity assumption in Equation (3) and how we can test for these violations. A first possible violation relates to changes in cost weight factors. As described in Section 2, cost weight factors are set at the federal level, and they are adjusted annually. If hospitals provide different types of services and if changes in the average cost weights of the services they provide are correlated with changes in base rates, this can cause an omitted variable bias in our estimates.

Ideally, we would like to control for the change in the average cost weight of each hospital conditional on that the initial composition of DRGs is kept constant over time. However, such a measure is not available in our data. Yet we know the case‐mix index. In column 1 of Table 3, we show that a 1% increase in base rates is associated with a decrease in the case‐mix index of around 0.003, conditional on covariates. This association can have two alternative explanations: (a) Hospitals react to reduced base rates by upcoding (Dafny, 2005; Jürges & Köberlein, 2015) and/or by providing treatment that is more intensive (Cutler, 1995). (b) Changes in average cost weights (for a constant composition of DRGs over time) are correlated with changes in base rates.

Table 3.

The role of changes in cost weights

	Case‐mix index	Log number of admissions	Log revenues (Log number of admissions*Case‐mix index)
	(1)	(2)	(3)
Δbase rate (2004–2009)	−0.285***	−0.200***	−0.389***
	(0.082)	(0.056)	(0.057)
Case‐mix index	No	−0.075 (0.049)	No
Year effects	Yes	Yes	Yes
Regional characteristics	Yes	Yes	Yes
Average base rate of competitors	Yes	Yes	Yes
Hospital fixed effects	Yes	Yes	Yes
N (hospitals)	788	788	788

Note. The table shows estimation coefficients of a fixed effects linear regression model. The sample includes observations for the years 2004 and 2009. Δbase rate (2004–2009) is defined as log(base rate 2009) − log(base rate 2004). Regional indicators include average age of men, average age of women, population density, and unemployment rate. All regional characteristics are measured for a hospital's catchment area. Parentheses show robust standard errors, clustered at the hospital level.

^* Significant at 10%.

^** Significant at 5%.

^*** Significant at 1%.

Although we are not able to distinguish between these two explanations in our study, we can obtain estimates that are unbiased if either of these two explanations is true. If explanation (a) is true, then the specification shown in column 1 of Table 2 is correct. If explanation (b) is true, then we should include case‐mix index as additional control variable in our estimation. Not controlling for the case‐mix index would lead to omitted variable bias. If both explanations contribute to the association in column 1 of Table 3, then, under some assumptions, we can interpret the coefficients with and without controlling for the case‐mix index as bounds for the true income effect.

In column 2 of Table 3, we show regression results that control for the case‐mix index as an additional control variable. The coefficient for changes in base rates is now −0.2 as compared with −0.14 in column 1 of Table 2. We interpret these two coefficients as bounds for the true income effect. Depending on the relative importance of explanations (a) and (b), the estimated income effects falls in the range between −0.14 and −0.2

Column 3 of Table 3 shows the effect of changes in base rate factors on total revenues from the DRG system. A 1% increase in base rates is associated with a 0.39% decrease in revenues. However, this coefficient should be interpreted with caution, because it could also be partly explained by changing cost weight factors.

5.3. Pre‐trends and post‐trends

A second potential violation arises if changes in base rates are correlated with unobserved underlying trends in hospital volumes. We can test for this violation by examining whether trends in hospital volumes before the year 2004 are related to subsequent changes in base rates between the years 2004 and 2009 based on the following linear regression model:

$$q_{i,t}=\sum _{t=2000}^{2009}{d}_t\mathrm{\Delta }\mathit{\text{base}}{\mathit{\text{rate}}}_{i,2004-2009}{\beta }_t+d_t{\gamma }_t+x_{r\left(i\right),t}\prime \delta +{\alpha }_i+{\epsilon }_{i,t}.$$ (4)

Figure 3 shows estimation coefficients of β_t and their 95% confidence intervals for each year t ∈ (2000,  …,  2009). The coefficients of β_t for the years t ∈ (2000,  …,  2003) are close to 0, and they are not statistically significant, neither individually nor jointly. Thus, we conclude that there are no significant pre‐trends in the years before 2004.

Figure 3.

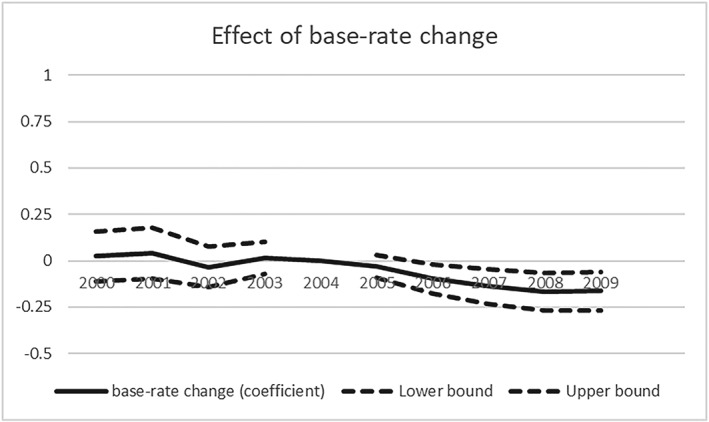
Pre‐trends and post‐trends for the effect of base rate changes on the number of admissions. Note: The figure shows the estimation coefficients and their 95% confidence intervals for the effect of changes in base rates (Δbase rate 2004–2009) between the years 2004 and 2009 on the number of admissions in each year between 2000 and 2009. Δbase rate (2004–2009) is defined as log(base rate 2009) − log(base rate 2004). The coefficients are based on estimation Equation (4). The sample includes all hospitals that are included in the baseline specification in Table 2, column 1. Standard errors are robust and clustered at the hospital level

5.4. Heterogeneous effects of the introduction of DRG payment

A third potential violation of the exogeneity assumption can arise because of the heterogeneous effects of the introduction of DRG payment. Price changes coincide with the time period just after the introduction of DRG payment in the year 2004. In our empirical model, we take time effects into account, but the effects of the introduction of DRG payment could be heterogeneous. For example, it could vary between small and large hospitals or between urban and rural hospitals. As a robustness check, we estimate a model that allows for time trends that vary with hospital and regional characteristics based on the regression equation below:

$$q_{i,t}=d_{2009}\mathrm{\Delta }\mathit{\text{base}}{\mathit{\text{rate}}}_{i,2004-2009}\beta +d_{2009}\gamma +x_{r\left(i\right),t}\prime \delta +d_{2009}{x}_{r\left(i\right),2004}\prime \lambda +d_{2009}{h}_{i,2004}\prime \kappa +{\alpha }_i+{\epsilon }_{i,t},$$ (5)

where t ∈ (2004,2009), x_r(i),2004, and h_i,2004 refer to the regional and hospital characteristics in the year 2004 at the beginning of the payment reform and d₂₀₀₉ is a binary indicator for the year 2009. In column 2 of Table 2, we show estimation results for the regression model in Equation (5). The coefficient of β is essentially unchanged compared with the baseline specification in column 1. Thus, our estimation results are robust to the inclusion of heterogeneous time trends with respect to observed hospital and regional characteristics.

5.5. Further robustness checks

Further potential violations of the exogeneity assumption may be caused by changes in ownership type, the spread of private hospital chains, or by mergers of hospitals. In column 3 of Table 2, we exclude hospitals from our sample that are situated in the states of Hesse or Bavaria where private hospital chains were most active during our study period. In column 4 of Table 2, we exclude hospitals from our sample that were affected by a change in the type of ownership during the 2004–2009 period. For both regressions, the estimation coefficient of β is very similar to the baseline specification. The coefficient of β is also essentially unchanged compared with the baseline specifications if we omit regional characteristics or the change in the average price of competitors from the regression equation (columns 5 and 6 of Table 2). There is also no statistically significant correlation between Δbase rate_{i,2004 − 2009} and an indicator for whether or not a hospital was involved in a merger during the 2004–2009 period (see Table S10 in the online appendix). Furthermore, we show that increases in admission numbers for hospitals with decreases in base rates cannot be explained by low‐initial capacity utilization (see Table S11 in the online appendix).

5.6. Nonlinear effects of price changes

Finally, we examine whether the effect of price changes on volume of care is nonlinear. For this purpose, we regress hospital volume on quintiles of price changes:

$$q_{i,t}=\sum _{k=1}^5{d}_{2009}\mathit{qu}\mathit{int}{\mathit{ile}}_{i,k}{\beta }_k+x_{r\left(i\right),t}\prime \delta +{\alpha }_i+{\epsilon }_{i,t},$$ (6)

where quintile_i,k is a binary indicator for whether hospital i falls in the kth quintile of the distribution of Δbase rate_{i,2004 − 2009} and β_k is a parameter. Column 1 of Table 4 shows the estimation results with the log number of admissions as outcome variable. For hospitals with strongly decreasing base rates (quintile 1), the number of admissions was 11% higher in the year 2009 compared with the year 2004, keeping covariates constant. For hospitals with strongly increasing base rates (quintile 5), the number of admissions was 6.9% higher in the year 2009 compared with the year 2004, keeping covariates constant. Although hospital volume increases more for hospitals with declining base rates (quintiles 1 and 2) than for hospitals with increasing base rates (quintiles 4 and 5), this effect is nonlinear. For example, the increase is larger for the second quintile than for the first quintile. A possible explanation could be that rules to limit growth in the number of admissions are more likely to be binding for hospitals with the largest price decreases such that further increases in the number of admissions become financially less attractive.

Table 4.

Nonlinear effects by quintiles of base rate changes

	Log number of admissions	Case‐mix index	Log revenues
	(1)	(2)	(3)
Quintile 1	0.110***	0.101***	0.192***
	(0.035)	(0.029)	(0.047)
Quintile 2	0.127***	0.002	0.145***
	(0.037)	(0.028)	(0.047)
Quintile 3	0.099***	0.006	0.119***
	(0.034)	(0.027)	(0.043)
Quintile 4	0.091***	0.006	0.115***
	(0.035)	(0.029)	(0.042)
Quintile 5	0.069*	−0.022	0.060
	(0.040)	(0.029)	(0.214)
Year effects	Yes	Yes	Yes
Regional characteristics	Yes	Yes	Yes
Average base rate of competitors	Yes	Yes	Yes
Hospital fixed effects	Yes	Yes	Yes
N (hospitals)	801	801	801

Note. The table shows estimation coefficients of a fixed effects linear regression model. The model includes hospital fixed effects. The dependent variables are the logarithmized number of admissions (column 1), the case‐mix index (column 2), and the logarithmized revenues (columns 3). Results for column 1 are also shown in Figure S6. Specifications refer to Equation (6). The sample includes observations for the years 2004 and 2009. Regional indicators include average age of men, average age of women, population density, and unemployment rate. All regional characteristics are measured for a hospital's catchment area. Parentheses show robust standard errors, clustered at the hospital level.

^* Significant at 10%.

^** Significant at 5%.

^*** Significant at 1%.

We also examine the effect of price changes on hospital volume separately for hospitals with increasing base rates and for hospitals with decreasing base rates based on the following linear model:

$$q_{i,t}=d_{2009}\mathrm{\Delta }\mathit{\text{base}}{\mathit{\text{rate}}}_{i,2004-2009}{\mathit{\text{incr}}}_i{\beta }_1+d_{2009}\mathrm{\Delta }\mathit{\text{base}}{\mathit{\text{rate}}}_{i,2004-2009}{\mathit{\text{decr}}}_i{\beta }_2+d_{2009}\gamma +x_{r\left(i\right),t}\prime \delta +{\alpha }_i+{\epsilon }_{i,t},$$ (7)

where incr_i is a binary indicator for hospitals with increasing base rates and decr_i is a binary indicator for hospitals with decreasing base rates. β₁ and β₂ are parameters. Column 1 of Table 5 shows that the effect of base rate changes on the number of hospital admissions is significantly negative for hospitals with increasing base rates. For hospitals with decreasing base rates, the effect of base rate changes is not significantly different from 0 and positive.

Table 5.

Nonlinear effects of increasing and decreasing base rates

	Log number of admissions	Case‐mix index	Log revenues
	(1)	(2)	(3)
Δbase rate (2004–2009)*increasing base rates	−0.189***	−0.198***	−0.371***
	(0.057)	(0.055)	(0.063)
Δbase rate (2004–2009)*decreasing base rates	0.152	−0.928***	−0.516***
	(0.135)	(0.316)	(0.136)
Year effects	Yes	Yes	Yes
Regional characteristics	Yes	Yes	Yes
Average base rate of competitors	Yes	Yes	Yes
Hospital fixed effects	Yes	Yes	Yes
N (hospitals)	801	801	801

Note. The table shows estimation coefficients of a fixed effects linear regression model. The model includes hospital fixed effects. The dependent variables are the logarithmized number of admissions (column 1), the case‐mix index (column 2), and the logarithmized revenues (Columns 3). Specifications refer to Equation (7). Regional indicators include average age of men, average age of women, population density, and unemployment rate. All regional characteristics are measured for a hospital's catchment area. Parentheses show robust standard errors, clustered at the hospital level.

^* Significant at 10%.

^** Significant at 5%.

^*** Significant at 1%.

The results in column 1 of Table 5 are in line with the results in column 1 of Table 4, but they are based on different comparison groups. Table 4 shows that the increase in admissions between the years 2004 and 2009 is larger for hospitals with weakly decreasing prices (quintile 2) than for hospitals with strongly decreasing prices (quintile 1). Correspondingly, Table 5 shows that the effect of price changes on the number of admissions is (insignificantly) positive if we restrict the sample to hospitals with decreasing prices—reflecting the higher coefficient for quintile 2 compared with quintile 1 in Table 4.

Finally, we examine whether the effects of price changes on the case‐mix index and total revenues are also nonlinear. Column 2 of Table 4 shows that between the years 2004 and 2009, the case‐mix index increases strongly and significantly for hospitals with strongly decreasing prices (quintile 1) whereas there is no significant change for all other groups. Column 2 of Table 5 shows that the coefficients for price changes are negative and significant at 1% level for both hospitals with increasing and with decreasing prices, but the negative effect is stronger for hospitals with decreasing prices. Column 3 of Table 4 shows that the relationship between price changes and changes in total revenues follows an approximate linear pattern. Column 3 of Table 5 shows that the coefficients for price changes on total revenues are negative and significant at 1% level for hospitals with both increasing and decreasing prices.

6. CONCLUSIONS

We examine the effect of changes in hospital reimbursement prices on the volume of care based on a reform of hospital financing in Germany. We find that a 1% across‐the‐board increase in payment rates for the period 2004–2009 leads to a decrease in the number of hospital admissions by between 0.14% and 0.2%, depending on our assumptions on the role of changing cost weight factors.

We interpret our findings as evidence for a negative income effect. This is not the same as evidence for physician induced demand. Physician induced demand is defined as care that is in the financial interest of the provider but not in the best interest of the patient (McGuire, 2000). In our study, we do not know the optimal volume of care, and we are unable to say whether or not the additional care provided in response to lower reimbursement prices was in the best interest of the patients.

Still our findings have important policy implications. First, our results suggest that existing rules to limit volume of care for German hospitals do not prevent hospitals from increasing treatment volumes in response to lower prices. Second, the negative income effect has implications for the budgetary impact of changes in regulatory prices for hospitals. Following the example of the Congressional Budget Office in the United States, policy makers in Germany should take the income effect into account in their decisions about setting prices in the hospital sector.

FUNDING

We gratefully acknowledge financial support of the Fritz Thyssen Foundation (project title: How do hospitals respond to price changes, Az 10.15.1.002WW).

CONFLICT OF INTEREST

The authors have no conflict of interests to declare.

Supporting information

Table S1: Descriptive statistics – comparison to universe of hospitals

Table S2: Distribution of base rates (Basisfallwerte)

Table S3: Determinants of base‐rate change and case‐mix index change

Table S4: Admissions with CMI as additional control variable

Table S5: Case‐mix index as outcome variable

Table S6: Revenues (sum of cost‐weights) as outcome variable

Table S7: Heterogeneous effects of base‐rate changes on number of admissions

Table S8: Heterogeneous effects of base‐rate changes on hospital revenues (sum of cost‐weights)

Table S9: Effect of base‐rate changes on number of admissions for specific diagnosis

Table S10: Robustness check – Relationship between initial base‐rate and subsequent mergers

Table S11: Alternative explanation – different capacity utilization before the reform

Figure S1: Convergence in base‐rates (empirical evidence)

Figure S2: Trends in number of admissions by tertiles of the distribution of base‐rate changes

Figure S3: Trends in number of admissions for two groups of base‐rate changes

Figure S4: Trends in case‐mix index by tertiles of the distribution of base‐rate changes

Figure S5: Trends in CMI for two groups of base‐rate changes

Figure S6: Non‐linear effects of base‐rates on number of admissions (based on quintiles of base‐rate changes)

Figure S7: Non‐linear effects of base‐rates on number of admissions

Figure S8: Non‐linear effects of base‐rates on number of admissions without extreme baserate changes

Figure S9: Non‐linear effects of base‐rates on cmi without extreme baserate changes

Figure S10: Non‐linear effects of base‐rates on revenues without extreme base‐rate changes

Salm M, Wübker A. Do hospitals respond to decreasing prices by supplying more services? Health Economics. 2020;29:209–222. 10.1002/hec.3973