Abstract
CircRNA is a special type of non-coding RNA, which is closely related to the occurrence and development of many complex human diseases. However, it is time-consuming and expensive to determine the circRNA-disease associations through experimental methods. Therefore, based on the existing databases, we propose a method named RWRKNN, which integrates the random walk with restart (RWR) and k-nearest neighbors (KNN) to predict the associations between circRNAs and diseases. Specifically, we apply RWR algorithm on weighting features with global network topology information, and employ KNN to classify based on features. Finally, the prediction scores of each circRNA-disease pair are obtained. As demonstrated by leave-one-out, 5-fold cross-validation and 10-fold cross-validation, RWRKNN achieves AUC values of 0.9297, 0.9333 and 0.9261, respectively. And case studies show that the circRNA-disease associations predicted by RWRKNN can be successfully demonstrated. In conclusion, RWRKNN is a useful method for predicting circRNA-disease associations.
Subject terms: Computational models, Computational models, Computational models, Data processing, Data processing
Introduction
CircRNA, as a star molecule in the recent years, is a kind of non-coding endogenous RNA with single-stranded, closed and circular structure1,2. Unlike the linear RNA, circRNA is the result of “back-splice” or derived from linear RNA. Hence, they lack 5′-3′ ends representing the RNA transcription’s start and stop3–6. The first circRNA was discovered by electron microscopy in RNA viruses7 and afterwards in eukaryotic cells8. Unfortunately, researchers regarded circRNA initially as a by-product of abnormal splicing without regulatory potential. Thus, circRNA did not attract much scientific attention9.
With the increasing researches on circRNAs, lots of circRNAs have been found in viruses, animals and plants6,10–12. So far, circRNA has been confirmed to regulate multiple major biological processes, like cell invasion, proliferation as well as apoptosis13,14. And circRNA is an important part in process of transcription15, mRNA splicing16, RNA translation and decay17. Thus, the regulatory mechanism of circRNA is closely related to the occurrence of disease, which was identified by advanced biotechnology. For instance, the expression level of hsa_circ_0001982 in breast cancer tissues is significantly high18. In addition, there are some circRNAs (Hsa_circ_001471719, CircMTO120, Circ-PRKCI21) that act as miRNA’s sponge to regulate tumorigenesis. Therefore, it can provide new ideas for the treatment of diseases with acquisition and utilization of information related to circRNAs and diseases.
In recent years, some circRNA-disease related databases have also been proposed to further investigate the associations between circRNAs and diseases, involving CircR2Disease22, circRNADisease23 and Circ2Disease24. The effective calculation methods based on these databases will effectively reduce the time consumption caused by the methods in biological experiments. Thus, it is urgent to use computational methods for exploring disease-related circRNA. Fan et al.25 raised a similarity-based method with KATZ measure called KATZHCDA on a heterogeneous network. Yan et al.26 advanced a kernel-based method with regularized least squares. Lei et al.27 proposed a path-weighted method (PWCDA) integrating disease functional similarities and circRNA semantic similarities. Xiao et al.28 put forward a model (MRLDC) using a weighted manifold regularized-based algorithm. Wei et al.29 proposed a factorization Machine (FM) based method called iCircDA-MF using matrix factorization. Zhao et al.30 developed a method (IBNPKATZ) integrating the KATZ measure and bipartite network projection. Zhang et al.31 proposed a label propagation method (CD-LNLP) based on linear neighborhood. However, these methods above rely on the information of circRNA-disease, circRNAs or diseases, and the number of datasets is relatively limited. Therefore, it is not very suitable to discover the relationship of new diseases and novel circRNAs. To solve the problem further, Deng et al.32 proposed a KATZ-based method (KATZCPDA) integrating the information of circRNAs, diseases and proteins. Due to bioinformatics analysis of protein information, KATZCPDA could predict potential association that cannot be inferred when only using information of circRNAs and diseases.
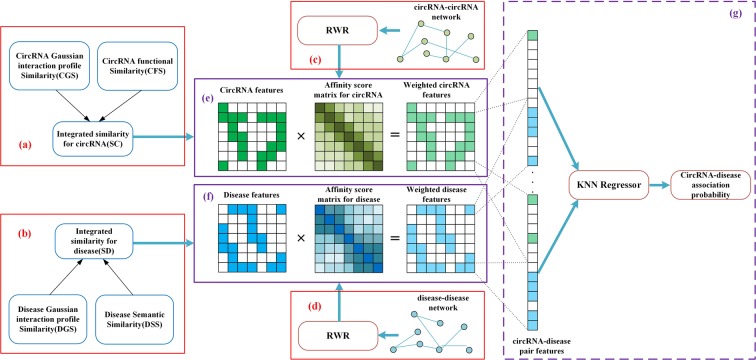
Inspired by Lee et al.33, a model weighting the features of circRNAs and diseases in the global network topology is put forward. In this work, all features of circRNA-disease pairs are weighted using the random walk with restart (RWR) algorithm. Firstly, we construct circRNA-disease associations, and calculate circRNA functional similarity, Gaussian interaction profile (GIP) kernel similarity of circRNAs, disease semantic similarity and GIP kernel similarity of diseases. Secondly, based on these similarities, we further construct two matrixes, i.e., circRNA-circRNA matrix, disease-disease matrix. Next, the RWR is performed on all nodes in circRNA-circRNA matrix and disease-disease matrix respectively. With affinity scores of all circRNA and disease nodes from RWR, features of circRNAs (diseases) consisting of integrated circRNA (disease) similarity are weighted. In the end, negative circRNA-disease pairs are selected randomly and a k-Nearest Neighbor (KNN) model get trained with weighted features (See Fig. 1).
Figure 1.
The flowchart of the computational method RWRKNN.
Results
Performance evaluation
Leave-one-out cross validation (LOOCV), 5-fold cross-validation(5CV) and 10-fold cross-validation(10CV) are utilized to evaluate the prediction performance of our model. For LOOCV, each positive sample is left out in turn as a testing sample, and the other positive samples are used to train the model with the negative samples. Different from the LOOCV, 5CV and 10CV randomly divide the positive samples into 5 equal parts and 10 equal parts respectively, and take out one part of them as testing samples while the rest of samples are regarded as training samples in turn. Next, the predicted scores are sorted in descending order. Further, we draw the receiver operating characteristics (ROC) curve via plotting the true positive rate (TPR) versus the false positive rate (FPR) at different score thresholds. TPR (FPR) refers to the percentage of positive (negative) cases that are correctly identified. Generally, the area under the ROC curve (AUC) is calculated and employed to evaluate the prediction performance. Specifically, the closer the AUC value is to 1, the better the prediction performance. As a result, in LOOCV, RWRKNN achieves an AUC of 0.9297. And concerning 5CV and 10CV, RWRKNN yields the average AUCs of 0.9333 and 0.9261 respectively. The results are shown in the Fig. 2.
Figure 2.
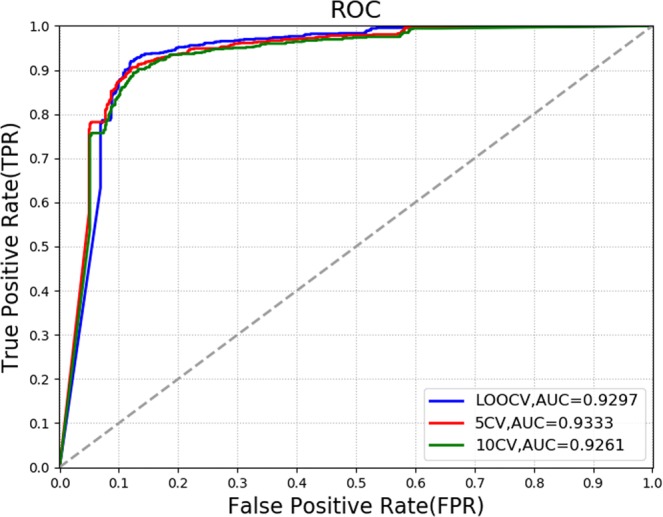
The ROC curves and AUCs of RWRKNN in LOOCV, 5CV and 10CV.
Adjustment of parameters
RWRKNN model involves four parameters: DA’s threshold value α, CA’s threshold value β, neighbors’ number k and distance metric p. The value of α and β might affect the weighted feature matrixes of circRNAs and diseases. The value of k and p probably influence KNN’s classification performance. Let α and β both range between 0.5 and 0.9. Let k be an integer value between 1 and 5 and p ∈ {1, 2, 3}. As a result, among these four parameters, RWRKNN (α = 0.6, β = 0.8, k = 5 and p = 1) gains the highest AUCs of 0.9333 in 5CV as shown in the Supplement. Specifically, p = 1 means the Manhattan distance metric.
Compared with other methods
To analyze the performance of RWRKNN model in predicting circRNA-disease associations, RWRKNN (α = 0.6, β = 0.8, k = 5 and p = 1) is compared with four methods. Firstly, to show the importance of weighting features, we compared RWRKNN with a model with unweighted features called raw_KNN (k = 5, p = 1). And in order to highlight the classification performance of KNN, Support Vector Machine (SVM) is compared with our model. In the end, we compare RWRKNN with KATZHCDA25 and DWNN-RLS26 previously mentioned. The ROC curves of each method using LOOCV are shown in Fig. 3. In addition, we also compared RWRKNN with other four methods in other evaluation criteria (see Fig. 4) including accuracy (ACC), F1-Score, Matthews Correlation Coefficient (MCC). And Precision-Recall (PR) curves and area under the PR curves (AUPRs) are also adopted to reflect the performance of these five methods (see Fig. 5). We can see that RWRKNN gets the satisfactory and optimal performance.
Figure 3.

The ROC curves and AUCs of five methods using LOOCV.
Figure 4.
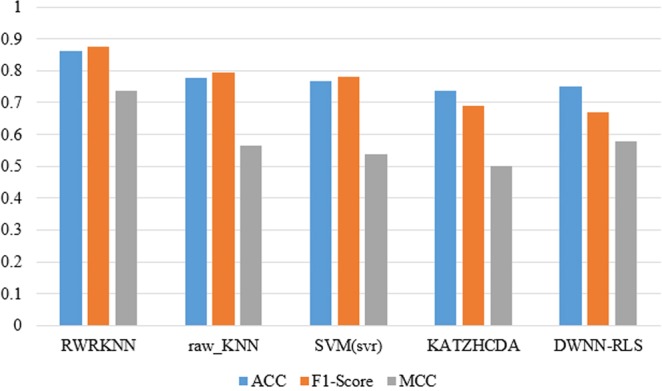
Comparison of five methods in ACC, F1-Score, MCC (LOOCV).
Figure 5.

Comparison of five methods in PR curves and AUPRs (LOOCV).
Case study
To further evaluate the prediction performance of RWRKNN (α = 0.6, β = 0.8, k = 5 and p = 1), we also carry out case studies on three common diseases, i.e., breast cancer, bladder cancer and colorectal cancer. Breast cancer is one of the most common cancer affecting women, and its incidence and mortality rates are expected to increase significantly the next years34. Bladder cancer is a kind of cancer with high incidence, morbidity and mortality35. Colorectal cancer is also one of the most common cancers worldwide36. However, the complex biology of the three types of diseases remains uncertain and unexplored. Therefore, it is necessary to explore the biological characteristics of these diseases by using computational methods. In this work, all known associations between the investigated disease and circRNAs are assumed to be unknown. Through the calculation of the model, the circRNAs with the top 10 scores are selected among all the predicted associations between the investigated disease and circRNAs. Through searching related literatures or databases, some circRNAs are confirmed to be related to the investigated disease. The results of the case studies of these diseases (breast cancer, bladder cancer and the colorectal cancer) are shown in Tables 1, 2 and 3, respectively.
Table 1.
Candidate circRNAs of breast cancer.
| Rank | CircRNA name | Evidences | Rank | CircRNA name | Evidences |
|---|---|---|---|---|---|
| 1 | hsa_circ_005239 | PMID:29037220 | 6 | hsa_circ_0108942 | PMID:29045858 |
| 2 | hsa_circ_0007534 | PMID:30139516 | 7 | hsa_circ_0001946 | PMID:28049499 |
| 3 | hsa_circ_0001982 | PMID:28933584 | 8 | hsa_circ_0006528 | PMID:30520151 |
| 4 | circRNA-000911 | PMID:29431182 | 9 | hsa_circ_0003575 | unconfirmed |
| 5 | hsa_circ_0001785 | PMID:29045858 | 10 | circDENND4C | PMID:31488193 |
Table 2.
Candidate circRNAs of bladder cancer.
| Rank | CircRNA name | Evidences | Rank | CircRNA name | Evidences |
|---|---|---|---|---|---|
| 1 | hsa_circ_0003221 | PMID:29125888 | 6 | hsa_circ_0007158 | circRNADisease |
| 2 | hsa_circ_0091017 | PMID:29151929 | 7 | hsa_circ_0041103 | circRNADisease |
| 3 | hsa_circ_0000284 | circRNADisease | 8 | hsa_circ_0008732 | unconfirmed |
| 4 | hsa_circ_0002768 | circRNADisease | 9 | hsa_circ_0005941 | unconfirmed |
| 5 | hsa_circ_0058058 | unconfirmed | 10 | hsa_circ_0002024 | PMID:30972190 |
Table 3.
Candidate circRNAs of colorectal cancer.
| Rank | CircRNA name | Evidences | Rank | CircRNA name | Evidences |
|---|---|---|---|---|---|
| 1 | hsa_circ_0007534 | PMID:29364478 | 6 | hsa_circ_0020397 | PMID:28707774 |
| 2 | hsa_circ_0001649 | PMID:29421663 | 7 | circ-BANP | PMID:28103507 |
| 3 | hsa_circ_0014717 | PMID:29571246 | 8 | hsa_circ_0000069 | PMID:28003761 |
| 4 | hsa_circ_0000567 | PMID:29333615 | 9 | hsa_circRNA_104700 | PMID:28349836 |
| 5 | circRNA0003906 | PMID:29123417 | 10 | hsa_circRNA_103809 | PMID:30249393 |
Conclusion
At circRNA level, identifying unknown associations of circRNA-disease get crucial for the study of biomarkers for disease diagnosis. In this study, a computational method (RWRKNN) is proposed, which integrates RWR and KNN regression. The existing circRNA-disease association from CircR2Disease is used to assign labels to circRNA-disease pairs. In view of constructing feature of circRNA-disease pairs and circRNA-circRNA associations CA and disease-disease associations DA, we take use of circRNA-disease associations, GIP kernel similarities of circRNAs and diseases, circRNA functional similarity and disease semantic similarity. For every circRNA (disease), we complement RWR on the constructed CA (DA) matrix to obtain affinity scores, which are employed to weight the features of circRNAs (diseases). After obtaining the global feature vectors of circRNAs (diseases), KNN regression model could output the possibility of inquired circRNA-disease association pairs. In addition, both multiple performance evaluation criteria and case studies on breast cancer, bladder cancer and colorectal cancer have illustrated the reliable prediction ability of RWRKNN. However, RWRKNN also has limitations. It relies on prior information about circRNAs and diseases. Therefore, it is slightly inadequate in uncovering the relationship between new diseases and new circRNAs.
Materials and Methods
Human circRNA-disease associations
To acquire circRNA-disease associations verified by biological experiments, we download the circRNA-disease associations from circR2Disease database (http://bioinfo.snnu.edu.cn/CircR2Disease/)22. CircR2Disease provides association information between circRNAs and diseases supported by experiments, including 725 circRNA-disease associations between 661 circRNAs and 100 diseases. In this study, we extract all circRNA and disease associations in the database and then construct a matrix A to reflect the adjacency associations of circRNA-disease. If a disease i has been confirmed to have an association with a circRNA j, A(i, j) = 1, otherwise A(i, j) = 0. The dimension of A is Nc × Nd, where Nc and Nd represent the number of the known circRNAs and the known diseases, respectively.
Disease similarity
The semantic similarity between diseases is calculated based on DAG (directed acyclic graph) topology. To be specific, the DAG of a disease d can be defined as DAG(d) = (d, T(d), E(d)), where T(d) is an ancestor set of disease d and E(d) includes the corresponding edges. According to Eqs. (1) and (2), the semantic value DSV(d) of disease d can be obtained37.
| 1 |
| 2 |
where the disease t ∈ T(d), ∆ (∆ = 0.5) is semantic contribution decay factor, and Dd(t) denotes the contribution of ancestor node t to d. Next, the semantic similarity between di and dj can be calculated as follows:
| 3 |
In the end, the semantic similarity matrix of diseases DSS is constructed.
GIP kernel similarity is calculated based on the topological structure of the association network of biological information nodes38. An assumption supporting this approach is that more similar diseases tend to be associated with the similar circRNAs38. Disease GIP kernel similarity is calculated with the known circRNA-disease associations, which is obtained according to the Eq. (4).
| 4 |
where IPd(i) represents the interaction profile of disease i as a binary vector reflecting whether disease i is associated with each circRNA or not. DGS(i, j) is the GIP kernel similarity between disease i and disease j. σd is influential in tuning the kernel bandwidth calculated by the Eq. (5).
| 5 |
where Nd is the number of all diseases, and is set to 1 as the initial value following the previous study38.
In order to make full use of the disease semantic similarity and the disease GIP kernel similarity, we construct a new disease similarity matrix SD (See Fig. 1b) by integrating DSS and DGS based on the Eq. (6).
| 6 |
CircRNA similarity
Similar to the calculation method of disease GIP kernel similarity, we use the Eq. (7) to calculate circRNA GIP kernel similarity.
| 7 |
where IPc(i) represents the interaction profile of circRNA i as a binary vector reflecting whether circRNA i is associated with each disease or not. CGS(i, j) is the GIP kernel similarity between circRNA i and circRNA j. σc is influential in tuning the kernel bandwidth calculated by the Eq. (8).
| 8 |
where Nc is the number of all circRNAs, and is set to 1 as the initial value following the previous study38.
We adopt a similar method to Wang’s method37 for calculating circRNA functional similarity to improve the accuracy of the calculation model. To be specific, the functional similarity score between a circRNA U and a circRNA V is obtained by calculating the semantic similarity between the two groups of circRNA-related diseases. First, let dx be any given disease, and Dy be a group of diseases defined as Dy = {dy1, dy2, dy3, …, dyr}. Then, the semantic similarity between dx and Dy can be calculated as follows:
| 9 |
Second, the functional similarity between circRNA U and circRNA V can be calculated as follows:
| 10 |
where Du is a group of circRNA U-related diseases and Dv is another group of circRNA V-related diseases. Dui ∈ Du and Dvj ∈ Dv. In the end, circRNA functional similarity matrix is constructed, which is symmetric and has all 1 s on its diagonal. CFS(i, j) represents the functional similarity between circRNA i and circRNA j.
Similar to the method of disease similarity integration, circRNA functional similarity and circRNA GIP kernel similarity are integrated to constitute a new circRNA similarity matrix SC (See Fig. 1a) based on the Eq. (11).
| 11 |
Human disease-disease associations
In order to get the disease association adjacency matrix DA, a threshold value α is set for the integrated disease similarity SD as shown in Eq. (12). If the similarity value is greater or equal to α, the corresponding position in DA has a value of 1, otherwise 0.
| 12 |
Human circRNA- circRNA associations
In order to get the circRNA association adjacency matrix CA, a threshold value β is set for the integrated circRNA similarity SC as shown in Eq. (13). If the similarity value is greater or equal to β, the corresponding position in CA has a value of 1, otherwise 0.
| 13 |
RWRKNN
After having constructed four matrixes, i.e., the integrated disease similarity matrix, the integrated circRNA similarity matrix, disease-disease association matrix and circRNA-circRNA association matrix, RWRKNN will do the following three steps, i.e., RWR for every circRNA and disease (Fig. 1c,d), feature weighting (Fig. 1e,f) and training KNN model (Fig. 1g).
Considering the input requirements of the KNN regression model, we transform the features of circRNA-disease pairs into vectors. Firstly, for diseases, we take each row of the integrated disease similarity SD as the feature vector of diseases with 100 dimensions. Similarly, with respect to circRNAs, we take each row of the integrated circRNA similarity SC as the feature vector of circRNAs with 661 dimensions.
To make predictions of circRNA-disease associations from a global network perspective, we could obtain affinity scores between a circRNA (disease) node and all circRNA (disease) nodes using the RWR algorithm on the CA (DA) network. RWR estimates affinity level (affinity score) between two nodes by repeatedly exploring the overall structure of a network. Starting at a seed node, the random walker diffuses its resources by (1) moving to a neighbor node with probability 1-c and (2) restarting from the seed node with restarting probability c. This process is iterated repeatedly until all nodes are traversed. At this time, the probability vector obtained contains the affinity scores of all nodes and the seed node. The affinity scores of all nodes during each step are represented by the Eq. (14).
| 14 |
where q is the starting vector whose seed node is set to 1 while the others are set to 0, and W is the normalized adjacency matrix, and p would finally reach a steady state after multiple iterations, and c is set to 0.7 according to Park et al.39’s work. Consequently, by multiplying the adjacency matrix, it diffuses its resources throughout the network. By the iteration of the pi value, i.e. the result of RWR for the seed node i, the affinity score matrix F could be obtained, whose element Fij refers to how closely node j is connected to seed node i. Finally, the (Nc × Nc) circRNA affinity score matrix Fc and the (Nd × Nd) disease affinity score matrix Fd are constructed, where Nc is the number of circRNAs and Nd is the number of diseases.
Next, we utilize the affinity scores to weight the circRNA and disease features. As regards the circRNA features, they are weighted using the Eq. (15).
| 15 |
where means the affinity score of circRNA c(i), which is a row vector. is the transpose of . And SC(c(i)) denotes the integrated similarity of circRNA c(i), which is also a row vector. WSC is the weighted feature matrix of circRNAs and WSC(c(i)) represents the weighted feature of circRNA c(i).
In the case of the disease features, Eq. (16) is used.
| 16 |
where means the affinity score of disease d(j), which is a row vector. is the transpose of . And SC(d(j)) denotes the integrated similarity of disease d(j), which is also a row vector. WSD(d(j)) represents the weighted feature of disease d(j) and WSD is the weighted feature matrix of diseases.
In the whole, the features of circRNAs and diseases are weighted by means of adding each feature of all nodes to a certain seed node via affinity scores from the RWR. The weighting can be conducted by multiplying feature matrix by affinity score matrix as depicted in Fig. 1e,f.
With the weighted features of the circRNAs and diseases, we link each feature vector of diseases and circRNAs together to compose a 761-dimensional feature vector for each circRNA-disease pair as the input of KNN regressor model. To train the KNN regressor model, we prepare positive samples and negative samples. The known circRNA-disease association pairs are used as positive samples. To get negative samples, the following steps are taken: (1) A circRNA i is selected at first, and then (2) calculate the number ndi of diseases associated with the circRNA i. (3) Next, select ndi diseases unassociated to the circRNA i. (4) Until all circRNAs are traversed, we end up with the same number of negative samples as positive samples. In RWRKNN model, the KNN regression could find k neighbors closest to a certain circRNA-disease pair based on the Minkowski distance metric (defined as Eq. (17)), which is a set of distance definitions.
| 17 |
Here, different values of p represent different distance metrics for calculating the distance between vectors a and b with n-dimension, and we set p = 1, which represents the Manhattan distance is used as a metric between vectors. In addition, considering the closer neighbors should have more weight, we take the inverse of the distance as the weight.
Supplementary information
Acknowledgements
We thank the financial support which comes from National Natural Science Foundation of China (61672334, 61972451, 61902230) and the Fundamental Research Funds for the Central Universities (No. GK201901010).
Author contributions
X.L. contributed to the conception of the study, the design of the method and writing of the manuscript. C.B. contributed to designing the method and carrying out the experiments. C.B. performed the data analyses and wrote the manuscript. X.L. revised the manuscript and polished the English expression. All the authors have read and approved the final manuscript.
Data availability
Data can be obtained by sending an email to the corresponding author upon reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
is available for this paper at 10.1038/s41598-020-59040-0.
References
- 1.Fan X, et al. Circular RNAs in Cardiovascular Disease: An Overview. BioMed research international. 2017;2017:5135781. doi: 10.1155/2017/5135781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Greene J, et al. Circular RNAs: Biogenesis, Function and Role in Human. Diseases. Frontiers in molecular biosciences. 2017;4:38. doi: 10.3389/fmolb.2017.00038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Nigro JM, et al. Scrambled exons. Cell. 1991;64:607–613. doi: 10.1016/0092-8674(91)90244-s. [DOI] [PubMed] [Google Scholar]
- 4.Zhang Y, et al. Circular intronic long noncoding RNAs. Molecular cell. 2013;51:792–806. doi: 10.1016/j.molcel.2013.08.017. [DOI] [PubMed] [Google Scholar]
- 5.Knupp D, Miura P. CircRNA accumulation: A new hallmark of aging? Mechanisms of ageing and development. 2018;173:71–79. doi: 10.1016/j.mad.2018.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Memczak S, et al. Circular RNAs are a large class of animal RNAs with regulatory potency. Nature. 2013;495:333–338. doi: 10.1038/nature11928. [DOI] [PubMed] [Google Scholar]
- 7.Sanger HL, Klotz G, Riesner D, Gross HJ, Kleinschmidt AK. Viroids are single-stranded covalently closed circular RNA molecules existing as highly base-paired rod-like structures. Proceedings of the National Academy of Sciences of the United States of America. 1976;73:3852–3856. doi: 10.1073/pnas.73.11.3852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hsu MT, Coca-Prados M. Electron microscopic evidence for the circular form of RNA in the cytoplasm of eukaryotic cells. Nature. 1979;280:339–340. doi: 10.1038/280339a0. [DOI] [PubMed] [Google Scholar]
- 9.Cocquerelle C, Mascrez B, Hetuin D, Bailleul B. Mis-splicing yields circular RNA molecules. FASEB journal: official publication of the Federation of American Societies for Experimental Biology. 1993;7:155–160. doi: 10.1096/fasebj.7.1.7678559. [DOI] [PubMed] [Google Scholar]
- 10.Danan M, Schwartz S, Edelheit S, Sorek R. Transcriptome-wide discovery of circular RNAs in Archaea. Nucleic. acids research. 2012;40:3131–3142. doi: 10.1093/nar/gkr1009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chu Q, et al. PlantcircBase: A Database for Plant Circular RNAs. Molecular plant. 2017;10:1126–1128. doi: 10.1016/j.molp.2017.03.003. [DOI] [PubMed] [Google Scholar]
- 12.Chen L, Huang C, Wang X, Shan G. Circular RNAs in Eukaryotic Cells. Current genomics. 2015;16:312–318. doi: 10.2174/1389202916666150707161554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Holdt LM, Kohlmaier A, Teupser D. Molecular roles and function of circular RNAs in eukaryotic cells. Cellular and molecular life sciences: CMLS. 2018;75:1071–1098. doi: 10.1007/s00018-017-2688-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Salzman J, Chen RE, Olsen MN, Wang PL, Brown PO. Cell-type specific features of circular RNA expression. PLoS genetics. 2013;9:e1003777. doi: 10.1371/journal.pgen.1003777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hansen TB, et al. Natural RNA circles function as efficient microRNA sponges. Nature. 2013;495:384–388. doi: 10.1038/nature11993. [DOI] [PubMed] [Google Scholar]
- 16.Qu S, et al. Circular RNA: A new star of noncoding RNAs. Cancer letters. 2015;365:141–148. doi: 10.1016/j.canlet.2015.06.003. [DOI] [PubMed] [Google Scholar]
- 17.Wang M, et al. Circular RNAs: A novel type of non-coding RNA and their potential implications in antiviral immunity. International journal of biological sciences. 2017;13:1497–1506. doi: 10.7150/ijbs.22531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tang YY, et al. Circular RNA hsa_circ_0001982 Promotes Breast Cancer Cell Carcinogenesis Through Decreasing miR-143. DNA and cell biology. 2017;36:901–908. doi: 10.1089/dna.2017.3862. [DOI] [PubMed] [Google Scholar]
- 19.Wang F, Wang J, Cao X, Xu L, Chen L. Hsa_circ_0014717 is downregulated in colorectal cancer and inhibits tumor growth by promoting p16 expression. Biomedicine & pharmacotherapy = Biomedecine & pharmacotherapie. 2018;98:775–782. doi: 10.1016/j.biopha.2018.01.015. [DOI] [PubMed] [Google Scholar]
- 20.Han D, et al. Circular RNA circMTO1 acts as the sponge of microRNA-9 to suppress hepatocellular carcinoma progression. Hepatology (Baltimore, Md.) 2017;66:1151–1164. doi: 10.1002/hep.29270. [DOI] [PubMed] [Google Scholar]
- 21.Qiu M, et al. The Circular RNA circPRKCI Promotes Tumor Growth in Lung Adenocarcinoma. Cancer research. 2018;78:2839–2851. doi: 10.1158/0008-5472.can-17-2808. [DOI] [PubMed] [Google Scholar]
- 22.Fan, C., Lei, X., Fang, Z., Jiang, Q. & Wu, F. X. CircR2Disease: a manually curated database for experimentally supported circular RNAs associated with various diseases. Database: the journal of biological databases and curation2018, 10.1093/database/bay044 (2018). [DOI] [PMC free article] [PubMed]
- 23.Zhao Z, et al. circRNA disease: a manually curated database of experimentally supported circRNA-disease associations. Cell death & disease. 2018;9:475. doi: 10.1038/s41419-018-0503-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Yao D, et al. Circ2Disease: a manually curated database of experimentally validated circRNAs in human disease. Scientific reports. 2018;8:11018. doi: 10.1038/s41598-018-29360-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Fan C, Lei X, Wu FX. Prediction of CircRNA-Disease Associations Using KATZ Model Based on Heterogeneous Networks. International journal of biological sciences. 2018;14:1950–1959. doi: 10.7150/ijbs.28260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Yan C, Wang J, Wu FX. DWNN-RLS: regularized least squares method for predicting circRNA-disease associations. BMC bioinformatics. 2018;19:520. doi: 10.1186/s12859-018-2522-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lei Xiujuan, Fang Zengqiang, Chen Luonan, Wu Fang-Xiang. PWCDA: Path Weighted Method for Predicting circRNA-Disease Associations. International Journal of Molecular Sciences. 2018;19(11):3410. doi: 10.3390/ijms19113410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Xiao Qiu, Luo Jiawei, Dai Jianhua. Computational Prediction of Human Disease- Associated circRNAs Based on Manifold Regularization Learning Framework. IEEE Journal of Biomedical and Health Informatics. 2019;23(6):2661–2669. doi: 10.1109/JBHI.2019.2891779. [DOI] [PubMed] [Google Scholar]
- 29.Wei, H. & Liu, B. iCircDA-MF: identification of circRNA-disease associations based on matrix factorization. Briefings in bioinformatics, 10.1093/bib/bbz057 (2019). [DOI] [PubMed]
- 30.Zhao Qi, Yang Yingjuan, Ren Guofei, Ge Erxia, Fan Chunlong. Integrating Bipartite Network Projection and KATZ Measure to Identify Novel CircRNA-Disease Associations. IEEE Transactions on NanoBioscience. 2019;18(4):578–584. doi: 10.1109/TNB.2019.2922214. [DOI] [PubMed] [Google Scholar]
- 31.Zhang W, Yu C, Wang X, Liu F. Predicting CircRNA-Disease Associations Through Linear Neighborhood Label Propagation Method. IEEE Access. 2019;7:83474–83483. doi: 10.1109/ACCESS.2019.2920942. [DOI] [Google Scholar]
- 32.Deng L, Zhang W, Shi Y, Tang Y. Fusion of multiple heterogeneous networks for predicting circRNA-disease associations. Scientific reports. 2019;9:9605. doi: 10.1038/s41598-019-45954-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Lee I, Nam H. Identification of drug-target interaction by a random walk with restart method on an interactome network. BMC bioinformatics. 2018;19:208. doi: 10.1186/s12859-018-2199-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Anastasiadi Z, Lianos GD, Ignatiadou E, Harissis HV, Mitsis M. Breast cancer in young women: an overview. Updates in surgery. 2017;69:313–317. doi: 10.1007/s13304-017-0424-1. [DOI] [PubMed] [Google Scholar]
- 35.Martinez Rodriguez RH, Buisan Rueda O, Ibarz L. Bladder cancer: Present and future. Medicina clinica. 2017;149:449–455. doi: 10.1016/j.medcli.2017.06.009. [DOI] [PubMed] [Google Scholar]
- 36.Brody H. Colorectal cancer. Nature. 2015;521:S1. doi: 10.1038/521S1a. [DOI] [PubMed] [Google Scholar]
- 37.Wang D, Wang J, Lu M, Song F, Cui Q. Inferring the human microRNA functional similarity and functional network based on microRNA-associated diseases. Bioinformatics (Oxford, England) 2010;26:1644–1650. doi: 10.1093/bioinformatics/btq241. [DOI] [PubMed] [Google Scholar]
- 38.van Laarhoven T, Nabuurs SB, Marchiori E. Gaussian interaction profile kernels for predicting drug-target interaction. Bioinformatics (Oxford, England) 2011;27:3036–3043. doi: 10.1093/bioinformatics/btr500. [DOI] [PubMed] [Google Scholar]
- 39.Park, K., Kim, D., Ha, S. & Lee, D. Predicting Pharmacodynamic Drug-Drug Interactions through Signaling Propagation Interference on Protein-Protein Interaction Networks. PLOS ONE10 (2015). [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data can be obtained by sending an email to the corresponding author upon reasonable request.