Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2020 Feb 7;10:2118. doi: 10.1038/s41598-020-58196-z

Low-frequency variability in photoplethysmographic waveform and heart rate during on-pump cardiac surgery with or without cardioplegia

Anton R Kiselev 1,2,3,✉, Ekaterina I Borovkova 3, Vladimir A Shvartz 1, Viktoriia V Skazkina 3, Anatoly S Karavaev 3,4, Mikhail D Prokhorov 4, Artak Y Ispiryan 1, Sergey A Mironov 1, Olga L Bockeria 1
PMCID: PMC7005763  PMID: 32034184

Abstract

We studied the properties of low-frequency (LF) heart rate variability (HRV) and photoplethysmographic waveform variability (PPGV) and their interaction under conditions where the hemodynamic connection between them is obviously absent, as well as the LF regulation of PPGV in the absence of heart function. The parameters of HRV and finger PPGV were evaluated in 10 patients during cardiac surgery under cardiopulmonary bypass (on-pump cardiac surgery) with or without cardioplegia. The following spectral indices of PPGV and HRV were ertimated: the total spectral power (TP), the high-frequency (HF) and the LF ranges of TP in percents (HF% and LF%), and the LF/HF ratio. We assessed also the index S of synchronization between the LF oscillations in finger photoplethysmogram (PPG) and heart rate (HR) signals. The analysis of directional couplings was carried out using the methods of phase dynamics modeling. It is shown that the mechanisms leading to the occurrence of oscillations in the LF range of PPGV are independent of the mechanisms causing oscillations in the LF range of HRV. At the same time, the both above-mentioned LF oscillations retain their activity under conditions of artificial blood circulation and cardioplegia (the latter case applies only to LF oscillations in PPG). In artificial blood circulation, there was a coupling from the LF oscillations in PPG to those in HR, whereas the coupling in the opposite direction was absent. The coupling from the LF oscillations in PPG to those in HR has probably a neurogenic nature, whereas the opposite coupling has a hemodynamic nature (due to cardiac output).

Subject terms: Cardiovascular biology, Cardiovascular biology

Introduction

Despite the relatively widespread use of photoplethysmography to assess the state of peripheral blood flow1,2, the question of the physiological interpretation of the frequency components of photoplethysmographic waveform variability (PPGV) remains largely debatable. Usually, the nature of high-frequency (HF) oscillations in photoplethysmogram (PPG) signal is explained by the mechanical effect of respiration3–5, while the low-frequency (LF) oscillations (with a characteristic frequency of about 0.1 Hz) in PPG are associated with sympathetic regulation of peripheral vascular resistance3,6,7. It should be noted that besides the PPG, the LF fluctuations at a similar frequency are detected also in the signals of heart rate (HR)8,9 and blood pressure (BP)10,11. Blood pressure variability (BPV) is primarily due to the vasomotor tone, which is not directly related to the heart control. Since blood flow through the distal arteries contributes to the formation of the finger PPG12, the autonomic regulation of BP can be indirectly assessed by the PPG signal.

In experiments with linearly increasing frequency of respiration, we have shown earlier the functional independence of LF oscillations in HR and PPG13. In healthy subjects, these LF oscillations are usually synchronized between themselves14. Quantitative estimation of the degree of synchronization between the LF oscillations in HR and PPG has potential clinical importance, for example, for assessing cardiovascular risk and controlling drug therapy14. However, how closely the mechanisms of the autonomic regulation of HR and BP are associated and whether they can function separately is not known. The nature of couplings between them (neurogenic or hemodynamic) also requires clarification.

The aim of this work was to study the properties and interaction of LF oscillations in HR and PPG under conditions where the hemodynamic coupling between them is certainly absent, and to study the LF regulation of PPGV in the absence of heart function. For this purpose, the parameters of heart rate variability (HRV) (if available) and finger PPGV were evaluated in patients during cardiac surgery under cardiopulmonary bypass (on-pump cardiac surgery) with or without cardioplegia. Such an approach allows us to understand better the principles of the functional organization of the autonomic regulation of blood circulation and increases the reliability of the analysis of biological signals in the experimental studies of cardiovascular system.

Materials and Methods

Ethical approval

The Ethics Committee of the Bakulev Scientific Center for Cardiovascular Surgery in Moscow, Russia approved the design of the study. All subjects gave informed consent. All procedures performed on humans fall under ethical regulations, including 1964 Helsinki Declaration and its later amendments.

Patients

We studied five men during coronary artery bypass grafting, aged 60.1 ± 8.2 years (mean ± standard deviation), and five men during surgical correction of valvular heart disease, aged 57.2 ± 9.3 years.

We excluded from the study the patients with severe cardiac failures, cancer, mental illness, organic diseases of nervous system and brain, endocrine pathology except for compensated diabetes, symptomatic hypertension, or abnormalities in peripheral microcirculation.

Surgical approach

All patients were operated using the standard cardiopulmonary bypass (CPB) (so-called, on-pump) technique. The on-pump coronary artery bypass grafting (CABG) was performed on a beating heart under the parallel perfusion and normothermia. Aorta was not cross-clamped and cardioplegic solution wasn’t administered. During the CPB a single two-stage cannula was installed into the right atrium through the free wall. For conduits we used radial artery, great saphenous vena, and the left internal thoracic artery, which in some cases was switched to internal thoracic artery from the right side. While forming the coronary anastomoses we stabilized myocardium with the “Octopus” (Medtronic, USA) or “Acrobat” (Maquet, Germany) vacuum stabilizers. After the CABG, all patients without contraindications underwent the intraoperative graft angiography in order to assess the quality of the formed anastomoses. In accordance with the standard procedure, we finished the operation with drainage of pericardial cavity and anterior mediastinum and stratification of the chest suturing wounds.

We performed the on-pump surgical correction of valvular heart disease under pharmacological cardioplegia and hypothermia. The correction included the aortic cannulation, the separate cannulation of the superior vena cava with an angled cannula, and the direct cannulation of the inferior vena cava through free wall of the right atrium. We performed the antegrade cardioplegia in aortic root or, if aortic valve was insufficient, we performed the retrograde cardioplegia through coronary sinus. While performing the cardioplegia, we administered Custodiol (Odyssey Pharmaceuticals Inc., Germany) cardioplegic solutions. In accordance with the standard procedure, we finished the operation with drainage of pericardial cavity and anterior mediastinum.

It is important to note that the flow of blood from the heart-lung machine into the aorta, distal to the place of its cannulation, does not occur laminarly, but is jerked, which is formed by the operation of a rotor motor. This generates blood flow oscillations in the peripheral channel, in particular, reflected in the PPGV. Depending on the surface area of the human body, in order to maintain the desired balance of the blood volume, the rotational speed of the rotary motor can vary in the range from 80 to 160 beats per minute. In patients without cardioplegia, the frequency of mechanical ventilation was ranged from 10 to 16 breaths per minute, while in patients with cardioplegia, this frequency was about 1–2 breaths per minute. In the case of cardioplegia, the circulating blood was cooled.

Biological signals recording

The signals of electrocardiogram (ECG) and PPG from the middle finger of the left hand were simultaneously recorded within 10 minutes in all patients during cardiac surgery. All signals were sampled at 250 Hz and digitized at 16 bits. We used PPG sensors based on the infrared light emitting diode (wavelength of about 960 nm IR-LED) operating on reflection.

Theoretical basis of research methods

We assessed the autonomic regulation of BP using PPGV analysis, taking into account the contribution of the distal arteries to the formation of the PPG finger signal12. Under CPB conditions, the hemodynamic coupling between the mechanisms of HRV and BPV autonomic regulation is largely destroyed (the crossed out dotted arrow in Fig. 1) and the neurogenic coupling from BPV to HRV (solid line in Fig. 1) is held. Under conditions of cardioplegia, there is no neurogenic coupling from LF oscillations in HR (as there is no mechanical and electrical function of the heart) to LF oscillations in BP (the crossed out thin line in Fig. 1c). The presence of such coupling in the absence of cardioplegia is an open question.

Figure 1.

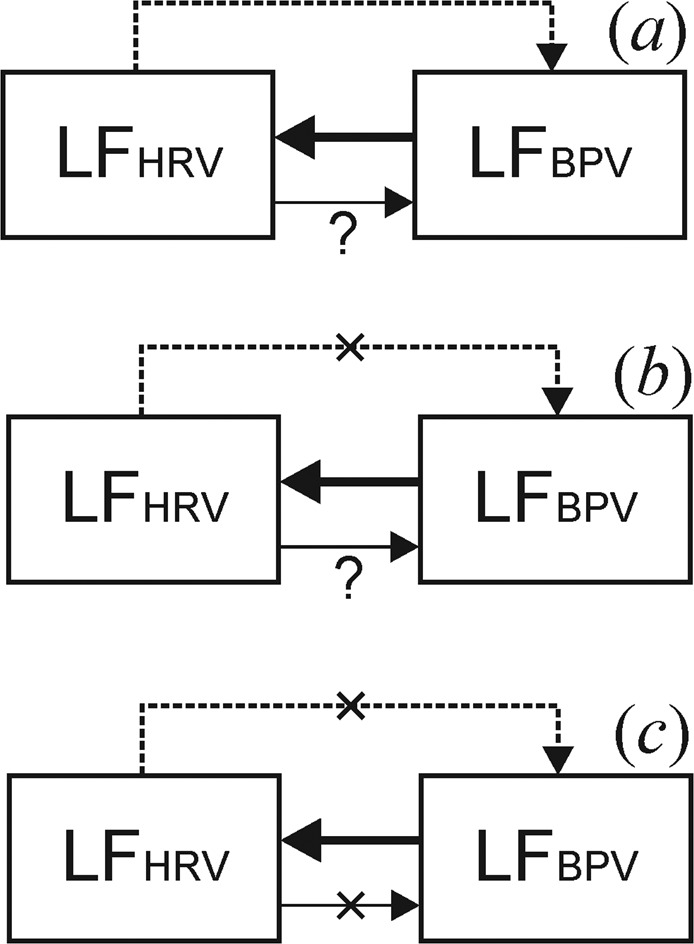
Figure 1

Open in a new tab

Schematic representation of the structure of couplings between the LF components in the signals of the systems of HR and vascular tone regulation in the normal state (a) and during cardiac surgery in CPB without cardioplegia (b) and under cardioplegia (c). Arrows indicate the directions of couplings. The dashed line is a hemodynamic coupling from HRV to BPV, the solid line indicates an autonomous regulatory influence from BPV to HRV and the thin line indicates an autonomous regulatory influence from HRV to BPV.

Signal processing and data analysis

Before the processing, the studied signals were filtered in the frequency range of 0.04–0.4 Hz (LF + HF band). The spectral analysis of HRV was carried out in accordance with the methodological recommendations15. We calculated the following indices of HRV: the total power of HRV spectrum (TP, ms2), the ratio of LF components of HRV spectrum to TP measured in percent (LF%), the ratio of HF components of HRV spectrum to TP measured in percent (HF%), and LF/HF ratio.

The PPGV power spectra were estimated directly from the PPG signals. The power spectrum was evaluated by the Welch method16 in one-minute windows with a shift of 20 seconds. A triangular spectral window was used for the spectrum estimation. A critical power value was calculated, above which spectral components were considered statistically significant (p = 0.05). For this, using the surrogate data, we tested the statistical hypothesis of normal noise bounded in the frequency band 0.04−0.4 Hz. Then we applied the standard HRV analysis technique to the PPGV spectra and calculated the spectral indices LF%, HF%, and LF/HF,

For the PPG data, it is difficult to interpret the absolute values of the waveforms. The output of the PPG sensors is proportional to the unknown coefficient, which depends on optical features of subject’s skin, BP values, sensors placement, optical and electrical characteristics of the sensor, the room illumination and temperature, and other factors. The interpretation of the PPGV absolute values is an open question and goes beyond the scope of the study; instead we used conventional units (cu) to measure the PPG signals. Conventional units are values of the PPG discrete samples and are proportional to the sensor output. Since the proportional coefficient between the blood flow and cu is unknown, it is difficult to interpret the absolute values of LF, HF, and TP. However, LF%, and HF% are dimensionless and have the same interpretation as the respective HRV indexes.

To estimate the synchronization between the LF oscillations in HR and PPG, we applied the method proposed by us recently14. Index S defines the relative time (in percents) of synchronization between the considered LF oscillations. Each synchronization index S was accompanied by an estimate of the probability of randomly obtaining the calculated S value for obviously nonsynchronous signals – p-value. To evaluate p, we used a method for generating surrogate data based on randomizing the phases of the Fourier harmonics of signals17,18 and adapted to assess the statistical significance of the results of synchronization detection in the systems under study13. In practice, the estimation of index S is considered to be statistically significant, if p < 0.05.

To analyze the relationship between the spectral components of the LF oscillations in HRV and PPGV, the coherence function С(f)19 and the corresponding critical significance level p = 0.05 were calculated. For this purpose, the method of generating surrogate data was used, based on the randomization of the phases of the Fourier harmonics of the signals17,18, as well as it was done in the previous method. When the critical significance level for С(f) was greater than p = 0.05 in the corresponding frequency range, the spectral components were considered statistically coherent.

The analysis of directional couplings was carried out using the method of phase dynamics modeling based on a comparison of the prognostic capabilities of individual and joint models describing the dynamics of instantaneous phases of analyzed signals20,21. The paper21 presents the formulas for estimating from time series the strength G of coupling between the systems under study together with a 95% confidence interval at different trial delays τ. Coupling is considered to be significant if G, together with its confidence interval is above zero. The calculation of characteristics of directional couplings was carried out for the time shifts between the time series from 0 to 20 seconds (up to two characteristic periods of oscillation). The parameter of increase of the instantaneous phase values at each iteration was chosen to be equal to the characteristic oscillation period of 10 seconds in accordance to the paper22. Before the processing, the studied signals were filtered in the frequency range of 0.06–0.14 Hz14.

Quantitative data are presented below as mean with standard deviation (M ± SD).

Results

Cardiopulmonary bypass without cardioplegia

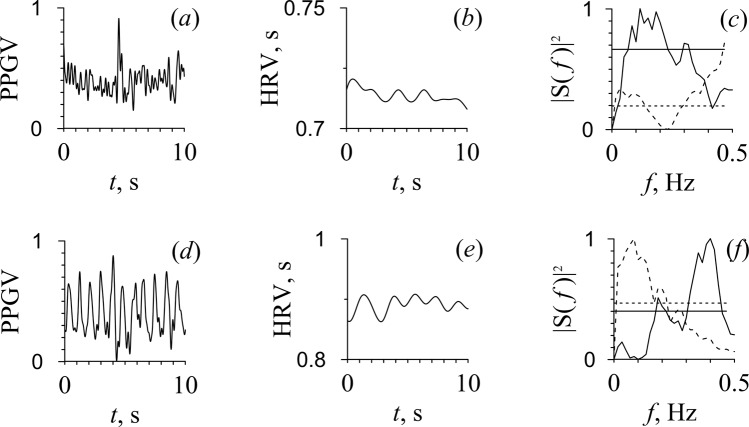
The low overall HRV level in all five patients and the very low amplitude of PPG (pulse waves were hardly noticeable by visual analysis) in three patients out of five draws attention. Figure 2 shows an example of signals from patient D with low amplitude PPG (Fig. 2a) and from patient A with a distinguishable pulse wave (Fig. 2d). At the same time, a pronounced peak at a frequency of about 0.1 Hz was observed in the spectra of HRV and PPG only in three patients. It should be noted that well-distinguished pulse waves in PPG and a peak at 0.1 Hz in the PPG spectrum were observed in different patients. In the PPGV spectrum, peaks were observed also at the pulsation frequencies generated by the pump oxygenator and mechanical ventilation.

Figure 2.

Figure 2

Open in a new tab

PPG signal (a,d), RR intervals (b,e), and their Fourier power spectra (c,f) depicted by solid line for PPG and by dashed line for RR intervals. The dashed and solid horizontal lines in (c,f) correspond to the critical power value (p = 0.05), estimated from RR intervals and PPG signals, respectively. The upper line (a–c) corresponds to patient D with low amplitude of PPG and bottom line (d–f) corresponds to patient A with a distinguishable pulse wave under CPB.

It was also found that in four of five patients, the power of the LF range in HRV and PPGV was less than the power of the HF range (Table 1).

Table 1.

Spectral components in HRV and PPGV in patients with and without cardioplegia.

Patients TPHRV LF%HRV HF%HRV LF/HFHRV LF%PPGV HF% PPGV LF/HFPPGV S, %
Patients without cardioplegia
Patient A 0.080 46 39 1.18 11 83 0.13 6
Patient B 0.042 20 73 0.27 49 44 1.11 26
Patient C 0.044 27 63 0.43 15 83 0.18 14
Patient D 0.041 33 54 0.61 36 61 0.59 12
Patient E 0.067 21 66 0.32 27 64 0.42 53
M ± SD 0.054 ± 0.018 30 ± 11 59 ± 13 0.56 ± 0.37 28 ± 15 67 ± 16 0.49 ± 0.40 22.2 ± 18.7
Patients with cardioplegia
Patient F 24 71 0.34
Patient G 36 57 0.63
Patient H 27 70 0.38
Patient I 47 42 1.13
Patient J 63 23 2.70
M ± SD 39 ± 16 53 ± 20 1.04 ± 0.98
Open in a new tab

M ± SD, mean with standard deviation.

The analysis of the directionality of couplings through the phase dynamics modeling revealed the presence of coupling from LF oscillations in PPG to LF oscillations in HR for three out of five patients. This result was statistically significant at a 0.05 level for lags from 3.5 to 14.0 seconds (Table 2). An example of phase dynamics analysis is presented in Fig. 3. In particular, in Fig. 3a, the GPPGV→HRV, together with a confidence interval, lies above zero for a set of values from 4 to 14 seconds. The duration of the interval of 10 seconds corresponds to one characteristic oscillation period, therefore it can be stated that PPGV has an effect on HRV in the LF range with a probability of random error of no more than 0.05. We did not obtain any indication of the presence of coupling from HRV to PPGV.

Table 2.

Intervals of time lags between the LF oscillations in PPG and HR in patients without cardioplegia.

Patients τGPPGV→HRV > 0,S
Patient A —
Patient B 4.0–14.0
Patient C —
Patient D 3.5–12.0
Patient E 5.0–14.0
Open in a new tab

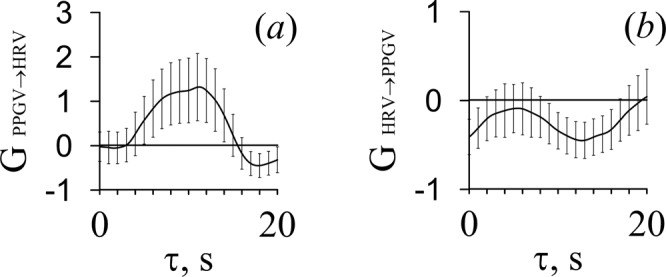
Figure 3.

Figure 3

Open in a new tab

The results of the analysis of directional coupling between the HRV and PPGV signals for patient E at different values of time lags. (a) The strength of coupling from PPGV to HRV in the LF range; (b) the strength of coupling from HRV to PPGV in the LF range. Vertical lines indicate 95% confidence interval (95% CI).

For all five subjects, the epochs of synchronization between the LF oscillations in HR and PPG were found out. However, in four patients the values of index S were rather small. Only in one case out of five, significant synchronization was revealed (patient E, S = 53%, p = 0.004) (Table 1).

The calculation of the coherence function C(f) showed that the coherence of the LF oscillations in HRV and PPGV is low and its significance level is close to p = 0.05 for four out of five patients. Figure 4a depicts C(f) for patient D. The values of C(f) are statistically significant (p = 0.05) over the 72% of the LF range. Figure 4b shows C(f) for patient E, for which the spectral components are statistically insignificant at a frequency of about 0.1 Hz. The maximum statistically significant values (p = 0.05) of the coherence function C(f) for the HRV and PPGV oscillations in the LF range are shown in Table 3.

Figure 4.

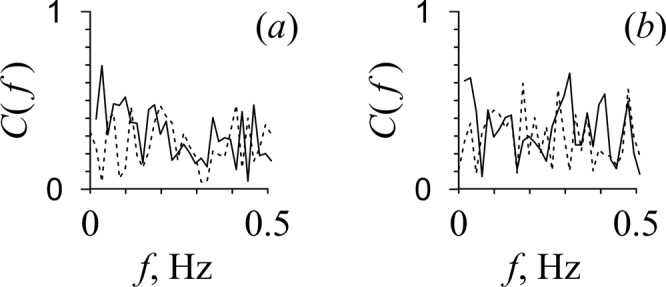
Figure 4

Open in a new tab

The results of the analysis of the coherence function C(f) for the HRV and PPGV signals in the LF and HF bands. C(f) is shown with solid line for patients D (a) and E (b). The 95% confidence interval is shown with dashed line.

Table 3.

Maximum statistically significant values (p = 0.05) of the coherence function C(f) for oscillations in the LF range of HRV and PPGV in patients without cardioplegia.

Patients С(f)
Patient A 0.66
Patient B 0.32
Patient C 0.59
Patient D 0.52
Patient E 0.45
Open in a new tab

Cardiopulmonary bypass with cardioplegia

Visually, pulse waves were not noticeable in the PPG signals of all patients (Fig. 5a). Only in three of five subjects the PPGV spectra showed peaks at a frequency of about 0.1 Hz (Fig. 5b). The peaks at the pulsation frequencies produced by the pump oxygenator were not identified in the power spectra. The spectral analysis of PPGV revealed that the power of LF oscillations was less than the power of HF oscillations in three out of five patients (Table 1).

Figure 5.

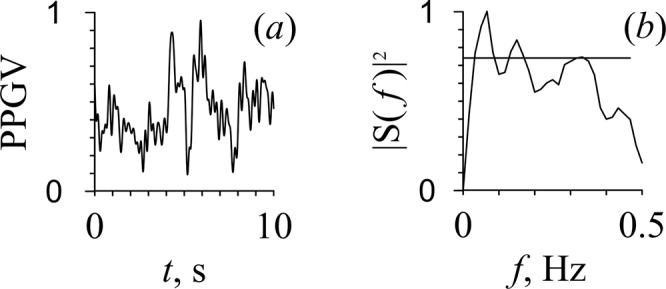
Figure 5

Open in a new tab

PPG signal (a) and its Fourier power spectrum (b) for patient G under cardiopulmonary bypass and cardioplegia.

Discussion

The obtained results agree with a conclusion that coupling from the heart to the peripheral vessels has a hemodynamic nature and the coupling from the vessels to the heart is carried out through the neural pathways23. In particular, for three out of five subjects, a significant impact of LF fluctuations in PPG on LF fluctuations in HR was detected. At the same time, in one case, this coupling from the vessels to the heart was so strong that it led to phase synchronization. In this case, there was no significant coherence between the spectral components at a frequency of about 0.1 Hz that eliminates the presence of leakage process (parasitic mixing of signals in the measurement channel), which could lead to a false detection of synchronization.

Detection of weak coupling between signals corrupted with noise is a complex problem. To solve this problem, we used the method based on phase dynamics modeling, which is one of the most sensitive techniques. However, even this method encounters difficulties caused by signal complexity. We revealed the presence of statistically significant coupling from LF oscillations in PPG to LF oscillations in HRV in three out of five patients. To ensure the reliability of the results, we inevitably have to sacrifice the sensitivity of the method. Obtaining a statistically insignificant result of the presence of coupling for the other two patients does not mean its absence, but only indicates that for these signals it is impossible to draw a reliable conclusion about the presence of coupling. For these two patients, the obtained result may be due to a higher noise level, a decrease in coupling strength, or the absence of noticeable oscillations in the studied frequency ranges. A more detailed analysis requires an increase in signal duration or direct registration of sympathetic nerve activity, which is impossible in practice. Therefore, we have to confine ourselves to conclusions based on the analysis of statistically significant results obtained for only a part of patients.

We have not got any results in favor of the hypothesis of the presence of a nervous coupling from the heart to the vessels. Under the hemodynamic dissociation of the heart and vascular bed through the use of CPB, the dynamics of the HRV parameters did not have any effect on the PPGV parameters, despite the continuing possibility of transmitting information from the heart to the vessels along the nerve pathways. We found out that neurogenic coupling from the peripheral vessels to the heart is characterized by small lag times. This may be the basis for the dominance of regulatory coupling from the peripheral vessels to the heart in adaptive processes in the circulatory system. Such coordination interactions are necessary to maintain the functional integrity of the circulatory system.

The presence of LF oscillations in PPG, even if clearly observed in several patients, in the absence of influences from the heart function, confirms the independence of the mechanisms of autonomic regulation of BP through modulation of vascular tone causing their occurrence in this signal. This is consistent with the results of other authors24, indicating a lack of changes in BPV in the background of CPB, which is caused by the stability of mechanisms for regulating BP to external influences. At the same time, both the renin-angiotensin and sympathetic systems are involved in the genesis of LF oscillations in BP24. According to some authors, the LF component of PPG may be a marker of patient separation according to the state of peripheral vascular resistance25.

A number of researchers have shown that the LF oscillations in mean BP are due to changes in peripheral vascular resistance26,27. Besides, the low correlation between the LF oscillations in BP and the cardiac state, for example, cardiac output, has been revealed28. However, the LF oscillations in cardiac output have shown good correlation with the LF oscillations in HRV27. The results of mathematical modeling also confirm the leading role of the tone of peripheral vessels in BP control29. Investigations of LF oscillations in BP (so-called Mayer waves) have shown that they are highly coherent with the oscillations in sympathetic nervous activity, baroreflectory control, and liberation of endothelium-derived nitric oxide, which may be important for the spontaneous control of the vessels tone30.

Considering data on the significant contribution of BPV to PPGV1,12, LF fluctuations in PPG also characterize the baroreflex regulation of BP. We believe that baroreflex regulation and sympathetic effects on vascular tone are components of a single central mechanism for regulating BP, which is involved in the formation of LF oscillations in BP and PPG.

The question of functional autonomy or the dependence of LF fluctuations in HR on the mechanisms of autonomic regulation of BP needs to be clarified. Earlier, we showed the phenomenon of separate capture of LF oscillations in HR and PPG13, indicating the autonomy of these oscillations. In the current study, in one patient under cardiopulmonary bypass, significant synchronization of LF oscillations in HR and PPG was also detected. Considering, as mentioned above, the lack of coupling in the direction from the heart to the vessels, but the presence of LF oscillations in HR, synchronization could be actively imposed by the processes of autonomic regulation of peripheral vascular resistance through the vasomotor centre. The lack of significant synchronization in the other patients under conditions of cardiac surgery with extracorporeal circulation is probably due to severe autonomic dysfunction against the background of chronic cardiovascular pathology and acute operational stress, which caused reduced activity of LF oscillations during the registration of physiological signals.

It should be noted that regarding the nature of LF oscillations in PPG, besides the hypothesis described above in the text, there are other opinions.

A number of authors consider the PPG oscillations in the LF range to be a reflection of vasomotions (vascular endothelial activity, myogenic autoregulation of blood flow, and regulation of skin temperature)31,32 and passive fluctuations in peripheral blood flow, which are conditioned by the response of elastic arteries and veins to the oscillations in BP, HR, and systolic blood flow33. Ferrario et al.34 showed the key role of central volume in the origin of LF oscillations of HR. Perhaps this result can be attributed to BPV. The complex nature of LF oscillations in PPG (for example, this issue was discussed in detail by Baselli et al.35) may involve all of the above-mentioned processes to some extent.

The lack of characteristic peaks in the LF range of the HRV and PPGV spectrum in some patients in the presence of significant coupling and synchronization may be due to difficulties in visualizing LF oscillations using spectral analysis methods because of the aforementioned marked reduction in their power. Also important is the fact of detecting a peak at 0.1 Hz in the spectrum of PPG even in patients with visually poorly noticeable pulse wave at PPG (including the case of cardioplegia), indicating the presence of these fluctuations in vascular tone under conditions of low blood filling.

Taking into account the features of the study (mechanical ventilation, CPB, cardioplegia, and cardiac surgery on the heart) we should carefully interpret the results of spectral analysis of HRV and PPGV, since there are no other studies with which to compare the results. For example, it is known that anesthesia can weaken the Mayer waves and decrease the spontaneous baroreceptor modulation36. However, such observations were not previously performed directly during cardiac surgery. Therefore, the obtained results of spectral analysis should be carefully compared with the results obtained for qualitatively different categories of subjects. The interpretation of the results should be carried out in conjunction with other methods of analysis.

We analyzed the data obtained under rather difficult experimental conditions. Therefore, the analyzed experimental ensemble is small. However, we investigated the qualitative effects. We believe that detecting these effects even in a few particular recordings is beneficial and forwards the understanding of cardiovascular system and its regulation. The conclusions we made are verified by careful statistical analysis based on the ensemble of surrogate signals that reproduce the statistical (spectral) characteristics of the experimental data. The surrogate data themselves can be considered as an extension of experimental data. This justifies the reliability of the obtained results and conclusions on a small experimental ensemble. However, the great variability in the characteristics of the cardiovascular system makes it desirable to expand the experimental ensemble. With a larger set of signals, it may be possible to uncover other effects that do not appear in analyzed recordings.

Conclusion

The mechanisms of autonomic regulation of peripheral vascular resistance, the activity of which is manifested in LF fluctuations in PPG, are autonomous from the mechanisms of autonomic regulation of the heart. Moreover, these mechanisms of regulation of the heart and blood vessels to some extent retain their activity under conditions of CPB and cardioplegia (the latter refers only to LF fluctuations in PPG). The coordinating coupling from the vessels to the heart is carried out by a neurogenic route, whereas the coupling in the opposite direction has a hemodynamic nature (due to cardiac output).

Acknowledgements

This work was supported by the Russian Science Foundation, Grant No. 18-74-10064.

Author contributions

A.R.K., V.A.S., A.S.K. and O.L.B. conceived and designed research. E.I.B., V.A.S., V.V.S., M.D.P., A.Y.I. and S.A.M. conducted experiments. A.R.K., V.A.S. and V.V.S. analyzed data. A.R.K., V.A.S., A.S.K. and M.D.P. wrote the manuscript. All authors read and approved the manuscript.

Competing interests

Vladimir A. Shvartz, Viktoriia V. Skazkina, and Artak Y. Ispiryan were supported by the Russian Science Foundation, Grant no. 18-74-10064. Other authors declare no potential conflict of interest.

Footnotes

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

References

  • 1.Allen J. Photoplethysmography and its application in clinical physiological measurement. Physiol. Meas. 2007;28:R1-9. doi: 10.1088/0967-3334/28/3/R01. [DOI] [PubMed] [Google Scholar]
  • 2.Moraes JL, et al. Advances in photopletysmography signal analysis for biomedical applications. Sensors (Basel) 2018;18:1894. doi: 10.3390/s18061894. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Bernardi L, et al. Autonomic control of skin microvessels: assessment by power spectrum of photoplethysmographic waves. Clin. Sci. (Lond.) 1996;90:345–355. doi: 10.1042/cs0900345. [DOI] [PubMed] [Google Scholar]
  • 4.Dash S, Shelley KH, Silverman DG, Chon KH. Estimation of respiratory rate from ECG, photoplethysmogram, and piezoelectric pulse transducer signals: a comparative study of timefrequency methods. IEEE Trans. Biomed. Eng. 2010;57:1099–1107. doi: 10.1109/TBME.2009.2038226. [DOI] [PubMed] [Google Scholar]
  • 5.Javed. F, et al. Frequency spectrum analysis of finger photoplethysmographic waveform variability during haemodialysis. Physiol. Meas. 2010;31:1203–1216. doi: 10.1088/0967-3334/31/9/010. [DOI] [PubMed] [Google Scholar]
  • 6.Middleton PM, et al. Fingertip photoplethysmographic waveform variability and systemic vascular resistance in intensive care unit patients. Med. Biol. Eng. Comput. 2011;49:859–866. doi: 10.1007/s11517-011-0749-8. [DOI] [PubMed] [Google Scholar]
  • 7.Middleton PM, et al. Peripheral photoplethysmography variability analysis of sepsis patients. Med. Biol. Eng. Comput. 2011;49:337–347. doi: 10.1007/s11517-010-0713-z. [DOI] [PubMed] [Google Scholar]
  • 8.Nollo G, Faes L, Porta A, Antolini R, Ravelli F. Exploring directionality in spontaneous heart period and systolic pressure variability interactions in humans: implications in the evaluation of baroreflex gain. Am. J. Physiol. Heart Circ. Physiol. 2005;288:H1777–H1785. doi: 10.1152/ajpheart.00594.2004. [DOI] [PubMed] [Google Scholar]
  • 9.Whittam AM, Claytont RH, Lord SW, McComb JM, Murray A. Heart rate and blood pressure variability in normal subjects compared with data from beat-to-beat models developed from de Boer’s model of the cardiovascular system. Physiol. Meas. 2000;21:305–318. doi: 10.1088/0967-3334/21/2/310. [DOI] [PubMed] [Google Scholar]
  • 10.Julien C, Malpas SC, Stauss HM. Sympathetic modulation of blood pressure variability. J. Hypertens. 2001;19:1707–1712. doi: 10.1097/00004872-200110000-00002. [DOI] [PubMed] [Google Scholar]
  • 11.Malpas SC. Neural influences on cardiovascular variability: possibilities and pitfalls. Am. J. Physiol. Heart Circ. Physiol. 2002;282:6–20. doi: 10.1152/ajpheart.2002.282.1.H6. [DOI] [PubMed] [Google Scholar]
  • 12.Rhee, S., Yang, B. H. & Asada, H. Theoretical evaluation of the influence of displacement on finger photoplethysmography for wearable health monitoring sensors in Symp. on Dynamics, Control, and Design of Biomechanical Systems ASME Int. Mechanical Engineering Congress and Exposition (Nashville, TN, 14–19 November, 1999).
  • 13.Karavaev AS, et al. Synchronization of low-frequency oscillations in the human cardiovascular system. Chaos. 2009;19:033112. doi: 10.1063/1.3187794. [DOI] [PubMed] [Google Scholar]
  • 14.Kiselev AR, et al. Method of estimation of synchronization strength between low-frequency oscillations in heart rate variability and photoplethysmographic waveform variability. Russ. Open Med. J. 2016;5:e0101. doi: 10.15275/rusomj.2016.0101. [DOI] [Google Scholar]
  • 15.Task Force of the European Society of Cardiology and the North American Society of Pacing and Electrophysiology Heart rate variability: standards of measurement, physiological interpretation, and clinical use. Circulation. 1996;93:1043–1065. doi: 10.1161/01.CIR.93.5.1043. [DOI] [PubMed] [Google Scholar]
  • 16.Welch PD. The use of Fast Fourier Transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Transactions on Audio and Electroacoustics. 1967;15:70–73. doi: 10.1109/TAU.1967.1161901. [DOI] [Google Scholar]
  • 17.Schreiber T, Schmitz A. Improved surrogate data for nonlinearity tests. Phys. Rev. Lett. 1996;77:635–638. doi: 10.1103/PhysRevLett.77.635. [DOI] [PubMed] [Google Scholar]
  • 18.Theiler J, Longtin A, Galdrikian B, Farmer J. Testing for nonlinearity in time series: the method of surrogate data. Physica D. 1992;58:77–94. doi: 10.1016/0167-2789(92)90102-S. [DOI] [Google Scholar]
  • 19.White LB, Boashash B. Cross spectral analysis of nonstationary processes. IEEE Trans. Inf. Theory. 1990;36:830–835. doi: 10.1109/18.53742. [DOI] [Google Scholar]
  • 20.Rosenblum MG, Pikovsky AS. Detecting direction of coupling in interacting oscillators. Phys. Rev. E. 2001;64:045202. doi: 10.1103/PhysRevE.64.045202. [DOI] [PubMed] [Google Scholar]
  • 21.Smirnov D, Bezruchko B. Estimation of interaction strength and direction from short and noisy time series. Phys. Rev. E. 2003;68:046209. doi: 10.1103/PhysRevE.68.046209. [DOI] [PubMed] [Google Scholar]
  • 22.Smirnov DA, Bezruchko BP. Detection of coupling in ensembles of stochastic oscillators. Phys. Rev. E. 2009;79:046204. doi: 10.1103/PhysRevE.79.046204. [DOI] [PubMed] [Google Scholar]
  • 23.Khorev VS, et al. Estimation of delay times in coupling between autonomic regulatory loops of human heart rate and blood flow using phase dynamics analysis. Open Hypert. J. 2017;9:16–22. doi: 10.2174/1876526201709010016. [DOI] [Google Scholar]
  • 24.Souza Neto EP, et al. Blood pressure and heart rate variability changes during cardiac surgery with cardiopulmonary bypass. Fundam. Clin. Pharmacol. 2004;18:387–396. doi: 10.1111/j.1472-8206.2004.00244.x. [DOI] [PubMed] [Google Scholar]
  • 25.Piepoli M, Garrard CS, Kontoyannis DA, Bernardi L. Autonomic control of the heart and peripheral vessels in human septic shock. Intensive Care Med. 1995;21:112–119. doi: 10.1007/BF01726532. [DOI] [PubMed] [Google Scholar]
  • 26.O’Leary DS, Woodbury DJ. Role of cardiac output in mediating arterial blood pressure oscillations. Am. J. Physiol. 1996;271:R641–R646. doi: 10.1152/ajpregu.1996.271.3.R641. [DOI] [PubMed] [Google Scholar]
  • 27.Elstad M, Walløe L, Chon KH, Toska K. Low-frequency fluctuations in heart rate, cardiac output and mean arterial pressure in humans: what are the physiological relationships? J. Hypertens. 2011;29:1327–1336. doi: 10.1097/HJH.0b013e328347a17a. [DOI] [PubMed] [Google Scholar]
  • 28.Aletti F, et al. Cardiac output is not a significant source of low frequency mean arterial pressure variability. Physiol. Meas. 2013;34:1207–1216. doi: 10.1088/0967-3334/34/9/1207. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Aletti F, Bassani T, Lucini D, Pagani M, Baselli G. Multivariate decomposition of arterial blood pressure variability for the assessment of arterial control of circulation. IEEE Trans. Biomed. Eng. 2009;56:1781–1790. doi: 10.1109/TBME.2009.2016845. [DOI] [PubMed] [Google Scholar]
  • 30.Julien C. The enigma of Mayer waves: Facts and models. Cardiovasc. Res. 2006;70:12–21. doi: 10.1016/j.cardiores.2005.11.008. [DOI] [PubMed] [Google Scholar]
  • 31.Anschutz S, Schubert R. Modulation of the myogenic response by neurogenic influences in rat small arteries. Br. J. Pharmacol. 2005;146:226–233. doi: 10.1038/sj.bjp.0706323. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Krupatkin AI. Blood flow oscillations at a frequency of about 0.1 Hz in skin microvessels do not reflect the sympathetic regulation of their tone. Hum. Physiol. 2009;35:183–191. doi: 10.1134/S036211970902008X. [DOI] [PubMed] [Google Scholar]
  • 33.Grinevich AA, Tankanag AV, Chemeris NK. Role of elasticity of blood vessels in formation of highly amplitude oscillations of a blood flow with frequency of 0.1 Hz. Math. Biol. Bioinformatics. 2014;9:341–358. [Google Scholar]
  • 34.Ferrario M, et al. The forgotten role of central volume in low frequency oscillations of heart rate variability. PLoS One. 2015;10:e0120167. doi: 10.1371/journal.pone.0120167. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Baselli G, Porta A, Pagani M. Coupling arterial windkessel with peripheral vasomotion: modeling the effects on low-frequency oscillations. IEEE Trans. Biomed. Eng. 2006;53:53–64. doi: 10.1109/TBME.2005.859787. [DOI] [PubMed] [Google Scholar]
  • 36.Shin WJ, et al. Link between heart rate and blood pressure Mayer wave during general anesthesia. Clin. Auton. Res. 2011;21:309–317. doi: 10.1007/s10286-011-0115-9. [DOI] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES