A Parametric Study on Overband Radial Build for a REBCO 800-MHz Insert of a 1.3-GHz LTS/HTS NMR Magnet

Abstract

A high-resolution 1.3-GHz/54-mm low-temperature superconducting/high-temperature superconducting (HTS) nuclear magnetic resonance magnet (1.3 G) is currently being built at Francis Bitter Magnet Laboratory, Massachusetts Institute of Technology. One of its key components is an 800-MHz HTS insert (H800) comprising three nested coils. Each coil is a stack of double-pancake coils wound with 6-mm-wide 75-μm-thick REBCO tape. For this H800 generating its self-field of 18.6 T and being exposed to a total field as high as 30.5 T, overbanding each pancake coil is necessary to keep the conductor strain at < 0.6%. Although electromagnetic and mechanical details of the H800 had been considered during its design stage, a parametric study on the overband radial build considering winding tension effect should further confirm the results of our previous analysis. Thus, in this paper, based on Maxwell’s equations and the equilibrium equations for mechanical deformation, we examine stress levels that the H800 experiences as H800 undergoes winding–energizing sequences during operation at 1.3 GHz. We also discuss the effects of overband radial build and winding tension on conductor stress in each coil. Finally, based on this analysis, we may further optimize the stainless-steel overbanding and winding tension on each H800 coil.

I. Introduction

BECAUSE magnetic field strength improves the resolution and sensitivity of nuclear magnetic resonance (NMR) signals, efforts to increase the magnetic field of NMR spectrometers have continuously progressed. Recently, the NMR experimental results on complex molecular structures have shown that their resolution would be optimized and improved in the range 1.2–1.4 GHz [1]. To achieve this field range, we at the Francis Bitter Magnet Laboratory are currently developing a 1.3-GHz/54-mm LTS/HTS NMR magnet (1.3 G): a combination of a 500-MHz LTS NMR magnet (L500) and an 800-MHz HTS insert (H800). Currently, BSCCO and REBCO high temperature superconducting tapes are both available in long lengths and are suitable for various applications at this field range [2], [3], thus, the H800 comprises three nested coils (coil1~3), each a stack of DP coils wound with 6-mm wide, 75-μm thick REBCO tape without turn-to-turn insulation [4]–[7]. When the 1.3 G is exposed to a field as high as ≥ 30.5 T, H800 will be under intense Lorentz forces, which in turn can lead to large strain on REBCO conductor at a nominal operating current of 251 A. It is important to keep the superconductor within its tolerable strains in design and operation of H800. Therefore, mechanical stress-strain analysis plays an important role [8], [9] in H800 magnet design.

Stress analyses based on simplified magnet winding models are available, e.g., [10], [11]. However, with finite element (FE) numerical methods, superconducting magnets may be analyzed to determine their stress distributions in more detail [12], [13]. These structural analyses have proven effective for high-field superconducting magnets. To retain the conductor critical current density at ≥95 % of its unstrained value, we designed H800 to limit the conductor strain in the REBCO tape to ≤ ~0.6 % [5]–[7]. For optimal design, however, it is still advisable to analyze the stress distributions inside the H800.

Since stainless steel overband and its winding tension are two major design parameters in H800 to meet the conductor strain requirement, in this paper, we mainly aim at analyzing the effects of overband radial build and its winding tension on conductor stress in the H800 coils during 1.3 G operation. A 2D axial-symmetric FE model under plane stress condition is applied to H800 coils in our numerical analysis; structural response of each coil in H800 consists of REBCO conductor and SS (stainless steel 316) overband. The commercial multiphysics package FlexPDE [14], which is a general purpose scripted finite element software, was used to solve simultaneously Maxwell’s and equilibrium equations. The radial stress and hoop stress distributions in the H800 coils were obtained numerically. The effects of overband radial build and its winding tension on stress in each coil are also discussed. The results on stress were also compared and confirmed with those of its first-cut design, whose methods had been proved for a DP coil by comparison of the experimental results [15], [16]. A parametric analysis has been conducted primarily for a better understanding of the structural behavior of H800, including the roles of overband radial build and winding tension. Based on this study, a set of optimal overband radial build and its winding tension on each H800 coil has been obtained.

II. Fundamental Equation and Modeling

H800 is comprised three nested coils (coil1 ~3), each a stack of double-pancake coils of 75-μm thick, 6-mm wide REBCO tape (SuperPower’s 2G HTS REBCO). Each coil requires an overband of 76-μm thick, 6-mm wide stainless steel [15]. When energized, H800 coils mainly experience large Lorentz forces that may exceed conductor’s 0.6% strain limit [6], [7].

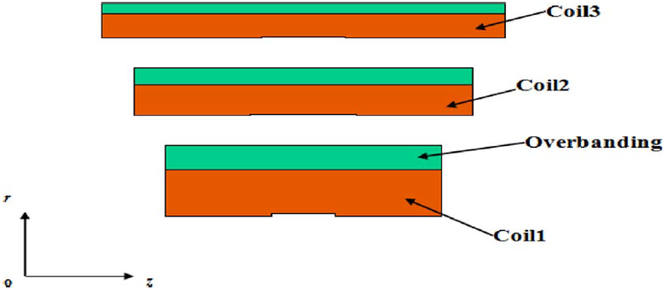
To simulate electromagnetic stress distributions within the axially symmetric overbanded H800 coils, we developed a 2-D finite element model in cylindrical coordinate (see Fig. 1). Each coil is composed of two hollow cylinders of different radii, one the winding and the other an overband of many turns of thin stainless steel strip. Each tape was treated as a monolithic block:

$$\nabla \times B={\mu }_{0}J,\nabla \cdot B=0\text{\hspace{0.17em}winding}$$ (1)

$$J\times B=-\nabla \cdot \sigma \text{ winding \& overband}$$ (2)

where J is winding overall current density vector, B is magnetic flux density vector and σ is stress tensor vector.

Fig. 1.

Two-dimensional axial symmetric model of H800 coils.

When H800 is energized, its magnetic field distribution may be computed by (1) and its stresses are mainly induced by the Lorenz force between operating current and magnetic field as given by (2). Based on plane stress condition and zero shear stress approximation, and using the local displacement in the radial direction u as a variable, we further combine (1) and (2) with generalized Hooke’s law and strain-displacement relation [10]

$$\frac{1}{1-v_i}\frac{\partial }{\partial r}\left(\left(\frac{\partial u_i}{\partial r}+\frac{u_i}{r}\right)\right)+\frac{1+v_i}{E_i}{J}_{\theta }{B}_z=0.$$ (3)

Here, u_i, E_i, v_i, respectively are the radial displacements, Young’s moduli and Poisson’s ratios of the coil package (i = 1) and overbanding (i = 2).

Once (3) is solved, we can simulate the circumferential and radial stress according to:

$${\sigma }_{\theta i}(r)=\frac{E_i}{1-v_i^2}\left(\frac{u_i}{r_i}+v_i\frac{\partial u_i}{\partial r}\right)$$ (4)

$${\sigma }_{ri}(r)=\frac{E_i}{1-v_i^2}\left(\frac{\partial u_i}{\partial r}+v_i\frac{u_i}{r_i}\right).$$ (5)

The commercial multiphysics package FlexPDE was used to solve the above equations in a different sub-domain. An iterative method was employed considering magneto-mechanical coupled effects of each coil in H800. For the purpose of comparison, in our simulation, the same material parameters of REBCO tape and the overband can be also both found in [16]. In addition, in our simulation, for the winding tension, a corresponding radial stress will be exerted to an individual turn as a boundary condition, as described in [10].

III. Validation

To verify the accuracy of the numerical model proposed, our results were compared and confirmed with the analytical results of our first-cut design [15]. As shown in Fig. 2, the distributions of hoop stresses and radial stress are perfectly consistent, when key parameters of the H800 are set identically as in [15]. Finally, in Table I, the % differences in results between two analyses are given; agreement is quite good. Based on these results, we can proceed to apply our analysis to optimize overband radial build on each H800 coil.

Fig. 2.

Comparison and distributions for H800 coils. (a) Radial stress. (b) Hoop stress.

TABLE I.

Maximum Differences Between Two Analyses

	Hoop Stress	Radial Stress
Coil1	2.7%	0.8%
Overbanding1	0.6%	0.7%
Coil2	2.5%	0.2%
Overbanding2	2.1%	0.4%
Coil3	2.0%	0.09%
Overbanding3	0.9%	0.1%

IV. Results and Discussion

We carried out optimizing stresses in the H800 coils by considering both the overband radial build and its winding tension. For our first-cut design, the following parameters were chosen: a winding tension of 50 N for both REBCO tape and SS overband strip for each H800 coil, overband radial builds of coil 1~3, respectively, 7 mm, 5 mm and 3 mm. Other key parameters for H800 can also be found in [15]. In our optimization, we simulated the detailed stress analyses of H800 coils in the background of the L500 magnet under different conditions: 1) A constant winding tension of 50 N and overband radial builds of 7 mm, 6.5 mm, 6 mm, 5.5 mm, 5 -mm for coil 1; 2) A constant overband radial build of 7 mm, 5 mm, 3 mm and overband winding tensions of 25 N, 50 N and 100 N for coils 1–3. In each simulation, H800 was set at 251 A. Radial and hoop equivalent Young’s moduli of H800 were set at 73 GPa and 142 GPa, respectively, and equivalent Young’s modulus of the SS overband was 180 GPa. Finally, the overband radial build effects on peak hoop stresses in coil 1 at three winding tensions are summarized and discussed.

A. Stress Analysis for Different Overband Radial Build in Coil1

First, to modify the stresses in coils, it can be useful to optimize overband radial build, so we simulated stress on overband radial build for coil 1 considering constant winding tension and energizing of 1.3-GHz LTS/HTS NMR Magnet. Fig. 3(a) show coil 1 radial stress versus radius plots for 5 overband radial builds. Note that radial stresses at r = a₁ and a₂, respectively, the innermost and outermost radii are zero. This is because of the mechanical boundary condition that the surface is traction free at end. Coil 1 and its overband, always under compressive stress, limit hoop strains during excitation. Also, the maximum radial stress is at the outermost turn. In addition, the radial compression is increased with overband radial build. For another, hoop stress is an important index in design of a high-field REBCO magnet: σ_θ on REBCO tape should be kept < 700 MPa and the overband < 1200 MPa. In our parametric study, coil 1 hoop stress versus radius plots, calculated on force equilibrium for five overband radial builds, are also depicted in Fig. 3(b). Thus the results show that coil hoop stress decreases with overband radial build and that tensile stress decreases with radius, as does magnetic field. A jump in each plot in Fig. 3(b) indicates the beginning of the overband. Thus, overband radial build in each H800 coil is an effective design parameter for limiting its radial stresses and hoop stresses.

Fig. 3.

(a) Magnetic radial stress versus radius plots for coil 1 at different overband radial builds for winding tension of 50 N. (b) Magnetic hoop stress versus radius plots for coil 1 at different overband radial builds for winding tension of 50 N.

B. Stress Analysis for Different Winding Tension of Overband in Coils 1~3

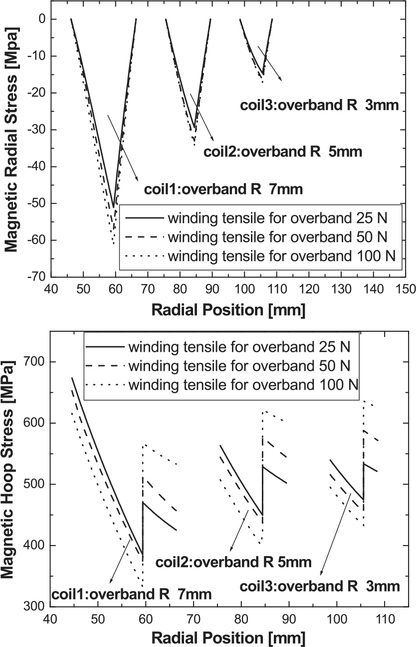
To further study on beneficial effects of overband, we analyzed the overband winding tension. In our simulation, we set overband radial builds for coils 1–3, respectively, at 7 mm, 5 mm, and 3 mm, and analyzed overband winding tensions of 25 N, 50 N and 100 N. Fig. 4(a) shows radial (compressive) stress versus radius plots for coils 1–3. The stress behaviors on winding tension are quite similar with those on overband radial build. One can see in Fig. 4(a) that radial stress is increased with winding tension. For coil l, the figure indicates that the maximum radial compressive stresses are 60 MPa, 55-MPa, and 49 MPa, at overband winding tensions, respectively of 100 N, 50 N, and 25 N. The winding tension effects are smaller for coils 2 and 3. The results illustrate that overband winding plays an important role in limiting stresses in a high-field coil. The computed hoop stresses show a significant difference between overband winding tensions of 25 N and 100 N in H800: 615 MPa versus 673 MPa; 504 MPa versus 563 MPa; and 495 MPa versus 539 MPa for coils 1–3, respectively (see Fig. 4(b)).

Fig. 4.

(a) Magnetic radial stress versus radius plots for coils 1–3 at overband winding tensions of 25, 50, and 100 N. (b) Magnetic hoop stress versus radius plots for coils 1–3 at overband winding tensions of 25, 50, and 100 N.

C. Further Discussion and Optimization

In this parametric study, one important result is peak hoop stress versus the overband radial build. Fig. 5(a) for coil 1 shows that peak stress in coil 1 decreases with overband radial build and winding tension. Thus, we believe that maximum hoop stress may be limited by the overband radial build and winding tension. In addition, Fig. 5(b) also show that the sensitivity on peak hoop stress in coil 1 depends on the overband radial build at different winding tensions. The values are normalized with respect to the maximum hoop stress for an overband radial build of 5 mm at different winding tensions. From Fig. 5(b), we can conclude that the peak hoop stress in coil 1 will be reduced about 5% when the overband build is increased by 1 mm. Finally, an overband radial build of 6 mm (down from original 7 mm) and an overband winding tension of 75 N (up from original 50 N) have been applied to coil 1.

Fig. 5.

(a) Peak hoop stress versus overband radial thickness plots in coil 1 at overband winding tensions of 25, 50, 75, and 100 N. (b) Sensitivity on normalized peak hoop stress versus overband radial build plots in coil 1 at overband tensions of 25, 50, 75, and 100 N.

V. Conclusion

This paper described results of parametric studies to compute stress induced by magnetic force on H800 during operation of 1.3-GHz LTS/HTS NMR magnet. About 800-MPa of 95%-Ic-retention tensile stress was reported for selected SuperPower REBCO conductors after ~10 000 load cycles at 77 K [17]. Based on this criterion, we analyze in detail the effects of overband radial build and its winding tension on conductor stresses in H800 coils for final assembly. As we have shown here, the stresses in H800 coils may be decreased with an overband of greater radial build and winding tension.