Abstract
Life is an emergent property of transient interactions between biomolecules and other organic and inorganic molecules that somehow leads to harmony and order. Measurement and quantitation of these biological interactions are of value to scientists and are major goals of biochemistry, as affinities provide insight into biological processes. In an organism, these interactions occur in the context of forces and the need for a consideration of binding affinities in the context of a changing mechanical landscape necessitates a new way to consider the biochemistry of protein–protein interactions. In the past few decades, the field of mechanobiology has exploded, as both the appreciation of, and the technical advances required to facilitate the study of, how forces impact biological processes have become evident. The aim of this review is to introduce the concept of force dependence of biomolecular interactions and the requirement to be able to measure force-dependent binding constants. The focus of this discussion will be on the mechanotransduction that occurs at the integrin-mediated adhesions with the extracellular matrix and the major mechanosensors talin and vinculin. However, the approaches that the cell uses to sense and respond to forces can be applied to other systems, and this therefore provides a general discussion of the force dependence of biomolecule interactions.
The development of life has evolved in the context of physical forces acting on biological systems. From individual molecules to organelles to cells, tissues, and organs, every part of every organism is exposed to and experiences forces. These forces, generated or experienced, impact every aspect of physiology;1−3 every cell interprets “classical” signaling pathways (growth factors, hormones, etc.) in the context of its physical environment.5−8
The purpose of this review is to provide a brief introduction to the concept of force-dependent binding constants, and we will introduce the study of how forces can impact biomolecular interactions. This review will be divided into three sections. The first section will be a general discussion of biomolecular interactions and their importance in biological processes; in particular, this section will focus on the protein interactions involved in mechanotransduction leading to the appreciation that many of these protein interactions have a force-dependent component. In the second section, we will discuss the modifications to the theory of binding constants required to enable force dependence to be considered. Finally, in the third section, we will discuss some of the novel approaches that are emerging and/or required to enable force-dependent binding constants to be measured.
Biomolecular Interactions
For the purposes of this review, we focus on interactions with proteins and DNA, although the concepts and principles can be applied to other systems. Interactions between proteins and other proteins, DNA, lipid membranes, inorganic metal ions, etc., are mediated by compatible interacting residues and surfaces, i.e., a surface on the substrate protein that has the optimal shape to recognize its ligand (a moiety that forms a complex with that biomolecule to serve a biologically relevant purpose). The ligand can be any biomolecule or non-organic molecule that interacts with the biomolecule in a meaningful way. Interacting surfaces that have important biological functions tend to be highly conserved through evolution, to preserve and maintain the interaction.
Equilibrium Dissociation Constant, Kd
The binding affinity of an interaction describes the strength of
the binding between a target molecule and its ligand. This binding
affinity is usually reported as the equilibrium dissociation constant, Kd. This quantity is defined as the ratio between
the off-rate, koff, typically in units
of s–1, and the on-rate, kon, typically in units of M–1 s–1. Therefore, the dissociation constant, 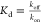 , has a dimension of concentration typically
expressed in molar concentration. Kd can
also be expressed by the equilibrium ratio of the fractions of the
bound target (αon) and that of the unbound target
(αoff = 1 – αon) molecules,
, has a dimension of concentration typically
expressed in molar concentration. Kd can
also be expressed by the equilibrium ratio of the fractions of the
bound target (αon) and that of the unbound target
(αoff = 1 – αon) molecules, 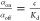 , where c is the
concentration
of free ligand molecules.
, where c is the
concentration
of free ligand molecules.
The recent rapid development of single-molecule
technologies has
made it possible to investigate binding of ligands to a single target
molecule, thus enabling determination of binding affinity Kd with a single-molecule level of accuracy.
Such quantification of Kd is mainly achieved
either by measuring the on- (kon) and
off-rates (koff) through the equation 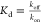 or by measuring the equilibrium probabilities
of the bound (pon) and unbound states
(poff = 1 – pon) of the target molecule through the equation
or by measuring the equilibrium probabilities
of the bound (pon) and unbound states
(poff = 1 – pon) of the target molecule through the equation 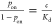 . At equilibrium, the ratio of
the bound
probability to the unbound probability should follow the Boltzmann
distribution,
. At equilibrium, the ratio of
the bound
probability to the unbound probability should follow the Boltzmann
distribution, 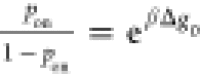 , where
, where 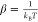 and Δg0 is the free energy difference between the unbound and bound states,
which is related to the dissociation constant by the equation Kd = ce–βΔg0.
and Δg0 is the free energy difference between the unbound and bound states,
which is related to the dissociation constant by the equation Kd = ce–βΔg0.
Measurement and quantitation of biological interactions are of value to scientists and are major goals of biochemistry, as affinities provide insight into biological processes. In drug discovery, measuring affinities is important to aid the design of drugs with a higher affinity for the target and thus a higher efficacy. If there are two potential ligands available to bind to a single target molecule, at similar concentrations, then the relative affinities of each for the biomolecules will dictate which binds preferentially. If one has a higher affinity (lower Kd), then it will bind preferentially. Modulation of the affinities for the two ligands (via post-translational modification, including alteration of conformation via mechanical force) can alter the complexes that form.
Forces in Biology
Life that lives under the sea has forces acting on it that are very different from those on land or the forces on those that take to the skies, and changes in mechanical signaling that arise from these different physical environments enable the stunningly beautiful diversity of creatures. Strikingly, despite this incredible diversity, the adhesive structures holding the cells in place, via contact with neighboring cells and the surrounding extracellular matrix, are largely made of the same building blocks. The appreciation of forces in biology has been the subject of many excellent reviews,10−13 and these all provide excellent accounts to which we refer the reader. The focus here is how these forces can be sensed by the cell and how they can alter signaling outcomes.
Forces on Biomolecules
Many forces exist in cells, arising from collisions, flow (both retrograde flow of proteins inside the cell and flow of blood past proteins on the surface of cells), force generation machinery and motor proteins (myosins, kinesins, etc.), and forces exerted from the outside world, gravity, pressure, friction, etc.14−16 All of these forces are sensed by mechanosensors in the cell and used to control cell behavior.17−19 As these forces are ubiquitous, it seems safe to assume that many biomolecules in the cell will experience forces and as such that the binding constants of interactions involving these molecules will have a force-dependent component.
Actomyosin Contraction
Motor proteins harness the energy from ATP hydrolysis to generate mechanical energy that drives conformational changes that act on other cellular structures (reviewed in refs (16) and (20)). In the case of myosin, its interaction against actin filaments enables motion, with the myosin either moving along the filament or pulling the actin filament toward it.21,22 These forces generated by myosin motors pulling on the actin filament is dubbed actomyosin contraction and is a major method the cell utilizes to generate and maintain forces. Much of the discussion herein will focus on the mechanisms with which the cell responds to this internally generated force.
For a force to act on a biomolecule, it requires the force generation machinery to couple to the protein. This coupling can be either direct, if the protein directly binds to the actin filament, or indirect, if the actomyosin pulls on another protein that acts on the protein. If the biomolecule is bound just to the force generator, then this will pull the biomolecule toward the force. Trafficking of proteins can occur in this manner; for instance, MyosinX can couple to cargo proteins and drag them along actin tracks to the tips of filopodia.23,24 In this scenario, the biomolecule is dragged along (and will experience the forces associated with drag).
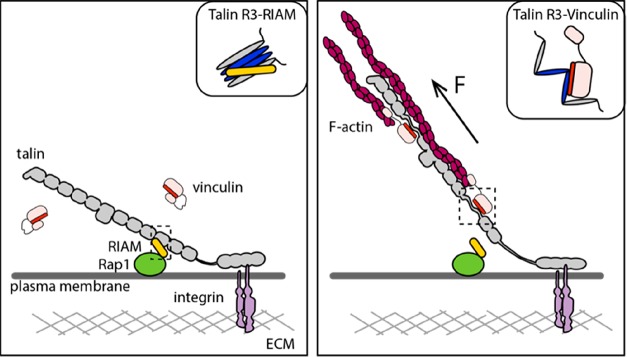
However, if a protein couples to the force generation machinery but is also tethered to a second less mobile system, then the forces “pull” on the tethered protein and the forces are exerted on all proteins constituting the force-transmission molecular linkage. An example of this tethered system is seen for talin, bound to the integrin–ECM complexes at the plasma membrane18,25 (Figure 1). Here, when actomyosin contractions act on talin, as the talin is tethered, the forces are exerted on the length of the molecule, and as these forces exceed force thresholds of stability for any talin domains, they can trigger domain unfolding (see the next section for a discussion of the consequences of domain unfolding).
Figure 1.
Talin serves as a force-dependent mechanochemical switch. Talin (gray) is shown bound to integrin and to F-actin. The 13 rod domains are shown arranged like beads on a string. The switch behavior of the R3 domain is shown. The left panel shows the talin–RIAM–Rap1 linkage. The inset shows the schematics of RIAM binding to folded talin R3. The right panel shows the talin–vinculin–F-actin linkage. The inset shows the schematics of full-length vinculin bound to exposed VBS in unfolded talin R3.
This action of actomyosin contraction pulling on a tethered protein is not exclusive to adhesion; any protein, DNA, or membrane that experiences forces has the potential to undergo changes in its shape and thus its function. Therefore, any consideration of the mechanobiology of biomolecules needs to consider where the force is originating, how it is acting on the biomolecule, and how the biomolecule will react, which will depend on its mobility (can it move, or is it tethered?).
Structural Mechanobiology
One exciting, though not altogether unsurprising, aspect of the mechanosensitive events identified to date is that knowledge of the structural basis of the interaction provides an atomic basis of the mechanosensitive mechanism of the interaction. For instance, in the case of talin it is possible to identify the exact amino acids that render the molecule mechanically sensitive. A striking example of this is the R3 domain of talin;25−27 this domain has reduced mechanical stability due to a cluster of four threonine residues in the central hydrophobic core, which due to their more polar nature destabilize the domain. Using this precise structural information, it is possible to modulate mechanosensing via targeted point mutations that alter mechanosensing. In the case of R3, modification of the four threonine residues to isoleucine and valine residues (a so-called “IVVI mutant”) results in stabilization of the R3 domain,25−27 shifting its mechanical stability to a higher level (i.e., the modified domain unfolds at a higher force at the same force loading rate). Therefore, a comprehensive appreciation of mechanobiology at the atomic level requires atomic-resolution structural biology.
Types of Force-Dependent Binding
There are many ways that force can impact binding, and these effects can quickly stack to give diverse responses. Here we offer a non-exhaustive summary of some of the common force dependencies. Protein–protein interactions can change their affinity by orders of magnitude under different force constraints, and as a result, biochemistry done in bulk solution in vitro captures only part of the picture and lacks consideration of the mechanical regulation of the interaction. As a consequence, it is necessary to consider the force dependence of biomolecular interactions.
The focus of this review is on equilibrium binding constants under mechanical force, Kd(F). Discussion of the Kd(F) will facilitate the description of forces impacting the affinity of binary interactions, autoinhibition, and the interplay of these factors. This will enable the description of two common force-dependent processes that regulate mechanosensitivity through talin, namely, exposure of cryptic binding sites, whereby force exposes hidden binding sites, a type of autoinhibition, and disruption of binding sites, where the binding site is accessible to the ligand, but force results in the domain unfolding and destroying the binding site. The talin rod contains 13 rod domains, R1–R13, which all combine both of these processes together, to create a series of mechanochemical switches25 (Figure 1).
Mechanochemical Switches
Tension-sensitive conformational change is a very rapid way for proteins to respond to mechanical force. In many ways, this can be considered as a post-translational modification; force alters the conformation of a protein, and if this change in shape elicits a change in biochemical function, then force can be converted into biological signals. If the conformational change is reversible, that is when force is released the domain reverts back to its low-force condition, then this provides incredible plasticity and can enable rapid and dynamic changes in signaling outcomes.
The theoretical basis of these processes will be discussed in the next section, but to illustrate this concept of force-dependent binding constants, consider the interactions of a talin rod domain (here the example is R3) with three different ligands.
Conventional Protein Interactions
Here, two proteins interact in a “classical” manner, whereby one ligand binds to a binding site on a folded domain (i.e., RIAM binding to the folded talin rod domain R3, as demonstrated in the left panel in Figure 1). In the absence of force, the talin domains are folded, so the interaction can occur. In this scenario, the level of binding is highest at low force and so the Kd is lowest. If the domain is unfolded by mechanical force, then the binding surface on the domain is destroyed, so force, above a certain threshold, drives a sharp decrease in the level of binding. Beyond this point, additional force has a weaker effect on the affinity of the interaction as the interaction is already destroyed.
Cryptic Binding Sites That in the Absence of Force Are Inaccessible to Binding
In conventional protein interactions, force results in the loss of ligands binding to folded rod domains; however, eight of the 13 talin rod domains contain vinculin binding sites (VBSs), amphipathic helices in which the vinculin binding epitope is buried inside the domain. At low force, the affinity of the VBS interaction with vinculin is weak (it has a high Kd) as the binding site is not accessible to vinculin. Here, the Kd profile with force is different, at low force, the Kd is high as binding is not possible, at forces above the unfolding threshold, then the Kd is low [exposed VBS bind tightly to the vinculin head, with a nanomolar Kd (although as we will see the vinculin itself is also regulated by forces acting on vinculin)]. However, the force dependence is complicated as at high forces the VBS helix can unfold and lead to a loss of vinculin binding.
Cryptic Binding Sites That Are Exposed Only When All Secondary Structure Is Destroyed
While no such ligand has yet been identified for talin, there is also the third scenario in which a fully extended talin polypeptide creates linear epitopes that bind ligands. Here, the affinity will be the highest at high force when the domain is completely unfolded.
Autoinhibition
Autoinhibition is not always considered to be mechanosensitive, but if proteins that are regulated by autoinhibition form part of the mechanical linkages in the cell, then the affinity of the protein for its ligands is directly correlated to the force on the system. The cryptic nature of VBS in talin is also a type of autoinhibition,28 and talin is further autoinhibited by the molecule folding up into a tight globular compact structure.29−31 Vinculin is also regulated by a head–tail interaction, where the binding sites for talin and actin are rendered cryptic.32,33 All of these layers of autoinhibition have a strong force-dependent component, as the affinity of autoinhibition is controlled by whether the protein is under force (if the autoinhibitory domains are held apart by mechanical force, then the protein is maintained in an activated state).27,34,35 What is emerging is that autoinhibition of proteins in force-transmitting pathways represents a major force-dependent mechanism to enable mechanotransduction.
Force-Dependent Kinetic Changes in Binding
Another key force dependence of interactions arises from scenarios in which forces alter the kinetics of the interactions. As the binding affinity is determined by the ratio of the dissociation rate to the association rate, the influence of force on the binding affinity must be through force-mediated changes in the dissociation and association rates. While a detailed discussion of these is beyond the scope of this review, it is worth mentioning these effects as they impact the mechanical functioning of force-dependent interactions. The force-dependent dissociation rate is of particular interest, as it defines the average lifetime of force-bearing molecular complexes once they are formed. The two most well characterized occurrences of force-dependent dissociation kinetics affecting biomolecular interactions are the slip bond and the catch bond.
Slip Bonds
A slip bond refers to the phenomenon in which the rate of dissociation of a molecular complex increases as the applied force increases. It indicates that a protein interaction is weakened under force, as the force pulls the two interacting components apart.
Catch Bonds
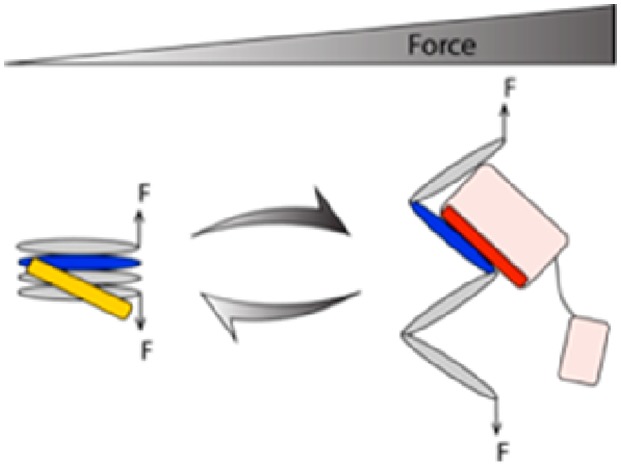
A catch bond refers to an anti-intuitive phenomenon in which the molecular lifetime of an interaction increases as force applied to the interacting molecules increases,36−39 which plays critical roles in cell–matrix and cell–cell adhesions.40−42 Interestingly, catch bond kinetics can have a geometric component, where the interaction exhibits catch bond behavior only when force is exerted in a particular pulling geometry. This leads to directionally asymmetric catch bonds as are seen for the interaction between vinculin and F-actin.43 Directional asymmetry can be rationalized at the atomic level by looking at the geometry of the force vectors on the interacting proteins (Figure 2). Here, the two extremes are “unzipping” and “shearing” geometries.44−47 The unzipping geometry typically exhibits slip bond kinetics, while in contrast, the shearing geometry often exhibits catch bond kinetics. At the same force, the dissociation rate is often faster for the unzipping force geometry than for the shearing force geometry. We refer the readers to our recent publications44,46 for the physical principles underlying the effects of pulling geometry on the force-dependent dissociation kinetics.
Figure 2.
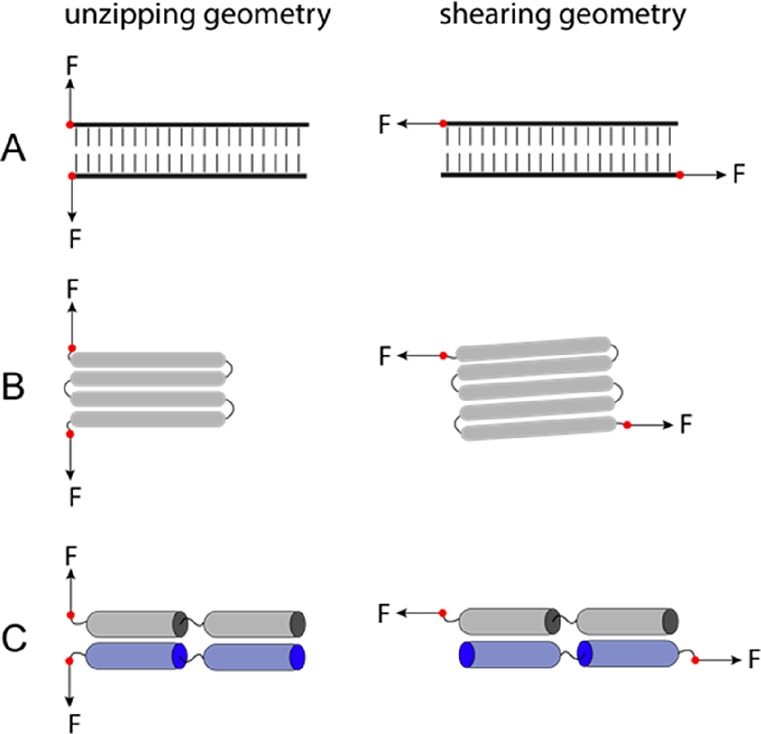
Two force geometries in rupturing/unfolding (A) double-stranded DNA, (B) a protein domain, and (C) a domain–domain interface. The left panel shows the unzipping geometry that typically exhibits slip bond kinetics with a faster dissociation rate. The right panel shows the shearing geometry that typically exhibits catch bond kinetics with a slower dissociation rate.
Intriguingly, many force-bearing protein–protein interactions, such as the integrin–talin connection, the talin–vinculin connection, and the vinculin–actin connection, are under shearing force geometry.43,48−50 These protein–protein interactions form the interfaces in various force-transmission supramolecular linkages in cells, to enable mechanosensing. Perhaps these linkages evolved to achieve high mechanical stability for their functions through making shearing–force connections. In contrast, both force geometries occur frequently in force-dependent unfolding of protein domains. For example, when force is exerted through the N- and C-termini of proteins, Ig domains and α-helix bundles consisting of an odd number of β-strands/α-helices are typically subjected to shearing force geometry, while domains with an even number of β-strands/α-helices are under the unzipping force geometry, as illustrated in Figure 2B.
While important to our understanding of mechanobiology, these two force-dependent kinetic phenomena will be the subject of a subsequent review and will not be considered further here.
Force-Dependent Binding Affinity, Kd(F)
The theoretical description of the dissociation constant defined in the previous section can be extended to include the effects of force dependence.
Two-State Binary Interactions
The
force-dependent affinity
of binary interactions has been discussed previously for simple two-state
interactions,51 where a molecule can exist
in either an unbound state or a bound state. When force is applied
to this target molecule, each state is associated with a force-induced
free energy, which is additional to the free energy change associated
with its ligand. Therefore, the applied force can cause an additional
change in the free energy from the bound to the unbound states, Δg(F) = Δg0 + Δϕ(F), where Δg0 is the binding energy (i.e., the free energy cost of
unbinding) at zero force and Δϕ(F) is
the force-dependent conformational free energy difference between
the unbound and bound states. On the basis of the Boltzmann distribution
of the states and the definition of the dissociation constant, 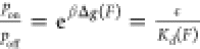 , it is straightforward to see that, for
a simple two-state binary interaction, Kd(F) = Kd0e–βΔϕ(F), where Kd = ce–βΔg0 is the dissociation constant in the
absence of force. Depending on the sign of Δϕ(F), force may increase or decrease the value of the dissociation
constant.
, it is straightforward to see that, for
a simple two-state binary interaction, Kd(F) = Kd0e–βΔϕ(F), where Kd = ce–βΔg0 is the dissociation constant in the
absence of force. Depending on the sign of Δϕ(F), force may increase or decrease the value of the dissociation
constant.
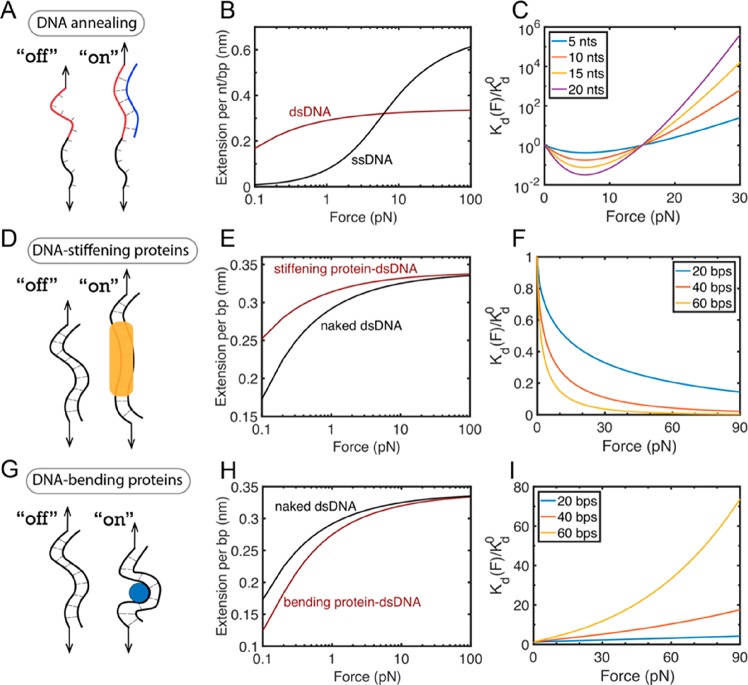
Therefore, the force-dependent affinity of such simple two-state binary interactions is solely determined by Δϕ(F), which can be calculated by the equation Δϕ(F) = −∫0FΔx(f) df. Here Δx(F) = xoff(F) – xon(F) is the extension difference between the unbound state and the bound state of the target molecule at the same applied force.52−54 Over more than a decade of single-molecule manipulation studies, the force–extension curves of many interesting molecules, such as double-stranded DNA (dsDNA), single-stranded DNA (ssDNA), folded protein domains, and unfolded protein peptide chains, have been investigated. Therefore, the Kd(F) of two-state binary interactions can be considered well understood. Figure 3 shows three test-case examples of force-dependent dissociation constants calculated on the basis of the well-characterized force–extension curves of DNA molecules. In each case, a ligand binding causes extension changes of the target DNA molecule at the same applied force (Figure 3B,E,H), which leads to force-dependent binding affinity Kd(F) (Figure 3C,F,I). In each of these scenarios, the strength of the interaction behaves markedly differently when force is exerted.
Figure 3.
Force-dependent dissociation constants, Kd(F), for three examples of two-state binary interactions. (A–C) Test case 1 is DNA annealing. DNA annealing causes a ssDNA to be paired with the complementary ssDNA to form a dsDNA. The change in the force-dependent conformational free energy Δϕ(F) can be explained by the distinct force–extension curves of naked ssDNA and dsDNA, which leads to the force-dependent interaction affinity of DNA annealing. (D–F) Test case 2 is DNA-stiffening protein binding to dsDNA. Force–extension curves of naked dsDNA and the dsDNA bound by a stiffening protein (e.g., H-NS4) that causes an increase in the persistence length of dsDNA from 53 to 174 nm. (G–I) Test case 3 is DNA-bending protein binding to DNA. Force–extension curves of naked dsDNA and dsDNA bound by a bending protein (e.g., IHF9) that causes an effective decrease in persistence length of dsDNA from 53 to 30 nm. Panels C, F, and I show the fold change of force-dependent Kd(F) relative to Kd0 for DNA annealing, the binding of DNA-stiffening protein to dsDNA, and the binding of DNA-bending protein to dsDNA. As each interaction shown in panels B, E, and H results in different effects on the DNA force–extension curves, the force dependence of the binding constant is markedly different.
Binary Interactions Involving Autoinhibition
Many proteins can adopt multiple conformational states, where the binding sites in these proteins are exposed at different levels of force. Autoinhibition is where the native state (i.e., the conformational state with the lowest energy) results in suppression of the accessibility of the binding site. In this scenario, binding can be discussed on the basis of a three-state model, which involves two unbound states (closed state “off,1” and exposed unbound state “off,2”) and one bound state (exposed bound state “on”). In the absence of force, on the basis of the Boltzmann distribution of the three states and the definition of the dissociation constant,
it can be shown that Kd0 = Kd,o(1 + eβμc), where Kd0 is the zero-force dissociation constant of the ligand molecule binding to the target molecule and Kd,o is the zero-force dissociation constant of the exposed binding site in a constitutively open conformation of the target molecule. μc = goff,2 – goff,1 is the autoinhibition energy, which is the chemical potential energy difference between the open conformation and the closed conformation of the target molecule. This reveals that the dissociation constant approximately increases exponentially as the autoinhibition energy increases.
Autoinhibition can be relieved via a number of mechanisms that reduce the value of μc, including biochemical processes such as phosphorylation or binding of an activating molecule.55−58 For force-bearing mechanosensing proteins, mechanical stretching provides another possible means of releasing autoinhibition, which has not been extensively studied in the field. Relief of autoinhibition by mutation is one way to study these processes, as this shifts the autoinhibition dynamics toward a more open conformation, effectively maintaining the protein in an open conformational state. Reducing the value of μc enables the lifetime of the open conformation to be extended as if the protein is under force. This provides an effective way to study protein dynamics that would normally be observed for the wild-type protein only when it is under force.
Here, we provide a succinct discussion of force-dependent release of autoinhibition and its impact on molecular interactions.
A binary interaction involving autoinhibition can still be understood
on the basis of the aforementioned three-state model. The only difference
from the zero-force binding case is that each state now contains an
additional force-dependent conformational free energy. A similar derivation
based on 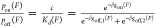 leads to an expression of the
force-dependent
dissociation constant of ligand binding to the autoinhibited target
molecule:
leads to an expression of the
force-dependent
dissociation constant of ligand binding to the autoinhibited target
molecule:
| 1 |
where Δϕ1,2(F) = ϕoff,1(F) – ϕoff,2(F) and Δϕon,2(F) = ϕon(F) – ϕoff,2(F).
Test case 4: ssDNA Binding to an Autoinhibited Region in a dsDNA Hairpin
We demonstrate the application of this equation using a “simple” model system of autoinhibition. Here, the annealing of a short single-stranded DNA (ssDNA) oligo, acting as the “ligand”, binds to a 10-nucleotide complementary region that is buried, cryptic, inside a 20-bp double-stranded DNA (dsDNA) hairpin (Figure 4A). The dsDNA hairpin can exist in two distinct unbound states: a closed hairpin state (state “off,1” in Figure 4A) and an open unzipped state (state “off,2” in Figure 4A). Considering the bound state (state “on” in Figure 4A) where the ligand ssDNA binds to the complementary region of the dsDNA hairpin, there are in total three states that need to be considered. In this case, eq 1 can be directly applied to calculate the force-dependent dissociation constant of ssDNA binding, where the autoinhibition energy, μc, is the base pairing energy in the hairpin. Under physiological conditions, a base pair energy is in the range of 1–4 kBT depending on the nearest-neighbor dinucleotide sequences.59,60 Assuming an average 2 kBT per base pair, for a 20-bp DNA hairpin, μc is around 40 kBT, which completely inhibits binding of the ligand ssDNA. However, such strong autoinhibition can be easily released by forces. On the basis of μc = 40 kBT and the force–extension curves of ssDNA and dsDNA, it is found that forces of ∼15 pN can decrease the dissociation constant (i.e., increase the binding affinity) by more than 1015 fold (Figure 4B).
Figure 4.

Kd(F) for binary interactions involving autoinhibition. (A and B) Test case 4: ssDNA binding to an autoinhibited region in a dsDNA hairpin. (C and D) Test case 5: vinculin D1 domain (red) binding to a VBS (blue) buried within a talin rod domain. Panels B and D show the ratio of force-dependent Kd(F) to Kd,o0 for the ssDNA binding to the dsDNA hairpin (eq 1) and Vd1 binding to a VBS-containing talin domain (eq 2), respectively.
Interestingly, the predicted Kd(F) has a biphasic force dependence, which can be divided into two regions: a monotonically decreasing function at forces below 15 pN due to the force-dependent release of autoinhibition, maximal binding affinity at 15 pN where the binding region is no longer autoinhibited, and a monotonically increasing function at forces above 15 pN due to force-dependent destabilization of the force-bearing DNA duplex.52 Even in this simple model system, the force dependence on the Kd is complex.
Test Case 5: Vinculin D1 Domain Binding to Talin
Another important example of autoinhibition affecting the Kd(F) is the binding of the vinculin D1 domain (Vd1) to a vinculin binding site (VBS) buried in a talin rod α-helical bundle. In the absence of force, the VBS is cryptic in the folded rod domains. In contrast to a dsDNA hairpin that can exist in only two distinct unbound states, an α-helical bundle can exist in three distinct unbound states: an autoinhibited folded state (state “off,1” in Figure 4C), an unfolded state in which the VBS exists in an α-helical conformation (state “off,2” in Figure 4C), and an unfolded state in which the VBS becomes an unstructured peptide polymer (state “off,3” in Figure 4C). Considering the bound state (state “on” in Figure 4C) where Vd1 binds to the α-helical conformation of VBS, there are in total four states that need to be considered. Denoting ε as the chemical potential energy between the unstructured and α-helical conformations of the VBS (broadly equivalent to the stability of one α-helix) and Kd,o0 as the zero-force dissociation constant of Vd1 for the exposed α-helical conformation of VBS, on the basis of a similar analysis of the force-dependent energies of the four states, we can show that
| 2 |
where Δϕ1,2(F) = ϕoff,1(F) – ϕoff,2(F) and Δϕ3,2(F) = ϕoff,3(F) – ϕoff,2(F), which can be computed on the basis of the force–extension curves of the states. Using a fixed μc value of 11 kBT, the fold change of Kd(F) relative to Kd,o0 can be calculated for several values of ε (Figure 4D). At these parameter values, a force of ∼5 pN can decrease the dissociation constant (i.e., increase the binding affinity) of Vd1 for the talin rod α-helical bundle by >10000 fold. In other words, the high autoinhibition energy μc of 11 kBT that limits vinculin binding in the absence of force can be released by a small force of ∼5 pN.
The predicted Kd(F) exhibits an overall biphasic profile, which can be divided into three regions. A monotonically decreasing function at forces of <5 pN resulted from force-dependent release of autoinhibition energy (μc = 11 kBT), an almost force-independent basin region, followed by a monotonically increasing function due to force-dependent destabilization of the α-helical conformation and thus the bound complex.27,34,61 In contrast to the sharp switch from the decreasing profile of Kd(F) to the increasing profile of Kd(F) at ∼15 pN in the case of ssDNA binding to an autoinhibited region in a dsDNA hairpin (Figure 4B), the switch is much less sharp in the case of Vd1 binding to a VBS-containing domain (Figure 4D). Here, after the domain unfolds and autoinhibition is relieved, the VBS binding helix is exposed and has maximal affinity for Vd1 all the while the VBS helix is folded. The more stable the VBS helix, the greater the force range over which binding affinity is maximal. As a result, maximal affinity is present over a range of forces, as seen by the force-independent basin region in Figure 4D with the force range of the basin determined by the stability, ε, of the VBS α-helix.
Mutually Exclusive Binary Interactions Involving Autoinhibition
The previous examples describe the scenarios of the complex force dependence on Kd(F) where the applied force can drastically increase the binding affinity between the target molecule and its ligand by releasing the autoinhibition of the target molecule, thus exposing the binding site(s) for its ligand, and where the applied force can also then decrease the binding affinity by destabilizing the conformation of the bound state.
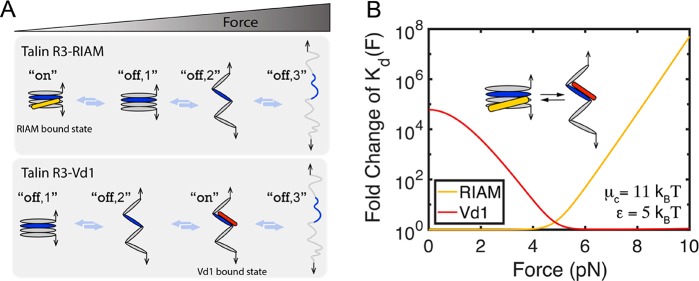
In the case of talin rod domains, these force-dependent components can be multiplexed, to create force-dependent switching of binding partners. The force-dependent switching of binding partners on talin rod domain 3 (R3) provides an example of this (Figure 1). At low forces, the Rap1 effector RIAM binds the α-helical bundle form of R3 where the VBSs are cryptic (Figure 1 and top panel in Figure 5A), whereas at high forces, the autoinhibition of VBSs in R3 is released and exposure of the VBSs significantly increases the binding affinity for Vd1 (Figure 1, Figure 4C,D, and bottom panel in Figure 5A). As such, force drives a change in binding partners.
Figure 5.
Force-dependent switching of Vd1 and RIAM binding to talin R3. (A) Schematics of states involved in R3–RIAM interaction and R3–Vd1 interaction. (B) Fold change in Kd(F) of talin R3–RIAM interaction [the yellow curve shows the ratio of Kd(F) to Kd0 in eq 3] and talin R3–Vd1 interaction [the red curve shows the ratio of Kd(F) to Kd,o in eq 2].
To be specific, the force-dependent binding constants Kd(F) of R3–RIAM interaction and R3–Vd1 interaction can be derived on the basis of a similar analysis of the force-dependent energies of all of the states involved. Via analysis of the four states involved in the R3–RIAM interaction (illustrated in the top panel in Figure 5A), the Kd(F) of R3–RIAM interaction can be derived via
| 3 |
where Kd0 is the zero-force dissociation constant of RIAM for the α-helical bundle form of R3, Δϕ2,1(F) = ϕoff,2(F) – ϕoff,1(F), and Δϕ3,1(F) = ϕoff,3(F) – ϕoff,1(F).
With regard to the R3–Vd1 interaction, there are two VBSs in talin R3, and in such a scenario, a complete description needs to consider the multiple bound states and the effect of volume exclusion. For the sake of simplicity of demonstrating the idea of force-dependent switching of binding partners, here we consider only binding to one VBS in R3. As such, there are one bound state and three unbound states (illustrated in the bottom panel of Figure 5A), and force-dependent dissociation constant Kd(F) of the R3–Vd1 interaction can be directly calculated by eq 2.
In eqs 2 and 3, μc is the chemical potential energy between the α-helical bundle form of R3 and its extended α-helix chain, and ε is the chemical potential energy between the unstructured and α-helical conformations of one α-helix. Using fixed values for μc of 11 kBT and ε of 5 kBT for the purpose of demonstration, the force-dependent switching between R3–RIAM and R3–Vd1 interactions can be shown in Figure 5B.
Measurement of Kd(F) in Experiments
To further explore the impact of forces on the affinity of binary interactions, direct measurement of Kd(F) in experiments will provide a straightforward understanding of the force dependence of binding affinity. This section is devoted to providing a brief discussion of the measurement of Kd(F) in experiments, which includes (i) the measurement of zero-force dissociation constant Kd(0) = Kd0 by bulk technology and (ii) the measurement of dissociation constant under force Kd(F) by single-molecule manipulation technology.
Bulk Technology for Measuring the Kd(0)
There are many methods for biochemically measuring zero-force dissociation constants, which are generally based on two approaches.
The first way to quantify the Kd(0)
is based on the measurement of the bound (αon) or
unbound fraction (αoff) of target molecules through 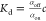 (where c is the ligend
concentration). For example, the electrophoretic mobility shift assay
(EMSA) can be used to quantify protein–DNA interaction. Here,
fluorescence DNA dyes are usually used to label the DNA molecules
that present the DNA targets in the bound and unbound states as two
bands migrating with different speeds in agarose or polyacrylamide
gel.62,63 The bound and unbound fractions are indirectly
estimated on the basis of the intensity ratio of the bands, under
an assumption that the intensity is proportional to the amount of
target molecules in the corresponding bands. Such methods require
an additional assumption that the bound and unbound fractions of the
target molecules remain fixed during the gel shift assay.
(where c is the ligend
concentration). For example, the electrophoretic mobility shift assay
(EMSA) can be used to quantify protein–DNA interaction. Here,
fluorescence DNA dyes are usually used to label the DNA molecules
that present the DNA targets in the bound and unbound states as two
bands migrating with different speeds in agarose or polyacrylamide
gel.62,63 The bound and unbound fractions are indirectly
estimated on the basis of the intensity ratio of the bands, under
an assumption that the intensity is proportional to the amount of
target molecules in the corresponding bands. Such methods require
an additional assumption that the bound and unbound fractions of the
target molecules remain fixed during the gel shift assay.
The
other commonly applied way to quantify the binding affinity
is based on the measurement of the association (kon) and dissociation rates (koff) through 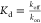 . The surface plasmon resonance
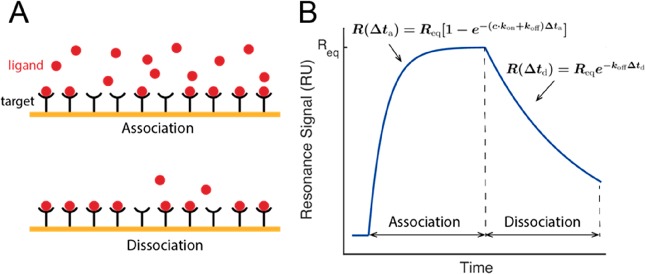
(SPR) technology
is a representative example, which detects binding of ligands to target
molecules tethered on a gold surface based on the binding-induced
shift in the resonant oscillation of conduction electrons (Figure 6A).64,65 In typical experiments (Figure 6B), SPR measures the evolution of the resonance signal
after flowing a ligand-containing solution until it reaches equilibrium.
On the basis of the most commonly used Langmuir model,66,67 this time evolution follows the single-exponential relation R(Δta) = Req[1 – e–(ckon+koff)Δta], where Req is the resonance signal
when the binding and unbinding of ligands reach equilibrium, c is the ligand concentration, and Δta is the time duration after flowing in the ligand-containing
solution. After the removal of the ligand from the solution, the bound
ligands dissociate, resulting in an SPR signal time evolution: R(Δtd) = Reqe–koffΔtd, where Δtd is the duration after the removal of the ligand from the
solution. By fitting the association and dissociation SPR data with
the two equations, one can obtain the values of association and dissociation
rates and thus Kd.
. The surface plasmon resonance
(SPR) technology
is a representative example, which detects binding of ligands to target
molecules tethered on a gold surface based on the binding-induced
shift in the resonant oscillation of conduction electrons (Figure 6A).64,65 In typical experiments (Figure 6B), SPR measures the evolution of the resonance signal
after flowing a ligand-containing solution until it reaches equilibrium.
On the basis of the most commonly used Langmuir model,66,67 this time evolution follows the single-exponential relation R(Δta) = Req[1 – e–(ckon+koff)Δta], where Req is the resonance signal
when the binding and unbinding of ligands reach equilibrium, c is the ligand concentration, and Δta is the time duration after flowing in the ligand-containing
solution. After the removal of the ligand from the solution, the bound
ligands dissociate, resulting in an SPR signal time evolution: R(Δtd) = Reqe–koffΔtd, where Δtd is the duration after the removal of the ligand from the
solution. By fitting the association and dissociation SPR data with
the two equations, one can obtain the values of association and dissociation
rates and thus Kd.
Figure 6.
Quantification of Kd based on measuring kinetic rates in SPR experiments. (A) Schematics of the association and dissociation phase in the Kd measurement. (B) Typical SPR signal. The kinetic rates (kon and koff) and binding affinity (Kd) can be determined by fitting the sensorgram data to an appropriate interaction model.
Besides the EMSA and the SPR assay, a number of other methods have been developed to quantify the binding affinity of molecules based on either measurement of the bound and unbound fractions of target molecules or measurement of the kinetic rates, which include (but are not limited to) fluorescence, fluorescence polarization (FP), nuclear magnetic resonance (NMR), isothermal titration calorimetry (ITC), stopped flow kinetics, etc., and these are discussed elsewhere.68−70 However, these biochemical assays are not applicable for the study of the force dependence of molecular interactions, because they do not apply mechanical constraints to molecules.
Single-Molecule Technology for Measuring Kd(F)
As mentioned above, single-molecule
technologies can also be used to determine the dissociation constant Kd either by quantifying the equilibrium binding
probability pon through the equation 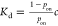 (where c is the ligand
concentration) or by quantifying the association constant kon and the dissociation rate koff through the equation
(where c is the ligand
concentration) or by quantifying the association constant kon and the dissociation rate koff through the equation 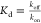 . Most of the single-molecule measurements
of Kd to date have been performed using
technologies such as single-molecule fluorescence imaging71−73 and single-molecule mechanical manipulation.74−77 For the measurement of Kd(F), single-molecule mechanical
manipulation is necessary to apply force to a target molecule and
measure its force-dependent interactions with the ligand. Therefore,
the following section will focus on the measurement of Kd(F) using single-molecule mechanical
manipulation technology.
. Most of the single-molecule measurements
of Kd to date have been performed using
technologies such as single-molecule fluorescence imaging71−73 and single-molecule mechanical manipulation.74−77 For the measurement of Kd(F), single-molecule mechanical
manipulation is necessary to apply force to a target molecule and
measure its force-dependent interactions with the ligand. Therefore,
the following section will focus on the measurement of Kd(F) using single-molecule mechanical
manipulation technology.
Single-molecule mechanical manipulation technologies78 can be categorized into two groups on the basis of the types of mechanical constraints they apply to a molecule. In one group represented by optical tweezers (OT)79 and atomic force microscopy (AFM),80 an external Hookean spring is attached to one end of the tethered molecule and its distance R from the other end of the molecule is controlled (Figure 7, top panel). In the other group, represented by magnetic tweezers (MT),81 centrifuge tweezers,82 and acoustic tweezers,83 an external force is applied to a bead attached to the tethered molecule and the level of force is controlled (Figure 7, bottom panel). Through a force-clamping feedback control, OT and AFM can also apply an external force control to molecules.84,85 To measure the force-dependent dissociation constant Kd(F), it is most convenient to measure the interaction across a range of constant forces.
Figure 7.
Schematics of two typical mechanical constraints applied to a target molecule in single-molecule manipulation technologies.
Because the measurement is performed on a single target molecule, it is desirable to record repetitive binding and unbinding events over a long duration of measurement. This imposes strong requirements on the stability of the instrument over long durations. Magnetic tweezers can make measurements over a time course of hours to days with negligible spatial and force drifts.86,87 The force-dependent binding to, and unbinding from, the mechanically manipulated target molecule can in principle be detected on the basis of integration of single-molecule fluorescence imaging with single-molecule manipulation.88 However, such integration has a drawback of photobleaching, which impairs the long duration measurement for interactions with slow kinetics.
Hence, it is important to develop label-free measurement approaches for detection and quantitation of single-molecular interactions under force. In a force–constraint single-molecule manipulation experiment, the target molecule is tethered between a coverslip surface at one end and a bead at the other end.89,90 A well-controlled stretching force, which can be calibrated at a sub-piconewton resolution, is applied to the target molecule through the bead; the bead height from the surface can be measured at nanometer resolution. Hence, it can detect molecular extension changes of a few nanometers. Utilizing this spatial resolution, label-free measurement of single-molecule interaction under force can be based on detecting (i) binding-induced deformation of the target molecule (Figure 8A,B) or (ii) binding-induced delay to a structural transition (Figure 8C,D). These two label-free detection approaches, discussed in the next section, have been applied in a number of recent studies to detect DNA–protein76,77,91,92 and protein–protein interactions.27,34 More recently, these detection approaches have been further developed to quantify the dissociation constant Kd(F).76,77
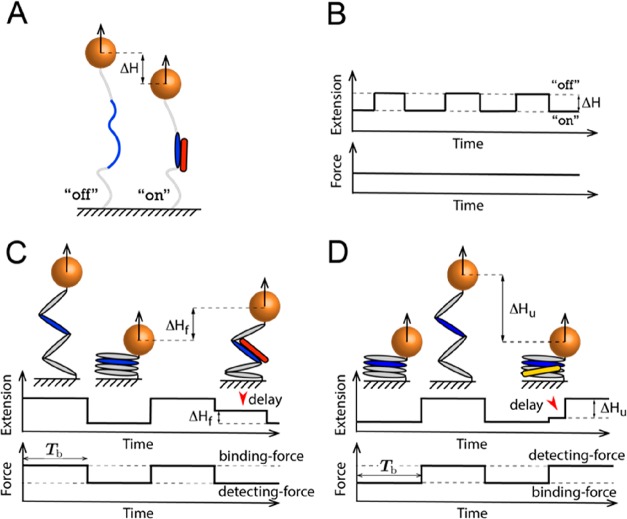
Figure 8.
Two typical label-free single-molecule manipulation detection approaches. (A and B) Schematics of detection based on ligand binding-induced target molecule deformation that causes a detectable extension change, ΔH, at a constant force. (C and D) Schematics of detection based on the delayed structural transition of the target molecule arising from the presence of a bound ligand. (C) A ligand bound on a mechanically exposed binding site at a higher force causes a delay in refolding after a force jump to a lower force. (D) A ligand bound on a folded structure at a lower force causes a delay in unfolding after a force jump to a higher force.
Detection Based on Target Molecule Deformation
Ligand
binding can be probed on the basis of the changes in the end-to-end
extension resulting from binding-induced structural transition or
deformation of the binding site (Figure 8A,B). This approach is suitable for ligands
that induce a detectable change in the extension of the tethered molecule.
An example of this is the interaction between Vd1 and the mechanically
exposed VBS in talin R327 and α-catenin.34 At forces of >15 pN, the exposed VBS exists
in a randomly coiled peptide conformation. Binding of Vd1 induces
the formation of the α-helical conformation of the VBS, resulting
in a detectable stepwise extension decrease of 2–3 nm depending
on the applied force. Similarly, when Vd1 dissociates, it will be
accompanied by a 2–3 nm stepwise extension increase (Figure 8A,B). This 2–3
nm step provides a visible and quantifiable readout of ligand binding
and unbinding. From the time trace of such two-state stepwise extension
fluctuation, the association and dissociation rates can be determined
by obtaining the dwell time in bound and unbound states; therefore,
the force-dependent dissociation constant can be determined by the
equation 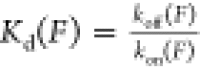 .
.
Detection Based on Delayed Structural Transitions
A bound ligand on a target molecule can also be detected if binding results in a delayed structural transition. This can be (i) delayed refolding if the ligand is bound on an unfolded structure via an exposed binding site (Figure 8C) and (ii) delayed unfolding if the ligand is bound on a folded structure (Figure 8D).
An example of delayed protein refolding due to ligand binding is the interaction between Vd1 and VBS in talin rod and α-catenin domains.27,34,35 Previous studies from our group have shown that Vd1 bound on the mechanically exposed VBS in the domains can keep the domains in the unfolded conformation for a longer duration after force is released, compared with in the absence of Vd1. This resulting longer extension (Figure 8C) can be detected and quantified.
A ligand bound on a folded target molecule can be detected similarly (Figure 8D). As the structural unfolding of the target molecule can happen only after the ligand dissociates, ligand binding can stabilize the target, which often results in a slower unfolding transition. Thus, if the ligand results in a detectable delay in the unfolding transition after jumping to a higher force, it becomes a readout on whether the target molecule is bound by a ligand or not right before the force jump. While delayed unfolding has mainly been applied to quantify protein–DNA interactions,77,91,92 the same principle can be utilized to detect ligand binding to a protein domain (e.g., RIAM binding to talin R3) and thereby quantify the force-dependent dissociation constant.
On the basis of these delayed structural transitions, the bound
and unbound states of the target molecule can be determined, which
enables the determination of the equilibrium binding probability pon(F) using a force jump assay.
In such an assay (Figure 8C,D), many cycles of force jump between two force levels are
used: (i) a binding force (F) at which the target
binding site is stable for a duration of 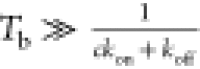 to
ensure binding equilibrium and (ii)
a detecting force at which the binding-induced delayed structural
transition can be observed. The probability of binding is then determined
by the ratio of the number of cycles where binding is detected (M) to the total number of cycles (N):
to
ensure binding equilibrium and (ii)
a detecting force at which the binding-induced delayed structural
transition can be observed. The probability of binding is then determined
by the ratio of the number of cycles where binding is detected (M) to the total number of cycles (N): 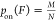 . From this, the force-dependent dissociation
constant can be determined with the equation
. From this, the force-dependent dissociation
constant can be determined with the equation 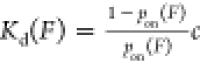 , where c is the ligand
concentration.
, where c is the ligand
concentration.
Discussion
In this short review, we have sought to provide a brief discussion of some of the force-dependent considerations at the heart of mechanobiology and outline some of the strategies for measuring and studying them. The requirement to consider the force dependence of binding constants in biology necessitates development of the existing mathematical descriptions of binding constants to include mechanical descriptors. In addition, we discuss the novel experimental approaches required to measure them.
The examples of force-dependent binding events illustrated in Figures 3–5 highlight some of the diverse and ingenious ways that biological systems sense, and respond to, forces. Even in these simplified in vitro systems, it is evident that the ways in which binding constants in each scenario are affected by force are complex and often biphasic. The consequence of these complex force dependencies is that the binding affinities between two ligands can change, either increasing or decreasing, by ≥1000 fold dynamically over a physiological force range. This creates incredible complexity in these mechanical linkages, with the same components assembling differently in different force environments.
Multivalent Interaction
Our review of the force-dependent affinity has been developed on the basis of single-site binary interactions. In many cases, such as antibody–antigen interactions, however, multivalent interactions play a crucial role in biological functions. In such cases, the binding strength of multivalent interactions cannot be formulated on the basis of a two-state model. The binding strength or the functional activity of such multivalent interactions is often termed “avidity”. Such multivalent interactions are also implicated in mechanosensing reactions. For example, talin contains 11 VBS.35 When multiple VBSs in talin are mechanically exposed for binding to vinculin, the functional activity of the force-dependent talin–vinculin interaction is expected to be further boosted.
Multiplexing Force-Dependent Factors
A hint about the immense amount of information that can be encoded by such mechanosensitive complexes is evident when you consider these principles in a simple two-component system and the multiplexing of the multiple force-dependent contributions that can emerge. Take, for example, the mechanosensitive interactions between talin and vinculin at the core of the focal adhesion. There is the well-documented force dependence of the exposure of cryptic VBS from within the core of the folded talin bundles discussed above. Above a certain threshold, talin bundles unfold exposing cryptic VBS and allowing vinculin to bind. The description in Figure 4 presents a single VBS binding a single vinculin. However, talin contains 11 VBS, and the mechanical response of talin is complex,35 with diverse force thresholds governing exposure of each VBS. This setup is further impacted by additional force-dependent considerations.
For instance, both talin and vinculin are further regulated by autoinhibition, and in both cases, the affinity of the autoinhibition (which is a head–tail interaction) is reduced when the protein is under force; here, the effective binding constant of the autoinhibition is massively increased as the two interacting domains (the head and the tail) are physically held apart from each other (Figure 1). As such, layers upon layers of inhibition exist on these molecules all exhibiting force dependence.93 The forces exerted on talin change constantly, and if the force decreases, then the talin rod domain and the head tail autoinhibition will have a higher effective affinity (they will no longer be held apart from each other) and can be trying to revert back to their closed inactive conformations.
There is also considerable hysteresis on talin domain refolding.25,35 A domain that unfolds at 15 pN will not refold when the force drops to <15 pN; instead, it requires forces of <3 pN to refold on a reasonable time scale. When refolding of the talin domains occurs, it will affect the exposure and thus the affinity of the talin–vinculin interactions. With up to 11 VBS in talin, many force linkages can be coupled.
However, additional force dependence is introduced by the connectivity of vinculin with the actin filaments. If vinculin engages talin via its head domain and couples to actin via its tail domain, then this will exert force on the talin–vinculin interaction, which will affect the affinity, and as the geometry of this force on the VBS–vinculin interaction is likely to be shearing force geometry, it means that force will strengthen this interaction (with catch bond kinetics). In addition, tethering vinculin to talin and actin also restricts vinculin autoinhibition, so the effective Kd of vinculin autoinhibition is also greatly increased, which will further enhance the VBS–vinculin interaction.
This description is complex but still does not include the potential force dependence of unfolding of vinculin domains, the strength of the talin linkages with the integrin and actin, or the recruitment, or displacement, of factors as a result of domain unfolding that might enhance or decrease contractility. All of these will further augment the mechanical connections. Therefore, even within this simplified description of the system, there are almost endless possibilities for diverse outcomes. When you layer on the myriad of other mechanoeffectors and regulators that assemble on this hyperplastic framework, it becomes apparent that there is a huge capacity in these linkages to encode vast amounts of data.25
Future Perspective
This review is centered around the molecular interactions involved in mechanosensing, with a focus on how force applied to a molecule may influence the affinity with its binding partners. In addition, the review also briefly discusses how force applied to interacting partners may affect the lifetime of the complex.
What has been missed in these discussions is how force applied to one molecule affects the binding and unbinding rates of its binding partners in solution. Because force can drastically change the affinity of the interaction, it should have a significant influence on the binding rate, the unbinding rate, or both. Compared to force-dependent affinity, the force-dependent kinetics of binary interactions have not been as extensively studied and remain less well understood. A deeper understanding of the force-dependent interaction kinetics is required because in cells many interactions do not reach equilibrium. The force-dependent reaction rates will provide crucial insights into how non-equilibrium molecular interactions under mechanical force in cells can be understood.
Another interesting topic, which is not included here, is how other types of mechanical constraints may affect interactions. Cytoskeleton filaments, such as actin filaments, are often subjected not only to tensile force but also to rotational constraint.94 The latter will result in torque in the filament, which is transmitted to the proteins, such as formin or other actin capping proteins, linked to the end of the actin filaments.95 Another example is that DNA in many topologically isolated chromatin domains is supercoiled, which also results in torque applied to the DNA.96,97 How torque may affect the affinity and the kinetics of the molecular interactions is currently poorly understood, which should be another interesting future direction.
The rapid advances in the field of mechanobiology are making great strides in advancing our understanding of these complex mechanosensing signaling systems.
Model and Parameters of Force–Extension Curves of Target Molecules
Two-State Binary Interactions. Single-stranded DNA
(ssDNA) is described by the worm-like chain (WLC) polymer model that
contains two parameters, bending persistence length AssDNA and contour length L = nntlnt, where nnt is the number of nucleotides. ssDNA has a
persistence length AssDNA of ∼0.7
nm and a contour length per nucleotide lnt of ∼0.7 nm.98 On the basis of
the WLC model, the force–extension curve of ssDNA xssDNA(F) can be obtained by solving the
inverse function of the Marko–Siggia formula:99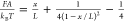 .
.
Double-stranded DNA (dsDNA) is described by the WLC model where the dsDNA has a persistence length AdsDNA of ∼50 nm and a contour length per base pair lbp of ∼0.34 nm.100 Similarly, the force–extension curve of dsDNA xdsDNA(F) can be obtained by solving the inverse function of the Marko–Siggia formula.
Stiffening protein–dsDNA and bending protein–dsDNA are both described by the WLC model where the only difference compared with the naked dsDNA is the bending persistence length. In panels E and F of Figure 3, the bending persistence length of stiffening protein–dsDNA (Asf–dsDNA) is taken to be ∼174 nm, which is adapted from the case of H-NS binding.4 In panels H and I of Figure 3, the bending persistence length of bending protein–dsDNA (Abd–dsDNA) is taken to be ∼30 nm, which is adapted from the case of IHF binding.9
Binary Interactions Involving Autoinhibition. The
dsDNA hairpin is described by the rigid body with a size Lhp of ∼2 nm, which is the width of dsDNA.101 Its force–extension curve is 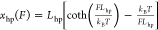 .
.
The α-helical bundle is described by the rigid body with a size Lbd of ∼3.4 nm, which is the N-terminus–C-terminus distance obtained from talin R10 (Protein Data Bank entry 2KVP).102
The α-helical
chain is described by the freely jointed chain
(FJC) polymer model where contour length Lahc = nahLah, where nah is the number of α-helices
and Lah is the size of each α-helix.
In Figures 4D and 5B, fixed values of nah and Lah are taken to be 4 and 4.8 nm,
respectively.102 Its force–extension
curve is 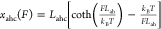 .
.
The α-helix form of VBS is described by the rigid body where size Lah,VBS = NVBSlah,aa, where NVBS = 25 is the number of amino acids in VBS103 and lah,aa = 0.15 nm is the extension per amino acid in the form of an α-helix.104,105
The unstructured peptide chain is described by the WLC model where the peptide chain has a persistence length Apt of ∼0.8 nm and a contour length per amino acid laa of ∼0.38 nm.106 Similarly, the force–extension curve of peptide chain xpt(F) can be obtained by solving the inverse function of the Marko–Siggia formula.
B.T.G. is funded by Biotechnology and Biological Sciences Research Council Grants BB/N007336/1 and BB/S007245/1. J.Y. and Y.W. are funded by the National Research Foundation (NRF), Prime Minister’s Office, Singapore, under its NRF Investigatorship Program (NRF Investigatorship Award NRF-NRFI2016-03) and by the Singapore Ministry of Education Academic Research Fund Tier1. B.T.G. and J.Y. are funded by Human Frontier Science Program Grant RGP00001/2016.
The authors declare no competing financial interest.
References
- Thompson D. W. (1942) On growth and form, Cambridge University Press. [Google Scholar]
- Turner C. H.; Pavalko F. M. (1998) Mechanotransduction and functional response of the skeleton to physical stress: the mechanisms and mechanics of bone adaptation. J. Orthop. Sci. 3, 346–355. 10.1007/s007760050064. [DOI] [PubMed] [Google Scholar]
- Owens G. K. (1996) Role of mechanical strain in regulation of differentiation of vascular smooth muscle cells. Circ. Res. 79, 1054–1055. 10.1161/01.RES.79.5.1054. [DOI] [PubMed] [Google Scholar]
- Lim C. J.; Lee S. Y.; Kenney L. J.; Yan J. (2012) Nucleoprotein filament formation is the structural basis for bacterial protein H-NS gene silencing. Sci. Rep. 2, 509. 10.1038/srep00509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardel M. L.; Schneider I. C.; Aratyn-Schaus Y.; Waterman C. M. (2010) Mechanical integration of actin and adhesion dynamics in cell migration. Annu. Rev. Cell Dev. Biol. 26, 315–333. 10.1146/annurev.cellbio.011209.122036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engler A. J.; Sen S.; Sweeney H. L.; Discher D. E. (2006) Matrix elasticity directs stem cell lineage specification. Cell 126, 677–689. 10.1016/j.cell.2006.06.044. [DOI] [PubMed] [Google Scholar]
- Ulrich T. A.; de Juan Pardo E. M.; Kumar S. (2009) The mechanical rigidity of the extracellular matrix regulates the structure, motility, and proliferation of glioma cells. Cancer Res. 69, 4167–4174. 10.1158/0008-5472.CAN-08-4859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Discher D. E.; Janmey P.; Wang Y.-l. (2005) Tissue cells feel and respond to the stiffness of their substrate. Science 310, 1139–1143. 10.1126/science.1116995. [DOI] [PubMed] [Google Scholar]
- Lin J.; Chen H.; Dröge P.; Yan J. (2012) Physical organization of DNA by multiple non-specific DNA-binding modes of integration host factor (IHF). PLoS One 7, e49885 10.1371/journal.pone.0049885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iskratsch T.; Wolfenson H.; Sheetz M. P. (2014) Appreciating force and shape—the rise of mechanotransduction in cell biology. Nat. Rev. Mol. Cell Biol. 15, 825. 10.1038/nrm3903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogel V.; Sheetz M. (2006) Local force and geometry sensing regulate cell functions. Nat. Rev. Mol. Cell Biol. 7, 265. 10.1038/nrm1890. [DOI] [PubMed] [Google Scholar]
- Vogel V. (2018) Unraveling the mechanobiology of extracellular matrix. Annu. Rev. Physiol. 80, 353–387. 10.1146/annurev-physiol-021317-121312. [DOI] [PubMed] [Google Scholar]
- Ingber D. (2003) Mechanobiology and diseases of mechanotransduction. Ann. Med. 35, 564–577. 10.1080/07853890310016333. [DOI] [PubMed] [Google Scholar]
- Baratchi S.; Khoshmanesh K.; Woodman O. L.; Potocnik S.; Peter K.; McIntyre P. (2017) Molecular sensors of blood flow in endothelial cells. Trends Mol. Med. 23, 850–868. 10.1016/j.molmed.2017.07.007. [DOI] [PubMed] [Google Scholar]
- Beck F.-X.; Burger-Kentischer A.; Müller E. (1998) Cellular response to osmotic stress in the renal medulla. Pfluegers Arch. 436, 814–827. 10.1007/s004240050710. [DOI] [PubMed] [Google Scholar]
- Kull F. J.; Endow S. A. (2013) Force generation by kinesin and myosin cytoskeletal motor proteins. J. Cell Sci. 126, 9–19. 10.1242/jcs.103911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grashoff C.; Hoffman B. D.; Brenner M. D.; Zhou R.; Parsons M.; Yang M. T.; McLean M. A.; Sligar S. G.; Chen C. S.; Ha T.; Schwartz M. A. (2010) Measuring mechanical tension across vinculin reveals regulation of focal adhesion dynamics. Nature 466, 263. 10.1038/nature09198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Margadant F.; Chew L. L.; Hu X.; Yu H.; Bate N.; Zhang X.; Sheetz M. (2011) Mechanotransduction in vivo by repeated talin stretch-relaxation events depends upon vinculin. PLoS Biol. 9, e1001223 10.1371/journal.pbio.1001223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riveline D.; Zamir E.; Balaban N. Q.; Schwarz U. S.; Ishizaki T.; Narumiya S.; Kam Z.; Geiger B.; Bershadsky A. D. (2001) Focal contacts as mechanosensors: externally applied local mechanical force induces growth of focal contacts by an mDia1-dependent and ROCK-independent mechanism. J. Cell Biol. 153, 1175–1186. 10.1083/jcb.153.6.1175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang W.; Lang M. J. (2009) Mechanical design of translocating motor proteins. Cell Biochem. Biophys. 54, 11–22. 10.1007/s12013-009-9049-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartman M. A.; Spudich J. A. (2012) The myosin superfamily at a glance. J. Cell Sci. 125, 1627–1632. 10.1242/jcs.094300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sellers J. R. (2000) Myosins: a diverse superfamily. Biochim. Biophys. Acta, Mol. Cell Res. 1496, 3–22. 10.1016/S0167-4889(00)00005-7. [DOI] [PubMed] [Google Scholar]
- Tokuo H.; Ikebe M. (2004) Myosin X transports Mena/VASP to the tip of filopodia. Biochem. Biophys. Res. Commun. 319, 214–220. 10.1016/j.bbrc.2004.04.167. [DOI] [PubMed] [Google Scholar]
- Bohil A. B.; Robertson B. W.; Cheney R. E. (2006) Myosin-X is a molecular motor that functions in filopodia formation. Proc. Natl. Acad. Sci. U. S. A. 103, 12411–12416. 10.1073/pnas.0602443103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goult B. T.; Yan J.; Schwartz M. A. (2018) Talin as a mechanosensitive signaling hub. J. Cell Biol. 217, 3776–3784. 10.1083/jcb.201808061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goult B. T.; Zacharchenko T.; Bate N.; Tsang R.; Hey F.; Gingras A. R.; Elliott P. R.; Roberts G. C. K.; Ballestrem C.; Critchley D. R.; Barsukov I. L. (2013) RIAM and vinculin binding to talin are mutually exclusive and regulate adhesion assembly and turnover. J. Biol. Chem. 288, 8238–8249. 10.1074/jbc.M112.438119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao M.; Goult B. T.; Chen H.; Cong P.; Sheetz M. P.; Yan J. (2015) Mechanical activation of vinculin binding to talin locks talin in an unfolded conformation. Sci. Rep. 4, 4610. 10.1038/srep04610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papagrigoriou E.; Gingras A. R.; Barsukov I. L.; Bate N.; Fillingham I. J.; Patel B.; Frank R.; Ziegler W. H.; Roberts G. C. K.; Critchley D. R.; Emsley J. (2004) Activation of a vinculin-binding site in the talin rod involves rearrangement of a five-helix bundle. EMBO J. 23, 2942–2951. 10.1038/sj.emboj.7600285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goksoy E.; Ma Y.-Q.; Wang X.; Kong X.; Perera D.; Plow E. F.; Qin J. (2008) Structural Basis for the Autoinhibition of Talin in Regulating Integrin Activation. Mol. Cell 31, 124–133. 10.1016/j.molcel.2008.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goult B. T.; Bate N.; Anthis N. J.; Wegener K. L.; Gingras A. R.; Patel B.; Barsukov I. L.; Campbell I. D.; Roberts G. C. K.; Critchley D. R. (2009) The Structure of an Interdomain Complex That Regulates Talin Activity. J. Biol. Chem. 284, 15097. 10.1074/jbc.M900078200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goult B. T.; Xu X.-P.; Gingras A. R.; Swift M.; Patel B.; Bate N.; Kopp P. M.; Barsukov I. L.; Critchley D. R.; Volkmann N.; Hanein D. (2013) Structural studies on full-length talin1 reveal a compact auto-inhibited dimer: Implications for talin activation. J. Struct. Biol. 184, 21–32. 10.1016/j.jsb.2013.05.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bakolitsa C.; Cohen D. M.; Bankston L. A.; Bobkov A. A.; Cadwell G. W.; Jennings L.; Critchley D. R.; Craig S. W.; Liddington R. C. (2004) Structural basis for vinculin activation at sites of cell adhesion. Nature 430, 583–586. 10.1038/nature02610. [DOI] [PubMed] [Google Scholar]
- Borgon R. A.; Vonrhein C.; Bricogne G.; Bois P. R. J.; Izard T. (2004) Crystal Structure of Human Vinculin. Structure 12, 1189–1197. 10.1016/j.str.2004.05.009. [DOI] [PubMed] [Google Scholar]
- Yao M.; Qiu W.; Liu R.; Efremov A. K.; Cong P.; Seddiki R.; Payre M.; Lim C. T.; Ladoux B.; Mege R. M.; Yan J. (2014) Force-dependent conformational switch of alpha-catenin controls vinculin binding. Nat. Commun. 5, 4525. 10.1038/ncomms5525. [DOI] [PubMed] [Google Scholar]
- Yao M.; Goult B. T.; Klapholz B.; Hu X.; Toseland C. P.; Guo Y.; Cong P.; Sheetz M. P.; Yan J. (2016) The mechanical response of talin. Nat. Commun. 7, 11966. 10.1038/ncomms11966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marshall B. T.; Long M.; Piper J. W.; Yago T.; McEver R. P.; Zhu C. (2003) Direct observation of catch bonds involving cell-adhesion molecules. Nature 423, 190. 10.1038/nature01605. [DOI] [PubMed] [Google Scholar]
- Thomas W. E.; Trintchina E.; Forero M.; Vogel V.; Sokurenko E. V. (2002) Bacterial adhesion to target cells enhanced by shear force. Cell 109, 913–923. 10.1016/S0092-8674(02)00796-1. [DOI] [PubMed] [Google Scholar]
- Dembo M.; Torney D.; Saxman K.; Hammer D. (1988) The reaction-limited kinetics of membrane-to-surface adhesion and detachment. Proc. R. Soc. B 234, 55–83. 10.1098/rspb.1988.0038. [DOI] [PubMed] [Google Scholar]
- Thomas W. E.; Vogel V.; Sokurenko E. (2008) Biophysics of catch bonds. Annu. Rev. Biophys. 37, 399–416. 10.1146/annurev.biophys.37.032807.125804. [DOI] [PubMed] [Google Scholar]
- Manibog K.; Li H.; Rakshit S.; Sivasankar S. (2014) Resolving the molecular mechanism of cadherin catch bond formation. Nat. Commun. 5, 3941. 10.1038/ncomms4941. [DOI] [PubMed] [Google Scholar]
- Doggett T. A.; Girdhar G.; Lawshé A.; Schmidtke D. W.; Laurenzi I. J.; Diamond S. L.; Diacovo T. G. (2002) Selectin-like kinetics and biomechanics promote rapid platelet adhesion in flow: the GPIbα-vWF tether bond. Biophys. J. 83, 194–205. 10.1016/S0006-3495(02)75161-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beste M. T.; Hammer D. A. (2008) Selectin catch–slip kinetics encode shear threshold adhesive behavior of rolling leukocytes. Proc. Natl. Acad. Sci. U. S. A. 105, 20716–20721. 10.1073/pnas.0808213105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang D. L.; Bax N. A.; Buckley C. D.; Weis W. I.; Dunn A. R. (2017) Vinculin forms a directionally asymmetric catch bond with F-actin. Science 357, 703–706. 10.1126/science.aan2556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan G.; Le S.; Yao M.; Qian H.; Zhou X.; Yan J.; Chen H. (2017) Elasticity of the Transition State Leading to an Unexpected Mechanical Stabilization of Titin Immunoglobulin Domains. Angew. Chem., Int. Ed. 56, 5490–5493. 10.1002/anie.201700411. [DOI] [PubMed] [Google Scholar]
- Guo S.; Tang Q.; Yao M.; You H.; Le S.; Chen H.; Yan J. (2018) Structural-elastic determination of the force-dependent transition rate of biomolecules. Chem. Sci. 9, 5871–5882. 10.1039/C8SC01319E. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo S.; Efremov A. K.; Yan J. (2019) Understanding the catch-bond kinetics of biomolecules on a one-dimensional energy landscape. Commun. Chem. 2, 30. 10.1038/s42004-019-0131-6. [DOI] [Google Scholar]
- Yan J.; Yao M.; Goult B. T.; Sheetz M. P. (2015) Talin dependent mechanosensitivity of cell focal adhesions. Cell. Mol. Bioeng. 8, 151–159. 10.1007/s12195-014-0364-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anthis N. J; Wegener K. L; Ye F.; Kim C.; Goult B. T; Lowe E. D; Vakonakis I.; Bate N.; Critchley D. R; Ginsberg M. H; Campbell I. D (2009) The structure of an integrin/talin complex reveals the basis of inside-out signal transduction. EMBO J. 28, 3623–3632. 10.1038/emboj.2009.287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izard T.; Vonrhein C. (2004) Structural basis for amplifying vinculin activation by talin. J. Biol. Chem. 279, 27667–27678. 10.1074/jbc.M403076200. [DOI] [PubMed] [Google Scholar]
- Kim L. Y.; Thompson P. M.; Lee H. T.; Pershad M.; Campbell S. L.; Alushin G. M. (2016) The structural basis of actin organization by vinculin and metavinculin. J. Mol. Biol. 428, 10–25. 10.1016/j.jmb.2015.09.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marko J. F.; Siggia E. D. (1997) Driving proteins off DNA using applied tension. Biophys. J. 73, 2173–2178. 10.1016/S0006-3495(97)78248-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouzina I.; Bloomfield V. A. (2001) Force-induced melting of the DNA double helix 1. Thermodynamic analysis. Biophys. J. 80, 882–893. 10.1016/S0006-3495(01)76067-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouzina I.; Bloomfield V. A. (2001) Force-induced melting of the DNA double helix. 2. Effect of solution conditions. Biophys. J. 80, 894–900. 10.1016/S0006-3495(01)76068-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cocco S.; Yan J.; Leger J. F.; Chatenay D.; Marko J. F. (2004) Overstretching and force-driven strand separation of double-helix DNA. Phys. Rev. E 70, 011910. 10.1103/PhysRevE.70.011910. [DOI] [PubMed] [Google Scholar]
- Dou H.; Buetow L.; Hock A.; Sibbet G. J.; Vousden K. H.; Huang D. T. (2012) Structural basis for autoinhibition and phosphorylation-dependent activation of c-Cbl. Nat. Struct. Mol. Biol. 19, 184. 10.1038/nsmb.2231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gresset A.; Hicks S. N.; Harden T. K.; Sondek J. (2010) Mechanism of phosphorylation-induced activation of phospholipase C-gamma isozymes. J. Biol. Chem. 285, 35836–35847. 10.1074/jbc.M110.166512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen H.; Choudhury D. M.; Craig S. W. (2006) Coincidence of Actin Filaments and Talin Is Required to Activate Vinculin. J. Biol. Chem. 281, 40389. 10.1074/jbc.M607324200. [DOI] [PubMed] [Google Scholar]
- Bois P. R. J.; O’Hara B. P.; Nietlispach D.; Kirkpatrick J.; Izard T. (2006) The Vinculin Binding Sites of Talin and a-Actinin Are Sufficient to Activate Vinculin. J. Biol. Chem. 281, 7228–7236. 10.1074/jbc.M510397200. [DOI] [PubMed] [Google Scholar]
- Santa Lucia J. Jr.; Hicks D. (2004) The thermodynamics of DNA structural motifs. Annu. Rev. Biophys. Biomol. Struct. 33, 415–440. 10.1146/annurev.biophys.32.110601.141800. [DOI] [PubMed] [Google Scholar]
- SantaLucia J. Jr. (1998) A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc. Natl. Acad. Sci. U. S. A. 95, 1460–1465. 10.1073/pnas.95.4.1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao Y.; Zorman S.; Gundersen G.; Xi Z.; Ma L.; Sirinakis G.; Rothman J. E.; Zhang Y. (2012) Single reconstituted neuronal SNARE complexes zipper in three distinct stages. Science 337, 1340–1343. 10.1126/science.1224492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fried M.; Crothers D. M. (1981) Equilibria and kinetics of lac repressor-operator interactions by polyacrylamide gel electrophoresis. Nucleic Acids Res. 9, 6505–6525. 10.1093/nar/9.23.6505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heffler M. A.; Walters R. D.; Kugel J. F. (2012) Using electrophoretic mobility shift assays to measure equilibrium dissociation constants: GAL4-p53 binding DNA as a model system. Biochem. Mol. Biol. Educ. 40, 383–387. 10.1002/bmb.20649. [DOI] [PubMed] [Google Scholar]
- Fägerstam L. G.; Frostell-Karlsson Å.; Karlsson R.; Persson B.; Rönnberg I. (1992) Biospecific interaction analysis using surface plasmon resonance detection applied to kinetic, binding site and concentration analysis. Journal of Chromatography A 597, 397–410. 10.1016/0021-9673(92)80137-J. [DOI] [PubMed] [Google Scholar]
- Nguyen H.; Park J.; Kang S.; Kim M. (2015) Surface plasmon resonance: a versatile technique for biosensor applications. Sensors 15, 10481–10510. 10.3390/s150510481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oshannessy D. J.; Brighamburke M.; Soneson K. K.; Hensley P.; Brooks I. (1993) Determination of rate and equilibrium binding constants for macromolecular interactions using surface plasmon resonance: use of nonlinear least squares analysis methods. Anal. Biochem. 212, 457–468. 10.1006/abio.1993.1355. [DOI] [PubMed] [Google Scholar]
- Langmuir I. (1916) The constitution and fundamental properties of solids and liquids. Part I. Solids. J. Am. Chem. Soc. 38, 2221–2295. 10.1021/ja02268a002. [DOI] [Google Scholar]
- Pollard T. D. (2010) A guide to simple and informative binding assays. Mol. Biol. Cell 21, 4061–4067. 10.1091/mbc.e10-08-0683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fielding L. (2003) NMR methods for the determination of protein-ligand dissociation constants. Curr. Top. Med. Chem. 3, 39–53. 10.2174/1568026033392705. [DOI] [PubMed] [Google Scholar]
- Williams M. (2016) Protein-Ligand Interactions, Humana Press, Totowa, NJ. [Google Scholar]
- Wang Y.; Guo L.; Golding I.; Cox E. C.; Ong N. (2009) Quantitative transcription factor binding kinetics at the single-molecule level. Biophys. J. 96, 609–620. 10.1016/j.bpj.2008.09.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowen M. E.; Weninger K.; Ernst J.; Chu S.; Brunger A. T. (2005) Single-molecule studies of synaptotagmin and complexin binding to the SNARE complex. Biophys. J. 89, 690–702. 10.1529/biophysj.104.054064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Oijen A. M. (2011) Single-molecule approaches to characterizing kinetics of biomolecular interactions. Curr. Opin. Biotechnol. 22, 75–80. 10.1016/j.copbio.2010.10.002. [DOI] [PubMed] [Google Scholar]
- Cao Y.; Balamurali M.; Sharma D.; Li H. (2007) A functional single-molecule binding assay via force spectroscopy. Proc. Natl. Acad. Sci. U. S. A. 104, 15677–15681. 10.1073/pnas.0705367104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleimann C.; Sischka A.; Spiering A.; Tönsing K.; Sewald N.; Diederichsen U.; Anselmetti D. (2009) Binding kinetics of bisintercalator Triostin a with optical tweezers force mechanics. Biophys. J. 97, 2780–2784. 10.1016/j.bpj.2009.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le S.; Chen H.; Cong P.; Lin J.; Dröge P.; Yan J. (2013) Mechanosensing of DNA bending in a single specific protein-DNA complex. Sci. Rep. 3, 3508. 10.1038/srep03508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gulvady R.; Gao Y.; Kenney L. J.; Yan J. (2018) A single molecule analysis of H-NS uncouples DNA binding affinity from DNA specificity. Nucleic Acids Res. 46, 10216–10224. 10.1093/nar/gky826. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neuman K. C.; Nagy A. (2008) Single-molecule force spectroscopy: optical tweezers, magnetic tweezers and atomic force microscopy. Nat. Methods 5, 491. 10.1038/nmeth.1218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moffitt J. R.; Chemla Y. R.; Smith S. B.; Bustamante C. (2008) Recent advances in optical tweezers. Annu. Rev. Biochem. 77, 205–228. 10.1146/annurev.biochem.77.043007.090225. [DOI] [PubMed] [Google Scholar]
- Zlatanova J.; Lindsay S. M.; Leuba S. H. (2001) Single molecule force spectroscopy in biology using the atomic force microscope. Prog. Biophys. Mol. Biol. 74, 37–61. 10.1016/B978-008044031-6/50031-8. [DOI] [PubMed] [Google Scholar]
- De Vlaminck I.; Dekker C. (2012) Recent advances in magnetic tweezers. Annu. Rev. Biophys. 41, 453–472. 10.1146/annurev-biophys-122311-100544. [DOI] [PubMed] [Google Scholar]
- Yang D.; Ward A.; Halvorsen K.; Wong W. P. (2016) Multiplexed single-molecule force spectroscopy using a centrifuge. Nat. Commun. 7, 11026. 10.1038/ncomms11026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ozcelik A.; Rufo J.; Guo F.; Gu Y.; Li P.; Lata J.; Huang T. J. (2018) Acoustic tweezers for the life sciences. Nat. Methods 15, 1021. 10.1038/s41592-018-0222-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nambiar R.; Gajraj A.; Meiners J.-C. (2004) All-optical constant-force laser tweezers. Biophys. J. 87, 1972–1980. 10.1529/biophysj.103.037697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lal R.; Ramachandran S.; Arnsdorf M. F. (2010) Multidimensional atomic force microscopy: a versatile novel technology for nanopharmacology research. AAPS J. 12, 716–728. 10.1208/s12248-010-9232-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen H.; Yuan G.; Winardhi R. S.; Yao M.; Popa I.; Fernandez J. M.; Yan J. (2015) Dynamics of equilibrium folding and unfolding transitions of titin immunoglobulin domain under constant forces. J. Am. Chem. Soc. 137, 3540–3546. 10.1021/ja5119368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popa I.; Rivas-Pardo J. A. s.; Eckels E. C.; Echelman D. J.; Badilla C. L.; Valle-Orero J.; Fernández J. M. (2016) A HaloTag anchored ruler for week-long studies of protein dynamics. J. Am. Chem. Soc. 138, 10546–10553. 10.1021/jacs.6b05429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- del Rio A.; Perez-Jimenez R.; Liu R.; Roca-Cusachs P.; Fernandez J. M.; Sheetz M. P. (2009) Stretching single talin rod molecules activates vinculin binding. Science 323, 638–641. 10.1126/science.1162912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen H.; Fu H.; Zhu X.; Cong P.; Nakamura F.; Yan J. (2011) Improved high-force magnetic tweezers for stretching and refolding of proteins and short DNA. Biophys. J. 100, 517–523. 10.1016/j.bpj.2010.12.3700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao X.; Zeng X.; Lu C.; Yan J. (2017) Studying the mechanical responses of proteins using magnetic tweezers. Nanotechnology 28, 414002. 10.1088/1361-6528/aa837e. [DOI] [PubMed] [Google Scholar]
- You H.; Lattmann S.; Rhodes D.; Yan J. (2017) RHAU helicase stabilizes G4 in its nucleotide-free state and destabilizes G4 upon ATP hydrolysis. Nucleic Acids Res. 45, 206–214. 10.1093/nar/gkw881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao X.; Peter S.; Droge P.; Yan J. (2017) Oncofetal HMGA2 effectively curbs unconstrained (+) and (−) DNA supercoiling. Sci. Rep. 7, 8440. 10.1038/s41598-017-09104-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gough R. E.; Goult B. T. (2018) The tale of two talins - two isoforms to fine-tune integrin signalling. FEBS Lett. 592, 2108–2125. 10.1002/1873-3468.13081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sase I.; Miyata H.; Ishiwata S. I.; Kinosita K. (1997) Axial rotation of sliding actin filaments revealed by single-fluorophore imaging. Proc. Natl. Acad. Sci. U. S. A. 94, 5646–5650. 10.1073/pnas.94.11.5646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu M.; Yuan X.; Lu C.; Le S.; Kawamura R.; Efremov A. K.; Zhao Z.; Kozlov M. M.; Sheetz M.; Bershadsky A.; Yan J. (2017) mDia1 senses both force and torque during F-actin filament polymerization. Nat. Commun. 8, 1650. 10.1038/s41467-017-01745-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bryant Z.; Stone M. D.; Gore J.; Smith S. B.; Cozzarelli N. R.; Bustamante C. (2003) Structural transitions and elasticity from torque measurements on DNA. Nature 424, 338. 10.1038/nature01810. [DOI] [PubMed] [Google Scholar]
- Koster D. A.; Croquette V.; Dekker C.; Shuman S.; Dekker N. H. (2005) Friction and torque govern the relaxation of DNA supercoils by eukaryotic topoisomerase IB. Nature 434, 671. 10.1038/nature03395. [DOI] [PubMed] [Google Scholar]
- Bosco A.; Camunas-Soler J.; Ritort F. (2014) Elastic properties and secondary structure formation of single-stranded DNA at monovalent and divalent salt conditions. Nucleic Acids Res. 42, 2064–2074. 10.1093/nar/gkt1089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marko J. F.; Siggia E. D. (1995) Stretching dna. Macromolecules 28, 8759–8770. 10.1021/ma00130a008. [DOI] [Google Scholar]
- Marko J. F.; Cocco S. (2003) The micromechanics of DNA. Phys. World 16, 37–41. 10.1088/2058-7058/16/3/40. [DOI] [Google Scholar]
- van Holde K. E. (1989) The Structures of DNA. In Chromatin, pp 31–68, Springer. [Google Scholar]
- Goult B. T.; Gingras A. R.; Bate N.; Barsukov I. L.; Critchley D. R.; Roberts G. C. (2010) The domain structure of talin: residues 1815–1973 form a five-helix bundle containing a cryptic vinculin-binding site. FEBS Lett. 584, 2237–2241. 10.1016/j.febslet.2010.04.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gingras A. R.; Ziegler W. H.; Frank R.; Barsukov I. L.; Roberts G. C.; Critchley D. R.; Emsley J. (2005) Mapping and consensus sequence identification for multiple vinculin binding sites within the talin rod. J. Biol. Chem. 280, 37217–37224. 10.1074/jbc.M508060200. [DOI] [PubMed] [Google Scholar]
- Bragg L.; Kendrew J. C.; Perutz M. F. (1950) Polypeptide Chain Configurations in Crystalline Proteins. Procroyasocilond Proceedings of the Royal Society of London. Proc. R. Soc. A 203, 321–357. 10.1098/rspa.1950.0142. [DOI] [Google Scholar]
- Pauling L.; Corey R. B.; Branson H. R. (1951) The structure of proteins; two hydrogen-bonded helical configurations of the polypeptide chain. Proc. Natl. Acad. Sci. U. S. A. 37, 205–211. 10.1073/pnas.37.4.205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winardhi R. S.; Tang Q.; Chen J.; Yao M.; Yan J. (2016) Probing Small Molecule Binding to Unfolded Polyprotein Based on its Elasticity and Refolding. Biophys. J. 111, 2349–2357. 10.1016/j.bpj.2016.10.031. [DOI] [PMC free article] [PubMed] [Google Scholar]