Abstract
In the western U.S., smoke from wild and prescribed fires can severely degrade air quality. Due to changes in climate and land management, wildfires have increased in frequency and severity, and this trend is expected to continue. Consequently, wildfires are expected to become an increasingly important source of air pollutants in the western U.S. Hence, there is a need to develop a quantitative understanding of wildfire‐smoke‐specific health effects. A necessary step in this process is to determine who was exposed to wildfire smoke, the concentration of the smoke during exposure, and the duration of the exposure. Three different tools have been used in past studies to assess exposure to wildfire smoke: in situ measurements, satellite‐based observations, and chemical‐transport model (CTM) simulations. Each of these exposure‐estimation tools has associated strengths and weakness. We investigate the utility of blending these tools together to produce estimates of PM2.5 exposure from wildfire smoke during the Washington 2012 fire season. For blending, we use a ridge‐regression model and a geographically weighted ridge‐regression model. We evaluate the performance of the three individual exposure‐estimate techniques and the two blended techniques by using leave‐one‐out cross validation. We find that predictions based on in situ monitors are more accurate for this particular fire season than the CTM simulations and satellite‐based observations because of the large number of monitors present; therefore, blending provides only marginal improvements above the in situ observations. However, we show that in hypothetical cases with fewer surface monitors, the two blending techniques can produce substantial improvement over any of the individual tools.
Keywords: smoke, wildfires, exposure, observations, satellites, models
Key Points
For the 2012 Washington wildfires, the number of in situ measurements allows for accurate interpolation of PM2.5 measurements
Blending interpolated measurements with model output and satellite observations only produced modest improvement over interpolation alone
Geographically Weighted Regression can substantially improve over interpolation in a simulated case with fewer measurements available
1. Introduction
Ambient air pollution is one of the leading causes of premature mortality worldwide [Forouzanfar et al., 2015]. Atmospheric aerosols are a major component of air pollution, and exposure to fine particles with aerodynamic diameters smaller than 2.5 µm (PM2.5) is associated with many negative health effects [Pope and Dockery, 2006]. While regulation has successfully reduced the anthropogenic contribution to ambient PM2.5 [Sheppard et al., 1999; Gauderman et al., 2015], nonanthropogenic emissions are more difficult to control. In the western U.S., nonanthropogenic biomass burning such as wildfires are a major source of PM2.5 [Mallia et al., 2015]. Wildfire activity is closely coupled with spring and summer time temperatures [Westerling et al., 2006]. Many metrics of drought and fire potential have been shown to increase in response to anthropogenic climate change [Abatzoglou and Williams, 2016], suggesting that the relative importance of wildfires for western U.S. air quality is likely to continue to increase [Yue et al., 2015].
Studies have attempted to quantify the impact of biomass burning PM2.5 smoke on human health [e.g., Lelieveld et al., 2015]. This has been done by using concentration‐response (CR) functions to link PM2.5 exposure to health effects. CR functions for PM2.5 exposure are developed from environmental epidemiology studies such as the Harvard Six Cities Study [Dockery et al., 1993] which examined incidence of disease in populations with different exposures to ambient PM2.5. These CR functions pertain to chronic exposure to low‐to‐moderate levels of PM2.5; they may not apply to transient pollution events lasting days to weeks with much higher levels of pollution, an exposure pattern more typical of wildfire smoke [Val Martin et al., 2013]. Furthermore, how particle composition impacts health is not well understood. As biomass‐burning aerosol has a different composition, it may also have a different toxicity than ambient mixtures of PM2.5 from other aerosol sources. However, many CR functions are developed for exposure to ambient total PM2.5, not for specific sources or components. Given this disconnect, as well as the increasing importance of wildfires to western U.S. air quality, there is a need to develop CR functions specific to wildfire smoke.
Environmental epidemiology uses many different techniques for determining the health effects of an environmental pollutant and for calculating CR functions [Samet et al., 2000; Miller et al., 2007]. However, these study designs require accurate estimates of pollutant exposure, reliable health data, and a large exposed population in order to ensure detection of a statistically significant change in health outcomes between the hazard and nonhazard periods. Because wildfire smoke events tend to occur in sparsely populated regions, statistical power can be challenging. Therefore, reducing exposure misclassification by producing increasingly accurate estimates of spatiotemporal smoke concentrations is even more necessary for the epidemiology to be effective [Liu et al., 2015]. The focus of this study is to produce accurate estimates of exposure to wildfire smoke across large areas, which can be used in an epidemiology study.
Previous studies on health effects due to wildfire‐smoke exposure have relied on three different tools to estimate smoke PM2.5 exposure: in situ monitors [e.g., Elliott et al., 2013], satellite‐based observations [e.g., Rappold et al., 2011], and chemical‐transport models (CTMs) [e.g., Alman et al., 2016]. While each of these tools has a different set of strengths, wildfire smoke presents different challenges for all three of these exposure‐estimation techniques.
In situ measurements: in the United States, the Environmental Protection Agency (EPA) consolidates surface PM2.5 measurements from state and local agencies into the Air Quality System (AQS) and Interagency Monitoring of Protected Visual Environments networks. These in situ measurements provide accurate information about PM2.5 concentrations at a single point in space; however, the spatial density of sites is inconsistent throughout the western U.S. and monitors are often insufficiently spaced to resolve steep spatial gradients associated with wildfire smoke. Furthermore, some measurement sites only record data every third day which can fail to measure changes in smoke concentrations that often occur on shorter time scales.
Satellite‐based observations: satellite‐based observations offer a good complement to in situ measurements due to their ability to make observations over large spatial areas. However, surface concentrations are hard to determine from a satellite‐based observation. Instead, most air‐quality satellite retrievals produce estimates of aerosol optical depth (AOD), which is the integrated extinction due to the total column aerosol mass and may not necessarily be indicative of surface PM2.5 concentrations. Satellite observations of AOD have been used in numerous studies of air quality and health [Henderson et al., 2011; Rappold et al., 2011] and are often combined with models or measurements for spatially improved PM2.5 estimates [e.g., van Donkelaar et al., 2006, 2011; Brauer et al., 2012].
CTMs: to fill the gap between satellite and in situ observations, modeling tools are often used [e.g., van Donkelaar et al., 2006]. A wide range of CTMs are used to estimate surface PM2.5 based on knowledge about emissions, chemical processing of emissions, and transport due to meteorology; because CTMs produce spatially continuous information about many different species, these tools are attractive for use in health studies [Alman et al., 2016]. However, CTMs are limited by our understanding of the underlying physical processes [Alvarado et al., 2015], as well as our ability to represent these processes in a computationally viable model. Specifically, accurate modeling of wildfire smoke requires detailed knowledge of fuel loading and moisture, fire behavior, and thermodynamic structure of the atmosphere to correctly predict emission species and mass, as well as pollutant injection height [Paugam et al., 2016], which are all crucial to predicting surface PM2.5 in smoke plumes [Baker et al., 2016]. With additional uncertainties in meteorology [Garcia‐Menendez et al., 2013] and subgrid‐scale parameterizations' effect on transport, accurate modeling of wildfire smoke is a challenging endeavor [Saide et al., 2015].
Given the limitations of these individual tools, several studies have examined the utility of combining information from each of these tools, as well as other data sets. Reid et al. [2015] combines CTM simulation results with AOD products from two satellite platforms, in situ monitor data, and other land use data and distance‐to‐fire data in a data‐adaptive machine‐learning framework consisting of 11 different algorithms. Yao and Henderson [2014] combined various remote‐sensing products with previous days' in situ measurements as well as a dispersion model in a regression model to predict surface PM2.5.
Henderson et al. [2011] compared the observed health signal by using models, monitors, and satellites separately to determine exposure and found that the exact technique used to determine exposure can impact the health response significantly. The recent review of wildfire‐smoke exposure literature by Liu et al. [2015] noted that while most studies find a signal for respiratory health effects of wildfire smoke exposure, cardiovascular morbidity and mortality signals are less consistently seen; however, there is a well‐known relationship between other sources of air pollution and adverse cardiovascular health effects [Dockery et al., 1993; Pope et al., 2004; Miller et al., 2007]. The absence of a detected relationship between wildfire smoke and cardiovascular health outcomes may be due to exposure misclassification, rather than the absence of a relationship [Liu et al., 2015]. Therefore, new strategies for assessing exposure to wildfire smoke exposure that reduce exposure misclassification are needed to resolve this discrepancy.
In this study, we evaluate the combination of model output with in situ measurements and satellite observations to produce estimates of population exposure to wildfire smoke. We compare the performance of this method to conventional exposure estimate techniques for the Washington 2012 wildfire season, and we simulate the performance of estimates for a hypothetical case with fewer in situ monitors.
The methods and results of the companion epidemiology study can be found in “A comparison of smoke estimation methods and their association with wildfire smoke and cardiopulmonary‐related hospital admissions during the 2012 Washington wildfires” [Gan et al., 2017].
2. Methods
2.1. Overview of Washington 2012 Wildfires
On 8 September 2012, a lightning storm ignited a series of fires in the east Cascade mountain range of Washington which burned close to 260,000 acres through the month of September. The fires produced spatially broad smoke plumes which severely impacted visibility and air quality in much of the central and eastern parts of the state. Figure 1b shows the locations of fires on 21 September 2012.
Figure 1.
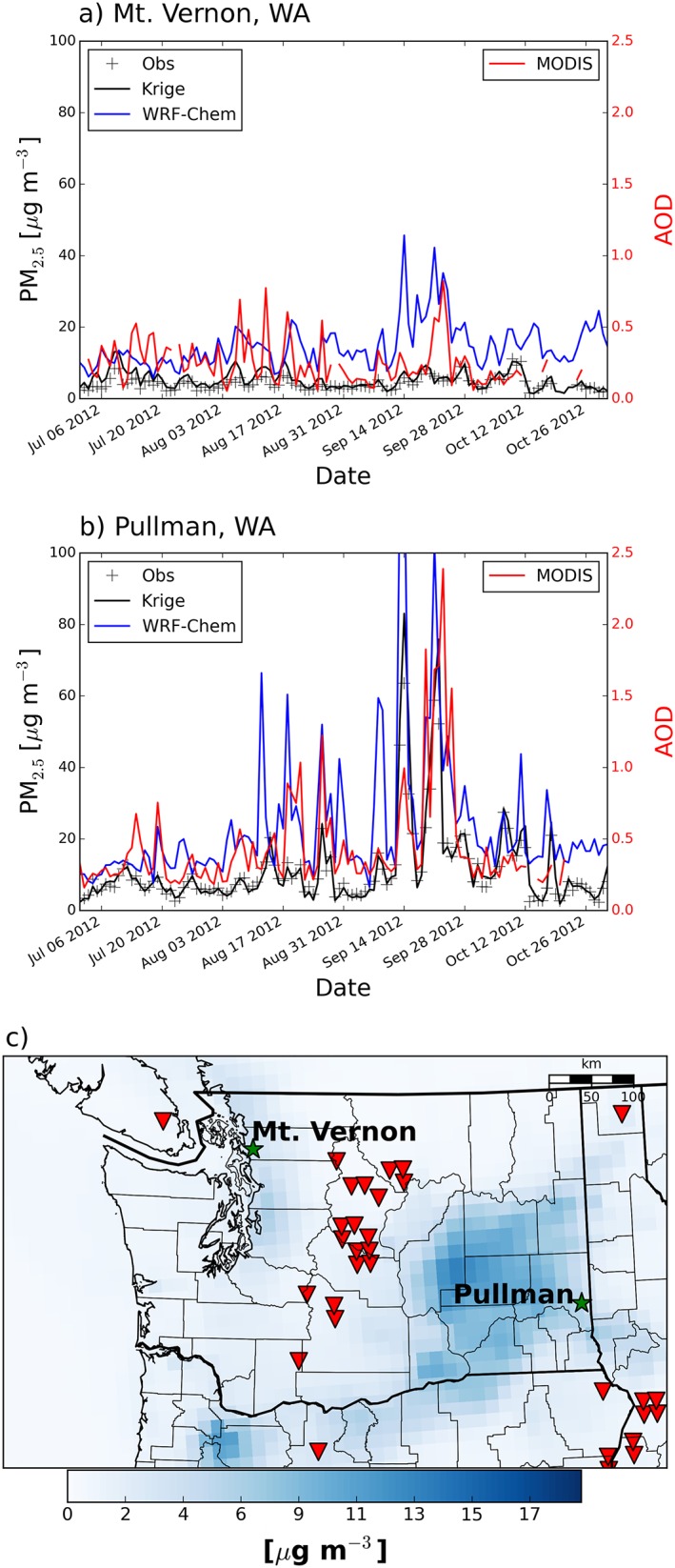
Time series plot showing in situ measurements alongside WRF‐Chem, interpolated estimates of PM2.5, and MODIS AOD. Plots are from (a) Mount Vernon, WA, which was not impacted by smoke during this time period, and (b) Pullman, WA, which was impacted by smoke. (c) The locations of these two measurement sites in Washington along with fire locations and surface concentrations on 21 September 2012.
For this study, we analyzed surface PM2.5 concentrations associated with these wildfires and the surrounding months as control. We estimated daily average surface PM2.5 concentrations from 1 July to 31 October 2012.
2.2. Exposure Estimation Tools
2.2.1. Weather Research and Forecasting Model With Chemistry Simulations
We use the Weather Research and Forecasting model with Chemistry (WRF‐Chem) [Grell et al., 2005] to simulate the wildfire event. We chose WRF‐Chem because it allows us to conduct simulations at higher resolution than some other CTMs (e.g., Goddard Earth Observing System model with Chemistry (GEOS‐Chem)) which is important for resolving steep spatial gradients associated with wildfires [Wu et al., 2006]. Furthermore, WRF‐Chem allows for chemical fields to feed back on meteorological variables. Dense aerosol layers associated with wildfire plumes can impact radiative transfer and cloud processes, which can in turn impact transport [Grell et al., 2011].
Simulations were conducted at 15 × 15 km resolution, with Global Forecast System analysis for meteorological initial/boundary conditions. Meteorological fields were reinitialized daily. We use output from the Model for Ozone and Related Tracers Version 4 (MOZART‐4) to initialize the model and establish boundary conditions for chemical species [Emmons et al., 2010]. Biomass‐burning emissions are based on the Fire Inventory from National Center for Atmospheric Research (NCAR) (FINN) v1.5 [Wiedinmyer et al., 2011], and anthropogenic emissions are based on 2011 EPA National Emissions Inventory. We use the MOZART gas‐phase chemical mechanisms [Emmons et al., 2010], with Goddard Chemistry Aerosol Radiation and Transport model [Chin et al., 2000] to simulate the evolution of the biomass‐burning plume. We use the YSU boundary layer parameterization [X.‐M. Hu et al., 2013] and the Morrison microphysics parameterization [Morrison and Gettelmen, 2008] subgridscale processes. The WRF‐Chem simulations produced hourly estimates of surface PM2.5 concentrations, from which 24 h averages were calculated. A detailed summary of our simulation parameters can be found in Table S1 in the supporting information.
2.2.2. In Situ Measurements and Interpolation
In situ monitor data for the state of Washington, as well as northern Oregon, western Idaho, and Montana were obtained from the EPA AQS for the months of July–October of 2012 (https://aqs.epa.gov/aqsweb/documents/data_mart_welcome.html). During smoky periods, the Washington Department of Ecology deployed additional PM2.5 monitors, which were also included in our analysis. Additional in situ measurements from Canada were obtained from Dr. Sarah Henderson at the University of British Columbia School of Population and Public Health. There were a total of 212 in situ measurement sites during our study period. All networks of in situ measurements use a combination of automated and manual filter‐based instruments, and reported in situ measurements are at varying temporal resolution as follows: Washington Department of Ecology supplemental sites reported hourly data, Canadian measurements reported daily data, and EPA AQS sites reported data every 3 or 7 days. A map denoting the location and parent network of the various in situ monitors can be found in Figure S1 in the supporting information. Because we produced exposure estimates at daily temporal resolution, all subdaily (e.g., hourly) observations were averaged to produce 24 h averages at those monitor locations.
Previous studies of all‐source PM2.5 exposure [e.g., Dockery et al., 1993; Samet et al., 2000; Miller et al., 2007; Bell and HEI Health Review Committee, 2012] have relied on nearest monitor observations to estimate exposure and have limited the study area to areas within a specified distance of a surface monitor. However, reducing the spatial area of the study has disadvantages because it reduces the sample size of the exposed population, and many health effects (especially cardiovascular effects) may be obscured by a lack of statistical power [Reid et al., 2016]. To avoid this issue, past studies have used an interpolation technique to estimate PM2.5 concentrations in between measurement sites and increase the statistical power in exposure estimates [Deligiorgi and Philippopoulos, 2011; Li et al., 2016]. Building off these approaches, we use ordinary kriging [Isaaks and Srivastava, 1989; Jerrett et al., 2005; Janssen et al., 2008] to interpolate in situ measurements of PM2.5. We used brute‐force optimization to fit an analytical semivariogram to our data as follows: (1) we guessed a shape and parameter values for an analytical semivariogram function, (2) we used the kriging weights derived from this semivariogram function to do a leave‐one‐out cross validation evaluation [Efron, 1982] (which is described in detail below) of the kriging model, and (3) we evaluated each kriging model by using slope, R2, mean average error (MAE), and mean bias (MB) statistics. On each day, we use all available measurements to fit a new kriging model for that day. We found that a spherical semivariogram shape with parameter values “sill” s = 3.0, “nugget” n = 0.1, and “range” r = 8.0 degrees produced the estimates with the best performance according to our summary statistics, and the results are discussed in section 3.2.2. We use this analytical semivariogram throughout our analysis. Because we use a constant semivariogram for the entire time period, we are only performing two‐dimensional spatial kriging; however, we do fit a kriging model for every day of our time period. The semivariogram and kriging weights are calculated by using the Python PyKrige module following Murphy [2014]. We evaluate our ordinary kriging estimates by using leave‐one‐out cross validation (LOOCV) [Efron, 1982] as follows: an individual in situ measurement site is removed from the interpolation algorithm, a PM2.5 estimate at the location of the removed site is calculated based on interpolation of the remaining PM2.5 measurements available on that date, and this estimate is compared with the measured value at that site. This process is repeated for every in situ measurement site, on every day that the measurement site reports a value.
LOOCV is a common interpolation evaluation technique [Efron, 1982] and was done as follows: for a given measurement site on a given day, all other measurements are used to interpolate to that point in space. The interpolated value is then compared to the measurement made at that location as a means of testing the skill of the interpolation strategy. This step is repeated for every measurement site, on every day that each measurement site reports a value.
2.2.3. Moderate Resolution Imaging Spectroradiometer Satellite Observations
For satellite observations, we use the Moderate Resolution Imaging Spectroradiometer (MODIS) instrument aboard the Terra and Aqua polar‐orbiting satellites. Both satellites provide measurements of the entire globe approximately once daily in the absence of clouds, with the Terra and Aqua overpasses occurring at ~10:30 A.M. and ~1:30 P.M. local time, respectively, with a swath width of 2330 km. MODIS instruments consist of radiometer measurements of the Earth at 36 wavelengths [Remer et al., 2005]. Aerosol optical depth (AOD) is a measure of the integrated optical extinction in the atmosphere due to the total amount of particulate matter in an atmospheric column. In many locations, AOD is often highly correlated with surface PM2.5 concentrations [Engel‐Cox et al., 2004]. However, there can be variability in the strength of the relationship which depends on many other variables [Ford and Heald, 2016].
For this analysis, we use the Level 2 AOD Dark‐Target Collection 6 retrieval at 10 km spatial resolution [Sayer et al., 2014]. The Terra (~10:30 A.M. local time) and Aqua (~1:30 P.M. local time) overpasses are composited together to produce a single AOD observation that is representative of the daytime period according to a procedure described in Text S1 in the supporting information. The Level 2 retrieval includes a cloud mask. However, in the case of wildfires, thick smoke is often mistaken as cloud by the retrieval and erroneously masked [van Donkelaar et al., 2011]. Changes were made in Collection 6 to account for this; however, some pixels are still flagged as cloudy when we believe that they represent dense smoke. When masked pixels are surrounded by elevated AOD values due to smoke, we assume that the retrieval failed on these pixels and we interpolate surrounding pixel values to estimate the AOD in that pixel.
The details of the compositing and masking procedures are discussed in Text S1. Additionally, we present a sensitivity analysis to demonstrate that these procedures do not introduce significant bias to our results.
2.3. Blending Techniques
2.3.1. Global Ridge Regression
We use linear regression to blend our three exposure estimate data sets together. Because each individual data set is an estimate of surface PM2.5 concentrations, we expect a high degree of multicollinearity between these three data sets. Therefore, this is an “ill‐posed” problem for a conventional regression technique (e.g., ordinary least squares) and may lead to an overfitted model that amplifies noise [Vogel, 2002]. To account for this, we use ridge regression, which penalizes the model as the norm of the regression coefficients grows and results in a more stable regression model for correlated inputs.
We use the ridge‐regression algorithm provided in the Python SKLearn module [Pedregosa et al., 2011] to train and implement our model. We evaluate this approach by using a leave‐one‐out cross validation (LOOCV) approach, where we use all but one in situ measurement site to train a set of regression coefficients, and then evaluate the model by using the data from the removed in situ measurement site. As inputs to our regression model, we use the LOOCV ordinary kriging estimate along with WRF‐Chem estimates and MODIS AOD estimates at each point and use the measured value at the site to train and evaluate the regression model, allowing us to simulate estimating PM2.5 concentrations with regression at a point far from a measurement site. This process is repeated for every measurement site. Therefore, we have a distribution of regression coefficients for each iteration of the cross validation, though each iteration of the LOOCV produces one set of regression coefficients for use throughout the domain. Because we aggregate data from many in situ measurement sites to train our regression model, we refer to this approach as a Global Ridge Regression (GRR) blend.
2.3.2. Geographically Weighted Ridge Regression
One limitation to the GRR approach is that we aggregate data across the full domain (the state of Washington in this case) to train the regression model. However, the inputs to the regression model may perform differently in different parts of our domain. For example, the performance of WRF‐Chem in the urban corridor in western Washington depends on the accuracy and precision of the anthropogenic emissions inventory, as well as the ability of the chemical mechanism to simulate the complex chemistry that occurs in this region. However, model performance in the central and eastern parts of the state is more determined by the emissions and transport of emissions from the wildfires in the central part of the state. Likewise, we expect our estimates from kriging of in situ measurements to perform better in regions where numerous surface sites are nearby.
In Geographically Weighted Regression (GWR), we can leverage the fact that different data sets can provide better estimates of surface PM2.5 in different locations. GWR [Brunsdon et al., 1998; Fotheringham et al., 2002] is a geostatistical technique that has been used before in urban air‐quality studies [Song et al., 2014] as well as national‐level studies that incorporated remote sensing [X. Hu et al., 2013; You et al., 2016].
In GWR, regression coefficients are calculated at each in situ measurement site. The regression coefficients are then interpolated by using a Gaussian kernel function:
| (1) |
where D i,j is the distance to the surface monitor and Bw is a bandwidth parameter (we used 100 km) which determines the length scale of the Gaussian kernel. The regression coefficients in a given grid cell in our domain (w) are given by the following interpolation formula:
| (2) |
where the index i denotes each surface monitor location and the index j refers to the grid cell. Using this interpolation approach, we are able to calculate a set of unique coefficients for each location in our analysis domain. We evaluate this technique by using LOOCV as described for GRR.
3. Results and Discussion
Figures 1a and 1b present in situ measurements of surface PM2.5 plotted alongside WRF‐Chem and interpolated estimates of surface PM2.5, as well as MODIS AOD for two in situ measurement locations for one example day during our study time period. Figure 1c shows the relative locations of these measurement sites with locations of major fires from the FINN inventory [Wiedinmyer et al., 2011].
Mount Vernon (Figure 1a) is located in the northwest part of Washington, which, based on the observed concentrations of PM2.5, was not impacted by smoke during this time period. Therefore, PM2.5 concentrations during this time period were dominated by nonwildfire sources. There was little variability in measured PM2.5 at this measurement location (standard deviation of 1.8 µg m−3), and concentrations were consistently <15 µg m−3. Our WRF‐Chem simulation not only overpredicted PM2.5 throughout the time period but also predicted increases in PM2.5 during September, when most of the fire activity in the region occurred. These relative increases were not corroborated by the surface measurements. However, there were increases in MODIS AOD during this time period, suggesting that smoke may have been lofted above the measurement site and the model may have erroneously kept the smoke at the surface. Throughout this time period, estimates of PM2.5 based on kriging of surrounding measurements appear to very closely follow the observed concentrations (note that the actual measurements taken at this observation site were left out of the kriging fit in order to evaluate the utility of kriging).
However, the other time series location in Pullman, WA (Figure 1b) was impacted by smoke during the time period, as reflected by elevated PM2.5 measurements close to 60 µg m−3. While WRF‐Chem estimates of PM2.5 appear to overestimate concentrations during the time period, the increases in measured concentrations correspond to increases in simulated PM2.5, which indicates that WRF‐Chem captures the variability in concentrations due to wildfire smoke, even if it overpredicts concentrations. These periods of elevated PM2.5 are also captured by MODIS AOD as well as kriging of surrounding measurement sites.
To assess the performance of these techniques throughout the domain, we compared our estimates of surface PM2.5 concentrations to measurements at every site throughout the domain. For these comparisons, we use the LOOCV estimates derived from kriging, as well as ridge regression and GWR based on the LOOCV kriged data set. We then compare these estimates to the actual measured value at that location. In doing so, we are simulating estimating PM2.5 concentrations in a location where measurements are hypothetically not available.
Figure 2 shows one‐to‐one scatterplots of the data, with performance statistics summarized in Table 1, while Figure 3 shows the coefficient of determination (R 2) between each estimate and measured PM2.5 at every measurement site in the domain. These results will be discussed in further detail in the following subsections.
Figure 2.
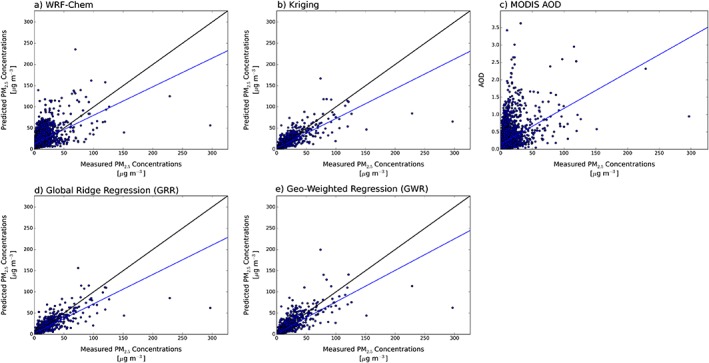
One‐to‐one plots of (a) WRF‐Chem, (b) kriging, (c) MODIS AOD, (d) Global Ridge Regression, and (d) Geo‐Weighted Ridge Regression predictions of surface PM2.5 versus measured PM2.5 concentrations for all measurement sites in Washington for 1 July 2012–2031 and October 2012.
Table 1.
Performance Statistics for Each Exposure Estimate, Aggregated Across All In Situ Measurement Sites 1 July 2012–2031 and October 2012
| Exposure Estimate | Slope | R 2 | Mean Absolute Error (µg m−3) | Mean Bias (µg m−3) |
|---|---|---|---|---|
| WRF‐Chem | 0.67 | 0.25 | 11.45 | 10.22 |
| Kriging | 0.70 | 0.69 | 2.09 | 0.00 |
| MODIS AOD | 0.01 | 0.18 | – | – |
| Global ridge regression | 0.70 | 0.69 | 2.14 | 0.01 |
| Geographically weighted regression | 0.78 | 0.66 | 2.40 | 0.37 |
Figure 3.

R 2 value for each in situ measurement site as compared to (a) WRF‐Chem, (b) kriged PM2.5 measurements, (c) MODIS AOD, (e) Global Ridge Regression, and (f) geo‐weighted ridge regression for 1 June 2012–2031 and October 2012. (d) The mean bias for the WRF‐Chem simulated PM2.5 at each in situ measurement site (note the different color scale).
3.1. Aggregate Results of Individual Estimates
3.1.1. WRF‐Chem Simulations
A comparison between the WRF‐Chem simulation and the surface observations indicates that the model overpredicts PM2.5 concentrations during the period of July–September 2012 throughout Washington (Figure 2). WRF‐Chem estimates have a slope of 0.67, R 2 of 0.25, mean absolute error (MAE) of 11.4, and mean bias (MB) of 10.2 µg m−3 (Table 1). The slope of less than 1 is driven by (1) an underprediction of surface PM2.5 for the few highest concentrations that were recorded and (2) a high PM2.5 bias in nonsmoke regions. Estimates from our WRF‐Chem simulation are on average biased high, and an overprediction of PM2.5 in nonfire regions makes a large contribution to this bias.
Much of the positive bias shown in Figure 2 is driven by the large number of monitors in western Washington that was not impacted by smoke (Figure 3d). WRF‐Chem is not capturing the variability at those surface monitors as indicated by the R 2 values near zero in Figure 3a. Model performance in these locations depends on a suite of factors including nonwildfire emissions, such as anthropogenic emissions, biogenic emissions, MOZART boundary conditions, or the choice of aerosol chemistry/physics scheme. In contrast, the mean absolute bias is much closer to zero, and R 2 values are much higher (0.5–0.7) in the central part of the state that was most severely impacted by smoke. In the eastern third of the state, WRF‐Chem‐simulated PM2.5 are also biased high with respect to the surface observations, but the R 2 values remain high (>0.5). This is consistent with our observations in Pullman, WA, where the time series in Figure 3c show that WRF‐Chem overpredicts ambient and wildfire PM2.5 but captures the variability in surface observations.
As previously mentioned, one of the main challenges for determining wildfire‐specific health effects is exposure misclassification bias [Liu et al., 2015]. Other studies that have attempted to use WRF‐Chem to characterize exposure to wildfire smoke [e.g., Alman et al., 2016] have acknowledged that exposure misclassification can occur when using models to estimate exposure and the extent of exposure misclassification is difficult to quantify. In particular, the Alman et al. [2016] study had a comparatively smaller number of in situ PM2.5 monitors in their study domain available against which to evaluate their exposure estimates. While it is possible in principle to use WRF‐Chem to generate highly accurate surface PM2.5 estimates, this may require optimizing the WRF‐Chem simulation to better account for parameters and processes that are more representative of each region. This would likely also require enough in situ monitors to comprehensively evaluate WRF‐Chem performance in the domain.
3.1.2. Kriging of In Situ Measurements
Using kriging to estimate PM2.5 appears to outperform our WRF‐Chem simulation throughout the domain with a slope of 0.7, R 2 of 0.69, mean absolute error (MAE) of 2.1 µg m−3, and mean bias (MB) of 0.0. The analogous one‐to‐one plot for our kriged PM2.5 estimates and R 2 map are shown in Figures 2b and 3b, respectively. The slope less than one is driven by an underprediction of the highest observed concentrations. This is expected, because interpolation techniques cannot predict local maxima or minima that do not impact a measurement site used in the interpolation. If there are local maxima and minima in between measurement sites, no interpolation strategy will successfully resolve these values. Likewise, when doing LOOCV, if one measurement site is experiencing a higher concentration than the surrounding sites, then there is no way to successfully predict that value based on other measurements through interpolation. On average, however, kriging is able to produce estimates that are close to the actual value, given the low MAE and bias.
Kriging produces the highest R 2 values in regions where surface monitors are closest together (Figure 3b). This is an expected result; the spatial autocorrelation of PM2.5 decays with distance, so sites in closer proximity are better able to capture the expected variability than more distant ones. However, there are individual sites with low R 2 values despite close proximity to other monitors. This low correlation may indicate a local source of PM2.5. Because the kriging model produces estimates with a lower error and bias, we consider this to be a more accurate estimate than our WRF‐Chem simulations for the 2012 Washington fires.
Our interpolation is able to represent surface concentrations with better‐than‐expected accuracy. There are two factors that contributed to this. (1) The state of Washington has an extensive in situ monitor network that was augmented in summer 2012 by the deployment of extra monitors. (2) The number and distribution of large wildfires (Figure 1) produced large areas of smoke impact instead of isolated plumes. While interpolation has been shown to be useful for characterizing PM2.5 concentrations for ambient air pollution [e.g., Jerrett et al., 2005; Li et al., 2012], relatively few studies have attempted to use interpolation to characterize smoke concentrations for wildfires, largely because the highly concentrated plumes of smoke often produce spatial PM2.5 concentration gradients that are too steep for in situ monitor networks to resolve [Wu et al., 2006]. Studies that do use in situ monitors to determine wildfire impacts on air quality either limit their study area to close to a monitor [Wu et al., 2006] or combine PM2.5 monitor data with other sources of information [e.g., Reid et al., 2015]. Though our method represented surface concentrations well, the method cannot capture local maxima or minima in PM2.5 concentrations between surface monitors. Other sources of information, such as the satellite observations and WRF‐Chem output, can add important information to exposure estimates in these locations.
3.1.3. MODIS AOD
MODIS AOD has been successfully used to identify wildfire smoke in previous studies [van Donkelaar et al., 2011; Rappold et al., 2011]. With the exception of thick smoke occasionally being erroneously classified as a cloud and cases where smoke is lofted above the boundary layer [van Donkelaar et al., 2011], AOD is well suited for identifying large changes in atmospheric aerosol loading. Variability in AOD:PM2.5 ratios may be due to variability in (1) the vertical profile of aerosol, e.g., due to lofted smoke; (2) the ambient relative humidity driving variability in aerosol water; (3) the aerosol size distribution or composition driving variability in the mass extinction efficiency; and/or (4) temporal/spatial variability in the 24 h PM2.5 not captured by the resolution of the satellite observation.
Figure 2c presents the relationship between MODIS AOD and in situ PM2.5 concentrations for our study region. There is a slope of 0.01 (Table 1); physically, this means that an increase in 0.01 AOD on average produces an increase of 1 µg m−3 in PM2.5 concentrations. The observations are bifurcated around the 1:1 line (either above or below), with few data points lying along the line. Our MODIS AOD data set is a composite of Terra and Aqua overpasses, so while it may describe the location of smoke well for the time period between 10 A.M. and 2 P.M. local time, we are comparing to 24 h average PM2.5 measurements. This temporal discrepancy is further explored in section S3 in the supporting information, though we do not find that this significantly biases our results. The R 2 value for MODIS AOD is 0.18. In Figure 3c, we see that, like with WRF‐Chem PM2.5, R 2 values for AOD are close to zero in western Washington, but R 2 values are as high as 0.6 at some surface monitors in the central and eastern portions of the state that were more heavily smoke impacted. Past studies have shown that AOD is well suited for identifying large changes in atmospheric aerosol loading, which explains its good performance in central and eastern Washington. Contrastingly, low variability in aerosol loading in western Washington, coupled with the presence of fog and stratus clouds, as well as uncertainties in the aerosol retrieval in coastal regions, produces lower performance.
Even in smoke‐impacted regions, we do not expect AOD to explain all of the variance in the surface PM2.5 concentrations, as there are still challenges associated with distinguishing surface PM2.5 from aerosol mass that are above the surface and not directly relevant to human health. Other studies have attempted to deal with this uncertainty in different ways; Rappold et al. [2011] used a binary exposure variable (e.g., smoke or no smoke based on fractional coverage of counties) applied at a coarse spatial resolution. At this level of spatial resolution, exposure misclassification is likely to occur from many sources, and the contribution due to uncertainty in smoke plume height may be relatively minor in comparison. van Donkelaar et al. [2011] combined satellite AOD with output from a chemical‐transport model to constrain population‐level exposure estimates. In the next section we combine MODIS AOD with WRF‐Chem output and kriged in situ measurements of PM2.5 to improve the accuracy of our estimates of PM2.5. We do not attempt to estimate exposure at subdaily time scales because the MODIS data set is a composite of overpasses between 10 A.M. and 2 P.M. on each day (representative of daytime concentrations), whereas the in situ PM2.5 measurements are 24 h averages. Our health data [Gan et al., 2017] are also at the daily resolution, but we acknowledge that this temporal mismatch between the satellite product and surface measurements might bias our comparisons (section S3).
3.2. Regression Results
We combined the simulated PM2.5 with the satellite and surface observations by using two different techniques: Global Ridge Regression (GRR) and Geographically Weighted Regression (GWR).
3.2.1. Global Ridge Regression
Global Ridge Regression (GRR) produces summary statistics (slope = 0.70, R 2 = 0.69, MAE = 2.14, MB = 0.01) that are almost identical to the kriging estimate (Table 1). The regression coefficients for GRR are shown in Table 2. We see that the GRR estimate is weighted heavily toward the estimate derived from kriging of measurements. If we use the mean AOD:PM2.5 ratio from Table 1 of 0.01 AOD/[µg m−3] to convert the GRR coefficient for AOD into the same units as the other GRR coefficients, we find that the relative weights are 0.91 for kriging, 0.07 for WRF‐Chem, and 0.01 for MODIS AOD. Consequently, the GRR model‐predicted PM2.5 is very close to the kriging‐predicted values and the performance statistics are similar. Because the kriging estimates comprehensively outperform both our WRF‐Chem simulation and MODIS AOD, the GRR heavily relies on the kriged PM2.5 estimates. The R 2 values across the different measurement locations for the GRR are also quite similar to the kriged PM2.5 estimate (Figures 3a and 3d). The only discernible difference is the absence of a few surface monitor locations in the GRR figure (Figure 3d), which is due to a lack of sufficient MODIS AOD observations at those locations.
Table 2.
Global Ridge Regression Coefficients as Output by Regression Model (and Normalized to the Same Units)
| Regression Coefficient | Mean Value | Standard Deviation |
|---|---|---|
| Intercept [µg m−3] ([µg m−3]/[µg m−3]) | −0.78 (−0.00) | 0.04 (0.00) |
| Kriging ([µg m−3]/[µg m−3] | 0.91 | 0.00 |
| WRF‐Chem ([µg m−3]/[µg m−3] | 0.07 | 0.00 |
| MODIS AOD [µg m−3/AOD] ([µg m−3]/[µg m−3]) | 0.87 (0.01) | 0.04 (0.00) |
We note that the three inputs to the regression model are expected to be highly correlated. While we address instabilities in the regression model by using ridge regression, one unavoidable complication is that the regression coefficients are not necessarily unique, due to multicollinearity. Information that is contained in multiple data sets is only added to the regression model once. Therefore, a set of coefficients could exist that relies more on either our WRF‐Chem PM2.5 or MODIS AOD to produce the same estimate of surface PM2.5.
3.2.2. Geographically Weighted Regression
For measurement sites near other sites, the GWR appears to perform the same or better than GRR, while isolated sites suffer a slight decrease in performance (Figure 3e). This may be due to the interpolation of regression coefficients, which adds another layer of estimation to the system for GWR relative to GRR. Table 1 shows the performance of the GWR model (slope = 0.76, R 2 = 0.66, MAE = 2.40, MB = 0.37). Although the resulting R 2 is lower than the R 2 determined from the kriging estimate and the GRR, the MAE, and MB are slightly higher, the slope is much closer to one. The increases in MAE and MB from 2.1 to 2.4 and 0 to 0.4 µg m−3 (relative to using the kriged PM2.5) are small, relative to the concentrations seen during the wildfire smoke events (e.g., 80 µg m−3).
Figure 4 shows the intercept and three regression coefficients calculated at each in situ monitor in the domain. In Figure 4b, we see that, at most of the in situ monitor locations, GWR relies heavily on the kriged PM2.5 measurements to produce the best estimate of surface PM2.5 concentrations. However, in Figures 4c and 4d, we see that there is a nonzero contribution from both WRF‐Chem and MODIS in the central and eastern parts of the state, where both data sets were shown to explain more of the variance in the in situ measurements (Figure 3). WRF‐Chem has negative coefficients at some of the smoke‐impacted monitors in central Washington, which shows that the best fit combinations at some sites are not always physically intuitive.
Figure 4.
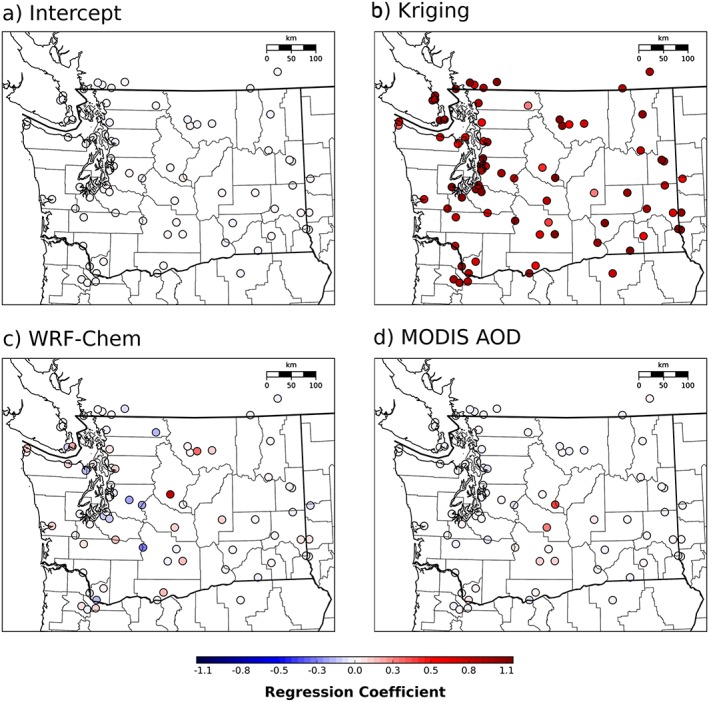
Geographically Weighted Regression (a) intercept and coefficients of (b) kriged surface PM2.5 measurements, (c) WRF‐Chem surface PM2.5 estimates, and (d) MODIS AOD. All coefficients have been converted to be dimensionless.
GWR allows the model more degrees of freedom to account for strengths/weaknesses of the three inputs in different regions, which is an advantage over GRR. A disadvantage of GWR is that the total amount of data used to calibrate model coefficients at each individual site is lower than the amount of data used to calibrate the single set of coefficients in GRR, where the data from all individual sites are pooled together. Thus, it is possible that the fits at the individual sites for GWR are less robust than the global fit for GRR. Furthermore, while sites outside the analysis domain were used as inputs to the kriging data set, they were not incorporated into the GWR analysis, so analysis grid boxes near the boundaries of the domain have fewer regression coefficients contributing to the GWR calculation and are also less reliable. In order to include sites outside of the boundaries of the analysis domain in GWR, we need a robust kriging model to estimate LOOCV concentrations outside the boundaries. To do this, we would need to use additional surface monitors even further from our domain. Because our model does not perform worse near the boundaries, and because the boundaries were not heavily impacted by smoke, this extra step would likely only produce marginal improvements. However, applying these techniques to a different fire or region may require this extra step.
Our techniques perform comparably to other studies that have also estimated smoke concentrations. The Yao and Henderson [2014] study of the 2003–2012 fire seasons in British Columbia, which combined prior days' PM2.5 concentrations with the NOAA Hazard Mapping System product, and MODIS‐measured fire radiative power, reported correlation coefficients of 0.84 (R 2 of 0.71) and a normalized root‐mean‐square error (NRMSE) of 55.6%, whereas our GWR model produces an R 2 of 0.66 and an NRMSE of 2%. Another study, Reid et al. [2015], combined many different types of land use and GIS data with in situ and satellite observations and CTM output in a multimethod, machine‐learning framework. Reid et al. [2015] found that a generalized boosting model (GBM) with 29 different variables input produced their best estimates, with a slope of 0.99, R 2 of 0.80, and a root‐mean‐square error (RMSE) of 1.5 µg m−3. In comparison to this study, we are able to achieve similar performance with our error statistic (MAE of 2.4 µg m−3 for GWR), but our slope and R 2 do not achieve the same level of performance. In large part, this is because the GBM uses more input variables (29 versus our 3), allowing for more degrees of freedom to train the model. Reid et al. [2015] also used a suite of 11 sophisticated statistical models and selected the top performer, whereas we use only one regression model. An advantage of our techniques is that they allow us to investigate the spatial dependence of different input data sets, which may be more difficult with esoteric machine‐learning techniques. While machine‐learning techniques do not require many different variables as predictors, Reid et al. [2015] used a wide range of environmental variables as inputs to their model such as wind direction, planetary boundary layer height, and distance to nearest fire, as well as land use and distance to highways. While we expect some of these to be related to surface PM2.5 concentrations, many of these variables (boundary layer height and U and V wind components) are not necessarily independent, and others (distance to highway) do not have a clear physical explanation for their ability to predict wildfire smoke concentrations (when all‐source PM2.5 measurements are used as the training and evaluation data), which limits our ability to gain a physical understanding of the results from these types of model. However, they do produce highly accurate results, which, in the context of a health study, is the primary objective. As in our study, they found that WRF‐Chem simulation output was relatively uncorrelated with their best predictor variable (GASP AOD).
3.3. Simulating Fewer Available Surface Measurements
For our case study, kriging interpolation of the in situ measurements produces better estimates of surface PM2.5 than WRF‐Chem and satellite observations. Furthermore, because of the disparity in performance between these three data sets, combining all three data sets in a regression model does not greatly improve on the kriging estimate. However, not every region or time period has an extensive in situ monitor network as Washington did during September 2012. In a more sparsely monitored region, satellite observations and CTMs may contribute more to the blended estimate. We explored this with a sensitivity study by lowering the number of monitors in Washington during September 2012.
We randomly selected between 12 and 212 (which corresponds to using all sites) surface monitors as inputs to our analysis. We then used ordinary kriging of this subset of the measurements to produce an interpolated estimate of PM2.5 concentrations. We evaluated this estimate with LOOCV as above, using the complete set of measurements for the evaluation step. Finally, we used our kriged estimates as inputs to our GRR and GWR calculations and evaluated those results as well. Because the location and number of observations from sites vary, not all sites provide the same amount of information to the kriging estimate and the resulting GRR and GWR estimates. To account for this, we repeated our analysis for a given number of sites included 100 times (for a total of 200,000 iterations). We calculated R 2, slope, and standard error statistics for each estimate and plotted the mean value of each statistics across the 100 trials as a function of sites included, with shading to represent between the 25th and 75th percentiles. The results are shown in Figure 5.
Figure 5.
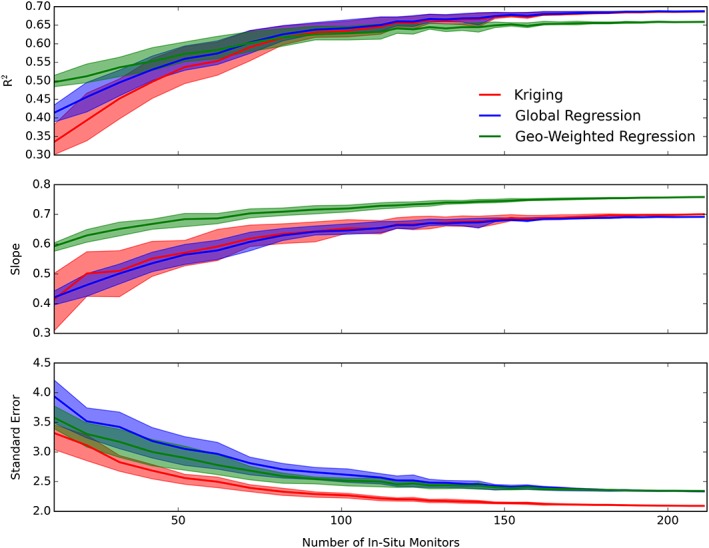
R 2, slope, and standard error (top) for kriging, (middle) Global Ridge Regression, and (bottom) Geographically Weighted Regression models as a function of measurement site number included in the analysis. The shaded regions represent 25th and 75th percentiles for each statistic from the 100 random trials.
On average, the GWR performs best with respect to slope for any number of input monitors. Furthermore, GWR achieves the highest R 2 when fewer than 50 monitors (corresponding to 25% of total available monitors) are input into the model. Kriging and GRR both achieve higher R 2 values than GWR when 120 monitors (i.e., 60% of total available monitors) have been included in the estimates. With respect to standard error, kriging performs best for any number of sites. However, all three models maintain a STDE between 2.0 and 4.0 µg m−3, which is small relative to the concentrations that are typically produced by wildfire smoke.
A limitation of this analysis is that we have not optimized any of these estimation strategies for the new number of in situ monitors. The kriging weights are calculated based on the semivariogram which produced the best performance with all sites included. The purpose of the semivariogram is to capture the dependence of physical semivariance (i.e., spatial autocorrelation) as a function of distance and should theoretically be independent of the number of in situ monitors used to inform the model. In principle, the performance of the kriging interpolation should not change significantly if we were to recalculate the optimal semivariogram for each configuration of surface sites. However, we acknowledge that using the semivariogram determined from all in situ measurements is not realistic for a sparsely monitored region, where the semivariogram would be based only on available measurements.
Likewise, the free parameter in the GRR estimate is α, which is adjusted depending on the degree of multicollinearity of the system. We do not expect the multicollinearity of the system to change significantly as surface monitors are removed from the system, so the previously calculated value should be sufficient. However, because α was tuned for a more extensively monitored region, the optimal choice of this parameter value may be more challenging to determine in a more realistic analysis of a sparsely monitored wildfire.
In contrast, GWR has a bandwidth parameter, which is the spatial scale at which the GWR coefficients influence a given part of the domain. We expect the optimal bandwidth parameter to change as a function of number and configuration of monitors, as clustering effects due to the spatial heterogeneity of measurement locations become potentially important. Therefore, this analysis can be thought of as a “lower bound” for GWR performance with fewer in situ measurement sites.
4. Conclusions
As wildfires become increasingly important for the air quality in the western U.S., there is a need to understand the risk to human health posed by wildfire smoke. Wildfires generate steep smoke gradients, which can be challenging for monitor networks to resolve. Furthermore, because smoke often impacts small populations, exposure misclassification can make epidemiological studies of wildfire smoke challenging.
This study uses three common techniques (chemical‐transport modeling, in situ measurements, and satellite observations) to determine population‐level exposure to air pollution in the context of the 2012 wildfire event in Washington state. Of the three techniques, interpolating between in situ measurements has the most predictive skill because (1) there was a dense network of measurements in this region for this time period and (2) the smoke plumes had a broad spatial extent. While WRF‐Chem and MODIS were both shown to have some predictive skill in the central parts of the state, poor performance in the urban corridor near the Puget Sound hampered the aggregated performance of both data sets.
We also investigated combining these three data sets into two regression models. For the first regression model (GRR), we aggregate data from all measurement sites to train one set of regression coefficients. Because the kriging data set produced estimates that outperformed the other two, this approach did not improve over the kriging data set on its own. The second regression approach (GWR) trained a unique set of coefficients for each in situ measurement site. These coefficients were then interpolated between sites to allow for estimation of smoke far from any individual measurement site. This approach allowed the regression model to use WRF‐Chem and MODIS in regions where both data sets were shown to have skill, while suppressing their influence in regions where they struggled. This approach was able to produce marginal improvements over the GRR and the kriging‐only approach.
Despite these improvements, wildfires still present challenges to exposure assessment, in large part due to the rapid changes in smoke concentration. This is because narrow, concentrated plumes are difficult to resolve, even with a relatively dense network of monitors. Therefore, accurate estimation of PM2.5 concentrations depends on a well‐modeled event and/or high‐resolution satellite observations. In terms of how the spikiness translates to different health outcomes, this is a major unknown and a major factor for why we are doing this research.
Finally, we investigated the skill of these approaches in a scenario with fewer in situ measurements available by withholding measurements from the analysis. As measurements become sparser, all three approaches lose skill, but the GWR approach outperforms the other two approaches at extremely low numbers of monitors, suggesting that this approach may be useful in less extensively monitored regions.
Supporting information
Supporting Information S1
Figure S1
Acknowledgments
We would like to acknowledge Kathleen McClean (University of British Columbia) and Sarah Henderson for providing us with in situ measurements from British Columbia. We would also like to acknowledge NASA for computing support, NASA Applied Sciences Program for supporting this work with grant NNX15AG35G, and Joint Fire Science Program for partially supporting this work with grant JFSP 13‐1‐1‐4. NCAR is operated by the University Corporation of Atmospheric Research under sponsorship of the National Science Foundation. Upon acceptance, all process data and code used in this analysis will be made available on the Colorado State University's publicly accessible digital data repository.
Lassman, W. , Ford B., Gan R. W., Pfister G., Magzamen S., Fischer E. V., and Pierce J. R. (2017), Spatial and temporal estimates of population exposure to wildfire smoke during the Washington state 2012 wildfire season using blended model, satellite, and in situ data, GeoHealth, 1, 106–121, doi: 10.1002/2017GH000049.
This article is a companion to Gan et al. [2017] doi:10.1002/2017GH000073.
References
- Abatzoglou, J. T. , and Williams A. P. (2016), Impact of anthropogenic climate change on wildfire across western US forests, Proc. Natl. Acad. Sci. U.S.A., 113(42), 11,770–11,775, doi: 10.1073/pnas.1607171113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alman, B. L. , Pfister G., Hao H., Stowell J., Hu X., Liu Y., and Strickland M. J. (2016), The association of wildfire smoke with respiratory and cardiovascular emergency department visits in Colorado in 2012: A case crossover study, Environ. Health, 15, 64, doi: 10.1186/s12940-016-0146-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alvarado, M. J. , et al. (2015), Investigating the links between ozone and organic aerosol chemistry in a biomass burning plume from a prescribed fire in California chaparral, Atmos. Chem. Phys., 15(12), 6667–6688, doi: 10.5194/acp-15-6667-2015. [DOI] [Google Scholar]
- Baker, K. R. , Woody M. C., Tonnesen G. S., Hutzell W., Pye H. O. T., Beaver M. R., Pouliot G., and Pierce T. (2016), Contribution of regional‐scale fire events to ozone and PM2.5 air quality estimated by photochemical modeling approaches, Atmos. Environ., 140, 539–554, doi: 10.1016/j.atmosenv.2016.06.032. [DOI] [Google Scholar]
- Bell, M. L. , and HEI Health Review Committee (2012), Assessment of the health impacts of particulate matter characteristics, Res. Rep. Health Eff. Inst., 161, 5–38. [PubMed] [Google Scholar]
- Brauer, M. , et al. (2012), Exposure assessment for estimation of the global burden of disease attributable to outdoor air pollution, Environ. Sci. Technol., 46(2), 652–660, doi: 10.1021/es2025752. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunsdon, C. , Fotheringham S., and Charlton M. (1998), Geographically Weighted Regression, J. R. Stat. Soc. Ser. Stat., 47(3), 431–443, doi: 10.1111/1467-9884.00145. [DOI] [PubMed] [Google Scholar]
- Chin, M. , Rood R. B., Lin S.‐J., Müller J.‐F., and Thompson A. M. (2000), Atmospheric sulfur cycle simulated in the global model GOCART: Model description and global properties, J. Geophys. Res., 105(D20), 24,671–24,687, doi: 10.1029/2000JD900384. [DOI] [Google Scholar]
- Deligiorgi, D. , and Philippopoulos K. (2011), Spatial interpolation methodologies in urban air pollution modeling: Application for the greater area of Metropolitan Athens, Greece, in Advanced Air Pollution, edited by Nejadkoorki F., InTech, Rijeka, Croatia, doi: 10.5772/17734. [DOI] [Google Scholar]
- Dockery, D. W. , Pope C. A., Xu X., Spengler J. D., Ware J. H., Fay M. E., Ferris B. G. J., and Speizer F. E. (1993), An association between air pollution and mortality in six U.S. cities, N. Engl. J. Med., 329(24), 1753–1759, doi: 10.1056/NEJM199312093292401. [DOI] [PubMed] [Google Scholar]
- Efron, B. (1982), The Jackknife, The Bootstrap and Other Resampling Plans, Society for Industrial and Applied Mathematics, Philadelphia, Pa. [Google Scholar]
- Elliott, C. T. , Henderson S. B., and Wan V. (2013), Time series analysis of fine particulate matter and asthma reliever dispensations in populations affected by forest fires, Environ. Health Global Access Sci. Source, 12, 11, doi: 10.1186/1476-069X-12-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Emmons, L. K. , et al. (2010), Description and evaluation of the Model for Ozone and Related chemical Tracers, version 4 (MOZART‐4), Geosci. Model Dev., 3(1), 43–67, doi: 10.5194/gmd-3-43-2010. [DOI] [Google Scholar]
- Engel‐Cox, J. A. , Holloman C. H., Coutant B. W., and Hoff R. M. (2004), Qualitative and quantitative evaluation of MODIS satellite sensor data for regional and urban scale air quality, Atmos. Environ., 38(16), 2495–2509, doi: 10.1016/j.atmosenv.2004.01.039. [DOI] [Google Scholar]
- Ford, B. , and Heald C. L. (2016), Exploring the uncertainty associated with satellite‐based estimates of premature mortality due to exposure to fine particulate matter, Atmos. Chem. Phys., 16(5), 3499–3523, doi: 10.5194/acp-16-3499-2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forouzanfar, M. H. , et al. (2015), Global, regional, and national comparative risk assessment of 79 behavioural, environmental and occupational, and metabolic risks or clusters of risks in 188 countries, 1990–2013: A systematic analysis for the Global Burden of Disease Study 2013, Lancet London Engl., 386(10,010), 2287–2323, doi: 10.1016/S0140-6736(15)00128-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fotheringham, A. S. , Brundson C., and Charlton M. (2002), Geographically Weighted Regression the Analysis of Spatially Varying Relationships, John Wiley, Hoboken, N. J. [Google Scholar]
- Gan, R. W. , Ford B., Lassman W., Pfister G., Vaiyanathan A., Volckens J., Pierce J. R., Magzamen S. (2017), Comparison of wildfire smoke estimation methods and association with cardiopulmonary‐related hospital admissions, GeoHealth, 1, doi: 10.1002/2017GH000073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Garcia‐Menendez, F. , Hu Y., and Odman M. T. (2013), Simulating smoke transport from wildland fires with a regional‐scale air quality model: Sensitivity to uncertain wind fields, J. Geophys. Res. Atmos., 118, 6493–6504, doi: 10.1002/jgrd.50524. [DOI] [Google Scholar]
- Gauderman, W. J. , Urman R., Avol E., Berhane K., McConnell R., Rappaport E., Chang R., Lurmann F., and Gilliland F. (2015), Association of improved air quality with lung development in children, N. Engl. J. Med., 372(10), 905–913, doi: 10.1056/NEJMoa1414123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grell, G. , Freitas S. R., Stuefer M., and Fast J. (2011), Inclusion of biomass burning in WRF‐Chem: Impact of wildfires on weather forecasts, Atmos. Chem. Phys., 11(11), 5289–5303, doi: 10.5194/acp-11-5289-2011. [DOI] [Google Scholar]
- Grell, G. A. , Peckham S. E., Schmitz R., McKeen S. A., Frost G., Skamarock W. C., and Eder B. (2005), Fully coupled “online” chemistry within the WRF model, Atmos. Environ., 39(37), 6957–6975, doi: 10.1016/j.atmosenv.2005.04.027. [DOI] [Google Scholar]
- Henderson, S. B. , Brauer M., MacNab Y. C., and Kennedy S. M. (2011), Three measures of forest fire smoke exposure and their associations with respiratory and cardiovascular health Outcomes in a population‐based cohort, Environ. Health Perspect., 119(9), 1266–1271, doi: 10.1289/ehp.1002288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu, X. , Waller L. A., Al‐Hamdan M. Z., Crosson W. L., Estes M. G. Jr., Estes S. M., Quattrochi D. A., Sarnat J. A., and Liu Y. (2013), Estimating ground‐level PM2.5 concentrations in the southeastern U.S. using Geographically Weighted Regression, Environ. Res., 121, 1–10, doi: 10.1016/j.envres.2012.11.003. [DOI] [PubMed] [Google Scholar]
- Hu, X.‐M. , Klein P. M., and Xue M. (2013), Evaluation of the updated YSU planetary boundary layer scheme within WRF for wind resource and air quality assessments, J. Geophys. Res. Atmos., 118, 10,490–10,505, doi: 10.1002/jgrd.50823. [DOI] [Google Scholar]
- Isaaks, E. H. , and Srivastava R. M. (1989), Applied Geostatistics, Oxford Univ. Press, New York. [Google Scholar]
- Janssen, S. , Dumont G., Fierens F., and Mensink C. (2008), Spatial interpolation of air pollution measurements using CORINE land cover data, Atmos. Environ., 42(20), 4884–4903, doi: 10.1016/j.atmosenv.2008.02.043. [DOI] [Google Scholar]
- Jerrett, M. , et al. (2005), Spatial analysis of air pollution and mortality in Los Angeles, Epidemiology, 16(6), 727–736. [DOI] [PubMed] [Google Scholar]
- Lelieveld, J. , Evans J. S., Fnais M., Giannadaki D., and Pozzer A. (2015), The contribution of outdoor air pollution sources to premature mortality on a global scale, Nature, 525(7569), 367–371, doi: 10.1038/nature15371. [DOI] [PubMed] [Google Scholar]
- Li, L. , Tian J., Zhang X., Holt J. B., and Piltner R. (2012), Estimating population exposure to fine particulate matter in the conterminous U.S. using shape function‐based spatiotemporal interpolation method: A county level analysis, GSTF Int. J. Comput., 1(4), 24–30. [PMC free article] [PubMed] [Google Scholar]
- Li, L. , Zhou X., Kalo M., and Piltner R. (2016), Spatiotemporal interpolation methods for the application of estimating population exposure to fine particulate matter in the contiguous U.S. and a real‐time Web application, Int. J. Environ. Res. Public Health, 13(8), doi: 10.3390/ijerph13080749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu, J. C. , Pereira G., Uhl S. A., Bravo M. A., and Bell M. L. (2015), A systematic review of the physical health impacts from non‐occupational exposure to wildfire smoke, Environ. Res., 136, 120–132, doi: 10.1016/j.envres.2014.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mallia, D. V. , Lin J. C., Urbanski S., Ehleringer J., and Nehrkorn T. (2015), Impacts of upwind wildfire emissions on CO, CO2, and PM2.5 concentrations in Salt Lake City, Utah, J. Geophys. Res. Atmos., 120, 147–166, doi: 10.1002/2014JD022472. [DOI] [Google Scholar]
- Miller, K. A. , Siscovick D. S., Sheppard L., Shepherd K., Sullivan J. H., Anderson G. L., and Kaufman J. D. (2007), Long‐term exposure to air pollution and incidence of cardiovascular events in women, N. Engl. J. Med., 356(5), 447–458, doi: 10.1056/NEJMoa054409. [DOI] [PubMed] [Google Scholar]
- Morrison, H. , and Gettelman A. (2008), A new two‐moment bulk stratiform cloud microphysics scheme in the Community Atmosphere Model, Version 3 (CAM3). Part I: Description and numerical tests, J. Clim., 21(15), 3642–3659, doi: 10.1175/2008JCLI2105.1. [DOI] [Google Scholar]
- Murphy, B. S. (2014), PyKrige: Development of a kriging toolkit for Python, Abstract H51K‐0753 presented at 2014 Fall Meeting, AGU, San Francisco, Calif., Dec.
- Paugam, R. , Wooster M., Freitas S., and Val Martin M. (2016), A review of approaches to estimate wildfire plume injection height within large‐scale atmospheric chemical transport models, Atmos. Chem. Phys., 16(2), 907–925, doi: 10.5194/acp-16-907-2016. [DOI] [Google Scholar]
- Pedregosa, F. , et al. (2011), Scikit‐learn: Machine learning in Python, J. Mach. Learn. Res., 12, 2825–2830. [Google Scholar]
- Pope, C. A. , and Dockery D. W. (2006), Health effects of fine particulate air pollution: Lines that connect, J. Air Waste Manage. Assoc., 56(6), 709–742, doi: 10.1080/10473289.2006.10464485. [DOI] [PubMed] [Google Scholar]
- Pope, C. A. , Burnett R. T., Thurston G. D., Thun M. J., Calle E. E., Krewski D., and Godleski J. J. (2004), Cardiovascular mortality and long‐term exposure to particulate air pollution, Circulation, 109(1), 71–77, doi: 10.1161/01.CIR.0000108927.80044.7F. [DOI] [PubMed] [Google Scholar]
- Rappold, A. G. , et al. (2011), Peat bog wildfire smoke exposure in rural North Carolina is associated with cardiopulmonary emergency department visits assessed through syndromic surveillance, Environ. Health Perspect., 119(10), 1415–1420, doi: 10.1289/ehp.1003206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reid, C. E. , Jerrett M., Petersen M. L., Pfister G. G., Morefield P. E., Tager I. B., Raffuse S. M., and Balmes J. R. (2015), Spatiotemporal prediction of fine particulate matter during the 2008 Northern California wildfires using machine learning, Environ. Sci. Technol., 49(6), 3887–3896, doi: 10.1021/es505846r. [DOI] [PubMed] [Google Scholar]
- Reid, C. E. , Brauer M., Johnston F., Jerrett M., Balmes J. R., and Elliott C. T. (2016), Critical review of health impacts of wildfire smoke exposure, Environ. Health Perspect., doi: 10.1289/ehp.1409277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Remer, L. A. , et al. (2005), The MODIS Aerosol Algorithm, Products, and Validation, J. Atmos. Sci., 62(4), 947–973, doi: 10.1175/JAS3385.1. [DOI] [Google Scholar]
- Saide, P. E. , et al. (2015), Revealing important nocturnal and day‐to‐day variations in fire smoke emissions through a multiplatform inversion, Geophys. Res. Lett., 42, 3609–3618, doi: 10.1002/2015GL063737. [DOI] [Google Scholar]
- Samet, J. M. , Dominici F., Curriero F. C., Coursac I., and Zeger S. L. (2000), Fine particulate air pollution and mortality in 20 U.S. cities, 1987–1994, N. Engl. J. Med., 343(24), 1742–1749, doi: 10.1056/NEJM200012143432401. [DOI] [PubMed] [Google Scholar]
- Sayer, A. M. , Munchak L. A., Hsu N. C., Levy R. C., Bettenhausen C., and Jeong M.‐J. (2014), MODIS Collection 6 aerosol products: Comparison between Aqua's e‐Deep Blue, Dark Target, and “merged” data sets, and usage recommendations, J. Geophys. Res. Atmos., 119, 13,965–13,989, doi: 10.1002/2014JD022453. [DOI] [Google Scholar]
- Sheppard, L. , Levy D., Norris G., Larson T., and Koenig J. Q. (1999), Effects of ambient air pollution on nonelderly asthma hospital: Epidemiology, LWW. [Available at http://journals.lww.com/epidem/Fulltext/1999/01000/Effects_of_Ambient_Air_Pollution_on_Nonelderly.6.aspx, accessed 2016‐11‐17.] [PubMed]
- Song, W. , Jia H., Huang J., and Zhang Y. (2014), A satellite‐based Geographically Weighted Regression model for regional PM2.5 estimation over the Pearl River Delta region in China, Remote Sens. Environ., 154, 1–7, doi: 10.1016/j.rse.2014.08.008. [DOI] [Google Scholar]
- Val Martin, M. , Heald C. L., Ford B., Prenni A. J., and Wiedinmyer C. (2013), A decadal satellite analysis of the origins and impacts of smoke in Colorado, Atmos. Chem. Phys., 13(15), 7429–7439, doi: 10.5194/acp-13-7429-2013. [DOI] [Google Scholar]
- van Donkelaar, A. , Martin R. V., and Park R. J. (2006), Estimating ground‐level PM2.5 using aerosol optical depth determined from satellite remote sensing, J. Geophys. Res., 111, D21201, doi: 10.1029/2005JD006996. [DOI] [Google Scholar]
- van Donkelaar, A. , Martin R. V., Levy R. C., da Silva A. M., Krzyzanowski M., Chubarova N. E., Semutnikova E., and Cohen A. J. (2011), Satellite‐based estimates of ground‐level fine particulate matter during extreme events: A case study of the Moscow fires in 2010, Atmos. Environ., 45(34), 6225–6232, doi: 10.1016/j.atmosenv.2011.07.068. [DOI] [Google Scholar]
- Vogel, C. R. (2002), 7. Regularization parameter selection methods, in Computational Methods for Inverse Problems, pp. 97–127, Society for Industrial and Applied Mathematics, Philadelphia, Pa. [Google Scholar]
- Westerling, A. L. , Hidalgo H. G., Cayan D. R., and Swetnam T. W. (2006), Warming and earlier spring increase western U.S. forest wildfire activity, Science, 313(5789), 940–943, doi: 10.1126/science.1128834. [DOI] [PubMed] [Google Scholar]
- Wiedinmyer, C. , Yokelson J., Emmons K., Soja J., Orlando J., and Al‐Saadi A. (2011), The Fire INventory from NCAR (FINN): A high resolution global model to estimate the emissions from open burning, Geosci. Model Dev., 4(3), 625, doi: 10.5194/gmd-4-625-2011. [DOI] [Google Scholar]
- Wu, J. , Winer A. M., and Delfino R. J. (2006), Exposure assessment of particulate matter air pollution before, during, and after the 2003 Southern California wildfires, Atmos. Environ., 40(18), 3333–3348, doi: 10.1016/j.atmosenv.2006.01.056. [DOI] [Google Scholar]
- Yao, J. , and Henderson S. B. (2014), An empirical model to estimate daily forest fire smoke exposure over a large geographic area using air quality, meteorological, and remote sensing data, J. Exposure Sci. Environ. Epidemiol., 24(3), 328–335, doi: 10.1038/jes.2013.87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- You, W. , Zang Z., Zhang L., Li Y., and Wang W. (2016), Estimating national‐scale ground‐level PM2.5 concentration in China using Geographically Weighted Regression based on MODIS and MISR AOD, Environ. Sci. Pollut. Res., 23(9), 8327–8338, doi: 10.1007/s11356-015-6027-9. [DOI] [PubMed] [Google Scholar]
- Yue, X. , Mickley L. J., Logan J. A., Hudman R. C., Martin M. V., and Yantosca R. M. (2015), Impact of 2050 climate change on North American wildfire: Consequences for ozone air quality, Atmos. Chem. Phys., 15(17), 10,033–10,055, doi: 10.5194/acp-15-10033-2015. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information S1
Figure S1


