Loss of Hyperconjugative Effects Drives Hydride Transfer during Dihydrofolate Reductase Catalysis

Abstract

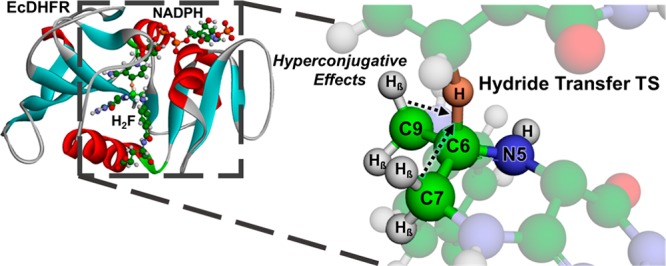
Hydride transfer is widespread in nature and has an essential role in applied research. However, the mechanisms of how this transformation occurs in living organisms remain a matter of vigorous debate. Here, we examined dihydrofolate reductase (DHFR), an enzyme that catalyzes hydride from C4′ of NADPH to C6 of 7,8-dihydrofolate (H₂F). Despite many investigations of the mechanism of this reaction, the contribution of polarization of the π-bond of H₂F in driving hydride transfer remains unclear. H₂F was stereospecifically labeled with deuterium β to the reacting center, and β-deuterium kinetic isotope effects were measured. Our experimental results combined with analysis derived from QM/MM simulations reveal that hydride transfer is triggered by polarization at the C6 of H₂F. The σ C_β–H bonds contribute to the buildup of the cationic character during the chemical transformation, and hyperconjugation influences the formation of the transition state. Our findings provide key insights into the hydride transfer mechanism of the DHFR-catalyzed reaction, which is a target for antiproliferative drugs and a paradigmatic model in mechanistic enzymology.

Introduction

Hydride transfer, a ubiquitous event found in all living organisms, has been subjected to intense investigation with the aim of deciphering the physicochemical basis of enzyme catalysis.^1,2 Despite a wealth of studies,³⁻⁸ a model that comprehensively illustrates the unparalleled catalytic power of enzymes is still lacking. Irrespective of whether electrostatics, dynamic coupling, and quantum tunneling contribute to an enzyme’s rate acceleration, all existing theories are built on the accepted principle of transition state stabilization.^9,10 Hence, the comprehensive characterization of enzyme transition states is essential.

Using dihydrofolate reductase (DHFR) as a model system, we explored the role played by hyperconjugation in driving hydride transfer. DHFR catalyzes the reduction of 7,8-dihydrofolate (H₂F) to 5,6,7,8-tetrahydrofolate (H₄F) via transfer of the C4′ pro-R hydride from NADPH to the C6 Re-face of H₂F (Figure 1).¹¹ DHFR is central in regulating the metabolic flux of the one-carbon cycle. Inhibitors of DHFR have broad applications in pharmacotherapy,¹² and trimethoprim, pyrimethamine, and methotrexate are frequently used in therapy.^13,14 There is, however, an emerging resistance to these drugs, and a better understanding of the mechanism underlying DHFR catalysis is needed to aid the design of new anti-DHFR drugs.¹³⁻¹⁷

Figure 1.

Reduction of 7,8-dihydrofolate (H₂F) in to 5,6,7,8-tetrahydrofolate (H₄F) catalyzed by dihydrofolate reductase (DHFR). Hydrogens located at the β positions of the C6 of H₂F are highlighted. pABA-Glu = p-aminobenzoyl-l-glutamate.

The kinetic isotope effect (KIE) is a powerful tool to investigate enzyme mechanisms.^8,9,18−20 During DHFR catalysis, hydride transfer to C6 and protonation of the N5 of H₂F occur (see Figure 1). Accordingly, both N5 and C6 of H₂F change from sp² to sp³ hybridization, while C4′ of NADPH alternates from sp³ to sp². Depending on the location of the isotopic label, there are two main classes of KIE that can be measured. Primary KIEs arise when atoms directly involved in the chemical transformation are replaced by their heavy counterparts.^6,19,21−23 Primary KIE measurements for NADPH(D) and heavy-atom (¹⁵N, ¹³C) isotope labeling of the primary reacting centers have generated evidence in support of a stepwise mechanism for DHFR from E. coli (EcDHFR).^21,22,24,25 Secondary α-deuterium KIEs (α-KIEs) arising from the rehybridization of C4′ of NADPH provide atomistic insights into local environmental changes during the chemical transformation, as isotopic substitution influences the rehybridization process of the primary atoms, which is reflected as a change in reaction rate.^23,26−28 However, despite EcDHFR being one of the most studied enzymes, the role of C6 rehybridization in H₂F has never been investigated in detail. Because the four hydrogens on C7 and C9 of H₂F are located in positions β to C6, secondary β-deuterium isotope effects (β-KIEs) can be measured to explore the extent of C6 rehybridization. In general, β-KIE values fall between 1.15 and 1.25, similar to those of α-KIEs (from 1.1 to 1.2),²⁹ and this has been attributed to hyperconjugation, a quantum mechanical effect where σ C_β–H(D) bonds partially donate electrons to the neighboring electron-deficient π-bond.^19,30−35 β-KIE measurements have been depicted in many enzyme catalysts,³⁶⁻⁴⁴ and they have been exploited to investigate reactions where hyperconjugation is likely to contribute to the stabilization of the enzymatic transition state. These include fumarate hydratase,³⁶ subtilisin,³⁷ β-lactamase,^38,39 chorismate synthase,⁴⁰ purine nucleoside phosphorylase,⁴¹ DNA glycosylases,^42,43 and enzyme-catalyzed acyl transfer reactions.⁴⁴ When the N5–C6 double bond is converted to a single bond during EcDHFR catalysis, the magnitude of this σ → π* effect can be different in the reactant and transition states (RS and TS), provoking a variation of the C_β–H stretching force constants and leading to a measurable β-isotope effect. Given the nature of hyperconjugation, β-KIEs are also conformation dependent, with the maximum magnitude being obtained when the σ C_β–H(D) bond is aligned to the electron-deficient π-network,^35,45−47 and hence an angular dependence of the β-KIEs is expected. Nevertheless, because the preparation of the corresponding deuterated H₂F remains a nontrivial task, the corresponding β-KIE measurement has not been conducted.

Here, a versatile synthetic strategy is described to produce H₂Fs that are regio- and stereospecifically deuterated at the C7 and C9 positions. The use of deuterated H₂Fs in β-KIE measurements combined with QM/MM simulations reveal that the C6 hydride acceptor of H₂F is polarized upon approaching the TS. Conformation-dependent hyperconjugative effects play a key role in the progression of the hydride transfer reaction from the RS to the TS.

Results and Discussion

Chemoenzymatic Synthesis of Folate Deuterated on C7 and C9

An adaptation of our chemoenzymatic synthesis of dihydrofolate (H₂F) was used for deuterium incorporation at C7 and C9 of H₂F (Figure 2).²⁵ Folic acid from a commercial source was transformed into 6-formylpterin (6-FP) by oxidation with sodium sulfite under acidic conditions.⁴⁸ Replacing exchangeable protons with their deuterated counterparts eventually leads to deuterium enrichment at the aldehydic position (93%). Upon reduction with dimethylaminoborane (DMAB) or its deuterated equivalent, 6-FP was converted to 6-hydroxymethylpterin (6-HMP) or 6-HMP with deuterium selectively incorporated at the C9 position (90% enrichment). Further reduction of 6-HMP with sodium dithionite led to 6-hydroxymethyl-7,8-dihydropterin (6-HMDP). Likewise, the use of D₂O in place of water led to the incorporation of a deuterium atom at the C7 position of the pterin ring (95% enrichment).⁴⁹

Figure 2.

Synthetic strategies to produce deuterium-labeled H₂Fs. (a) Folic acid was converted into 6-formylpterin (6-FP) by oxidation with sodium sulfite under acidic conditions.⁴⁸ Subsequently, 6-FP was reduced to 6-hydroxymethylpterin (6-HMP) by dimethylaminoborane (DMAB). Further reduction of 6-HMP by sodium dithionite affords 6-hydroxymethyl-7,8-dihydropterin (6-HMDP),⁴⁹ which was enzymatically transformed to H₂F by the combined actions of 6-hydroxymethyl 7,8-dihydropterin pyrophosphokinase (HPPK) and dihydropteroate synthase (DHPS).²⁵ (b) Reduction of deuterated 6-FP (6-FP-d) with either (S)- or (R)-alpine borane offers an alternative route to stereoselectively introduce a deuterium in 6-HMP.⁵¹ Cofactor recycling was operated by myokinase (MK) and pyruvate kinase (PK).^25,50 Details can be found in the Supporting Information.

6-HMDP is a metabolite of the folate de novo biosynthetic pathway and thus can be transformed in vitro to H₂F (Figure 2a) with 6-hydroxymethyl 7,8-dihydropterin pyrophosphokinase (HPPK) and dihydropteroate synthase (DHPS).²⁵ In the first step, 6-HMDP was added with pyrophosphate by HPPK. Formation of 6-hydroxymethyl-7,8-dihydropterin diphosphate uses 1 equiv of ATP (6-HMDPpp); therefore, a regeneration system of the cofactor based on myokinase (MK) and pyruvate kinase (PK) was included.⁵⁰ 6-HMDPpp was subsequently combined with p-aminobenzoyl-l-glutamic acid (pABA-Glu) to afford H₂F. The use of deuterated reagents in each synthetic step allowed the production of [7-²H], [9-²H], [9,9-²H₂], [7,9-²H₂] and [7,9,9-²H₃] H₂F, respectively.

Since hyperconjugation relies on the position of the β C_β–H bond with respect to the π*-bond, we predict that the magnitude of the β-KIE is dependent on the dihedral angle between C_β–H and C6–N5.^35,45−47 Consequently, (S)- and (R)-[9-²H] H₂F were produced by further modifying the synthetic pathway (Figure 2b). Deuterated 6-FP (6-FP-d) was reduced to (S)- and (R)-[9-²H] 6-HMP with (R)- and (S)-alpine borane, respectively (Midland reduction, Figure 2b),^51,52 and their absolute configurations were determined by a Mosher ester analysis (Supporting Information).⁵³ As detailed above, (R)- and (S)-[9-²H] 6-HMP were chemoenzymatically converted in (S)- and (R)-[9-²H] H₂F, respectively. It should be noted that the stereochemistry at C9 undergoes inversion during the nucleophilic displacement catalyzed by DHPS from R to S and vice versa.⁵⁴ Because both (S)- and (R)-[9-²H] H₂F share the same isotope source, 6-FP-d, the degree of isotopic enrichment (93%) between them is identical.

Experimental and Theoretical Determination of β-KIEs

To investigate rehybridization of C6 of H₂F in the hydride transfer TS of EcDHFR, deuterated H₂Fs produced in this work were used to measure experimental β-KIEs (Figure 2, Figures S1–S24, and Table 1). At pH 7.0 under pre-steady-state conditions between 5 and 35 °C, inverse β-KIEs were obtained (Table 1, Tables S1–S5, and Figures S26–S29; see the Supporting Information for data collection and processing). For racemic [7-²H] and [9-²H] H₂Fs, the average β-KIEs were of 0.96 ± 0.01 and 0.96 ± 0.01, respectively, over the examined temperature range (Table S1).

Table 1. β-KIEs Measured between 5 and 35 °C for Deuterated H₂Fs^a.

	R1	R2	R3	R4	β-KIEav
[7-2H] H2F	H	H	H/D (racemic)		0.96 ± 0.01
[9-2H] H2F	H/D (racemic)		H	H	0.96 ± 0.01
(R)-[9-2H] H2F	D	H	H	H	0.960 ± 0.009
(S)-[9-2H] H2F	H	D	H	H	0.980 ± 0.005
[9,9-2H2] H2F	D	D	H	H	0.952 ± 0.006
[7,9-2H2] H2F	H/D (racemic)		H/D (racemic)		0.95 ± 0.01
[7,9,9-2H3] H2F	D	D	H/D (racemic)		0.924 ± 0.006

^aEach value represents the average of the β-KIEs measured at 5, 10, 15, 20, 25, 30, and 35 °C for each compound (Table S1). Errors are intended as standard deviations of the mean values.

β-Deuterium isotope effects mainly originate from hyperconjugation between an electron-deficient π-orbital and a vicinal σ-donor.³⁵ As previously shown in solvolysis reactions,^45,46 hyperconjugation is dependent on the dihedral angle (ϕ) between the σ C_β–H(D) and an electron-deficient π-orbital, as they must align perpendicularly for maximum σ→ π* donation.^35,45,46 Such a spatial requirement indicates that the magnitude of the β-KIE is dependent on how the C_β–H(D) bond aligns to the electron-deficient π orbital. (R)-[9-²H] and (S)-[9-²H] H₂F (93% enrichment) gave average β-KIEs of 0.960 ± 0.009 and 0.980 ± 0.005, respectively (Tables S1 and S5 and Figure S26). The use of mono-, di-, and trideuterated H₂Fs revealed that the magnitude of the inverse β-KIE was proportional to the increase in deuterium enrichment (Tables S1–S5 and Figures S26–S29). The magnitudes of the β-KIEs measured for monodeuterated H₂Fs ([7-²H] and [9-²H] H₂F) are lower than those measured with [7,9-²H₂] (0.95 ± 0.01) and [9,9-²H₂] H₂F (0.952 ± 0.006) (Table S1). This phenomenon becomes increasingly evident when [7,9,9-²H₃] H₂F is used, where the β-KIE value was 0.924 ± 0.006 between 5 and 35 °C (Table S1 and Figure S26).

Initial structures of the RS and TS were selected from QM/MM simulations corresponding to the minimum and maximum of the reaction free energy profiles, which are computed in terms of a potential of mean force (see the Supporting Information for details and Figure S30). These structures were fully optimized at the M06-2X/MM level with the 6-31G* basis set considering the full flexible protein solvated in a box of water molecules. It is important to point out that the potential energy barriers, which could slightly change if a larger basis set was employed, are insensitive to isotopic substitution; consequently, possible errors do not affect the final evaluation of the KIEs. The resulting structures were then characterized as being real minima (for the RS structures) or saddle points (TS structures) by inspection of the corresponding Hessian matrices. Similar to the case in previous studies,⁵⁵⁻⁵⁷ Hessians were used to compute the partition functions for each of the structures in the range of temperatures of the experiments. KIEs were evaluated for each pair of TS and RS structures from the ratio between their partition functions. In this regard, considering that the β-H(D) is not transferred during the present process and evaluation of the rate constant is not required for KIE calculations, quantum tunneling effects have not been considered. The final averaged KIE values are found as the arithmetic mean of all individual values for all the pairs of TS and RS structures. While it would produce results that are negligibly different from a numerical point of view, another possible strategy would be to obtain the full averaged partition functions and then calculate the KIE.⁵⁸ Our results are in excellent agreement with the experimental values (Tables S1 and S6–S12). AM1 values, also reported in this work (see Tables S6–S12), are very similar to those obtained at the M06-2X/6-31G* level, pointing out the convergence of our results with respect to the quantum description.

The inverse β-KIEs, observed when the pro-R and/or pro-S hydrogen atoms (H_R and H_S) of the C7 and C9 positions of H₂F are substituted by deuterium, originate from an increase in the force constants associated with the movements of these hydrogen atoms during the evolution from the RS to the TS. The averaged values of the stretching and bending force constants associated with these hydrogen atoms were obtained at the M06-2X/MM level (Table 2). The values provided in Table 2 illustrate an increase in the stretching force constants of the four hydrogen atoms (H7_R, H7_S, H9_R, and H9_S) as the hydride transfer advances from the RS to the TS, which can be related to hyperconjugation (see above). A natural bond order (NBO) analysis performed with Gaussian16 on the optimized structures confirms that the delocalization of the electronic density of the σ C_β–H orbital on the antibonding N5–C6 π-orbital stabilizes the system by a quantity up to 3.36 ± 0.09 kcal mol^–1 in the RS.^59,60

Table 2. M06-2X/MM Averaged Force Constants for C_β–H Stretching and H–C_β–H Bending Motions at the Reactant State (RS) and Transition State (TS)^a.

	RS	TS
C7–HR	5.23 ± 0.04	5.27 ± 0.03
C7–HS	5.40 ± 0.03	5.45 ± 0.02
C9–HR	5.26 ± 0.02	5.34 ± 0.02
C9–HS	5.25 ± 0.02	5.34 ± 0.04
HS–C7–HR	0.564 ± 0.001	0.596 ± 0.006
HS–C9–HR	0.637 ± 0.004	0.655 ± 0.007

^aUnits are mdyn Å^–1 and mdyn Å rad^–2, respectively.

An analysis of the optimized structures shows how the interatomic N5–C6 distance increases from 1.29 ± 0.01 Å at the RS to 1.39 ± 0.03 Å at the TS. The change in distance indicates that the π-bond between these two atoms is broken, and it is associated with a decrease of electron density at C6 which facilitates hydride transfer (the charges on C6 of an isolated H₂F are 0.34 ± 0.01 and 0.49 ± 0.01 au at the RS and TS geometry, respectively). The hyperconjugative effect vanishes while the double bond is transformed into a single bond, and then the electron population of the σ C_β–H(D) bond is increased. At the TS, the maximum stabilization energy due to the mixing of the σ C_β–H and the antibonding N5–C6 π-orbitals, as determined by the NBO analysis, is 2.54 ± 0.19 kcal mol^–1. Consequently, the stretching force constant of this bond is larger at the TS than that at the RS, resulting in an inverse β-KIE when the respective hydrogens are replaced with deuteriums. The ordering of the stretching force constants associated with H_R and H_S in the TS can be rationalized by considering the degree of overlap between the σ C_β–H(D) bonds and the N5–C6 π-bond (Figure 3). The N5–C6–C7–H_R and N5–C6–C7–H_S dihedral angles (ϕ) at the TS are −98 ± 4 and 147 ± 4°, respectively, indicating a larger overlap with the N5–C6 bond and hence a greater electron donation effect in the case of the C7–H_R bond. This explains the smaller value of the force constant of this hydrogen with respect to that of C7–H_S. For the C9 position, the values of the two N5–C6–C9–H dihedral angles are much closer (−127 ± 2 and 120 ± 1° for H_R and H_S, respectively), in agreement with the observed similarity between the two stretching force constants (Table 2). This correlation between the bond orientation and the force constants reinforces our interpretation of the observed inverse KIEs.

Figure 3.

Representative snapshots of thecomputed EcDHFR hydride transfer TS with relevant dihedral angles defining the position of the four β-hydrogen atoms indicated. (a) Overall view of protonated H₂F approached by NADPH. Perspective views of the hydride transfer TS from (b) C7 and (c) C9 of protonated H₂F.

According to the calculations, other force constants associated with the hydrogen atoms in β positions are also partially responsible for the inverse β-KIE. The bending motions of H_R–C_β–H_S show a substantial increase in the corresponding force constant (Table 2); we attribute this phenomenon to a “packing” effect at the TS. Effectively, the hydrogen atoms on C7 and C9 experience a more crowded environment at the TS than at the RS, thereby provoking a tighter bending mode. In particular, the cofactor is substantially closer to the substrate at the TS than at the RS on one side to facilitate hydride transfer. The cofactor approaches the substrate from the side of the H9_R and H7_S atoms (Figure 3), replacements of which with deuterium lead to a greater magnitude of inverse β-KIEs (Tables S11 and S12). The distance of the H7_S atom of the substrate to the closer hydrogen atom of the cofactor is reduced from 2.51 ± 0.09 Å at the RS to 2.16 ± 0.05 Å at the TS. On the other side, some active site residues also approach the substrate to stabilize the TS. Thr46 is closer to C9 of the substrate at the TS (the Cγ46-H9_R distance is reduced from 3.83 ± 0.03 to 3.47 ± 0.05 Å), while Ile94 is in proximity to the C7 center (the O94–H7_S distance is reduced from 2.54 ± 0.03 Å at the RS to 2.39 ± 0.01 Å at the TS). The “packing” effect around the TS also contributes to increasing the force constants associated with the β-hydrogens, resulting in a larger zero-point energy and an inverse KIE upon deuterium substitution. Interestingly, this packing effect was also described in a recent theoretical study focused exclusively on protonation of N5 of H₂F.⁶¹ Electrostatic stabilization clearly affects the whole N5–C6 double bond and surrounding β-hydrogens in the EcDHFR-H₂F complex, implying that the role of the “packing effect” stabilization goes well beyond modulating protonation of N5 of H₂F.

Conclusions

In conclusion, our work illustrates how polarization triggers hydride transfer in the DHFR catalysis. C6 of H₂F possesses strong carbenium ion character when it approaches the TS, and the buildup of a partially positive charge is stabilized by the surrounding σ C_β–H bonds through hyperconjugation, a phenomenon that is revealed here as an inverse β-KIE. Furthermore, as hyperconjugation is most effective when the σ C_β–H bond is perpendicular to the π*-bond, the magnitude of β-KIE depends on the stereochemistry. Computation indicates an increase in the force constants of the bond motions (stretching and bending) surrounding the β positions. The charge distribution at the TS is stabilized by EcDHFR-H₂F interactions, which also contribute to the increase in the force constant associated with β H(D) atom motions. Since C6 of H₂F must be polarized for hydride transfer to occur, our results are in agreement with a stepwise mechanism where protonation precedes hydride transfer.^{21,22,24,25,62} Because polarization of the N5–C6 double bond in H₂F and the hyperconjugative effects play a non-negligible role in the buildup of the TS of hydride transfer, those elements cannot be ignored when DHFR is used as a model to answer fundamental enzymology questions. Importantly, TS analysis has been shown to be a powerful approach to the design of enzyme inhibitors,^9,20 and information derived from the work reported here can be exploited for the design of DHFR transition state analogues.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscatal.9b02839.

• Details of the experimental procedures, pre-steady-state kinetic and computational data, and coordinates of the transition structures (PDF)

The authors declare no competing financial interest.