Ionic and Electronic Conduction in TiNb₂O₇

Abstract

TiNb₂O₇ is a Wadsley–Roth phase with a crystallographic shear structure and is a promising candidate for high-rate lithium ion energy storage. The fundamental aspects of the lithium insertion mechanism and conduction in TiNb₂O₇, however, are not well-characterized. Herein, experimental and computational insights are combined to understand the inherent properties of bulk TiNb₂O₇. The results show an increase in electronic conductivity of seven orders of magnitude upon lithiation and indicate that electrons exhibit both localized and delocalized character, with a maximum Curie constant and Li NMR paramagnetic shift near a composition of Li_0.60TiNb₂O₇. Square-planar or distorted-five-coordinate lithium sites are calculated to invert between thermodynamic minima or transition states. Lithium diffusion in the single-redox region (i.e., x ≤ 3 in Li_xTiNb₂O₇) is rapid with low activation barriers from NMR and D_Li = 10^–11 m² s^–1 at the temperature of the observed T₁ minima of 525–650 K for x ≥ 0.75. DFT calculations predict that ionic diffusion, like electronic conduction, is anisotropic with activation barriers for lithium hopping of 100–200 meV down the tunnels but ca. 700–1000 meV across the blocks. Lithium mobility is hindered in the multiredox region (i.e., x > 3 in Li_xTiNb₂O₇), related to a transition from interstitial-mediated to vacancy-mediated diffusion. Overall, lithium insertion leads to effective n-type self-doping of TiNb₂O₇ and high-rate conduction, while ionic motion is eventually hindered at high lithiation. Transition-state searching with beyond Li chemistries (Na⁺, K⁺, Mg²⁺) in TiNb₂O₇ reveals high diffusion barriers of 1–3 eV, indicating that this structure is specifically suited to Li⁺ mobility.

Introduction

Next-generation energy storage materials with fast recharging and high power capability are of immediate interest to accelerate widespread electric vehicle adoption.¹ Improved high-rate and high-capacity energy storage performance would also enable quick-charging portable devices and power-intensive tools, as well as not yet feasible applications that require power higher than that of conventional batteries and charge storage greater than that of supercapacitors. For negative electrodes (anodes) in rechargeable lithium ion batteries, graphite and other materials (e.g., silicon) that store a large quantity of lithium in a potential range close to the Li⁺/Li redox couple are favored for high-energy density applications. However, large overpotentials and spatial overpotential inhomogeneities at high current densities can lead to lithium plating on the surface of low-voltage electrodes.²⁻⁶ When lithium deposits as mossy or dendritic structures⁷⁻¹⁰—rather than plating smoothly onto a Li anode—the cell can short-circuit and undergo rapid heating that may lead to a battery fire/explosion.¹¹⁻¹⁴

In order to overcome the inherent challenges associated with the use of low-voltage electrode materials in high-rate applications, a series of higher-voltage anode material candidates are emerging. Lithium titanate spinel, Li₄Ti₅O₁₂, is the most established of these with an average voltage of 1.55 V vs Li⁺/Li and an accessible capacity of about 150 mA h g^–1, while other candidates include bronze-related TiO₂(B),¹⁵⁻¹⁸ T-Nb₂O₅,¹⁹⁻²² Nb₁₈W₁₆O₉₃,²³ and crystallographic shear (cs) structures such as Nb₁₆W₅O₅₅²³ and TiNb₂O₇.²⁴⁻³¹ An average lithiation potential of ca. 1.5 V lowers the energy density at the full cell level in comparison to the standard graphite anode at ca. 0.1 V; however, high-voltage oxide anodes preclude dendrite formation even under very high current density lithiation, limit SEI formation, do not suffer the degradation of graphite at high rates, and can still offer reasonable cell energy with high density atomic structures and particle morphologies.

Crystallographically, TiNb₂O₇ belongs to a family of compounds known as Wadsley–Roth phases: block phases exhibiting crystallographic shear planes at the borders of ReO₃-like regions (blocks) of corner-shared octahedra. TiNb₂O₇ (Figure 1) comprises blocks that are three octahedra wide and three octahedra long, and the blocks are infinitely connected in each plane (as opposed to blocks separated by tetrahedra in e.g. TiNb₂₄O₆₂ or the niobium tungsten oxides); this motif is denoted (3 × 3)_∞. TiNb₂O₇, the most titanium-rich ternary member of the mixed TiO₂–Nb₂O₅ series,^32,33 has demonstrated promise for its high rate capability in various nanostructures and its high theoretical capacity. A capacity of 232.7 mA h g^–1 would be expected on the basis of one-electron reductions of Ti⁴⁺ to Ti³⁺ and Nb⁵⁺ to Nb⁴⁺ (i.e., Li₃TiNb₂O₇), with additional capacity reported through multielectron redox or “overlithiation” beyond one lithium per transition metal (Li/TM). Previous studies have focused on aspects of the structural mechanism of lithiation in TiNb₂O₇^34,28,35 and performance-optimizing synthetic strategies.^{26−28,30,36−41} In addition to the generic challenges associated with implementing nanostructured particles for energy storage—cost, stability, and scalability⁴²—TiNb₂O₇ also specifically exhibits problematic gas evolution that is exacerbated by high-surface-area morphologies.⁴¹ In this work, we approach the fundamental aspects of electrochemical energy storage in TiNb₂O₇ by studying the lithiation of low-surface-area, micrometer-scale particles. A combined experimental and computational quantitative analysis is performed to understand the lithium and electron transport properties that enable high-rate performance in large particles of this wide-band-gap oxide. This has implications for many other insulating early-transition-metal oxide electrode candidates with d⁰ electron configurations.

Figure 1.

Crystal structure of the Wadsley–Roth phase TiNb₂O₇. (a) The (3 × 3)_∞ blocks of ReO₃-like octahedra are shaded; purple and green shaded blocks are offset by 1/2b in the structure. (b) Thirty-atom unit cell structure of TiNb₂O₇ used in DFT calculations. The five symmetrically distinct transition-metal (M) sites are labeled M₁–M₅, following the nomenclature of Perfler et al.¹ The two types of infinite tunnels along the b axis are labeled T1 and T2.

Solid-state nuclear magnetic resonance (NMR) spectroscopy is a versatile probe of local atomic and electronic structure, as well as ion dynamics, that has been widely applied to study transport and failure mechanisms in electrochemical energy storage materials.^43,44 As NMR spectra are sensitive to localized paramagnetism and delocalized Pauli paramagnetic effects (known as Knight shifts) as well as diamagnetic shielding from local coordination environments, we follow the changes that lithium insertion induces in the electronic and magnetic properties of TiNb₂O₇.

Nuclear magnetic relaxation is mediated by fluctuations on the time scale of the nuclear Larmor frequency (ω₀). Thus, when diffusion modulates the NMR couplings (e.g., dipolar, quadrupolar, and/or hyperfine), T₁ relaxation serves as a probe of atomic motion.⁴⁵⁻⁴⁷ The time variation of the ⁷Li z magnetization can be derived from the spectral density function of the motion, J(ω). Assuming that the correlation function for the diffusional motion is monoexponential, it is possible to compute the spectral density; this is the basis of the well-established Bloembergen–Purcell–Pound (BPP) model for analyzing relaxation due to atomic motion.⁴⁸ Here, the ⁷Li NMR relaxation in Li_xTiNb₂O₇ is examined over a wide temperature range, ca. 300–1000 K, and motional activation energies are extracted as a function of lithiation, i.e. state of charge. In favorable cases, where a T₁ minimum can be identified, it is possible to extract the lithium diffusivity via the Einstein–Smoluchowski relation. These NMR results are correlated with complementary analyses including magnetic susceptibility, electronic conductivity, and multipurpose density functional theory (DFT) calculations.

Ab initio calculations complement the experimental results by evaluating the cation configurations and predicting diffusion pathways and energy barriers, as well as the local environments. First of all, calculations on the host TiNb₂O₇ crystallographic shear structure set the scene for further calculations of lithium kinetics and spectroscopic signatures. Due to the mixed occupancy of Ti and Nb on the five crystallographically-distinct octahedral metal sites in TiNb₂O₇, cation configurations were enumerated and their energies minimized and thermodynamically ranked. Once lithium ions were added, a single-ended transition state searching method based on hybrid eigenvector following (HEF) was used in this work to explore minima and transition states on the complex potential energy landscape, without prior knowledge of the final states along the reaction pathway.⁴⁹ Using the HEF approach, the facile and highly anisotropic nature of Li diffusion in TiNb₂O₇ is rationalized. In principle, established double-ended transition state searching methods such as the nudged elastic band (NEB) approach^50,51 can also be used to determine the activation barrier for e.g. lithium or sodium hopping⁵² when the initial and final states along the conduction pathway are known, such as in layered oxides and spinels with well-defined ionic diffusion pathways. However, given the lack of prior knowledge of the transition and final states along the reaction pathways in TiNb₂O₇, the HEF approach is more appropriate for initial exploration of the landscape.

There have been a few reports on Na⁺ intercalation into TiNb₂O₇, in which the bulk material exhibited very low capacity, although the performance could be improved by nanosizing of the particles.⁵³⁻⁵⁶ There have been a dearth of reports of intercalation of other promising “beyond Li ion” cations such as K⁺ and Mg²⁺ into the TiNb₂O₇ structure, and yet this, and related phases, show tunnel structures that should be able to accommodate these ions. After establishing the HEF theoretical framework to determine lithium mobility, it is straightforward to extend the method to other intercalants, as illustrated in this work.

Overall the work shows that the high-rate capability of TiNb₂O₇ is related to rapid lithium mobility within the Wadsley–Roth block motifs down the tunnels along the b axis and also between intrablock tunnels. The specific activation energies are a function of the Ti/Nb ordering; however, irrespective of cation ordering, cross-block diffusion is negligible due to the high electrostatic repulsion at the shear planes of edge-sharing octahedra. Electronically, the structure undergoes a transition from (partially) localized to delocalized behavior as the concentration of lithium increases, with evidence that localization occurs primarily on titanium.

Experimental and Computational Methods

Synthesis

The samples investigated in this work were prepared by ball-milling a 1:1 stoichiometric ratio of TiO₂ (Alfa, 99.9%, anatase) and Nb₂O₅ (Alfa, 99.9985%, H polymorph) for 90 min in a zirconia ball mill (Spex 8000 M Mixer/Mill), pressing the powder into pellets at 600 MPa with a stainless-steel die set, sanding the pellet surfaces, and heating the pellets in air at 1623 K for 96 h with a 10 K min^–1 heating rate and natural cooling in the furnace (Carbolite, HTF 1700).

X-ray Diffraction

Phase purity was examined by X-ray diffraction on a laboratory Panalytical Empyrean diffractometer with a Cu Kα source and a rotating sample stage in Bragg–Brentano reflection geometry. The data were recorded from 5 to 80° 2θ in steps of 0.0167° at a rate of 3.75° min^–1. Data analysis and Rietveld refinement⁵⁷ were performed with GSAS-II,⁵⁸ and the structure visualization utilized VESTA 3.4.⁵⁹

Scanning Electron Microscopy (SEM)

SEM was conducted on a Sigma VP instrument (Zeiss) at 3.0 kV with secondary electron detection. To prepare the sample, TiNb₂O₇ powder was suspended in ethanol and dropped from a pipette onto a holey-carbon Cu-grid TEM sample holder.

X-ray Photoelectron Spectroscopy (XPS)

A Kratos Axis Ultra instrument was used to perform XPS with a monochromatic Al Kα source at 14.87 keV. Photoelectrons at pass energies of 80 eV were detected with a multichannel detector. The spectrum was analyzed using the CasaXPS software.

Diffuse Reflectance Spectroscopy

UV–visible spectrophotometry was measured with a Varian Cary 50 Bio instrument from 200 to 800 nm wavelengths. The sample was measured as a dry powder dispersed onto a quartz slide; the background was subtracted, and three measurements were averaged.

Tap Density

Powder tap density was recorded on an AutoTap (Quantachrome Instruments) instrument operating at 257 taps per minute. The measurement was performed according to ASTM international standard B527-15, modified to accommodate a 10 cm³ graduated cylinder.

Electrochemistry

Composite electrode films for electrode performance studies were prepared with bulk TiNb₂O₇ powder, conductive carbon (Super P, Timcal), and a polymeric binder (polyvinylidene difluoride, Kynar, HSV 900) in an 8:1:1 mass ratio. First, the oxide and carbon were ground together with an agate mortar and pestle. This mixture was then homogenized in a solution of PVDF dissolved in N-methyl-2-pyrrolidone (NMP, Sigma, 99.5%, anhydrous) to create a viscous slurry that was spread onto Cu foil with a doctor blade. Residual solvent was removed from the film by drying in a furnace at 60 °C overnight. Circular electrodes of 1.27 cm² were cut with a punch press with a low electrode active material loading of 1.0 mg cm^–2 to minimize overpotentials and focus on inherent micrometer particle properties; no calendaring steps were used in this work. Pure Li_xTiNb₂O₇ pellet electrodes of 100–550 mg were prepared for physical property measurements and structure characterization studies by pressing the powder into circular or bar-shaped free-standing pellets at 150 MPa without the presence of any conductive additive or binding agent (up to x ≤ 3.5). Highly lithiated samples (x ≥ 3.75 in Li_xTiNb₂O₇) for ex situ spectroscopic characterization required some conductive additive and binder and were prepared as free-standing pellets in an 8:1:1 mass ratio with Super P carbon (Timcal) and polytetrafluoroethylene (PTFE, Sigma, spheres) without the use of solvents or current collectors. After cycling, pellets were extracted from the cells and rinsed three times with 2 mL of dimethyl carbonate (DMC, Sigma, ≥ 99%, anhydrous). Electrochemical testing and sample preparation were conducted in stainless-steel 2032-type coin cells or Swagelok cells (conductivity measurements only) with a lithium metal anode (99.95%, LTS Research) and 1.0 M LiPF₆ in ethylene carbonate/dimethyl carbonate (1/1 v/v, Sigma, battery grade) liquid electrolyte. Electrochemical measurements were performed with Biologic potentiostat/galvanostat instruments. All potentials in this work are quoted relative to Li⁺/Li, and C rates are defined with respect to the reduction of one electron per transition metal (e.g., C/5 = 232.6 mA h g^–1/5 h = 46.5 mA g^–1).

Solid-State Nuclear Magnetic Resonance Spectroscopy

Measurements of ⁶Li and ⁷Li solid-state NMR were performed at 11.75 T (Bruker Ascend wide-bore magnet) and 16.44 T (Bruker Ultrashield wide-bore magnet) with Bruker Avance III spectrometers; variable-temperature ⁷Li NMR experiments were conducted at 9.402 T (Bruker Ultrashield wide-bore magnet) with a Bruker Avance spectrometer. The ⁶Li Larmor frequency is 103.0 MHz at 16.44 T and 73.60 MHz at 11.75 T. The ⁷Li Larmor frequency is 272.1 MHz at 16.44 T, 194.4 MHz at 11.75 T, and 155.6 MHz at 9.402 T. For ambient-temperature measurements, samples were packed into a 4.0 mm ZrO₂ rotor with a Kel-F cap and measured in a Bruker 4.0 mm magic angle spinning (MAS) probe at 12.5 kHz MAS frequency. Variable-temperature (VT) NMR relaxometry was performed with a Bruker 7.0 mm laser probe with samples packed into a 7.0 mm ZrO₂ rotor with a ZrO₂ cap and spun at 4 kHz MAS frequency. Temperature calibration of these experiments was performed with KBr (Sigma, ≥ 99.0%).⁶⁰ Sample temperatures are reported with an estimated accuracy of ±10 K for 293–473 K and ±20 K for 473–973 K.⁴⁷ Higher-resolution high- and low-temperature VT NMR was performed on Li_0.60TiNb₂O₇ center-packed with polytetrafluoroethylene (PTFE) ribbon in a 4.0 mm ZrO₂ rotor with a ZrO₂ cap and spun at 10 kHz MAS frequency. Temperature calibration of the 4.0 mm probe measurements was performed ex situ with Pb(NO₃)₂ (Sigma) with an estimated accuracy of ±5 K. One-dimensional ⁷Li experiments at 9.402 T were performed with a 2.5 μs π/2 excitation pulse and a recycle delay of 1.5–3.0 s, based on the observed T₁ relaxation such that the recycle delay was always greater than 5T₁ to ensure ≥99.3% quantitative spectra. T₁ relaxation times were measured with a saturation recovery pulse sequence. One-dimensional ⁶Li and ⁷Li spectra at 11.75 T were recorded with 1.0 and 2.0 μs π/2 pulses and relaxation delays of 3–20 and 5 s, respectively. Phase-cycled single pulse (π/2–acquire) and rotor-synchronized Hahn echo (π/2−τ–π–τ–acquire) experiments were performed. Due to the low natural abundance (nonenriched samples) and low Larmor frequency of ⁶Li, between 512 and 18828 time-domain free induction decays (FIDs) were coadded before Fourier transform to achieve signal to noise (S/N) >50. For all ⁷Li 1D spectra, 64 scans were sufficient for S/N >500 for the central transition. ⁶Li and ⁷Li NMR shifts were externally referenced to a 1.0 M aqueous solution of LiCl at 0.0 ppm.

The isotropic shift δ_iso is defined in the Haeberlen convention with the chemical shift anisotropy CSA taken as CSA = δ_ZZ – δ_iso and the shift asymmetry η_CSA given by 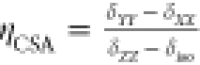. In this definition, the principal components of the shift tensor are ordered such that |δ_ZZ – δ_iso| ≥ |δ_XX – δ_iso| ≥ |δ_YY – δ_iso|. N.b.: this definition of CSA is sometimes referred to as the reduced anisotropy, which is equal to two-thirds of the “full” anisotropy 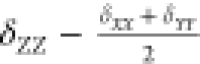used by some authors and programs. The quadrupolar coupling constant C_Q is defined by the nuclear quadrupole moment Q (Q_Li-7 = −4.00(3) fm²)⁶¹ and the largest principal component of the electric field gradient (EFG) at the nucleus V_ZZ according to where e is the electric charge and h is Planck’s constant. The quadrupolar asymmetry parameter η_Q is also defined by the EFG tensor components as 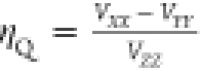ordered such that |V_ZZ| ≥ |V_YY| ≥ |V_XX|.

Magnetic Susceptibility

The magnetic susceptibility of Li_xTiNb₂O₇ was measured with a Quantum Design Magnetic Property Measurement System 3 (MPMS) superconducting quantum interference device (SQUID) magnetometer. Samples of ∼20 mg of pure Li_xTiNb₂O₇ powder were packed into a polypropylene holder, snapped into a brass rod, and wrapped with a single layer of Kapton tape. Lithiated samples were packed in an argon glovebox containing less than 1 ppm of oxygen or water. Field-cooled susceptibility was measured from 400 to 2 to 400 K in an applied field of 0.1 T. The small-field approximation was used for the susceptibility, assuming χ(T) = dM/dH ≈ M/H, where M is the magnetization and H is the magnetic field intensity.

Electric Conductivity

The conductivity of bar pellets of Li_xTiNb₂O₇ were measured under vacuum from room temperature to 150 K with a home-built four-point probe apparatus. The lithiated pellets were prepared by cold pressing pure TiNb₂O₇, assembling the pellets into Swagelok cells vs Li metal (as above), electrochemically lithiating to a desired stoichiometry, extracting and rinsing the lithiated pellets with dimethyl carbonate in an argon glovebox, and applying contacts with a silver epoxy onto the surface of the pellet. The nominal composition of each pellet was determined coulometrically, which assumes that every electron transferred corresponds to a Li ion intercalating into the host; this assumption is reasonable over the voltage window within the stability region of the organic carbonate electrolyte and in the absence of carbon or binder.

Density Functional Theory Calculations

The computational methods and codes are outlined here; see the Supporting Information for an expanded technical description. All electronic energies and forces in this work were calculated with DFT using the Perdew–Burke–Ernzerhof (PBE) functional⁶² in the VASP code⁶³ with projector augmented wave (PAW) pseudopotentials.⁶⁴ The energetics of Ti and Nb disorder were studied by enumerating all symmetrically distinct Ti/Nb orderings in a Ti₃Nb₆O₂₁ cell using the CASM package.^65,66 Changes in the electronic structure at the initial stages of lithiation were studied in a 1 × 3 × 1 supercell of TiNb₂O₇ produced from one of the lowest energy Ti/Nb orderings found from enumeration. To study the nature of electronic charge localization in the TiNb₂O₇ structure, a single electron was doped into the ordered supercell in the presence of a charge-neutralizing background. As it has previously been demonstrated that standard DFT fails to predict the correct localization behavior of electronic charge in analogous systems such as TiO₂^67,68 and Nb₁₂O₂₉,⁶⁹ the electronic structure was also studied with the inclusion of a Hubbard U correction (DFT+U).⁷⁰ The rotationally invariant form of DFT+U proposed by Liechtenstein et al. was used with the PBE functional (PBE+U).⁷¹U values of 5.2 eV were applied to Ti and Nb (U_Ti:Nb) or Ti only (U_Ti). An exchange parameter, J, of 1 eV was applied in both cases. To create a distortion of the lattice to promote polaron localization, ab initio molecular dynamics (AIMD) calculations were performed with either PBE or PBE+U at 400 K.⁷²

Single-ended transition state searches of Li transport were performed using the hybrid eigenvector following (HEF) approach^49,73,74 in the OPTIM code, with energies and forces taken from VASP using standard PBE. For an initial input structure, the HEF approach uses a variational procedure to find the smallest Hessian eigenvalue and corresponding eigenvector by minimizing the Rayleigh–Ritz ratio, followed by tangent space minimization as outlined in ref (73). The eigenvectors found by the variational procedure are then followed uphill until the transition state is reached. Once the transition state geometry has been located, the corresponding minima are found by displacing atoms at the transition state along the transition state eigenvector in the positive and negative directions followed by optimization of the atomic positions. The energies of the transition state, E_T, and initial and final minima, E_initial and E_final, respectively, are computed with the single-ended HEF approach without previous knowledge of the final state.

The ⁷Li paramagnetic NMR properties of the different local Li environments in the TiNb₂O₇ supercell were calculated with the VASP code with standard PBE according to the methodology as described in detail in previous studies.⁷⁵⁻⁷⁷ The size of the Fermi contact shift on ⁷Li was predicted by calculating the unpaired spin density, ρ_N(0), at the Li nuclear position in the ferromagnetic state with nominally 0 K DFT. ρ_N(0) can be related to the isotropic hyperfine coupling constant A_iso as outlined in refs (75 and 78). The value of A_iso at 0 K was then scaled into the paramagnetic regime with a scaling factor, Φ, to give an isotropic Fermi contact shift, δ_iso, via the relation 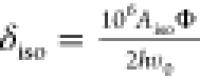, where ν₀ is the Larmor frequency of ⁷Li.⁷⁵ For a system with Curie–Weiss type magnetization, Φ is defined as 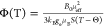, where g_e is the free electron g factor, μ_B is the Bohr magneton, B₀ is the external magnetic field, μ_eff is the effective magnetic moment, S is the formal spin, T is the temperature, and Θ is the Weiss constant. The values of δ_iso in this work were calculated in supercell structures with a single electron on a d¹ transition metal, and so the formal spin-only values of S = 1/2 and μ_eff = 1.73 μ_B were used with Θ set to 0 K. A value of T = 340 K was used to account for frictional heating during MAS. The anisotropic components of the hyperfine tensor, A_D, were also calculated at 0 K and scaled into the paramagnetic regime with Φ, analogous to the equation for δ_iso, to give the electron–nuclear dipolar shift components, δ_Dⁱⁱ where ii = xx, yy, zz corresponds to the principal axis of the tensor.^75,78 The reduced electron–nuclear dipolar anisotropy, Δδ_D, and asymmetry, η_D, are defined analogously to CSA and η_CSA. In addition to the hyperfine parameters, the EFG tensor V at the ⁷Li nucleus was also calculated and used to compute C_Q.

Results

Electrochemical Features and Lithium Ion Battery Performance of Bulk TiNb₂O₇

The electrochemical properties of TiNb₂O₇ have been reported for a variety of particle sizes/morphologies and electrode preparations.^{79,24,28,37,80} In this work, a series of analytical and performance tests on undoped, bulk TiNb₂O₇ establish a base from which to understand our experimental and computational results on the inherent or native host properties of the material. The material was prepared with standard high-temperature solid-state synthesis methods and analyzed for phase and compositional purity with powder X-ray diffraction and X-ray photoelectron spectroscopy (Figure S1 in the Supporting Information). Electrodes of micrometer-scale TiNb₂O₇ particles (Figures S2 and S3 in the Supporting Information) with a tap density of 2.8(1) g cm^–3 were assembled in standard coin cells and cycled against lithium metal. Electrodes with low areal mass loading levels were used to explore the inherent properties of these micrometer-sized particles. At a modest rate of C/5, the discharge and charge profiles (Figure 2a) can be divided into three regions: (i) an initial sloping profile for ca. 60 mA h g^–1, (ii) a flatter, “plateau-like” region until ca. 150–200 mA h g^–1, and (iii) another sloping region that extends into the multielectron redox region beyond 232.6 mA h g^–1 and continues below 1.0 V (Figure S4 in the Supporting Information). X-ray absorption spectra at the Ti and Nb K-edges indicate that both titanium and niobium are simultaneously reduced throughout discharge.²⁸ These regions can also be observed in the derivative plot (Figure 2b). Though we reserve the discussion until later in the text, we note here that the electrochemical regions are less well-defined in TiNb₂O₇ than in some other cs phases. The charge storage capacity attained at C/5 was between 300 and 350 mA h g^–1, depending on the lower voltage limit (V_min) (Figure 2c). The accessible capacity drops noticeably to 225–250 mA h g^–1 at 2C, decreasing further at higher rates but maintaining 100–140 mA h g^–1 at 20C. The bulk particles are also stable for at least 1000 cycles with >90% capacity retention (Supplementary Figure S5). Similarly to several other niobium-based oxides,^21,23,81 the electrochemical results suggest that, under these conditions, there is little apparent benefit from nanostructuring these materials for energy storage applications. The influence of mass loading, electrode calendering, and various carbon or electrolyte additives are important to optimize battery performance but are outside the scope of this fundamental study.

Figure 2.

Electrochemical profiles and performance of TiNb₂O₇ vs Li as a function of rate from C/5 to 100C. (a) Galvanostatic potential vs capacity profiles and (b) dQ/dV curves. In the dQ/dV plot, discharge curves have negative values and charge curves have positive values. (c) Rate test data under galvanostatic conditions with no potentiostatic hold (i.e., CC cycling) obtained on cycling the materials from 3.0 V to 1.0, 1.1, and 1.2 V. The discharge and charge curves in (a) and (b) correspond to the middle cycle of the variable rate data in (c) with a lower voltage cutoff limit of 1.2 V.

Electronic and Magnetic Evolution

The reaction of lithium with TiNb₂O₇ to form ca. Li_0.80TiNb₂O₇ is associated with a sloping voltage region from the start of discharge (∼2.0 V) to 1.66(1) V. Magnetic susceptibility (χ) measurements (Figure 3 and Figure S6 in the Supporting Information) indicate paramagnetic behavior in this region: the Curie constant (C), which measures the localized paramagnetism, increases linearly with introduced electrons, and thus lithium content, at low lithium concentrations. Beyond ca. Li_0.75TiNb₂O₇, the temperature-independent contribution (χ₀) to the total magnetic susceptibility increases (Figure 3). Despite the increase in d electrons at higher lithiation, the absolute magnitude of C is less for Li_1.50TiNb₂O₇ than for the less lithiated samples. This effect is even more dramatic when the localized paramagnetic contribution is normalized to the number of lithium and electrons transferred (C per Li). The increase in χ₀ and decrease in C are both signatures of the emergence of Pauli paramagnetism from delocalized electrons. Overall, Li_xTiNb₂O₇ evolves from a diamagnetic insulator at x = 0 to host variable amounts of localized and delocalized electrons as a function of lithium content. On the basis of the magnetic measurements, the proportion of localized electrons is largest for low lithium contents, while at high lithium contents, most electrons delocalize. This suggests the emergence of metallic conductivity upon electrochemical lithiation.

Figure 3.

Magnetic constants of Li_xTiNb₂O₇. The temperature-dependent Curie constant (C) and temperature-independent contribution to magnetic susceptibility (χ₀) are shown normalized to the amount of sample (mol^–1) and of lithium (mol_Li^–1); the latter is equivalent to the number of d¹ electrons in the system. The effective magnetic moment per lithium (i.e., per d¹ electron) indicates partial Curie–Weiss paramagnetism at low x and nearly zero Curie–Weiss paramagnetic contribution at high x.

Four-point probe resistivity (ρ) measurements were recorded for Li_xTiNb₂O₇ as a function of lithium content on non-sintered, polycrystalline, cold-pressed bar pellets (Table 1). From the previous measurements of Xing et al., a room-temperature resistivity for TiNb₂O₇ of 10⁹ Ω cm can be predicted.⁸² However, upon lithiation to Li_0.25TiNb₂O₇ (0.083 Li/TM, 19 mA h g^–1) the room temperature resistivity is 5 × 10¹ Ω cm (Table 1 and Figure S7 in the Supporting Information), a decrease of over seven orders of magnitude. Clearly the n-doping of insulating d⁰ TiNb₂O₇ via electrochemical reduction increases the carrier concentration to convert this electronic insulator into an effective conductor.

Table 1. Room-Temperature Resistivity of Li_xTiNb₂O₇.

nominal composition	Li/TM	capacity (mA h g–1)	resistivity @ 294 K (Ω cm)
TiNb2O7	0	0	1 × 109a
Li0.25TiNb2O7	0.083	19	5 × 101
Li0.50TiNb2O7	0.17	39	1 × 102
Li1.00TiNb2O7	0.33	78	7 × 102
Li1.50TiNb2O7	0.50	116	2 × 103
Li2.25TiNb2O7	0.75	174	2 × 103
Li3.00TiNb2O7	1.00	233	8 × 102

^aRoom-temperature resistivity of TiNb₂O₇ extrapolated from 450–1100 °C data of Xing et al.⁸² This polycrystalline sample was sintered at high temperatures; the lithiated samples were not sintered.

The lithiated polycrystalline samples were not hot-pressed out of concern for stability at the high temperatures required for densification of refractory oxides. It is thus likely that there is a significant grain boundary contribution to the measured resistances and the values reported here really represent a lower limit on the inherent conductivity of Li_xTiNb₂O₇. Cava et al. observed that resistivity measurements on non-sintered, polycrystalline, cold-pressed bar pellets of crystallographic shear niobium oxides typically exhibit resistivity that is two orders of magnitude higher than would be measured on single crystals and one order of magnitude higher than would be measured on a sintered pellet.⁸³ The resistivity appears to increase for greater lithiation, but this too may have microstructural origins related to grain boundaries and/or pellet expansion. These effects account for the fact that the bulk resistivity measurements do not show the metallic temperature dependence that would have been expected on the basis of the magnetic susceptibility measurements. Nevertheless, the resistivities of all samples over the range Li_0.25TiNb₂O₇ to Li_3.00TiNb₂O₇ are many orders of magnitude lower than that of the host compound and compare favorably with other electrode materials.⁸⁴ The conductivity of highly lithiated TiNb₂O₇ is quantitatively similar to the measurement that Cava et al. recorded on lithiated H–Nb₂O₅, which exhibited a room-temperature resistivity of 4 × 10³ Ω cm for H-Li_1.8Nb₂O₅.⁸³

Electronic Structure Calculations

Cation Ordering

Partial ordering of Ti and Nb ions over the five distinct transition metal sites (M₁–M₅; Figure 1) has been observed from single-crystal X-ray and powder neutron diffraction studies of TiNb₂O₇.^35,85,86 In this work, the cation ordering was investigated from first-principles calculations with the PBE functional in a 30-atom (Ti₃Nb₆O₂₁) cell (Figure 1b) to determine the enthalpic ground-state host structure. The connectivity of the adjacent 3 × 3 blocks leads to two different types of tunnels along the b axis of the cell, labeled T1 and T2 in Figure 1b. Two Ti⁴⁺ ions occupied the M₅ metal sites at the edge of tunnel T2 in the four lowest energy structures, which is consistent with the experimental studies. In the enumerated structures, the third Ti⁴⁺ ion occupied one of the possible M₁–M₄ sites. In the lowest energy structure, the M₄ site on the edge of the ReO₃-like block was occupied by Ti⁴⁺, although the energy difference between the other structures with Ti⁴⁺ at the M₁ (40 meV f.u.^–1), M₂ (20 meV f.u.^–1), or M₃ (30 meV f.u.^–1) sites was small. The highest energy structure contained Ti⁴⁺ ions solely on the M₁ and M₂ sites, and was 660 meV f.u.^–1 above the ground state. At the synthesis temperature of 1623 K, the thermal energy is approximately 140 meV, which suggests that there will be significant disorder between Ti⁴⁺ and Nb⁵⁺, particularly on the M₁–M₄ sites.

Electronic Structure

It has been previously shown that, on lithiation, the Ti⁴⁺ and Nb⁵⁺ species are both reduced as electrons are introduced into the structure,²⁸ with Mulliken charges suggesting a greater degree of reduction taking place on the metal sites at the corners of the blocks (M₃ and M₅).³⁵ In transition-metal oxides, the localization of charge is often accompanied by a local distortion of the lattice, forming a polaron defect. To study the changes in the electronic structure on initial reduction, an “ordered” 1 × 3 × 1 supercell of TiNb₂O₇ containing Ti⁴⁺ ions on the M₅ and M₁ sites was used. This structure was chosen over the marginally lower energy Ti/Nb ordering with Ti on M₅ and M₄ sites, due to the higher symmetry of the former case, which decreased the number of inequivalent M sites. A second, “disordered” 1 × 3 × 1 supercell was also created in which the Ti and Nb ions were randomly distributed over the Ti and Nb sites. After full structural optimization with the PBE functional, the energy of the disordered TiNb₂O₇ cell was only 80 meV f.u.^–1 higher in energy than the lowest energy TiNb₂O₇ structure found previously. A single electron was then doped into the ordered and disordered structures in the presence of a charge-neutralizing background. A local distortion of the lattice was produced with AIMD at 400 K (see Supplementary Methods in the Supporting Information), followed by optimization of the atomic positions with PBE or PBE+U (U_Ti = 5.2 eV and U_Ti:Nb = 5.2 eV). The lattice parameters for both systems were fixed to the undoped cell as optimized with PBE. The densities of states of the optimized structures are shown in Figure 4 and Figure S8 in the Supporting Information.

Figure 4.

Density of states (DOS) for (a) pristine and (b) electron-doped TiNb₂O₇ supercell calculated with the PBE functional. (c) DOS of the electron-doped structure calculated with a Hubbard U correction on Ti (U_Ti = 5.2 eV). An enlarged view of the localized polaron state within the gap is shown with a red box. The dashed black line indicates the Fermi energy (E_F). Magnetization density isosurface for (d) delocalized and (e) localized electronic states predicted with PBE and PBE+U, respectively. Spin density isosurfaces are shown in purple. Isosurface levels of 0.001 and 0.005 a₀^–3 were used for (d) and (e), respectively. The gray lines in (d) and (e) indicate the edges of the unit cell.

For the pristine ordered TiNb₂O₇ structure without an additional electron (Figure 4a), the electronic structure calculated with PBE has an optical gap of 1.87 eV between the valence and conduction bands, which is consistent with previous DFT studies.⁸⁷ The underestimation of the energy gap in comparison to the experimentally measured optical gap (3.06 eV, Figure S9 in the Supporting Information) is due to the self-interaction error in standard DFT leading to an overly delocalized wave function.

The introduction of an electron into the ordered TiNb₂O₇ structure results in a metallic state. During the AIMD calculation there was a partial localization of the electron spin (∼0.1 e^–) on the M₅ sites on the edges of the tunnels as a result of local bond distortions. After structural optimization with standard DFT, a spin-polarized state at the bottom of the conduction band was formed (Figure 4b). The magnetization density of the DFT structure (Figure 4d) is delocalized over multiple Ti/Nb sites, forming a spin-polarized metallic state. The greatest amount of spin density is again localized on the M₅ sites at the edge of tunnel T2, with the least spin density on the M₁ sites in the center of tunnel T1. The formation of a similar spin-polarized metallic state is also observed for the disordered TiNb₂O₇ supercell calculated with standard DFT (Figure S10 in the Supporting Information).

For both the ordered and disordered structures, the addition of a U correction results in a localized electronic state within the original energy gap. In the ordered TiNb₂O₇ structure, U_Ti (Figure 4c) or U_Ti:Nb (Figure S8 in the Supporting Information) corrections lead to a localized state that is primarily of Ti character from the DOS, with integrated local magnetic moments of 0.83 and 0.85 μ_B, respectively. The magnetization density (purple) of the structure with U_Ti = 5.2 eV is shown in Figure 4e. A localization of the magnetization is clearly present on a single Ti at the M₅ site, which is coupled to an elongation of the Ti–O bonds (Table S1 in the Supporting Information), corresponding to the formation of a small polaron. By starting the structural optimization from the metallic DFT structure obtained with PBE, it was also possible to stabilize a spin-polarized metallic state, analogous to Figure 4b, for a structure with a U_Ti correction applied. The resulting delocalized state was 0.101 eV higher in energy than the localized, polaron state.

In the disordered structure, the application of a U_Ti correction resulted in a localized polaron on an M₃ site at the corner of tunnel T1, as shown in Figure S10b in the Supporting Information, with a local magnetic moment of 0.87 μ_B. Application of a U correction on both Ti and Nb (U_Ti:Nb), resulted in a localized polaron on two adjacent M₅ Nb sites (Figure S10c in the Supporting Information). The magnetic moments of the two Nb sites in the polaron state were 0.33 and 0.36 μ_B.

The localization of charge with the application of a U parameter, as opposed to the metallic state found with standard DFT, is more consistent with the localized magnetic moments observed from magnetic measurements and the Li NMR spectra (vide infra). Although a spin-polarized state is not obtained with standard DFT, the preferential reduction of the different M sites is still in qualitative agreement with previous hybrid DFT studies.³⁵ The exact location of polaron defects in the TiNb₂O₇ structure is sensitive to the initial structure and nature of the U correction, and the different site preference between the ordered and disordered cells also suggests that the local Ti/Nb environments will affect the charge localization.

Lithium Solid-State NMR Spectroscopy

To understand the lithium insertion process of TiNb₂O₇, ⁶Li and ⁷Li solid-state MAS NMR spectra were recorded as a function of lithium content from Li_0.10TiNb₂O₇ (0.033 Li/TM) to Li_5.50TiNb₂O₇ (1.83 Li/TM) (Figure 5). At the start of discharge a ⁷Li resonance is observed at the composition Li_0.10TiNb₂O₇ that fits well to a single Gaussian–Lorentzian (pseudo-Voigt) line (Figure S11 in the Supporting Information). Upon further lithiation, two resonances are observed; the major signal (ca. 90% integrated intensity) shifts to lower frequencies on increasing lithiation, reaching −10.7 ppm at Li_0.60TiNb₂O₇ (Figure 5 and Figure S12 in the Supporting Information), which is well outside the typical range of diamagnetic lithium. Hahn echo MAS NMR experiments also indicate a shorter T₂ spin–spin relaxation constant for the negatively shifted resonance (Figure S13 in the Supporting Information). Both the negative resonant frequency and the shorter T₂ of this signal suggest an increased paramagnetic shift contribution, arising from localized electrons on the niobium and titanium ions as they are reduced from d⁰ to d¹ electronic states in the first electrochemical region. This is in agreement with the magnetic susceptibility data at low lithium content. Given the paramagnetic origin of this shift, it is then surprising to observe narrow NMR line shapes. To investigate this, high-resolution variable-temperature ⁷Li MAS NMR spectra of Li_0.60TiNb₂O₇ were recorded below and above room temperature (Figure S14 in the Supporting Information). The low-temperature NMR spectra show dramatic broadening of the negatively shifted resonance, while the high-temperature spectra show further line narrowing. These experiments suggest that the paramagnetic resonance is partially motionally narrowed at room temperature—another indication of the lithium mobility under ambient conditions in the TiNb₂O₇ host material. Furthermore, the magnitude of the paramagnetic shift decreases with increasing temperature, i.e. the shift becomes less negative, confirming that the shift is paramagnetic in origin (Figure S14 in the Supporting Information).

Figure 5.

⁶Li (solid lines) and ⁷Li (dashed lines) MAS NMR spectra of Li_xTiNb₂O₇. Single-pulse spectra were collected in the range x = 0.10–5.50 (8–426 mA h g^–1) at an MAS frequency of 12.5 kHz and B₀ = 11.7 T.

As the structure is further lithiated, the resonance shifts back toward 0 ppm and the line shape can again be well described by a single peak for Li_1.20TiNb₂O₇. The NMR line widths (full width at half-maximum, fwhm) decrease for samples within the second, pseudoplateau-like electrochemical feature, indicating increased motional averaging.

The NMR spectra of lithium concentrations corresponding to the third, sloping region of the electrochemical profile are characterized by a broad, asymmetric signal centered around 0 ppm; this signal can be described with a simple two-component model (Figures S11 and S12 in the Supporting Information) for all lithium contents greater than Li₂TiNb₂O₇. While the fewest possible peaks were used to fit each NMR line shape, more lithium sites and thus resonances are expected from the crystal structure; this anomaly could be due to either very small shift differences between lithium in magnetically inequivalent sites or lithium exchange between different sites with an exchange frequency greater than the separation between their isolated NMR shifts. Both effects likely coexist in Li_xTiNb₂O₇ with a small shift range and rapid lithium mobility. The small shift also suggests that the Knight shift contributions, which could be core-polarization or orbital in nature, either are very small or effectively cancel out.

⁷Li NMR spectroscopy was complemented by high-resolution ⁶Li NMR spectroscopy (Figure 5) across the entire lithiation series: the dipolar and quadrupolar broadening mechanisms are suppressed for ⁶Li vs ⁷Li due to the smaller Larmor frequency and quadrupole moment, respectively, of ⁶Li. The similarity of the isotropic resonance line width trends between ⁶Li and ⁷Li for Li_xTiNb₂O₇ is evidence that the changes in broadening are not caused by dipolar coupling between nuclei or quadrupolar coupling between the nuclear quadrupole and the electric field gradient at the nucleus but rather are due to nucleus-independent effects such as solid-state exchange kinetics and distributions of environments.

⁷Li Paramagnetic NMR Calculations

The ⁷Li NMR parameters of the local Li minima (Li_A–Li_G) in the ordered supercell (LiTi₉Nb₁₈O₆₃) were determined from first-principles calculations to aid the assignment of the experimental NMR (Table S2 in the Supporting Information and discussion therein). An in-depth discussion of the Li positions will be given below in the context of the first-principles Li diffusion calculations. All of the Li sites have a small, negative ⁷Li NMR Fermi contact shift, ranging from −1 to −19 ppm, which is consistent with experiment, accounting for motional exchange. The different local environments in Table S2 in the Supporting Information also experience different C_Q values. The largest C_Q value is computed for the square-planar (LiO₄) site in TiNb₂O₇ (see Lithium Diffusion Mechanism), as it has the most anisotropic local environment. Smaller C_Q values in the range of 30–70 kHz are predicted for sites with higher coordination (approximately LiO₅) that leads to a more spherical charge distribution. The experimental SSB manifold widths (Figure S15 in the Supporting Information) correspond to C_Q values of ca. 70–250 kHz, which are in partial agreement with the calculations, while they suggest that the effects of nondilute lithium content, especially above 1.0 Li/TM, lead to larger C_Q values and thus more distorted Li environments.

Variable-Temperature ⁷Li NMR Spectroscopy

Variable-temperature NMR spectra were recorded over a large temperature range with a laser-heated probe to measure lithium mobilities and activation energies from motionally-induced nuclear relaxation, as well as to investigate line shape evolution as a function of temperature. For lithiated TiNb₂O₇, given the size of the quadrupolar interaction relative to homonuclear dipolar coupling under MAS, the motionally-induced fluctuations in the quadrupolar interaction dominate the T₁ relaxation, and hence the relaxation data were converted to motional correlation times (τ) according to BPP theory via the expression

where ω₀ is the Larmor frequency, C_Q is the nuclear quadrupolar coupling constant, η is the quadrupolar asymmetry parameter, and I is the nuclear spin (I = 3/2 for ⁷Li). This predicts that the T₁ will exhibit a minimum when ω₀τ ≈ 1, from which the correlation time can be determined directly at the temperature corresponding to the T₁ minimum. The observed T₁ minima correspond to C_Q values, within this model, of 130 kHz at low lithium content to 200–210 kHz at high lithium content. In reality, there will be multiple, possibly partially averaged, quadrupolar constants for the different lithium sites and there should also be contributions to the relaxation from dipolar interactions and unpaired electrons, but the single-parameter quadrupolar model corresponds to C_Q values that are consistent with the spectra. T₁ minima were used directly to determine diffusion coefficients. The activation energies (E_a) were extracted from Arrhenius fits (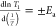) to regions on either side of the T₁ minimum; temperatures below the T₁ minimum correspond to long τ, while temperatures above the T₁ minimum correspond to short τ. Obtained E_a values were very small, in the range of 20–85 meV in the low-temperature, slower hopping region (ω₀τ > 1) and 60–390 meV in the high-temperature, faster hopping region (ω₀τ < 1) (Figure 6 and Table S3 in the Supporting Information). The observed asymmetry between the long- and short-τ regimes has been ascribed to short- vs long-range mobility and differences in dimensionality, which are both relevant in the case of TiNb₂O₇ (see Lithium Diffusion Mechanism). The activation barrier for this lithium motion is thus within a small factor of room-temperature thermal energy (k_BT = 25.7 meV at 298 K). The activation energy for lithium hopping, especially in the high-temperature region, increases drastically at high lithium content (Table S3 in the Supporting Information). This agrees with the analysis of lithium kinetics from the galvanostatic intermittent titration technique (GITT) (Figure S16 in the Supporting Information), which shows that the chemical diffusion coefficient of lithium is relatively constant during lithiation until the composition reaches Li₃TiNb₂O₇, noting that values during the pseudoplateau feature cannot be analyzed by conventional GITT if they correspond to the presence of multiple phases.⁸⁸ The lithium diffusion in lithium-stuffed concentrations (>1 Li/TM) is nearly two orders of magnitude lower than that in lithium-dilute concentrations.

Figure 6.

⁷Li spin–lattice relaxation constants for Li_xTiNb₂O₇ on an Arrhenius plot. T₁ constants at 4 kHz MAS and 9.4 T were extracted from saturation recovery experiments as a function of lithium composition and variable temperature via laser heating.

At the T₁ minima, ω₀τ ≈ 1; thus, at this field the correlation time is τ ≈ 6 ns. This can be converted to a self-diffusion coefficient (D_Li) via the Einstein–Smoluchowski relation

where l is the lithium hop distance and d is the dimensionality of diffusion. As we will see from the DFT calculations (vide infra), the dimensionality of local ion hopping in TiNb₂O₇ is restricted 3D (restricted by crystallographic shear planes), while long-range diffusion is 1D along the parallel tunnels present in all Wadsley–Roth phases. From the Einstein–Smoluchowski equation with d = 1 and l = 3.8 Å, D_Li in Li_xTiNb₂O₇ is ca. 10^–11 m² s^–1 at the temperature of the observed T₁ minimum of 525–650 K for x ≥ 0.75.

Under these spectroscopic conditions (4 kHz MAS, 9.4 T), one asymmetric signal was resolved for all samples (Figure 7 and Figure S17–S23 in the Supporting Information) with the exception of Li_0.75TiNb₂O₇ from 370 to 670 K (Figure S18 in the Supporting Information). This sample exhibited a considerably lower temperature T₁ minimum of 425 K for the paramagnetically-shifted low-frequency peak, suggesting that this lithium reservoir at this composition is more mobile.

Figure 7.

High-temperature ⁷Li MAS NMR spectra of Li_0.30TiNb₂O₇. The (a) central transition and (b) spinning sideband manifold are depicted as a function of temperature from 295 to 670 K (ascending). The dashed vertical line in (a) indicates the average shift in the ambient-temperature δ(⁷Li) spectrum. Spectra were recorded at 4 kHz MAS and 9.4 T. See also Figures S17–S22 in the Supporting Information.

The ⁷Li shifts and spinning sideband patterns undergo significant changes over the investigated temperature range (Figure 7 and Figures S17–S23 in the Supporting Information). As the temperature increases, the average frequency of the paramagnetically shifted resonances moves toward the diamagnetic region centered around zero, as expected for localized paramagnetism. The sideband evolution with temperature is complicated but hints at differential and changing dynamics. Numerical simulations of the quadrupolar powder patterns indicate that essentially the entire sideband intensity comes from the nuclear satellite transitions (−3/2 ↔ −1/2, +1/2 ↔ +3/2) for ⁷Li (I = 3/2) in this system. As we also saw in the ambient-temperature high-resolution NMR spectra (Figure S15 in the Supporting Information), the ambient-temperature laser-probe spectra (Figure S23 in the Supporting Information) exhibit relatively small sideband patterns, and hence C_Q values, upon lithiation up to Li_1.50TiNb₂O₇; the C_Q value then increases drastically at and above Li_3.00TiNb₂O₇.

By 400–450 K, increasing sideband intensity appears for x ≤ 1.50 in Li_xTiNb₂O₇, whereas the intense sideband manifold decreases for x ≥ 3.00 at elevated temperatures. Spectral broadening occurs when the rate of exchange is of the same order of magnitude as the interaction that is being averaged by the exchange,^89−91,47 in this case quadrupolar coupling of the order 50–250 kHz. Taken together, the variable-temperature lithium NMR spectra reveal several trends in lithium mobility.

In samples with low lithium content (x ≤ 1.50), the intercalated lithium ions are in an intermediate motional regime, with partial averaging giving rise to broad central and sideband resonances. At higher temperatures (ca. 400–600 K; Figure 7 and Figures S17–S20 in the Supporting Information), the sideband amplitude increases as the sidebands become sharp. This is attributed to averaging of the dipolar coupling (likely major) and the shift tensor (likely minor) but not of the quadrupolar coupling. At very high temperatures (ca. ≥700 K), the quadrupolar interaction is averaged and the full spectral width of the satellite transitions decreases. The onset of motional averaging shifts to higher temperatures at higher states of lithiation.

Highly lithiated TiNb₂O₇ (>1.50 Li/TM) experiences slower ionic mobility, as evidenced from GITT and NMR relaxometry, which results in larger quadrupolar and dipolar interactions, and hence the sideband manifold (Figures S21 and S22 in the Supporting Information) and fwhm (Figure 5) are broad at room temperature. Upon heating, the individual SSBs broaden and overlap (compare e.g. Figures S20 and S21 in the Supporting Information at intermediate temperatures). Sideband narrowing then occurs above 800 K; averaging of the quadrupolar interaction is obscured by the broadened sidebands but may also be occurring at very high temperatures. For context, motional broadening of the dipolar-broadened ⁷Li–⁷Li satellite transition SSBs in Li₂CO₃ does not occur until around 570 K, with motional narrowing setting in at higher temperatures.⁴⁷ Even to 970 K, only marginal averaging of the relatively small quadrupolar coupling (C_Q ≈ 70 kHz) is observed in that relatively nonconducting system.⁴⁷

Given the high lithium mobility of TiNb₂O₇, ⁷Li pulsed field gradient (PFG) NMR spectroscopy was performed with the aim of directly measuring a macroscopic diffusion coefficient, but the short T₁ and T₂ relaxation coefficients prevented the measurement of a decaying static signal. Operando ⁷Li NMR spectroscopy (Figure S24 in the Supporting Information) was also performed to track real-time changes and look for metastable intermediates, but the static nature of operando electrochemical NMR, combined with the small (10 ppm) isotropic shift range of Li_xTiNb₂O₇ that overlaps with the large electrolyte resonance, meant that no considerable changes were observed (other than in the Knight-shifted Li metal resonance at 248 ppm from varying intensity and from microstructural effects^43,92).

Lithium Diffusion Mechanism

Previous experimental and theoretical studies have highlighted that there are multiple possible sites for Li insertion into the TiNb₂O₇ structure.^87,93 Catti et al. proposed that there are two main types of Li coordination: five-coordinate (LiO₅) square-pyramidal sites on the edges of the 3 × 3 blocks and four-coordinate (LiO₄) square-planar sites within the 3 × 3 block.⁹³ Here, first-principles calculations were used to explore the possible Li insertion sites and associated ion motion barriers. A single-ended transition state searching approach based on hybrid eigenvector following (HEF) was adopted to locate local minima and transition states in the Ti/Nb “ordered” TiNb₂O₇ supercell described previously. Although it was previously shown (vide supra) that the formation of localized polaron states is sensitive to the inclusion of a Hubbard U parameter, the description of the electronic structure without a U correction is in qualitative agreement with experiment. For the remainder of this study we therefore used standard DFT to capture the mechanisms associated with ionic diffusion, without the presence of additional electron transfer processes, an approach commonly adopted in other transition-metal oxide battery materials.⁵²

Transition state searches were initiated by placing a single Li atom close to the center of a LiO₄ window for all possible LiO₄ and LiO₅ sites in the structure. Once the transition state was found, the corresponding minima along the reaction pathway were located by displacing the atoms along the single negative eigenvector at the saddle point in both the positive and negative directions, followed by optimization of the atomic positions. The diffusion mechanisms and associated activation barriers of the “ordered” TiNb₂O₇ cell are shown in Figure 8. Movies depicting the various ionic hopping pathways are included in the Supporting Information.

Figure 8.

Li conduction pathways and corresponding activation barriers in eV located via the hybrid eigenvector following approach along the (a) b axis and (b) ac plane of an “ordered” TiNb₂O₇ supercell structure. Li minima (Li_A–Li_G) and transition states (configurations i–viii) are shown in red and gray, respectively. Curved black arrows show the direction of Li hops. The energies of the local minima (red squares) and kinetically-resolved activation barriers (eq 1 in the Supporting Information) to the transition states (gray squares) are shown relative to configuration C at 0 eV. An interpolation of the energy between the initial and final minima for each hop is shown. The local bonding environments of in-tunnel Li minima (Li_A–Li_C) are also displayed (red box).

Within the blocks, three minima were located: sites Li_A and Li_B in tunnel T2 and site Li_C in tunnel T1, as shown in Figure 8a. Li_C is the lowest energy position in the Ti/Nb ordered TiNb₂O₇ supercell and corresponds to a distorted site in which the Li ion is displaced toward the center of tunnel T1. Hopping between Li_C sites along the b axis of the cell requires a moderate activation energy of 0.39 eV. Interestingly, in the dilute limit, the square-planar (LiO₄) site within tunnel T1 corresponds to the transition state (configuration ii) along the Li_C–Li_C diffusion path and not a local minimum. Site Li_B adopts a five-coordinate square-pyramidal site, distorted toward the center of tunnel T2, similar to site Li_C in tunnel T1. Site Li_B is analogous to the distorted five-coordinate Li site observed at low levels of lithiation in the related compound V₆O₁₃.⁹⁴ The energy difference between the Li_B and Li_C sites (0.11 eV) is small, suggesting that both may be populated at room temperature. In tunnel T2, the square-planar site, Li_A, along the b axis is a local minimum, which is 0.16 eV higher in energy than the five-coordinate Li_B site. The activation energy for Li_A–Li_B diffusion (0.18 eV) is also low, suggesting that b axis conduction down tunnel T2 will be facile.

The conduction mechanisms between sites within the ac plane are shown in Figure 8b. In addition to the in-tunnel sites (Li_A–Li_C), square-pyramidal (LiO₅) sites (Li_D–Li_F) were also located with the HEF approach on the edges of the blocks, in agreement with previous studies.^87,93 In the ordered TiNb₂O₇ supercell, the Li_E and Li_F sites on the edges of the tunnels are the highest in energy while the Li_B and Li_C sites within the tunnels are the lowest in energy, suggesting preferential lithiation of the tunnels in the first stages of lithiation. However, as will be shown below, the relative energies of the different sites are subtly related to the Ti/Nb ordering. Within the blocks, conduction between the Li_B and Li_C sites can occur along the a axis or c axis through the square-planar (LiO₄) windows (configurations iii and iv, respectively). The small kinetically-resolved activation energies of 0.10 and 0.18 eV for a and c axis diffusion, respectively, suggest that Li⁺ can rapidly diffuse between tunnels T1 and T2. The activation barriers between the square-pyramidal sites and Li_B/Li_C sites (configurations v–viii) are larger (0.41–0.65 eV), indicating that diffusion within the ac plane to these sites will be slower.

The square-pyramidal sites on the edges of one block share a common edge with the square-pyramidal sites in an adjacent block, creating a possible pathway for cross-block diffusion. As can be seen in Figure 9, significantly larger barriers (0.71–1.00 eV) are observed for cross-block diffusion, suggesting that these pathways do not contribute significantly to the overall diffusion process, at least at dilute levels of lithiation. At the transition state of the cross-block diffusion (configurations ix–xi), the diffusing Li⁺ has a distorted-octahedral (LiO₆) configuration that is face-sharing with four transition-metal (MO₆) octahedra, resulting in a large electrostatic repulsion. This is consistent with a previous computational study on the related system TiO₂(B), in which diffusion across the tunnels is higher in energy than down-tunnel diffusion.⁹⁵ These results agree with and lend quantitative support to the simplified picture provided by bond valence sum mapping (Figure S25 in the Supporting Information).

Figure 9.

Cross-block Li diffusion pathways and corresponding activation energies in eV. Li minima (Li_D–Li_G) and transition states (configurations ix–xi) are shown in red and gray, respectively. The energies of the local minima and kinetically-resolved activation energies (eq 1 in the Supporting Information) relative to configuration C are displayed on the conduction barrier plots (blue). An interpolation of the energy between the initial and final minima for each Li hop is shown.

In a real TiNb₂O₇ sample, the disordered arrangement of Nb and Ti sites also leads to a local distribution of neighbors for each Li site. To capture the effect of transition-metal disorder, the previously observed Li ion activation barriers in the ordered supercell were investigated in the disordered supercell. Transition state searches involving a single Li ion were initiated from all of the possible LiO₄ windows in the structure using the approach described previously. The energies of the local Li minima and activation barriers found in the disordered TiNb₂O₇ supercell are shown in Figure 10a,b, respectively.

Figure 10.

Energies of (a) local Li minima and (b) kinetically-resolved activation barriers in the disordered TiNb₂O₇ supercell. Li sites Li_A–Li_G correspond to the Li positions observed in the ordered TiNb₂O₇ structure in Figure 8. The energies of all minima are referenced to the lowest energy Li_D site at 0 eV.

The transition-metal disorder leads to a distribution of energies for all of the local minima (Li_A–Li_G) in Figure 10, which is related to the different electrostatic potential experienced by the Li ion with different arrangements of Ti⁴⁺/Nb⁵⁺ neighbors around a given site. In the disordered supercell, the trend in the relative site energies remains the same as that found for the ordered TiNb₂O₇ supercell, in which the in-tunnel environments (Li_A–Li_C) are lower in energy than the square-pyramidal environments Li_E–Li_G on the edges of the tunnels. The square-pyramidal environment Li_D on the edge of tunnel T1 was, however, found to be a low-energy site for several local Li orderings. The results above regarding the possible Li environments are only strictly applicable for dilute levels of Li doping in TiNb₂O₇, as Li–Li interactions and transition-metal reduction Mⁿ⁺ → M^(n–1)+ at higher levels of Li insertion will affect the relative energies of the different sites. However, the similarity between the energies of the different Li configurations suggests that there will be a significant population of square-planar (Li_A), distorted-five-coordinate (Li_B and Li_C), and square-pyramidal (Li_D) sites on initial lithiation.

For several of the diffusion pathways connected to in-tunnel local environments (Li_B and Li_C) in the disordered supercell, the single-ended transition state searches from neighboring sites resulted in a splitting of the positions found in the ordered supercell into different local Li positions within the same tunnel (Figure S26 in the Supporting Information). The activation barrier between two split Li_C sites was calculated using the HEF approach and was found to be 0.04 eV. This result suggests that the presence of Ti/Nb disorder subtly changes the in-tunnel sites, creating multiple shallow local minima that can rapidly exchange. This behavior is analogous to the rapid diffusion between adjacent sites within the same block in the perovskite solid electrolyte material Li_3xLa_(2/3)–xTiO₃ (LLTO).⁹⁶

The trend in the relative activation energies between different diffusion mechanisms previously found in the ordered supercell remains the same in the disordered supercells (Figure 10b), with a distribution of the energies in the latter case. Activation barriers for b axis diffusion of 0.10–0.14 and 0.11–0.55 eV were found for configurations i and ii, respectively, using the HEF approach. From an analysis of the transition state structures of configuration ii, it is evident that the activation barrier for ionic conduction through the square-planar window is lowest when transition-metal site M₄ on the edge of the block is occupied by Ti⁴⁺, which results in a lower electrostatic repulsion than that for Nb⁵⁺. A deeper understanding of the effect of disorder and Ti/Nb local environments on the activation barriers could be gained through a cluster expansion-type approach,^65,97 although this is beyond the scope of the current study.

The activation energies of the pathways within the ReO₃-like blocks between tunnels T1 and T2 (via configurations iii and iv) remain low (0.06–0.25 eV) for all of the pathways calculated, suggesting that rapid transport between tunnels T1 and T2 will still occur for a range of different local Nb/Ti orderings. The range of activation barriers (0.18–0.44 eV) for diffusion between square-pyramidal site Li_D and site Li_C (configuration v) was similar to that of b axis diffusion, whereas the range of activation barriers for diffusion to the higher energy square-pyramidal sites (Li_E–Li_G) was larger (0.27–0.59 eV). The energy of the cross-block barriers (configurations ix–xi) remained very high (0.60–1.03 eV) for all local Ti/Nb orderings, suggesting that 3D diffusion between blocks is limited.

The change in the Li diffusion barriers at higher levels of lithiation (Li_xTiNb₂O₇) was investigated for a limited number of concentrations (x = 2.667, 4) in the ordered and disordered TiNb₂O₇ structures (Figures S27 and S28 in the Supporting Information). At higher levels of lithiation, the square-planar transition state configurations ii and iii (Figure 8) in the ReO₃-like blocks become stable sites for Li. The energy preference to create Li vacancies at different square-planar and square-pyramidal sites in the structure was found to be sensitive to both the Li composition and Ti/Nb ordering. The activation barriers for down-tunnel Li diffusion were also found to be sensitive to the Li composition with values ranging from 0.29 to 0.44 eV in the ordered x = 2.667, 4 structures. Li diffusion at higher levels of lithiation occurs via a vacancy-based mechanism, and so the diffusivity observed experimentally will be sensitive to the concentration of vacancies on different square-planar and square-pyramidal sites in the structure. The barriers for cross-block diffusion were found to be considerably higher, from 0.85 to 0.9 eV, suggesting that cross-block diffusion does not play a significant role at high or low levels of lithiation. While we examined some key Li compositions—(i) dilute, (ii) near the end of the second discharge region, and (iii) Li stuffed—a more in-depth analysis of the change in the Li hopping barriers as a function of Li content is an important topic and could also be approached with a more intensive cluster expansion based methodology,⁶⁵ although this is beyond the scope of the current work.

Behavior of “Beyond-Li” Cations

To test how the nature of the cation affects the motional activation barrier, the Li⁺ ion in the transition state configurations associated with b axis diffusion (configurations i and ii) of the ordered TiNb₂O₇ supercell was replaced with a Na⁺, K⁺, or Mg²⁺ ion. The corresponding activation barriers were then found with HEF approach, as shown in Figure 11. For all of the beyond-Li cations, the barriers for b axis diffusion along tunnel T1 or tunnel T2 are considerably larger than the corresponding Li barriers with ΔE_Li⁺ ≪ ΔE_Mg²⁺ < ΔE_Na⁺ ≪ ΔE_K⁺. For the Na⁺ and K⁺ systems, the minima in both tunnels in Figure 11 occur when the Na⁺/K⁺ ion occupies the 12-coordinate site at the center of the tunnel. In both tunnels, the transition state occurs when Na⁺/K⁺ passes through the square-planar configuration, which corresponds to minimum Li_A (tunnel 2) and transition state configuration ii (tunnel T1), in the Li system. The increase in the activation barrier along the series Li → Na → K can be related to the increase in the ionic radius 0.76 → 1.02 → 1.38 Å, respectively, which leads to increased repulsion as the A⁺ ion passes through the square-planar AO₄ transition state.

Figure 11.

b axis diffusion mechanisms of Li⁺, Na⁺, K⁺, and Mg²⁺ in the ordered supercell structure of TiNb₂O₇ initiated from (a) configuration i in tunnel T2 and (b) configuration ii in tunnel T1 (Figure 8a). The energies for each system are scaled relative to the lowest energy minimum in (b).

For the Mg²⁺ system, the minimum in tunnel T1 (Figure 11b) corresponds to the distorted-square-pyramidal site analogous to position Li_C and the transition state corresponds to the square-planar position analogous to configuration ii. From Bader charge analysis,^98,99 the charge on the Mg ion in configuration ii was +1.75 e^–, consistent with the full ionization of Mg to Mg²⁺. In tunnel T2 (Figure 11a), two local minima were found for Mg²⁺: a square-pyramidal site (0.2 eV), analogous to position Li_B, and a highly distorted square planar site (0.64 eV), analogous to Li_A. Although the positions of the local minima are the same between the Li and Mg systems, the higher charge in the latter case results in an increase in the electrostatic repulsion at the transition state and thus a higher activation barrier (∼1 eV). Although only a selected number of pathways were investigated for Na⁺, K⁺, and Mg²⁺, these results suggest that the diffusion barriers for these ions are intrinsically much larger than for Li⁺, which explains the requirement for nanosizing in the Na⁺ system.⁵³⁻⁵⁶

Discussion

Implications of Electronic Conductivity

Battery electrodes are mixed ionic–electronic conductors; therefore, low electrical resistivity is required, especially for operation at high current densities. Thus, TiNb₂O₇ might not be an obvious choice for a high-rate electrode material from e.g. band structure screening for small-band-gap materials, as it is a white, wide-band-gap insulator with a measured optical band gap of 3.06(2) eV (Figure S9 in the Supporting Information). Indeed, the experimental resistivity of a sintered pellet of TiNb₂O₇ is estimated from Xing et al.⁸² to be ∼10⁹ Ω cm at room temperature, by Arrhenius extrapolation from higher-temperature measurements. However, TiNb₂O₇ does show good rate performance, indicating that this picture is incomplete because it does not account for the step-change increase in electronic conductivity upon lithiation. It is a general feature of shear structures that their conductive properties make it possible to lithiate, at least up to one Li/TM, pure polycrystalline pellets without the need for conductive additives or binder; this enables a variety of intrinsic measurements as a function of lithium content with relatively high precision.^21,23,34

Due to the low conductivity of pristine TiNb₂O₇, many studies have focused on improving the this parameter via transition-metal doping,^29,100 partial reduction under a low oxygen partial pressure,¹⁰¹ or partial nitridation.³⁸ Furthermore, these strategies are also being applied to related shear structures.^102−106 In light of the changes in resistivity as a function of lithiation, this approach should be reevaluated: while those methods do improve the transport by decades vs the insulating host, lithium intercalation has the same effect. For battery electrodes, which vary significantly in composition and often exhibit large changes in properties during operation, it is important to consider the full compositional range, not only the host structure and/or end point.

Crystallographic Shear Structure: Electronic/Ionic Property Relationships

Analogies can be drawn between ternary TiNb₂O₇ upon reduction by lithium and the crystallographic shear structures of binary Nb₂O_5−δ, which are reduced by oxygen deficiency. Cava et al.^107−109 studied the magnetism of these latter phases and found effective magnetic moments—normalized to the number of d¹ electrons (μ_eff^e–)—of 1.18, 1.17, 1.39, and 1.14 for Nb₂₅O₆₂, Nb₄₇O₁₁₆, Nb₂₂O₅₄, and both orthorhombic and monoclinic (o,m)-Nb₁₂O₂₉, respectively. The magnitude of μ_eff for both Li_0.30TiNb₂O₇ and Li_0.60TiNb₂O₇ is 1.09, corresponding to localization of only 43% of the electron density if we take both Nb⁴⁺ and Ti³⁺ to be d¹, S = 1/2, g = 2. All of these Nb₂O_5−δ shear structures exhibit low resistivity at room temperature (ρ = 3 × 10^–1 to 4 × 10^–3 Ω cm) and behave as metals or heavily doped semiconductors.¹⁰⁷ Furthermore, m-Nb₁₂O₂₉ was shown to simultaneously display metallic conductivity and local moment magnetism with low-temperature antiferromagnetic ordering.^109,110 This intriguing behavior has been assigned to two subsets of the structure and the electron character—an itinerant electron within the crystallographic shear planes, which conducts along the b axis,¹¹¹ and a localized electron within the ReO₃-like block.⁶⁹ If one electron per formula unit is assumed to be itinerant and one assumed to be localized in Nb₁₂O₂₉, the one-electron μ_eff^e– value becomes 1.61, in agreement with expectations for this 4d¹ configuration.¹⁰⁷

In a systematic single-crystal study, Rüscher convincingly demonstrated that Nb₂O_5−δ shear structures exhibit metallic behavior along the b axis, i.e. down the tunnels, and insulator-like properties in the ac plane perpendicular to the tunnels,¹¹¹ consistent with electronic band structure calculations of niobium suboxides.⁶⁹ Crystal structure analysis of TiNb₂O₇ and niobia crystallographic shear phases shows significantly shorter metal–metal interatomic distances via edge-shared octahedra along the shear planes (3.2–3.4 Å) in comparison to the ac planar cross-block metal–metal pathways (≥3.8 Å). In contrast to the perovskite structure with 180° −M–O–M– orbital interactions, the edge-sharing planes of the crystallographic shear structures provide electric “wires” running parallel to the columns. This suggests that long-range electronic conduction is down the b axis in TiNb₂O₇ and the other shear oxides,⁶⁹ which is also the direction of long-range ionic conduction.

Altogether, comparisons of the magnetic and electronic behavior of TiNb₂O₇ with Nb₂O_5−δ crystallographic shear structures suggest that the hierarchical crystal structure comprising shear planes and block motifs may enable some degree of room-temperature electron delocalization as well as the observed local moments. The partially localized, partially delocalized electronic behavior may explain the large increase in conductivity due to lithium insertion in TiNb₂O₇, even at low doping levels and in the presence of Curie–Weiss paramagnetism. Meanwhile, TiNb₂O₇ differs from Nb₂O_5−δ due to the presence of Ti and of cation mixing. One effect of this, elucidated from the DFT calculations, is that the electron localization in TiNb₂O₇ is associated with Ti atoms; Ti atoms, though disordered, preferentially occupy shear plane sites so that spin density is observed at block edges in TiNb₂O₇ vs block centers in Nb₂O_5−δ.⁶⁹ The localized state roughly 1 eV within the band gap of TiNb₂O₇ (Figure 4) is consistent with the electronic localization in n-type TiO₂¹¹² and suggests that the electronic localization in 3d Ti-containing crystallographic shear phases is stronger than in 4d niobium oxides or 4d–5d niobium tungsten oxides with larger d orbitals, which has implications for the electronic conductivity.

The cation disorder also has implications for the ionic conductivity upon lithiation. Four- and five-coordinate Li sites can be either ground states or transition states depending on the tunnel and cation configuration. Additionally, metal cation disorder creates local structural effects such as split Li sites with very small intrasite hopping barriers. The small blocks of TiNb₂O₇ (3 × 3) require that every tunnel straddles shear planes and central corner-shared octahedra. An interesting future direction will be to examine the different ionic transport properties through central tunnels vs edge tunnels in crystallographic shear structures with larger block sizes, on top of the role of cation disorder.

High-Temperature NMR Spectroscopy

For a fast ion conductor at room temperature, motional narrowing of NMR line shapes is expected, but in the case of crystallographic shear titanium niobium oxide, it might appear that only limited line narrowing is observed from 295 to ca. 1000 K. There are significant changes to the spinning sideband manifold from the satellite transitions at high temperatures and resolved peaks do appear within the central transition. The high-temperature line shapes are neither pseudo-Voigt nor quadrupolar. However, a fit to the whole pattern can be obtained by the combination of a series of shift-distributed narrow pseudo-Voigt lines (Figure 12). Individual peaks have a fwhm of ca. 80 Hz (0.5 ppm) with the edges of the line shape constraining the maximum line width of the components. The obtained fit was produced with the shift and quadrupolar tensor parameters in Table 2. The unusual central and sideband peak distribution is observed in all spectra with the exception of Li_0.75TiNb₂O₇; the peaks emerging within the central transition resonance and sidebands are most prominent at low lithiation. Strikingly similar line shapes were observed in the ¹⁹F NMR spectra of a niobium fluoride due to ¹J(¹⁹F,⁹³Nb) indirect coupling to the I = 9/2 ⁹³Nb nucleus (2I + 1 = 10) with partial motional averaging of the dipolar coupling under MAS-induced or VT heating.¹¹³ We would expect the ²J(⁷Li,⁹³Nb) coupling to be weaker. This is also consistent; a ¹J(¹⁹F,⁹³Nb) value of 204(2) Hz was found in the former case, and a ²J(⁷Li,⁹³Nb) value of 90(10) Hz would be consistent with the spectra presented here. Increased residual dipolar coupling is expected in the lithium-rich compositions, remaining even under MAS at high temperatures, due to the persistence of homonuclear ⁷Li–⁷Li dipolar coupling^47,89,114 relative to heteronuclear ⁷Li–⁹³Nb dipolar coupling. Alternatively, it is possible that this effect could arise from residual dipolar¹¹⁵ or J(116) coupling between quadrupolar nuclei in the presence of anisotropic motion.

Figure 12.

⁷Li MAS NMR spectrum of Li_0.30TiNb₂O₇ at ca. 670 K. The unique line shapes of the (a) central transition and (b) spinning sideband manifold were fit as described in the text. The spectrum was recorded at 4 kHz MAS and 9.4 T. Fitting parameters are given in Table 2. Experimental data are given in black, individual fit components are given in blue, and the sum of the fit is given in orange. This is not necessarily a unique or an optimized fit but rather a reproduction of the observed spectrum with minimum variables.

Table 2. NMR Shift and Quadrupolar Tensors Fit to the ⁷Li NMR Spectrum of Li_0.30TiNb₂O₇ at ca. 670 K^a.

param	site 1	sites 2–11
δ(7Li) (ppm)	–0.5	site (N – 1) + 0.5
CSA (ppm)	10 (10)	10 (10)
ηCSA	0	0
CQ (kHz)	12 (2)	55 (5)
ηQ	0	0

^aN indicates the site number. η values were set to zero and not refined. The fits were also not very sensitive to CSA for values below 20 ppm. Line broadening of 100 Hz was used for each site (1:1 Gaussian:Lorentzian line shape).

Lithium Diffusion

On comparison of the DFT-computed conduction barriers with the activation energies from NMR, for dilute Li contents, the small energies from NMR within the low-temperature regime (0.020–0.085 eV) can be tentatively assigned to the rapid Li exchange between split sites within the same ReO₃-like cage. At high states of lithiation, the DFT calculations show a transition from an interstitial to a vacancy diffusion mechanism, which eliminates rattling between split sites within the blocks. NMR measurements on highly lithiated samples do not show these ultralow barrier processes, consistent with the DFT results. The activation energies (0.060–0.390 eV) from NMR at higher temperatures can then be tentatively assigned to a combination of Li diffusion along the b axis (configurations i and ii), aided by facile hopping between tunnels T1 and T2 (configurations iii and iv) and diffusion between square-pyramidal sites on the edges of the tunnel (configuration v), primarily Li_D sites. The large activation barriers between blocks (configurations ix–xi) for all local Ti/Nb orderings suggests that the diffusion mechanism in Li-doped TiNb₂O₇ is primarily 1D in nature. The situation is analogous to the rapid down-tunnel diffusion but high cross-tunnel energies in LiFePO₄¹¹⁷ and TiO₂(B),⁹⁵ the important difference in TiNb₂O₇ and other crystallographic shear structures²³ being the multiple parallel tunnels with low intrablock hopping energies between tunnels.

High-Rate Energy Storage

Among crystallographic shear structures for lithium ion batteries, the gravimetric capacity of TiNb₂O₇ is one of the highest at lower C rates but drops precipitously at higher rates even at the low mass loadings used here, due in part to the rapid increase in E_a as lithiation approaches 1 Li/TM. In TiNb₂O₇, the dQ/dV peak width measured for the discharge process is always broader than that of the charge process (Figure 2b), indicating a more kinetically hindered process for lithium insertion than for lithium extraction. This behavior is atypical for crystallographic shear structures. Although dQ/dV curves are not widely reported as a function of rate, there is no evidence for this noticeable lithiation–delithiation asymmetry in Nb₁₂WO₃₃,^118,119 Nb₁₆W₅O₅₅,²³ TiNb₂₄O₆₂,³³ or H-Nb₂O₅.²¹ A kinetic limitation on discharge in a half-cell is in agreement with numerous reports that lithiation is the rate-limiting step for TiNb₂O₇.^26,28,30,120 In a full cell configuration, TiNb₂O₇ is the negative electrode and lithium insertion occurs on charging; the implication is that the full cell charging rate could be lower than the discharge rate: i.e., high power output but comparatively slower charging. The niobium tungsten oxides, even at higher mass loadings, show higher gravimetric capacity and symmetric lithiation/delithiation voltage curves at high C rates while having 20–30% higher density.²³ Among the emerging complex oxide anode materials, further electrode engineering and electrochemical testing is required to determine the crossing points in the tradeoffs between gravimetric vs volumetric capacity and low-to-intermediate rate performance vs high rate performance. The demands of the application will ultimately determine the optimal material selection.

While lithium experiences low activation barriers to move through the crystallographic shear structure of TiNb₂O₇, larger alkali cations and divalent cations are considerably more hindered. This compound may not be suitable for “beyond lithium” rechargeable batteries, but a related phase with similar structural motifs and larger tunnels may enable intercalation of alternative species.

Conclusion

Via experiment, theory, and comparisons to related crystallographic shear structures, we conclude that ionic and electronic conduction are strongly anisotropic in TiNb₂O₇ to the extent that they can be approximated as one-dimensional in the direction along the tunnel (b axis). The anisotropy in both Li⁺ and e^– conduction arises due to the crystallographic shear planes that disrupt transport in the ac plane. Nevertheless, the bulk structure is capable of high-rate (de)lithiation. The ReO₃-like blocks of octahedra in this complex oxide allow facile Li diffusion characterized by activation barriers of <100 meV from variable-temperature NMR, at lithium concentrations below one lithium per transition metal (Li₃TiNb₂O₇), and 100–200 meV from single-ended transition state searching calculations. Lithium diffusivity decreases rapidly at and above one-electron redox capacities, as evidenced by high-temperature ⁷Li NMR (E_a = 300–400 meV), ^6/7Li NMR spectral line widths, and GITT measurements, which explains the lower lithium storage capacities at higher rates. The crystallographic shear planes, while essentially prohibiting Li⁺ diffusion perpendicular to the tunnels, hold the framework open and provide structural stability. Electronically, n-type doping of TiNb₂O₇ by the addition of Li atoms (Li⁰ = Li⁺ + e^–) increases the electronic conductivity of the host by ca. seven orders of magnitude even at low doping concentrations. At low lithium concentrations, localized paramagnetism is observed via measurements of the magnetic susceptibility and ^6/7Li NMR spectroscopy, though the magnetic moment is smaller than expected. This result suggests the possibility of the simultaneous presence of localized and delocalized electrons. At higher lithium concentrations, NMR and magnetic susceptibility measurements suggest that the system becomes metallic. Li can occupy a range of four- and five-coordinate sites within the ReO₃ blocks, and the energies of the local minima and transition states are subtly related to the presence of the Ti/Nb local ordering. The availability of multiple adjacent Li minima with similar energies is a crucial factor that leads to the facile conduction in the TiNb₂O₇ structure. At high lithium concentrations, the activation barriers for intersite Li hopping are relatively unchanged in comparison to the dilute limit. However, the diffusion mechanism transitions from interstitial-mediated to vacancy-mediated and the vacancy formation energetics—specifically for inner block sites that lead to long-range Li⁺ diffusion—may become rate-determining. With the framework established for Li ground-state and transition-state searching, the diffusion of intercalant species Na⁺, K⁺, and Mg²⁺ was examined. These cations all exhibit very high diffusion barriers of at least ca. 1.0 eV, suggesting minimal conduction at room temperature.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.9b06669.

• Supplementary methods; structural characterization; additional electrochemical measurements, including GITT, magnetic, electrical, and optical property curves; additional lithium NMR spectra with a range of compositions, temperatures, and effects of an echo pulse sequence; bond valence sum map of TiNb₂O₇; additional kinetic barrier figures at dilute and concentrated Li contents for ordered and disordered Ti/Nb configurations; and calculated local structures and NMR parameters. Data supporting this work are available at www.repository.cam.ac.uk. (PDF)

• Movie of lithium hopping pathway from site A, through transition state i, to site B (MPG)

• Movie of lithium hopping pathway from site B, through transition state iii, to site C (MPG)

• Movie of lithium hopping pathway from site B, through transition state vii, to site F (MPG)

• Movie of lithium hopping pathway from site B, through transition state viii, to site G (MPG)

• Movie of lithium hopping pathway from site C, through transition state ii, to site C (MPG)

• Movie of lithium hopping pathway from site C, through transition state iv, to site B (MPG)

• Movie of lithium hopping pathway from site C, through transition state v, to site D (MPG)

• Movie of lithium hopping pathway from site E, through transition state vi, to site C (MPG)

• Movie of lithium hopping pathway from site E, through transition state x, to site E (MPG)

• Movie of lithium hopping pathway from site F, through transition state ix, to site D (MPG)

• Movie of lithium hopping pathway from site G, through transition state xi, to site G (MPG)

Author Contributions

^# K.J.G. and I.D.S. contributed equally.

The authors declare the following competing financial interest(s): K.J.G. and C.P.G. are major shareholders in a start-up company developing fast-charging batteries based on high-rate anode materials.