Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2019 Jun 5;35(27):8896–8902. doi: 10.1021/acs.langmuir.8b04277

Regimes of Head-On Collisions of Equal-Sized Binary Droplets

Yi Ran Zhang †, Kai H Luo ‡,*
PMCID: PMC7007249  PMID: 31244244

Abstract

graphic file with name la8b04277_0008.jpg

Through molecular dynamics simulations, head-on collision processes of two identical droplets with a diameter of 10.9 nm are elaborately scrutinized over a wide range of impact Weber numbers (from 6.7 to 1307) both in vacuum and in an ambient of nitrogen gas. As the impact Weber number exceeds a certain critical value, a hole or multiple holes in apparently random locations are observed in the disklike structure formed by two colliding droplets. We name this a new “hole regime” of droplet collisions, which has not yet been reported in previous studies. As the impact Weber number increases, the number of holes increases. The hole or holes may disappear unless a second critical impact Weber number is exceeded, when the merged droplet is likely to experience dramatic shattering. It is also found that the existence of ambient gas provides a “cushion effect” which resists droplet deformation, thus delaying or even preventing the appearance of hole formation and shattering regimes. Moreover, increasing ambient pressure suppresses hole formation. A model based on energy balance is proposed to predict droplet behaviors, which provides a more accurate estimate of the maximum spreading factor compared to previous models. Finally, we further extend the current nanoscale droplet collision regime map and analyze the similarities and dissimilarities between nano- and macroscale droplet collision. Our study extends the current understanding on nanodroplet collisions.

1. Introduction

Droplet collisions are encountered in both natural and industrial processes,1−4 for example, the formation of rain drops,5 the operation of nuclear reactors,6 and the process of spraying.7 Experiments have been first conducted for head-on droplet collisions and four distinct regimes are identified: coalescence, bounce, coalescence followed by separation, and shattering.8 Other investigations using experimental and numerical methods9−11 such as the level set, volume of fluid, and lattice Boltzmann method (LBM) provide a rich picture of droplet collision outcomes, but the details of the collision dynamics are difficult to obtain through experiments and continuum numerical methods, especially when the approaching droplets are within a distance comparable to the molecular mean-free path. In a recent study, we have employed molecular dynamics (MD) simulations to investigate head-on collisions of nanodroplets, which successfully reproduced the head-on collision and bounce-back regime for the first time by any numerical simulation. Such phenomena have only been observed in head-on collisions of microdroplets in experiments.12 Previous numerical studies, including those by discrete, mesoscopic LBMs,13−18 failed to predict this regime because the interfacial region of thickness comparable to the molecular mean-free path was not resolved. When the impact Weber number is high, the shattering and the separation phenomena are observed in nanoscale and macroscale droplet collisions, respectively. In general, nanoscale droplets have shown some different behaviors from their macro-, meso-, or micro-counterparts in recent studies.19,20 Currently, our understanding of high impact Weber number collisions is still very limited, and an effective model that can predict the spreading factor of droplet collisions is still missing at nanoscales. Our study successfully observed a new hole regime in nanoscale droplet collision at high impact number and proposed a model based on energy balance to estimate the spreading factor of the merged droplet.

In this paper, the methodology of MD is introduced in Section 2. Section 3.1 introduces the hole regime discovered at high impact Weber numbers. Section 3.2 shows a model based on energy balance to predict the droplet maximum spreading factor. Sections 3.3 and 3.4 discuss the influence of ambient pressure and impact Weber number. A new regime map of nanodroplet collisions is constructed in Section 3.5. The conclusion of the research is discussed in Section 4.

2. MD Simulations

Figure 1 illustrates the initial setup of the simulation system with two nanodroplets submerged in the nitrogen ambient. The simulation box is a 2000 Å × 1000 Å × 1000 Å block with the origin of coordinates at the left bottom back corner. The two identical droplets with a diameter of 10.9 nm were initially placed along the x direction at the central part of the box with x coordinates being 500 and 1500 Å, respectively (Figure 1). The whole simulation system in vacuum comprises 108 108 atoms in total. The NVT ensemble was selected with a Nose–Hoover thermostat at 300 K with an initial Gaussian velocity distribution.

Figure 1.

Figure 1

Open in a new tab

Initial setup of the simulation system. Two nanodroplets with a diameter of 10.9 nm (107 572 water molecules) are submerged in nitrogen-ambient gas and approach each other along the x direction.

The TIP3P water model21−23 with a bond length rOH = 0.9572 Å and a bond angle θHOH = 104.52° has been adopted for water molecules because it offers a sufficient description of intermolecular forces in water in MD simulations. The TIP3P water model specifies a three-site rigid water molecule with charges and Lennard-Jones parameters assigned to each of the three atoms. Nitrogen molecules were treated as Lennard-Jones particles. The intermolecular interactions between water and nitrogen include both Coulombic and Lennard-Jones (L-J) 12–6 potentials,24−26 as shown in eq 1.

2. 1

In eq 1, r is the distance between any two atoms, and σ and ε represent the zero energy separation distance and the minimum energy, respectively. The subscripts i and j are the atom indexes. The Lorentz–Berthelot mixing rule was employed for calculating the potential parameters between water and nitrogen molecules. L-J parameters used in this research are summarized in Table 1. Periodic boundary conditions were applied to all three directions and a cutoff distance of 16 Å was adopted.

Table 1. Values of Potential Parameters for the TIP3P Water Model.

atom σ (Å) ε (kcal/mol)
O–O 0.102 3.188
H–H 0.000 0.000
N–N 0.072 3.320
O–N 0.086 3.254
H–N 0.000 0.000
Open in a new tab

Equilibration simulations of droplets and ambient gases were conducted before the droplet collision simulations. For droplets, the equilibration procedure was undertaken in vacuum at a temperature of 300 K for about 2 ns and then the canonical ensemble (NVT) was employed. After equilibrium, a single droplet can be generated by removing all the vaporized molecules around. The second droplet was obtained by duplicating the first one. Meanwhile, ambient nitrogen molecules were also equilibrated at 300 K in a parallel equilibrium simulation.

After equilibrium, the two droplets were first placed in the required positions and then equilibrated ambient gas molecules were added to fill the remaining space of the box. A further simulation was conducted for 2 ns to equilibrate the final system consisting of both droplets in the ambient gas. In the droplet collision simulations, each droplet was assigned the same impact speed along the x direction. A time step of 1 fs was assigned, and the dynamic trajectories and thermos data were recorded every 1 ps. The droplet density, surface tension, and viscosity are ρ = 0.997 g/cm3, υ = 0.851 Pa·s, and γ = 66 mN/m, respectively.

All the MD simulations are performed using the LAMMPS platform27 on ARCHER, the UK national supercomputing service. Visual MD28 and OVITO29 are used to display simulation results and the system configurations.

3. Results and Discussion

3.1. Hole Regime

Weber number is an important dimensionless number in droplet collision, which is defined as

3.1.

where R is the radius of droplet, ρ is the density, U is the impact speed, and σ is the surface tension. Weber number measures the relative importance of droplet’s inertia compared to its surface tension. Droplet collisions were first simulated in vacuum with the impact Weber number varying in a broad range from 6.7 to 540 (Re = 2.6–23.2). By systematically varying the impact Weber number, the collision outcomes can be classified into different regimes. At a low impact Weber number (<265), the collision outcome is consistent with previous studies,31 that is, a coalescence regime: the two droplets experienced very small deformation as they approached each other before eventually coalescing into a larger droplet (Figure S1). However, as the impact Weber number increased, interesting phenomena emerged (Figure 2). When the impact Weber number reached 265, the two droplets first merged into a large droplet and gradually expanded to a planar disk. The maximum spreading factor βmax is defined as βmax = Dmax/D0, where Dmax is the maximum spreading diameter and D0 is the initial diameter. After 0.13 ns, when the maximum spreading factor reached 2.66, two holes close to each other appeared that lasted about 0.03 ns. The two holes first increased in size, then merged into a larger hole with a maximum diameter of 3.2 nm, and finally decreased until the hole was completely submerged in the merged droplet. Similar phenomena were observed at the impact Weber number of 281 and 299, albeit with one larger hole. When the impact Weber number reached 315, the maximum spreading factor was 2.91 at this point. After 0.108 ns, eight tiny holes with diameters ranging from 1.3 to 4.3 nm appeared randomly on the disk. Another 0.144 ns later, these holes gathered together and merged into a larger hole with a diameter of 10.3 nm in the vicinity of the merged droplet center. Then, the holes extended to the peripheral region until a ringlike structure was formed. Finally, the hole contracted and disappeared, as the large droplet reached its stable state because of surface tension. When the impact Weber number was further increased to 540, the maximum spreading factor is 3.43. More and bigger holes appeared throughout the merged droplet. A “spider web”-like structure was formed. The surface tension was not enough to pull the structure together, and consequently, the spider web disintegrated into “spaghetti”-like structures. At the final stage, the spaghetti-like structures broke up into small satellite droplets. This breaking process coincides with the shattering regime.32 The above dynamic processes with the formation of single and multiple holes have not been observed in droplet collisions before. The existence of initial holes was previously observed in droplet impingement on substrates and attributed to air entrapment in surface crevices.33 This explanation, however, would not hold true for our simulations, as holes can still be observed even when the collision occurred in vacuum.

Figure 2.

Figure 2

Open in a new tab

Transition from coalescence regime to hole regime and shattering regime.

To further clarify the mechanisms behind the different regimes of droplet collision dynamics, we also investigate the droplet collisions in an ambient gas with different pressures. An ambient of nitrogen gas consisting of 85 890 and 343 560 nitrogen molecules provided a pressure of 2.7 and 8 atm, respectively. The hole regime is observed in p = 2.7 atm as shown in Figure 3. The threshold impact Weber number for this regime at 2.7 and 8 atm is larger than in vacuum. Detailed analysis will be conducted in the following section.

Figure 3.

Figure 3

Open in a new tab

Series of images of representative droplet collisions at different ambient pressures at We = 326 and 540. (a) We = 326 and (b) We = 540.

3.2. Spreading Factor

From the above findings, the spreading factor is an important parameter in predicting the droplet collision outcomes, especially for the hole and shattering regimes.34 Previous studies on the spreading factor mainly focused on macrodroplets impacting on substrates. There have been few if any studies on predicting the spreading factor of droplet collisions, especially nanodroplets. In this section, we will propose a model for predicting the maximum spreading factor for nanodroplet collisions. First, we can write the energy balance equation for the initial and the maximum spreading states as follows

3.2. 3

where Ek and Ep represent the kinetic and gravitational potential energy, respectively, and W represents the viscous dissipation. In our MD simulations, gravity is negligible because it is too small compared with other forces. The initial kinetic energy Ek1 is 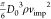Inline graphic and the initial surface energy is 2πD02σ. From previous nanodroplet impinging studies,32 the viscous dissipation from the initial state to a maximum spreading state has been evaluated as

3.2. 4

where μ is the kinematic viscosity coefficient, vimp is the impact velocity, D0 is the droplet diameter, and β is the maximum spreading factor. The estimation of viscous dissipation takes nanoscale flow properties into consideration. First, the velocity gradient exists in the entire droplet instead of just in the boundary layer. Second, the height of the droplet during spreading should not be replaced by the value at the maximum spreading state simply. Assuming cylindrical shape for the disklike spreading droplet, at the maximum spreading state, the surface area is

3.2. 5

Combining all the above equations, we can obtain the maximum spreading factor as a function of Re and We

3.2. 6

With the impact Weber number ranging from 6.7 to 375, the present model predictions and obtained MD simulation results are compared with those of other macrodroplet collision models, as shown in Figure 4. From the comparison between different results, the macrodroplet predictions either overestimate or underestimate the droplet collision dynamic behavior while the present new model shows a more accurate prediction because of the more accurate viscous dissipation estimation. The model developed by Sander et al. can only be applied to larger Weber numbers.30 In Sander’s assumption, half of the initial kinetic energy is transformed into surface energy. In nanoscale, this assumption underestimates the viscous dissipation and therefore massively overestimates the maximum spreading factor. In Pan’s macrodroplet model, the velocity gradient only exited in the boundary layer which is the cross section of the disk, while in nanoscale, the boundary layer does not exist in the velocity field because the length scale from the center to the edge of the disk is very small. Our new model is very accurate up to an impact Weber number of 250. When the hole regime starts (at the impact Weber number larger than 265), our model slightly underestimates the spreading factor. It might be related to the overestimate of the surface energy and viscous dissipation. When holes appear, the surface energy at the maximum spreading state is lower than the complete disk without holes. To better describe the spreading dynamics in the hole formation regime, the viscous dissipation and surface energy in the spreading process need to be reevaluated. In the shattering regime (for impact Weber number larger than 540), the concept of the spreading factor is no longer valid because the droplet tends to break up into fragments.

Figure 4.

Figure 4

Open in a new tab

Comparison among spreading factors predicted by different models and MD simulation results.

3.3. Influence of Ambient Pressure

As shown in Section 3.1, single or multiple holes appear when two droplets collide in vacuum, which is an extreme case of decreasing ambient pressure. To investigate the ambient pressure effects, we have also simulated the binary collisions with different ambient pressures. A total of 85 890 and 343 560 nitrogen molecules were introduced to create an ambient pressure of 2.7 and 8 atm, respectively. The spreading factor at different Weber number and pressure is shown in Figure 5. At the same Weber number in Figure 5, the black line representing the spreading factors in vacuum is always larger compared to the other two lines at 2.7 and 8 atm. At 2.7 atm, when the impact Weber number reached 282, the two droplets finally merged into a larger droplet after expanding to a planar disk, without any appearance of holes during the whole process. However, when the impact Weber number continuously rose to 530 and the spreading factor reached 2.90, similar holes as seen in collisions in vacuum began to appear, but no shattering regime was observed. When the impact Weber number rose to 667 and the spreading factor reached 3.63, more holes appeared and then the shattering phenomenon occurred. Here, the ambient gas acts as a “cushion”, which resists droplet deformation including hole formation and shattering. The “cushion effect” was first proposed in our previous paper,34 where the ambient gas acted like a cushion to prevent the droplets approaching each other. In this study, the “cushion effect” of the ambient gas also acts to resist droplet deformation. From the atomic perspective, a higher ambient pressure contributes to a more compact layout of molecules and shorter intermolecule distances and thus stronger interatomic or intermolecular interactions. Consequently, droplets would find it more difficult to be deformed and the maximum spreading factor of the coalesced droplet decreases. The appearance of the hole and shattering regimes requires a threshold maximum spreading factor of around 2.66 and 3.64, respectively. Therefore, the threshold impact Weber number for the hole and shattering regimes at 2.7 atm is larger than in vacuum. The maximum spreading state under the above conditions is shown in Figure S2.

Figure 5.

Figure 5

Open in a new tab

Comparison among different spreading factors under different ambient gas pressure.

3.4. Impact of Weber Number

For all the low impact Weber number collisions in different environments, the coalescence regime appears. The two droplets approach each other and merge into a larger droplet, which is consistent with previous experimental and computational studies.35 From our proposed model, the maximum spreading factor increases with increasing impact Weber number. As shown in Figure 6, the thickness of the spreading disklike droplet becomes smaller and smaller until it becomes a thin liquid film, especially in the droplet center. When the maximum spreading factor is beyond a threshold value (2.66), the liquid film becomes unstable and rupture, leading to hole formation. Surface tension, however, tends to pull back any deformation including the formation of holes. Provided that the impact Weber number is not too high, surface tension would eventually “repair” the hole(s), leading to a merged larger droplet. When the impact Weber number further increases beyond a second critical value, the shattering regime appears, when surface tension is too weak to hold the droplet together. It is worth noting that the ambient pressure also tends to resist droplet deformation. As a result, the critical impact Weber numbers for the onset of hole formation and shattering are delayed by increasing ambient pressure.

Figure 6.

Figure 6

Open in a new tab

Front view and side view of the disklike spreading droplet around the maximum spreading state. The width of the disk is shown in the figure.

3.5. Nanodroplet Collision Regimes

Our study extends the current nanodroplet collision regime map, which is different from their macro- or microcounterparts.36,37 The new hole regime should be added to the nanoscale droplet collision regime map, which includes coalescence, bounce, coalescence, and separation; hole formation; and shattering regime (Figure 7). The bounce regime is absent from both nano- and macrodroplets when collision occurs in vacuum, which validates previous nanodroplet collision studies.38 In macroscale collision, the droplet collision regime map includes coalescence, bounce, coalescence, separation, and shattering regime.9 As a result, the separation regime existing in macroscale collision is absent in nanoscale collision while the hole regime existing in nanoscale collision is absent in macroscale collision. Compared to macroscale droplet collision, the bounce regime occurs in a very narrow Weber number range and there is no bounce—coalescence—bounce transition. Additionally, the similarities between nanodroplet collision and impingement require more analysis. Because of the “cushion effect” of the ambient gas, the threshold impact Weber number for different regimes increases with increasing pressure at both nano- and macroscales. Our simulation results are quantitatively validated in nanoscale and qualitatively validated in macroscale droplet collisions.

Figure 7.

Figure 7

Open in a new tab

Nanoscale and macroscale droplet collision regime maps under different pressures. (a) Nanoscale droplet collision regime map. (b) Macroscale droplet collision regime map.

4. Conclusions

In summary, using MD simulation, we found a new phenomenon called the hole regime in the head-on collision of binary nanodroplets. In vacuum, when the impact Weber number reached 265 and the maximum spreading factor reached 2.66, holes were formed in the planar disk in seemingly random locations before they finally coalesced. As the impact Weber number rose, holes were less likely to vanish once formed, and the collisions were more likely not shift to the shattering regime. The hole regime is attributed to the instability of the thin liquid film, and the liquid film instability increases with increasing maximum spreading factor (and consequently thinner film). The presence of ambient gas served as a cushion which was able to delay or suppress the hole formation as well as the shattering occurrence. The cushion effect increased with increasing ambient pressure. The cushion effect can be attributed to the interactions between water molecules and nitrogen molecules. Additionally, we proposed a model based on energy balance to estimate the spreading factor of the merged droplet. This model predicted the droplet dynamics behavior much better than previous models. These results show that collision outcomes are a function of the ambient pressure and impact Weber number. As a result, a new and complete regime map of head-on collisions of nanodroplets is constructed, which is contrasted with the regime map for macrodroplet collisions.

Acknowledgments

The authors gratefully acknowledge that simulations were partly performed on the Tsinghua High-Performance Parallel Computer and partly on ARCHER funded under the EPSRC projects “UK Consortium on Mesoscale Engineering Sciences (UKCOMES)” (grant nos. EP/L00030X/1 and EP/R029598/1) and “High Performance Computing Support for United Kingdom Consortium on Turbulent Reacting Flow (UKCTRF)” (grant no. EP/K024876/1).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.langmuir.8b04277.

  • Series of images of representative droplet collisions and maximum spreading state of droplet collisions under different pressures and Weber numbers (PDF)

The authors declare no competing financial interest.

Supplementary Material

la8b04277_si_001.pdf (341.4KB, pdf)

References

  1. Adam J. R.; Lindblad N. R.; Hendrick C. D. The Collision, Coalescence, and Disruption of Water Droplets. J. Appl. Phys. 1968, 39, 5173–5180. 10.1063/1.1655940. [DOI] [Google Scholar]
  2. Ashgriz N.; Poo J. Y. Coalescence and separation in binary collisions of liquid drops. J. Fluid Mech. 1990, 221, 183–204. 10.1017/s0022112090003536. [DOI] [Google Scholar]
  3. Pan K.-L.; Chou P.-C.; Tseng Y.-J. Binary droplet collision at high Weber number. Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. 2009, 80, 036301. 10.1103/physreve.80.036301. [DOI] [PubMed] [Google Scholar]
  4. Yarin A. L. Drop impact dynamics: Splashing, spreading, receding, bouncing. Annu. Rev. Fluid Mech. 2006, 38, 159–192. 10.1146/annurev.fluid.38.050304.092144. [DOI] [Google Scholar]
  5. Falkovich G.; Fouxon A.; Stepanov M. G. Acceleration of rain initiation by cloud turbulence. Nature 2002, 419, 151–154. 10.1038/nature00983. [DOI] [PubMed] [Google Scholar]
  6. Faeth G. M. CURRENT STATUS OF DROPLET AND LIQUID COMBUSTION. Prog. Energy Combust. Sci. 1977, 3, 191–224. 10.1016/0360-1285(77)90012-0. [DOI] [Google Scholar]
  7. Focke C.; Kuschel M.; Sommerfeld M.; Bothe D. Collision between high and low viscosity droplets: Direct Numerical Simulations and experiments. Int. J. Multiphase Flow 2013, 56, 81–92. 10.1016/j.ijmultiphaseflow.2013.05.008. [DOI] [Google Scholar]
  8. Hawa T.; Zachariah M. R. Coalescence kinetics of unequal sized nanoparticles. J. Aerosol Sci. 2006, 37, 1–15. 10.1016/j.jaerosci.2005.02.007. [DOI] [Google Scholar]
  9. Jiang Y. J.; Umemura A.; Law C. K. An experimental investigation on the collision behaviour of hydrocarbon droplets. J. Fluid Mech. 1992, 234, 171–190. 10.1017/s0022112092000740. [DOI] [Google Scholar]
  10. Kuan C.-K.; Pan K.-L.; Shyy W. Study on high-Weber-number droplet collision by a parallel, adaptive interface-tracking method. J. Fluid Mech. 2014, 759, 104. 10.1017/jfm.2014.558. [DOI] [Google Scholar]
  11. Lycett-Brown D.; Luo K. H.; Liu R. H.; Lv P. M. Binary droplet collision simulations by a multiphase cascaded lattice Boltzmann method. Phys. Fluids 2014, 26, 023303. 10.1063/1.4866146. [DOI] [Google Scholar]
  12. Qian J.; Law C. K. Regimes of coalescence and separation in droplet collision. J. Fluid Mech. 1997, 331, 59–80. 10.1017/s0022112096003722. [DOI] [Google Scholar]
  13. Willis K.; Orme M. Binary droplet collisions in a vacuum environment: an experimental investigation of the role of viscosity. Exp. Fluids 2003, 34, 28–41. 10.1007/s00348-002-0526-4. [DOI] [Google Scholar]
  14. Pan K.-L.; Law C. K.; Biao Z. Experimental and mechanistic description of merging and bouncing in head-on binary droplet collision. J. Appl. Phys. 2008, 103, 064901. 10.1063/1.2841055. [DOI] [Google Scholar]
  15. Kalweit M.; Drikakis D. Collision dynamics of nanoscale Lennard-Jones clusters. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 74, 235415. 10.1103/physrevb.74.235415. [DOI] [Google Scholar]
  16. Monaco E.; Brenner G.; Luo K. H. Numerical simulation of the collision of two microdroplets with a pseudopotential multiple-relaxation-time lattice Boltzmann model. Microfluid. Nanofluid. 2014, 16, 329–346. 10.1007/s10404-013-1202-0. [DOI] [Google Scholar]
  17. Lycett-Brown D.; Luo K. H. Improved forcing scheme in pseudopotential lattice Boltzmann methods for multiphase flow at arbitrarily high density ratios. Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. 2015, 91, 023305. 10.1103/physreve.91.023305. [DOI] [PubMed] [Google Scholar]
  18. Lycett-Brown D.; Luo K. H. Cascaded lattice Boltzmann method with improved forcing scheme for large-density-ratio multiphase flow at high Reynolds and Weber numbers. Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. 2016, 94, 053313. 10.1103/physreve.94.053313. [DOI] [PubMed] [Google Scholar]
  19. Li Q.; Luo K. H.; Kang Q. J.; He Y. L.; Chen Q.; Liu Q. Lattice Boltzmann methods for multiphase flow and phase-change heat transfer. Prog. Energy Combust. Sci. 2016, 52, 62–105. 10.1016/j.pecs.2015.10.001. [DOI] [Google Scholar]
  20. Kalweit M.; Drikakis D. Collision dynamics of nanoscale Lennard-Jones clusters. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 74, 235415. 10.1103/physrevb.74.235415. [DOI] [Google Scholar]
  21. MacKerell A. D.; Bashford D.; Bellott M.; Dunbrack R. L.; Evanseck J. D.; Field M. J.; Fischer S.; Gao J.; Guo H.; Ha S.; Joseph-McCarthy D.; Kuchnir L.; Kuczera K.; Lau F. T. K.; Mattos C.; Michnick S.; Ngo T.; Nguyen D. T.; Prodhom B.; Reiher W. E.; Roux B.; Schlenkrich M.; Smith J. C.; Stote R.; Straub J.; Watanabe M.; Wiórkiewicz-Kuczera J.; Yin D.; Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
  22. Liao M.-L.; Ju S.-P.; Yang S.-H. Coalescence behavior of water nanoclusters: temperature and size. J. Phys. Chem. C 2007, 111, 6927–6932. 10.1021/jp066246t. [DOI] [Google Scholar]
  23. Nikolopoulos N.; Bergeles G. The effect of gas and liquid properties and droplet size ratio on the central collision between two unequal-size droplets in the reflexive regime. Int. J. Heat Mass Transfer 2011, 54, 678–691. 10.1016/j.ijheatmasstransfer.2010.09.002. [DOI] [Google Scholar]
  24. Nikolopoulos N.; Strotos G.; Nikas K. S.; Bergeles G. The effect of Weber number on the central binary collision outcome between unequal-sized droplets. Int. J. Heat Mass Transfer 2012, 55, 2137–2150. 10.1016/j.ijheatmasstransfer.2011.12.017. [DOI] [Google Scholar]
  25. Beckers J. V. L.; Lowe C. P.; De Leeuw S. W. An iterative PPPM method for simulating Coulombic systems on distributed memory parallel computers. Mol. Simul. 1998, 20, 369–383. 10.1080/08927029808022044. [DOI] [Google Scholar]
  26. Verlet L. Computer “Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules. Phys. Rev. 1967, 159, 98–103. 10.1103/physrev.159.98. [DOI] [Google Scholar]
  27. Aktulga H. M.; Fogarty J. C.; Pandit S. A.; Grama A. Y. Parallel reactive molecular dynamics: Numerical methods and algorithmic techniques. Parallel Comput. 2012, 38, 245–259. 10.1016/j.parco.2011.08.005. [DOI] [Google Scholar]
  28. Humphrey W.; Dalke A.; Schulten K. VMD: Visual molecular dynamics. J. Mol. Graphics Modell. 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
  29. Stukowski A. Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. 10.1088/0965-0393/18/1/015012. [DOI] [Google Scholar]
  30. Wildeman S.; Visser C. W.; Sun C.; Lohse D. On the spreading of impacting drops. J. Fluid Mech. 2016, 805, 636–655. 10.1017/jfm.2016.584. [DOI] [Google Scholar]
  31. Dhiman R.; Chandra S. Rupture of thin films formed during droplet impact. Proc. R. Soc. A 2010, 466, 1229–1245. 10.1098/rspa.2009.0425. [DOI] [Google Scholar]
  32. Li B.-X.; Li X.-H.; Chen M. Spreading and breakup of nanodroplet impinging on surface. Phys. Fluids 2017, 29, 012003. 10.1063/1.4974053. [DOI] [Google Scholar]
  33. Zhang Y. R.; Jiang X. Z.; Luo K. H. Bounce regime of droplet collisions: A molecular dynamics study. J. Comput.Sci. 2016, 17, 457–462. 10.1016/j.jocs.2016.03.011. [DOI] [Google Scholar]
  34. Willis K. D.; Orme M. E. Experiments on the dynamics of droplet collisions in a vacuum. Exp. Fluids 2000, 29, 347–358. 10.1007/s003489900092. [DOI] [Google Scholar]
  35. Yarin A. L.Drop impact dynamics: Splashing, spreading, receding, bouncing. Annual Review of Fluid Mechanics; Annual Reviews: Palo Alto, 2006; Vol. 38, pp 159–192. [Google Scholar]
  36. Tang C.; Zhang P.; Law C. K. Bouncing, coalescence, and separation in head-on collision of unequal-size droplets. Phys. Fluids 2012, 24, 022101. 10.1063/1.3679165. [DOI] [Google Scholar]
  37. Fei L.; Scagliarini A.; Montessori A.; Lauricella M.; Succi S.; Luo K. H. Mesoscopic model for soft flowing systems with tunable viscosity ratio. Phys. Rev. Fluid. 2018, 3, 104304. 10.1103/physrevfluids.3.104304. [DOI] [Google Scholar]
  38. Chun I.-B.; Ha M.-Y.; Jang J.-K.; Yoon H.-S. Molecular Dynamics Study on the Binary Collision of Nanometer-Sized Droplets of Liquid Argon. Bull. Korean Chem. Soc. 2011, 32, 2027–2031. 10.5012/bkcs.2011.32.6.2027. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

la8b04277_si_001.pdf (341.4KB, pdf)

Articles from Langmuir are provided here courtesy of American Chemical Society

RESOURCES