High mobility in a van der Waals layered antiferromagnetic metal

We introduce a van der Waals material that exhibits a very high electronic mobility and antiferromagnetism and can be exfoliated.

Abstract

Van der Waals (vdW) materials with magnetic order have been heavily pursued for fundamental physics as well as for device design. Despite the rapid advances, so far, they are mainly insulating or semiconducting, and none of them has a high electronic mobility—a property that is rare in layered vdW materials in general. The realization of a high-mobility vdW material that also exhibits magnetic order would open the possibility for novel magnetic twistronic or spintronic devices. Here, we report very high carrier mobility in the layered vdW antiferromagnet GdTe₃. The electron mobility is beyond 60,000 cm² V⁻¹ s⁻¹, which is the highest among all known layered magnetic materials, to the best of our knowledge. Among all known vdW materials, the mobility of bulk GdTe₃ is comparable to that of black phosphorus. By mechanical exfoliation, we further demonstrate that GdTe₃ can be exfoliated to ultrathin flakes of three monolayers.

INTRODUCTION

Van der Waals (vdW) materials are the parent compounds of two-dimensional (2D) materials, which are currently actively studied for new device fabrications (1) involving the creation of heterostructure stacks (2) or twisted bilayers (3) of 2D building blocks. Ferromagnetic and antiferromagnetic vdW materials have recently led to the observation of intrinsic magnetic order in atomically thin layers (4–12), which was followed by exciting discoveries of giant tunneling magnetoresistance (MR) (13–16) and tunable magnetism (17–19) in these materials.

So far, the known ferromagnetic or antiferromagnetic vdW materials that can be exfoliated are limited to a few examples, such as CrI₃ (4), Cr₂Ge₂Te₆ (5), FePS₃ (6, 7), CrBr₃ (8, 9), CrCl₃ (10–12), Fe₃GeTe₂ (17, 20), and RuCl₃ (21–23). Out of these, only Fe₃GeTe₂ is a metallic ferromagnet, and there is no known vdW-based 2D antiferromagnetic metal. Moreover, no evidence of high carrier mobilities has been reported in any of these exfoliated thin materials or even in their bulk vdW crystals. In general, high mobility is limited to very few vdW materials, such as graphite (24) and black phosphorus (25). A material with high electronic mobility and a corresponding high mean free path (MFP) might be critical for potential magnetic “twistronic” devices (3), where a large MFP could enable interesting phenomena in a Moiré supercell–induced flat band. In addition, conducting antiferromagnetic materials are the prime candidates for high-speed antiferromagnetic spintronic devices (26). Here, we report the realization of a very high electronic mobility in a vdW layered antiferromagnet, GdTe₃. We note that “layered” reflects the crystal structure and not the magnetic structure. We further demonstrate the mechanical exfoliation of bulk GdTe₃ crystals down to a few layers. In thin-flake samples of ~20 nm thickness, a relatively high mobility is retained.

We chose to study GdTe₃, because rare-earth tritellurides (RTe₃, R = La-Nd, Sm, and Gd-Tm) are structurally related to topological semimetal ZrSiS (27, 28) while being known to exhibit an incommensurate charge density wave (CDW) (29–31) and rich magnetic properties (32) and becoming superconducting under high pressure (R = Gd, Tb, and Dy) (33). Combined, these properties hint that they could exhibit both high mobility and magnetic order. Without considering the CDW, RTe₃ phases crystallize in an orthorhombic structure with the space group Bmmb. The structure is formed by double Te square-net sheets (perpendicular to the c axis), separated by double-corrugated RTe slabs, as illustrated in Fig. 1A. The RTe₃ crystal structure additionally exhibits a vdW gap between the two neighboring Te square-net sheets, which allows us to exfoliate RTe₃ bulk crystals into 2D thin flakes.

Fig. 1. GdTe₃ crystal structure and antiferromagnetism.

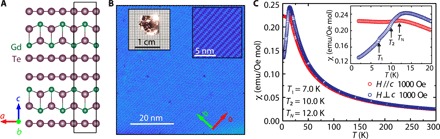
(A) Illustration of the GdTe₃ crystal structure: A vdW gap is located between the two neighboring Te sheets. The rectangular box indicates the unit cell if no CDW is considered. (B) STM image of the GdTe₃ surface at 72 K with a tip bias of 0.2 V. The CDW vector is along the b axis. The left inset shows a typical GdTe₃ crystal. The right inset shows a zoom-in image with atomic resolution. (C) Temperature-dependent magnetization of a bulk GdTe₃ crystal under zero-field cooling conditions. H//c and H⊥c indicate the applied field perpendicular and parallel to the basal plane, respectively. The arrows indicate the three transitions. Photo credit: Shiming Lei, Princeton University.

RESULTS AND DISCUSSION

High-quality plate-like GdTe₃ crystals, with lateral sizes up to ~8 mm × ~8 mm in the basal plane (inset in Fig. 1B), were grown by the self-flux technique (see Materials and Methods and fig. S1). Despite the existence of a CDW along the b axis below 379 K (fig. S1C) (34), the GdTe₃ crystals show excellent metallicity. Under zero magnetic field, they reveal a large residual resistivity ratio [RRR; defined as ρ_xx (300 K)/ρ_xx (2 K)] reaching up to 825 (for a list of explored samples in this work, see table S1), therefore demonstrating very high crystal quality with low defect concentrations. Figure 1B shows a representative scanning tunneling microscopy (STM) image of the cleaved GdTe₃ surface, indicating the CDW modulation (fig. S2). The defect concentration evaluated from this image is one defect per 200 nm² or one defect per ~1000 unit cells. We note that this low defect concentration is a rough estimate of one STM image and not based on a statistical analysis. However, it was measured on a sample whose RRR is roughly 300, resulting in a conservative estimate. For the GdTe₃ crystals with larger RRR, the defect concentration might be lower.

The antiferromagnetic order is confirmed by temperature-dependent DC magnetization of bulk GdTe₃ (Fig. 1C), which reveals three transitions: the Néel transition at T_N = 12.0 K and two further transitions at T₁ = 7.0 K and T₂ = 10.0 K; the T₁ transition has previously not been noted in the literature. Independently, these three transitions are confirmed by zero-field heat capacity (fig. S1E) and temperature-dependent resistivity measurements under an applied magnetic field (fig. S1F). The broad peak features at T₂ and T_N in the heat capacity measurement suggest a magnetic phase transition, while a sharp peak at T₁ in the heat capacity (fig. S1E) as well as a sudden jump at T₁ in the resistivity curve (fig. S1F) indicate that this transition is of first order and might be structural. The exact magnetic structure remains to be determined.

Quantum oscillation (QO) measurements demonstrate a very long single-particle quantum lifetime in GdTe₃ crystals. Figure 2A shows very detailed de Haas–van Alphen (dHvA) oscillations that appear in the AC magnetic susceptibility measurements. The fast Fourier transformation (FFT) of the dHvA oscillations (inset in Fig. 2A) reveals five oscillation frequencies: F(α) = 60 T, F(β₁) = 472 T, F(β₁) = 506 T, F(γ₁) = 813 T, and F(γ₂) = 847 T. By performing the Lifshitz-Kosevich (L-K) analysis (Fig. 2B) on the three strong QO components (β₁, β₂, and γ₂), the quantum lifetime is determined to be 13.5 × 10⁻¹⁴ to 17.5 × 10⁻¹⁴ s, resulting in a mobility of 1400 to 1700 cm² V⁻¹ s⁻¹ (for more details, see table S2).

Fig. 2. QOs of bulk GdTe₃.

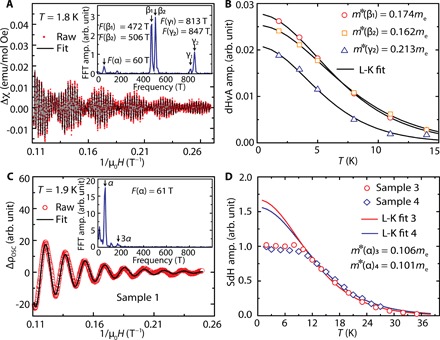
(A) dHvA oscillations at 1.8 K with L-K fit. The inset shows the FFT spectrum, with five indicated oscillation frequencies. (B) Temperature dependence of the amplitudes of β₁, β₂, and γ₂ oscillations from dHvA measurements. The solid lines are fits to the L-K formula. (C) SdH oscillations after subtracting the polynomial background from field-dependent resistivity measurements (ρ_xx) for sample 3. The inset shows the FFT spectrum, with resolved α oscillation and its third harmonics. (D) Temperature dependence of the amplitude of the α oscillation from SdH measurements. The solid line is a fit to the L-K formula above T_N, resulting in the effective masses of m*(α)₃ and m*(α)₄ for samples 3 and 4, respectively.

Besides dHvA oscillations, Shubnikov–de Haas (SdH) oscillations, which appear in the field-dependent resistivity measurement (fig. S3), provide an additional insight into the overall Fermi surface (FS) geometry. Although different samples show slight difference in the relative peak intensities in the FFT spectra (see Fig. 2C and fig. S3D), the sizes of FS pockets revealed by SdH oscillations are overall in good agreement with those determined from dHvA oscillations, with additional FS pockets (η, δ₁, and δ₂) appearing at higher frequencies of 2230, 3708, and 3948 T, respectively (fig. S3D; also see table S2 for comparison). Furthermore, the higher-frequency oscillations (β, η, γ, and δ) are much weaker than the α oscillation and its harmonics. Possibly because of this reason, the weak γ₁ is not resolved in the SdH measurements. By comparing the β and γ pockets that are accurately determined from QO measurements to the published calculated ones (30), we find a very good agreement. This indicates that the β and γ pockets arise because of the effect of bilayer splitting, and the pairing of each one (β₁/β₂ and γ₁/γ₂) is associated with “neck” and “belly” extremal orbits of the corrugated FS along k_z. For a detailed discussion of the FS, see the Supplementary Materials.

The dominant α oscillation in SdH oscillations allows the evaluation of the quantum lifetime of α FS pocket. The results from two samples (#3 and #4) are shown in Fig. 2D. Sample 3 has an RRR of 315, while sample 4 has an RRR of 188. Unlike the larger FS pockets (Fig. 2B), the amplitude of α oscillation (Fig. 2D) shows clear deviation from the L-K formula and appears to reach a plateau in the magnetically ordered regime (T < T_N). This suggests a substantial interplay of the antiferromagnetic order to the conducting electrons in the small α pocket but a negligible effect of the antiferromagnetic order in the larger FS pockets. L-K fits of the temperature dependence of the oscillation amplitude above T_N yield a very light cyclotron effective mass of m*(α) = 0.101 to 0.106m_e (m_e is the free electron mass) and a quantum lifetime up to 12.1 × 10⁻¹⁴ s, resulting in a mobility up to 2012 cm² V⁻¹ s⁻¹ (see table S2). We notice that the SdH oscillations in GdTe₃ have previously been reported in (35). However, in this study, only the α pocket was resolved, resulting in F(α) ≈ 56 T and m*(α) ≈ 0.1m_e. This result on the α FS pocket is consistent with our measurement.

For high-speed device applications, it is crucial to determine the transport mobility and not just the mobility derived from the quantum lifetime. Hall measurements provide an important overview on the transport mobility and carrier concentration. Figure 3 (A and B) shows their temperature dependence on sample 1, based on fits to the Hall resistivity, ρ_yx, assuming a two-band model. Ideally, one should attempt to determine the carrier concentration (n_i) and mobility (μ_i) for each of the pockets. However, the proliferation of fit parameters strongly degrades the robustness of the fits. Multiple sets of “good” parameters can lead to several broad minima of the error function even if the values are unphysical or very remote from the actual values. This would not be helpful for understanding the materials’ real transport properties. A better approach is to group the two (rather similar) electron pockets (β and γ) as one “electron band” with an average electron mobility and the two larger hole pockets (η and δ) as one “hole band” with an average hole mobility and carry out the two-band model fits. We regard the inferred electron (hole) concentrations and mobilities as the average values for the group of electron (hole) pockets. The justification of this model is that the fits yield (average) carrier concentrations that are quite consistent between Hall and QO measurements and across the measured samples with low and high mobilities (see section S5). At 2 K, the electron and hole concentrations are evaluated to be 1.0 × 10²¹ cm⁻³ and 2.5 × 10²¹ cm⁻³, respectively, and the electron and hole transport mobilities are determined to be μ_t (e) = 28,100 cm² V⁻¹ s⁻¹ and μ_t (h) = 8300 cm² V⁻¹ s⁻¹, respectively (also see Table 1). For accuracy, a two-band model fit is also performed on the low-field Hall conductivity, σ_xy. It results in μ_t (e) = 37,700 cm² V⁻¹ s⁻¹ and μ_t (h) = 13,500 cm² V⁻¹ s⁻¹ (see fig. S5 and Table 1). The results from these two methods reasonably agree with each other. Among all measured samples, the highest achieved electron and hole mobilities are μ_t (e) = 61,200 to 113,000 cm² V⁻¹ s⁻¹ and μ_t (h) = 15,000 to 23,500 cm² V⁻¹ s⁻¹ (fig. S4). The lower and higher bounds come from the Hall conductivity and resistivity fits (see more details in Table 1). Unexpectedly, the electron transport mobility is found to be more than 14 times larger than the mobility (μ_q) estimated from QO (table S2). Such a large difference is associated with the different scattering processes. Essentially, the classical transport mobility is only susceptible to the large-angle scattering processes that relax the current, whereas the mobility derived from the quantum lifetime is sensitive to all scattering processes that cause Landau level broadening, including forward scattering (36). Therefore, μ_t is generally larger than μ_q, and the difference reflects the relative importance of small-angle scatterings. Experimentally, a large ratio of μ_t/μ_q up to ~10⁴ has been reported in the 3D Dirac semimetal Cd₃As₂, which was interpreted to indicate severely reduced backscattering (36). In GdTe₃, μ_t/μ_q reaches up to ~30, which also suggests a reduced backscattering process, although it is much less prominent than that of Cd₃As₂.

Fig. 3. Carrier concentrations and transport mobilities of bulk GdTe₃ and a 22-nm flake.

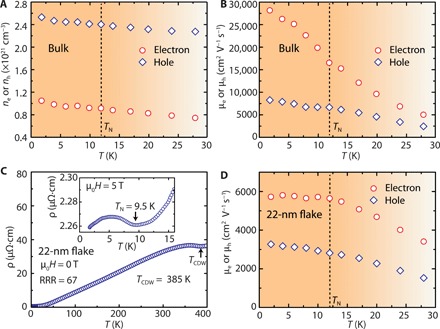
(A and B) Temperature-dependent carrier concentrations and mobilities from Hall measurements of bulk GdTe₃. The dashed lines indicate T_N. (C) Temperature-dependent resistivity on a 22-nm-thin flake, showing both the existence of the CDW and the antiferromagnetic transition. The inset shows the low-temperature resistivity under an applied field of 5 T, revealing the magnetic transition. (D) Temperature-dependent electron and hole mobilities of the 22-nm-thin flake.

Table 1. Carrier concentrations and mobilities from Hall measurements.

The results outside and inside the parentheses are from fits to the Hall resistivity (ρ_xy) and Hall conductivity (σ_xy), respectively.

Sample number	ne (×1021 cm−3)	nh (×1021 cm−3)	μt (e) (cm2 V−1 s−1)	μt (h) (cm2 V−1 s−1)	Sample geometry
1	1.05 (0.61)	2.53 (2.03)	28,100 (37,700)	8,300 (13,500)	Bulk
3	0.96 (0.62)	2.41 (2.02)	17,700 (23,300)	6,000 (8,400)
4	1.07 (1.15)	2.70 (2.75)	14,000 (12,000)	5,100 (5,400)
5	1.59 (2.28)	2.74 (3.43)	113,000 (61,200)	15,000 (23,500)
6	1.01 (1.12)	2.15 (2.05)	5,700 (5,400)	3,300 (3,300)	Thin flake

While the transport mobility might seem low compared to some nonmagnetic topological semimetals, such as Cd₃As₂ [mobility of 9 × 10⁶ cm² V⁻¹ s⁻¹ at 5 K (36)], it is among the highest reported for any magnetically ordered (either ferromagnetic or antiferromagnetic) compound. For reference, Table 2 presents a list of known layered, magnetically ordered materials (that cannot necessarily be exfoliated) with high mobility. The structurally related nonmagnetic topological semimetal ZrSiS (28), as well as high-mobility delafossite PdCoO₂ (37), graphite (24), and black phosphorus (25), is also listed. GdTe₃ stands out as the material with the highest mobility in the category of (quasi-)layered magnetically ordered materials and even compares to nonmagnetic black phosphorus. Among all the listed magnetically ordered materials, GdTe₃ is the only vdW layered material and thus the only one that can be easily exfoliated.

Table 2. A compilation of bulk materials with magnetic order, in addition to ZrSiS, PdCoO₂, graphite, and black phosphorus, for which high mobilities are reported, in comparison to GdTe₃.

For the transport mobility (μ_t) estimated from Hall measurement, the values outside and inside the parentheses represent the electron and hole carriers, respectively. For the quantum lifetime–derived mobility (μ_q) and effective mass (m*) estimated from SdH and dHvA oscillations, a range with lower and upper bounds is provided. For the transport mobility estimated from a combination of the QO and residual resistivity measurements, we denote it as “hybrid.” The transport mobility estimated from MR is listed when it is considered to be more accurate than the Hall mobility. The mobilities of PdCrO₂ and PdCoO₂ were deduced by the hybrid method because no quantum lifetime or Hall carrier mobility is reported in the literature. The mobility of EuMnBi₂ from the hybrid method is also listed for comparison with the Hall carrier mobility. NA, not available.

Material	μq or μt (cm2 V−1 s−1)	m*/me	Method	Reference
SrMnBi2	250	0.29	SdH	(44)
CaMnBi2	488	0.53	SdH	(45)
Sr1−yMn1−zSb2	570	0.04–0.05	SdH	(46)
YbMnBi2	689	0.27	SdH	(47)
YbMnSb2	1,584 1,072 6,538 (1,310)	0.134 0.108 NA	SdH dHvA Hall	(48) (48) (48)
EuMnBi2	1.6 (520) (14,000)	NA NA	Hall Hybrid	(49) (50)
BaMnSb2	1,280 1,300	0.052–0.058 NA	SdH Hall	(51) (51)
GdPtBi	Not reported (1,500–2,000)	0.23 NA	SdH Hall	(52) (52)
PdCrO2	8,700	0.33–1.55	Hybrid	(53)
BaFe2As2*	1,130	NA	MR	(54)
GdTe3	1,165–2,012 >61,200 (>15,000)	0.101–0.213 NA	SdH and dHvA Hall	This work
ZrSiS	1,300–6,200 4,219–10,000 20,000 (2,800)	0.1–0.14 0.025–0.052 NA	SdH dHvA Hall	(28) (55) (28)
PdCoO2	51,000	1.45–1.53	Hybrid	(37)
Graphite†	1,263,000	NA	MR	(24)
Black phosphorus‡	(65,000)	NA	Hall	(25)

*The average mobility value from Hall data is 376 cm² V⁻¹ s⁻¹, but it was considered to be inaccurate. Therefore, the MR was used to evaluate the average mobility.

†The average mobility is adopted.

‡The hole mobility in p-type black phosphorus is adopted as it is higher than the electron mobility n-type one.

The reason for such a high mobility in a magnetically ordered phase is closely related to the crystal structure of GdTe₃. Materials containing a square net as a structural motif frequently exhibit very steeply dispersed bands (38). In general, high mobility (μ) is described by two factors in a conducting material: a low effective mass, m*, and a long scattering time, τ. While the long scattering time benefits from the high crystal quality, the low effective mass is related to the steep conduction bands resulting from the square net. To confirm the latter, we performed angle-resolved photoemission spectroscopy (ARPES) measurements (fig. S6) and extracted the Fermi velocity (V_F) of the bands composing the pockets around $\overline{X}$ to be 1.1 × 10⁶ to 1.2 × 10⁶ m s⁻¹, which is a slightly conservative value compared to that of other RTe₃ compounds (1.5 × 10⁶ m s⁻¹) (39). Nevertheless, these numbers are comparable to that of graphene (40). Because the sizes of β and γ pockets were accurately determined by QO measurements and are in reasonably good agreement with the ARPES results (fig. S6), the knowledge of Fermi velocity allows the evaluation of their effective masses. Assuming a parabolic band dispersion, the effective masses are estimated to be m*(β) = 0.11 to 0.13m_e and m*(γ) = 0.15 to 0.17m_e, which is in reasonably good agreement with the cyclotron effective masses determined from QO measurements (Fig. 2B). Besides the square-net structure, the CDW might also play an important role in contributing to the high mobility. The scattering time can be enhanced because of partial gap opening of the FS.

Last, we provide evidence for the exfoliation capability of GdTe₃ and the persistence of high electronic mobility and antiferromagnetic order in a thin flake. Using a micromechanical exfoliation approach in inert atmosphere, we first created a 22-nm thin device of GdTe₃. Note that the thin flakes are degraded with heating or long exposure to air (fig. S7). To ascertain that magnetic order is retained in these thin flakes, we performed transport measurements on the 22-nm flake. The temperature-dependent resistivity (Fig. 3C) under an applied magnetic field shows the magnetic phase transition, visible in the slope change of the resistivity, similar to the bulk (fig. S1F). Therefore, we conclude that antiferromagnetism still exists in these thin flakes. On the basis of the thin-flake transport measurements, the electron and hole mobilities are determined to be 5700 and 3300 cm² V⁻¹ s⁻¹, respectively (Fig. 3D). While these values are lower than those in the bulk, the mobility is still slightly higher than that reported for black phosphorus flakes with similar thickness (41). The lower mobility in the GdTe₃ flake compared to the bulk might be related to slight sample degradation, possibly because of short exposure to air, which results in a lower RRR of 67. Nonetheless, it is very likely that future effort that aims for improvements of the thin-flake device fabrication, with, for example, hexagonal boron nitride (h-BN) encapsulation (42), will enhance the mobility and realize the full potential of this material. There are some additional observations that can be made from the transport experiment on the thin flake. For once, the resistivity measurement (Fig. 3C) suggests the persistence of the CDW; however, the transition temperature is slightly higher than in the bulk. Therefore, GdTe₃ may additionally provide a platform to study the thickness dependence of CDWs. Furthermore, the SdH measurements on a 19-nm flake (fig. S3, E and F) hint a reduction of the FS pockets in size with sample thickness, although no clear difference of carrier concentrations can be found between the bulk samples and the 22-nm flake.

We extended the exfoliation procedure and were able to reach GdTe₃ flakes with a minimum thickness of 3.8 nm (Fig. 4, A and B), which corresponds to three monolayers (where a monolayer is half a unit cell). The structural integrity (on flakes down to 7.5 nm) was confirmed by Raman spectroscopy measurements in inert atmosphere (fig. S8). Therefore, we are confident that mono- or bilayer devices of GdTe₃ will be accessible with further optimized exfoliation conditions.

Fig. 4. Exfoliation of GdTe₃ ultrathin flakes.

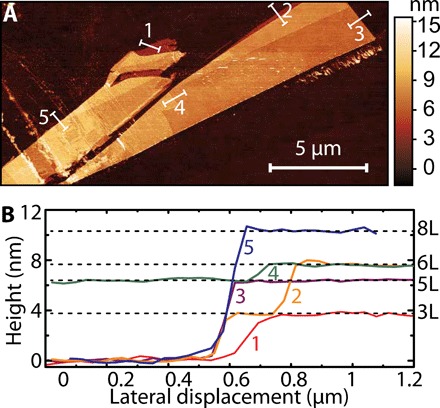
(A and B) An AFM image of exfoliated GdTe₃ ultrathin flakes and its cross-sectional height profiles. Note that the height profiles are translated into the number of GdTe₃ layers on the right vertical axis in (B). One layer corresponds to half a unit cell (shown in Fig. 1A).

In summary, we showed that GdTe₃, as a vdW layered antiferromagnet, exhibits high electronic mobility. It stands out as the material that shows the highest mobility within all known structurally (quasi-)layered and magnetically ordered materials, to the best of our knowledge. Among all known vdW materials, the dominant carrier mobility of GdTe₃ is only surpassed by graphite but comparable to black phosphorus. We also demonstrated that GdTe₃ can be exfoliated to ultrathin flakes, reaching three monolayers (or 1.5 unit cells). In a GdTe₃ flake of 22 nm, a relatively high carrier mobility is maintained, while the CDW and antiferromagnetic order persists. Overall, GdTe₃ can be considered to be the first high-mobility, magnetically ordered vdW material. The combination of these properties provides a huge potential for novel 2D spintronic or twistronic devices. We believe that the establishment of a vdW layered, magnetically ordered material with high mobility provides numerous exciting opportunities for future studies.

MATERIALS AND METHODS

GdTe₃ crystal growth and x-ray diffraction

High-quality GdTe₃ single crystals were grown in an excess of tellurium (Te) via a self-flux technique. Te (metal basis, >99.999%; Sigma-Aldrich) was first purified to remove oxygen contaminations and then mixed with gadolinium (Gd) (>99.9%; Sigma-Aldrich) in a ratio of 97:3. The mixture was sealed in an evacuated quartz ampoule and heated to 900°C over a period of 12 hours and then slowly cooled down to 550°C at a rate of 2°C/hour. The crystals were obtained by a decanting procedure in a centrifuge. The as-grown crystals were characterized by x-ray diffraction using a Bruker D8 Advance Eco diffractometer in reflection geometry with Cu Kα radiation and a STOE STADI P diffractometer in a transmission geometry with Mo Kα radiation. The room temperature lattice parameters evaluated this way are 4.316, 4.325, and 25.6 Å along a, b, and c axes, respectively, without considering the CDW modulations. For the exfoliated samples, we call a flake “ultrathin” when it is less than 3 unit cell thick, while it is “thin” when it is above 3 unit cell thick and below ~100 nm.

STM imaging

Bulk GdTe₃ samples were cleaved and measured at 72 K in ultrahigh vacuum with a variable temperature STM. A mechanically sharpened platinum-iridium tip was used for topography and spectroscopy measurements. The STM tip was treated on a Cu (111) surface before the experiment to ensure its metallic character. STM spectra were taken using a lock-in amplifier with a setpoint current of 60 pA, a bias of 800 mV, and a modulation bias of 8 mV.

Magnetization and dHvA measurements

Temperature-dependent DC magnetization measurements were performed on a Quantum Design PPMS DynaCool system via the vibrating sample magnetometer (VSM) option. The AC magnetic susceptibility measurements were performed via the ACMS option. The dHvA oscillation was obtained by subtracting a polynomial background from the AC susceptibility data. An FFT was performed to reveal the frequency of each QO component. To quantify the amplitude of the three dominant QO components of β₁, β₂, and γ₂, the dHvA oscillation was fitted with a superposition of three exponentially decaying sinusoidal functions (30). The amplitude of each fitted QO component at the envelope peak location of 7.8 T was adopted for the evaluation of their respective cyclotron effective mass. For the dHvA oscillation, the temperature-dependent QO damping is described by the L-K formula

$$\mathrm{\Delta }M\propto -B^{1/2}\frac{\mathrm{\lambda }T}{\text{sinh}(\mathrm{\lambda }T)}{e}^{-\mathrm{\lambda }{T}_{\mathrm{D}}}\text{sin}\left[2\mathrm{\pi }\right(\frac{F}{B}-\frac{1}{2}+\mathrm{\beta }+\mathrm{\delta }\left)\right]$$ (1)

where λ = (2π²k_Bm*)/(ℏeB), k_B is the Boltzmann constant, ℏ is the reduced Planck’s constant, T_D is the Dingle temperature, F is the QO frequency, and 2πβ is the Berry phase. In Eq. 1, δ is a phase shift, which is 0 and $\pm \frac{1}{8}$ for the 2D and 3D systems, respectively. Because of the dominant contribution of the sinusoidal function in Eq. 1 to the oscillatory component of the AC magnetic susceptibility (∆χ), ∆χ can be derived as

$$\mathrm{\Delta }\mathrm{\chi }\propto -B^{-3/2}F\frac{\mathrm{\lambda }T}{\text{sinh}(\mathrm{\lambda }T)}{e}^{-\mathrm{\lambda }{T}_{\mathrm{D}}}\text{cos}\left[2\mathrm{\pi }\right(\frac{F}{B}+\mathrm{\beta }+\mathrm{\delta }\left)\right]$$ (2)

In Eq. 2, a thermal factor can be defined as

$$R_T=\frac{\mathrm{\lambda }T}{\text{sinh}(\mathrm{\lambda }T)}$$ (3)

to describe the temperature-dependent damping of the dHvA oscillations. At a constant field, this thermal factor only depends on the cyclotron effective mass and temperature. The effective masses of QO components of β₁, β₂, and γ₂ were thus determined. The following step involves a refitting of the dHvA oscillation at 1.8 K to a superposition of three QO components, as described by Eq. 2. The Dingle temperature (T_D) was then determined. The quantum lifetime (τ_q) and mobility (μ_q) were derived by ${\mathrm{\tau }}_{\mathrm{q}}=\raisebox{1ex}{$\mathrm{\hslash }$}\!\left/ \!\raisebox{-1ex}{$2\mathrm{\pi }{k}_{\mathrm{B}}{T}_{\mathrm{D}}$}\right.$ and ${\mathrm{\mu }}_{\mathrm{q}}=\raisebox{1ex}{$e{\mathrm{\tau }}_{\mathrm{q}}$}\!\left/ \!\raisebox{-1ex}{$m^{*}$}\right.$, respectively.

Electrical transport and SdH oscillation measurements

The temperature- and field-dependent in-plane resistivities were measured in a standard four-terminal geometry in a Quantum Design PPMS DynaCool system. A constant AC current with an amplitude of 10 mA was applied. The angle-dependent SdH oscillations were measured with the aid of PPMS Horizontal Rotator. For the evaluation of the SdH oscillations, a polynomial background was subtracted from the symmetrized MR data. The cyclotron effective mass and Dingle temperature of the α FS pocket were determined in a similar manner to that in dHvA oscillation. The SdH oscillation is described by the L-K formula

$$\mathrm{\Delta }\mathrm{\rho }\propto \frac{\mathrm{\lambda }T}{\text{sinh}(\mathrm{\lambda }T)}{e}^{-\mathrm{\lambda }{T}_{\mathrm{D}}}\text{cos}\left[2\mathrm{\pi }\right(\frac{F}{B}-\frac{1}{2}+\mathrm{\beta }+\mathrm{\delta }\left)\right]$$ (4)

To evaluate the transport mobility and carrier concentration, Hall measurements (ρ_xx and ρ_yx) were performed in a standard Hall bar geometry. Assuming a two-band model, the Hall resistivity is expressed as (43)

$${\mathrm{\rho }}_{yx}(B)=\frac{B}{e}\frac{(n_{\mathrm{h}}{{\mathrm{\mu }}_{\mathrm{h}}}^2-n_{\mathrm{e}}{{\mathrm{\mu }}_{\mathrm{e}}}^2)+(n_{\mathrm{h}}-n_{\mathrm{e}}){({\mathrm{\mu }}_{\mathrm{e}}{\mathrm{\mu }}_{\mathrm{h}}B)}^2}{{({\mathrm{n}}_{\mathrm{e}}{\mathrm{\mu }}_{\mathrm{e}}+n_{\mathrm{h}}{\mathrm{\mu }}_{\mathrm{h}})}^2+{(n_{\mathrm{h}}-n_{\mathrm{e}})}^2{({\mathrm{\mu }}_{\mathrm{e}}{\mathrm{\mu }}_{\mathrm{h}}B)}^2}$$ (5)

where B = μ₀H (μ₀ is the free-space permeability); e is the elementary charge; n_e and n_h are electron and hole carrier concentrations, respectively; and μ_e and μ_h are the electron and hole carrier mobilities, respectively. According to the two-band model, the zero-field resistivity, ρ_xx(0), is related to the carrier concentration and mobility through the following equation

$${\mathrm{\rho }}_{\mathit{xx}}(0)=\frac{1}{e}\frac{1}{n_{\mathrm{e}}{\mathrm{\mu }}_{\mathrm{e}}+n_{\mathrm{h}}{\mathrm{\mu }}_{\mathrm{h}}}$$ (6)

The carrier concentration and mobility were determined by fits of the Hall resistivity to Eq. 5 on the condition of Eq. 6.

On the basis of Eq. 5, one can see that the field-dependent Hall resistivity becomes linear at high fields; the slope is

$${\frac{\mathrm{d}{\mathrm{\rho }}_{yx}}{\mathrm{d}B}\mid }_{B\text{is large}}=\frac{1}{(n_{\mathrm{h}}-n_{\mathrm{e}})e}$$ (7)

which solely depends on the difference in carrier concentration. This behavior is observed in our transport measurements on GdTe₃. For completion, fits to the two-band model are also performed on the Hall conductivity (σ_xy) data, which is converted from ρ_xx and ρ_yx. σ_xy is related to the carrier concentration and mobility through the expression

$${\mathrm{\sigma }}_{\mathit{xy}}(B)=\mathit{eB}(\frac{n_{\mathrm{h}}{{\mathrm{\mu }}_{\mathrm{h}}}^2}{1+{{\mathrm{\mu }}_{\mathrm{h}}}^2{B}^2}-\frac{n_{\mathrm{e}}{{\mathrm{\mu }}_{\mathrm{e}}}^2}{1+{{\mathrm{\mu }}_{\mathrm{e}}}^2{B}^2})$$ (8)

While the high-field Hall resistivity provides information on the carrier concentration difference, the low-field Hall conductivity is sensitive to the specific carrier type that has a higher mobility, even if it is the minority carrier. The Hall conductivity fits were performed with the constraint conditions of known carrier concentration difference and the zero-field resistivity. The mobilities evaluated from the Hall resistivity and Hall conductivity fits are considered as the two boundaries. The real carrier mobilities are considered to lie in between.

GdTe₃ thin-flake exfoliation and device fabrication

GdTe₃ crystals were micromechanically exfoliated using scotch tape and deposited directly onto 285-nm SiO₂/Si substrates. We performed the exfoliation tests both inside and outside the inert gas glovebox. The thin flakes were identified under an optical microscope based on the optical contrast on the substrate. Their thickness and structural integrity were directly measured in inert atmosphere through an NMI ezAFM40 and a WITec alpha300 Raman microscope. For Raman, a 100× objective was used with a 532-nm laser. To avoid damage and overheating, the laser power was kept below 50 μW. For thin-flake device fabrications, the prepatterned Hall bar electrode (25-nm Au with 5-nm Ti as the sticking layer) was deposited on a 285-nm SiO₂/Si substrate by standard E-beam lithography and evaporation procedure. To achieve a smooth top surface of the electrode, we used double-layer poly(methyl methacrylate) (PMMA) as the resist (PMMA 495 A2 as the bottom layer and PMMA 950 A2 as the top layer). Afterward, GdTe₃ thin flakes were exfoliated onto a SiO₂/Si substrate in an argon-filled glovebox and transferred onto the prepatterned electrode by standard dry transfer techniques for 2D materials using a poly(bisphenol A carbonate) (PC)/polydimethylsiloxane (PDMS) stamp. To protect the flake from air exposure, the PC film was left on top of the device. The device was then transported to a PPMS for further electrical characterizations. In the whole process, the air exposure was limited to less than 30 min. After the measurement, the PC film was dissolved in chloroform, and the thickness of thin flake was measured by atomic force microscopy (AFM).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/6/eaay6407/DC1

Section S1. Crystal structure, composition, magnetization, heat capacity, and in-plane resistivity

Section S2. STM topography and spectroscopy

Section S3. MR and SdH oscillations

Section S4. Comparison of the FS pockets from QO measurements to the calculated ones

Section S5. Carrier concentration estimations from QO measurements versus Hall measurements

Section S6. ARPES measurement

Section S7. Air sensitivity study and Raman spectroscopy of GdTe₃ thin flakes

Section S8. Additional notes on mobility for materials shown in Table 2

Table S1. An overview of the GdTe₃ samples (bulk and thin-flake geometries), on which we have performed transport measurements in this work.

Table S2. Material properties derived from QO measurements.

Fig. S1. X-ray diffraction pattern, magnetization, and in-plane resistivity measurements on bulk GdTe₃ crystals.

Fig. S2. CDW revealed by STM on a GdTe₃ crystal.

Fig. S3. MR and SdH oscillations.

Fig. S4. Two-band model fits to the Hall resistivity and conductivity at various temperatures on multiple samples.

Fig. S5. Temperature-dependent carrier concentrations and mobilities from two-band model fits to the Hall conductivities measured on sample 1.

Fig. S6. FS measured by ARPES and gap opening by the CDW in GdTe₃.

Fig. S7. Air sensitivity of GdTe₃ thin flakes.

Fig. S8. Raman spectroscopy on a series of GdTe₃ thin flakes with varying thicknesses.

References (56–62)