SUMMARY
The connectomes of organisms of the same species show remarkable architectural and often local wiring similarity, raising the question: where and how is neuronal connectivity encoded? Here, we start from the hypothesis that the genetic identity of neurons guides synapse and gap-junction formation and show that such genetically driven wiring predicts the existence of specific biclique motifs in the connectome. We identify a family of large, statistically significant biclique subgraphs in the connectomes of three species and show that within many of the observed bicliques the neurons share statistically significant expression patterns and morphological characteristics, supporting our expectation of common genetic factors that drive the synapse formation within these subgraphs. The proposed connectome model offers a self-consistent framework to link the genetics of an organism to the reproducible architecture of its connectome, offering experimentally falsifiable predictions on the genetic factors that drive the formation of individual neuronal circuits.
In Brief
The origins of the reproducible wiring of the connectome remain a mystery. Barabási and Barabási propose a connectome model that links gene expression to detectable subgraphs in the connectome.
INTRODUCTION
While the tools of network science are often used to study the brain, the connectome poses unique challenges for the field (Sporns et al., 2004; Bassett and Bullmore, 2006; Ercsey-Ravasz et al., 2013; Nicosia et al., 2013; Betzel and Bassett, 2017; Kaiser, 2017). An important unexplained fact is the high degree of reproducibility in some of the observed networks: despite small local variations, the connectome of the roundworm Caenorhabditis elegans is believed to be largely identical for most worms (Jarrell et al., 2012; Walker et al., 2017). In higher organisms, while experience, learning, and epigenetic effects are known to induce variations in micro-wiring, there are multiple local circuits, like the early visual or olfactory systems, that are highly reproducible within a species (LaVail et al, 1978; Hong and Luo, 2014; Bernardo-Garcia et al., 2017). The presence of the reproducible local and global architectural features of the connectome raises a fundamental question: where, and how, is the neuronal connectivity information encoded in an organism?
While answers to these questions are undoubtedly rooted in the biological details of brain development (Holguera and Desplan, 2018), a satisfying framework must also answer a deeper theoretical question: how does a brain wire, to varying degree of reproducibility, a network of billions of nodes and trillions of links? Current generative models of neuronal wiring successfully capture several known spatial and topological features of the connectome (Sporns et al., 2004; Bassett and Bullmore, 2006; Ercsey-Ravasz et al., 2013; Nicosia et al., 2013; Betzel and Bassett, 2017; Kaiser, 2017). Yet these, as well as most models used in the wider context of network science (Caldarelli, 2010; Zitin et al., 2014; Barabási, 2016), are inherently stochastic, thus unable to reproduce specific circuits.
To explore the mechanisms responsible for wiring reproducibility, we must first decide how similar is the wiring of two connectomes. This is a graph isomorphism problem, one of the most challenging computational problems in graph theory (Babai, 2016). If, however, each node has a unique address (label), which is shared by both graphs, for the resulting labeled graphs it is easy to check isomorphism. This suggests that, if developmental processes result in somewhat reproducible connectomes in different individuals within the same species, each neuron participating in such a reproducible circuit must possess a unique label shared across individuals. With that in mind, the wiring of the connectome raises a previously unaddressed theoretical question: how does the brain encode in a reproducible manner the links between genetically stereotyped neurons? Here, we show that by acknowledging the genetic roots of neuronal wiring, we can explain the observed reproducibility.
Here, we propose a connectome model that builds on the hypothesis that the formation of neuronal connections is determined by specific combinations of expressed genes. We show that this hypothesis predicts the emergence of specific network biclique motifs. Furthermore, the model predicts that the biclique motifs should be characterized by similarities in the gene expression patterns of participating neurons, allowing us to identify the genes responsible for the observed local circuits.
RESULTS
Encoding Neuronal Identity
While neurons are clustered into broad classes based on their morphology, function, and location, these differences are expected to be rooted in the differential expression patterns of their genes and proteins, controlled by combinations of transcription factors (TFs) (Marcus, Marblestone and Dean, 2014; Zeisel et al., 2015; Hobert, Glenwinkel and White, 2016; Tasic et al., 2016; Paul et al., 2017). Hence, without loss of generality, we start from the hypothesis that (1) neuronal identity is uniquely encoded by the expression patterns of a neuron’s genes (or TFs, which in turn control the expression of the genes) and (2) each TF can be in two possible states, expressed (1) or not (0), ignoring for the moment that the coding may depend on the degree of expression of each TF. With these approximations, that can be relaxed if needed, we assume that neuronal identity is encoded by the state of b distinct TFs. Such encoding can be rather efficient, as an organism needs only b = log2(N) TFs to offer a unique TF-based label (barcode) to each of its N neurons, with much smaller than the number of TFs known to be present in various organisms (Table S1). In other words, by relying on a small fraction of its TFs, an organism can turn its connectome into a labeled graph.
While TF-based encoding of neuronal identity is well established (Marcus, Marblestone and Dean, 2014; Zeisel et al., 2015; Hobert, Glenwinkel and White, 2016; Tasic et al., 2016; Paul et al., 2017), there are several caveats to our starting hypothesis. First, it is unlikely that the number of TFs included in neuronal encoding is limited to the theoretical minimum, b = log2(N), but likely more TFs participate, allowing for coding robustness. Second, we do not need to assume that the b TFs are exclusively used for establishing neuronal identity—the same TFs likely play multiple developmental and functional roles. Third, though in this viewpoint we follow the traditional approach of referring to TFs as the drivers of cellular identity; our framework can be formulated in terms of individual genes as well, which we will do later when we focus on the role of innexins in gap-junction formation. Fourth, neuronal identity is determined by temporally and spatially induced signaling developmental programs, and a series of equally complex processes that guide the physical location of each neuron (Holguera and Desplan, 2018). Here, we do not aim to address these developmental processes but assume that differentiation has progressed to a state where neuronal identity is well established; hence, the proteins relevant for synapse formation are already expressed. Finally, other regulatory factors also shape neuronal identity, such as epigenetics, alternative splicing, or post-translational regulation by miRNA. Given the paucity of systematic data in this area, we are not able to address their role here. Yet, the only requirement of the presented framework is the existence of some differential expression patterns, like those displayed by TFs or genes, which help us distinguish neurons from each other, allowing us to model the connectome as a labeled graph. Hence, with improved data, such additional regulatory effects can be incorporated. We develop our framework in the context of C. elegans, where wiring is reproducible down to the level of individual neurons and show later its relevance to other organisms.
Encoding Reproducible Synapses via Selective Coding
The wiring of a connectome is uniquely described by its adjacency matrix, B, with Bij = 1 if there is a directed link (synapse, gap junction) from neuron i to neuron j, and Bij = 0 otherwise. To reproducibly generate two similar connectomes, the system must somehow store its adjacency matrix, representing bits of information. It is unclear where this extraordinary amount of information is encoded in the brain. While TFs can offer unique identity to each neuron, a neuron with k links will need k·log2(N) bits to store the addresses of the neurons it synapses with, representing nearly 60% of all available TFs in C. elegans and almost three times the total documented number of TFs in Drosophila. Hence, direct transcriptional encoding of the whole adjacency matrix is not feasible.
To identify the biological mechanisms that could contribute to the reproducible encoding of the connectome, consider surface membrane proteins, whose interactions seed synapse and gap-junction formation in the brain (Südhof, 2018). Gap junctions are formed by the interaction of innexin or connexin protein families and synapses require the combinatorial expression of multiple surface proteins (Carrillo et al., 2015). The specificity of synapse formation between some neuron pairs, and the inability of other pairs to synapse, even if they come in physical contact (Williams, de Wit and Ghosh, 2010), suggests that gap-junction and synapse formation specificity is governed by biological mechanisms linked to neuronal identity, ultimately encoded by specific TF expression patterns (Wester et al., 2019). We mathematically formulate this biological mechanism as an operator O, whose role is (1) to inspect the TF signatures of neurons i and j, and (2) to decide whether to facilitate (or to block) the formation of a directed i → j link between them. This operator can encode the actions of external agents, like glia cells, which select specific neurons and facilitate synapse formation between them (Rapti et al., 2017), but can also detect the combinatorial expression of surface proteins, whose protein-protein interactions catalyze synapse formation. We will discuss the potential biological implementation of the operator O later, but, as we show next, it is sufficient to assume the existence of such operators O to offer testable predictions on connectome wiring.
Consider the simplest case, corresponding to an operator O capable of identifying the full TF profile of two neurons, i and j (defined as a vector of elements Xi = {0, 1, 0,…}, each capturing the 0 or 1 expression of a specific TF) and initiate the formation of a directed link (synapse, gap junction) i → j between them. One could encode the full connectome by using a different operator O for each link (gap junction, synapse), but such coding is highly inefficient. It also lacks robustness, as it is unlikely that a biological mechanism can reliably read all TFs of a neuron. Most importantly, such accurate encoding is not necessary. For example, in C. elegans the expression of the appropriate innexin proteins is sufficient for neurons i and j to form a gap junction. In other words, the operator O governing gap-junction formation only needs to detect the presence of the appropriate innexin proteins, driven by the state of the TFs that control innexin expression. We therefore hypothesize that the wiring of the connectome is determined by selective operators, that detect the expression pattern of only a subset of TFs, rather than all TFs. As we show next, such selective operators predict the emergence of detectable and reproducible network motifs in the connectome, offering falsifiable tests of our modeling framework.
Selective Operators and Bicliques
Let us start with a hypothetical connectome consisting of eight neurons, A–H, whose identity is uniquely determined by the differential expression of three TFs (Figure 1A). An O1 operator that reads the full barcode of each neuron, recognizing a unique source (F, 101) and destination (E, 100) neuron’s expression pattern, will encode a single directed link from neuron F to neuron E (Figure 1B). However, a more selective operator O2, that reads only the first two TFs of the destination neuron, and ignores the third, will generate directed links from a single source neuron (G, 110) to two different destination neurons (E, 100, and F, 101), as it is unable to distinguish the expression-based differences between E and F (Figure 1C). A third operator O3, that recognizes only a single TF in the source neurons, and two TFs in the destination neurons, will generate eight links, connecting each of the four source neurons with TFs 0XX, to any neurons with TFs 11X (Figure 1D). In general, the more selective an operator O is (i.e., the fewer TFs it recognizes), the more directed links it can encode: if a total of q elements are X’s in the operator O, it will encode the formation of a maximum of 2q directed links in the connectome. Note that in our model a single neuron can participate in multiple wiring rules, driven by the expression patterns of different gene/TF subsets. For example, neurons E and F participate in both O1 and O2, and G participates first in the source set of O2, then in the destination set of O3.
Figure 1. Connectome Model.
(A) A neuronal system consisting of eight neurons, the identity of each neuron being encoded by the distinct expression pattern of its three TFs.
(B) Abiclique operator O1 that recognizes the neuron with barcode identity 101 and generates a single directed link to destination neuron 100.
(C) Biclique operator O2 recognizes two TFs in the destination neuron set; hence, it encodes two links (G → E and G → F) that form a bi-fan motif.
(D) Biclique operator O3 recognizes a single TF in the source neurons and two in the destination neurons and generates a 4x2 directed biclique in the connectome.
(E) The joint action of the three biclique operators shown in (B)–(D) leads to the connectome shown in (E), where each link is rooted in a distinct respective biclique, as indicated by the color of the links.
Figures 1B-1D summarize the first prediction of the connectome model: each biological mechanism that relies on a subset of TF signatures to initiate synapse formation will generate an imprint in the connectome in the form of a unique network motif, known as directed biclique in graph theory (Zelinka, 2002). A directed biclique is a subgraph that consists of two sets of nodes (S, D), where each node of the source (S) set is connected with a directed link to every node of the destination (D) set. The simplest biclique is a single link (Figure 1B), but, as shown in Figures 1C and 1D, the fewer TFs the operator O recognizes, the larger the resulting biclique. In other words, the connectome model makes an explicit, falsifiable prediction: if neuronal wiring is determined by specific TF combinations, then the connectome must contain specific large biclique motifs. Each of these bicliques corresponds to a selective, TF-dependent and genetically encoded biological mechanism mathematically described by an operator O.
To unveil the biological mechanism behind each operator, we need an accurate connectome and single-cell expression data for each neuron, which is currently unavailable for any organism. Yet, as we show next, we can test the model’s key predictions in C. elegans, an organism whose full connectome is mapped (Varshney et al., 2011; Cook et al., 2019). We begin validating the connectome model’s predictions on the synaptic connectome defined by 279 neurons connected by 3,503 links, each link corresponding to one or several synapses (Cook et al., 2019). As we show in the STAR Methods, the model’s predictions are verified in other reconstructions, as well as in the connectome determined by gap junctions.
Bicliques in C. elegans
If the wiring of the connectome is determined by TF-dependent selective operators, the connectome model predicts the existence of multiple biclique motifs that should be detectable in the connectome. As within each biclique, there are multiple smaller bicliques; here, we focus on maximal bicliques, representing the largest possible fully connected biclique among a set of nodes. Identifying all maximal bicliques in a graph is an NP-complete problem (Dias et al., 2007). However, given the limited size of the C. elegans connectome, we were able to identify all maximal bicliques using the Maximal Biclique Enumeration Algorithm (MBEA, see STAR Methods) (Zhang et al., 2014). The algorithm identified 9,431 maximal bicliques in the C. elegans synaptic connectome, which can be classified into 182 distinct maximal biclique motif types.
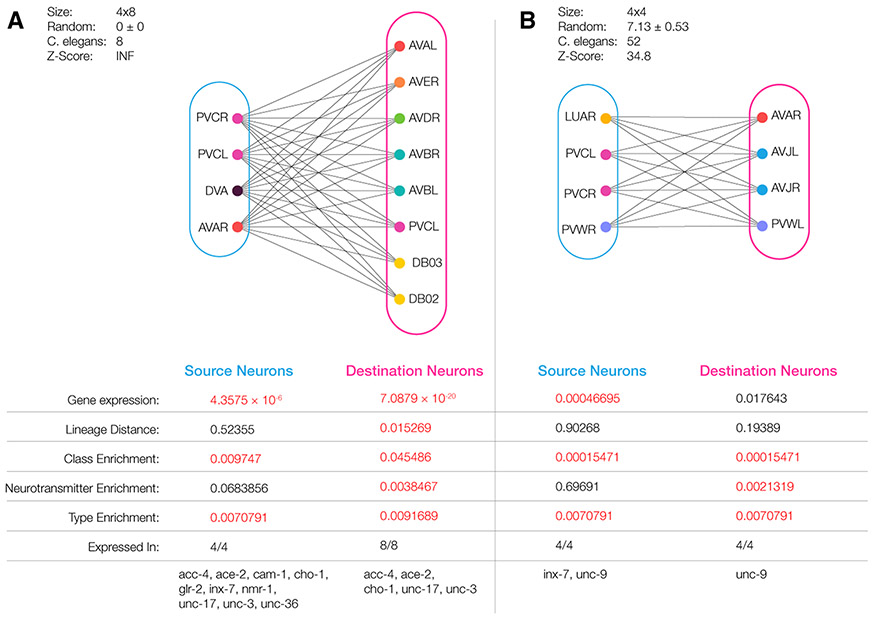
Given the dense wiring of the C. elegans connectome, some of the observed maximal bicliques could emerge by chance. As standard in network science, we use degree preserving randomization (Maslov and Sneppen, 2002) to test the statistical significance of the observed maximal bicliques. We generated 1,000 networks whose size and degree sequence matches the C. elegans connectome and identified all maximal biclique motifs in each random realization of the original network. For example, we find 0.91 ± 1.21 maximal bicliques of size 3 x 6 in the randomized networks (Figure 2A). Yet, the real C. elegans connectome has 173 maximal bicliques of size 3 x 6, outnumbering with Z = 142 SDs the number of such motifs in a randomized network. This indicates that these maximal bicliques could not have emerged by chance but may be rooted in the genetic mechanisms that determine the wiring of the connectome. In Figure 2D, we cataloged all observed maximal bicliques in C. elegans, finding that 98 of the 182 distinct maximum bicliques are statistically overrepresented (Z > 3.4, after multiple testing correction). Some of the larger and denser motifs are so rare that they never appear in the 1,000 random configurations we generated, yet we find multiple copies of them in the C. elegans connectome. Examples of such large maximal biclique motifs found in the C. elegans connectome are shown in Figure 3.
Figure 2. Evidence of Bicliques in the C. elegans Connectome.
(A) Maximal bicliques of size 3x6 are significantly overrepresented in the chemical synapse connectome: 173 maximal bicliques of size 3x6 are found in C. elegans connectome, but only 0.91 ± 1.21 are observed under degree-preserving randomization (Z score = 142).
(B) Average numdber of maximal bicliques observed under degree-preserving randomization. Rows indicate the size of the source (S) set, and columns indicate the size of the destination (D) set.
(C) Number of unique maximal bicliques of a given size observed in the synaptic connectome of C. elegans. Note how small maximal bicliques are less common than in the randomizations.
(D) Z scores of maximal bicliques of various sizes. Orange squares show maximal bicliques that are underrepresented in the real connectome compared to the random reference (Z < −3.4)–they capture small maximal bicliques (2 → n, or n → 2) that often emerge by chance. Green squares capture maximal bicliques that are overrepresented in the real connectome (Z > 3.4)–these are the ones that we expect to have genetic origins. Gray maximal bicliques are observed, but their numbers are non-significant (−3.4 < Z < 3.4). The white region corresponds to maximal bicliques that are absent in the chemical connectome. Similar plots describe the gap-junction connectome, as well as the synaptic and gap-junction connectomes of the other C. elegans reconstruction (Figure S1).
Figure 3. Biological Significance of the Observed Bicliques.
(A) An observed chemical synapse maximal biclique of size 4 x 8. Neurons are colored by class, with all neurons in the source set synapsing onto all neurons in the destination set. The neurons present in this maximal biclique play a functional role in the locomotion of C. elegans. Both the source and destination sets co-express a statistically significant number of genes in all neurons. Furthermore, the source set is significant in genetic expression (p < 4.36*10−6), class enrichment (p < 0.00975) and type enrichment (p < 0.00708). The destination set is significant for all measures.
(B) A maximal biclique of size 4x4 in the gap-junction connectome of C. elegans. We find that both source neurons all express inx-7 and unc-9, known to code for proteins forming gap junctions, and the destination neurons express unc-9. Furthermore, the source set was found to be significant in genetic expression (p < 0.000468), class enrichment (p < 0.000155), and type enrichment (p < 0.00708). The destination set was significant for all measures except genetic expression and lineage distance.
The exceptional statistical significance of these large maximal bicliques is our first evidence for the validity of the proposed connectome model. We also find that 94.6% of all synapses of the C. elegans connectome are part of at least one maximal biclique of statistical significance, suggesting that almost all synaptic connections could be explained by the genetic mechanisms captured by the connectome model. Small motifs, like bifans and feedforward loops, were previously documented in the C. elegans connectome (Reigl et al., 2004; Itzkovitz and Alon, 2005; Qian et al., 2011). The proposed connectome model may be able to explain the genetic origins of these as well and, in addition, predicts the existence of specific large motifs, the bicliques, that, given their size, could not be detected by previous analyses. Each of these potentially represents an imprint of a transcriptional mechanism that shapes the wiring process. Finally, note that other mechanisms, like physical proximity or network development, may also contribute to the observed bicliques.
Biological Significance of Bicliques
The second prediction of the connectome model goes beyond wiring and pertains to the identity of the S (or D) neuron sets within each biclique: the expression pattern of the TFs recognized by the corresponding O operator are expected to display significant overlap (Figures 1C and 1D). In other words, the neurons participating in a specific biclique are not chosen randomly but are expected to have common expression patterns. A comprehensive test of this prediction ideally requires single-cell expression data of each C. elegans neuron throughout development. Lacking this, we tested the predictions using gene expression data available for 935 genes in 279 C. elegans neurons, compiled in the WormBase repository (Harris et al., 2010). We start by testing the prediction that the gene expression pattern of the S (or D) neurons within each biclique motif must display a degree of expression-based similarity that cannot be explained by chance. Evidence for this is offered by the maximal biclique shown in Figure 3A. We find that the four source neurons (PVCR, PVCL, DVA, AVAR) have significantly similar expression patterns (S set: p < 10−5). The same is true for the eight destination neurons in the D set (p < 10−19). To generalize this observation, we used a 2-sample Kolmogorov-Smirnov test to evaluate the expression-based similarity of the S and D gene set in each maximal biclique in C. elegans, finding statistical significance in 1,964 S sets and 3,570 D sets (see STAR Methods). When using gene expression data, we implemented multiple hypothesis correction; hence, significance represents p < 0.0125.
The connectome model also predicts that the observed statistically significant similarity of the neurons found in the same S (or D) set is rooted in the identical expression of the TFs recognized by the operator O, and the genes driven by these. In other words, we should be able to explicitly identify the genes or the TFs each operator recognizes, helping us unveil the potential genetic mechanism behind each maximal biclique motif. To achieve this, for each S (and D) neuron set we identified the number of genes with identical expression patterns (expressed, 1, or not, 0). We also estimated the expected number of common genes for the same nS (or nD) randomly selected neurons (see STAR Methods), finding that 1,433 S sets, and 2,874 D sets share a statistically significant number of common genes. For example, in the S set of the maximal biclique of Figure 4A we find that 11 genes are expressed in all four neurons (acc-4, ace-2, cam-1, cho-1, glr-2, glr-5, inx-7, nmr-1, unc-17, unc-3, unc-36). Given that for four randomly selected neurons the number of genes with shared expression pattern is expected to be 0.2, the observed pool of 11 genes in common has a p < 10−4 significance (see STAR Methods). The significance persists even if we correct for the fact that PVCL and PVCR are assigned identical expression patterns in WormBase (p < 0.0037). We observe a similar pattern if we inspect the eight destination neurons of the same motif (DB02, DB03, PVCL, AVBL, AVBR, AVDR, AVER, AVAL), each of them previously implicated in locomotion. These eight destination neurons share five genes (acc-4, ace-2, cho-1, unc-17, unc-3), whose significance (p < 0.0001) persists even if we correct for the identical expression patterns of ALBL/R and DB02/3 pairs, as well as if we choose a more conservative random reference, correcting for the degrees of the neurons, and class-based expression biases (see STAR Methods). Of the shared genes, unc-3 was found to be crucial for presynaptic function (Harris et al., 2010), and unc-36 plays a role in presynaptic organization and morphology (Harris et al., 2010), in line with our expectation that some of the genes recognized by the operator O should play a known role in neuronal identity and wiring.
Figure 4. Unveiling the Biological Roots of the Biclique Operators.
(A and B) (A) The 4 x 4 chemical synapse maximal biclique shows significant co-expression patterns in both its source and destination neurons, partially driven by the set of three genes with common expression in the S set and three genes in the D set. This suggests that the maximal biclique is generated by the operator shown in (B) that recognizes the three genes on the source side and the three genes on the destination side.
(C and D) (C) The bipartite network with all neurons expressing inx-2 in the source, and inx-3 in the destination set, predicted by the operator shown in (D), based on the hypothesis that inx-2 and inx-3 expression can seed gap-junction formation. We find that 7 of the possible 32 connections are present in the gap-junction connectome (solid lines); however, only 2 potential connections are missing when we only consider neurons that are touching (dashed lines).
As the TFs recognized by O contribute to a neuron’s transcriptional identity, we expect that the neurons in the same S (or D) sets should also be similar to each other across multiple detectable morphological, functional, and developmental characteristics (see STAR Methods). We therefore asked whether the S/D neuron sets selected by the biclique motifs have similar lineage distance, measuring the coalescence distances between neurons defined by the developmental lineage in C. elegans. We also explored whether the neurons in the S and D sets have similar anatomical characteristics, defined by the 103 neuronal classes of neurons with similar morphology (White et al., 1986). Further, we checked for neurotransmitter enrichment, using as a proxy the seven unique neurotransmitters each neuron uses (Pereira, 2015). Finally, we examined neuron functional type, segmented into sensory neurons, motor neurons, and interneurons. We find significant enrichment of neurons with similar lineage, class, neurotransmitters, and type in both S and D sets, not only for the maximal bicliques shown in Figure 3 but in many large maximal bicliques (see STAR Methods). Although correlations between cell identity measures would be expected, past work has shown that lineage branching shows limited correlations with gene expression, functional type, neurotransmitter expression, or anatomical class (Hobert, 2005; Packer et al., 2019).
Finally, we also identified the maximal bicliques present in the gap-junction connectome, identifying the statistical significance of each maximal biclique, and its potential biological origins. In Figure 3B, we show a 4 x 4 maximal biclique whose neurons are connected by gap junctions. Once again the S and D neurons show biological significance across expression patterns, as well as class and type enrichment. Furthermore, unc-9, the gene expressed in both S and D sets, has been experimentally implicated in gap-junction formation in C. elegans (Starich et al., 2009).
Taken together, we find that the neurons selected by the maximal bicliques found in the C. elegans connectome display highly significant genetic, morphological, and lineage-based similarity in both the synaptic and the gap-junction-based connectomes, supporting our hypothesis that each maximal biclique motif represents the imprint of a genetic operator that determines the local, reproducible wiring of the connectome.
The Biological Nature of the Biclique Operators
According to the connectome model, each observed maximal biclique (Figures 3 and 4) is rooted in a biological operator O, which mathematically describes a transcription-based process responsible for synapse or gap-junction formation between the neurons forming the maximal biclique. The formalism behind the model can unveil the biological mechanisms behind each operator O, if we have access to single-cell expression data that captures the expression level of each gene in each neuron. Currently, such data cover only 935 of the 20,000 protein coding genes of C. elegans. Yet, as we show next, we can still rely on this incomplete data to illustrate how to unveil the biology behind some of these operators.
Let us start from the 4 x 4 maximal biclique shown in Figure 4A, observed in the chemical connectome. Both the S neurons and the D neurons have three genes expressed in common, and both sets are significant (p < 0.025). These jointly expressed genes allow us to reconstruct a potential operator that may be responsible for the wiring behind the maximal biclique (Figure 4B), suggesting that the joint expression of cam-1, glr-1, and unc-47 in the source neurons predestines them to link to neurons that express simultaneously acc-4, ace-2, and unc-6. This does not mean that only these genes drive the synapse formation—as the available expression data cover less than 5% of the genes, the expression of these genes may be driven by some other, yet-unmapped TFs that define the identify of these neurons, or may correlate with some of the surface proteins that drive synapse formation. However, if we apply the operator of Figure 4B to the expression data of all neurons in C. elegans, we find 7 S neurons and 27 D neurons; i.e., the operator of Figure 4B defines neuron sets that are an extension of the maximal biclique of Figure 4A. Of the 189 potential connections the operator of Figure 4B would predict, only 31 are actually present. In other words, we observe an incomplete biclique, corresponding to the case when genetic rules predict a fully connected biclique, but only a subset of the predicted links are observed. While incomplete, this biclique is highly significant—given the link density of C. elegans; if we observe 189 random links, we are expected to have 8.51 links by chance; hence, the significance of the observed incomplete biclique is p < 10−8. One important reason for this biclique’s incompleteness is rooted in spatial effects: two neurons may have the genetic makeup to connect, but they never meet physically to form a gap junction. Indeed, using the C. elegans physical adjacency data (Cook et al., 2019), we find that 153 of the missing links can be explained by the lack of physical proximity. In other words, only 5 of the 36 predicted gap junctions are missing. This example illustrates how to use the connectome model to unveil the potential genetic mechanisms driving synapse formation, a process that can be mathematically formalized (unpublished data).
Another approach is to start from the known genetic drivers of link formation and then unveil the associated biclique. We illustrate this route using gap-junction formation, known to be driven by innexin-innexin interactions in C. elegans (Hall, 2017). There are 25 innexin proteins in C. elegans, but only 15 gap junction-related proteins are expressed in the nervous system (Bhattacharya et al., 2019). Lacking extensive data on innexin interactions in C. elegans, here we consider the potential role of a protein interaction between inx-2 and inx-3 proteins. Inx-3 has previously been shown to play a role in gap-junction formation (Landesman et al., 1999) and to be essential for development in C. elegans (Starich et al., 2003). If the expression of these proteins alone can seed gap-junction formation in C. elegans (a hypothesis that needs to be experimentally confirmed), the underlying operator O will recognize any neuron that expresses inx-2 and will prompt them to form a gap junction with any neuron that expresses inx-3 (Figure 4D). We find that two neurons (AVKL and AVKR) express inx-2, and 16 neurons express inx-3; hence, a potential interaction between the two proteins predicts the operator shown in Figure 4D, leading to a 2 x 16 biclique (Figure 4C). In line with this prediction, we do find a bipartite motif with seven gap junctions linking the two inx-2-expressing source neurons, AVKL and AVKR, to five of the 16 destination neurons that express inx-3 (Figure 4C). Again, we observe an incomplete biclique, that is still highly significant (p < 0.001)–given the link density of C. elegans, these two sets of neurons (2 x 16) are expected to have 1.72 links by chance. If we also consider the C. elegans physical adjacency data (Cook et al., 2019), we find that 23 of the missing links can be explained by the lack of physical proximity. In other words, only two of the 9 predicted gap junctions are missing (AVKR-DVA and AVKR-ALNL), and 7 are present, underlining once again the accuracy the connectome model offers in uncovering a plausible genetic interactions between neurons that express inx-2 and inx-3.
Taken together, Figure 4 illustrates two different avenues we can follow to unveil the genetic roots of the operators responsible for the observed maximal bicliques–starting from the maximal bicliques observed in the connectome (Figures 4A and 4B) or starting from the known biology of gap-junction formation (Figures 4C and 4D). Given the incomplete expression data, the operators shown in Figure 4 are expected to be incomplete—they serve only to illustrate the procedure of unveiling the biology behind each maximal biclique. Advances in single-cell expression profiling could allow us to systematically unveil the genetic roots of each synapse or gap junction, ultimately offering experimentally falsifiable predictions.
DISCUSSION
The connectome model allows us to integrate, using a single theoretical framework, information about the wiring and the genetics of each neuron, offering several testable predictions: (1) the existence of a reproducible structural imprint of each genetically induced operator O in the connectome, represented by a maximal biclique motif; (2) the expression-based similarity of the neurons within each biclique. We find that such biclique motifs are indeed present in multiple connectome, supporting (1). Gene expression data in C. elegans reveal that the neurons forming these motifs share common expression patterns, as predicted by (2). Further, we show how to use the set of genes jointly expressed in the source or destination neurons of a biclique to unveil the potential biological mechanism responsible for the wiring of the biclique.
For completeness, we analyzed all the commonly utilized connectomes of C. elegans (synaptic connectome and a gap-junction network, from two reconstructions), finding significant maximal bicliques in each map, and largely indistinguishable maximal biclique significance diagrams (Figure 2C; Figure S1), supporting the existence of unique, genetically driven mechanisms. The fact that we find significant results despite the limited expression coverage (covering 935 of around 20,000 genes in C. elegans) suggests that the patterns we observe are robust to data incompleteness.
The predictions of the connectome model can be tested in any species for which neuronal-level connectomes are available. For example, in addition to C. elegans, we have identified the maximal biclique subgraphs in C. intestinalis CNS (N = 205, L = 2,974) (Ryan et al, 2016) and the D. melanogaster larva olfactory circuit (N = 387, L = 3,690) (Berck et al., 2016; Eichler et al., 2017), finding statistically significant maximal bicliques in each (see STAR Methods), together with a maximal biclique distribution that is very similar to the one observed in C. elegans (Figure 2E; Figure S2), suggesting that our findings generalize to larger networks. Definite evidence will eventually be provided by full connectome maps currently under development in multiple organisms, complemented with matched gene expression data. Extrasynaptic signaling, leading to a wireless connectome, also plays a key role in brain function (Bentley et al., 2016) and can be addressed within the framework introduced above, helping us identify bicliques specific for each neuromodulator. In this case, a biclique captures an S-set of neurons expressing systems to release octopamine and a D-set that expresses octopamine receptors.
The evidence we offered for C. elegans and other simple organisms raises the question whether the connectome model could also help formalize the processes driving mammalian wiring. Mammalian wiring is greatly affected by learning and experience, potentially resulting in different local connectomes in individuals of the same species (Edelman, 1987). Yet, the large-scale architecture of mammalian brains, as captured by fMRI scans and other tools (McGonigle et al., 2000; Telesford et al., 2010; Choe et al., 2015), show remarkably reproducible patterns across individuals of the same species, suggesting that genetic factors shape some architectural features of the underlying connectome (English et al., 2017; Han et al., 2018). Further, biclique-like structures are observed in the reconstruction of the mouse retina wiring (Söhl et al, 2005). The biology behind the underlying operator O can be linked to gap-junction proteins, like connexin-36 (CX36), that couples rods and cones through gap junctions. Further evidence is available in D. melanogaster olfactory circuits: olfactory receptor neurons expressing the same olfactory receptor (OR) converge onto the same set of projection neurons (PNs); hence, the olfactory circuits are wired by a set of biclique operators that recognize the OR identity of neurons and connect them onto a complementary set of PNs. It remains to be seen whether similar biclique structure can be found in other circuits, particularly in brain areas where random connectivity dominates for PN axon projections (Caron et al., 2013).
These studies hint that the connectome model, perhaps applied to neuronal classes, rather than single neurons, may help describe the genetic and developmental roots of the structural connectivity established during development, guiding the brain’s large-scale architecture. For instance, experimental perturbations of a single TF in mice, changing the identity of neuronal classes, have altered the native wiring patterns of affected regions (Wester et al., 2019), supporting the TF-driven wiring that the connectome model relies on. Nevertheless, the cellular level connectome collected at mammalian adulthood is expected to be significantly rewired by experience-driven learning; thus, the wiring rules may only be observable if we pair connectomic and genetic measurements through the course of development. Thus, while the ideas behind the connectome model may be fruitful for hypothesis building, testing its applicability to mammals requires further development of the proposed framework.
As we ponder the applicability of the model to C. elegans and beyond, we must realize that the biclique operator defines only the genetic potential of two neurons to connect. In both the worm and, in particular, in higher organisms, given the highly compartmentalized nature of the brain, neurons require a wide range of additional genetic signals to synapse: two neurons that have the complementary surface proteins may lack the routing directions to meet and connect, resulting in incomplete biclique motifs, similar to the one seen in Figure 4C. Further, incomplete bicliques may result from activity dependent pruning or rewiring, such as the retinal waves involved in activity patterning in the visual cortex (Ackman et al., 2012). Our ability to reconstruct wiring rules that jointly consider genetic factors and spatial guidance may be best informed by considering more general types of bipartite structures, which have a rich literature in economic networks (Saracco et al., 2017; Straka et al., 2017, 2018). Such techniques may also better account for overlapping bicliques, where multiple genetic wiring rules can code for the same connections. The mathematical formalism behind the connectome model can be expanded to systematically account for spatial effects and their impact on the observed biclique distribution (unpublished data). These developments could help us deconvolute axon routing from connectomic matching, jointly utilizing projectomic and connectomic datasets.
Such spatial effect also raises the question whether spatial constraints could fully explain the reproducible wiring of the connectome. Our analysis shows that brain models that connect neurons based on their spatial proximity do indeed generate some maximal bicliques (Ercsey-Ravasz et al., 2013). Yet, these maximal bicliques are rooted in the fully connected local cliques these models generate, which are absent in the C. elegans connectome (see STAR Methods; Figure S3). As we show in the STAR Methods, the observed maximal bicliques cannot be explained by the canonical network models used in network science either.
The hypothesis that genetic factors may contribute to neuronal wiring emerged originally in the context of the chemoaffinity hypothesis (Sperry, 1963). It states that synaptic connections are driven by selective attachment mediated by specific molecular identifiers encoded in the genome. Since its formulation in the 1960s, the hypothesis has helped identify genes that disrupt the development of neuronal circuitry (Kaufman et al., 2006), including axon guidance genes (sax-3, unc-34, unc-40) (Yu et al., 2002), attractive and repulsive interactions (unc-6, unc-40, and unc-5) (Hedgecock et al., 1990; Lim and Wadsworth, 2002; Adler et al., 2006), presynaptic input modulation (unc-4, unc-37) (Winnier et al., 1999), presynaptic differentiation (sad-1) (Crump et al., 2001), and synaptic specificity genes (syg-1, syg-2) Shen et al., 2004). Evidence also comes from the HSNL neuron (Shen et al., 2004), helping discover that the transmembrane proteins syg-1 and syg-2 bind together and guide the neuron to form correct synapses. Candidate genes contributing to synapse formation include the Dscam gene in Drosophila (Chen et al., 2006) and the Protocadherin (Pcdh) proteins (Shapiro and Colman, 1999) and connexin genes (Belousov and Fontes, 2013) in vertebrates. The connectome model builds on the chemoaffinity hypothesis to offer a framework to systematically combine the connectome with expression data in order to formulate experimentally falsifiable predictions for the wiring of each specific subcircuit.
The connectome model represents a generative model for complex networks, capable of generating graphs with a wide range of network characteristics. We can, for example, generate a pure random network by utilizing a separate operator for each link, in which case the number of operators (or the necessary biological mechanisms) scale as . This raises an important question: what is the minimal number of distinct biological mechanisms (i.e., distinct operators, O) required to explain the full connectome? Formally the answer is within the grasp of graph theory, as it corresponds to the minimum number of maximal bicliques required to cover all links in the connectome, a difficult (and likely NP- complete) algorithmic problem. Yet, limit theorems common in combinatorial graph theory could predict this minimal number, helping us estimate the smallest number of biological hypotheses needed to describe a connectome (Bollobás, 2001).
Finally, a major remaining challenge lies in developing computational tools to systematically identify combinatorial genetic rules of neuronal wiring. Our work offers the theoretical framework to aid efforts that aim to reconstruct wiring rules from genetic data (Kaufman et al., 2006; Varadan, Miller and Anastassiou, 2006; Baruch et al., 2008). One could also use Bayesian inference to predict rules of connectivity and the underlying genetic rules, given spatial information and clustering-based cell identity (Jonas and Kording, 2015). A formal matrix description of the connectome model (unpublished data), incorporating spatial, genetic, and connectomic data, offers a strong foundation for inferring such wiring rules, with the added benefit of predicting rewiring patterns under genetic perturbations. Further validation of the connectome model, or other inference frameworks for the genetic basis of wiring, would benefit from the recent availability of neuron-resolved single-cell RNA expression in C. elegans (Taylor et al., 2019), as well as techniques for development-resolved connectivity and gene expression (Farrell et al., 2018; Wagner et al., 2018).
STAR ★ METHODS
LEAD CONTACT AND MATERIALS AVAILABILITY
Further information and requests for resources should be directed to the Lead Contact, Albert-László Barabási (a.barabasi@northeastern.edu).
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Data Sources for C. elegans Connectome
The neural system of C. elegans consists of chemical synapses and gap junctions between 302 neurons. Graph theoretical analyses of C. elegans connectomes typically restrict the circuit to the connected somatic nervous system of 279 neurons, excluding 20 neurons in pharyngeal nervous system and 3 somatic neurons (CANL/R and VC06) that, in the Varshney et al. (2011) reconstruction, do not synapse with other neurons. Each reconstruction offers two separate adjacency matrices: a directed chemical synapse network, and an undirected gap junction network. We studied two different reconstructions:
The Varshney et. al. reconstruction maps the connectome relying on a combination of the White et. al. electron microscopy images (White et al., 1986), and recent reconstruction updates. The resulting adjacency matrices contain 6,393 chemical synapses, 890 gap junctions, and 1,410 neuromuscular junctions between 279 neurons. For this reconstruction, the synaptic adjacency matrix has 2,194 directed links, and the gap junction network has 517 links, of which 3 are self-loops.
Cook et. al. reconstruct a chemical synapse adjacency matrix with 3,503 links, and a gap junction network with 1,051 undirected links, including 11 self-loops (Cook et al., 2019). This reconstruction is utilized in the body of the paper, unless otherwise noted.
Data Sources of C. elegans Cell Identity
We obtained binary gene expression data from WormBase, which aggregates expression information of individual genes in C. elegans from the literature. The data were hand-curated by experts to ensure “true zeros,” meaning that “1”s in the data indicate that a reporter transgene was found to be expressed in a given neuron, and “0”s are in the case where the gene is not expressed. Some neurons in the dataset express as few as 9 genes, while others over 140 genes, with an average of 32 expressed.
METHOD DETAILS
Brain Sizes Across Organisms
To generate in a reproducible manner the connectome of an organism, we need: (i) a way to create a labeled graph by offering a unique ID to each neuron (cellular identity), and (ii) a method of storing the links between them (adjacency matrix). As we discuss in the main text, b = log2(N) TFs are sufficient for (i), generating a labeled network of N neurons. As Table S1 indicates, such encoding requires only a small portion of the available TFs in C. elegans (9 needed out of 934 available) or in higher organisms (in humans, 33 TFs are sufficient, out of the 1,391 known TFs) (White et al., 1986; Tang et al., 2001; Herculano-Houzel and Lent, 2005; Reece-Hoyes et al., 2005, 2011; Ananthanarayanan et al., 2009; Azevedo et al., 2009; Vaquerizas et al., 2009; Lagercrantz et al., 2010; Zhang et al., 2011; Varshney et al., 2011; Zheng et al., 2018).
Encoding the full adjacency matrix requires N2 bits of information. Let us assume that each neuron i “remembers” the address of the other neurons it links to. The most efficient way to encode this is for each neuron i to remember and recognize only the addresses of ki neurons it links to, ignoring the addresses of the N-ki >> ki neurons it does not synapse with. Yet, even such minimal encoding imposes considerable information burden. For example C. elegans, with 302 neurons, must devote at least log2(302) = 9 of its TFs to uniquely label each neuron. In principle, each neuron could use its remaining TFs to “store” the barcode of the neurons it connects to, in log2(N) chunks. Naively, this implies that AVAR, a neuron with k = 62, must reserve k * log2(N) = 558 of its TFs to encode the address of the 62 neurons it can synapse with, or 60% of the available TFs. For higher organisms, we can approximate the information required using < k > *log2(N), which significantly exceeds the number of available TFs (Table S1), requiring 1,700 TFs in Drosophila and nearly 700,000 in humans. This suggests, that the brain cannot encode each link at the TF level. It can do so, however, if it uses selective coding, as described by the proposed connectome model.
Maximal Biclique Enumeration Algorithm
Enumerating all biclique motifs in a network is a computationally intensive problem. Indeed, a naive approach must test all 22N possible biclique subsets of the N source and destination nodes. Specifically, we are interested in non-induced bicliques, in which the source and destination sets can overlap. Furthermore, we wish to account for all maximal bicliques, meaning that we focus on the largest non-induced bicliques that can be constructed, and not their sub-sets. For instance, if we find a biclique that links {a,b,c} to {c,d,e}, and no further nodes can be added to the set (i.e., there is no node f such that a, b, and c all connect to f as well), we do not want to count separately the biclique, such as {b,c} connecting to {c,e}, a subset of the larger biclique.
We used the Maximal Biclique Enumeration Algorithm (MBEA) to identify all maximal bicliques in a bipartite graph (Zhang et al., 2014). The algorithm considers the input to be a bipartite graph, assuming the source and destination sets to be distinct, thereby generating non-induced bicliques (separate provisions to eliminate non-induced bicliques would require extra computational steps). The algorithm develops recursion trees to perform the biclique searches, constantly building maximal bicliques from growing subsets of the source and destination nodes. The efficiency of the algorithm is boosted by eliminating from the search space regions of the graph where maximal bicliques are absent. The algorithm runs in minutes even on large networks (782 x 45,137 bipartite graph) (Zhang et al., 2014). However, larger connectomes are expected to exceed this size (the fly brain is estimated to contain 100,000 neurons), thus more efficient algorithms may be needed to explore the connectomes of higher organisms.
Degree-Preserving Randomization
When examining the importance of bicliques in the connectome, it is important to understand whether such subgraphs can naturally emerge in a network of similar size and degree sequence. For this, we compare the observed subgraphs with subgraphs in appropriately randomized networks. We started with full randomization (preserving only N and density, i.e., turning the random reference into Erdős-Rényi random networks), which shows high significance. Given the unique degree sequence of the C. elegans connectome, with its hubs forming a rich-club (Colizza et al., 2006; Towlson et al., 2013), degree-preserving randomization offers a more appropriate reference frame (Maslov and Sneppen, 2002). More elaborate randomization techniques also exist that better account for dense graphs (Zlatic et al., 2009), or, as in exponential random graph models, account for noise in the network reconstruction process by utilizing the overall network statistics, rather than the exact degrees observed (Cimini et al., 2019). We utilize the MATLAB software developed by Sergei Maslov (Maslov and Sneppen, 2002) for degree-preserving randomization of directed graphs for the chemical synapse connectome, and undirected degree-preserving randomization for gap junctions. The algorithm randomly chooses two edges (e.g., A → B and C → D) and swaps the involved nodes (e.g., A → D and C → B), thereby preserving the total number of connections each node makes. This process is performed 4L times, where L is the number of connections in the network.
QUANTIFICATION AND STATISTICAL ANALYSIS
Bicliques in the C. elegans Connectome
Using MBEA, we enumerate all unique maximal bicliques in the C. elegans connectomes (Figure S1) as well as in their degree-randomized version. We find that in both synaptic connectomes the number of maximal bicliques significantly outnumbers the number of maximal bicliques observed after degree-preserving randomization, with Z-scores ranging from 3 to 20 (Figure S1A).
To calculate the significance of the number of maximal bicliques, we performed multiple testing corrections for the number of unique SxD biclique sizes observed in the network that are randomized. For instance, in Figure 2, we find 182 biclique types, thus significance was considered at p = 0.05/182 = 0.00027, corresponding to a Z-threshold of 3.4. We define over-represented bicliques as Z > 2*, where * indicates the correction. Under-represented bicliques are Z < −2*, and non-significant bicliques are −2* < Z < 2*.
We find that larger maximal bicliques are significantly overrepresented in the connectome (Figure 2). At the same time, smaller maximal bicliques are often under-represented in the connectome, or, in the case of the Varshney et. al. reconstruction, not statistically significant. We find larger maximal bicliques in the Cook et. al. reconstruction (e.g., 5x8 maximal bicliques are not present at all in Varshney et. al.), however this can again be attributed to the higher density of the Cook et. al. reconstruction.
We ran MBEA on the two gap junction connectomes as well, treating it as an undirected network. As with the chemical synapses, we find that the number of maximal bicliques is significantly larger than expected in the degree-preserved random reference connectome (Table S2), and that larger maximal bicliques are significantly overrepresented.
Gene Expression Patterns
Similarity Metrics
To quantify how similar is the expression pattern of two neurons, we use the mean square contingency coefficient (MSCC) which was shown (Arnatkeviciūtė et al., 2018) to be less biased by sparse expression data than the Jaccard index or Yule’s Q:
Here nxy enumerates possible binary pairings, such that n01 = ∑iδxi,0δyi,1 and n1* = ∑iδxi,1, where * stands for “or.” The MSCC is maximal (rϕ = 1) when two neurons express exactly the same set of genes and minimal (rϕ = −1) when the expression patterns of the two neurons mirror each other (i.e., one has 0 the other has 1).
To establish the statistical significance of the expression based similarity for a given set of S or D neurons in a biclique, we measure all pairwise similarities between the number of neurons, and use a two-sample Kolmogorov-Smironov test to decide if the pairwise distribution’s empirical cdf is larger than the distribution of pairwise genetic similarities between all 279 neurons. We find 1,964 source sets and 3,570 destination sets significant using this metric, with 955 maximal bicliques showing significance for both S and D sets. For all gene expression analyses we consider statistical significance to be p < 0.0125 to correct for multiple comparisons.
Gene Co-Expression
The connectome model (Figure 1) predicts that each biological operator recognizes a set of genes, suggesting that the neurons in an S or D set of the same biclique do not represent a random subset of neurons, but have common TF expression patterns, reflecting the biological mechanism captured by the operator O. In other words, the expression pattern of multiple TFs recognized by O (and the genes directly driven by them) must be in common. This suggests that the expression pattern of the neurons must display detectable similarities. To test this, for each S or D set we count the number of co-expressed genes, and compare it to the number of co-expressed genes expected in 1,000 similarly sized sets of randomly chosen neurons. We find that 1,279 source and 2,263 destination sets are significant under this metric.
To check the robustness of this result, we performed multiple randomizations that are better informed on the selection of comparable nodes:
Class-Based Expression Patterns
When experiments map the genes of neurons, often class-based indicators are used, meaning that every neuron in the same class is assumed to express a gene, even if it is only observed to be expressed in a single neuron of the class. To account for this, we reduced each maximal biclique to the number of unique classes present in them and compared with distributions of 1,000 randomizations of similar size. For instance, in a set of size 4, where two neurons are of the same class, we compare with random choices of three nodes for different classes. We find that 509 Source sets and 1,006 Destination sets remain significant under this more stringent metric.
Degree Preservation
Given the finding that rich-club hub nodes show higher degree of correlations in gene expression (Arnatkeviciūtė et al., 2018), as a second robustness metric we normalize for degree. For this, we group nodes into three degree categories (‘low’, ‘medium’, and ‘high’) and always replace nodes within their degree category during the 1,000 randomizations. We find that 768 source sets and 1,647 destination sets remain significant under this more stringent metric.
Additional Test for Biological Significance
Given the extensive characterization of the C. elegans neurons, we can use additional metrics of cell identity to test the genetic similarity of the S and D sets selected by the bicliques. As the TFs recognized by the biological operator O contribute to a neuron’s transcriptional identity, we predict that the neurons in the same S (or D) sets should also be similar to each other across multiple morphological, functional, and developmental characteristics. Next we offer evidence of the validity of this prediction.
Lineage Distance
The developmental lineage in C. elegans defines the coalescence distances between neurons, which captures their developmental similarity. We identified pairwise lineage distances between all source-source and destination-destination neuron combinations, and used a two-sample Kolmogorov-Smironov test to test the alternative hypothesis that the real pairwise distribution’s empirical cdf is smaller than the distribution of pairwise lineage distances between all 279 neurons. In lineage distances a smaller value indicates that the two cells have fewer divisions between them. Looking at all maximal bicliques, we find 1,494 significant source sets and 1,717 destination sets, with 235 maximal bicliques significant for both source and destination neurons.
Neuronal Classes
The C. elegans neurons have been classified into 118 neuronal classes based on their anatomical similarities, each class containing 1 to 13 neurons. The restricted connectome of 279 neurons contains 103 of these classes. As a neuron’s morphological features are ultimately driven by gene expression, class membership represents a coarse-grained proxy for expression pattern similarity. According to our model, the neurons found in the same S or D set should share the expression of the genes selected by the corresponding operator O. We therefore expect that each biclique set should be enriched in class membership.
To test the validity of the above prediction, we tested for class enrichment in each biclique by finding the size of the largest class in each S/D set. For instance, if a source set of 8 neurons has 3 neurons in class A, 2 in class B, and the remaining 3 neurons alone in classes C, D, and E, we take class A to be the largest class. We calculate the probability of finding 3 neurons of the same size of class together when we randomly select 8 neurons. This probability can be written as
where U is the set size, M is the max number of neurons of one class found in the set, C is the number of neurons in the largest class, and num(C) indicates the multiplicity of size C classes. Extending this analysis to all maximal biclique motifs, we find 1,973 significant source and 3,070 significant destination sets, with 845 maximal bicliques showing significance for both source and destination neurons.
Neurotransmitter Enrichment
C. elegans neurons utilize seven unique neurotransmitters, with 11 neurons expressing more than one neurotransmitter and 24 neurons have unknown neurotransmitters. The remaining 244 neurons each have a unique neurotransmitter assigned, one of the seven. As neurotransmitter expression also acts as a proxy for neuronal identity, we examined the neurotransmitter enrichment in the S and D sets for each biclique motif. Enrichment was found similar to class enrichment: the most commonly expressed neurotransmitter was identified in a given set and compared to the probability of finding that same number of similar neurotransmitter in a random reference set of neurons. When we extend the analysis to all maximal bicliques, we find 1,519 source and 1,641 destination sets significant in the chemical synapse data, and 261 maximal bicliques have significant enrichment in neurotransmitters for source and destination neurons.
Type Enrichment
Neurons have also been categorized in three classes, sensory, interneuron, or motor neuron, according to the function they play in C. elegans, once again offering a proxy for neuronal identity. We determined enrichment for neuronal type in bicliques with methods similar to those utilized for neurotransmitter and class enrichment. Under type enrichment, we find 1,955 source sets and 2,710 destination sets to show significant enrichment, with 564 maximal bicliques displaying significance for both S and D sets.
Biclique Motifs in Other Organisms
Although C. elegans offers the only complete connectome for a full organism, partial reconstructions in other organisms are available, which allows us to test the network-level predictions of the connectome model.
Ciona Intestinalis
A recent connectome for a tadpole larva of a sea squirt, Ciona intestinalis, offers a partial mapping of a second central nervous system (Ryan, Lu and Meinertzhagen, 2016). The published data consider 177 neurons and the cells they synapse with, resulting in a 205x215 adjacency matrix with 7.04% density. We restricted our analysis to the largest connected component of the complete subgraph of the dataset, to better compare with the complete mapping of C. elegans, resulting in a 197x197 matrix with 7.66% density (< k > = 15.1).
Using MBEA, we found 29,689 maximal bicliques in the chemical synapse connectome, while only 15,494 ± 333 maximal bicliques under degree preserving randomization, resulting in Z = 44.612. This finding indicates that, just like C. elegans, there is a highly significant number of maximal bicliques that can’t be explained by the degree distribution. As with the C. elegans chemical synapse connectome, we find that large maximal bicliques are overrepresented in the connectome, and smaller maximal bicliques are either under expressed or not significant (Figure S2). This indicates that the maximal biclique structure predicted by our model is not limited to C. elegans but is present in other organisms as well.
Drosophila
Ongoing efforts to map the wiring of Drosophila fruit flies have yielded EM reconstructions of both the adult and larval fly, resulting in the published connectome of the early olfactory system (Berck et al., 2016; Eichler et al., 2017). We investigated the maximal biclique structure of the mushroom body, consisting predominantly of Kenyon Cells and Projection Neurons. In order to account for noise in the reconstruction, we considered connections with a weight of at least 5 synapses. The resulting network includes 387 neurons with 3,690 links between them, at 2.46% density and < k > = 9.53.
We found 34,080 maximal bicliques among the chemical synapses, a number that by itself is highly significant compared to the 27,100 ± 1,100 maximal bicliques found under degree-preserving randomization (Z = 6.48). We also found much larger maximal bicliques than in C. instestinalis and C. elegans, and the large maximal bicliques continue to be significantly overrepresented (Figure S2).
Bicliques in Network Models
Could the existing models of complex networks explain the exceptional density and the nature of bicliques observed in C. elegans? To answer that, we explored several reference models: the Erdős-Rényi model of random networks (ER) (Erdös and Rényi, 1959), a growth model of scale-free (SF) networks (Barabási and Albert, 1999), and the neuronal network model built on the exponential distance rule (EDR) (Ercsey-Ravasz et al., 2013), proposed to capture the linking probabilities of interareal networks.
Erdős-Rényi Model
While there are some smaller maximal bicliques in networks generated by the ER model, none of them are significant. This is a direct consequence of the fact that the reference randomized networks used to determine the statistical significance of the observed maximal bicliques, are indistinguishable from the random network we are exploring. The same is true for networks generated by the configuration model (independent of the underlying degree distribution), meaning that while these networks may generate some maximal bicliques, the observed maximal bicliques lack statistical significance by construction.
Exponential Distance Rule Model
The EDR model was proposed to describe brain wiring, its rules integrating the empirically observed distances of brain regions. Inspired by EDR measurements in C. elegans (Ahn, Jeong and Kim, 2006), we generated networks of density of 4.5% by placing N = 279 nodes on a square lattice with periodic boundary conditions, connecting nodes with probability p(d) = exp(−λd), where d is the Euclidean distance between nodes and λ = 10.88, which was chosen to match the link density of C. elegans (Ercsey-Ravasz et al., 2013). The maximal biclique analysis does identify statistically significant maximal bicliques. Yet, a close inspection of the maximal bicliques generated by the EDR model indicate that they are different from those observed in C. elegans, being rooted in fully connected cliques.
Indeed, by connecting most nodes within the same geographic vicinity, the model generates fully connected cliques, i.e., specific type of maximal bicliques that have not only direct S→D links, but also the nodes in the D and the S sets are also significantly (or fully) linked to each other. Indeed, we find that of the maximal bicliques generated by the EDR model, all sets have a statistically significant number of links among the D (or S) nodes. In contrast, in C. elegans only 37.9% S sets show statistically significant number of links (p < 0.05, defined as greater than 25% link density), and 35.2% for the D sets. If we disregard the maximal bicliques with densely connected D or S sets (i.e., those that show statistical significance), all statistically significant maximal bicliques disappear from the EDR model. In contrast, the same procedure applied to the C. elegans maximal bicliques leaves most statistically significant maximal bicliques unperturbed.
Scale-free Model
We implemented a growth model of SF networks (mindful of the fact that the C. elegans network is too small to decide the nature of its precise degree distribution, and measurements point toward an exponential P(k)). We generated using the SF model (Barabási and Albert, 1999) a network with m = 13 and N = 279, chosen to match the size and the link density of the C. elegans connectome, and identified the maximal bicliques, and their statistical significance. We do find statistically significant maximal bicliques that are rooted in the evolutionary nature of the model. Indeed, the first m nodes tend to acquire the most links, which become the hubs of the resulting network. With a non-zero probability, the later nodes connect their m links to the first (and the largest) m nodes, generating multiple maximal bicliques.
This observation predicts two features: (i) The maximal biclique significance spectrum is not stationary, but as the network grows, it will lead to larger and larger out-degree (S) maximal bicliques, all linked to subsets the first m-nodes. (ii) The maximal outdegree of the statistically significant maximal bicliques will be m (D set). Simulations confirm both predictions (Figure S3).
To test our insights that the observed maximal bicliques are all anchored on the first m nodes, we removed these m nodes from the network, which results in the loss of statistical significance of the remaining maximal bicliques (Figure S3).
Taken together, we find that current network models cannot explain the maximal biclique structure observed in C. elegans and other organisms. Evolving models, like the SF model, generate a non-stationary maximal biclique structure, in which all maximal bicliques are anchored on the first m nodes with the highest degrees. Spatial models, in contrast, generate (almost) fully connected cliques, different from the structure of the maximal bicliques observed in C. elegans. This suggests that we need to invoke biological mechanisms to explain the roots of the observed maximal bicliques structure seen in brain networks. Nevertheless, an open question is how to systematically incorporate the spatial nature of the connectome into the framework. This is possible once we mathematically formulate the spatial contribution to the connectome model (unpublished data).
DATA AND CODE AVAILABILITY
We provide MATLAB code for the identification and analysis of bicliques in connectomes in the public repository with https://doi.org/10.5281/zenodo.2699419. The analyses of the study utilized a number of publicly available software packages which could not be reproduced in the repository, but can be found through in-text citations and the Key Resources Table.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited Data | ||
| WormBase Gene Expression | WormBase, Oliver Hobert (curation) | July 15th, 2016 release |
| Lineage Identity | WormAtlas | https://www.wormatlas.org/neuronalwiring.html |
| Neurotransmitter Identity | Pereira et al., 2015 | https://elifesciences.org/articles/12432#tbl2 |
| C elegans Connectome 1 | Varshney et al., 2011 | https://journals.plos.org/ploscompbiol/article?id+10.1371/journal.pcbi.1001066 |
| C elegans Connectome 2 | Cook et al., 2019 | https://www.nature.com/articles/s41586-019-1352-7 |
| Ciona intestinalis Connectome | Ryan et al., 2016 | https://elifesciences.org/articles/16962 |
| Drosophila Connectome | Eichler et al., 2017 | https://www.ncbi.nlm.nih.gov/pubmed/28796202 |
| Software and Algorithms | ||
| MBEA | Zhang et al., 2014 | https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4038116/ |
| Degree Preserving Randomization | Sergei Maslov | http://maslov.bioengineering.illinois.edu/matlab.htm |
| MATLAB | MathWorks | R2018a-2019b |
| GNU Parallel | Ole Tange: GNU 2018 | https://www.gnu.org/software/parallel/ |
Supplementary Material
Highlights.
Modeling the genetic roots of the connectome
Predicting genetically encoded biclique motifs
Predicting genes potentially responsible for neural wiring
Validating in the connectomes of three species
ACKNOWLEDGMENTS
We wish to thank István Kovács, Emma Towlson, Hamza Giaffar, Petra Vertes, and Armen Stepanyants for fruitful discussions and Alice Grishchenko for help in designing the figures. D.L.B. was supported by NIH NIGMS T32 GM008313. A.-L.B. was supported by the NSF award 1734821 and by the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 810115 - DYNASNET.
Footnotes
SUPPLEMENTAL INFORMATION
Supplemental Information can be found online at https://doi.org/10.1016/j.neuron.2019.10.031.
DECLARATION OF INTERESTS
D.L.B. declares no competing interests. A.-L.B. is the founder of Scipher, Foodome, and Nomix and sits of the boards of these companies. He is co-inventor on several patents in the area of network science and network medicine.
REFERENCES
- Ackman JB, Burbridge TJ, and Crair MC (2012). Retinal waves coordinate patterned activity throughout the developing visual system. Nature 490, 219–225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Adler CE, Fetter RD, and Bargmann CI (2006). UNC-6/Netrin induces neuronal asymmetry and defines the site of axon formation. Nat. Neurosci 9, 511–518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahn Y-Y, Jeong H, and Kim BJ (2006). Wiring cost in the organization of a biological neuronal network. Physica A 367, 531–537. [Google Scholar]
- Ananthanarayanan R, Esser SK, Simon HD, and Dharmendraand SM (2009). The cat is out of the bag: cortical simulations with 109 neurons, 1013 synapses. Proceedings of the Conference on High Performance Computing Networking, Storage and Analysis, 63. [Google Scholar]
- Arnatkeviciute A, Fulcher BD, Pocock R, and ad Fornito A (2018). Hub connectivity, neuronal diversity, and gene expression in the Caenorhabditis elegans connectome. PLOS Comput. Biol Published online February 12, 2018. 10.1371/journal.pcbi.1005989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azevedo FAC, Carvalho LR, Grinberg LT, Farfel JM, Ferretti RE, Leite RE, Jacob Filho W, Lent R, and Herculano-Houzel S (2009). Equal numbers of neuronal and nonneuronal cells make the human brain an isometrically scaled-up primate brain. J. Comp. Neurol 513, 532–541. [DOI] [PubMed] [Google Scholar]
- Babai L (2016). Graph isomorphism in quasipolynomial time. arXiv, arXiv:1512.03547. https://arxiv.org/abs/1512.03547. [Google Scholar]
- Barabási AL (2016). Network Science, First Edition (Cambridge University Press; ). [Google Scholar]
- Barabási A-L, and Albert R (1999). Emergence of scaling in random networks. Science 286, 509–512. [DOI] [PubMed] [Google Scholar]
- Baruch L, Itzkovitz S, Golan-Mashiach M, Shapiro E, and Segal E (2008). Using Expression Profiles of Caenorhabditis elegans Neurons to Identify Genes that Mediate Synaptic Connectivity. PLoS Comput. Biol Published online July 11,2008. 10.1371/journal.pcbi.1000120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett DS, and Bullmore E (2006). Small-world brain networks. Neuroscientist 12, 512–523. [DOI] [PubMed] [Google Scholar]
- Belousov AB, and Fontes JD (2013). Neuronal gap junctions: making and breaking connections during development and injury. Trends Neurosci. 36, 227–236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bentley B, Branicky R, Barnes CL, Chew YL, Yemini E, Bullmore ET, Vértes PE, and Schafer WR (2016). The Multilayer Connectome of Caenorhabditis elegans. PLoS Comput. Biol Published online December 16, 2016. 10.1371/journal.pcbi.1005283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berck ME, Khandelwal A, Claus L, Hernandez-Nunez L, Si G, Tabone CJ, Li F, Truman JW, Fetter RD, Louis M, Samuel ADT, and Cardona A (2016). The wiring diagram of a glomerular olfactory system. eLife 5, 1–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernardo-Garcia FJ, Humberg TH, Fritsch C, and Sprecher SG (2017). Successive requirement of Glass and Hazy for photoreceptor specification and maintenance in Drosophila. Fly 11, 112–120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Betzel RF, and Bassett DS (2017). Generative models for network neuroscience: prospects and promise. J. R. Soc. Interface 14, 20170623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhattacharya A, Aghayeva U, Berghoff EG, and Hobert O (2019). Plasticity of the electrical connectome of C. elegans. Cell 176, 1174–1189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bollobás B (2001). Random Graphs (Cambridge University Press; ). [Google Scholar]
- Caldarelli G (2010). Scale-Free Networks: Complex Webs in Nature and Technology, Scale-Free Networks: Complex Webs in Nature and Technology. Published online January 2010. 10.1093/acpro-f:oso/9780199211517.001.0001. [DOI] [Google Scholar]
- Caron SJC, Ruta V, Abbott LF, and Axel R (2013). Random convergence of olfactory inputs in the Drosophila mushroom body. Nature 497, 113–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrillo RA, Özkan E, Menon KP, Nagarkar-Jaiswal S, Lee PT, Jeon M, Birnbaum ME, Bellen HJ, Garcia KC, and Zinn K (2015). Control of Synaptic Connectivity by a Network of Drosophila IgSF Cell Surface Proteins. Cell 163, 1770–1782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen BE, Kondo M, Garnier A, Watson FL, Püettmann-Holgado R, Lamar DR, and Schmucker D (2006). The molecular diversity of Dscam is functionally required for neuronal wiring specificity in Drosophila. Cell 125, 607–620. [DOI] [PubMed] [Google Scholar]
- Choe AS, Jones CK, Joel SE, Muschelli J, Belegu V, Caffo BS, Lindquist MA, van Zijl PC, and Pekar JJ (2015). Reproducibility and temporal structure in weekly resting-state fMRI over a period of 3.5 years. PLoS ONE 10, e0140134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cimini G, Squartini T, Saracco F, Garlaschelli D, Gabrielli A, and Cardarelli G (2019). The statistical physics of real-world networks. Nature Rev. Phys 1, 58–71. [Google Scholar]
- Colizza V, Flammini A, Serrano MA, and Vespignani A (2006). Detecting rich-club ordering in complex networks. Nat. Phys 2, 110–115. [Google Scholar]
- Cook SJ, Jarrell TA, Brittin CA, Wang Y, Bloniarz AE, Yakovlev MA, Nguyen KCQ, Tang LT, Bayer EA, Duerr JS, et al. (2019). Whole-animal connectomes of both Caenorhabditis elegans sexes. Nature 571, 63–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crump JG, Zhen M, Jin Y, and Bargmann CI (2001). The SAD-1 kinase regulates presynaptic vesicle clustering and axon termination. Neuron 29, 115–129. [DOI] [PubMed] [Google Scholar]
- Dias VMF, de Figueiredo CMH, and Szwarcfiter JL (2007). On the generation of bicliques of a graph. Discrete Appl. Math 155, 1826–1832. [Google Scholar]
- Edelman G (1987). Neural Darwinism (Neural Darwinism; ). [Google Scholar]
- Eichler K, Li F, Litwin-Kumar A, Park Y, Andrade I, Schneider-Mizell CM, Saumweber T, Huser A, Eschbach C, Gerber B, et al. (2017). The complete connectome of a learning and memory centre in an insect brain. Nature 548, 175–182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- English DF, McKenzie S, Evans T, Kim K, Yoon E, and Buzsáki G (2017). Pyramidal Cell-Interneuron Circuit Architecture and Dynamics in Hippocampal Networks. Neuron 96, 505–520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ercsey-Ravasz M, Markov NT, Lamy C, Van Essen DC, Knoblauch K, Toroczkai Z, and Kennedy H (2013). A predictive network model of cerebral cortical connectivity based on a distance rule. Neuron 80, 184–197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Erdös P, and Rényi A (1959). On random graphs. Publ. Math 6, 290–297. [Google Scholar]
- Farrell JA, Wang Y, Riesenfeld SJ, Shekhar K, Regev A, and Schier AF (2018). Single-cell reconstruction of developmental trajectories during zebrafish embryogenesis. Science. Published online June 1, 2018. 10.1126/science.aar3131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall DH (2017). Gap junctions in C. elegans: Their roles in behavior and development. Dev. Neurobiol 77, 587–596, 10.1002/dneu.22408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han Y, Kebschull JM, Campbell RAA, Cowan D, Imhof F, Zador AM, and Mrsic-Flogel TD (2018). The logic of single-cell projections from visual cortex. Nature 556, 51–56, 10.1038/nature26159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris TW, Antoshechkin I, Bieri T, Blasiar D, Chan J, Chen WJ, De La Cruz N, Davis P, Duesbury M, Fang R, et al. (2010). WormBase: a comprehensive resource for nematode research. Nucleic Acids Res. Published online January 2010. 10.1093/nar/gkp952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hedgecock EM, Culotti JG, and Hall DH (1990). The unc-5, unc-6, and unc-40 genes guide circumferential migrations of pioneer axons and mesodermal cells on the epidermis in C. elegans. Neuron 4, 61–85. [DOI] [PubMed] [Google Scholar]
- Herculano-Houzel S, and Lent R (2005). Isotropic fractionator: a simple, rapid method for the quantification of total cell and neuron numbers in the brain. J. Neurosci 25, 2518–2521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hobert O (2005). Specification of the nervous system. WormBook: The Online Review of C. elegans Biology (WormBook). Published online August 8, 2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hobert O, Glenwinkel L, and White J (2016). Revisiting Neuronal Cell Type Classification in Caenorhabditis elegans. Curr. Biol 26, R1197–R1203. [DOI] [PubMed] [Google Scholar]
- Holguera I, and Desplan C (2018). Neuronal specification in space and time. Science 362, 176–180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hong W, and Luo L (2014). Genetic control of wiring specificity in the fly olfactory system. Genetics 196, 17–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Itzkovitz S, and Alon U (2005). Subgraphs and network motifs in geometric networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys 71, 026117. [DOI] [PubMed] [Google Scholar]
- Jarrell TA, Wang Y, Bloniarz AE, Brittin CA, Xu M, Thomson JN, Albertson DG, Hall DH, and Emmons SW (2012). The connectome of a decision-making neural network. Science 337, 437–444. [DOI] [PubMed] [Google Scholar]
- Jonas E, and Kording K (2015). Automatic discovery of cell types and microcircuitry from neural connectomics. Elife. Published online April 30, 2015. 10.7554/eLife.04250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaiser M (2017). Mechanisms of Connectome Development. Trends Cogn. Sci 21, 703–717. [DOI] [PubMed] [Google Scholar]
- Kaufman A, Dror G, Meilijson I, and Ruppin E (2006). Gene expression of Caenorhabditis elegans neurons carries information on their synaptic connectivity. PLoS Comput. Biol 2, e167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lagercrantz H, Hanson MA, Ment LR, and Peebles DM (2010). The Newborn Brain: Neuroscience and Clinical Applications (Cambridge University Press; ). [Google Scholar]
- Landesman Y, White TW, Starich TA, Shaw JE, Goodenough DA, and Paul DL (1999). Innexin-3 forms connexin-like intercellular channels. J. Cell Sci 112,2391–2396. [DOI] [PubMed] [Google Scholar]
- LaVail JH, Nixon RA, and Sidman RL (1978). Genetic control of retinal ganglion cell projections. J. Comp. Neurol 182, 399–421. [DOI] [PubMed] [Google Scholar]
- Lim Y, and Wadsworth WG (2002). Identification of domains of netrin UNC-6 that mediate attractive and repulsive guidance and responses from cells and growth cones. J. Neurosci 22, 7080–7087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marcus G, Marblestone A, and Dean T (2014). Neuroscience. The atoms of neural computation. Science 346, 551–552. [DOI] [PubMed] [Google Scholar]
- Maslov S, and Sneppen K (2002). Specificity and stability in topology of protein networks. Science 296, 910–913. [DOI] [PubMed] [Google Scholar]
- McGonigle DJ, Howseman AM, Athwal BS, Friston KJ, Frackowiak RS, and Holmes AP (2000). Variability in fMRI: an examination of intersession differences. Neuroimage 11, 708–734. [DOI] [PubMed] [Google Scholar]
- Nicosia V, Vértes PE, Schafer WR, Latora V, and Bullmore ET (2013). Phase transition in the economically modeled growth of a cellular nervous system. Proc. Natl. Acad. Sci. USA 110, 7880–7885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Packer JS, Zhu Q, Huynh C, Sivaramakrishnan P, Preston E, Dueck H, Stefanik D, Tan K, Trapnell C, Kim J, et al. (2019). A lineage-resolved molecular atlas of C. elegans embryogenesis at single-cell resolution. Science. Published online September 5, 2019. 10.1126/science.aax1971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paul A, Crow M, Raudales R, He M, Gillis J, and Huang ZJ (2017). Transcriptional Architecture of Synaptic Communication Delineates GABAergic Neuron Identity. Cell 171, 522–539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pereira L, et al. (2015). A cellular and regulatory map of the cholinergic nervous system of C. elegans. eLife. 10.7554/eLife.12432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian J, Hintze A, and Adami C (2011). Colored Motifs Reveal Computational Building Blocks in the C. elegans Brain. PLoS ONE. Published online March 7, 2011. 10.1371/journal.pone.0017013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rapti G, Li C, Shan A, Lu Y, and Shaham S (2017). Glia initiate brain assembly through noncanonical Chimaerin-Furin axon guidance in C. elegans. Nat. Neurosci 20, 1350–1360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reece-Hoyes JS, Deplancke B, Shingles J, Grove CA, Hope IA, and Walhout AJ (2005). A compendium of Caenorhabditis elegans regulatory transcription factors: a resource for mapping transcription regulatory networks. Genome Biol. 6, R110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reece-Hoyes JS, Diallo A, Lajoie B, Kent A, Shrestha S, Kadreppa S, Pesyna C, Dekker J, Myers CL, and Walhout AJ (2011). Enhanced yeast one-hybrid assays for high-throughput gene-centered regulatory network mapping. Nat. Methods 8, 1059–1064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reigl M, Alon U, and Chklovskii DB (2004). Search for computational modules in the C. elegans brain. BMC Biol. 2, 25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ryan K, Lu Z, and Meinertzhagen IA (2016). The CNS connectome of a tadpole larva of Ciona intestinalis (L.) highlights sidedness in the brain of a chordate sibling. eLife. Published online December 6, 2016. 10.7554/eLife.16962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saracco F, Straka MJ, Di Clemente R, Gabrielli A, Caldarelli G, and Squartini T (2017). Inferring monopartite projections of bipartite networks: an entropy-based approach. arXiv, arXiv:1607.02481. [Google Scholar]
- Shapiro L, and Colman DR (1999). The diversity of cadherins and implications for a synaptic adhesive code in the CNS. Neuron 23, 427–430. [DOI] [PubMed] [Google Scholar]
- Shen K, Fetter RD, and Bargmann CI (2004). Synaptic specificity is generated by the synaptic guidepost protein SYG-2 and its receptor, SYG-1. Cell 116,869–881. [DOI] [PubMed] [Google Scholar]
- Söhl G, Maxeiner S, and Willecke K (2005). Expression and functions of neuronal gap junctions. Nat. Rev. Neurosci 6, 191–200. [DOI] [PubMed] [Google Scholar]
- Sperry RW (1963). Chemoaffinity in the Orderly Growth of Nerve Fiber Patterns and Connections. Proc. Natl. Acad. Sci. USA 50, 703–710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns O, Chialvo DR, Kaiser M, and Hilgetag CC (2004). Organization, development and function of complex brain networks. Trends Cogn. Sci 8, 418–425. [DOI] [PubMed] [Google Scholar]
- Starich TA, Miller A, Nguyen RL, Hall DH, and Shaw JE (2003). The Caenorhabditis elegans innexin INX-3 is localized to gap junctions and is essential for embryonic development. Dev. Biol 256, 403–417. [DOI] [PubMed] [Google Scholar]
- Starich TA, Xu J, Skerrett IM, Nicholson BJ, and Shaw JE (2009). Interactions between innexins UNC-7 and UNC-9 mediate electrical synapse specificity in the Caenorhabditis elegans locomotory nervous system. Neural Dev. 4, 16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Straka MJ, Caldarelli G, and Saracco F (2017). Grand canonical validation of the bipartite international trade network. Phys. Rev. E 06, 022306. [DOI] [PubMed] [Google Scholar]
- Straka MJ, Caldarelli G, Squartini T, and Saracco F (2018). From ecology to finance (and back?): A review on entropy-based null models for the analysis of bipartite networks. J. Stat. Phys 173, 1252–1285. [Google Scholar]
- Südhof T (2018). Neuron. 10.1016/j.neuron.2018.09.040. [DOI] [Google Scholar]
- Tang Y, Nyengaard JR, De Groot DM, and Gundersen HJ (2001). Total regional and global number of synapses in the human brain neocortex. Synapse 41, 258–273. [DOI] [PubMed] [Google Scholar]
- Tasic B, Menon V, Nguyen TN, Kim TK, Jarsky T, Yao Z, Levi B, Gray LT, Sorensen SA, Dolbeare T, et al. (2016). Adult mouse cortical cell taxonomy revealed by single cell transcriptomics. Nat. Neurosci 19, 335–346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor SR, Santpere G, Reilly M, Glenwinkel L, Poff A, McWhirter R, Xu C, Weinreb A, Basavaraju M, Cook SJ, et al. (2019). Expression profiling of the mature C. elegans nervous system by single-cell RNA-Sequencing. bioRxiv. 10.1101/737577v2. [DOI] [Google Scholar]
- Telesford QK, Morgan AR, Hayasaka S, Simpson SL, Barret W, Kraft RA, Mozolic JL, and Laurienti PJ (2010). Reproducibility of graph metrics in FMRI networks. Front. Neuroinform 4, 117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Towlson EK, Vértes PE, Ahnert SE, Schafer WR, and Bullmore ET (2013). The rich club of the C. elegans neuronal connectome. J. Neurosci 33, 6380–6387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaquerizas JM, Kummerfeld SK, Teichmann SA, and Luscombe NM (2009). A census of human transcription factors: function, expression and evolution. Nat. Rev. Genet 10, 252–263. [DOI] [PubMed] [Google Scholar]
- Varadan V, Miller DM, and Anastassiou D (2006). Computational inference of the molecular logic for synaptic connectivity in C. elegans. Bioinformatics 22, 497–506. [DOI] [PubMed] [Google Scholar]
- Varshney LR, Chen BL, Paniagua E, Hall DH, and Chklovskii DB (2011). Structural Properties of the Caenorhabditis elegans Neuronal Network. PLoS Comput. Biol Published online February 3, 2011. 10.1371/journal.pcbi.1001066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner DE, Weinreb C, Collins ZM, Briggs JA, Megason SG, and Klein AM (2018). Single-cell mapping of gene expression landscapes and lineage in the zebrafish embryo. Science 360, 981–987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker DS, Chew YL, and Schafer WR (2017). The Oxford Handbook of Invertebrate Neurobiology In Genetics of Behavior in C. elegans, Byrne JH, ed. (Oxford University Press; ). [Google Scholar]
- Wester JC, Mahadevan V, Rhodes CT, Calvigioni D, Venkatesh S, Maric D, Hunt S, Yuan X, Zhang Y, Petros TJ, et al. (2019). Neocortical Projection Neurons Instruct Inhibitory Interneuron Circuit Development in a Lineage-Dependent Manner. Neuron 102, 960–975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White JG, Southgate E, Thomson JN, and Brenner S (1986). The structure of the nervous system of the nematode Caenorhabditis elegans. Philos. Trans. R. Soc. Lond. B Biol. Sci 314, 1–340. [DOI] [PubMed] [Google Scholar]
- Williams ME, deWit J, and Ghosh A (2010). Molecular mechanisms of synaptic specificity in developing neural circuits. Neuron 68, 9–18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winnier AR, Meir JY, Ross JM, Tavernarakis N, Driscoll M, Ishihara T, Katsura I, and Miller DM 3rd (1999). UNC-4/UNC-37-dependent repression of motor neuron-specific genes controls synaptic choice in Caenorhabditis elegans. Genes Dev. 13, 2774–2786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu TW, Hao JC, Lim W, Tessier-Lavigne M, and Bargmann CI (2002). Shared receptors in axon guidance: SAX-3/Robo signals via UNC-34/Enabled and a Netrin-independent UNC-40/DCC function. Nat. Neurosci 5, 1147–1154. [DOI] [PubMed] [Google Scholar]
- Zeisel A, Muñoz-Manchado AB, Codeluppi S, Lönnerberg P, La Manno G, Juréus A, Marques S, Munguba H, He L, Betsholtz C, et al. (2015). Brain structure. Cell types in the mouse cortex and hippocampus revealed by single-cell RNA-seq. Science 347, 1138–1142. [DOI] [PubMed] [Google Scholar]
- Zelinka B (2002). On a problem of E. Prisner concerning the biclique operator. Math. Bohem 127, 371–373. [Google Scholar]
- Zhang H-M, Chen H, Liu W, Liu H, Gong J, Wang H, and Guo AY (2011). AnimalTFDB: a comprehensive animal transcription factor database. Nucleic Acids Res 40, D144–D149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Phillips CA, Rogers GL, Baker EJ, Chesler EJ, and Langston MA (2014). On finding bicliques in bipartite graphs: a novel algorithm and its application to the integration of diverse biological data types. BMC Bioinformatics 15, 110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng Z, Lauritzen JS, Perlman E, Robinson CG, Nichols M, Milkie D, Torrens O, Price J, Fisher CB, Sharifi N, et al. (2018).A Complete Electron Microscopy Volume of the Brain of Adult Drosophila melanogaster. Cell 174, 730–743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zitin A, Gorowara A, Squires S, Herrera M, Antonsen TM, Girvan M, and Ott E (2014). Spatially embedded growing small-world networks. Sci. Rep 4, 7047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zlatic V, Bianconi G, Díaz-Guilera A, Garlaschelli D, Rao F, and Caldarelli G (2009). On the rich-club effect in dense and weighted networks. Eur. Phys. J 67, 271–275. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
We provide MATLAB code for the identification and analysis of bicliques in connectomes in the public repository with https://doi.org/10.5281/zenodo.2699419. The analyses of the study utilized a number of publicly available software packages which could not be reproduced in the repository, but can be found through in-text citations and the Key Resources Table.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Deposited Data | ||
| WormBase Gene Expression | WormBase, Oliver Hobert (curation) | July 15th, 2016 release |
| Lineage Identity | WormAtlas | https://www.wormatlas.org/neuronalwiring.html |
| Neurotransmitter Identity | Pereira et al., 2015 | https://elifesciences.org/articles/12432#tbl2 |
| C elegans Connectome 1 | Varshney et al., 2011 | https://journals.plos.org/ploscompbiol/article?id+10.1371/journal.pcbi.1001066 |
| C elegans Connectome 2 | Cook et al., 2019 | https://www.nature.com/articles/s41586-019-1352-7 |
| Ciona intestinalis Connectome | Ryan et al., 2016 | https://elifesciences.org/articles/16962 |
| Drosophila Connectome | Eichler et al., 2017 | https://www.ncbi.nlm.nih.gov/pubmed/28796202 |
| Software and Algorithms | ||
| MBEA | Zhang et al., 2014 | https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4038116/ |
| Degree Preserving Randomization | Sergei Maslov | http://maslov.bioengineering.illinois.edu/matlab.htm |
| MATLAB | MathWorks | R2018a-2019b |
| GNU Parallel | Ole Tange: GNU 2018 | https://www.gnu.org/software/parallel/ |