Causal evidence supporting the proposal that dopamine transients function as temporal difference prediction errors

Abstract

Reward-evoked dopamine transients are well-established as prediction errors. However the central tenet of temporal difference accounts – that similar transients evoked by reward-predictive cues also function as errors – remains untested. Here we addressed this by showing that optogenetically-shunting dopamine activity at the start of a reward-predicting cue prevents second-order conditioning without affecting blocking. These results indicate that cue-evoked transients function as temporal-difference prediction errors rather than reward predictions.

One of the most fundamental questions in neuroscience concerns how associative learning is implemented in the brain. Key to most implementations is the concept of a prediction error – a teaching signal that supports learning when reality fails to match predictions ¹. The greater the error, the greater the learning. In computational accounts, these errors are calculated by the method of temporal difference ^2,3, in which time (t) is divided into states, each containing a value prediction (V) derived from past experience that is the basis of a rolling prediction error. This error (δ is the difference between successive states. The most famous of these is temporal difference reinforcement learning (TDRL) ³, whose prediction error:

$$\mathrm{\delta }\left(\mathrm{t}\right)=\mathrm{V}\left(\mathrm{t}\right)-\mathrm{V}\left(\mathrm{t}-1\right)$$

has been mapped onto millisecond-resolution changes in dopamine neuron firing ⁴.

While this mapping has been one of the signature success stories of modern neuroscience, one pillar of this account that has not been well-tested is that the transient increase in firing evoked by a reward-predicting cue is a temporal difference error, propogated back from the reward and functioning to support learning about predictors of that cue. Evidence for true, gradual backpropogation of this signal is sparse, as is evidence that it exhibits signature features that define the error at the time of reward, such as suppression on omission of the cue when it has been predicted by an earlier cue, and transfer back to such earlier predictors (in the absence of the primary reward itself). Further, there is little or no causal evidence that cue-evoked dopamine serves as an error signal to support learning. Indeed, the cue-evoked signal is often described as if it encodes the cue’s significance or value derived from its prediction of future reward. Such language is imprecise, leading at best to confusion about the theorized unitary function of the dopamine transient and at worst to a true dichotomization of the function of cue- versus reward-evoked activity. This situation is especially curious, since the appearance of the dopamine transient in response to reward-predictive cues is a lynchpin of the argument that the dopamine neurons signal a temporal difference error ¹.

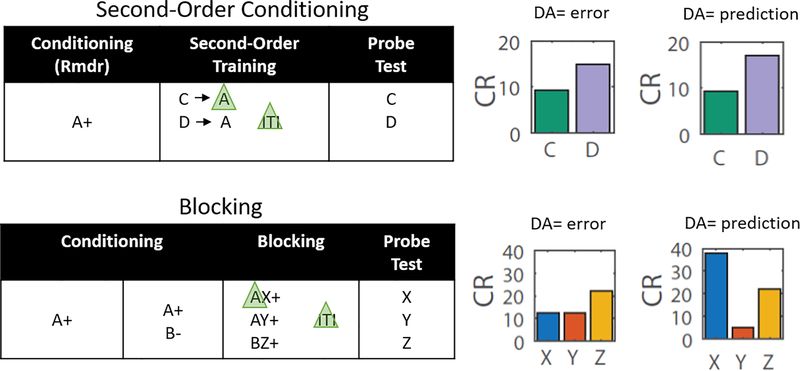
A logical way to address this question is to test, using second-order conditioning ⁵, whether optogenetic blockade or shunting of dopamine activity at the start of a reward-predictive cue prevents learning about this cue in the same way that optogenetic shunting of dopamine activity at reward delivery prevents learning about reward ⁶. If this signal is a temporal difference error, δ(t_cue) in the terms of the above equation, then blocking it will prevent such learning (Fig. 1, Extended Data Fig. 1), which shows an experimental design for second-order conditioning and computational modeling of the effect of eliminating δ(t_cue). However, while this seems at first like a conclusive experiment, it is not, since the same effect is obtained by eliminating the cue’s significance or ability to predict reward for the purposes of calculating the prediction error (Fig. 1, Extended Data Fig. 1). This occurs because the ability of the cue to predict reward is the source of V(t_cue), which is the basis of the cue-evoked prediction error. If shunting the transient eliminates the cue-evoked prediction, then it could also eliminate the cue-evoked prediction error. Consequently, the disruption of second-order conditioning by shunting of the dopamine transient would show that this signal is necessary for learning, but it would not distinguish whether this because it is a prediction error or a reward prediction.

Figure 1: Modeling Results.

Experimental designs for second-order conditioning (top row) and blocking (bottom row), along with bar graphs modeling the predicted results of shunting of the dopamine transient at the start of the reward-predictive cue, A, in each procedure. Green triangles indicate light delivery to shunt dopamine transients at the start of the cue in TH-Cre rats expressing halorhodopsin in VTA neurons. The left column of bar graphs shows modeled results under the hypothesis that the cue-evoked dopamine transient signals a prediction error; the right column shows them under the hypothesis that it signals a reward prediction. Elimination of either signal would impair second-order conditioning (top graphs, C versus D), but only elimination of a prediction would affect blocking (bottom graphs, X vs Y/Z). Note the output of the classic TDRL model was converted from V to conditioned responding (CR) to better reflect the behavioral output actually measured in our experiments (see methods for details). See Extended Data Fig. 1 for modeling of behavior in the full experiments, culminating in these displays.

This confound can be resolved by combining the above experiment with an assessment of the effects of the same manipulation (ideally in the same subjects) on blocking ⁷. Blocking refers to the ability of a cue to prevent or block other cues from becoming associated with the predicted reward; blocking is thought to reflect the reduction in prediction error at the time of reward, δ(t_rew), caused by the cue’s contribution to the reward prediction in the reward state (V(t_rew −1)). If the cue-evoked dopamine transient is carrying the cue’s reward prediction, then optogenetically-shunting it should diminish or prevent blocking, because in the absence of the cue’s reward prediction the reward would still evoke a prediction error (Fig. 1, Extended Data Fig. 1), which shows an experimental design for blocking and computational modeling of the effect of eliminating V(t_rew −1). On the other hand, if the cue-evoked dopamine signal reflects only the actual prediction error occurring at the start of the cue, δ(t_cue), then its removal should have no impact on the blockade of the prediction error evoked by the reward and, thus, no impact on blocking (Fig. 1, Extended Data Fig. 1).

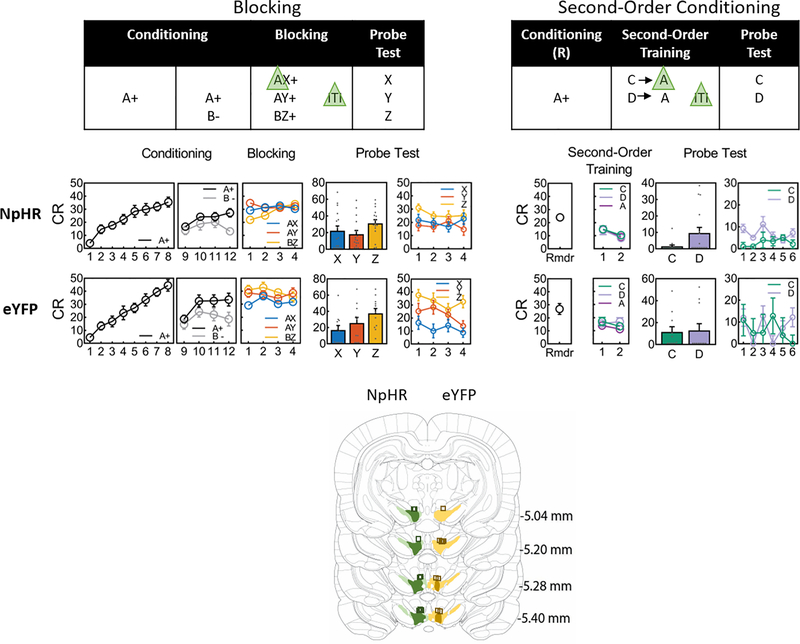
Armed with these contrasting, computationally-validated predictions, we conducted a within-subjects version of the designs (Fig 1, Extended Data Fig. 1). Sixteen Long-Evans transgenic rats expressing Cre recombinase under control of the tyrosine hydroxylase promoter (TH-Cre+/−) served as subjects. Four weeks prior to the start of testing, the rats underwent surgery to infuse a Cre-dependent viral vector carrying halorhodopsin (AAV5-EF1α-DIO, eNpHR3.0- eYFP) into the VTA bilaterally and to implant optical fibers targeting this region (Extended Data Fig. 2). Rats were food restricted immediately prior to the start of testing and then trained to associate a visual cue, A, with reward. Food port approach (percent time spent) was taken as a measure of the level of conditioning. The blocking experiment was carried out in the same rats before the SOC experiment to ensure that any effect of non-reinforcement during SOC training would not disrupt blocking. However, to align with the logic of our modeling, we present the SOC data first here.

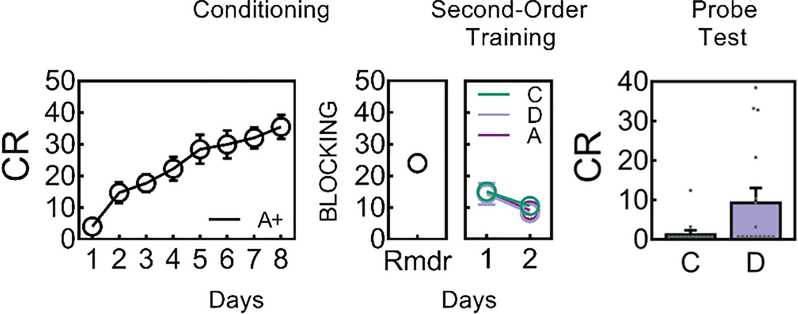
Second-order training consisted of 2 sessions in which A was presented without reward, preceded on each trial by one of two 10s novel auditory cues, C or D. On C→A trials, continuous laser light (532nm, 18–20mW output) was delivered into the VTA for 2.5s, starting 0.5s prior to the onset of A in order to disrupt any dopamine transient normally occurring at the start of the reward-predicting cue, in this case, A. We model this as shunting, since we have found that similar duration patterns of inhibition disrupt learning from positive errors without inducing aversion or learning from negative errors ^6,8,9. On D→A trials, the same 2.5s light pattern was delivered during the intertrial interval at a random time point 120–180s after termination of A. Following this training, rats underwent probe testing, in which C and D were presented alone and without reward (Fig. 2, with supporting statistics described in the legend). There was no difference in responding on C→A versus D→A trials, indicating that the optogenetic manipulation did not deter responding during second-order training. However in the probe test, responding to C was significantly lower than responding to D, indicating that light delivery at the start of A prevented second-order conditioning of C. Identical results were obtained in a separate experimental group that underwent the same training without the prior experience with blocking, described below (Extended Data Fig. 3), whereas eYFP controls that underwent the same training after being transfected with a virus lacking NpHR2.0 showed high levels of responding to both C and D (Extended Data Fig. 2).

Figure 2: The cue-evoked dopamine transient is necessary for second-order conditioning.

Behavioral responding (Mean ± SEM, n = 16 rats) during A increased during Conditioning (ANOVA: F_1,15 = 65.6, p < 0.005) and following Blocking during reminder (Rmdr) training (ANOVA: F_1,15 = 38.0, p < 0.001). Responding to C (i.e., C→A trials) and D (i.e., D→A trials) did not differ (Friendman analysis of variance: D1 χ2(1,31) = 0.6, p = 0.439; for D2 χ2(1,31) = 0.29, p = 0.593) during second-order training when shunting of VTA transients took place at the start of the reward-predictive cue, A (as illustrated in Figure 1). A Wilcoxon signed rank test was used to analyze the data on Test. Responding to C was lower compared to D (z = 1.9, p = 0.03, effect size r = 0.34), showing that inhibition of the VTA DA signal at the start of A prevented A from supporting second-order conditioning to C whereas identical inhibition during the ITI left learning to D intact. Rmdr, reminder training post-blocking. CR or conditioned responding is percent time spent in the magazine during the last 5s of the cue.

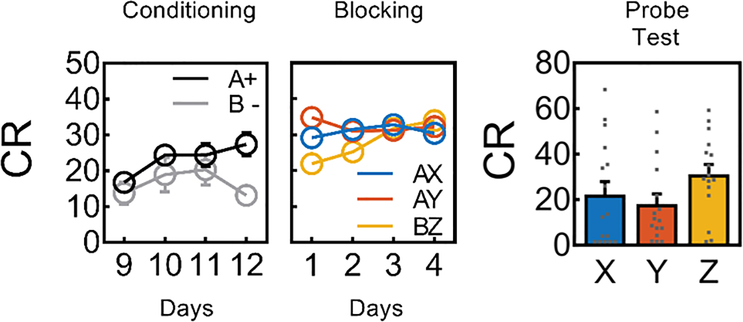
Blocking consisted of 4 sessions in which A was presented in compound with two novel 10s auditory cues, X and Y, followed by reward. On AX trials, continuous laser light (532nm, 18–20mW output) was delivered into the VTA for 2.5s, starting 0.5s prior to the onset of A; on AY trials, the same 2.5s light pattern was delivered during the intertrial interval at a random time point starting 120–180s after termination of the compound. In addition, as a positive control for learning about a compound cue, the rats also received presentations of two additional cues, B and Z, followed by the same reward. B was a visual cue, which was presented four times without reward on each of the last four days of conditioning (Extended Data Fig. 2). Z was a third novel auditory cue. Following this training, rats underwent probe testing, in which X, Y, and Z were presented alone and without reward (Fig. 3, with supporting statistics described in the legend). During blocking, responding to BZ was lower at the start of training but reached that of the AX and AY compounds by the end of training. There were no differences in responding on AX versus AY trials across blocking, indicating that the optogenetic manipulation did not deter responding. In the probe test, responding to the positive control cue, Z, was significantly higher than responding to two blocked cues, X and Y, indicating that pre-training of A blocked learning for these two cues. Further, there was no difference in responding to X and Y, indicating that light delivery at the start of A on AX trials had no effect on blocking. Identical results were obtained in eYFP control rats (Extended Data Fig. 2).

Figure 3: The cue-evoked dopamine transient is not necessary for blocking.

Behavioral responding (Mean ± SEM, n = 16 rats) during conditioning was greater to the reinforced A compared to the non-reinforced B (ANOVA: F_1,15 = 14.9, p = 0.002, see also online methods). During Blocking responding to the control compound (BZ) was lower compared to that seen to the blocking compounds (AX and AY) on the first day of training for NpHR (ANOVA: F_1,15 = 12.9, p = 0.003) but smilar on subsequent days (ANOVA: max F_1,15 = 2.7, p = 0.122); shunting of the VTA DA transient took place at the start of the reward-predicting cue, A (as illustrated in Figure 1), yet responding to AX and AY was similar on each day (ANOVA: max F_1,15 = 1.3, p = 0.272). A Wilcoxon signed rank test was used to analyze the data on Test. The rats showed a blocking effect: there was higher level of responding to the control cue (Z) compared to the blocked cues (X and Y) (z = 2.22, p = 0.01, effect size r = 0.39) on the first trial pooled across both Probe tests. There was no effect of VTA DA inhibition on blocking as responding to the blocked cues (X vs. Y) did not differ (z = 0.05, p = 0.48, effect size r = 0.009). CR or conditioned responding is percent time spent in the magazine during the last 5s of the cue.

These data provide clear and concise evidence that transient increases in the firing of dopamine neurons at the start of reward-predictive cues function as prediction errors to support associative learning in much the same way that reward-evoked changes have been shown to do. As noted in our introduction, such evidence is important because the proposal that the cue-evoked dopamine transient is a prediction error is the lynchpin of the hypothesis that dopaminergic error signals integrate information about future events, thereby providing a temporal difference error. The finding that dopamine neuron activity at the start of a reward-predicting cue is necessary for second-order conditioning but not blocking provides strong support for this idea, while at the same time ruling out alternative proposals that this signal – at least at the level of the spiking of dopamine neurons – reflects the actual associative significance of the cue with respect to predicting reward (but see ¹⁰). Importantly, our findings are agnostic with regard to the nature of the information in the temporal difference signal or the specific type of learning that it supports. This is a noteworthy caveat, since temporal difference errors can be limited to representing information about value ^2,3 or they can be construed more broadly as representing errors in predicting other value-neutral information ^2,11. Recent studies using sensory preconditioning and reinforcer devaluation provide evidence that dopamine transients can support learning orthogonal to value in line with the latter account ^9,11,12. Here we used second-order conditioning, which has been proposed to rely on an associative structure that bypasses the representation of the outcome and links a stimulus and a response ¹³. Sensory pre-conditoning, by contrast, is supported by the association of two neutral stimuli, leaving no opportunity for direct links with a reward-based response. That dopamine transients in the VTA are now causally implicated in supporting both forms of learning supports a much broader role for these signals in driving associative learning than is envisioned by current dogma, one in which the content of the learning supported is determined by the learning conditions.

Methods

Methods and any associated references are available in the online version of the paper.

Online Methods

Modeling

Simulations of the behavioral designs were run using a one-step temporal difference learning algorithm, TD(0)¹⁴. This algorithm was used to estimate the value of different states of the behavioral paradigm with states being determined by the stimuli present at any particular time. Linear function approximation was used in order to estimate the value, V, of a given state, s_t, by the features present during that state according to

$$\widehat{V}(s_t)\approx \sum _j{w}_j{x}_j\left(s_t\right)$$

where j is indexed through all possible components of the feature vector x and corresponding weight vector w. The feature vector is considered to be the set of possible observed stimuli such that if stimulus j is present during state s at time t, then x_j(s_t) = 1, and zero otherwise. The weights are adjusted over time in order to best approximate the value of each state given the current set of stimuli. Weights, w_j, corresponding to each feature, x_j, are updated at each time step according to the TD error rule

$${\delta }_t=\left[r_t+\gamma \widehat{V}(s_t)-\widehat{V}(s_{t-1})\right]$$

under linear value function approximation where γ is the temporal discouting factor. The weights are updated as

$$\mathrm{\Delta }{w}_j=\alpha x_j\left(s_t\right){\delta }_t$$

in which the scalar α is the learning rate. The linear value approximation reduces the size of the possible state space by generalizing states based on the features present. This approximation results in the calculation of the total expected value of a state as the sum of the expected value of each stimulus element present in the current state, a computation which is consistent with a global prediction error as stipulated by the Rescorla-Wagner model¹⁵.

Modeling of optogenetic manipulation of midbrain dopamine activity

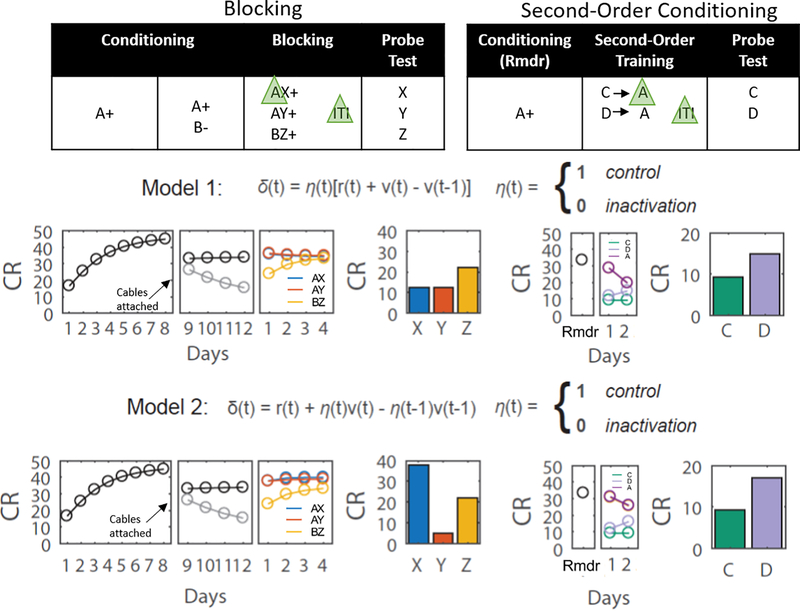
Optogenetic inhibition of dopaminergic neurons was modeled two different ways to align with the different hypotheses of dopamine function described in the main text.

Model 1: Dopamine transients correspond to TD errors

For this model, inhibition of dopaminergic activity disrupts solely the error signal¹¹

$${\delta }_t={\mathit{\eta }}_{\mathit{t}}\left[r_t+\gamma \widehat{V}(s_t)-\widehat{V}(s_{t-1})\right]\eta =\{\begin{array}{cc}0& “laseron”\\ 1& “laseroff”\end{array}$$

where η is a binary value determining whether the inhibition was present or not during state s_t.

Model 2: Dopamine transients correspond to expected value

In this case, the dopaminergic inhibition disrupts the future expected value during the current state, and, since this becomes the prior expected value in the next state, the inhibition disrupt this as well

$${\delta }_t=\left[r_t+\gamma {\mathit{\eta }}_{\mathit{t}}\widehat{V}(s_t)-{\mathit{\eta }}_{\mathit{t}-\mathbf{1}}\widehat{V}(s_{t-1})\right]\eta =\{\begin{array}{cc}0& “laseron”\\ 1& “laseroff”\end{array}$$

where η again determines whether the inhibition was present.

Model Parameterization

Generalization of value across stimuli was modeled by setting the initial weights, w_j, of a stimulus to 0.7 for stimuli of the same modality and 0.2 for stimuli of different modalities.

Conditioned responding to the food cup, CR, at each state was was modeled using a logistic function

$$CR(s_t)=\frac{c}{1+e^{-b\left(V\right(s_t)-a)}}$$

in which the parameters were determined based on empirical estimates of the maximal responding, c, the baseline responding, a, as well as the steepness of the learning curve, b. These were set as 55, 0.4, and 3 respectively for all simulations. Reduced responding to the foodcup while rats were attached to the patch cables was modeled as a reduction in the maximal responding to 40.

All simulations were performed with α = 0.05 and γ = 0.95. To ensure that order of cue presentations did not affect the findings, cue presentations during each stage of conditioning were pseudo-randomized and results of the simulations were averaged over 100 repetitions of the model. Simulations were performed using custom-written functions in MATLAB (Mathworks, Natick, MA), which are available in the Supplementary Software and are posted on Github (https://github.com/mphgardner/Basic_Pavlovian_TDRL/tree/Maes_2018).

Subjects

A total of 45 experimentally naïve Long-Evans transgenic rats expressing Cre recombinase under control of the tyrosine hydroxylase promoter (TH-Cre+/−) were used in the experiments reported here. The rats were approximately three months of age at the start of the experiment. Sixteen of those rats were bred inhouse at the National Institute on Drug Abuse (NIDA, Bayview, Baltimore, USA; male: n=9, 390–587; female: n=7, 302–370g) and 14 rats were bred inhouse at Concordia University (Montreal, Canada; (male: n=5, 382–515; female: n=7, 247–289g) and infused with a viral vector carrying NpHR (see below); the remaining 15 rats were bred inhouse at NIDA (male: n=8, 450–630g; female: n=7, 250–330g) and infused with a control viral vector (eYFP only, see below). Samples sizes were chosen based on published work^6,8,9. Four rats were excluded from the Concordia-bred cohort due to no virus expression (n=1), failure to consume the pellets during conditioning (n=1) or failure to receive stimulation due to broken ferrules (n=1) or cables (n=1). Four rats were excluded from the eYFP group due to no virus expression (n=2), failure to receive stimulation due to broken cables (n=1) and due to a significant outlier result accoding to Grubb’s test (n=1; Zc = 2.55, Z = 2.8, p < 0.05, https://www.graphpad.com/quickcalcs/Grubbs1.cfm) There were no effects of sex across the different phases in our study (NpHR: max F_{1, 14} = 2.1, p = 0.17; eYFP: max F_{1, 14} = 4.0, p = 0.08). The rats were implanted with bilateral optical fibers in the ventral tegmental area (VTA) at approximately 4 months of age. Please refer to Life Sciences Reporting Summary for additional information.

Surgical Procedures

Surgical procedures have been described elsewhere^8,9. Rats were infused bilaterally with 1.2μL AAV5-EF1α-DIO-eNpHR3.0-eYFP or AAV5-EF1α-DIO-eYFP into the VTA at the following coordinates relative to bregma: AP: −5.3mm; ML: ±0.7mm; DV: −6.55mm and −7.7 (females) or −7.0mm and −8.2mm (males). The viral vector was obtained from the Vector Core at University of North Carolina at Chapel Hill (UNC Vector Core). During surgery, ferrules carrying optical fibers were implanted bilaterally (200μm diameter, Precision Fiber Products, CA) at the following coordinates relative to bregma: AP: −5.3mm; ML: ±2.61mm, and DV: −7.05mm (female) or −7.55mm (male) at an angle of 15° pointed toward the midline.

Apparatus

The within-subjects NpHR and eYFP experiments was conducted using 8 behavioral chambers (Coulbourn Instruments, Allentown, PA) which were individually housed in light- and sound-attentuating cabinets. The replication of the second-order conditioning study was conducted using 8 behavioural chambers (Med-Associates, Fiarfax, VT) which were individually housed in light-attentuating custom-made cabinets. Each chamber was equipped with a pellet dispenser that delivered 45-mg sucrose pellets into a recessed magazine when activated. Access to the magazine was detected by means of infrared detectors mounted across the opening of the recess. Two light panels (NIDA: differently shaped; Concordia: identical) were located on the right-hand wall of the chamber above and on either side of the magazine. At NIDA the chambers contained a speaker housed within the chambers whereas at Concordia the chambers contained two speakers located outside the testing chamber but inside the housing cabinet. The speakers were connected to a custom-built Arduino device containing wave files of the stimuli used (NIDA: 5Hz clicker, white noise, tone, siren, chime; Concordia: white noise, 4Hz clicker). Stimulus intensity was 72–74 dB. A computer equipped with Coulbourn Instruments GS3 or Med-Associates Med-IVR software controlled the equipment and recorded the responses.

Housing

Rats were housed singly and maintained on a 12-hour light-dark cycle, where behavioral experiments took place during the light cycle at NIDA and during the dark cycle at Concordia. Rats had ad libitum access to food and water unless undergoing behavioral testing, during which they received sufficient chow to maintain them at ~85% of their free-feeding body weight. All experimental procedures conducted at the NIDA-IRP were in accordance with the Institutional Animal Care and Use Committee of the US National Institute of Health guidelines, and those conducted at Concordia University were in accordance were treated in accordance with the approval granted by the Canadian Council on Animal Care and the Concordia University Animal Care Committee.

General behavioral procedures

Trials consisted of 13s visual and 10s auditory cues as described below; visual cues were 3s longer and their onset was 3s prior to auditory cue onset in the blocking part of the study; in the second-order conditioning part of the study the auditory cues preceded the visual cues with auditory cue offset coinciding with visual cue onset. In the second-order conditioning replication study done at Concordia University, the visual and auditory cues were 10s long. These cue arrangements allowed for optogenetic manipulation of the dopamine transient at the start of visual cue A without any interference with the processing of other cues. Trial types were interleaved in miniblocks, with the specific order unique to each rat and counterbalanced across groups. Intertrial intervals varied around a 6 min mean (4–8 min range). All rats were trained between 10am and 8pm. Five auditory stimuli (tone, clicker, white noise for X, Y, Z in blocking; chime and siren (NIDA) or white noise and clicker (Concordia) for C and D in second-order conditioning) and two visual stimuli (flashing light and steady light for A and B) were used. The stimuli were counterbalanced across rats within each modality, and the reward used throughout consisted of two 45mg sucrose pellets (NIDA: no flavour; Concordia: chocolate-flavoured, 5TUT; TestDiet, MO).

Training for the bocking/second-order conditioning within-subjects experiment consisted of six phases: Conditioning, Blocking, Blocking Probe Test, Reminder Training, Second-Order Conditioning, Second-Order Probe Test. These are described below. Training for the second-order replication experiment follows.

Conditioning

Conditioning took place across 12 days (8 untethered days, 4 tethered days) and each day consisted of 14 presentations of A→2US, where a 13s presentation of A was immediately followed by two 45mg sucrose pellets (5TUT; TestDiet, MO). Towards the end of Conditioning (on tethered days 9–12), the rats also received four trials per day of non-reinforced presentations of B. This was done to reduce unconditioned orienting to the novel visual stimulus that would detract from learning on the first few trials of the compound stimulus ¹⁶. Conditioning data were normally distributed (NpHR: for A p = 0.739; for B p = 0.084; eYFP: for A p = 0.984; for B p = 0.118). Responding (Figure 2 and Extended Data Fig 2: Conditioning) to A increased across the first 8 days of conditioning (NpHR: F_1,15 = 65.6, p < 0.005; eYFP: F_1,10 = 94.4, p < 0.005). During the subsequent 4 days of discrimination training, responding was higher for A compared to B (Figure 3 and Extended Data Fig 2: Conditioning NpHR: F_1,15 = 14.9, p = 0.002; eYFP: F_1,10 = 16.3, p < 0.001) but it remained stable (NpHR: F_1,15 = 3.0, p = 0.106; eYFP: F_1,10 = 3.1, p = 0.099) and there was no interaction (NpHR: F_1,15 = 5.2, p = 0.038; eYFP: F_1,10 = 6.6, p < 0.021).

Blocking

Following Conditioning, all rats received four days of Compound Conditioning, that is Blocking. Blocking followed the initial Conditioning phase because it was paramount that the reinforced cue had not been experienced in the absence of reiforcement (as in second-order conditioning) as this could compromise its effectivenss to block learning. During this phase two compounds consisting of the pre-trained cue A and a novel auditory cue, X or Y, and a third compound consisting of the pre-exposed cue B and a novel auditory cue Z were presented. Each compound received six reinforced trials with the same reward (AX→2US; AY→2US; BZ→2US). This yielded two blocking compounds AX, AY, and a control compound, BZ. The presentation of the blocking and blocked cues were offset (see also ¹⁷) such that the 13s visual cues began 3s prior to onset of the 10s auditory cues. On AX trials, continuous laser light (532nm, 18–20mW output, Shanghai Laser & Optics Century Co., Ltd) was delivered into the VTA for 2.5s starting 0.5s prior to the onset of A; on AY trials, the same light pattern was delivered during the intertrial interval, 120–180s after termination of the compound. Data during the blocking phase were normally distributed (NpHR: for AX p = 0.560, for AY p = 0.802, for BZ p = 0.568; eYFP: for AX p = 0.555, for AY p = 0.675, for BZ p = 0.875). During blocking (Figure 3 and Extended Data Fig 2: Blocking), responding to the control compound (BZ) was lower compared to that seen to the blocking compounds (AX and AY) on the first day of training for NpHR (F_1,15 = 12.9, p = 0.003) but not for eYFP (F_1,10 = 2.0, p = 0.19) but was similar on subsequent days (NpHR: D2 F_1,15 = 2.7, p = 0.122; D3 F < 1, p = 0.934; D4 F < 1, p = 0.422; eYFP: D2 F_1,15 = 1.1, p = 0.328; D3_1,10 F = 2.7, p = 0.134; D4 F<1, p = 0.950). Responding to the blocking compounds (AX and AY) did not differ across this phase of training for NpHR (D1 F_1,15 = 1.3, p = 0.272; D2 F < 1, p = 0.918; D3 F < 1, p = 0.703; D4 < 1, p = 0.593) nor eYFP except for D1 (D1 F_1,10 = 5.8, p = 0.037; D2 F < 1, p = 0.702; D3 F_1,10 = 1.3, p = 0.281; D4 F_1,10 = 2.0, p = 0.185). The lack of differences between AX and AY provide evidence that shunting DA firing during the start of A did not disrupt processing of A.

Blocking Probe Test

To confirm learning and determine the effect of inhibition of TH+ neurons in the VTA, rats received a probe test in which each of the auditory cues (X, Y, and Z) was presented four times alone and without reward for a total of 12 trials. Rats received the same probe test again two days afterwards, which allowed for behavioural recovery. The two test sessions were collapsed. Analyses focused on the pooled data from the initial trial in each test. The first trial eliminates any within-session effects of non-rienforcement, which can mask behavioural differences (see also ¹⁸). Data from the test were not all normally distributed (NpHR: for X p = 0.017, for Y p = 0.012, for Z p = 0.441; eYFP: for X p = 0.022, for Y p = 0.244, for Z p = 0.854), therefore the Wilcoxon signed rank test was used to analyze differences between the conditions (see Figure 3 legend in main text). On Test, the rats showed a blocking effect: there was higher level of responding to the control cue (Z) compared to the blocked cues (X and Y) (NpHR: Figure 2, z = 2.22, p = 0.01, effect size r = 0.39; eYFP: Extended Data Fig 2, z = 1.96, p = 0.03, effect size r = 0.42). There was no effect of VTA DA inhibition (i.e., NpHR condition) on blocking as responding to the blocked cues (X vs. Y) did not differ (z =0.05, p = 0.48, effect size r = 0.009). There was also no effect of VTA light stimulation (eYFP condition) as responding to the blocked cues (X vs. Y) did not differ (z = 0.97, p = 0.17, effect size r = 0.206). We also compared the pooled data from all trials for both the NpHR and eYFP groups of rats together. There was no effect of group (F<1, p = 0.573), there was a difference between the control (Z) compared to the blocked cues (X and Y; F_4,2 = 7.6, p = 0.01), but this difference did not interact with group (F<1, p = 0.561), there was no difference between the blocked cues (F < 1, p = 0.850), and no interaction between the blocked cues with group (F < 1, p = 0.430).

Reminder training

Prior to the start of Second-Order Conditioning, all rats received a single reminder session for A, which consisted of re-training of the A→2US contingency across 14 trials as described above. This was done to offset any effects of probe testing without reward at the end of blocking. Magazine responding to the re-trained cue A (Figure 2 and Extended Data Fig 2) was normally distributed (NpHR: p = 0.432; eYFP: p = 0.348) and was found to increase across trials (NpHR: F_1,15 = 38.0, p < 0.001; eYFP: F_1,15 = 25.6, p < 0.001).

Second-Order Conditioning

Following retraining, rats received two sessions of second-order conditioning consisting of six presentations of C and six presentations of D each paired with A (C→A; D→A). No rewards were delivered during this phase. On C→A trials, continuous laser light 532nm, 18–20mW output, Shanghai Laser & Optics Century Co., Ltd) was delivered into the VTA at the start of A in the same manner as that used in Blocking; on D→A trials, the same light pattern was delivered during the intertrial interval, 120–180s after termination of A. Responding during this phase was generally not normally distributed (NpHR: for C p = 0.024; for D p = 0.009; for A(C) p = 0.069; for A(D) p = 0.041; eYFP: for C p = 0.019; for D p = 0.213; for A(C) p < 0.001; for A(D) p = 0.026). Therefore, the Friedman analysis of variance was used to analyze responding during this phase. Responding to C and D (see Figure 2 and Extended Data Fig 2: Second-order training) did not differ across second-order conditioning (NpHR: for D1 χ2(1,31) = 0.6, p = 0.439; for D2 χ2(1,31) = 0.29, p = 0.593; eYFP: for D1 χ2(1,21) = 0.11, p = 0.739; for D2 χ2(1,21) = 1.8, p = 0.180), there was no effect of trials (NpHR: for D1 χ2(2,47) = 0.25, p = 0.883; for D2: χ2(2,47) = 0.5, p = 0.779; eYFP: for D1 χ2(2,20) = 0.45, p = 0.798; for D2: χ2(2,20) = 0.36, p = 0.834) and no differences between C and D on each of the trial blocks (NpHR: for D1 maxχ2(1,31) = 0.82, p = 0.366; for D2 max χ2(1,31) = 0.5, p = 0.480; eYFP: for D1 maxχ2(1,21) = 0.1, p = 0.739; for D2 max χ2(1,21) = 2.0, p = 0.157). Similarly, responding to A following C or D did not differ (NpHR: for D1 χ2(1,31) = 0.29, p = 0.593; for D2 χ2(1,31) = 0.08, p = 0.782; eYFP: for D1 χ2(1,21) = 0.11, p = 0.739; for D2 χ2(1,21) = 0.11, p = 0.739), there was no effect of trials (NpHR: for D1 χ2(2,47) = 0.57, p = 0.752; for D2 χ2(2,47) = 0.37, p = 0.832; eYFP: for D1 χ2(2,32) = 1.09, p = 0.581; for D2 χ2(2,32) = 2.59, p = 0.273), nor any differences on each of the trial blocks (NpHR: for D1 max χ2(1,31) = 2.57, p = 0.109, for D2 max χ2(1,31) = 0.4, p = 0.527; eYFP: for D1 max χ2(1,11) = 0.82, p = 0.366; for D2 max χ2(1,21) = 2.78, p = 0.096). Therefore, responding to A was combined.

Second-Order Probe Test

Following this training, rats received a probe test where cue C and D were each presented six times in the absence of any reinforcement (Figure 2 and Extended Data Fig. 2: Probe Test). Responding during the first trial of the second-order probe test was not normally distributed (NpHR: for C p < 0.001; for D p < 0.001; eYFP: for C p = 0.002; for D p < 0.001), therefore the Wilcoxon signed rank test was used to analyze differences between the conditions (see Figure 2 legend in main text). Responding to C was lower compared to D in NpHR rats (z = 1.9, p = 0.03, effect size r = 0.34), but not in eYFP rats (z = 0.140, p = 0.444, effect size r = 0.03). In addition to analyzing the first trial of test, we also examined responding across the whole test, which confirmed the effects reported on Trial 1. Responding across the entire test was genereally not normally distinbuted (NpHR: for C p = 0.001, for D p = 0.213; eYFP: for C p = 0.030, for D p = 0.003). A Wilcoxon signed rank test confirmed that the difference between C and D persisted across the entire second-order conditioning test for NpHR rat (z = 2.38, p = 0.009, effect size r = 0.421) and the lack of difference for eYFP (z = 0.153, p=0.439, effect size r = 0.033).

As mentioned in the main text, the differential effects of VTA DA shunting during A in second-order conditioning and blocking as well as the lack of a difference in the eYFP rats in the second-order test provide evidence that the disruptive effect of halorhodposin on VTA DA signalling during second-order learning is not due to light artifacts serving to hinder processing of A. If so, then, we would see a disruption of the blocking effect as well (i.e., learning about X). These results support temporal difference accounts by providing causal evidence that cue-evoked dopamine transients function as prediction errors.

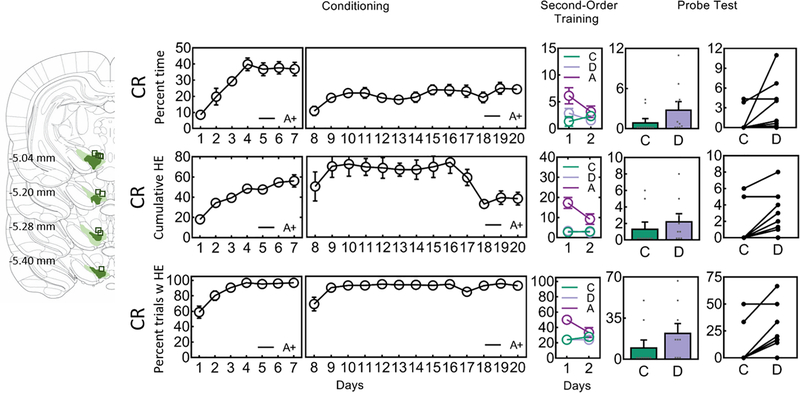
Second-Order replication experiment (Concordia)

Rats received 20 daily conditioning trials between A, a visual cue (flashing light or steady light), and two sucrose pellets (2US) across 17 days. On days 18–20 the rats received 10 A→2US as well as 10 lever→2US conditioning trials. Pavlovian Lever→2US conditioning was done in order to maintain high levels of responding during the subsequent phases of the study. That is, across second-order conditioning and test, 6 daily lever→2US trials were given interleaved with the critical X→A and Y→A second-order conditioning trials and the non-reinforced X and Y test trials. Respodning to the lever is not of interest and therefore was not reported.

Conditioned responding for this experiment was reported using three measures: percent time spent in the magazine during the cue (as described above), cumulative head entries during the cue period across a session, and percent trials with a head entry relative to all trials. Conditioned responding to A was normally distributed for the cumulative head entries measure (Days 1–7 pre-tether: p = 0.473; Days 8–20 post-tether: p = 0.104) and percent trials with a head entry (Days 1–7 pre-tether: p = 0.842; Days 8–20 post-tether: p = 0.112) but not for percent time spent in the magazine (Days 1–7 pre-tether: p = 0.017; Days 8–20 post-tether: p = 0.048). A within-subjects ANOVA revealed a linear trend across days (Cumulative Head Entries: Days 1–7 pre-tether, F_1,9 = 63.78, p < 0.001; Days 8–20 post-tether, F_1,9 = 7.66, p = 0.022; Percent Trials with Head Entries: Days 1–7 pre-tether, F_1,9 = 34.26, p < 0.001; Days 8–20 post-tether, F_1,9 = 7.52, p = 0.023). A Mann-Kendall test for percent time spent in the magazine also reported an increase in responding to A across days (Days 1–7 pre-tether: p < 0.001; Days 8–20 post-tether: p < 0.001).

Second-order conditioning took place during the subsequent two days and was identical to that described above with one exception, the lever continued to be paired with sucrose pellets for a total of six trials distributed amongst the second-order conditioning trials. Responding during this phase (see Extended Data Fig. 3) was normally distributed for all cues using percent trials with a head entry (for C p = 0.140, for D p = 0.198, for A p = 0.406), but not for cumulative head entries (for C p = 0.064, for D p = 0.044, for A p = 0.578), nor for percent time spent in the magazine (for C p < 0.001, for D p < 0.001, for A p = 0.244). A t-test revealed no differences in Percent Trials with Head Entries between C and D (Day 1 t₉ = 0, p = 1.0, Day 2 t₉ = 0.198, p = 0.847). The Wilcoxon signed rank test was used to analyze the cumulative head entries for C and D during this phase (Day 1 z = 0.526, p = 0.599,, Day 2 z = 0.281, p = 0.779). The Friedman analysis of variance was used to analyze percent time spent in the magazine during this phase for C and D. There was no difference between C and D across second-order conditioning (for D1 χ2(1,19) = 0.11, p = 0.739; for D2 χ2(1,19) = 0.14, p = 0.706), there was an effect of trials for Day 1 (χ2(2,29) = 6.08, p = 0.048) but not for D2 χ2(2,29) = 2.77, p = 0.250), and no differences between C and D on each of the trial blocks (for D1 max χ2(1,19) = 0.14, p = 0.706, for D2 max χ2(1,19) = 0.67, p = 0.414). Similarly, responding to A following C or D did not differ across any of the measures on any of the days (Cumulative Head Entries: Day 1 t₉ = 1.116, p = 0.293, Day 2 t₉ = 1.035, p = 0.327; Percent Trials with a Head Entry: Day 1 t₉ = 0.208, p = 0.840, Day 2 t₉ = 0.176, p = 0.864). For percent time spent in the magazine responding to A following C or D did not differ (for D1: F_1,9 < 1, p = 0.378; for D2: F < 1, p = 0.919), there was an effect of trials on Day 1 (F_1,9 = 9.20, p = 0.014) but not on Day 2 (F < 1, p = 0.714), and no interactions (for D1: F < 1, p = 0.542; for D2: F <1, p = 0.704).

Following second-order training, rats received a probe test where cues C and D were each presented six times in the absence of any reinforcement, but in the presence of six reinforced lever trials distributed amongst the C and D nonreinforced trials. Responding during the second-order probe test was generally not normally distributed (Cumulative Head Entries: for C p < 0.001, for D p = 0.106; Percent Trials with Head Entries: for C p < 0.001, for D p = 0.067; Percent Time Spent in Magazine: for C p < 0.001, for D p = 0.012), therefore the Wilcoxon signed rank test was used to analyze differences between the conditions. Responding to C was lower compared to D (Cumulative Head Enties: z = 2.214, p = 0.013, effect size r = 0.50; Percent Trials with Head Entry: z = 2.264, p = 0.012, effect size r = 0.51; Percent Time in Magazine: z = 2.197, p = 0.014, effect size r = 0.49).

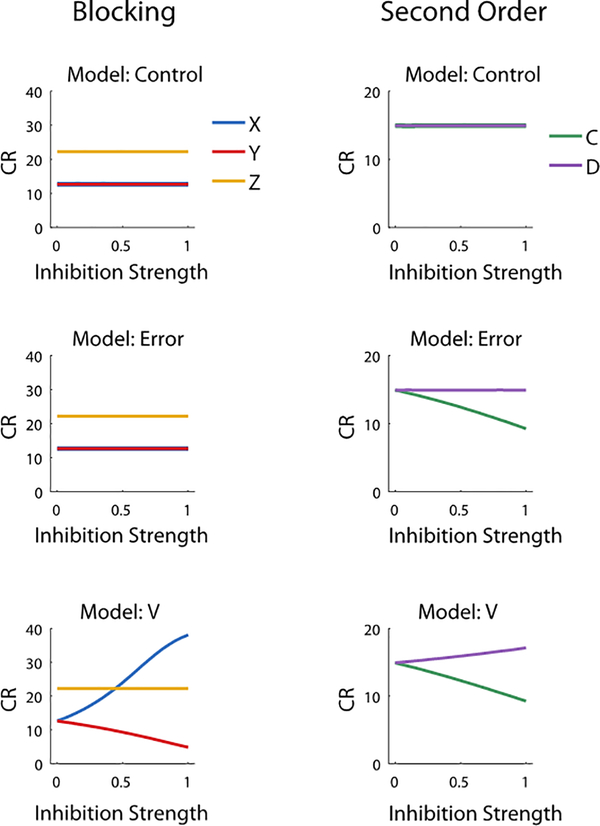
Finally, we carried out additional modelling examining the effect of different strengths of inhibition (0 for no inhibition, 0.5 for partial inhibition, 1 for full inhibition) on learning to the cues in blocking (X, Y, Z) and second-order conditioning (C and D) in each of our models: the prediction model (Model: V), the prediction-error model (Model: Error), and a control for which all η values were zero. These data are captured in Extended Data Fig. 4.

Histology

The rats were euthanized with an overdose of carbon dioxide (NIDA) or a sodium pentobarbitual (Euthanyl, Concordia University) and perfused with phosphate buffered saline (PBS) followed by 4% Paraformaldehyde (Santa Cruz Biotechnology Inc., CA). Fixed brains were cut in 40μm sections, images of these brain slices were acquired and examined under a fluorescence microscope (NIDA: Olympus Microscopy, Japan; Concordia: Carl Zeiss Microscopy, USA). The viral spread and optical fiber placement (see Extended Data Fig. 2 and 3) was verified and later analyzed and graphed using Adobe Photoshop.

Data collection and statistics

Data we collected using Colbourne Instruments or Med-Associates automated software and the text file output was analyzed using a custom-made script in Matlab (Mathworks, Natick, MA) or a custom-made excel macro courtesy of Steve Cabilio (Concordia University). Data from each phase of the experiments were checked for normality using the Shapiro-Wilk test in SPSS. In cases where the data were normally distributed parametric tests were conducted. In cases where the data were not normally distributed non-parametric tests were used. As we tested specific hypotheses based on our modeling results, the directionality of the data were pre-determined. Therefore, we used Analyses of Variance (ANOVA) and planned orthogonal contrasts in PSY2000 for parametric tests, and the Friedman ANOVA, the Wilcoxon signed-rank test and Mann-Kendall test for non-parametric analyses. Non-parametric effect sizes (r) were calculated for the Probe Tests as per ¹⁹. The Grubb’s test was used to check for outliers.

Data availability

Behavioural data will be made available upon request.

Code availability

Simulations were performed using custom-written functions in MATLAB (Mathworks, Natick, MA), which are posted on Github (https://github.com/mphgardner/Basic_Pavlovian_TDRL/tree/Maes_2018).

Extended Data

Extended Data Fig 1.

Experimental design for within-subjects blocking and second-order conditioning as used in our study, along with graphs modeling the predicted results of shunting of the dopamine transient at the start of the reward-predictive cue, A, in each procedure. In Model 1 the VTA DA signal encodes a prediction error and in Model 2 it encodes a reward prediction. Bar graphs are reproduced from Figure 1 in the main text; other panels model results of training in the other phases. Note the output of the classic TDRL model was converted from V to conditioned responding (CR) to better reflect the behavioral output actually measured in our experiments. The major impact of the neural manipulation was on responding to X in Model 2. Elimination of the prediction on AX trials in this model causes a positive prediction error on reward delivery in the blocking phase. This results in unblocking of X.

Extended Data Fig 2.

During Conditioning, responding to A but not B increased across days, and this responding was higher for A compared to B. During Blocking, responding to the control compound (DZ) was lower compared to blocking compound (AX, AY) at the start, but equivalent by the end of training, with no difference between the blocking compounds. Responding during the first trial of the Probe Test showed evidence of blocking (X and Y vs. Z) and no difference between the blocking cues (X vs Y, see Fig 3 legend for statistics). Differences disappeared on subsequent trials. Responding to the retrained cue A increased across reminder (Rmdr) trials while that to C (i.e., C→A trials) and D (i.e., D→A trials) did not differ across second-order training. On Probe Test, responding to C was lower compared to D (see Fig 2 legend for statistics) on the first trial as well as across the entire test. eYFP: The pattern of data obtained for the NpHR rats was similar to that obtained for the eYFP rats with one critical exception: there was no difference between C and D on Probe Test in the eYFP rats. Some data are reproduced from Figures 2 and 3 in the main text. CR or conditioned responding is percent time spent in the magazine during the last 5s of the cue. Drawings to the left illustrate the extent of expression of NpHR and eYFP and location of fiber tips within VTA.

Extended Data Fig 3.

Drawings to the left illustrate the extent of expression of NpHR and location of fiber tips within VTA. The three panels of behavioral responding show behavioral data across the three phases of the second-order conditioning experiment represented using three different CRs (top – percent time spent in the magazine; middle – cumulative head entries during the CS across a single day of training; bottom – percent trials containing a head entry). Behavioral responding during A increased during Conditioning (see online methods for statistics). Responding to C (i.e., C→A trials) and D (i.e., D→A trials) did not differ (see online methods) during second-order training when shunting of VTA transients took place at the start of the reward-predictive cue, A. On Test, responding to C was lower compared to D (see online methods for statistics for each of the CRs), showing that inhibition of the VTA DA signal at the start of A prevented A from supporting second-order conditioning to C whereas identical inhibition during the ITI left learning to D intact.

Extended Data Fig 4.

The modeling data show how different inhibition strength (i.e., η = 0, 0.5, 1 as used in the models, see also Figure S1) affects the predicted conditioned responding on Probe Test across the different models. Model Control represents eYFP controls in which inhibition is not effective. Model Error represents the dopamine signal acting as a prediction-error in which increases in inhibition strength do not affect conditioned responding to X in blocking but lead to reduced conditioned respdoning to the C in second-order conditioning. Model V represents the dopamine signal as prediction in which increases in inhibition strength lead to greater conditioned responding to X in blocking (i.e., unblocking) and reduced conditioned responding to C in second-order conditioning.