Guided transition waves in multistable mechanical metamaterials

Significance

Mimicking material-level phenomena using macroscopically architected materials has gained popularity and enabled novel engineering applications such as photonic, acoustic, mechanical, and topological metamaterials. An interesting microstructural phenomenon observed in phase-transforming materials is the dissipative motion of topological defects such as phase and domain boundaries. With a few one-dimensional exceptions, structural analogs of dynamic phase-transforming materials are still rare, owing to their complicating strong nonlinearity. Through experiments, models, and simulations, we demonstrate a concept for tailoring propagating transition fronts in periodic structures in arbitrary dimensions. This significantly increases the design space of metamaterial performance and functionality and finds application in programming soft robotic locomotion, in controlling energy absorption (or release), and in mechanical logic devices.

Abstract

Transition fronts, moving through solids and fluids in the form of propagating domain or phase boundaries, have recently been mimicked at the structural level in bistable architectures. What has been limited to simple one-dimensional (1D) examples is here cast into a blueprint for higher dimensions, demonstrated through 2D experiments and described by a continuum mechanical model that draws inspiration from phase transition theory in crystalline solids. Unlike materials, the presented structural analogs admit precise control of the transition wave’s direction, shape, and velocity through spatially tailoring the underlying periodic network architecture (locally varying the shape or stiffness of the fundamental building blocks, and exploiting interactions of transition fronts with lattice defects such as point defects and free surfaces). The outcome is a predictable and programmable strongly nonlinear metamaterial motion with potential for, for example, propulsion in soft robotics, morphing surfaces, reconfigurable devices, mechanical logic, and controlled energy absorption.

Mechanical metamaterials have been riding on a (transition) wave in recent decades, transforming the way in which we think of material behavior—no longer as nature-given but rather as tailorable for enhanced performance and functionality in everyday applications (1–3). Testament to this development is the now well-established phononic and acoustic metamaterials to control mechanical waves in unprecedented ways (4) and to facilitate applications such as nonreciprocal transmission (5, 6), cloaking (7), and noise reduction (8–10). Common to all these systems is that they operate in the linear regime and take advantage of spectral gaps in frequency (11), possibly tailorable by finite predeformation such as in bistable systems (12, 13). By contrast, nonlinear dynamic counterparts are still rare, even though they have shown tremendous potential for controlling mechanical signals (14–17) and unraveling unique effects such as unidirectional wave motion (18). The most prominent cause of nonlinearity in those examples is a nonconvex, multiwelled energy landscape, which was shown to support the stable propagation of topological defects (19).

Natural materials systems are rich in propagating transition fronts that separate distinct phases (or domains) through phase (or domain) boundaries. Examples range from temperature- and stress-induced solid–solid phase transformations in crystalline materials (20, 21); to domain wall motion in ferroelectrics, ferromagnetics, and multiferroics (22–24); to deformation twinning in metals and ceramics (25). In each case, a nonconvex potential energy landscape is responsible for the existence of multiple stable equilibrium states (e.g., multiple phases or domains), and the application of external stimuli drives transition fronts between domains. The multiwelled energy landscape renders the resulting system kinetics inherently nonlinear and the associated transition phenomena complex to describe (26, 27) and to imitate in artificial systems. Demonstrated structural analogs so far have been limited to one-dimensional (1D) periodic chains (15, 18); extensions to 2D configurations have been limited to numerical studies of grounded systems with each unit cell attached to a bistable on-site potential (28)—making the resulting architectures immobile and of limited applicability.

In this work, we use a combination of analysis and experiments to demonstrate transition waves in a class of 2D architectures previously employed only for static reconfiguration. Specifically, we focus on monostable unit cells which, when tessellated, form an untethered and ungrounded network in which each unit cell displays multistability. The transition from monostability to bistability emerges from the suppression of rotational rigid-body modes of individual unit cells by the enforcement of periodicity in tessellated networks. We leverage a continuum mechanical model of solid–solid phase transitions to qualitatively and quantitatively describe the observed dynamic effects and to aid in the design process. Then, guided by simulations, we experimentally demonstrate the steering of transition fronts through carefully engineered topological defects (akin to point defects and free surfaces in crystal lattices; Fig. 1). This leads to morphing and reconfigurable structures with not only tailored initial and final configurations but the entire kinetic transformation path—including the wave travel direction, trajectory, and velocity—geared toward a time-dependent deployment history with programmable intermediate states. Besides enabling opportunities for actuated all-soft, substrate-free engineering applications from soft robotics to “4D printing” (29–31), our work also highlights avenues to replicate rich material-level kinetic phenomena at the structural level.

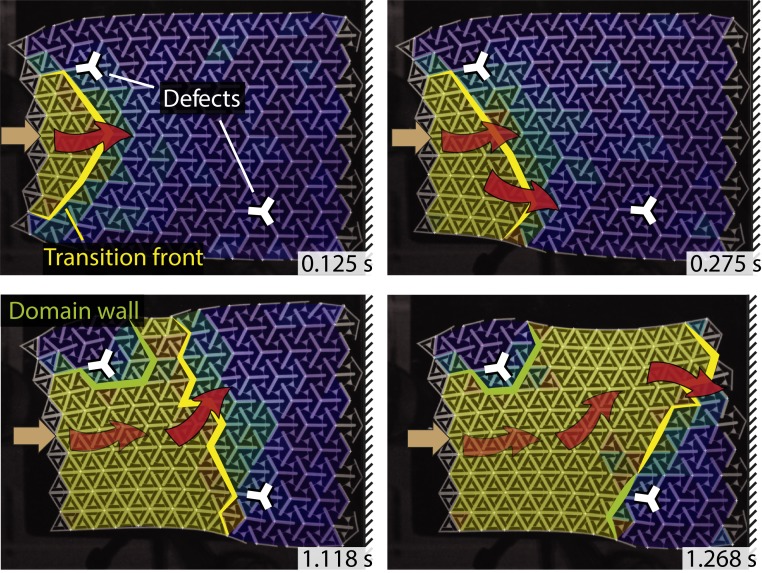
Fig. 1.

Upon initiation by an impulse (orange arrow), a transition front propagates through a 2D periodic multistable network, transforming unit cells from an open (strained) to a closed (unstrained) state as the domain wall passes by. Lattice defects and boundaries can be used effectively to predicatively guide the wave in the laser-cut polymer sheet (the right boundary acts as a rigid wall here).

Multistable Structural Networks

The point of departure is a structural network whose unit cells, once periodically connected, experience two stable configurations: the unstrained ground state and a strained (here, volumetrically expanded) equilibrium state of higher strain energy (Fig. 2). This setup is akin to solid–solid phase transitions and represents our starting point for guiding transition fronts. Multistability is key to achieving topological domain boundaries in the structural network between open (strained) and closed (unstrained) unit cells. The high level of elastic strain energy in partially open or closed unit cells favors the formation of large domains of uniform equilibrium strain, separated by domain boundaries of generally diffuse character and accommodated by transitioning unit cells of high energy (collectively contributing interface energy). Stable static configurations of the structural network are hence minima of its total energy, subject to particular boundary conditions. Upon changes to the loading, domain boundaries move, and transition fronts propagate (Fig. 1 and Movie S1).

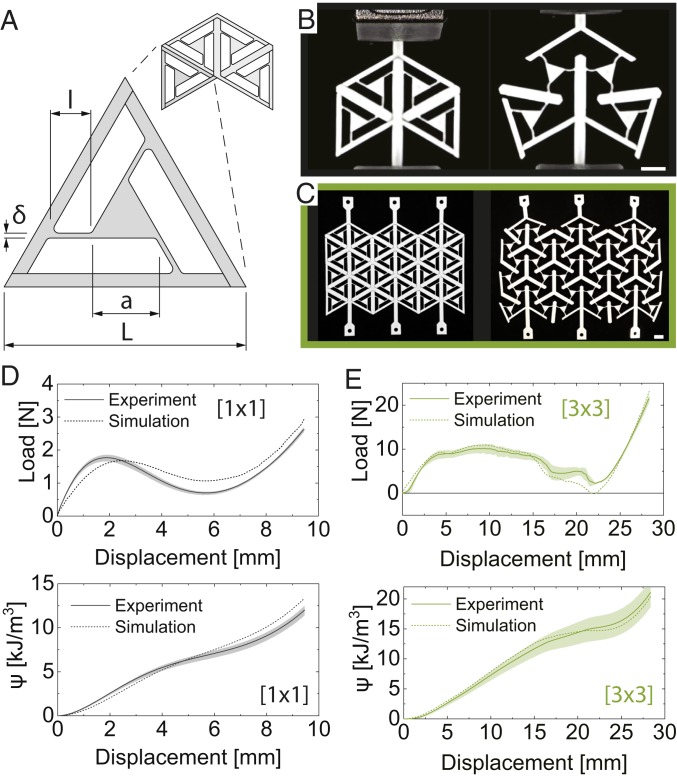
Fig. 2.

Unit cell geometry, tessellation, and response. (A) Geometric parameters defining the unit cell, which consists of four triangular building blocks (material is gray, voids are white). (B) Snapshots of an individual unit cell in the undeformed configuration and loaded by an applied displacement of 9.45 mm. Note that, since a single unit cell is monostable, the structure returns to the undeformed configuration as soon as the clamps used to stretch the structure are removed. (C) Snapshots of a $3\times 3$ unit cell tessellation in the undeformed configuration and in the stable expanded configuration. Since the tessellation is multistable, it remains in the expanded state when the clamps used to stretch it are removed. (Scale bars for B and C, 10 mm.) (D and E) Load–displacement curves and associated potential energy densities $\psi$ (defined by first fitting a fifth-degree polynomial to the measured force–displacement data and then integrating) for (D) a single unit cell and (E) a $3\times 3$ tessellation. Both experimental (continuous line) and finite element results are shown.

As shown in Fig. 2 A and B, the unit cell is based on four triangular building blocks containing slender joints that admit large reversible local rotations, producing auxetic expansion upon loading (32, 33), and pins that stiffen the unit cell in compression (SI Appendix, Fig. S3). Its geometry is defined by the dimensionless ratios $l/L$, $\delta /L$, and $a/L$, where $l$, $\delta$, $a$, and $L$ denote, respectively, the hinge length, hinge thickness, core length, and unit cell size. While variation in these parameters enables control of the energy landscape (33), our experimental prototypes in this study are characterized by $l/L=0.15$, $\delta /L=0.02$, and $a/L=0.3$ (with $L=27$ mm). We find that such unit cells are monostable if free-standing but bistable when tessellated (SI Appendix, Figs. S6 and S7). More specifically, while a free-standing unit cell exhibits a single equilibrium in the undeformed ground state (Fig. 2D), our simulations indicate a bistable behavior for the $3\times 3$ tessellation, as the load vanishes in the expanded state at an applied displacement of ca. 22 mm (Fig. 2E and SI Appendix, Figs. S4–S6; note that experiments record a small positive force in that state, which is attributed to friction in the clamps and the resolution of the load cell). Therefore, as in classical phase transitions (34), the overall sample size of our multistable metamaterials and the particular boundary conditions have an essential impact on the (multi)stability of the network (here demonstrated by the influence of the number of columns and rows per sample; SI Appendix, Fig. S8).

Finally, in addition to free surfaces, the introduction of zeroth-order lattice defects in the form of isolated point defects (modified unit cells) affects the stability as well as the domain nucleation and the domain wall migration within samples (Fig. 2)—the latter being reminiscent of Zener drag on domain walls by point defects (35). As shown in Fig. 1, all such architectural features can be exploited to guide transition fronts of complex shapes and paths.

Continuum Mechanical Model

Having demonstrated the fundamental concept of transition fronts in multistable structural networks (Fig. 1), we introduce a continuum model to describe and efficiently simulate the domain formation and growth processes. The model will be used for the exploration of the design space of 1D, 2D, and 3D transition waves with and without defects.

Leveraging the analogy to solid–solid phase transitions (20, 36, 37), we borrow from continuum mechanics to describe the observed domain kinetics by a simple analytical model, based on the observations that 1) each unit cell has two energy-minimizing strain states, 2) inertial effects of the thin structure and ground friction play a negligible role, and 3) the lossy base material leads to viscous dissipation during deformation. As in classical homogenization, we consider a separation of scales between the unit cell size $L$ and the overall sample dimensions, so that the sample deformation can be described by a continuous displacement field $\mathit{u}\left(\mathit{x},t\right)$ at a location $\mathit{x}$ at time $t$. Assuming linearized kinematics, the strain tensor follows as $\mathit{\epsilon }=sym\left(\nabla \mathit{u}\right)$. Acknowledging that the bistability is linked to volumetric straining (in $d$ dimensions), we decompose the strains into the scalar volumetric strain $\theta =tr\mathit{\epsilon }/d$ and the deviatoric (volume-preserving) strain tensor $\mathit{e}=\mathit{\epsilon }-\theta \mathit{I}$. Based on this kinematic description and the above constitutive observations, we postulate an isotropic elastic energy density $W\left(\mathit{\epsilon }\right)=\psi \left(\theta \right)+\mu \hspace{0.17em}\mathit{\epsilon }\cdot \mathit{\epsilon }$, where $\psi \left(\cdot \right)$ denotes the bistable energy landscape identified from the volumetric straining of the unit cell (SI Appendix, Fig. S9), and $\mu >0$ acts as an effective shear modulus penalizing strain variations between unit cells (hence contributing energy in the interfaces between domains). $\psi$ is chosen as a quartic polynomial to approximate the bistable energy obtained from finite element analysis (FEA) and calibrated by experiments, whereas $\mu$ is identified by homogenization of the discrete unit cell energy (SI Appendix, section 3).

Following the Coleman–Noll procedure of continuum mechanics, this energy density defines the elastic stress tensor as ${\mathit{\sigma }}_e=\partial W/\partial \mathit{\epsilon }$. To account for material-intrinsic damping, we decompose the total stress tensor into elastic and viscous contributions, that is,

$$\mathit{\sigma }={\mathit{\sigma }}_e+{\mathit{\sigma }}_v=\frac{\partial W}{\partial \mathit{\epsilon }}+\eta \hspace{0.17em}\stackrel{\cdot }{\mathit{\epsilon }}=\eta \hspace{0.17em}\stackrel{\cdot }{\mathit{\epsilon }}+\frac{\psi \prime \left(\theta \right)}{d}\mathit{I}+\mu \hspace{0.17em}\mathit{e},$$ [1]

where $\eta >0$ represents a Newtonian viscosity, and dots denote partial derivatives with respect to time. The point-wise equation of motion for the mechanical system, linear momentum balance in the absence of inertial effects and body forces (gravity acting perpendicular to the plane), becomes

$$\nabla \cdot \mathit{\sigma }=0\iff \eta \hspace{0.17em}\nabla \cdot \stackrel{\cdot }{\mathit{\epsilon }}+\frac{{\psi }^{″}\left(\theta \right)}{d^2}\nabla \theta +\mu \hspace{0.17em}\nabla \cdot \mathit{e}=0.$$ [2]

When discreteness effects can be neglected, Eq. 2 describes the mechanics of the multistable network at the continuum level (in principle, in arbitrary dimensions $d$), which is solved numerically for the displacement field $\mathit{u}\left(\mathit{x},t\right)$, using a finite element spatial discretization and implicit time integration. Simulations start from a fully stretched equilibrium configuration and predict the time evolution upon applied loading—leading to a transition wave that reconfigures the structure into its collapsed equilibrium state. The only calibration parameter, $\eta$, is chosen by direct comparison of transition wave speeds obtained from this continuum model and experiments of uniaxial (1D) transition waves (Fig. 3).

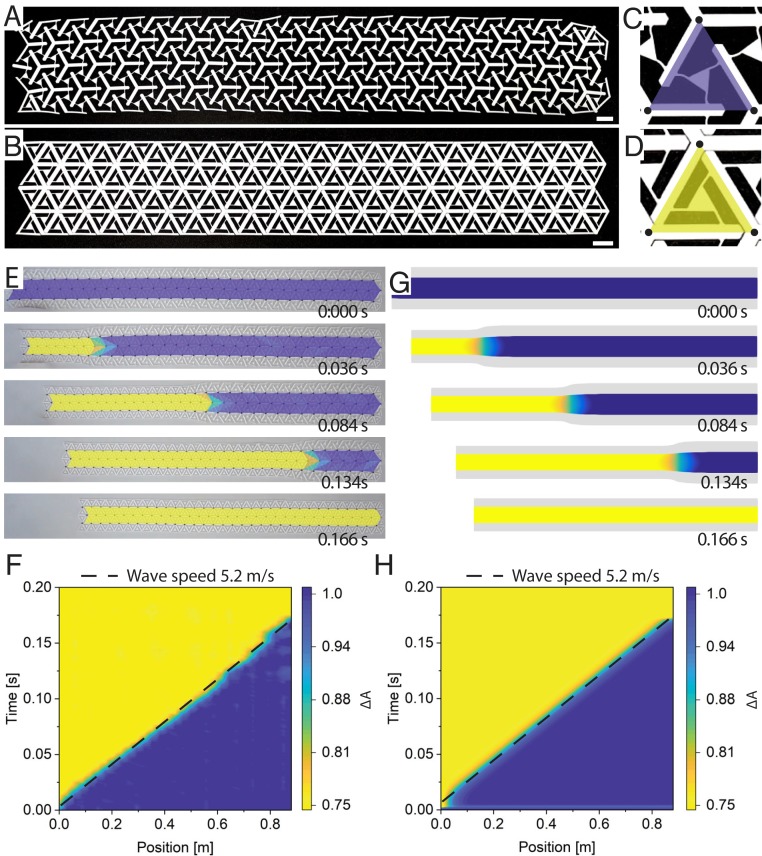
Fig. 3.

The 1D transition waves. (A and B) Tessellations of bistable unit cells in their (A) open and (B) closed equilibrium states. (Scale bars, 20 mm.) (C and D) A color map shows the relative change in unit cell area, here indicating closed as blue and open as yellow. (E) Upon initiation from the left, a 1D transition wave travels through the structure, whose (F) $x$–$t$ diagram confirms the approximately constant wave speed. (G) The transition front motion is reproduced by the continuum model in agreement with the experiment, also seen in (H) the $x$–$t$ diagram.

Uniaxial Transition Waves

Long and slender chains comprising $32\times 2$ unit cells are initialized in their stretched equilibrium state (Fig. 3A) and compressed by a gradually increasing indenter force until a transition wave is triggered and subsequently propagates through the chain (Movie S2). The experimental snapshots in Fig. 3E confirm that a phase boundary propagates through the 1D body, gradually transforming unit cells from the open (high-energy) to the closed (low-energy) equilibrium state. To quantify this transition, we use the relative change in area,

$$\mathrm{\Delta }A=\left|\frac{A}{A_0}\right|,$$ [3]

as a continuous metric for phase identification (with $A$ and $A_0$ denoting the measured current and initial unit cell size, respectively). The average wave speed measures 5.2 m/s, requiring 0.166 s to traverse the entire chain (a constant speed is reached within the first unit cell, after the decay of transient effects due to the initiation). Interestingly, defective unit cells (as seen, e.g., in the upper boundary region of Fig. 3A) show a vanishing impact on the propagating transition wave, demonstrating the robustness of the system against fabrication-induced imperfections.

Importantly, results obtained from describing the 1D chain dynamics by the above continuum model (Fig. 3 G and H) reveal convincing agreement with experiments, for example, comparing the measured and simulated wave profiles at time stamps 0.036, 0.094, 0.134, and at 0.166 s, confirming the applicability of the chosen linear kinetics and of the continuum description (Movie S2). Simulations yield a constant wave speed (and hence constant slope in the $x$–$t$ diagram, Fig. 3H) after the decay of transient effects, while disturbances in experimental data (Fig. 3G) are attributed to fabrication imperfections and unavoidable frictional losses. It is remarkable that the wave speed shows little dependence of the triggering impulse (as long as it is sufficient to induce the transition front). Similar to grounded 1D chains (19), the constant speed is the result of a balance between energy release from transforming unit cells, on the one hand, and energy consumption due to viscous losses and kinetic energy of the growing tail end of the chain undergoing rigid-body motion, on the other hand (the latter being of minor importance here due to negligible inertial effects).

Controlling Transition Waves by Defects in Two Dimensions

Assembling unit cells into multistable 2D structures adds more than an additional dimension: Analogous to domain wall interactions with lattice defects in crystalline solids, the introduction of point and line defects in two dimensions provides opportunities for complex transition front guidance (SI Appendix, Fig. S10). Contrary to topological defects utilized to facilitate localized soft modes in a structure (38, 39), we here introduce stiff defects (akin to, e.g., precipitates or solute atoms in a crystal) that locally interact with—and thereby pin or redirect—the propagating transition front (see SI Appendix, Fig. S10 for details of the induced defects). Similarly, boundaries (such as stress-free surfaces; SI Appendix, Figs. S11 and S12) interact with the transition front and locally alter the propagation speed, thus affecting the front profile and shape.

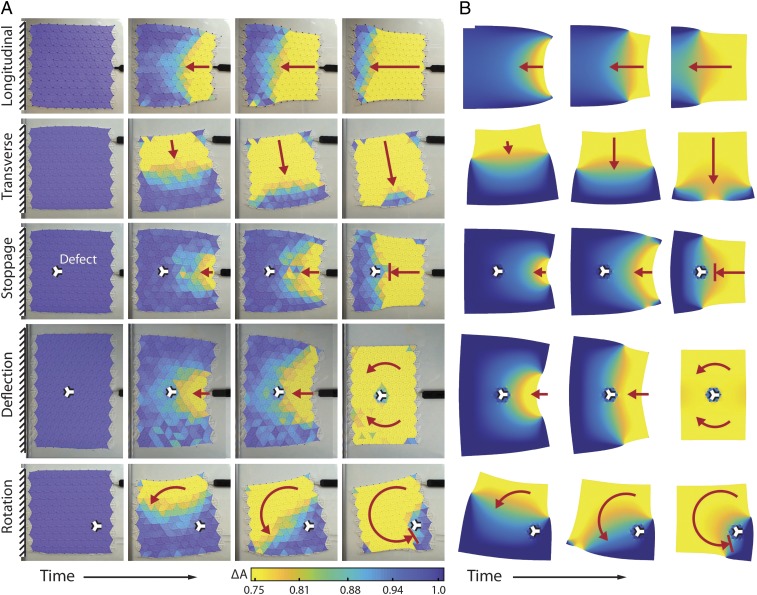
Fig. 4 illustrates five examples of propagating transition fronts (comparing experiments and simulations for each; Movie S3), demonstrating the influence of defects and boundary conditions on the path of the transition wave. When the 2D body is indented symmetrically by a point load (Fig. 4A, row 1), a 1D front propagates, here showing edge effects that arise from the free boundaries and producing a convex shaped front. By contrast, when initiating the wave asymmetrically, for example, by an eccentric point load (Fig. 4A, row 2), a wave is generated in the transverse direction with a concave front, ultimately propagating orthogonally to the direction of initiation.

Fig. 4.

The 2D transition waves. (A) Experimental observations of transition waves propagating through 2D structures (after initialization in the fully open configuration, each transition wave is triggered by a point load applied by the black indenter). Waves are controlled by boundary conditions (e.g., boundary application sites) as well as by defects (e.g., point defects realized by nontransforming open unit cells). Examples show free transition wave propagation in two directions, wave pinning, wave deflection, and rotation. (B) Numerical results obtained from the continuum model are in good agreement with experimental findings (differences stemming mainly from imperfections and size effects).

Stiff point defects (namely, open unit cells of the same size but constrained to not collapse under load) interact with propagating transition fronts by local pinning in the bulk of the structure. For example, when adding a defect at the center of a symmetric structure, the transition front is locally deflected and travels around the defect (Fig. 4A, row 4). If the sample is sufficiently small (Fig. 4A, row 3), the front may also be fully arrested due to the large driving force required to unpin the wave [akin to, e.g., the inverse scaling of the strength of Zener pinning (35) with the distance between two defects]. Deliberately tailoring defect locations, in combination with free boundaries, can hence be exploited to guide transition fronts in a complex fashion. Repeating, for example, the scenario of Fig. 4A, row 2, but with a point defect in the bottom right corner, results in a transition front that propagates around the defect (Fig. 4A, row 5).

Fig. 4B summarizes analogous simulation results for those five cases and demonstrates the power of the continuum model toward predicting transition fronts. Of course, differences between experiments and simulations are expected due to, for example, fabrication imperfections, imperfect boundary conditions, and size effects. Considering the relatively small size of samples and the large ratio of unit cell to sample size (whereas the model assumes a separation of scales), it is remarkable that the simple model captures the qualitative transition front behavior well—thus offering predictive support in the design of tailored configurations for guided transition fronts.

Expansion of the Design Space

Having demonstrated the general feasibility of the approach and the agreement between model predictions and measurements through the above prototype experiments, we use the continuum model (and its finite element implementation) to explore the design space beyond the limitations of current fabrication constraints (Movie S4).

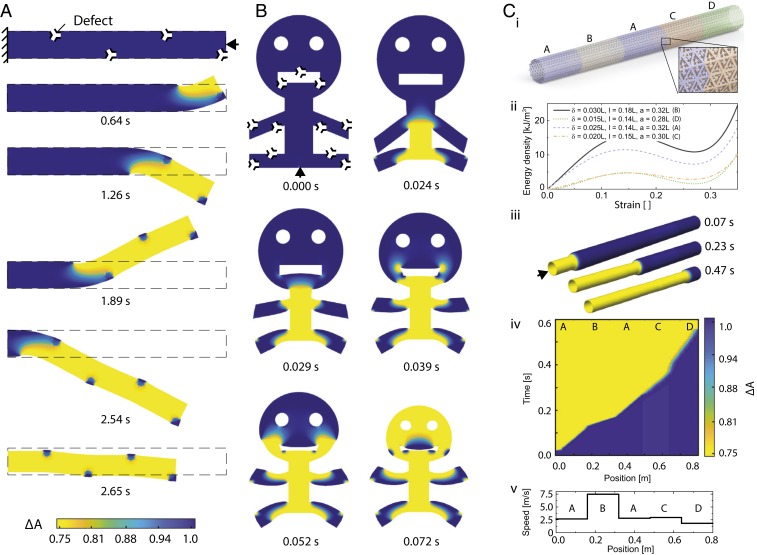
We start by considering a slender structure with point defects alternating on opposite surfaces (Fig. 5A). An impulse applied to the right end of the sample (the left end is kept fixed) excites a wave that propagates at constant speed and amplitude between defects. However, the locally circular motion around each defect collectively results in a snake-like motion of the overall structure, suggesting opportunities for utilization in soft robotic motion.

Fig. 5.

The 3D waves and expansion of the design space. (A) By combining the effects of point defects and free surfaces, a transition fronts is designed to produce an alternating serpentine motion with potential for locomotion of soft robots. (B) Combining point defects with complex shapes having interior and exterior surfaces adds functionality such as splitting and merging of waves, resulting in reconfigurable devices. (C) Forming a 2D multistable sheet into a 3D structure: (i) hollow tube made of a multistable sheet; (ii) four different unit cell geometries produce four distinct energy landscapes, which correspond to four different wave speeds; (iii) simulated wave propagation at different time steps; (iv and v) quantifying the wave speed along a tube made of five sections with the above energy landscapes shows a wave that adjusts its speed in each section. The colormap shows the relative change in unit cell area; see Eq. 3.

Next, to achieve functional shape morphing, we combine multiple point defects with a more complex sample shape with internal and external free boundaries. Fig. 5B visualizes an example whose defect and boundary arrangement leads to wave splitting and merging as well as to overall shape changes, from a sitting figure with a neutral face and hanging arms to a standing one with a smiley face and upward arms. Once the transition is initiated by an impulse at the bottom center, the front propagates vertically and splits into three waves deforming the legs and torso, then again splitting into three waves to deform the arms, and, finally, reaching and reconfiguring the head shape and facial expression (the redirection around the mouth being of similar nature as the circular motion around point defects shown previously).

Finally, we study a 3D architecture capable of supporting transition waves, created by shaping 2D multistable sheets into 3D surfaces without altering the essential transition behavior or kinetics discussed in two dimensions (2D). Fig. 5C shows a reconfigurable circular pipe created by rolling a multistable sheet (based on the unit cell of Fig. 3) into a hollow tube. To control the wave speed along the tube, we divide it into five sections and modify the unit cell geometry in each of those. Remarkably, we find that the front seamlessly propagates from section to section, rapidly changing its speed within approximately a single unit cell when entering a new section. This is confirmed by the numerically measured speed profile (Fig. 5 C, v) with velocities ranging from 1.8 m/s to 7.45 m/s (a difference of $>300$%).

Summary and Conclusion

To summarize, we have demonstrated, via a combination of theory, simulations, and experiments, that periodically bistable networks show structural phase transition fronts that propagate with many of the characteristics classically known from crystalline solids, including the interaction mechanisms with lattice defects. Homogeneous networks resulted in constant-speed transition fronts (emerging from the balance between energy dissipation by damping and release of stored mechanical energy), whereas the presence of defects was shown to redirect or pin transition waves, as well as to split, delay, or merge propagating wave fronts. Unlike their crystalline counterparts, the presented structures allow for full control of the network architecture (and an efficient performance prediction through the presented continuum mechanical model), and are thus amenable to tailored wave motion and optimized reconfiguration kinetics. We further note that the behavior of the networks is robust and minimally affected by imperfections introduced during either fabrication or testing, such as broken ligaments. Like all mechanical analogs, the presented metamaterial features some but certainly not all aspects of phase transformations in solids, excluding, for example, statistical effects such as those arising from finite temperature. Admittedly, transition waves in the shown examples are one-time effects without automatic resetting; however, unlike in previous approaches (15, 18), each structural network is easily reset by applying mechanical loads to expand all unit cells—a task that can be realized, for example, using pneumatic actuators.

The multistable structures presented here serve as representative examples of the more general concept of employing structural transition fronts for guided motion and reconfiguration in arbitrary dimensions and of arbitrary complexity. The same principles (and the same model) apply to 3D unit cells, which widens the untapped design space. Moreover, graded networks of spatially changing unit cells promise local wave speed modulation, which is of interest, for example, for mechanical logic (15, 40, 41), 4D printing (29–31), and morphing surfaces and reconfigurable devices (42–44). The simple yet powerful link between multistable energy landscape and resulting wave speed provides fruitful grounds to engage in extending concepts classically used for linear waves—such as transformation optics for wave focusing (45, 46)—to the strongly nonlinear transition front motion reported here.

Materials and Methods

Details of the materials and fabrication methods are summarized in SI Appendix, section 1. The experimental procedures, including the uniaxial tensile tests, microscopy, and analysis of planar waves, are described in SI Appendix, section 2. FEA procedures, continuum model, and numerical implementations are detailed in SI Appendix, section 3.

Data Availability

The data that support the findings of this study are openly available in Figshare under https://doi.org/10.6084/m9.figshare.10048724.