Far-field midinfrared superresolution imaging and spectroscopy of single high aspect ratio gold nanowires

Significance

Traditional optical microscopy methods are limited by diffraction. This makes it hard to image and study nanostructures in the midinfrared, a relatively unexplored spectral region of chemical significance. Here we use infrared (IR) photothermal heterodyne imaging (IR-PHI), a far-field superresolution optical technique, to study the Fabry–Pérot resonances of single gold nanowires in the 2,800 to 4,000-cm⁻¹ region. Because the spatial resolution of IR-PHI is on the order of a few hundred nanometers, we are able to directly resolve the structure of the Fabry–Pérot resonances and assign the mode order. This cannot be done with traditional optical measurements. IR absorption spectra recorded using IR-PHI show narrow linewidths, in several cases below the limit imposed by Au’s Drude relaxation parameter.

Abstract

Limited approaches exist for imaging and recording spectra of individual nanostructures in the midinfrared region. Here we use infrared photothermal heterodyne imaging (IR-PHI) to interrogate single, high aspect ratio Au nanowires (NWs). Spectra recorded between 2,800 and 4,000 cm⁻¹ for 2.5–3.9-μm-long NWs reveal a series of resonances due to the Fabry–Pérot modes of the NWs. Crucially, IR-PHI images show structure that reflects the spatial distribution of the NW absorption, and allow the resonances to be assigned to the m = 3 and m = 4 Fabry–Pérot modes. This far-field optical measurement has been used to image the mode structure of plasmon resonances in metal nanostructures, and is made possible by the superresolution capabilities of IR-PHI. The linewidths in the NW spectra range from 35 to 75 meV and, in several cases, are significantly below the limiting values predicted by the bulk Au Drude damping parameter. These linewidths imply long dephasing times, and are attributed to reduction in both radiation damping and resistive heating effects in the NWs. Compared to previous imaging studies of NW Fabry–Pérot modes using electron microscopy or near-field optical scanning techniques, IR-PHI experiments are performed under ambient conditions, enabling detailed studies of how the environment affects mid-IR plasmons.

Plasmonic materials have uses in a wide range of applications, such as photovoltaics, the generation of solar fuels, and chemical sensing (1–4). Key properties of plasmonic structures are the ability to confine light to subwavelength dimensions, along with related enhancements of local electromagnetic fields (2). Conventional plasmonic materials have resonances in the near-infrared (near-IR) to visible regions of the spectrum (5, 6). While this is useful for solar energy conversion, there are important applications in other parts of the spectrum as well. Thus, realization of the full potential of plasmonics requires exploring new materials and geometries, which enable access to unexplored spectral regions such as the midinfrared (mid-IR) (7–10) or the near-UV (11, 12). In particular, mid-IR plasmonic materials open the door to ultrasensitive, label-free chemical sensing via surface-enhanced IR absorption (SEIRA) spectroscopy (9).

A variety of different systems have been developed for mid-IR plasmonics, including metal nanostructures (7–10), and doped metal-oxide and metal-chalcogenide semiconductor nanocrystals (13–17). Single-particle spectroscopy measurements have shown that mid-IR plasmonic materials possess narrow linewidths, which implies long plasmon lifetimes (18–20). This is surprising, as the structures for mid-IR plasmonics are usually large, with sizes where conventional near-IR/visible plasmonic resonators suffer severe radiation damping (21–23). Here we examine the “Fabry–Pérot”-type resonances of single noble-metal nanowires (NWs) (24–32). The frequencies of these resonances have been extensively studied by ensemble measurement (24–26, 28, 29). However, ensemble measurements do not provide reliable linewidth information (21–23). Studies of individual NWs in the mid-IR have been performed with electron energy loss spectroscopy (EELS) and cathodoluminescence experiments (10, 19, 31–34), as well as through direct optical extinction (18). However, there is still a need for systematic studies of the size- and environmental dependencies of mid-IR NW plasmon linewidths.

The lack of linewidth information for mid-IR plasmonic materials is due, in part, to the difficulty of performing single-particle experiments in this spectral region. Techniques in addition to EELS and cathodoluminescence capable of imaging and detecting single nanostructures in the mid-IR include near-field optical microscopy measurements (20, 35–40) and atomic force microscopy-detected IR absorption (41, 42). However, these techniques are experimentally complex and difficult to perform in different environments. In this paper, the mid-IR Fabry–Pérot resonances of single gold NWs are examined using IR photothermal heterodyne imaging (IR-PHI)––a superresolution, far-field optical imaging and spectroscopy technique (43–45). Compared to the methods listed above, IR-PHI is a simple tabletop approach for characterizing the mid-IR properties of individual nanostructures, that can operate under ambient conditions. The spectral resolution of IR-PHI is also much better than that of EELS measurements––a few cm⁻¹ compared to tens of cm⁻¹ (46–48). The mid-IR spectra of individual gold NWs are measured for NW lengths between 2.5 and 3.8 μm. Spatial maps of the mid-IR plasmon modes are also recorded. These maps, which are only possible due to the superresolution capabilities of IR-PHI (43–45), allow an unambiguous assignment of the mode order of the Fabry–Pérot resonances probed in the measurements. The results of the experiments are compared to finite-element simulations that describe both the absorption spectra and the IR-PHI images.

Results and Discussion

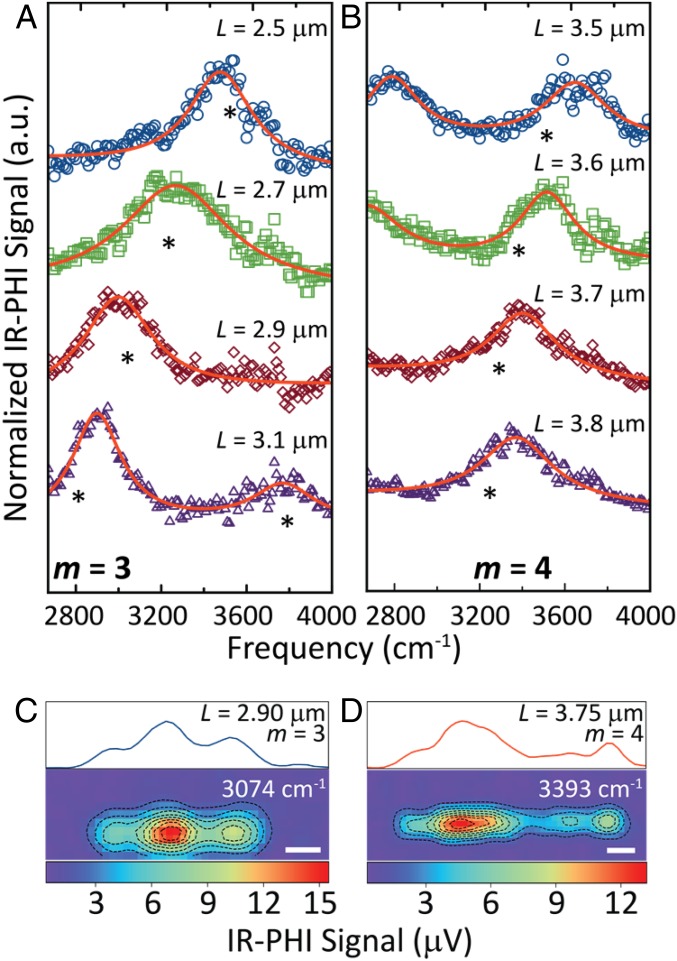
IR absorption spectra for single NWs with lengths (L) between 2.50 and 3.80 μm are presented in Fig. 1. The NWs in this study were created by nanofabrication, and were designed to be 50 nm high and 100 nm wide, with lengths ranging from 1.00 to 9.95 μm in 0.05-μm steps. Fig. 1A shows spectra for L = 2.50–3.10-μm NWs, and Fig. 1B shows spectra for L = 3.50–3.80-μm NWs. The resonance frequencies red-shift with increasing length from 3,670 to 2,880 cm⁻¹ in Fig. 1A, and from 3,650 to 3,360 cm⁻¹ in Fig. 1B. The shift in the resonances to progressively lower frequencies as L increases is expected for NW Fabry–Pérot modes (24–32). Specifically, a simple expression for NW Fabry–Pérot resonance frequencies ${\nu }_{\text{res}}$ is (26, 30, 31, 49, 50)

$${\nu }_{\text{res}}=\frac{c_0}{2n_{\text{eff}}}\frac{m}{L},$$ [1]

where $n_{\text{eff}}$ is an effective index for the mode, $c_0$ is the speed of light, and m is the mode order. Eq. 1 is derived by considering the interference between forward and backward propagating SPPs in the NW (26, 30, 49). In this picture $n_{\text{eff}}$ is related to the phase velocity of the surface plasmon polariton (SPP) modes: $c_{SPP}=c_0/n_{\text{eff}}$. For metal NWs on a surface $n_{\text{eff}}$ can be estimated from finite-element method (FEM) simulations using a two-dimension mode analysis calculation. These calculations yield a value of $n_{\text{eff}}$ of 1.63 for NWs excited by light with a free-space wavelength of 3 μm (the middle of the spectral range investigated in this paper). The observation of two resonances in the L = 3.10-μm and L = 3.50-μm spectra suggests that two Fabry–Pérot modes are present with different mode orders, with the higher-frequency mode being the one tracked in Fig. 1B (26, 51).

Fig. 1.

(A and B) IR-PHI spectra of individual Au NWs with lengths L = 2.50–3.80 μm. Asterisks denote positions of the (A) m = 3 and (B) m = 4 resonances from Eq. 1. Solid red lines are Lorentzian fits to the data. (C and D) False-color IR absorption maps obtained at 3,074 and 3,393 cm⁻¹ for Au NWs with lengths of L = 2.90 and 3.75 μm, respectively. Averaged line profiles are presented above each IR absorption map. (Scale bars, 0.5 μm.)

To investigate the order of the modes excited in Fig. 1 A and B, IR absorption images are acquired. Because the spatial resolution of IR-PHI is dictated by the visible probe wavelength (43, 44), this technique can in principle resolve the mode structure of mid-IR Fabry–Pérot resonances. Representative IR absorption images of the Fabry–Pérot modes corresponding to the resonances in Fig. 1 A and B are presented in Fig. 1 C and D, respectively. Fig. 1C shows an image of an L = 2.90-μm NW that exhibits three lobes across the nanostructure. Fig. 1D is an image for an L = 3.75-μm NW that has a more complex structure, consistent with this resonance arising from a higher-order Fabry–Pérot mode. The IR-PHI images reflect the spatial distribution of the absorbed IR light and, thus, report on the interference pattern of the Fabry–Pérot mode excited in the experiments (43, 44). Finite-element simulations (vide infra) show that m = 3 Fabry–Pérot absorption maps have a three-lobe structure that is similar to that observed in Fig. 1C. Therefore, this resonance, and the resonances tracked in Fig. 1A for the L = 2.50–3.10-μm NWs, are assigned to m = 3 Fabry–Pérot modes.

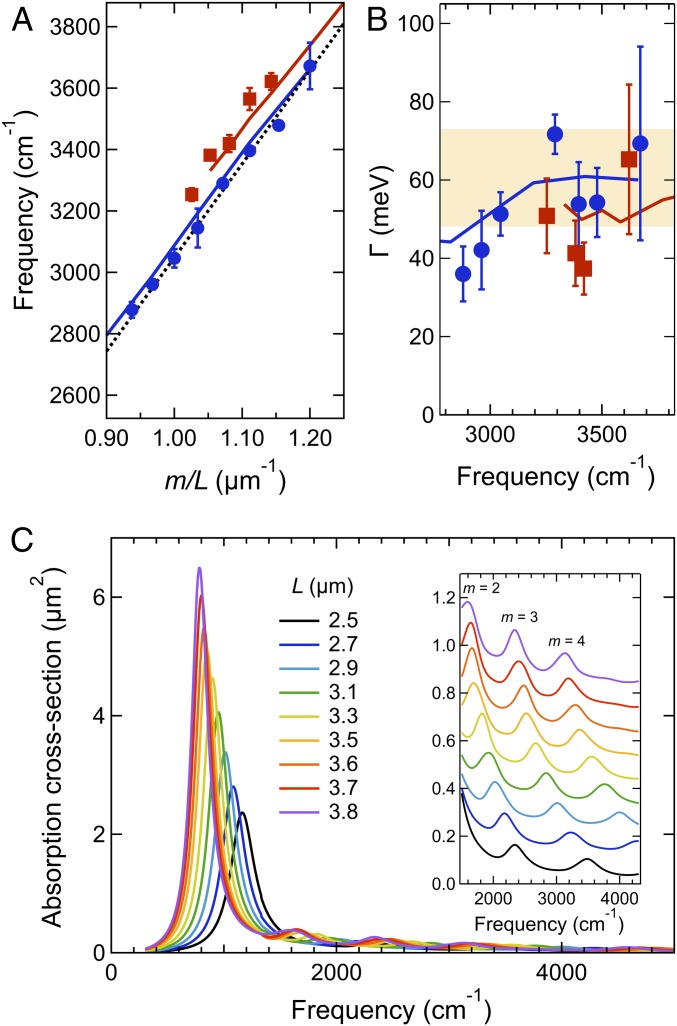
Fig. 2A shows the resonance frequencies for the NWs versus $m/L$, which is proportional to the plasmon wavevector. In Fig. 2B the linewidths $\left(\text{Γ}\right)$ determined from Lorentzian fits to the spectra (solid red lines in Fig. 1 A and B) are plotted versus resonance frequency. Error bars represent SDs from at least three measurements on nominally identical NWs. The dashed black line in Fig. 2A is a fit to the m = 3 Fabry–Pérot mode data using Eq. 1. This fit gives a value of $n_{\text{eff}}=1.64$. This value is consistent with the estimate of $n_{\text{eff}}$ from the mode analysis calculations, and also with previous studies of the dispersion of Fabry–Pérot modes of metal NWs (25, 26, 31, 49). The good agreement between calculated and measured frequencies shows that Eq. 1 is a reasonable description of the mid-IR plasmon resonances of the Au NWs. Using the value of $n_{\text{eff}}$ determined from the m = 3 Fabry–Pérot mode data allows us to assign the resonances tracked in Fig. 1B to the m = 4 Fabry–Pérot modes. Note that under normal incidence excitation only odd-order modes (m = 1, 3, 5, …) are expected to be observed in absorption due to parity (26, 30, 49). However, even-order modes can be detected when the NWs are excited using nonnormal incident light (26, 30, 49). In our experiments, the 0.65-numerical aperture (N.A.) Cassegrain objective used to focus the IR pump beam creates a range of excitation angles, allowing the excitation of both the odd- and even-order modes (26, 30, 49).

Fig. 2.

(A) Resonance frequencies as a function of inverse length times mode order $\left(m/L\right)$ and (B) average linewidths $\left(\mathrm{\Gamma }\right)$ versus frequency for the m = 3 (blue circles) and m = 4 (red squares) Fabry–Pérot resonances of the gold NWs. Data collected from at least three NWs with error bars representing SDs. The dashed black line in A shows the frequencies calculated from Eq. 1. The shaded area in B shows the range of values for the Drude relaxation parameter for Au (55, 56). The solid red and blue lines in A and B are the results from the 3D FEM simulations. (C) Spectra for different length NWs calculated from FEM simulations. The lowest-frequency features are the m = 1 Fabry–Pérot resonances. (Inset) An expanded view of the higher-energy m = 2, 3, and 4 resonances (the spectra have been offset for clarity).

Three-dimensional FEM simulations were used to calculate Au NW IR absorption spectra. In these simulations the NWs were modeled as having rectangular cross-sections with a 100-nm width and 50-nm height on a glass substrate. Calculated spectra are presented in Fig. 2C and are dominated by the m = 1 Fabry–Pérot mode. Fig. 2C (Inset) shows an expanded view of the higher-frequency region, where the m = 2, 3, and 4 resonances are more clearly observed. The calculated resonance frequencies for the m = 3 and m = 4 Fabry–Pérot modes are plotted versus $m/L$ in Fig. 2A as the solid blue and red lines, respectively. In the simulations the dielectric constant of the substrate ${\mathit{ϵ}}_{sub}$ was adjusted so that the calculated and measured frequencies match for the m = 3 mode of the L = 2.50-μm NWs. Simulations were then performed for a range of NW lengths using this value of ${\mathit{ϵ}}_{sub}$. The calculated frequencies are in excellent agreement with the experimental measurements for both the m = 3 and m = 4 modes over the full range of lengths, confirming our assignment of the mode order and validating the calculations. The value of the substrate dielectric constant obtained from the fitting procedure $\left({\mathit{ϵ}}_{sub}=2.45\right)$ is slightly larger than the experimental dielectric constants of glass in the mid-IR. This is attributed to differences in the exact shape of the NWs in the experiments and simulations (the mode frequencies are sensitive to the aspect ratio of the NWs).

A major attribute of the single-particle spectra in Fig. 1 is that they provide meaningful information about plasmon linewidths $\left(\text{Γ}\right)$. $\text{Γ}$-values in Fig. 2B range from 35 to 70 meV, which correspond to plasmon dephasing times $T_2=2\overline{h}/\text{Γ}$ between 40 and 20 fs, respectively (52). In the absence of radiation damping, the linewidths for the localized surface plasmon resonances of metal nanostructures can be estimated using (53, 54)

$$\mathrm{\Gamma }=\frac{2{\mathit{ϵ}}_2}{\sqrt{{\left(\partial {\mathit{ϵ}}_1/\partial \omega \right)}^2+{\left(\partial {\mathit{ϵ}}_2/\partial \omega \right)}^2}},$$ [2]

where ${\mathit{ϵ}}_1$ and ${\mathit{ϵ}}_2$ are the real and imaginary parts of the metal bulk dielectric constant, respectively. In the mid-IR, the dielectric constants of noble metals are well described by the Drude model, and in this case $\text{Γ}$ is simply given by the Drude relaxation parameter (53, 54). Literature values for the Drude relaxation parameter for Au vary from 73 meV in ref. 55 to 48 meV in ref. 56, and are shown as the shaded area in Fig. 2B. The majority of the measured linewidths fall within the range of the literature values. However, longer NWs (lower resonance frequencies) have significantly smaller linewidths than expected from Eq. 2 for both the m = 3 and m = 4 modes. The colored lines in Fig. 2B show the linewidths from the FEM simulations. The simulations show the same trend as the experimental data: the linewidths decrease as the NWs get longer.

The linewidths in Fig. 2B are among the narrowest reported to date for Au nanostructures. In the near-IR to visible spectral region, the smallest linewidths reported are ∼70 meV for the longitudinal plasmon resonance of gold nanorods (the m = 1 Fabry–Pérot mode) (57). Resonance linewidths of ∼65 meV were observed in mid-IR absorption spectroscopy studies of the m = 1 mode of smaller aspect ratio Au NWs (18). Narrow linewidths are expected for Au NWs in mid-IR experiments for two reasons: First, because of their large dimensions the NWs do not suffer from electron-surface scattering (21, 23, 53, 54). Second, radiation damping is suppressed in the mid-IR because of the low resonance frequencies and consequent diminished electromagnetic density of states (58, 59). However, it is still surprising that the measured dephasing times are longer than the bulk gold Drude relaxation time (32). We believe that the reduced linewidths for the Fabry–Pérot modes relative to the Drude limit are due to decreased confinement of the electric field in the mid-IR (60), leading to reduced resistive heating losses. Note that the linewidths estimated from the FEM simulations are slightly larger than the experimental linewidths (Fig. 2B). This is attributed to the choice of dielectric functions used in the simulations––the Drude damping parameter for the dielectric constant data in ref. 55. overestimates the damping for Au (56). Using the dielectric constant data from Olmon et al. (56) would reduce the calculated linewidths and bring them into better agreement with experiment.

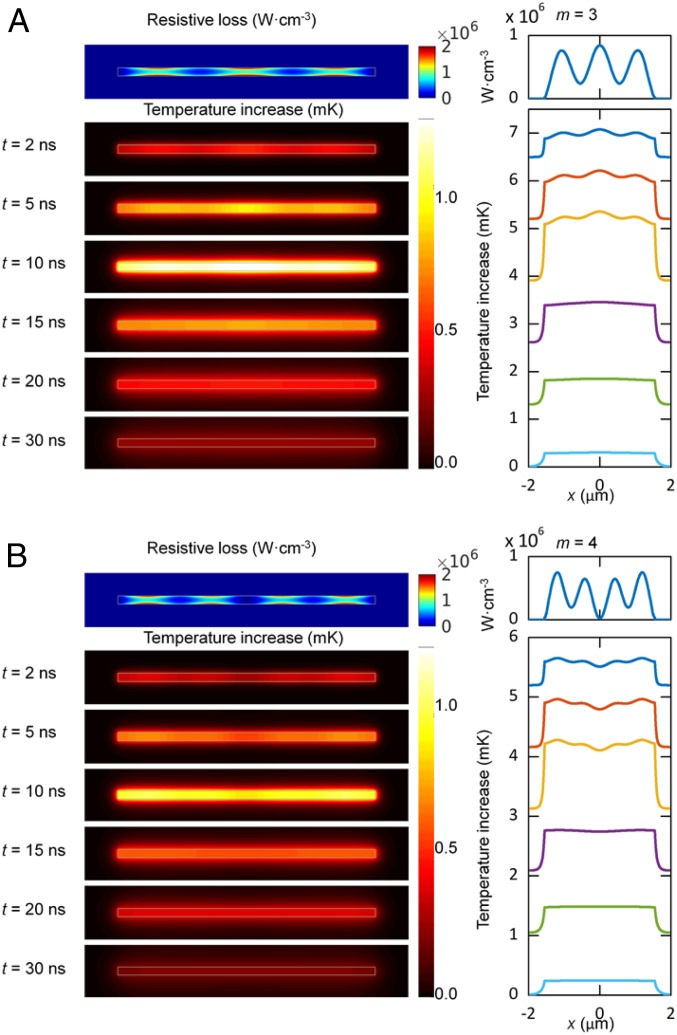
It is important to note that the m = 4 mode structure in Fig. 1D is not as well defined as that for the m = 3 mode in Fig. 1C. Several parameters determine the fidelity of the IR-PHI images. The IR-PHI contrast mechanism relies on local, heat-induced changes to the optical properties of the sample (43, 44). The images are, however, affected by heat diffusion, which naturally smears out the mode structure in the experiments. The effects of heat diffusion are expected to be more severe for the higher-order modes, as they have smaller length-scale features. To understand the effects of heat diffusion, FEM simulations are used to model light absorption and thermal transport in the nanowires.

Fig. 3 shows maps of the spatially dependent absorption for the m = 3 and m = 4 Fabry–Pérot modes of an L = 3.1-μm NW, along with images of the time-dependent temperature changes in the system. Absorption maps are generated by setting the angle of incidence for the excitation beam to ±15° off normal to account for the effect of the focusing objective (see SI Appendix for details). The time-dependent temperature is calculated assuming a 10-ns square-pulse excitation with an integrated energy equivalent to the energy per pulse of the pump beam (the start of the pulse is at 0 ns). During the pulse the spatial distribution of the temperature increase reflects the structure of the NW Fabry–Pérot modes. However, as time progresses thermal diffusion smears out this structure, creating a homogeneous temperature distribution within the NW. This occurs before there is any significant heat transfer to the surroundings.

Fig. 3.

FEM simulation maps of the resistive heating and time-dependent temperature changes for an L = 3.1-μm-long Au NW on a glass substrate for the (A) m = 3 and (B) m = 4 Fabry–Pérot modes. (Top) Images in each panel shows maps of the IR absorption of the NWs. (Bottom) Images show the time-dependent temperature changes in the system. The excitation wavelength for the simulations is chosen to be at the maximum for each resonance. Note that the temperature profiles in the right-hand panels in A and B have been offset for clarity.

The fact that the structure from the Fabry–Pérot modes in the simulations is quickly washed out after the pump pulse implies that the signal in these experiments does not arise from the conventional PHI contrast mechanism, that is, change in the refractive index of the surroundings induced by absorption of the pump beam (61). One possibility is that we are actually detecting a transient absorption signal in these experiments. The probe laser in our measurements is resonant to the transverse plasmon band of the NWs (SI Appendix, Fig. S2), which will be modified by pump laser excitation. Transient absorption signals in metal nanostructures decay rapidly in time due to electron–phonon coupling (54, 62). Because of this the associated images are not sensitive to thermal diffusion (63). Further experiments and simulations are being performed to understand the contrast mechanism in IR-PHI measurements of metal nanostructures, with the goal of improving the quality of associated images.

The last point addressed here is the angle of incidence dependence of the absorption maps. The images in Fig. 3 were generated using a symmetrical excitation scheme (the images are an average of ±15° incident-angle simulations). Simulations performed with unsymmetrical excitation produce absorption maps that are also unsymmetrical, similar to what is observed in Fig. 1D (see SI Appendix for details). Unsymmetrical excitation could arise from misalignment through the Cassegrain objective used to focus the IR beam, and we believe that this is the primary reason for the differences between the experimental and simulated mages for the m = 4 modes in Figs. 1 and 3.

Summary and Conclusions

We have demonstrated an all-optical, far-field, tabletop technique with the spatial resolution and sensitivity to image and spectrally characterize the mid-IR Fabry–Pérot modes of single-metal NWs. The obtained spectra show two resonances that are assigned to the NW m = 3 and m = 4 Fabry–Pérot modes from analysis of the IR absorption images. Comparison of the measured frequencies to the results of FEM simulations validate the experimental mode order assignment. Average linewidths as low as 35 meV are measured for the Fabry–Pérot modes, which are among the smallest values reported to date for any plasmonic system, in either the visible or IR regions of the electromagnetic spectrum. Narrow linewidths correspond to long dephasing times and imply that long-lived enhancements to local electromagnetic fields can be achieved in the mid-IR. This is an important issue for SEIRA applications of the metal nanostructures, as the SEIRA enhancement factor depends on the quality factor for the plasmon resonance, which is directly related to the lifetime.

Materials and Methods

Nanostructure Synthesis.

Gold NWs are fabricated on 0.17-mm-thick glass substrates via electron-beam lithography (JEOL 9300FS) using a lift-off process. To mitigate charging, a thin (10 nm) chromium layer is deposited on top of the resist layer. Following electron-beam exposure the chromium layer is wet chemical etched and the poly (methyl methacrylate) resist is then developed using methyl isobutyl ketone:isopropyl alcohol (IPA) (1:3) for 60 s. Finally, 50 nm of Au is sputter deposited onto the substrates followed by soaking in acetone, rinsing with IPA and deionized water, and then drying under nitrogen. Resulting samples consist of eight identical arrays of gold NWs with each array containing NWs with lengths ranging from 1.00 to 9.95 μm in 0.05-μm steps. In all cases, NWs are 100 nm wide and 50 nm thick. The NWs are spaced by 50 μm to prevent any optical coupling between structures. Representative scanning electron microscope (SEM) images of the NWs can be found in SI Appendix.

IR-PHI Measurements.

A tunable, pulsed infrared pump source (M-Squared, 2,670–4,010-cm⁻¹ frequency range, 150-kHz repetition rate, 10-ns pulsewidth) is focused onto individual Au NWs using a reflective Cassegrain objective (0.65 N.A., Edmund Optics) with the output linearly polarized along the NW long axis. A counterpropagating continuous-wave, visible probe laser (640 nm, Coherent OBIS) is simultaneously focused onto the NW using a conventional, high-N.A. refractive objective (0.9 NA, Plan Apo, Nikon). The probe is linearly polarized along the NW length using a half-wave plate (Thorlabs). The average intensity of the pump beam at the sample is 10–20 mW/cm². Reflected probe light is collected with the refractive objective and is directed onto an avalanche photodiode (Thorlabs, APD110A).

The IR pump laser induces heating in the NW, which changes its dielectric constant as well as the dielectric constant of the immediate environment. This produces a small change in probe-beam reflectivity, which is detected using a high-frequency lock-in amplifier (Stanford Research, SR 844) referenced to the IR pump laser repetition rate. Tuning the IR laser while recording the PHI signal yields IR absorption spectra of individual Au NWs. Corresponding absorption images are obtained by raster scanning the sample through the pump and probe focus using a piezostage (Physik Instruments, P-517.3CL). The spatial resolution of the IR-PHI images is determined by the probe laser, and is ∼0.3 μm for the current experiments.

FEM Simulations.

Three-dimensional FEM simulations (performed using COMSOL Multiphysics) are used to calculate the IR absorption of the NWs, as well as the time dependence of the heat transfer process. The light source profile is taken to be a plane wave since the spot size of the pump beam in the experiment is much greater than the NW dimensions. Oblique incidence (±15° incident angle) is used to excite both the bright and dark optical modes of the NW. In the light-absorption calculations the permittivity of Au is taken from ref. 55, and the permittivity of the glass substrate is set as 2.45. In the conductive heat transfer calculations, the following parameters are used for the thermal conductivity (κ), mass density (ρ), and specific heat capacities (c_p) of air, Au, and glass: $\kappa$_air = 0.024 W·m⁻¹⋅K⁻¹, ρ_air = 1.2 × 10^−3⋅g·cm⁻³, c_p,Air = 1.012 J·g^−1⋅K⁻¹; $\kappa$_Au = 310 W·m⁻¹·K⁻¹, ρ_Au = 19.32 g·cm⁻³, c_p,Au = 0.129 J·g⁻¹⋅K⁻¹; $\kappa$_glass = 1.4 W·m⁻¹⋅K⁻¹, ρ_glass = 2.65 g·cm⁻³, c_p,glass = 0.840 J·g⁻¹·K⁻¹. Two-dimensional FEM mode analysis calculations are also used to determine the effective index for the propagating SPP modes of the NWs in the mid-IR (64, 65). More details about the FEM simulations are presented in SI Appendix.

Data Availability Statement.

All data discussed in the paper (IR-PHI spectra and images, SEM images of the samples, computer assisted design drawings for nanofabrication processes, and FEM simulations programs) will be made available to readers upon request.