Computing Relative Binding Affinity of Ligands to Receptor: An Effective Hybrid Single-Dual Topology Free Energy Perturbation Approach in NAMD

Abstract

An effective hybrid single-dual topology protocol is designed for the calculation of relative binding affinities of small ligands to a receptor. The protocol was developed as an expansion of the NAMD molecular dynamics program, which exclusively supports a dual-topology framework for relative alchemical free-energy perturbation (FEP) calculations. In this protocol, the alchemical end states are represented as two separate molecules sharing a common substructure identified through maximum structural mapping. Within the substructure, an atom-to-atom correspondence is established, and each pair of corresponding atoms are holonomically constrained to share identical coordinates at all time throughout the simulation. The forces are projected and combined at each step for propagation. Following this formulation, a set of illustrative calculations of reliable experiment/simulation data, including relative solvation free energies of small molecules and relative binding affinities of drug compounds to proteins are presented. To enhance sampling of the dual-topology region, the FEP calculations were carried out within a replica-exchange MD scheme supported by the multiple-copy algorithm module of NAMD, with periodic attempted swapping of the thermodynamic coupling parameter λ between neighboring states. The results are consistent with experiments and benchmarks reported in the literature, lending support to the validity of the current protocol. In summary, this hybrid single-dual topology approach combines the conceptual simplicity of the dual topology paradigm with the advantageous sampling efficiency of the single topology approach, making it an ideal strategy for high throughput in silico drug design.

Graphical Abstract

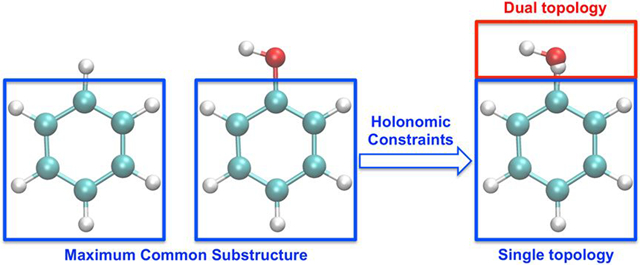
1. Introduction

Protein-ligand binding plays a fundamental role in a vast number of biological processes. Accurate calculations of ligand binding affinity to a protein help understand the microscopic mechanism of molecular recognition and association, while accelerating discovery of novel drugs in pharmaceutical sciences and engineering.^1–6 From a conceptual standpoint, free-energy calculations can be formally distinguished in terms of geometrical and alchemical transformations.^7–8 In stark contrast with the former, which imply mapping the potential of mean force (PMF) with respect to order parameters of the molecular objects at play, the latter exploit the malleability of the potential energy function and the virtually infinite possibilities of computer simulations to transform between chemically distinct states. Methodologies based on alchemical free-energy perturbation (FEP) as well as on geometrical PMF with explicit solvent have proven to be a powerful and robust tool to calculate the absolute binding affinity of drug compounds to a protein target.^9–13 Recent advances include incorporation of sampling enhancement algorithms^14–15 and implementation on graphical processing unit (GPU)-based architectures.¹⁶ While state-of-the-art methodologies enable the calculation of the absolute binding free energy of ligands, estimation of relative binding free energies is in general less costly and has broader application in biophysical and pharmaceutical research and drug development.^17–20 In drug-discovery campaigns, alchemical FEP calculations have played a predominant role in achieving high-throughput virtual drug design.

Alchemical FEP algorithms have been implemented in a number of popular academic molecular dynamics (MD) software packages, such as CHARMM,²¹ GROMACS²² and Amber.²³ These algorithms rely either on a single- or a dual-topology setup. Both represent viable and rigorous routes to carry out this type of computations. Strict dual-topology implies that there is an inherent duplication of a part of the system; the atoms of the two end-state molecules are present at all stages of the calculation, while they do not interact with each other. The system is transformed from one end state to the other by means of a thermodynamic coupling parameter, λ. At one end state (λ=0), one molecule is fully interacting (coupled) with its environment, while the other molecule is non-interacting (decoupled); this is inverted at the other end state (λ=1). NAMD supports such a traditional dual-topology alchemical setup, which may be applied to perform both absolute and relative FEP calculations.²⁴ Conceptually, dual topology is the most straightforward approach when the two end-state molecules are structurally very dissimilar. However, a dual-topology calculation is essentially the same as two absolute free energy calculations, coupling (creation) and decoupling (annihilation), executed simultaneously in opposite directions. This paradigm is a source of complications as the two independent end-state molecules can drift apart, which may result in slow convergence. For this reason, dual topology is often combined with some form of spatial restraints to keep the two end-state molecules spatially coupled.^25–26 For two structurally similar end-state molecules, a dual-topology approach appears somewhat wasteful and cumbersome, especially when the two end-state molecules share a common core. In contrast, single topology seeks to exploit the topological and structural similarity of the two end-state molecules of interest.^27–28 In single topology, only one connected molecular entity is created and transformed along the coupling parameter, λ, to represent one molecule at one end state (λ=0) and another one at the other end state (λ=1). When the number of atoms is different in the two end states, a number of non-interacting “dummy” atoms must necessarily be introduced to hold the place of vanishing/appearing physical atoms in order to balance out the number of atoms at both end states. Dummy atoms have no non-bonded interactions in the end states, but normally retain some of their bonded terms, so that they do not drift away unhindered in the simulation cell. Single topology can be implemented by mixing force-field parameters, or by mixing the potential energy functions of the end states.²⁹ When the term “single topology” was coined, it referred to a mixing of the force-field parameters and each interaction term would be evaluated only once.³⁰ The force-field parameters of each term are scaled as a function of the alchemical coupling parameter, λ. This single-topology approach is still used in GROMOS³¹ and GROMACS²², and recently a parameter interpolation thermodynamic integration (PI-TI) method within the Amber package has been reported.³² In contrast, mixing the potential energy functions of the end states is essentially an approach that combines a single coordinate set with a dual topology setup, whereby each interaction term is calculated twice with the same coordinates, and the resulting energies and forces are mixed as a function of the alchemical coupling parameter. Such a single topology setup mixing potential energy functions of end states could be implemented within the existing dual-topology implementation of NAMD³³ without major modifications to the existing code. However, while a strict single-topology method is often advantageous from the standpoint of reduced sampling cost, it may encounter difficulties if it is enforced for regions of the end-state molecules that are chemically dissimilar. Furthermore, practical applications often require some manual intervention to properly setup the single-topology ligand with appropriate common chemical core and dummy atoms, and a simple and conceptually clear strategy amenable to automated high throughput calculations would be desirable.

To address this issue, we describe here the implementation of a hybrid single-dual topology approach in NAMD. The basic idea is to start from the dual-topology representation of the two end-state molecules, and then selectively apply “holonomic” constraints to the common substructure of these molecules, such that each pair of corresponding atoms will share identical coordinates throughout the simulation. The task of pre-identifying and selecting the common substructure between two arbitrary molecules should be handled separately to avoid cluttering the MD code. Within the substructure, single-topology transformation is achieved based on virtual particles and force projection, and forces are exerted only on those atoms pertaining to one molecule to perform integration. This strategy bears some similarities with the SANDERS module of AMBER, whereby the atoms of the common substructure identified from two separate ligands represented in dual topology are synchronized (coordinates and velocities) at every time-step of MD.^34–35 By virtue of the hybrid single-dual topology strategy, the explicit creation of dummy atoms is obviated through the dual-topology representation of the atoms that are unaffected by the holonomic constraints, thus resulting in considerable conceptual simplicity and clarity. Further, different intermediates are coupled in a Hamiltonian exchange simulation to increase sampling efficiency. In the subsequent sections, the detail of the implementation in the NAMD source code is presented and combination with Hamiltonian exchange is discussed. The practical advantage of the proposed hybrid single-dual topology approach is illustrated in a series of representative relative FEP applications.

2. Implementation Details

2.1. Hybrid Single-Dual Topology

Introducing the thermodynamic coupling parameter λ, the objective is to design a methodology enabling the free energy calculation between two end states designed to represent molecular entity Mol0 at λ=0, and Mol1 at λ=1. The calculated free energy difference corresponding to the transformation U [λ = 0] → U [λ = 1]. In the process of varying λ from 0 to 1, Mol0 is said to be “outgoing” and Mol1 is said to be “incoming”. A subset of atoms in Mol0 and Mol1, referred to as the single (S) topology region, is identified and selected as a common chemical core. Within this region, holonomic constraints enforce an exact one-to-one correspondence between the atomic coordinates of Mol0 and Mol1 (each pair of atoms from Mol0 and Mol1 have identical coordinates during MD). The remaining atoms of Mol0 and Mol1 that are not part of the single topology region are ascribed to the dual (D) topology region. The common chemical core between Mol0 and Mol1 can be determined using a maximum common substructure (MCS) search algorithm,^36–37 yielding a specific atom-to-atom structural mapping. As illustrated in Figure 1, the common core region plays the role of “single topology”, while the other atoms are treated as a “dual topology” region.

Figure 1:

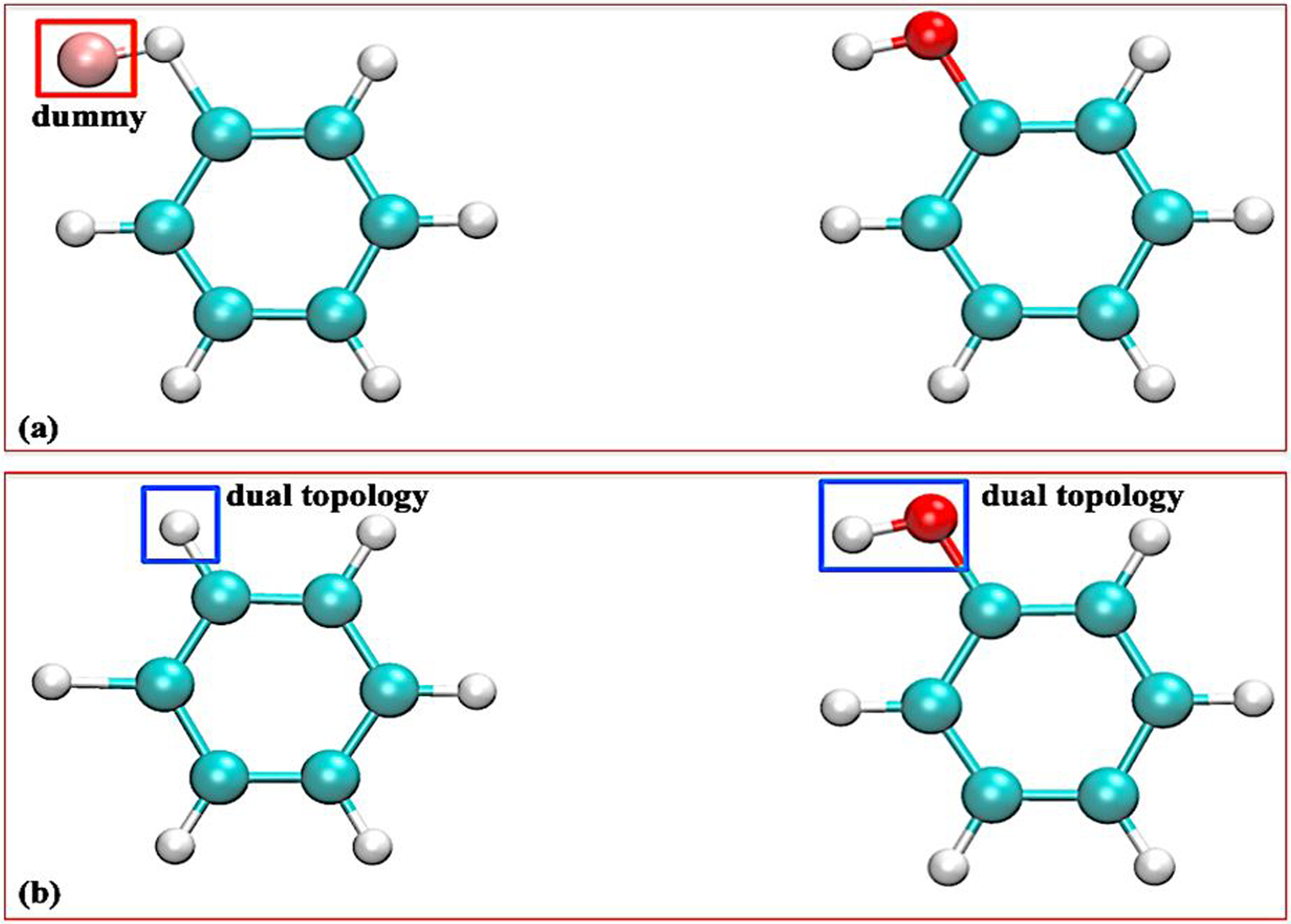
Alchemical transformation between benzene to phenol as an illustrative example for the current hybrid single-dual topology protocol. Panel (a) presents a strict one-to-one correspondence between the two molecules aided with explicit dummy atom; Panel (b) presents a flexible hybrid single-dual topology implementation on the top of a MCS region.

In order to produce a thermodynamically valid free energy difference between the two end states, a number of energy terms involving Mol0 and Mol1 must be scaled appropriately. First and foremost, the nonbonded (NB) Lennard-Jones (LJ) and electrostatic charges parameters of Mol1 are scaled to zero at λ=0, while the nonbonded parameters of Mol0 are scaled to zero at λ=1. This scaling rule essentially converts the atoms in the dual topology region with nonbonded parameters scaled to zero into “dummy” atoms, like in the traditional single topology framework. Thus, the scaling rule for the atom-based nonbonded parameters is straightforward. The scaling rules for the internal energy term (bonds, angles, and dihedrals), however, require a careful analysis because they involve multiple atoms that may lie within the single (S) or dual (D) topology region.

One can distinguish S-S, D-D and S-D internal terms. Because the corresponding atoms are holonomically constrained within the single topology region, it is valid to scale to zero the S-S internal terms of Mol1 at λ=0, and scale to zero the S-S internal terms of Mol0 at λ=1. Obviously, the S-S internal terms of Mol0 at λ=0 and of Mol1 at λ=1 must not be scaled. Similarly, it is valid to keep the D-D internal terms unscaled, as this does not directly affect the configurational distribution of the opposite molecule in the uncoupled state. The more delicate issue is the treatment of the S-D internal terms of Mol0 at λ=1 and of Mol1 at λ=0 because it may result in an undesirable bias on the atoms in the single topology region. If a group of atoms in the dual topology region is linked to the single topology region via a single bond, it can be shown that there is no unwanted bias as long as one keeps only one valence angle and one dihedral angle.³⁸ Accordingly, scaling all but one S-D bond, one S-D valence angle and one S-D dihedral angle is a possible avenue that would yield a thermodynamically meaningful free energy difference between the end states. It should be noted this strategy can be extended to dummy atom group that forms multiple S-D bonds with the single topology region, by perturbing extra S-D bond(s).¹⁸ The implication is that a single link (1 bond, 1 angle, and 1 dihedral) must be kept for an entire group of atoms in the dual topology region in order to result in unbiased results. The three selected S-D terms of each transformed atom group, not only retain unbiased statistical distribution of single topology region, but also are poised to reduce sampling cost while an end-state molecule is being decoupled, analogous to the translational restraint in absolute binding free energy computation based on double decoupling protocol.^{11, 25–26, 39} The selection of unperturbed S-D bonded terms can be automated based on four criteria: (1) no hydrogen atom can be selected from single topology region; (2) each S-D bonded term contains one dual topology atom only to provide a stable translational reference for alchemically altered moieties; (3) if one end molecule contains multiple disjoint transformed atom groups, the multiple sets of selected S-D bonded terms from one end molecule do not share any single topology atom to avoid spurious coupling among single topology atoms; (4) if a transformed moiety is connected to the rest of the molecule via multiple S-D bonds, such as ring topology change, only one link remains unperturbed while all S-D bonded terms associated with other links are scaled. The unperturbed S-D bond, valence angle and dihedral terms and perturbed S-D bond selected with three representative transformations in this report are presented in the Supporting Information.

In the following, we will designate the unperturbed internal covalent S-D terms retained for the connectivity as $U_{\text{SD}}^{\text{Mol}}(1\text{bond,}\text{1}\text{angle,}\text{1}\text{dihedral})$ for the specified molecule (Mol0 or Mol1) and the remainder of the S-D terms as $U_{\text{SD}}^{\text{Mol}}$. Likewise, the unperturbed S-S and D-D terms are designated as $U_{\text{SS}}^{\text{Mol}}$ and $U_{\text{DD}}^{\text{Mol}}$. Thus, in the hybrid single-dual topology method, the potential energy U [λ] expressed as a function of the three thermodynamic coupling parameter λ, is,

$$U\left[\lambda \right]=U_0+U_{\text{NB}}^{\text{Mol}0}\left[1-\lambda \right]+U_{\text{NB}}^{\text{Mol}1}\left[\lambda \right]+\left(1-\lambda \right)U_{\text{SS}}^{\text{Mol}0}+\lambda U_{\text{SS}}^{\text{Mol}1}+\left(1-\lambda \right)U_{\text{SD}}^{\text{Mol}0}+U_{\text{SD}}^{\text{Mol}0}\left(1\text{bond},1\text{angle},1\text{dihedral}\right)+\lambda U_{\text{SD}}^{\text{Mol}1}+U_{\text{SD}}^{\text{Mol}1}\left(1\text{bond},1\text{angle},1\text{dihedral}\right)+U_{\text{DD}}^{\text{Mol}0}+U_{\text{DD}}^{\text{Mol}1}$$ (1)

where U₀ is the potential energy that is unperturbed, and U_NB [λ] is the nonbonded contribution for the specified molecule (Mol0 or Mol1),

$$U_{\text{NB}}\left[\lambda \right]={\lambda }_{\text{LJ}}\left[\lambda \right]{\epsilon }_{ij}\left[{\left(\frac{{\left(R_{ij}^{\text{min}}\right)}^2}{r_{ij}^2+\delta \left(1-{\lambda }_{\text{LJ}}\left[\lambda \right]\right)}\right)}^6-2{\left(\frac{{\left(R_{ij}^{\text{min}}\right)}^2}{r_{ij}^2+\delta \left(1-{\lambda }_{\text{LJ}}\left[\lambda \right]\right)}\right)}^3\right]+{\lambda }_{\text{elec}}\left[\lambda \right]\frac{q_i{q}_j}{4\pi {\epsilon }_0{\epsilon }_1{r}_{ij}}$$ (2)

where δ is a radius-shifting coefficient of the modified soft-core LJ interactions during alchemical free energy calculations (U_NB [λ] depends non-linearly on λ). The soft-core potential^40–41 serves to scale gradually the short-range LJ potential along the alchemical transformation to avoid any numerical instabilities in MD. It should be noted that the two coupling parameter λ_LJ or λ_elec are not varying independently as their values are controlled internally in NAMD by a unique global thermodynamic parameter λ via a switching NB scheduler,⁴², shown by Figure 2. Throughout the perturbation, a holonomic constraint is applied to the coordinates of the Mol0 and Mol1 atoms that are part of the single topology region.

Figure 2:

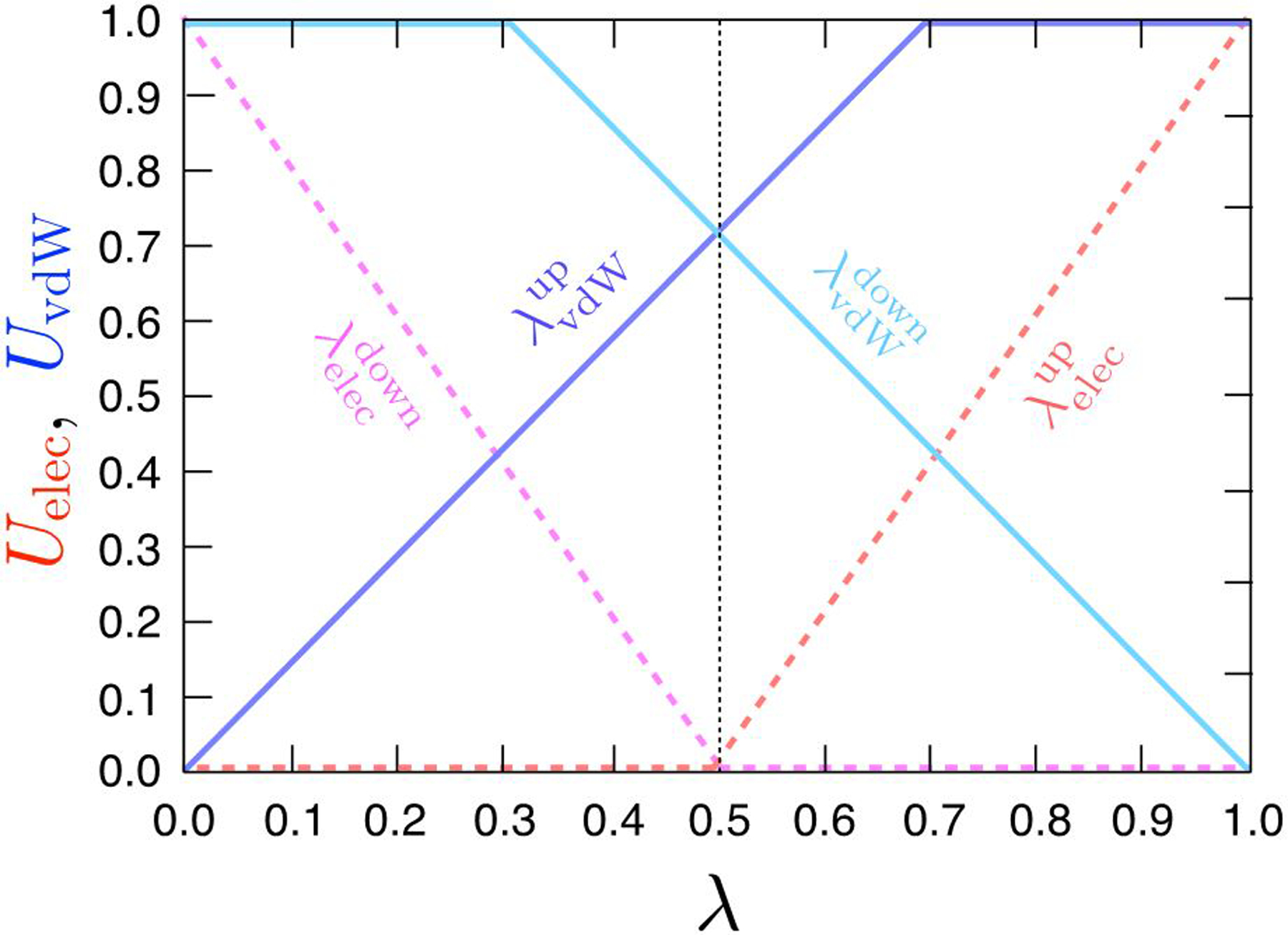
Evolution of thermodynamic coupling parameters for vdW and electrostatic interaction between the initial and final state. The progressions of the four thermodynamic coupling parameters are functions of a “master” λ.

The present hybrid single-dual topology implementation extends the multiple-partition data structure of the alchemical module in NAMD, but retains the existing input/output data structure to obviate the need for fundamental modifications in the source tree. Following the traditional alchemical index file of NAMD for the dual-topology FEP scheme, the incoming and outgoing atoms are respectively noted “1” and “−1” in the coordinate file (the user can choose from the O, B, or x, y, z columns), whereas unperturbed atoms are noted as “0”. In the hybrid single-dual topology, the value for a single-topology incoming and outgoing atom is noted “2” and “−2”, respectively. The extended multiple-partition data structure, however, does not complicate the existing Particle Mesh Ewald (PME) implementation for long-range electrostatics of alchemical transformations. Within the multiple-grid framework of PME in NAMD,⁴³ the incoming (or outgoing) atoms of a single topology share identical PME grids and thermodynamic coupling parameters with the incoming (or outgoing) atoms of the dual topology. Thus, the composition of PME grids and computations of PME force/energy remain unchanged. A segment of a sample alchemical index file for the hybrid single-dual topology is presented in the Supporting Information.

To facilitate structural mapping of the two end-states, a lightweight hybrid structure preparation tool based on MCS search was designed and will be published with the next official NAMD release. This scheme essentially aims at maximum overlap,⁴⁴ with the idea that a maximal single-topology description leading to a minimal number of vanishing/appearing atoms is the most efficient protocol.⁴⁵ Alternatively, users can turn to another popular hybrid structure preparation tools such as AmberTools²³ or FESetup,⁴⁶ and then convert the generated CHARMM-formatted input files into the proper NAMD format. In single topology setup, explicit dummy atoms²⁹ are attached (Figure 1a), so that the two end states have the same number of atoms and share identical coordinates. However, it must be stressed that such a strict one-to-one topology correspondence may result in a number of problems. Artificial effects of dummy atoms, which are independent of topology setup, on the computed relative free energies have been a long-standing issue. Their nonphysical contribution cancels out only if the bonded terms of dummy atoms are handled correctly.^{29, 38} In the current hybrid single-dual topology, artificial effects due to the bonded interactions between dummy atoms and the rest of molecule are removed by keeping one link unperturbed, demonstrated in Eq. 1. The existence of the dual-topology region allows the transforming moieties to sample configurational space while being decoupled. Hamiltonian exchange along the alchemical transformation path can further help to enhance the conformational sampling.⁴⁷ Within each step, the rescaled bonded and nonbonded forces of each pair of atoms in the common chemical core region are combined into a single force. In the NAMD source code we adopted a solution of force redistribution/combination and atom repositioning in the common chemical core region to obtain an effective single topology, in a similar spirit with the algorithm used in NAMD to handle lone pairs.⁴⁸ The combined force of each pair of atoms applies to the Mol0 atom only, while no force is assigned to the Mol1 atom. Since the initial/end-state atoms share identical coordinates, such force redistribution does not require any virial correction. After completion of an integration step for the Mol0 atoms, the coordinates of the Mol1 atoms are updated with those of the corresponding Mol0 atoms, and their contribution to the kinetic energy is zeroed out. The above force projection with rescaled bonded interactions of single-topology atoms avoids force duplication on the initial-state atoms, and, thus, facilitates construction of a customized single-topology region, where pairs of corresponding atoms in Mol0 and Mol1 can have different bonded and nonbonded parameters. In practice, a user could redefine the single- and dual-topology regions to satisfy any special need. Some specific transformation in proteins involve atom-type changes on both the backbone and the side chains, e.g., transformation from amide to ester.⁴⁹ In such instances, the end-user can manually design a single-dual topology region without assistance of an MCS search algorithm.

2.2. FEP/λ-REMD Simulation Protocol

In stark contrast with a FEP staging simulation protocol adopted for absolute free-energy calculations,^{11, 50} in a relative FEP calculation the van der Waals and electrostatic interactions can be scaled concurrently⁴³ in each window due to less severe sampling requirements. According to the switching NB scheduler of NAMD,⁴² the electrostatic interaction is switched on later than the van der Waals interaction, which then they scale up together for incoming atoms/end state. Likewise, for outgoing atoms/initial state, the electrostatic interaction is scaled down together with the van der Waals interaction, but the former is switched off earlier than the latter. The combined potential energy of an intermediate window is expressed with the aid of separate coupling parameters, λ_elec and λ_LJ, that control the electrostatics and the non-bonded Lennard-Jones potentials, which are implemented as a function of a single global thermodynamic coupling parameter, λ (see Figure 2).

With the multiple partition module of charm++/NAMD,⁵¹ all FEP windows can be launched together and run concurrently in a single job managed by communication-enabled Tcl scripting propagated with a replica-exchange algorithm following the conventional Metropolis-Hastings exchange criterion⁵² with λ-swap moves,

$$\text{exp}\left[\left(U\left({\lambda }_m,r_m\right)+U\left({\lambda }_n,r_n\right)-U\left({\lambda }_m,r_n\right)-U\left({\lambda }_n,r_m\right)\right)/k_{B}T\right]\ge \text{random}\left(0,1\right)$$ (3)

where U denotes the potential energy of the underlying replica, and λ_m and r_m denotes the staging parameters (the subscripts m and n denote the indexes of two neighboring windows/replicas with n = m + 1) and coordinates, respectively. In NAMD’s communication-enabled Tcl interface, communication between two neighboring windows involves instant potential-energy value exchange and generates four potential energy outputs for each parameter-swap attempt U (λ_m, r_m), U (λ_n, r_n), U (λ_m, r_n) and U (λ_n, r_m). These potential energy outputs can be straightforwardly introduced in the simple overlap sampling (SOS) free-energy estimator⁵³

$$\text{exp}\left(-\frac{\mathrm{\Delta }{G}_{mn}}{k_{\text{B}}T}\right)=\frac{{\langle \text{exp}\left(-\left(U\left({\lambda }_n,r_n\right)-U\left({\lambda }_m,r_m\right)\right)/2k_{\text{B}}T\right)\rangle }_m}{{\langle \text{exp}\left(\left(U\left({\lambda }_m,r_n\right)-U\left({\lambda }_n,r_m\right)\right)/2k_{\text{B}}T\right)\rangle }_n}$$ (4)

where the ΔG_mn denotes the free energy difference between the two neighboring intermediate states and the summation of ΔG_mn along the thermodynamic axis yields the relative free energy change.

3. Applications

3.1. Simulation Methodology

In this work, two types of free-energy calculations were carried out to probe our new implementation, namely relative solvation free-energy and relative binding free-energy calculations. High-frequency λ-exchange was performed to aid sampling of the altered chemical moieties. FEP/λ-exchange is launched with a customized Tcl scripting interface, which was employed previously for absolute free-energy calculations. All the FEP calculations at the binding site were performed on the IBM Blue Gene/Q cluster Mira of the Leadership Computing Facility at Argonne National Laboratory. The simulations were carried out in a high performance mode with version 2.10 of the NAMD program,⁴³ which was modified and extended for the present study. All the simulations were performed with periodic boundary conditions in the isobaric-isothermal ensemble. The initial binding structures of T4 Lysozyme/L99A^{11, 54–55} and Myeloid Cell Leukemia 1 (MCL1)⁵⁶ were constructed from the crystallographic structure (PDB 181L and 4HW3) with CHARMM-GUI Ligand Binder^57–58. Hybrid structures of ligand pairs were generated with the hybrid-structure preparation tool, which will be made publicly available, and then mapped into the initial binding structures. All crystallographic ions and waters were kept and counter ions were randomly positioned by the CHARMM-GUI web server, amid the aqueous solvent. Chemical bonds involving hydrogen atoms were constrained to their equilibrium length by means of the RATTLE algorithm.⁵⁹ Water molecules were constrained to their equilibrium geometry with the SETTLE algorithm.⁶⁰ The equations of motion were integrated with a 2 fs time step, using Langevin dynamics at a temperature of 300K. The pressure was maintained at a constant value of 1 atm with the Langevin piston pressure control.⁶¹ For both the binding-site and solvation free-energy calculations, production runs were performed with a replica-exchange frequency of 1/100 steps. The generalized CHARMM force field parameters (CGenFF)⁶² for all the small molecules were determined with the CHARMM-GUI Ligand Binder module.^49–50 The protein and its aqueous environment were described by the CHARMM36 force field and the TIP3P water model.⁶³

In the FEP/λ-REMD simulation, 16 λ-windows were employed with general soft-core potentials applied to Lennard-Jones interactions to avoid the so-called “end-point catastrophe”. In a test run of 200 ps with FEP/λ-REMD, the exchange acceptance ratio distributions among the 16 neighboring replica pairs ranged from ~30% to ~35%. For all applications, both the intramolecular nonbonded interactions and bonded interactions within the two end molecules are perturbed. For relative binding free energy applications, no gas phase calculation is necessary as the two end points (binding site and bulk solution) are always subtracted from one another to get the net free energy change. However, for relative solvation free energy applications, a gas phase FEP/λ-REMD simulation must be performed to close the thermodynamic cycle. In all calculations, the exchange attempt history and the corresponding potential energy evaluation of Metropolis-Hastings trial move of each replica exchange were collected during the production run, and post-processed using the SOS algorithm. To monitor the convergence of the binding-site free-energy calculation, 150 consecutive FEP calculations (150×100 ps) were performed for each system, each starting from the configuration saved at the end of the previous run. The data generated during the last 100 FEP calculations were used for free-energy estimation and data analysis. For each system of solvated hybrid molecules, two sets of absolute FEP calculations were run for the initial molecule and the final molecule. The relative solvation free energy determined from two separate absolute FEP calculations is expected to provide a self-consistent comparison with the current single-topology protocol.

3.2. Relative Solvation Free Energy

Alchemical transformation of a sodium ion to a potassium ion constitutes a prototypical single-topology setup, although it can also be simulated using a traditional dual-topology scheme with positional restraints. The transformation only involves nonbonded force recombination and atom repositioning. The relative solvation free energy of sodium to potassium ion was estimated to be equal to 18.7 ± 0.0 kcal/mol, in agreement with the experimental value of 17.2 kcal/mol,⁶⁴ and the value resulting from two absolute FEP calculations in the present study for sodium ion and potassium ion, i.e., 18.7 ± 0.0 kcal/mol.

Transformation from benzene to phenol involves all elements of a hybrid single-dual topology setup. The aromatic ring clearly represents the MCS region. In the alchemical perturbation, a hydrogen atom must be transformed into a hydroxyl group. With this simple, albeit representative problem, we show that construction of a customized single-topology region is feasible based on the present force projection with rescaled bonded interactions. Three different topology setups were employed to calculate the relative free energy: (1) a strict single-topology setup with an explicit dummy atom attached to the hydrogen atom of benzene (Figure 1a); (2) the definition of a single-topology region containing the hydrogen atom of benzene and the oxygen atom of phenol, while the hydrogen atom of the hydroxyl group moves without coordinate constraint; (3) the definition of the aromatic ring as the single-topology region, while the hydrogen atom of benzene and the hydroxyl group are defined as a dual topology. With setup (1) extra bonded parameters including bonds, valence angles and dihedral angles are defined for the dummy atom, corresponding to those of hydrogen in a hydroxyl group. Essentially setup (1) and (2) are equivalent and can be employed together to underscore the stability of the present implementation. The relative solvation free energies calculated with the three setups result in essentially the same value: −4.7 ± 0.1 kcal/mol (1), −4.7 ± 0.1 kcal/mol (2) and −4.7 ± 0.2 kcal/mol (3). This includes a gas phase calculation needed to close the thermodynamic cycle. The results are all in agreement with the experimental value of −5.27 kcal/mol,⁶⁵ as well as previous simulation results from the literature.^66–67 In the subsequent binding affinity calculations, the MCS is defined as a single-topology region, while the other moieties are defined as dual topology (Figure 1b).

3.3. Relative Binding Free Energy

Molecular dynamics simulations at the binding site often experience a number of sampling issues, among which are solvent equilibration within buried binding pockets and the large reorganization of the surrounding structure. Two proteins with hydrophobic binding pockets, T4L/L99A and MCL1, are selected. The hydrophobic nature of their binding pocket makes them free from solvent sampling issue. For the T4L/L99A target, transformation from benzene to o-xylene was simulated. Experiment has shown that both benzene and o-xylene do not induce any structural change at the binding pocket.⁵⁵ For target MCL1, four transformations, 65 → 60, 57 → 42, 49 → 56 and 33 → 44, at the rigid binding pocket were simulated. Here, all the MCL1 binders are numbered in accordance with previous reports of simulations and experiments.^{17, 56} All these transformations are depicted in Figure 3, where it can be seen that the changed moieties range from single-atom mutation to replacement of functional groups, to a large-ring topology change. Listed in Table 1, the calculated binding free energies are in agreement with experiment and previous simulations,^{11, 17} falling within ±1.0 kcal/mol. It ought to be noted that among the five transformations, 33 → 44 involves a significant ring- topology transformation, in which ligand 33 undergoes ring extension at the end state, i.e., ligand 44. Ring-topology change is a longstanding challenge in relative free-energy calculations. The associated bond breaking/creation process significantly modifies local topology/atomic connectivity and can give rise to severe sampling issue in MD simulations.^{18, 68}

Figure 3:

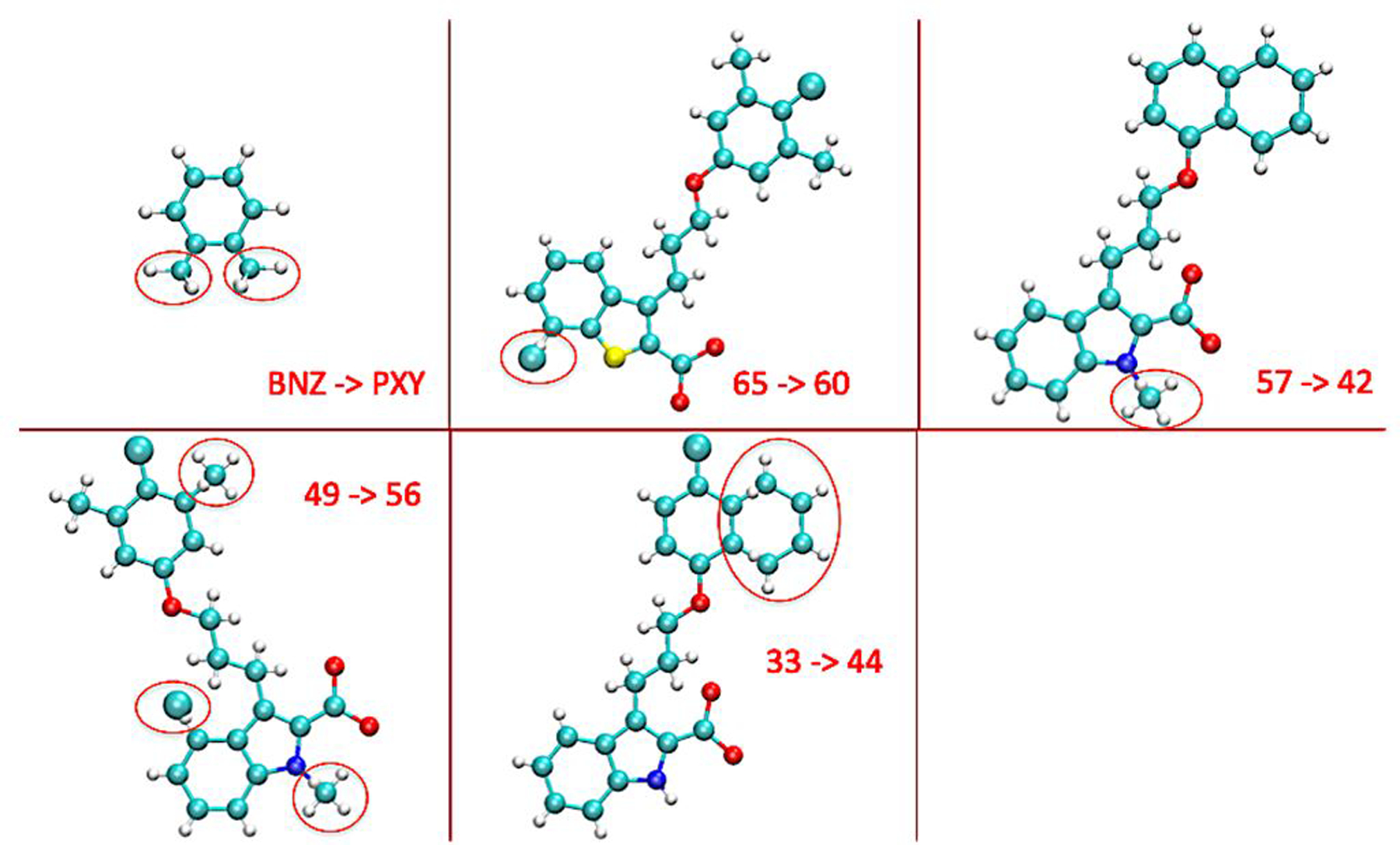
Alchemical transformations in relative binding free energy calculations. The red circles denote dual topology region while the other part is single topology (MCS) region. In the five transformations, the initial and final moieties in the dual topology regions, respectively, are two hydrogen atoms to two methyl groups for BNZ -> PXY, a chloride atom to a hydrogen atom for 65 -> 60, a methyl group to a hydrogen atom for 57 -> 42, a chloride atom, two hydrogen atoms to a hydrogen atom and two methyl groups for 49 -> 56, and two hydrogen atoms to a six-membered aromatic ring (except the two anchor carbon atoms) for 33 -> 44.

Table 1.

Calculated Relative Binding Free Energies in This Report (all values in kcal/mol)

	ΔΔGsite	ΔΔGbulk	ΔΔG	Exp. ΔΔG	Ref. 17 ΔΔG
Benzene → o-xylene	15.0±0.1	14.5±0.1	0.5±0.1	0.6	N/A
65 → 60	−9.6±0.2	−9.4±0.1	−0.2±0.2	−0.5	−0.8
57 → 42	8.3±0.2	7.8±0.1	0.5±0.2	0.14	−1.0
49 → 56	−13.7±0.2	−12.7±0.1	−1.0±0.2	−0.9	−2.3
33 → 44	14.5±0.2	16.1±0.1	−1.6±0.2	−1.8	−2.6

ΔΔG_site, ΔΔG_bulk and ΔΔG represent the simulated relative free energy in binding site and bulk solution without subtracting gas phase transformations, and net relative binding free energy, respectively. The simulated net binding free energy is compared with experimental results Exp. ΔΔG, and previous theoretical results, Ref. 17 ΔΔG. For target MCL1, the previous theoretic and experiment results can be looked up in lines 78–119, spreadsheet ‘ja512751q_si_003.xlsx’ of the Supporting Information of Ref. 17. The experiment results of target MCL1 also can be found in Table 3 of Ref. 56. The experiment results of target T4L/L99A can be looked up in Table 2 of Ref. 11 or Ref. 55.

While there are some bond distortions, we observe here that the extended ring of molecule 44 in the binding site conserves its topology even at the decoupled end state (see snapshot of the decoupled end-molecule 44 in the binding site after 15 ns FEP/λ-REMD simulation in Supporting Information). The overall integrity of ring geometry is maintained in this system, which is well sampled with λ-REMD. To provide a robust computational test, two separate absolute FEP simulations for the solvation of 33 and 44 were performed. It turns out that the relative solvation free energy values obtained from the two different simulations, 0.7±0.1 kcal/mol (from the single-dual topology FEP) and 0.4±0.1 kcal/mol (from the two separate absolute FEP), agree within 0.3 kcal/mol, suggestive that this approach can be used for ring-topology transformation problems. However, it needs to be stressed that in ring-topology/scaffold hopping transformations,¹⁸ including the ring opening/closing, extension and size-change problems, the dummy group might experience diverse conformational distortions at decoupled states, and the present ring extension problem itself does not represent general cases. Generalization of the present approach to general ring-topology transformation problems is our current research.

4. Conclusion

An effective hybrid single-dual topology setup for relative free-energy calculations was constructed with a single-coordinate dual-molecule protocol, and extends the multiple-partition data structure of the alchemical module in NAMD. A maximum common substructure (MCS) algorithm is used to identify the atom-to-atom correspondence between the two structurally similar ligands. The single-topology transformation is achieved as a local holonomic constraint in MD propagation via force combination and coordinates of the two common substructures. The hybrid single-dual topology setup minimizes the sampling cost of two structurally similar ligands by virtue of the single topology region, while the alchemically altered moieties are free to sample the configurational space by virtue of the dual topology region. It must be noted that, artificial effects due to the bonded interactions between dummy atoms and the rest of molecule are removed by retaining a single unperturbed S-D link per dummy atom group.³⁸ The end-user can define the dual-topology region based on chemical similarity or to satisfy sampling requirements. The implementation performs well on the set of solvation and binding free-energy calculations considered here, displaying the practical convenience of a hybrid single-dual topology approach that combines the robust conceptual simplicity of the dual topology together with the well-established sampling efficiency of the single topology approach. The conceptual clarity and simplicity of the proposed hybrid single-dual topology method makes it an ideal strategy for automated high-throughput relative alchemical FEP calculations for compound optimization.