MR-based cardiac and respiratory motion correction of PET: Application to static and dynamic cardiac ¹⁸F-FDG imaging

Abstract

Motion of the myocardium deteriorates the quality and quantitative accuracy of cardiac PET images. We present a method for MR-based cardiac and respiratory motion correction of cardiac PET data and evaluate its impact on estimation of activity and kinetic parameters in human subjects. Three healthy subjects underwent simultaneous dynamic ¹⁸F-FDG PET and MRI on a hybrid PET/MR scanner. A cardiorespiratory motion field was determined for each subject using navigator, tagging and golden-angle radial MR acquisitions. Acquired coincidence events were binned into cardiac and respiratory phases using electrocardiogram and list mode-driven signals, respectively. Dynamic PET images were reconstructed with MR-based motion correction (MC) and without motion correction (NMC). Parametric images of ¹⁸F-FDG consumption rates (K_i) were estimated using Patlak’s method for both MC and NMC images. MC alleviated motion artifacts in PET images, resulting in improved spatial resolution, improved recovery of activity in the myocardium wall and reduced spillover from the myocardium to the left ventricle cavity. Significantly higher myocardium contrast-to-noise ratio and lower apparent wall thickness were obtained in MC versus NMC images. Likewise, parametric images of K_i calculated with MC data had improved spatial resolution as compared to those obtained with NMC. Consistent with an increase in reconstructed activity concentration in the frames used during kinetic analyses, MC led to the estimation of higher K_i values almost everywhere in the myocardium, with up to 18% increase (mean across subjects) in the septum as compared to NMC. This study shows that MR-based motion correction of cardiac PET results in improved image quality that can benefit both static and dynamic studies.

INTRODUCTION

Motion associated with respiratory and cardiac functions is a well-known source of image quality degradation in cardiac Positron Emission Tomography (PET) studies. The magnitude of regular heart displacements is indeed substantial, particularly when viewed in comparison to the ~4–5 mm intrinsic spatial resolution of PET cameras. For example, respiration typically shifts the heart by more than 10 mm along the superior-inferior direction [1], whereas cardiac contraction moves the base of the myocardium toward the apex by an average of ~12.8 mm [2] and at the same time thickens the myocardium wall by 4.0–6.1 mm [3]. The continuous movement of the heart during scanning introduces artifacts that alter quantification of tracer concentration in cardiac tissues and deteriorate the diagnostic quality of PET images. Two types of image artifacts directly result from motion: One presents as a spatially-dependent blurring of the reconstructed activity distribution that can lead to underestimation of the local tracer uptake and even impair the detection of small lesions in some cases. The second type of artifact, resulting from spatially inconsistent emission and attenuation distributions, manifests primarily in regions adjacent to large attenuation gradients (e.g. at heart/lung or liver/lung interfaces) and can introduce artefactual myocardial defects. Its impact on image diagnostic quality has been extensively documented in cardiac PET/CT [4], [5].

Motion correction of cardiac PET has been an area of active research for more than two decades [6]–[11] (see reviews in [12], [13]). It is hoped that artifact-free PET images will translate into more accurate assessment of myocardial perfusion, metabolism and cardiac function, leading to improved diagnosis and staging of cardiovascular diseases [14], [15]. For studies performed on standalone PET or PET/CT systems, motion has generally been tackled using the following multistep framework: First, the measured emission data are gated, i.e. assigned to specific cardiac and respiratory phases based on surrogate signals measured with external sensors (e.g. EKG, respiratory bellows, optical tracking) or the PET data themselves [16]. Second, an image volume is reconstructed for each motion phase. Third, motion vector fields (i.e. dense sets of 3-D displacements) mapping the voxel-to-voxel correspondence between every motion phase and a reference phase are estimated by registration of the gated PET volumes. Fourth, the motion fields are used to correct the PET data for motion by being either applied to the gated images directly [17] or modeled within motion-compensated image reconstruction [18]. A well-known limitation of this approach, however, is the fact that motion estimation relies on gated PET volumes, which are characterized by their low signal-to-noise ratio (SNR) especially when dual (i.e. cardiac + respiratory) gating is employed. Furthermore, image registration is generally complicated by the overall lack of anatomical landmarks in cardiac PET images: for instance, certain intramural components of contractile motion (e.g. torsion) are nearly impossible to track accurately due to the uniformity of myocardium in PET images [6]. Finally, low tracer accumulation in diseased cardiac tissues could further confound local estimation of the motion field with PET images.

In addition to its clinical potential in cardiovascular imaging [19], [20], a unique feature of hybrid PET and Magnetic Resonance Imaging (MRI) is that it provides a robust solution to the problem of motion in PET. Indeed, owing to its lack of ionizing radiation, excellent soft-tissue contrast, high SNR and good spatiotemporal resolution, MRI has ideal characteristics for measuring organ motion. In simultaneous PET/MR scanners, the acquired motion information can be leveraged to correct the PET data for motion. MR-based motion correction of PET has been investigated extensively over the past few years, with applications in imaging of malignancies [21]–[30], brain [31]–[33] and heart [14], [25], [34]–[41] (refer to [42]–[46] for comprehensive reviews on the topic). In their vast majority, these works have focused on static (i.e. single time-point) PET scanning and have evaluated the impact of motion correction on various semi-quantitative image metrics such as target-to-background ratio or SUV. However, much less attention has been given to evaluating MR-based motion correction in the context of fully quantitative cardiac PET studies based on dynamic imaging.

We have previously presented and evaluated a method for MR-based motion correction of dynamic PET data in a pre-clinical porcine model of myocardial perfusion [25]. Cardiac motion correction only was performed in that study, due to the small amplitude of respiration-induced myocardium motion in this animal model. Here, we extend the method to human subjects and perform MR-guided correction of both cardiac and respiratory motion of dynamic ¹⁸F-FDG PET data. The impact of the technique on PET image quality and estimates of myocardial ¹⁸F-FDG consumption rates was evaluated in healthy subjects.

MATERIALS AND METHODS

Overview of motion correction methodology and enabling assumptions

Dynamic ¹⁸F-FDG PET and MRI data were simultaneously acquired during free-breathing in three healthy human subjects. The PET events for each dynamic frame were reconstructed in two different ways: with the proposed MR-based cardiac/respiratory motion correction (MC) method and without motion correction (NMC). Improvement in cardiac PET image quality was assessed by quantifying the apparent thickness of the myocardium wall as well as the myocardium contrast-to-noise ratio (CNR) in a late dynamic frame. The Patlak analysis method [47], [48] was applied to both MC and NMC dynamic sets to estimate voxel-wise ¹⁸F-FDG uptake rate constants (K_i) in cardiac tissues.

Overview of proposed methodology

The motion correction method for dynamic scan data comprises four key components: (1) Surrogate signals for the cardiac and respiratory cycles that are acquired continuously during the experiment and are used to assign a cardiac and respiratory phase index to every measured coincidence event. (2) A deforming cardiorespiratory tissue motion model which assigns a given cardiorespiratory motion phase (i.e. paired cardiac and respiratory phase) index to a specific 3-D deforming motion vector field. The motion field for a specific phase encodes the movement of each voxel of tissue between said phase and a chosen reference one. As detailed hereinafter, the model is constructed by means of navigator, tagging and golden-angle radial MR acquisitions. Importantly, the MRI motion tracking measurements are performed while also collecting surrogate signals, allowing us to establish the correspondence between the surrogate signals and motion fields. (3) A motion-dependent attenuation model (i.e. one attenuation map per motion phase), generated by deforming an acquired attenuation map with the motion model. (4) A motion-compensated PET reconstruction algorithm which incorporates the motion fields and motion-dependent attenuation data to produce a motion corrected image volume for each frame. Importantly, all coincidences detected during a frame are used to form the final image and therefore the reconstruction method preserves the SNR in each frame. A detailed description of each component is provided afterwards.

Enabling assumptions

Several assumptions are made to simplify the measurement of heart motion and facilitate motion correction of dynamic scan data. One, we assume that myocardium motion due to cardiac contractions is superimposed on top of the respiration motion. Accordingly, one can measure each component separately and subsequently compose the two vector fields to obtain the complete cardiorespiratory motion model. Two, we assume that the positions of tissues are the same for a given state of both the cardiac and respiratory surrogate signals at any time during the dynamic experiment. Therefore, the motion model can be used to correct any acquired event throughout the scan based on the knowledge of surrogate signals only. This implies that cardiac and respiratory motion do not change significantly during the scan and that bulk body motion is absent or negligible.

Imaging data acquisition

Imaging protocol

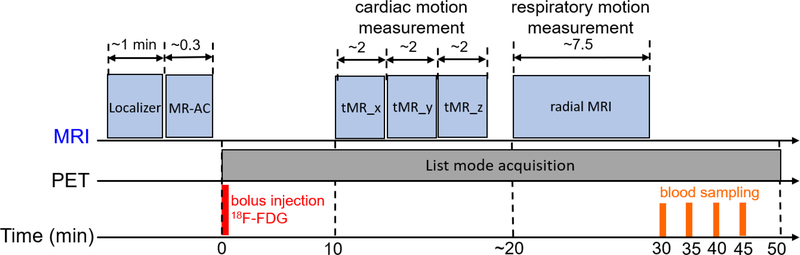
Figure 1 presents a schematic timeline of the imaging protocol. All scans were acquired on a Siemens Biograph mMR, a whole-body integrated 3T PET/MR system. The characteristics and imaging performance of the system have been described elsewhere [49]. Approval for the studies was obtained from the Institutional Review Board at Massachusetts General Hospital and all the subjects provided written informed consent. Study subjects were instructed to fast for 6 hours prior to the start of the experiment. At about 45 min prior to tracer administration, the subjects were instructed to drink a glucose-rich beverage to promote ¹⁸F-FDG uptake in the myocardium. Subjects were prepared for PET/MR imaging, equipped with a 3-lead Electrocardiogram (EKG) system and positioned head first supine on the scanner’s bed. Subjects were then sent in the scanner gantry after a flexible receiving surface coil was placed on the chest. Acquisition of imaging data commenced with the vendor’s MR-based attenuation correction sequence (MRAC) during a breath-hold at end-exhalation to measure an attenuation map. Shortly afterwards, a bolus of ¹⁸F-FDG (average radioactivity: ~10 mCi) was administered intravenously and a 50-min list mode PET acquisition was initiated. Subjects were instructed to relax and breath freely during the scan. At about 10 min after the start of PET acquisition, MR pulse sequences (described afterwards) were played sequentially to track motion due to cardiac contraction and respiration. Four venous blood samples were drawn at 30, 35, 40 and 45 min after tracer administration. After the scan ended, concentrations of radioactivity in the whole-blood and plasma samples were measured on a well counter.

Figure 1:

Schematic timeline of data acquisition. MR-AC: MR-based attenuation correction sequence, ‘tMR_x’: tagged MRI sequence with tag lines orientation parallel to x-axis.

Measurement of cardiac contractile motion

We employed a navigated, cardiac-gated MRI tagging sequence [25], [37] to measure the contractile motion of the myocardium during free breathing. “Tagging” is a magnetization preparation technique which consists in perturbing the magnetization in a spatially-dependent manner before the acquisition of MR imaging data to create temporary fiducial markers (“tags”) within tissues. Because tags result from perturbations of the magnetization of the tissue itself, changes in the shape of tags during imaging reflect the movement of the underlying tissue [50], [51]. The tagging sequence acquires line-tagged, multi-slice cardiac cine MR data sets using SPAMM [52] and a gradient recalled echo acquisition method. Imaging data acquisition is performed at a chosen respiratory phase (end-exhalation in this case) using a pencil-beam navigator intersecting the right lung-diaphragm interface in the superior-inferior direction. Each time an R-wave is detected, a navigator is measured (acquisition time: ~20 msec), and the diaphragm position is calculated; if the position is within a predefined range, the sequence proceeds to acquire the imaging data in all cardiac phases; if not, acquisition remains on standby until the next R-wave. To track motion in 3D, acquisition of line-tagged data was repeated three times, each with a different line tag orientation, corresponding to the three orthogonal Cartesian axes. Two of the three tag acquisitions were performed with transverse slices and the other with sagittal slices, ensuring that tag lines orthogonally intersect the imaging plane. Ten volumes corresponding to ten cardiac phases were acquired for each orientation with the following parameters: TE = 1.97 ms, TR = 4.8–10.2 ms, flip angle = 5–7°, in-plane resolution = 2.3×2.3 mm², acquisition matrix = 128×104, slice thickness = 8 or 10 mm, tag line distance = 8 mm and number of slices = 10. Data acquisition for each tag line orientation took ~1.5–2 min, depending on the subject’s cardiac and respiratory rate.

Measurement of respiratory motion

We used a free-breathing, navigated multi-slice radial sequence with a golden-angle spoke acquisition scheme [28], [53] to measure respiratory motion. For each TR, the sequence first acquires a 1D slice-projection navigator oriented along the superior-inferior direction and intersecting the right lung-diaphragm interface to track the diaphragm position. Afterwards, the same spoke (i.e. with the same in-plane orientation) is acquired in all the prescribed slices. From one TR to the next, spoke orientation is incremented according to the golden-angle formula [54]. The imaging parameters were: TE = 1.53 ms, TR = 3.49 ms, flip angle = 30°, in-plane resolution = 2.3×2.3 mm², acquisition matrix = 128×128, slice thickness = 6 mm, image plane = coronal and number of slices = 24. We let the sequence ran until a total of 5120 spokes per slice were acquired for a total acquisition time of ~7.5 min. During data post-processing, the navigator, acquired for each TR, was used to assign a respiratory phase index to each acquired spoke. The golden-angle encoding scheme provides pseudo-uniform coverage of the k-space for an arbitrary number of acquired spokes, thereby enabling flexible a posteriori binning of spokes into respiratory bins.

Data processing

Tagged MRI

For each subject, the tag data sets comprise three image volumes (two transverse and one sagittal), each with orthogonal tag line directions, for every cardiac phase. To estimate cardiac motion in 3D, the three volumes for each phase were re-oriented and resampled onto the same spatial grid (isotropic 2×2×2 mm³ voxels) and then summed. This procedure yielded ten cardiac volumes tagged along all three Cartesian axes. Note that the tagged volumes depict tissues in the end-exhalation respiratory phase.

Golden-angle radial MRI

The following procedure was employed to process the golden-angle MR data: First, we used the slice-projection navigators to obtain a respiratory trace by tracking the diaphragm position over time. The trace was obtained by selecting a reference navigator signal and by calculating Pearson correlation coefficients between the reference and all other time points. We then applied a previously proposed histogram-guided navigator sorting technique [28] to the trace to assign the acquired spokes to five respiratory bins. The sorting method adapts the amplitude of each bin to obtain approximately the same number of spokes in each bin. Next, iterative reconstruction of the MR data was performed for each bin. Let ${\mathbf{m}}_{{\mathrm{r}}_{\mathbf{k}}}$ denote the set of spokes corresponding to respiratory bin (or ‘phase’) r_k, k ∈ [1; R] (R=5 in this study). The reconstruction of each slice in each phase was performed by preconditioned conjugate gradient-based minimization of a cost-function comprised of a data consistency term including the non-uniform fast Fourier transform (NUFFT) operator [55], and a total-variation regularization term that helps reduce streak artifacts and noise in the reconstructed images [56]:

$$\widehat{{\mathbf{I}}_{{\mathrm{r}}_{\mathrm{k}}}}=\underset{{\mathbf{\lambda }}_{{\mathrm{r}}_{\mathrm{k}}}}{\arg \min }{\Vert \mathbf{F}\cdot \mathbf{C}\cdot {\mathbf{I}}_{{\mathrm{r}}_{\mathrm{k}}}-{\mathbf{m}}_{{\mathrm{r}}_{\mathrm{k}}}\Vert }_2^2+\mathrm{\beta }{\Vert \mathbf{S}\cdot {\mathbf{I}}_{{\mathrm{r}}_{\mathrm{k}}}\Vert }_1$$ Eq. 1

where ${\mathbf{I}}_{{\mathrm{r}}_{\mathrm{k}}}$ denotes the 2-D MR image for respiratory phase r_k, F is the NUFFT operator, C are the estimated 2-D coil sensitivity maps, ‖∗‖₁ and ‖∗‖₂ denote the L-1 and L-2 norms, respectively, S is the total-variation operator [57] and β is a regularization parameter (scalar). This procedure yielded five respiratory-resolved MR volumes that were subsequently used to determine the respiratory motion fields. Note that because cardiac gating was not applied during data reconstruction, the reconstructed MR volumes represented an average cardiac position.

Surrogate signals

As mentioned earlier, the motion correction method relies on surrogate signals to monitor the respiratory and cardiac cycles of the subject during the dynamic scan. EKG is a straightforward and robust approach to monitor the cardiac cycle. Throughout the PET acquisition, the scanner’s physiological monitoring unit inserts a trigger event in the list mode data stream each time an R-wave is detected by the EKG sensor. These trigger events can then be retrieved in the list mode file and a specific cardiac phase can be assigned to each event based on its relative time of arrival with respect to a directly preceding R-wave event. Monitoring of respiration, however, is not as straightforward: for instance, MR navigators are considered as one of the most accurate approaches to monitoring breathing, since unlike respiratory bellows or other external sensors, they can directly measure the position of internal organs (e.g. diaphragm) with high temporal resolution. The disadvantage of using navigators, however, is the fact that their measurement interferes with the MR acquisition and it is therefore impractical to use navigators for continuously monitoring respiration during a long PET acquisition. In this study, we opted for a previously proposed list mode-driven approach to monitor respiration during the dynamic scan [16], and directly compared the method to diaphragmatic navigator acquisitions. First, we obtained a “raw” respiratory curve by counting the total number of coincidences detected within a non-overlapping 100-ms sliding window. Because rapid changes in tracer distribution during the early frames of the scan can deteriorate the quality of the gating signal, this procedure was only applied to events detected after the first-pass delivery of ¹⁸F-FDG, i.e. starting from 1 min after tracer injection. The respiratory trace was obtained by filtering the raw curve using a band-pass filter with cutoff frequencies at [0.1–0.4] Hz. The cutoffs were selected to remove slow trends in the data (e.g. radioactive decay, tracer washout) as well as high frequency components (e.g. counting noise, cardiac contraction), while at the same time preserving the expected frequency range of respiratory fluctuations.

PET data

The list mode data for each subject were sorted into a series of 20 time frames (8 × 15 sec, 4 × 60 sec and 8 × 300 sec) covering a total of 46 min acquisition. The prompt events for each of the last sixteen frames (i.e. after ¹⁸F-FDG first-pass) were binned into 10 cardiac phases and 5 respiratory phases using the surrogate signals (i.e. EKG and list mode-driven respiratory curve), resulting in a total of 50 sinograms per frame. Cardiac phases were defined by dividing each cardiac cycle (i.e. R-R interval) in temporal bins of equal duration. Respiratory phases were defined by applying the histogram-guided sorting method to the list mode-driven respiratory trace [28]. A sinogram of delayed events for each frame was also obtained for correction of random coincidences.

Calculation of cardiorespiratory motion model

The tagging and golden-angle MR volumes were used to measure motion due to cardiac and respiratory functions, respectively. For both data sets, motion field estimation was performed using a nonrigid registration method based on a 3-D tensor product B-spline parametric model [58], [59]. Given two image volumes to register, the algorithm seeks to estimate a diffeomorphic nonrigid transformation by conjugate gradient-based optimization of a cost-function comprised of a standard sum-of-squared-differences data consistency term and a quadratic regularization term. To improve convergence speed and robustness, the algorithm employs a bilevel multiresolution scheme in both image and transformation domains. For both tag and golden-angle MR data sets, rather than directly registering the volume of each phase to the reference phase, we registered consecutive pairs of volumes for estimation of inter-phase (or “partial”) motion fields. The reference phases for cardiac and respiratory motion were chosen as end-diastole and end-exhalation, respectively. The complete cardiac and respiratory motion fields were computed by accumulating the displacements from the partial fields. Let c_n, n ∈ [1; C] and r_k, k ∈ [1; R] denote indices for cardiac and respiratory phases, respectively, and vector $\left(\begin{array}{l}{\mathrm{c}}_{\mathrm{n}}\\ {\mathrm{r}}_{\mathrm{k}}\end{array}\right)$ denote a cardiorespiratory phase. For simplicity, end-diastole and end-exhalation (i.e. reference phases for cardiac and respiration motion) are indexed with n, k = 1. The procedure described earlier yielded two distinct fields:

• ${\left\{{\mathbf{D}}_{\left(\begin{array}{l}{\mathrm{c}}_1\\ {\mathrm{r}}_1\end{array}\right)\to \left(\begin{array}{l}{\mathrm{c}}_{\mathrm{n}}\\ {\mathrm{r}}_1\end{array}\right)}^{\mathrm{card}}\right\}}_{\mathrm{n}=1\dots \mathrm{C}}$, the cardiac displacement field estimated using tagged MRI data, which encodes the 3-D displacement of each voxel between cardiorespiratory phases $\left(\begin{array}{l}{\mathrm{c}}_1\\ {\mathrm{r}}_1\end{array}\right)$ and $\left(\begin{array}{l}{\mathrm{c}}_{\mathrm{n}}\\ {\mathrm{r}}_1\end{array}\right)$.

• ${\left\{{\mathbf{D}}_{{\mathrm{r}}_1\to {\mathrm{r}}_{\mathrm{k}}}^{\mathrm{resp}}\right\}}_{\mathrm{k}=1\dots \mathrm{R}}$, the respiratory displacement field estimated using the golden-angle MRI data, which encodes the 3-D displacement of each voxel between respiratory phases r₁ and r_k. Note that since no cardiac gating was used during data acquisition and reconstruction, these MR volumes represent an average cardiac position. However, we assume that the estimated respiratory motion field apply to any cardiac phase.

We obtain the complete cardiorespiratory motion model by first resampling the two fields on a common voxel grid and then sum the results:

$${\mathbf{D}}_{\left(\begin{array}{c}{\mathrm{c}}_1\\ {\mathrm{r}}_1\end{array}\right)\to \left(\begin{array}{c}{\mathrm{c}}_{\mathrm{n}}\\ {\mathrm{r}}_{\mathrm{k}}\end{array}\right)}^{\mathrm{resp}+\mathrm{card}}\cong {\mathbf{D}}_{\left(\begin{array}{c}{\mathrm{c}}_1\\ {\mathrm{r}}_1\end{array}\right)\to \left(\begin{array}{c}{\mathrm{c}}_{\mathrm{n}}\\ {\mathrm{r}}_1\end{array}\right)}^{\mathrm{card}}+{\mathbf{D}}_{\left({\mathrm{r}}_1\right)\to \left({\mathrm{r}}_{\mathrm{k}}\right)}^{\mathrm{resp}},\mathrm{n}\in [1,\mathrm{C}],\mathrm{k}\in [1,\mathrm{R}]$$ Eq. 2

The combined motion field model D^resp+card describes the 3-D displacement of each voxel between the end-diastolic, end-exhalation phase $\left(\begin{array}{l}{\mathrm{c}}_1\\ {\mathrm{r}}_1\end{array}\right)$ and all other cardiorespiratory phases. The fields were then converted to a set of 3-D image warping operators {W_1→m}, m ∈ [1, M = R × C] for incorporation within PET reconstruction.

Attenuation correction

The vendor’s MRAC method was used to acquire an attenuation map during an end-exhalation breath-hold. MRAC employs Dixon acquisition and tissue segmentation to produce a 4-classes attenuation map (air, lung, fat, soft-tissue). The following procedure was used to generate a motion-dependent attenuation map from breath-hold MRAC scans: First, we non-rigidly registered the water volume produced by MRAC to the end-exhalation golden-angle MR volume using mutual-information based B-spline registration. Second, the estimated transformation was applied to the 4-classes attenuation map to ensure spatial consistency between the motion model and the attenuation map. Third, the cardiorespiratory warping operators were used to deform the resulting attenuation map to all other motion phases.

PET reconstruction

The dynamic PET data for each subject were reconstructed with and without motion correction on a frame-by-frame basis. As mentioned earlier, the prompt events detected in each of the last sixteen dynamic frames were binned into cardiac and respiratory phases, yielding a total of M=50 sinograms per frame. Let ${\mathbf{y}}_{\mathrm{f}}^{\mathrm{m}}\in {\mathrm{ℝ}}^{\mathrm{I}}$ denote the sinogram of prompt events with I bins in dynamic frame f and motion phase m ∈ [1; M]. It is assumed that the elements of ${\mathbf{y}}_{\mathrm{f}}^{\mathrm{m}}={\{{\mathrm{y}}_{\mathrm{f}}^{\mathrm{i},\mathrm{m}}\}}_{\mathrm{i}=1\dots \mathrm{I}}$ are realizations of statistically independent Poisson random variables with expected values ${\overline{\mathbf{y}}}_{\mathrm{f}}^{\mathrm{m}}={\{{\overline{\mathrm{y}}}_{\mathrm{f}}^{\mathrm{i},\mathrm{m}}\}}_{\mathrm{i}=1\dots \mathrm{I}}$. Accordingly, the forward PET model for multi-phase sinogram data in a given temporal frame is:

$$\left[\begin{array}{c}{\overline{\mathbf{y}}}_{\mathrm{f}}^1\\ ⋮\\ {\overline{\mathbf{y}}}_{\mathrm{f}}^{\mathrm{M}}\end{array}\right]=\left[\begin{array}{c}{\mathrm{\Delta }}_{\mathrm{f}}^1\mathbf{S}{\mathbf{A}}^1\mathbf{G}{\mathbf{W}}_{1\to 1}\\ ⋮\\ {\mathrm{\Delta }}_{\mathrm{f}}^{\mathrm{M}}\mathbf{S}{\mathbf{A}}^{\mathrm{M}}\mathbf{G}{\mathbf{W}}_{1\to \mathrm{M}}\end{array}\right]{\mathbf{x}}_{\mathrm{f}}+\left[\begin{array}{c}{\overline{\mathbf{s}}}_{\mathrm{f}}^1\\ ⋮\\ {\overline{\mathbf{s}}}_{\mathrm{f}}^{\mathrm{M}}\end{array}\right]+\left[\begin{array}{c}{\overline{\mathbf{r}}}_{\mathrm{f}}^1\\ ⋮\\ {\overline{\mathbf{r}}}_{\mathrm{f}}^{\mathrm{M}}\end{array}\right]$$ Eq. 3

where ${\overline{\mathbf{y}}}_{\mathrm{f}}^{\mathrm{m}}$, ${\overline{\mathbf{s}}}_{\mathrm{f}}^{\mathrm{m}}$ and ${\overline{\mathbf{r}}}_{\mathrm{f}}^{\mathrm{m}}$ all $\in {\mathrm{ℝ}}^{\mathrm{I}}$ are sinograms of expected prompt, scattered and random coincidences, respectively, ${\mathbf{x}}_{\mathrm{f}}\in {\mathrm{ℝ}}^{\mathrm{J}}$ is the motion-corrected image (i.e. distribution of ¹⁸F-FDG at end-diastole/end-exhalation) with J voxels that we seek to estimate from the sinograms, ${\mathbf{W}}_{1\to \mathrm{m}}\in {\mathrm{ℝ}}^{\mathrm{J}\times \mathrm{J}}$ is an image warping operator that deforms the PET image in the reference phase to phase m (note that W_1→1 = I), $\mathbf{G}\in {\mathrm{ℝ}}^{\mathrm{I}\times \mathrm{J}}$ is the geometric probability matrix, ${\mathbf{A}}^{\mathrm{m}}\in {\mathrm{ℝ}}^{\mathrm{I}\times \mathrm{I}}$ is a diagonal matrix containing the attenuation coefficients for phase m, $\mathbf{S}\in {\mathrm{ℝ}}^{\mathrm{I}\times \mathrm{I}}$ is a diagonal matrix containing the sensitivity coefficient for each sinogram bin, and ${\mathrm{\Delta }}_{\mathrm{f}}^{\mathrm{m}}$ is a scalar corresponding to the ratio between the number of events detected in phase m and the total number of events detected in the frame. Image reconstruction for each frame was performed by maximizing the corresponding Poisson log-likelihood density function using ordered subset expectation maximization [60]. For reconstruction without motion correction (NMC), the forward model in Eq. 3 was modified by setting ${\left\{{\mathbf{W}}_{1\to \mathrm{m}}\right\}}_{\mathrm{m}=1\dots \mathrm{M}}=\mathbf{I}$ and A^m = A¹ (i.e. no motion warping and motion dependent attenuation correction performed). For both MC and NMC reconstructions, sinograms of scattered coincidences were calculated using the single scatter simulation technique [61] and sinograms of randoms using the smoothed delayed window approach. The distributions of scatters and randoms were assumed to be independent of motion, i.e. ${\left\{{\overline{\mathbf{s}}}_{\mathrm{f}}^{\mathrm{m}}\right\}}_{\mathrm{m}=\mathrm{1..}\mathrm{M}}={\left\{{\mathrm{\Delta }}_{\mathrm{f}}^{\mathrm{m}}{\overline{\mathbf{s}}}_{\mathrm{f}}\right\}}_{\mathrm{m}=\mathrm{1..}\mathrm{M}}$ and ${\left\{{\overline{\mathbf{r}}}_{\mathrm{f}}^{\mathrm{m}}\right\}}_{\mathrm{m}=\mathrm{1..}\mathrm{M}}={\left\{{\mathrm{\Delta }}_{\mathrm{f}}^{\mathrm{m}}{\overline{\mathbf{r}}}_{\mathrm{f}}\right\}}_{\mathrm{m}=\mathrm{1..}\mathrm{M}}$, where ${\overline{\mathbf{s}}}_{\mathrm{f}}$ and ${\overline{\mathbf{r}}}_{\mathrm{f}}$ represent scatter and random sinograms estimated using all events in the frame regardless of motion. All PET images were reconstructed on a 2.08×2.08×2.03 mm³ voxel grid with 4 iterations and 12 subsets.

PET images analyses

Evaluation of image quality

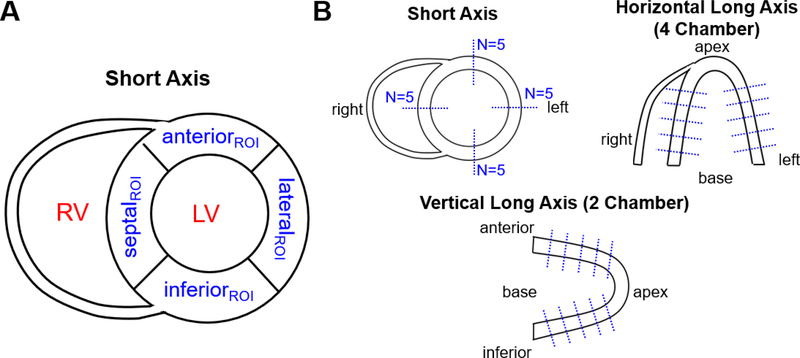
For each subject, we evaluated the quality of MC and NMC images by comparing myocardium contrast-to-noise ratio (CNR) and apparent myocardial wall thickness in a late (40 min after injection) 5-min frame. Activity images were first re-sliced in short axis orientation and five evenly spaced planes sampling the heart from apex to base were selected. For each plane, four regions of interest (ROI) were manually positioned in the septal, lateral, anterior and inferior walls (see Figure 2 A). A spherical ROI (4 mm radius) was also drawn in the mid left-ventricular blood cavity. Next, CNR [9] was calculated for each ROI as:

$$\mathrm{CNR}=\frac{\mathrm{Mean}\left({\mathrm{Myoc}}_{\mathrm{ROI}}\right)-\mathrm{Mean}\left({\mathrm{LV}}_{\mathrm{ROI}}\right)}{\mathrm{SD}\left({\mathrm{LV}}_{\mathrm{ROI}}\right)}$$ Eq. 4

where Mean and SD are the voxel-wise mean and standard deviation of activity values in a ROI, Myoc_ROI and LV_ROI refer to ROIs taken in the myocardium and left-ventricle blood bool respectively. To measure the apparent thickness of the myocardium in septal, lateral, anterior and inferior walls, we extracted line profiles in short axis (SA), horizontal long axis (‘HLA’, approximating the four-chamber view [62]) and vertical long axis (‘VLA’, approx. the two-chamber view) planes, as illustrated in Figure 2 B. More specifically, we extracted 20 profiles along the septal, lateral, anterior and inferior walls in 5 SA slices spread-out evenly over the length of the myocardium, 10 profiles in the septal and lateral walls in the selected HLA plane, and 10 profiles in the anterior and inferior walls in the VLA plane. The exact same slices were selected for MC and NMC images. This procedure yielded a total of 40 profiles for each volume. Thickness of the wall was quantified as the full-width at half maximum of a 1-D Gaussian function fitted to each profile.

Figure 2:

Illustration of positioning of (A) ROIs for one short-axis plane and (B) line profiles for calculation of myocardium CNR and apparent wall thickness, respectively.

Calculation of myocardial ¹⁸F-FDG uptake rates

Parametric images of net ¹⁸F-FDG influx rate (K_i, with units of min⁻¹) were calculated by applying the Patlak plot method [63] to the last 40 min of the dynamic acquisition. The first frames were omitted during the analysis to obtain steady-state equilibrium between the reversible and plasma compartments. To compute input functions for kinetic modeling, we extracted a whole-blood time-activity curve (TAC) in a spherical ROI (4 mm radius) located in the base of the left ventricle blood pool in both MC and NMC image sets. Next, arterial plasma input functions were computed by scaling whole-blood TACs to the plasma activity concentrations measured in the four blood samples. Patlak analysis was then applied on a voxel-wise basis for both MC and NMC dynamic sets using the corresponding input functions. The operational equation for the Patlak model is defined according to:

$$\frac{{\mathrm{C}}_{\mathrm{T}}(\mathrm{t})}{{\mathrm{C}}_{\mathrm{p}}(\mathrm{t})}={\mathrm{K}}_{\mathrm{i}}\frac{{\int }_0^{\mathrm{t}}{\mathrm{C}}_{\mathrm{p}}(\mathrm{t})\mathrm{d}\mathrm{t}}{{\mathrm{C}}_{\mathrm{p}}(\mathrm{t})}+V_b$$ Eq. 5

where C_T(t) and C_p(t) are instantaneous concentrations of activity in myocardium tissue and arterial plasma, respectively, and V_b is the intercept. Parameters of the Patlak model were estimated for each voxel by linear least-square regression. The resulting parametric images were resliced to short-axis view using the transformation parameters applied to the activity images. Average K_i values were then calculated in the previously defined 20 myocardium ROIs. According to Eq. 5, an increase in reconstructed myocardium activity concentration following motion correction should translate into higher K_i values.

Statistical Analysis

All statistical tests were performed using a two-tailed paired t-test. A p-value lower than 0.05 was considered significant.

RESULTS

Figure 3 presents examples of images and displacement fields obtained using tagging and golden-angle radial MR acquisitions for various cardiac and respiratory phases. The motion fields estimated with tagged MRI (Figure 3 A) depict the movement of the myocardium between the reference end-diastolic phase (C₁) and all other cardiac phases. Note that due to T1 recovery, the contrast of the tag lines progressively decreases towards the end of the cardiac cycle, which may impact the accuracy of motion estimation in the late cardiac phases. The displacement fields overlaid on top of the respiratory-gated radial MRI slices (Figure 3 B) show the movement of thoracic tissues, including heart and liver, between the reference end-exhalation phase (R₁) and other respiratory phases. Note that non-rigid registration techniques, such as the one employed in this work cannot guarantee accurate estimation of motion in areas with uniform intensities such as the left-ventricle blood pool.

Figure 3:

Examples of images and motion fields estimated using tagged (A) and golden-angle radial (B) MR acquisitions in subject 1. Tagged and golden-angle images are shown in transverse and coronal orientations, respectively. The motion fields estimated with tagged (resp. golden-angle radial) MRI capture the movement of voxels between the reference end-diastolic (resp. end-exhalation) phases and all other cardiac (resp. respiratory) phases. The blue arrow in (B) indicates the placement of the navigator. LV: left ventricle, RV: right ventricle.

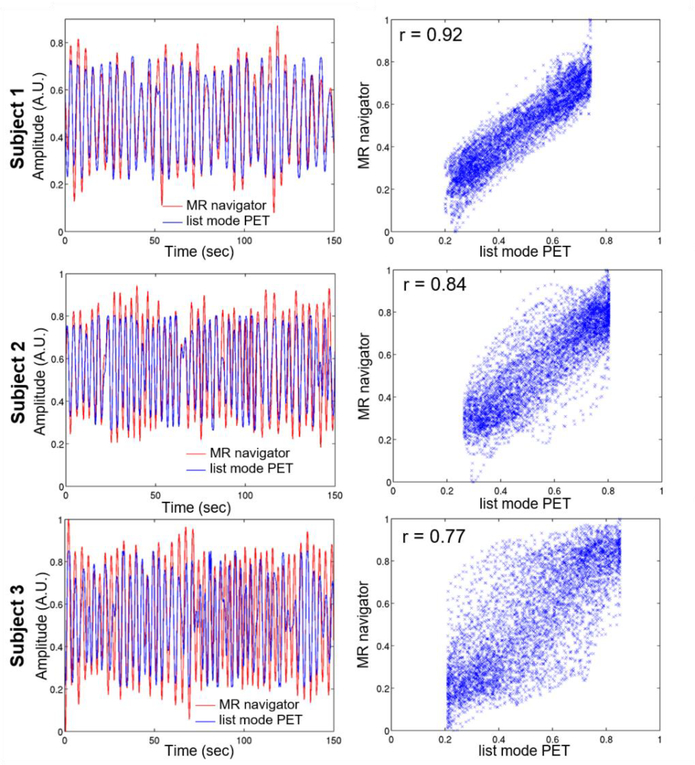
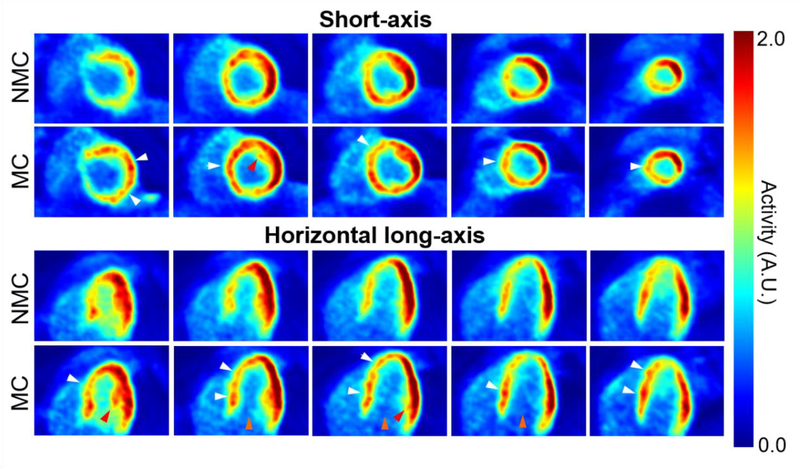
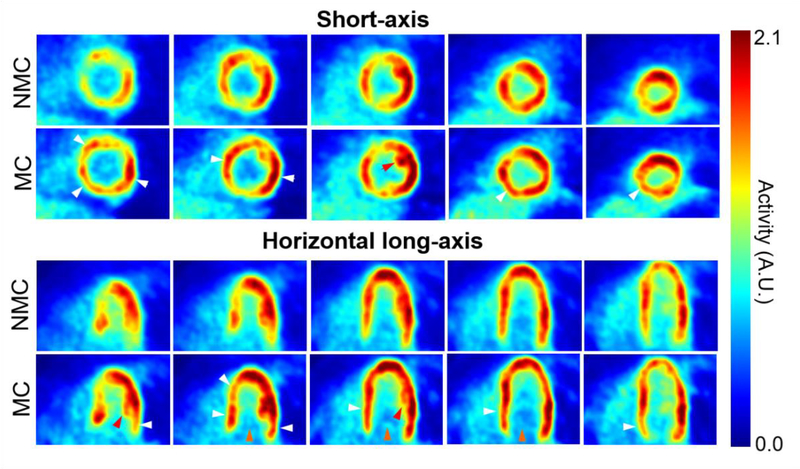
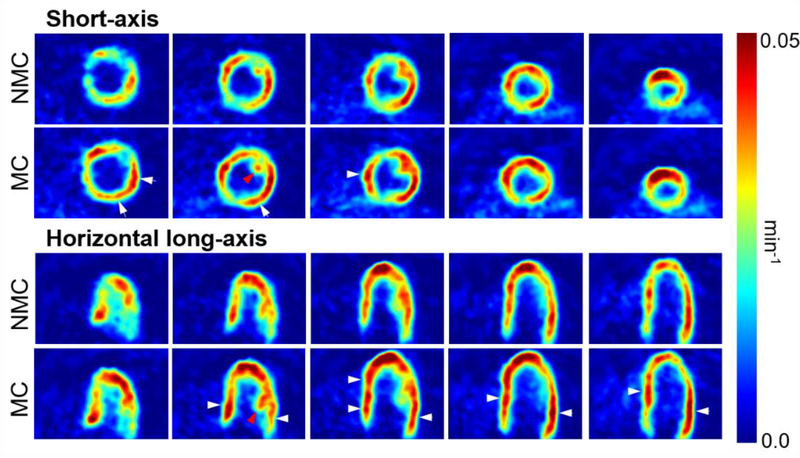
Figure 4 compares the traces obtained using the list mode-driven method and the MR navigator measured during the golden-angle radial scan for all three subjects. There was a strong correlation between the navigator and list mode-driven signals for all subjects, in agreement with findings from other groups [64]. Figures 5 and 6 display five evenly spaced short-axis and horizontal long-axis images of a late dynamic frame reconstructed with MC and NMC for subject 1 and 2, respectively. MC images showed visibly higher spatial resolution than NMC images as evidenced by the improved delineation of papillary muscles (red arrows), higher myocardium wall signal (white arrows), reduced spillover of activity from the myocardium to the left-ventricle blood pool (yellow arrows) and thinner wall. Visually, the impact of motion correction was most substantial in the septum, especially at the basal level.

Figure 4:

Respiratory traces generated for all three subjects using list mode and MR navigator-based techniques. The left panels show plots of the two curves for a 150-sec window, while the right panels show the corresponding scatter plots.

Figure 5:

Short-axis and horizontal long-axis images of a late dynamic frame reconstructed with MC and NMC for subject 1. White arrows indicate locations where reconstructed wall activity is clearly higher in MC compared to NMC. Red arrows point to papillary muscles whose structure is more visible in MC images, indicating improved spatial resolution. Orange arrows indicate areas where spillover from the myocardium to the left-ventricle cavity is visibly reduced in MC images.

Figure 6:

Short-axis and horizontal long-axis images of a late dynamic frame reconstructed with MC and NMC for subject 2. White arrows indicate locations where reconstructed wall activity is clearly higher in MC compared to NMC. Red arrows point to papillary muscles whose structure is more visible in MC images, indicating improved spatial resolution. Orange arrows indicate areas where spillover from the myocardium to the left-ventricle cavity is visibly reduced in MC images.

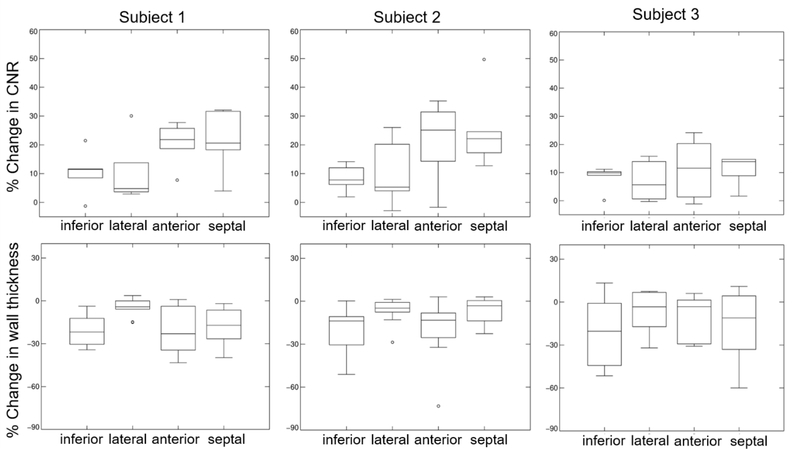
Table 1 presents CNR and wall thickness values extracted in MC and NMC images for different sectors of the myocardium for all three subjects. Figure 7 plots percent differences in myocardium CNR and thickness between MC and NMC (i.e. $\frac{(\mathrm{MC}-\mathrm{NMC})}{\mathrm{NMC}}\times 100\mathrm{\%}$). For all subjects, MC yielded significantly higher myocardium CNR (all p<0.05) and lower apparent wall thickness than NMC (all p<0.05). CNR increased by an average of up to 20.1% in the septal wall and 16.4% in the anterior wall for MC compared to NMC. Apparent wall thickness decreased by an average of 18.9% in the inferior wall and 18.4% in the septal wall as compared to NMC. Overall, the impact of motion correction was lower in subject 3 than in the other two subjects. One possible reason for this is the lower quality of the list mode-based respiratory gating curve for this subject, which was noisier and exhibited a weaker correlation with the navigator-based signal. The lower performance of event-based gating may have been caused by the relatively lower apparent ¹⁸F-FDG myocardium uptake in subject 3 compared with the other subjects.

Table 1.

Contrast-to-noise-ratio (CNR) and apparent thickness of the inferior, lateral, anterior and septal walls for the two reconstruction methods (mean ± SD)

Subject no.		CNR		Thickness (mm)
		MC	NMC	MC	NMC
1	inferior	16.2±2.3	14.7±2.1	15.5±3.9	18.7±4.3
	lateral	21.0±3.7	19.2±4.3	14.7±2.7	15.4±2.6
	anterior	17.8±2.8	14.9±2.6	11.8±2.9	14.1±3.4
	septal	14.6±2.4	12.0±1.2	13.6±2.8	16. 2±4.5
2	inferior	17.3±0.8	16.1±1.4	16.1±4.4	19.3±5.8
	lateral	22.9±3.5	21.1±4.9	14.8±4.5	15.7±4.5
	anterior	19.9±2.9	16.9±4.9	11.5±1.6	13.6±2.8
	septal	17.3±0.9	14.0±1.8	14.8±3.2	15.8±3.8
3	inferior	6.9±0.6	6.4±0.7	16.2±3.1	20.2±7.1
	lateral	9.0±0.85	8.5±1.1	16.7±4.8	17.5±5.7
	anterior	8.8±1.4	7.9±0.7	15.1±1.9	16.9±4.1
	septal	5.1±0.7	4.5±1.2	15.6±3.4	19.4±6.7

Figure 7:

Percent changes in myocardium CNR and wall thickness between MC vs. NMC images for all three subjects. Overall, MC images have higher CNR and lower wall thickness than NMC in all four myocardium sectors.

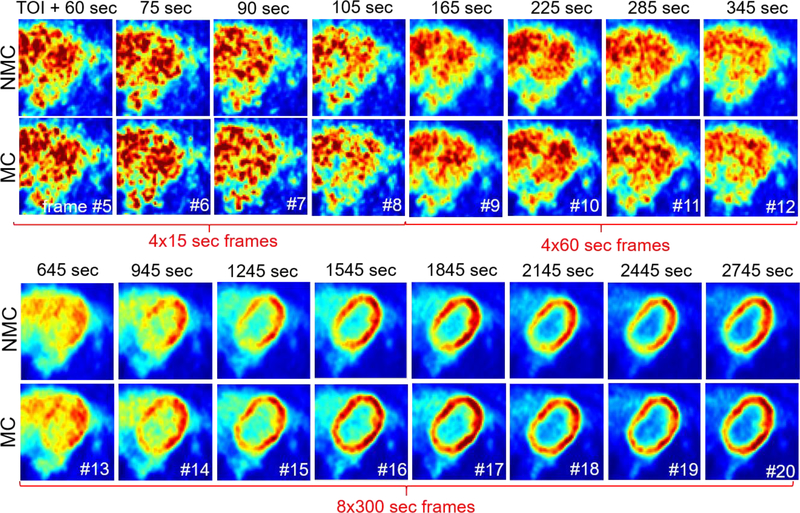
Figure 8 shows the same transverse slice in the various dynamic frames reconstructed using NMC and MC methods for subject 2. Supplementary Figure 1 presents the same data for subject 1. In general, we found that for the frames acquired up to ~4 min after administration of ¹⁸F-FDG (frame #5 to 10), MC led to a slightly lower reconstructed myocardium activity concentration as compared to NMC, which is consistent with reduced spillover effects from the blood cavity to the myocardium. When the activity distribution is uniform (e.g. frame #11 and 12), with similar blood and myocardium signals, MC does not seem to have much effect, which is likewise consistent with expectations. The impact of the correction becomes more pronounced for the later frames (e.g. frame #13–20) as the tracer accumulates in the myocardium and the contrast between myocardium and blood increases.

Figure 8:

Same transverse slice across dynamic frames for NMC and MC methods (subject 2). Note that, to facilitate comparison of NMC and NMC images, the display range was adapted specifically for each dynamic frame. The first 4 frames after injection are not included in the figure as they were not corrected for motion. TOI = time of injection.

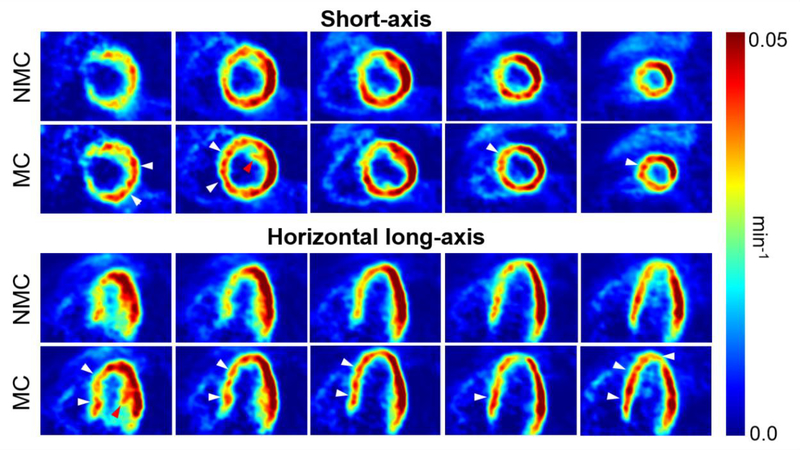
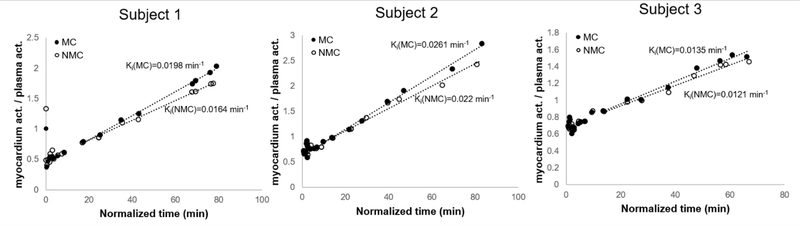
Parametric images of ¹⁸F-FDG influx rate (K_i, with units of min⁻¹) were calculated as described in Methods for all three subjects. Figures 9 and 10 display short and horizontal long-axis K_i slices computed with MC and NMC data for subjects 1 and 2, respectively. Note that the presented slices correspond to those shown in Figures 5 and 6. As can be seen, MC dynamic data yielded K_i maps with overall higher values in the myocardium and improved spatial resolution as compared to NMC images. Figure 11 shows examples of Patlak plots for MC and NMC in one ROI taken in the basal section of the septum, where motion correction was found to have the most impact.

Figure 9:

Short-axis and horizontal long-axis K_i slices obtained using MC and NMC dynamic images for subject 1. MC yielded higher K_i values than NMC, especially in regions evidenced by white arrows. Structures such as papillary muscles are also easier to delineate in MC K_i maps (see red arrows).

Figure 10:

Short-axis and horizontal long-axis K_i slices obtained using MC and NMC dynamic images for subject 2. MC yielded higher K_i values than NMC, especially in regions evidenced by the white arrows. Structures such as papillary muscles are also easier to delineate in MC K_i maps (see red arrows).

Figure 11:

Examples of Patlak plots for MC and NMC in one ROI taken in the base of the septum. (normalized time: integrated plasma activity over [0-t] / plasma activity (t)).

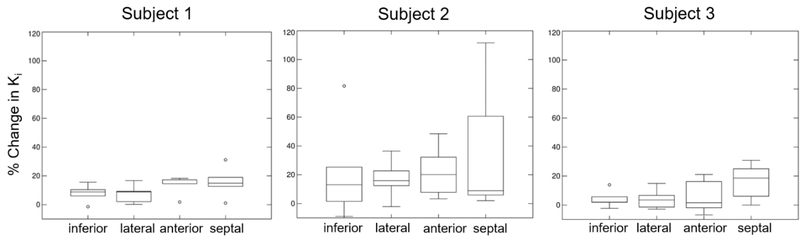
Table 2 shows MC and NMC K_i values for the different myocardium regions in all three subjects. Figure 12 displays box plots of K_i percent differences between MC and NMC. Motion correction yielded significantly higher K_i values for all subjects as compared to NMC (all p<0.05). Higher K_i values were obtained everywhere, especially in the septum where average K_i increased by 18% as compared to NMC.

Table 2.

K_i values in the inferior, lateral, anterior and septal walls for the two reconstruction methods (mean±SD)

		Ki (min−1)
Subject no.		MC	NMC
1	inferior	0.031±0.004	0.029±0.004
	lateral	0.038±0.007	0.035±0.007
	anterior	0.031±0.005	0.027±0.005
	septal	0.027±0.002	0.023±0.001
2	inferior	0.034±0.002	0.029±0.006
	lateral	0.035±0.006	0.030±0.004
	anterior	0.035±0.006	0.029±0.009
	septal	0.033±0.006	0.027±0.010
3	inferior	0.050±0.005	0.048±0.005
	lateral	0.063±0.007	0.061±0.010
	anterior	0.064±0.011	0.060±0.006
	septal	0.037±0.008	0.033±0.008

Figure 12:

Percent differences in myocardium K_i for MC vs. NMC for all three subjects. Motion correction yields higher K_i values almost everywhere but especially in the septum.

DISCUSSION

Motion of the myocardium deteriorates the spatial resolution and quantitative accuracy of cardiac PET images. We developed a methodology for MRI-based cardiac and respiratory motion correction of PET data and evaluated its impact on image quality as well as quantification of myocardial ¹⁸F-FDG uptake rates in three healthy subjects. The results obtained suggest that the proposed correction method alleviates motion artifacts in PET images, resulting in visibly improved spatial resolution, increased recovery of activity in the myocardium and reduced spillover of activity from the myocardium to the left ventricle cavity. As a result, significantly higher CNR (up to 20.1% mean CNR increase in septum across subjects) and lower apparent wall thickness (up to 18.9% mean thickness decrease in inferior wall) were obtained in the resulting motion corrected images as compared to non-corrected ones. Likewise, motion correction yielded parametric images of ¹⁸F-FDG uptake rates (K_i) with improved spatial resolution. The correction led to the estimation of higher K_i values almost everywhere in the myocardium, with up to 18% increase in septal K_i (mean across subjects) as compared to non-corrected data. Overall, the impact of motion correction was the greatest in the basal regions of the myocardium in all subjects.

A key component of the correction technique is the recording of respiration as a function of scanning time. In this study, we used a previously proposed sensitivity-based event-driven method to derive a surrogate signal for the respiratory cycle. In agreement with works from other groups [22], a strong correlation was obtained for all subjects between the obtained respiratory curves and diaphragm position readouts using navigators (see Figure 4). Therefore, the event-driven signal was considered accurate enough to bin PET events into the different respiratory phases. It is important to highlight that, in a dynamic PET scan, the raw signal extracted using the sensitivity method (i.e. number of counts as a function of time) will be correlated not only to respiratory and cardiac motion, but also to decay and tracer kinetics. The latter factor can produce either high or low frequency components in the signal depending on timing with respect to tracer injection: typically, it is expected that tracer kinetics will introduce high frequency changes in early frames (first-pass of the tracer) and lower frequency contributions (e.g. tracer washout) in later frames. In this study, to minimize the influence of tracer kinetics, event-driven gating was applied after the first-pass of ¹⁸F-FDG and band-pass Fourier filtering was used to isolate the respiratory component. Further investigations are needed to study the accuracy of event-driven gating methods in early frames, especially in the context of cardiac blood flow studies.

We employed a combination of sequential tag and golden-angle MR acquisitions to obtain a cardiorespiratory motion field for each subject. MR tagging is considered as one of the most accurate approaches to measure cardiac contractile motion in that it provides “features” in cardiac tissues that non-tagged MRI lacks and thereby facilitates estimation of intramural motion. Another advantage of tagging is that it naturally offers contrast between heart muscle and blood cavity, as tagging of blood protons rapidly vanishes with blood circulation within the ventricles during the cardiac cycle. A drawback of 3D MR tagging, however, is the long time needed to acquire the data. Here, to limit scan times, the acquisition of the three tagged MRI data sets was performed using a relatively coarse slice resolution (8–10 mm), which will necessarily impact the accuracy of the motion fields. Parallel imaging or compressed sensing could be employed to drastically accelerate data acquisition without significantly degrading motion field accuracy [37]. T1 recovery-induced tag line fading, which can be appreciated by inspecting the tagged images in Figure 3 A, is another well-known limitation of tagged MRI that can lead to a deterioration of the quality of the motion field estimates, especially in the late cardiac phases. Nevertheless, since the largest displacements occur during the first phases of the cardiac cycle which exhibit good tag contrast, the impact of fading on the motion corrected PET images should remain relatively small. Moreover, our tagged MRI sequence assumes that the subject’s respiratory phase, determined by a navigator readout prescribed immediately after each R-wave, does not change during the R-R interval length whose duration is typically ~0.7–1.0 sec in resting conditions. In reality, however, the respiratory phase may change during this time period, which can introduce respiratory motion artifacts, especially towards the end of the cardiac cycle. Lastly, in the current version of the sequence, the duration of the data acquisition window after R-wave detection is fixed and must be pre-defined by the operator based on the average cardiac cycle rate of the subject. Therefore, difficulties could arise when imaging a patient with a very irregular cardiac cycle.

Respiratory motion was tracked in each subject using a navigated, golden-angle based radial MR sequence. As mentioned earlier, we let the sequence run until a total of 5,120 spokes per slice (and thus 5,120 navigators) were acquired, leading to a ~7.5 min scan. All acquired spokes were then binned into 5 respiratory phases based on the navigator-measured diaphragm position. As a result, the reconstruction of each slice in each respiratory phase was performed using ~1,000 spokes, which is about 5-fold higher than the number of spokes prescribed by the Nyquist sampling criterion. Therefore, it is important to underline that while we deliberately chose to acquire a large number of spokes in this study in order to obtain a robust estimate of the correlation between the navigator and event-driven respiratory curves, the scan time for measuring respiratory motion using this sequence could be drastically shortened in practice. Furthermore, because the main components of respiratory motion are along head-feet and antero-posterior directions [65], the use of sagittally-oriented slices should be more optimal for capturing respiratory motion. Here, we chose to acquire coronal rather than sagittal orientation because it allows for imaging, and hence motion estimation, of the whole thorax using a relatively smaller number of slices, while keeping the primary motion component (head-feet) within the imaging plane. It is indeed important that the cardiorespiratory motion model includes not only the heart but also other moving tissues (e.g. liver) within the PET field-of-view for accurate motion correction of projection measurements. Finally, it should be noted that irregular breathing patterns and large variations in respiratory motion amplitude would make the measurement and correction of respiratory motion more challenging. Further investigations are needed, especially in patients with cardiovascular diseases, to understand how the current approach should be modified to account for such effects.

The proposed motion tracking and modeling method relies on the assumption that cardiac motion is superimposed on top of respiratory motion and that the two motions can therefore be measured separately. A limitation of this approach is that it does not account for possible variations in cardiac motion patterns in the different respiratory phases. Furthermore, it is known that respiratory motion can show hysteretic effects in some subjects [66], [67], whereby the same diaphragm position corresponds to different heart positions at inspiration and expiration. Although this has not been explored in the present study, it is in principle possible to account for hysteresis by assigning the PET and MR data to different phases according to the respiratory state (i.e. inspiration or expiration).

Although motion correction generally led to a decrease in apparent wall thickness and an increase in CNR and K_i as compared to no motion correction, it should be noted that this was not the case everywhere, as in some areas, MC images exhibited similar or even slightly lower CNR and K_i values as well as greater apparent wall thickness than NMC images (see box plots in Figure 7 and 12). A possible reason for this might be local errors in the cardiorespiratory motion field that may deteriorate the quality of the correction in relevant areas.

In general, by alleviating spillover from myocardium to blood and vice-versa in reconstructed PET images, motion correction (MC) is expected to reduce bias in estimates of activity concentration and kinetic parameters. In this population of healthy subjects, motion correction led to an increase in reconstructed myocardium activity in the frames used for kinetic modeling, which resulted in the estimation of overall higher K_i values as compared to non-corrected data. However, it should be noted that motion correction of dynamic cardiac PET scan data may not always translate into an increase in estimated K_i values. For instance, in diseased myocardium with low tracer uptake, one expects motion corrected images to exhibit lower activity concentration in the defect as compared to non-corrected images [35], which might lead to the estimation of lower K_i values in relevant segments [41].

To evaluate the relative impact of respiratory and cardiac motion correction, Supplemental Figures 2–5 compare images of activity and K_i obtained without motion correction to those obtained by applying respiratory-only, cardiac-only and ‘dual’ (i.e. respiratory and cardiac, as used throughout the paper) motion correction. Overall, we found that correcting respiratory or cardiac motion effects alone lead to noticeable improvement in image quality as compared to no motion correction. By visual inspection of the estimated activity and K_i images, it is clear that correction of both cardiac and respiratory motion had the most impact on image quality (e.g. compare delineation of papillary muscles and septal wall in left-most HLA slice in Supplemental Figures 2 and 4).

Long dynamic scans are associated with an increased likelihood of body movement during the acquisition, especially in patients with cardiac disease. Body motion is unpredictable and can occur for numerous reasons including subject discomfort, coughing or deep breathing. Such motion can have a severe impact on image quality and confound kinetic parameter estimation [68], [69]. In principle, estimates of body motion (e.g. obtained using registration of dynamic PET images [70]) could be employed to adapt the cardiorespiratory motion model to each dynamic frame based on patient position. This will be part of future technical developments.

Another potential issue that comes along with extended PET scans is the possibility of changes in cardiac and respiratory motion patterns that could result in inaccurate modeling and correction of motion for some portions of the scan. Further works are needed to investigate how the motion model could be modified to account for such variation. Nevertheless, the fact that motion correction led to estimation of parametric images with improved resolution suggests that the motion model was relatively accurate for the whole dynamic scan in this study.

Myocardial perfusion imaging protocols typically involve the acquisition of two PET scans, one in resting conditions and the other during pharmacological stress. The administration of vasodilators (e.g. regadenoson) for stress imaging will cause an increase heart rate and may also substantially change the breathing pattern of the patient [11]. Therefore, it is possible that distinct cardiorespiratory motion models need to be obtained for both scanning conditions, although this warrants further investigations.

The number of subjects in this study was small as we only scanned three subjects. Another limitation of this work is the lack of motion-free reference standard for validation of the motion correction methodology. Indeed, due to the drastic increase in noise associated to rejecting events in dynamic frames, we did not apply kinetic modeling to dual-gated PET images. Nevertheless, comparisons of motion corrected vs. non-corrected results could demonstrate the effectiveness of the method and its impact on activity and kinetic parameter quantification. However, further investigations in patients with cardiac diseases are needed to determine whether motion correction improves the diagnostic value of cardiac PET.

CONCLUSION

In this work, we presented a method for MR-based cardiac and respiratory motion correction of cardiac ¹⁸F-FDG PET data and evaluated its impact on quantification of activity and kinetic parameters in healthy volunteers. The method was shown to substantially improve the spatial resolution and contrast of cardiac ¹⁸F-FDG images. Motion correction yielded parametric images with improved spatial resolution and produced a significant increase in K_i estimates, consistent with increased reconstructed myocardial activity in the frames used during kinetic analyses.