Design and analysis of a clinical trial using previous trials as historical control

Abstract

Background/Aims:

For single arm trials, a treatment is evaluated by comparing an outcome estimate to historically reported outcome estimates. Such a historically controlled trial is often analyzed as if the estimates from previous trials were known without variation and there is no trial to trial variation in their estimands. We develop a test of treatment efficacy and sample size calculation for historically controlled trials that considers these sources of variation.

Methods:

We fit a Bayesian hierarchical model, providing a sample from the posterior predictive distribution of the outcome estimand of a new trial, which, along with the standard error of the estimate, can be used to calculate the probability that the estimate exceeds a threshold. We then calculate criteria for statistical significance as a function of the standard error of the new trial and calculate sample size as a function of difference to be detected. We apply these methods to clinical trials for amyotrophic lateral sclerosis (ALS) using data from the placebo groups of sixteen trials.

Results:

We find that when attempting to detect the small to moderate effect sizes usually assumed in ALS clinical trials, historically controlled trials would require a greater total number of patients than concurrently controlled trials, and only when an effect size is extraodinarily large is a historically controlled trial a reasonable alternative. We also show that utilizing patient level data for the prognostic covariates can reduce the sample size required for a historically controlled trial.

Conclusion:

This paper quantifies when historically controlled trials would not provide any sample size advantage, despite dispensing with a control group.

Introduction

The gold standard for clinical trials is to use randomization to generate a concurrent control group that differs, in principle, only with respect to use of the intervention under study. Often the team designing the study discusses an alternative, the historically controlled trial (HCT), where the investigator compares their results from patients treated on an experimental arm to outcomes observed in one or more previous trials of patients given the usual treatment. Such trials are more common when the experimental arm is a new treatment and the trial is designed to help decide whether to do additional trials to show efficacy, a so called Phase II trial. This paper focuses on one aspect of the discussion of whether or not to conduct an HCT, which is how to determine the sample size required for such a trial when properly accounting for variation in the historical control group outcomes. These results are one consideration that can help inform the discussion as to whether or not it is acceptable to do such an HCT. In effect, we show how to quantitatively evaluate the claim made by Paul Meier,¹ that if you correctly accounted for the trial-to-trial variability then there would be little advantage to the use of historically controlled trials. We also quantify one of the rules for HCTs published in the New England Journal of Medicine in 1990,² which states that HCTs are only appropriate when the expected treatment effect is large.

The usual analysis of an HCT is to compare a statistic such as the mean response rate, median survival time, or mean rate of change from the experimental group to the same statistic from the historical comparator trials without fully accounting for uncertainty in the historical estimate. We denote the statistic used to assess the results of a trial as the outcome of the trial in what follows. When variability in the outcomes of the historical comparator trials are ignored, an HCT appears to require one fourth the number of patients that would be required to detect the same magnitude of treatment effect in a randomized controlled trial (RCT) that assigns treatments equally to two groups.³ This is true because the sample size is halved by removing the control group and then halved again because the variability of the control group outcome is treated as zero. The ignored variability in this calculation derives from patient-to-patient variability and unexplained trial-to-trial variability. This variability could reflect factors such as differences from trial to trial in the types of centers involved (academic, community-based, etc.) that could lead to variation in the manner in which the experimental (and other) treatments are delivered, differences in the nature of the underlying study target populations, and differences in the actual patients enrolled (covariate distributions). We conceptualize the problem as follows: investigators running an HCT perform a single trial from a population of potential trials. Repetitions of the trial would not all yield the same outcome. The outcome of each individual trial is subject to a random trial effect as well as variation due to sampling. If there is a true treatment effect it would be added to this trial effect. When the trial data are compared to historical data, this random trial effect could make the difference look significant when there was no effect of treatment, or perhaps worse, it could make the difference look insignificant when there was a difference.

The purpose of this paper is to develop a criterion based on control group (usual care) data from multiple clinical trials that can be used to assess significance of the outcome of a single arm study while appropriately acknowledging the presence of trial-to-trial variation. Our approach uses a Bayesian hierarchical model to account for variability in the historical trials and our uncertainty in estimating it. We demonstrate how to determine the required sample size for trials that would use this criterion. Through our derivation, we quantify the guidance given in Byar et al.² that HCTs are appropriate when the effect of treatment is large or only large differences are of interest. Given the strong interest of patients, researchers, and funders in conducting efficient and timely trials, this insight can guide the decision of when an HCT is reasonable.

We consider two scenarios. The first is where the historical outcome data are a list of trial outcomes and their standard errors. Such historical data can be compiled from the published literature or online.⁴ We show how to develop a control chart that can be used to determine whether the estimated treatment effect from any future HCT is greater than would be expected by chance. In addition, we show how to develop a sample size chart that shows how large such an HCT should be. The second scenario requires patient level data from multiple trials and we discuss how prognostic covariates might reduce the trial effect and thereby increase the efficiency of HCTs.

There is an extensive literature on whether to conduct HCTs. For instance, Gehan and Freireich⁵ created controversy in the cancer community by advocating that single arm trials be used and others have discussed this issue in the literature.⁶, ⁷ The use of a Bayesian hierarchical model to analyze HCTs was suggested in Meier¹ but was not implemented. He brought forward this method as an argument that if you correctly accounted for the trial-to-trial variability then there would be little advantage to the use of historically controlled trials. Although Meier doesn’t elaborate, one assumes that he is comparing the number of patients in the experimental group in the historically controlled trial with the number of patients in the combined experimental plus control group in the randomized trial. We implement his suggestion in this paper and show that his statement is true for a study in Amyotrophic Lateral Sclerosis (ALS) in the sense that the historically controlled trial would require more patients than a randomized trial (with two groups) to detect a treatment difference associated with an effective therapy in this disease.⁸

One could also use a Bayesian hierarchical model to pool concurrent control group data with historical control groups. Pooling historical data with a randomized control group also has an extensive literature beginning with Pocock et al. ⁹ and more recently reviewed by others. ^10-12. The Galway paper¹² contrasts various approaches including a Bayesian hierarchical model using a simulated example. Despite this literature, pooling historical and concurrent data does not seem to be commonly used in clinical trials.

The outline of this paper is as follows. We describe the Bayesian hierarchical model that we used and how we calculated the predictive distribution of the outcome parameter for clinical trials. We then show how this distribution can be used both to generate criteria for evaluating an HCT and for calculating the required sample size. We discuss the issue of using a machine learning-based predictive model based on covariates to reduce the sample size even further. Finally, we apply this approach using data from the PRO-ACT data base¹³ as an example of applying these criteria to amyotrophic lateral sclerosis (ALS) clinical trials.

Methods

Using estimates of means and standard errors from multiple groups

We start with the situation where patient-level data from historical trials are unavailable. What are available are estimates of the parameter of interest from the control groups from m clinical trials, say ${\widehat{\mu }}_1$, ${\widehat{\mu }}_2$, … , ${\widehat{\mu }}_m$. These parameters might be the mean of an outcome variable, a proportion, or any summary that could be used to evaluate the results for the treatment and control group. Suppose also that we have the standard error of each ${\widehat{\mu }}_1$, ${\widehat{\mu }}_2$, … say τ₁, τ₂, … . In most fields such statistics are available or could be easily derived from published manuscripts. In what follows, for i indexing trial, we consider ${\widehat{\mu }}_i$ to be random variables but we consider each τ_i to be known exactly. The method we use is described in Gelman et al.¹⁴ and is their paradigmatic example of a Bayesian analysis. We need to treat τ_i as known exactly because, as in the example in Gelman et al.,¹⁴ in most situations the clinical trials would have slightly different designs. As a result although the estimands would be the same, the standard errors, would not be a patient level standard deviation divided by $\sqrt{n}$, where n is the sample size, and more importantly they would not be proportional to $1∕\sqrt{n}$ with the same proportionality constant. We assume the sample size of each of the trials would have to be large enough so that the variability of the standard error due to sampling variation is negligible. An alternative approach is to treat the standard deviation as an estimate having a distribution, which is more appropriate for small sample sizes as is discussed later in this section.

We assume a hierarchical model where ${\widehat{\mu }}_i$ is an estimate of μ_i. where the later has a normal distribution with mean μ and standard deviation σ. The parameter σ is the trial-to-trial variability in the outcome. The full hierarchical model of the observed data is: ${\widehat{\mu }}_i~\mathrm{Normal}({\mu }_i,{\tau }_i)$, μ_i ~ Normal(μ, σ). The priors for μ σ were the uniform priors that STAN uses by default. To develop a criteria for significance for a new trial we generate values of the Bayesian predictive distribution of a the outcome of a new trial, say μ^*. This calculation can be easily performed using STAN¹⁵ or WinBugs¹⁶ although the latter requires the prior distributions of μ and σ to be supplied explicitly.

We then created a function which uses this sample to calculate the probability that the results of a new clinical trial will estimate a parameter that exceeds a specified threshold, say t. Suppose δ is the actual improvement due to the new treatment, where δ = 0 if it isn’t effective, the trial result has standard error τ and p(μ^*) is the predictive distribution. Then $P(\widehat{\mu }>t)=\int (\Phi (({\mu }^{\ast }+\delta -t)∕\tau )p({\mu }^{\ast }))d{\mu }^{\ast }$. This can be estimated using the mean of Φ((μ^* + δ − t)/τ) over our sample from the predictive distribution of μ^*. We assume that the new trial is reasonably large, that is large enough so the normal approximation to it’s distribution is valid for the measured treatment effect in the new trial. With this function it is straight forward to plot the criteria for significance at any level, as a function of τ. Such a control chart could be used to determine the significance of a historically controlled trial. In the example, we used STAN for this calculation with 12,000 iterations of the MCMC sampler where half were then used for the calculation, the first 6000 is used as a burn in. All the parameters in STAN were set at their default. The program we used is available in CRAN¹⁷ with the name of HCT. If there are only a small number of historical control groups it might be better to put a more informative distribution on μ and σ however, for the results to be believable one would need this distribution to be wide enough to be universally acceptable.

The derivation above doesn’t use the sample sizes n_i of the previous clinical trials, nor does it use the sample size of the HCT under consideration, as in the example in Gelman et al.¹⁴ Clearly large trials will have smaller values of τ_i. The algorithm effectively subtracts out the sampling variation in ${\widehat{\mu }}_i$ using τ_i when it calculates the posterior distribution of μ. When the criteria above are used to evaluate an HCT, one will have an estimate of the standard error, τ for the HCT (which we will consider fixed) from the output of whatever statistical package is used to analyze the data. In this case, the sample size of the HCT can be ignored, as long is it is large enough for the normal approximation of the outcome to hold. For planning trials τ is needed as a function of the sample size n in order to calculate the power of a clinical trial. In the simplest situation where ${\widehat{\mu }}_i$ is a mean, $\tau =s∕\sqrt{n}$ where s is the patient level standard deviation of the efficacy measure. The value of s can be calculated from the historical trial data by the average value of ${\tau }_i\sqrt{n}$. As a sensitivity analysis we considered a more complicated model where the square of the standard deviation is considered to be s²/[n(n − 1)] times a a Chi-Squared distribution with n − 1 degrees of freedom and the s for each trial is considered a draw from a log-normal distribution with unknown mean and standard deviation which are given non-informative priors. This would be the preferred analysis if one had small trials rather than large ones in the historical database. In the ALS example, to follow, none of the probability calculations changed appreciably.

Often ${\widehat{\mu }}_i$ is the estimated parameter of a model. In this case, ${\tau }_i\propto 1∕\sqrt{n_i}$, where the constant of proportion, which we will still call s, depends on the study design. In a survival study where $\widehat{\mu }$ is the log-hazard ratio, s will depend on the duration of the accrual and follow-up periods and a formula can be found in Schoenfeld.¹⁸ In a longitudinal study s will depend on the number and timing of the study visits. A formula for a random effects model can be found in Liu and Liang.¹⁹. An R package is available.²⁰. In general s² is the element of the inverse of the information matrix that corresponds to the parameter estimate that measures the treatment effect. If the design of the proposed HCT is quite similar to that of all of the historical trials then s can be estimated by the average value of ${\tau }_i\sqrt{n_i}$ and used as if the outcome were a sample mean.

What we are doing is similar to a random effects meta analysis, where we assume that ${\widehat{\mu }}_1$, ${\widehat{\mu }}_2$, … , ${\widehat{\mu }}_m$ have a normal distribution with a N(μ′ + θ, τ) distribution and θ is a random effect with standard deviation σ. The advantage of a Bayesian approach where you put a uniform prior on the unknown value of μ′ and σ is that the Bayesian approach appreciates the role of the number of control groups m. The Bayesian predictive distribution of μ^* will have more variability if m is small, while the results of a random effects meta analysis will not.

Use of patient level data with covariates

When patient-level data are available, such as demographics, disease severity, etc., the sample size of an HCT might be reduced by using these data to match patients or to predict the patient outcome used to measure efficacy. Differences in the distributions of prognostic covariates might be one cause of the variation in the outcomes of the trials. In addition including covariates might reduce the value of τ_i. Both of these might improve the efficiency of an HCT.

We focus on a strategy that allows the implementation of a control chart, in a similar manner to the one that can be generated from published data. To do this, we need a method of letting $\widehat{\mu }$ for each trial be the difference between the observed outcome and the prediction based on covariates. Then we can duplicate the algorithm described for the use of published data, replacing the outcome by it’s deviation from the prediction and it’s standard error by the standard error of the deviation.

The principal difficulty with this approach is that if you develop a prediction model from the pooled historical data it will tend to over-fit these data, and both the between trial variation and the standard error of the outcome will be understated. To prevent this, we hold out the data for each trial and develop the prediction equation from the other trials. We then predict the data from the held out trial and use the deviation from the prediction as the value of ${\widehat{\mu }}_i$ for that trial. An alternative would be to use the same covariates in the model for all the trials, in which case all the standard errors as well as the among trail variability may be reduced.

Example

Background

ALS is characterized by a progressive loss of motor neurons. Patients face increasing disability leading to complete paralysis including the breathing and swallowing muscles, which eventually causes death. The ALS functional Rating Scale Revised (ALSFRS-R) is a 12-item questionnaire which rates functional abilities in four domains (bulbar, fine motor, gross motor, and respiration) from 4-normal to 0-completely absent. The score is a sum of the ratings of each of the 12 functions. The average rate of decline in ALSFRS-R among ALS patients is approximately one point per month. The score is used as the primary efficacy measure in phase II and in some phase III ALS trials. Usually a random-slopes model is used to analyze the data,²¹ with the trial outcome being the mean slope. This model specifies that the observed ALSFRS-R is a patient-specific random intercept and slope plus a visit-specific residual deviation from the patient-specific trajectory. A normal distribution is postulated for the patient-specific intercepts, slopes and deviations. Although the disease is eventually fatal, mortality is not used as an endpoint in early phase trials because the one-year survival is over 80%.

In 2014 with funds from several philanthropic organizations, Prize4Life and the Neurology Clinical Trials Unit at the Massachusetts General Hospital created the PROACT database to house data from clinical trials conducted by industry and academia. The database currently contains records of 23 Phase II/III clinical trials. This database provided the opportunity to conduct a meta-analysis using the methods described above.

Analysis based on estimated control group means and standard errors

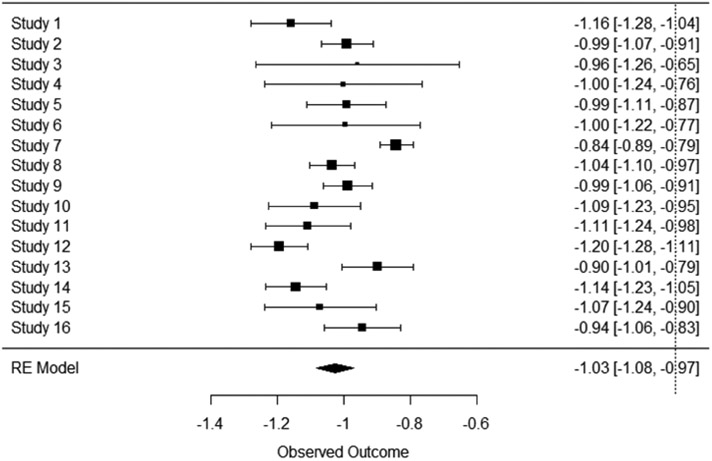
The database that is publicly distributed does not identify the trial source for each patient and one cannot identify which patients were in the same trial; however the organizers of the database have this information, and were willing to calculate the statistics for the control group of each trial for us to use in this analysis. We assumed that a phase II HCT would be six months in duration, so we removed the data for each patient that occurred more than 220 days after randomization. In addition, we did not want to include trials that were shorter than six months in duration, so if a trial had no observations taken after 150 days the whole trial was excluded. Figure 1 shows a forest plot of mean slope of the ALSFRS-R per month for the included trials.

Figure 1.

Forest Plot of the control groups of clinical trials in the PROACT database. The mean and error bars for the mean change in ALSFRS-R per month are shown.

We used RSTAN¹⁵ for the computation. Of the 23 trials in the database, there where 16 that were included based on the criteria above. The mean of μ, the rate of change of ALSFR-R, was −1.03 points/month and the mean of σ was 0.11 points/month. The standard deviation of μ was 0.03 points/month and the variation of σ was 0.026. The average value of s was 0.995 points/month.

If one considered the historical control mean to be fixed, then one could assume that a new drug worked if an HCT with 100 patients clinical trial had a mean slope of greater than $(-1.03+1.96\times s∕\sqrt{100})=-0.83$ points/month. The criteria based on our model was −.73 (points/month) to declare significance at a two sided p=0.05 significance level.

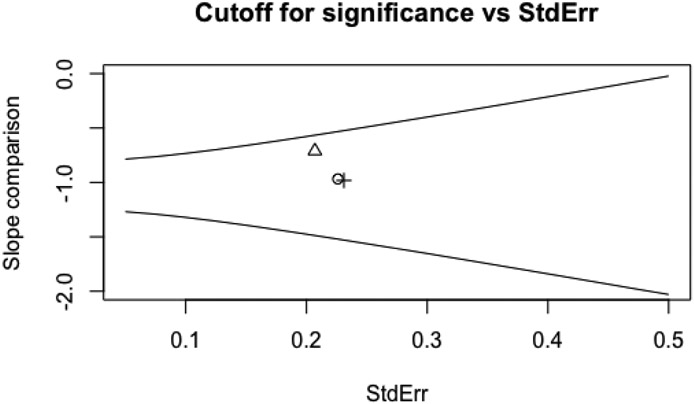
Figure 2 is the control chart that could be used to determine statistical significance of a new treatment in an HCT. One would plot the estimated slope per month against its standard error. If the point was above the top line running from slope= −.8 to slope= −.4 points/month, then the HCT would provide evidence of a significant beneficial effect; if it were below the bottom line running from −1.3 to −1.6 points/month, then the HCT would provide evidence of a significant harm. The three points on the graph are the results from three 20-patient clinical trials of exercise, showing neither benefit nor harm.²²

Figure 2.

Control chart for judging significance of an HCT with ALSFRS-R slope estimated over 6 months as the outcome.

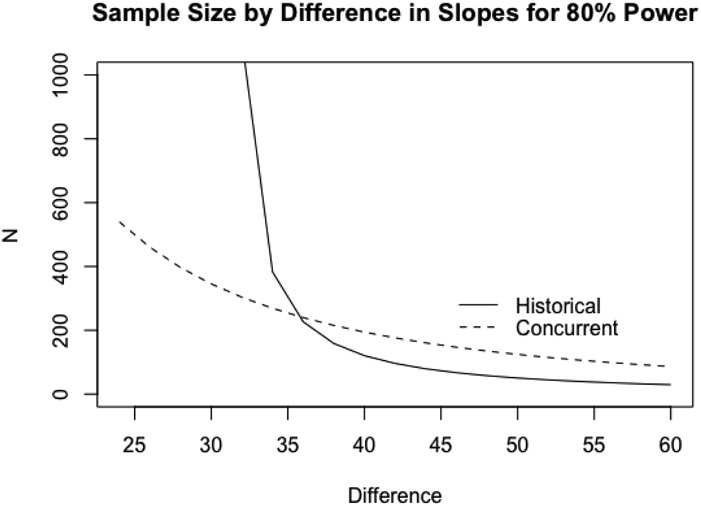
Figure 3 plots required sample size for 80% power comparing a concurrently controlled trial (RCT) to an HCT. The solid line shows the sample size needed for an HCT as a function in the % decrease in ALSFRS-R slope and the dashed line shows the corresponding total sample size for an RCT, with equal randomization to each arm. We assumed s = 0.995 which was the average value from our historical database. The standard times to measure the ALSFRS-R are 0,1,2,4 and 6 months, and most of the variation in the random-effects model is due to variation in each patient’s slope, so the effect of different designs on s would be minimal. However if one wanted to calculate s, let X be a two column matrix with first column ones and second column the visit times. Then $s^2=({\sigma }_0^2{X}^{\prime }X+X^{\prime }\Sigma X{)}_{2,2}^{-1}$, where σ₀ is the standard deviation of the error term and Σ is the variance covariance matrix of the random effects. Then the sample size should be s/0.995 times the sample size from the chart in Figure 3.

Figure 3.

Total Sample Size as a function of difference in slope as %change for an HCT and an RCT

The sample size for an HCT increases rapidly as the effect size is reduced with a vertical asymptote near 30%. To see why this is so, we note that if the new trial had a very large sample size so that the estimated outcome $\widehat{\mu }$ had a negligible standard error then the power to detect a 29% difference would be approximately $P(\widehat{\mu }>\mu +1.96\sigma )=1-\Phi \{(\mu +1.96\ast \sigma -(\mu +\delta ))∕\sigma \}=1-\Phi \{(-1.03+1.986\ast .11-0.71\ast (-1.03))∕.11\}=0.78$. where in this case μ, σ are the mean and standard deviation of the predictive distribution, and an 80% power could not be achieved whatever the sample size.

Many phase II-III trials in ALS of oral drugs are designed to achieve 80% power to detect a 30% differnce. However, it would be reasonable to posit a 50% difference for trials of particularly expensive or invasive treatments, such as gene or stem cell therapy. In this case, an HCT would require ≈ 50 patients versus ≈ 130 for a RCT.

The point at which the two sample size curves cross provides a quantification of the general guidance that HCTs should be considered when investigating dramatic treatment effects, e.g., the use of penicillin in pneumococcal pneumonia.²³

Analysis using patient-level data for covariate adjustment

For covariate adjustment we needed a prediction that could be computed for most of the data in the PRO-ACT database and would accurately predict patients’ ALSFRS-R scores over time. Prize4Life had previously conducted a data mining contest for developing a predictor with just those properties, so we chose to use this algorithm.²⁴ A non-linear, nonparametric gradient boosting algorithm²⁵ was trained using the PROACT data. The model was trained to predict raw ALSFRS-R scores longitudinally from a set of features extracted from baseline trial visits. The feature set chosen to train the model was based on an evaluation of features that had a similar distribution across all trials in the PRO-ACT database to reduce bias due to high proportions of missing data within a subset of trials. Final feature selection, optimization of tuning parameters and imputation of missing data were performed based largely on previous exploratory analyses and models.

The model was fit for this paper by considering the trials in groups of three, training the model on the trials not in that group of three, and then using the model to make predictions for each patient in the group of three trials. These predictions were subtracted from the observed ALSFRS-R scores and the result used as the data for a random slopes model.

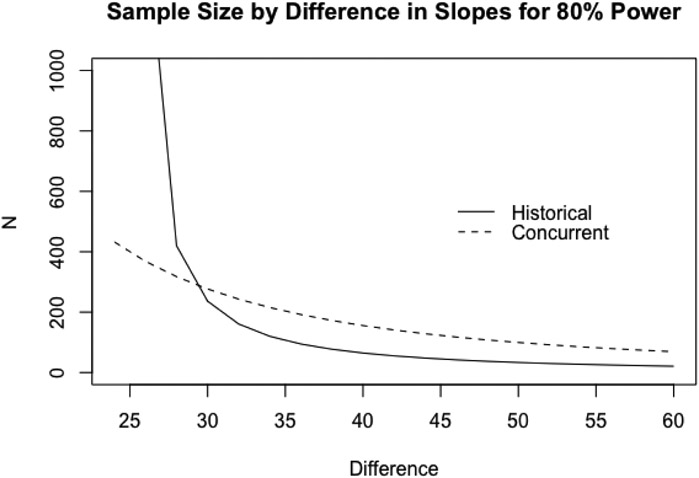
Figure 4 shows how this would change the sample size requirements for HCTs and RCTs. In this case, it appears that an HCT and an RCT designed to detect a 30% difference would need to be the same size, but an HCT would require fewer patients to test for larger differences.

Figure 4.

Total sample size as a function of difference in slope(% change), using covariate adjustment

Interpretation

A common effect size of ALS phase II trials is a 25-30 percent reduction in the decline of the ALSFRS-R slope. Assuming this treatment effect, an RCT would require no more total patients than an HCT. Thus, using HCTs to detect these differences would be inadvisable and the conjecture given in Meier¹ that the HCT offers no advantage turns out to be true.For the ALS example, we show that the HCT would not be smaller than the randomized trial. This may be counterintuitive to patients and physicians who believe an HCT will reach a conclusion more rapidly. However, in ALS, where improvements are likely to be moderate, the HCT will not have sufficient power to detect (even an important) benefit. For larger differences, HCTs would require smaller sample sizes, especially if we use covariates. However, the use of covariates as described here is fairly difficult to implement. The algorithm we used would need it to be run on the data of the clinical trial in order to analyze the trial. Also, in the planning phase, one would have to assume that future patients would be enough like the patients in the PRO-ACT database such that the sample size considerations developed using this database would be relevant. For instance, the exclusion and inclusion rules would need to be similar and their expected rates of progression would need to be similar. In particular, one would need to consider whether the standards of care external to the trial were constant enough to make the historical data relevant. The risk, if the new trail recruits are substantially different patients, is that the study would be underpowered and miss a potentially promising therapy. This can happen for example if the a new treatment becomes standard and improves patient outcome, resulting in a lower control group rate. In ALS, there is concern that the approval of edaravone for ALS²⁶might change the natural history if many patients opt to receive it. In time, the control groups of trials conducted after the introduction of edaravone could be used to develop new criteria for HCTs.

Discussion

There are many issues about historically controlled trials that were not discussed in this paper. One concern in using historical data is if there is a secular trend, where trial outcomes improve over the years due to changes in diagnostic criteria or improvements in treatment or other care so the historical patients would be too different to use as a control group. This trend could be directly modeled if patient level historical data are available. While we did not have such data from the PRO-ACT trial, this database is being actively curated, with contemporary trials being continually added.

In Qureshi et al.²⁷ secular trends in mean ALSFRS-R were not detectable. Occasionally there are advances in patient care that might radically change the prognosis of the control group. Two examples would be the introduction of a new effective therapy or changes in care or diagnosis criteria. This may have happened in ALS with the introduction of a recently approved therapy²⁶. In that case one would need quite a few new trials to estimate the new mean outcome. This could be accomplished by introducing a new parameter measuring the difference caused by the change in standard of care. If one assumed that the trial-to-trial variability also changed one would need a completely new set of trials.

A second issue which is not readily resolvable is whether eliminating the placebo control group would fundamentally change the patient population. In particular, there is already a known difference in the demographic makeup of patients who participate in clinical trials from the broader patient population.²⁸ It is unknown whether that difference would be exacerbated if patients knew that they would be receiving treatment.

An important area where alternatives to placebo controlled trials are required is the advent of increasingly invasive treatments for relatively rare diseases, such as surgical placement of stem cells. In these cases, there is a clear desire to find viable alternative strategies to a sham placebo, which would likely be unethical. However, these trials may have the issue that they require younger, healthier patients who have better prognosis but for whom no historical data exist.

Another issue is how often the analysis of historical data needs to be repeated. The Bayesian approach has the advantage that uncertainties in the estimation of the mean drop in ALSFRS-R and the trial-to-trial variation are incorporated into the criteria for significance and the sample size calculations. Thus, as more trials are added to the database, the power of HCT will increase modestly.

This analysis could be repeated for other diseases that are extensively studied. Since the analysis does not require patient-level data, it could be included in meta-analyses to give guidance for interpreting future single arm trials in the literature. Software is available for fitting these models.¹⁷

The focus of this paper has been on phase II trials that are designed to screen new drugs for further study. It is not our intention to suggest replacing randomized phase III clinical trial when they are ethically possible. The data from an HCT can never be as convincing as that from an RCT.

There are other approaches to phase II trials such as using master protocols to select the most promising phase II drug among several.^29,30 However, an HCT is an alternative when expected effect sizes are large and master protocols aren’t possible. In ALS it appears that this would be an unusual situation because the usual effect sizes are too small to make HCTs practical.