Abstract
The sugar-phosphate backbone of DNA near single-stranded (ss)—double-stranded (ds) junctions likely fluctuates within a broad distribution of conformations to permit the proper binding of genome regulatory proteins that function at these sites. In this work, we use absorbance, circular dichroism (CD), and two-dimensional fluorescence spectroscopy (2DFS) to study the local conformations and conformational disorder within chromophore-labeled DNA constructs. These constructs employ dimers of the fluorescent chromophore Cy3, which are site-specifically incorporated into the sugar-phosphate backbones of DNA strands at ss-ds DNA fork junctions. We show that these data can be analyzed to determine the local conformations of the (Cy3)2 dimer, and the degree of conformational disorder. Our analysis employs an essential-state Holstein-Frenkel Hamiltonian model, which takes into account the internal electronic-vibrational motions within each Cy3 chromophore, and the resonant electronic interaction that couples the two chromophores together. Our results suggest that this approach may be applied generally to understand local backbone conformation and conformational disorder at ss-ds DNA fork junctions.
I. Introduction
The structure of genomic DNA is generally pictured as the static B-form conformation of the Watson-Crick (W-C) duplex (1). However, many centrally important biological processes involve dynamic molecular events that require local regions of DNA to open spontaneously, thus allowing proteins to gain access to either single-stranded DNA base sequences, or to secondary structure motifs that depart from the stable W-C structure (2). For example, the elongation events of DNA replication involve the binding of proteins to non-sequence-specific positions at or near single-stranded (ss)—double stranded (ds) DNA junctions. To facilitate elementary biochemical steps of the elongation process, the sugar-phosphate backbone of DNA near ss-ds junctions likely fluctuates into a broad distribution of functionally relevant conformations to permit the proper binding of replication proteins. Thus, the nature and extent of conformational disorder at DNA junctions may be central to the molecular mechanisms of the binding and the subsequent function of the protein-DNA complexes involved.
The carbocyanine dye Cy3 is often used as a chromophore label for proteins and nucleic acids. Such fluorescently labeled biomolecular constructs are employed in diverse applications, from rapid screening of single-molecules to imaging of subcellular components (3–10). The Cy3 chromophore is comprised of an electronically conjugated trimethine group, which bridges two indole-like substituents (see Fig. 1A). The lowest energy π → π* electronic transition occurs when the molecule is in its all-trans ground state configuration, with electric dipole transition moment (EDTM) polarized parallel to the long axis of the trimethine bridge. The absorbance spectrum of Cy3 labeled constructs exhibits a pronounced vibronic progression with energy spacing ℏω0 ~ 1,100 cm−1 (3). The presence of the vibronic progression indicates that the electronic transition is effectively coupled (as characterized by the Huang-Rhys parameter, λ2 ≈ 0.55) to at least one local vibrational mode of relatively high frequency (11–13), such as the Raman-active symmetric stretch of the trimethine bridge at ~ 1,200 cm−1 (14).
Figure 1.
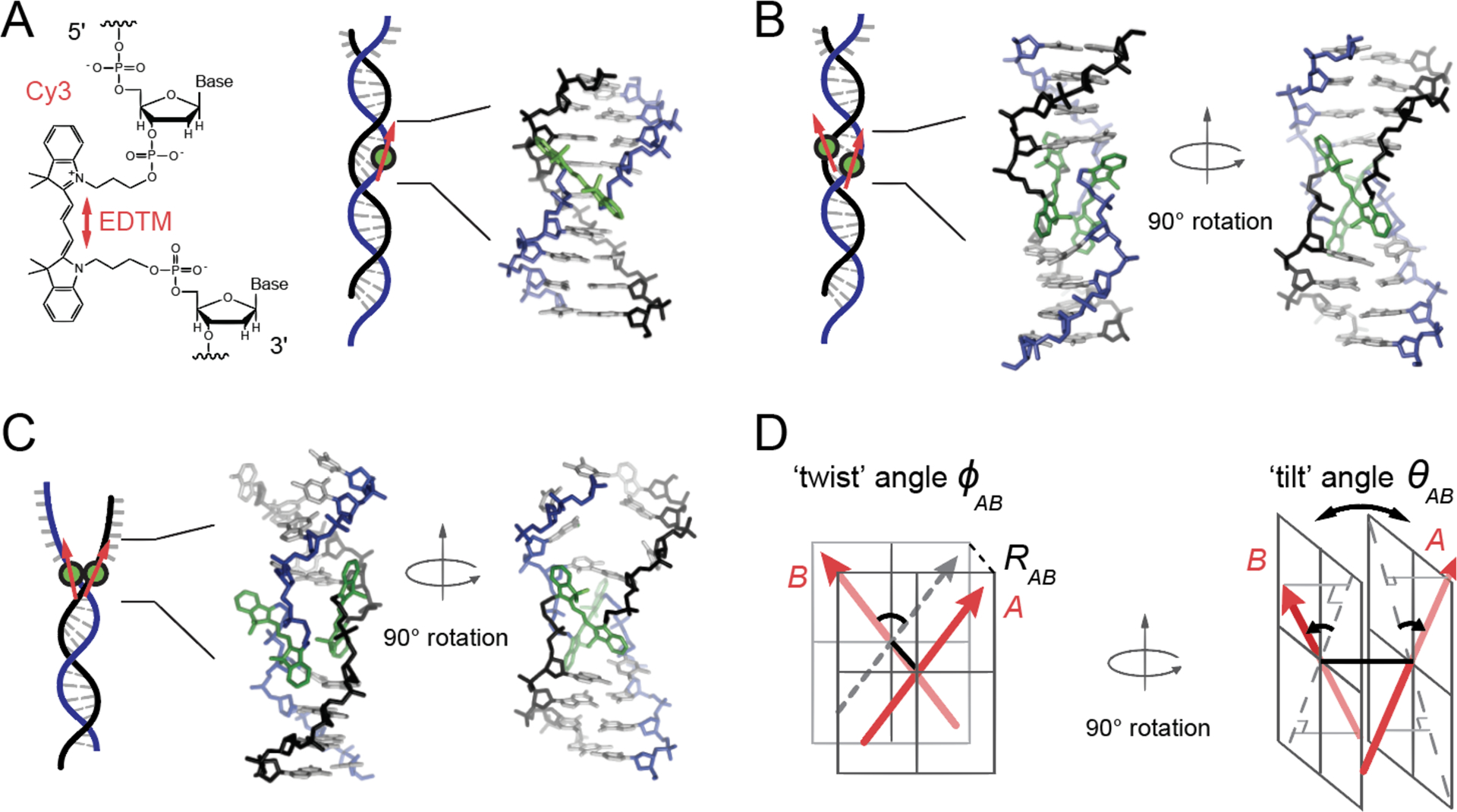
Model structure of the internally labeled Cy3 monomer and (Cy3)2 dimer in dsDNA. (A) The structural formula of the internally labeled Cy3 chromophore is shown with its insertion linkages to the 3’ and 5’ segments of the sugar-phosphate backbone of ssDNA. A red double-headed arrow indicates the orientation of the electric dipole transition moment (EDTM), which lies parallel to the axis of the trimethine bridge in the all-trans configuration. (B) A (Cy3)2 dimer-dsDNA construct is formed by annealing two complementary DNA strands, which each contain a site-specifically positioned Cy3 chromophore. Space-filling structural models performed using the Spartan program (Wavefunction, Inc.) suggest that the dimer exhibits the same approximate D2 symmetry as right-handed (B-form) helical dsDNA (17). (C) A (Cy3)2 dimer-fork DNA construct contains the dimer probe near the ss-ds DNA fork junction. The local conformation of the (Cy3)2 dimer probe is expected to reflect the disruption of base-stacking interactions that occurs near the fork junction. In panels (A – C), the sugar-phosphate backbones of the conjugate strands are shown in black and blue, the bases in gray, and the Cy3 chromophores in green. (D) The structural parameters that define the local conformation of the (Cy3)2 dimer are the inter-chromophore separation vector RAB, the twist angle ϕAB, and the tilt angle θAB.
Cyanine chromophores can be chemically attached to a nucleic acid base or to an amino acid side chain via a flexible linker (3, 9). Cy3 and Cy5 are often used as a double-label pair to perform Förster resonance energy transfer (FRET) experiments (15). Such studies can provide information about inter-chromophore separation based on the resonant electronic coupling J between the optically excited Cy3 ‘donor’ and the unexcited Cy5 ‘acceptor.’ The relative fluorescence intensities of the Cy3 / Cy5 donor-acceptor pair depends on the magnitude of J, which is most sensitive to changes in inter-chromophore separation on the scale of the Förster radius R0 ~ 50 Å. FRET experiments are performed in the ‘weak-coupling regime’ (16), where the magnitude of J is small in comparison to the interactions between the chromophore and its local environment at room temperature (~kBT ≈ 210 cm−1) (11).
An alternative labeling scheme is to site-specifically incorporate the Cy3 chromophores ‘internally’ within the sugar-phosphate backbone of a single strand of DNA (see Fig. 1) (3, 8, 9). By annealing two complementary DNA strands, each containing a single internally-labeled Cy3 chromophore, a DNA construct can be formed with a (Cy3)2 dimer (or a Cy3 monomer) at a predetermined position relative to a single-stranded (ss) – double-stranded (ds) DNA fork junction. The resulting chiral conformation of the (Cy3)2 dimer is sterically constrained by the stabilizing interactions of the adjacently stacked bases within the DNA duplex. Conversely, the conformation of the (Cy3)2 dimer can be destabilized by increasing the sample temperature or by positioning the probes close to the DNA fork junction where base stacking interactions are disrupted. Such internally-labeled Cy3 probes are thought to have only a minimal effect on the local DNA structure, as their presence in relatively short oligomeric dsDNA constructs (~ 30 base pairs) does not significantly alter the denaturation temperature (Tm = 65 °C) (9).
Due to the relatively small inter-chromophore separations within internally-labeled (Cy3)2 dimer-DNA constructs (RAB ~ 5 Å), the magnitude of the resonant coupling can be significantly greater than kBT, approaching values comparable to the vibrational relaxation energy (λ2ℏω0 ~ 600 cm−1) (17). In this ‘intermediate-to-strong coupling regime’ (16), the (Cy3)2 dimer forms delocalized excitons comprised of symmetric and anti-symmetric superpositions of the electronic-vibrational product states of the component Cy3 monomers (18, 19). While FRET-based experiments can provide limited information about inter-chromophore separation, experiments that can resolve the relative intensity contributions from the symmetric and anti-symmetric excitons of internally-labeled (Cy3)2 dimer-DNA constructs can reveal detailed information about local dimer conformation and the ways in which fluctuations of the local environment broaden spectra and perturb the coupling. As we discuss further below, this information can be sensitively probed using absorbance, circular (CD), and two-dimensional fluorescence spectroscopy (2DFS) (17).
In previous work, we used absorbance and CD spectroscopy to study the monomer Cy3 and the dimer (Cy3)2 duplex DNA constructs depicted in Fig. 1A and 1B, respectively, over the temperature range 15—60 °C below the dsDNA denaturation transition (Tm = 65 °C) (17). We analyzed our results with the aid of the Holstein-Frenkel Hamiltonian model for an electronically coupled dimer of two-electronic-level molecules, each with their electronic transition coupled to a single vibrational (harmonic) mode (19). We found that the conformation of the (Cy3)2-dsDNA construct undergoes systematic variation as a function of temperature, in terms of the inter-chromophore separation RAB, the twist angle ϕAB (defined in Fig. 1D) and the degree of structural disorder. In the current work, we extend our approach to examine the local conformations of the (Cy3)2 dimer-labeled fork DNA construct depicted in Fig. 1C. DNA forks and other ss-ds DNA junctions are sites of interaction for proteins that participate in DNA replication, recombination and repair (20, 21). The local conformation of the sugar-phosphate backbone and conformational disorder at the fork junction is a consequence of DNA ‘breathing’ – i.e., thermally activated fluctuations of the folded secondary structure – that is a key factor affecting the assembly and stability of protein components (2). To characterize the local conformations of the (Cy3)2 dimer-labeled fork DNA construct, we introduce the structural parameter of the inter-chromophore tilt angle θAB (defined in Fig. 1D) to account for the disruption of hydrogen bonds and stacking of bases within the ss region adjacent to the (Cy3)2 dimer. With the inclusion of this additional orientational parameter, we use the (Cy3)2 dimer-labeled fork DNA construct as a test system to examine the reliability of the point-dipole approximation in estimating the resonant coupling strength J.
In general, the resonant electronic coupling J is determined by integrating the Coulomb interactions between electric transition charge densities of the component monomers (11). Direct calculation of the atomic transition charge density by quantum chemical methods would provide the most accurate determination of the coupling strength, albeit at a significant computational cost (22). For expediency, the point-dipole approximation is often invoked, where the transition charge density is focused at a single point, and J is described as the interaction between two point-dipole moments. Of course, for inter-chromophore separations comparable to the monomer size, the point-dipole approximation cannot reflect the details of the transition charge density, which is extended across the length of the trimethine bridge and indole substituents of the Cy3 molecule. To examine the reliability of the point-dipole model we here implement an extended-dipole model (23), which includes a displacement parameter to account for the length over which the transition charge q is distributed. In the extended dipole model, the displacement parameter is oriented parallel to the EDTM , and the magnitudes of the transition charge and displacement satisfy ql = μ (22–24). We have performed our analyses for both the (Cy3)2-ds DNA and (Cy3)2-fork DNA constructs using both the point-dipole and extended dipole models. Our results indicate that both models yield very similar values for the structural parameters of these DNA constructs over the full range of temperatures studied.
In addition to determining the average local conformations adopted by the backbone labels within the (Cy3)2-dsDNA and (Cy3)2-fork DNA constructs, we further examine structural disorder by interpreting inhomogeneous spectral line broadening as an indicator of this effect. Molecular dynamics simulations suggest that the Cy3 chromophore(s), when incorporated internally within the DNA duplex, may exist in a variety of conformations (25). This dispersion is due to the coupling between the Cy3 probe chromophores and the fluctuating local DNA environment, which induces the transition energies of the Cy3 probes to occur over a broad spectral range. We show that the results of 2DFS experiments performed on these systems – taken in combination with absorbance and CD spectroscopy – can be used to determine the homogeneous and inhomogeneous line broadening and the corresponding degree of structural disorder.
II. Experimental Methods
Sample Preparation.
We show in Table I the sequences and nomenclature of the internally labeled Cy3 monomer and (Cy3)2 dimer DNA constructs used in this work. Oligonucleotide samples were purchased from Integrated DNA Technologies (IDT, Coralville, IA) and used as received. For our absorbance, circular dichroism (CD), and two-dimensional fluorescence spectroscopy (2DFS) measurements, we prepared solutions with sample concentrations of 1 μM and a standard aqueous buffer of 10 mM Tris, 100 mM NaCl, and 6 mM MgCl2. We combined complementary oligonucleotide strands to form the Cy3 monomer- and (Cy3)2 dimer-labeled DNA constructs, which contain both ds and ss regions. The Cy3 monomer-labeled constructs contained a thymine base (T) in the complementary strand position directly opposite to the Cy3 probe chromophore. For the ‘duplex’ constructs, the Cy3 probes are positioned deep within the double-stranded region of the DNA. For the ‘fork’ constructs, the Cy3 probes are positioned near the ss — ds DNA fork junction. Prior to the experiments, the sample solutions were annealed by heating to 95 °C for 3 minutes before they were allowed to slowly cool to room temperature. For our control 2DFS experiments performed on the Cy3 chromophore in methanol (see SI section), we purchased 1,1’-diethyl-3,3,3’,3’-tetramethylindocarbocyanine iodide (Cy3) from Toronto Research Chemicals, Inc., which we used without further purification. Spectroscopic grade methanol was used to prepare solutions of concentration 1 × 10−3 M.
Table I.
Base sequences and nomenclature for the Cy3 monomer and (Cy3)2 dimer labeled DNA constructs used in these studies. The horizontal line indicates the regions of complementary base pairing.
| DNA construct | Nucleotide base sequences |
|---|---|
| Cy3 monomer duplex DNA | 3’-GTC AGT ATT ATA CGC TCy3C GCT AAT ATA TAC GTT TTT TTT TTT TTT TTT TTT TTT TTT TTT T-5’ |
| 5’-CAG TCA TAA TAT GCG A T G CGA TTA TAT ATG CTT TTA CCA CTT TCA CTC ACG TGC TTA C-3’ | |
| (Cy3)2 dimer duplex DNA | 3’-GTC AGT ATT ATA CGC TCy3C GCT AAT ATA TAC GTT TTT TTT TTT TTT TTT TTT TTT TTT TTT T-5’ |
| 5’-CAG TCA TAA TAT GCGACy3G CGA TTA TAT ATG CTT TTA CCA CTT TCA CTC ACG TGC TTA C-3’ | |
| Cy3 monomer fork DNA | 3’-GAG GGA GCA CAG CAG AGG TCA GTA TTA TAC GCT Cy3CG CTG GTA TAC CAC GTT T (x29)-5’ |
| 5’-CTC CCT CGT GTC GTC TCC AGT CAT AAT ATG CGA T AT GCT TTT ACC ACT TTC ACT CAG GTG CTT A-3’ | |
| (Cy3)2 dimer fork DNA | 3’-GAG GGA GCA CAG CAG AGG TCA GTA TTA TAC GCT Cy3CG CTG GTA TAC CAC GTT T (x29)-5’ |
| 5’-CTC CCT CGT GTC GTC TCC AGT CAT AAT ATG CGA Cy3AT GCT TTT ACC ACT TTC ACT CAG GTG CTT A-3’ |
Absorbance and CD Measurements.
We performed absorbance measurements using a Cary 3E UV-Vis spectrophotometer, and CD using a Jasco model J-720 CD spectrophotometer. Temperature-dependent measurements were performed over the range 15 – 75 °C. Samples were held in a 1 cm quartz cuvette, and the temperature was controlled to within 0.1 °C using a Peltier thermoelectric heating block. We determined all spectra over the range 200 – 700 nm to examine the spectral region of the native bases (~275 nm), in addition to that of the Cy3 probe(s) (~540 nm). For all of the samples, we confirmed that the ds region adopted the anticipated Watson-Crick B-form conformation by examination of the ultraviolet absorbance and CD of the native bases (26).
In Fig. 2, we show absorbance and CD spectra at 25 °C for the Cy3 monomer- and dimer-labeled duplex DNA constructs, and the (Cy3)2 dimer-labeled fork DNA construct. We note that the spectra of the Cy3 monomer fork DNA construct (not show) are qualitatively similar to those of the corresponding duplex construct. The absorbance spectra of the Cy3 monomer duplex and fork DNA constructs exhibit a progression of vibronic features with the first (0–0) peak centered at 549 nm (18,280 cm−1). The vibronic progression is still present in the spectrum of both the (Cy3)2 dimer-labeled duplex DNA construct and the dimer-labeled fork DNA construct. However, individual vibronic features of the dimer are broadened relative to those of the monomer, and the ratio of the 0–0 to 1–0 vibronic peak intensities has decreased relative to that of the monomer . While the monomer CD signal is very weak (as expected), the CD of both the dimer duplex and fork constructs exhibit a progression of bisignate lineshapes (i.e. a change of sign within a given vibronic band), which is a signature of vibronic excitons in a chiral dimer (19, 27, 28). Furthermore, the CD spectra of the (Cy3)2 dimer-duplex and fork DNA constructs have opposite signs, indicating that the two systems have opposite chiral symmetries.
Figure 2.
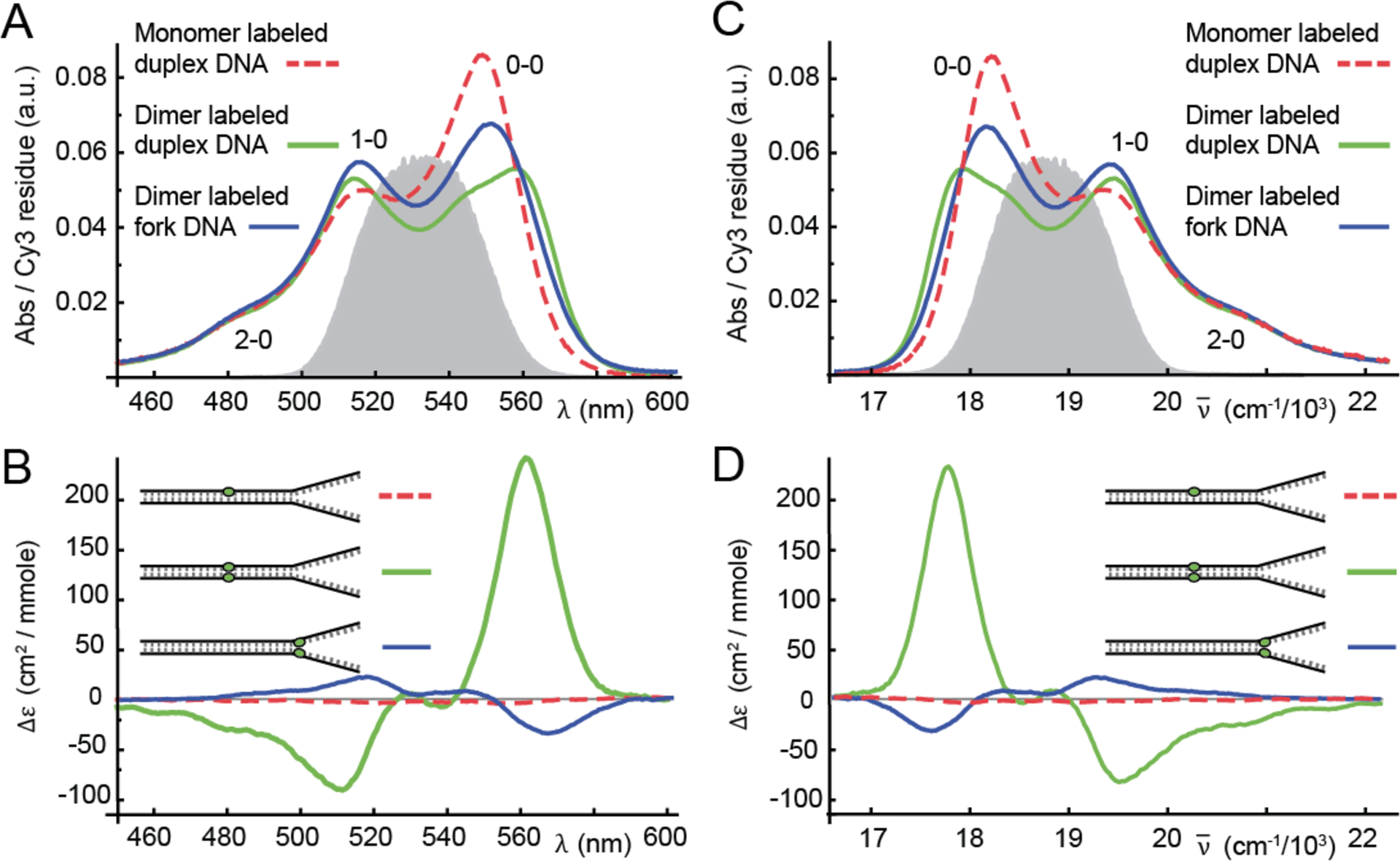
Room temperature (25 °C) absorbance (A & C) and CD (B & D) spectra for Cy3 monomer duplex (dashed red), (Cy3)2 dimer duplex (solid green), and (Cy3)2 dimer fork (solid blue) DNA constructs. The Here Δε is the differential absorbance of left and right circular polarized light. Nucleotide sequences and placement of the chromophore probes are indicated in Table I. The spectra are shown as a function of optical wavelength (A & B) and as a function of wavenumber (C & D). The vibronic features of the monomer absorption spectra are labeled ne – 0, where ne (= 0, 1, 2) indicates the vibrational occupancy of the electronically excited monomer. An example laser spectrum used for 2DFS experiments is shown in gray. The laser spectrum spans a region containing both the 0–0 and 1–0 vibronic sub-bands.
Phase Modulated Two-Dimensional Fluorescence Spectroscopy (2DFS).
To obtain estimates of the homogeneous line widths for the samples listed in Table I, we performed phase-modulated 2DFS experiments. These measurements were carried out as previously described (29–32). 2DFS utilizes a train of four collinear laser pulses. The relative phase of pulses 1 and 2, and that of pulses 3 and 4, are continuously swept at the frequencies Ω21 = 5 kHz and Ω43 = 8 kHz, respectively. Fluorescence from the optically excited sample is detected as a function of the time delay between the first two pulses (t21) and that of the second two pulses (t43). For the experiments reported here, the delay between pulses two and three (t32) is set to zero. The phase-selective fluorescence detection method (29, 33) is used to extract the fourth-order population signals (30), which vary in time at the sum [(Ω43 + Ω21)= 13 kHz] and difference [(Ω43 − Ω21) = 3 kHz] modulation frequencies associated with the non-rephasing (NRP) and rephasing (RP) signals, respectively.
The four laser pulses were generated using a single high-repetition-rate non-collinear optical parametric amplifier (NOPA) with the excitation centered at 532 nm (18,796 cm−1) and a FWHM bandwidth of 31 nm (1,100 cm−1) for experiments on all samples performed at room temperature, and a bandwidth of 37 nm (1,300 cm−1) for control 2DFS measurements performed on the Cy3 chromophore in methanol (see SI section). Fluorescence was detected using a 615 nm long-pass filter (Chroma, HQ615LP), which served to reject scattered excitation light. To eliminate optical saturation effects, solutions were continuously circulated through the cuvette using a peristaltic pump. Pulses were compressed using a quadruple-pass fused-silica prism pair to compensate for dispersive media in the optical path preceding the sample. Pulse widths were characterized by placing a beta-barium borate (BBO) frequency doubling crystal at the sample position, where a phase-modulated train of pulse-pairs was incident. The frequency-doubled signal output was detected using a lock-in amplifier, which was referenced to the ac carrier signal used to modulate the relative phase of the pulses, as previously described (29). We thus minimized the pulse width ΔτL = ~14 fs by performing a pulse-pulse autocorrelation. We measured the laser bandwidth ΔλL centered at λL = 532 nm using an Ocean Optics mini-spectrometer. The measured time-bandwidth product was thus ~ ~ 0.55, which is within 25% of the optimal value (0.44) for Fourier-transform-limited Gaussian pulses. Results from these measurements are presented below.
III. Theoretical Modeling
Absorbance and CD Spectra.
Building upon previous work (17), we implemented the Holstein-Frenkel (H-F) model to describe the electronic-vibrational structure of the (Cy3)2 dimer probe, similar to the approach taken by others (19, 34–38). The H-F model accounts for the interactions between electronic and vibrational degrees of freedom internal to each chromophore, and the conformation-dependent resonant electronic coupling J between chromophores. The presence of both types of interactions (excitonic and vibronic) gives rise to delocalized symmetric and anti-symmetric transitions of well-defined energies and polarizations, which feature prominently in absorbance and CD spectra. Because the positions and amplitudes of the spectroscopic features depend sensitively on the conformation of the (Cy3)2 dimer, an optimization procedure that compares simulated to experimental spectra (17) allows us to extract structural information about the (Cy3)2 dimer.
In the H-F model, each Cy3 monomer is treated as a two-electronic-level molecule with ground state |g〉, excited state |e〉, and transition energy εeg. The monomers are labeled A and B, with electric dipole transition moment (EDTM) . The electronic transition of each Cy3 monomer is coupled to a single harmonic mode with frequency ω0. The monomer Hamiltonian is given by
| (1) |
In Eq. (1), the electronic-vibrational coupling is characterized by the Huang-Rhys parameter λ2 = d2ω0/2ℏ, where d is the vibrational coordinate displacement of the electronic excited state potential minimum relative to the electronic ground state. The value of λ2 is the number of vibrational quanta absorbed by the system upon optical excitation. The operator creates (annihilates) a vibrational excitation in the un-shifted electronic potential surface. The dimer Hamiltonian is
| (2) |
where the final term couples the singly excited electronic states of the monomers. Here |eg〉 is the state in which monomer A is electronically excited and monomer B is unexcited, and |ge〉 is the state in which the A and B labels are interchanged. The resonant electronic coupling J depends on dimer conformation in terms of the Coulomb interaction between monomer site transition charge densities (11)
| (3) |
where .
The delocalized excitons and corresponding energies of the coupled AB dimer are obtained by diagonalization of the Hamiltonian given by Eq. (2) (17). The singly excited states are symmetric (+) and anti-symmetric (−) superpositions of electronic-vibrational products . Here, the coefficients depend on the vibrational coordinates of monomers A and B, ng(e) (= 0, 1, …) are the number of vibrational excitations in the un-shifted (shifted) potential of an unexcited (excited) monomer, and α (= 0, 1, …) is an index in order of increasing state energy (19).
The absorbance spectrum is the sum of symmetric (+) and anti-symmetric (−) exciton features
| (4) |
where , is the collective EDTM, and is a Lorentzian function that represents the homogeneous lineshape of the transition with eigen-energy ε±,α and FWHM line width ΓH. Similarly, the CD spectrum is the sum of symmetric and anti-symmetric rotational strengths
| (5) |
where . In the above expressions, we have defined the ground electronic-vibrational state of the AB dimer |0〉 = |gg〉. Because the dimer conformation is subject to disorder due to DNA breathing, the homogeneous absorbance and CD line shapes are convolved with an inhomogeneous distribution function , which is centered at the average transition energy and has standard deviation σI. The final expressions for the absorbance and CD spectra are given by the Voigt profiles and , respectively.
Two-Dimensional Fluorescence Spectroscopy.
We simulate 2DFS spectra based on the H-F Hamiltonian using previously developed methods (30, 39). We use |v〉 to represent the electronic ground state with vibrational quantum number v = vA + vB. For example, the state |0〉 is the electronic ground state with zero vibrational occupancy. The states |e〉 and |e′〉 represent any two of the symmetric and anti-symmetric excitons within the singly excited manifold, and the state |f〉 represents any one state within the doubly excited manifold. Rephasing (RP) and non-rephasing (NRP) response functions are written (30)
| (6) |
and
| (7) |
In Eqs. (6) and (7), the first two terms on the right hand side of the proportionalities represent, respectively, ground state bleach and stimulated emission. The final two terms are excited state absorption for the singly and doubly excited state manifolds, respectively. The parameter Γ2D, which may assume values between zero and two, is the fluorescence quantum yield of the doubly excited state manifold relative to that of the singly excited state manifold. When the effects of inhomogeneous broadening are included in the response function (40), the individual terms are written for RP:
| (8) |
| (9) |
| (10) |
and for NRP:
| (11) |
| (12) |
| (13) |
In Eqs (8) – (13), the factors denote the four-point product that takes into account the projections of the transition dipole moments onto the (parallel) plane polarizations of the four laser pulses, which are averaged over an isotropic distribution of dimer orientations. The complex-valued 2DFS spectra are obtained by Fourier transformation of the RP and NRP response functions [Eqs. (6) and (7)] with respect to the delay variables t21 and t43.
Estimation of the Resonant Electronic Coupling.
In the point-dipole approximation, the electronic coupling is given by (30)
| (14) |
where and are unit vectors that specify the monomer EDTM directions (see Fig. 1D). The point-dipole approximation provides a reasonable value for J when the inter-chromophore separation is much greater than the molecular size (11). In our previous studies, we estimated the long-axis dimension of the Cy3 chromophore to be ~ 14 Å and the inter-chromophore separation to be RAB ~ 6 Å (17). In our current work, we have carried out additional analyses using the extended-dipole model (23, 24), which includes a one-dimensional displacement parameter to account for the finite size of the chromophore. Each dipole is represented as two point charges of equal magnitude and opposite sign (±q) separated by the distance l. The direction of is the same as that of the monomer EDTM. The resonant coupling between monomers A and B in the extended-dipole model is
| (15) |
where ql = μeg and the distances between point charges are , , and (24). For all of the calculations that follow, we used the measured EDTM value μeg = 12.8 D, which we determined by integration of the absorbance lineshapes of the Cy3 monomer duplex and fork DNA constructs (17). We estimated l = 7 Å by assuming the same value that was used by Knoester and co-workers to model the coupling between carbocyanine dyes of similar structure to Cy3 (24). The above values imply q = 0.38e (with e the charge of an electron). In both extended- and point-dipole models, the value of J depends on structural parameters that specify the Cy3 dimer conformation – i.e., the inter-chromophore separation RAB, the twist angle ϕAB, and the tilt angle θAB (see Fig. 1D).
In Fig. 3, we compare the results of calculations for the resonant electronic coupling based on the point-dipole model (shown in green) versus the extended-dipole model (shown in blue). In these calculations, we have set the inter-chromophore separation RAB ~ 5 Å, which is close to the value obtained from our previous analyses for the (Cy3)2 dimer duplex DNA construct (17). In Figs. 3A – 3C, the twist angle ϕAB is varied for fixed values of the tilt angle θAB = 0, 60 and 100°, respectively. For small θAB, the point-dipole and extended-dipole models exhibit qualitatively similar sinusoidal dependences on ϕAB. However, the point-dipole approximation generally overestimates the magnitude of the coupling strength for arbitrary angles. The effect of the finite size of the chromophores, which is qualitatively captured by the extended-dipole model, is revealed for the case of a side-by-side geometry with ϕAB = 0°, and subsequently varying the tilt angle (see Fig. 3D). Here the extended-dipole model exhibits divergences at θAB = 90 and 270°, which are due to the repulsive close-encounters between like charges, and a local minimum at the head-to-tail geometry of θAB = 180°, which is dominated by the attractive interaction between opposite charges. This ‘finite-size effect’ is entirely neglected by the point-dipole model, which varies smoothly with tilt angle, and reaches a local maximum at θAB = 180°. The stability of the head-to-tail conformation is most significant for increasing values of ϕAB (see Figs. 3E and 3F), in which case the repulsive barriers that are present for small values of ϕAB vanish. The above comparison indicates that, in principle, very different results might be obtained from analyses that employ the point-dipole model versus the physically more realistic extended-dipole model. Nevertheless, as we discuss further below, the results of our optimization analysis for the (Cy3)2 dimer DNA constructs reveal that the two models produce very similar values for the conformational parameters, thus suggesting that the states accessible to the dimer are those for which the two models agree.
Figure 3.
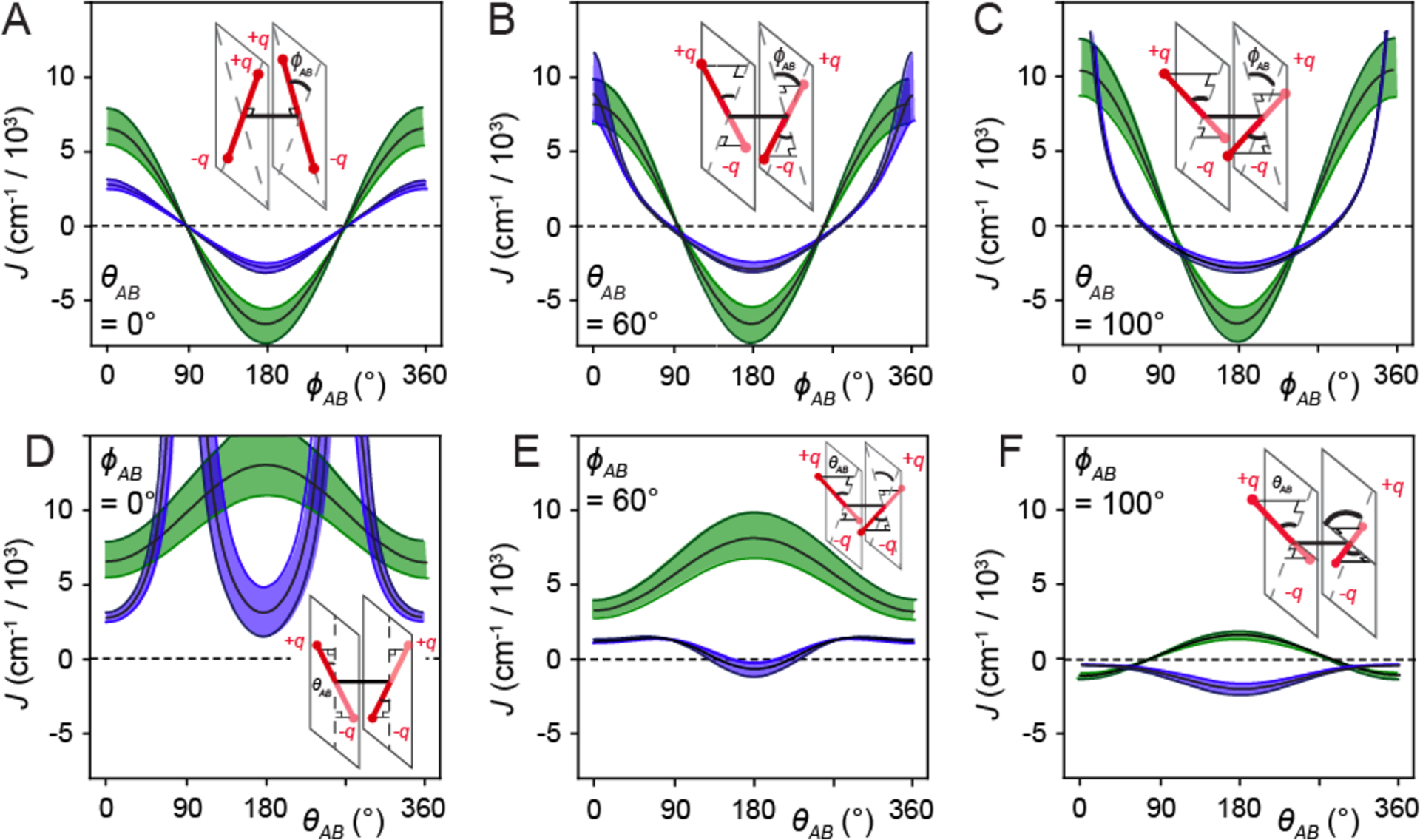
Calculations of the resonant electronic coupling J based on the point-dipole (shown in green) and extended-dipole (shown in blue) models. In the top row, J is plotted as a function of the twist angle ϕAB for tilt θAB = 0° (A), 60° (B), and 100° (C), and in the bottom row as a function of θAB for ϕAB = 0° (D), 60° (E), and 100° (F). In these calculations, we have used the following values for the transition dipole moment μeg = 12.8 D, the extension length l = 7 Å, the transition charge q = 0.38e, and the inter-chromophore separation RAB = 5 ± 0.3 Å. The error bars in J correspond to the upper and lower values adopted for RAB = 5 ± 0.3 Å.
Multi-Parameter Optimization Procedure.
To efficiently explore the space of structural parameters needed to model the absorbance, CD and 2DFS of the (Cy3)2 dimer DNA constructs, we implemented an automated multi-variable regression analysis. The procedure is similar to one we have used in the past (17, 30, 39, 41), in which a random search algorithm generates an initial set of input parameters, and commercial software (KNITRO) (42) is used to refine the corresponding solutions. For each set of input trial parameters, we calculate a linear least-squares target function χ2, which guides the selection of parameter values for subsequent iterations. The optimized solutions correspond to minimization of the target function. Error bars associated with the optimized parameters were determined by a 1% deviation of the target function from its minimized value. The results of our optimization analysis of the dimer spectra are presented in Table II and Table III, and discussed further below.
Table II.
Structural parameters of the (Cy3)2 dimer DNA duplex construct at various temperatures using, alternatively, the point-dipole and extended-dipole models for the resonant coupling J. The reported values are based on optimized fits of the Holstein-Frenkel Hamiltonian model to absorbance and circular dichroism spectra. The calculations use as inputs the EDTM μeg = 12.8 D, the homogeneous line width ΓH = 186 cm−1 (17), and for each temperature, the electronic transition energy εeg, the vibrational mode frequency ω0, and the Huang-Rhys parameter λ2 obtained from analyses of the Cy3 monomer DNA construct absorbance spectra (see Table S1 and Table S2 of the SI section). For the extended dipole model calculations, the extension length l = 7.1 Å and the effective charge q = 0.38e were used. The parameters listed are the resonant coupling strength J, the inter-chromophore twist angle ϕAB, the inter-chromophore tilt angle θAB, the inter-chromophore separation RAB, and the standard deviation of the Gaussian inhomogeneous disorder function σI,dim. Structural parameters are presented at temperatures below the melting transition at 65 °C, for which the dimer model may be reasonably applied. Error bars were calculated based on a 1% deviation of the target function from its optimized value.
| Point Dipole Model | |||||
|---|---|---|---|---|---|
| T (°C) | J (cm−1) | ϕAB (°) | θAB (°) | RAB (Å) | σI,dim (cm−1) |
| 15 | 527 +32/−11 | 82.9 ± 0.14 | 1.52 +6.2/−9.2 | 5.8 ± 0.04 | 292 ± 5.3 |
| 25 | 512 +33/−11 | 79.9 ± 0.22 | 7.02 +4.4/−18 | 6.6 ± 0.05 | 302 ± 5.1 |
| 35 | 495 +34/−12 | 76.0 ± 0.32 | 0.00 ± 10.5 | 7.4 ± 0.06 | 313 ± 5.2 |
| 45 | 482 +35/−13 | 72.0 ± 0.44 | 6.90 +6.7/−20 | 8.1 ± 0.07 | 325 ± 5.2 |
| 55 | 465 +33/−13 | 70.2 ± 0.48 | 9.28 +5.8/−24 | 8.4 ± 0.07 | 336 ± 5.0 |
| 65 | 361 +40/−10 | 73.5 ± 0.5 | 0.71 +14/−16 | 8.6 ± 0.10 | 336 ± 8.2 |
| Extended Dipole Model | |||||
| T (°C) | J (cm−1) | ϕAB (°) | θAB (°) | RAB (Å) | σI,dim (cm−1) |
| 15 | 532 +24/−38 | 80.7 +0.2/−0.1 | 18.1 +2.9/−2.1 | 3.7 ± 0.1 | 289 ± 5.2 |
| 25 | 514 +14/−29 | 79.6 ± 0.21 | 10.2 +6.4/−27 | 4.4 ± 0.07 | 302 ± 5.1 |
| 35 | 496 +26/−19 | 76.0 ± 0.32 | 3.0 +13/−19 | 5.5 ± 0.08 | 315 ± 5.5 |
| 45 | 483 +32/−16 | 71.9 ± 0.43 | 7.7 +8.5/−24 | 6.4 ± 0.08 | 325 ± 5.2 |
| 55 | 467 +31/−15 | 70.4 ± 0.46 | 7.0 +8.4/−22 | 6.8 ± 0.09 | 336 ± 5.0 |
| 65 | 354 +34/−17 | 73.7 ± 0.6 | 5.4 +11/−22 | 7.1 ± 0.13 | 353 ± 5.1 |
Table III.
Structural parameters of the (Cy3)2 dimer DNA fork construct at various temperatures using, alternatively, the point-dipole and extended-dipole models to determine the resonant coupling J. The parameters and conditions for performing these calculations are the same as those described in Table II.
| Point Dipole Model | |||||
|---|---|---|---|---|---|
| T (°C) | J (cm−1) | ϕAB (°) | θAB (°) | RAB (Å) | σI,dim (cm−1) |
| 15 | −538 +74/−65 | 103 ± 0.48 | 44.1 +2.7/−2.5 | 6.4 ± 0.10 | 356 ± 12 |
| 25 | −488 +86/−91 | 101 ± 0.45 | 44.2 +2.9/−3.0 | 6.1 ± 0.13 | 364 ± 13 |
| 35 | −390 +64/−68 | 101 ± 0.41 | 44.7 +2.6/−2.5 | 6.5 ± 0.13 | 362 ± 10 |
| 45 | −351 +58/−62 | 98 ± 0.16 | 54.0 +1.0/−1.0 | 5.0 ± 0.10 | 364 ± 7.0 |
| 55 | 366 +29/−28 | −11 ± 7.9 | 73.0 +2.3/−2.4 | 14.4 ± 0.23 | 347 ± 7.0 |
| 65 | 380 +34/−34 | −23 ± 3.4 | 69.5 +2.5/−2.6 | 13.9 ± 0.25 | 414 ± 8.1 |
| Extended Dipole Model | |||||
| T (°C) | J (cm−1) | ϕAB (°) | θAB (°) | RAB (Å) | σI,dim (cm−1) |
| 15 | −537 +68/−79 | 101 ± 0.67 | 47.3 +4.2/−4.5 | 5.3 ± 0.1 | 355 ± 12 |
| 25 | −489 +84/−91 | 101 ± 0.82 | 44.2 +5.4/−6.5 | 5.4 ± 0.07 | 364 ± 13 |
| 35 | −390 +62/−69 | 101 ± 0.74 | 44.4 +6.1/−7.4 | 6.1 ± 0.08 | 364 ± 10 |
| 45 | −352 +57/−61 | 96 ± 0.52 | 58.2 +3.2/−3.5 | 5.6 ± 0.08 | 365 ± 9.5 |
| 55 | 366 +33/−31 | −11 ± 7.3 | 73.0 +2.2/−2.3 | 14.4 ± 0.09 | 349 ± 7.5 |
| 65 | 384 +40/−38 | −23 ± 3.2 | 69.6 +2.4/−2.5 | 13.7 ± 0.13 | 407 ± 8.8 |
Comparison Between Point-Dipole and Extended-Dipole Models.
We performed optimization calculations to simulate the absorbance and CD spectra of the Cy3 labeled DNA constructs (see Table I). For these calculations, we used values that were previously established for the monomer EDTM, μeg = 12.8 D, and the homogeneous line width, ΓH = 186 cm−1 (17). For calculations of the Cy3 monomer duplex and fork DNA constructs, we applied the monomer Hamiltonian given by Eq. (1) to our temperature-dependent data, and thereby determined optimized values for the monomer electronic transition energy εeg, the Huang-Rhys parameter λ2, the vibrational frequency ω0, and the spectral inhomogeneity for the monomer specified by the Gaussian standard deviation σI,mon. The results of this analysis for the Cy3 monomer duplex and Cy3 monomer fork DNA constructs are listed in Table S1 and Table S2 of the SI section, respectively. For both duplex and fork DNA constructs, the Cy3 monomer (intra-chromophore) parameters εeg, λ2, and ω0 do not exhibit significant temperature dependences, while the monomer inhomogeneity parameter σI,mon increases with temperature.
We next performed calculations for the (Cy3)2 dimer duplex and fork DNA constructs based on the dimer Hamiltonian given by Eq. (2). For each temperature, we used as inputs the corresponding monomer parameters listed in Table S1 and Table S2 of the SI section. We thus determined optimized values for the (Cy3)2 inter-chromophore separation RAB, the inter-chromophore twist angle ϕAB, the inter-chromophore tilt angle θAB, and the spectral inhomogeneity parameter for the dimer, σI,dim. As described above, we performed these calculations using, alternatively, the point-dipole [Eq. (14)] and the extended-dipole [Eq. (15)] model for the resonant coupling. In Fig. S1 of the SI section, we directly compare the results of our optimizations using either method to experimental spectra taken at 15 °C, for both the (Cy3)2 dimer duplex and fork DNA constructs. We find that equally favorable agreement between experimental and simulated spectra can be achieved using either the point-dipole or the extended-dipole models. Moreover, both models produce similar values for the optimized parameters J, ϕAB, θAB, and σI,dim, while the extended-dipole model generally produces smaller values for inter-chromophore separation RAB than does the point-dipole model. This behavior is consistent with the relatively small values of the tilt angle θAB for both the duplex and fork DNA constructs, where the primary difference between the point-dipole and extended-dipole models is the overestimation of the resonant coupling by the point-dipole model (see Fig. 3). In Table II and Table III, we list the results of our optimization analyses for the (Cy3)2 dimer duplex and fork DNA constructs, respectively. In the discussion that follows, we focus on the results of the extended-dipole model, which are qualitatively the same as those of the point-dipole model.
IV. Discussion of Results
Determination of (Cy3)2 Dimer Conformation and Conformational Disorder using Absorbance and CD Spectroscopy.
We studied the temperature-dependence of the absorbance and CD spectra of the (Cy3)2 dimer-labeled duplex and fork DNA constructs. In Fig. 4, we present experimental absorbance and CD spectra of these samples at representative temperatures. Overlaid with the experimental data are simulated symmetric (+, shown in blue) and anti-symmetric (−, shown in red) exciton components resulting from our optimization procedure, and which are based on the extended-dipole model. The agreement between experiment and theory is very good over the full range of temperatures that we studied. In Table II and Table III, we list as a function of temperature the optimized values of the inter-chromophore structural parameters (i.e., J, ϕAB, θAB, RAB, and σI,dim) for the (Cy3)2 dimer-labeled duplex and fork DNA constructs, respectively. We note that for both of these dimer-labeled DNA constructs at temperatures above the melting transition (Tm ≈ 65 °C), the spectra appear indistinguishable from those of the corresponding Cy3 monomer DNA constructs, signifying the complete separation between the conjugated single DNA strands.
Figure 4.
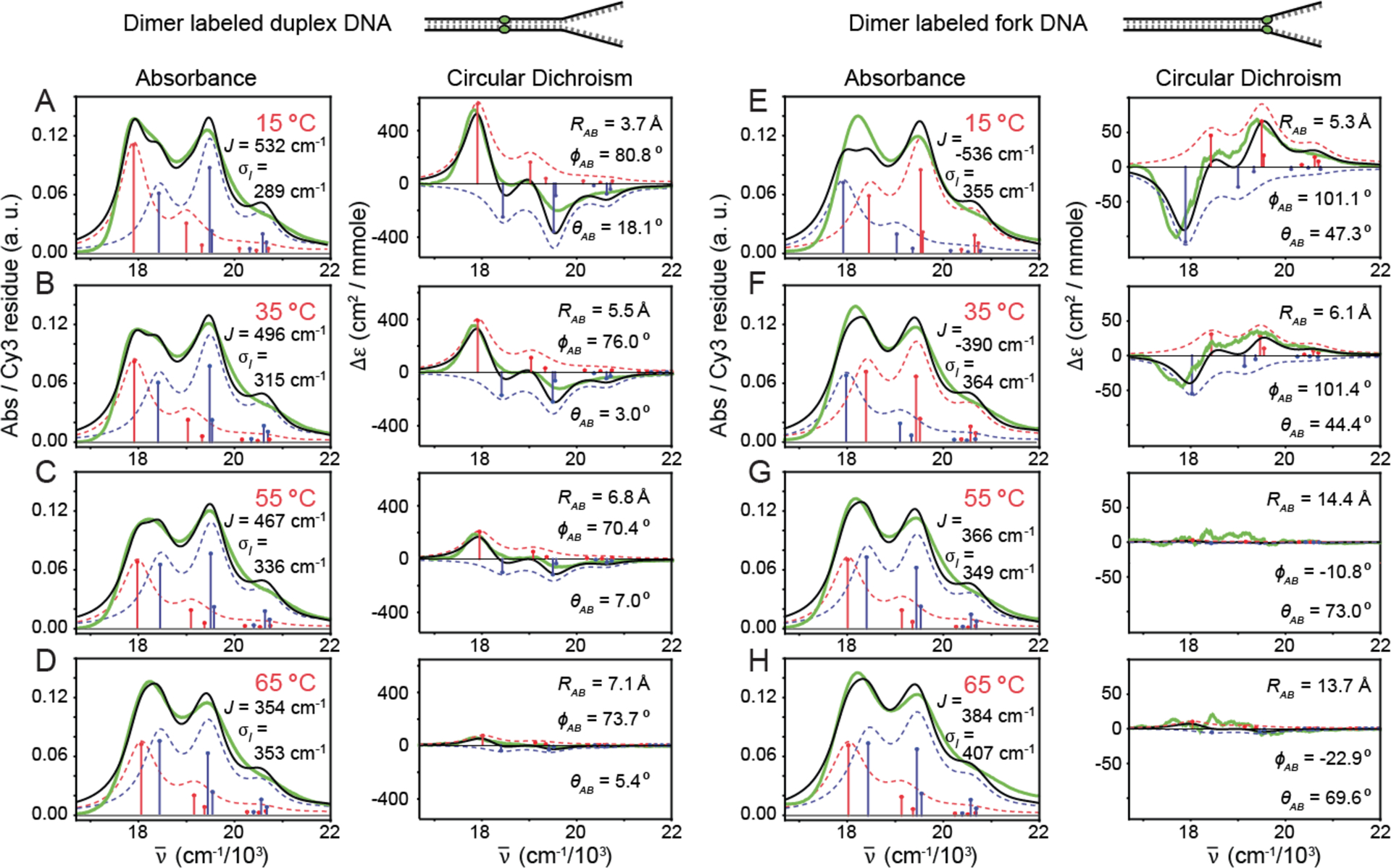
Temperature-dependent absorbance and CD spectra for (Cy3)2 dimer labeled duplex DNA construct (A-D), and for the (Cy3)2 dimer labeled fork DNA construct (E-H). Experimental spectra are shown in solid green, and the simulated total lineshapes (inhomogeneous-plus-homogeneous) are shown in solid black. The optimized parameters shown in the insets were obtained using the extended-dipole model for the resonant coupling. Symmetric and anti-symmetric transitions determined from the model are shown as blue and red sticks, respectively. Symmetric and anti-symmetric contributions to the inhomogeneous lineshapes are shown as dashed blue and red curves, respectively.
Our temperature-dependent analyses of the absorbance and CD spectra shown in Fig. 4 reveal that for both (Cy3)2 dimer-labeled duplex and fork DNA constructs, the individual vibronic bands are well separated into symmetric and anti-symmetric exciton components with energy spacings that depend on the coupling strength J. For both types of DNA constructs, each exciton component contributes with comparable intensities to the absorbance spectra [as described by Eq. (4)], which – as we discuss further below – is due to the occurrence in both species of the nearly orthogonal twist angles ϕAB. Moreover, we see from our analyses that the pronounced bisignate line shapes within individual vibronic bands of the CD spectra are due to the opposite sign contributions of the symmetric and anti-symmetric excitons [see Eq. (5)].
We first discuss our results for the (Cy3)2 dimer-labeled duplex DNA construct (see Fig. 4A) at 15 °C. The optimized values for the structural parameters are J = 532 cm−1, ϕAB = 80.7°, θAB = 18.1°, RAB = 3.7 Å, and σI,dim = 289 cm−1. These values for RAB, ϕAB, and θAB are consistent with space-filling models for the local conformation of the (Cy3)2 dimer depicted in Fig. 1B, which shows the two Cy3 monomers positioned closely within the DNA duplex with an approximately coplanar and orthogonal relative orientation. Furthermore, this dimer conformation reflects the anticipated structure of the opposing segments of the sugar-phosphate backbone deep within the duplex region of the DNA construct. The value of the resonant coupling strength J is positive, indicating that the symmetric (anti-symmetric) exciton manifold is blue- (red-) shifted relative to the transition energy of the uncoupled monomers. The positive sign of J corresponds to the right-handed chirality of the dimer (with ϕAB < 90°), which manifests as a positive Cotton effect in the CD spectrum (43). For both duplex and fork constructs, the magnitude of J is greater than that of the spectral inhomogeneity σI,dim, which is a necessary condition for the dimer to support delocalized excitons (11). Because the coupling strength is comparable to the intramolecular vibrational relaxation energy (i.e. J ~ λ2ℏω0 = 602 cm−1, where we have used λ2 = 0.54 and ℏω0 = 1,116 cm−1), the dimer exists in the intermediate-to-strong exciton-coupling regime.
The results for the (Cy3)2 dimer-labeled duplex DNA construct discussed above serve to confirm our general expectations for the right-handed helical structure of B-form DNA. In contrast, much less is known about local conformations of the sugar-phosphate backbone near DNA fork junctions. It is therefore interesting to compare our results for the two different (Cy3)2 dimer-labeled DNA constructs. The optimized structural parameters for the dimer-labeled DNA fork construct at 15 °C (see Fig. 4E) are J = −537 cm−1, ϕAB = 101°, θAB = 47.3°, RAB = 5.3 Å, and σI,dim = 355 cm−1. Here the values for RAB, ϕAB, and θAB are consistent with the local conformation of the (Cy3)2 dimer depicted in Fig. 1C, for which the two Cy3 monomers are positioned closely at the DNA fork junction with a non-coplanar and nearly orthogonal orientation. The increased value of the tilt angle θAB reflects the loss of cylindrical symmetry at the fork junction. While the magnitude of the resonant coupling J is nearly the same for the fork and duplex constructs, the sign of the coupling is negative for the DNA fork construct. This indicates that the symmetric (anti-symmetric) exciton manifold is red- (blue-) shifted relative to the transition energy of the uncoupled monomers. Thus, near the DNA fork junction the local backbone segments labeled by the (Cy3)2 dimer has adopted a left-handed chiral symmetry (i.e. ϕAB > 90°) such that the CD exhibits a negative Cotton effect. The spectral inhomogeneity for the dimer-labeled fork DNA construct is greater than that of the duplex. This latter finding is consistent with the notion that the distribution of backbone conformations near the DNA fork junction may be broadened due to biologically significant ‘breathing’ fluctuations, which uniquely occur at this position (2).
As the temperature was increased over the range 15 – 65 °C, (see Fig. 4) the splittings between the symmetric and anti-symmetric exciton components decreased continuously, as did the finite amplitudes of the CD signal. The CD signal of the DNA fork construct decreased much more rapidly with increasing temperature than that of the DNA duplex, which is due to a loss of chiral symmetry at ~ 55 °C, well below the denaturation transition. For both the (Cy3)2 dimer-labeled DNA duplex and fork constructs, the temperature-dependent properties are correlated to systematic changes in the resonant coupling strength J. This is due to the temperature sensitivity of cooperative interactions between constituent nucleic acid bases (i.e., base stacking interactions, Watson-Crick hydrogen bonding, etc.), which stabilize the right-handed helical structure of the duplex DNA construct, and only partially stabilize the left-handed conformation that we observe at the DNA fork junction. The temperature-dependent disruption of local DNA secondary structure is reflected by systematic changes in the conformation of the (Cy3)2 dimer DNA duplex and DNA fork constructs characterized by the structural parameters listed in Table II and Table III, respectively, and are plotted in Fig. 5.
Figure 5.
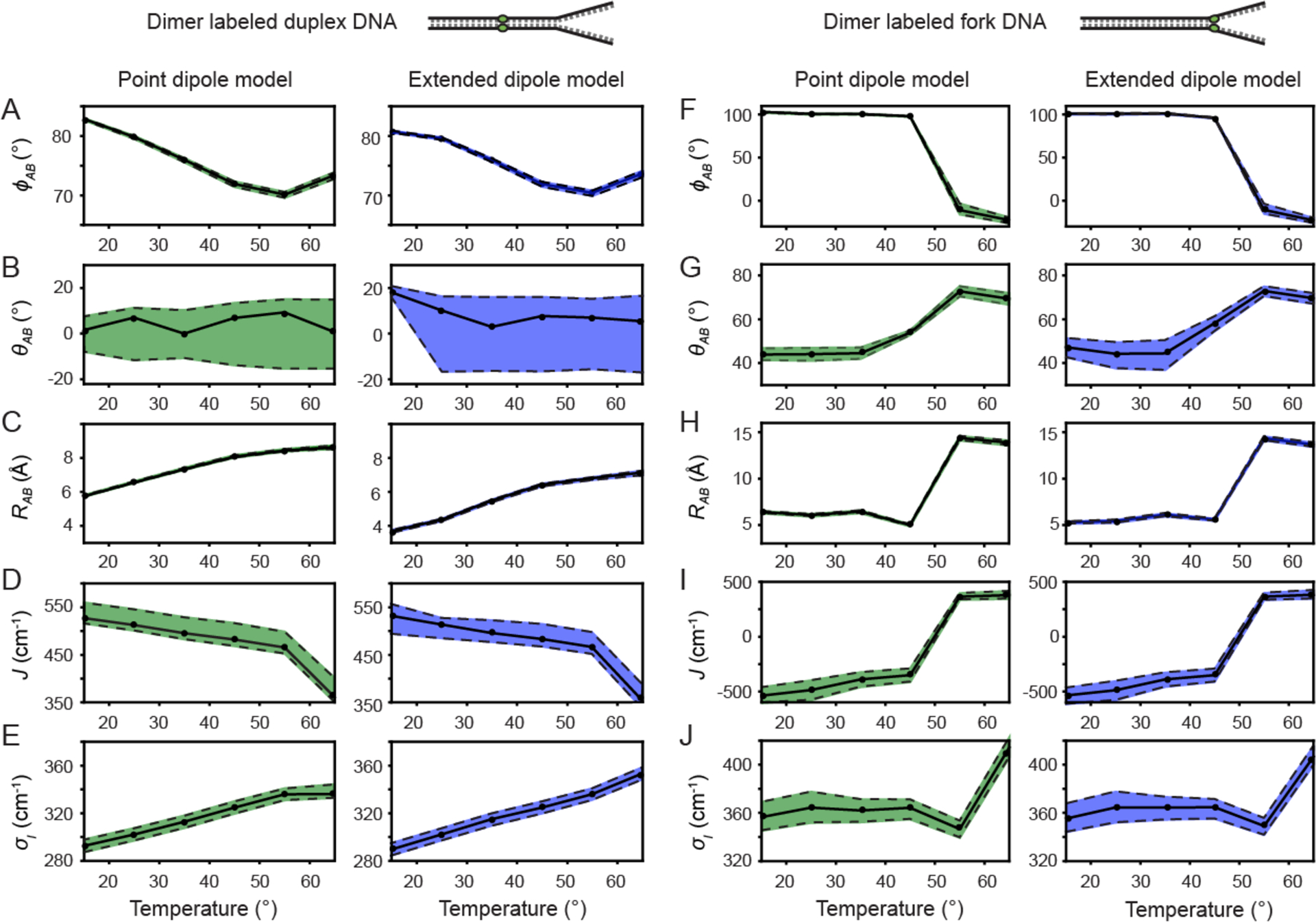
Temperature-dependent optimized parameters from (Cy3)2 dimer absorption and CD spectra. Error bars were calculated based on a 1% deviation of the target function from its optimized value. The dashed line at 65 °C indicates the melting transition temperature Tm of the DNA constructs. (A) Inter-chromophore twist angle; (B) Resonant electronic coupling parameter; (C) Inter-chromophore separation; and (D) Spectral inhomogeneity parameter associated with the Cy3 monomer and the (Cy3)2 dimer DNA constructs.
As shown in Fig. 5, the majority of structural parameters of the (Cy3)2 dimer-labeled DNA duplex and fork constructs vary continuously over the range of temperatures 15 – 55 °C. As discussed above, our results are nearly indistinguishable using either the point-dipole (shown in green) or the extended-dipole (shown in blue) models for the resonant coupling strength J. For our remaining discussion, we focus on the values given by the extended-dipole model.
For the (Cy3)2 dimer-labeled duplex DNA construct, the inter-chromophore separation RAB increases from 3.7 – 6.8 Å, the inter-chromophore twist angle ϕAB decreases from 80.7 – 70.4°, the tilt angle θAB decreases relatively quickly from 18.1 – 7.0°, the resonant coupling J decreases from 532 – 467 cm−1, and the spectral inhomogeneity parameter σI,dim increases from 289 – 336 cm−1. The spectral inhomogeneity is a measure of the disorder of the local DNA environment experienced by the chromophores. In Table S1 of the SI, we list the spectral inhomogeneity for the Cy3 monomer-labeled duplex DNA construct as a function of temperature. The values of both parameters σI,mon and σI,dim increase with temperature, which suggests that for both the monomer and dimer labeled duplex DNA constructs, there exists a distribution of thermally populated conformational sub-states separated by thermal barriers, which are overcome with increasing temperature. The level of disorder appears to be greater in the monomer versus the dimer duplex DNA construct. The disorder parameter of the monomer σI,mon increases monotonically with temperature over the range 15 – 45 °C, and then undergoes a gradual decrease over the range 45 – 65 °C to nearly the same value as that of the dimer σI,dim at the melting transition. This is likely a reflection of the less favorable packing conditions of the Cy3 monomer within the duplex DNA construct, for which a single thymine base is positioned across from the Cy3 chromophore on the opposing DNA single-strand (see Table I).
For the (Cy3)2 dimer-labeled fork DNA construct, the inter-chromophore separation RAB increases from 5.3 – 14.4 Å, the inter-chromophore twist angle ϕAB decreases from 101 to −11°, the tilt angle θAB increases from 47.3 – 73.0°, and the resonant coupling J increases from −537 – 366 cm−1. An interesting property of the dimer-labeled fork DNA construct is that the spectral inhomogeneity parameter σI,dim remains essentially constant (~ 365 cm−1) over the temperature range 15 – 55 °C, before abruptly increasing to 407 cm−1 at the denaturation temperature 65 °C. This weak temperature dependence of the inhomogeneity parameter suggests the absence of thermal barriers separating the broad distribution of conformational sub-states associated with the probe labels at the fork junction. It is interesting to compare the temperature-dependent inhomogeneity parameter of the Cy3 monomer-labeled DNA fork construct (see Table S2 of the SI) to that of the (Cy3)2 dimer fork DNA construct. At 15 °C, we see that the value of σI,mon is approximately equal to the value of σI,dim. However, over the temperature range that the dimer disorder parameter remains constant, the monomer disorder increases monotonically with temperature, approaching a value of 405 cm−1, which is nearly equal to that of the dimer σI,dim at the denaturation temperature 65 °C.
Determination of Inhomogeneous Line Widths using Two-Dimensional Fluorescence Spectroscopy.
From our previous analyses of the linear absorbance and CD spectra of the (Cy3)2 dimer-labeled DNA constructs, we see that it is possible to obtain significant information about the average conformation and conformational disorder of the chromophore probes within the local DNA framework. These analyses made use of a separate determination of the room temperature homogeneous line width parameter ΓH = 186 cm−1 (17). To achieve a more accurate characterization of local conformation and conformational disorder, we extend our analysis to include the results of 2DFS experiments, as described in Section II. When combined with absorbance and CD, these 2DFS measurements can separately measure homogeneous and inhomogeneous contributions to the spectral lineshapes.
The rephasing (RP) and non-rephasing (NRP) 2DFS signals are complex-valued response functions described by Eqs. (6) and (7), respectively [Tekavec, Perdomo]. These signals are Fourier transformed with respect to the inter-pulse delays t21 and t43 to produce the complex-valued RP and NRP 2DFS spectra as a function of the frequency variables and , respectively. The RP and NRP spectra may be combined to produce the total correlation (TC) spectra (i.e., RP + NRP = TC). From Eqs. (8) – (10), we see that the RP spectra have the property that inhomogeneous line broadening does not contribute to the 2D lineshapes along the anti-diagonal direction , while homogeneous line broadening does contribute along both the diagonal and the anti-diagonal directions. From Eqs. (11) – (13), we see that the NRP spectra contain both inhomogeneous and homogeneous contributions along the diagonal and the anti-diagonal directions. These properties of 2DFS spectral lineshapes allow us to separately resolve homogeneous and inhomogeneous parameters.
As a control study, we performed 2DFS measurements of the Cy3 chromophore in methanol solution at 25 °C (see Fig. S2 of the SI section). For these measurements, the laser center wavelength was set to 532 nm (18,796 cm−1) with bandwidth 37 nm (1,300 cm−1). This laser spectrum spans the 0 – 0 and 1 – 0 vibronic sub-bands of the Cy3 absorbance spectrum, which occurs over the wavelength range 515 – 550 nm (18,200 – 19,400 cm−1). In Fig. S2C, we show the real and imaginary parts of the NRP (left column), RP (middle column), and TC (right column) spectra. The 2DFS spectra are dominated by the 0 – 0 vibronic transition, with a minor contribution from the 1 – 0 transition. The effect of these two overlapping vibronic features on the 2DFS spectra is to produce quasi-elliptical 2D lineshapes with long (short) axes oriented along the anti-diagonal (diagonal) directions of the NRP (RP) spectra. The combination of RP and NRP spectra produces a TC spectrum that is relatively symmetric with respect to diagonal and anti-diagonal axes. We note that there are only minor cross-peak intensities that appear to couple the 0 – 0 and 1 – 0 transitions. From an analysis of the diagonal and anti-diagonal cross-sectional line widths (17), we obtain values for the homogeneous Lorentzian FWHM parameter ΓH = 400 cm−1, and the inhomogeneous Gaussian standard deviation σI = 250 cm−1.
We next discuss the results of our 2DFS measurements performed on the Cy3-labeled DNA constructs at 25 °C. In Fig. 6, we present experimental absorbance spectra (top row), experimental RP 2DFS spectra (middle row) and simulated RP 2DFS spectra (bottom row) corresponding to the Cy3 monomer-labeled duplex DNA construct (Fig. 6A), the (Cy3)2 dimer-labeled duplex DNA construct (Fig. 6B), and the (Cy3)2 dimer-labeled fork DNA construct (Fig. 6C). Overlaid with the experimental absorbance spectra are the exciton features resulting from our analyses of the absorbance and CD spectra, which we discussed in previous sections. Also shown is a representative laser spectrum with center wavelength 532 nm and bandwidth 31 nm (1,100 cm−1). In all cases, the laser spectrum spans the 0 – 0 and 1 – 0 vibronic sub-bands. Similar to the RP 2D spectra obtained from the Cy3 chromophore in methanol (see Fig. S2C), the RP 2D spectra of the Cy3 DNA constructs exhibit a dominant feature associated with the 0 – 0 transition, and a minor feature associated with the 1 – 0 transition. Yet the most striking observation for all three of the DNA constructs is the overall asymmetry of the 2D spectra, which indicates the presence of overlapping diagonal peaks and off-diagonal cross-peaks. Furthermore, the 2D lineshapes of individual spectral features are disproportionately broadened along the diagonal direction of the 2D spectrum due to the influence of conformational disorder, which uniquely affects the RP spectrum for each of the DNA constructs.
Figure 6.
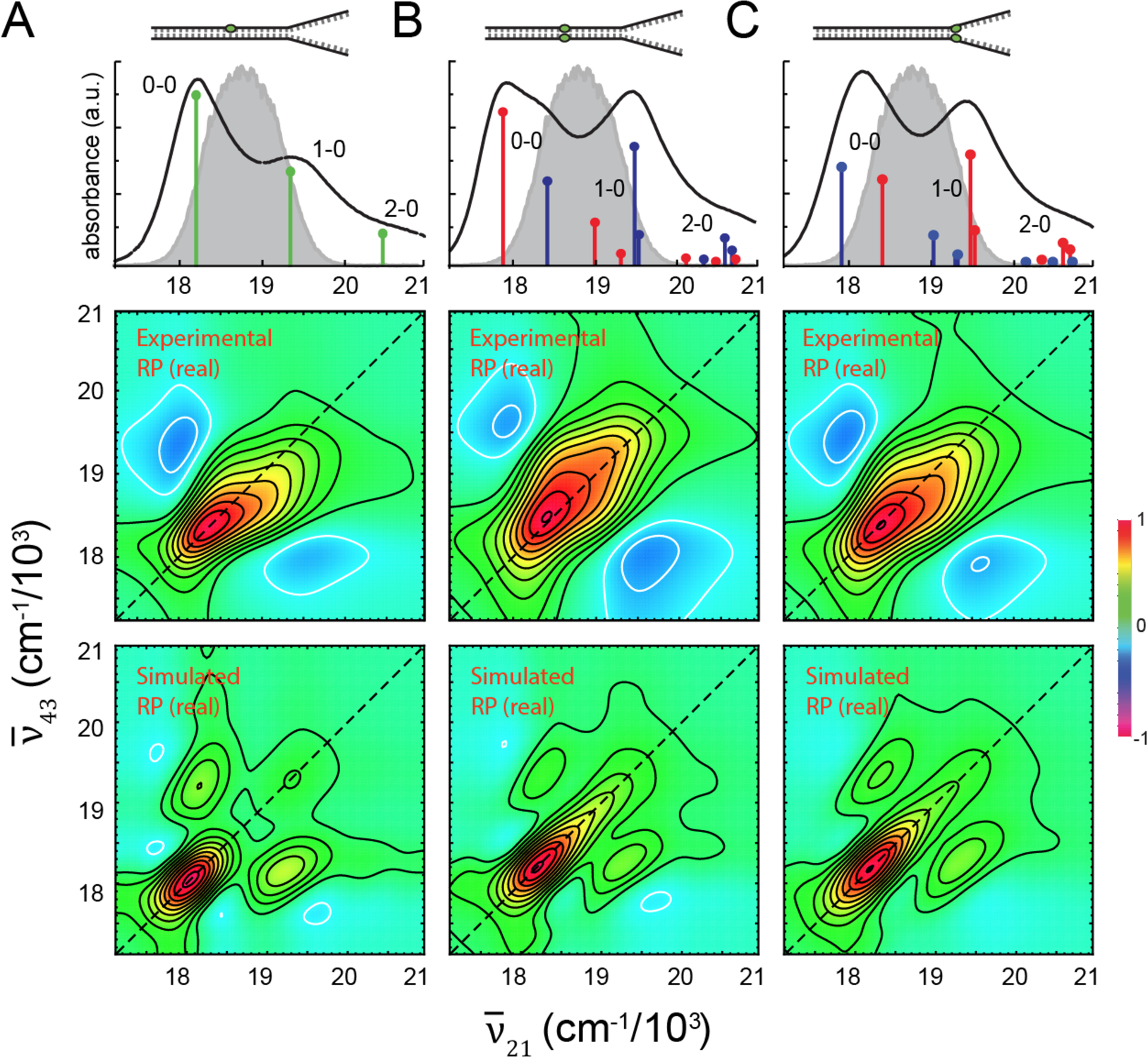
Room temperature (25 °C) experimental and simulated 2DFS measurements performed on (A) the Cy3 monomer duplex DNA construct, (B) the (Cy3)2 dimer duplex DNA construct, and (C) the (Cy3)2 dimer fork DNA construct. Absorbance spectra are shown overlaid with the vibronic spectral features obtained from the H-F Hamiltonian given by Eq. (1) and Eq. (2). The associated parameters are listed in Table S1 for the monomer duplex DNA construct, in Table II for the dimer duplex DNA construct, and in Table III for the dimer fork DNA construct. Also shown is the laser spectrum (in gray) with center frequency = 18,796 cm−1 (λL= 532 nm) and FWHM bandwidth = 1,100 cm−1 (ΔλL = 31 nm). The laser spectrum spans a region containing both the 0–0 and 1–0 vibronic sub-bands. Experimental RP spectra (middle row) are compared to simulated RP spectra (bottom row). Simulated spectra are based on the homogeneous line width parameter ΓH = 186 cm−1, the fluorescence quantum yield parameter Γ2D = 0.5 [Eq. (6)], the structural parameters obtained from our analyses of absorbance and CD spectra, and inhomogeneous lineshape parameters (A) σI = 125 cm−1, (B)σI = 125 cm−1 and (C) σI = 250 cm−1.
In Fig. 6 (bottom row), we present simulated RP spectra that assume as input structural parameters the same values that we obtained from our optimization analyses for the corresponding Cy3-labeled DNA construct. In these calculations, we have used the homogeneous line width parameter ΓH = 186 cm−1, in accordance with our previous analyses. We also used the value Γ2D = 0.5, which characterizes the relative fluorescence quantum yield of the doubly excited state relative to the singly excited state manifolds [see Eqs. (6) and (7)]. We note that our simulated 2D spectra for the (Cy3)2 dimer system are relatively insensitive to the value of Γ2D. For each of the simulated RP spectra, we adjusted the inhomogeneous line broadening parameter to obtain the most favorable comparison to the experimental data. For both the Cy3 monomer-labeled duplex DNA construct (Fig. 6A) and the (Cy3)2 dimer-labeled duplex DNA construct (Fig. 6B), we obtain the value σI = 125 cm−1. For the (Cy3)2 dimer-labeled fork DNA construct, we obtain the value σI = 250 cm−1. We note that the agreement between experimental and simulated RP spectra is good. The simulated spectra exhibit diagonal peaks and off-diagonal cross-peaks that give rise to the spectral features seen in the experiment. The effects of disorder can be understood in terms of their disproportionate contribution along the diagonal to the various 2D spectral line shapes. These results are in agreement with those of our previous analyses, which indicate that there is significantly greater conformational disorder associated with the (Cy3)2 dimer-labeled fork DNA construct than that exhibited by the Cy3 monomer- and (Cy3)2 dimer-labeled duplex DNA constructs.
V. Conclusions
We studied the absorbance, circular dichroism (CD) and two-dimensional fluorescence (2DFS) spectra of a (Cy3)2 dimer that was site-specifically positioned within the sugar-phosphate backbone at the single-stranded (ss)—double-stranded (ds) DNA fork junction. We compared our results to those obtained from a (Cy3)2 dimer that was positioned deep within the DNA duplex. We adopted the Holstein-Frenkel (H-F) Hamiltonian model to characterize the symmetric and anti-symmetric excitons supported by the dimer over a range of temperatures below the denaturation transition of the dsDNA. From this analysis, we obtained a temperature-dependent parameterization of the average dimer conformation and the degree of conformational disorder (see Table III). We compared the results of our analyses using alternatively the point-dipole and the extended-dipole models, and we found that both models yield essentially the same temperature-dependent values for the conformational parameters.
At the lowest temperature we studied (15°C), the (Cy3)2 dimer-labeled DNA fork construct exhibits intermediate-to-strong resonant coupling (J ~ −537 cm−1), comparable in magnitude to the vibrational relaxation energy of the constituent monomers (λ2ℏω0 ~ 600 cm−1). Under these conditions, the dimer can support delocalized excitons composed of symmetric and anti-symmetric superpositions of electronic-vibrational product states. The delocalized electronic structure is a consequence of the (Cy3)2 dimer being held within the sugar-phosphate backbone at a very small inter-chromophore separation (RAB = 5.3 Å) and a nearly orthogonal inter-chromophore twist angle. The conformation of the (Cy3)2 dimer at the DNA fork junction lacks cylindrical symmetry with tilt angle θAB = 47.3° and inter-chromophore twist angle ϕAB = 101°, which markedly deviates from the Watson-Crick B-form structure that we observe in the DNA duplex.
As the temperature is increased towards the ds – ss DNA denaturation temperature (Tm = 65 °C), the resonant electronic coupling strength of the (Cy3)2 dimer-labeled DNA fork construct gradually decreases in magnitude over a ~ 200 cm−1 range, and undergoes a sign inversion at ~ 55 °C. The Hamiltonian parameters characteristic of the Cy3 monomer-labeled DNA fork construct (i.e. the transition energy εeg, the Huang-Rhys electronic-vibrational coupling parameter λ2, and the vibrational frequency ω0) remain approximately independent of temperature (see Table S1 of the SI). This behavior is due to the sensitivity of the local secondary structure of the (Cy3)2 dimer-labeled fork (and duplex) DNA construct(s) to temperature, which affects the inter-chromophore separation, twist angle, and tilt angle, but not the electronic-vibrational properties internal to each Cy3 monomer.
While the magnitude of spectral inhomogeneity (~365 cm−1) is significant across the 15 – 65°C temperature range, the effects of exciton delocalization within the (Cy3)2 dimer are not dominated by spectral inhomogeneity. The spectral inhomogeneity parameter of the Cy3 monomer-labeled fork DNA construct increases systematically over the 15 – 65 °C temperature range (σI,mon = 355 – 398 cm−1), signifying that the monomer probe experiences locally disordered, thermally activated regions of the DNA fork, well below the melting transition. However, the inhomogeneity parameter of the (Cy3)2 dimer-labeled fork DNA construct is relatively constant over the 15 – 55 °C temperature range (σI,dim ~ 365 cm−1) before abruptly increasing to 407 cm−1 at the denaturation temperature 65 °C. Our observation of a weak temperature-dependence for the inhomogeneity parameter σI,dim suggests that thermal activation does not play a significant role in populating a broad distribution of (Cy3)2 dimer conformational sub-states at the ss-ds DNA fork junction. This finding is consistent with the hypothesis that the sugar-phosphate backbone of DNA near ss-ds junctions fluctuates into a broad distribution of conformations to permit the proper binding of genome regulatory proteins.
Our accompanying two-dimensional fluorescence spectroscopy (2DFS) measurements allow us to test our H-F Hamiltonian model based on the analysis of absorbance and CD data, and to potentially examine the effects of conformational disorder in more detail. We find that our room temperature 2DFS data are consistent with the H-F Hamiltonian parameters that we determined from our analysis of absorbance and CD, in addition to our previously determined value for the homogeneous spectral line width (FWHM ΓH = 186 cm−1). Furthermore, rephasing (RP) spectra are extremely sensitive to the effects of disorder, which contribute disproportionately to the 2D lineshapes along the diagonal and anti-diagonal axis directions. Although our current analysis confirms that disorder at the DNA fork junction exceeds that within the DNA duplex, the magnitude of the disorder determined by 2DFS appears to be less (~ 100 cm−1) than that determined from our analyses of linear spectra. Additional temperature-dependent analyses of RP and NRP spectral lineshapes should provide a comprehensive description of disorder at the ss-ds DNA fork junction.
Although the H-F model for the exciton-coupled (Cy3)2 dimer is relatively simple as it assumes a single internal vibrational mode for each Cy3 monomer, the model appears to capture the essential features of the experimental absorbance, CD and 2DFS spectra. Temperature variation corresponds to systematic changes in local dimer conformation that allows the resonant coupling strength to be ‘tuned’ across the intermediate-to-strong exciton-coupling regime. The significant spectral inhomogeneity is due to the presence of local structural fluctuations of the DNA backbone and base stacking that influence the packing of the chromophore probes. Such local fluctuations of DNA are termed DNA ‘breathing,’ which likely play a functional role in the binding and assembly of gene regulatory proteins (2).
Supplementary Material
Acknowledgements
We thank members of the von Hippel group for useful discussions pertaining to DNA breathing and other factors that affect DNA stability. We also thank Prof. Michael Raymer and Prof. Brian Smith for useful discussions about exciton coupled molecular networks. This work was supported by the John Templeton Foundation (RQ-35859 to A.H.M. as a co-PI), by the National Science Foundation Chemistry of Life Processes Program (CHE-1608915 to A.H.M.), and by the National Institutes of General Medical Sciences (NIGMS Grant GM-15792 to A.H.M. and P. H. vH. as co-PIs).
Footnotes
Supplementary Material
Supplementary material contains temperature-dependent optimized parameters of model Hamiltonian fits to the absorbance spectra of Cy3 monomer duplex and fork DNA constructs. A comparison is shown between optimized fits to absorption and CD spectra using a point-dipole versus an extended-dipole model of the resonant coupling. Two-dimensional fluorescence spectroscopy (2DFS) measurements are presented for the Cy3 chromophore in methanol.
References
- 1.Alberts B, Johnson A, Lewis J, Raff M, Roberts K, and Walter P, Molecular Biology of The Cell (Garland Science, New York, 2008), 5th edn., [Google Scholar]
- 2.von Hippel PH, Johnson NP, and Marcus AH, 50 Years of DNA ‘Breathing’: Reflections on Old and New Approaches. Biopolymers 99, 923–954, (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Levitus M, and Ranjit S, Cyanine Dyes in Biophysical Research: The Photophysics of Polymethine Fluorescent Dyes in Biomolecular Environments. Quat. Rev. Biophys 44, 123–151, (2011). [DOI] [PubMed] [Google Scholar]
- 4.Mishra A, Behera RK, Behera PK, Mishra BK, and Behera GB, Cyanines During the 1990s: A Review. Chem. Rev 100, 1973–2011, (2000). [DOI] [PubMed] [Google Scholar]
- 5.Würthner F, Kaiser TE, and Saha-Möller CR, 75 Years of J-aggregates. Angew. Chem. Int. Ed 50, 3376–3410, (2000). [DOI] [PubMed] [Google Scholar]
- 6.Resch-Genger U, Grabolle M, Cavaliere-Jaricot S, Nitschke R, and Nann T, Quantum Dots Versus Organic Dyes as Fluorescent Labels. Nature Meths. 5, 763–775, (2008). [DOI] [PubMed] [Google Scholar]
- 7.Sanborn ME, Connolly BK, Gurunathan K, and Levitus M, Fluorescence Properties and Photophysics of the Sufoindocyanine Cy3 Linked Covalently to DNA. J. Phys. Chem. B 111, 11064–11074, (2007). [DOI] [PubMed] [Google Scholar]
- 8.Lee W, Jose D, Phelps C, Marcus AH, and von Hippel PH, A Single-Molecule View of the Assembly Pathway, Subunit Stoichiometry and Unwinding Activity of the Bacteriophage T4 Primosome (Helicase-Primase) Complex. Biochemistry 52, 3157–3170, (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lee W, von Hippel PH, and Marcus AH, Internally Labeled Cy3 / Cy5 DNA Constructs Show Greatly Enhanced Photostability in Single-Molecule FRET Experiments. Nucleic Acids Res 42, 5967–5977, (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Phelps C, Lee W, Jose D, von Hippel PH, and Marcus AH, Single-Molecule FRET and Linear Dichroism Studies of DNA ‘Breathing’ and Helicase Binding at Replication Fork Junctions. Proc Natl Acad Sci U S A 110, 17320–17325, (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Valkunas L, Abramavicius D, and Mančal T, Molecular Excitation Dynamics and Relaxation: Quantum Theory and Spectroscopy (Wiley-VCH, 2013), [Google Scholar]
- 12.Azumi T, and Matsuzaki K, What Does the Term “Vibronic Coupling” Mean? Photochem. and Photobiol. 25, 315–326, (1977). [Google Scholar]
- 13.Fischer G, Vibronic Coupling: The Interaction Between the Electronic and Nuclear Motions (Academic Press, London, 1984), [Google Scholar]
- 14.Aydin M, Dede Ö, and Akins DL, Density Functional Theory and Raman Spectroscopy Applied to Structure and Vibrational Mode Analysis of 1,1’,3,3’-Tetraethyl-5,5’,6,6’-Tetrachloro-Benzimidazolocarbocyanine Iodide and its Aggregate. J. Chem. Phys 134, 064325-1–12, (2011). [DOI] [PubMed] [Google Scholar]
- 15.Roy R, Hohng S, Ha T, A Practical Guide to Single-Molecule FRET. Nature Meths. 5, 507–16, (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Förster T, Delocalized Excitation and Excitation Transfer (Florida State University, Tallahassee, Florida, 1965), Vol. Bulletin No. 18, Division of Biology and Medicine, U.S. Atomic Energy Commission, [Google Scholar]
- 17.Kringle L, Sawaya NPD, Widom J, Adams C, Raymer MG, Aspuru-Guzik A, Marcus AH, Temperature-Depednent Conformations of Exciton-Coupled Cy3 Dimers in Double-Stranded DNA. J. Chem. Phys 148, 085101-1–13, (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Spano FC, The Spectral Signatures of Frenkel Polarons in H- and J-Aggregates. Acc. Chem. Res 43, 429–439, (2010). [DOI] [PubMed] [Google Scholar]
- 19.Kistler KA, Pochas CM, Yamagata H, Matsika S, and Spano FC, Absorption, Circular Dichroism, and Photoluminescence in Perylene Diimide Bichromophores: Polarization-Dependent H- and J-Aggregate Behavior. J. Phys. Chem. B 116, 77–86, (2012). [DOI] [PubMed] [Google Scholar]
- 20.von Hippel PH, McGhee JD, DNA-Protein Interactions. Annu. Rev. Biochem 41, 231–300, (1972). [DOI] [PubMed] [Google Scholar]
- 21.von Hippel PH, From “Smple” DNA-Protein Interactions to the Macromolecular Machines of Gene Expression. Annu. Rev. Biophys. Biomol. Struct 36, 79–105, (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Howard IA, Zutterman F, Deroover G, Lamoen D, Van Alsenoy C, Approaches to Calculation of Exciton Interaction Energies for a Molecular Dimer. J. Phys. Chem. B 108, 19155–19162, (2004). [Google Scholar]
- 23.Czikklely VHDF, Kuhn H, Extended Dipole Model for Aggregates of Dye Molecules. Chem. Phys. Lett 6, 207–210, (1970). [Google Scholar]
- 24.Didraga C, Pugžlys A, Hania PR, von Berlepsch H, Duppen K, Knoester J, Structure, Spectroscopy, and Microscopic Model of Tubular Carbocyanine Dye Aggregates. J. Phys. Chem. B 108, 14976–14985, (2004). [Google Scholar]
- 25.Stennett EMS, Ma N, van der Vaart A, Levitus M, Photophysical and Dynamical Properties of Doubly Linked Cy3-DNA Constructs. J. Phys. Chem. B 118, 152–163, (2014). [DOI] [PubMed] [Google Scholar]
- 26.Cantor CR, Schimmel PR, Biophysical Chemistry Part II: Techniques for the Study of Biological Structure and Function (Freeman, New York, 1980), Vol. 2, Biophysical Chemistry, [Google Scholar]
- 27.Charney E, The Molecular Basis of Optical Activity: Optical Rotatory Dispersion and Circular Dichroism (John Wiley & Sons, New York, 1979), [Google Scholar]
- 28.Berova N, and Nakanishi K, in Circular Dichroism: Principles and Applications, edited by Berova N, Nakanishi K, and Woody RW (John Wiley & Sons, Inc., New York, 2000), pp. 337–382. [Google Scholar]
- 29.Tekavec PF, Lott GA, and Marcus AH, Fluorescence-Detected Two-Dimensional Electronic Coherence Spectroscopy by Acousto-Optic Phase Modulation. J. Chem. Phys 127, 214307, (2007). [DOI] [PubMed] [Google Scholar]
- 30.Perdomo A, Widom JR, Lott GA, Aspuru-Guzik A, Marcus AH, Conformation and Electronic Population Transfer in Membrane Supported Self-Assembled Porphyrin Dimers by Two-Dimensional Fluorescence Spectroscopy. J. Phys. Chem. B 116, 10757–10770, (2012). [DOI] [PubMed] [Google Scholar]
- 31.Widom JR, Johnson NP, von Hippel PH, Marcus AH, Solution Conformation of 2-Aminopurine (2-AP) Dinucleotide by Ultraviolet 2D Fluorescence Spectroscopy (UV-2D FS). New Journal of Physics 15, 025028, (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Karki KJ, Widom JR, Seibt J, Moody I, Lonergan MC, Pullerits T, Marcus AH, Coherent Two-Dimensional Photocurrent Spectroscopy in a PbS Quantum Dot Photocell. Nature Comm. 5, 5869-1–7, (2014). [DOI] [PubMed] [Google Scholar]
- 33.Tekavec PF, Dyke TR, Marcus AH, Wave Packet Interferometry and Quantum State Reconstruction by Acousto-Optic Phase Modulation. J. Chem. Phys 125, 194303-1–19, (2006). [DOI] [PubMed] [Google Scholar]
- 34.Polyutov S, Kühn O, and Pullerits T, Exciton-Vbrational Coupling in Molecular Aggregates: Electronic Versus Vibronic Dimer. Chem. Phys 394, 21–28, (2012). [Google Scholar]
- 35.Eisfeld A, Braun L, Stunz WT, Briggs JS, Beck J, and Engel V, Vibronic Energies and Spectra of Molecular Dimers. J. Chem. Phys 122, 134103-1–10, (2005). [DOI] [PubMed] [Google Scholar]
- 36.Tiwari V, Peters WK, Jonas DM, Electronic Resonance with Anticorrelated Pigment Vibrations Drives Photosynthetic Energy Transfer Outside the Adiabatic Framework. Proc Natl Acad Sci U S A 110, 1203–1208, (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Halpin AJ, P. J. M., Tempelaar R Murphy RS, Knoester J, Jansen TLC, and Miller RJD, Two-Dimensional Spectroscopy of a Molecular Dimer Unviels the Effects of Vibronic Coupling on Exciton Coherences. Nature Chem. 6, 196–201, (2014). [DOI] [PubMed] [Google Scholar]
- 38.Duan H-G, Nalbach P, Prokhorenko VI, Mukamel S, and Thorwart M, On the Origin of Oscillations in Two-Dimensional Spectra of Excitonically-Coupled Molecular Systems. New Journal of Physics 17, 072002, (2015). [Google Scholar]
- 39.Lott GA, Perdomo-Ortiz A, Utterback JK, Widom JR, Aspuru-Guzik A, and Marcus AH, Conformation of Self-Assembled Porphyrin Dimers in Liposome Vesicles by Phase-Modulation 2D Fluorescence Spectroscopy. Proc Natl Acad Sci U S A 108, 16521–6, (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Grégoire P, Kandada ARS, Vella E, Tao C, Leonelli R, Silva C, Incoherent Population Mixing Contributions to Phase-Modulation Two-Dimensional Coherent Excitation Spectra. J. Chem. Phys 147, 114201-1–9, (2017). [DOI] [PubMed] [Google Scholar]
- 41.Phelps C, Israels B, Jose D, Marsh M, von Hippel PH, and Marcus AH, Using Microsecond Single-Molecule FRET to Determine the Assembly Pathways of T4 ssDNA Binding Protein onto Model DNA Replicatoin Forks. Proc Natl Acad Sci U S A 114, E3612–E3621, (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Byrd RH, Nocedal J, and Waltz RA, KNITRO: An Integrated Package for Nonlinear Optimization. (Springer-Verlag, Berlin, Germany, 2006), Large-Scale Nonlinear Optimization, 35–59. [Google Scholar]
- 43.Nordén B, Rodger A, and Dafforn T, Linear Dicrhoism and Circular Dichroism: A Textbook on Polarized-Light Spectroscopy (RSC Publishing, Cambridge, UK, 2010), [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


