Update: use of the benchmark dose approach in risk assessment

Abstract

The Scientific Committee (SC) reconfirms that the benchmark dose (BMD) approach is a scientifically more advanced method compared to the NOAEL approach for deriving a Reference Point (RP). Most of the modifications made to the SC guidance of 2009 concern the section providing guidance on how to apply the BMD approach. Model averaging is recommended as the preferred method for calculating the BMD confidence interval, while acknowledging that the respective tools are still under development and may not be easily accessible to all. Therefore, selecting or rejecting models is still considered as a suboptimal alternative. The set of default models to be used for BMD analysis has been reviewed, and the Akaike information criterion (AIC) has been introduced instead of the log‐likelihood to characterise the goodness of fit of different mathematical models to a dose–response data set. A flowchart has also been inserted in this update to guide the reader step‐by‐step when performing a BMD analysis, as well as a chapter on the distributional part of dose–response models and a template for reporting a BMD analysis in a complete and transparent manner. Finally, it is recommended to always report the BMD confidence interval rather than the value of the BMD. The lower bound (BMDL) is needed as a potential RP, and the upper bound (BMDU) is needed for establishing the BMDU/BMDL per ratio reflecting the uncertainty in the BMD estimate. This updated guidance does not call for a general re‐evaluation of previous assessments where the NOAEL approach or the BMD approach as described in the 2009 SC guidance was used, in particular when the exposure is clearly smaller (e.g. more than one order of magnitude) than the health‐based guidance value. Finally, the SC firmly reiterates to reconsider test guidelines given the expected wide application of the BMD approach.

Short abstract

http://onlinelibrary.wiley.com/doi/10.2903/sp.efsa.2017.EN-1147/full

Summary

Considering the need for transparent and scientifically justifiable approaches to be used when risks are assessed by the Scientific Committee (SC) and the Scientific Panels of the European Food Safety Authority (EFSA), the SC was requested in 2005 by EFSA (i) to assess the existing information on the utility of the benchmark dose (BMD) approach, as an alternative to the traditionally used the no‐observed‐adverse‐effect level (NOAEL) approach, (ii) to provide guidance on how to use the BMD approach for analysing dose–response data from experimental animal studies and (iii) to look at the possible application of this approach to data from observational epidemiological studies.

A guidance document on the use of the benchmark dose approach in risk assessment was published in 2009. In 2015, the SC reviewed the implementation of the BMD approach in EFSA's work; the experience gained with its application and the latest methodological developments in regulatory risk assessment, and concluded that an update of its guidance from 2009 was necessary. Most of the modifications made to the SC guidance of 2009 concern the section providing guidance on how to apply the BMD approach in practice. Model averaging is now recommended as the preferred method for calculating the BMD confidence interval, while acknowledging that the respective tools are still under development. As these tools may currently not be easily accessible to every risk assessor, the simpler approach of selecting or rejecting models is still considered as a suboptimal alternative. The set of default models to be used for the BMD analysis has been reviewed, and the Akaike information criterion (AIC) has been introduced instead of the log‐likelihood to characterise the relative goodness of fit of different mathematical models to a dose–response data set. A flowchart has also been inserted in this update to guide the reader step‐by‐step when performing a BMD analysis, as well as a chapter on the distributional part of dose–response models and a template for reporting a BMD analysis in a complete and transparent manner. Finally, it is recommended to always report the BMD confidence interval rather than the value of the BMD. The lower bound (BMDL) is needed as a potential Reference Point (RP), and the upper bound (BMDU) is needed for establishing the BMDU/BMDL ratio, which reflects the uncertainty in the BMD estimate.

The SC reconfirms in this updated guidance that the BMD approach, and more specifically model averaging, should be used for deriving a RP from the critical dose–response data to establish health‐based guidance values (HBGVs) and margins of exposure. This updated guidance does not call for a general re‐evaluation of previous assessments where the NOAEL approach or the BMD approach as described in the 2009 SC guidance was used, in particular when the exposure is clearly smaller (e.g. more than one order of magnitude) than the HBGV. The application of this updated guidance to previous risk assessments where the 2009 guidance was used might result in different RPs, in particular in the case of continuous response data (due to the updated procedure of selecting models from the nested model families).

The SC recommends that training in dose–response modelling and the use of BMD software continues to be offered to experts in the Scientific Panels and EFSA Units. EFSA should establish a Standing Working Group on the BMD analysis to be consulted by EFSA experts and staff members if needed, e.g. when alerts are identified or when applying the BMD approach to specific data such as histopathological (ordinal) data. A network on BMD, coordinated by EFSA, should also be considered to exchange experience and develop expertise with the EFSA Partners (Member States competent, EU sister agencies, DG Santé Scientific Committees and international organisations).

The SC also identifies the need for a specific guidance on the use of the BMD approach to analyse human data.

Finally, the SC firmly reiterates the need for current toxicity test guidelines to be reconsidered given the expected wide application of the BMD approach.

1. Introduction

As per EFSA's Founding Regulation (EC) No 178/2002 of the European Parliament and of the Council, ‘the EFSA Scientific Committee shall be responsible for the general coordination necessary to ensure the consistency of the scientific opinion procedure, in particular with regard to the adoption of working procedures and harmonisation of working methods’. The EFSA Science Strategy 2012–2016 echoes this key responsibility of the Scientific Committee (SC) by setting the development and harmonisation of methodologies and approaches to assess risks associated with the food chain as one of the four strategic objectives for the European Food Safety Authority (EFSA).

In May 2009, the SC adopted its guidance on the use of the benchmark dose (BMD) approach in risk assessment (EFSA, 2009a). When deriving a Reference Point (point of departure), the guidance document recommends using the BMD approach instead of the traditionally used the no‐observed‐adverse‐effect level (NOAEL) approach, since it makes a more extended use of dose–response data and it allows for a quantification of the uncertainties in the dose–response data. The BMD approach is applicable to all chemicals in food, irrespective of their category or origin.

Feedback was gathered by EFSA's Secretariat regarding the implementation of this approach by EFSA's Scientific Panels during the last 7 years; several issues were highlighted as worth further clarification. During its 67th Plenary meeting (see minutes), the Scientific Committee agreed with the proposal to update the guidance document on the use of the benchmark dose approach in risk assessment.

1.1. Terms of Reference as provided by EFSA

EFSA requests the SC to update the existing guidance to clarify the following issues:

1. The current SC guidance recommends specific mathematical models to be fit for quantal and continuous dose–response data. The list of recommended models should be reviewed.

2. The approach for selecting the best model when dealing with a family of nested models should be reviewed; suggestion was made to deviate from the approach recommended in the SC guidance and use directly the full versions of the nested family of models, i.e. the Exponential and Hill four parameters models when dealing with continuous data (Slob and Setzer, 2014).

3. The need and relevance to constrain some of the model parameters so that they reflect the biology should be reviewed and guidance should be provided on when or when not to constrain models.

4. Further guidance should be provided on how to deal with poor data sets. Criteria regarding acceptable BMDL1 –BMD or BMDL–BMDU2 intervals to derive a Reference Point (RP) should be provided, as well as recommendations on how to deal with data sets that do not comply with these criteria.

5. Further guidance should be provided on using covariate analysis and when combining data for a BMD analysis.

This list is non‐exhaustive and may be expanded with additional issues identified during the updating process, if deemed worth further clarification.

2. Assessment

2.1. Introduction

This document addresses not only the analysis of dose–response data from experimental studies but also considers the application to data from observational epidemiological studies. Toxicity studies are conducted to identify and characterise the potential adverse effects of a substance. The data obtained in these studies may be further analysed to identify a dose that can be used as a starting point for risk assessment. The dose used for this purpose, however, derived is referred to in this opinion as the RP. This term has been used already by EFSA in the opinion of the SC on a harmonised approach for risk assessment of substances which are both genotoxic and carcinogenic (EFSA, 2005), and is therefore preferred to the equivalent term Point of Departure (PoD), used by others such as the US EPA.

The NOAEL has been used historically as the RP for estimating the health‐based guidance values (HBGVs) such as acceptable daily intakes (ADIs), tolerable daily intakes (TDIs) or tolerable weekly intakes (TWIs) in risk assessment of non‐genotoxic substances.

EFSA (2005) and the Joint FAO/WHO Expert Committee on Food Additives (JECFA, 2006a) have proposed the use of the BMD approach for deriving the RP used to calculate the margins of exposure (MOE) for substances that are both genotoxic and carcinogenic. As the NOAEL is known to have some limitations (see following sections), the SC concluded in 2009 that the benchmark dose (BMD) approach is the best approach for defining a RP also for non‐genotoxic substances (EFSA, 2009a). The methodology discussed in this guidance document has subsequently been applied for deriving RPs (i.e. BMDLs) for various types of chemicals (e.g. pesticide, additives and contaminants). The SC reviewed in 2015 the implementation and the experience of the BMD approach in EFSA's work, as well as the latest methodological developments in regulatory risk assessment to prepare the present update of its guidance document.

In Sections 2.1–2.3 of this guidance document, the concepts underlying both the NOAEL and BMD approaches are discussed with some illustrative examples. In these sections, it is outlined why the SC considers the BMD approach as the more powerful approach. Section 2.4 discusses the potential impact of using the BMD approach for hazard/risk characterisation and risk communication. Section 2.5, which provides guidance on how to apply the BMD approach in practice, has been significantly modified compared to the 2009 version of the guidance document: model averaging is more strongly emphasised as the preferred method for calculating the BMD confidence interval. Further, the set of default models to be used for the BMD analysis has been revised while the evaluation of model performance is now based on the so‐called Akaike information criterion (AIC) instead of the log‐likelihood. At the end of Section 2.5, two examples, one based on quantal data and the other on continuous data, are provided to illustrate the application of the BMD approach in practice and how to report the results. A template for BMD analysis reporting has been inserted in Appendix B.

The present guidance is primarily aimed at the EFSA Units and Panels and other stakeholders, for example applicants, performing dose–response analyses. The SC considers that the use of the BMD approach is always better than the NOAEL approach to define a RP; therefore, the application of this guidance document is unconditional for EFSA and is strongly recommended for all parties submitting assessments to EFSA for peer‐review (see EFSA Scientific Committee, 2015).

2.2. Hazard identification: selection of potential critical endpoints

Toxicity studies are designed to identify the adverse effects produced by a substance and to characterise the dose–response relationships for the adverse effects detected. While in some cases human dose–response data are available, most risk assessments rely on data from animal studies. The aim of hazard identification is to identify potential critical endpoints that may be of relevance for human health. An important component is the consideration of dose dependency of observed effects. Traditionally, this is done by visual inspection, together with conventional statistical tools. The SC recommends using dose–response modelling approaches instead (see Section 2.5.5). When no statistical evidence is found for a dose‐related trend, that data set would normally not be used for deriving a RP. For a given assessment (compound), the number of data sets with statistical evidence of a dose‐related trend may be large, and in such cases, visual inspection may be used to preselect those data sets that appear to show effects at lower doses than other data sets. Ideally, however, as visual inspection is not well suited for taking sampling error into account, selection of the critical dataset(s) would ideally be based on a BMD analysis of all relevant data sets. This will easily be possible as soon as the current BMD software is extended with the possibility to analyse a series of data sets in a single run. However, the selection of the critical effect should not be based on the statistical procedures only. Importantly, additional toxicological arguments should be taken into account in the evaluation of a full toxicological data package. Use of the BMD approach does not remove the need for a critical evaluation of the response data3 and an assessment of the relevance of the effect to human health.

The result of this first step is the identification of potential critical endpoints that should be analysed in more detail as described in the next sections.

2.3. Using dose–response data in hazard characterisation

The nature of the dose–response relationships is explored in detail in hazard characterisation. For most toxicological effects, the overall aim of the process is to identify a dose without appreciable adverse health effects in the test animals under the experimental conditions. The RP from the toxicity studies is then used to establish a level of human intake at which it is confidently expected that there would be no appreciable adverse health effects, taking into account uncertainty and variability such as inter‐ and intraspecies differences, suboptimal study characteristics or missing data.

Hazard characterisation in risk assessment requires the use of a range of dose levels in animal toxicity studies. Doses are needed that produce different effects sizes providing information on both the lower and higher part of the dose–response relationship to characterise the full dose–response relationship.

Experimental and biological variations affect response measurements; in consequence, the mean response at each dose level will include sampling error. Therefore, dose–response data need to be analysed by statistical methods to prevent inappropriate biological conclusions being drawn because of statistical errors associated with the data. Currently, there are two statistical approaches available for deriving a RP: the NOAEL approach and the BMD approach. This section reviews these two approaches, and provides a comparison of the strengths and limitations of each method.

2.3.1. The NOAEL approach

The NOAEL approach is applicable to all toxicological effects considered to have a threshold.

The study NOAEL is derived as follows:

• For each adverse effect/endpoint, identify the highest experimental dose level where effects were not detected, using expert opinion and statistical tests to compare each dose group with the control group.

• The study NOAEL is the lowest relevant NOAEL obtained for any of the adverse effects detected in the study (i.e. for the critical effect of the study).

Hence, the NOAEL is the highest dose tested without evidence of an adverse effect in the particular experiment. The numerical value of the NOAEL is thus dependent upon the selection of dose levels when the study was designed and on the ability of the study to detect adverse effects. Since studies with low power (e.g. small group sizes) and/or insensitive methods are able to detect only relatively large effects, these tend to result in higher NOAELs. If there is a statistically significant effect at all dose levels, the lowest dose used in the study is usually selected as the lowest‐observed‐adverse‐effect‐level (LOAEL).

It should be noted that in general, identification of the NOAEL is not always a purely statistically based decision. This has advantages and disadvantages. It allows the assessor to reject a NOAEL which is not well supported by the data, but it can also lead to different decisions. Factors that may be taken into account in identification of the NOAEL include whether there is a consistent dose–response relationship and the magnitude of the change in (mean) response. When the observed change in response is small, even if statistically significant, some assessors may consider it non‐adverse and use a higher dose as the NOAEL. In contrast, where there is a small, non‐significant increased response in the dose group below the statistically significant effect, some assessors may identify this response still as an adverse effect (i.e. being a LOAEL). Such decisions are based on expert judgement and different assessors may reach different decisions, as happened in the past, e.g. in the evaluation of residues of the veterinary drug ractopamine by JECFA (2006b) and the EFSA Panel on Additives and Products or Substances used in Animal Feed (FEEDAP) (EFSA, 2009b).

2.3.2. The BMD approach

The BMD approach is applicable to all toxicological effects. It makes use of all of the dose–response data to estimate the shape of the overall dose–response relationship for a particular endpoint. The BMD is a dose level, estimated from the fitted dose–response curve, associated with a specified change in response, the benchmark response (BMR), (see Section 2.5.2). The BMDL is the BMD's lower confidence bound, and this value is normally used as the RP.

The key concepts in the BMD approach are illustrated in Figure 1 and its legend. This figure shows that a BMDL that is calculated, e.g. for a BMR of 5%, can be interpreted as follows:

Figure 1.

Key concepts for the BMD approach, illustrated using hypothetical continuous data.

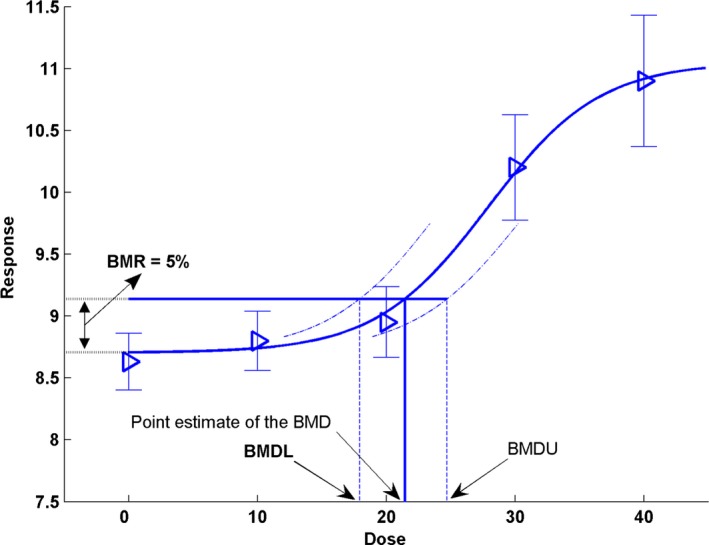
• The observed mean responses (triangles) are plotted, together with their confidence intervals. The solid curve is a fitted dose–response model. This curve determines the point estimate of the BMD, which is generally defined as a dose that corresponds to a low but measurable change in response, denoted the benchmark response (BMR). The dashed curves represent, respectively, the upper and lower 95% confidence bounds (one sided)4 for the effect size as a function of dose. Their intersections with the horizontal line are at the lower and upper bounds of the BMD, denoted BMDL and BMDU, respectively. It should be noted that the BMR is not defined as a change with regard to the observed mean background response, but with regard to the background response predicted by the fitted model. This distinction is important because, in general, the fitted curve does not hit the observed background response exactly (so that adding the BMR to the observed background response will in general not provide the correct intersection with the dose–response at the BMD). In the Figure, the BMD corresponds to a 5% change in response relative to background (BMR = 5%). The fitted curve yields an estimated background response of 8.7, and a 5% increase of that equals 9.14 (= 8.7 + 0.05 × 8.7). Thus, the BMD ₀₅ of 21.50 is obtained from the intersection of the horizontal line, at a response of 9.14, with the fitted dose–response model. In this example, the BMDL ₀₅ has a value of 18

BMDL₀₅ = dose where the change in response is likely to be smaller than 5%

where the term ‘likely’ is defined by the statistical confidence level, usually 95% confidence.

The essential steps involved in identifying the BMDL for a particular study are:

• Specification of a response level, e.g. a 5% or 10% increase or decrease in response compared with the background response. This is called the BMR (see Section 2.5.2).

• Fitting a set of dose–response models (Section 2.5.3), and calculation of the BMD confidence interval for each of the models that describe the data according to statistical criteria, resulting in a set of BMD confidence intervals.

• Deriving a single BMD confidence interval from the set of BMD confidence intervals for that particular adverse effect/endpoint, preferably by model averaging (Section 2.5.6).

• An overall study BMDL, i.e. the critical BMDL of the study, is selected from the obtained set of BMD confidence intervals for the different potentially critical endpoints (see Section 2.5.7).

In principle, the BMD approach could be applied to every endpoint measured in the relevant studies. The critical effect would then be selected in an analogous way as in the NOAEL approach, that is, not only as the endpoint resulting in the lowest BMDL, but also taking additional toxicological arguments into account, just as in the case of the NOAEL approach. However, it is recommended to make use of one of the strengths of the BMD approach, and select the study BMDL based on considering the complete BMD confidence intervals for the endpoints considered and combine the information on uncertainties in the underlying data with biological considerations (see Section 2.5.7). In the NOAEL approach, the decision to accept a data set for deriving a NOAEL as a potential RP is important since poor or limited data (e.g. due to high variability within the dose groups, high limit of quantification of analytical methods, small sample sizes) will tend to result in high NOAELs. Acceptability of the data will therefore depend upon expert judgement. In contrast, the BMD approach itself provides a formal quantitative evaluation of data quality, by taking into account all aspects of the specific data. When the data are relatively poor or uninformative, the resulting BMD confidence interval for that data set will tend to be wide, and the BMDL might be much lower than the true BMD. But the meaning of the BMDL value remains as it was defined: it reflects a dose level where the associated effect size is unlikely to be larger than the BMR used.

Nonetheless, it might happen that the data are so poor that using the associated BMDL as a potential RP appears unwarranted. This might be decided when the BMD confidence interval is wide or when different models result in widely different BMDL values. This issue is further discussed in Section 2.5.7.

The most well‐known BMD software are the benchmark dose software (BMDS) developed by the US EPA (http://www.epa.gov/bmds), and the PROAST software developed by RIVM (http://www.rivm.nl/proast). When the same models are fitted to the same data using the same assumptions, BMDS and PROAST will lead to the same answer (possibly with minor numerical differences). However, there are differences in running the software (e.g. different default settings, differences in output format) and in modelling options, as summarised in Appendix A.

2.3.3. Interpretation and properties of the NOAEL and the BMDL

The NOAEL is a dose level where generally no statistically significant differences in response are observed, compared with the background response. This implies that the NOAEL could reflect a dose level where effects are too small to be detected in that particular study, and therefore, the size of the possible effect at the NOAEL remains unknown. A straightforward way of gaining insight into this is by calculating a confidence interval for the observed change in response between the control group and the NOAEL dose group.

For a limited number of substances, the SC determined upper bounds for the effect size that are summarised in Table 1. Here, the size of effect for quantal responses is expressed as extra risk. Extra risk is defined as an absolute change in frequency of response (additional risk in %) divided by the non‐affected fraction in the control population (100 minus the background response in %).5 For continuous responses, the effect size is expressed as a per cent change in mean response. For quantal endpoints, the upper bounds (which relate to extra risk) vary between around 3% and 30%. This illustrates that in some cases the extra risk at the NOAEL could be greater than 10%, which is the recommended BMR level for quantal data (see Section 2.5.2). Similarly, for this limited number of substances, it is found that the upper bound of the effect size at the NOAEL for continuous endpoints could be as small as 3%; but more often it was in the order of 10%, which is high compared with the 5% recommended for the BMR for continuous data (see Section 2.5.2). In one of the examples, with a highly variable clinical chemistry parameter, the upper bound of effect was as high as 260%.

Table 1.

Illustrations of upper boundsa of effect at NOAELs related to 10 substances evaluated previously by JMPR or EFSA

Substance (source +year)	Endpoint	Quantal data	Continuous data	References
		Upper bound extra risk (%)b	Upper bound percent change (%)c
Thiodicarb (JMPR, 2000)	Splenic extramedullary haematopoiesis	21		http://www.inchem.org/documents/jmpr/jmpmono/v00pr09.htm
Carbaryl (JMPR, 2001)	Vascular tumours	15		http://www.inchem.org/documents/jmpr/jmpmono/2001pr02.htm
Spinosad (JMPR, 2001)	Thyroid epithelial cell vacuolation	2.7		http://www.inchem.org/documents/jmpr/jmpmono/2001pr12.htm
Flutolanil (JMPR, 2002)	Erythrocyte volume fraction		9	http://www.inchem.org/documents/jmpr/jmpmono/2002pr07.htm
	Haemoglobin concentration		9.7
	Mean corpuscular haemoglobin		3
	Decreased cellular elements in the spleen	30
Metalaxyl (JMPR, 2002)	Serum alkaline phosphatase activity		260	http://www.inchem.org/documents/jmpr/jmpmono/2002pr09.htm
	Serum AST		100
Cyprodinil (JMPR, 2003)	Spongiosis hepatis	5.1		http://www.inchem.org/documents/jmpr/jmpmono/v2003pr03.htm
Famoxadone (JMPR, 2003)	Cataracts	29		http://www.inchem.org/documents/jmpr/jmpmono/v2003pr05.htm
	Microscopic lenticular degeneration	29
Tributyltin (EFSA, 2004)	Testis weight		9.1	http://www.efsa.europa.eu/EFSA/efsa_locale-1178620753812_1178620762916.htm
Fumonisin (EFSA, 2005)	Nephrosis	8.6		http://www.efsa.europa.eu/EFSA/efsa_locale-1178620753812_1178620807204.htm
Deoxynivalenol (EFSA, 2004)	Body weight		10.5	http://www.efsa.europa.eu/EFSA/efsa_locale-1178620753812_1178620763160.htm
Ethyl lauroyl arginate (EFSA, 2007)	White blood cell counts		23	http://www.efsa.europa.eu/EFSA/efsa_locale-1178620753812_1178622334379.htm

^aAs calculated by the Scientific Committee.

^bTwo‐sided 90%‐confidence interval for extra risk was calculated by the likelihood profile method.

^cTwo‐sided 90% confidence interval was calculated for the difference on log‐scale, and then transformed back, resulting in the confidence interval for per cent change (see Slob (2002) for further statistical assumptions).

The NOAEL is therefore not necessarily a ‘no adverse effect’ dose, although it is often interpreted as such. Indeed, as the review studies discussed in Section 2.5.2, the size of the estimated effect at the NOAEL is, on average over a number of studies, close to 10% (quantal responses) or 5% (continuous responses). For an individual NOAEL, the size of effect remaining statistically non‐significant might be smaller, or greater than these values. As illustrated in Table 1, it is possible to calculate an upper bound for the effect size at the NOAEL. Similarly, Sand et al. (2011) estimated that the median of the upper bounds of extra risk at the NOAEL was close to 10% based on analysis of about 800 data sets from the US National Toxicology Program cancer bioassay database. However, the confidence interval of the effect size at the NOAEL is generally not reported in current applications. In the BMD approach, the potential size of the effect (i.e. the benchmark response, BMR) is by definition known.

For human (epidemiological) data, lower BMR values may be used because the observed response is often lower than 10% (see Section 2.5.2).

The BMD approach involves a statistical method, which uses the information in the complete data set instead of making pairwise comparisons using subsets of the data. In addition, the BMD approach can interpolate between applied doses, while the NOAEL approach is restricted to these doses. Therefore, a BMDL is always associated with a predefined effect size for which the corresponding dose has been calculated, while a NOAEL represents a predefined dose and the corresponding potential effect size is mostly not calculated. Therefore, a BMDL value gives more information than a NOAEL, by explicitly indicating the upper bound of effect at that dose as defined by the BMR.

An inherent consequence of the BMD approach is the evaluation of the uncertainty in the (true) BMD, which is reflected by the BMD confidence interval. This is a difference with the NOAEL approach where the uncertainty associated with the NOAEL cannot be evaluated from a single data set.

The data requirements of the NOAEL approach for the purpose of risk assessment have been incorporated into internationally agreed guidelines for study design, e.g. OECD guidelines for the testing of chemicals. However, the utility of the data depends not only on these global aspects regarding study design (e.g. number of dose groups, group sizes), but also on aspects of the quality of the specific study, such as actual doses selected and variability in the responses observed. While in the NOAEL approach, the utility of the data is based to a considerable extent on a priori considerations such as study design, a BMD analysis is less constrained by these factors, as discussed above. In addition, it goes further, by evaluating the data taking the specifics of the particular data set into account (e.g. the scatter in the data, dose–response information). In this way, a more informed decision on whether a data set is acceptable for deriving the RP is possible. It should be noted that the BMD confidence interval has already accounted for the limitations of the particular data set, so that data limitations (e.g. sample size) is a less crucial issue than it is for the NOAEL.

Although the current international guidelines for study design have been developed with the NOAEL approach in mind, they offer no obstacle to the application of the BMD approach. The current guidelines may, however, not be optimal given that the BMD approach allows for more freedom in balancing between number of dose groups and group sizes (Slob, 2014). As these guidelines are revised, e.g. within the OECD Test Guidelines Programme, the possibility to recommend study designs that tend to result in better dose–response information (e.g. more dose levels with the same total number of animals) should be taken into account.

2.3.4. NOAEL and BMD approach: some illustrations

This section provides some illustrations of the NOAEL and BMD approaches to dose–response assessment. In the first and second example, real dose–response data from toxicity studies are used to illustrate the NOAEL approach vs the BMD approach, in the case of continuous and quantal response data, respectively. The third example relates to human (observational) dose–response data.

Example 1: Continuous dose–response data

This example relates to body weights measured in a subchronic National Toxicology Program (NTP) study. The BMR in continuous responses should be interpreted as a measure of the degree or severity of the effect, as opposed to the BMR in quantal data which reflects a change in incidence (see Example 2).

To illustrate the differences between the NOAEL and BMD approaches, both will be applied to this particular data set. In the NOAEL approach, each dose group is compared with the response in the control group, and, as shown in the last column of Table 2, effects at doses of 215 and 419 mg/kg are statistically significantly different at p < 0.05, while the other doses are not. Based on the criterion of a statistically significant result, 76 mg/kg would be designated as the NOAEL. Nonetheless, the upper 95%‐confidence bound (one sided) of the effect that could occur at this dose level is a 4.7% decrease in body weight (Table 2).

Table 2.

Pairwise comparison of dose groups, data from Figure 2

Dose (mg/kg bw)	N	Geometric mean (g)	ES (%)	Lower 95% confidence bound (one sided) of ES (%)a	Upper 95% confidence bound (one sided) of ES (%)a	t‐statistic	p‐value
0	10	26.3
8	10	26.0	−1.3	−5.7	3.3	0.491	0.31
25	10	25.7	−2.6	−6.9	2.0	0.962	0.17
76	10	26.3	−0.24	−4.7	4.4	0.087	0.47
215	10	25.0	−5.1	−9.4	−0.71	1.93	0.029
419	10	20.8	−21	−25	−17	8.64	0.000

ES: effect size (in per cent change compared to response at dose zero).

^aTwo‐sided 90% confidence interval was calculated for the difference on log‐scale, and then transformed back, resulting in the confidence interval for per cent change (see Slob (2002) for further statistical assumptions).

To illustrate the BMD approach for the same data set, a dose–response model (y = a exp(bx ^d)) was fitted to the data, and a BMR representing a 5% decrease in body weight was used (see Figure 2). The output of this model results in a BMDL₀₅ (at BMR = 5%) of 170 mg/kg (see legend of Figure 2).

Figure 2.

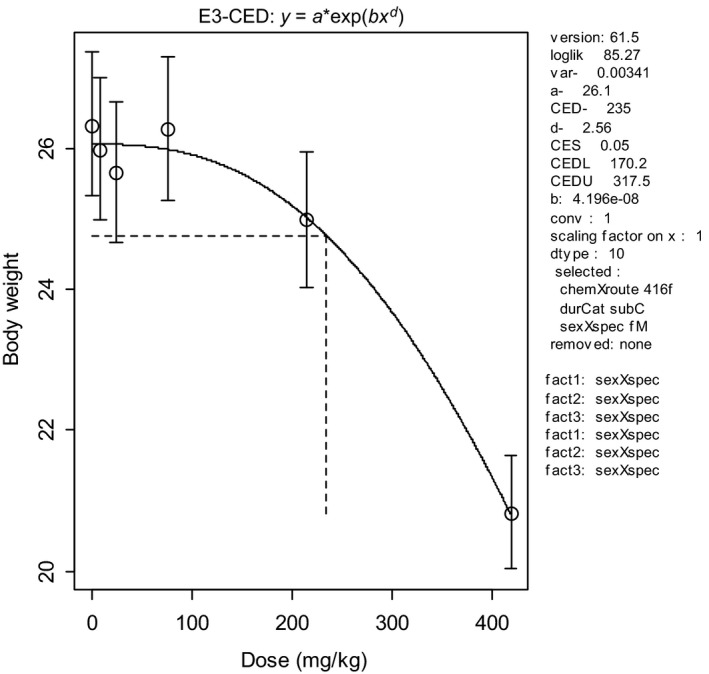
Body weights in 10 individual animals per dose plotted against dose in mg/kg body weight (bw) (data from NTP study 416). Circles represent (geometric) group means, with 90% confidence intervals. The solid curve is the fitted dose–response model using PROAST v. 61.5. The dashed lines indicate the BMD at a BMR of 5%. CED = BMD, CEDL = BMDL, CEDU = BMDU

In this data set, the BMDL₀₅ is higher than the NOAEL (170 vs 76 mg/kg). Nonetheless, it can be stated that the effect size at the BMDL₀₅ of 170 mg/kg is smaller than 5% (with 95% confidence). Note that the pairwise comparison (see Table 2) led to the conclusion that the effect size at 76 mg/kg is smaller than 4.7% (again with 95% confidence), similar to the BMR used for the BMDL of 170 mg/kg. For the BMD approach to result in a BMDL similar to the NOAEL of 76 mg/kg, the BMR needs to be set at 1.3% in this data set. In other words, while the NOAEL can only state that effects smaller than 4.7% are unlikely, the BMD approach can state that effects smaller than 1.3% are unlikely, at the same dose, and using the same data. This greater precision illustrates that the BMD approach makes better use of the information in the data by analysing the complete data set, rather than making comparisons between single dose groups and the control group.

Example 2: Quantal response data

For quantal data, the BMR is defined as a specified increase in incidence over background. A BMR of 10% (extra risk) is used in the following example, illustrated in Figure 3.

Figure 3.

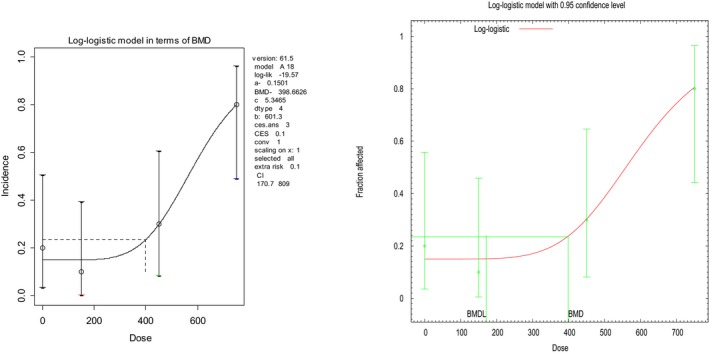
Analysis of quantal data as obtained by PROAST and BMDS software. Fraction of affected animals in a toxicity study with 10 animals in each dose group (endpoint investigated: gastric impaction). A dose–response model has been fitted to the data (solid curve) and the horizontal line indicates the BMR of 10% extra risk compared to the response at zero dose (according to the curve). Log‐logistic model was fitted by PROAST (v. 61.5) and BMDS (v. 2.6) (see Table 3); the figures presented reflect the way in which the software generates the graphs

Here, the mid‐dose and low‐dose incidences are not statistically significantly different from the background response. Hence, the middle dose of 450 mg/kg is the NOAEL for this endpoint in this study. In this case, a pairwise comparison with the background response results in a very large upper 95% confidence bound (one sided) for the effect size at the NOAEL: an extra risk6 value of around 47%.

Modelling the dose–response data (see Figure 3) using a log‐logistic model as an illustration results in a BMDL₁₀ of 171 mg/kg, 2.6‐fold lower than the NOAEL.

The BMD approach allows for the statement that the associated effect at the BMDL is not greater than 10% (with 95% confidence), which is considerably lower than the upper bound of effect of around 47% at the NOAEL, as calculated based on a pairwise comparison of the background response and the NOAEL dose group.

Example 3: Human dose–response data

The analysis of human dose–response data can be more complicated than that of typical dose–response data from animal studies, due to confounders for which accounting is needed, and imprecision in the exposure estimates. The example provided here does not deal with these complexities and aims only to illustrate one particular aspect of human data that may occur, that of very small exposure groups. In specific cases, the exposure levels are estimated for each individual person. The NOAEL approach could then only be applied if the doses are lumped into a limited number of dose categories. However, such would result in a loss of information. In contrast, the BMD approach can be applied without categorisation, as illustrated in Figure 4. In this example, every person was scored as showing either normal (= 0) or abnormal (= 1) eye–hand coordination. It is hard to detect any dose–response relationship by visual inspection for these types of observations. It is, however, feasible to fit a dose–response model to these data, and demonstrate the existence of a dose‐related response. In this example, the curve associated with the fitted model represents the probability of any person responding at a given exposure level. The fitted model resulted in a statistically significant improvement of the fit compared with a fitted horizontal line, indicating that there is a statistically significant effect of the exposure. The BMD approach uses this curve to estimate the exposure level where the extra risk is 10% (see Section 2.5.7), together with the BMD confidence interval.

Figure 4.

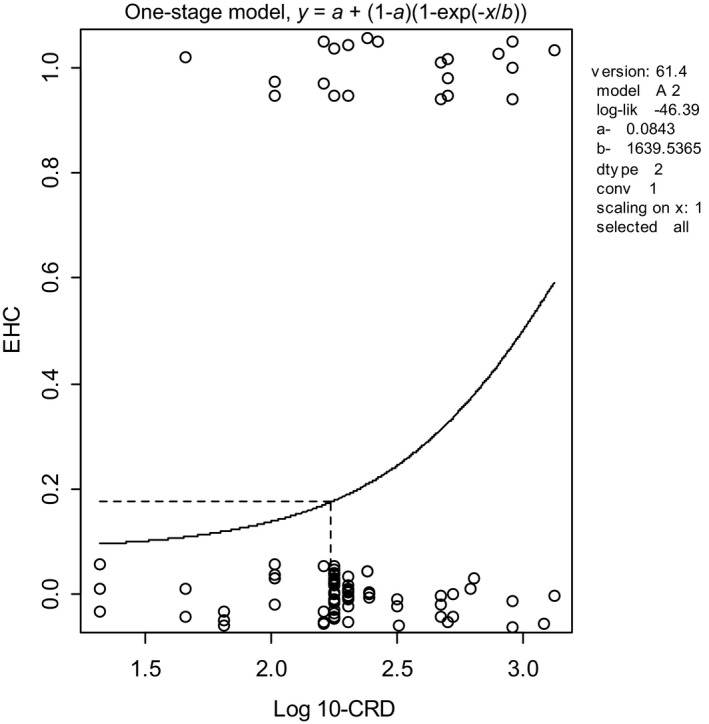
BMD analysis of human dose–response data with individual exposures. Observed eye–hand coordination scores (0.0 = normal, 1.0 = abnormal) in individual workers (plotted as circles with some artificial vertical scatter to make the ties visible for individuals having the same exposure) as a function of exposure (CRD). A dose–response model has been fitted to these data using PROAST v. 61.4; the BMD ₁₀ (see dashed lines) was 173, and the BMDL ₁₀ was 92. A BMR of 10% extra risk was used

The example further illustrates that the BMD approach may apply in situations without any controls: the background response level can in principle be estimated by the fitted dose–response curve, while the confidence interval for the estimated background indicates how well it could be estimated, given the data available.

2.4. Consequences for hazard/risk characterisation

In the previous section, the BMD approach has been introduced in the context of deriving a RP. This RP will be used in hazard characterisation for establishing HBGVs, such as ADIs for food additives and pesticide residues, and TDIs or TWIs for contaminants. It will also be used in risk characterisation of substances that are both genotoxic and carcinogenic, i.e. in establishing MOEs.

2.4.1. Establishing health‐based guidance values

In establishing a HBGV, such as an ADI or TDI, from a RP, uncertainty factors are applied to the NOAEL (WHO 1987). It has been suggested that larger or additional uncertainty factors might be appropriate when a BMDL is used as the RP. The argument used is that the BMDL does not reflect a ‘no‐effect’ dose, in contrast to the NOAEL. This argument is based on the false assumption that a NOAEL is associated with the complete absence of any adverse effect. As discussed (in Section 2.5.2), the default values of the BMR are such that the BMDL on average coincides with the NOAEL. Further, it was shown in Section 2.3.3 that the potential magnitude of the effect at the NOAEL can be even greater than the specified effect size (BMR) associated with the BMDL. Taking these considerations into account, an additional uncertainty factor, beyond those normally applied is not necessary (it might actually be argued that an additional uncertainty factor would be needed when using the NOAEL rather than the BMDL, see IPCS, 2014). The HBGV derived from the BMDL can be expected to be as protective as the one derived from the NOAEL, i.e., on average over a large number of risk assessments. In conclusion, the default values for uncertainty factors (or chemical‐specific adjustment factors) currently applied to the NOAEL are equally applicable to the BMDL.

In some studies, there may be an effect at the lowest dose tested which is statistically significantly different from the response in the control group and biologically relevant (LOAEL). In the NOAEL approach, the LOAEL is traditionally divided by an additional uncertainty factor. However, in the BMD approach, it is usually possible to derive a BMDL from such data at the desired BMR and there would be no need for such an additional uncertainty factor. If the desired BMR would imply substantial extrapolation outside the observed dose‐range from the fitted model (see Section 2.5.2), then a higher BMR can be selected but an additional uncertainty factor to the BMDL may be necessary.

2.4.2. Risk assessment of substances which are both genotoxic and carcinogenic

The SC (EFSA, 2005) concluded that, from the options considered, the MOE approach would be the most appropriate one in the risk assessment of substances that are both genotoxic and carcinogenic. They proposed to use the BDML₁₀ as the RP, i.e. the BMDL₁₀ should constitute the numerator of the MOE.

2.4.3. Potency comparisons

Comparisons of the potencies of different substances, or of the same substance under different exposure conditions, require information on the doses necessary to produce the same size of effect/response. The BMD approach is a suitable tool for such analyses, as it enables the estimation of equipotent doses by interpolation between applied doses. For the same reason, the BMD approach is also suitable for the derivation of relative potency factors (RPFs) or toxic equivalency factors (TEF) for individual substances in a mixture that share a common mode of toxicological action. The BMD approach has been used to provide relative potency estimates for different organophosphates (Bosgra et al., 2009). More recently, the BMD approach has been used for estimating equipotent doses in in vivo and in vitro genotoxicity tests which so far has only been used for (qualitative) hazard identification (e.g. Bemis et al., 2015; Soeteman‐Hernández et al., 2015a,b; Wills et al., 2015). Further, the BMD approach can be used for testing if dose addition applies in chemical mixtures (Kienhuis et al., 2015).

2.4.4. Probabilistic risk assessment

Probabilistic approaches in risk assessment are receiving increasing attention, regarding both exposure assessment (e.g. Gibney and van der Voet, 2003; Tressou et al., 2004; Fryer et al., 2006) and hazard characterisation (e.g. Baird et al., 1996; Swartout et al., 1998; Van der Voet and Slob, 2007; IPCS, 2014; Chiu and Slob, 2015). The BMD approach is compatible with probabilistic hazard characterisation, as the uncertainty in the BMD can be quantified in the form of a distribution (Slob and Pieters, 1998). Further, the dose–response modelling behind the BMD approach provides a means of estimating the magnitude of a potential health effect in the human population, given a particular exposure level (e.g. the current exposure in the population). This has been done, for example, for the mycotoxin deoxynivalenol (Pieters et al., 2004), and for a number of genotoxic carcinogens (Slob et al., 2014).

2.4.5. BMDL vs NOAEL: Perception of safety

It has been argued that the introduction of the BMD approach may raise problems in communication with risk managers, politicians, consumer organisations and the public because the BMDL is perceived as an effect level. On the other hand, the NOAEL is sometimes perceived incorrectly as a level that is without any effects. However, as explained in Section 2.4.1, use of the BMDL in risk assessment does not fundamentally change the basic approach or assumptions.

An argument in favour of the BMD approach is that this approach provides a higher level of confidence in the conclusions in any individual case since the BMDL takes into account the statistical limitations of the data better than the NOAEL. This does not imply that re‐evaluation of all previous data is needed, because as stated in Section 2.4.1, the NOAEL and BMDL are expected to be similar on average. A re‐evaluation would certainly not be necessary in circumstances where large margins exist between the estimated daily intake and the HBGV, e.g. ADI. For substances where the actual estimated daily intake appears to be close to or exceeding the HBGV, a refined risk assessment might result from a re‐evaluation of the data, using the BMD approach.

It also has to be recognised that there are a number of sources of uncertainty in a risk assessment, and dose–response modelling is only one of these. In assessing the likely benefits of applying the BMD approach in a given risk assessment, some consideration should be given to the sources of uncertainty, their magnitude and the likely impact in the assessment. The latter can be done in a probabilistic way, as recommended by the IPCS (2014). Such information will help to determine whether the likely refinement provided by the BMD approach will result in a substantial change in the risk assessment.

In addition, when a HBGV is based on the BMD approach, it takes into account all the data from the dose–response curve. The BMD method provides a better basis to quantify the risk in situations where the HBGV is exceeded, and, thus, is a better basis for risk communication.

Finally, it is important to realise that HBGVs like ADIs or TDIs provide levels to which humans may be exposed daily over their lifetime without appreciable health risk, and this definition does not change when the HBGV is derived from a BMDL instead of a NOAEL.

2.5. Guidance to apply the BMD approach

This section provides an overview of how to derive a BMD confidence interval from dose–response data and recommendations are given on particular choices to be made. The guidance refers not only to in vivo data but could be applied also to other types of data (e.g. in vitro data). Although currently available software allows for the application of the BMD approach without detailed knowledge of computational technicalities, a conceptual understanding of the method, as described in this opinion, is a prerequisite for correct interpretation of the results.

The application of the BMD approach may be summarised as a process involving the following steps:

1. Specification of type of dose–response data (Section 2.5.1)

2. Specification of the BMR (Section 2.5.2)

3. Selection of candidate dose–response model(s) (Sections 2.5.3 and 2.5.4)

4. Fitting the candidate models and calculate the BMD confidence interval for each model (Section 2.5.5)

5. Combining the results from the various models into one single BMD confidence interval, with the lower bound (BMDL) as the RP (Section 2.5.7).

These steps are further discussed below.

2.5.1. Specification of type of dose–response data

Response data may be of various types, including continuous, quantal and ordinal. The distinction between data types is important for statistical reasons (such as assumption of underlying statistical distribution), but also for the interpretation of the BMR. See Section 2.3.4 (examples 1 and 2) for the interpretation of the BMR in continuous and in quantal data. Ordinal data may be regarded as an intermediate data type: they arise when a severity category (minimal, mild, moderate, etc.) is assigned to each individual (as in histopathological observations). Ordinal data could be reduced to quantal data, but this implies loss of information, and is not recommended. Models for analysing ordinal data are available in different software package, e.g. in PROAST or CatReg in BMDS (US EPA, 2016).

For continuous data, the individual observations should ideally serve as the input for a BMD analysis. When no individual but only summary data are available, the BMD analysis may be based on the combination of the mean, the standard deviation (or standard error of the mean), and the sample size for each treatment group. Using summary data may lead to slightly different results compared with using individual data (Slob, 2002; Shao et al., 2013). For quantal data, the number of affected individuals and the sample size are needed for each dose group.

2.5.2. Specification of BMR

The BMR is a specific value of the effect size selected for estimating the associated dose (the ‘true’ BMD). Before thinking about what value may be specified for the BMR, it is necessary to make clear in what terms the BMR is defined, i.e. what metric is used for reflecting the magnitude of the effect. Both for continuous and for quantal data there are various options, and the most important ones will be discussed below.

Quantal data

For quantal data, the BMR is defined in terms of an increase in the incidence of the lesion/response scored, compared with the background incidence. In toxicology, the two common metrics for reflecting such an increase are the additional risk (incidence at a given dose minus incidence in the controls), and the extra risk, i.e. the additional risk divided by the non‐affected fraction of the population (see Section 2.3.3, footnote5). Epidemiologists more often use relative risk, where a given incidence (prevalence) is divided by the control incidence.

For quantal response data observed in experimental animals, BMR values of 1%, 5% or 10% (extra or additional risk) were initially proposed (Crump, 1984; EPA, 1995). Various studies estimated that the median of the upper bounds of extra risk at the NOAEL was close to 10%, suggesting that the BMDL₁₀ may be an appropriate default (Allen et al., 1994; Fowles et al., 1999; Sand et al., 2011). Also, a BMR of 10% appears preferable for quantal data because the BMDL can become substantially dependent on the choice of dose–response model at lower BMRs (Sand et al., 2002).

Continuous data

For continuous data, the metric for the BMR could be defined in various ways. One option is to define the BMR as a change in the mean response relative to the variation in the control group, as measured by the standard deviation (SD). The US EPA Benchmark Dose Technical Guidance (US EPA, 2012) recommends to always report the estimate of the BMD associated with BMR in terms of a difference in means equal to 1 SD. However, one of the weaknesses of this definition of BMR is that the associated (true) BMD then depends on the particular study, due to study‐specific factors (measurement error; dosing error; heterogeneity in experimental conditions). Another problem of using the 1 SD metric is that the estimate of the associated BMD cannot be translated into an equipotent dose in populations with larger within‐group variation, including humans. Another option is to define the BMR as a per cent change in mean response; the BMD associated with such a BMR does not depend on the within‐group variation and therefore is more stable among different studies examining the same dose response, as well as among different populations. Therefore, the SC recommends defining the BMR as a per cent change in the mean response as compared to the background response.

A re‐analysis of a large number of NTP studies (Bokkers and Slob, 2007) showed that the BMDL₀₅ was, on average, close to the NOAEL derived from the same data set (see Figure 5), while in most individual data sets they differed within one order of magnitude. Similar observations have also been made in studies of fetal weight data (Kavlock et al., 1995). While the BMR of 5% for continuous data is recommended as a default, it might be modified based on toxicological or statistical considerations. For example, a 20% change in a liver enzyme in serum might still be considered sufficiently small for deriving an RP, based on biological considerations. As a statistical consideration, one might consider to select a BMR higher than 5% for endpoints that tend to show a relatively large within‐group variation (in terms of coefficient of variation), and/or a relatively high maximum response (if known, based on experience with that endpoint over a larger number of studies (Slob and Setzer, 2014)). Increasing the BMR (in terms of a percent change) for data showing a relatively large maximum response is somewhat similar to using a BMR defined as a change equal to 1 SD (Slob, 2016); an important difference is that the BMR expressed in terms of a per cent change allows for comparison among studies and populations that differ in within‐group variation.

Figure 5.

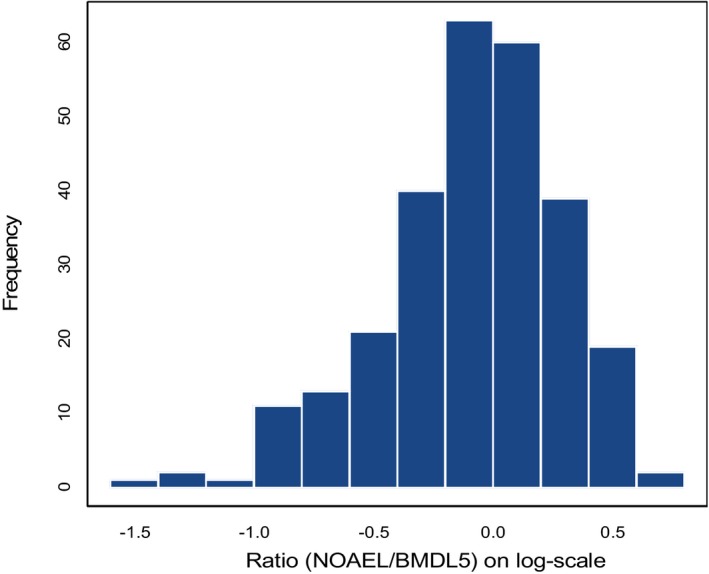
Histogram of 395 NOAEL/BMDL ₀₅ ratios (log₁₀ scale) for the same dose–response data in rat and mouse (NTP) studies (Bokkers and Slob, 2007). The BMDL ₀₅ relates to a BMR of 5%. Six endpoints were considered: bw, relative and absolute liver and kidney weight, red blood cell counts. The geometric mean of the ratios is close to 1, i.e. on average the NOAEL is similar to the BMDL ₀₅

In conclusion, for experimental animal studies, the SC proposes that a default BMR value of 5% (change in mean response) be used for continuous data and 10% (extra risk) for quantal data. As stated previously, the default BMR may be modified based on statistical or biological considerations. For example, if the BMR is considerably smaller than the observed response(s) at the lowest dose(s), leading to the need to extrapolate substantially outside the observation range, a larger BMR may be chosen. The biological relevance of changing the BMR value should be discussed and whether this should give reason to change for example the assessment factor when establishing an HBGV. The rationale for deviating from the default BMR should be described and documented.

2.5.3. Recommended dose–response models

In the current opinion, the term dose–response model is used for a mathematical expression (function) that describes the relationship between (mean) response and dose. This section will deal with dose–response models in that sense. The distributional part of dose–response models will be discussed in Section 2.5.4.

Ideally, the relationship between dose and response would be described by a biologically based model that describes (models) the essential toxicokinetic and –dynamic processes related to the specific compound. For most compounds, such models are not available, and therefore, the BMD approach uses fairly simple models that do not describe the underlying biology in any detail, and should be treated as purely statistical models. As the purpose of a BMD analysis is not to find the best estimate of the (true) BMD but rather to find all plausible values of the (true) BMD, given the data available, not only the best‐fitting model but also the models resulting in a slightly poorer fit need to be taken into account. After all, it could well be that the second (or third, …) best‐fitting model is closer to the true dose–response than the best‐fitting model. This type of uncertainty is called ‘model uncertainty’, and implies that the BMD confidence interval needs to be based on the results from various models, instead of just a single (‘best’) model.

Table 3 summarises the recommended models for analysing toxicological data sets. These models are considered suitable for analysing toxicological data sets in general. If other software is used, it is recommended to apply the same set of candidate models. As can be seen from this table, the models for continuous or quantal data differs; they will be discussed below. There are, however, two special models that relate to both types of data: the so‐called full (or saturated) model and the null model. The full model describes the dose–response relationship simply by the observed (mean) responses at the tested doses, without assuming any specific dose–response. It does, however, include the (same) distributional part of the model (see next section) and thus it may be used for evaluating the goodness of fit of any dose–response model (see Section 2.5.5). The null model expresses the situation that there is no dose‐related trend, i.e. it is a horizontal line, and may be used for statistically evaluating the presence of a dose‐related trend (see Section 2.5.7). It should be noted that in this document the phrase ‘dose–response models’ does not exclude the full and null models.

Table 3.

Expressions of the recommended models for use in the BMD approach, with (mean) response (y) being a function of dose (x), both on the original scale. See Table A.2 in Appendix A for the equivalent model expressions used in BMDS software

Model	Number of model parameters	Model expression mean response (y) as function of dose (x)	Constraints
Full modela	Number of dose groups including background	Set of observed means or incidences at each dose
Null modelb	1	y = a	a > 0 for continuous data 0 < a < 1 for quantal data
Continuous data
Exponential family
3‐parameter modelc	3	y = a exp(bx d)	a > 0, d > 1
4‐parameter modeld	4	y = a [c−(c−1)exp(−bx d)]	a > 0, b > 0, c > 0, d > 1
Hill family
3‐parameter modelc	3	y = a [1−x d/(b d + x d)]	a > 0, d > 1
4‐parameter modeld	4	y = a [1 + (c−1)x d/(b d + x d)]	a > 0, b > 0, c > 0, d > 1
Quantal data
Logistic	2	y = 1/(1 + exp(−a−bx))	b > 0
Probit	2	y = CumNorm(a + bx)	b > 0
Log‐logistic	3	y = a + (1−a)/(1 + exp(−log(x/b)/c))	0 ≤ a ≤ 1, b > 0, c > 0
Log‐probit	3	y = a + (1−a) CumNorm(log(x/b)/c)	0 ≤ a ≤ 1, b > 0, c > 0
Weibull	3	y = a + (1−a) exp((x/b)c)	0 ≤ a ≤ 1, b > 0, c > 0
Gamma	3	y = a + (1−a) CumGam(bx c)	0 ≤ a ≤ 1, b >0, c > 0
LMS (two‐stage) model	3	y = a + (1−a)(1−exp(−bx−cx 2))	a > 0, b> 0, c > 0
Latent variable models (LVMs) based on the continuous models abovee	Depends on underlying continuous model	These models assume an underlying continuous response, which is dichotomised into yes/no response based on a (latent) cut‐off value that is estimated from the data	See continuous models

a, b, c, d: unknown parameters that are estimated by fitting the model to the data.

CumNorm: cumulative (standard) normal distribution function.

CumGam: cumulative Gamma distribution function.

^aThe full model will result in the maximum possible value of the log‐likelihood (given the statistical assumptions) for the data set considered.

^bThe null model can be regarded as a model that is nested within any dose–response model: it reflects the situation of no dose response (= horizontal line).

^cCalled model 3 in PROAST, and similarly (for the exponential model) in BMDS.

^dCalled model 5 in PROAST, and similarly (for the exponential model) in BMDS.

^eThe latent variable models are implemented in PROAST.

Models for continuous data

For continuous data, both the exponential family and the Hill family of models are recommended. These models have the following properties:

• they always predict positive values, e.g. organ weight cannot be ≤ 0,

• they are monotonic (i.e. either increasing or decreasing),

• they are suitable for data that level off to a maximum response,

• they have been shown to describe dose–response data sets for a wide variety of endpoints adequately, as established in a review of historical data (Slob and Setzer, 2014),

• they allow for incorporating covariates in a toxicologically meaningful way (see Section 2.5.5),

• they contain up to four parameters, which have the same interpretation in both model families, in particular: a is the response at dose 0, b is a parameter reflecting the potency of the chemical (or the sensitivity of the population), c is the maximum fold change in response compared to background response and d is a parameter reflecting the steepness of the curve (on log‐dose scale). The four parameters are summarised in Figure 6.

Figure 6.

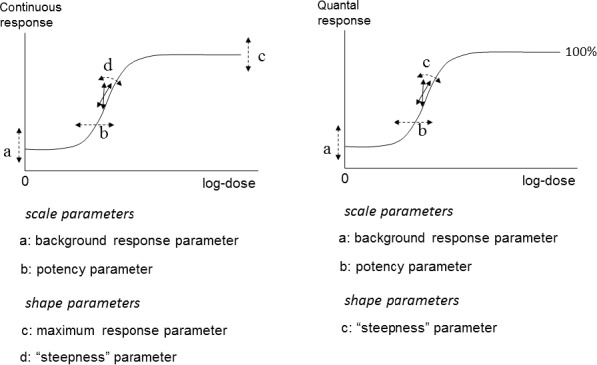
The four model parameters a, b, c and d and their interpretation for continuous and quantal data. The dashed arrows indicate how the curve would change when changing the respective parameter

The SC recommends more parametric dose–response models with the above characteristics to be developed for continuous data.

For both the exponential and the Hill family of models, Table 3 presents for each family two different models, respectively: one with three parameters and one with four parameters. The previous guidance (EFSA, 2009a) included for each family two other members, but these are no longer recommended, as BMD confidence intervals tend to have low coverage7 when parameter d is in reality unequal to one.

In the model expressions for continuous data, parameter a (reflecting the background response) is included multiplicatively, in line with defining the BMR as a per cent change (rather than a difference) compared to background response (Slob, 2016). Further, it matches the common way of normalising responses in different subgroups to 100% response. Occasionally, dose–response data may be expressed such that they include negative values, for instance, body weight gains decreasing from positive to negative values at high doses. In those cases, the recommended models that are strictly positive are no longer valid and models with an additive background parameter would be needed. Preferably, however, the body weight gains should be expressed as ratios (per cent changes) rather than differences, if the individual body weight data are available.

The US EPA BMDS includes some additional models for continuous data, in particular, the power model and the polynomial (including the linear) model. These models are additive with respect to the background response, which could result in fitted curves predicting negative values. Therefore, the SC does not recommend using these models.

Quantal data

Table 3 lists the models that are recommended to be used for quantal data. The two‐stage model is a member of the nested family of linearised multistage models (LMS). The two‐stage model is recommended to be used from this family as it has next to the scale parameters (a and b) one single shape parameter (c), just like most other quantal models. Furthermore, general experience has shown that the three‐stage model (recommended in the previous version of this guidance document) rarely provides a better fit to the data; consequently, this model has now been removed from the table of recommended models.

While the logit and probit model are listed as recommended models in Table 3, they have only two parameters. A minimum of three parameter appears, however, to be minimally needed (see right panel of Figure 6: one for background, one for potency, and one for steepness). Indeed, it is general experience that these two models provide poor fits to real data sets that include more than the usual number of doses (three plus controls).

The last row in Table 3 mentions the latent variable models. These models are implemented in PROAST, and have been found to adequately describe quantal data in general. For more details see the PROAST manual (http://www.proast.nl). They may be included in the BMD analysis, in particular when model averaging is applied.

Parameter constraints in modelling continuous or quantal data

To avoid the models having undesirable properties, certain constraints are imposed on the model parameters. For instance, since continuous responses are usually positive, the background response parameter (a) is constrained to be positive in the continuous models. In quantal models, it is constrained to be between 0 and 1 (i.e., 0% and 100% response).

Next to the parameter constraints shown in Table 3, an additional parameter constraint has often been applied in practice (US EPA, 2012). This constraint relates to the shape parameter that can be viewed as reflecting the steepness of the curve, i.e. parameter c in the quantal dose–response models (c > 1), and parameter d in the continuous (exponential and Hill) models (d > 1). The rationale behind this constraint was to avoid that the dose–response would have infinite slope at dose zero. In most models, this may be achieved by constraining the steepness parameter to be larger than one (rather than larger than zero). At first sight, this appears to be a reasonable restriction from a biological point of view. However, as shown in Slob and Setzer (2014), this constraint is based on a false argument and contradicted by real dose–response data. One way to see this is by imagining a study with eight doses between 50 and 0.000005 mg/kg, dose spacing being a factor of 10. The study results in the (quantal) responses are illustrated in Figure 7. In the upper panel, the responses are plotted against dose. Fitting a model would result in the steepness parameter c being smaller than one, i.e. the dose–response curve has infinite slope at dose zero. In the lower panel, however, the same data are plotted against log‐dose, which shows that there is in fact a large range of doses with virtually no change in response.

Figure 7.

A dose–response data set where the response is plotted against the dose (upper panel) and against the log‐dose (lower panel). The slope appears infinite when the response is plotted against the dose, while it appears to be ‘threshold‐like’ when plotted against the log‐dose. The lower doses are squeezed to dose zero when plotted against dose, and hence not visible. When plotted against log‐dose they become visible, showing that in reality there is a large range of doses with virtually no effect

The constraint that the steepness parameter should be larger than one is inappropriate and should not be applied, as it may lead to artificially high BMDLs. A practical consequence of omitting this constraint is that the BMDL in some cases can be much lower as compared to analysis where the constraint is applied. Section 2.5.7 discusses how to deal with BMDLs that are orders of magnitude lower than the associated BMDUs.

2.5.4. The distributional part of dose–response models

The dose–response models introduced and discussed in the previous section describe the mean response as a function of dose, assuming that there was no random sampling error. As this is unrealistic, the dose–response model also needs to describe the within‐(dose‐)group variation. This may be called the ‘distributional part’ of the dose–response model.

In continuous data, the within‐group variation can be directly observed as the scatter of the individual data around the fitted curve at the respective dose. This scatter can be characterised by a statistical distribution. Basic choices include two‐parameter distributions such as the log‐normal, gamma, Weibull, inverse‐Gaussian distribution, etc. Although different choices can be considered for different data sets, the log‐normal distribution has shown to be an appropriate choice across a variety of data sets, and therefore is proposed as the default choice. When individual data are available, the SC recommends to check the log‐normality assumption (e.g. using a normal probability plot – also called QQ‐plot) and to consider alternative distributions, if considered necessary. However, one should always realise that a deviation from log‐normality could also be the result of another misspecification of the distributional part of the model (e.g. litter effects were not taken into account), or by specific problems in the data (e.g. outliers).

The log‐normal distribution has two parameters: the mean and standard deviation of the response on the log‐scale at a given dose. Taking the exponential function (depending on the base of the log used) of the mean and the standard deviation results in the geometric mean (= median) and geometric standard deviation on the original response scale, respectively (Slob, 1994). With the default log‐normality assumption, the models in Section 2.5.3 describe the geometric mean as a function of dose. In the default application of these models; it is assumed that the standard deviation for the log‐responses (or, equivalently, the geometric standard deviation) does not depend on dose. When there is evidence that the geometric standard deviation does change with dose, an extended model, which considers dependence of the standard deviation on dose can be used. Ignoring that dependency (while in reality it exists), the fitted dose–response model for the mean and the BMD estimate are in general expected to be still appropriate. However, the standard errors of the parameter estimates are expected to be larger, resulting in lower and hence more conservative BMDLs. For this reason, and because it is not easy to decide whether the within‐group variation does indeed depend on dose (given the impact of sampling error on the observed standard deviations) the assumption of constant variability among dose groups is recommended as the default practice.

In quantal data, the within‐group variation is normally not directly visible, given that most quantal data sets only have one observed incidence per dose. Yet, this observed incidence is subject to random sampling error just as well. When the experimental units do not show any dependencies (like litter effects) the sampling error in observed incidences will be binomially distributed. Therefore, the binomial distribution is the default assumption for quantal data.

When there are litter effects, they need to be taken into account. Ignoring them will result in a to small BMD confidence interval. One way to take litter effects into account is by assuming an additional (e.g. beta) distribution that describes the variation among the dams. In PROAST, all usual quantal models can be fitted while taking the litter effects into account based on that principle. In BMDS, three quantal models are available that can account for litter effects.

2.5.5. Fitting models

The currently available BMD software from the US EPA and RIVM takes care of fitting a model, which means finding the values of the unknown parameters in the model that make the associated dose–response curve approach the data as closely as possible. This is called the best fit of that model and is achieved by maximising the log‐likelihood that can be reached by that model.

Convergence

The available BMD software fit the recommended models by applying numerical algorithms, which are optimisation procedures: the fit of the model is re‐evaluated over and over again for different values of the parameters, until the log‐likelihood can no longer be improved. If the algorithm is able to find the maximum likelihood, while this holds for just one set of parameter values, the software will report that the algorithm has ‘converged’. It may happen, however, that the algorithm reports that no convergence was reached. There could be various reasons for that, but usually this indicates that the data did not provide sufficient information to appropriately estimate all the parameters in the model. For instance, there may be different sets of parameter values that would result in similar log‐likelihood values. Clearly, this would hamper the establishment of the statistically best estimate of the BMD, but for risk assessment purposes the BMD confidence interval is of interest. Simulations showed that convergence may not be critical in providing a reliable BMD confidence interval, and therefore a message of non‐convergence does not necessarily imply that the model should be rejected. However, non‐convergence does typically indicate that the data are not informative enough to estimate all parameters for the model at hand, and this should be considered as an alert.

The AIC criterion

For the purpose of comparing the fit of different models, the AIC is a convenient criterion as it directly integrates the log‐likelihood and the number of model parameters in one single value. The AIC is calculated as −2 log(L) + 2p with log(L) the log‐likelihood of the model, and p the number of parameters. The first term, −2 log(L) will decrease when the model gets closer to the data. To penalise for the number of parameters, AIC includes the term 2p, which increases the value of AIC when the number of parameters increases. Thus, the model with a relatively low AIC may be considered as providing a good fit without using too many parameters.

According to Burnham and Anderson (2004), different models that result in AICs not differing by more than two units may be regarded as describing the data equally well. Further, the full model tends to show the smallest AIC and the null model the largest, although deviations may occur when there is a large number of dose groups.

The AIC criterion can be used to check if there is statistical evidence of a dose‐related trend. For a fitted model to show statistical evidence of a dose‐related trend, the SC proposes that its AIC should be lower than the AIC_null−2.

The AIC criterion can also be used to compare the fit of any model with that of the full model. Theoretically, the AIC of a fitted model should be no more than two units larger than the full model's AIC. If the model with the minimal AIC is more than two units larger than that of the full model (AIC_min > AIC_full + 2), this could be due to the use of an inappropriate dose–response model (e.g. it contains an insufficient number of parameters), or to misspecification of the distributional part of the model (e.g. litter effects are ignored), or to non‐random errors in the data (see Section 2.5.7).

Covariates

Besides fitting dose–response models to single data sets, it is possible to fit a given model to a combination of data sets which differ in a specific aspect, such as sex, species or exposure duration, but are similar otherwise. In particular, the response parameter (endpoint) needs to be the same. By fitting the dose–response model to the combined data set, with the specific factor included in the analysis as a so‐called covariate, it can be examined in what sense the dose–responses in the subgroups differ from each other, based on statistical principles (like AIC).

In general, there are three possible outcomes of such an analysis. First, it may be found that the subgroups show similar dose–responses, and that a single curve may be used to describe all subgroups combined. Second, the subgroups may be found to differ in dose–response but only partially so. For instance, they may show different background responses (at dose zero) but be equally sensitive to the chemical. Or, they may differ in sensitivity but their dose–responses may otherwise have the same shape. In the latter case, the analysis will result in subgroup‐specific BMD confidence intervals. The third possible outcome is where the subgroups appear to differ in all parameters in the model. In this case, the result of the combined dose–response analysis will be identical to analysing the subgroups separately. With the appropriate software (e.g. PROAST), a combined analysis can be performed, and will indicate how the combined data set could be best described.

Combining data sets in a dose–response analysis with covariate(s) may have two reasons. The first is that it provides a powerful method for examining and quantifying potential differences in dose–response between the subgroups. For instance, the problem formulation might indicate that the assessment should specifically focus on sex differences, in which case it would be important to know if the data provide evidence that both sexes actually differ in sensitivity to the test material, and if so, to have a precise estimate of the difference in (true) BMDs between male and female animals. As another example, by combining different chemicals affecting the same endpoint an effective estimate of the relative potencies will be obtained (Bosgra et al., 2009). Or, one might be able to link the more precise information on the potencies of various chemicals to mechanism of action hypotheses (Wills et al., 2015).

The second reason for combining data sets and applying the covariate approach is to improve the precision of the estimated BMD(s), i.e. to obtain a smaller BMD confidence interval. This is particularly relevant when the individual data sets provide relatively poor dose–response information (for an illustration see Figure 11 in Slob and Setzer, 2014). As long as at least one of the parameters in the model does not appear to differ among the subgroups, it is useful to include the factor that discriminates the subgroups as a covariate in the analysis: the common parameter can then be estimated from all data combined, and hence will be known more precisely, resulting in a more precise estimate of the (true) BMD(s).

2.5.6. Model averaging

As discussed in Section 2.5.3, the BMD approach does not aim to find the single statistically best estimate of the BMD but rather all plausible values that are compatible with the data. Therefore, the goal is not to find the single best fitting model, but rather to take into account the results from all models applied. The recommended way to do that is by the so‐called Model Averaging approach.

It has been shown that multimodel estimation and inference using model averaging is the best way to account for model uncertainty and at the same time for the uncertainty related to the sampling errors in the data (Burnham and Anderson, 2004; Wheeler and Bailer, 2007, 2008, 2009). In model averaging, the individual model results are combined using weights, with higher weights for models that fit the data better. These weights are often defined in terms of the AIC.

Briefly, model averaging consists of two main steps. First, the average response is calculated for a large number of doses, by taking the weighted average from the fitted dose–response models involved. The BMD can now be calculated for the average model. Second, a large number of artificial data sets are generated based on the average model, and for each data set the first step is repeated. This results in a large number of BMDs: the lower and higher 5th percentiles define the BMD 90% confidence interval.

In this document, the MADr‐BMD program as described in Wheeler and Bailer (2008) has been used to perform example model averaging analyses (see Section 2.5.9, Example 2).

2.5.7. Establishing the BMD confidence interval

BMD confidence interval for a given data set

The flow chart of Figure 8 shows how to proceed once the models are fitted to the data.

Figure 8.

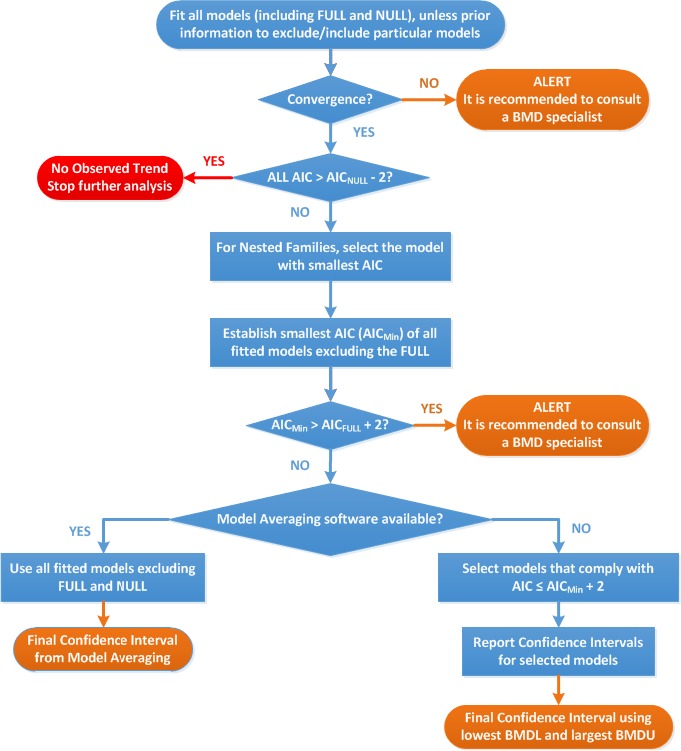
Flow chart to establish the BMD confidence interval and BMDL for dose–response data set of a specified endpoint. AIC: Akaike information criterion (indicative of the goodness of fit of the model considered); AIC_null: AIC value of the Null Model; AIC_full: AIC value of the Full Model; AIC_min: AIC value of the model with the lowest AIC value, the null and full models being excluded

When the software reported ‘no convergence’ for one or more models, this may be taken as an alert: apparently, the data are not very informative, or the model may be over‐parameterised. In cases of non‐convergence, it is recommended to consult a specialist on dose–response modelling on how to proceed with the BMD analysis. At the EFSA level, a standing working group will be established to assist the EFSA Experts and Staff on BMD‐related issues (see Section 4). Preliminary simulations have shown that non‐convergence may have little impact on the BMD confidence interval.

The next step consists in checking if at least one of the models revealed a dose‐related trend, i.e. one of the model's AIC is lower than the AIC of the null model + 2 units. If this is not fulfilled, there is no dose‐related trend and the BMD analysis can stop.

If nested models have been used (i.e. for continuous data), one single member is selected per model family: the one that resulted in the lowest AIC. Then, from all (non‐nested) models, the lowest AIC is determined. If this lowest AIC exceeds the AIC of the full model by more than two units, this may be considered as an alert. A first thing to consider in that case is whether the distributional part of the model needs to be adjusted (see Section 2.5.4). Then, it should be explored if there might be other problems in the data, e.g. systematic errors caused by some unintended experimental factor differing among dose groups. This would be more likely if the study was not performed according to an appropriate study protocol (e.g. randomising animals and order of treatments, avoiding cage effects as a confounding factor). Associated non‐random data errors may result in an AIC_min that is substantially larger than the AIC_full. An indication of non‐random errors may be found by checking whether the confidence intervals around the (mean) responses at each dose are hit by the fitted dose–response curve; if not, this may indicate that there is more error in the data than expected from random sampling error. If non‐random errors appear to be the most likely explanation of the alert, the BMD analysis can in principle continue according to the flow chart, in particular when the impact on the estimated shape of the dose–response is minor.

In principle, another reason for AIC_min > AIC_full + 2 could be that none of the models was appropriate for that data set although this has been rarely observed in relatively good data sets (Slob and Setzer, 2014).

Finally, the results from the fitted models need to be combined to establish the final BMD confidence interval. The ideal way to proceed is by model averaging (see Section 2.5.6), where each of the models that was fitted is taken into account, including the models that showed a less good fit. The latter does not harm as model averaging uses the AIC as a weight, so that poorly fitting models will hardly contribute to the final BMD confidence interval.

If the required model averaging software is not available, a distinction is made between models with a relatively good and those with a relatively poor fit. The set of relatively good models include the model with the minimum AIC and all models with an AIC no more than two units larger than that. The lowest BMDL and highest BMDU from these selected models will then be used to define the BMD confidence interval. It should be noted that no confidence level can be associated with this interval; in general it will be larger than the nominal value of 90% used for the BMD confidence intervals obtained with individual models. Hence, the BMDL will generally be smaller than the final BMDL derived from model averaging. Further, it should be noted that the choice of two units difference between AICs, as substantiated by Burnham and Anderson (2004), constitutes a somewhat arbitrary way of defining the cut‐off between relatively good and relatively poor models. In specific cases, one may decide to use a larger value than 2, for example, when it would lead to the selection of just one model. This problem is avoided in the approach of model averaging.

Before deciding to use a larger value than 2 for the AIC criterion or in situations where there is an alert, the SC recommends to consult a specialist in BMD analysis.

Judging the width of the BMD confidence interval for a given data set

Ideally, when the experimental data provide sufficient information on the dose–response relationship, the different models will result in similar confidence intervals, thereby providing an adequate basis to define a RP for the establishment of a health‐based guidance value or for the calculation of a MOE (see Section 2.4).

In some cases, however, the dose–response relationship may not be well defined by the data. For instance, there may be large gaps between consecutive response levels, or the lowest non‐zero dose already resulted in a response much larger than the BMR. Therefore, it may occur that the applied models result in widely different BMD confidence intervals, or that some, or all of them, are very wide (several orders of magnitude). When the width of the combined BMD confidence interval is found to cover orders of magnitude, the BMDL could be orders of magnitude lower than the true BMD, had better data been available. Therefore, the resulting RP, and the HBGV or MOE eventually derived from it, might have been much higher or larger, respectively. In such cases, one might explore the possibility to request for better data. However, in many cases this would not be possible. Alternatively, the data could be re‐analysed, taking into account prior information on typical values of the shape parameters, if available from historical data, e.g. by constraining the shape parameters or by applying prior distributions in a Bayesian approach. Whatever option is applied, this should be clearly documented. This option may be considered when the combined confidence interval is wide for various reasons related to limitations in the data, such as (i) a small total number of animals (or other experimental units) in the study, (ii) considerable scatter in the consecutive (mean) responses with increasing dose, (iii) few doses in the study design, or few doses with distinct responses, (iv) relatively small response in the top dose(s), and (v) relatively high response at the lowest dose (see previous bullet).

Determining the RP for a given substance

The flow chart results in a final BMD confidence interval for a given dose–response data set related to a specific endpoint. The BMD confidence interval should be derived for all data sets considered relevant (potentially leading to the RP), resulting in a set of confidence intervals indicating the uncertainty ranges around the true BMD for the endpoints considered. This set of BMD confidence intervals concisely reflects the information provided by the available data and provides the starting point for the risk assessor to derive the RP. One way to proceed is to simply select the endpoint with the lowest BMDL and use that value as the RP. However, this procedure may not be optimal in all cases, and the risk assessor might decide to use a more holistic approach, where all relevant aspects are taken into account, such as the BMD confidence intervals (rather than just the BMDLs), the biological meaning of the relevant endpoints, and the consequences for the HBGV or the MOE. This process will differ from case to case and it is the risk assessor's responsibility to make a substantiated decision on what BMDL will be used as the RP. One example is a situation where the BMD confidence interval with the lowest BMDL is orders of magnitude wide. This means that the true BMD might be much higher than the BMDL, which raises the question if that BMDL would be an appropriate RP. To answer that question, following aspects may be considered:

• If the HBGV established based on a particular BMDL would still be much higher than the exposure estimate, or the MOE much larger than 10,000, then the high uncertainty in the RP, as indicated by the wide confidence interval, has no consequence for the hazard characterisation. It should be, however, kept in mind that an exposure estimate is not a fixed value (it may well change in the future) and is therefore uncertain.8

• In some cases, the selected RP may not be the lowest BMDL, for example, when this lowest BMDL concerns an effect that is also reflected by other endpoints (e.g. the combination of liver necrosis and serum enzymes) that resulted in much smaller confidence intervals but with higher BMDLs. In that case, it might be argued that the true BMDs for those analogous endpoints would probably be similar, but one of them resulted in a much wider confidence interval (e.g. due to large measurement errors).

2.5.8. Epidemiological dose–response data

In principle, the BMD approach would also be applicable to human data. BMD analysis of human data will be the subject of a separate guidance document of the EFSA SC.

2.5.9. Reporting of the BMD analysis

The results of a BMD analysis should be reported in such a way that others are able to follow the process.

In reporting a BMD analysis for a particular study, it is not necessary to provide information on all the endpoints analysed but only for the critical one(s) in that study. It should be made clear in a narrative why this (these) endpoint(s) was (were) selected.

The following information should be provided:

1. A summary table of the data for the endpoint(s) for which the BMD analysis is reported. For quantal endpoints, both the number of responding animals and the total number of animals should be given for each dose level; for continuous endpoints the mean responses and the associated SDs (or SEMs) and sample sizes9 should be given for each dose level.

2. The value of the BMR chosen, and, if deviating from the default value, the rationale for that.

3. The software used, including version number.

4. Settings and statistical assumptions in the model fitting procedure when they deviate from the recommended defaults in this opinion, together with the rationale for doing so.

5. A table presenting the models used (preferably in the order of Table 3), including the null and full model and their AICs, with the BMD confidence intervals. BMDL and BMDU values should be reported with two significant figures – see Examples.

6. A plot of the fitted average model. If model averaging was not used, a plot of all the models fitted to the data for the critical endpoint(s). In case of nested families, a plot of the selected model for each family.

7. Conclusion regarding the selected BMDL to be used as a RP.

A template is annexed to ensure a standardised reporting of the above‐mentioned information (Appendix B).

The reporting of a BMD analysis is illustrated below for specific continuous and a quantal datasets.

While efforts have been made in this opinion to provide guidance on the use of BMD software, users should be aware that such software still evolves, just like the BMD approach itself. The version of the software available at the time of use may not be the same as that referred to here, but, the reporting structure should remain the same.

Example 1: Continuous data

The BMD analysis given below may serve as an example of how to report the results from a BMD analysis of a continuous data set in an EFSA opinion. This example was run using the PROAST software (see Appendix A for an overview of the differences between PROAST and BMDS).

The data in this example relate to a 2‐year study in male mice. A dose‐related decrease in body weight was observed. This endpoint is assumed to be the critical effect.

A. The data

Dose (mg/kg bw per day)	Body weight, group mean (g)	SD	n	Sex
0	43.85	2.69	37	M
0.1	43.51	2.86	35	M
0.5	40.04	3.00	43	M
1.1	35.09	2.56	42	M

bw: body weight; SD: standard deviation.

B. BMR: Default value (per cent change = 5%)

C. Software used: PROAST v. 61.6

D. Additional assumptions: None

E. Table of results

Model	No. of parameters (variance excluded)	AIC		BMDL05 (mg/kg)		BMDU05 (mg/kg)
		Exponential	Hill	Exponential	Hill	Exponential	Hill
Null model	1	−234.06
Model 3	3	−388.50a	−388.58a	0.198	0.205	0.410	0.412
Model 5	4	−386.72	−386.72
Full model	4	−386.72

AIC: Akaike information criterion; BMDL: lower confidence limit of the benchmark dose; BMDU: upper confidence limit of the benchmark dose.

^a Selected model, based on lowest AIC.

F. Figure of fitted models

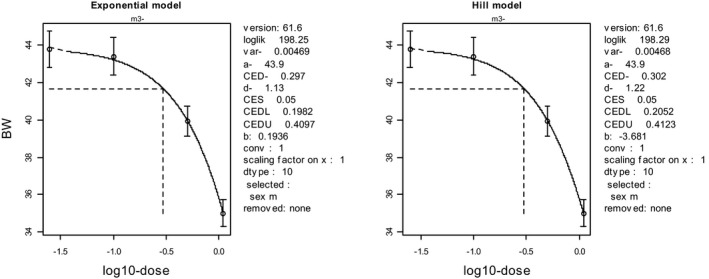
Fitted curves for model 3 from the exponential model family (left panel) and model 3 from the Hill model family (right panel). Vertical whiskers represent 95% confidence intervals for the responses. Dose is plotted on log‐scale for better readability; the response in the controls is shown at an arbitrary level lower than the lowest non‐zero dose (as zero dose is situated at minus infinity on log‐scale).

G. Conclusion

There were no alerts (the fit was reached under convergence and the AICs of both models differed less than two units from the full model).

For both the exponential and the Hill family of models, model 3 was selected, based on the lowest AIC. The two associated BMD confidence intervals were similar. Therefore, model averaging would hardly provide a different result, and it was decided to select the lowest BMDL and highest BMDU from both models (in this case, they were the same for both models when using two significant figures).

The combined BMD confidence interval was (0.20, 0.41) mg/kg.

The BMDL₀₅ for this data set is 0.20 mg/kg.

Example 2: quantal data

This example relates to a 2‐year study in rats, where three doses of a substance were administered to the animals. Dose‐related changes in thyroid epithelial cell vacuolisation were found, and these data were used for a BMD analysis. The BMD analysis given below may serve as an example of how to report the results from a BMD analysis of a quantal data set in an EFSA opinion.

A. The data

Dose (mg/kg day)	No of animals with thyroid epithelial vacuolisation	No of animals in dose group	Sex
0	6	50	F
3	6	50	F
12	34	50	F
30	42	50	F

B. BMR: Default value (extra risk = 10%)

C. Software used: EFSA BMD Platform (under development) + PROAST v. 61.6

D. Additional assumptions: None

E. Table of results

Model	No of parameters	AIC	BMDL10	BMDU10 a
Null Model	1	276.38	–	–
Gamma	3	192.99	1.21	2.67a
Logistic	2	198.47	3.31	4.90a
Log‐Logistic	3	189.81b	1.84	5.00a
Probit	2	199.07	3.37	NA
Log‐Probit	3	189.73c	1.98	5.11a
Weibull	3	193.55	1.10	4.01a
LMS (Two stage)	3	194.20	1.35	3.10
Full Model	4	188.04	–	–

AIC: Akaike information criterion; BMDL: lower confidence limit of the benchmark dose; BMDU: upper confidence limit of the benchmark dose.

^a Calculated by PROAST, as BMDS does not yet provide BMDUs except for the two‐stage model.

^b AIC differs less than two units from lowest AIC.

^c Model with lowest AIC.

F. Figure of fitted model

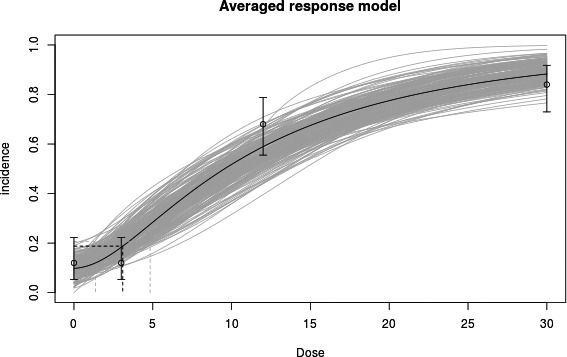
‘Average model’ from model averaging analysis of the observed incidences of animals with thyroid epithelial cell vacuolisation. The average model was constructed via averaging all weighted‐model results at a finite set of points (i.e., doses) in order to generate curve. The EFSA BMD platform (under development) was used.

If model averaging software was not available, the plots of the recommended models should be shown:

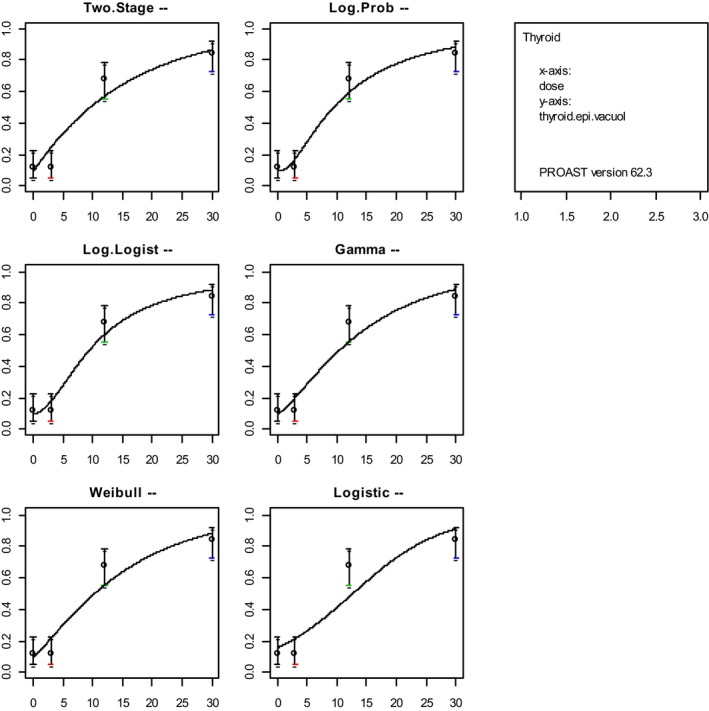
The recommended models fitted to the observed incidences of animals with thyroid epithelial cell vacuolisation, with 95% confidence intervals at each response. PROAST v. 62.3 was used.

G. Conclusion

There were no alerts (the fit was reached under convergence and the AIC differed less than two units from the full model).

The preferred way of combining the results is by model averaging. The MADr‐BMD program as described in Wheeler and Bailer (2008) can be used for that purpose. In this approach, all models are taken into account with a weight that is derived from the AIC. The following weights were used for this data set:

Model	Weight	AIC
Log‐probit	0.411	189.73
Log‐logistic	0.395	189.81
Gamma	0.080	192.99
Weibull	0.061	193.54
Multistage 2°	0.044	194.20
Logistic	0.005	198.47
Probit	0.004	199.07

The current MADr‐BMD program does not calculate the BMDU; it only calculates a BMDL (and a BMD point estimate). The BMDL for this data set was found to be 1.5 mg/kg based on model averaging.

If model averaging software is not available, the surrogate method may be used, where the lowest BMDL and highest BMDU is taken from the models that showed an AIC differing less than two units from the lowest AIC. In this data set only, the log‐probit and the log‐logistic models meet that criterion. Combining these two models results in a BMD confidence interval of (1.8 and 5.1) mg/kg.

The fact that the model averaging software resulted in a slightly lower BMDL is due to the fact that the other models were taken into account as well (although with low weight).

3. Conclusions

This revised guidance takes account of the experience accumulated in BMD analysis over the last 7 years.

The SC confirms that the BMD approach is a scientifically more advanced method compared to the NOAEL approach for deriving a RP, since it makes extended use of dose–response data and it provides a quantification of the uncertainty in the estimated RP resulting from the statistical limitations in the dose–response data. Using the BMD approach results in a more consistent RP, as a consequence of the specified BMR. HBGVs derived using the BMD approach can be expected to be as protective as those derived from the NOAEL approach, i.e. on average over a large number of risk assessments. Therefore, the default values for uncertainty factors currently applied are equally applicable.

The SC does not consider it necessary to repeat all previous evaluations using the NOAEL approach by the BMD approach, because, on average, the two approaches give comparable results. Similarly, the SC does not consider it necessary to repeat previous risk assessments related to quantal endpoints that used the 2009 version of the BMD guidance, given the modifications proposed in the updated version of the guidance for this type of data. Regarding previous risk assessments where the 2009 BMD guidance was applied to continuous data sets, the updated guidance might result in lower RPs, in particular when model 2 of the nested families was selected to derive the RP.

As indicated above, on average the NOAEL and BMDL approaches will result in comparable RPs; however, in individual cases, the resulting RP may differ substantially (e.g., by one order of magnitude) between both approaches. Hence, when the estimated exposure to the compound was evaluated to be close (e.g. within one order of magnitude) to the HBGV (and similarly for the MOE), then a re‐evaluation might be considered. In such cases, the BMD approach as described in this guidance should be applied.

The BMD approach is applicable to all chemicals in food, independently of their category or origin, e.g. pesticides, additives or contaminants, for identifying RPs to establish HBGVs or to calculate MOE. The BMD approach can be used for dose–response assessment of experimental animal data as well as for epidemiological data, although the latter is not addressed in this guidance document and will be subject to a separate guidance of the EFSA SC.

4. Recommendations

• The SC strongly recommends that the BMD approach, and more specifically model averaging, is used for the determination of the RPs for establishing HBGVs and for calculating margins of exposure. As the preferred approach is model averaging, appropriate software should be developed.

• The SC recommends that training in dose–response modelling and the use of BMD software continues to be offered to experts in the Scientific Panels and EFSA Units.

• The SC is firmly of the view that, given the expected increased use of the BMD approach, current toxicity test guidelines should be reconsidered with the purpose of optimising the study design for the determination of the RP for establishing the HBGV, e.g. increase the number of dose levels without changing the total number of animals used in the experiment.

• The SC recommends EFSA to establish a BMD Standing Working Group to be consulted by EFSA experts and staff members on BMD analysis issues if needed, e.g. when alerts are identified or when applying the BMD approach to histopathological (ordinal) data. A network on BMD, coordinated by EFSA, should also be considered to exchange experience and develop expertise with EFSA Partners (Member States competent, EU sister agencies, DG Santé Scientific Committees and international organisations).

• The SC identified the need for a specific guidance on the use of the BMD approach to analyse human data.

Abbreviations

ADI

acceptable daily intake

AIC

Akaike information criterion

BMD

benchmark Dose

BMDL

lower confidence limit of the benchmark dose (equivalent term: CEDL)

BMDS

benchmark dose software

BMDU

upper confidence limit of the benchmark dose (equivalent term: CEDU)

BMR

benchmark response

bw

body weight

CEDL

see BMDL

CEDU

see BMDU

FAO

Food and Agriculture Organization of the United Nations

FEEDAP

EFSA Panel on Additives and Products or Substances used in Animal Feed

GUI

Graphical User Interface

HBGV

health‐based guidance value

IPCS

WHO International Programme on Chemical Safety

JECFA

Joint FAO/WHO Expert Committee on Food Additives

JMPR

Joint FAO/WHO Meeting on Pesticide Residues

LOAEL

lowest‐observed‐adverse‐effect‐level

MOE

margins of exposure

NOAEL

no‐observed‐adverse‐effect level

OECD

Organisation for Economic Co‐operation and Development

PoD

point of Departure

RP

Reference Point

RPF

relative potency factors

SC

Scientific Committee

SD

standard deviation

SEM

standard error of the mean

TDI

tolerable daily intake

TEF

toxic equivalency factor

TWI

tolerable weekly intake

US

US Environmental Protection Agency

WHO

World Health Organization

Appendix A – Summary of the differences between BMDS and PROAST

1.

A summary of the main differences between the BMDS and PROAST software is provided in Table A.1.

Table A.1.

Comparison of BMDS and PROAST

	BMDS	PROAST
Environment	Can be run immediately (as an executable) under Windows	R (free software) is required Also runs under Linux and Mac OS X
First use	Easy to get started	Higher threshold; requires basic understanding of R
User interaction	Graphical User Interface (GUI)	Both a menu version and a GUI version available. GUI is suitable for most standard analyses; the menu version covers more options
Continuous data	Yes	Yes
Nested continuous data, e.g. for litter effects	No	Yes
Quantal data	Yes	Yes (in menu version)
Nested quantal data, e.g. for litter effects	Yes	Yes
Ordinal data	A program on categorical regression is implemented	Yes
BMDU calculated	No, except for Multistage Cancer model	Yes
Default assumption of distribution continuous data	normal	log‐normal
Option to change default distribution continuous data	Only for exponential model	Yes (in menu version)
Confidence interval based on profile likelihood	Yes	Yes
Confidence interval based on bootstrapping	No	Yes (in menu version)
Covariates	No (except for nested quantal models)	Yes
Model fitting for (nested) exponential models	Yes	Yes
Model fitting for (nested) Hill models	No, only four‐parameter model	Yes
Automatic model fitting for recommended suite of quantal models	Yes	Yes
Graphical output	Yes, but only original scales for y‐axis and x‐axis	Yes, including options to change scales (e.g. log‐scales)
Evaluation of dose addition	No	Yes

For continuous data, the default assumptions regarding the distribution of the data differ between BMDS and PROAST. As a default, data are assumed to be normally distributed in BMDS while they are assumed to be log‐normally distributed in PROAST. If this is the only difference (i.e. the same model, BMR, and other settings) in a specific dose–response analysis, this should result in only slight differences in the BMD and BMDL when the within‐group variation is small (Shao et al., 2013); larger deviations may occur with data showing large within‐group variation. In view of this guidance document, it is important to note that BMDS lacks the option of setting the distribution to log‐normal in the Hill model.

The procedure in PROAST for fitting the family of exponential models is available in the BMDS, but the family of Hill models cannot be fitted in BMDS. In view of this guidance document, an important gap in BMDS is that the three‐parameter Hill model cannot be fitted.

It should also be noted that the parameterisation of the Hill model differs between BMDS and PROAST, but the models may still be regarded as equivalents. Besides the four‐parameter Hill model and the nested family of exponential models, BMDS also includes three additional models (power, linear and polynomial) for continuous data. These models are, however, not recommended in this opinion. Table A.2 lists the models used in BMDS that are equivalent to those recommended in Table 3.

Table A.2.

Dose–response models for continuous and quantal data in BMDS (US EPA, 2012)

Continuous models
Hill model $\mathit{\mu }\left(X\right)=\mathit{\gamma }+\mathit{\nu }\frac{X^{\mathit{\eta }}}{{\mathit{\kappa }}^{\mathit{\eta }}+X^{\mathit{\eta }}}$	Exponential models (a set of nested models) Model 3: $\mathit{\mu }\left(X\right)=\mathit{\gamma }+e^{{\left(kX\right)}^d}$ Model 5:$\mathit{\mu }\left(X\right)=\mathit{\gamma }\left(c-(c-1)e^{-{\left(kX\right)}^d}\right)$
Quantal models
Logistic model $p\left(X\right)=\frac{1}{1+e^{-\left(\mathit{\alpha }+\mathit{\beta }X\right)}}$ Log‐logistic model $p\left(X\right)=\mathit{\gamma }+\frac{1-\mathit{\gamma }}{1+e^{-\left(\mathit{\alpha }+\mathit{\beta }lnX\right)}}$ Probit model a $p\left(X\right)=\frac{1}{\sqrt{2\mathit{\pi }}}\underset{-\infty }{\overset{\mathit{\alpha }+\mathit{\beta }X}{\int }}{e}^{\frac{-x^2}{2}}dx$ Log‐probit model a $p\left(X\right)=\mathit{\gamma }+\frac{1-\mathit{\gamma }}{\sqrt{2\mathit{\pi }}}\underset{-\infty }{\overset{\mathit{\alpha }+\mathit{\beta }lnX}{\int }}{e}^{\frac{-x^2}{2}}dx$	Weibull model $p\left(X\right)=\mathit{\gamma }+\left(1-\mathit{\gamma }\right)\left(1-e^{-\mathit{\beta }{\left(X\right)}^{\mathit{\alpha }}}\right)$ Gamma model b $p\left(X\right)=\mathit{\gamma }+\left(1-\mathit{\gamma }\right)\frac{1}{\mathrm{\Gamma }\left(\mathit{\alpha }\right)}\underset{0}{\overset{\mathit{\beta }X}{\int }}{x}^{\left(\mathit{\alpha }-1\right)}{e}^{-x}dx$ Multistage model $p\left(X\right)=\mathit{\gamma }+\left(1-\mathit{\gamma }\right)\left(1-e^{-\sum _{j=1}^n{\mathit{\beta }}_j{X}^j}\right)$

For continuous models, the variance across dose group may either be assumed to be constant or non‐constant (a power function of the mean response).

^aIn the model, $\frac{1}{\sqrt{2\mathit{\pi }}}{e}^{\frac{-x^2}{2}}$is the standard normal density function.

^bIn the model, $\mathrm{\Gamma }\left(\mathit{\alpha }\right)=\underset{0}{\overset{\infty }{\int }}{x}^{\left(\mathit{\alpha }-1\right)}{e}^{-x}dx$ is the gamma function.

For continuous data, the variance can be either specified as constant or it can be modelled as a function of the mean response in BMDS, while PROAST always assumes the variance to be constant on log‐scale (i.e. constant coefficient of variation). A constant coefficient of variation is a special case of the non‐constant variance model in BMDS, i.e. the case when the parameter ‘rho’ equals 1.

In BMDS, four ways of defining the BMR are available for continuous data: standard deviation (Std. Dev), relative deviation (Rel. Dev), absolute deviation (Abs. Dev) and Point. In PROAST, only the options called ‘Rel. Dev.’ and ‘Std. Dev.’ in BMDS are available.

For most models in BMDS, only the lower bound of the confidence interval is calculated, i.e. the BMDL, while both the lower and upper bound are computed by PROAST for all models. In view of this guidance document recommending the consideration of the BMD confidence interval, the lack of BMDUs in the BMDS output is a limitation.

For analysis of quantal data, BMDS and PROAST are essentially the same. Similar to the case for the Hill model, however, many of the quantal models differ in parameterisation between BMDS and PROAST, but they do provide similar results.

Appendix B – Template for reporting a BMD analysis

1.

A Data description

Brief general description of the data. This section should include a table summarising the data. In case that raw data is obtained or provided, resulting in a too large table, summary statistics may be given instead.9 For quantal endpoints, both the number of responding animals and the total number of animals should be given for each dose level; for continuous endpoints, either the individual responses or the mean responses and the associated SDs (or SEMs) and sample sizes should be given for each dose level.

Table B.1.

Example of table for continuous dose–response data

Dose	Endpoint mean	SD	N	Covariates (gender)
0	43.85	2.69	37	M
0.1	43.51	2.86	35	M
0.5	40.04	3.00	43	M
1.1	35.09	2.56	42	M
0	41.54	6.26	36	F
0.1	38.71	4.73	42	F
0.5	33.76	3.92	37	F
1.1	28.55	2.08	38	F

In case that several control groups are reported in the publication or provided by the applicant, they should all be presented in the table. However, these will be handled in the analysis needs a case‐by‐case consideration.

Table B.2.

Example of table for quantal dose–response data

Dose	Number of animals with event of interest	N	Covariates (gender)
0	2	50	M
3	4	50	M
12	32	49	M
30	45	50	M
0	6	50	F
3	6	50	F
12	34	50	F
30	42	50	F

In case different endpoints are to be analysed, they should be described in different subsections, containing information pertaining to each endpoint.

The following steps apply for each endpoint considered.

B Selection of the BMR

The value of the BMR used in the analysis. The rationale behind the choice made should be described, in particular when it deviates from the default.

C Software used

The software used including version number should be reported. In case another non‐publicly available software was used, the script for the BMD analysis should be provided as an appendix.

D Specification of deviations from default assumptions

• In case model averaging software is available and another approach was used, rationale for deviating from the recommended approach should be provided.

• Assumptions made when deviating from the recommended defaults in this guidance document (e.g. gamma distributional assumption instead of log‐normal, heteroscedasticity instead of homoscedasticity).

• Other models than the recommended ones listed in Table 3 of this guidance document that were fitted should be listed, with the reasons to include them.

• Description of any deviation from the procedure described in the flow chart (Figure 8) to obtain the final BMD confidence interval (e.g. using AIC + 3 instead of AIC + 2 for model selection).

E Results

The results of the BMD analysis should contain:

• a table presenting results of the models fitted, including number of parameters in the model, AIC, BMDL and BMDU (see Table B.3);

• report whenever convergence issues were encountered;

• report whenever the full model performed better than any of the fitted models according to the criterion AIC_min > AIC_full + 2. Indicate if this could be due to problems in the data (see study protocol) or something else, and whether or not this affected the conclusions;

• highlight the models complying with the rule AIC ≤ AIC_min + 2.

Table B.3.

Result table for continuous data

Model	Number of parameters	Log‐likelihood	AIC	BMDL	BMDU
Null	1
Full
Exp Model 3
Exp Model 5
Hill Model 3
Hill Model 5

AIC: Akaike information criterion; BMDL: lower confidence limit of the benchmark dose; BMDU: upper confidence limit of the benchmark dose.

F Plots of fitted models

In case model averaging is used, show the plot of the data with confidence intervals for the responses, together with the resulting model average fit. If no model averaging software is available, or the decision was made to deviate from the model averaging recommendation, show the plot with all the models fitted (in case of nested model families, the plot of the selected model for each nested family).

Figure B.1.

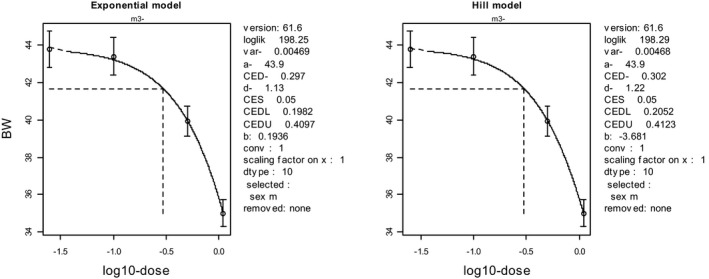
Plot of the selected models from each model family in the case of continuous data (plots shown here are from PROAST)

G Conclusions

This section should summarise the results for each endpoint (data set) that was analysed and provide a discussion of the rationale behind selecting the critical endpoint.

The BMD confidence interval of the critical endpoint (and the BMDL selected as RP) should be reported and discussed.

Suggested citation: EFSA Scientific Committee , Hardy A, Benford D, Halldorsson T, Jeger MJ, Knutsen KH, More S, Mortensen A, Naegeli H, Noteborn H, Ockleford C, Ricci A, Rychen G, Silano V, Solecki R, Turck D, Aerts M, Bodin L, Davis A, Edler L, Gundert‐Remy U, Sand S, Slob W, Bottex B, Abrahantes JC, Marques DC, Kass G and Schlatter JR, 2017. Update: Guidance on the use of the benchmark dose approach in risk assessment. EFSA Journal 2017;15(1):4658, 41 pp. doi: 10.2903/j.efsa.2017.4658