Vesicle Shrinking and Enlargement Play Opposing Roles in the Release of Exocytotic Contents

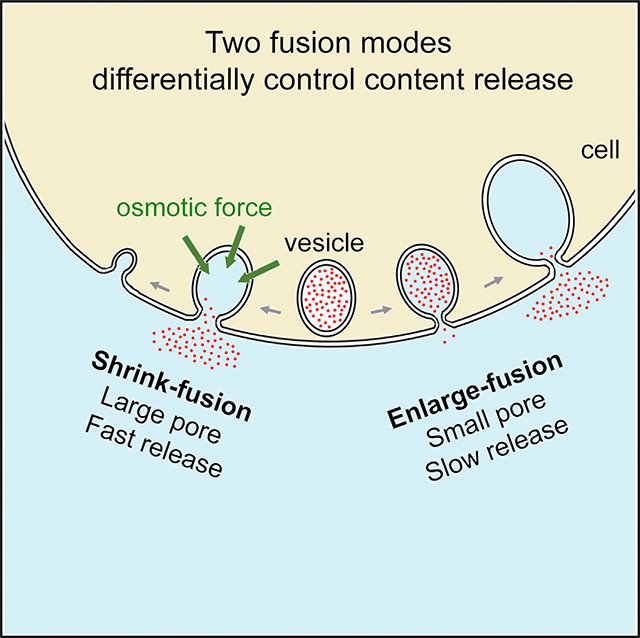
SUMMARY

For decades, two fusion modes were thought to control hormone and transmitter release essential to life; one facilitates release via fusion pore dilation and flattening (full collapse), and the other limits release by closing a narrow fusion pore (kiss-and-run). Using super-resolution stimulated emission depletion (STED) microscopy to visualize fusion modes of dense-core vesicles in neuroendocrine cells, we find that facilitation of release is mediated not by full collapse but by shrink fusion, in which the Ω-profile generated by vesicle fusion shrinks but maintains a large non-dilating pore. We discover that the physiological osmotic pressure of a cell squeezes, but does not dilate, the Ω-profile, which explains why shrink fusion prevails over full collapse. Instead of kiss-and-run, enlarge fusion, in which Ω-profiles grow while maintaining a narrow pore, slows down release. Shrink and enlarge fusion may thus account for diverse hormone and transmitter release kinetics observed in secretory cells, previously interpreted within the full-collapse/kiss-and-run framework.

In Brief

Shin et al. discover two fusion modes; one involves fused vesicle shrinking that employs a large pore to facilitate content release, and the other involves vesicle enlargement with a small pore that slows down release. Shrinking is energetically preferred over the generally assumed full-collapse fusion, because osmotic pressure squeezes fused vesicles.

Graphical Abstract

INTRODUCTION

Hormone and transmitter release by endocrine cells and neurons mediates many important functions, such as stress responses, immune response, control of blood glucose with relevance to diabetes, and synaptic transmission, which is essential for cognition and coordinated motor activity (Jahn and Fasshauer, 2012; Saheki and De Camilli, 2012; Alabi and Tsien, 2013; Wu et al., 2014; Chang et al., 2017; Sharma and Lindau, 2018). Regulation of the amount and rate of release is physiologically crucial, and much research has addressed the mechanisms involved. From decades of research, a widely held view emerged that content release by neurons and endocrine cells is controlled by two modes of fusion: (1) full collapse, in which the fusion pore dilates while the vesicle flattens into the membrane, resulting in rapid and complete release; and (2) kiss-and-run, when a narrow fusion pore opens and then closes, giving a slow and/or partial release of contents (Jahn and Fasshauer, 2012; Saheki and De Camilli, 2012; Alabi and Tsien, 2013; Wu et al., 2014; Chang et al., 2017; Sharma and Lindau, 2018).

This view has been questioned in two respects. First, inconsistent with the assumed narrow pore, fusion pore conductance measurements revealed large conductance during some kiss-and-run events (Alés et al., 1999; He et al., 2006), and a recent imaging study directly visualized pores of ~60–490 nm during some kiss-and-run events (Shin et al., 2018). Second, while full collapse was proposed on the basis of electron microscopy (EM) data (Heuser and Reese, 1981), it has not been observed in live cells. Imaging in endocrine cells shows shrinking fusion spots rather than growing fusion spots that subsequently disappear, as would be expected from full collapse (Chiang et al., 2014; Wen et al., 2016). It was proposed that the shrinking spots indicated a fusion mode termed shrink fusion, in which the vesicle shrinks while retaining its shape without pore dilation, and shrink fusion was suggested to be mediated by F-actin-dependent plasma membrane (PM) tension (Wen et al., 2016).

While these observations imply the possibility of replacing full collapse with shrink fusion, direct evidence of shrink fusion is lacking. To demonstrate shrink fusion would require visualization of vesicle membrane profile shape changes and evidence that the pore does not dilate. Such visualization is also required to eliminate other possibilities, including rapid budding of clathrin-coated vesicles at the fusion-generated Ω-profile as recently suggested (Bittner et al., 2013; Abbineni et al., 2018). Direct visualization is indeed feasible, as shown in recent studies that visualized Ω--shaped membrane profiles and their pores (Zhao et al., 2016; Shin et al., 2018). However, these studies did not investigate Ω-profile shrinking or pore dynamics during shrinking.

The proposal of shrink fusion in replacement of full collapse raises the questions of why shrinking is preferred to the intuitively appealing full-collapse pathway, whether shrink fusion promotes release, and by what mechanism. The observation that kiss-and-run may not limit content release (Alés et al., 1999; Shin et al., 2018) raises the question of whether there is a fusion mode specifically for the limiting of content release. Here, we addressed these fundamental questions by super-resolution stimulated emission depletion (STED) imaging of vesicular membrane profiles and fusion pore dynamics, confocal imaging of content release, electron microscopy (EM) and realistic mathematical modeling in neuroendocrine chromaffin cells. We found that facilitation of content release is mediated not by full collapse but by shrink fusion with a large fusion pore and that inhibition of release is mediated not by kiss-and-run but by enlarge-fusion mode, in which Ω-profiles increase in size but maintain a narrow pore. We found that cells’ physiological osmotic pressure squeezes, but does not dilate, the Ω-profile, explaining why shrink fusion rather than full collapse is the default fusion mode for merging vesicles with the PM and promoting content release. We conclude that shrink and enlarge fusion control the yin and yang of exocytotic content release.

RESULTS

Direct Observation of Fused Vesicle Shrinking and Enlargement in Live Cells

To study how vesicles merge with the PM, we transfected bovine adrenal chromaffin cells in primary cultures with EGFP or mNeonGreen attached to the phospholipase C delta PH domain (PH_G; either PH-EGFP or PH-mNeonGreen). PH_G binds to PtdIns(4,5)P2 (PIP₂) at the PM cytosolic-facing leaflet and thus labels PM (Figure 1A) (Zhao et al., 2016; Shin et al., 2018). We added Atto 532 (A532) in the bath (Figure 1A), which enters the fusing Ω-profile to confirm the structural changes revealed by PH_G imaging (Chiang et al., 2014; Shin et al., 2018). We induced vesicle fusion using 1-s depolarization from −80 to +10 mV (depol_{1 s}) through a pipette in the whole-cell configuration, which induced calcium currents and capacitance changes reflecting robust exo- and endocytosis (Figure 1A). STED imaging of A532 and PH_G was performed in the microscope xz plane at a fixed y location near the cell bottom every 26–300 ms (xz/y_fix imaging) before and after depol_{1 s} for ~20–30 s. Each cell was subjected to only one depol_{1 s}, which induced fusion mostly during and ~3 s after depol_{1 s} (Chiang et al., 2014; Shin et al., 2018).

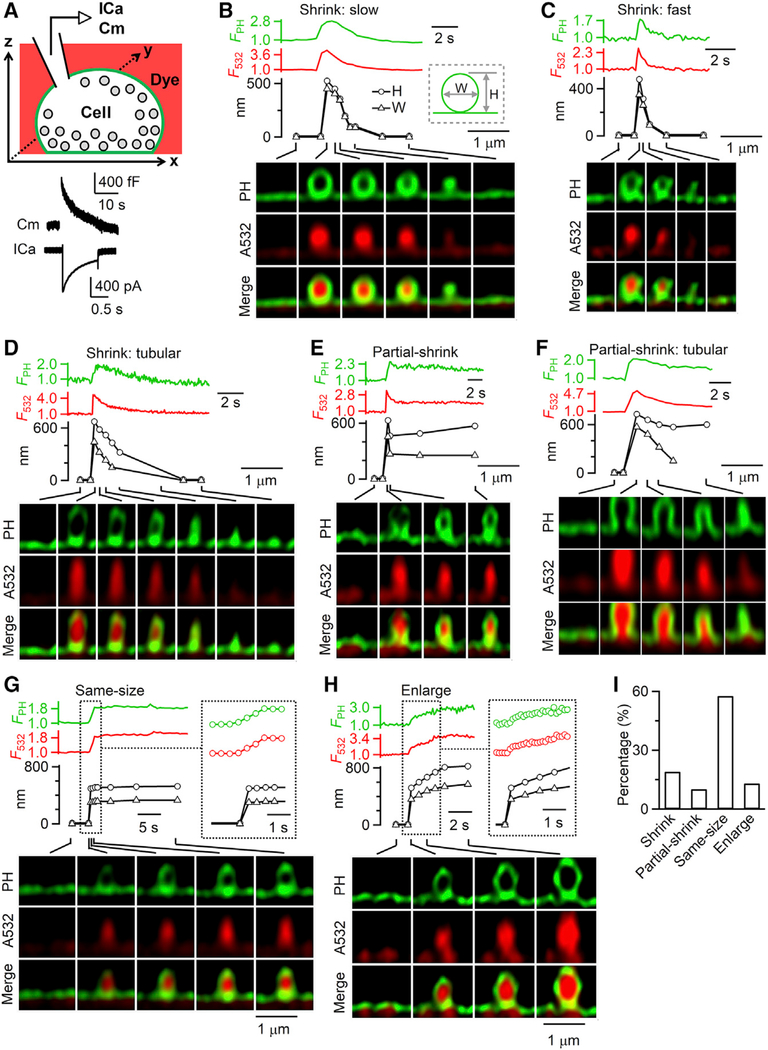
Figure 1. Visualization of Ω-Shaped Membrane Profile Shrinking and Enlargement.

(A) Top: setup drawing. The cell membrane is labeled with PH_G (green) and bath labeled with A532 (red). Calcium current (ICa) and capacitance (Cm) are recorded at the whole-cell voltage-clamp configuration. Bottom: Sampled ICa and Cm change induced by depol_{1 s}.

(B–H) PH-Ω fluorescence (F_PH; normalized to baseline), A532 spot fluorescence (F₅₃₂; normalized to baseline), PH-Ω height (H; circles), PH-Ω width (W; triangles), and sampled images at times indicated with lines showing different modes of fusion: (B–D) shrink fusion (B, slow; C, fast; and D, tubular intermediates observed); (E and F) partial shrink fusion (E, reduced-size Ω-profile; and F, reduced-size tubular structure); (G) same-size fusion; and (H) enlarge fusion. The inset in (G) and (H) is shown at the same timescale (right). When PH-Ω was too dim or smaller than our resolution, PH-Ω height and width were not measured. Images were acquired with STED xz/y_fix scanning.

(I) The percentage of shrink fusion, partial shrink fusion, same-size fusion, and enlarge fusion (total PH-Ω number: 236; from 202 cells).

See also Figures S1 and S2.

Depol_{1 s} induced PH_G-labeled Ω-shape profiles (PH-Ωs) filled with A532 (Figures 1B–1H), reflecting diffusion of PH_G and A532 from PM and bath into the fusion-generated Ω-profile. PH-Ω without A532, which reflected hemi-fusion (Zhao et al., 2016), was not analyzed here. In ~20% of cells, we observed a depol_{1 s}-induced, fusion-generated A532-filled PH-Ω with a clear membrane outline. Following PH-Ω appearance (236 events, 202 cells; Figure S1A), the Ω-profile (1) shrank while maintaining an Ω-shape until it became undetectable (shrink fusion, 45 events; Figures 1B–1D); (2) shrank partially and then maintained a reduced-size Ω-profile (partial shrink fusion, 24 events; Figures 1E and 1F); (3) maintained its Ω-profile and A532 spot size (same-size fusion, 136 events; Figure 1G); or (4) increased in size while maintaining its Ω-shape (enlarge fusion, 31 events; Figure 1H; summarized in Figure 1I). Figure S1B illustrates these four fusion modes schematically. The PH-Ω width (see Figure S1C for measurements) at the fusion onset was similar for these four fusion modes (Figure S1D).

Shrink fusion was rapid, with a 20%–80% shrinking time mostly <2 s (Figures 1B–1D). During shrinking episodes (both shrink fusion and partial shrink fusion), in most cases, the Ω shape was preserved as the width and height decreased proportionally (Figures 1B, 1C, and 1E). However, in some instances of shrink fusion, PH-Ω had an extended tubular shape with a height considerably greater than the width (Figures 1D and 1F). We did not observe vesicle budding off the PH-Ω during shrink fusion (n = 45), excluding this as the mechanism that shrinks the PH-Ω.

Enlarge fusion was slower than shrink fusion, with a 20%–80% time of ~2–20 s (Figure 1H). Enlarge fusion was detected if the PH-Ω’s width at 20–30 s after fusion onset (516 ± 18 nm) increased by >15% of that at the fusion onset (352 ± 13 nm, n = 31; t test, p < 0.001). The width of PH-Ω at 20–30 s after the onset of enlarge fusion (516 ± 18 nm, n = 31) was significantly larger than that of same-size fusion (374 ± 7 nm, n = 136; t test, p < 0.001). The width and height of the PH-Ω increased approximately proportionally during enlarge fusion (Figure 1H). Additional vesicle fusion at the PH-Ω was not observed during enlarge fusion (n = 31), excluding compound fusion as the origin of enlarge fusion.

Three sets of evidence showed that shrinking or enlargement was not due to Ω-profile movement in the xy plane. First, random Ω-profile movement generally involves displacements in both the x and y directions, whereas during shrinking or enlargement captured by STED xz/y_fix imaging, the Ω-profile did not shift in the x direction (n = 69; Figures 1B–1H). Second, STED xy-plane imaging at a fixed z-focal plane (xy/z_fix imaging) showed that depol_{1 s} induced the appearance of PH-labeled rings containing A532 spots (Figures S2A–S2C), which reflected fusion-generated Ω-profiles induced by depol_{1 s} (Chiang et al., 2014; Shin et al., 2018). These PH-labeled rings shrank, remain unchanged or enlarged but did not move in the xy plane (Figures S2A–S2C; 102 events, 7 cells). Third, in cells treated with high-potassium solution (70 mM, 45 s) and fixed with 4% paraformaldehyde, all PH-Ω (59 PH-Ω in 39 cells) did not change in width during 20–30 s STED xz/y_fix imaging (Figure S2D). Thus, PH-Ω size changes observed in live cells are not due to microscopic y axis drift.

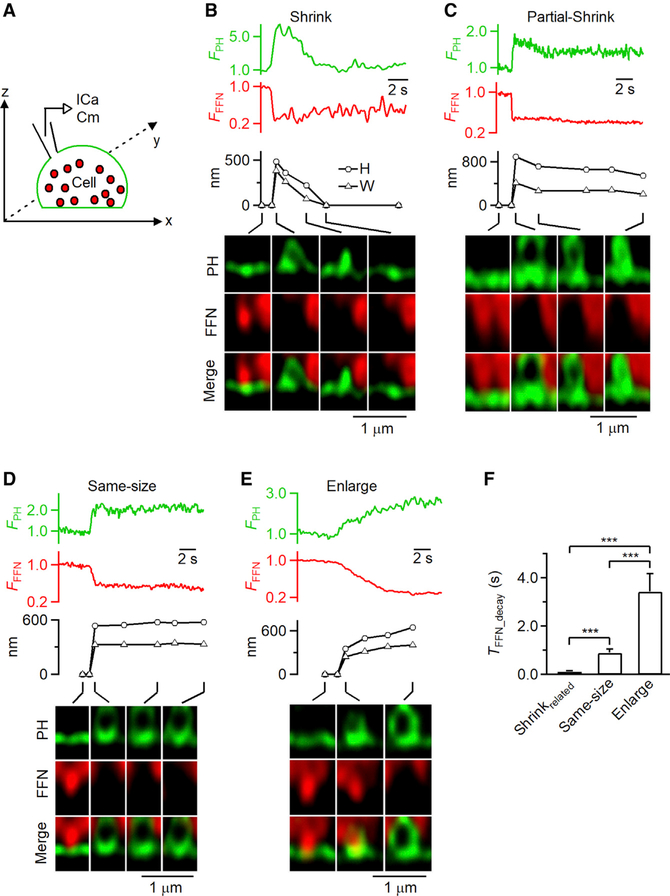
To verify that the PH-Ω size changes reflect post-fusion structural changes, we loaded vesicles with fluorescent false neurotransmitter FFN511 via bath application (Figure 2A) (Gubernator et al., 2009). We observed the appearance of PH-Ω that released FFN511, as detected with STED xz/y_fix imaging of PH_G and FFN511 (Figures 2A–2E; n = 92 events, 71 cells) (Shin et al., 2018). Similar to STED PH_G/A532 imaging, we observed shrink fusion (n = 8), partial shrink fusion (n = 13), same-size fusion (n = 53), and enlarge fusion (n = 18; Figures 2B–2E). The 20%–80% FFN511 release time depended on the fusion mode (Figure 2F), which will be further described later. We concluded that the PH-Ω size changes reflect post-fusion vesicle size changes.

Figure 2. Observation of Ω-Shaped Membrane Profile Shrinking and Enlargement while Releasing FFN511.

(A) Setup diagram. Vesicles were loaded with FFN511 (red, pseudo-color), the PM was labeled with PH_G (green), and ICa and Cm were recorded via a pipette.

(B–E) F_PH, FFN511 fluorescence (F_FFN; normalized to baseline), PH-Ω height (H; circles) and width (W; triangles), and sampled images at times indicated with lines showing release of FFN511 for shrink fusion (B), partial shrink fusion (C), same-size fusion (D), and enlarge fusion (E).

(F) 20%–80% decay time of FFN511 (T_{FFN_decay, mean + s.e.m.}) for shrink fusion (8 events), partial shrink fusion (13 events), same-size fusion (53 events), and enlarge-fusion (18 events). Data are from 71 cells under STED xz/y_fix imaging of PH_G/FFN511. ***p < 0.001; ANOVA test.

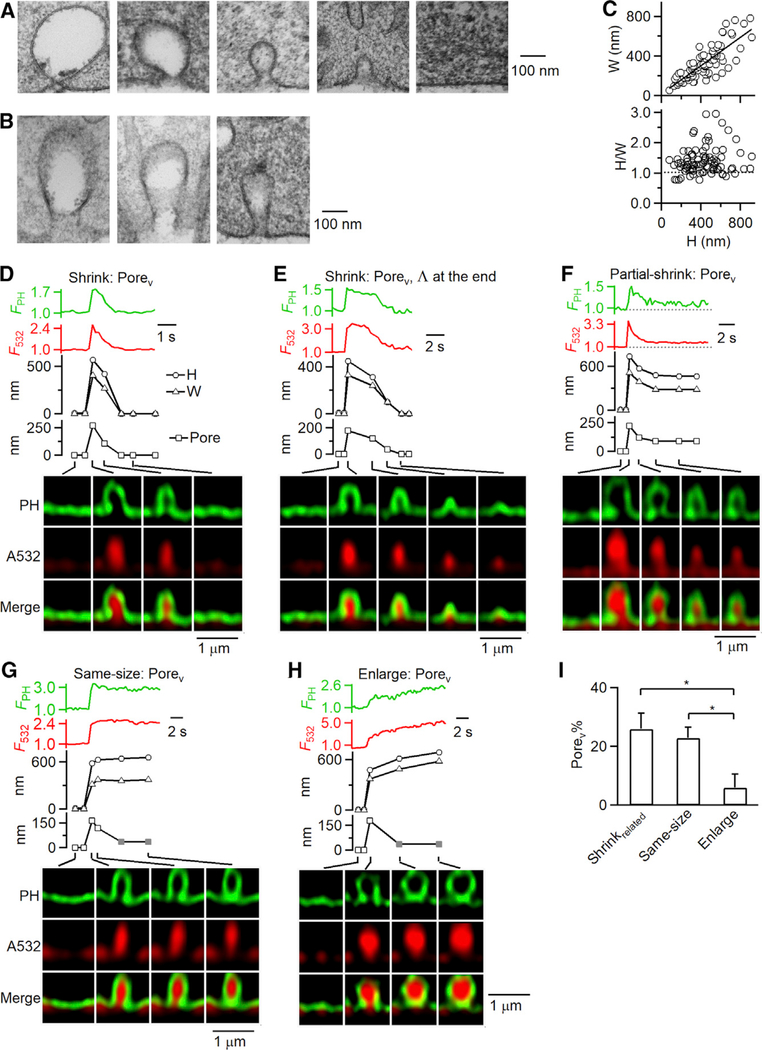
Consistent with Ω-profile shrinking and enlargement (Figure 1), EM revealed Ω-profiles of various sizes, some of which approached a tubular shape (Figures 3A and 3B); widths ranged from 56 to 784 nm, and larger width was correlated with larger height (Figure 3C, top). The height/width ratio of most Ω-profiles was >1 (85% of cases; Figure 3C, bottom), indicating that Ω-profiles were mostly somewhat elongated with some approaching a tubular shape, consistent with STED observation of mostly elongated Ω-profiles (e.g., Figures 1B–1H and 3D–3H). The pore size range measured with EM was similar to the STED-measured visible pore (Pore_v) range, as shown in a previous study (Shin et al., 2018).

Figure 3. Fusion Pore Dynamics during Shrink, Partial Shrink, Same-Size, and Enlarge Fusion.

(A and B) Electron microscopic images of Ω-profiles (A) or elongated Ω-profiles resembling cylinders (B) with different sizes. Cells were in 70 mM KCl for 90 s.

(C) The width (W) and the ratio between the height (H) and width (H/W) of Ω-profiles observed with EM (each circle: 1 Ω-profile; 84 Ω-profiles from 800 cell cross sections). The line (upper panel) is a linear regression fit (correlation coefficient: 0.81). Dotted line (lower panel) indicates H/W = 1.

(D–H) F_PH (PH-Ω fluorescence), F₅₃₂ (A532 fluorescence), H (PH-Ω height, circles), W (PH-Ω width, triangles), pore (PH-Ω pore size, squares), and sampled images at times indicated with lines showing pore dynamics during shrink fusion (D and E), partial shrink fusion (F), same-size fusion (G), and enlarge fusion (H). Gray squares (G and H), pore remained open, but below our STED resolution of ~60 nm.

(I) The percentage of observing a Pore_v (Pore_v%, mean + s.e.m.) during shrink_related fusion (including shrink fusion and partial shrink fusion), same-size fusion, and enlarge fusion (total fusion event number: 236; from 202 cells). *p < 0.05, ANOVA test.

See also Figure S3.

As the PH-Ω shrank, remained unchanged in size or enlarged, in some cases the pore closed. This was reflected as decay of the spot A532 fluorescence (F₅₃₂; strong excitation) to the baseline while PH-Ω size remained unchanged due to pore closure that prevented exchange of the bleached A532 (caused by strong excitation) with fluorescent A532 in the bath (Figure S3A; STAR Methods) (for details, see Chiang et al., 2014; Zhao et al., 2016).

Resolving Fusion Pore during Vesicle Shrinking or Enlargement

At fusion onset, sampled every 26–300 ms, ~21% of PH-Ω (51 of 236 PH-Ω) showed a Pore_v larger than ~60 nm, our STED resolution (Figures 3D–3H; see Figure S3B for Pore_v measurement). The pore in the remaining PH-Ω could not be resolved, mostly because it was below STED resolution (Shin et al., 2018). The percentage of Pore_v (Pore_v%) for shrink-related fusion (shrink_related fusion), which denotes both shrink fusion (e.g., Figures 3D and 3E) and partial shrink fusion (e.g., Figure 3F), was significantly larger than that for enlarge fusion (e.g., Figure 3H) but not significantly larger than that for same-size fusion (e.g., Figure 3G) (summarized in Figure 3I). Results similar to those in Figure 3I were obtained when pore closure events were excluded (Figure S3C). Thus, fusion pores are larger for shrink_related fusion than enlarge fusion. This finding suggests that shrink_related fusion releases contents faster than enlarge fusion, a conjecture that was experimentally verified, as described in the next section.

We noticed that in 3 of 14 shrink-fusion events with a Pore_v, following substantial shrinking of the Ω-profile so that the width had become smaller than the pore size, the Ω-shape changed into a Λ-shape during the final stages (e.g., Figure 3E). Such Λ-profiles were not observed during shrink fusion with no Pore_v (31 out of 31 events; e.g., Figures 1B–1D). Thus, only ~7% of shrink-fusion events showed a late-stage Λ-profile. These results suggest that as the shrinking Ω-profile approaches the size of its own pore, a conversion to a Λ-profile occurs before finally merging with the flat PM.

Shrink Fusion Releases Contents Much Faster than Enlarge Fusion

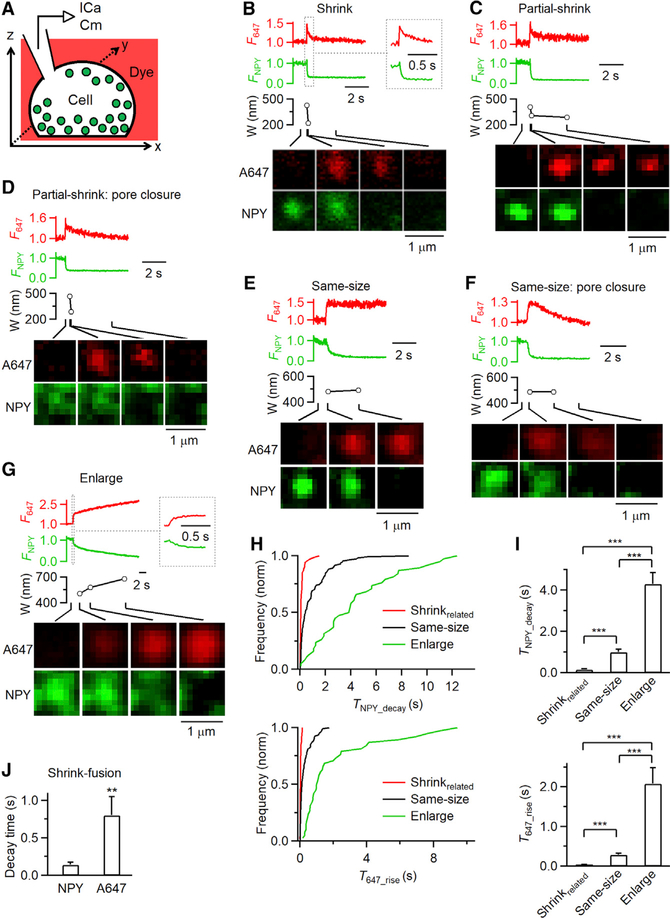
To determine whether shrink fusion and enlarge fusion are associated with different release kinetics, we overexpressed a vesicular lumen protein neuropeptide Y-EGFP (NPY-EGFP) and performed confocal imaging of NPY-EGFP with Alexa Fluor 647 (A647; in the bath) in the xy/z_fix configuration ~200 nm above the cell bottom (Figure 4A). Depol_{1 s} induced NPY-EGFP spot release (218 spots, 28 cells; Figures 4B–4G), accompanied by sudden A647 spot appearance and fluorescence (F₆₄₇) increase due to A647 diffusion from the bath to the fusion-generated Ω-profile (Chiang et al., 2014).

Figure 4. Imaging NPY-EGFP Release and Structural Changes of A647-Labeled Fusing Vesicles.

(A) Schematic drawing of a cell containing NPY-EGFP-labeled vesicles (green) bathed with a solution containing A647 (red).

(B–G) F₆₄₇ (A647 spot fluorescence), F_NPY (NPY-EGFP spot fluorescence), A647 spot width (W; full-width-half-maximum), and A647/NPY-EGFP confocal xy-images at times indicated with lines for various rates of NPY-EGFP release at various fusion modes: (B) shrink fusion (inset shows traces in larger timescale); (C) partial shrink fusion; (D) partial shrink fusion followed by pore closure; (E) same-size fusion; (F) same-size fusion followed by pore closure; and (G) enlarge fusion (inset shows traces in larger timescale).

(H and I) Cumulative frequency (H; normalized) or the mean (I; mean + s.e.m.) of T_{NPY_decay} (20%–80% F_NPY decay time, top) and T_{647_rise} (20%–80% F₆₄₇ rise time, bottom) for shrink_related fusion (69 events, 28 cells), same-size fusion (111 events, 28 cells), and enlarge fusion (38 events, 28 cells). ***p < 0.001, ANOVA test.

(J) 20%–80% decay time of NPY-EGFP (T_{NPY_decay}) and A647 fluorescence during shrink fusion (mean + SEM, 41 events). A647 fluorescence decay was measured after the peak was reached. **p < 0.01, t test.

See also Figure S4.

Under strong excitation, we observed four distinct patterns of evolution of A647 spots (218 spots, 28 cells) (see Chiang et al., 2014 for systematic characterizations). First, shrink fusion was reflected as A647 spot width shrinking until it was undetectable while F₆₄₇ decayed to the baseline (Figure 4B; 41 events). Second, the A647 spot width could shrink partially with partial F₆₄₇ decrease and then maintain a spot of reduced size, which reflected partial shrink fusion (Figures 4C and 4D; 28 events). The reduced-size spot was sometimes followed by spot F₆₄₇ decay to baseline while the spot size did not change further, reflecting pore closure that prevented exchange of bleached A647 in the spot with fluorescent A647 in the bath (partial shrink fusion with pore closure; Figure 4D) (Chiang et al., 2014). Third, A647 spot size and F₆₄₇ could remain unchanged (same-size fusion; Figure 4E; 111 events), sometimes followed by F₆₄₇ decay to baseline without spot size change (same-size fusion with pore closure; Figure 4F). Fourth, spot width and F₆₄₇ could increase (enlarge fusion; Figure 4G; 38 events), occasionally followed by spot F₆₄₇ decay to baseline without further change in spot size (enlarge fusion with pore closure; not shown). Consistent with STED xy/z_fix imaging (Figure S3A), we used these A647 spot behaviors to identify shrink fusion, partial shrink fusion, same-size fusion, and enlarge fusion (for detail, see Chiang et al., 2014).

The percentages of shrink fusion (19% ± 4%, n = 28 cells) and enlarge fusion (17% ± 5%, n = 28 cells) were not significantly different compared to those without NPY-EGFP overexpression (shrink fusion: 18% ± 3%; enlarge fusion: 10% ± 2%, n = 60 cells). Thus, NPY-EGFP overexpression is not crucial in determining whether a vesicle undergoes shrink or enlarge fusion.

NPY-EGFP release was detected as decay of NPY-EGFP fluorescence (F_NPY; Figures 4B–4G) (Taraska et al., 2003; Perrais et al., 2004). The F_NPY 20%–80% decay time (T_{NPY_decay}) ranged from 12 ms to 12 s, in most cases less than ~2 s. Of 218 spots, 6 did not release or else partially released NPY-EGFP due either to rapid pore closure (5 out of 95 pore closure events) or to a narrow pore (1 out of 82 same-size fusion or enlarge fusion without pore closure) (Shin et al., 2018). These 6 events were excluded from further analysis.

T_{NPY_decay} for shrink_related fusion was much shorter than that for same-size fusion, whereas enlarge fusion showed a much longer T_{NPY_decay} than that of either same-size fusion or shrink_related fusion (Figures 4H and 4I, top; 212 events, 28 cells). Similar results were obtained when pore closure events were excluded (Figures S4A and S4B; 122 events, 28 cells), or partial shrink fusion was excluded from shrink_related fusion (Figures S4C and S4D). Thus, shrink_related fusion and enlarge fusion are associated with faster and slower content release, respectively.

STED xz/y_fix imaging of FFN511 release further confirmed that shrink_related fusion and enlarge fusion are associated with faster and slower content release, respectively. The 20%–80% decay time of FFN511 (T_{FFN_decay}) during shrink_related fusion, as observed with STED xz/y_fix imaging, was much shorter than that for same-size fusion, whereas enlarge fusion observed with STED xz/y_fix imaging showed the longest T_{FFN_decay} (e.g., Figures 2B–2E, summarized in Figure 2F; 92 events, 71 cells). These results were analogous to different T_{NPY_decay} observed during shrink_related, same-size, and enlarge fusion (Figure 4I).

Three sets of evidence suggest that to facilitate content release, shrink_related fusion employs a larger fusion pore than enlarge fusion. First, as mentioned above, Pore_v% of shrink_related fusion was significantly larger than that of enlarge fusion (Figure 3I). Second, release of either NPY-EGPF or FFN511 was fastest for shrink_related fusion, slower for same-size fusion, and the slowest for enlarge fusion (Figures 2F and 4I, top), supporting that these different release time courses are controlled by the fusion pore size differences. Third, the F₆₄₇ 20%–80% rise time (T_{647_rise}) was shortest for shrink_related fusion, significantly longer for same-size fusion, and longest for enlarge fusion (Figures 4H and 4I, bottom), mirroring the order of the respective T_{NPY_decay} values for the three classes of events (Figures 4H and 4I, top). The same order for the time course of content release and A647 entry into the fusing vesicle further suggests that this order reflects the fusion pore size differences.

Both T_{NPY_decay} and T_{647_rise} were shorter for shrink_related fusion than for same-size fusion (Figures 4H and 4I), suggesting that shrink_related fusion employs a larger fusion pore than same-size fusion. We could not detect a difference in Pore_v% values for shrink_related fusion and same-size fusion (Figure 3I), likely due to our limited STED resolution (~60 nm). Although shrink fusion was associated with fast NPY release, shrinking was apparently not the cause of this fast release, because NPY release time, T_{NPY_decay} (0.14 ± 0.03 s, n = 41), was much faster than the time for the vesicle to shrink, the 20%–80% decay time of F₆₄₇ during shrink fusion (0.80 ± 0.25 s, n = 41, t test, p < 0.01; e.g., Figure 4B, summarized in Figure 4J).

Mechanisms Underlying Shrink Fusion

What mechanism leads to shrink fusion, and why is this pathway preferred to the full-collapse pathway envisaged in the classical picture? To address this, we mathematically modeled the merging of a fused vesicle with the chromaffin cell PM (Figure 5A; STAR Methods, Mathematical modeling) and verified the model’s predictions with experimental data.

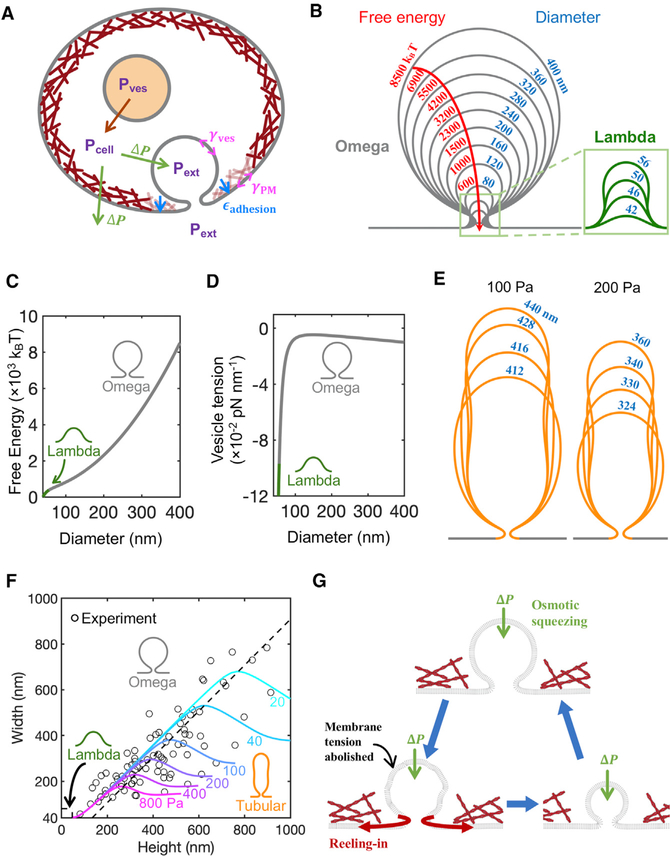
Figure 5. Mathematical Model of Vesicle Evolution during Exocytosis.

(A) Schematic of the model (not to scale). Cells maintain an outward (swelling) osmotic pressure ΔP=P_{cell –} P_ext (green arrows), with cell pressure P_cell exceeding extracellular pressure P_ext. Intact vesicles maintain swelling pressure (red arrow), with vesicle pressure P_ves >P_cell. Following fusion with PM, rapid equilibration between the vesicle lumen and extracellular medium is assumed, so P_ves =P_ext. The vesicle osmotic pressure then equals ΔP but is now an inward squeezing pressure. The model calculates the vesicle tension, γ_ves, while the PM tension, γ_PM, and the adhesion energy ε_adhesion to the actin cortex (maroon layer adjacent to PM) are taken from experiment (see Table 1).

(B) Predicted shrink fusion sequence. Computed vesicle shapes and free energies for squeezing pressure ΔP = 100 Pa and the indicated effective diameters D (such that vesicle area equals πD2). A transition occurs at D = 56 nm from Ω to Λ shape (defined as a profile lacking overhang).

(C and D) Free energy (C) and vesicle membrane tension (D) plotted versus diameter for the vesicles in (B).

(E) Predicted tubular shapes for two squeezingpressures (100 or 200 Pa). Tubular vesicles are predicted for large squeezing pressure or large vesicle area.

(F) Three classes of vesicle shape are predicted (Ω, tubular, and Λ), each corresponding to one sector in the vesicle width-height plane. Predicted isobars are shown for the indicated osmotic squeezing pressures. The EM data of Figure 3C are also plotted. Each experimental point belongs to one isobar, representing the predicted squeezing pressure for the observed vesicle.

(G) Shrink fusion mechanism predicted by themodel. Osmotic squeezing deflates the vesicle and abolishes its membrane tension, so the membrane is reeled into the PM by the PM tension and PM adhesion to the actin cortex.

See also Figure S5

The vesicle membrane is treated as a continuous surface, with bending and osmotic pressure energy contributions following the well-established Helfrich theory (Helfrich, 1973). The membrane connects to the PM in a small area assumed free of actin cortex (Table 1; Figure 5A), and elsewhere, the PM is assumed adhered to the actin cortex, likely via actin-binding transmembrane and membrane-associated proteins (Dai and Sheetz, 1999; Borghi and Brochard-Wyart, 2007; Porat-Shliom et al., 2013; Wen et al., 2016; Shi et al., 2018). Using a method similar to a previous study (Jenkins, 1977), we obtained differential equations whose solution yielded the minimum energy shape and volume (see STAR Methods, Mathematical modeling). All model parameters were fixed by experiment, either from the present study or published data (Table 1).

Table 1.

Model Parameters

Symbol	Meaning	Value	Reference
κ	membrane bending modulus	20 kBT	Rawicz et al., 2000
w	diameter of actin cortex-free zone	80 nm	Figure 3Aa
γPM	PM tension	0.04 pN nm−1	Tinevez et al., 2009
εadhesion	membrane-cortex adhesion energy density	0.02 pN nm−1	Dai and Sheetz, 1999

^aModel solutions with w = 80 nm had ∼30-nm-diameter fusion pores, consistent with the experimental Ω-shapes of Figure 3A. The solutions exhibited a Ω-to-Λ transition at vesicle diameter 56 nm (slightly less than the STED resolution limit), consistent with the finding that 93% of shrink fusion events lacked a visible Λ-sequence in STED measurements.

A key model assumption is that during shrink fusion, the vesicle and extracellular pressures are equal, because fusion pores are large enough to allow rapid pressure equilibration, unhindered by vesicular lumen contents (Figure 5A). Several observations support this assumption. First, ~26% of shrink-fusion events involved pores >60 nm (Figure 3I). Second, shrink-fusion events permitted rapid ~0.14 s release of the ~4 nm NPY-EGFP (Palm et al., 1997) (Figure 4J), which is much faster than the Ω-profile shrinking time (~0.80 s, Figure 4J, p < 0.01). Thus, content release precedes Ω-profile shrinking. Consistent with this, chromogranin A, a major vesicular matrix component, was released in ~0.1 s during high potassium application (Abbineni et al., 2019), which might induce mostly shrink fusion (Wen et al., 2016). Once the contents are gone, pressure equilibration is almost instantaneous; even for a small 4-nm-diameter pore, we estimate unhindered pressure equilibration requires only milliseconds (see STAR Methods, Mathematical modeling).

Pressure equalization has significant consequences; since cells maintain a swelling osmotic pressure (ΔP = intracellular osmotic pressure – extracellular osmotic pressure) (Stewart et al., 2011), it follows that the fused vesicle experiences a squeezing osmotic pressure, ΔP, equal to the cell swelling pressure but acting in reverse (Figure 5A). Computed shapes are shown in Figure 5B for a typical squeezing pressure of ΔP = 100 Pa and vesicle sizes up to effective diameter D = 400 nm, typical for shrink-fusion onset. The sequence follows a shrink-fusion trajectory of mildly prolate Ω-shapes, with height/width ratios of ~1.2–1.5, which is close to our EM measurements (Figure 3C).

We calculated the free energies of the vesicle states in Figure 5B and found the free energy monotonically decreased with decreasing vesicle size, demonstrating that the shrink-fusion trajectory is indeed selected (Figures 5B and 5C; STAR Methods, Mathematical modeling). The decrease originated in the osmotic squeezing force, which deflated the vesicle and abolished its tension to negative values (Figures 5D and S5A). Thus, a powerful membrane tension gradient reels in membrane, from the tensionless vesicle into the PM, driven by the PM tension and the PM-actin cortex adhesion forces (Figure 5G). For a membrane area ΔA reeled onto the PM, we find a free energy decrease ΔF = −(ε_adhesion + γ_{PM −} γ_ves) ΔA, where ε_adhesion, γ_PM, γ_ves are the membrane-cytoskeleton adhesion energy, the PM tension, and the vesicle membrane tension, respectively (STAR Methods, Mathematical modeling).

In the late stages of the shrink-fusion sequence (Figure 5B), the model generated Λ shapes similar to those in STED images (Figure 3E). The Ω→Λ shape transition depended on the diameter w of the actin cortex-free zone where the vesicle joins the PM (Figure 5A). For example, if w = 80 nm, Ω→Λ transition occurred as vesicle diameter D shrank to ~56 nm (Figure 5B); the transition was delayed to D = 14 nm if w = 20 nm (Figures S5B–S5F). The merging of a Λ-shaped membrane with the PM is a full-collapse subsequence; thus, full-collapse shapes are realized only in the latest stages of the trajectory.

From the computed shapes (Figure 5B), we measured pore diameters, defined as the minimum width near the PM for Ω shapes, or the vesicle width at a fixed height for Λ shapes (Figure S5F). Down to a height of ~200 nm in the shrink-fusion sequence of Figure 5B, the pore size increases gradually from 16 to 23 nm and then increases more sharply to 42 nm before decreasing to zero during the Λ-shape sequence as the vesicle flattens into the PM (Figure S5F). The qualitative behavior is similar for larger diameters of the actin cortex-free zone w, but with somewhat larger pores (Figures S5B–S5F). These pore size changes were not observed with STED imaging, likely in part due to limited STED resolution. When PH-Ω’s pore was detected with STED microscopy, Pore_v often constricted during shrink_related fusion (Figures 3D–3F). This was likely due to dynamin-mediated constriction of the fusion pore, as recently reported (Shin et al., 2018), and/or changes in w during shrink fusion, both of which are beyond the scope of the present model, which focused on modeling shrinking of the entire Ω-profile.

For even larger vesicles (e.g., D > 400 nm at ΔP = 100 Pa), the model reproduced the remarkable tubular shapes that we observed in cells, a vivid consequence of squeezing forces (Figure 5E). Tubular vesicles had large height-to-width ratios and widths that decreased with height, asymptoting a pressure-dependent width for large heights (Figure 5F).

Agreeing with experiment, the model identified three vesicle classes: Ω-shaped, tubular-shaped, and Λ-shaped. In Figure 5F, model-predicted isobars (constant ΔP) are plotted in the vesicle height-width plane, together with the EM data of Figure 3C. Each experimental point belongs to one of the three vesicle shape sectors and to a certain isobar, illustrating how measurement of vesicle shape enables the model to predict the squeezing pressure on that vesicle. The data in Figure 5F suggest vesicles in cells were subject to squeezing pressures from ~40 to ~400 Pa.

Four specific model predictions are confirmed by experimental observations, considerably strengthening our model’s conclusions. (1) During shrink fusion, predicted vesicle shapes have mild prolateness (height greater than width) and a late transition to Λ-shape before flattening into the PM (Figure 5B). This is experimentally confirmed (Figures 1 and 3). (2) Tubular shapes are predicted for large squeezing pressures or vesicle size, a vivid manifestation of osmotic squeezing closely related to the spherical-to-prolate first-order transition previously predicted for closed vesicles under high squeezing pressure (Jenkins, 1977). Tubular-shaped vesicles were predicted to be shrinking (Figure 5E), consistent with our observations of large shrinking tubular vesicles (Figures 1 and 3). (3) Lowering the osmotic squeezing driving force by increasing extracellular osmolarity or (4) lowering the reeling-in force by compromising adhesion between the PM and the actin cortex is predicted to reduce the shrink-fusion frequency (Figure 5A). Both predictions were confirmed in a recent study, where increased extracellular osmolarity or inhibition of F-actin by latrunculin A, cytochalasin D, or actin knockout significantly reduced the percentage of shrink fusion detected by confocal imaging of fusion spots (Wen et al., 2016).

DISCUSSION

Recent imaging of dense-core vesicle fusion in chromaffin cells shows that fusion spots may shrink or enlarge in size and that F-actin-dependent PM tension is needed for shrinking (Chiang et al., 2014; Wen et al., 2016). The present work advanced over these studies in three aspects. First, with STED imaging of PH_G-labeled fused vesicular membrane dynamics and the dynamics of FFN511 release from vesicular lumen in chromaffin cells, we directly visualized, and thus verified, two fusion modes associated with size changes: shrink fusion (or shrink_related fusion) and enlarge fusion (Figures 1, 2, and 3). Second, we found that shrink_related fusion is associated with a large pore that promotes rapid content release, whereas enlarge fusion is associated with a narrow pore that slows down content release (Figures 2, 3, and 4). These two fusion modes may contribute to explain diverse release rates reported in decades of studies that had interpreted release under the framework of full-collapse and kiss-and-run fusion modes (Saheki and De Camilli, 2012; Alabi and Tsien, 2013; Wu et al., 2014). Third, we discovered the underlying mechanism of shrink fusion; the swelling osmotic pressure maintained by cells squeezes the Ω-profile and abolishes the Ω-profile membrane tension, producing a tension gradient (from PM to Ω-profile) that reels Ω-profile membrane into the PM (Figure 5). The requirement of the PM-to-Ω-profile tension gradient explains why F-actin-dependent PM tension is needed to mediate shrink fusion, as suggested recently (Wen et al., 2016). The squeezing pressure is equal in magnitude to the swelling osmotic pressure of the cell (Diz-Muñoz et al., 2010; Boulant et al., 2011; Stewart et al., 2011; Tsujita et al., 2015; Wen et al., 2016), once the fused vesicle equilibrates with the extracellular medium (Figure 5A). With squeezing force and membrane-reeling-in force, Ω-profile shrinking is free energetically favored over full collapse (Figures 5, S5G, and S5H), challenging the traditional view that full collapse is the default fusion mode (Alabi and Tsien, 2013; Wu et al., 2014).

Our findings as summarized above, together with a recent finding that most fusion pore closure events (kiss-and-run) on average do not slow down content release (Shin et al., 2018), lead us to suggest that shrink and enlarge fusion are the yin and yang of fusion modes that control the rate of content release. This suggestion challenges the classical view that full collapse and kiss-and-run serve as the yin and yang fusion modes accounting for rapid and slow release observed in endocrine cells and neurons (Saheki and De Camilli, 2012; Alabi and Tsien, 2013; Wu et al., 2014). Decades of studies on the release rates (Saheki and De Camilli, 2012; Alabi and Tsien, 2013; Wu et al., 2014) that interpret exocytosis with the classical view may need to be re-examined with the fusion modes reported here.

Our finding that cells use shrink fusion instead of full collapse to promote content release has broad implications for two reasons. First, swelling osmotic pressure and membrane-actin cortex adhesion, both required for shrink fusion (Figure 5), are general properties of cells (Dai and Sheetz, 1999; Diz-Muñoz et al., 2010; Boulant et al., 2011; Stewart et al., 2011; Tsujita et al., 2015; Wen et al., 2016). Consequently, shrink fusion may serve as the fusion mode that facilitates exocytotic content release in many cell types. Second, shrink fusion may describe exocytosis of various sizes of vesicles, because Ω-profile shrinking was observed down to our STED resolution limit of ~60 nm (Figure 1). A recent study had speculated that as the width of the Ω-profile shrinks to an extent that is smaller than its pore, the Ω-profile may appear as a collapse-like Λ-shaped profile before flattening at the PM (Wen et al., 2016). Modeling and imaging in the present work showed that during the final stage of shrinking, the Ω-profile undergoes a transition to a Λ-profile (Figures 3 and 5). Indeed, such Λ-profiles, observed with EM, are the basis for the full-collapse fusion hypothesis (Heuser and Reese, 1981; Alabi and Tsien, 2013; Wu et al., 2014). Thus, we propose a shrink-collapse fusion mode in which Ω-profile shrinking is followed by a transition to a Λ-profile and then flattening to unify the apparently contradictory observations of shrink fusion and full collapse.

Although vesicles smaller than 60 nm, such as synaptic vesicles (~20–60 nm), are beyond our detection limit, it is likely that these vesicles display shrink collapse, with shrinking as the main component for larger vesicles (near 60 nm) and collapse as the main component for smaller vesicles (near 20 nm). It would be of great interest to verify this possibility in the future. The forces involved in mediating shrink fusion, as described here (Figure 5), could not account for same-size and enlarge fusion. Additional unknown mechanisms must be involved in mediating same-size and enlarge fusion.

The suggestion that shrink and enlarge fusion regulate content release by controlling the fusion pore is further supported by our finding that shrink_related fusion facilitates FFN511 and NPY-EGFP release, whereas enlarge-fusion slows down release of them (Figures 2 and 4). While we emphasized these two fusion modes in controlling fusion pore size and content release rate, other factors may also regulate fusion pore and release. For example, some fusion pore closure events (kiss-and-run) may release only a fraction of large protein molecules, such as NPY-EGFP and tissue plasminogen activator (Taraska et al., 2003; Perrais et al., 2004; Shin et al., 2018), although a large fraction of kiss-and-run events fully release contents (Alés et al., 1999; Shin et al., 2018). Fusion pore dynamics and lifetime are regulated by many factors, such as the vesicular lumen protein NPY, chromogranin A, tissue plasminogen activator, the vesicular membrane protein synaptotagmin, and the GTPase dynamin (Rao et al., 2014; Weiss et al., 2014; Rao et al., 2017; MacDougall et al., 2018; Shin et al., 2018; Abbineni et al., 2019). Whether and how these regulators affect shrink and enlarge fusion are unclear. Consequently, our mathematical model did not include these potential regulators but focused on elucidating the impacts of the biophysical properties of the vesicle and PM on shrink fusion. Although beyond the scope of the present work, it would be of interest to study how shrink and enlarge fusion are regulated by factors known to regulate fusion pore. The present work showed that overexpression of NPY-EGFP does not significantly affect the percentage of shrink and enlarge fusion, ruling out overexpressed NPY-EGFP as a regulator of shrink or enlarge fusion.

Various sizes of Ω-, tubular, and Λ-profiles have been reported in electron microscopy studies (Heuser and Reese, 1973, 1981). The present work revealed that these structures can originate from the dynamic processes of shrink, partial shrink, and enlarge fusion. For example, large Ω-profiles were previously presumed to result from bulk endocytosis, phagocytosis, or compound exocytosis of large vesicles formed by vesicle-vesicle fusion (Saheki and De Camilli, 2012; Wu et al., 2014; Kononenko and Haucke, 2015). We showed that they may alternatively originate from enlarge fusion. Enlarge fusion may not be limited to chromaffin cells; capacitance recordings in mast cells show that the capacitance up-step is sometimes followed by a larger down-step, suggesting that retrieved vesicles can be larger than fused vesicles (Monck et al., 1990). Fusion pore closure after enlarge fusion may thus be a mechanism to generate large endosome-like structures previously attributed to bulk endocytosis. What controls vesicle size is largely unclear; our work suggests that fusion pore closure after partial shrink fusion and enlarge fusion may produce different sizes of vesicles. The origin of tubular membrane structures is unclear and often attributed to bulk endocytosis (Saheki and De Camilli, 2012; Wu et al., 2014; Kononenko and Haucke, 2015). The present work reveals that partial shrink fusion, mediated by the osmotic squeezing forces, may generate tubular membrane shapes. Pore closure of these tubular structures may thus constitute a mechanism to generate tubular vesicles widely observed.

STAR★METHODS

LEAD CONTACT AND MATERIALS AVAILABILITY

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact Ling-Gang Wu (wul@ninds.nih.gov). This study did not generate new unique reagents.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Primary cell culture

Fresh adult (21 – 27 months old) male bovine adrenal glands purchased from a local abattoir (J. W. Treuth and Sons, Inc.) were used to prepare primary chromaffin cell culture, which are widely used for the study of exo- and endocytosis (Wu et al., 2014; Sharma and Lindau, 2018).

METHOD DETAILS

Chromaffin cell culture

We prepared primary bovine adrenal chromaffin cell culture as described previously (Chiang et al., 2014). Fresh adult (21 – 27 months old) bovine adrenal glands (from a local abattoir) were immersed in pre-chilled Locke’s buffer on ice containing: NaCl, 145 mM; KCl, 5.4 mM; Na2HPO4, 2.2 mM; NaH2PO4, 0.9 mM; glucose, 5.6 mM; HEPES, 10 mM (pH 7.3, adjusted with NaOH). Glands were perfused with Locke’s buffer, then infused with Locke’s buffer containing collagenase P (1.5 mg/ml, Roche), trypsin inhibitor (0.325 mg/ml, Sigma) and bovine serum albumin (5 mg/ml, Sigma), and incubated at 37°C for 20 min. The digested medulla was minced in Locke’s buffer, and filtered through a 100 μm nylon mesh. The filtrate was centrifuged (48 xg, 5 min), re-suspended in Locke’s buffer and re-centrifuged until the supernatant was clear. The final cell pellet was re-suspended in pre-warmed DMEM medium (GIBCO) supplemented with 10% fetal bovine serum (GIBCO).

Electroporation and plating

Cells were transfected by electroporation using Basic Primary Neurons Nucleofector Kit (Lonza), according to the manufacturer’s protocol and plated onto glass coverslips with mouse Laminin coating over PDL layer (Neuvitro). The cells were incubated at 37°C with 9% CO2 and used within 5 days.

Plasmids and fluorescent dyes

The PH-EGFP (phospholipase C delta PH domain attached with EGFP) was obtained from Dr. Tamas Balla. NPY-EGFP was purchased from Addgene. PH-mNeonGreen construct was created by replacing the EGFP tag of PH-EGFP with mNeonGreen (Allele Biotechnology) (Shaner et al., 2013). Both PH-EGFP and PH-mNeonGreen are abbreviated as PH_G. For imaging, the dye concentration in the bath solution was: Atto 532 (A532, Sigma), 30 μM; Alexa 647 (A647, Sigma), 30 μM. For FFN511 (Abcam) imaging, cells were bathed with FFN511 (5–10 μM) for 10 min and images were performed after washing out FFN511 in the bath solution.

Overexpression of PH_G or NPY-EGFP did not significantly affect the basic properties of exo- and endocytosis, because 1) whole-cell capacitance measurements and imaging show robust exo- and endocytosis, and similar percentages of close-fusion and non-close-fusion as control (Chiang et al., 2014; Zhao et al., 2016), and 2) Ω-profile’s pore could also be resolved by imaging extracellularly applied mCLING-A488 or by EM (Shin et al., 2018).

Electrophysiology

At room temperature (20 – 22°C), whole-cell voltage-clamp and capacitance recordings were performed with an EPC-10 amplifier together with the software lock-in amplifier (PULSE, HEKA, Lambrecht, Germany) (Lindau and Neher, 1988; Chiang et al., 2014). The holding potential was −80 mV. For capacitance measurements, the frequency of the sinusoidal stimulus was 1000 – 1500 Hz with a peak-to-peak voltage ≤ 50 mV. The bath solution contained 125 mM NaCl, 10 mM glucose, 10 mM HEPES, 5 mM CaCl₂, 1 mM MgCl₂, 4.5 mM KCl, 0.001 mM TTX and 20 mM TEA, pH 7.3 adjusted with NaOH. The pipette (2 – 4 MΩ) solution contained 130 mM Cs-glutamate, 0.5 mM Cs-EGTA, 12 mM NaCl, 30 mM HEPES, 1 mM MgCl₂, 2 mM ATP, and 0.5 mM GTP, pH 7.2 adjusted with CsOH. These solutions pharmacologically isolated calcium currents.

For stimulation, we used a 1 s depolarization from the holding potential of −80 mV to +10 mV (depol_{1 s}). We used this stimulus, because it induces robust exo-endocytosis as reflected in capacitance recordings (Figure 1A) (Engisch and Nowycky, 1998; Perrais et al., 2004; Chiang et al., 2014). In a fraction of experiments during FFN511 imaging, we used 10 pulses of 400-ms depolarization from −80 mV to +10 mV at 2 Hz.

Confocal image acquisition

Imaging with A647 and NPY-EGFP were performed with an inverted confocal microscope (TCS SP5II, Leica, Germany, 100 × oil objective, numerical aperture: 1.4), where A647 (30 μM in bath, Sigma) and NPY-EGFP were excited by a Diode laser at 640 nm (maximum power: 40 mW) and an Argon laser at 488 nm (maximum power: 50 mW), respectively. The 640 nm laser was set at 50% of the maximum power, which could bleach A647 inside the Ω-profile within a few seconds once the Ω-profile closed (Chiang et al., 2014). The 488 nm laser was set at 1.5–2% to avoid significant bleaching of NPY-EGFP. A647 fluorescence was collected with a photomultiplier at 650 – 720 nm, whereas NPY-EGFP, at 498 – 580 nm. Both excitation and fluorescence collection were done simultaneously at the XY/Z_fix scanning mode at the cell bottom (XY-plane with Z focal plane fixed). Confocal imaging area was ~70 – 160 μm2 at the XY plane with a fixed Z axis focal plane ~100–200 nm above the cell-bottom membrane. Images were collected every 10–33 ms at 50 – 70 nm per pixel at the XY/Z_fix scanning mode.

Fusion mode identification during confocal imaging

During confocal imaging of A647 (strong excitation, 50% maximal power) and NPY-EGFP (weak excitation: 1.5%–2% maximal power) at the cell-bottom, we identified fusion modes based on A647 imaging as characterized in detail in the main text (for detail, see Chiang et al., 2014). Upon fusion pore closure, continuous strong excitation of A647 gradually bleached A647 inside the closed Ω-profile, resulting in F₆₄₇ decay to baseline with a time constant of ~2.9 s, during which the spot size remained unchanged (Chiang et al., 2014). Although shrink-fusion also reduced spot F₆₄₇ to baseline, F₆₄₇ decay was generally much faster (time constant: ~1.1 s), and the decay was accompanied by the spot width decrease (Figure 4B) (Chiang et al., 2014).

Pore closure detected with spot F₆₄₇ bleaching by strong excitation is not due to a narrow pore smaller than A532 molecule size, because after spot dimming, bath application of an acid solution cannot quench the pH-sensitive VAMP2-EGFP or VAMP2-pHluorin overexpressed at the same spot, indicating that the spot is impermeable to H+ or OH−, the smallest molecules, and thus is closed (Chiang et al., 2014; Zhao et al., 2016). Furthermore, the closure time course calculated from spot dimming matches approximately with whole-cell endocytosis time course (Chiang et al., 2014), and inhibition of dynamin by dynamin inhibitors, dynamin dominant-negative mutant dynamin 1-K44A or dynamin knockdown blocks not only whole-cell endocytosis but also pore closure detected with the spot dimming method (Chiang et al., 2014; Zhao et al., 2016). These results further confirm that spot dimming under strong excitation reflects pore closure.

STED imaging

STED images were acquired with Leica TCS SP8 STED 3 × microscope that is equipped with a 100 × 1.4 NA HC PL APO CS2 oil immersion objective and operated with the LAS-X imaging software. Excitation was with a tunable white light laser and emission was detected with hybrid detectors. In time-gated STED mode, PH-EGFP and A532 were sequentially excited at 470 and 532 nm, respectively, with the 592 nm STED depletion beam, and their fluorescence collected at 475–525 nm and 540–587 nm, respectively. PH-mNeonGreen and A532 were sequentially excited at 485 and 540 nm, respectively, with the 592 nm STED depletion beam, and their fluorescence collected at 490–530 nm and 545–587 nm, respectively. PH-mNeonGreen and FFN511 were sequentially excited at 505 and 442 nm, respectively, with the 592 nm STED depletion beam, and their fluorescence collected at 510–587 nm and 447–490 nm, respectively.

The excitation power for A532 was 10% of the maximum, at which fluorescent A532 can be bleached within a few seconds. This feature was used to distinguish whether the fusion pore is closed or not, because pore closure prevents bleached A532 (caused by strong excitation) from exchange with fluorescent A532 in the bath, resulting in A532 spot fluorescence decay (Chiang et al., 2014). In contrast, an open pore would not cause A532 spot fluorescence decay, because an open pore allows for continuous exchange of bleached A532 in the Ω-profile with fluorescent A532 in the bath (Chiang et al., 2014).

STED imaging generally causes more photobleaching and phototoxicity. Severe phototoxicity could cause loss of the whole-cell giga seal during patch-clamp recording (Chiang et al., 2014). We avoided severe phototoxicity by applying only one depol_{1 s} and imaging for only ~30–40 s per cell. With this setting, we have not noticed significant differences in the exo- and endocytosis properties obtained under confocal and STED imaging conditions (Chiang et al., 2014; Zhao et al., 2016). For imaging of PH_G and A532, continuous exchange of bleached PH_G or A532 with fluorescent ones from non-imaging areas lessened the photobleaching problem.

STED scanning modes

STED images were acquired at the cell bottom with the XZ (perpendicular to the coverslip) scanning mode with the y axis focal plane fixed at about the cell center (Figure 1A, XZ/Y_fix scanning mode), at which images were acquired every 26–300 ms at 15 nm per pixel in an XZ area of 19.4 μm x 0.7–1.5 μm (Shin et al., 2018). We used 300 ms per XZ frame at the beginning of this project, but used 26–100 ms as we realized the importance of catching fast events with fast imaging rates.

The STED resolution for imaging PH_G (PH-EGFP or PH-mNeonGreen) in our conditions was ~60 nm on the microscopic X- and y axis (parallel to cell-bottom membrane or coverslip), and ~150–200 nm on the microscopic Z axis. We observed on average about 0.2 PH-Ω-profile with clear outline per XZ/Y_fix scan after depol_{1 s}. STED images were deconvolved using Huygens software (Scientific Volume Imaging).

Electron microscopy

Bovine chromaffin cells were stimulated for 90 s using a solution containing 70 mM KCl, 60 mM NaCl, 10 mM glucose, 10 mM HEPES, 2 mM CaCl₂, and 1 mM MgCl₂ (pH 7.3). The cells were then immediately fixed with 2% glutaraldehyde, 2% paraformaldehyde and 4% tannic acid in 0.1 M cacodylate buffer (pH 7.4) solution for 15 min, followed by the same fixative without tannic acid for additional 15 min. The cells were washed first with a solution of 100 mM glycine in 0.1 M sodium cacodylate buffer for 1 min at room temperature, and then with 0.1 M sodium cacodylate. After post-fixation in 1% OsO₄ for 1 h on ice, the samples were dehydrated in ethanol series. During dehydration the specimens were stained with 2% uranyl acetate in 70% ethanol for 30 min following 70% ethanol step. All preparations were embedding in Embed-812 resin (EMS). 70–90 nm ultrathin sections were cut in an ultramicrotome with Diamond knife (Diatome). The sections were placed onto pioloform-coated 200 mesh grids. Images were collected at up to 73,000x magnification in a JEOL JEM-200CX transmission electron microscope (voltage used 120kV) equipped with an AMT XR-100 CCD camera.

Mathematical modeling

Estimating pressure equilibration time

We estimate here an upper bound of the time required, during shrink fusion, for the pressure inside the fused vesicle to decrease and become equal to the extracellular pressure. The equilibration is assumed unhindered by vesicular contents, which are assumed released before shrink fusion commences (see main text). During this equilibration, a small volume of fluid flows out of the vesicle and the membrane tension of the fused vesicle decreases simultaneously. This tension change is due to an increase in lipid density at a constant number of lipids, as lipid flow from the vesicle to the plasma membrane is much slower than the flow of the content fluid (Shi et al., 2018). We calculate the timescale of tension relaxation below, which is the same as the timescale for pressure relaxation as the two are related according to Laplace’s law.

We first estimate the volume change ΔV_ves needed to let the vesicle membrane tension relax to zero. We assume a linear stress-strain relation for the membrane tension (Hochmuth et al., 1973):

$$\mathrm{\Delta }\gamma =-\frac{E_{\text{m}}\mathrm{\Delta }\rho }{{\rho }_0},$$

where E_m is the area expansion modulus of the vesicle membrane and ρ₀ is the lipid density under zero tension.

We assume the total number of lipids does not change as stated earlier, so the area of the membrane is inversely proportional to lipid density. Then the area change is given by ΔA_ves = − A_iΔγ/E_m, where A_i is the initial membrane area. For simplicity we assume the vesicle remains a sphere, so the corresponding change in volume ΔV_ves to completely abolish the tension is given by

$$\mathrm{\Delta }{V}_{\text{ves}}=\frac{\pi D_{\text{i}}^3{\gamma }_{\text{i}}}{2E_{\text{m}}},$$

where D_i is the initial vesicle diameter and γ_i the pre-fusion vesicle tension. This volume change is relatively small compared to the initial vesicle volume V_i as ΔV_ves/V_i≈γ_i/E_m ≪ 1.

The flux Q of the content fluid through a fusion pore with a diameter D_pore is given by $Q\sim D_{\text{pore}}^2\overline{v}$, where $\overline{v}$ is the mean vertical velocity across the cross-section of the fusion pore. This flux is caused by the high initial vesicle pressure ΔP_i, set by initial tension γ_i following Laplace’s law ΔP_i = 4γ_i=D_i. The mean velocity $\overline{v}$ is estimated by the Stokes equation (ignoring inertial terms) $\eta \overline{v}/D_{\text{pore}}\sim \mathrm{\Delta }{P}_{\mathrm{i}}$, where η is the viscosity of the content fluid. Thus, the flux is given by

$$Q\sim \frac{\mathrm{\Delta }{P}_{\mathrm{i}}{D}_{\text{pore}}^3}{\eta }$$

The pressure relaxation time τ_relax is given by

$${\tau }_{\text{relax}}\sim \frac{\mathrm{\Delta }{V}_{\text{ves}}}{Q}\sim \frac{D_{\text{i}}^4\eta }{E_{\text{m}}{D}_{\text{pore}}^3}.$$

We use the following parameter values from experiment: D_i = 350 nm, the mean diameter of large dense-core vesicles in chromaffin cells (Plattner et al., 1997); η = 1.1 cP, the measured cytoplasmic viscosity in fibroblast cells (Bicknese et al., 1993); and E_m = 250 pN nm⁻¹, measured expansion modulus of phosphatidylcholine bilayers (Rawicz et al., 2000). For a relaxation time of ~1 ms, D_pore ~4 nm. This is an upper bound for the relaxation time as larger pores have been observed (Figure 3D). These have much smaller relaxation times as ${\tau }_{\text{relax}}\sim D_{\text{pore}}^{-3}$.

Calculation of fused vesicle shapes

Our procedure yields the shape of a fused vesicle corresponding to an area A_ves, an actin cortex-free zone of diameter w, and a squeezing pressure ΔP (Table 1). Such a shape has a local balance of forces and moments, which are produced by osmotic pressure ΔP, membrane tension γ_ves, and force q that arises from membrane bending. The membrane bending energy is given by $F_{\text{bend}}=\kappa /2\int {(2H)}^{2}dS$ (the integral is over the entire surface of the vesicle) (Helfrich, 1973), where k is the bending modulus and H is the mean curvature. These force and moment balance equations stated below were derived by Jenkins (1977).

We assume the vesicle shape is axisymmetric with the vertical axis being the symmetry axis. We numerically solve a system of six first order equations for the height coordinate z, the cross-sectional radius r, the angle between the tangent plane and the z axis ϕ, mean curvature H, force that arises from bending q, and membrane tension γ_ves. All the six variables (except ϕ) as well as the parameter ΔP are nondimensionalized as

$$\tilde{r}=r{R}_{\text{ves}}^{-1},\tilde{z}=z{R}_{\text{ves}}^{-1},\tilde{H}=H{R}_{\text{ves}},\tilde{q}=q{(2\kappa )}^{-1}{R}_{\text{ves}},$$

$$\tilde{\gamma }={\gamma }_{\text{ves}}{(2\kappa )}^{-1}{R}_{\text{ves}}^2,\tilde{p}=\mathrm{\Delta }P{(2\kappa )}^{-1}{R}_{\text{ves}}^3,$$

where $R_{\text{ves}}=\sqrt{A_{\text{ves}}/4\pi }$. These quantities are obtained as a function of an angle S as defined by Jenkins (Jenkins, 1977), which ranges from 0 to π, where S = 0 and π denote the top and the bottom of the fused vesicle respectively (the vesicle membrane joins the cytoskeleton-attached plasma membrane at the bottom). The six first order equations are

$$\frac{d\tilde{r}}{dS}=\frac{sinS}{\tilde{r}}sin\varphi$$

$$\frac{d\tilde{z}}{dS}=-\frac{sinS}{\tilde{r}}cos\varphi$$

$$\frac{d\varphi }{dS}=\frac{2sinS}{\tilde{r}}\tilde{H}+\frac{sinS}{{\tilde{r}}^2}cos\varphi$$

$$\frac{d\tilde{H}}{dS}=\frac{sinS}{{\tilde{r}}^2}\tilde{q}$$

$$\frac{d\tilde{q}}{dS}=-\tilde{p}sinS-2\tilde{H}sinS\left(\tilde{\gamma }+{\tilde{H}}^2+\frac{cos\varphi }{\tilde{r}}\left(2\tilde{H}+\frac{cos\varphi }{\tilde{r}}\right)\right)$$

$$\frac{d\tilde{\gamma }}{dS}=0$$

for 0≤S≤π. Of the following six boundary conditions, the first is vanishing force at $r^{\sim }=0$ and the others are geometric constraints.

$$\tilde{q}(0)=0,\varphi (0)=\varphi (\pi )=\frac{\pi }{2},\tilde{r}(0)=0,\tilde{r}(\pi )=\frac{\tilde{w}}{2},\tilde{z}(\pi )=0,$$

Here, $\tilde{w}=W/R_{\text{ves}}$ is the normalized diameter of the cortex-free zone.

These differential equations are solved using the solver ‘bvp4c’ in MATLAB® using an absolute error tolerance of 10⁻⁴ and a relative error tolerance of 10⁻² (MathWorks, Natick, MA). We get the sequence of shapes and tensions along one isobar by solving these equations for different R_ves values, and by repeating this procedure for different ΔP values, several isobars were achieved (Figure 5F). For one isobar, the vesicle adopts Ω shapes for small sizes and tubular ones for large sizes. The Ω-tubular boundary is defined as points where the vesicle width is a maximum for a given pressure value (Figure 5F, dashed line).

Evaluation of free energy changes

We estimate the free energy change during shrink-fusion using the shapes and tensions of a fused vesicle at a constant squeezing pressure calculated as described above. For each shape which has area A_ves and volume V_ves, the squeezing pressure ΔP = P_cell − P_ves and the vesicle membrane tension γ_ves are related to partial derivatives of the membrane bending energy F_bend (Seifert et al., 1991),

$$\mathrm{\Delta }P=-{\frac{\partial F_{\text{bend}}}{\partial V_{\text{ves}}}|}_{A_{\text{ves}}}$$

$${\gamma }_{\text{ves}}=-{\frac{\partial F_{\text{bend}}}{\partial A_{\text{ves}}}|}_{V_{\text{ves}}}.$$

The evaluation of the free energy change during shrink-fusion involves not only the membrane bending energy F_bend, but also the contribution from the vesicle interior (whose free energy is denoted as $F_{\text{ves}}^{\text{i}}$), the cell interior $(F_{\text{cell}}^{\text{i}})$, and the cell membrane $(F_{\text{cell}}^{\text{m}})$. The total free energy F is the sum of the above four free energies, given by

$$F=F_{\text{ves}}^{\text{i}}\left(V_{\text{ves}}\right)+F_{\text{bend}}\left(A_{\text{ves}},V_{\text{ves}}\right)+F_{\text{cell}}^{\text{i}}\left(V_{\text{cell}}\right)+F_{\text{cell}}^{\text{m}}\left(A_{\text{cell}}\right),$$

where V_cell is the cell volume and A_cell is the cell membrane area. We assume the chemical potential of the content molecules is the same between the vesicle and the extracellular solution, hence their free energy does not appear in F. The differential of F is given by

$$dF=\frac{\partial F_{\mathrm{ves}}^{\mathrm{i}}}{\partial V_{\text{ves}}}d{V}_{\text{ves}}+\frac{\partial F_{\text{bend}}}{\partial V_{\text{ves}}}d{V}_{\text{ves}}+\frac{\partial F_{\text{bend}}}{\partial A_{\text{ves}}}d{A}_{\text{ves}}+\frac{\partial F_{\mathrm{cell}}^{\mathrm{i}}}{\partial V_{\text{cell}}}d{V}_{\text{cell}}+\frac{d{F}_{\mathrm{cell}}^{\mathrm{m}}}{d{A}_{\text{cell}}}d{A}_{\text{cell}}=-P_{\text{ves}}d{V}_{\text{ves}}-\mathrm{\Delta }Pd{V}_{\text{ves}}-{\gamma }_{\text{ves}}d{A}_{\text{ves}}-P_{\text{cell}}d{V}_{\text{cell}}-\gamma d{A}_{\text{cell}},$$

where γ is the sum of plasma membrane tension γ_PM and membrane-cortex adhesion energy density ε_adhesion (Table 1).

As total fluid volume and membrane area are conserved, dV_ves + dV_cell = 0 and dA_ves + dA_cell = 0. Thus, the above equation can be simplified as

$$dF=\left({\gamma }_{\text{PM}}+{\epsilon }_{\text{adhesion}}-{\gamma }_{\text{ves}}\right)d{A}_{\text{ves}}.$$

Integrating, we get the free energy of a fused vesicle with area A

$$F(A)=\underset{A0}{\overset{A}{\int }}\left({\gamma }_{\text{PM}}+{\epsilon }_{\text{adhesion}}-{\gamma }_{\text{ves}}\right)d{A}_{\text{ves}}.$$

The reference area A₀ is πD₀2 where D₀ = 42 nm. We numerically calculated the free energy change as shown in Figure 5C using the above equation with the equilibrated vesicle shapes and tensions γ_ves calculated as described before at a constant squeezing pressure ΔP = 100 Pa.

Free energy landscape of fusion pore dilation

We developed a Monte Carlo (MC) method to calculate the minimum energy shapes of vesicles with a fixed pore diameter, which allows determination of free energy landscape of fusion pore expansion by measuring the forces to expand or constrain the fusion pore. The contour of the axially symmetric vesicle is described by a function r(z) (r and z are defined same as in the previous section) and discretized into N points ((z_i,r_i), i = 1, 2, …N) which are uniformly distributed along the z axis. The MC method seeks the shape that minimizes the vesicle free energy

$$F_{\text{ves}}=F_{\text{bend}}+V_{\text{ves}}\mathrm{\Delta }P+\frac{k_{\text{membrane}}}{2}{\left(A_{\text{ves}}-A_{\text{ves}}^0\right)}^2+\frac{k_{\text{pore}}}{2}{\left(d_{\text{pore}}-d_{\text{pore}}^0\right)}^2,$$

where two quadratic terms serve to constrain the vesicle membrane area A_ves and fusion pore diameter d_pore to their set values $A_{\text{ves}}^0$ and $d_{\text{pore}}^0$ (F_bend, V_ves and ΔP are defined same as in the previous section). The vesicle membrane tension is given by ${\gamma }_{\text{ves}}=k_{\text{membrane}}\left(A_{\text{ves}}-A_{\text{ves}}^0\right)$ and the force to constrain the fusion pore $f_{\text{pore}}=k_{\text{pore}}\left(d_{\text{pore}}-d_{\text{pore}}^0\right)$, which are obtained from partial derivatives of F_bend. As one expands the fusion pore, the variation of the free energy of the vesicle with respect to fusion pore diameter d is given by

$$F_{\text{expansion}}(d)=\underset{d0}{\overset{d}{\int }}-f_{\text{pore}}d\left(d_{\text{pore}}\right),$$

where d₀ is the fusion pore diameter of the reference state.

The simulation investigates the free energy landscape of fusion pore expansion of a fused vesicle with effective diameter D = 200 nm (A_ves = πD²) with subject to a squeezing pressure ΔP = 100 Pa, and the reference state is d_pore = 6 nm. The vesicle contour is discretised into N = 401 points. To ensure the calculated vesicle area and fusion pore diameter fall within ± 1% of the set value, k_membrane = 4 ×10⁻⁶ pN nm⁻³ and k_pore = 10³ pN nm⁻¹ were chosen. The simulation runs at zero temperature and a move that generates a new shape will be accepted only if it leads to a lower free energy F_ves. Each move is either a local radial change (neighboring r_i) with a maximum displacement of 10⁻⁴ nm or a change in vesicle height of 10⁻⁴ nm (all z_i scale with the same factor). All the simulations are equilibrated after 2×10⁸ MC steps as in the final 2×10⁷ steps F_ves only decreases by ~0.05 k_BT.

QUANTIFICATION AND STATISTICAL ANALYSIS

Data selection

For every cell recorded with a pipette under the whole-cell configuration, the data within the first 2 min at the whole-cell configuration were used, which avoided rundown of endocytosis (gradual disappearance of endocytosis) as previously reported under the whole-cell configuration for a long time (Smith and Neher, 1997; Chiang et al., 2014). Cells expressed with PH_G (or PH-mCherry) were used for visualization of PH-Ω. The criteria for selecting PH-Ωs for analysis during XZ/Y_fix scanning are described in Figure S2 of Shin et al., 2018.

Visible pores of PH-Ω (Pore_v) containing A532 at the XZ frame are identified based on two criteria: 1) the Ω-profile pore is visible as judged by eyes and A532 spot is inside the Ω-profile, and 2) the F_PH line profile across the pore region shows a V-shape valley with an amplitude at least three times larger than the standard deviation of the same F_PH line profile before fusion (for detail, see Shin et al., 2018).

Analysis of PH-Ω structural changes

STED images of PH-Ω were analyzed with ImageJ and LAS X (Leica). While Ω-profiles labeled with PH_G, but filled with no A532 may appear due to hemi-fusion (Zhao et al., 2016), we only analyzed Ω-profiles labeled with PH and filled with A532 throughout the work.

During XZ/Y_fix scanning, some depol_{1 s}-induced PH-Ω-profiles were out of the Y_fix focal plane, as the outline of the Ω-profile was vague or unclear (for detail, see Shin et al., 2018). These out-of-focus Ω-profiles were not included for analysis. The criteria for the selection of the Ω-profile are described in detail in Figure S2 of Shin et al., 2018. PH-Ω’s width and height were measured as described in Figure S1C of the present work.

Pores labeled with PH_G were identified based on the image and the fluorescence intensity line profile. We first identified the fluorescently labeled Ω-profiles with an open pore, the edge of which was continuous with the plasma membrane. The intensity line profile in the pore region should show a valley with a peak at least three times larger than the baseline fluctuation (standard deviation) in the non-pore region (for detail, see Shin et al., 2018). The full-width-half-maximum of the valley of the intensity line profile across the pore (Figure S3B) was proportional to the pore diameter, as shown with simulation (Shin et al., 2018). Thus, this method was used for pore size measurements.

The percentage of Pore_v was calculated as the number of PH-Ω showing a Pore_v divided by the total number of PH-Ω induced by a depol_{1 s} during a XZ/Y_fix scanning (~30–40 s) in each cell. Normally we observed 0 or 1 PH-Ω per cell during a XZ/Y_fix scanning. Occasionally, we observed 2 PH-Ω. Thus, the percentage of Pore_v in a recorded cell was either 0%, 50% or 100%. These individual values were averaged to obtain the mean ± s.e.m. for the percentage of Pore_v.

During XZ/Y_fix imaging, A532 was excited at a high laser power so that fluorescent A532 can be bleached with a time constant of 1.5–3.5 s. Pore closure was identified as the gradual dimming of the A532 spot fluorescence to baseline during XZ/Y_fix PH_G/A532 imaging while PH_G image remained unchanged or dimmed gradually without changing the PH-Ω size (Figure S3A) (Shin et al., 2018).

Our STED XZ/Y_fix sampling was 26–300 ms per frame. The width of the PH-mNG-labeled Ω-profile could be measured within 50–300 ms after fusion. Thus, we measured the PH-mNG-labeled Ω-profile’s width from 50–300 ms after the fusion onset to 20–30 s afterward. If the width was increased by more than 15% within the recording time period (~20–30 s), it was defined as the enlarge-fusion mode.

Confocal image analysis

Confocal images were analyzed with ImageJ and LAS X (Leica). The fluorescence intensity from an area covering the fluorescence spot was measured at every image frame. The spot width was measured as the full-width-half-maximum from intensity profiles of 1 – 4 lines across the spot center. The time course of NPY-EGFP release was quantified as the time the NPY-EGFP spot fluorescence decayed from 20% to 80% of the maximal decrease (T_{NPY_decay}). Similarly, the 20%–80% risetime of A647 spot fluorescence (T_{647_rise}) was quantified; the 20%–80% decay time of A647 spot fluorescence during shrink-fusion was quantified after A647 spot fluorescence reached the peak.

Statistical tests

Data were expressed as mean ± s.e.m. Replicates are indicated in results and figure legends. N represents the number of cells, pores, or Ω-profiles as indicated in results and figure legends. The statistical test used is t test or ANOVA. Although the statistics were performed based on the number of cells or pores, and Ω-profiles, each group of data was collected from at least four primary chromaffin cell cultures. Each culture was from at least two glands from one bovine.

DATA AND CODE AVAILABILITY

All experimental data produced for this manuscript are available from the Lead Contact (wul@ninds.nih.gov) upon reasonable request. All data and code for the computational analysis are available from the corresponding author (bo8@columbia.edu) upon reasonable request.

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, Peptides, and Recombinant Proteins
DMEM medium	GIBCO	Cat#11885092
Fetal bovine serum	GIBCO	Cat#10082147
German glass coverslips with mouse Laminin coating over PDL layer	Neuvitro	GG-25-Laminin
Atto 532	Sigma	88793
Alexa 647	Sigma	A20502
Trypsin inhibitor	Sigma	T9253; CAS: 9035-81-8
Bovine serum albumin	Sigma	A2153; CAS: 9048-46-8
Embed-812	EMS	Cat#13940
Collagenase P	Sigma	COLLP-RO Roche 11249002001
Critical Commercial Assays
Basic Primary Neurons Nucleofector Kit	Lonza	Cat#VVPI-1003
Experimental Models: Primary Cell Culture
Bovine adrenal chromaffin cell	J. W. Treuth and Sons, Inc.	Adrenal Glands
Recombinant DNA
PH-EGFP	Varnai and Balla, 1998	Addgene Plasmid #51407
mNeonGreen	Allele Biotechnology	ABP-FP-MNEONSB
PH-mNeonGreen	Shin et al., 2018	Allele Biotechnology
NPY-EGFP	Taraska et al., 2003	Addgene Plasmid #74629
Software and Algorithms
Huygens Professional	Scientific Volume Imaging	https://svi.nl/Huygens-Professional
ImageJ	NIH	https://imagej.nih.gov/ij/
LAS X	Leica	https://www.leicabiosystems.com/
Igor Pro	WaveMetrics	https://www.wavemetrics.com/products/igorpro
MATLAB	MathWorks	https://www.mathworks.com/products/matlab.html
Python v3.5.2	Python Core Team	https://www.python.org

Highlights.

• Visualizing fused vesicular membrane shrinking and enlargement with STED microscopy

• Shrinking is mediated by physiological osmotic pressure that squeezes fused vesicles

• Vesicle shrinking facilitates content release by employing a large fusion pore

• Vesicle enlargement slows down content release by employing a small fusion pore