Cognitive Modeling Suggests That Attentional Failures Drive Longer Stop-Signal Reaction Time Estimates in Attention Deficit/Hyperactivity Disorder

Abstract

Mean stop-signal reaction time (SSRT) is frequently employed as a measure of response inhibition in cognitive neuroscience research on ADHD. However, this measurement model is limited by two factors which may bias SSRT estimation in this population: 1) excessive skew in “go” RT distributions, and 2) trigger failures, or instances in which individuals fail to trigger an inhibition process in response to the “stop” signal. We use a Bayesian parametric approach, which allows unbiased estimation of the shape of entire SSRT distributions and the probability of trigger failures, to clarify mechanisms of stop-signal task deficits in ADHD. Children with ADHD displayed greater positive skew than their peers in both “go” RT and SSRT distributions. However, they also displayed more frequent trigger failures, which appeared to drive ADHD-related stopping difficulties. Results suggest that stop-signal task performance in ADHD reflects impairments in early attentional processes, rather than inefficiency in the stop process.

Executive functions, a broadly-defined cluster of neurocognitive processes involved in the top-down control of cognition and actions, are central to theoretical models of Attention Deficit Hyperactivity Disorder (ADHD: Barkley, 1997; Killeen, Russell, & Sergeant, 2013; Rapport et al., 2008; Willcutt, Doyle, Nigg, Faraone, & Pennington, 2005), and to current cognitive neuroscience research aimed at clarifying the condition’s etiology (Coghill, Nigg, Rothenberger, Sonuga-Barke, & Tannock, 2005; Fair, Bathula, Nikolas, & Nigg, 2012; Roberts, Martel, & Nigg, 2017). Of these constructs, deficits in response inhibition, the ability to stop a pre-potent or ongoing response that is no longer adaptive given the current demands of the environment (Logan & Cowan, 1984; Miyake et al., 2000), are thought to be some of the most robust findings in group comparisons between children with ADHD and their typically-developing peers (Crosbie et al., 2013; Nigg, 1999; Willcutt et al., 2005).

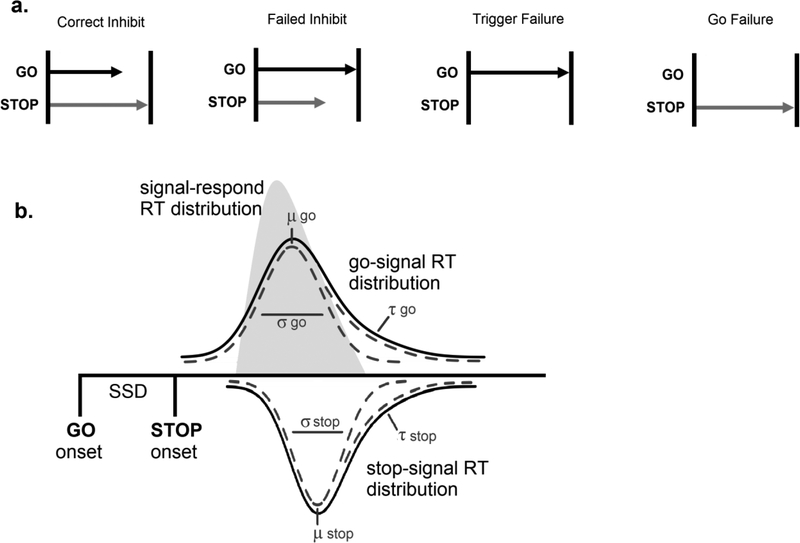
Many such findings rely on the measurement of response inhibition provided by the stop-signal paradigm (Logan, 1994; Logan & Cowan, 1984; for a recent review, see: Matzke, Verbruggen & Logan, 2018), in which individuals complete a choice response time (RT) task (e.g., deciding whether a letter stimulus is an “X” or an “O”), and are signaled to inhibit their response on a subset of trials after the presentation of the choice stimulus. This measurement method assumes that the stop signal produces a horse race between a “go” process, triggered by the presentation of the choice stimulus, and a “stop” process, triggered by the presentation of the stop signal (Figure 1a). Whether an individual ultimately inhibits their response is dependent on whether the “stop” or “go” process finishes first. The speed of the latent “stop” process is typically estimated using the “mean” method (Verbruggen, Chambers, & Logan, 2013) in combination with a “staircase tracking” procedure (Levitt, 1971), in which the difference between the onset of the go stimulus and the onset of the stop signal, or “stop-signal delay” (SSD), is dynamically adjusted based on the participant’s performance to produce a roughly 50% probability of inhibition. Once this rate is achieved, an individual’s mean “stop-signal reaction time” (SSRT) can be estimated by subtracting the mean SSD from their mean “go” RT (Verbruggen et al., 2013).

Figure 1.

Schematics of the horse race and ex-Gaussian models of stop-signal task performance. a) Demonstration of single trial horse races (assuming SSD=0) in which the stop process wins the race (correct inhibit), in which the go process wins the race (failed inhibit), in which the stop process fails to be triggered (trigger failure), and in which the go process fails to be triggered (go failure). b) Schematic of the ex-Gaussian race model, adapted from Matzke et al. (2017), in which the signal-respond RT distribution (light gray) is given by a go RT distribution censored by a stop-signal RT distribution, both of which is assumed to be ex-Gaussian in shape.

Mean SSRT is thought to index the efficiency of a top-down control process that allows individuals to inhibit actions (Logan & Cowan, 1984; Matzke, Verbruggen, & Logan, 2018), and this metric is frequently adopted in the ADHD literature as a measure of individuals’ response inhibition ability. Under this measurement assumption, theoretical accounts of ADHD that highlight impaired response inhibition have been supported by robust findings of group differences in mean SSRT between individuals with the disorder and their typically-developing peers (Martel, Nikolas, & Nigg, 2007; Nigg, 1999; Willcutt et al., 2005), with overall effect sizes falling in the medium range (Lipszyc & Schachar, 2010). Furthermore, mean SSRT appears to be improved by stimulant medication treatments for ADHD (Aron, Dowson, Sahakian, & Robbins, 2003; Rosch et al., 2016), and display heritability patterns consistent with the idea that slow SSRT is a plausible endophenotype of genetic risk for the disorder (Crosbie et al., 2013; Nigg, Blaskey, Stawicki, & Sachek, 2004), although recent work using polygenetic risk scores has cast doubt on the latter finding (Nigg et al., 2018).

However, there are multiple indications that the prevailing interpretation of stop-signal task performance, as primarily reflecting top-down inhibitory control, may be more tenuous than is typically assumed. First, the “mean” method can lead to artificially slow estimates of mean SSRT, and do so to a greater extent when “go” RTs are more positively skewed (Verbruggen et al., 2013). As RT distributions of individuals with ADHD are characteristically more positively skewed than those of their peers (Epstein et al., 2011; Kofler et al., 2013), longer SSRT estimates may result from the bias associated with this skew, rather than a core inhibition deficit.

Although the “block-wise integration” method of estimating SSRT provides a way to address this challenge (Verbruggen et al., 2013), it cannot address a second major challenge: the possibility that the inhibition process fails to be triggered by the stop signal on a subset of trials (see Figure 1a). These instances, known as “trigger failures” (Matzke, Love, & Heathcote, 2017) have been long acknowledged by Logan (1994), and result in failed inhibits that are due to the “stop” process never entering the race. Applications of Bayesian parametric methods have estimated that trigger failures occur on roughly 7–10% of stop-signal trials in healthy adult populations, and can lead to the dramatic overestimation of SSRTs if they are not accounted for (Matzke, Love, et al., 2017). Adults diagnosed with schizophrenia display trigger failure rates as high as 18% (Matzke, Hughes, Badcock, Michie, & Heathcote, 2017). Evidence for non-trivial rates of trigger failure in healthy populations and even higher rates in clinical groups suggests that trigger failures could also play a role in the stop-signal task performance of children with ADHD. Specifically, greater trigger failure rates in ADHD may cause systematic overestimation of SSRT in children with this disorder. If true, this would indicate that aberrant performance on the stop-signal task in ADHD reflects impairments in early perceptual or attentional processes rather than, or in addition to, inefficiency in the top-down inhibitory control process.

A novel parametric approach in which the entire distribution of SSRTs and go RTs (rather than just the mean) are estimated in a Bayesian framework (Matzke, Dolan, Logan, Brown, & Wagenmakers, 2013), provides a promising way of addressing both pitfalls of SSRT measurement and indexing the incidence of trigger failures in ADHD. In common with other methods of estimating SSRT, this approach assumes the distribution of go RTs is the same for go trials and for stop-signal trials (i.e., context independence), so that the signal-respond RT distribution (i.e., RTs on stop-signal trials, or failed inhibits) can be treated as a go RT distribution censored by the latent SSRT distribution (Figure 1b). Finishing times for the go and stop processes are assumed to follow an ex-Gaussian distribution, which is a Gaussian distribution, defined with mean μ and standard deviation σ, convolved with an exponential distribution with mean τ (i.e., the slow tail of the distribution). Previous simulation work has suggested that, although μ, σ, and τ do not selectively index underlying cognitive processes, reduced efficiency of cognitive processing leads to increases in both the mean and variability of ex-Gaussian distributions (Matzke & Wagenmakers, 2009). Hence, increases in the latency or variability of the stop process’s RT distribution would suggest inefficiencies in the stop process. Since positive skew of the go RT distribution is explicitly modeled in this framework, the method provides an index of the stop process that is not biased by this feature of performance. To index the incidence of trigger failures, Matzke et al. (2017) extended the ex-Gaussian race model to include a trigger failure parameter (PiF), which quantifies the probability that an individual will fail to trigger the stop process on a given stop-signal trial.

Hence, the full ex-Gaussian race model may be able to advance the literature on stop-signal task performance in ADHD and related psychopathologies in two ways. First, it could provide a measurement method for estimating processes of theoretical interest while controlling for other potentially confounding features of task performance in ADHD (e.g., skew in the go RT distribution), which may, in turn, improve researchers’ ability to link these processes to clinical outcomes or neural correlates of the disorder. Second, although the ADHD field has largely assumed that SSRT measurements provide an index of trait-level response inhibition (but see: Alderson, Rapport, & Kofler, 2007; Alderson, Rapport, Sarver, & Kofler, 2008; Lijffijt, Kenemans, Verbaten, & van Engeland, 2005), the ex-Gaussian race model allows for a more nuanced and mechanistic understanding of individual variation in this ability. If response inhibition is defined as the functional ability to inhibit pre-potent responses (i.e., how frequently an individual is able to prevent a “go” response), individual variation in this ability may be due to individual differences in either 1) mechanisms that allow top-down inhibitory control processes to be triggered in response to environmental cues, or 2) the integrity of the top-down inhibitory control processes themselves. By indexing the former mechanism with P_TF and the latter with the ex-Gaussian parameters of the SSRT distribution, the model allows these separate determinants of response inhibition ability to be measured and explicitly distinguished.

To this end, the current study applies the ex-Gaussian race model with the P_TF parameter to stop-signal task data from a large existing sample of children with ADHD and age-matched controls. The first goal of the study is to use the Bayesian parametric approach to estimate entire distributions of children with ADHD’s SSRTs, and compare them to those of their peers. Although ex-Gaussian analyses of choice RT tasks have revealed robust τ increases in the disorder (Epstein et al., 2011; Kofler et al., 2013), features of the SSRT distribution have never been previously evaluated in this group. In doing so, our second goal is to determine whether children with ADHD display greater latency or variability of SSRTs when skew in their go RT distributions is accounted for. If so, this finding would support the prevailing view of children with ADHD as displaying deficits in top-down inhibitory control processes. Finally, our third goal is to estimate the prevalence of trigger failures in ADHD, and determine whether increases in these rates can partially, or fully, explain differences in stop-signal task performance between these children and their typically-developing peers. The latter outcome would indicate that stop-signal task deficits in ADHD reflect impairments in early perceptual or attentional processes instead of, or in addition to, impairments in inhibitory control processes.

Methods

Sample

An initial sample of 234 children with ADHD and 108 age-matched typically-developing controls completed the stop-signal task as part of a larger battery of tests administered in an ongoing study of childhood ADHD. The study was approved by the Pennsylvania State University’s institution review board, and was carried out in accordance with the provisions of the Declaration of Helsinki. This initial sample included all children who had met the larger study’s full inclusion criteria (detailed below) and had completed the stop-signal paradigm by the time that the current study was first conceived by the authors (December 2015). Of this initial sample, 25 children with ADHD (11%) and 9 controls (8%) were excluded prior to modeling due to data quality concerns (described below), leaving a final sample (Table 1) of 209 children with ADHD and 99 controls. Although the sample size was not determined a priori, it was sufficient to accomplish the study’s goal of investigating between-groups effects in parameter values¹, and no additional data were added to the sample after analyses began. The larger study included a number of other experimental paradigms in addition to the stop-signal task, and description of these measures is beyond the scope of the current study. However all experimental conditions of the stop-signal task and all data exclusions are reported in the current manuscript. This study was not pre-registered because this practice was less-commonly required of authors at the time data analyses began, and because the primary goals of this study were exploratory.

Table 1.

Descriptive, demographic and behavioral summary statistics of each group in the final sample. Means are displayed with standard deviation in parentheses. All ratings scales reported in T-scores. For subtypes: H = Hyperactive, I = Inattentive, C = Combined. For comorbidities: MDD = Major Depressive Disorder, GAD = Generalized Anxiety Disorder, ODD = Oppositional Defiant Disorder, CD = Conduct Disorder. Frequentist inferences (p-value), Bayesian inferences (BF), and frequentist point estimates of effect size (d) were drawn from independent samples t-tests conducted in JASP.

	Control	ADHD	p	BF	d
N(Males:Females)	99(46:53)	209(140:69)	-	-
#Subtypes (H,I,C)		5,85,119	-	-
Age	10.23(1.26)	10.20(1.31)	.874	.14	.03
Estimated Full Scale IQ	103.79(7.61)	103.47(12.18)	.814	.14	.02
Hyperactivity/Impulsivity
Total # of symptoms	.28(.54)	5.49(2.93)	<.001	>10,000	2.14
Parent BASC-2	42.42(5.41)	65.03(13.69)	<.001	>10,000	1.93
Parent Conners	45.83(3.34)	67.09(14.12)	<.001	>10,000	2.69
Teacher BASC-2	43.74(3.42)	60.30(13.07)	<.001	>10,000	1.52
Teacher Conners	45.53(2.80)	59.45(12.41)	<.001	>10,000	1.35
Inattention
Total # of symptoms	0.54(.69)	8.02(1.30)	<.001	>10,000	6.59
Parent BASC-2	43.47(6.42)	66.62(6.72)	<.001	>10,000	3.50
Parent Conners	45.74(3.87)	70.12(10.68)	<.001	>10,000	2.69
Teacher BASC-2	43.52(5.36)	62.27(6.98)	<.001	>10,000	2.88
Teacher Conners	46.15(4.55)	60.35(11.37)	<.001	>10,000	1.46
Comorbidity (past year)
MDD	0	9	-	-	-
GAD	0	23	-	-	-
ODD/CD	3/0	82/15	-	-	-
Task Summary Statistics
Go Mean RT	0.771 (0.149)	0.818 (0.146)	.01	3.13	.32
Signal-Respond Mean RT	0.666 (0.119)	0.720 (0.125)	<.001	58.62	.44
Go Accuracy	0.976 (0.039)	0.949 (0.053)	<.001	2716.18	.56
Signal-Respond Accuracy	0.970 (0.051)	0.937 (0.069)	<.001	589.30	.52
Mean SSD	0.454 (0.180)	0.394 (0.204)	.012	2.66	.31
Mean SSRT Estimate	0.317 (0.105)	0.424 (0.162)	<.001	>10,000	.72
Overall P(response)	0.528 (0.060)	0.577 (0.099)	<.001	2012.00	.56

Children in the study were community recruited from several sites in Pennsylvania, which spanned urban, suburban and semi-rural settings and represented the ethnic and racial demographics of the region (78% Caucasian/non-Hispanic, 5% Caucasian/Hispanic, 2% other Hispanic, 6% African American, 1% Asian, 6% mixed, and 3% unknown/missing). Children’s average annual family income fell between $60,000 and $80,000. To qualify for a diagnosis of ADHD, children had to meet full DSM-IV criteria, including age of onset, duration, cross-situational severity, and impairment, which were determined using parent report on the Diagnostic Interview Schedule for Children version IV (DISC-IV) (Shaffer, Fisher, & Lucas, 1997). The DISC-IV was administered to one parent, either father or mother, by trained research assistants. In addition, at least one parent report (from the same parent who was administered the DISC) and one teacher report of behavior on the Attention, Hyperactivity, or ADHD subscales of the Behavioral Assessment Scale for Children (BASC-2: Reynolds & Kamphaus, 2004) or the Conners’ Rating Scales (Conners’: Conners, 2008) was required to exceed the 85^th percentile (T-score>61). The “or” algorithm was used to integrate DISC-IV and teacher reports of symptoms, following DSM-IV field trials (Lahey et al., 1994), to establish symptom counts. Non-ADHD controls did not meet the DSM-IV criteria, had never been previously diagnosed or treated for ADHD, and all of the above listed rating scales were below the 80^th percentile (T-score≤58) for both parent and teacher report.

To ensure that group differences could not be attributed to differences in general intelligence, IQ was estimated from the 2-subtest short form (Vocabulary, Matrix Reasoning) of the Wechsler Intelligence Scale for Children—IV (WISC-IV: Wechsler, 2003). Non-ADHD controls with an estimated IQ>115 and children in both groups with an IQ<80 were excluded. Children with ADHD who were prescribed a psychostimulant medication (N = 69) ceased taking their medication 24–48 hours in advance of the day of testing (median washout = 57 hours). The presence of common psychiatric comorbidities, including generalized anxiety disorder, major depression, oppositional defiant disorder, and conduct disorder, was assessed on the DISC-IV and rating scales. However, these diagnoses (Table 1) were not exclusionary. We chose to include individuals with comorbidity because comorbidity in ADHD is the rule, not the exception (Angold, Costello, & Erkanli, 1999; Larson, Russ, Kahn, & Halfon, 2011), and exclusion of children with co-occurring disorders would therefore limit the generalizability of our results.

Stop-Signal Task

Children completed the stop-signal task seated in front of a computer monitor in the presence of a trained graduate or undergraduate research assistant. Each trial began with a 200ms fixation cross presented in the center of the screen, followed by the 1000ms presentation of a letter stimulus (either an “X” or an “O”) in the same location and a 2300ms inter-stimulus interval, during which the screen was blank. Participants were instructed to indicate whether an “X” or an “O” had appeared at any time during the stimulus presentation period or subsequent inter-stimulus interval by pressing response box buttons labeled with each response. Children completed a 20-trial practice round, followed by five blocks of 40 trials presented in a pseudorandom order, with an optional rest period before each block. An auditory tone was played on 25% of experimental trials (a total of 50 trials, interspersed pseudorandomly) signaling that the participant should inhibit their response. The SSD on each trial was determined using a standard “staircase” algorithm, in which, on the first stop trial, the tone was presented 250ms before a running average of the participant’s RT across all previous trials. If the participant successfully inhibited a response, the next stop signal was presented 200ms before the participant’s mean RT at that time. If they failed to inhibit a response, however, the next stop signal was presented 300ms before the mean RT. In this way, the SSD was dynamically adjusted throughout the task in increments of 50ms and locked to the updated average of RT.

Model-Based Analyses

The ex-Gaussian race model was specified and estimated using the Dynamic Models of Choice software (DMC: Heathcote et al., 2018) consisting of a free set of R (Team, 2015) functions for conducting model-based choice RT analyses in a Bayesian framework.

Prior to model-fitting, data quality checks were used to exclude individuals with data that indicated noncompliance or inadequate understanding of the task, or that violated key assumptions of the model. Exclusion criteria were selected by the authors after visual inspection of group distributions of relevant summary statistics (e.g., accuracy and omission rates) with the goals of 1) retaining as many children with ADHD as possible, so as to have a representative sample, while also 2) excluding participants for whom there was clear evidence of problematic data (e.g., we made the assumption that individuals with accuracy rates <55% were likely not performing the task above chance, and were therefore likely to be noncompliant). First, children who were unable to maintain accuracy levels greater than 55%, or who had an excessive proportion of omissions on go trials (>40%) were excluded from analysis (20 ADHD, 6 Control). Second, because the model assumes that an individual’s mean RT does not speed up or slow down significantly over the course of the task, regression slopes were calculated to measure the change in RT over time for each individual. Any participant who displayed an RT reduction or increase of >500ms throughout the task was excluded from analysis (5 ADHD, 3 Control).

Excessive error trials can distort SSRT estimates from parametric methods (Matzke, Curley, Gong, & Heathcote, in press: http://dora.erbe-matzke.com/papers/InhibitingDifficultChoices.pdf), and it is common for researchers to exclude participants or experimental blocks that do not have high accuracy rates (e.g., >70–95%: Ashare & Hawk, 2012; Matzke, Hughes, et al., 2017; Matzke, Love, et al., 2017; Nigg, 1999). However, due to developmental differences in cognitive ability, maintaining such criteria would preclude the retention of a representative sample of children. To address this issue, we conducted two model-based analyses: 1) our main analysis, described below, for which we use an inclusion criteria of >55% accuracy, and a modification of the ex-Gaussian race model (Matzke et al., in press) that explicitly accounts for error RTs, and 2) a secondary analysis, reported in the Supplemental Materials, using the standard model that does not account for go errors (Matzke, Love, et al., 2017). This secondary analysis only included correct RTs from children with >95% accuracy rates (N = 121 ADHD, 88 Control). As between-group effects in the secondary analysis were not substantively different from those in the main analysis, we report results using the modification of the race model that allows for the inclusion of a more representative sample of children.

The modified ex-Gaussian race model (Matzke et al., in press) explains the accuracy of RTs by postulating one go process for each go response as well as a stop process (i.e., a race with three runners). In line with evidence accumulator models of choice RT (Brown & Heathcote, 2008; Logan, Van Zandt, Verbruggen, & Wagenmakers, 2014), this framework assumes that correct responses occur when the “matching” go process (e.g., the process triggering an “X” response when the stimulus is an “X”) finishes before the “mismatch” go process (e.g., the process triggering an “O” response), while error responses occur when the mismatch process finishes first. Preliminary analyses that attempted to fit a model which estimated all three ex-Gaussian parameters (μ, σ, τ) separately for the mismatch process revealed that these parameters were poorly constrained and led to convergence problems, potentially because of the relatively low number of go errors per participant, or the relatively high level of positive skew in children with ADHD’s RT distributions. We therefore estimated separate μ and σ parameters for the match (μ_go-match, σ_go-match) and mismatch (μ_go-mismatch, σ_go-mismatch) RT distributions, but assumed that both distributions shared the same τ parameter (τ_go), as this parameterization led to more stable and well-constrained estimates.

The shape of the SSRT distribution was described with three separate parameters (μ_stop, σ_stop, τ_stop), while a “trigger failure” parameter (P_TF) estimated the probability that the stop-signal tone fails to trigger an inhibition process on a given trial. Previous research on trigger failures in the ex-Gaussian race model, which was conducted using data from adult subjects (Matzke, Hughes, et al., 2017; Matzke, Love, et al., 2017), did not consider the possibility of “go failures”, or instances in which the go process, rather than the stop process, fails to be triggered. However, as many children in the current sample displayed relatively high rates of omissions on go trials, it was possible that go failures were present in the data, and would bias estimates of the other model parameters if not accounted for. Therefore, we also estimated a “go failure” (Matzke et al., in press; Tannock, Schachar, Carr, Chajczyk, & Logan, 1989) parameter (P_GF) for the probability that the go process fails to be triggered. Although mechanistic interpretations of go failures are beyond the scope of this study, results reported below suggest that both children with ADHD and their peers display non-trivial rates of go failure.

We used a hierarchical modelling approach which treats subject-level parameters as random effects described by group-level distributions. On average, this method 1) provides more accurate estimates of individual-level parameters, because the group-level parameters serve as priors that constrain individual estimates (parameter “shrinkage”), and 2) allows for robust estimation of the mean and standard deviation of the individual parameters for each group, even in situations with relatively sparse observations at the individual level. For the current model, all ten individual-level parameters were assumed to follow (truncated) normal distributions, specified by location (M: which gives the group mean for non-truncated distributions) and scale (S: which gives the group standard deviation for non-truncated distributions) parameters, estimated separately for each group. Because the current data set contains a relatively low number of trials at the individual level, but a relatively large sample of participants in each group, the group-level parameters provided a robust summary of the groups, despite high levels of uncertainty in the individual-level estimates. Thus, only the group-level parameters were used for inference.

Prior to estimation, RTs <200ms were excluded from analysis as fast guesses (<1% of trials) following standard procedures for fitting choice RT models (Ratcliff & Tuerlinckx, 2002). Differential Evolution Markov chain Monto Carlo simulations (Turner, Sederberg, Brown, & Steyvers, 2013) were used to sample from the posterior distribution of all group- and individual-level model parameters. Following previous work (Matzke, Hughes, et al., 2017), sampling for the P_TF and P_GF parameters used probabilities that were projected onto the real line using a probit transformation. Relatively broad and uninformative priors were posited for all group-level parameters, although limits were placed on some parameters to prevent the estimation of impossible values (for example, group location and scale parameter values for the μ, σ, and τ parameters that fall below 0ms). Priors for all group scale (S) parameters simply consisted of exponential distributions with a scale of 1, while priors for group location (M) parameters were truncated normal distributions with the following locations, scales, and bounds (note that probability parameters are on the probit scale):

$${\mu }_{go-match}~TN\left(\text{location }=1,\text{ scale }=2,\text{ lower }=0,\text{ upper }=3\right)$$

$${\sigma }_{go-match}~TN\left(\text{location }=.5,\text{ scale }=2,\text{ lower }=0,\text{ upper }=1\right)$$

$${\mu }_{go-mismatch}~TN\left(\text{location }=1,\text{ scale }=2,\text{ lower }=0,\text{ upper }=3\right)$$

$${\sigma }_{go-mismatch}~TN\left(\text{location }=.5,\text{ scale }=2,\text{ lower }=0,\text{ upper }=1\right)$$

$${\tau }_{go}~TN\left(\text{location }=.5,\text{ scale }=2,\text{ lower }=0,\text{ upper }=1\right)$$

$${\mu }_{stop}~TN\left(\text{location }=.5,\text{ scale }=2,\text{ lower }=0,\text{ upper }=3\right)$$

$${\sigma }_{stop}~TN\left(\text{location }=.25,\text{ scale }=2,\text{ lower }=0,\text{ upper }=1\right)$$

$${\tau }_{stop}~TN\left(\text{location }=.25,\text{ scale }=2,\text{ lower }=0,\text{ upper }=1\right)$$

$$P_{GF}~TN\left(\text{location }=-1,\text{ scale }=2,\text{ lower }=\infty ,\text{ upper }=\infty \right)$$

$$P_{TF}~TN\left(\text{location }=-1,\text{ scale }=2,\text{ lower }=\infty ,\text{ upper }=\infty \right)$$

Start points of the sampling process for all parameters were determined using the means and variance of samples from earlier non-hierarchical fits at the individual-subject level. A total of 30 chains (three times the number of parameters) were used for sampling of each group- and individual-level parameter. An initial burn-in period using a migration step with 5% migration probability (Turner et al., 2013) was followed by a second burn-in period with migration turned off. This second period lasted until both visual inspection of chains and the Gelman-Rubin statistic (Gelman & Rubin, 1992) indicated convergence (Gelman-Rubin < 1.1 for all parameters). After convergence, a final sample of 100 iterations was retained for analysis, providing a total of 3000 (30 × 100) posterior samples for each parameter. The goodness-of-fit of the model was explored with posterior predictive plots (Supplemental Materials).

Hypothesis Testing

Behavioral summary statistics (accuracy, RT, SSD) were analyzed using both frequentist significance tests (p-values) and Bayes Factors (BFs) from t-tests and ANOVAs conducted in JASP (JASP Team, 2018), a free software package designed to replicate the functionality of SPSS for frequentist analyses and allow Bayesian versions of the same analyses to be easily conducted by users. BFs quantify the probability of the data under a research hypothesis, such as the hypothesis that the effect size is not 0, relative to the probability of the data under the null hypothesis. A BF of 10, for example, indicates that the data are 10 times more likely under the research hypothesis, while a BF of .25 indicates that the data are 4 times more likely under the null hypothesis². According to commonly-used guidelines (Jeffreys, 1961), BFs between 1 and 3 provide only “anecdotal” or ambiguous evidence for the research hypothesis, while BFs of 3 to 10 provide substantial evidence, BFs >10 provide strong evidence, and BFs>100 provide decisive evidence.

Group differences in model parameters were quantified using Bayesian p-values, following previous studies using the ex-Gaussian race model (Matzke, Hughes, et al., 2017). These p-values were calculated for each group difference by subtracting the posterior distribution of the group that had lower values, overall, from the posterior distribution of the other group, and counting the proportion of posterior samples for which this difference was positive. Thus, p-values close to 0 provided evidence that one group’s parameter value was greater than that of the other group. The null-hypothesis testing convention of rejecting the null hypothesis if p<.05 does not apply to Bayesian p-values. Rather, they quantify the degree to which the posterior distribution of the difference between groups is consistent with the hypothesis that a group difference exists.

Results

Behavioral Summary Statistics

For analyses of summary statistics (Table 1), BFs were used as the primary method of quantifying evidence for the presence or absence of effects, but frequentist statistics are also reported for ease of interpretation. In mean RT, there was positive evidence for a main effect of Group, _F(1,306)=9.69, η² =.03, p=.002, BF=11.76, indicating that children with ADHD had longer RTs than their peers. A main effect of Stop-Signal, F(1,306)=781.64, η² =.72, p<.001, BF>10,000, indicated that RTs were shorter on signal-respond trials (responses on trials with a stop signal) than on go trials. There was evidence for the absence of a Group × Stop-Signal interaction, F(1,306)=1.14, η² =.001, p=.286, BF=.18. The Group effect is consistent with previous research on ADHD, while the Stop-Signal effect was expected because the race model assumes that the inhibition process on stop-signal trials censors longer RTs. Children with ADHD were less accurate than their peers, F(1,306)=22.29, η² =.07, p<.001, BF=3386.11, and signal-respond responses were less accurate than go trial responses F(1,306)=11.46, η² =.04, p<.001, BF=168.03, but evidence for an interaction was ambiguous, F(1,306)=1.16, η² =.004, p=.282, BF=1.01. The effect of Stop-Signal on accuracy suggested that error RTs were faster than correct RTs, as fast responses would be censored to a lesser extent on signal-respond trials. Indeed, error RTs were faster, on average, than correct RTs, t(281)=4.26, p<.001, BF=407.2³. This pattern could indicate that a proportion of RTs are fast guesses, where participants make a random response before considering evidence for the decision, or that participants emphasized speed over accuracy, which commonly produces fast error RTs (Ratcliff & Rouder, 1998).

Despite the flaws, discussed above, of the “mean method” for estimating SSRT, we used this method to compare our results with those commonly reported in previous studies of SSRT in ADHD where this method was used (e.g., Karalunas & Huang-Pollock, 2013; Nigg, 1999; Rosch et al., 2016). When SSRT was estimated in this way, there was strong evidence that individuals with ADHD displayed longer mean SSRTs than their peers, t(306)=5.98, d=.73, p<.001, BF>10,000. Thus, findings based on this index are consistent with previous research on ADHD.

Model-Based Analyses

Posterior predictive checks (Supplemental Materials) suggested that the model provided a good description of go RTs, signal-respond RTs, and inhibition functions in both groups. The group-level location (M: which approximates the group mean) and scale (S: which approximates the group standard deviation) parameters were directly used to assess group differences in the means and standard deviations of race model parameters, with two exceptions. First, the group-level M parameters for the trigger- (P_TF) and go-failure (P_GF) parameters were transformed back to the probability scale using an inverse-probit transformation, which allowed us to approximate the group medians on the probability scale⁴. Second, as group distributions of the SSRT variability parameters (σ_stop, and τ_stop) displayed severe truncation at 0 (i.e., the appearance of an exponential, rather than normal, shape because the parameter values of many subjects were clustered close to 0), the group-level M and S parameters for σ_stop, and τ_stop do not provide an accurate description of the central tendency and between-subjects variability of these parameter values. To address this issue, the posterior samples for the group-level M and S parameters were transformed⁵ to the mean and standard deviation of the group-level truncated normal distributions. The transformed parameters were then used to make inferences about group differences in means and variability of σ_stop, and τ_stop.

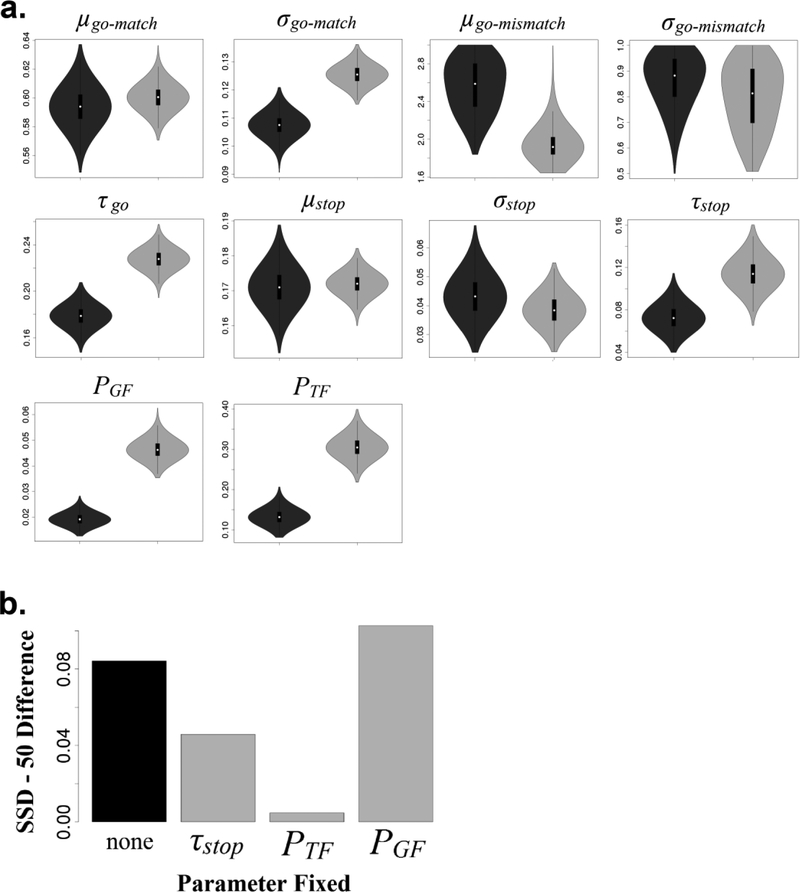
Posterior distributions of group M parameters are displayed as violin plots in Figure 2a, while posterior medians for group M and S parameters are displayed in Table 2 along with Bayesian p-values for group differences. For go RT distributions, there was little evidence for a differences in Gaussian mean (μ_go-match), p=.330, but strong evidence for greater values of Gaussian variability (σ_go-match) p<.001, and exponential variability (τ_go), p<.001, in the ADHD group. Although τ_go was collapsed across match and mismatch accumulators, our secondary analysis of only correct RTs (Supplemental Materials) also found group differences in τ_go. Thus, consistent with previous findings, children with ADHD appear to display increased Gaussian and exponential RT variability on go trials. For parameters that described the RT distributions of signals that are mismatched with the stimulus, children with ADHD displayed evidence of lower μ_go-mismatch, p=.031, but little evidence for differences in σ_go-mismatch, p=.355, compared to their typically-developing peers. The lower μ_go-mismatch in ADHD likely reflects how the model explains the ADHD group’s increased error rate; in addition to having more variable match signal RTs than controls, mismatch signal RTs in children with ADHD also have a slightly shorter latency, leading to the higher incidence of errors.

Figure 2.

a) Violin plots representing posterior distributions of the group-level location (M) parameters of typically-developing controls (dark gray) and children with ADHD (light gray). For go- and stop-signal RT distributions, μ = Gaussian mean, σ = Gaussian variability, and τ = exponential variability; P_TF = probability of trigger failures, P_GF = probability of go failures. Due to concerns about truncation (detailed in the text), posterior samples for σ_stop, and τ_stop have been transformed to the mean of the group-level truncated normal distributions. The group-level parameters for P_TF and P_GF have been transformed back to the probability scale for clarity, and approximate the median values for each group. b) Results of the simulation studies aimed at determining the relative contributions of τ_stop, P_TF and P_GF to stopping difficulties in ADHD. The group difference in SSD-50 values is displayed for the simulation that used estimated parameter values of each group (black) and each simulation in which specific values for the ADHD group were “normalized” by setting them to the value of the Control group (gray).

Table 2.

Posterior medians of all group-level parameters and Bayesian p-values for each group difference. For go- and stop-signal RT distributions, μ = Gaussian mean, σ = Gaussian variability, and τ = exponential variability; P_TF = probability of trigger failures, P_GF = probability of go failures; M = group location (approximates the mean of the individual parameters), S = group scale (approximates the standard deviation of the individual parameters). Due to concerns about truncation (detailed in the text), the group-level M and S parameters for σ_stop, and τ_stop have been transformed to the mean and the standard deviation of the truncated normal group-level distribution. Here we report results for the untransformed as well as the transformed (subscripted with “Mean” and “SD”) posterior samples. M parameters for P_TF and P_GF have been transformed to the probability scale for clarity, which approximate the medians of the group distributions.

Group M
Parameter	Control Post. Median	ADHD Post. Median	Bayesian p-value
μgo-match	.594	.601	.330
σgo-match	.108	.125	<.001
μgo-mismatch	2.587	1.918	.031
σgo-mismatch	.882	.813	.355
τgo	.179	.228	<.001
μstop	.171	.172	.429
σstop	.017	.014	.428
τstop	.027	.027	.480
σstop Mean	.043	.038	.300
τstop Mean	.072	.114	.006
PGF	.019	.047	<.001
PTF	.134	.305	<.001
Group S
Parameter	Control Post. Median	ADHD Post. Median	Bayesian p-value
μgo-match	.120	.114	.302
σgo-match	.033	.043	.007
μgo-mismatch	.577	.434	.123
σgo-mismatch	.169	.030	<.001
τgo	.076	.099	.013
μstop	.040	.029	.010
σstop	.045	.041	.300
τstop	.076	.128	.001
σstop SD	.030	.027	.282
τstop SD	.051	.083	.002
PGF	.755	.893	.187
PTF	.446	.485	.051

For SSRT distributions, there was little evidence of group differences in μ_stop and σ_stop (all p>.30), but children with ADHD appeared to display greater exponential variability (τ_stop) than their peers, p=.006, suggesting inefficiency in the top-down inhibition process. There was also strong evidence, p<.001, for a large increase in trigger failures (P_TF) in the ADHD group; children with ADHD appeared to have over twice the incidence of trigger failures (31% of trials) compared to their typically-developing peers (13% of trials), who had rates slightly higher than those of healthy adults reported in previous investigations (ranging from 7–10%: Matzke, Hughes, et al., 2017; Matzke, Love, et al., 2017). Consistent with the deficits in early perceptual or attentional processing implied by the P_TF findings, there was also strong evidence, p<.001, for increased go failures (P_GF) in ADHD, although these rates were much lower overall than the rates of trigger failures (5% for ADHD and 2% for Controls). Taken together, this pattern of results suggests that trigger failures occur at relatively high rates for both children with ADHD and their typically-developing peers, and that group differences in stop-signal task performance can be attributed to larger trigger failure rates, in addition to differences in the integrity of the top-down inhibition process itself.

Although the group S parameters, which quantify the level of between-subject variability in a group, were not the primary focus of the study, there was evidence for several effects (displayed in Table 2) that are potentially informative given recent findings of cognitive and neurophysiological heterogeneity in ADHD (Fair et al., 2012; Karalunas, Fair, et al., 2014). Specifically, the ADHD group displayed greater between-subject variability in two parameters that describe intraindividual variability in go RT distributions, σ_go-match, p=.007, and τ_go, p=.013, suggesting that children with ADHD not only have greater Gaussian and exponential variability in the go process, but also have more between-subject heterogeneity in these types of variability. More relevant to the current study, there was strong evidence that children with ADHD displayed greater between-subject variability in T_stop, p=.002, and suggestive evidence of greater between-subject variability in P_TF, p=.051. Taken together, these effects indicate that both parameters are more heterogeneous in the ADHD group, which suggests that there may be considerable individual differences in the causes of children with ADHD’s impaired performance on the task. As the current sample does not have enough trials at the individual level to reliably assess individual differences (our primary reason for focusing on the group-level parameters for inference), future work with larger samples of stop-signal trials would be instrumental in exploring this possibility.

Simulations to Determine Parameter Contributions to Stopping Impairments

The analyses reported above suggested that differences in both exponential variability of the SSRT distribution (τ_stop) and the probability of trigger failures (P_TF) contribute to children with ADHD’s difficulty stopping a dominant response. However, the degree to which each of these processes contributes is unclear. To determine the relative contributions of each parameter to stopping deficits in the disorder, a simulation study was conducted. First, the group-level M posteriors for each group were used to simulate stop-signal task data in order to determine the magnitude of stopping difficulties experienced by children with ADHD, which was quantified by identifying the SSD for which each group had a .50 probability of responding (SSD-50). This metric relies on the well-supported assumptions that 1) greater stopping difficulties, regardless of whether they are due to trigger failures or slow/variable SSRTs, will necessarily increase probability of responding at a given SSD, and 2) probability of responding increases with SSD latency. Under these assumptions, a group’s SSD-50 will necessarily increase with increases in stopping difficulties. The SSD-50 was determined by simulating a total of 5000 trials at each SSD (a large number to produce stable estimates) over a range of .300 to .600 seconds at .010 second increments and using R’s approx() function to identify the exact SSD value for which each group showed a .50 probability of responding. Next, the SSD-50 value for the ADHD group was subtracted from the SSD-50 value for the Control group to obtain an estimate of the magnitude of children with ADHD’s stopping difficulties (SSD-50 difference).

Following this, two separate simulations were conducted in which: 1) the τ_stop parameter of the ADHD group was set to the τ_stop parameter value of the Control group and 2) the P_TF parameter of the ADHD group was set to the P_TF parameter value of the Control group. As this procedure would “normalize” the ADHD group’s deficits in τ_stop and P_TF, respectively, reductions in the magnitude of the SSD-50 difference in each simulation (Figure 2b) are reflective of these parameters’ individual contributions to stopping difficulties in the disorder. To assess the contributions of P_GF deficits, which would be expected to have the opposite effect on stopping difficulties (with more “go failures”, the probability of responding on a stop-signal trial would be decreased), we also conducted a simulation in which the P_GF parameter was “normalized” in ADHD.

Relative to the SSD-50 difference suggested by the parameters estimated from the empirical data (.084 seconds), fixing the τ_stop parameter to be the same between groups reduced the magnitude of ADHD-related stopping difficulties to roughly half (.046 seconds). However fixing the P_TF parameter to be the same between groups led to an SSD-50 difference of almost 0 (.005 seconds). Thus, this analysis suggests that if children with ADHD’s average P_TF was similar to that of their typically-developing peers, their ability to stop the dominant response would be roughly comparable to that of their peers. As expected, fixing P_TF to be the same between groups increased the ADHD-related SSD-50 difference (.117 seconds). Taken together, the outcome of these simulations suggests that, although children with ADHD display evidence of increased variability in SSRTs, failure to trigger the inhibition process in response to the stop signal is, on aggregate, the primary driver of stopping difficulties in the disorder.

Discussion

The goal of this study was to use the ex-Gaussian race model (Matzke, Dolan, Logan, Brown, & Wagenmakers, 2013; Matzke, Love, et al., 2017), a Bayesian parametric approach for estimating stop-signal RT distributions and the incidence of trigger failures, to better clarify the latent cognitive mechanisms responsible for ADHD-related performance differences on the stop-signal task. The model-based analysis indicated that children with ADHD display more variable SSRTs than their typically-developing peers, and specifically more positive skew in their SSRT distributions, a finding that was, notably, also present in their distributions of go RTs. However, their difficulties stopping the dominant “go” response appeared to primarily be driven by failures to trigger the inhibition process, rather than impairments in the inhibition process itself. Furthermore, the P_GF parameter revealed low overall rates of failure to initiate the “go” process, but a disproportionate difficulty in ADHD, suggesting that ADHD-related deficits on the stop-signal task reflect broad problems with initiating goal-directed behaviors in response to relevant cues. Although previous lines of work have questioned the common interpretation that stop-signal task performance differences in ADHD reflect impairments in inhibitory control processes (Alderson et al., 2007; Alderson et al., 2008; Lijffijt et al., 2005), the current study is the first to use a parametric approach to identify specific cognitive mechanisms that can explain these differences.

The ability to rapidly utilize cues or changes in the environment to guide goal-directed behavior is essential for the implementation of cognitive control (Verbruggen, McLaren, & Chambers, 2014; Verbruggen, Stevens, & Chambers, 2014). In turn, effective detection and utilization of such cues has been hypothesized to be dependent on the top-down biasing of attentional competition towards stimuli that are most relevant to behavior (Desimone & Duncan, 1995), or a ventral frontoparietal neural network that re-orients attention towards previously unattended, but task-relevant, environmental stimuli (Corbetta, Patel, & Shulman, 2008; Corbetta & Shulman, 2002). Studies using visuospatial orienting tasks and those that manipulate visual perceptual load have suggested that early selective attention processes are largely intact in ADHD (Huang-Pollock & Nigg, 2003; Huang-Pollock, Nigg, & Carr, 2005). However, children with ADHD show marked impairment on tasks that require the active maintenance of goals or rules to guide behavior over a longer time scale, such as working memory paradigms (Kasper, Alderson, & Hudec, 2012; Rapport et al., 2008) and decision-making tasks that require the updating of action rules (Shahar, Teodorescu, Karmon-Presser, Anholt, & Meiran, 2016). Thus, rather than reflecting early selection deficits, trigger failures may reflect “goal neglect” (Duncan, Emslie, Williams, Johnson, & Freer, 1996), in which the goals of a task are understood and are possible for the individual to accomplish, but the top-down biasing of attention towards stimuli that are task-relevant is poorly or inconsistently implemented.

In line with this account, a previous investigation of trigger failures in schizophrenia (Matzke, Hughes, et al., 2017) found a relationship between the P_TF parameter and the latency of an electrophysiological waveform commonly associated with attentional processes (the N1). Furthermore, similar to the schizophrenia literature (Hughes, Fulham, Johnston, & Michie, 2012), neuroimaging studies of ADHD have revealed aberrant activity in the right inferior frontal gyrus during stop-signal task performance (Janssen, Heslenfeld, van Mourik, Logan, & Oosterlaan, 2015; Rubia, Smith, Brammer, Toone, & Taylor, 2005). This region is strongly associated with the stop-signal task (Aron & Poldrack, 2006), but also appears to be broadly involved in the detection of task-relevant cues, regardless of whether these cues lead to inhibition (Hampshire, Chamberlain, Monti, Duncan, & Owen, 2010), which lends support to an attentional account of stop-signal task deficits.

Between-group differences in τ_stop were also detected, but they did not appear to be a major driver of stopping difficulties in ADHD. Furthermore, we also found an increase in the exponential variability of “go” process RTs in ADHD, consistent with the previous literature applying ex-Gaussian analyses to choice tasks in the disorder (Epstein et al., 2011; Kofler et al., 2013). Thus, τ_stop deficits, rather than reflecting specific impairments in inhibitory control, may simply reflect the positive skew that is ubiquitous in processing time distributions of individuals with ADHD. This finding extends the work of Kofler et al. (2013), who provided compelling meta-analytic evidence that RT distributions of children with ADHD are primarily characterized by greater τ, in that it demonstrates that their latent distributions of stop-signal RTs show the same feature. Although ex-Gaussian parameters do not correspond to unique cognitive constructs (Matzke & Wagenmakers, 2009), formal sequential sampling models of choice tasks (Ratcliff, Smith, Brown, & McKoon, 2016) have consistently suggested that greater positive skew in the RT distributions of children with ADHD reflects less efficient information processing (Huang-Pollock, Karalunas, Tam, & Moore, 2012; Karalunas & Huang-Pollock, 2013; Karalunas, Huang-Pollock, & Nigg, 2012; Metin et al., 2013; Weigard & Huang-Pollock, 2016). Less efficient processing in ADHD has, in turn, been hypothesized to reflect impairments in top-down attentional systems related to arousal and state-regulation (Karalunas, Geurts, Konrad, Bender, & Nigg, 2014), suggesting a possible attentional link between RT variability and trigger failures.

Taken together, the overall pattern of results suggests that mechanistic accounts which posit inhibitory control as a core deficit in ADHD are not supported by features of stop-signal task performance in the disorder. However, children with ADHD have also been found to display poorer performance on other tasks that are putative indices of inhibitory control, including go/no-go (Wright, Lipszyc, Dupuis, Thayapararajah, & Schachar, 2014), Flanker, and Simon paradigms (Mullane, Corkum, Klein, & McLaughlin, 2009). The ex-Gaussian race model only describes the stop-signal task, but it is possible that parameters similar to P_TF, which index the probability that control processes fail to be initiated, could be added to formal models of these other tasks in future work to evaluate the hypothesis that such parameters can account for poor performance across response inhibition measures. As formal models that describe go/no-go and interference tasks are already being developed and evaluated (Ratcliff, Huang-Pollock, & Mckoon, 2016; White, Servant, & Logan, 2018), this research direction would likely provide a strong and comprehensive test of this hypothesis.

Beyond evidence from controlled experimental tasks, the “disinhibition” hypothesis of ADHD is also appealing because it intuitively explains behavioral impulsivity, a core symptom of the disorder. We note that, if the combined evidence from this and future studies involving a range of response inhibition tasks ultimately demonstrates that performance deficits are due to trigger failures, such evidence would not invalidate the idea that behavioral symptoms of ADHD are caused by difficulties with inhibiting impulsive responses. Instead, it would suggest a different mechanistic explanation for behavioral impulsivity by supporting theories which posit that individuals with ADHD have difficulty initiating control processes in response to corresponding cues and changes in the environment (Nigg & Casey, 2005) as opposed to difficulty enacting top-down control of cognition or behavior. Indeed, tentative findings of error processing abnormalities in ADHD (Shiels & Hawk, 2010), and evidence that children with the diagnosis have difficulty adjusting their performance strategy in response to subtle changes in task demands (Weigard & Huang-Pollock, 2014; Weigard, Huang-Pollock, & Brown, 2016) also support this general conceptualization.

Although the evidence for this account is preliminary, prior work that has emphasized the involvement of state-regulation processes in ADHD suggests a plausible mechanism for trigger failures and more general difficulties initiating top-down control processes in response to cues. ADHD-related deficits in arousal, or “vigilance,” which are commonly indexed by measures from formal response time models (drift rates) and signal detection theory (d’), have recently shown promise as a putative endophenotype of the disorder (Nigg et al., 2018). Such deficits have been hypothesized to reflect dysfunction in noradrenergic systems that modulate attentional states in response to task demands, leading children with ADHD to exhibit greater RT variability and greater difficulty parsing task-relevant signal from task-irrelevant noise (Karalunas, Geurts, et al., 2014; Weigard, Huang-Pollock, Brown, & Heathcote, 2018). Difficulties parsing task-relevant information from noise would likely impact an individual’ s ability to attend to the stop signal and other task-relevant cues. Therefore, it is plausible that deficient arousal causes trigger failures and other difficulties with the initiation of top-down control processes. However, until a clear link between trigger failures and measures of arousal is established, this idea remains speculative. A crucial direction for future research on the causes of trigger failures in ADHD would be to experimentally assess the effects of arousal, as well as secondary factors such as motivation and affective state, on parameters of the race model. The complex etiology of ADHD also requires that future work longitudinally link ex-Gaussian race model parameters to other factors that are likely relevant to the development of ADHD, such as genetic, affective, environmental variables.

Several additional research directions are also essential. First, the fact that P_TF estimates of typically-developing children were slightly higher than those reported in previous studies of healthy adults (Matzke, Hughes, et al., 2017; Matzke, Love, et al., 2017) suggests that there are developmental differences in the incidence of trigger failures. However, an investigation of performance on a stop-signal task with similar parameters across multiple age bands is needed to clarify developmental differences. Second, further investigation of the construct validity of the novel P_GF parameter would be helpful; although we interpreted this parameter as an index of attentional processing, it could be argued that, due to the high salience of the choice stimuli, this parameter is more of an index of non-compliance. Furthermore, as neuroimaging research and animal models of the stop-signal task suggest that the go and stop processes have distinct neural bases (Aron et al., 2007), additional work is necessary to qualify our assumption that P_GF and P_TF index similar constructs. In addition, findings of greater between-subject variability in the τ_stop and P_TF parameters in ADHD, which suggest possible mechanistic subtypes of individuals with inhibition vs. trigger failure deficits, are consistent with the emerging literature on neuropsychological and neurophysiological heterogeneity in the disorder (Fair et al., 2012; Gates, Molenaar, Iyer, Nigg, & Fair, 2014). However, as the individual-level parameter estimates from this analysis were too uncertain to explore individual differences, application of the ex-Gaussian race model to a different data set with a larger number of trials at the individual level would be instrumental for exploring the possibility of mechanistic subtypes and selective relationships with relevant covariates (e.g., symptom dimensions, neural measures).

The current study has several additional limitations. First it is possible that parameters added to the model to account for features of the data set (e.g., the addition of the P_GF parameter and the ex-Gaussian parameters for mismatch RTs to account for omission rates and errors) may have led to problems related to “overfitting” the model to the data in this sample (Pitt & Myung, 2002). However, as the same parameters have recently been added to the ex-Gaussian race model for analyses of different data sets, and were found to be necessary to account for behavior in those samples (Matzke et al., in press), it is unlikely that these additions reflect overfitting. Relatedly, due to the low per-subject number of error trials, the τ_go parameter was fixed for match and mismatch process RTs to constrain the model. Although our secondary analysis suggested that most effects of group on model parameters were robust to this decision, this modification of the ex-Gaussian race model it may have led to misfits of the model to error RTs (see Supplemental Materials), and prevented the model from providing a comprehensive description of behavior. Therefore, this limitation underscores the importance of replicating our results in a data set with more trials at the individual level. A final limitation of the current study is that the analysis plan was not pre-registered, which would have reduced the likelihood that researcher degrees of freedom may have influenced results. Hence, pre-registered replication of our findings in independent samples is necessary.

In sum, the current study provided evidence that performance aberrations observed in children with ADHD on the stop-signal task are, on aggregate, more likely to be due to problems with triggering goal-directed processes in response to environmental cues than to specific deficits in top-down inhibitory control processes. Crucially, these findings not only challenge the common interpretation of stop-signal task performance in ADHD, but also advance a mechanistic explanation for stop-signal task deficits that can be tested with a formal model and can, ideally, be more closely linked to causal explanations at the neurophysiological level in future research. More broadly, as originally argued by Matzke and colleagues (2017), the results demonstrate that trigger failures must be considered when using the stop-signal task to answer clinical and other applied questions, and that Bayesian parametric methods provide an ideal approach for doing so.