Abstract
Classical molecular dynamics simulations and free energy methods have been used to obtain a better understanding of the molecular processes occurring prior to the first nucleation event for calcium phosphate biominerals. The association constants for the formation of negatively charged complexes containing calcium and phosphate ions in aqueous solution have been computed, and these results suggest that the previously proposed calcium phosphate building unit, [Ca(HPO4)3]4–, should only be present in small amounts under normal experimental conditions. However, the presence of an activation barrier for the removal of an HPO42– ion from this complex indicates that this species could be kinetically trapped. Aggregation pathways involving CaHPO4, [Ca(HPO4)2]2–, and [Ca(HPO4)3]4– complexes have been explored with the finding that dimerization is favorable up to a Ca/HPO4 ratio of 1:2.
Short abstract
Classical molecular dynamics simulations and free energy methods have been used to obtain a better understanding of the molecular processes occurring prior to the first nucleation event for calcium phosphate biominerals. The association constants for the formation of negatively charged complexes containing calcium and phosphate ions in aqueous solution have been computed, and these results suggest that the previously proposed calcium phosphate building unit, [Ca(HPO4)3]4−, should only be present in small amounts under normal experimental conditions. However, the presence of an activation barrier for the removal of an HPO42− ion from this complex indicates that this species could be kinetically trapped. Aggregation pathways involving CaHPO4, [Ca(HPO4)2]2−, and [Ca(HPO4)3]4− complexes have been explored with the finding that dimerization is favorable up to a Ca/HPO4 ratio of 1:2.
1. Introduction
Calcium phosphate minerals are ubiquitous in nature and are found extensively in both geological settings and within living systems. The most studied crystalline phase of this mineral family is hydroxyapatite (HA). A carbonated form of HA is found in human bones where it is crucial as a structural element and as a mineral reservoir. It has also been extensively studied due to its wide range of properties, which leads to a wealth of potential applications including the development of new biomaterials or engineered bone tissue replacement,1,2 catalysis,3 liquid column chromatography,4 and heavy metal removal from soils.5 Nonetheless, the pathway by which this mineral nucleates from solution is still under debate, and understanding the molecular mechanism behind this process is essential to improve our ability to control the structure and tailor the final properties of this mineral for a desired application.
Many recent studies have tried to probe the structures arising from the association of solutes prior to the initial nucleation event (i.e., the formation of critical size nuclei). Recent interest was spurred by the observation of structures considerably larger than the ion pair, using analytical ultracentrifugation, before nucleation in the calcium carbonate mineral system.6 This observation was subsequently supported by cryo-TEM7 and further analysis using molecular dynamics simulations, which showed that clusters with linear, branched, and ring structures composed of close to a one-to-one mixture of Ca2+ and CO32– ions can form.11,23 Whether these clusters simply follow a classical cluster distribution and therefore do not offer a significant change in the classical approach to nucleation remains a debate within the community. Recent work by Smeets et al.9 indicates that the clusters are unstable at high concentrations leading to the formation of a dense liquid phase, implying a two-step approach to the nucleation problem.10
The importance of clusters larger than the ion pair has long been argued for in calcium phosphate, and they have been observed under various experimental conditions. Posner was the first to suggest both the existence of a calcium phosphate amorphous precursor and that formation of hydroxyapatite occurred through the aggregation of Ca9(PO4)6 clusters, later called Posner’s clusters.12 These have been subsequently investigated both experimentally and via computational methods.13−16 The experiments of Onuma and Ito (using atomic force spectroscopy and dynamic light scattering to study the growth of hydroxyapatite) showed the presence of clusters with sizes between 0.7 and 1.0 nm in solution, which they proposed to be Ca9(PO4)6 clusters. Additionally, they observed that hydroxyapatite grew in steps of 0.8–1.6 nm, suggesting that these clusters are the growth unit.15 Mancardi et al. have used unbiased molecular dynamics to simulate the aggregation of calcium phosphate species toward the formation of Posner’s clusters.17 However, no quantitative thermodynamics was reported, and the simulations utilized a water model that is now known to freeze at ambient conditions.18,19 Kanzaki et al. used ab initio methods to study the thermodynamic stability of various cluster sizes and aggregates of Ca3(PO4)2, observing that a number of stable configurations existed on the potential energy surfaces of [Ca3(PO4)2]3. From the decrease of the energy as a function of the number of Ca3(PO4)2 units, they also proposed that the aggregation of these units could be an alternative to the formation of Posner’s clusters.13 However, the formation of neutral clusters, as suggested in that study, does not explain the recent observation that the amorphous precursor to the nucleation and growth of calcium phosphate minerals is negatively charged due to a calcium-deficient structure.20,21 This is almost certainly because the calculations of Kanzaki et al. considered the stability of clusters in vacuo, and the absence of solvent will have had profound consequences for the thermodynamics.
Investigation of the nucleation and growth of HA within living systems, specifically in murine and zebra fish, has shown that crystallization occurs through the initial precipitation of an amorphous structure22−25 (which is also a common mechanism for the crystallization of calcium carbonate26). Intriguingly, recent analysis in vitro showed that, in contrast to previous observations where the calcium to phosphate ratio (Ca/P) was observed to be between 1.1 and 1.5,27 this structure carries a negative charge arising from a calcium deficiency that leads to a Ca/P ratio of 0.67.20,21 A similar structure appears to be important in vivo as well. Analysis of osteoblast vesicles lining the growth front of murine calvarial bone using electron dispersive spectroscopy showed a Ca/P ratio of 0.75.25 A recent in vitro investigation of biomimetic calcium phosphate precipitation by Habraken et al. proposed, by monitoring the pH and composition of the solution, that the inorganic polymeric chains observed before nucleation using cryo-TEM are composed of monomeric units of calcium trihydrogen phosphate complexes,21 [Ca(HPO4)3]4–. They suggested that these complexes interact through a double hydrogen bond within the polymeric chains; however, this could not be verified. Subsequent densification of the cluster would then occur by the addition of a further calcium ion leading to an amorphous structure composed of [Ca2(HPO4)3]2– fractals.21
Previous analysis of the formation of clusters for the calcium phosphate system using molecular dynamics simulations and ab initio methods has shown a wealth of potential clusters in solution. Zahn looked at the thermodynamics of association of calcium and hydrogen phosphate using molecular mechanics and ab initio calculations58 and proposed that the stable initial complexes were (Ca2HPO4)2+ units; however, other potential pathways were not examined. Mancardi, Terranova, and De Leeuw recently analyzed the formation of the negative calcium phosphate complex proposed by Habraken et al. by means of ab initio simulations.32 While they found a minimum in the free energy curve, the simulations used a small unit cell, and the free energy was sampled only up to 7 Å. Since the Bjerrum length for this reaction is 14 Å, it is therefore impossible to extract the standard free energy change. Furthermore, the length of time sampled was relatively short due to the computationally demanding nature of such simulations, and therefore any slow degrees of freedom (e.g., exchange of bound water at calcium) could not be fully explored. In other studies, Almora-Barrios et al. and Ma et al. looked at the interaction between calcium and phosphate ions in highly concentrated solutions in the presence of collagen using molecular dynamics simulations.33,34 They both observed the formation of calcium phosphate clusters. De Leeuw et al. analyzed solutions with only PO43– anions present which are unlikely to exist in solution at a pH of 7.4 (the approximate pH of living systems). In contrast, Ma et al.34 did investigate solutions containing HPO42–, and a number of clusters carrying a charge were reported. However, Ma et al. obtained their force field for the HPO42– molecule directly from the CHARMM database, and the ability of this parameter set to model the bulk structures of any calcium phosphate minerals has not yet been demonstrated, which may mean that the interactions are not fully reliable.34 This year, concurrently with the present work, a study by Yang et al.35 on calcium phosphate prenucleation clusters was published which represents the most rigorous investigation thus far as it included extensive sampling of the free energy landscape via bias enhanced sampling. Like the work of Ma et al., it used the CHARMM force field and attempted to validate the parametrization by comparing the ion pairing free energy to experiment and to the earlier values from the Demichelis et al. force field.36 Yang et al. reported an ion pairing free energy of −27.2 kJ/mol (compared to the experimental value of −15 kJ/mol37 and the Demichelis value of −17.9 kJ/mol) indicating that the CHARMM force field overestimates the stability of Ca2+ and HPO42– binding. As a consequence, they describe a mechanism by which the addition of further phosphate ions leads to a monotonic increase in stability despite the increasing overall negative charge of the cluster.
In the present study, we use molecular dynamics simulations based on a force field parametrized specifically for thermodynamic properties36 to probe the formation, structure, stability, and potential mechanisms of aggregation that can lead to the formation of the initial species containing two calcium ions in aqueous solution. Free energy profiles for both the formation of the monomeric complexes and their aggregation will be presented, allowing us to calculate their relative concentrations in solution. The results agree in part with previous experimental analysis and show that the complex suggested experimentally as part of the aggregation mechanism, [Ca(HPO4)3]4–, has an exergonic formation. Even though our results suggest that it will not be the dominant species present in the solution, it could become kinetically trapped. However, [Ca2(HPO4)6]8–, the dimer of [Ca(HPO4)3]4–, is endergonic, making it unlikely that dimerization is the method by which growth occurs. Additional potential species and aggregates were also found, giving new insights into the molecular mechanisms behind the initial precipitation of amorphous calcium phosphate minerals.
2. Methods
Classical molecular dynamics simulations were used to probe the formation of calcium and hydrogen phosphate complexes and their subsequent aggregation using a force field specifically parametrized with a thermodynamic focus.36 This force field reproduces the thermodynamics of the phosphate and calcium ions in solution and has been recently used to explore the water structure and dynamics at a surface of the calcium phosphate mineral brushite.38 A similar method was previously used to obtain a force field for the calcium carbonate system and was shown to capture the stability of the different polymorphs, as well as the solubility, more accurately than previous models.45 The water molecules were simulated using the flexible SPC/Fw force field.59
In order to be able to simulate the full speciation of phosphates, the force field developed by Demichelis et al. includes parameters for all the relevant anions. Here we concentrate on the hydrogen phosphate anion (HPO42–) because experimentally21 it was observed to be the main species during the initial association with Ca2+ ions. In the subsequent text, the different oxygens of the HPO42– ion and water will be defined as OP in the case of the nonprotonated oxygens, OHP for the protonated one, and OW for water.
Multiple-walker41 well-tempered metadynamics42 was used to explore the possible association mechanisms involving [CaHPO4]0, [Ca(HPO4)2]2–, [Ca(HPO4)3]4–, [Ca(HPO4)4]6–, [Ca2(HPO4)2]0, [Ca2(HPO4)3]2–, [Ca2(HPO4)4]4–, [Ca2(HPO4)5]6–, and [Ca2(HPO4)6]8– complexes. (All the reactions sampled are summarized in Table S1.) Molecular dynamics was performed using LAMMPS43 with the PLUMED 2.444 plug-in in order to bias the collective variables and compute the pairing free energies. All simulations were run using a 1 fs time step within the isothermal–isobaric ensemble with a Nosé–Hoover thermostat and barostat. Ions were placed in a cubic box of water molecules with a cell length of 49.843 Å that initially contained 4178 water molecules. Overlapping water molecules were removed leading to systems with between 4142 and 4174 waters, depending on the species inserted. Equilibration for 500 ps resulted in box sizes with cell lengths of 49.6–49.9 Å. All simulations were run at 300 K and 1 atm. Metadynamics simulation times were greater than 150 ns, with specific simulation times per association reported in Table S1.
One of the main challenges in mapping the free energy landscape for cluster formation is in determining the optimal set of collective variables (CVs) onto which to project the free energy. Unfortunately, the simulation cost rapidly increases with the number of CVs, due to the dimensionality of the free energy surface, while the analysis also becomes complex. Hence, we have limited the number of simultaneously used collective variables to three. Thus, for the systems with a single Ca2+ and up to three hydrogen phosphate ions, it was possible to define a CV between each anion and Ca2+, e.g., an association of the form Ca2+ + HPO42– + HPO42– + HPO42– → Ca(HPO4)34–, such that a cluster can form from initially separate ions within a single simulation and theoretically could fully explore multiple aggregation pathways. However, even here this requires the assumption that water exchange at Ca2+ is fast on the simulation time scale and that the relative orientation and position of hydrogen phosphate ligands is similarly fully sampled. Once the situation is reached where there are two Ca ions and multiple ligands, then three CVs are generally insufficient to unambiguously map the pathways for association from single ions. In such cases, a stepwise association was performed, e.g., an association of the form Ca2+ + HPO42– → Ca(HPO4) + Ca(HPO4) → Ca(HPO4)2 and Ca(HPO4) + Ca(HPO4) → Ca2(HPO4)2. There are now two simulations, but they each require fewer CVs. Here the assumption is made that any reacting species, such as ion pairs, remain bound during aggregation, and this is enforced through applying restraints. To verify that the use of different restraints for different reactions did not lead to a significant error, the stability of all complexes was determined via multiple pathways (see Table S2 for all summed paths). By comparing the overall thermodynamics for different routes between the same species, Hess’s Law was used to check the consistency of the free energy cycles. In some cases, the reduction of number of CVs through restraints was used to allow the inclusion of the Ca–OW coordination number(s) to account for the expectation that the slowest degree of freedom will be the exchange of water molecules around the cation.
The coordination number (CN) collective variables for both biasing and restraints were defined using the continuous differentiable function:
For the definition of the Ca–OW CN, n = 4, m = 10, and ri is the distance between Ca and OW,i. When used to constrain clusters to remain together, n = 6, m = 12, and ri was taken to be the distance between Ca and Pi. The coordination number parameters for Ca (d0 = 3.6 Å for Ca–P, d0 = 2.1 Å for Ca–OW) were chosen using the position of the first peak of the pair distribution function for Ca + HPO4 and Ca + H2O. In some cases, additionally, upper walls (UW) were used to limit cluster separation. These were defined using a half-harmonic restraint for xi> ai;
where ki is the force constant (for restraining a cluster to remain bound the upper wall ki = 2 eV/Å2, and for limiting the distance of separation between two species the upper wall ki = 10 eV/Å2), and the position of the upper wall (ai = 3.78 Å) between calcium and HPO4 was chosen based on the pair distribution function between Ca and HPO4. The necessity of an ion pair upper wall was tested by running a simulation without this restraint, but the ion pairs were observed to break apart during the association process being mapped.
Once free energy curves are obtained as a function of separation, it is possible to obtain the free energy change for the formation of the different ionic complexes under standard conditions. Following the method detailed elsewhere45 and restated in the Supporting Information, the curves were offset so as to align with the analytic curve for the free energy in the long-range asymptotic limit, as shown in Figure 1. The maximum cluster separation was originally 16 Å for all associations, but for larger associations, where the curve was still not well-aligned to the long-range asymptotic limit, a larger separation of ai = 20 Å was used (see Supporting Information for details of values for each specific association reaction). The maximum distance for the bound state depended on the specific association type and was chosen based on the furthest bound of a minimum which is discernible visually (generally 8–11 Å). In this way, the free energy of the solvent-separated association was included in the calculation, thus preventing discrepancies between associations where there is a clear barrier between nonsolvent and solvent-separated associations (for example, all cases in Figure 1) and those where there was no significant barrier (for example, Figure S10). The specification of the upper bound for the association is important since it determines the volume of the complex relative to that for a 1 M concentration, thereby allowing the computed free energies to be corrected to the standard values.
Figure 1.
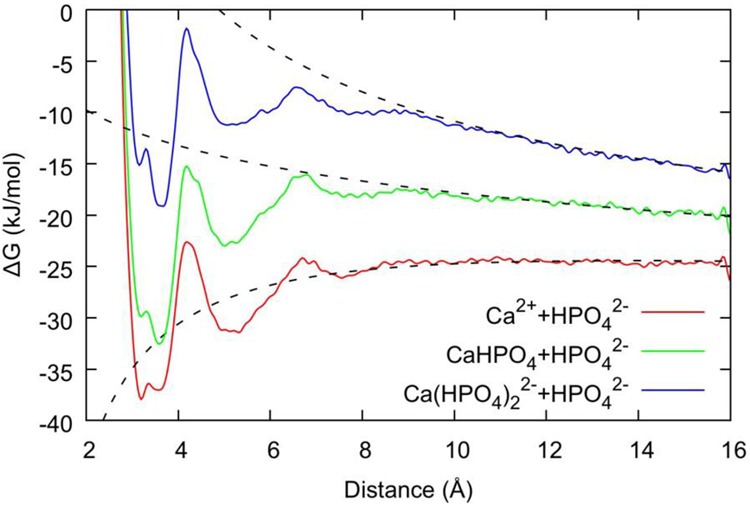
Free energy plotted as a function of the distance between Ca2+ and P within a (HPO4)2– group. The red, green, and blue lines are the free energy profiles for Ca2++ HPO42–→ [CaHPO4]0, [CaHPO4]0+ HPO42–→ [Ca(HPO4)2]2–, [Ca(HPO4)2]2–+ HPO42–→ [Ca(HPO4)3]4–, respectively. The corresponding dashed lines represent the analytic solution in the long-range limit, which is used to align the absolute free energy. Note that the anomalous data points very close to 16 Å are due to the presence of the confining wall.
Gaussians were laid every 1 ps along all CVs with a width of 0.1 Å and an initial height of kbT. Using the multiple-walker algorithm, 30 parallel simulations were run for each energy profile with a bias factor of 5 for the well-tempering. In the cases where a bias factor of 5 returned an energy significantly larger than 15 kJ/mol, the simulations for that CV were rerun with a bias factor of 15 to ensure that the larger barrier was overcome by the simulations. Representative cluster geometries were chosen by determining the lowest free energy configuration via analysis of the free energy as a function of the CVs (see Supporting Information).
3. Results and Discussion
3.1. Formation of [Ca(HPO4)n]−2n+2 Complexes
Given that the experimental results suggest that negatively charged [Ca(HPO4)3]4– complexes form prior to nucleation21 and that calcium-deficient amorphous calcium phosphate (ACP)20,21 forms subsequently, it is important to probe the mechanisms by which these complexes can form and their relative stabilities in aqueous solution. The free energy profiles (as a function of the distance between the Ca and P atoms in the system) are shown in Figure 1 for the formation of the following species: [CaHPO4]0, [Ca(HPO4)2]2–, and [Ca(HPO4)3]4–. The ion pair shows a split minimum at a distance of 3.3 Å, which corresponds to two configurations with a small barrier separating the states. The inner configuration relates to the presence of a bidentate interaction (i.e., the HPO42– ion is interacting with the Ca2+ ion via two OP atoms), while the outer configuration is due to a monodentate interaction via a single OP. The OHP, bonded to a hydrogen, tends to remain in solution and interacts with OW through both OHP–HW bonding and HHP–OW bonding. As HPO42– ions are added to the Ca2+ ion, the inner bidentate state shifts from being the most stable configuration to a higher energy relative to the monodentate one. The contact ion pair basin at 3.4 Å is separated from the solvent-shared ion pair (SSIP) by a barrier at 4.2 Å. This barrier is 15 kJ mol–1 for [CaHPO4]0, while for both [Ca(HPO4)2]2– and [Ca(HPO4)3]4– it is slightly higher at 17 kJ mol–1. All the curves also show one additional shallow minimum at approximately 5.1 Å due to the formation of the solvent-separated ion pair.
The present structural model, described above, accords with X-ray near-edge structure results,52 which suggest that when a HPO42– ion forms a contact ion pair with a Ca2+ ion, two water molecules are displaced from the coordination shell of the metal cation (see Table 1 and Figure 2), although this does not lead to a more centrosymmetric arrangement around the cation since the hydrogen phosphate prefers to bind with two oxygens. As more HPO42– ions are added to the Ca2+ ion, the number of displaced water molecules per addition decreases, mostly due to the shift of the preferred HPO42– binding configuration from a bidentate to a monodentate one.
Table 1. Thermodynamic and Structural Properties of Different Complexes of Ca2+ with Hydrogen Phosphate Anions in Watera.
| species | number of OW in coordination shell | change in OW in coordination shell | ΔGassn (kJ/mol) | ΔGfrom ions (kJ/mol) |
|---|---|---|---|---|
| Ca2+ | 7.2245 | |||
| [CaHPO4]0 | 5.06 | –2.16 | –17.9 | –17.9 |
| [Ca(HPO4)2]2– | 4.05 | –1.01 | –12.0 | –29.9 |
| [Ca(HPO4)3]4– | 3.05 | –1.00 | +1.1 | –28.7 |
The average number of water oxygens (OW) in the hydration shell of the calcium cation, either as an isolated ion in water or within an ion pair or complex, is given in the second column. The change in water coordination number and free energy of one association (ΔGassn) are given relative to the species on the previous line of the table in the third and fourth columns, respectively. The free energy of the species formed from ions is reported in the fifth column.
Figure 2.
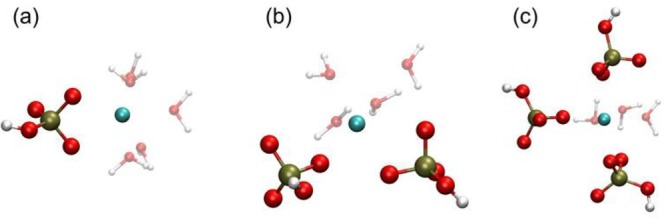
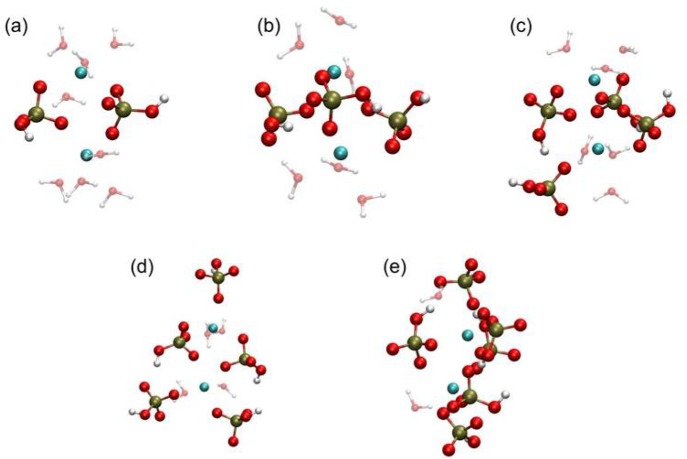
Representative geometries for configurations taken from the local minima of the free energy curves of Figure 1 for the contact ion pair state of (a) [CaHPO4]0; (b) [Ca(HPO4)2]2–; and (c) [Ca(HPO4)3]4–. Ca is cyan, P is tan, O is red, and H is white. Only those water molecules coordinated to calcium are shown for clarity.
As detailed in the Methods, it is possible to obtain the free energy change for the formation of the different ionic complexes under standard conditions from Figure 1. For the ion pair, the value obtained for the free energy of association is exergonic, −17.9 kJ mol–1, and within a few kJ mol–1 of the experimental value,37 as previously reported and shown in Table 1. Exergonic binding was also observed for the formation of the [Ca(HPO4)2]2– complex with a free energy change of −12.0 kJ mol–1. Despite the Coulomb repulsion between two anions, the further addition of a HPO42– ion to this complex, leading to the [Ca(HPO4)3]4– complex described by Habraken et al.,21 also showed an energy minimum at a Ca–P distance of 3.6 Å but did result in a slightly endergonic addition (+1.1 kJ mol–1).
By summing consecutive associations, we can report the free energy of association of the clusters compared to isolated ions (see Table 1), which is a different way of showing the same trend that the [Ca(HPO4)2]2– and [Ca(HPO4)3]4– complexes are roughly energetically equal. These results differ from the recent work of Yang et al.35 where it is suggested that addition of HPO42– ions leads to a systematic decrease in the free energy compared to isolated clusters in solution. In addition to the possible overstabilization due to the CHARMM force field, when we recalculate binding for their free energy curves by alignment to the asymptotic limit, rather than using the force integration method, we get values that are increasingly discrepant as the total charge increases (see Table S3 and Figure S21). In the case of [Ca(HPO4)3]4–, Yang et al. report a binding of −81 kJ/mol for the cluster relative to the isolated ions in solution; recalculated using alignment this value is −57 kJ/mol. This value is still twice our reported value, but given that the ion pair binding of Yang et al. is 1.8 times more negative than the experimental value this result is consistent given the systematic overbinding.
By using the changes in free energies detailed in Table 1 and above, it is possible to calculate the concentration of the different species in solution for a given starting concentration and ionic strength. Using a concentration of 0.006 M Ca2+ ions and 0.005 M HPO42– ions, approximately that used by Habraken et al.,21 and the same ionic strength (i.e., I = 0.02 M), the result suggests that in an equilibrated solution approximately 74% of the Ca2+ ions would be unbound, 16% would form ion pairs, and 11% would form a complex, namely, [Ca(HPO4)2]2–. The percentage of [Ca(HPO4)3]4– under these conditions would be insignificant. Similarly, under the conditions used by Xie et al., 0.00122 M Ca2+ and 0.0073 M HPO42–, 64% of the Ca2+ ions would be free ions, 18% would form ion pairs, and 18% would form [Ca(HPO4)2]2–, again with an insignificant concentration of [Ca(HPO4)3]4–. However, depending on the solution mixing conditions, [Ca(HPO4)3]4– complexes could form and then be kinetically trapped for a short period, as the barrier to removal of an HPO42– ion from this complex is 17 kJ mol–1.
The differences between our simulations and the experiments of Habraken21 et al. and of Xie20 et al. may arise from not accounting for all the phosphate species that will be present in the solution at a pH value of 7.4. Under these conditions, approximately half of the phosphate species will be present as H2PO4– due to the acid–base equilibria of phosphate in solution. This is, however, likely to further decrease the fraction of HPO42– complexes, rather than increase it. Another potential reason, as suggested in the section above, is that in the experimental solution the complexes are kinetically trapped due to the initial mixing protocol. Moreover, the presence of other solutes in the experiments, such as trisaminomethane (TRIS, used as a buffer) and a high concentration of NaCl might affect the equilibrium. In a series of dynamic light scattering experiments, Onuma et al. looked at reference solutions to compare the size of the cluster observed when both Ca2+ and HPO42– were present.15 The particle distribution obtained for the solution composed of NaCl, K2HPO4·3H2O, TRIS, and HCl showed a bias toward slightly larger particle sizes compared to the other reference solutions, potentially indicating that HPO42– and TRIS interact to form small aggregates.15 However, it is important to emphasize that our results indicate that negatively charged complexes in solution already represent stable structures, even without a countercation. When these complexes form, they could then become kinetically trapped due to the height of the activation barrier that must be surmounted to escape the contact state.
3.2. Aggregation of the Different Complexes in Solution
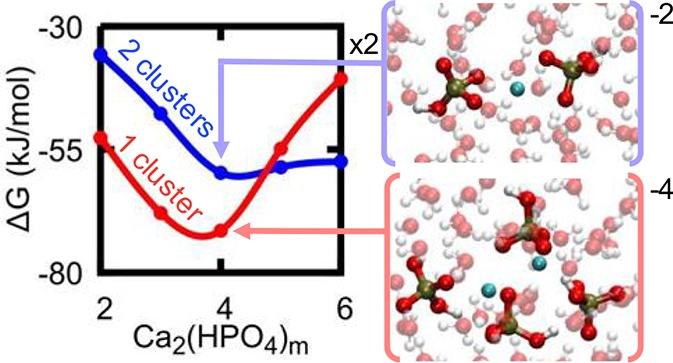
According to the computed equilibria for the [Ca(HPO4)n]−2n+2 complexes under representative experimental conditions, the main bound species present in solution are CaHPO4 and [Ca(HPO4)2]2–. As the concentration of phosphate increases, the more negative [Ca(HPO4)3]4– complex could also become important. To form larger stable complexes or aggregates, as seen experimentally, these species need to interact favorably in solution. The calcium phosphate complexes could aggregate directly in their current form, through the interaction with counterions or by the loss of HPO42–. The free energy changes presented in Figure 3 show some of the possible association pathways of [CaHPO4]0, [Ca(HPO4)2]2–, [Ca(HPO4)3]4–, and [Ca(HPO4)4]6– to form dimeric prenucleation species [Ca2(HPO4)n]−2n+4. The free energy curves for the pathways to form [Ca2(HPO4)2]0, [Ca2(HPO4)3]2–, [Ca2(HPO4)4]4– and [Ca2(HPO4)5]6– exhibit a similar shape, with no significant activation barrier to forming the cluster and with a minimum at a Ca–Ca distance of ∼4 Å, where the formation of [Ca2(HPO4)3]2– and [Ca2(HPO4)4]4– are the most exergonic (the association free energies for the complexes are [Ca2(HPO4)2]0: −15.3 kJ/mol; [Ca2(HPO4)3]2–: −19.5 kJ/mol; [Ca2(HPO4)4]4–: −8.8 kJ/mol; ([Ca2(HPO4)5]6–: −2.7 kJ/mol). However, for the reaction leading to [Ca2(HPO4)6]8– (given in Figure 3), the free energy of binding is endergonic (+10.9 kJ/mol), though again with a local minimum around ∼4 Å. These values agree with the averages reported in Table 2 computed from multiple pathways generally within a few kJ/mol.
Figure 3.
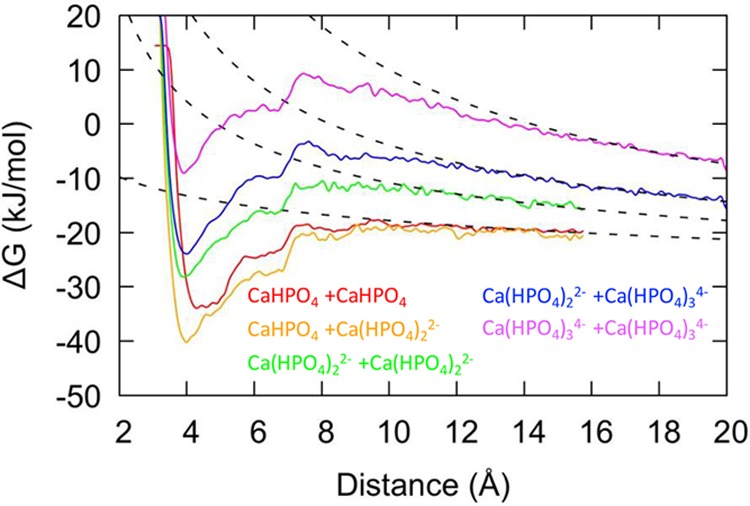
Free energy for association of pairs of calcium hydrogen phosphate clusters plotted as a function of the distance between the Ca atoms. Lines for formation of [Ca2(HPO4)2]0, [Ca2(HPO4)3]2–, [Ca2(HPO4)4]4–, [Ca2(HPO4)5]6–, [Ca2(HPO4)6]8– are colored red, orange, green, dark blue, and magenta, respectively. The free energies for [Ca2(HPO4)2]0, [Ca2(HPO4)3]2–, and [Ca2(HPO4)4]4– stop at 16 Å due to the position of an upper wall, whereas for the other associations shown the upper wall is at 20 Å.
Table 2. Thermodynamic and Structural Properties of Dimeric Calcium Hydrogen Phosphate Clustersa.
| species | number of OW in Ca coordination shell | change in OW in coordination shell from 2[Ca(HPO4)n]−2n+2 | ΔG (kJ/mol) |
|---|---|---|---|
| [Ca2(HPO4)2] | 8 | –2 | –16.4 |
| [Ca2(HPO4)3]2– | 6 | –3 | –20.5 |
| [Ca2(HPO4)4]4– | 6 | –2 | –11.3 |
| [Ca2(HPO4)5]6– | 4 | –3 | +1.4 |
| [Ca2(HPO4)6]8– | 2 | –4 | +15.6 |
Column two gives a summary of the average number of water oxygens (OW) in the two hydration shells of the calcium cations to the nearest integer. The change in water coordination number is given relative to [Ca(HPO4)j,k]−2n+2 (where j+k = n is the number of phosphate species in the cluster; if there is an even number of phosphate species then j = k and if odd j = k – 1). The free energy (ΔG) relative to 2[Ca(HPO4)n]−2n+2 is given as the average over the different pathways for formation, as listed fully in Table S2.
It might be expected that there would be a systematic increase in free energy (i.e., lowering of stability) with the increasing charge of the cluster dimers. However, the computed trend is slightly more nuanced. An initial decrease in free energy with respect to the dissociated clusters is followed by a subsequent increase. Examining the change in water oxygen coordination around calcium (Table 2) and the configurations of the clusters at the minima (Figure 4) enables us to postulate a cause for this trend. We see a nonsystematic decrease in the water coordination to calcium for all clusters, leading to a corresponding increase in number of bonds to phosphate anions (except going from [Ca2(HPO4)3]2– to [Ca2(HPO4)4]4– when there is no change). This is a possible partial explanation of why association occurs despite the high overall negative charge, alongside entropic effects due to the release of water back to solution as previously seen in the neutral calcium carbonate system.48 In Figure 4, we observe that there is a tendency for 2–3 phosphate ions to be bound to both Ca atoms and the remaining phosphate ions to be bound to just one Ca. This trend results in an observable symmetry for the [Ca2(HPO4)2]0 and [Ca2(HPO4)3]6– clusters, while the other species are skewed to allow for water coordination. The interplay between symmetry and entropic stabilization from released water molecules may result in the trend in free energy despite the increasing negative charge.
Figure 4.
Representative geometries for configurations taken from the minima in the region of calcium–calcium distances of ∼4 Å for the free energy curves shown in Figure 3 for (a) [Ca2(HPO4)2]0; (b) [Ca2(HPO4)3]2–; (c) [Ca2(HPO4)4]4–; (d) [Ca2(HPO4)5]6–; and (e) [Ca2(HPO4)6]8–. Ca is cyan, P is tan, O is red, and H is white. Only those water molecules coordinated to calcium are shown for clarity.
We have established the free energy change from [Ca(HPO4)n]−2n+2 to [Ca2(HPO4)m]−2m+4, but, in order to gauge the stability of [Ca2(HPO4)m]−2m+4 clusters, we need to compare the free energies of formation between clusters. In Figure 5, we summarize these free energies and show that the dimeric cluster is more stable than the sum of the relevant monomers until [Ca2(HPO4)5]6– is reached, where the free energy for association is essentially zero to within the level of statistical convergence (see Supporting Information, Tables S1–S2). The formation from ions of the [Ca(HPO4)3]28– cluster is higher than the free energy of formation for two [Ca(HPO4)3]2– separate ions. Conversely the smaller, lower charge [Ca2(HPO4)3]2– exhibits the largest exergonic formation compared to its component clusters [Ca(HPO4)2]2– and CaHPO4, which is consistent with the ACP composition found by Habraken et al. The recent work by Yang et al. suggests that [Ca2(HPO4)3]2– is the most stable intermediate cluster during aggregation. However, they do not report results on the [Ca2(HPO4)4]4– complex, which we find to be the most stable species.
Figure 5.
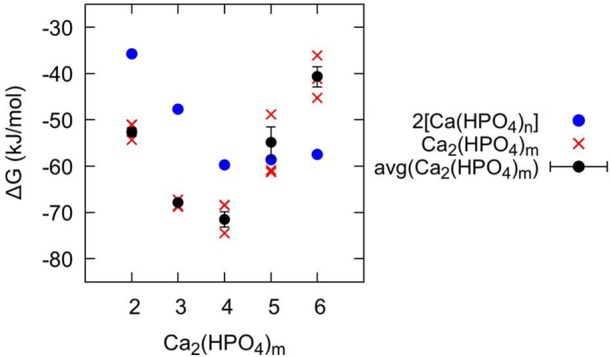
Free energy of formation from the component ions (ΔG) for dimeric clusters [Ca2(HPO4)m]−2m+4 shown in red, compared to the sum of the corresponding free energies for the single calcium species [Ca(HPO4)j,k]−2n+2 shown in blue (where j + k = m). The individual data points for the three methods for calculating ΔG[Ca2(HPO4)m]−2m+4, as outlined in Table S2, are shown with red crosses, while the averages of the two methods giving the largest discrepancy are shown with black circles, where the error bar corresponds to the standard error.
Following the nucleation analysis of Hu et al.,49 the formation of a state of comparable or lower thermodynamic stability should not increase the barrier to nucleation and so could lie on the nucleation pathway. For all but the [Ca(HPO4)3]28– cluster, this is the situation observed here under standard conditions. As the clusters increase in size, the free energy initially decreases until [Ca2(HPO4)4]4– and then begins to increase again (see Figure 5). By way of contrast, in the calcium carbonate system,6,50−51 simulations and potentiometric measurements and titrations have suggested that association of ions into larger structures is driven by an almost monotonic decrease in the free energy per ion pair of addition.8,51 The other key difference is that the clusters observed in simulations for the carbonate system are neutral, while in the phosphate case they exhibit a thermodynamic preference to possess an overall negative charge, at least in the case of small clusters.
4. Nucleation Pathways
From the results discussed above, a number of conclusions can be drawn concerning the nucleation mechanism of calcium phosphate. However, it is important to emphasize that we are not claiming to have demonstrated a definite pathway to nucleation and crystallization since this lies beyond the scale that is readily accessible with current atomistic simulations. In this article, the aim was to critique, using molecular simulations, the conclusions drawn from experimental results reported for the nucleation and growth of calcium phosphate minerals by Habraken et al. and Xie et al. This gives a greater understanding of the mechanism involved and which molecular species could play an important role.20,21 The observation of a calcium-deficient amorphous precursor formed via the interaction of negatively charged complexes is surprising as it is not usual to think of natural processes evolving through electrically unbalanced reactions, and it is thus important to verify its existence.
The calcium phosphate complexes proposed by Habraken et al., [Ca(HPO4)3]4–, are shown here to be (meta)stable. However, at experimental concentrations, the simulations suggest that 11% of the Ca2+ ions would form [Ca(HPO4)2]2–, while 19% would form ion pairs and the rest would be free in solution. Even though equilibrium calculations suggest that [Ca(HPO4)3]4– complexes would form in negligible quantities (0.19%) in solution, they could become kinetically trapped for a short period as the calcium and phosphate solutions are mixed together. Additionally, the amount of each complex present in the solution will depend upon a number of factors that include the solution composition, the presence of organic molecules, and the physical constraints applied to the solution. In the experimental work suggesting the formation of [Ca(HPO4)3]4–, a TRIS buffer was used and could have stabilized this complex. It is well-known that organic molecules can have an important impact on the nucleation and growth of minerals from solution.53−56
This study shows that, for calcium phosphate, the formation of aggregates from the units that could be present in solution, i.e., CaHPO4, [Ca(HPO4)2]2–, and [Ca(HPO4)3]4–, is favorable for the smaller clusters. However, as the aggregation continues, the states become metastable with respect to the smaller clusters and could be important during nucleation. The work by Hu et al. used a modified version of classical nucleation theory (CNT).20,21 Hu et al. argued that if, in contrast to most presentations of CNT, we do not assume that the interfacial energy for clusters is the same as that for the bulk phase, but allow it to change as a function of the size of the forming nuclei, reaching a negligible value for the ion pair, then the transition free energy barrier will be scaled by
where C is a factor that depends on various parameters, including the shape of the cluster, the cluster radius, but most importantly the excess free energy of the cluster. Here α is the interfacial free energy and σ depicts the favorable energy arising from the association of ions in solution. B is a constant that varies according to the shape and density of the nucleating solid. Whether there is a plus or minus sign in the denominator depends on whether the energy minimum occupied by the cluster is of higher or lower energy than the ions (or ion pair) in solution. In the latter case, a minus sign will apply, and the barrier to nucleation will be increased. In the former case, the barrier will be decreased, and the complexes are likely to lie on the nucleation pathway. As we found metastable states for the aggregation of complexes that could be present in solution, following the analysis of Hu et al., these could lie on the nucleation pathway. Habraken et al. extended the approach of Hu et al. to consider the case where the unit of growth for the critical nucleation cluster was a molecular cluster rather than individual ionic species. Evidence for such clusters was seen in their experiments. This implies a different nucleation pathway to that envisaged by simple classical nucleation theory. Our results in Figure 5 show that clusters with fewer than five HPO42– ions are more stable than the units from which they are built. As argued above, this will tend to increase the nucleation barrier. However, it is still possible that the overall barrier is lower because the pathway is different. Unfortunately, it is beyond the ability of simulation to investigate this at present. The most we can say is simply repeating the dimerization process is unlikely to be the only mechanism for the precipitation of amorphous calcium phosphate. The dimer of [Ca(HPO4)3]4– is much higher in energy compared to its separate state, suggesting that [Ca(HPO4)3]28– is unlikely to be required for amorphous growth.
5. Conclusions
Our results, obtained from classical molecular dynamics simulations, provide further evidence that negatively charged complexes of calcium phosphate can indeed form and are stable in solution confirming previous experimental observations. However, calculation of the equilibrium constant for the different calcium phosphate complexes suggests that, in the experimental conditions used by Habraken et al.21 and other authors,20 the ion pair would be the dominant calcium phosphate species in solution. The barrier inhibiting the loss of an HPO42– ion, 17 kJ mol–1, suggests that [Ca(HPO4)3]4– complexes formed could be kinetically trapped to some extent. In this scenario, the large negative charge could attract Ca2+ ions, which would then be able to bridge complexes to form larger charged aggregates, which are (meta)stable, as shown using metadynamics. These inorganic clusters are chemically similar to the amorphous calcium phosphate found experimentally in two separate studies. Additionally, the fact that vesicles in osteoblasts present at the growth front of bone showed a Ca/P ratio of 0.75 suggests the potential importance of this pathway for the in vivo mineralization of calcium phosphate.
The aggregation of CaHPO4 and [Ca(HPO4)2]2– leads to configurations that are more stable in energy than the separated state, suggesting that they could lie on the nucleation pathway. This would increase the barrier to nucleation as above. However, the idea that nucleating clusters could be made from units of molecular complexes, used by Habraken et al. to explain how amorphous calcium phosphate could form at their studied supersaturation, is still viable since the corresponding nucleation pathway could still have a lower barrier overall. Incorporating a dependence on cluster size of the interfacial energy was shown to decrease the nucleation barrier of amorphous calcium phosphate to a reasonable value.
Acknowledgments
This project has been funded by the Australian Research Council (DP160100677) and Curtin University; J.D.G., P.R., and R.D. also acknowledge the Australian Research Council for their Laureate Fellowship (FL180100087) and Future Fellowships (FT130100463 and FT180100385), respectively. The Australian National Computational Infrastructure (NCI) and the Pawsey Supercomputing Centre are acknowledged for the provision of computing resources. J.H.H. and C.L.F. acknowledge an EPSRC Programme Grant (Grant EP/R018820/1), which funds the Crystallization in the Real World consortium. The authors would like to thank Wouter Habraken (Max Planck Institute for Colloids and Interfaces, Potsdam) and Shaun A. Hall for several useful conversations during the course of this work.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.cgd.9b00889.
Supplementary methods containing an explanation on the determination of the lowest free energy structure; table containing every association reaction performed and its corresponding standard free energy, time simulated, biased CV(s), and walled CV(s); table containing the standard free energies for formation of each ion cluster with the corresponding uncertainty; recalculated free energies for formation of each ion cluster from the previous work of Yang et al. for comparison based on alignment of the free energy to the long-range asymptotic limit; figures containing the free energy as a function of distance and/or calcium-water coordination number and a minimum geometry for each association performed; free energy as a function of distance recreated from the previous work of Yang et al. for comparison; supplementary discussion on the alignment of free energy profiles (PDF)
Author Present Address
# Department of Biochemistry, Radboud Institute for Molecular Life Sciences, Radboud University Medical Center, Nijmegen, The Netherlands.
The authors declare no competing financial interest.
Supplementary Material
References
- Zhou H.; Lee J. Nanoscale hydroxyapatite particles for bone tissue engineering. Acta Biomater. 2011, 7 (7), 2769–2781. 10.1016/j.actbio.2011.03.019. [DOI] [PubMed] [Google Scholar]
- Suchanek W.; Yoshimura M. Processing and properties of hydroxyapatite-based biomaterials for use as hard tissue replacement implants. J. Mater. Res. 1998, 13 (1), 94–117. 10.1557/JMR.1998.0015. [DOI] [Google Scholar]
- Ghantani V. C.; Lomate S. T.; Dongare M. K.; Umbarkar S. B. Catalytic dehydration of lactic acid to acrylic acid using calcium hydroxyapatite catalysts. Green Chem. 2013, 15 (5), 1211–1217. 10.1039/c3gc40144h. [DOI] [Google Scholar]
- Freitag R.; Hilbrig F. Isolation and purification of recombinant proteins, antibodies and plasmid DNA with hydroxyapatite chromatography. Biotechnol. J. 2012, 7 (1), 90–102. 10.1002/biot.201100015. [DOI] [PubMed] [Google Scholar]
- Corami A.; Mignardi S.; Ferrini V. Cadmium removal from single- and multi-metal (Cd plus Pb plus Zn plus Cu) solutions by sorption on hydroxyapatite. J. Colloid Interface Sci. 2008, 317 (2), 402–408. 10.1016/j.jcis.2007.09.075. [DOI] [PubMed] [Google Scholar]
- Gebauer D.; Voelkel A.; Coelfen H. Stable Prenucleation Calcium Carbonate Clusters. Science 2008, 322 (5909), 1819–1822. 10.1126/science.1164271. [DOI] [PubMed] [Google Scholar]
- Pouget E. M.; Bomans P. H. H.; Goos J. A. C. M.; Frederik P. M.; de With G.; Sommerdijk N. A. J. M. The Initial Stages of Template-Controlled CaCO3 Formation Revealed by Cryo-TEM. Science 2009, 323 (5920), 1455–1458. 10.1126/science.1169434. [DOI] [PubMed] [Google Scholar]
- Quigley D.; Freeman C. L.; Harding J. H.; Rodger P. M. Sampling the structure of calcium carbonate nanoparticles with metadynamics. J. Chem. Phys. 2011, 134 (4), 044703. 10.1063/1.3530288. [DOI] [PubMed] [Google Scholar]
- Demichelis R.; Raiteri P.; Gale J. D.; Quigley D.; Gebauer D. Stable prenucleation mineral clusters are liquid-like ionic polymers. Nat. Commun. 2011, 2, 590 10.1038/ncomms1604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smeets P. J. M.; Finney A. R.; Habraken W. J. E. M.; Nudelman F.; Friedrich H.; Laven J.; De Yoreo J. J.; Rodger P. M.; Sommerdijk N. A. J. M. A classical view on non-classical nucleation. Proc. Natl. Acad. Sci. U. S. A. 2017, 114, E7882. 10.1073/pnas.1700342114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henzler K.; Fetisov E. O.; Galib M.; Baer M. D.; Legg B. A.; Borca C.; Xto J. M.; Pin S.; Fulton J. L.; Schenter G. K.; Govind N.; Siepmann J. I.; Mundy C. J.; Huthwelker T.; De Yoreo J. J. Supersaturated calcium carbonate solutions are classical. Sci. Adv. 2018, 4 (1), eaao6283 10.1126/sciadv.aao6283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Betts F.; Posner A. S. X-ray radial-distribution study of amorphous calcium-phosphate. Mater. Res. Bull. 1974, 9 (3), 353–360. 10.1016/0025-5408(74)90087-7. [DOI] [Google Scholar]
- Kanzaki N.; Treboux G.; Onuma K.; Tsutsumi S.; Ito A. Calcium phosphate clusters. Biomaterials 2001, 22 (21), 2921–2929. 10.1016/S0142-9612(01)00039-4. [DOI] [PubMed] [Google Scholar]
- Treboux G.; Layrolle P.; Kanzaki N.; Onuma K.; Ito A. Existence of Posner’s cluster in vacuum. J. Phys. Chem. A 2000, 104 (21), 5111–5114. 10.1021/jp994399t. [DOI] [Google Scholar]
- Onuma K.; Ito A. Cluster growth model for hydroxyapatite. Chem. Mater. 1998, 10 (11), 3346–3351. 10.1021/cm980062c. [DOI] [Google Scholar]
- Wang L.; Li S.; Ruiz-Agudo E.; Putnis C. V.; Putnis A. Posner’s cluster revisited: direct imaging of nucleation and growth of nanoscale calcium phosphate clusters at the calcite-water interface. CrystEngComm 2012, 14 (19), 6252–6256. 10.1039/c2ce25669j. [DOI] [Google Scholar]
- Mancardi G.; Tamargo C. E. H.; Tommaso D. D.; de Leeuw N. H. Detection of Posner’s clusters during calcium phosphate nucleation: a molecular dynamics study. J. Mater. Chem. B 2017, 5, 7274–7284. 10.1039/C7TB01199G. [DOI] [PubMed] [Google Scholar]
- Van Maaren P. J.; Van Der Spoel D. Molecular Dynamics Simulations of Water with Novel Shell-Model Potentials. J. Phys. Chem. B 2001, 105, 2618. 10.1021/jp003843l. [DOI] [Google Scholar]
- Raiteri P.; Demichelis R.; Gale J. D. Development of Accurate Force Fields for the Simulation of Biomineralization. Methods Enzymol. 2013, 532, 3–23. 10.1016/B978-0-12-416617-2.00001-1. [DOI] [PubMed] [Google Scholar]
- Xie B.; Halter T. J.; Borah B. M.; Nancollas G. H. Tracking Amorphous Precursor Formation and Transformation during Induction Stages of Nucleation. Cryst. Growth Des. 2014, 14, 1659–1665. 10.1021/cg401777x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Habraken W.; Tao J. H.; Brylka L. J.; Friedrich H.; Bertinetti L.; Schenk A. S.; Verch A.; Dmitrovic V.; Bomans P. H. H.; Frederik P. M.; Laven J.; van der Schoot P.; Aichmayer B.; de With G.; DeYoreo J. J.; Sommerdijk N. Ion-association complexes unite classical and non-classical theories for the biomimetic nucleation of calcium phosphate. Nat. Commun. 2013, 4, 1507 10.1038/ncomms2490. [DOI] [PubMed] [Google Scholar]
- Beniash E.; Metzler R. A.; Lam R. S. K.; Gilbert P. U. P. A. Transient Amorphous Calcium Phosphate in Forming Enamel. J. Struct. Biol. 2009, 166 (2), 133–143. 10.1016/j.jsb.2009.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akiva A.; Kerschnitzki M.; Pinkas I.; Wagermaier W.; Yaniv K.; Fratzl P.; Addadi L.; Weiner S. Mineral Formation in the Larval Zebrafish Tail Bone Occurs via an Acidic Disordered Calcium Phosphate Phase. J. Am. Chem. Soc. 2016, 138 (43), 14481–14487. 10.1021/jacs.6b09442. [DOI] [PubMed] [Google Scholar]
- Mahamid J.; Sharir A.; Gur D.; Zelzer E.; Addadi L.; Weiner S. Bone mineralization proceeds through intracellular calcium phosphate loaded vesicles: A cryo-electron microscopy study. J. Struct. Biol. 2011, 174 (3), 527–535. 10.1016/j.jsb.2011.03.014. [DOI] [PubMed] [Google Scholar]
- Meldrum F. C.; Coelfen H. Controlling Mineral Morphologies and Structures in Biological and Synthetic Systems. Chem. Rev. 2008, 108 (11), 4332–4432. 10.1021/cr8002856. [DOI] [PubMed] [Google Scholar]
- Dorozhkin S. V. Amorphous calcium (ortho)phosphates. Acta Biomater. 2010, 6 (12), 4457–4475. 10.1016/j.actbio.2010.06.031. [DOI] [PubMed] [Google Scholar]
- Zahn D. Mechanisms of Calcium and Phosphate Ion Association in Aqueous Solution Z. Anorg. Allg. Chem. 2004, 630, 1507–1511. 10.1002/zaac.200400151. [DOI] [Google Scholar]
- Mancardi G.; Terranova U.; de Leeuw N. H. Calcium phosphate prenucleation complexes in water by means of ab initio Molecular Dynamics simulations. Cryst. Growth Des. 2016, 16 (6), 3353–3358. 10.1021/acs.cgd.6b00327. [DOI] [Google Scholar]
- Almora-Barrios N.; De Leeuw N. H. Molecular Dynamics Simulation of the Early Stages of Nucleation of Hydroxyapatite at a Collagen Template. Cryst. Growth Des. 2012, 12 (2), 756–763. 10.1021/cg201092s. [DOI] [Google Scholar]
- Ma J. A molecular dynamics study on the nucleation of calcium phosphate regulated by collagen. J. Mater. Sci. 2014, 49 (8), 3099–3106. 10.1007/s10853-013-8011-4. [DOI] [Google Scholar]
- Yang X.; Wang M.; Yang Y.; Cui B.; Xu Z.; Yang X. Physical origin underlying the prenucleationcluster-mediated nonclassical nucleation pathways for calcium phosphate. Phys. Chem. Chem. Phys. 2019, 21, 14530. 10.1039/C9CP00919A. [DOI] [PubMed] [Google Scholar]
- Demichelis R.; Garcia N. A.; Raiteri P.; Innocenti Malini R.; Freeman C. L.; Harding J. H.; Gale J. D. Simulation of Calcium Phosphate Species in Aqueous Solution: Force Field Derivation. J. Phys. Chem. B 2018, 122, 1471–1483. 10.1021/acs.jpcb.7b10697. [DOI] [PubMed] [Google Scholar]
- Busenberg E.; Plummer N. L. Thermodynamics of Magnesian Calcite Solid-Solutions at 25 C and 1 Atm Total Pressure. Geochim. Cosmochim. Acta 1989, 53, 1189–1208. 10.1016/0016-7037(89)90056-2. [DOI] [Google Scholar]
- Garcia N. A.; Raiteri P.; Vlieg E.; Gale J. D. Water Structure, Dynamics and Ion Adsorption at the Aqueous {010} Brushite Surface. Minerals 2018, 8 (8), 334. 10.3390/min8080334. [DOI] [Google Scholar]
- Raiteri P.; Demichelis R.; Gale J. D. Thermodynamically consistent force field for Molecular Dynamics simulations of alkaline-earth carbonates and their aqueous speciation. J. Phys. Chem. C 2015, 119 (43), 24447–24458. 10.1021/acs.jpcc.5b07532. [DOI] [Google Scholar]
- Wu Y.; Tepper H. L.; Voth G. A. Flexible simple point-charge water model with improved liquid-state properties. J. Chem. Phys. 2006, 124 (2), 024503. 10.1063/1.2136877. [DOI] [PubMed] [Google Scholar]
- Raiteri P.; Laio A.; Gervasio F. L.; Micheletti C.; Parrinello M. Efficient Reconstruction of Complex Free Energy Landscapes by Multiple Walkers Metadynamics. J. Phys. Chem. B 2006, 110 (8), 3533–3539. 10.1021/jp054359r. [DOI] [PubMed] [Google Scholar]
- Barducci A.; Bussi G.; Parrinello M. Well-Tempered Metadynamics: A Smoothly Converging and Tunable Free-Energy Method. Phys. Rev. Lett. 2008, 100 (2), 20603. 10.1103/PhysRevLett.100.020603. [DOI] [PubMed] [Google Scholar]
- Plimpton S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117 (1), 1–19. 10.1006/jcph.1995.1039. [DOI] [Google Scholar]
- Bonomi M.; Branduardi D.; Bussi G.; Camilloni C.; Provasi D.; Raiteri P.; Donadio D.; Marinelli F.; Pietrucci F.; Broglia R. A.; Parrinello M. PLUMED: A portable plugin for free-energy calculations with molecular dynamics. Comput. Phys. Commun. 2009, 180 (10), 1961–1972. 10.1016/j.cpc.2009.05.011. [DOI] [Google Scholar]
- Zhang Q.; Jiang Y.; Gou B.-D.; Huang J.; Gao Y.-X.; Zhao J.-T.; Zheng L.; Zhao Y.-D.; Zhang T.-L.; Wang K. In Situ Detection of Calcium Phosphate Clusters in Solution and Wet Amorphous Phase by Synchrotron X-ray Absorption Near-Edge Spectroscopy at Calcium K-Edge. Cryst. Growth Des. 2015, 15 (5), 2204–2210. 10.1021/cg5018505. [DOI] [Google Scholar]
- Kellermeier M.; Raiteri P.; Berg J. K.; Kempter A.; Gale J. D.; Gebauer D. Entropy Drives Calcium Carbonate Ion Association. ChemPhysChem 2016, 17 (21), 3535. 10.1002/cphc.201600653. [DOI] [PubMed] [Google Scholar]
- Hu Q.; Nielsen M. H.; Freeman C. L.; Hamm L. M.; Tao J.; Lee J. R. I.; Han T. Y. J.; Becker U.; Harding J. H.; Dove P. M.; De Yoreo J. J. The thermodynamics of calcite nucleation at organic interfaces: Classical vs. non-classical pathways. Faraday Discuss. 2012, 159, 509–523. 10.1039/c2fd20124k. [DOI] [Google Scholar]
- Gebauer D.; Coelfen H. Prenucleation clusters and non-classical nucleation. Nano Today 2011, 6 (6), 564–584. 10.1016/j.nantod.2011.10.005. [DOI] [Google Scholar]
- Li Q. X.; Song B. Z.; Yang Z. Q.; Fan H. L. Electrolytic conductivity behaviors and solution conformations of chitosan in different acid solutions. Carbohydr. Polym. 2006, 63 (2), 272–282. 10.1016/j.carbpol.2005.09.024. [DOI] [Google Scholar]
- Wallace A. F.; Hedges L. O.; Fernandez-Martinez A.; Raiteri P.; Gale J. D.; Waychunas G. A.; Whitelam S.; Banfield J. F.; De Yoreo J. J. Microscopic Evidence for Liquid-Liquid Separation in Supersaturated CaCO3 Solutions. Science 2013, 341 (6148), 885–889. 10.1126/science.1230915. [DOI] [PubMed] [Google Scholar]
- Freeman C. L.; Harding J. H.; Quigley D.; Rodger P. M. Structural Control of Crystal Nuclei by an Eggshell Protein. Angew. Chem., Int. Ed. 2010, 49 (30), 5135–5137. 10.1002/anie.201000679. [DOI] [PubMed] [Google Scholar]
- Gower L. B.; Odom D. J. Deposition of calcium carbonate films by a polymer-induced liquid-precursor (PILP) process. J. Cryst. Growth 2000, 210 (4), 719–734. 10.1016/S0022-0248(99)00749-6. [DOI] [Google Scholar]
- Olszta M. J.; Cheng X.; Jee S. S.; Kumar R.; Kim Y.-Y.; Kaufman M. J.; Douglas E. P.; Gower L. B. Bone structure and formation: A new perspective. Mater. Sci. Eng., R 2007, 58 (3–5), 77–116. 10.1016/j.mser.2007.05.001. [DOI] [Google Scholar]
- Evans J. S. ″Tuning in″ to Mollusk Shell Nacre- and Prismatic-Associated Protein Terminal Sequences. Implications for Biomineralization and the Construction of High Performance Inorganic-Organic Composites. Chem. Rev. 2008, 108 (11), 4455–4462. 10.1021/cr078251e. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.