Organizing and analyzing the activity data in NHANES

Abstract

The NHANES study contains objectively measured physical activity data collected using hip-worn accelerometers from multiple cohorts. However, using the accelerometry data has proven daunting because: 1) currently, there are no agreed upon standard protocols for data storage and analysis; 2) data exhibit heterogeneous patterns of missingness due to varying degrees of adherence to wear-time protocols; 3) sampling weights need to be carefully adjusted and accounted for in individual analyses; 4) there is a lack of reproducible software that transforms the data from its published format into analytic form; and 5) the high dimensional nature of accelerometry data complicates analyses. Here, we provide a framework for processing, storing, and analyzing the NHANES accelerometry data for the 2003–2004 and 2005–2006 surveys. We also provide an NHANES data package in R, to help disseminate high quality, processed activity data combined with mortality and demographic information. Thus, we provide the tools to transition from “available data online” to “easily accessible and usable data”, which substantially reduces the large upfront costs of initiating studies of association between physical activity and human health outcomes using NHANES. We apply these tools in an analysis showing that accelerometry features have the potential to predict 5-year all cause mortality better than known risk factors such as age, cigarette smoking, and various comorbidities.

1. Introduction

The National Health and Nutrition Examination Survey (NHANES) is a large, stratified, multistage survey conducted by the Centers for Disease Control (CDC) which collects health and nutrition data on the US population. According to the NHANES website, this data is collected with the intent that it will be analyzed to “help develop sound public health policy, direct and design health programs and services, and expand the health knowledge for the Nation” [2]. NHANES is one of the largest and most important studies in terms of size, scope, diversity, and accessibility of the data. Moreover, NHANES was the first study to make public a large dataset containing activity information measured using accelerometers when they released accelerometry data from the 2003–2004 and 2005–2006 samples. Recently, the UK Biobank has made public accelerometry data on approximately 100, 000 individuals from the UK, who will be followed up for up to 20 years [27]. This is another extraordinary resource, but our focus for this paper is the NHANES. As NHANES is representative for the non-institutionalized US population, results are generalizable to well-defined sub-populations of the US by using survey re-weighting techniques. Moreover, NHANES over-samples underrepresented groups (racial minorities, elderly, etc.) and can be linked to US national mortality data. This allows for the study of cross-sectional associations between individual characteristics and health outcomes as well as their association with future mortality. In this paper we are especially interested in the prediction of mortality, ranking of the most predictive covariates, the relative effects of accelerometry-derived predictors of mortality, and building of parsimonious prediction models based on the NHANES data.

The association between activity and health outcomes and mortality is an area of active research in a wide range of scientific applications including sleep, mood disorders, neurodegenerative diseases, diabetes, obesity, and aging [3,9,11,10,23,24,26]. In addition to providing objective measures of overall physical activity (PA), the minute-level resolution of most accelerometry data is sufficiently high to identify daily patterns of PA and their potential association with health and mortality. NHANES collected objectively measured PA data using hip-worn accelerometers in the 2003–2004 and 2005–2006 waves. More recently, NHANES has transitioned to wrist-worn accelerometers, but that data is not currently publicly available.

While the NHANES data is publicly available, actually analyzing the data requires a non-trivial amount of background information, data processing and linking, as well as knowledge of survey weighting and accelerometry data. Since there is currently no comprehensive reference for how to begin working with this data, each working group undergoes a lengthy learning process. This process is highly inefficient because it: 1) deters interested researchers from using the data; 2) requires considerable time and resources to go through the learning process; and 3) increases the chances that errors are made by independently repeating the same complex process with different research groups. We address these problems by providing reference datasets via the R [21] data package rnhanesdata [13] and provide detailed information about the data processing steps. Our hope is that the package will be used by multiple research groups, which could improve reproducibility and generalizability of results.

This document is organized as follows. In Section 2, we describe the NHANES study, accelerometry data transformation procedure, and how to begin working quickly with the NHANES data. In Section 3.1, we present two approaches for identifying interpretable features of accelerometry data which can be used as predictors in regression analyses. In Section 3.3, we identify key predictors of mortality in the NHANES study. Finally, we conclude with a discussion in Section 4.

2. Data

The NHANES data is publicly available from the Center for Disease Control at https://www.cdc.gov/nchs/nhanes/index.htm and is broadly categorized into six areas: demographics, dietary, examination, laboratory, questionnaire, and limited access. The accelerometry data for a particular NHANES cohort can be downloaded from the “Physical Activity Monitor” subcategory under the “Examination Data” tab. The NHANES uses an alphabetic naming convention to differentiate data for various waves, starting with the 1999–2000 wave. For example, data file names from the 2003–2004 wave end in “_C.ext” where .ext is the file extension (.csv, .xpt, etc.). Similarly, data file names for the 2005–2006 wave end in “_D.ext”. Currently, only the 2003–2004 (“PAXRAW_C.XPT”) and 2005–2006 (“PAXRAW_D.XPT”) waves of accelerometry data have been released, but data for subsequent waves will be released on a semi-regular schedule.

2.1. Accelerometry Data

The NHANES accelerometry data is initially provided as zipped .xpt files (SAS XPORT), which, once unzipped, can be loaded into most statistical software packages. The unzipped files are large at approximately 2.5Gb per wave, which makes them difficult to use. The size of the NHANES files is due to the long data storage format, with one row per subject-minute. The columns of the long format data correspond to: 1) SEQN - a unique subject identifier; 2) PAXSTAT - data reliability flag; 3) PAXCAL - device calibration flag; 4) PAXDAY - day of the week; 5) PAXN - sequential observation number; 6) PAXHOUR - hour of the day; 7) PAXMINUT - minute of the hour; 8) PAXINTEN - intensity value (activity count); and 9) PAXSTEP - device step count (not available for the 2003–2004 wave). See Figure 1 for an illustration of the data format. Here, subject 31128 does not have data quality issues and has observed activity counts of 166, 27, and 0 for the first three minutes on the day the device was activated (00:00–00:01, 00:01–00:02, and 00:02–00:03). This data storage structure results in a data matrix of dimension 72, 250,027 × 9 for the 2005–2006 wave; we call this the long format of the data.

Fig. 1:

First 3 rows of the ‘PAXRAW_D.XPT’ file, the 2005–2006 accelerometry data file available for download from the CDC website

The long format makes even simple analyses challenging and computationally expensive. For example, even calculating the average activity between 10:00AM and 11:00AM for all subjects is not straightforward since subjects have a varying number of observed minutes due to missing patterns. Keeping track of missing minutes would require careful coding (indexing) and even adding columns to the data which would substantially increase the memory footprint of the data. Moreover, identifying wear-time is a prominent concern and a key methodologic challenge in analyzing the NHANES accelerometry data. Using the long format of the data makes calculating the amount of wear-time within a day more complex and less intuitive than our proposed alternative, which we call the 1440+ format.

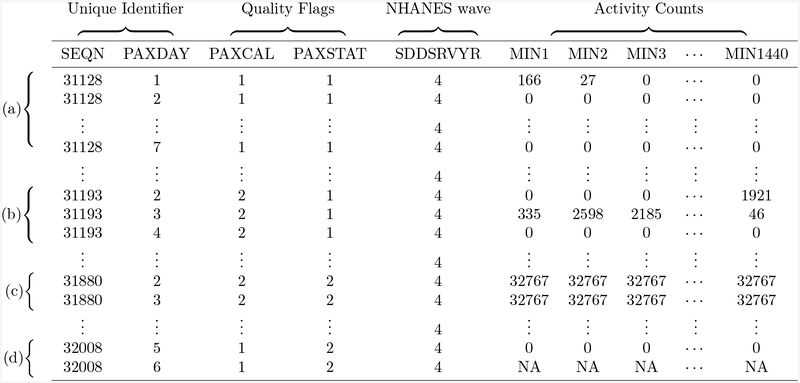
To address the problems associated with the long data format, we propose to store the data as one row per subject-day. That is, for each NHANES wave with N_w participants with accelerometry data, the accelerometry data will be stored as an (7 * N_w) × 1440 data matrix, where 7 refers to the number of days each subject was instructed to wear the accelerometer device and 1440 corresponds to the number of minutes in a day. To the accelerometry data we add columns for subject identifier, day of the week, the two data quality flags, and NHANES wave identifier. This results in a data matrix of size (7* N_w) × 1445, with rows ordered first by subject, and then by chronological, descending order within subjects. See Figure 2 for an example of this data format. We call this the 1440+ format and we suggest it as the standard format for analyzing aggregated accelerometry data at the minute level. Some studies have recorded the data at other fractions of the minute level (e.g. half a minute or two minutes); the same format can easily be used for such studies. Storing the data in the 1440+ format reduces the file size by nearly 80% and streamlines the process of identifying non-wear time.

Fig. 2:

Several rows from the processed 2005–2006 wave accelerometry data with various combinations of data quality indicators and missing data patterns. Specifically, (a) corresponds to a subject with 7 full days of activity data, no data quality flag indicators, and no missing data; (b) shows a subject where the device was marked as uncalibrated upon return to NHANES; (c) presents a subject with both an uncalibrated device and data reliability issue; and (d) illustrates a subject with their last two days of data missing (other missing day not shown).

In NHANES, participants were asked to wear the device 7 consecutive days during waking hours with the exception of swimming and bathing. Using established criteria for identifying periods of non-wear, it can be seen that non-compliance is highly prevalent among subjects. That is, many subjects either forgot to take off the device when they slept, forgot to put the device on upon waking, or generally forgot/refused to wear the device for one or more days. As a result, there are many subjects with less/more than the expected amount of wear-time in an given day, as well as subjects with fewer than 7 days of data. To account for the non-wear time, we create a data matrix of non-wear flags separately for each wave. The processed non-wear flags in the rnhanesdata package are derived using an algorithm implemented in the accelerometry package [29], which is a slight modification of [28]. This algorithm requires the specification of several parameters which control how aggressively the algorithm detects non-wear flags. Users are able to create their own matrix of non-wear flags using different algorithm parameters via the process_flags() function.

Once the activity data has been transformed and non-wear flags have been calculated, the data is ready to be merged with covariate and survey weight data. In NHANES, demographic data are generally straightforward to use (e.g. race, gender), however several covariates need additional processing to be expressed in the expected format (e.g. alcohol consumption, smoking).

NHANES does not have a simple random sample from the US population, instead it has a complex survey design. Features of the sampling strategy include oversampling, adjustment for non-response, and post-stratification. Taking all these design aspects into consideration, NHANES assigns a sample weight to each participant. That sample weight indicates the number of people in the population who are “represented” by that particular individual. Survey weights need to be addressed in order to obtain results that are generalizable to the US population. Even simple plots such as histograms can be misleading without incorporating survey weight information. The survey [16] package in the statistical software R [21] has many tools to perform survey weighted analyses and create survey weighted exploratory plots. However, an issue arises in the context of missing data. More specifically, if an analysis requires subsetting NHANES participants based on missing data, unless the data is missing completely at random, the analysis sample is potentially no longer representative of the non institutionalized US population, even accounting for survey weights. This can result in biased estimates for model parameters, the degree of which can grow substantially as rates of missingness increase. Fundamentally, addressing the problem of missing data while retaining generalizability involves either: 1) re-weighting individuals in the data; or 2) imputing the missing data. While a full discussion of approaches for handling missing data is beyond the scope of this paper, one approach that is implemented in the rnhanesdata package is to assume that within certain age, sex, and ethnicity categories, individuals for whom data is completely observed are representative of those for whom data is missing. Although this re-weighting procedure is used in other applications and packages [30,18], we believe the issue of re-weighting will need to be revisited in the future. We discuss our approach to this issue further in Section 2.4.

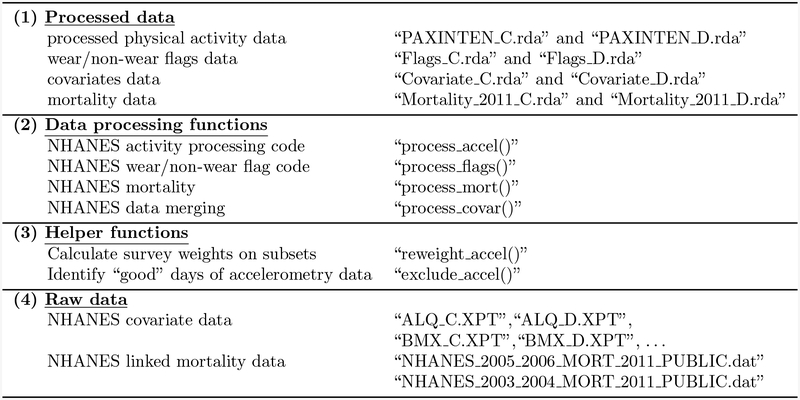
We aim to provide a template for processing and analyzing accelerometry data in the context of the NHANES study, though the standards and methods apply more generally. In addition to the processed data, the supplemental material contains all code necessary to replicate our results. Our hope is to enhance reproducibility of future analyses using the NHANES accelerometry data, reduce substantially the learning time for new users, and reduce the number of potential errors associated with multiple research group specific pre-processing pipelines. The data package (rnhanesdata) can be downloaded from GitHub at https://github.com/andrew-leroux/rnhanesdata. Figure 3 describes the contents and structure of the data package. With this data package, getting started with NHANES is simple. Even though we have been working with accelerometry data for years, the time investment required to understand the NHANES accelerometry data structure, derive non-wear flags, understand the survey structure of NHANES, design a processing pipeline, and create a data package was substantial. With this data package and tutorial paper we would have saved an immense amount of productive time across multiple individuals in our working group.

Fig. 3:

Data package structure and contents. Note that all “.rda” files referenced in the Processed data section are in matrix format and can be readily written to .csv or other standard formats. Although the long format accelerometry data is not available in the data package due to file sizes, the original data can be downloaded directly from the CDC and processed using the process-accel() function.

2.2. Covariate Data

Demographic and personal information collected by NHANES is reported in questionnaire format. Some questions are fairly straightforward, such as those inquiring about individuals’ age and education. However, producing other variables of interest requires merging information from multiple questions. For example, creating the variable indicator of whether or not an individual smokes cigarettes requires information from two separate questions. Similarly, creating a variable associated with alcohol consumption which categorizes individuals into ‘non-drinker’, ‘moderate drinker’, or ‘heavy drinker’, requires information from 4 different questions. Thus, the creation of both variables contains a set of decisions and choices regarding the definition of said variables that would be hard to reproduce and communicate without associated software. The code in the rnhanesdata package provides these details to ensure reproducibility of the covariate building process. In particular, we provide a vignette that walks through the creation of each of the processed demographic and lifestyle variables included in the package. An additional complexity is that NHANES covariate data is stored across multiple .xpt files. The rnhanesdata package contains several of these files which include demographic information (including survey weights). In addition, the function process_covar() will search all .xpt files in a directory (locally, or in the package datasets) for variables either by name or return all variables in a data matrix format. This can be used to easily access and merge variables across many different NHANES data files and waves, including those waves without accelerometry data.

2.3. Mortality Data

The National Center for Health Statistics provides a mechanism for linking NHANES waves with death certificate records from the National Death Index (NDI) [19]. The particular records used are publicly available and can be downloaded directly from ftp://ftp.cdc.gov/pub/Health_Statistics/NCHS/datalinkage/linked_mortality/ and are updated semi-regularly. The raw mortality data is not in an analysis ready format. To facilitate use of this mortality data, the rnhanesdata package provides both processed and raw versions of this data, as well as the code used to process it via the function process_mort(). The current mortality data in the package was released in 2011, however we intend to update the package with future data releases. We use the naming convention ”Mortality_**_*” where ** indicates the mortality data release year and * denotes NHANES wave. In the interest of reproducibility, moving forward we will retain mortality data from previous releases in the data package.

2.4. Survey Weights

The survey weight in NHANES for one individual correspond to the number of individuals in the US population that “are represented by” that particular individual. Each individual may have several survey weights depending on whether they participated in sub-studies within NHANES. As a general rule, an analysis should use the survey weight associated with the “innermost” sub-study among variables included in the analysis. For example, if one is interested in modelling mortality as a function of household income (collected at the household interview) and the accelerometry data, the analysis should use the “examination weights” (WTMEC2YR) as the accelerometry data is collected on a sub-sample of the interview portion of the study. An additional step is required when combining data from multiple waves. In the case of the 2003–2004 and 2005–2006 waves, this adjustment corresponds to dividing the survey weights by a factor of 2.

In addition to adjustments required for combining data across waves, it may be desirable to adjust survey weights when there is missing data in order to retain the generalizability of results. There are many ways this re-weighting can be done and each analysis should involve careful consideration of whether and how to re-weight. In the rnhanesdata package we take a very general approach that uses three variables which are recorded for all participants and is similar to the procedure implemented in the SAS routine reweight.pam [18,31]. More specifically, we stratify individuals by age, gender, and ethnicity, then re-weight each individual with complete data within each strata to be representative of the “total” strata size.

The stratification approach described above implicitly assumes that within these age, gender, and ethnicity strata, individuals with complete data are representative of the corresponding strata in the general population. Care needs to be taken when using this approach such that the age strata used for re-weighting are appropriate given any exclusion criteria. For example, it would not make sense to set one of the age strata to be [50, 60) but exclude any subjects under 59. This would result in those aged [59, 60) being highly up-weighted in order to make them representative of everyone age [50, 60) in the larger population. In addition, any subsetting based on age should be done using the age that corresponds to the survey weight of interest. That is, individuals’ age at the interview (RIDAGEMN) is generally not the same as their age at the exam (RIDAGEEX).

Finally, normalizing the survey weights helps with numerical stability for the estimation procedures employed by statistical software packages and is in fact necessary for obtaining accurate point estimates and standard errors outside of specialized survey software. The rnhanesdata package contains the function reweight_accel() which will automatically re-calculate a suite of the survey weights and normalized survey weights for a subset of the 2003–2004 and 2005–2006 waves, either separately or combined using the re-weighting procedure described above. The default age strata used in the re-weighting procedure correspond to the age categories targeted in the NHANES 2003–2004 and 2005–2006 waves for white Americans [4], though this can be specified by a user.

3. Data Application - Mortality in NHANES

We apply our data package to identify features of activity associated with mortality in the NHANES study, and assess their predictive value in combination with major demographic and health predictors. Specifically, we are interested in predicting 5-year mortality. If Y_i denotes the outcome Dead/Alive after 5 years and W_i denotes a column vector of covariates then we fit logistic regressions of the form

$$\{\begin{array}{ll}{Y}_i\hfill & ~\text{ Bernoulli }\left(p_i\right);\hfill \\ \text{log }\left(\frac{p_i}{1-p_i}\right)\hfill & ={\mathbf{W}}_i^t\beta \hfill \end{array}$$ (1)

Throughout this paper we use bold font to indicate data vectors and matrices and regular font to indicate data scalars. To conduct the analysis we exclude individuals based on age, missing data, and number of days of accelerometry data. In total, the NHANES 2003–2004 and 2005–2006 waves has 14, 631 participants with some accelerometry data. We excluded individuals who were: 1) younger than 50 or 85 and older at the time they wore the accelerometer; 2) missing any demographic predictor variables we adjust for; 3) had fewer than 3 days of data with at least 10 hours of estimated wear time; 4) missing mortality information; 5) alive with follow up less than 5 years. This set of exclusion criteria yielded a sample size of 3,198 participants. The vast majority of individuals were excluded based on the age criteria (10, 859 participants). Of the 3, 772 individuals who met our age criteria, the majority of individuals excluded were removed for accelerometer calibration/data quality issues (239) or too few days of “good” accelerometer data (278). The remaining 57 individuals excluded were removed for missing mortality or predictor data. As a final note, there were an additional 335 individuals who participated in the examination portion of the study who meet our age criteria but who have no accelerometry data.

Table 1 presents summary statistics comparing participants who had accelerometry data stratified by exclusion from our study. Both unadjusted and survey weight adjusted results are reported. Survey weighting was performed using the tableone package [35] in R which interfaces with the survey package [16]. The survey weighted results indicate that individuals who were excluded tend to be less educated (p = 0.002), more likely to have missing alcohol data (p < 0.001), be current smokers (p = 0.002), have a body mass index that qualifies as obese (p = 0.002), higher rates of Diabetes (p = 0.013), Stroke (p = 0.046), and self reported mobility problems (p = 0.001). In addition, although not statistically significant for a type-I error rate of 0.05, mortality is higher in the excluded group (15.2% vs 11.4%). Taken together, these results suggests that individuals who were excluded from our study were in general less healthy than those who were included, which does not support a missing completely at random hypothesis. However, it is not clear to what extent the re-weighting procedure described in Section 2.4 will address any differential missingness as the two groups appear to be fairly similar in terms of racial, gender, and age composition. We acknowledge this potential limitation of our analyses and proceed forward using the adjusted (re-weighted) survey weights.

Table 1:

Unadjusted and survey-weighted population characteristics of individuals excluded from the analysis for a reason other than age. Note that adjusting for survey weights can result in non-integer estimates for categorical variables (i.e. 444.7 individuals with Diabetes included in the analysis). We rounded the survey weighted categorical variables to the nearest integer. P-values associated with continuous variables were calculated using t-tests, while chi-squared tests were used for categorical variables.

	Unadjusted			Survey weighted
	Included (n = 3,198)	Excluded (n = 574)	p-value	Included (n = 3,243)	Excluded (n = 529)	p-value
Age (mean (sd))	65.97 (9.68)	65.78 (9.94)	0.674	62.97 (9.48)	63.21 (9.74)	0.723
Gender (% Female)	1587 (49.6)	283 (49.3)	0.923	1733.1 (53.4)	277.0 (52.4)	0.718
Race (%)			0.175			0.183
White	1862 (58.2)	310 (54.0)		2609.2 (80.5)	405.1 (76.6)
Mexican American	572 (17.9)	101 (17.6)		128.7 (4.0)	26.6 (5.0)
Other Hispanic	61 (1.9)	10 (1.7)		78.3 (2.4)	11.8 (2.2)
Black	601 (18.8)	132 (23.0)		288.8 (8.9)	63.0 (11.9)
Other	102 (3.2)	21 (3.7)		138.2 (4.3)	22.3 (4.2)
Education (%)			0.001			<0.001
Less than high school	1021 (31.9)	216 (38.0)		603.2 (18.6)	131.8 (25.2)
High school	792 (24.8)	152 (26.8)		875.1 (27.0)	165.5 (31.6)
More than high school	1385 (43.3)	200 (35.2)		1764.9 (54.4)	226.3 (43.2)
Cigarette smoking (%)			0.001			0.002
Never	1430 (44.7)	236 (41.4)		1479.2 (45.6)	210.9 (40.0)
Former	1229 (38.4)	202 (35.4)		1209.8 (37.3)	193.4 (36.7)
Current	539 (16.9)	132 (23.2)		554.2 (17.1)	122.5 (23.3)
Alcohol consumption (%)			<0.001			<0.001
Moderate Drinker	1512 (47.3)	230 (40.1)		1680.1 (51.8)	251.3 (47.5)
Non-Drinker	1362 (42.6)	256 (44.6)		1191.9 (36.8)	196.7 (37.2)
Heavy Drinker	188 (5.9)	26 (4.5)		233.7 (7.2)	27.4 (5.2)
Missing alcohol	136 (4.3)	62 (10.8)		137.6 (4.2)	53.4 (10.1)
Body mass index (%)			<0.001			0.002
Underweight	30 (0.9)	12 (2.2)		34.8 (1.1)	10.6 (2.1)
Normal	827 (25.9)	125 (23.2)		875.8 (27.0)	120.2 (24.0)
Overweight	1218 (38.1)	174 (32.3)		1219.9 (37.6)	146.8 (29.3)
Obese	1123 (35.1)	228 (42.3)		1112.7 (34.3)	223.9 (44.6)
Diabetes (% Yes)	570 (17.8)	137 (23.9)	0.001	444.7 (13.7)	101.1 (19.1)	0.014
Congestive heart failure (% Yes)	189 (5.9)	46 (8.0)	0.068	161.1 (5.0)	32.2 (6.1)	0.312
Coronary heart disease (% Yes)	265 (8.3)	54 (9.4)	0.419	244.0 (7.5)	48.0 (9.1)	0.360
Stroke (% Yes)	192 (6.0)	48 (8.4)	0.041	151.0 (4.7)	32.9 (6.2)	0.055
Cancer (% Yes)	503 (15.7)	69 (12.0)	0.027	527.3 (16.3)	74.9 (14.2)	0.328
Mobility problem (% Any Difficulty)	1035 (32.4)	242 (42.2)	<0.001	876.9 (27.0)	195.1 (36.9)	0.001
Months mortality follow-up (mean (sd))	77.27 (20.90)	70.91 (23.60)	<0.001	77.63 (18.96)	71.38 (21.64)	<0.001
Mortality at follow-up (% Dead)	500 (15.6)	113 (19.9)	0.013	360.8 (11.1)	76.8 (14.7)	0.074

An additional observation from Table 1 is that while unadjusted and survey weighted summary statistics are frequently similar, they can also be quite different for specific characteristics. For example, because NHANES over-samples black and Mexican Americans, the ethnicity estimates vary dramatically between the unweighted and survey weighted results. This highlights the important risk of obtaining biased results when analyses do not adjust for survey weights [15,14].

After applying our exclusion criteria, there is one individual who has 501 minutes of missing activity count data on a day which qualifies as “good” using the 10 hour wear-time criteria. We impute these minutes as 0 activity counts. We do not attempt to impute activity counts for periods identified as non-wear. However, there are some minutes which are identified as non-wear which have non-zero activity counts, though none with activity counts greater than 99. Any periods identified as non-wear are replaced with 0 activity counts. This highlights an important point of working with the 2003–2006 NHANES accelerometry data: we are unable to disentangle non-wear, sleep, and sedentary behaviors. However, the hope is that by applying a 10 hour minimum wear time criteria for days of accelerometry data we are able to capture the majority of waking activities. Thus, we hope that the majority of non-wear time corresponds to either sleep or sedentary behaviors, though this assumption is untestable in practice.

3.1. Accelerometry Feature Extraction

One challenging aspect of working with accelerometry data is addressing the dimensionality of the data. Indeed, there are 1, 440 observations per subject, per day, which makes both visualization and analyses difficult. To reduce complexity and improve translation of results, many analyses use simple summary statistics, including but not limited to: 1) mean or total activity count (TAC); 2) mean or total log transformed activity count (TLAC); 3) total sedentary time; and 4) total minutes of moderate/vigorous physical activity (MVPA). This is an effective strategy, but could result in loss of information due to the extreme reduction in dimensionality.

It is our experience that often, additional features of the data are associated with an outcome of interest. One method for identifying these features is to apply dimensionality reduction tools from functional data analysis (FDA) [22]. Here we focus on Functional Principal Component Analysis (FPCA) and functional regression to select features that are strongly associated with 5-year mortality. After the accelerometry data features are identified, we construct accelerometry measures that are interpretable from a scientific/public health perspective. The feature extraction procedures described subsequently do not directly account for the NHANES survey weights. Accounting for survey weights in dimensionality reduction is an entirely new topic, which is beyond the scope of the current paper. However, we account for survey weights in identifying variables that are predictive of 5-year mortality in Section 3.3. In addition to not accounting for survey weights, the feature extraction methods discussed below do not account for non-wear time in the sense that we can not differentiate between sleep, non-wear time, or sedentary behaviors. However, the hope is that by having excluded all days of data with fewer than 10 hours of wear time, we only use those days where individuals were largely compliant with study protocol and we capture the majority of individuals’ waking activity patterns, though this is an untestable assumption on our part.

3.1.1. Functional Principal Component Analysis

To reduce the high degree of skewness in the activity count data we first transform the data at each minute using the transformation x = log(1 + a), where a denotes the activity count. This transformation has the added benefit that it transforms 0 counts to 0 [24]. We conduct Functional principal component analysis (FPCA) on the transformed matrix. FPCA is a technique analogous to principal component analysis, but with additional steps for smoothing the data [22]. Let J_i be the number of days of accelerometry data for subject i = 1, …, N and $J={\sum }_{i=1}^N{J}_i$ be the total number of days of data. The log transformed “activity count” data matrix, X, is J × 1440 dimensional. To perform FPCA, we use the fast covariance estimation (FACE) approach [34], which can be used in this high dimensional context. FACE is implemented in the fpca.face() function of the refund [8] package in R [21]. Even for this high dimensional data fpca.face() ran in under ten seconds on a standard laptop.

The FPCA approach presented here does not account for the within-person correlation when calculating the principal components (PCs). Two alternatives for recovering this variability are to either: 1) use average activity profiles across days within an individual and perform FPCA on average activity profiles; or 2) use multilevel FPCA [5,36,25]. The first option calculates the PCs and recovers the day-to-day variability by projecting day-specific data on the resulting PCs. This can be problematic when the within-person patterns of variability are different from between-persons patterns of variability. The second approach is a viable option for analyzing day-to-day variability but beyond the scope of this tutorial paper. For simplicity of presentation we also ignore issues associated with non-wear time in terms of estimating the principal components.

Although we are not aware of any software which can estimate survey weighted FPCA, we compared our results to survey weighted non-functional PCA estimated via the svyprcomp() function from the survey package and obtained nearly identical shapes (up to a sign) for the first 16 principal components, though the proportion of variability explained by each component varied. While we don’t present these results here, the supplemental material contains code which performs both PCA methods and plots the results.

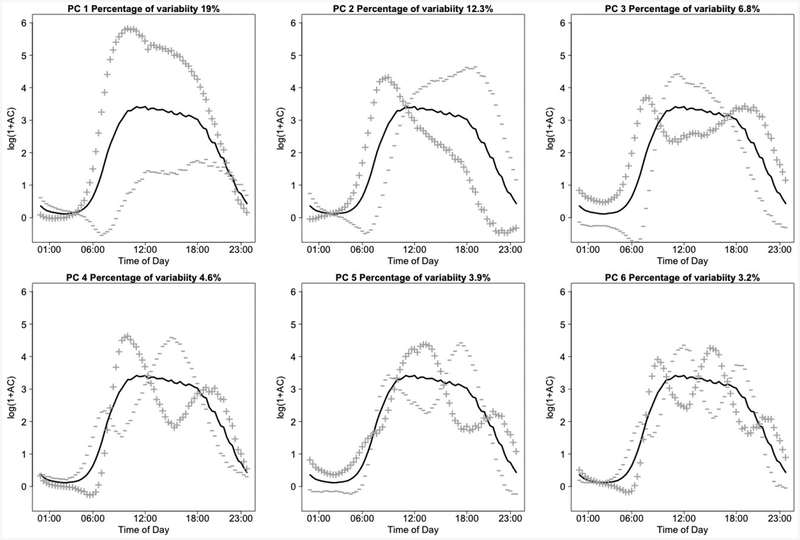
The first 6 PCs estimated using FPCA explain approximately 57% of the observed variability in the log transformed activity counts and are presented in Figure 4. Given how noisy the data is, 57% variability explained is substantial. For each subject and day we obtain a score on each PC and calculate the mean and standard deviation of these subject-specific scores. More specifically, let z_ijk be the score for subject i, on day j and PC k. Then we construct the additional 2K variables (2 for each of the first K = 6 PCs)

$$m_{ik}={\overline{z}}_{ik}=\frac{1}{J_i}\sum _{j=1}^{J_i}{z}_{ikj},s_{ik}= \text{sd} \left(z_{ik}\right)=\sqrt{\frac{{\sum }_{j=1}^{J_i}{\left(z_{ijk}-{\overline{z}}_{ik}\right)}^2}{J_i-1}}i=1,\dots ,Nk=1,\dots ,K=6$$

Fig. 4:

First 6 principal components calculated on the population, minute level NHANES accelerometry data using functional principal component analysis. Solid lines represent the population average curve, +, — lines denote the effect of being 2 standard deviations from a score of 0 on the particular principal component.

The subject- and component-specific mean and standard deviations, m_ik and s_ik, are then used as predictors in regression models. We denote by m_i = (m_i1, …, m_iK)^t and s_i = (s_i1, …, s_iK)^t the K × 1 dimensional vectors of score means and standard deviations. We fit a logistic regression of the form

$$\text{logit}\left(p_i|{\mathbf{W}}_i,m_i,s_i\right)=\alpha +W_i^t\beta +m_i^t\gamma +s_i\delta ,$$ (2)

where p denotes the probability of death in 5 years, W_i contains the standard demographics, behavioral and comorbidity covariates used in published NHANES mortality papers. The demographic covariates include age, gender, body mass index (BMI), race, and education level. The behavioral covariates include smoking status and alcohol consumption. The comorbidity covariates include self reported presence of a mobility problem, diabetes, coronary heart disease (CHD), congestive heart failure (CHF), cancer, and stroke. The precise definitions for each of these variables can be found in the data documentation for the rnhanesdata package. We used backward selection to identify the m_ik and s_ik covariates that are associated with survival time while always keeping the covariates W_i in the model. The backward selection was performed using complex survey Akaike’s Information Criteria (AIC) [17]. Using this procedure we find that the average scores for the first PC (m_i1) as well as the standard deviation of the first PC (s_i1), fifth PC (s_i5), and the sixth PC (s_i6) are retained at the end of the backward selection procedure. To interpret these results, we refer back to the shapes of principal components in Figure 4. Potential interpretations and possible surrogate measures calculated on the raw count data are proposed in Table 2 below.

Table 2:

Interpretation of the results of FPCA plus suggestions for possible surrogate measures which can be calculated directly on the activity count data. The “Result” column (−)/(+) indicates a negative/positive association of the predictor with 5-year mortality in a model adjusting for demographics, lifestyle factors, and the other predictors in this table.

Result	Possible Interpretation	Possible Surrogate Measure(s)
(−) association: mi1	Higher overall levels of low/light activity during the day, and increased early afternoon activity relative to early AM is associated with lower risk of 5-year mortality.	Average total log activity counts (TLAC) Average difference of early AM versus early PM activity
(+) association: si1	Increased variability in overall levels of low/light activity is associated with higher risk of 5-year mortality.	Standard deviation of total log activity counts (TLAC)
(−) association: si5	Increased variability in the timing of peak activity is associated with lower risk of 5-year mortality.	Standard deviation of “wake up” time Standard deviation of “winding down” time
(−) association: si6	Increased variability in the start time of daily activity is associated with lower risk of 5-year mortality. This could be an employment effect.	standard deviation of the difference in average activity during the peaks/troughs highlighted by PC6

With the interpretations presented in Table 2, we explored a number of potential surrogate measures that are interpretable on the original scale of the data and can easily be derived directly from the count data at the minute level without conducting FPCA. Although ratios comparing relative activity during key periods seem appealing, they are challenging to use in practice due to the large number of 0 activity counts present in the data. To avoid this problem we propose using differences in average log transformed activity counts between said key periods of time. The precise measures considered are presented in Table 3.

Table 3:

Actual surrogate measures identified for use in prediction models. All standard deviations are day-to-day standard deviations calculated for each participant.

Result	Quantity Measured	Calculation
(−) association: mi1	Average total log activity count (TLAC)	$\frac{1}{J_i}\sum _{j=1}^{J_i}\sum _{t=1}^{1440}{X}_{ij}(t)$
(+) association: si1	Standard deviation of total log activity counts	$\text{sd}\left(\sum _{t=1}^{1440}{X}_{ij}(t)\right)$
(−) association: si5	Standard deviation of difference in average log transformed activity counts comparing 10AM-3PM to 4PM-7PM	$\text{sd}\left(\frac{{\sum }_{t=661}^{900}{X}_{ij}\left(t\right)}{240}-\frac{{\sum }_{t=961}^{1140}{X}_{ij}\left(t\right)}{180}\right)$
(−) association: si6	Standard deviation of difference in average log transformed activity counts comparing {8AM-10AM, 3PM-5PM, 10PM-12AM} to {5AM-7AM, 11AM-1PM, 6PM-8PM }	$\text{sd}\left(\frac{{\sum }_{t\in t_a}{X}_{ij}\left(t\right)}{\left|t_a\right|}-\frac{{\sum }_{t\in t_b}{X}_{ij}\left(t\right)}{\left|t_b\right|}\right)$ ta = {481,…, 600, 901,…, 1020, 1321,…, 1440} tb = {301,…, 420, 661,…, 780, 1081,…, 1200}

To justify a particular surrogate measure, we considered the correlation between our surrogate measure and the results of FPCA. In general, correlations of at least 0.75 were considered sufficiently high to warrant inclusion in subsequent prediction models. For example, the correlation of our proposed surrogate measure for m_i1, total log activity counts (TLAC), has an observed correlation of 0.88 with m_i1. This procedure involved substantial amount of “guess and check”, and, correspondingly, the results of Section 3.3 should be interpreted as exploratory and not confirmatory.

3.2. Scalar on Function Regression

An alternative to signal extraction via FPCA followed by regression is to conduct functional regression directly on the patterns of activity. While some papers on functional regression in the context of survival data exist [7,12,33], this is a relatively new area of research. In order to keep results comparable with those in other sections and for simplicity of presentation, we continue to focus on the binary outcome Dead/Alive at 5 years.

3.2.1. Functional regression model

Denote the smoothed log transformed activity count data obtained from the FPCA performed in Section 3.1.1 as ${\tilde{X}}_{ij}(s)$ for subject i on day j at time s. Our logistic functional regression model is then a slight modification of Model (2)

$$\text{logit} \left(p_i|W_i,{\tilde{\mathbf{X}}}_i\right)=\alpha +W_i^t\beta +{\int }_0^1\left\{\frac{1}{J_i}\sum _{j=1}^{J_i}{\tilde{X}}_{i,j}(s)-\overline{X}(s)\right\}\gamma (s)ds,$$ (3)

where Wi contains the same predictors as the logistic regression in Section 3.1.1 and $\overline{X}(s)$ denotes the population average activity count at time s. That is, our functional predictor is the average of the smoothed activity profiles at each time point across days, centered at each time point. The centering is done to prevent confounding of the functional coefficient with the intercept term α and aid in interpretation. This model ignores potential effects of day-of-the-week, week-end, or day-to-day variability on 5-year survival. The functional parameter, γ(s), can be thought of as a weight function that expresses the relative contribution of an individual’s average daily activity profile as compared to the population average, $\frac{1}{J_i}{\sum }_{j=1}^{J_i}{\tilde{X}}_i\left(s\right)-\overline{X}(s)$, at each minute s towards the log odds ratio of 5-year mortality. The functional regression parameter can be approximated as

$$\gamma (s)=\sum _{k=1}^{k_b}{b}_k{\varphi }_k(s),$$

where $\varphi (s)={\left\{{\varphi }_1(s),\dots ,{\varphi }_{k_b}(s)\right\}}^t$ is a spline basis over s. Our primary interest in this section is to estimate and interpret the functional coefficient γ(s). We estimate γ(s) using cyclic penalized B-splines of dimension 30 to account for the natural periodicity in the data. Indeed, we expect the effect to be smooth around 12:00AM with very similar values at 11:59PM and 00:01AM across days. Because we do not account for differential non-wear, either within or across individuals, our model, and the resulting functional coefficient γ(s), may be combining the effect of 0 activity counts with periods of non-wear if non-wear time is associated with 5-year mortality. The additional predictors in the model, W_i, are the same demographic, lifestyle, and comorbidity variables described in Section 3.1.1.

The model fitting is performed using the refund [8] package in R which contains wrapper functions for the gam() function in the mgcv package to perform functional regression. Estimation is performed using the normalized survey weights. Even though we account for survey weights, the estimated standard errors may be inaccurate due to the multistage survey nature of NHANES. That is, because we only account for survey weights, and not survey design, our standard errors are likely underestimated. A re-sampling procedure could be used to estimate standard errors, but is beyond the scope of this paper as we use functional regression in an exploratory capacity. To the best of our knowledge, no software currently exists which will fit penalized functional regression models for complex survey designs. Note that using non-normalized survey weights with standard functional regression software may substantially affect both point estimates and estimated standard errors.

3.2.2. Results

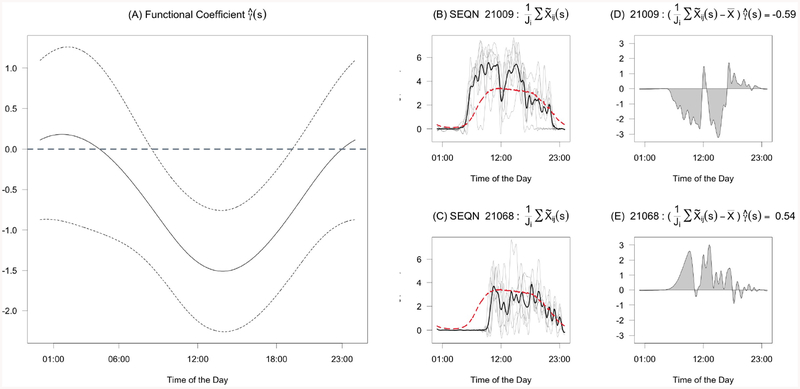
Figure 5(A) depicts $\widehat{\gamma }(s)$, the estimated functional coefficient, as a solid line. The dashed lines are pointwise 95% confidence intervals. Because $\widehat{\gamma }(s)$ is a weight on activity levels, larger magnitudes indicate that being above the population average activity at a particular time is associated with increased contribution to the log odds of 5-year mortality for that time of day. The coefficient function is estimated to be positive only during the late evening and early hours of the morning (approximately 11AM to 3AM), indicating that increased activity relative to the population average during this time period is associated with higher risk of mortality, after accounting for the other covariates, though the magnitude of the coefficient during this period is close to 0. The coefficient function is estimated to be most negative around 1PM-3PM, indicating that increased activity relative to the population during this period is associated with lower risk of mortality given a particular level of overall activity during any other part of the day. The pointwise confidence intervals contain zero for all times except roughly between 8AM-6PM. This suggests that the effects of activity outside of the interval 8AM-6PM is not particularly strong if we condition on the activity in this interval. This may, at least in part, be due to the fact that NHANES participants were instructed to remove the device while sleeping.

Fig. 5:

(A) Estimated Functional Coefficient For Daily Activity Patterns γ(s) with 95% pointwise confidence intervals presented as thin dashed lines. (B)/(C) Smoothed activity counts for one day of data for two different NHANES participants. The grey lines denote individual daily smoothed profiles. The black line denotes the average profile, $\frac{1}{J_i}{\sum }_{j=1}^{J_i}{\tilde{X}}_{ij}\left(s\right)$. The dashed red line is the population average profile $\overline{X}(s)$. The difference between the solid black line and the red dashed line is the functional predictor in model 3. (D)/(E) Contribution to the log odds for these example days of accelerometry data.

To interpret the functional coefficient, we compare the implied contribution to log odds of 5-year mortality for two individuals with markedly different daily activity patterns. Figure 5(B)/(C) displays their smoothed minute-level activity for all days (grey lines), the average across days (the black line), and the population average, ${\tilde{X}}_{ij}(s),\frac{1}{J_i}{\sum }_{j=1}^{J_i}{\tilde{X}}_{ij}\left(s\right)$, and $\overline{X}(s)$, respectively. The first person (labeled 21009) is, on average, active in the morning, has a dip in activity around 12PM, is active again in the early afternoon, and then has decreasing activity after 2PM. The second person (labeled 21068) wakes up late, and then has below average activity throughout most of the day. Figure 5(D)/(E) depicts $\left\{\frac{1}{J_i}{\sum }_{j=1}^{J_i}{\tilde{X}}_i\left(s\right)-\overline{X}\right\}\widehat{\gamma }(s)$, which is the pointwise product of each individual’s activity data and the estimated functional coefficient. The shaded area is the contribution to the log odds of the average activity profile, where more shaded area above 0 indicates an increased risk of 5-year mortality. This shaded area is equal to −0.59 for subject 21009 and 0.54 for subject 21068, indicating that subject 21009’s average activity profile is associated with an odds of 5-year mortality that, adjusting for the other covariates in the model, is exp(—0.59) = 0.55 times that of an individual with the population average activity profile. In contrast, subject 21068’s average profile is associated with an odds of 5-year mortality that is exp(0.54) = 1.72 times that of a comparable subject with average activity profile equal to the population average. For reference, in this model, each year of age is associated with 0.069 higher log odds of 5-year mortality, which suggests the difference in these two activity profiles is roughly comparable to the expected change in log odds for individuals who are 16.4 years apart in age.

These results suggest that activity during the day-time reduces the risk of 5-year mortality and that given an overall budget of activity, allocating more activity to early afternoon may be most associated with reduced risk of 5-year mortality. A closer inspection of results suggests that they may be driven by the afternoon average activity, which is highly correlated with the total or average activity count. Thus, it is likely that functional regression is picking up on a similar signal to that captured by m_i1 described in Section 3.1.1. In fact, the correlation between the linear predictor associated with the functional coefficient and m_i1 is 0.95. As a result, we consider our surrogate for m_i1 (TLAC) as sufficiently capturing the signal associated with the functional coefficient and do not add an additional candidate for predicting 5-year mortality based on the results of functional regression.

3.3. Prediction of Mortality in NHANES

In this section we aim to identify the best predictors of 5-year mortality among demographics, comorbidities, and lifestyle factors commonly used as confounding variables in NHANES survival analyses as well as features of activity identified as being predictive of mortality from Section 3.1.1 (surrogate measures for m_i1, s_i1, s_i5, s_i6 described in Table 3). In these models 5-year mortality is the outcome and we consider a set of non-activity predictors: age, gender, ethnicity, education, body mass index (BMI), smoking status, drinking status, diabetes, congestive heart failure, coronary heart disease, cancer, and mobility limitation. With respect to accelerometry derived predictors, we consider the features of activity identified as being predictive of mortality from Sections 3.1.1. We also include average daily wear time and time spent in moderate-to-vigorous activity (MVPA), which are standard predictors in the accelerometry literature. The activity count threshold used to determe moderate-to-vigorous activity was ≥ 2020 [28]. In addition, we considered total activity counts (TAC) which measure volume of activity. In contrast to total log activity counts (TLAC) which is associated with low/light activities, TAC is more highly associated with moderate/vigorous activities [32].

Finally, we consider three measures which involve the estimation of sedentary behaviors: total time spent in engaging in sedentary behaviors, as well as two measures of sedentary-active fragmentation: active to sedentary transition probability (ASTP) and sedentary to active transition probability (SATP)[6]. The standard practice is to consider sedentary behaviors during wake time as distinct from inactivity associated with sleep. However, as mentioned in Section 3, in NHANES we can not differentiate between non-wear, sedentary behaviors, and sleep. Therefore, in calculating these three measures typically derived from sedentary behaviors, we use “sedentary, sleep, or non-wear” in place of “sedentary”, which we assume to consist mostly of non-wear and sleep time due to our exclusion of days with fewer than 10 hours of wear-time. Although our non-standard construction complicates the interpretation of models which include these variables as predictors, it allows us to bypass the complexities associated with constructing transition probabilities in the context of intermittent non-wear and adjusting sedentary time for non-wear time. In order to differentiate our measures from those discussed in [6], we denote our transition probabilities as ASTP_sl/nw and SATP_sl/nw. We use an activity count threshold of < 100 counts to identify sedentary behaviors.

In our prediction models we do not consider interactions between predictors or alternative functional forms of continuous predictors (i.e. non-linear effects). This was done to simplify the forward selection procedure, but will not necessarily produce the “best” prediction model possible using the variables considered here.

3.3.1. Model Selection

Our intent is to rank each predictor in terms of their individual predictive value, and identify a set of “most” predictive variables using forward selection. Our procedure for ranking single predictors of 5-year mortality is to quantify the relative importance of variables for mortality prediction using univariate logistic regression models. Each variable was ranked according to 10-fold cross validated area under receiver operating characteristic curve (AUC) and complex survey Akaike’s information criterion (AIC) [17]. Forward selection is performed using the cross validated AUC criterion. In order to assess the sensitivity of forward selection to the survey re-weighting procedure described in Section 2.4, we performed the forward selection separately using: 1) our re-weighted (“adjusted”) survey weights; 2) unadjusted survey weights; and 3) no survey weights. Cases (deceased) and controls (alive) were split and partitioned separately to ensure approximately equal numbers of events in each of the 10-folds. The same partition of the data was used for the entire forward selection procedure.

3.4. Results

Table 4 shows individual predictors ranked using univariate logistic regression models based on AUC for each of the three sets of survey weights discussed in Section 3.3.1. These models are univariate in that all models have just one covariate. Regardless of which set of survey weights is used, eight of the top ten predictors are accelerometry-based measures, which may explain the explosive interest in objective measures of activity using wearable devices. TAC, MVPA, and Age provide best discrimination (AUC of 0.783, 0.756, and 0.747, respectively using the adjusted survey weights) among the 24 predictors. However, due to the relatively high correlation between some of these variables (TAC and MVPA or ASTP_sl/nw and SATP_sl/nw, for example), it is not terribly surprising that they would perform similarly. Still, the predictive performance of measures of vigorous activity (TAC, MVPA), overall low/light activity (TLAC), inactivity (Sedentary, sleep, or non-wear time) and the fragmentation measures (ASTP_sl/nw, SATP_sl/nw) as stand-alone variables is exceptional given that so many other well-known strong predictors of mortality have a much lower AUC.

Table 4:

Ranking of individual mortality predictors importance based on AUC criteria in from univariate logistic regressions.

	Adjusted Weights		Unadjusted Weights		Unweighted
Rank	Variable	AUC	Variable	AUC	Variable	AUC
1	TAC	0.783	TAC	0.784	TAC	0.753
2	MVPA	0.756	MVPA	0.757	Age	0.735
3	Age	0.747	Age	0.746	MVPA	0.729
4	ASTPsl/nw	0.745	Sedentary, Sleep, or Non-wear	0.745	ASTPsl/nw	0.727
5	Sedentary, Sleep, or Non-wear	0.744	ASTPsl/nw	0.745	Sedentary, Sleep, or Non-wear	0.724
6	TLAC	0.736	TLAC	0.738	TLAC	0.714
7	Mobility problem	0.679	Mobility problem	0.679	SATPsl/nw	0.654
8	SATPsl/nw	0.673	SATPsl/nw	0.675	Surrogate for si6	0.654
9	Surrogate for si6	0.662	Surrogate for si6	0.661	Mobility problem	0.651
10	Alcohol consumption	0.612	Alcohol consumption	0.609	Gender	0.582
11	Education	0.596	Education	0.597	Alcohol consumption	0.578
12	Cigarette smoking	0.594	Cigarette smoking	0.596	Surrogate for si1	0.573
13	Cancer	0.585	Cancer	0.585	Cigarette smoking	0.570
14	Surrogate for si1	0.580	Surrogate for si1	0.582	Cancer	0.568
15	Congestive heart failure	0.566	Congestive heart failure	0.567	Education	0.566
16	Gender	0.561	Gender	0.565	Congestive heart failure	0.558
17	Body mass index	0.559	Body mass index	0.560	Race	0.551
18	Diabetes	0.555	Diabetes	0.555	Body mass index	0.549
19	Coronary heart disease	0.548	Coronary heart disease	0.550	Diabetes	0.540
20	Stroke	0.540	Stroke	0.539	Coronary heart disease	0.540
21	Race	0.518	Race	0.518	Stroke	0.540
22	Wear time	0.444	Wear time	0.440	Wear time	0.493

Moving from univariate logistic regressions to multiple logistic regression, Table 5 presents the results from forward selection. The variables are presented in order of selection. Cells with a gray background indicate the AIC stopping criteria was met (i.e. AIC increases with the next variable included), while a black text box surrounding a variable communicates that the cross-validated AUC criteria was met (AUC decreases when another variable is added). AUC tended to be more optimistic than AIC in forward selection. Both the adjusted survey weights and unweighted procedure identified 11 and 14 variables using the AIC and AUC criteria, respectively, though the exact variables selected and their ordering differed slightly. The unadjusted weights identified 10 variables using both the AIC and AUC criteria. Overall there was perfect overlap between the weighting methods for the first 7 variables, and a high degree of overlap for the next several variables when comparing the two survey weighting methods.

Table 5:

Results from forward selection procedure using each of the three weighting procedures. For each weighting procedure, variables are presented in descending order by their inclusion. Variables are added to the model using cross-validated AUC criteria. Cells with a gray background indicate that the forward selection procedure would have stopped based on improvement in complex survey AIC. Cells with which are boxed indicate the forward selection procedure would have stopped based on improvement in cross-validated AUC.

	Adjusted Weights		Unadjusted Weights		Unweighted
Rank	Variable	AUC	Variable	AUC	Variable	AUC
1	TAC	0.783	TAC	0.784	TAC	0.753
2	Age	0.799	Age	0.799	Age	0.778
3	Gender	0.810	Gender	0.810	Gender	0.791
4	Mobility problem	0.816	Mobility problem	0.817	Mobility problem	0.801
5	Alcohol consumption	0.824	Alcohol consumption	0.825	Cigarette smoking	0.807
6	Cigarette smoking	0.830	Cigarette smoking	0.831	Alcohol consumption	0.812
7	Surrogate for si6	0.834	Surrogate for si6	0.834	Surrogate for si6	0.816
8	Congestive heart failure	0.835	Congestive heart failure	0.836	ASTPsl/nw	0.819
9	Body mass index	0.836	Body mass index	0.836	Cancer	0.821
10	Cancer	0.837	Cancer	0.838	Congestive heart failure	0.822
11	ASTPsl/nw	0.838	Stroke	0.838	Body mass index	0.823
12	Sedentary, Sleep, or Non-wear	0.838	Education	0.837	Sedentary, Sleep, or Non-wear	0.824
13	SATPsl/nw	0.841	Surrogate for si1	0.837	SATPsl/nw	0.826
14	Diabetes	0.841	Diabetes	0.838	TLAC	0.826
15	Education	0.841	Coronary heart disease	0.837	Diabetes	0.826
16	TLAC	0.841	ASTPsl/nw	0.836	Coronary heart disease	0.826
17	Surrogate for si1	0.840	Sedentary, Sleep, or Non-wear	0.836	MVPA	0.825
18	Stroke	0.840	SATPsl/nw	0.838	Education	0.824
19	Coronary heart disease	0.839	TLAC	0.838	Surrogate for si1	0.823
20	Wear time	0.838	Wear time	0.837	Wear time	0.823
21	MVPA	0.837	MVPA	0.835	Stroke	0.822
22	Race	0.832	Race	0.830	Race	0.818

Even though AIC was more conservative than 10-fold cross-validated AUC in selecting variables, any observed increases in AUC associated with adding additional variables beyond the first 7 are marginal, suggesting that even the AIC criteria may be overly optimistic. Recognizing this issue, we present the point estimates and 95% Wald confidence intervals obtained from the “Adjusted Weights” model using the first 7, 11, and 14 predictors obtained from forward selection in Table 6. In Table 6 all continuous predictors except age have been standardizes such that the odds ratios presented represent the expected change in odds of 5-year mortality for a one standard deviation increase in the predictor. Estimates and confidence intervals are obtained using the svyglm() function, accounting for both the survey weights and complex survey design of NHANES.

Table 6:

Estimated odds ratios and 95% confidence intervals from three different logistic regression models fit using adjusted survey weights. In each model 5-year mortality is the outcome. The order of variables is presented in order of their inclusion based on the forward selection AUC criteria, and models are nested in order from left to right. The 7 variable model corresponds to the first 7 variables identified by the forward selection procedure. Similarly, the AIC model and AUC model contain the variables selected using the AIC and AUC stopping criteria, respectively. Variables which are derived from accelerometry are highlighted in gray. The intercept for each model is not presented here as variables are not centered and the resulting value is not particularly interpretable.

Variable	7 Variable Model	AIC Model	AUC Model
TAC	0.562 (0.324, 0.977)	0.845 (0.439, 1.627)	0.656 (0.303, 1.420)
Age	1.071 (1.052, 1.090)	1.066 (1.046, 1.087)	1.066 (1.045, 1.087)
Female	0.475 (0.341, 0.661)	0.467 (0.329, 0.663)	0.449 (0.318, 0.636)
Mobility problem	2.112 (1.375, 3.244)	2.040 (1.349, 3.086)	1.979 (1.299, 3.013)
Alcohol consumption
Non-Drinker	1.992 (1.454, 2.730)	1.978 (1.425, 2.745)	1.929 (1.377, 2.701)
Heavy Drinker	2.122 (1.002, 4.496)	2.088 (0.985, 4.429)	2.142 (0.998, 4.597)
Missing alcohol	2.493 (1.286, 4.832)	2.389 (1.169, 4.883)	2.382 (1.153, 4.923)
Cigarette smoking
Former	1.615 (1.045, 2.495)	1.577 (1.014, 2.451)	1.570 (0.995, 2.475)
Current	2.611 (1.900, 3.590)	2.217 (1.656, 2.969)	2.238 (1.670, 2.999)
Surrogate for si6	0.735 (0.626, 0.862)	0.792 (0.669, 0.937)	0.791 (0.674, 0.929)
Congestive heart failure		2.137 (1.416, 3.223)	2.058 (1.348, 3.142)
Body mass index
Underweight		2.029 (0.738, 5.576)	2.091 (0.714, 6.122)
Overweight		0.539 (0.374, 0.777)	0.532 (0.366, 0.773)
Obese		0.614 (0.431, 0.875)	0.593 (0.415, 0.845)
Cancer		1.578 (1.122, 2.219)	1.614 (1.161, 2.245)
ASTPsl/nw		1.458 (1.090, 1.949)	1.979 (1.308, 2.995)
Sedentary, Sleep, or Non-wear			0.401 (0.193, 0.832)
SATPsl/nw			0.611 (0.436, 0.858)
Diabetes			1.270 (0.853, 1.889)

Interpreting the results shown in Table 6, we see the odds of experiencing 5-year mortality increase with age, presence of a mobility problem, and self reported comorbidities. Interestingly, adjusting for the other variables in the model, individuals with an BMI considered overweight or obese have a lower risk compared to those with normal BMI. Although this seems counterintuitive, this “obesity paradox” has been seen many times in the epidemiologic literature, including in analyses of NHANES data. Other studies have found that conditioning on health status eliminates the protective effect of being overweight on survival among healthy individuals [1]. For example, [20] found that conditioning smoking status eliminates the protective effect of being overweight among never-smokers, and indeed we see this same phenomena in our data (results not shown). As investigating any potential underlying causal mechanisms and addressing the issues of reverse-causality are beyond the scope of this paper, we simply acknowledge this emergent phenomena. Regarding lifestyle factors, former/current smokers have significantly higher mortality risk relative to non smokers. Individuals who consume alcohol moderately have lower risk of mortality compared to non-drinkers, a well known result that may be confounded by socioeconomic status and by individuals who do not drink alcohol as a result of a pre-existing health condition.

Interpreting the observed associations of activity summary measures with mortality is complicated by the dependencies among them. Consider the association of total volume of activity (TAC) with 5-year mortality. Although the direction of the association consistently indicates that increased volume of activity is associated with lower risk of 5-year mortality, adding the transition probabilities (ASTP_sl/nw/SATP_sl/nw) and sedentary, sleep, or non-wear time to the model markedly influences both the point estimate and variability associated with the coefficient for TAC. Despite the presence of dependencies among these predictors, the direction of effects is generally consistent with our expectations. That is, increased activity (TAC) or probability of transitioning to activity from sedentary, sleep, or non-wear (SATP_sl/nw) is associated with lower risk. In contrast, increased probability of transitioning from active to sedentary, sleep, or non-wear is associated with higher risk. Additionally, the observed protective association of our surrogate measure for s_i6 is consistent with the results from Section 3.1. The one association that does not seem to fit our expectations is the protective effect of increased sleep, sedentary time, or non-wear time. However, we need to remember that the protective effect is “adjusting for” total volume of activity as well as transition probabilities of sedentary to active and vice versa. We caution against looking too much into this particular result as forward selection does not necessarily produce models which “make sense” from an interpretation perspective.

4. Discussion

Here, we have provided a data package that is intended to considerably reduce the upfront time investment needed to begin working with NHANES accelerometry data. Assuming no changes to the format of future NHANES data releases, all code provided for the pipeline naturally extends to future NHANES data, including accelerometry and mortality data. In addition, we provide a framework for structuring accelerometry data that is in line with current best practices and is compatible with existing R code for accelerometry data. Moreover, through the use of three analytic examples, we provide users with a step-by-step guide for working with the NHANES accelerometry data, including adjusting for survey weights. All code, figures, and results in this manuscript are fully reproducible using code available in the supplemental material. This analysis will be added to the rnhanesdata package as a vignette in the near future.

Our results should be considered exploratory and not confirmatory given the extensive exploratory analysis performed to identify accelerometry derived predictors of mortality. However, we think that providing a list of highly predictive accelerometry metrics will be extremely useful in future confirmatory studies. A limitation of our approach is that we do not consider non-linear associations between continuous predictors and survival, nor do we consider interactions between predictors. Such models should be considered in future studies using the variables identified here as being predictive of 5-year mortality.

Ultimately, our package contains the content, the tools, and the context needed to empower users to begin working with NHANES data quickly (accelerometry, or otherwise). Most importantly, we integrate these features in a concise and well documented fashion that is accessible to users with varying degrees of statistical sophistication and is fully reproducible. Our hope is that this paper will result in increased utilization of this extremely rich, public resource.