Patient-Tailored, Connectivity-Based Forecasts of Spreading Brain Atrophy

SUMMARY

Neurodegenerative diseases appear to progress by spreading via brain connections. Here we evaluated this transneuronal degeneration hypothesis by attempting to predict future atrophy in a longitudinal cohort of patients with behavioral variant frontotemporal dementia (bvFTD) and semantic variant primary progressive aphasia (svPPA). We determined patient-specific “epicenters” at baseline, located each patient’s epicenters in the healthy functional connectome, and derived two region-wise graph theoretical metrics to predict future atrophy: (1) shortest path length to the epicenter and (2) nodal hazard, the cumulative atrophy of a region’s first-degree neighbors. Using these predictors and baseline atrophy, we could accurately predict longitudinal atrophy in most patients. The regions most vulnerable to subsequent atrophy were functionally connected to the epicenter and had intermediate levels of baseline atrophy. These findings provide novel, longitudinal evidence that neurodegeneration progresses along connectional pathways and, further developed, could lead to network-based clinical tools for prognostication and disease monitoring.

In Brief

Brown et al. show that unique atrophy “epicenters” can be detected in individual patients with behavioral variant frontotemporal dementia and semantic variant primary progressive aphasia and used in a connectivity-based model to accurately predict the longitudinal spread of atrophy.

INTRODUCTION

Neurodegenerative diseases, including frontotemporal lobar degeneration (FTLD) and Alzheimer’s disease, result in diverse clinical syndromes whose features reflect damage to specific large-scale brain networks (Seeley et al., 2009). These diseases are associated with protein misfolding and aggregation, which progress through predictable anatomical patterns (Braak and Braak, 1991; Broe et al., 2003), potentially via transsynaptic spread (de Calignon et al., 2012; Frost and Diamond, 2010; Goedert et al., 2010; Guo and Lee, 2014; Liu et al., 2012; Porta et al., 2018). One proposed mechanism for network-specific degeneration is onset of disease within a focal brain region, or “epicenter,” whose connectivity guides the spread of misfolded protein into new regions (Seeley, 2017). While evidence for this mode of progression has come from cross-sectional studies in groups of patients with various dementia syndromes (Mutlu et al., 2017; Torok et al., 2018; Zeighami et al., 2015; Zhou et al., 2012), the critical test of the model, however, is whether network connectivity can predict longitudinal spread of atrophy in individual patients. Achieving this goal would also provide a key step toward applying prediction algorithms in a clinical setting.

Frontotemporal dementia (FTD) syndromes, the clinical manifestations of underlying FTLD pathology, make compelling test cases for evaluating network-based spreading models due to their focal and circumscribed atrophy patterns (Rosen et al., 2002). The behavioral variant of FTD (bvFTD) presents with a variable combination of social-emotional symptoms that result from atrophy most prominent in frontoinsular and anterior cingulate cortices, striatum, and amygdala (Landin-Romero et al., 2017; Perry et al., 2017; Rascovsky et al., 2011; Seeley et al., 2008). These regions form a “salience network” in the healthy brain, detectable with task-free functional magnetic resonance imaging (tf-fMRI) (Seeley et al., 2007) that is the primary network targeted in bvFTD (Seeley et al., 2009). Semantic variant primary progressive aphasia (svPPA), in contrast, presents with loss of knowledge related to words, objects, people, and emotions, resulting from atrophy involving a semantic network made up of the anterior temporal lobes and connected regions including the ventral and medial temporal lobe, amygdala, and orbitofrontal cortex (Brambati et al., 2009; Chan et al., 2001; Garrard and Hodges, 2000; Gorno-Tempini et al., 2011; Guo et al., 2013; Rohrer et al., 2012). While regions of shared atrophy are seen across patients with bvFTD or svPPA, group studies obscure the heterogeneity seen in individual patients with bvFTD (Ranasinghe et al., 2016; Whitwell et al., 2009) and svPPA (Edwards-Lee et al., 1997; Seeley et al., 2005; Thompson et al., 2003). This well-documented heterogeneity leads to the main hypothesis of this study: within each syndrome, individual patients harbor distinct epicenters that create subtly different atrophy patterns by templating distinct patterns of transneuronal spreading.

Here, we introduce a network-based model for predicting longitudinal brain atrophy in individual patients using only a baseline MRI scan. First, we derived individual patient atrophy maps for patients with bvFTD and svPPA. We then used tf-fMRI data from a cohort of healthy older subjects to identify patient-tailored epicenters by comparing atrophy maps to a library of 194 intrinsic functional connectivity maps derived from seed regions spanning the entire cerebral cortex. Next, we projected the patient’s epicenter(s) and baseline atrophy map onto the healthy functional connectome to determine two hypothesized predictors of subsequent atrophy: (1) shortest path length, in network space, to the epicenter (SPE, Zhou et al., 2012) and (2) “nodal hazard,” a novel measure quantifying atrophy within a given region’s network neighbors. Finally, we implemented a generalized additive model to estimate future region-wise atrophy for a given subject, based in part on SPE and nodal hazard. We demonstrate that a patient-tailored model using network-based predictors can accurately estimate the spatial pattern of subsequent atrophy, creating a path toward precision prognosis and disease-monitoring.

RESULTS

Patients with bvFTD and svPPA Show Diverse but Predictable Epicenters

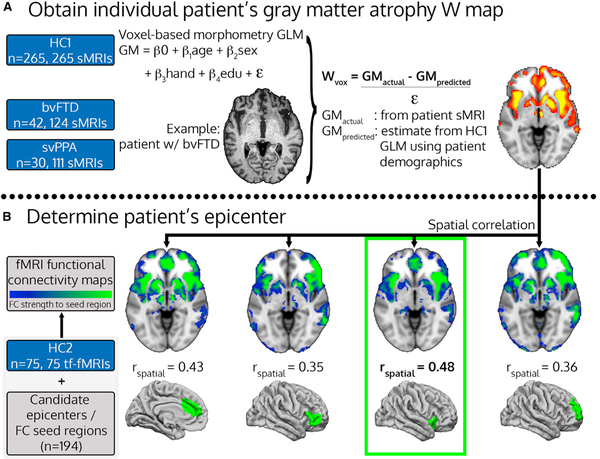
We performed statistical analysis of structural (T1-weighted) MRI scans to identify each subject’s unique gray matter atrophy pattern after controlling for age, sex, handedness, and other relevant covariates (Table 1). Using these maps, we then identified each patient’s epicenter, defined as the region whose intrinsic connectivity map in controls most strongly resembled the patient’s atrophy map (Figure 1).

Table 1.

Patient Demographic and Clinical Information

	bvFTD (n = 42)	svPPA (n = 30)
Age (years)	61.9 ± 6.8	63.8 ± 6.4
Sex (F/M)	19/23	13/17
Education (years)	16 ± 3	17 ± 3
Handedness (R/L/A)	38/3/1	28/1/1
Clinical Dementia Rating (CDR)	1.2 ± 0.6	0.6 ± 0.3
CDR Sum of Boxes	6.5 ± 3.0	3.2 ± 1.8
MMSE	23.6 ± 4.6	25.9 ± 3.7
# longitudinal time points	3 ± 1	3.7 ± 1
Interscan interval (days)	312 ± 117	314 ± 125

Figure 1. Patient-Tailored Epicenter Identification.

(A and B) Workflow for determining individual patient gray matter atrophy W maps (A) and patient-tailored epicenters, based on the spatial correlation between patient atrophy maps and healthy intrinsic functional connectivity maps (B). The procedure is illustrated for a single time point from a single representative patient with bvFTD, a 63-year-old right-handed man with 22 years of education, whose epicenter was identified as the right frontoinsular cortex. HC: healthy controls; bvFTD: behavioral variant frontotemporal dementia; svPPA: semantic variant primary progressive aphasia; sMRI: structural MRI; tf-fMRI: task-free functional MRI; GLM: general linear model; GM: gray matter; FC: functional connectivity.

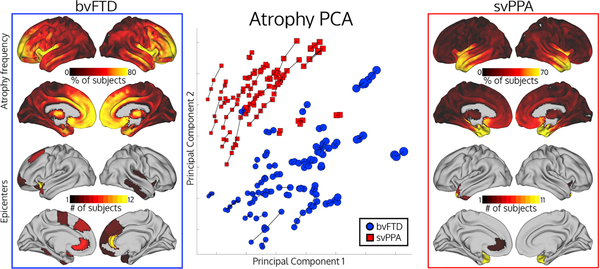
Based on the baseline MRI, patients with bvFTD had epicenters in the anterior cingulate cortex and frontoinsular cortex, as predicted by previous group-level analyses (Zhou et al., 2012), and less commonly in the anterior temporal lobe and medial prefrontal cortex (Figure 2, lower left; Figure S1; epicenter counts in Table S3). All of these regions had significant atrophy in most patients (Figure 2, upper left). Patients with svPPA had epicenters in the anterior temporal lobe (Figure 2, lower right; Figure S1; epicenter counts in Table S3), the most consistently atrophied region (Figure 2, upper right) (see STAR Methods for region definitions), as expected (Zhou et al., 2012). There was moderate spatial correspondence between the patient’s atrophy W-score map and the best matched seed-based functional connectivity map (mean r = 0.32 ± 0.08). While the epicenter was always located squarely within atrophied regions, the epicenter region and the region with maximal atrophy were identical in only 13/72 patients (1 bvFTD, 12 svPPA). The average Euclidean distance between epicenter and the atrophy peak was small but not negligible (mean = 36 ± 28 mm). Thus, while the epicenter and atrophy peak were always near each other, the spatial distribution of atrophy was better recapitulated by the healthy FC spatial pattern of the epicenter regions, arguing that the epicenter detection step offers an advantage versus using the atrophy peak as the point of origin for predicting subsequent network-based spread. We next considered whether the identified epicenter for each subject was a significantly better fit than other lower ranking candidate epicenters. The second ranked region had a GOF score that was within 96.2% of the top-ranked region (Figure S2), and the largest difference in ranking was between the first and second scoring regions (3.8%). The relatively small difference in GOF scores is unsurprising given the substantial similarity in FC maps derived from different seed regions in the same ICN. A non-parametric permutation test of the Z-transformed GOF scores for the first and second-ranked regions showed that the first-ranked epicenter provided a significantly better fit (one-tailed test, Z = 1.65, p = 0.05), indicating that a single-epicenter model may be justified. We subsequently compared predictive models of future atrophy based on (a) path length from the epicenter versus path length from the peak atrophy region, and (b) path length from a single epicenter versus path length from all epicenters with GOF scores within 5% of the top-ranked region (see A Connectivity-Based Model Predicts Longitudinal Atrophy in Individual Patients).

Figure 2. Patient Brain Atrophy, Epicenters, and Clustering.

Top left/top right: atrophy frequency for patients with svPPA or bvFTD, showing the percentage of patients with voxel atrophy value W-score > 1.5. Bottom left and bottom right: number of patients with a given epicenter. Middle: principal component analysis showing the first two atrophy components for atrophy maps for all time points from all subjects. Longitudinal scans from the same subject are connected by lines. Dot radius represents scan mean atrophy W-score.

To visualize the heterogeneous atrophy patterns that give rise to the diversity of observed epicenter locations, we used principal component analysis on the atrophy maps for all patients at all time points to determine the atrophy latent space. Patients with a given syndrome could be discriminated by a linear boundary in this 2D space with 94% accuracy, indicating that the two clinical syndromes have highly distinct atrophy patterns, as expected. Within each syndrome, however, there was substantial atrophy pattern variability. This variability is illustrated by (a) the numerous areas where only a subset of patients had substantial atrophy (based on a liberal W-score threshold of 1.5; Figure 2, top left and right), particularly in bvFTD, (b) the wide distribution of patients within a given syndrome in atrophy latent space (Figure 2, middle), and (c) the spatially varying latent atrophy factors (Figure S5). We further characterized atrophy latent space with a clustering analysis on patient atrophy maps and discovered four clusters, which seemed to group patients according to atrophy severity within each syndrome (Figure S3; Table S6). The regions contributing most positively to component 1 were the same regions showing predominant atrophy in bvFTD, and the component 2-associated regions were those most atrophied in svPPA (Figure S4). We also confirmed that identified epicenter locations were highly consistent within subjects longitudinally (Table S7). Overall, the latent space analysis demonstrated atrophy pattern variability between subjects with the same clinical syndrome, which, in turn, explains the variability of epicenter locations (Figure S1). Despite the epicenter variability across subjects, identified epicenters are stable within subjects over time, suggesting that our method is well suited for predicting progression across disease stages.

Network Connectivity Properties Hypothesized to Drive Disease Spread

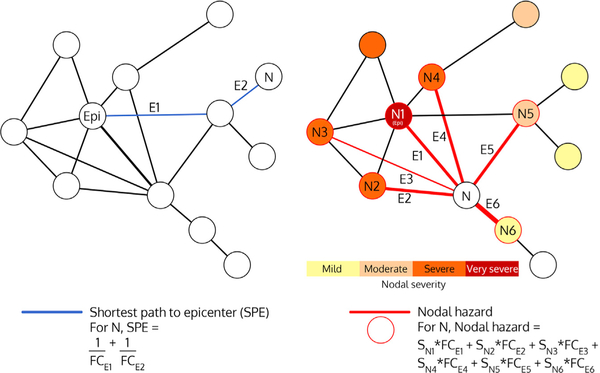
We hypothesize that multiple network properties may influence where disease spreads from an epicenter. Previously, we showed that regional atrophy severity depends on the shortest path length to the epicenter (SPE), a measure that captures the functional connectivity between a purported disease onset region and any other given region (Figure 3, left). These findings, however, were based on group-derived epicenters and averaged cross-sectional atrophy. As disease becomes more widespread, the connectional distance from the epicenter to a given region may lose some of its influence on that region’s risk for subsequent atrophy. Instead, a region’s risk of future degeneration may reflect the prevailing disease burden within that region’s immediate network neighbors. To model this concept, we defined a new regional risk measure, nodal hazard (Figure 3, right), expecting that a region with higher collective atrophy among its first-degree connected neighbors would undergo greater subsequent atrophy, especially when that region has strong connections to heavily affected neighboring nodes.

Figure 3. Schematic Depictions of Shortest Path to Epicenter (SPE) and Nodal Hazard (NH).

In SPE, E1 + E2 represents the path length between node N and node Epi. In nodal hazard, E1–E6 represent the functional connectivity strengths between node N and nodes N1–N6. Note that each node’s contribution to the nodal hazard weighted by its atrophy severity and adjusted for its Euclidean distance to the node of interest. Epi: epicenter; N: node; E: edge; FC: functional connectivity strength; S: severity.

A Connectivity-Based Model Predicts Longitudinal Atrophy in Individual Patients

Using each patient’s identified epicenter and each region’s path length to that epicenter and nodal hazard score, we specified a model to predict subsequent longitudinal atrophy. We used a generalized additive model, combining data from all patients and all regions to fit a single unified model. Generalized additive models are well suited for modeling spatiotemporal change because they can fit predictors in a flexible, non-linear fashion with safeguards against overfitting (see STAR Methods). These models can also include linear terms, random effect terms, and adjustment for spatial correlation among neighboring regions. Our model included non-linear terms for path length to the epicenter, nodal hazard, regional baseline atrophy, Euclidean distance to the epicenter and two random effects: a random intercept for subject and a random slope for each region’s relationship between baseline atrophy and subsequent atrophy. In the single-epicenter model, SPE, nodal hazard, and baseline atrophy were all significant predictors of change (Table 2).

Table 2.

Significance and Interpretation of Each Predictor on Subsequent Longitudinal Atrophy

Measure	t/F Statistic	p Value	Relationship to Change
Shortest path to epicenter	80.87 (F)	<2×10−16	Higher, less change (Figure 4C)
Nodal hazard	73.53 (F)	<2×10−16	Higher, more change (Figure 4C)
Baseline atrophy	118.62 (F)	<2×10−16	Intermediate, most change (Figure 4C)
Euclidean distance to epicenter	73.84 (F)	<2×10−16	Higher, less change
SPE * CDR-SB	19.98 (F)	8.05×10−11	Higher CDR-SB, positive-shifted SPE curve
Nodal hazard * CDR-SB	41.56 (F)	<2×10−16	Higher CDR-SB, positive-shifted Nodal hazard curve
CDR-SB baseline	−0.30 (t)	0.77	Not significant
CDR-SB change	−9.67	<2×10−16	More clinical worsening, less change
Interscan interval	14.50 (t)	<2×10−16	Longer, more change
Diagnosis	0.01 (t)	0.99	Not significant
Sex	−0.06 (t)	0.95	Not significant
Cortical/subcortical node	15.29 (t)	<2×10−16	Subcortical, more change
Global intercept	1.86 (t)	0.06	Subjects change on average (trend)
Age	0.01 (t)	0.99	Not significant
Subject intercept	157.54 (F)	<2×10−16	Different subjects have different amounts of change
Node random slope	25.41 (F)	<2×10−16	Different nodes have different baseline atrophy/change relationships
Spatial autocorrelation	89.77 (F)	<2×10−16	Adjacent nodes have more similar amounts of change

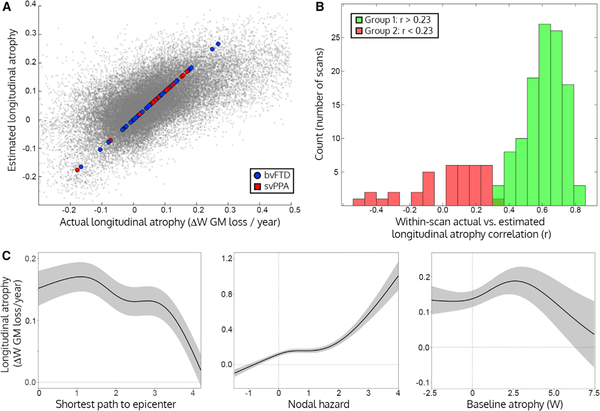
We evaluated the performance of the model for predicting atrophy first by correlating actual longitudinal atrophy and predicted longitudinal atrophy across all regions and all scans. Overall, the model explained an average of 37% within-scan variance in longitudinal atrophy (Figure 4A; root mean squared error W = ±0.105). When assessing the prediction accuracy across all regions for a given longitudinal scan, the predictions fell into “accurate” and “inaccurate” categories, with correlation accuracies greater or less than r = 0.23 (p greater than or less than 0.001). The prediction accuracies followed a bimodal distribution according to a Gaussian mixture model (see STAR Methods). 125 scans were accurately predicted (median r = 0.65 ± 0.15, Figure 4B, green) while predictions for 27 scans were much less accurate (median r = [C0]0.04 ± 0.20, Figure 4B, red). The generalizability of the model was tested using leave-one-subject-out cross validation. The leave-one-out models were still able to accurately predict subsequent longitudinal atrophy (accurate group LOO median r = 0.62 ± 0.15, root mean squared prediction error W = ±0.118; inaccurate group LOO mean r = −0.07 ± 0.19; root mean squared prediction error W = ±0.176). The strong performance of the model in predicting future atrophy suggests that the connection patterns of atrophied regions are a major factor influencing atrophy progression.

Figure 4. Network Model for Predicting Longitudinal Atrophy.

(A) Actual longitudinal atrophy for each node plotted against the estimated atrophy for that node from the full generalized additive model. Each subject’s mean longitudinal atrophy (as fit by the subject random intercept term) is shown as a larger dot with colors corresponding to their atrophy cluster membership (from Figure 2).

(B) Longitudinal prediction correlation per scan, based on the mixed effects model. Histogram indicating the frequency of Pearson correlations between the measured and estimated longitudinal atrophy across the 242 regions is shown. The green and red portions represent two groups detected by a Gaussian mixture model, representing scans with accurate (Group 1/green) or inaccurate predictions (Group 2/red).

(C) Effect plots for the three main predictors of interest, where shaded bands correspond to ± 2 × SE of the fit (95% confidence interval). Left: regions with a shorter path length to the patient’s epicenter had higher subsequent longitudinal atrophy, accounting for all other factors in the generalized additive model. Middle: regions with higher nodal hazard had higher subsequent longitudinal atrophy. Right: regions with intermediate levels of baseline atrophy had higher subsequent longitudinal atrophy than regions with low or high baseline atrophy.

Next, we determined which factors made some subjects’ atrophy progression more challenging to predict with our model. We used logistic regression to predict prediction accuracy group (Group 1/accurate or Group 2/inaccurate) and found scans in Group 2 were predominantly from patients with bvFTD (clinical diagnosis term t = 3.16, p = 0.001), especially those with lower levels of baseline atrophy (bvFTD diagnosis x mean baseline atrophy interaction term t = 2.03 p = 0.04), and subjects with a poorer fitting epicenter (epicenter GOF term t = 3.91 p = 0.0001). Scan quality (image quality rating determined by CAT12, see STAR Methods) or mean baseline level of atrophy did not have a significant impact on prediction accuracy (p > 0.05). An ROC curve based on region-wise prediction accuracy pooled across subjects revealed accurate performance in both syndrome groups (Figure S6; bvFTD AUC = 0.81, svPPA = 0.82). We noted that the 27 inaccurately predicted scans came from 16 subjects, 13 with a diagnosis of bvFTD, of which 4 had a C9orf72 mutation. Of these subjects, 9 had deceased and 8 autopsies had been completed, determining a diverse group of pathological diagnoses: corticobasal degeneration (bvFTD), TDP-43 unclassifiable (bvFTD), argyrophilic grain disease (bvFTD), TDP-43 type B with amyotrophic lateral sclerosis (bvFTD), Huntington’s disease (bvFTD), TDP-43 type B with motor neuron disease (bvFTD), TDP-43 type B (svPPA), and TDP-43 type C (svPPA). These findings suggest that patients who have poor epicenter fit, particularly if they have bvFTD and mild atrophy, are not ideal candidates for predicting future atrophy with a network-based model.

Shortest Path Length to the Epicenter, Nodal Hazard, and Regional Baseline Atrophy Have Non-linear Relationships with Subsequent Atrophy

Our brain-region-based predictors of subsequent atrophy were SPE, nodal hazard, and baseline atrophy. These terms were fit as non-linear “smooth” effects in the generalized additive model, which require visual interpretation to describe the relationship between the predictor and the outcome. The effect plots for SPE, nodal hazard, and baseline atrophy are shown in Figure 4C, displaying the effect of each term on longitudinal atrophy, accounting for all other terms in the model. Regions with the highest longitudinal atrophy were not at the epicenter but adjacent to the epicenter in network space, representing first-degree network neighbors (Figure 4C, left), This finding suggests that the epicenter regions may have slowed their rate of change due to an atrophy “ceiling” effect, where substantial previous atrophy has left little remaining gray matter available to lose, at the same time that epicenter neighbors showed peak change. Regions with a SPE of 2–3 had a less longitudinal atrophy, and regions farthest from the epicenter had the least longitudinal atrophy. Regions with higher nodal hazard showed greater longitudinal atrophy (Figure 4C, middle), with a non-linear acceleration for regions with nodal hazard > 1 (i.e., regions in the top 5% of nodal hazard values). Regions with intermediate levels of baseline atrophy had the most longitudinal atrophy (Figure 4C, right), while regions with low and high levels of baseline atrophy showed lower subsequent atrophy. This curve suggests a sigmoidal disease course in each region over time (Jack et al., 2010). The impact of clinical disease stage on network-based spread was considered by including CDR interactions with SPE and nodal hazard in the model. Both the SPE and nodal hazard effects had a higher intercept for higher levels of CDR, indicating greater global longitudinal atrophy with increasing baseline clinical severity. The relationship between subsequent atrophy and simultaneous clinical change was significant, consistent with a model in which clinical change lags in time behind gray matter atrophy.

We then investigated the possibility that atrophy may emanate from either a single or multiple independent epicenters or spread in both a spatial and a connectional pattern. A single-epicenter model was a significantly better overall predictor of subsequent atrophy than an otherwise identical multi-epicenter model (Likelihood ratio test, χ² = 81.5, p < 23×10⁻¹⁶; single-epicenter model: Akaike Information Criterion (AIC) score = −51251; multi-epicenter model AIC = −51171). The single-epicenter model also outperformed a model using path length from the region with peak atrophy (χ² = 226.9, p < 2×10⁻¹⁶; peak atrophy model AIC = 51028). When comparing the single and multi-epicenter model[C0]for only the 35 subjects with multiple high likelihood epicenters, the multi-epicenter model was slightly more significant (χ² = 21.02, p = 0.0001). We compared the single-epicenter model against two alternative models. First, a set of randomly connected null network-based models (n = 1000) all made significantly less accurate predictions than the true model (mean χ² = 1059.2 ± 39.6, all p < 2×10⁻¹⁶; mean AIC = −49671 ± 39) and substantially lower predictive power for network-based predictors (null SPE median F = 7.02 versus true SPE F = 80.87; null hazard median F = 8.43 versus true hazard F = 73.53). To further ensure that spatial autocorrelation in FC was not driving the results, we adjusted the connectome FC weights for Euclidean distance using regression. Similar results were obtained when generating null network-based models derived using this adjusted connectome (mean χ² =857.5 ± 40.1, all p < 2×10⁻¹⁶; mean AIC = −49758 ± 39). Second, a pure spatial spread model using only a[C0]”spatial hazard” term without network-based predictors (see STAR Methods) also made less accurate predictions than the true model (χ² = 328.68, p < 2×10⁻¹⁶, AIC = −50529; spatial hazard F = 156.06, p < 2×10⁻¹⁶). When predictions from the network-based and spatial-based models were compared, the network-based model was more accurate in areas physically distant from the baseline atrophy peak, such as the posterior cingulate/precuneus in bvFTD and the right anterior temporal lobe in svPPA (Figure S7). The spatial model mademore accurate predictions in subcortical areas physically proximal to the baseline atrophy peak, particularly in the thalamus in bvFTD and the striatum and thalamus and svPPA. When updating the single-epicenter network-based model with an additional term for spatial hazard, the new model outperformed the original (χ2 = 358.37, p < 2×10⁻¹⁶) with statistically significant explanatory power for baseline atrophy, shortest path to the epicenter, nodal hazard, Euclidean distance to epicenter, and spatial hazard (see Table S8 for individual termF-statistics). We assessed the accuracy of model predictions for nodes that were spatially near or far from the epicenter (less than or greater than 50 mm Euclidean distance) or found that the overall variances explained were similar (mean within-scan r = 0.58 ± 0.18 versus r = 0.60 ± 0.16, two-group comparison t = −1.15, p = 0.25). Overall, these findings suggest that while a model of connectivity-based spread from a single epicenter and hazard from connected neighboring nodes provides the best overall predictions of future brain atrophy, a multi-epicenter model may better capture patients with multiple high likelihood epicenters, and predictors based on spatial spread make a significant complementary contribution.

Predicting Diverse Patterns of Longitudinal Atrophy: Group Findings and Single Case Illustrations

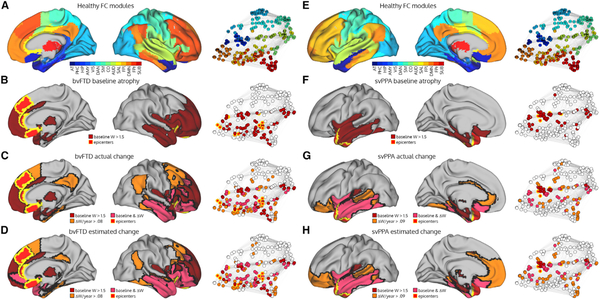
To demonstrate the anatomical prediction accuracy of the model, we generated actual and predicted longitudinal atrophy maps for the bvFTD (Figures 5A–5D) and svPPA (Figures 5E–5H) groups. BvFTD showed progressive atrophy spreading posteriorly and dorsally from the regions affected at baseline, infiltrating the posterior cingulate cortex and precuneus, inferior parietal lobule, posterior inferior temporal cortex, and dorsal prefrontal cortex both medially and laterally (Figure 5C). Importantly, spread bypassed some regions that were spatially adjacent but connectionally more distant from atrophied regions, such as the primary motor and sensory cortices. This observation is clearest when visualizing the connectome, where longitudinal atrophy is apparent in the default mode and fronto-parietal networks, while not involving regions in the sensory-motor network (Figure 5C). The model accurately predicted the presence or absence of longitudinal atrophy in each of these areas (Figure 5D). In the svPPA group, atrophy progressed both anteriorly and posteriorly into the ventral/orbital frontal cortex and posterior temporal lobe, and wrapped around the anterior and mid-cingulate cortices (Figure 5G). A number of regions showing the highest rates of longitudinal atrophy were in FC modules connectionally adjacent to the epicenter-containing FC modules. Overall, our unified model provided a striking congruence between measured and predicted atrophy spread in two anatomically distinct neurodegenerative syndromes.

Figure 5. Baseline, Longitudinal, and Predicted Longitudinal Atrophy Patterns in bvFTD and svPPA.

(A and E) The modules in the healthy functional connectome and the corresponding network graph.

(B and F) The bvFTD/svPPA group baseline atrophy map shown on the more severe hemisphere (right for bvFTD, left for svPPA), coloring nodes with a mean W-score > 1.5. Regions where > = 5 subjects had an epicenter are labeled as epicenters. Atrophied nodes and epicenters are also shown on the network graph.

(C and G) The annualized mean actual longitudinal atrophy map, coloring nodes with a mean W-score > 0.08 in bvFTD or W-score > 0.09 in svPPA (equivalent to the top 25% of regions).

(D and H) The annualized mean predicted longitudinal atrophy map, coloring nodes with a mean predicted W-score > 0.08 in bvFTD or predicted W-score > 0.09 in svPPA (equivalent to the top 25% of regions). AT: anterior temporal; PHC: parahippocampal; HIP: hippocampal; AMY: amygdala; VIS: visual; DAN: dorsal attention network; SM: sensory-motor; CO: cingulo-opercular; AUD: auditory; SAL: salience; FPl: left fronto-parietal; DMN: default mode network; FPr: right fronto-parietal; SUB: subcortical.

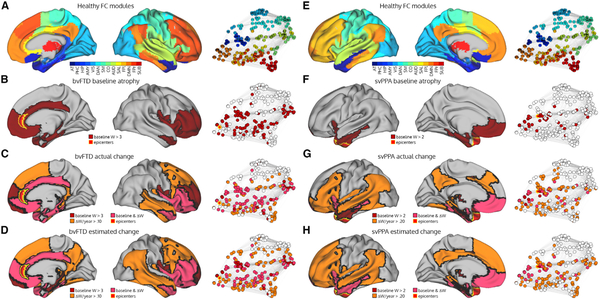
To illustrate the prediction accuracy of our model in individual patients, we plotted the predicted and actual longitudinal atrophy in one with bvFTD and one with svPPA who had predictions accuracies at the group median level. The first was a representative 64-year-old woman with bvFTD whose epicenter was located in pregenual anterior cingulate cortex. In the patient’s baseline MRI, atrophy was greatest in the anterior cingulate, anterior insula, ventral frontal lobe, and anterior temporal lobe (Figure 6B). Subsequently, atrophy worsened most in the ventral frontal lobe, insula, anterior temporal lobe, and cingulate while progressing into the dorsal frontal lobe, posterior temporal lobe, retrosplenial cortex, and parahippocampal cortex (Figure 6C), regions connectionally adjacent to the regions atrophied at baseline. The model was able to predict longitudinal atrophy in each of these areas (Figure 6D), while overestimating atrophy in the inferior and medial parietal lobe. The overall correlation between actual and predicted longitudinal atrophy was high (Pearson r = 0.64).

Figure 6. Regions with Greatest Baseline, Longitudinal, and Predicted Longitudinal Atrophy in bvFTD and svPPA Case Studies.

(A and E) The modules in the healthy functional connectome, shown on the brain and on the network graph.

(B and F) The patients’ baseline atrophy map shown on the more severe right hemisphere for bvFTD and the left hemisphere for svPPA. The epicenters are in the right pregenual anterior cingulate for the bvFTD patient and left ventral temporal pole for the svPPA are shown in yellow. Maps were thresholded at the 25^th percentile of atrophy baseline/change W-scores at the group level, based on these patients’ respective demographic and clinical variables, and are not intended to represent statistical thresholds.

(C and G) The patients’ actual annualized longitudinal atrophy map, coloring nodes with a mean W-score > 0.10 for the bvFTD patient or W-score > 0.2 for the svPPA patient (manually selected).

(D and H) The patients’ predicted longitudinal atrophy map, coloring nodes with a predicted W-score > 0.10 for the bvFTD patient or predicted W-score > 0.2 for the svPPA patient.

The second patient was a 51-year-old man with svPPA. His epicenter was located in left ventral anterior temporal lobe. At baseline, atrophy was most substantial in the anterior temporal lobe, anterior insula, and ventromedial prefrontal cortex (Figure 6F). Longitudinally, atrophy worsened most in the ventromedial prefrontal cortex while spreading into the posterior temporal lobe, inferior and medial parietal lobe, insula, lateral and medial frontal lobe, and cingulate (Figure 6G). As seen in the patient with bvFTD, the regions that showed longitudinal atrophy were connectionally adjacent to the regions atrophied at baseline. Our prediction model provided an accurate forecast, with a high correlation between predicted and observed atrophy (Pearson r = 0.67). Atrophy was accurately predicted to spread both in ventral anterior and posterior directions, while overestimated in the dorsal medial frontal lobe. Together, these case studies demonstrate the flexibility of our unified model to predict atrophy in different individual patients with distinctly different atrophy patterns and epicenters.

DISCUSSION

With an increasing number of candidate neurodegenerative disease therapies entering clinical trials, there is an urgent need to forecast and monitor disease progression in individual patients. In previous work, we developed a network-based neurodegeneration framework based on regional atrophy patterns seen in groups of patients at baseline. Here, we have developed an individualized, longitudinal atrophy prediction model and applied the model to patients with bvFTD and svPPA. We identified patient-derived “epicenters” by comparing each brain region’s connectivity pattern to the patient’s unique pattern of baseline atrophy. We then used each patient’s epicenter to derive graph theoretical properties for each brain region, again based on the healthy connectome, including that region’s connectional distance from the epicenter and the atrophy severity within the region’s closest network neighbors. We used these properties to build a statistical model of future atrophy in each brain region that could predict the whole-brain longitudinal atrophy pattern in most patients. In addition to providing new human evidence that neurodegenerative disease spreads, at least in part, between functionally connected areas, the findings represent a key step along the path toward clinical application of the network-based neurodegeneration framework.

Previous studies have identified “epicenters” in FTD, Alzheimer’s disease, and Parkinson’s disease based on the spatial patterns of atrophy or hypometabolism (Mutlu et al., 2017; Zeighami et al., 2015; Zhou et al., 2012). These efforts were based on group-level analyses that assumed a common epicenter or epicenters among all patients with a given syndrome. The anatomical heterogeneity seen within syndromes (Ranasinghe et al., 2016; Seeley et al., 2005; Thompson et al., 2003; Whitwell et al., 2009), however, suggested the need for a patient-tailored approach. Importantly, our procedure was able to avoid circularity by identifying each patient’s epicenter from their baseline scan and then using it to predict change in future scans. A key question related to this framework is whether disease begins within and spreads from a single epicenter or arises in a simultaneous or staggered manner in multiple, independent regions. Although we cannot rule out the presence of multiple, independent epicenters based on our data, we found that the dropoff in epicenter “goodness of fit” was greatest between the 1^st- and 2^nd-ranked epicenters. Furthermore, a single-epicenter model provided marginally but significantly more accurate predictions than did a multi-epicenter model. In the subjects where we detected multiple epicenters—those subjects for whom multiple regions had GOF scores within 5% of the top-ranked region—the multi-epicenter model slightly outperformed the single epicenter model. It remains an open question whether the multiple epicenters represent independent point sources in a staggered multi-focal neurodegeneration process (Seeley, 2017) or downstream amplification regions, “seeded” by a single onset region that proved potent because of specific cellular, synaptic, or other regional properties, such as a high concentration of neurons with a vulnerable phenotype. The single-epicenter model also outperformed a model of progression based exclusively on spatially contiguous spread, although the spatial hazard term had a significant contribution to predicting future atrophy. This observation suggests that connectivity and spatial proximity are complementary factors influencing progression. An important caveat of our approach is that we evaluate epicenter likelihood based on correspondence between atrophy and singleseed intrinsic connectivity networks. However, in a simulated model of network-based disease spread from a single point source throughout a modular network, infection will not remain confined to the original module for long, instead spreading into other modules once the process reaches connector hubs (van den Heuvel and Sporns, 2013). We employed two methods to address this issue—allowing for the possibility of multiple epicenters and including nodal hazard as a measurement of cumulative network burden. An important recent study by Torok and colleagues used a network diffusion model to infer heterogenous “seed” locations in different patients with Alzheimer’s disease (Torok et al., 2018). We expect that future studies will advance simulated network spread modeling (Iturria-Medina et al., 2014; Mi šić et al., 2015; Raj et al., 2015) to improve epicenter detection and make more precise predictions about an individual’s future pattern of disease progression.

Despite the striking accuracy seen across the group as a whole and in many individual patients (Figures 5 and 6), our model did not make accurate predictions in all patients. For 27 of 152 scans, the model produced weak predictions (median r = 0.04), leading us to seek out characteristics that might have rendered our model less useful in these patients. Most scans in this category came from patients with bvFTD (23/27 scans), particularly those with moderate atrophy (16/27 scans) and poorer-fitting epicenters. Considering the clinical, anatomical, genetic, and pathological diversity of patients with bvFTD (Perry et al., 2017), we suspected that our model may have failed in some patients based on a different underlying biology such as the presence of a C9orf72 expansion or other genetic mutation. Indeed, 4 out 6 C9orf72 carriers had poorly predicted scans, while one subject who came to autopsy had underlying Huntington’s disease. Some patients, particularly those with C9orf72 expansion, may have subcortical epicenters (Lee et al., 2016) that were excluded by our chosen methods, and future efforts could explore the value of retaining subcortical areas during epicenter selection. Patients with svPPA had more accurate predictions overall, which is due in part to a more stereotypical pattern of progression than in bvFTD and the ability of the model to learn spatial factors of progression that are consistent within subsets of the cohort through the terms for spatial correlation and node random effect. When applying a predictive model, one should consider the balance of leveraging group-wide patterns to improve prediction accuracy while maintaining sufficient flexibility to predict diverse patterns of change in individual patients. We expect that near-term efforts to improve the atrophy prediction accuracy will use both biologically principled and data-driven models (Young et al., 2018; Zhang et al., 2016), perhaps in tandem.

Accounting for a patient’s disease stage is critical when predicting the subsequent rate of neurodegeneration, given that changes in gray matter volume over time are non-linear (Jack et al., 2010). In this study we evaluated whether network-based progression exhibits a disease stage-dependence in two main ways: (1) using a non-linear generalized additive model and (2) defining a new regional risk factor, nodal hazard. Nodal hazard is the risk that a region faces for subsequent atrophy based on the cumulative atrophy burden of its mostly strongly connected neighbors. Overall, nodal hazard was a significant predictor of subsequent atrophy, explaining unique variance in our model above and beyond that explained by regional baseline atrophy and SPE. Nodal hazard’s explanatory power may suggest a “contagion” mechanism of disease spread, in which affected nodes downstream of the epicenters become additional amplifiers and spreaders of disease, rather than acting as passive relays. Future molecular imaging studies could help test this idea. If amplification is a factor in disease progression, one can expect exponential growth and plateau phases, which together constitute a sigmoidal progression of atrophy (Newman, 2018). Our model provided three additional pieces of support for non-linear rates of progression. First, the relationship between regional baseline atrophy and subsequent atrophy change was non-linear. Regions with intermediate levels of baseline atrophy showed greater subsequent longitudinal atrophy than regions with low or high baseline atrophy. This suggests a non-constant rate of change over time, as is the case for a sigmoidal curve where the rates of change are highest at the inflection point and slower in the ramp-up and ramp-down phases (Jack et al., 2012). Second, epicenter regions showed slightly lower longitudinal atrophy than their adjacent connected neighbors, suggesting that the epicenters had reached an atrophy “ceiling” effect. And third, longitudinal clinical change was negatively correlated with longitudinal atrophy, consistent with a mode of progression in which non-linear gray matter change precedes non-linear clinical change.

The central assumption of our connectivity-based prediction approach is that disease pathology spreads directly between anatomically connected brain regions. The two most common molecular pathologies underlyingbvFTD and svPPA involve pathological misfolding of tau (FTLD-tau) and TAR DNA-binding protein 43 (TDP-43; FTLD-TDP) within neurons and glia. There is accumulating evidence for trans-synaptic spread of tau through a prion-like mechanism (de Calignon et al., 2012; Liu et al., 2012). While there is evidence for cell-to-cell propagation of TDP-43 oligomers in vitro (Feiler et al., 2015), it remains unclear whether intracellular transmission occurs in vivo (Brettschneider et al., 2015; Hock and Polymenidou, 2016), although recent evidence supports transmissibility and some degree of spreading (Porta et al., 2018). Even if TDP-43 does not spread trans-synaptically, this does not rule out the possibility of cascading transneuronal degeneration in FTLD-TDP driving network-based spread of atrophy (Fornito et al., 2015), due to propagating cell-autonomous and non-cell-autonomous processes such as loss of trophic support (Perlson et al., 2010), hypometabolism (Bejanin et al., 2019), or Wallerian degeneration (Beirowski et al., 2005). Future neuroimaging studies with longitudinal tau PET in FTLD-tau will further our understanding of systems mechanisms underlying progressive neurodegeneration, while autopsy and animal studies will be necessary for resolving the cellular basis of disease spread.

We demonstrate that a network-based model can accurately predict the mean level of subsequent atrophy for most patients. In FTD and other neurodegenerative diseases, gray matter atrophy typically precedes subsequent clinical decline (Bateman et al., 2012; Jack et al., 2010; Rohrer et al., 2015). Here we found this type of relationship between clinical severity change and simultaneous rates of atrophy, which might be expected for patients in the mild-to-moderate clinical stage. The primary goal of this study, however, was to make accurate predictions about the severity of future atrophy using a baseline MRI scan. This type of patient-tailored biomarker may prove useful as a proof-of-concept indicator in an early-to-mid-stage clinical trial, where the aim is to demonstrate efficacy on an objective biological measure. In this setting, less-than-expected atrophy would provide an encouraging sign of treatment efficacy, helping industry stakeholders take the next step toward a confirmatory trial. This type of biomarker differs from a surrogate endpoint, which can be used as a substitute for clinical efficacy in a confirmatory trial. One additional reason to consider MRI-based atrophy as a clinical trial biomarker in FTD is the limited sensitivity of tau PET imaging in bvFTD (Tsai et al., 2019), the ambiguity of tau PET positivity in svPPA patients where TDP-43 type C pathology is expected (Bevan-Jones et al., 2018; Makaretz et al., 2018), and the absence of a TDP-43 PET ligand.

A limitation of our study is the use of a single functional connectome derived from healthy control subjects. Human brain connectome mapping has undergone continual refinement in the past decade (Crossley et al., 2014; Hagmann et al., 2008; Power et al., 2011; Yeh et al., 2018), though each connectome mapping modality has its limitations. Head motion is a concern in fMRI-based functional connectomes (Power et al., 2012), and systematic false positives are present in diffusion-weighted MRI tractography-based anatomical connectomes (Maier-Hein et al., 2017). The connectome used in this study was taken as group average from a cohort of healthy older control subjects (n = 75) selected on the basis of (1) similar age to the patients in the study, (2) data acquisition on the same scanner in the same center, and (3) particularly low head motion. We used the functional connectome to model network-based spread of atrophy because fMRI is currently better at capturing long-range, distributed brain networks, including the default mode network and dorsal attention network, while these long-range connections can be difficult to detect with diffusion-weighted tractography (Reveley et al., 2015; Thomas et al., 2014). Furthermore, functional intrinsic connectivity networks are highly reliable across individuals (Damoiseaux et al., 2006; Gordon et al., 2017; Gratton et al., 2018; Shehzad et al., 2009), represent stable anatomical subdivisions (Glasser et al., 2016), and have common gene expression profiles (Hawrylycz et al., 2015; Richiardi et al., 2015). A next step for patient-tailored, connectivity-based models of spread will be to incorporate the patient’s own functional and/or anatomical connectome and evaluate how disease-related changes in connectivity modulate the further spread of atrophy.

STAR★METHODS

LEAD CONTACTS AND MATERIAL AVAILABILITY

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, William Seeley (bill.seeley@ucsf.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Patient Diagnostic Criteria

Patients and control subjects were recruited between 2005 and 2016 through ongoing studies at the University of California San Francisco (UCSF) Memory and Aging Center (MAC). All subjects or their surrogates provided informed consent according to the Declaration of Helsinki and the procedures were approved by the Institutional Review Board at UCSF. All patients and control subjects underwent a clinical history, physical examination, neuroimaging, and comprehensive neuropsychological assessment within 90 days of scanning (Rosen et al., 2002). None of the patients had significant history of other neurological diseases or structural brain abnormalities inconsistent with bvFTD or svPPA. The patient group consisted of 72 patients who received a research diagnosis of either behavioral variant frontotemporal dementia, based on the criteria from the International Behavioral Variant Frontotemporal Dementia Criteria Consortium guidelines (Rascovsky et al., 2011), or semantic variant primary progressive aphasia based on published consensus criteria (Gorno-Tempini et al., 2011). All diagnoses were made within 90 days of the patients’ baseline MRI scan. We opted to include patients with shifting diagnoses to test the ability to predict future progression for subjects who had met the clinical criteria for a bvFTD or svPPA diagnosis at their original visit. All subjects with svPPA had consistent diagnoses at each visit, while 4/42 patients with bvFTD had diagnoses that shifted to either svPPA, Alzheimer’s disease, progressive supranuclear palsy syndrome, or corticobasal syndrome. Patients also received tests for the most common FTLD-causing mutations. Among patients with bvFTD, 6 had pathogenic variants in C9orf72, 3 in GRN, and 1 in MAPT. One patient with svPPA carried a pathogenic variant in TARDBP (Figure S5). At the time of writing, 28 patients had died and 20 of these had undergone autopsy and a post-mortem neuropathological assessment at the UCSF Alzheimer’s Disease Research Center (Figure S5). This cohort included patients with pathological diagnoses of corticobasal degeneration (n = 3), Pick’s Disease (n = 1), argyrophilic grain disease (n = 1), Huntington’s Disease (n = 1), TDP-43 type A (n = 2), TDP-43 type B (n = 5), TDP-43 type C (n = 5), and TDP-43 unclassifiable (n = 2). Among patients with TDP-B, one patient also comorbid amyotrophic lateral sclerosis, two patients had comorbid motor neuron disease, and one patient had a secondary unclassifiable tauopathy.

Healthy control criteria

Inclusion criteria for healthy control subjects included normal cognitive performance, lack of any major brain structural abnormalities, and absence of neurological, psychiatric, or other major medical illnesses. 288 subjects were selected to serve as controls for the structural analysis (HC1; Table S1). 100 subjects were considered as candidate functional controls, from which we selected a subset of 75 (HC2) that had the lowest head motion based on a combination of no or very few motion spikes (mean number of spikes = 0.17) and low relative head displacement (mean sum displacement = 42 mm; Table S2).

METHOD DETAILS

Neuroimaging acquisition

All patients (n = 72, Table 2) were scanned at the UCSF Neuroscience Imaging Center on a Siemens Trio 3T scanner. A T1-weighted MP-RAGE structural scan was acquired with an acquisition time = 8 min 53 s, sagittal orientation, a field of view of 160 × 240 × 256 mm with an isotropic voxel resolution of 1 mm³, TR = 2300 ms, TE = 2.98 ms, TI = 900 ms, flip angle = 9°. Healthy control subjects receiving structural MRI (n = 288) were scanned either on the Trio 3T scanner (n = 220) or on a Siemens 1.5 Tesla Magnetom scanner at UCSF (n = 68) using a MP- RAGE sequence with a voxel resolution of 1.0 × 1.0 × 1.5 mm, TR = 10ms, TE = 4ms, TI = 300ms, flip angle = 15°. Healthy control subjects receiving task-free functional MRI (n = 75) were scanned on the Trio 3T scanner, using a T2*-weighted echoplanar scan with an acquisition time = 8 min 6 s, axial orientation with interleaved ordering, field of view = 230 × 230 × 129 mm, matrix size = 92 × 92, effective voxel resolution = 2.5 × 2.5 × 3.0 mm, TR = 2000 ms, TE = 27 ms, for a total of 240 volumes. Subjects were instructed to remain awake with their eyes closed.

Structural image processing

MP-RAGE scans were first visually assessed by trained technicians and to ensure that excessive motion artifact (ringing or blurring) was not apparent. Images were subsequently processed with the CAT12 toolbox (http://www.neuro.uni-jena.de/cat/), which measures the image Noise Contrast Ratio, Inhomogeneity Contrast Ratio, and Root Mean Square Resolution and combines these measures to yield an Image Quality Rating (IQR). For the 235 scans, the IQR mean = 2.10 ± 0.23, ranging from a rating of “good” (1.85) to “satisfactory” (2.80). MP-RAGE scans for all time points for a given subject were then registered to one another using the symmetric diffeomorphic registration incorporated in the serial longitudinal anatomical MRI package in SPM12 (Ashburner and Ridgway, 2013). This procedure is optimized for longitudinal analysis by correcting for intensity inhomogeneities and creating an average T1 image for each subject, avoiding asymmetric bias that can result from using a particular time point (e.g., the baseline image) as the reference image. Default parameters were used for warping regularization and bias regularization. Jacobian determinant and divergence maps were produced that represent the amount of longitudinal brain contraction and expansion. We then applied unified normalization/segmentation to register the midpoint average T1 images to standard space (Ashburner and Friston, 2005) with light regularization, a 60 mm bias FWHM cutoff, and Gaussians per tissue type of [2,2,2,3,4,2]. The gray matter tissue segmentation for the midpoint average was multiplied by the deformation fields for each time point to obtain time point-specific gray matter maps. These images were then warped to standard space using the deformation fields from the unified normalization/segmentation procedure. The resulting normalized gray matter maps were smoothed with an 8 mm FWHM Gaussian kernel.

Functional image processing

For each fMRI scan, the first five volumes were discarded. SPM12 (https://www.fil.ion.ucl.ac.uk/spm/software/spm12/) and FSL (where explicitly specified; https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/) software was used for subsequent fMRI preprocessing. The remaining 235 volumes were slice-time corrected, realigned to the mean functional image and assessed for rotational and translational head motion. Volumes were next co-registered to the MP-RAGE image, then normalized to the standard MNI-152 healthy adult brain template using SPM segment, producing MNI-registered volumes with 2 mm³ isotropic resolution. These volumes were spatially smoothed with a 6 mm radius Gaussian kernel and temporally bandpass filtered in the 0.008–0.15Hz frequency range using fslmaths. Nuisance parameters in the preprocessed data were estimated for the CSF using a mask in the central portion of the lateral ventricles and for the white matter using a mask of the highest probability cortical white matter as labeled in the FSL tissue prior mask. Additional nuisance parameters included the 3 translational and 3 rotational motion parameters, the temporal derivatives of the previous 8 terms (WM/CSF/6 motion), and the squares of the previous 16 terms (Satterthwaite et al., 2013). No global signal regression was performed, although white matter and CSF regressors are likely to capture a portion of the variance from motion-associated global signals (Ciric et al., 2017). All subjects had maximum relative head motion less than 3 mm, maximum relative rotation less than 3 degrees, and the maximum number of motion spikes (relative motion > 1 mm) less than 10% of the total number of frames.

QUANTIFICATION AND STATISTICAL ANALYSIS

Determination of individual patient gray matter atrophy patterns

We derived voxelwise gray matter maps from a large set of older healthy controls (n = 288; Table S1) using the same normalization procedure described earlier (see Structural image processing). We then ran multiple regression for each voxel to estimate gray matter volume as a function of age, sex, handedness, years of education, total intracranial volume, & MRI scanner. Then, for a patient, we entered their demographic values into that regression model to estimated their gray matter volume for a given voxel. The voxel W-score was then calculated as the difference between actual gray matter volume and the estimated gray matter volume, divided by the standard error of the model fit in controls (La Joie et al., 2012) (Figure 1). The W-score approach is useful for creating voxelwise individualized maps of gray matter atrophy while accounting for covariates that may influence gray matter density.

Identification of disease epicenter for each patient

We used a whole-brain parcellation of 246 cortical and subcortical regions from the Brainnetome atlas (Fan et al., 2016; http://www.brainnetome.org/). This atlas was selected because of its joint validation using both functional and structural anatomy and connectivity, coherent with the design and aims of the current study. Furthermore, the Brainnetome atlas is one of the few publicly available atlases that includes data-derived subcortical parcels, which are commonly affected and of interest in bvFTD and svPPA. We screened regions for insufficient fMRI BOLD signal intensity by first calculating each region’s mean BOLD signal across all 75 scans. We sorted the regional BOLD intensity values from largest to smallest, and found the “elbow” of this distribution using the pairwise differences. The largest elbow was between regions 242 and 243, which led us to exclude 4 regions: left/right anterior parahippocampal gyrus, and left/right posterior inferior temporal gyrus. In the remainder of the analysis, we therefore used 242 regions. Each of these parcels was used as the seed region to generate a tf-fMRI seed-based intrinsic functional connectivity map from a set of healthy control subjects age matched to our patients (n = 75; Table S2). We obtained voxelwise FC maps by extracting the mean BOLD timeseries from a parcel and regressing it versus each voxel’s timeseries, covarying for the 32 nuisance parameters. Then for each parcel, we entered the voxelwise FC parameter estimate maps for the 75 control subjects into a second-level, one-sample t test to obtain a single group-level statistical parametric (t-statistic) FC map. These group-level FC seed t-statistic maps were then used to identify each patient’s atrophy epicenter. We limited our set of parcels to cortical regions, excluding parcels in the parahippocampal cortex, hippocampus, amygdala, basal ganglia, and thalamus, leaving a pool of 194 candidate epicenters. There is evidence that structural MRI registration procedures like the one used in this study may inflate estimates of gray matter loss in periventricular structures, sulci, and fissures (Callaert et al., 2014). This tradeoff must be weighed against the limitations of more complex registration algorithms when applied to brains with atrophy (Pereira et al., 2013).

To identify the epicenter for a given atrophy W map, we performed spatial correlation of the voxelwise gray matter atrophy W-scores with the voxelwise FC values (Z statistics) in the gray matter for each of the seed FC maps. The parcel whose FC map had the highest correlation with the atrophy W map (the epicenter goodness of fit score, GOF) was selected as the epicenter. This procedure was an adapted version of our previous protocol (Zhou et al., 2012) that eliminated statistical thresholding of W/FC maps for three reasons: 1) selection of statistical thresholds for “significant” atrophy/FC is essentially arbitrary, 2) inclusion of all voxels may enable detection of epicenters in earlier stage patients with subthreshold atrophy, and 3) in this study, where the goal is to predict future longitudinal atrophy, there is less risk of introducing circularity bias in the modeling of network spread when correlating continuous atrophy from the baseline scan and FC values, rather than binarizing atrophy/FC maps and measuring the amount of overlap. For a number of scans, we observed that several candidate epicenters had scores that were within 5% of the top GOF score. In such cases, less statistical confidence can be placed on a single epicenter. For this reason, we evaluated a multi-epicenter model in parallel to the single-epicenter model. We deemed any node whose epicenter score was within 5% of the top ranked node as a member of the set of multiple epicenters (Figure S2). A post hoc test indicated that the top epicenter regions across subjects (n = 25) had significantly lower weighted degree in the healthy functional connectome than non-epicenters (n = 169; t = −2.58, p = 0.01) but had no difference in within-module weighted degree Z-score (t = −0.58, p = 0.56).

Examination of atrophy subtypes

K-means clustering was performed on the 242 region x 235 scan data matrix to assign each scan to 1 of 4 clusters representing atrophy subtypes. Principal component analysis was then run on the same 242 × 235 matrix to visualize the clustering of atrophy maps on the first 2 principal components (Figure 2). Regional atrophy W-score correlations with component loading scores were determined for the first two components (p < 0.0002, corrected for multiple comparisons, corresponding to b > 0.05) (Figure S5).

Network analysis of the healthy FC connectome

We generated the 242 × 242 healthy control functional connectome (n = 75) by extracting the mean BOLD timeseries from each region (referred to equivalently as a network node), calculating the pairwise Pearson correlation coefficients, performing an r-to-Z transformation, and averaging across subjects. Graph theory analyses were run using the Brain Connectivity Toolbox (BCT; https://sites.google.com/site/bctnet/) and custom MATLAB code (https://github.com/jbrown81/connect_metrics). We determined the shortest path between all pairs of nodes by taking the unthresholded connectivity matrix, calculating the inverse to obtain a weight-to-distance mapping, and then using Dijkstra’s algorithm in the BCT to determine shortest paths and their path lengths:

$$d_{ij}=\sum _{a_{uv}\in gi\leftrightarrow j}\frac{1}{a_{uv}}$$

where d is the shortest path length from node i to node j, a is one edge comprising that shortest path that connects intermediate nodes u and v, g_ij is the shortest path from i to j, and path length is quantified as the inverse of the Z-transformed functional connectivity strength (Rubinov and Sporns, 2010). We used the Louvain algorithm (Blondel et al., 2008) to assess modularity in this network, as implemented in BCT, running 1000 iterations with the default parameters, choosing the partition that maximizes the Q value. We determined the modularity on the unthresholded graph in order to maintain consistency with the unthresholded seed-based FC maps that were used for epicenter detection. This yielded 4 modules, a relatively small number given the typical partitioning into 7 or more modules (Yeo et al., 2011). However, this small number of modules is typical when partitioning unthresholded graphs. We therefore chose to run the modularity algorithm a second time within each module, to detect 14 sub-modules, each of which corresponded to a known intrinsic connectivity network (Figure 5A).

Finally, we defined the formula for our new graph measure, nodal hazard, as:

$$N{H}_i=\sum _{j=1}^n\frac{a_j*e_{ij}}{d_{ij}}$$

where j are the neighboring nodes of node i, e is the edge weight between i and j, a is the atrophy W-score for node i, and d is the Euclidean distance between i and j (Figure 3), and n = 5. We limited the neighborhood to the five most strongly connected neighbors, which had a mean edge weight Z = 0.94, representing the 97.5^th percentile of connection strengths in the network. To give a qualitative sense of the size of a local neighborhood in the calculation of nodal hazard, when our modularity algorithm was applied at a third level it yielded 32 sub-sub-modules, which contained an average of 7.5 regions. Thus, a 6 region neighborhood (a region and its top 5 neighbors) roughly corresponded to the size of a module subcomponent, for example the anterior portion of the default mode network. The Euclidean distance scaling factor was included to adjust hazard for the pathological transit time, given that cumulative protein propagation over time is likely to depend on the physical distance between the regions (DeVos et al., 2018). As an alternative to a connectivity-based model for predicting subsequent atrophy, we calculated a “spatial hazard” measure. Spatial hazard was derived identically to nodal hazard, except that the Euclidean distance was used instead of functional connectivity strength for determining a node’s 5 closest neighbors. Models based exclusively on spatial spread included the proximity hazard for each node and each node’s Euclidean distance to the node with peak atrophy.

Null connectomes (n = 1000) were created by rewiring the true connectome 50000 times using the null_model_und_sign function in the BCT. This algorithm preserves the degree and strength distribution of the graph, a necessary constraint for making valid network comparisons (Rubinov and Sporns, 2011), albeit limiting the extent to which the network can be truly “randomized.” Such limited reconfiguration helps explain why the null network-model based predictions of longitudinal atrophy still found slightly positive F-statistics for SPE and hazard, though substantially reduced from the true network model (see Results).

Statistical evaluation of network spread

In each patient, for each time point, we determined the shortest path length from every node to their overall epicenter (for single-epicenter models) or the nearest epicenter based on path length (for multi-epicenter models). We then set up a generalized additive model to estimate longitudinal atrophy rate of gray matter change in each node. All modeling was done with the mgcv package (Wood, 2017) in R (https://www.r-project.org/) and models were statistically compared using likelihood ratio tests from the lmtest package. Generalized additive models are able to include linear terms, random effect terms for intercepts and slopes, and non-linear “smooth” terms that are fit using spline basis functions with a penalty to maximize smoothness by minimizing the function’s second derivative. Atrophy rates were calculated for each node as the W-score difference in a node between sequential time points. The nonlinear smooth fixed-effect predictors were shortest path length from epicenter (SPE), nodal hazard, baseline atrophy W-score, Euclidean distance to epicenter, and clinical dementia rating baseline score (CDR) interactions with SPE and nodal hazard. Each of these terms was restricted to have a maximal non-linear basis of 5 by setting k = 5 in the model formula (Gennatas et al., 2017). The linear fixed effects were interscan interval length, age, sex, diagnosis (bvFTD or svPPA), and a binary variable that identified a node as cortical or subcortical. The model also included a spatial autocorrelation term to account for the non-independence of spatially neighboring regional measurements. The spatial autocorrelation term was based on the Euclidean distance between each region’s center of gravity coordinate, using the Gaussian process option in mgcv with a Matern correlation function, a range of 167 mm, and k = 10. The model included random intercepts for subject. For leave-one-subject-out cross validation tests, no random intercept was estimated for the left out subject. We chose to exclude random intercepts for node because a model with this term suffered from “mode collapse,” simply predicting the group mean atrophy change pattern for each subject. We intentionally selected a model that maximized two values, the overall variance explained, and the diversity of predictions across individuals. The mixed effect model with random slopes for node fulfilled this criteria and has validity as a possible model configuration (Barr et al., 2013). A model without the spatial correlation and node random slope factors made substantially less similar predictions across subjects, with the across-scan similarity r = 0.60 ± 0.17 with these predictors and r = 0.46 ± 0.23 without them, indicating that these factors capture shared spatial patterns of change across subjects. We only tested our model on the set of scans for which a CDR-SB score was available (152 out of 163 follow-up time points).

Visualization

All plots were produced using MATLAB and R. MRI slice views were created with fsleyes (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/FSLeyes) and brain surface views with Connectome Workbench (https://www.humanconnectome.org/software/connectome-workbench). Network graph views were created with Networkx (https://networkx.github.io/) and matplotlib (https://matplotlib.org/). Network layout was determined on the healthy control functional connectome using t-SNE (van der Maaten and Hinton, 2008) with 5000 iterations and a perplexity of 100.

DATA AND CODE AVAILABILITY

Code for fMRI preprocessing and seed FC map derivation is available at: https://github.com/seeleylab/SeeleyToolbox. Code and data for derivation of network-based predictors is available at: https://github.com/jbrown81/neuron_2019.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited Data
Brainnetome atlas	Fan et al., 2016	http://www.brainnetome.org/
Software and Algorithms
MATLAB	Mathworks	RRID:SCR_001622; https://www.mathworks.com
SPM	The Wellcome Centre For Human Neuroimaging	https://www.fil.ion.ucl.ac.uk/spm/
FSL	FMRIB; (Smith et al., 2004)	https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/
CAT12 toolbox		http://www.neuro.uni-jena.de/cat/
R	Open source	https://www.r-project.org/
Brain Connectivity Toolbox	Rubinov and Sporns, 2010	https://sites.google.com/site/bctnet/
custom MATLAB code		https://github.com/jbrown81/connect_metrics; https://github.com/jbrown81/neuron_2019
Connectome Workbench		https://www.humanconnectome.org/software/connectome-workbench
Networkx		https://networkx.github.io/
matplotlib		https://matplotlib.org/
t-SNE	van der Maaten and Hinton, 2008	https://www.mathworks.com/help/stats/tsne.html

Highlights.

• Patient-tailored “epicenters” identified

• Connectivity-based model can predict longitudinal spread of atrophy

• Generalized additive model shows nonlinear spatial and temporal progression