Cell Mechanical and Physiological Behavior in the Regime of Rapid Mechanical Compressions that Lead to Cell Volume Change

Abstract

Cells respond to mechanical forces by deforming in accordance with viscoelastic solid behavior. Studies of microscale cell deformation observed by high speed video microscopy have elucidated a new cell behavior in which sufficiently rapid mechanical compression of cells can lead to transient cell volume loss and then recovery. Our work has discovered that the resulting volume exchange between the cell interior and the surrounding fluid can be utilized for efficient, convective delivery of large macromolecules (2000 kDa) to the cell interior. However, many fundamental questions remain about this cell behavior, including the range of deformation time scales that result in cell volume loss and the physiological effects experienced by the cell. In this study, we establish a relationship between cell viscoelastic properties and the inertial forces imposed on the cell that serves as a predictor of cell volume loss across human cell types. We determine that cells maintain nuclear envelope integrity and demonstrate low protein loss after the volume exchange process. These results define a highly controlled cell volume exchange mechanism for intracellular delivery of large macromolecules that maintains cell viability and function for invaluable downstream research and clinical applications.

Graphical Abstract

Studies of rapid cell deformation have discovered the phenomenon of cell volume exchange for efficient, convective intracellular macromolecule delivery. This paper characterizes a controlled cell volume exchange mechanism dependent on strain rate and cell viscoelastic properties that can predict volume change for multiple human cell types. This process maintains cell viability and function for invaluable downstream cell engineering applications.

1. Introduction

Studies of the mechanical behavior of various human cell types have demonstrated the innate ability of cells to change and recover shape in response to mechanical deformations.^[1–9] The mechanical response of cells to deformations has been shown to depend on the time scale of onset and duration of deformation. At deformation onset time scales >0.01 s, cells have been observed to have elastic behavior governed by soft-glass rheology dynamics.^[10–14] At shorter deformation onset time scales, cells demonstrate viscoelastic behavior in which apparent cell modulus increases with a decrease in the deformation time scale.^[11,14,15] Over the duration of compression at a constant strain, cells exhibit an initial elastic deformation response followed by a slower viscoelastic creep perpendicular to the compression.^[9,16,17] Cell deformation behavior at time scales >0.01 s has been characterized by micropipette aspiration and atomic force microscopy (AFM). However, these methods face challenges when attempting to explore regimes of cell deformation using fast time scales (<1 ms) of onset and duration.

Flow-through microfluidic cell compression systems coupled with high speed imaging are able to rapidly impose and observe large strain deformations on cells to explore cell mechanical behavior from compressions at time scales <1 ms.^[1,18,19] In studies of this rapid deformation regime, cells exhibited a loss of intracellular volume.^[9,16,20] Cells were observed to recover to their previous volume and shape as cells relax upon leaving the compression. This effect was also shown to deliver extracellular liquid and target molecules into the cell on convective fluid currents. Target molecule delivery was found to be non-endosomal and distributed throughout the cell interior.^[20] Therefore the phenomenon resulting from brief, rapid compressions can cause a transient exchange of fluid and macromolecules between the cell interior and its surroundings for intracellular macromolecule delivery.^[20,21] Yet to date there has not been a study of how the imposed deformations and biophysical properties of cells bring about cell volume loss. In this work, we explore the transition of time scales from slow compression to fast compression that leads to the volume change phenomenon, and its dependence on cell biomechanical properties.

Published work has shown that compression-mediated cell volume change increases with higher cell strain.^[9,16,20] However, studies have yet to quantify the dependence of cell volume change on compression rate and cell physical properties. The study of this dependence will define a relation between cell viscoelastic behavior and rapid compression as a potential predictor of cell volume loss. In addition, understanding the effects of cell volume loss on cell physiology will inform the use of this method in research and clinical intracellular delivery applications. While cells that undergo volume change were shown to maintain viability, other factors of interest such as nuclear envelope integrity and intracellular protein loss have not yet been characterized.

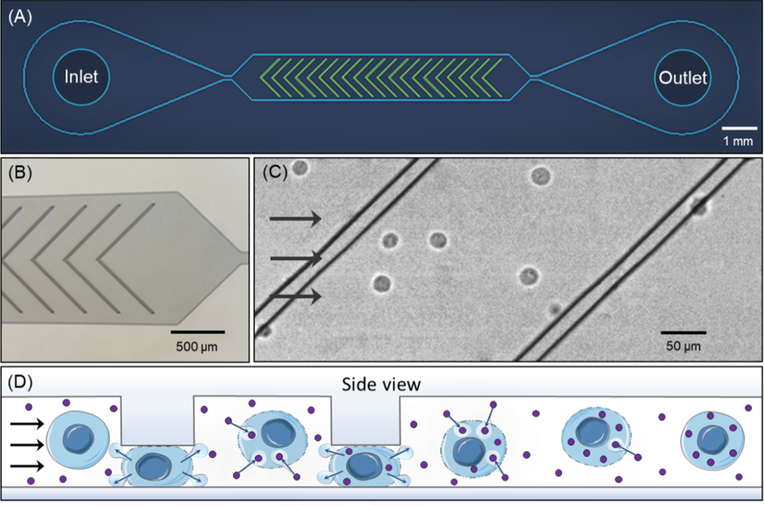
The cell volume exchange phenomenon is implemented in a microfluidic system that uses ridges to briefly impose compressions (Figure 1A, B). Cells suspended in buffer and flowed through the device rapidly pass through a microchannel in which they undergo sudden deformations under the ridges (Figure 1C), resulting in an abrupt change in shape. This compression is designed to have a rapid onset (on the order of 10–100 μs) and brief duration (~1 ms), resulting in a cell behavior regime of fast cell volume loss and recovery.^[20,21] The volume loss and recovery can cause cells to uptake surrounding molecules suspended therein (Figure 1D), a phenomenon called cell volume exchange for convective transfer (cell VECT). This cell behavior has been used to deliver macromolecules to the interior of various human cell types using convection, which is not restrained by molecule size for the range tested (4–2000 kDa).^[20]

Figure 1.

Microfluidic ridge-based cell compressions cause volume exchange. (A) Schematic of device layout. See Experimental Section for device design details. (B) Optical micrograph of microchannel with chevron ridge geometry. (C) Still-frame image from video of K562 cells flowing through the microchannel and ridges under light microscopy. (D) Schematic of cell permeabilization and volume loss, subsequent recovery, and repeated volume exchange with compressions.

We now aim to further characterize the biomechanical mechanisms of cell volume loss and its effects on cell physiology. We look to understand the relation between cell volume loss and compression rate and cell mechanics. We also analyze the physiological effects of rapid compression on cell nuclear envelope integrity, long term viability, and cell protein composition.

2. Results and Discussion

2.1. Varying cell compression rate

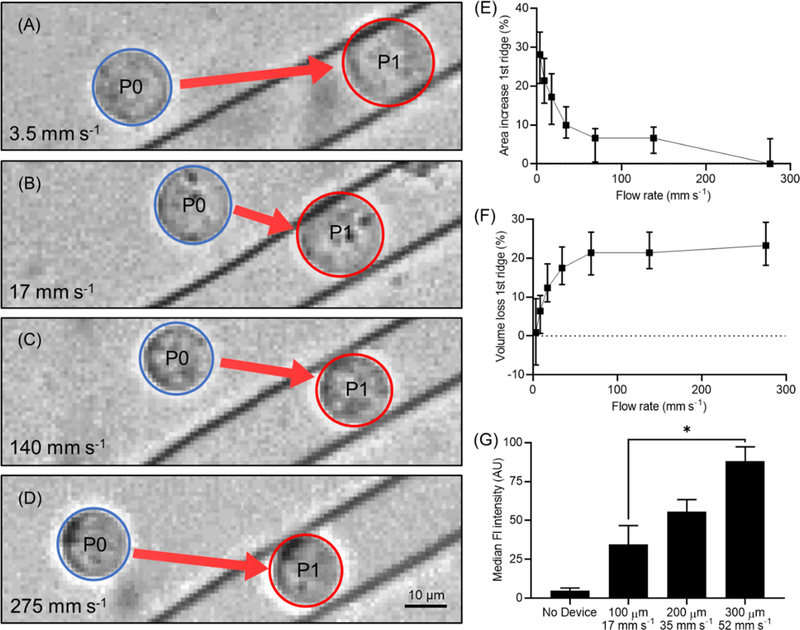
Cells were flowed through the ridged microchannel at varying flow rates to observe the effects of compression rate on cell volume change. Flow rate through the microchannel was varied from 3.5 mm s⁻¹ to 275 mm s⁻¹ with high speed video recording to observe cell responses during mechanical compression. A compression gap of 9 μm, previously characterized to cause volume change in K562 myelogenous leukemia cells, was used for this study.^[20] When calculating cell volume from 2-dimensional imaging, the uncertainty of the 3-dimensional shape of the compressed cell is a potential source of error. Using a cell deformation model combined with area analysis of high-speed videos of individual cells in the microfluidic channel, we calculated the compressed cell volume as a truncated ellipsoid under the first ridge compared to the volume of the ellipsoid cell before compression.^[22] See Experimental Section for more information on the truncated ellipsoid model used to calculate compressed cell volume.

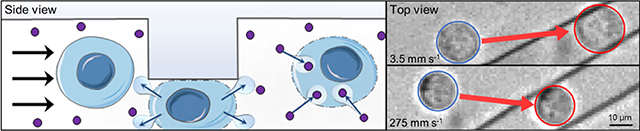
At low flow rates, cells were observed to expand in area when compressed underneath the ridge (Figure 2A,B). At higher flow rates, cells did not exhibit area expansion under the ridge (Figure 2C,D). As flow rate increases, the cell area expansion decreases, eventually approaching no area change compared to the uncompressed cell (Figure 2E). This cell area expansion results in overall conservation of cell volume at slow flow rates, whereas high flow rates cause cell volume loss (Figure 2F). This behavior suggests that, as cells undergo more rapid compressions, they are unable to expand under the ridge, resulting in increased volume loss. This trend plateaued at the highest flow rates we tested, wherein the cells appeared to maintain the same area under the compression compared to before compression, indicating a maximized volume change for that compression gap size of 9 μm.

Figure 2.

Analysis of cell response to compression time scale. K562 cells in 9 μm gap device. (A) Cells at the slowest flow rate, 3.5 mm s⁻¹, exhibit visible area expansion between P0 (before the first compression) and P1 (under the first compression). (B) Area expansion is diminished but still visible at 17 mm s^-1. (C) As flow moves faster, 140 mm s⁻¹, cell area expansion decreases until (D) at 275 mm s⁻¹ the area under the ridge remains the same compared to before the ridge. (E) Plot of cell area increase percentage compared to before the cells enter the ridge as a function of fluid flow rate. N ≈ 150 cells, bars represent interquartile range. (F) Plot of cell volume loss percentage under the first ridge as a function of fluid flow rate. N ≈ 150 cells, bars represent interquartile range. (G) Intracellular delivery of 2000 kDa FITC-dextran increased with compression rate. Cell recovery time between ridges is kept constant by scaling inter-ridge spacing with flow rate. *P < 0.05, N = 3 experiments, bars represent standard deviation.

We characterized the effects of compression rate on overall cell volume exchange by using 2000 kDa FITC-dextran (Sigma-Aldrich) as a fluorescent tracer molecule for intracellular delivery. Flow cytometry results from these experiments indicated that intracellular delivery of FITC-dextran increased with faster compression rate (Figure 2G). Therefore, increased cell volume loss due to faster compression results in greater intracellular delivery.

2.2. Cell physical properties

To better understand the physical mechanisms that govern cell VECT, we investigated the effect of cell physical properties, including cell size, elasticity, and viscosity, on volume change. At constant compression gap size, we observed that larger cells exhibited increased volume loss at every flow rate tested. At slower flow rates we observed a broader distribution of cell volume change behavior based on cell diameter (Figure 3A). At faster flow rates the cell volume change shows a stronger correlation with size (Figure 3B). These observations suggest that cell volume change is highly dependent on cell size at faster flow rates. However, at slower flow rates, other cell physical properties, like cell viscosity or elasticity, could dominate.

Figure 3.

Cell physical properties govern compression response. (A) At slow flow rate, K562 cell volume change has a broad distribution in relation to cell area. N = 110 cells, linear regression R² = 0.319 (B) At fast flow rate, volume change shows strong correlation with cell size. N = 150 cells, linear regression R² = 0.819 (C,D) Treatment of K562 cells with CD to decrease cell Young’s modulus did not have a significant impact on cell volume change. N = 50, bars represent SD, P > 0.34. (E) Both K562 and HL-60 cells slow down relative to the surrounding fluid flow when they interact with the first ridge. (F) Highly viscous HL-60 cells show more volume loss at slow flow rates compared to K562 cells. As flow rate increases the volume change converges. **P < 0.0001, *P < 0.005, N ≈ 100 cells, whiskers represent 10–90 percentile, 9 μm gap devices used. (G) A plot of volume change for multiple cell types shows sigmoidal relation with Ericksen number (Er). Cell types include leukocyte cell lines K562, HL-60, and formaldehyde-treated K562F, and epithelial cell lines HEY and OVCAR-3. N ≥ 25, bars represent standard error.

To test the impact of cell elasticity on volume change, high speed video analysis was performed on K562 cells treated using a cytochalasin-D (CD) protocol previously characterized to lower the cell Young’s Modulus from 0.40 ± 0.22 kPa to 0.21 ± 0.061 kPa.^[22] However, CD treatment did not exhibit a statistically significant impact on cell volume loss at two different flow rates and concentrations of CD (Figure 3C,D). Similarly, a study of cells treated with 20 μм blebbistatin to reduce Young’s modulus also did not show a statistically significant change in cell volume loss at multiple flow rates (Figure S1).^[23,24] Therefore we conclude that these changes in cell Young’s modulus using CD and blebbistatin did not significantly change volume loss.

The cell viscoelastic creep response has been shown to play an important role in transducing in-plane stresses to out-of-plane stresses and deformations.^[9,16,17] Therefore we explored viscosity as a governing factor of cell volume change response by comparing HL-60 promyelocytic leukemia cells to K562 cells. HL-60 cells were characterized by AFM to have higher viscosity and Young’s modulus than K562 cells (Figure S2).^[25] Studies have shown that cells increasingly behave as a viscous material at faster deformation rates.^[26,27] Video analysis of cells deforming under the first microfluidic ridge determined that both K562 and HL-60 cells decrease in translational velocity relative to the surrounding fluid flow when under the ridge (Figure 3E). The K562 and HL-60 cell experiments were controlled for flow rate and cell size to subject the cells to the same magnitude and rate of compression. Yet the two cell types demonstrated different volume change behavior. We found that at slow flow rates, more viscous HL-60 cells did not expand in area under the compression as much as K562 cells, and therefore showed higher volume change (Figure 3F). As flow rate increases, the volume change of the two cell types converge, suggesting cells of comparable size lose similar volume at faster flow rates.

To further test the hypothesis that cell viscoelastic properties govern cell area expansion and volume loss during compression, we characterized the deformation response of K562 cells crosslinked with formaldehyde. Treatment of K562 cells with 4% formaldehyde has been shown to significantly increase Young’s modulus and decrease viscosity.^[22,25] Therefore, formaldehyde-treated K562 cells (K562F) exhibit more elastic and less viscous behavior. We observed that K562F cells exhibited more area expansion and less volume change than untreated K562 cells at the same fluid flow rates (Figure S3A). Modifications to viscoelastic properties in K562F cells also shift the time scale at which volume change occurs. K562F cells required a faster compression time scale than untreated K562s in order to achieve the same volume change (Figure S3B). Therefore, K562F cells exhibited more elastic behavior, expanding more under the ridge and therefore losing less volume than untreated K562s at the same compression rates.

More viscous cells exhibit slower out-of-plane expansion during both the onset and duration of deformation, while elastic cell behavior is characterized by rapid expansion.^{[7,9,16,28–30]} These observations suggest that cells with higher viscosity exhibit less expansion in the initial elastic phase and slower expansion during the viscoelastic creep phase. We visualize this behavior in a qualitative plot of out-of-plane expansion for a more viscous and less viscous cell, based on a model of the cell as a viscoelastic solid consisting of an elastic cortical shell surrounding a viscous fluid (Figure S4).^[16,30] Therefore, at the same rate, magnitude, and duration of compression, a more viscous cell would be expected to exhibit less expansion and therefore more volume loss than a less viscous cell. To parameterize inertial force divided by viscous force, we calculated Reynolds number (Re) for the vertical compression of multiple cell types with mechanical properties measured by AFM (Figure S2). However, a plot of Re did not produce a single trend of correlation between Re and volume change among multiple cell types (Figure S5A). A dimensionless ratio of inertial force to elastic force also did not converge to a single trend for multiple cell types. (Figure S5B). Therefore, it appears that the volume change behavior of multiple cell types over different compression rates is not well explained by considering viscous and elastic forces individually.

We next evaluated the observed cell behavior by considering the combined effects of cell viscosity, elasticity, and compression rate on the resultant volume change. The relation between cell viscosity and elasticity during deformation is parameterized using the dimensionless Ericksen number (Er), which determines the relation between viscous and elastic forces.^[31,32]

$$\mathrm{Ericksen}\mathrm{number}=\frac{\mathrm{Viscous}\mathrm{force}}{\mathrm{Elastic}\mathrm{force}}=\frac{\mu VL}{EA}=\frac{T_v}{T_c}\frac{\Delta LL}{A}$$ (1)

The cell is modeled as a Maxwell viscoelastic material with dynamic viscosity μ = T_v E,^[33–35] where E is the Young’s Modulus and T_v is the viscous time constant as measured by AFM (Figure S2). Viscous force is dependent on cell compression velocity (V = ΔLT_c⁻¹ where T_c is the compression time measured by video analysis) and a characteristic length (L is the relaxed cell diameter, ΔL = L – compression gap). The elastic force is defined by Young’s Modulus and A, cell area.

At slow flow rates, and therefore low Er values, the cell exhibits elastic deformation behavior, expanding in area during initial compression.^[9–14,16] The slow flow rate also results in longer duration of compression, so the cell also expands transversely due to viscoelastic creep, resulting in volume conservation. Higher flow rates result in larger Er values, wherein the cell enters a viscoelastic behavior regime during compression onset that causes decreased initial elastic deformation.^[11,14,15] In addition, the shorter duration of compression allows less time for viscoelastic creep expansion during compression, resulting in an overall decrease in cell volume.^[5,9,16]

We find that several cell types follow the same sigmoidal trend of volume change dependence on Ericksen number, as determined by nonlinear regression performed on data points from multiple leukocyte and epithelial cell lines (Figure 3G). To account for differences in cell size and compression gap in these data, we examined a ratio of the observed cell volume change and the maximum attainable volume change, where the cell does not expand in area during compression.

At conditions in which Er >>1, in which cell volume change occurs, we observe that the time scale (T_c) at which cells transition from fully uncompressed to fully compressed under the first ridge is significantly faster than the cell viscous time constant (T_v). At these conditions, the cell must deform very rapidly and does not demonstrate the area expansion that was observed at small Er conditions. In the cell behavior regime of rapid deformation (T_c << T_v), cells are forced to compress at a time scale too fast for cytoplasmic remodeling and mechanical stimulus transmission to occur.^[36]

In order to understand the physical basis of the time scales of cell responses, it is intriguing to note that the T_c at which the cell is unable to expand transverse to the applied force is of the same order of magnitude (~2 ms) as the time scale of mechanical signal transmission in the viscoelastic cytoskeleton (~1 ms).^[36] We assume that the cytoskeleton behaves as a hydrated viscoelastic network consisting of cytoskeletal filaments and the surrounding cytosol. We hypothesize that as T_c approaches the time scale of mechanical stimulus transmission in the cytoskeleton, deformation occurs too quickly for the viscoelastic cytoskeleton to expand transverse to the compression. The cell membrane is also unable to undergo transverse expansion since it is attached to the compressed cytoskeleton. Therefore, the internal fluid pressure increases rapidly, and fluid leaves the cell as a result. On the other hand, for lower deformation speeds, both fluid and cytoskeleton have sufficient time to undergo transverse expansion, and the cell volume is conserved. We therefore hypothesize that rapid deformation necessitates that the cell loses some of its volume to accommodate the compression time scale.

The convergence plot of cell volume change behavior with relation to Ericksen number provides a dimensionless parameterization of cell volume loss in response to mechanical forces. The collapse of multiple cell types to a single trend of relation between volume change and Er was not seen in other parameterizations that do not include both viscosity and elasticity. Therefore cell deformation behavior is governed by the viscoelastic properties of the cell as a whole, and cannot be fully characterized by individual cell components. Various subcellular components, including the cytoskeleton and cytosol, can however be contributing factors to the viscoelastic mechanical response of the cell. When mechanical forces cause cells to deform at a time scale that exceeds the limits set by cell viscoelastic behavior, the cell undergoes permeabilization. This biological phenomenon may also result in cell damage, as seen in various cell and tissue injuries caused by mechanical trauma.^[37–42] This permeabilization can have lasting physiological effects, particularly in nerve cells.^[39,42] However, numerous human cell types, including epithelial cells, chondrocytes, and leukocytes, have demonstrated the ability to recover from mechanical compression without significant impact on viability and function.^{[9,16,20,21,43,44]}

2.3. Analysis of nuclear envelope disruption

We next sought to understand the physiological impact of these rapid mechanical compressions on cells. While it has been shown that the cell cytoplasm has a high capacity for deformation and recovery even at high strains, the nucleus – typically one of the largest and stiffest organelles – has been shown to be a rate-limiting factor in cell deformation.^[45,46] The demonstrated exchange in volume and macromolecules between the cell and its outside environment suggests that the cell membrane is compromised by fast compressions,^[20,21,43] but the integrity of the nuclear envelope has not been characterized. Nuclear envelope rupture is important to characterize because it has been associated with genome instability, aneuploidy, and DNA damage.^[45,47] Severe nuclear disruption can cause material to leave the nucleus, leading to chromatin protrusions, nuclear fragmentation, and chromothripsis.^[47,48]

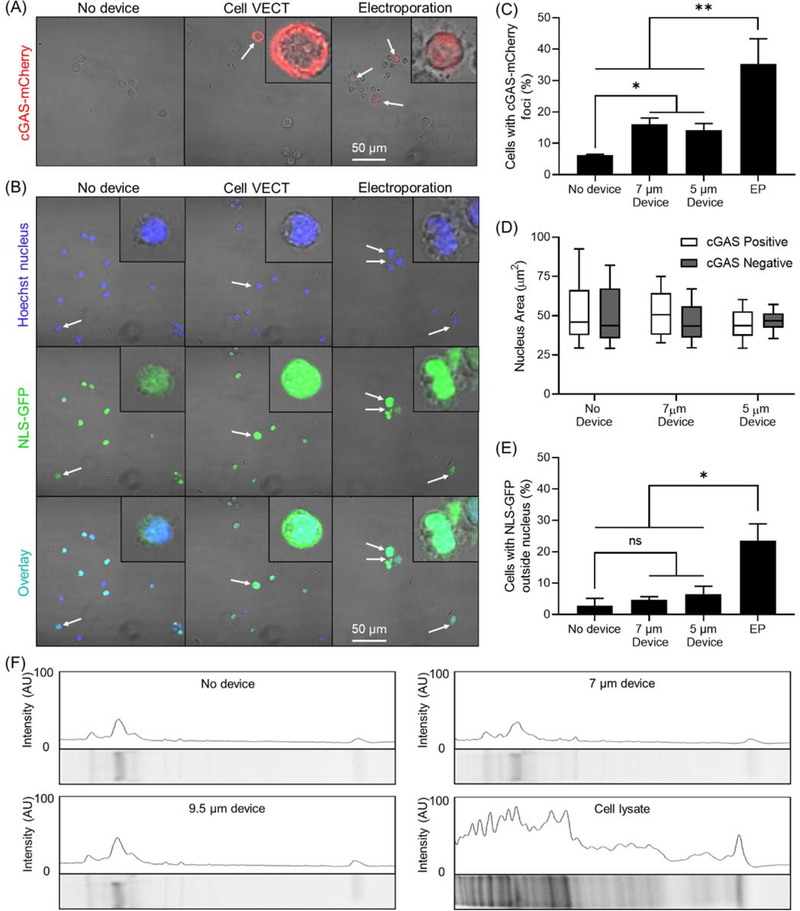
We used HEK-293 cells transduced with fluorescently labeled genes to indicate nuclear envelop disruption and loss of nuclear contents to the cytoplasm. The cyclic GMP-AMP synthase (cGAS-mCherry) is a cytosolic protein that binds DNA at sites of nuclear envelop rupture. Nuclear envelope disruption is indicated by cGAS-mCherry accumulation in and around the nucleus at sites of rupture (Figure 4A). The nuclear localization signal (NLS-GFP) allows the visualization of loss of nuclear contents to the cytoplasm.^{[45,47,49–51]} Nuclear content loss was determined by analyzing colocalization of NLS-GFP with a Hoechst nucleus stain (Figure 4B). We used devices with compression gap of 7 μm and 5 μm. On HEK-293 cells in suspension, these gaps impose cell strains of ~0.4 and ~0.6 respectively, which is a typical range of strains used in cell VECT.^[20] Electroporation was used as a positive control for nuclear envelope disruption. Compression of cells using cell VECT resulted in ~10% increase in number of cells with nuclear envelope disruption (Figure 4C). Varying the compression gap size between 7 μm and 5 μm did not appear to impact percentage of nuclear rupture. Cells that were positive for nuclear envelope rupture did not exhibit a difference in overall nucleus size (Figure 4D).

Figure 4.

Analysis of nuclear envelope disruption and protein loss. (A) Confocal microscopy shows cGAS-mCherry foci (white arrows) present in a minority of 7 μm gap device-processed cells and a significant portion of electroporated cells. Cells in insets are zoomed in 5X. (B) Confocal imaging shows colocalization of NLS-GFP to the Hoechst-stained nucleus in the majority of No device and 7 μm gap device cells, with NLS-GFP outside the nucleus in a small minority of cells (white arrows). NLS-GFP can be observed outside the nucleus in electroporated cells. Cells in insets are zoomed in 5X. (C) Cell VECT treated cells demonstrated ~10% increase in number of cells expressing cGAS-mCherry nuclear envelope disruption indicator compared to No Device control. Electroporation used as positive control. *P < 0.05, **P < 0.01, N = 3 (D) There is not a statistically significant correlation between nucleus size and nuclear envelope disruption. (E) Compressed cells exhibit NLS-GFP outside the nucleus in <10% of cells but is not statistically significant compared to No Device control. Electroporation used as positive control. *P < 0.01, N = 3. (F) Protein gel imaging shows device groups have very similar protein band intensity profiles to No device control. Cell lysate control group has much higher protein content.

Cells processed with cell VECT displayed a small (<5%) increase in NLS-GFP loss to the cytoplasm, but this increase was not statistically significant (Figure 4E). Therefore, we find that rapid, brief compressions with cell VECT causes nuclear envelope disruption in a small minority of cells. However, the disruptions do not appear to be significant enough to cause nuclear contents to leave the nuclear envelope. Therefore, it appears that the extent or duration of nuclear disruption is not sufficient to allow for exchange of materials between the nucleus and cytoplasm. This observation suggests that materials in the cytoplasm cannot enter the nucleus for direct nuclear delivery of target molecules.^[45,47,51] Overall the findings indicate that the compression conditions typically used in cell VECT have minimal impact on nuclear integrity, which indicates a low risk of associated negative effects such as DNA damage.

2.4. Impact on cell viability and protein content

Understanding the physiological impact of compression-based cell volume loss not only confers a deeper understanding of this phenomenon, but also informs its use in research and clinical settings. Characterization of long-term viability in K562 cells up to 5 days after microfluidics indicated <5% viability loss compared to No Device and Negative controls (Figure S6A). Negative controls were maintained in culture, while No Device controls were exposed to the same buffer and out-of-culture conditions as Device groups. Additionally, device-treated cells demonstrated rapid proliferation over 5 days on par with that of No Device and Negative control groups, doubling roughly once per day (Figure S6B). These results were not significantly impacted by decreasing the cell compression gap from 9.5 μm (~0.4 strain) to 7 μm (~0.6 strain) (Figure S6A,B).

To evaluate whether volume loss during rapid compression led to loss of intracellular proteins, we isolated the flow buffer after K562 cells underwent microfluidic compressions and concentrated the protein content. We then performed gel electrophoresis of the concentrated extracellular proteins with a SYPRO Ruby protein gel stain (ThermoFisher). Gel imaging revealed that the device groups had very similar band intensity compared to the No device control. The overall intensity and number of protein bands was much lower in the device and No device groups compared to the Cell lysate group (Figure 4F).

The concentrated extracellular protein from device processing was analyzed with mass spectrometry to further quantify the type and amount of protein present. The mass spectrometry results showed the overall peptide-spectrum matches (PSMs) were low in the device and No device groups. The composition of proteins in the buffer was unchanged in the 9.5 μm gap device compared to the No device group. The 7 μm gap device group appears to be selectively enriched for certain intracellular proteins, particularly the cytoskeletal proteins actin and myosin (Table S1). Overall the extracellular buffer of the No device and device groups showed very low PSMs compared to cell lysate control, indicating low protein content. The No device group had only 1.6% of the total PSMs of the cell lysate control, while the 7 μm and 9.5 μm device had 4.4% and 1.6% respectively. The overall conclusion is that the amount of protein lost during this compression-based cell volume loss is not significant, as the results with both protein gel and mass spectrometry are very similar to the No device control.

The observation of low protein loss could be explained by the sponge-like behavior of the cytoskeleton, which is believed to play a role in intracellular solute retention during transmembrane volume transport.^[52–54] These results suggest minimal cell lysis or loss of intracellular contents, which is consistent with maintained cell viability and proliferation. Cells have also demonstrated to ability to modulate cytosolic ion concentration rapidly (on the order of seconds). Ion modulation is achieved through ion exchange across membranes and release of intracellularly stored ions,.^[55–57] These ion exchange pathways have been shown to correct disturbances to ion homeostasis after membrane permeabilization. Studies of electroporated cells show that Na⁺/K⁺ pumps promote repolarization and restoration of intracellular Na⁺ and K⁺ concentrations.^[58–60]

3. Conclusions

In this paper we utilize high speed imaging of microfluidic cell compression coupled with AFM measurements of intrinsic cell mechanical properties to characterize cell deformation behavior in the regime of rapid compression. These studies show that cell compression behavior transitions from elastic deformation with conserved volume to viscoelastic deformation with cell volume loss. This volume loss is governed by compression time scale and cell mechanical properties. We report the Ericksen number as a dimensionless parameterization of compression rate and cell viscoelastic properties that can predict the resulting cell volume loss. This relation may inform the implementation of cell VECT for a wide variety of human cell types. This study also finds that cell VECT has minimal impact on nuclear envelop integrity, protein loss, and long term cell viability and proliferation. These findings help validate future potential applications for cell VECT in both research and clinical settings.

4. Experimental Section

Device design

The microfluidic device design uses constrictions in the form of angled ridges in a microchannel for the rapid processing of high numbers of cells. The channel allows a multitude of cells to pass simultaneously under each ridge while hydrodynamic flow forces maintain cell velocity through the constrictions, allowing cell processing to continue rapidly even after many constrictions. The angled ridges also serve as an escape mechanism for nonviable cells and cell aggregates that would otherwise clog the device. A chevron ridge design was chosen to focus cells to the center of the ridge field.^[19,61] Therefore, this design functioned effectively even with localized clogs that could be rapidly self-cleared. A multi-channel design of this device successfully processed 50 million cells in 10 minutes without clogging.

Fabrication of microfluidic channels

The microfluidic features of this device were molded onto polydimethylsiloxane (PDMS) and plasma bonded to a glass slide. A reusable SU-8 mold was made using standard two-step photolithography on a silicon wafer. To fabricate the devices, a 10:1 ratio of PDMS and crosslinking agent was mixed and poured onto the SU-8 mold to form the microfluidic channel features by replica molding. The PDMS was then degassed in a vacuum chamber and cured for 1 hr at 80°C. The cooled PDMS was then removed from the molds and outlets and inlets were punched using biopsy punches. The PDMS was then bonded to clean glass slides using a plasma bonder (PDC-32G Harrick) followed by 1 hr in a 80°C oven. After cooling, the channels were passivated using 1% bovine serum albumin (BSA) for an overnight incubation at 4°C.

Microfluidic experimental setup

Cells were resuspended in a cell flow buffer consisting of DPBS (−/−) with 0.1% BSA, 0.04% EDTA. Experiments in which video was taken used cell flow buffer with the addition of 25% Percoll to maintain cell suspension in buffer without settling. The cells were isolated from culture media and resuspended in buffer at ~1–5×10⁶ cells ml⁻¹ with the desired concentration of target molecules. The cell-buffer suspension was infused into the microfluidic device at a controlled rate using syringe pumps (PHD 2000, Harvard Apparatus). Following collection from the outlets, the cells were washed 2X with DPBS (−/−) to remove residual molecules external to the cells. It has previously been determined that increased volume loss results in a higher intracellular delivery due to the uptake of surrounding volume and molecules as the cell recovers. This volume uptake increases as cells are provided more time to recover volume between compressions. Therefore, to isolate the impact of compression rate on volume exchange, we varied the spacing between ridges proportional to the volumetric flow rate to keep the cell recovery time between compressions constant. Devices with 7 ridges were used to avoid saturation or maximization of delivery that would otherwise obscure the effects of compression rate.^[20]

Cell culture

K562 cells from ATCC were cultured in RPMI-1640 supplemented with 10% fetal bovine serum (FBS) and 1% penicillin-streptomycin. HL-60 cells from ATCC were cultured in IMDM with 20% FBS and 1% penicillin-streptomycin. HEY cells from MD Anderson Cancer Center in Houston, TX were cultured in RPMI-1640 with 10% FBS and 1% penicillin-streptomycin. OVCAR-3 cells from the National Cancer Institute (NCI) in Bethesda, MD were cultured in RPMI-1640 with 20% FBS and 1% penicillin-streptomycin. HEK-293 cells, a generous gift from Lammerding lab, were cultured in EMEM with 10% FBS and 1% penicillin-streptomycin and passaged using 0.25% Trypsin-EDTA. The cells were incubated at 37°C with 5% CO₂.

Plasmids and generation of fluorescently labeled cell lines

HEK-293-TN (System Biosciences, SBI) cells were stably modified with lentiviral vectors to express the nuclear rupture reporter NLS-GFP (pCDH-CMV-NLS-copGFP-EF1-blastiS) and/or cGAS-mCherry (pCDH-CMV-cGAS^E225A/D227A-mCherry2-EF1-Puro).^[45] cGAS is a cytosolic DNA binding protein; we used a cGAS mutant (E225A/D227A) with abolished enzyme activity and interferon production, but that still binds DNA and serve as a nuclear envelope rupture reporter.^[62] To generate stable lines, pseudoviral particles were produced as described previously.^[45] In brief, HEK-293-TN cells (System Biosciences, SBI) were co-transfected with the lentiviral plasmid, packaging and envelope plasmids using PureFection (SBI), following manufacturer protocol. Lentivirus-containing supernatants were collected at 48 hours and 72 hours after transfection and filtered through a 0.45 μm filter. Cells were seeded into 6-well plates so that they reached 50–60% confluency on the day of infection and transduced with the viral supernatant in the presence of 8 μg ml⁻¹ polybrene (hexadimethrine bromide). After 24 hours, the viral solution was replaced with fresh culture medium, and cells were cultured for 72 hours before selection with 1 μg ml⁻¹ of puromycin or 2 μg ml⁻¹ blasticidin S for 2–5 days. After selection, cells were subcultured and maintained in their recommended medium without the continued use of selection agents.

Protein gel

K562 cells were washed 3X with PBS (−/−) to remove serum protein and resuspended in serum-free RPMI-1640 at 2×10⁶ cells ml^-1. For the cell lysate control, cells were mixed with Halt™ Protease Inhibitor Cocktail, EDTA-Free (ThermoFisher), then underwent a 30-second liquid nitrogen snap freeze before thawing on ice for 10 minutes. The freeze-thaw process was repeated 5X. Cell lysate was centrifuged at 20,000xg for 15 min at 15°C and the supernatant was collected. Cells were processed with 7 and 9.5 μm gap microfluidic devices, plus a No device control. Device and No device samples, 2.5 ml each, were centrifuged at 200xg. 1.5 ml of supernatant was collected and centrifuged again. Only 1 ml of supernatant was collected to avoid contamination from cell debris. All samples were mixed with protease inhibitor and then concentrated 10-fold using a Vivaspin® 5 kDa molecular weight cut-off spin concentrator (Sigma-Aldrich). Supernatant proteins were characterized by protein gel electrophoresis using pre-cast SDS-polyacrylamide gel (Bio-Rad) according to manufacturer protocol. Sample loaded gel was run at constant voltage 200V. Gel was stained with SYPRO Ruby protein gel stain (Thermo Fisher) according to manufacturer protocol. Stained gel was imaged on a Bio-Rad ChemiDoc imager.

Mass Spectrometry

The proteins in each sample were reduced, alkylated and digested with trypsin according to the FASP protocol.^[63] The peptides were analyzed by nano-LC-MS/MS, and peptide identification as previously described with the following modifications.^[64] Reverse phase chromatography was performed using an in-house packed column (40 cm long X 75 μm ID X 360 OD, Dr. Maisch GmbH ReproSil-Pur 120 C18-AQ 1.9 μm beads) and a 120 min gradient. The Raw files were searched using the Mascot algorithm (ver. 2.5.1) against a protein database constructed by combining the human UniProt protein database (downloaded April 24, 2018, 20,303 entries), and a contaminant database (cRAP, downloaded 11–21-16 from http://www.thegpm.org) via Proteome Discoverer 2.1. Only peptide-spectrum matches with expectation value of less than 0.01 (“High Confidence”) were used. ^[64]

High speed video microscopy

The experiments were carried out on the stage of an inverted bright-field microscope (Eclipse Ti, Nikon), with a high-speed camera attachment (Phantom v7.3, Vision Research). PDMS microchannel deformation was analyzed using extra-fine objective focusing on the beginning of the ridge field, where deformation would be highest. Our studies were conducted at flow rates in which deformation of the microchannel and ridges was not detectable (<1 μm). The minimum flow rate of 3 μL min⁻¹ was the slowest flow rate at which cells would pass under the ridges. High speed (>1,000 fps) videos were taken of cells during processing at various segments of the device. Higher resolution imaging was conducted with 8-fold increased resolution (from 1 pixel μm⁻² to 8 pixels μm⁻²), which confirmed the volume loss results (Figure S7).

Video analysis for cell volume change

To measure the cell volume inside the device, we calculated measurements of the cell area from video data and applied volume assumptions based on a cell deformation model. For each manual measurement, we took the ellipse that fit to the pixels of the sharpest gray scale intensity gradient to represent the maximum projected cell boundary. We calibrated the length scales of each image based on known ridge dimensions, which enabled us to translate the number of pixels into an area measurement. For each cell, we measured the area before it entered the ridge region of the device to determine its uncompressed volume and the area when completely under each ridge to determine the compressed volumes. The volume of the unperturbed suspension cell was taken as an ellipsoid where radius was extracted from cell area measurement and used to calculate volume. The process of calculating a volume measurement from a 2-dimensional image of a compressed cell has potential sources of error due to the uncertainty of the 3-dimensional shape of the cell under the ridge. To address this uncertainty, we considered two cases for cell shape that represent the upper and lower limits of possible cell volume. The smallest possible cell volume corresponds to the unperturbed ellipsoid case, where the cell maintains an ellipsoid shape with a diameter in the Z-plane (into the image plane) equal to the known ridge compression gap as measured by profilometry. The largest possible cell volume corresponds to the cylindrical case, where the Z-plane height of the cylindrical cell is equal to the known ridge compression gap. To reconcile these two cell shape cases, we modeled the compressed cell as a truncated ellipsoid. To calculate the volume of a truncated ellipsoid cell, we applied the ellipsoid procedure to the compressed cell area and cut away equal caps that represent the volume of the ellipsoid that intersected with the known constraints of the ridge and channel bottom. This was considered the maximum reasonable volume for the compressed cell as it approached the cylindrical case for larger cells and collapsed back to the unperturbed ellipsoid case for smaller cells.

Statistical analysis

GraphPad Prism was used to perform statistical analysis (ANOVA and t-test) and generate plots. The curve for Er vs volume change was obtained by transforming the Er values for all five cell types to log, then performing a nonlinear regression to a sigmoidal function.

Flow cytometry

The BD Accuri C6 Flow Cytometer was used to characterize cell uptake of fluorescent target molecules. Samples processed with FITC-dextran were excited with a 488 nm wavelength laser and emission was detected with a 533/30 filter. The viability of the cells was tested by propidium iodide staining per manufacturer protocol and excited with a 488 nm wavelength laser and emission was detected with a 670 LP filter.

Electroporation

Electroporation of HEK-293 cells was carried out using an Amaxa Nucleofector II and Amaxa Cell Line Nucleofector Kit V using manufacturer protocols. Cells were electroporated using Nucleofector Program Q-001 in an Amaxa cuvette.

Confocal microscopy

Confocal microscopy of HEK-293 cells was done using the Zeiss LSM 700 with a 40X oil lens to analyze the expression of NLS-GFP and cGAS-mCherry. These cells were stained with Hoechst nucleus stain per manufacturer protocol prior to microfluidics. After processing, cells were fixed with 4% PFA, resuspended in imaging buffer (RPMI-1640 plus 1 mg ml⁻¹ ascorbic acid), and mounted onto glass coverslips using clear nail polish for imaging.

Confocal image analysis

For image analysis of cells with cGAS-mCherry, NLS-GFP, and Hoechst, the raw fluorescence channel values from the fluorescent images were exported as an 8-bit tag image file format (TIFF) image using Zen Lite software by Zeiss International. The fluorescent image stacks were then imported into ImageJ and the fluorescence profile was modulated by a threshold intensity value of 20 to reduce background fluorescence. To determine nucleus location, the outer edges of the Hoechst stained areas were found, and using a circular profile estimator, the areas of the cell nuclei could be calculated for each layer. The cell area data was organized and averaged using MATLAB. Cells in which NLS-GFP has left the nucleus were identified by the presence of GFP fluorescence signal outside the defined Hoechst stained nucleus area. In determining the presence of a nuclear breach, the fluorescence data from the cGAS-mCherry was modulated by increasing the multiplier for the intensity values for ease of viewing. Positive nuclear disruption was marked by small areas of higher intensity mCherry fluorescence (foci) or marked by an outline of the nucleus by a ring of higher mCherry fluorescence intensity. Cells that presented these mCherry fluorescence signals were counted towards positive nuclear disruption and paired with the calculated average cell area for that cell.

Atomic force microscopy

To characterize the mechanical properties of the ovarian cancer cell lines, we used force spectroscopy to obtain force-indentation curves with an MFP-3D atomic force microscope (Asylum Research) with an integrated optical microscope (Nikon) on a vibration isolation table. Cells were grown on glass FluoroDishes (World Precision Instruments). For better global measurements of the cell, 5.46 μm spherical polystyrene particles were attached to tipless silica nitride cantilevers (Bruker Probes) using a two-part epoxy and dried for >24 hours. The AFM was calibrated by taking a single force curve on a clean FluoroDish. The Sader calibration method was used to obtain cantilever spring constants (k is approximately 10–25 pN nm⁻¹) based on the thermal vibration of the cantilever. Cells were indented at 2 μm s⁻¹ until a force trigger of 10 nN was reached. The z position of the cantilever was held in place for 5 seconds, dwelling towards the surface, allowing for viscous relaxation of the cell before the cantilever was retracted. See Figure S2 for schematic of AFM setup, force curve acquisition, and fit. We used custom R code to fit the dwell region of the force curve to an exponential decay function to extract the viscous rate constant. To extract the cell Young’s modulus, we used custom R code relying on the Hertzian contact model.