Problems with centrality measures in psychopathology symptom networks: Why network psychometrics cannot escape psychometric theory

Abstract

Understanding patterns of symptom co-occurrence is one of the most difficult challenges in psychopathology research. Do symptoms co-occur because of a latent factor, or might they directly and causally influence one another? Motivated by such questions, there has been a surge of interest in network analyses that emphasize the putatively direct role symptoms play in influencing each other. In this critical paper, we highlight conceptual and statistical problems with using centrality measures in cross-sectional networks. In particular, common network analyses assume that there are no unmodeled latent variables that confound symptom co-occurrence. The traditions of clinical taxonomy and test development in psychometric theory, however, greatly increase the possibility that latent variables exist in symptom data. In simulations that include latent variables, we demonstrate that closeness and betweenness are vulnerable to spurious covariance among symptoms that connect subgraphs (e.g., diagnoses). We further show that strength is redundant with factor loading in several cases. Finally, if a symptom reflects multiple latent causes, centrality metrics reflect a weighted combination, undermining their interpretability in empirical data. Our results suggest that it is essential for network psychometric approaches to examine the evidence for latent variables prior to analyzing or interpreting patterns at the symptom level. Failing to do so risks identifying spurious relationships or failing to detect causally important effects. Altogether, we argue that centrality measures do not provide solid ground for understanding the structure of psychopathology when latent confounding exists.

Introduction

One of the most difficult challenges faced by clinicians and researchers alike is how best to conceptualize the co-occurrence of symptoms of psychopathology. Do certain symptoms co-occur because they reflect an underlying clinical entity (i.e., a disease category) or a shared latent trait (Krueger & Markon, 2006)? Or, do symptoms exacerbate and amplify each other, eventually generating clinical states recognized as mental disorders (Cramer, Waldorp, van der Maas, & Borsboom, 2010)? By extension, should the presumed underlying causes or the observed symptoms be the primary focus of interventions? Motivated by such questions, there has been a surge of interest in network analyses of psychopathology that could potentially reveal potentially causal relationships among symptoms (Borsboom et al., 2016; Hofmann, Curtiss, & McNally, 2016).

The network perspective rests on a mutualism model in which symptoms directly and reciprocally cause each other (Cramer et al., 2010; Van Der Maas et al., 2006). A central assumption of this approach is that symptoms, as measured by single psychometric items or scale scores, are the atomic units of psychopathology (Nesselroade & Molenaar, 2016). In much of the network psychometrics literature, this conceptualization has been contrasted and placed in direct contention with latent variable models — especially factor models — of psychopathology (e.g., McNally, 2012). This raises the question, do network analyses provide interpretable and novel information relative to established latent variable models? In this critical review, we address this important question, focusing particularly on the performance of symptom centrality measures in data where latent variables underlie covariance patterns.

Although improving the taxonomy of mental illness is an important goal, we assert that network analyses of cross-sectional symptom data rest on shaky ontological assumptions, emphasize data-driven algorithms over extant theory, and are limited in the novel information they can provide. Specifically, through a series of simulations, we demonstrate that relative to structural equation models (SEM), symptom (i.e., ‘node’) centrality metrics provide potentially misleading and at times redundant information about the relationships among symptoms when a common cause (e.g., an underlying disorder or trait) is present. Furthermore, we show that if symptoms reflect multiple independent causes (e.g., a pathophysiological process and gender bias in clinician judgment), nodal metrics reflect an unknown combination of these causes, undermining their utility in empirical analyses. As we articulate below, such latent confounding is likely to be present in most, if not virtually all, cross-sectional symptom data.

A Shift in Perspective

The pattern of covariance among symptoms both within and across disorders has traditionally been described using factor models, often within an SEM framework (Forbush & Watson, 2013; Kotov, 2011; Krueger, Chentsova-Dutton, Markon, Goldberg, & Ormel, 2003; Sharp et al., 2015; Watson, 2005). One of the most widely replicated findings from this literature is that the co-occurrence of mental disorders partly reflects two superordinate dimensions, internalizing and externalizing, that serve as shared liability factors with potentially distinct separable genetic and neurobiological substrates (Krueger & Markon, 2006; Salvatore et al., 2014). Indeed, some studies have found that these broad dimensions, rather than specific disorders, are better predictors of future psychopathology and negative health outcomes (e.g., Eaton et al., 2013).

By contrast, the network approach to psychopathology is built on a particle physics metaphor (Marsman et al., 2018), such that within an individual, it is the direct, potentially causal interactions among symptoms over time that putatively lead to the emergence and resolution of psychological problems. For example, an individual who experiences insomnia one night is more likely to suffer from fatigue and malaise the next day. The key argument is that mental illness is a dynamic phenomenon that involves activation of some symptoms, spread of activation to other symptoms, and disorder states that ultimately achieve stability through mutual reinforcement, even after triggering conditions have resolved (i.e., hysteresis; for additional details on this account, see Borsboom, 2017). Hofmann and colleagues (2016, p. 598) provide a useful synopsis: “Hence, a disorder is not the underlying cause of symptoms; it constitutes a network of symptoms that interact in ways that tend to maintain themselves. Accordingly, a stressful event does not activate an underlying entity called depression, which then causes the emergence of symptoms. Rather, stressful events activate certain symptoms that, in turn, activate other symptoms, and when the requisite number of symptoms occurs, an episode of disorder may be diagnosable.” Although the motivation of network psychometrics is to understand dynamic relationships among features of psychopathology over time, the data employed to test these questions have largely been cross-sectional (Fried et al., 2018; Heeren, Jones, & McNally, 2018; Kendler, Aggen, Flint, Borsboom, & Fried, 2018; McNally et al., 2015).

In a series of papers, scientists advocating a network psychometric approach to symptom co-occurrence have highlighted potential problems with the ontology of diagnostic entities and assumptions of conventional factor models (Borsboom & Cramer, 2013; Borsboom et al., 2016; Fried & Cramer, 2017; Hofmann et al., 2016; McNally, 2012). For example, if fatigue occurs in depression and anxiety disorders, it is possible that fatigue directly causes related problems such as appetite loss or distractibility in both disorders. This causal effect of one symptom on another could hold true without the need to invoke a latent variable such as a diagnosis or putative dimension of psychopathology.

In a recent methodological study, Marsman and colleagues (2018) demonstrated that the Ising model, which is commonly used in network analyses of observed binary variables, is statistically equivalent to some latent variable models from item response theory, particularly the Rasch model and a multidimensional two-parameter logistic model. This builds on earlier demonstrations that latent variable models can be transformed into directed network models without latent variables that are equivalent in their statistical fit (Molenaar, 2003, 2010; Molenaar, van Rijn, & Hamaker, 2007). Importantly, however, latent variable and network models differ considerably in their conceptual accounts. As Marsman and colleagues note, the statistical equivalence of some network and latent variable models suggests that, “the associations can be interpreted to arise from a direct influence between variables or due to an underlying and unobserved (set of) common cause(s)” (p. 31). In the case of equivalent models, experimentally manipulating key variables in the model or adding instrumental variables can help disambiguate alternative accounts (Pearl, 2009). Furthermore, additional research is needed to clarify what forms of network and latent variable models are equivalent in order to develop a deeper understanding of what conceptual models are tenable and distinct in psychopathology data.

Summarizing Key Features of a Symptom Network Using Nodal Statistics

A detailed treatment of how to resolve the challenges of alternative conceptual models that provide equivalent statistical fit is beyond the scope of this paper (for additional information, see Pearl, 2009). We note, however, that the equivalencies between latent variable and network models that have been identified to date exist at the level of the symptom covariance matrix (for details, see Graphical and Latent Variable Models of Cross-Sectional Symptoms below). On the other hand, empirical studies of symptom networks have primarily focused on nodal metrics from graph theory to explore whether particular symptoms are central in a network (e.g., McNally et al., 2015). Nodal metrics aggregate information from the overall covariance structure to summarize the properties of one symptom relative to another. In this way, even if there are cases in which network and latent variable models provide equivalent global fit, nodal centrality estimates, by definition, provide local information about symptoms within a co-occurrence network. Furthermore, nodal statistics are estimated from a given network structure and, thus, are not isomorphic with formal parameters in latent variable models such as factor loadings.

Centrality within a symptom co-occurrence network, it has been argued, may help to identify important clinical targets that play a crucial role in precipitating other problems or that may be particularly salient indicators of a given disorder (Hofmann et al., 2016). For example, the strength of a node is defined as the sum of its edge weights (i.e., partial correlations)¹ to other nodes:

$$s_i=\sum _j{W}_{ij}$$

Other centrality metrics such as closeness and betweenness derive from the concept of distance, which builds on the physical nature of many traditional graph theory applications, including railways and computer networks (Newman, 2010). In association networks such as those based on symptoms, the idea of network distance does not have a physical referent (e.g., number of miles of fiber optic cable), but instead reflects a quantitative summary of correlation strength.

Nodal centrality metrics describe an important aspect of graph topology but are not integrally linked to the estimation of the network itself. That is, metrics such as strength do not reflect the likelihood of the data given the parameters and model. Rather, for continuous data, the model-implied covariance matrix is usually derived from the Gaussian Graphical Model (GGM) whose free parameters are partial correlations (i.e., edges) among symptoms. Given this structure, we wish to underscore that graph metrics such as strength or closeness are secondary statistics in that they build upon characteristics of the formal model parameters. Consequently, it is not usually straightforward to estimate the uncertainty of a nodal statistic using asymptotic theory, though this can partly be circumvented using nonparametric bootstrapping (Epskamp, Borsboom, & Fried, 2018). By contrast, because the free parameters are typically of substantive interest in SEM and estimation uncertainty is an integral part of maximum likelihood estimation, it is straightforward to compare parameters or groups statistically.

The Ubiquity of Latent Variables in Taxonomy and Symptom Assessment

It is possible that at the level of ontology, symptoms directly and reciprocally cause one another. If this is the case, then focusing on symptom centrality metrics as the primary target of inference may help to clarify co-occurrence patterns. On the other hand, as noted above, there is substantial evidence that symptoms of psychopathology can be viewed within a hierarchical framework (Kotov et al., 2017; Markon, Krueger, & Watson, 2005) that conceptualizes broader dimensions as the latent causes of symptoms. Furthermore, it is important to note that symptoms themselves are often hypothetical constructs (e.g., anhedonia) that may have many plausible realizations.

Setting aside these thorny ontological questions, the intellectual traditions and research practices of both psychiatry and psychology provide reasons to be skeptical that trustworthy symptom networks can be identified from extant measures without the need to invoke latent variables. There is a rich history in psychometric theory (Nunnally & Bernstein, 1994) and test development (Clark & Watson, 1995) that builds on the idea of differentiating a hypothetical construct from its measurable manifestations. In their classic text on construct validity, Cronbach and Meehl (1955) argued that evidence for a hypothetical construct depends on defining key concepts and their relationships to each other, articulating observable manifestations of these concepts, and empirically testing whether the relationships among observables align with the theory. Thus, in test construction, researchers typically build item pools that measure content domains that emerge from theory, then use factor analysis to cull items that do not appear to measure a domain well (e.g., weak primary loading or strong cross-loading; Loevinger, 1957).

Moreover, there is increasing public awareness about mental illness, particularly from a biological perspective that emphasizes categorical diagnoses (Schomerus et al., 2012). This trend is likely to influence response patterns on self-report symptom inventories insofar as respondents may have a tendency to conceptualize their symptoms vis-à-vis a diagnostic construct. In short, the result is that most, if not all, psychological tests have a strong degree of latent structure that results from core principles of psychometric theory and/or public conceptions of mental illness.

Likewise, in defining the diagnostic criteria of mental disorders, the descriptive psychiatry tradition of the mid-20^th century (Feighner et al., 1972) shaped the psychometric properties of the diagnostic manuals from DSM-III onward. Relative to earlier editions, the DSM-III emphasized the psychometric reliability and validity of diagnoses and sought to untether diagnosis from theories of etiology (Gunderson & Singer, 1975; Robins & Guze, 1970). Although there are many problems with boundary overlap among disorders (e.g., Widiger & Trull, 2007) and evidence in favor of dimensional over categorical taxonomy (Kotov et al., 2017), the process of defining diagnoses in the DSM continues to depend in part on interrater agreement and test-retest reliability of multi-item symptom inventories (Narrow et al., 2013; Regier et al., 2013). Thus, there is a high probability that clinician ratings of psychopathology also have substantial latent structure that reflects both training practices in diagnosis and the psychometric legacy of the diagnostic system.

In sum, whether it is items from psychometric scales or symptoms from diagnostic interviews, these are the variables most often used in network analyses. As such, a latent variable architecture of some sort may be inherent to the data, and network methods need to be sensitive to such structure (cf. Spirtes & Zhang, 2016). If network psychometric analyses provide erroneous or limited information about symptom networks in which latent confounding exists, this could undermine the value of this approach.

The Current Study

Given the above concerns about potential latent confounding in cross-sectional symptom data, our study sought to characterize the performance of nodal centrality metrics in cross-sectional symptom data. More specifically, in simulations we examined how nodal metrics derived from GGMs represent a variety of datasets whose structure reflects one or more latent causes (i.e., factors). In line with the network psychometrics literature (e.g., Epskamp et al., 2018), we examined three nodal centrality measures: strength, closeness, and betweenness. Closeness is the sum of the shortest path lengths between a specific node and all other nodes. Betweenness quantifies how often the shortest paths among all nodes traverse a given node (i.e., how much traffic flows through the node). Previous research has focused on symptoms that have high betweenness as potentially serving a “bridging” role such that comorbidity between two disorders may reflect a symptom that is in common between them (Cramer et al., 2010).

Although there have been previous treatments of the alignment between latent variable and network models (Epskamp, Kruis, & Marsman, 2017; Marsman et al., 2018; Marsman, Maris, Bechger, & Glas, 2015), these have addressed a restricted set of models (e.g., the Rasch model). In parallel, there has been recent interest and debate about whether networks are reproducible within and across samples (Forbes, Wright, Markon, & Krueger, 2017; Fried et al., 2018) and whether different symptom thresholds yield different conclusions about network structure (Hoffman, Steinley, Trull, & Sher, 2018). Relative to these contributions, our study provides a detailed characterization of nodal centrality measures, which have been the primary focus in empirical studies. A secondary goal of our study was to compare formal SEM parameters, particularly factor loadings, with centrality measures under a variety of conditions.

If nodal centrality metrics are directly relevant to inferring the clinical and theoretical significance of specific symptoms, it is important to understand their sensitivity to different sources of covariance. More specifically, the network perspective assumes that differences in relative symptom centrality reflect particularly meaningful, distinct covariance patterns for specific symptoms in the context of the broader covariance structure. For example, in a network analysis of posttraumatic stress disorder (PTSD) symptoms, McNally and colleagues (2015) found that hypervigilance had greater strength and closeness centrality than other symptoms. From this, the authors inferred that hypervigilance may be a defining characteristic of PTSD that has particularly strong, direct associations with other symptoms.

The validity of such inferences depends on, minimally, whether 1) centrality measures are sensitive to the dominant sources of covariation in the data, 2) changes in symptom centrality measures are proportional to changes in the underlying covariance structure, and 3) centrality measures provide meaningful information about the relative importance of symptoms across a range of causal structures, including those that include latent variables. For instance, regarding proportionality, if a centrality metric such as betweenness changes dramatically due to very small differences in the covariance matrix (e.g., one cell decreases by 5%), this could undermine the interpretability of centrality differences in empirical studies. By contrast, if there is a proportional, monotonic relationship between changes in centrality measures and changes in symptom-relevant covariance, this would bolster the argument that nodal centrality may have conceptual centrality in understanding co-occurrence patterns. For example, if the correlation of a candidate symptom with all other symptoms is increased by 10%, by definition, strength centrality for the candidate will increase by 10%.

We conducted three latent structure simulations in an SEM framework in order to assess the extent to which symptom centrality measures provide meaningful information about symptom covariance patterns when the data contain at least one latent variable that confounds bivariate relationships among symptoms. Importantly, our simulations were intended to provide a set of test cases to examine how centrality measures varied as a function of unique versus shared sources of covariance. Thus, we were explicitly interested in using simulations to understand what inferences one might make in empirical data if one applied network psychometric approaches (using current best practice recommendations; Epskamp et al., 2018; Epskamp & Fried, 2018) to plausible symptom covariance patterns. This approach is unlike many simulation studies that are motivated to understand the performance of an estimator or model across a variety of conditions in which one examines differences between population parameters and estimated statistics (e.g., Rhemtulla, Brosseau-Liard, & Savalei, 2012). We note that the statistics of interest in our study — symptom centrality measures — are not part of the underlying population model (either factor models or graphical models) and, thus, do not have groundtruth parameter values.

The first simulation sought to map the correspondence between nodal centrality metrics and factor loadings. This builds on previous work arguing that centrality and factor loadings are incommensurable statistics in symptom networks (Cramer et al., 2010), yet to our knowledge, their relationship has not been examined in data generated by variants of the common factors model. We hypothesized that strength, which reflects the sum of edge weights incident to a given node, would be highly correlated with factor loadings in single- and multi-factor models. We further anticipated that closeness and betweenness, which depend on measuring shortest path lengths among nodes, would not show a strong correspondence with factor loadings in multi-factor models due to the presence of relatively disconnected subgraphs. Finally, we examined the extent to which centrality measures were affected by sampling variability that introduced small correlations among items from different latent causes.

The second simulation focused on the effects of common variance due to latent factors versus a specific bivariate relationship between two target psychometric items. This extends from the network psychometrics notion of a “bridge” symptom that connects partially nonoverlapping symptom clusters — here, conceptualized as distinct factors. We simulated datasets along a specific-to-general gradient in order to test how centrality measures varied as a function of the source of covariation. We hypothesized that strength would scale linearly along this gradient such that it was maximized when the targeted node was explained solely as a function of the latent factor. By contrast, we expected that allowing specific covariation between items that loaded on different factors would increase their betweenness, consistent with the idea of a bridge symptom. Extending the idea of proportional changes above, this simulation was also motivated to understand the form and magnitude of changes in centrality measures as a function of linear changes in the specific-to-general covariance gradient between the two target psychometric items.

The third simulation examined how network metrics from GGMs handle multiple latent causes for a given psychometric item. This was motivated in part by many applications in latent variable modeling, including how best to handle cross-loadings (Asparouhov, Muthén, & Morin, 2015), bifactor models (Reise, 2012), multi-trait multi-method analyses (Kenny & Kashy, 1992), and mitigating response biases (McLarnon, Goffin, Schneider, & Johnston, 2016). Such applications share an interest in modeling multiple sources of covariation such that substantively interesting structural covariance relationships can be identified even in the presence of other reasons for responses on psychometric tests. By contrast, the conditional independence assumption in GGMs only permit unitary direct associations among observed items. We hypothesized that network metrics would reflect a combination of latent causes, suggesting that in empirical (as opposed to simulated) data, centrality cannot be interpreted in unambiguously substantive terms.

Overview of Models and Simulation Methods

Graphical and Latent Variable Models of Cross-Sectional Symptoms.

Both SEM and network analyses of cross-sectional symptom data seek to represent the sample covariance matrix, S, accurately while also minimizing the number of free parameters (i.e., maintaining positive degrees of freedom). In SEM, the fit of a model is based on the discrepancy between S and a model-implied covariance matrix, $\mathbf{\Sigma }\left(\widehat{\mathbf{\theta }}\right)$, which reflects a set of structural equations across conceptually distinct parameter matrices (for an overview, see Lei & Wu, 2007). The Gaussian Graphical model (GGM) is the most common formal basis for networks composed of multivariate normal psychometric data (Epskamp, Rhemtulla, & Borsboom, 2017). More specifically, GGMs capture the covariation among symptoms according to a set of edges (i.e., connections) that represent pairwise conditional association. That is, if two symptoms are independent of each other (i.e., uncorrelated) after conditioning on all other symptoms, no edge would be included in the graph. Mathematically, a GGM can be estimated by inverting and standardizing the sample covariance matrix. This yields a partial correlation matrix, $\widehat{\mathbf{K}}$, in which each cell represents the conditional association of X_i and X_j net all other symptoms, X_−ij. That is, if a given cell is zero, then X_i and X_j are conditionally independent given the other nodes: X_i ⫫ X_j | X_−ij.

The prevailing approach to network analyses of cross-sectional symptom data builds on network discovery algorithms (Friedman, Hastie, & Tibshirani, 2008; Lauritzen, 1999) that seek to identify unique relationships among symptom pairs after accounting for all other symptoms (Epskamp et al., 2018). As we will return to below, most algorithms assume that there is no latent confounding that could explain relationships among nodes in the network (cf. Ogarrio, Spirtes, & Ramsey, 2016). Furthermore, many algorithms such as the graphical least absolute shrinkage and selection operator (GLASSO), assume that the underlying causal network is sparse, such that the observed covariance matrix, S, can be explained by a fraction of partial correlations among variables (Epskamp, Kruis, et al., 2017). Finally, most network models reflect a data-driven approach to symptom covariance that does not incorporate the researcher’s a priori knowledge about mental illness or the structure of the data (e.g., a distinction between variables representing patient report versus clinician judgment).

Although there is a deep link between SEM and network models (Molenaar, 2010; Pearl, 2012), traditional SEM with latent variables has a fundamentally different view of the data generating processes. In particular, conditional independence relationships among symptoms and the overall sparsity (i.e., the explicit omission of free parameters that could explain covariance) largely reflect the researcher’s a priori model specification. Furthermore, researchers using SEM are exhorted to test and compare multiple models that instantiate distinct hypotheses about latent and observed relationships in order to bolster their interpretation of the preferred model (Tomarken & Waller, 2005).

Network models share the goal of obtaining a parsimonious, overidentified approximation of symptom covariance, but achieve this by controlling the number of estimated edges (i.e., partial correlations). In GGMs, the decision to estimate or omit a given edge between nodes is typically based on algorithms that optimize a statistical fit criterion during a network search. To reduce the influence of small, spurious relationships and handle the problem of more parameters than observations (i.e., the p ≫ n problem; Johnstone & Titterington, 2009), it is common to regularize the network estimation (Epskamp & Fried, 2018) by applying a penalty on the number of non-zero edges. Here, we focus specifically on the GLASSO algorithm, which has been promoted in this literature (Epskamp et al., 2018).

General Methods Used Across Simulations.

All data were simulated from confirmatory factor models using continuous, Gaussian indicators in an SEM framework. Across population models, we standardized latent factors (i.e., variance = 1.0) and equated residual item variances. Covariance matrices were simulated using the simsem (Jorgensen, Pornprasertmanit, Miller, & Schoemann, 2017) package in R 3.4.0 (R Core Team, 2017) and fit within a confirmatory factor analysis (CFA) framework using lavaan (Rosseel, 2012). In CFA analyses, we provided the correct population model (i.e., no misspecification of the structural or measurement models), but factor loadings, residual variances, and covariances (if relevant) were free parameters. The conditional associations among variables in each dataset were fit as a GGM using the EBIC + GLASSO algorithm (EBICglasso function in the qgraph package; Epskamp, Cramer, Waldorp, Schmittmann, & Borsboom, 2012).

The GLASSO algorithm depends on a tuning parameter, λ, that controls the proportion of edges that are shrunk to exactly zero according to an L1 penalty, thereby eliminating a free parameter (Friedman et al., 2008). Here, we chose λ according to the extended Bayesian Information Criterion (EBIC). Importantly, the EBIC + GLASSO algorithm (hereafter called EBICGLASSO for simplicity) depends on a hyperparameter, γ, that is chosen by the researcher and controls the preference for simple versus complex models (Foygel & Drton, 2010). Consistent with the defaults of the bootnet and qgraph packages, we used a γ of 0.5, which assumes a sparser graph compared to lower values of γ, resulting in higher specificity (i.e., more likely to omit spurious associations; Epskamp et al., 2018).

Based on the absolute value of the estimated coefficients of the GGM — that is, the conditional associations among items — we computed nodal statistics from the weighted undirected graph using the igraph package (Csardi & Nepusz, 2006). Because closeness and betweenness depend on the length of paths connecting nodes, it is necessary to provide an operational definition of distance when the edge weights reflect association. Consistent with previous work on correlation/communication networks (e.g., Latora & Marchiori, 2003), when computing closeness and betweenness, we used the reciprocal of the partial correlation as the edgewise distance metric.

Simulation 1: Correspondence of Centrality Metrics and Factor Loadings

The first simulation focused on the correspondence between nodal centrality metrics and factor loadings across single- and multi-factor latent trait models.

Methods

In Simulation 1, we generated data from factor models having 10 indicators per factor and a sample size of 400. Factor loadings were drawn from a random uniform distribution between .4 and .95. To ensure that our findings were not specific to a given set of random loadings, we repeated this process 50 times, yielding 50 population models. For each population model, we simulated 100 replication datasets and fit these using CFA (with no misspecifiation) and GGM using the EBICGLASSO method. We then computed the relationships between nodal centrality metrics — strength, closeness, and betweenness — and fitted factor loadings.

To illustrate how the number of factors and the correlation between them affects the relationship between factor loadings and nodal centrality, we simulated data for one-, two-, and three-factor models. In the two- and three-factor models, we assumed simple structure (i.e., no cross-loadings); we further tested conditions in which factors were orthogonal (r = 0) or moderately correlated (r = 0.4). In order to compare across models, we combined graph metrics and factor loadings across all population models and replications. In multilevel regressions conducted using the lme4 package (Bates, Mächler, Bolker, & Walker, 2015), we regressed a given graph metric (e.g., strength) on the corresponding fitted factor loading, as well as the number of factors (one, two, or three) and the correlation condition (orthogonal versus correlated). We modeled crossed random effects of node, replication, and population model, allowing random intercepts of each. To quantify the relative level of variance explained in nodal statistics across predictors, we computed squared semipartial correlations following the approach of Nakagawa & Schielzeth (2013).

Results

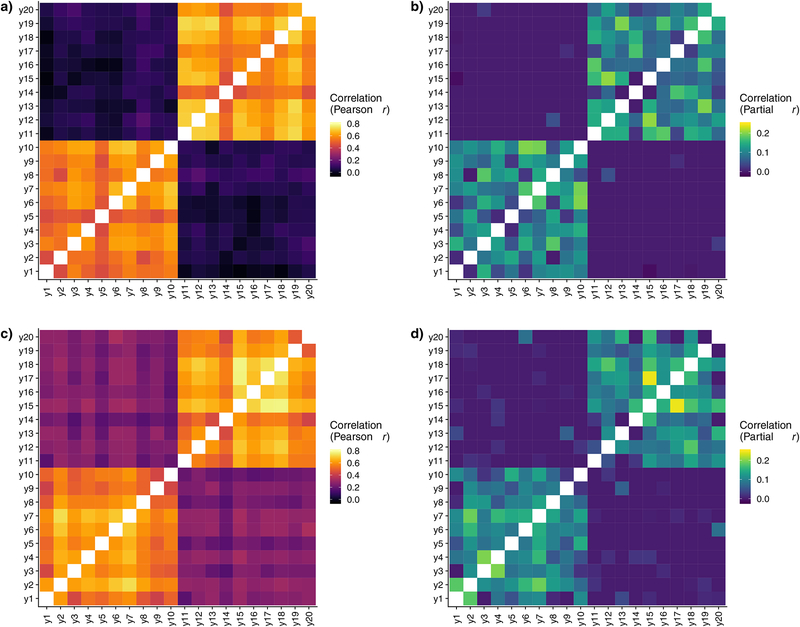
Representative marginal and regularized partial correlations among items for the two-factor orthogonal and correlated models are depicted in Figure 1. Weighted analyses of nodal centrality in the one-factor CFA revealed a strong correspondence between factor loadings and centrality statistics (Table 1). A similar, but weaker pattern, was observed for closeness and betweenness, which are based on path length among nodes.

Figure 1.

Example correlation matrices based on marginal association (a, c) and regularized partial correlation (b, d). The top row depicts the two-factor orthogonal Pearson (a) and EBICGLASSO partial (b) correlations for a representative covariance matrix. The bottom row depicts the correlated factors model (r = 0.4) for Pearson (c) and EBICGLASSO partial (d) correlations. Indicators y1–10 load onto one factor, whereas indicators y11-y20 load onto another.

Table 1.

Correspondence between nodal centrality statistics and fitted factor loadings

Model	M r with strength (SDbw, SDwi)	M r with closeness (SDbw, SDwi)	M r with betweenness (SDbw, SDwi)
One-factor CFA	0.98 (.005, .01)	0.94 (.01, .03)	0.74 (.05, .13)
Two-factor CFA, Orthogonal	.98 (.007, .01)	.42 (.06, .31)	0.37 (.08, .27)
Two-factor CFA, Correlated	0.97 (.007, .01)	.51 (.07, .27)	.44 (.07, .25)
Three-factor CFA, Orthogonal	0.98 (.007, .01)	.42 (.06, .31)	.31 (.07, .28)
Three-factor CFA, Correlated	0.97 (.009, .01)	.55 (.06, .26)	.41 (.06, .26)

Note. SD_bw reflects the standard deviation of the association between factor loadings and centrality metrics across independent examples/population models (n = 50). SD_wi reflects the standard deviation of the association between factor loadings and centrality metrics within replication samples from a given population model (n = 100).

In the model with two orthogonal factors, the association between strength and factor loadings remained, changing negligibly compared to the one-factor model. The association of closeness with factor loadings, however, dropped precipitously for the two-factor compared to one-factor model, Δr = −.52, d = −10.20. We also observed a large drop in the correspondence of betweenness and factor loadings, Δr = −.37, d = −5.41. Declines in graph metric-factor loading correspondence for the correlated two-factor model were qualitatively similar to the orthogonal model (Table 1). In the three-factor models, the correspondence between strength and factor loadings remained very high (r = .97). The correspondence of factor loadings with closeness and betweenness was much lower in the three-factor than the one-factor model, mirroring association decreases for the two-factor model.

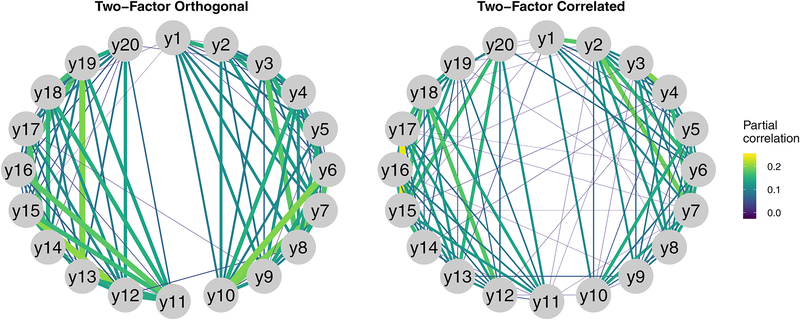
In network terms, a model with orthogonal factors and simple structure (i.e., no substantial cross-loadings) results in a structure with essentially disconnected subgraphs (each representing a factor; for an example, see Figure 2, left panel). By contrast, the correlated factors model yields a pattern of strong item correlations within factors and weaker associations between factors (see Figure 2, right panel). As described above, both closeness and betweenness are dependent on the connectedness of the entire graph, whereas strength is only concerned with edges incident to a given node. As a result, in multi-factor models, any edges among the subgraphs (i.e., edges that connect the factors), even if small, could potentially lead to substantial increases in closeness and betweenness centrality. Such edges have been of particular theoretical interest in the network psychometrics literature because they could putatively “bridge” between disorders and therefore explain patterns of comorbidity (Cramer et al., 2010). Furthermore, the presence of such “bridging” edges could explain the precipitous drop in the correspondence of closeness and betweenness with factor loadings.

Figure 2.

Adjacency matrices for two-factor orthogonal (left; cf. Figure 1b) and correlated (right; cf. Figure 1d) example graphs using the EBICGLASSO method. Note that indicators y1–10 load onto one factor, whereas indicators y11-y20 load onto another.

To interrogate this possibility, we computed the sum of the off-factor elements of the adjacency matrix that represented the associations of items that loaded on different factors². In the orthogonal factors case, this sum reflects spurious association among items due to sampling variability; in the population model, these items are conditionally independent. In the correlated factors case, the off-factor sum reflects both sampling variability and the weak association of items across factors due to the factor correlation (r = 0.4). For comparison, we computed the sum of the associations among items within a given factor. In the orthogonal factors design the sum of within-factor associations for each indicator was approximately 100 times larger than the summed associations with indicators of other factors, EBICGLASSO within/between M = 97.98, SD = 5.48. In the correlated factors case, this ratio was smaller, within/between M = 22.55, SD = .69.

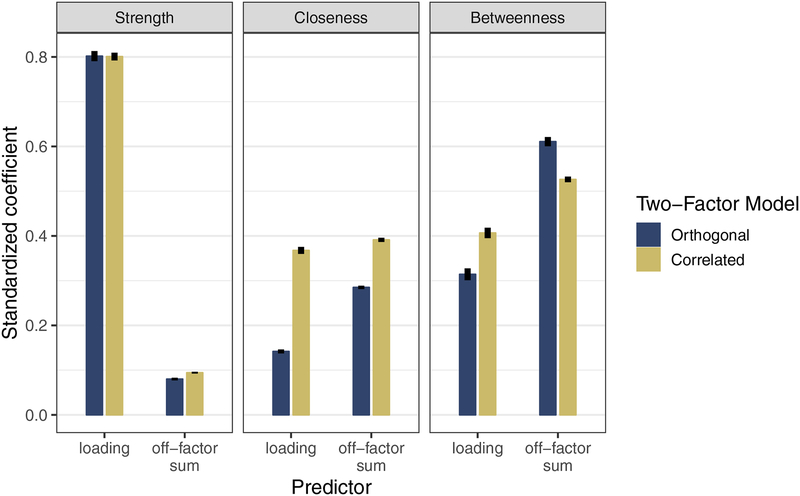
Although associations among indicators of orthogonal factors reflect sampling variability, not latent structure, these nevertheless played a key role in estimates of strength, closeness, and betweenness. Consistent with the correspondence statistics reported above (Table 1), strength had a relatively weak dependence on off-factor associations (sr² = .04) relative to the primary factor loading, (sr² = .82); see Figure 3, left panel³. By contrast, closeness centrality showed a dependency on the off-factor associations, with the off-factor influence (sr² = .08) accounting for about four times as much variance as the factor loading (sr² = .02; Figure 3, middle panel). Betweenness depended even more strongly on off-factor associations (sr² = .33); this effect was approximately three times the magnitude of the factor loading-betweenness relationship (sr² = .11; Figure 3, right panel). The pattern was qualitatively similar for the correlated two-factor model, but with more equal contributions of factor loadings and off-factor sums to closeness and betweenness estimates (Figure 3, righthand bars). We note that in the correlated factors case, the off-factor sums reflect both sampling variability and model-implied correlation due to the factor correlation.

Figure 3.

The effects of factor loading and summed off-factor associations on graph metrics in orthogonal (panel a) and correlated (panel b) two-factor CFAs. Bars denote the standardized coefficients from a multilevel model in which a given nodal graph metric (e.g., strength) is regressed on corresponding fitted factor loadings and the sum of the node’s conditional associations with items from the other latent factor. Black bars denote the 99% confidence limits on the standardized coefficients.

Simulation 2: Effects of Common Versus Specific Sources of Covariation on Network Metrics

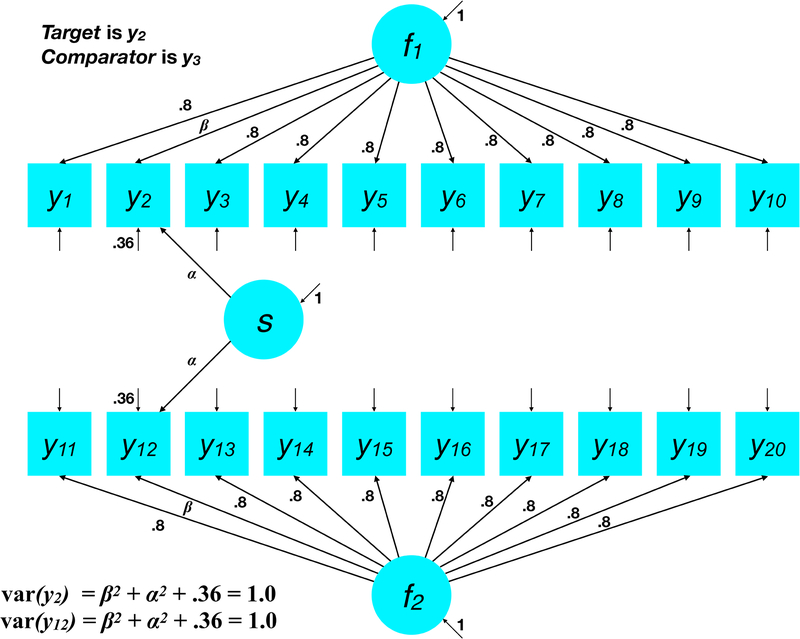
In Simulation 1, we were surprised to learn that small conditional associations between indicators of different factors, even if spurious, influenced closeness and betweenness. This finding suggests that even in the presence of robust associations due to a shared latent trait, smaller specific relationships between items could have nonlinear effects on nodal metrics. In Simulation 2, we focused specifically on this concern by manipulating the degree to which variance in two items, y2 and y12, reflected a common factor versus a specific bivariate relationship (i.e., a direct link) with an indicator of another factor (Figure 4). Simulation 2 sought to examine the functional form of network metrics along a gradient from common to specific variance. We anticipated that strength would scale linearly with factor-related variance. Because our simulation parametrically manipulated the specific covariance of items from different factors, we anticipated that the corresponding edge between them would have nonlinear effects on closeness and betweenness, which are based on paths between nodes.

Figure 4.

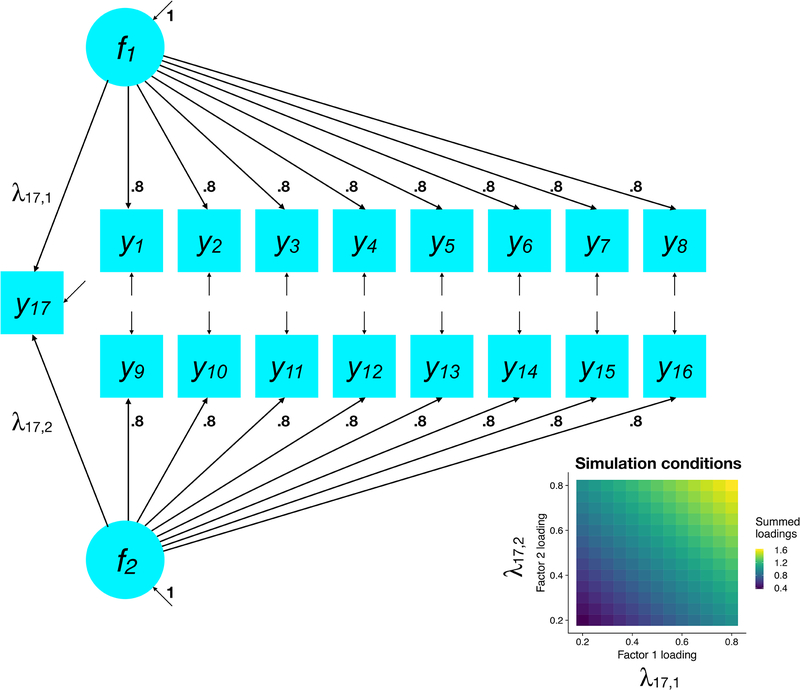
The orthogonal factor model for Simulation 2. The association between y2 and y12 varied parametrically between r = 0 and r = 0.64 according to the loading, α, on the specific factor, s. Standardized loadings for all other indicators were fixed at 0.8, whereas loadings for y2 and y12 varied to hold constant the explained item variance across conditions.

Methods

Simulation 2 generated data from an orthogonal factor model with ten indicators per factor in which there was a specific association between two indicators, y2 and y12. These items loaded on different latent factors, f1 and f2, respectively, and the specific association between them varied between r = 0 to r = 0.64 (see Figure 4). We implemented the specific association between y2 and y12 using a two-indicator latent variable, s, with equated loadings, but a model that captured a residual association between these items in the Θ matrix would be equivalent. Standardized factor loadings for all other indicators were fixed to 0.8; residual variances were fixed at 0.36 for all items.

For indicators that were conditionally independent after accounting for the latent factor (e.g., y3 or y14), the variance explained reflected the squared factor loading alone. In the case of the correlated indicators, y2 and y12, the simulations varied along a gradient that traded off variance due to specific association versus latent factor. More specifically, we parametrically varied the factor loadings such that variance explained by the shared factor varied from 0% to 64% in 1% increments: $r_{\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{o}\mathrm{r}}^2+r_{\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{f}\mathrm{i}\mathrm{c}}^2=.64$. Thus, there were 65 population models, and we simulated 100 replications from each using a sample size of 400. At one extreme of the variance gradient, the model reflected a simple two-factor orthogonal model: $r_{\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{f}\mathrm{i}\mathrm{c}}^2=0$; at the other extreme, y2 and y12 were not indicators of the latent factors, but reflected unique bivariate association alone.

For simplicity, we aggregated across replications within a given population model and used polynomial regression to capture the relationship between each metric and the difference in variance explained by the common factor versus specific association. Results were substantively similar using multilevel models that retained replication variability within each population model. Finally, we compared the effects of the variance manipulation on both a target node, y2, and comparator node, y3. Variance in y2 was explained by both factor and specific association with y12, whereas variance in y3 was attributable to the latent factor, f1, alone.

Results

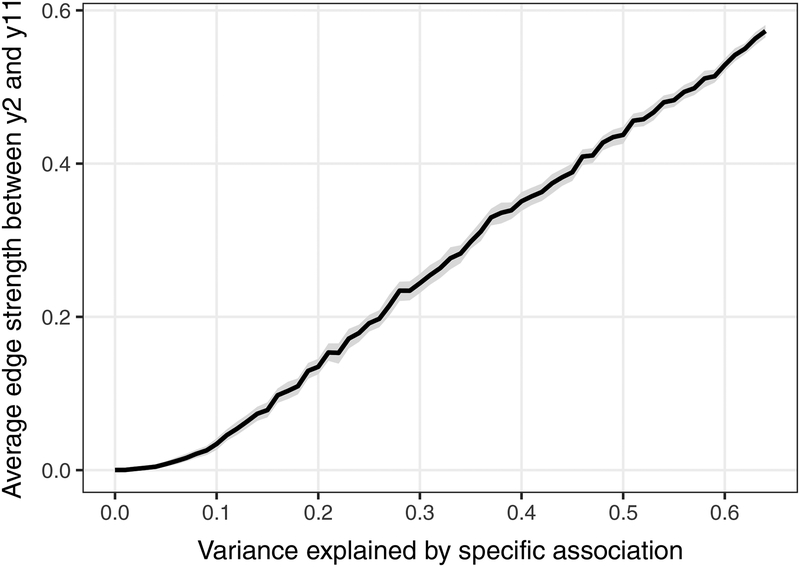
We first tested whether the magnitude of the edge (i.e., partial correlation) between y2 and y12 followed the underlying parametric gradient between common factor variance and specific association. As depicted in Figure 5, there was a strong correspondence between the specific association of y2 and y12 and the corresponding edge weight between them, r(63) = 0.997; there was a slight nonlinearity in the relationship below 0.1 (Figure 5, lower left corner).

Figure 5.

Edge strength between correlated items as a function of variance explained by a specific bivariate association. In all conditions, 64% of the variance in y2 and y12 was accounted for by the model. When zero variance was explained by the factor (i.e., the factor loadings were zero for y2 and y11), all variance was explained by the unique (marginal) association. Conversely, when all variance was explained by the factor, y2 and y11 had no specific association. Lines denote the mean edge strength across the 100 replications of each condition. Gray ribbons around the lines denote the bootstrapped 99% confidence interval.

These tests confirmed that the EBICGLASSO method was highly influenced by unique covariation between items in the presence of other sources of covariation – here, the covariation due to a common latent factor. Building on this basic test, we next examined the effect of specific versus common sources of covariation on strength, closeness, and betweenness. Overall, there was a nonlinear effect of the source of covariation (shared versus unique) on nodal metrics (Figure 6).

Figure 6.

Nodal graph metrics as a function of variance explained in the target nodes, y2 and y12, by common factor or unique sources (see Figure 4). Note that the scale of the y axis varies substantially across panels. The × axis represents difference in the variance explained by these sources, with the far left-hand side denoting variation completely due to a bivariate relationship between y2 and y12 (no factor effect). The far right-hand side denotes a condition in which all variation is due to common latent factors (no specific bivariate association). Lines denote the mean across replications within a condition; ribbons denote the 99% bootstrapped confidence limits of the mean. The target node depicts the effects of the simulation conditions on y2, whereas the comparator node depicts effects on y3, whose variance was not manipulated by the simulation.

Strength

We found a moderate main effect of the specific-to-shared variance balance on strength estimates, ${\eta }_G^2$ = .20 (Table 2). There was also a strong main effect of node type, ${\eta }_G^2$ = .51, such that strength was higher for comparator nodes compared to targets on average (Figure 6a). These effects were qualified by a variance balance × node type interaction, ${\eta }_G^2$ = .17. On average, strength for target nodes increased substantially as a greater proportion of variation was attributable to the shared factor. To interrogate the functional form of this interaction more specifically, however, we used orthogonal polynomial contrasts.

Table 2.

Effects of variance balance and node type on nodal metrics in Simulation 2

Metric	Effect	F (df1, df2)	Generalized η2
Strength	Variance balance (unique to shared)	45.42 (64, 6435)	.20
	Node type (target versus comparator)	15320.34 (1, 6435)	.51
	Variance balance × node type	47.62 (64, 6435)	.17
Closeness	Variance balance (unique to shared)	249.71 (64, 6435)	.68
	Node type (target versus comparator)	26350.16 (1, 6435)	.34
	Variance balance × node type	145.54 (64, 6435)	.15
Betweenness	Variance balance (unique to shared)	64.44 (64, 6435)	.24
	Node type (target versus comparator)	26772.13 (1, 6435)	.68
	Variance balance × node type	78.63 (64, 6435)	.29

For the target nodes (y2 and y12), strength varied substantially as a function of variance balance, ${\eta }_G^2$ = .40. The relationship between strength and variance balance followed a cubic pattern, R²_linear = .48, R²_quadratic = .64, R²_cubic = .98. More specifically, strength tended to increase as variance in the target was explained by the factor relative to the unique bivariate association. However, strength increased rapidly with small increases in factor-related variance, plateaued when there was a relative balance between factor and unique variance, then increased again as factor variance predominated. By comparison, if networks were defined using marginal, not partial, correlation, strength of the target increased asymptotically as factor variance predominated (Supplementary Figure S1).

For comparator nodes (i.e., items whose variance was explained only by the shared factor), strength was only weakly dependent on the variance balance of the target node, ${\eta }_G^2$ = .03. As depicted in Figure 6a, the difference in range for strength was much smaller across conditions for comparator nodes compared to target nodes.

Closeness

We found a strong main effect of target node variance balance on closeness, ${\eta }_G^2$ = .68. There was also a relationship between node type and closeness, ${\eta }_G^2$ = .34. These were qualified by a moderate interaction between variance balance and node type, ${\eta }_G^2$ = .15. As depicted in Figure 6b, there was an inverse quadratic relationship between source of variance and closeness for both target (R²_quadratic = .95) and comparator nodes (R²_quadratic = .96), though the peak of the quadratic component was higher for the target than comparator node, node type × squared variance source F(1, 124) = 168.25, p < .0001. For both target and comparator nodes, closeness was highest when there was slightly more factor variance than unique variance.

Betweenness

There were strong main effects of variance balance and node type on betweenness, ${\eta }_G^2$ = .24 and .68, respectively. These were qualified by a variance balance × node type interaction ${\eta }_G^2$ = .29. Whereas betweenness varied strongly for target nodes as a function of variance balance (${\eta }_G^2$ = .52), betweenness in comparator nodes was only weakly associated with the variance balance of targets (${\eta }_G^2$ = .03). As depicted in Figure 6c, betweenness increased substantially for target nodes when they had even a small degree of both factor and unique variance. This relationship could be approximated by a quartic polynomial model (R²_quartic = .92), cubic versus quartic $\Delta R^2$ = .04, F(1, 60) = 27.19. For comparator nodes, there was a weak tendency for betweenness to be greater when most of the variance in the target was explained by either unique or shared variance (R²_quadratic = .64).

Simulation 3: Effects of multiple latent causes on nodal graph metrics

Simulation 2 revealed that the specific bivariate relationship between items loading on different common factors (i.e., relaxing the conditional independence assumption of the factor model) resulted in substantial and often nonlinear changes in graph metrics. Although the primary goal of Simulation 2 was to examine common versus specific sources of covariation, the target items can also be viewed in terms of multiple latent causes. That is, variance in y2 and y12 was jointly explained by both common (f1 and f2) and specific (s) factors. Simulation 3 built on this notion, as well as our interest in understanding how symptom networks would represent multiple latent causes such as method factors versus substantive traits. In Simulation 3, we examined how nodal metrics vary when a node is a function of two latent causes. We hypothesized that network metrics would reflect a weighted combination of these latent causes.

Methods

We independently manipulated the loadings of a target item, y17, on two latent factors, f1 and f2 (see Figure 7). Factor loadings of the target item on f1 and f2 varied between 0.2 and 0.8 in 0.05 increments. Altogether, this yielded 169 possible combinations (13²) of loadings for the target item. All other loadings were fixed on their respective factors at 0.8 and residual item variance was held at 0.3 for all items across conditions. As with the other simulations, for each condition, we simulated 100 replication datasets with N = 400. As in Simulation 2, we averaged across replications within a given population model and used polynomial regression to capture the relationship between graph metrics and factor loadings. To examine the effect of target factor loadings on other nodes, we analyzed a comparator node, y10, which loaded on f2.

Figure 7.

The orthogonal two-factor model with cross-loadings used in Simulation 3. As depicted in the inset panel, the loadings of y17 (target) on f1 and f2 varied independently between 0.2 and 0.8 in 0.05 increments. Standardized loadings for all other indicators were fixed at 0.8, and residual item variances were fixed at 0.3.

Our primary focus was on the association between graph metrics for the target node, y17, and the population factor loadings across conditions. We also compared the effect of simulation condition on a comparator node, y10, whose loadings were fixed to 0.8 in all population models. Crucially, unlike network metrics, there was not a significant association between the fitted factor loading for the comparator node and both the population and fitted loadings of the target node, R² < .001. That is, manipulating the target factor loading did not bias the estimated loading of the comparator node. For simplicity, we averaged graph metrics across replications to understand their association with factor loadings, but multilevel models that captured replications nested within condition provided substantively identical results.

Results

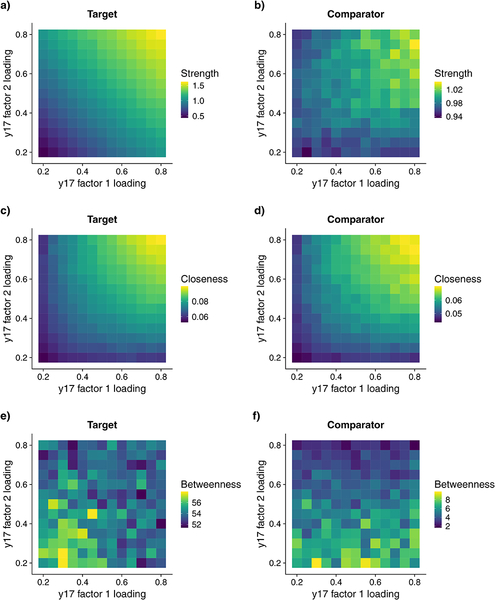
For the target node, strength was an equally weighted combination of the factor 1 and factor 2 loadings, B_f1 = 0.94 (SE = .007), B_f2 = 0.94 (SE = .007), R² = 1.0 (Figure 8a). Across replications, strength of the target node varied largely as a function of both factor 1 (${\eta }_G^2$ = 0.88) and factor 2 (${\eta }_G^2$ = 0.88) loadings, and very weakly as a function of their interaction (${\eta }_G^2$ = 0.02). Variation in strength for the comparator was much smaller across conditions (Figure 8b, top right panel), but it was weakly associated with target factor 1 loading (${\eta }_G^2$ = 0.05), factor 2 loading (${\eta }_G^2$ = 0.05), and their interaction (${\eta }_G^2$ = 0.02). Averaging across replication datasets, factor loadings of the target, including the factor 1 × factor 2 interaction, explained 82% of the variance in the comparator after accounting for the comparator factor loading. Finally, to quantify the similarity of condition effects on target and comparator nodes, we computed the correlation between average strength of target and comparator nodes across conditions. This revealed a high similarity for strength, r(167) = .84 (cf. patterns in Figure 8a,b).

Figure 8.

The effects of independent latent causes on nodal graph metrics for target (y17) and comparator (y10) nodes. Data were generated from an orthogonal two-factor model in which the cross-loading of the target on the latent factors was independently manipulated between 0.2 and 0.8 (see Figure 7). Color tiles in each panel depict the mean graph metric value in that simulation condition (i.e., as a function of factor 1 and factor 2 loadings).

For closeness, we found that the effect of condition on the target was strongly related to factor 1 loading (${\eta }_G^2$ = 0.63), factor 2 loading (${\eta }_G^2$ = 0.63), and their interaction (${\eta }_G^2$ = 0.20). The relationship between loadings and closeness was best captured by a model that included both linear and quadratic terms for the factor loadings, as well as the interaction of the linear terms, R² = .99 (Supplementary Table 1). As depicted in Figure 8c, closeness was particularly high when both factor 1 and 2 loadings were high. Although the comparator node had lower closeness on average, it nevertheless varied substantially as a function of the factor loadings for the target, factor 1 ${\eta }_G^2$ = 0.33, factor 2 ${\eta }_G^2$ = 0.33, factor 1 × factor 2 ${\eta }_G^2$ = .06. More specifically, variation in comparator closeness across conditions was largely predicted by a model that included linear and quadratic terms of the target’s loadings, R² = 0.98 (Supplementary Table 1). Furthermore, there was a very strong association in the effect of condition on closeness between target and comparator nodes, r(167) = 0.99 (cf. Figure 8c,d).

For betweenness, the effect of condition on the target was very weak, factor 1 ${\eta }_G^2$ = .003, factor 2 ${\eta }_G^2$ = .003, factor 2 × factor 2 ${\eta }_G^2$ = .009. Averaging across replications, betweenness was somewhat associated with both factor loadings, as well as their interaction, R² = .43 (Supplementary Table 2). As depicted in Figure 8e, betweenness for the target was greatest when loadings for both factors were relatively weak, diminishing as either factor loading increased. Variation in betweenness for the comparator node was very weakly related to the simulation condition for the target, factor 1 ${\eta }_G^2$ = .01, factor 1 ${\eta }_G^2$ = .01, factor 1 × factor 2 ${\eta }_G^2$ = .009. Betweenness in the comparator node, y10, was predicted by the factor loading of the target on same factor. More specifically, when y17 (target) had a smaller loading on the same factor as y10 (comparator), the betweenness of the comparator was higher (note the bottom-to-top color gradient depicted in Figure 8f), R² = 0.70 (Supplementary Table 2). The effect of condition on betweenness was only modestly related between target and comparator nodes, r(167) = 0.35.

Discussion

The goal of this paper was to examine the performance of network psychometric approaches to cross-sectional symptom data in which the covariance patterns reflect at least one latent variable. We focused on the relationship between estimates of formal parameters from a latent variable model and estimated nodal centrality measures in graph analyses, which are the primary focus of empirical studies (e.g., Fried et al., 2015). By contrast, previous research has examined the performance of network search algorithms in the accurate detection of edges (i.e., conditional bivariate relationships), or the convergence of selected network and latent variable models (Forbes et al., 2017; Marsman et al., 2018). Across three simulation studies, we observed a number of patterns in nodal centrality measures that undermine their interpretability in empirical studies of symptom co-occurrence.

In the first simulation, we examined the correspondence between nodal centrality metrics and factor loadings when data were generated from a factor model. Given the large literature on latent variable approaches to psychiatric comorbidity (Krueger & Markon, 2006), it is important to understand potential points of correspondence and disjunction between network psychometric analyses and traditional factor models. In defining symptom centrality as a construct, Cramer and colleagues (2010) state, “a latent variable model renders all symptoms equally central and thus exchangeable. … Within a latent variable framework, factor loadings cannot be measures of symptom centrality as we view the concept since those loadings are simply reliability estimates” (p. 144). Although exchangeability is an optional feature of latent variable models (e.g., by equating factor loadings in a τ-equivalent model), our first simulation demonstrated that when a latent factor underlies symptom correlations, nodal strength is perfectly correlated with loadings using the EBICGLASSO algorithm. Furthermore, this redundancy held true in correlated multi-factor models. This finding suggests that in empirical analyses, a node with higher strength may not necessarily denote a distinctly important symptom, but instead a symptom that is strongly associated with an underlying latent construct such as a diagnosis.

The notion that latent variable models render all symptoms equally central is both philosophically and quantitatively at odds with the results of our strength centrality findings. Classical test theory emphasizes the importance of exchangeability in part because item properties are not taken into account when test scores reflect equally weighted item sums (Nunnally & Bernstein, 1994). A modern approach to psychometric theory, however, explicitly incorporates item properties into the measurement of latent traits (McDonald, 1999). In so doing, the strength of the relationships between a putative latent variable and its manifestations can be indexed by the factor loadings (Bartholomew, Knott, & Moustaki, 2011). Consequently, although network psychometric studies have interpreted relative differences in strength in terms of the unique importance of specific symptoms, our findings are consistent with the interpretation that symptoms with higher strength centrality may simply be better indicators of a latent variable. Even if one adopts the narrow view that factor loadings are ‘simply reliability estimates,’ the equivalence of loadings and strength estimates in our simulations suggests that one could interpret symptoms with higher strength as being more reliable indicators of a latent variable, which has not been the view articulated in empirical network psychometric studies.

Our findings for closeness and betweenness revealed a more complex relationship between latent structure and nodal metrics. In our orthogonal multi-factor models, symptoms loading on different factors were, by definition, conditionally independent of each other (i.e., causally unrelated). However, in a given sample, there will be small associations between symptoms of different factors due to sampling variability. We found that closeness and betweenness were better explained by such spurious sampling variability than by the primary factor loading despite item correlations within a factor being nearly 100 times greater than spurious associations among items of uncorrelated factors. The magnitude of this sensitivity to sampling variability was larger for betweenness than for closeness. Such extreme sensitivity to small associations may partly explain the instability of these network metrics across samples (Forbes et al., 2017) or subsamples of the same dataset (Epskamp et al., 2018).

This result has particularly important implications for so-called “bridge” symptoms (Cramer et al., 2010) or “causal bridges” (Fried & Cramer, 2017) such as fatigue, which co-occur in different mental disorders. From a network psychometrics perspective, bridge symptoms are thought to explain disorder comorbidity. One would expect bridge symptoms to have greater betweenness, reflecting that symptoms of different disorders are connected via a path that includes the bridge. Likewise, a bridge symptom would typically have elevated closeness, reflecting relatively short distances (here, larger average partial correlations) to all other symptoms in the network, even if indirect. Our findings indicate that both nodal closeness and betweenness may be substantially elevated in empirical studies due to small, and even spurious, associations between symptoms that help to connect relatively disconnected subgraphs (here, resulting from orthogonal latent factors). One would almost certainly avoid interpreting such dubious results by a visual inspection of the marginal correlation matrix (e.g., Figure 1a). As is typical in the SEM literature (McDonald & Ho, 2002), we believe that it is important for network psychometric studies to report both marginal and partial correlation matrices used in their analyses. Failing to do so prevents a detailed examination of associations and requires the reader to interpret relationships using graphical depictions alone. Network diagrams often use color or line width to encode key information; these channels have limited bandwidth and are subject to constraints on graphical perception (Munzner, 2014).

Our second simulation examined more specifically how nodal metrics were affected when the variance of a target psychometric item was attributable to a broad latent factor (here, having 10 indicators) versus a specific bivariate relationship with a symptom of a different factor. By trading off variance along a general-to-specific gradient, this simulation tested both the accuracy of the specific edge between target items (Figure 4), as well as broader effects on network topology. Consistent with previous research on the sensitivity of the EBICGLASSO method to edgewise variation (e.g., van Borkulo et al., 2015), we found that the specific edge strength between target items was recovered well across simulation conditions. However, when examining the performance of nodal metrics, there were strong nonlinear effects along the general-to-specific gradient (Figure 6). As articulated above, the interpretability of centrality statistics rests, in part, on the extent to which they capture the dominant sources of covariation in the symptom matrix and whether they scale in proportion to changes in the underlying data-generating model.

We found that strength for target items increased as the node was more factor-related, consistent with the broader pattern of correlations that would be expected for an indicator of a latent factor relative to a specific bivariate correlation. Notably, strength increased rapidly as the target node had even weak factor-related variance but plateaued when specific and unique variance were relatively balanced. Closeness was maximized for the target item when there was a balance between factor-related and specific variance, following an inverse quadratic pattern of change. This is conceptually sensible insofar as a node should be closer to all other nodes in the graph when it links across otherwise disconnected subgraphs (here, factors). Importantly, however, we observed a similar, but smaller, inverse quadratic pattern for closeness of comparator nodes even though marginal associations among comparator items did not vary as a function of the target. This indicates that if any node connects subgraphs, then all nodes become closer, which is a correct description of the graph in terms of average correlational distances. Nevertheless, this suggests that researchers should exercise caution when interpreting closeness because it may change in parallel for two nodes that are conditionally independent of each other.

Likewise, we urge caution when interpreting the causal importance of betweenness in symptom networks. Even small correlations that connect subgraphs were associated with substantial changes in betweenness, but this metric was largely insensitive to variation in the relative balance of factor-related versus specific variance over most conditions tested (Figure 6c). This aligns with the findings from the first simulation, where small spurious correlations that connected subgraphs were associated with changes in betweenness.

Altogether, our findings from the second simulation indicate that researchers should be aware of the potentially nonlinear and heterogeneous changes in nodal metrics when variance in an item is attributable to a direct bivariate association relative to a broader latent factor. If nodal metrics are to be the primary emphasis of empirical studies, our findings suggest that remarkably different estimates could be obtained from relatively similar underlying structures. We recommend that researchers interested in network psychometrics use simulation studies to test how nodal metrics vary across plausible causal structures for their data. Likewise, researchers should be cognizant of the possibility that there could be relatively distinct modules (e.g., cognitive versus affective symptoms of depression; for an overview of modularity, see Newman & Girvan, 2004) such that edges connecting symptoms within a given module are stronger than edges between modules. Most nodal metrics capture aspects of the overall graph structure, but are not based on knowledge of modules, subgraphs, or latent factors. Without examining how metrics vary across alternative causal models, our findings suggest that the interpretation of strength, closeness, and betweenness may be ambiguous in empirical studies.

Extending such concerns, our third simulation examined how nodal metrics varied when symptom covariance reflected multiple latent causes. For example, some researchers have argued that psychopathology reflects a combination of broad liability factors such as internalizing or the ‘p-factor’ (i.e., omnibus risk for mental illness), as well as specific risk factors for particular forms of mental illness (Caspi et al., 2013; Kotov et al., 2017; Sharp et al., 2015). This view can be instantiated by bifactor models in which items reflect both general and specific factors (for a network-based objection, see van Bork, Epskamp, Rhemtulla, Borsboom, & van der Maas, 2017). Other researchers have sought to separate nuisance factors, such as method variance or response biases, from substantive factors that reflect hypothetical constructs (Eid, 2000; McLarnon et al., 2016). For example, Cole and colleagues (2007) demonstrated that omitting correlations among residuals that are attributable to the study design (e.g., items that were completed by a given informant) undermines the interpretability of substantive latent factors.

We found that nodal metrics reflect a weighted and at times nonlinear combination of the simulated latent causes. More specifically, if variation in a target node was due to two independent latent factors, nodal statistics depended on both factors (Figure 8). Although this is unsurprising in some ways, it has troubling implications for empirical studies. For example, strength was an equally weighted combination of the factor loadings of the two independent causes. Thus, in empirical studies, strength will be just as sensitive to nuisance factors (e.g., method variance) as substantive factors (e.g., personality traits). Furthermore, to our knowledge, network psychometric studies have exclusively used observed items from symptom inventories or clinical interviews without accounting for their psychometric properties, including measurement error, method variance, or response bias factors. Without explicitly modeling nuisance factors, it is impossible in an empirical analysis to unmix what portion of nodal metrics reflects substantively interesting covariation versus undesirable features of the psychological test. By contrast, there are many applications of SEM that are explicitly motivated by the goal of examining method variance such as in cross-informant agreement about symptoms (e.g., Grigorenko, Geiser, Slobodskaya, & Francis, 2010), as well as methodological techniques for mitigating common method variance (Williams, Hartman, & Cavazotte, 2010).

Moreover, if a given psychometric item is truly multidimensional — that is, influenced by multiple traits — nodal metrics cannot inform an understanding of which trait is conceptually more influential. For example, from an interpersonal circumplex perspective, stronger endorsement of extraversion items could be viewed in terms of elevations on the dimensions of dominance and affiliation (Wiggins & Pincus, 2002). This dilemma can be seen in the top-left-to-bottom-right diagonal of Figure 8a, where equal estimates of nodal strength were obtained despite substantial differences in the magnitudes of the latent causes.

Consistent with the dependencies observed in simulation 2, we found that there were echoes of the target item’s factor loadings on nodal metrics for other items (see patterns between Target and Comparator panels in Figure 8). This was true despite there being no relationship between factor loadings for the target and those for comparators. Neither did the fitted factor loadings show any dependency in the simulation. In particular, the closeness of comparator nodes was strongly associated with the closeness of the target, being maximized when factor loadings for the target were both high. Altogether, the factor model maintained a kind of firewall between conditionally independent items across conditions — that is, estimated factor loadings for target and comparator nodes were uncorrelated. This necessarily follows from the structure of the latent variable model, where indicators were independent after conditioning on the latent factor. Nevertheless, nodal metrics, which depend on the overall structure of the graph, were contaminated by a node that reflected multiple causes.

Why Network Psychometrics Cannot Escape Psychometric Theory

One of the major implications of our third simulation is that researchers must exercise extreme caution in selecting symptoms to enter into network analysis. In particular, any source of nuisance variation such as similar item phrasing or variation in assessment method (e.g., self-report versus clinical interview) should be minimized to avoid undermining the interpretability of nodal metrics. Furthermore, if two symptoms are likely to reflect the same underlying construct, these should probably be excluded from the analysis. For example, if the items “I worry a lot” and “I can’t get certain troubles off of my mind” were included in a symptom network, it is possible that their centrality estimates could reflect strongly overlapping content, rather than a substantive role in the broader pattern of generalized anxiety symptoms. Ideally, symptoms in network analyses should reflect conceptually distinct constructs such that the edges among them are akin to the structural model of an SEM.

The notion that nodes should reflect conceptually distinct constructs has been articulated in some of the network psychometrics literature. For example, in distinguishing a network approach from a typical latent trait approach to personality, Cramer and colleagues (2012) state, “we propose that every feeling, thought or act is a potential component of personality if it is associated with a unique ‘causal system’ … The component must thus be unique in the sense that its causal system differs from that of other (potential) components. This means that a personality component is, to a certain degree, causally autonomous and, as such, not ‘exchangeable’ with other components” (p. 415). Importantly, however, most network studies of psychopathology symptoms have selected nodes that are drawn from a given diagnosis or syndrome (e.g., Fried et al., 2015; McNally et al., 2015). As we have described above, extant symptom measures are typically constructed following a latent variable approach in which items that load strongly onto a factor are retained, while items with poor loadings are culled. Likewise, the development of psychiatric classification systems has been strongly informed by considerations of interrater agreement and internal consistency of a symptom set.

In short, implementing the recommendation to include symptoms that are conceptually and causally distinct may be possible in some circumstances, but we have doubts about the promise of this direction given the current structure of symptom measures and datasets. This is not to say that symptom co-occurrence necessarily reflects latent variables at the ontological level. Rather, if proponents of network approaches believe that psychopathology is composed of causally distinct components, it is essential that new measures be developed using methods that capture these components while discouraging the presence of latent confounding in the resulting item covariance matrices.

The Challenges of Latent Confounding in Graph Analyses

A primary goal of this paper was to examine the interpretability of nodal metrics when symptom correlations partly reflect latent confounding. In the causal network discovery literature, there is increasing awareness of the need to accurately identify conditional independence relationships in the presence of latent confounding (Chandrasekaran, Parrilo, & Willsky, 2012; Ogarrio et al., 2016; Spirtes & Zhang, 2016). Crucially, graphical models representing causal relationships among nodes assume that there are no key omitted variables (Pearl, 2000). In a commentary on this dilemma, Yuan (2012) noted, “the difficulty comes from the fact that the validity of conditional independence relationships implied by a graphical model relies critically on the assumption that all conditional variables are observed, which of course can be unrealistic” (p. 1968).

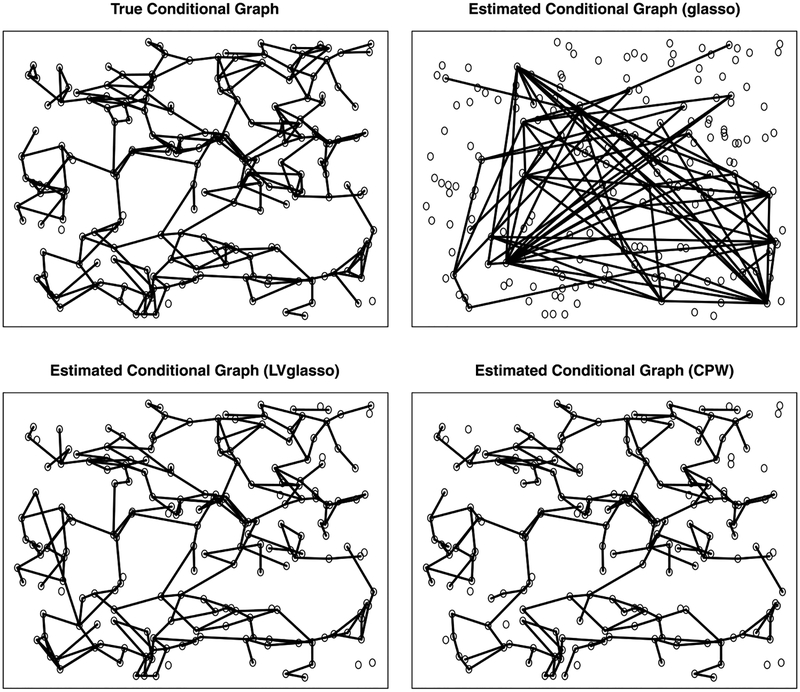
Ignoring the possibility of latent confounding can fundamentally misrepresent symptom relationships. If, in truth, the co-occurrence of anhedonia, dysphoria, and hopelessness reflect depression as a latent cause, omitting depression (a so-called “hidden” variable in the network literature) from the graphical model yields a structure in which edges among symptoms may be spurious, or important direct relationships are omitted. The consequences of this problem are visually evident in Figure 9 (reprinted from Yuan, 2012), which shows the poor performance of the GLASSO algorithm in the presence of latent confounding. This is a known limitation of GLASSO that has been described in the causal networks literature, with extensions that specifically seek to handle unknown latent variables (e.g., Agakov, Orchard, & Storkey, 2012). Indeed, when confronted with a set of highly correlated variables, as may occur among items measuring a given construct, a LASSO approach typically retains only a subset of plausible edges, and the subset is often sample dependent (Hastie, Tibshirani, & Friedman, 2009).

Figure 9.

The performance of three algorithms (glasso, LVglasso, CPW) in recovering a graph structure (upper left panel) that depends on latent variables. The glasso algorithm has been used extensively in the network psychometrics literature, but performs rather poorly in the presence of latent confounding (upper right panel). By contrast, the LVglasso and CPW algorithms, which seek to identify latent variables as part of estimating the graph, recover the structure reasonably well. LVglasso = latent variable graphical lasso; CPW = latent variable graphical model selection method of Chandrasekaran, Parrillo, and Willsky (2012). Figure reprinted from Yuan (2012); with permission.

Exploratory factor analysis (EFA) is a classical approach to identifying hidden variables in covariance matrices that can help to understand structural, and potentially causal, relationships (Loehlin, 2003). EFA is particularly useful when a researcher has relatively weak a priori knowledge about latent structure. Although network discovery algorithms have developed substantially in the past 15 years (Spirtes & Zhang, 2016), many approaches, including GLASSO, are based on searching for causal relationships among observed variables. Importantly, however, there is some evidence that network search algorithms that are sensitive to latent confounding can outperform EFA when the data generating model is complex (Silva, Scheines, Glymour, & Spirtes, 2006). Thus, although we have criticized network psychometric approaches in their current form, we believe that network science may provide useful methods for understanding the causes of symptom co-occurrence, both hidden and observed.

Furthermore, if researchers have a priori knowledge of latent structure — for example, based on validation studies of a psychological test — we recommend that this be formally incorporated into covariance structure analyses. Indeed, the fit of CFA models can be compared to GGMs, and conventional model selection strategies (e.g., based on global fit statistics) can inform an understanding of what model best describes the structure of symptom covariance (Epskamp, Rhemtulla, et al., 2017). We also believe that it is crucial for network models and more conventional SEMs to be compared in terms of fit versus parsimony (Krueger, Deyoung, & Markon, 2010), interpretability vis-à-vis theory, and reproducibility (Forbes et al., 2017) in order to promote a multi-model selection approach based on relative evidence (Burnham & Anderson, 2002). For example, Epskamp and colleagues (2017) recently developed an approach that integrates latent trait models with network search algorithms.

The Important Debate About the Ontology of Psychopathology

Advocates of network psychometrics have asserted that the assumption of local independence in common factor models — that is, that two indicators of a latent factor are independent after accounting for the factor — may not hold true in some datasets (Cramer et al., 2010). Although our study used factor models to examine the performance of network psychometrics in the presence of latent confounding, we do not make a strong assertion that common symptoms of psychopathology are caused by a diagnostic entity such as depression or a broad liability factor such as internalizing. Likewise, we acknowledge that factor models may not adequately describe some patterns of symptom co-occurrence. Such limitations have motivated, for example, extensions such as exploratory SEM, that allows the researcher to specify a measurement and structural model based on theory while also allowing for data-driven deviations from theory, particularly item cross-loadings (Marsh, Morin, Parker, & Kaur, 2014; also see Muthén & Asparouhov, 2012). Furthermore, we acknowledge that our study generated data from factor models and fit them using network models, but we did not examine the converse.

Understanding the formal relationships between network and factor models is a topic of active inquiry (Marsman et al., 2018). We have previously shown that factor models can be transformed into directed path models lacking latent variables (the so-called Houdini transformation; Bentler & Molenaar, 2012; Molenaar, 2003). This highlights the challenge of distinguishing between models that are conceptually distinct, but statistically equivalent. Future work should examine the conditions under which typical latent variable models accurately capture data generated from a network model such as the GGM. Ultimately, model fitting alone is typically insufficient to disambiguate equivalent models, and other approaches such as experimental manipulation or alternative metrics of model quality are needed (Williams, 2012).

These limitations notwithstanding, for the reasons stated above, we believe that it is highly plausible and often likely that latent variables are present in cross-sectional symptom covariance data. Our results, along with deeper treatments of latent confounding (Chandrasekaran et al., 2012), suggest that it is essential that network psychometric approaches examine the evidence for hidden variables prior to analyzing or interpreting patterns at the symptom level. Failing to do so risks identifying spurious relationships or failing to detect causally important effects. In this vein, one recent study contextualized nodal metrics vis-à-vis symptom modules that may represent latent variables, rather than emphasizing metrics such as closeness that are blind to subgraph structure (Blanken et al., 2018).

Returning to the conceptual model underlying cross-sectional network psychometric approaches (Borsboom, 2017), we wish to highlight three key ontological assumptions:

1. Two symptoms (manifest variables) can be uniquely associated with each other without implying a latent clinical entity (e.g., depression) or dimensional trait (e.g., negative affect). That is, symptoms are the atomic units of psychopathology.

2. The relationship between two symptoms can best be understood when common variation with other symptoms is partialed out. That is, the symptoms should have some direct relationship with each other, rather than simply being associated through many indirect effects.

3. Observed variables provide direct evidence of a symptom of interest, rather than being an indicator of a hypothetical construct. A corollary of this assumption is that measurement error is not important in characterizing the association among symptoms.

A fundamental difficulty with these assumptions is that many, if not most, symptoms could themselves be considered hypothetical constructs. For example, there is a literature on different facets of fatigue, as well as many psychometric items to measure each facet (Beurskens et al., 2000). Moreover, there are substantial advantages of accounting for measurement error in latent variable analyses, such as mitigating the attenuation of validity coefficients or improving power to detect structural relationships (Furr, 2017). We also question whether causal relationships between two symptoms will be identified under the assumption that the specific association is conditioned on all other symptoms. What is the meaning of a conditional association between fatigue and insomnia after accounting for all other symptoms of mood and anxiety disorders? By extension, the breadth of symptoms included in a network analysis is an implicit statement about the confounders that could obscure a unique bivariate causal relationship. Thus, the researcher’s decision about whether to include symptoms of a disorder (e.g., depression), family (e.g., mood disorders), or superordinate spectrum (e.g., internalizing pathology) fundamentally alters the causal assumptions of a given graphical model.

In short, network psychometrics cannot escape psychometric theory and should not attempt to do so. Rather, to advance a quantitative approach to the classification of mental illness, we believe that models should incorporate and test researchers’ a priori theory and build on extant knowledge of the latent structure of psychopathology. Such structures are likely to include latent variables such as diagnoses or liability factors (Krueger & Markon, 2006), and formally incorporating measurement models is likely to advance the validity of network analyses. At present, network psychometrics have applied exploratory data-driven algorithms that require minimal input from the scientist and optimize a fit criterion, rather than seeking to test a specific hypothesis about covariance structure. These approaches have operated almost exclusively at the level of observed variables, precluding the possibility of latent factors.

Our simulations provide a proof of concept that network psychometric approaches may provide ambiguous or misleading guidance in empirical studies. Nodal metrics are secondary statistics that may reflect an array of causes and do not directly link with the underlying conditional independence relationships of a given graphical model. Although arguments for a network approach have largely been cast in ontological terms (e.g., McNally, 2012), our results suggest that network psychometrics in their current form do not overcome key epistemic hurdles. In particular, network analyses based on observed variables alone fail to provide scientists with knowledge of whether or not latent confounders are likely to exist in the data. We believe that the classification of mental illness will be best advanced by examining parameters from formal models that are sensitive to latent structure and that instantiate specific hypotheses about the basis of symptom co-occurrence.