A New Approach for Inferring Traffic-Related Air Pollution: Use of Radar-calibrated Crowd-Sourced Traffic Data

Abstract

Background:

Crowd-sourced traffic data potentially allow prediction of traffic-related air pollution at high temporal and spatial resolution.

Objectives:

To examine associations (1) of radar-based traffic measurements with congestion colors displayed on crowd-sourced traffic data maps and (2) of black carbon (BC) levels with radar and crowd-sourced traffic data.

Methods:

At an off-ramp of an interstate and a small one-way street in a mixed-use area in New York City, we used radar devices to obtain vehicle speeds and flows (hourly counts) for cars and trucks. At these radar sites and at an additional non-radar equipped site at a 2-way street, we monitored BC levels using aethalometers in the summer and early fall of 2017. At all three sites, free-flow traffic conditions typically did not occur due to the nearby presence of traffic lights and forced turns. We also downloaded real-time traffic maps from a crowd-sourced traffic data provider and assigned an ordinal integer congestion color code CCC to the congestion colors, ranging from 1 (dark red) to 5 (gray).

Results:

CCC increased with vehicle speed. Traffic flow was highest for intermediate speeds and intermediate CCC. Regression analyses showed that BC levels increased with either segregated or total vehicle flows. At the off-ramp, time-dependent BC levels can be inferred from time-dependent CCC and radar-derived mean vehicle flow data. A unit decrease in CCC for a mean traffic flow of 100 vehicles/hr was associated with a mean (95% CI) increase in BC levels of 0.023 (0.028, 0.018) μg/m³. At the small 1-way and the 2-way street, BC levels were also negatively associated with CCC, though at a >0.05 significance level.

Conclusions:

Use of inexpensive crowd-sourced traffic data holds great promise in air pollution modeling and health studies. Time-dependent traffic-related primary air pollution levels may be inferred from radar-calibrated crowd-sourced traffic data, in our case radar-derived mean traffic flow and widely available CCC data. However, at some locations mean traffic flow data may already be available.

1. INTRODUCTION

Combustion-engine powered vehicles significantly contribute to traffic-related air pollution (TRAP).¹ TRAP includes a wide variety of toxic chemicals, including black carbon (BC), polycyclic aromatic hydrocarbons (PAHs), carbon monoxide, nitrogen oxides, sulfur oxides, particulate matter (PM), and BTEX (benzene, toluene, ethylbenzene and xylenes) volatile organic compounds (VOCs). TRAP has been linked to multiple adverse health outcomes including respiratory² and cardiovascular disease,^3,4 cancer,⁵ and is considered an ischemic stroke trigger.^6,7

The distance between a location of interest (e.g. home address) and roadways can serve as proxy for air pollution^8–10 and has been linked to adverse health outcomes.^11,12 Land-use regression models (LURs) have also been used to predict air pollution^1,13–17 and associated health outcomes.¹⁸ However, neither approach accounts for temporal variations in traffic. Accounting for spatio-temporal variations in air pollution at an hourly resolution may be important to assessing acute health effects due to differences in exposure to TRAP at different times of day and across a city. For instance, a recent study suggested that ischemic stroke onset risk was highest when the exposure to TRAP, in this case via BC (often used as a tracer for diesel truck emissions¹⁹), occurred 12 to 14 hours prior to the event.⁶

Key to predicting temporal variations in TRAP is the measurement of temporal variations in traffic conditions. Traditional technologies for counting vehicles in-situ²⁰ include pneumatic tube counters,^19,21,22 piezo-electric sensors, and inductive loops laid on roadways.^23,24 More recently, video-camera based systems^25,26 and radar-based systems^27,28 have become available. These systems can provide information about vehicle speed and “traffic flow” (vehicle counts per unit time²⁹) and have been used to examine the impacts of traffic on local hourly air pollution levels.^{19,22,30–34}

Evaluation of data obtained from GPS-enabled mobile phones collocated in driving vehicles offers the opportunity of inexpensive, real-time traffic monitoring of entire street networks,³⁵ which cannot be done with traditional traffic monitors. Traffic maps based on such crowd-sourced data are nowadays broadcasted in virtually real time via the Internet. There is great potential of using such data in air pollution studies. For instance, Google traffic travel time data along five routes were recently used to examine the effects of high-occupancy vehicle restrictions.³⁶ In this study, our objectives are (1) to examine associations of congestion colors displayed on crowd-sourced traffic data maps with radar-based measurements of traffic, and (2) to develop statistical models based on regression analysis for the mobile-source contributions to air pollution levels that account for measured traffic and meteorological data. Such models could potentially allow estimating the effects of additional traffic or traffic interventions on air pollution. While some of the models we will develop account for radar data (for comparison with other studies^19,22,37), it was our primary objective to examine whether mobile-source contributions to air pollution can be inferred from crowd-sourced traffic data and mean traffic flow.

2. METHODS

2.1. Study sites

Data collection occurred in the summer and early fall of 2017 in the Mott Haven/Port Morris neighborhoods in the South Bronx in New York City, NY, where we conducted a pilot study to examine associations between truck traffic and air pollution. Vehicles were counted at two locations impacted by truck traffic. It would have been desirable to count at additional locations, but the project budget did not allow for this. To minimize measurement error, we installed the radar devices at locations with at most one-lane traffic on each of the two sides of the device, thereby avoiding vehicle occlusion.³⁸ The devices were attached to street light poles with approval from the Department of Transportation (DOT). To examine contrasting traffic and pollution patterns, the two locations (see Figure A.1) differed in average daily vehicle counts:

• Site A: An exit ramp from US Interstate I-87. The radar device provides the combined flow of one-way traffic on the ramp as it gently slopes uphill (to the North of the counter) and one-way traffic on East 134^th Street (to the South). For the most part, East 134^th Street appears to serve its relatively few residents (in row homes) living in front of the traffic counting location, while the ramp traffic serves huge industrial hubs including the Harlem River Yard and Hunts Point. Field visits confirm that eastbound traffic on East 134^th Street at the radar location is negligible; as such, we interpret the radar counts as only representing the exit ramp. Traffic flow was affected by a downstream traffic light at the intersection between Bruckner Blvd. and Brown Place. A BC Aethalometer (AE21, Magee Scientific) was located in a residential building on the South side of East 134^th Street. The air inlet was located 4 m above street level and 6 m from the curb, which is abutted by a lane typically used for residential parking.

• Site B: A one-way street, which primarily serves vehicles visiting industrial areas in the Harlem River Yards and in Hunts Point. At the end of the block, the street leads to a T-intersection where vehicles need to make either a left or right turn. A BC micro-aethalometer monitor (MA350, AethLabs) was located on the flat roof of a commercially used warehouse on the East side of Willow Ave. inside of an environmental chamber that had Peltier heating and air-conditioning to keep the temperature inside the box at a constant 32.8°C. The air inlet was located 9 m above street level and 8 m from the curb. The roof was enclosed by an about 1-m tall parapet wall.

  In addition, BC measurements were performed at a site where no radar was installed.

• Site C: A two-way street, which serves vehicles visiting industrial areas in the Harlem River Yards. Traffic flow was affected by traffic lights at the intersection between St. Ann’s Ave. and Bruckner Blvd. and the intersection between St. Ann’s Ave and 134^th St. A BC Aethalometer (AE16, Magee Scientific) was located in a residential building on the East side of St. Ann’s Ave. The air inlet was located 8 m above street level and 12 m from the curb. Average daily traffic counts for a location on St. Ann’s Ave to the North of Site C were obtained from DOT: 6,863 vehicles per day.³⁹

All three sites typically did not allow drivers to select their own speed due to the presence of traffic lights or a downstream T-intersection. Therefore, conditions of free-flow traffic were typically not met. Also, both rack-mounted aethalometer and MA350 instruments use the same approach for BC measurements (transmission/adsorption at 880 nm) and collocation experiments have shown that they provide very similar concentrations (as quantified by the slope-intercept line^40,41) with high correlation (R² > 0.95).

The study was approved by the Columbia University Institutional Review Board and informed was consent obtained; participants were identified with the assistance of our community partner.

2.2. Radar-based traffic counting

We used radar devices (Armadillo traffic counter, Houston Radar) to make physical measurements of traffic conditions. The devices measure vehicle speed and traffic flow. As compared to pneumatic counters, radar devices have the advantage that they do not require study personnel to walk onto roads when installing the devices and are not damaged by street cleaners, thus significantly reducing maintenance and risk of injury.

For each detected vehicle, the radar device records the following data: time and date of the event, radar-derived vehicle speed (RS), and vehicle class (small, medium or large vehicle). According to the manufacturer, the accuracy of speed measurements is 0.4%, and up to 97% of vehicles are counted for the local road configurations for typical free flowing traffic, with worse accuracy for stop and go traffic⁴² as is typical for many other traffic monitoring techniques including pneumatic counters and video-based systems. The manufacturer indicates that vehicles with a length <4 m are counted as small vehicles, between 4 and 7 m as medium vehicle, and >7 m as large vehicles. In this paper, we interpret small- and medium-sized vehicles as “cars” and large vehicles as “trucks.” From the event logs, one can determine total traffic flow Q_tot, truck flow Q_tr and car flow Q_car.

2.3. Collection of crowd-sourced traffic data

During the course of our field study, we used a Unix “cron” job to automatically download crowd-sourced traffic data maps of the study area from a leading provider (with no service contract) onto a personal computer every minute and store them as digital images. In the maps, road segments are shown in different colors (green, orange, light and dark red) indicating speeds of vehicles and collocated phones. The bounding colors green and dark red indicate relatively free-flowing and congested traffic, respectively. Gray is displayed if not a sufficient number of drivers supply their GPS position to the traffic data provider via their cell phones. For each road segment for which a congestion color had been assigned, we converted the five colors into an ordinal variable, the congestion color code CCC, as follows:

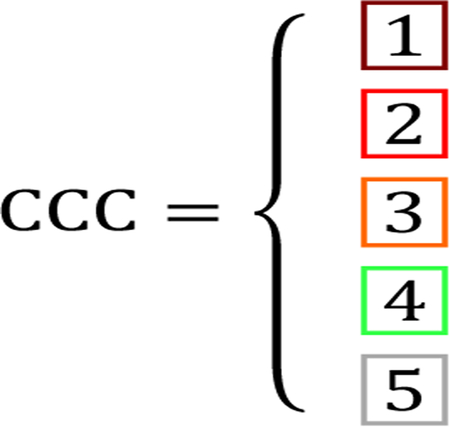
where the color of the square box indicates the congestion color displayed on the traffic maps and the number in the box indicates CCC. Since downloaded traffic maps were “true color” with 16.8 million possible colors, we converted the true-color images into indexed images with a total of 128 colors such that different shades of the five identified colors were reduced to a total of five colors.

Assuming that the fraction of GPS-enabled cell phones in moving traffic is independent of the congestion color, our color scheme assumes gray to be indicative of little traffic, allowing drivers to proceed at highest speeds. Thus CCC should increase monotonically with vehicle speed. By determining CCC for the road segments where the air pollution monitors and/or radar devices were mounted, we obtained CCC time series at a 1-minute resolution. The road segments used to characterize crowd-sourced traffic conditions at Sites A, B and C are indicated in Figure 1a and were 110, 80 and 80 m long, respectively.

Figure 1:

Crowd-sourced traffic data for our study site. (a) Sample traffic map for the entire study area. Dashed ovals for Sites A and B indicate the segments of the single-lane streets for which congestion colors CCC were extracted for analysis. Dashed half oval for Site C indicates the segment for Northeast bound traffic on the two-way street used for analysis. (b) Sample time series of congestion color at Site B. Weekend days are in-between the dotted and dashed lines. Hours refer to local time.

2.4. Sampling periods

At Site A, data collection occurred from June 19 to October 11, 2017. Two major gaps occurred in the BC data: (1) between August 8 to 17, because the aethalometer ran out of filter tape; and (2) between September 3 and 27, because the aethalometer pump broke down. One major gap occurred in the radar data: between October 3 and 13 due to memory overflow of the data logger in the radar device. At Site B, data collection occurred from July 31 to October 11, 2017. No major gaps in BC and radar data occurred. At Site C, data collection occurred from June 27 to October 15, 2017. Radar data were not collected, and a major gap in BC data collection occurred from August 22 to September 20 due to issues related to advancing the aethalometer’s filter tape. At Site A, complete data sets (BC, radar and CCC data) were collected for a total of 70 days, and at Site B for 71 days. At Site C, complete data sets (BC and CCC data) were collected for 80 days. Figure A.2 illustrates sampling periods and data gaps.

2.5. Meteorological data

Hourly surface weather data (temperature, wind speed and direction, relative humidity, precipitation depth) were obtained for the nearby LaGuardia airport (~3 miles away) from the US National Climatic Data Center.⁴³ Upper air radiosonde data were obtained from the US National Oceanic and Atmospheric Administration and the US Earth System Research Laboratory⁴⁴ for the closest out of the three radiosonde station in the state of New York: Brookhaven, NY which is ~50 miles away. While the regression coefficients for mixing height of the models for BC we developed could potentially be biased due to this 50-mile distance, we do not believe that this has a major impact on the regression coefficients for traffic variables that our paper presents. From the surface and upper air data, the mixing layer height was estimated each hour using AERMET, software developed by the U.S. Environmental Protection Agency.⁴⁵

2.6. Data synthesis and descriptive analyses

Different types of data were collected at different temporal resolutions. We normalized the data to 1-min, 5-min, 15-min and 60-min observational windows²² as explained in Appendix A. To explore diurnal variations in traffic conditions and pollution levels, we plotted for each hour of the day mean hourly BC levels and total traffic flow Q_tot averaged over the entire sampling period and stratified by weekdays and weekends. We used box plots to explore two kinds of relationships between pairs of 15-min time-dependent variables: (1) between two out of the five traffic variables (RS, Q_tot, Q_tr, Q_car, CCC) to examine how radar measurements are related to crowd-sourced traffic data, and (2) between BC levels and one traffic variable to get clues about which traffic conditions are related to low and high BC levels, even though these relationships might be confounded, e.g., by meteorological variables.

Since traffic maps cannot be expected to reflect changes in traffic conditions instantaneously (due to data transfer and analysis) we determined the time lag t_lag by calculating the cross-correlation⁴⁶ $R_{\text{GCC,RS}}(\tau )=\underset{-\infty }{\overset{\infty }{\int }}\text{GCC}(t)\text{RS}(t+\tau )dt$ between radar speed RS(t) and color code CCC(t) time series for a 1-min observational window, the temporal resolution of the CCC data. The lag t_lag is given by the τ value, for which the absolute value of $R_{\text{GCC,RS}}(\tau )$ is maximal. Matlab™’s “finddelay” routine was used to determine t_lag.

2.7. Statistical analyses

To examine how BC levels are affected by one or more traffic variables, we employed generalized additive models (GAMs)⁴⁷ using the 15-min time series of the measured traffic, air pollution and meteorological data. In our study, five different time-dependent traffic variables could be used to infer BC levels: segregated traffic flows Q_car(t) and Q_tr(t), total traffic flow Q_tot(t) including its mean ${\overline{Q}}_{tot}$ representing the average over the entire sampling period, radar speed RS(t), and color code CCC(t). Not all five traffic variables were used at the same time, because they may contain redundant information (an extreme example for redundancy is caused by the relation Q_car + Q_tr = Q_tot). Even though we were primarily interested in examining whether BC levels can be inferred from CCC, we fitted the following six regression models to the measured data so that we could compare radar-derived regressions to other published studies:

$$\text{ln}\left(\frac{\text{BC}(t)}{{\text{BC}}_0}\right)=\{\begin{array}{ll}{\alpha }_{tr}{Q}_{tr}(t)+{\alpha }_{car}{Q}_{car}(t)+{\beta }_{rad}{\overline{Q}}_{tot}\text{RS}(t)\text{+}\text{Met}(t)\text{ + }s(t)\hfill & (1)\hfill \\ {\alpha }_{tot}{Q}_{tot}(t)+{\beta }_{rad}{\overline{Q}}_{tot}\text{RS}(t)\text{+}\text{Met}(t)\text{ + }s(t)\hfill & (2)\hfill \\ {\alpha }_{tot}{Q}_{tot}(t)+{\beta }_{\text{GCC}}{\overline{Q}}_{tot}\text{CCC}(t)\text{+}\text{Met}(t)\text{ + }s(t)\hfill & (3)\hfill \\ {\alpha }_{tot}{Q}_{tot}(t)\text{+}\text{Met}(t)\text{ +}s(t)\hfill & (4)\hfill \\ {\beta }_{\text{GCC}}{\overline{Q}}_{tot}\text{CCC}(t)\text{+}\text{Met}(t)\text{ +}s(t)\hfill & (5)\hfill \\ {\beta }_{rad}{\overline{Q}}_{tot}\text{RS}(t)\text{+}\text{Met}(t)\text{ +}s(t)\hfill & (6)\hfill \end{array}$$

where the constant BC₀ = 1 μg/m³ makes sure the equation is dimensionally correct. The first model (Eq. 1) is the only model that accounts for fleet composition by using all the radar data collected, i.e., segregated flows and radar-derived vehicle speed. The second and third models (Eq. 2 and 3) account only for total flow and one measure for vehicle speed, either RS or CCC. Comparing the two models allows evaluating the potential equivalency of RS and CCC data. The fourth model (Eq. 4) represents the conventional approach for modeling time-dependent air pollution and accounts only for time-dependent vehicle flow data.²² The fifth model (Eq. 5) allows examining our primary conjecture that BC levels can be predicted from crowd-sourced traffic data. The sixth model (Eq. 6) was added to evaluate again the potential equivalency of RS and CCC data.

Even though BC should be expected to scale linearly with traffic flows, we log-transformed the BC data to improve both normality and to resolve heteroscedasticity issues. Thus the interpretation of the α’s became less straightforward. However, in case of the products αQ < 1 (with subscripts car, tr, tot), the regression coefficients α_car, α_tr and α_tot represent the mobile-source contributions to BC levels, quantifying the increase in BC levels due to an increase in traffic flow, either of all vehicles or segregated (cars vs. trucks). Similarly, the regression coefficients β_rad and β_CCC can be interpreted as speed slope factors, which describe the change in BC levels due to a change in vehicle speed (if flow remains constant). Both the β_rad and β_CCC coefficients were multiplied by ${\overline{Q}}_{tot}$ to improve comparability between sites with different mean flows, where for Sites A and B ${\overline{Q}}_{tot}$ was derived from our radar measurements while for Site C the DOT estimate was used. Units of β_rad and β_CCC are chosen such that the numerical value represents the change in BC levels in units of μg/m³ if the vehicle speed changes by 10 mph and CCC changes by 1, respectively, for a traffic flow of 100 vehicles per hour.

The regression models account explicitly for meteorological variables through the Met(t) term, because meteorological conditions could potentially confound the relationship the relationship between BC levels and CCC, which would in turn lead to biased estimates of the traffic-related regression coefficients. Furthermore, even if meteorological variables do not confound the CCC–BC association,^48,49 including them in the regression model can help account for some of the error variance, and doing so can increase the precision of the parameter estimates for the traffic-related regression coefficients. Similar to previous studies on TRAP,^22,50,51 we assumed that the Met. term could be represented by the following linear model:

$$\text{Met}(t)={\gamma }_{H}H+{\gamma }_{\text{WS}}\text{WS}+{\gamma }_{T}T+{\gamma }_{\text{RH}}\text{RH}+{\gamma }_{\text{PD}}\text{PD}+{{\sum }_i{\gamma }_{\text{WD},i}\text{WD}}_i$$ (7)

where H is the height of the mixing layer, WS is wind speed, T is temperature, RH is relative humidity, PD is precipitation depth, and WD_i is a categorical wind direction. T and RH are accounted for, because they affect the size distribution of vehicle exhaust particles and hence their subsequent fate in the atmospheric environment.⁵² Precipitation was accounted for, because it may affect traffic density and BC levels through washout of air particulate matter.⁵³ Wind speed WS was accounted for, because it affects atmospheric dispersion of BC. Wind direction was accounted for because it can affect TRAP.^54–56 Continuous meteorological variables were excluded from a regression specified by site ID (A, B, C) and model number (1, 2, …, 6) if their significance levels were >0.05. The categorical predictor variable WD was excluded if an ANOVA test showed that regressions results obtained with and without WD did not differ from one another at a level >=0.05.

Unmeasured confounding factors such as vehicle BC emissions from roads surrounding each site, maritime traffic, domestic and industrial sources, and wider urban BC inputs are accounted for by the penalized spline s(t). We examined the dependence of the regression coefficients on the number of knots in the spline function s(t) used to represent contributions from these additional BC sources. To illustrate the temporal variations of these contributions, we determined for each site “background” BC levels, which we define here as the levels that would occur if traffic at the site was not present or constant. These levels can be predicted with the fitted regression model by setting the flows to zero (Q_tot = Q_tr = Q_car = 0), vehicle speed variables (RS, CCC) to their medians, and maintaining the values of meteorological prediction variables.

GAM models generally assume that errors are mutually independent, which is not necessarily true. Due to expected autocorrelation in the time series of the model residuals,²² our regressions accounted for autoregressive (AR) errors. The AR(1) model was accounted for by the “bam” regression routine (R’s mgcv library); bam requires specifying a correlation parameter “rho” which we estimated from the lag-1 autocorrelation of the time series of model residuals obtained by first running a regression without accounting for AR errors. Moreover, we performed regressions using mgcv’s “gamm” routine which can account for AR(n) models. Unlike bam, gamm does not require specifying correlation parameters. We performed regressions for lag n up to 3. Since our measured time series were interrupted (e.g., due to data downloads from the monitors or equipment failures), the autocorrelation analyses excluded these data gaps.

We compared the bam regression routine, which accounts for AR(1) errors, to the gamm routine, which can account for AR(n) errors. For the gamm routine, we found that the autocorrelation between model residuals decreased substantially for increasing values of n. However, background BC levels could not be represented by the spline s(t) in a meaningful way. Even though we started the regression with 1 knot per measurement day, the final estimated degree of freedom (EDF) of the spline s(t) was very small, much less than 10, for n >= 2 close to 1. Therefore, the gamm regression could not account for confounding factors. At the same time, the explained variation R² was very small and decreased with increasing order n, e.g., to 1% for n = 3. In contrast, the bam routine substantially reduced the autocorrelation of model residuals while retaining the capability of modeling confounding background BC levels. Our findings are consistent with the mgcv documentation (page 90 in⁵⁷) which states that gamm is not quite as numerically robust as gam (bam being a variation of gam). We therefore used the bam routine in the final regressions.

For the spline function s(t), we chose a number of knots for which the regression coefficients for the traffic variables did not markedly change.⁵⁸ This was fulfilled for 1 spline knot per day of data collection. Thus BC variations due to diurnal variations in traffic and meteorological conditions were not smoothed out. To support our choice, we varied the number of knots for each final regression (with insignificant meteorological regression variables removed) and examined the dependence of regression coefficients on the EDF of s(t).

Analyses were conducted using the R Statistical Software, version 3.4.3 (Foundation for Statistical Computing, Vienna, Austria).

3. RESULTS

3.1. Illustration of traffic data

Figure 1a shows an example of one of the crowd-sourced maps we downloaded every minute. Using these data, time series of the congestion color code CCC can be developed for the entire street network shown in the map. In this work, we only analyzed traffic at the three locations with aethalometers. Figure 1b shows the times series of CCC for Site B collected in July 2017, a subset of all data collected. Diurnal fluctuations in traffic conditions as well as differences between weekdays and weekends can be easily discerned with this type of plot that synthesizes the crowd-sourced traffic data for a single road segment.

3.2. Temporal variations

Figure 2 shows average traffic flow and BC levels versus the hour of the day, stratified by weekdays and weekends. At the two sites where radar measurements were performed (Sites A and B), total traffic flow Q_tot peaked at about 6–7 am and 3–4 pm on weekdays, the rush hours. Truck flow Q_tr peaked from 4–8 am and from 2–3 pm with truck flow having been higher in the afternoon rush hour. On weekends, traffic was overall less, particularly truck traffic.

Figure 2:

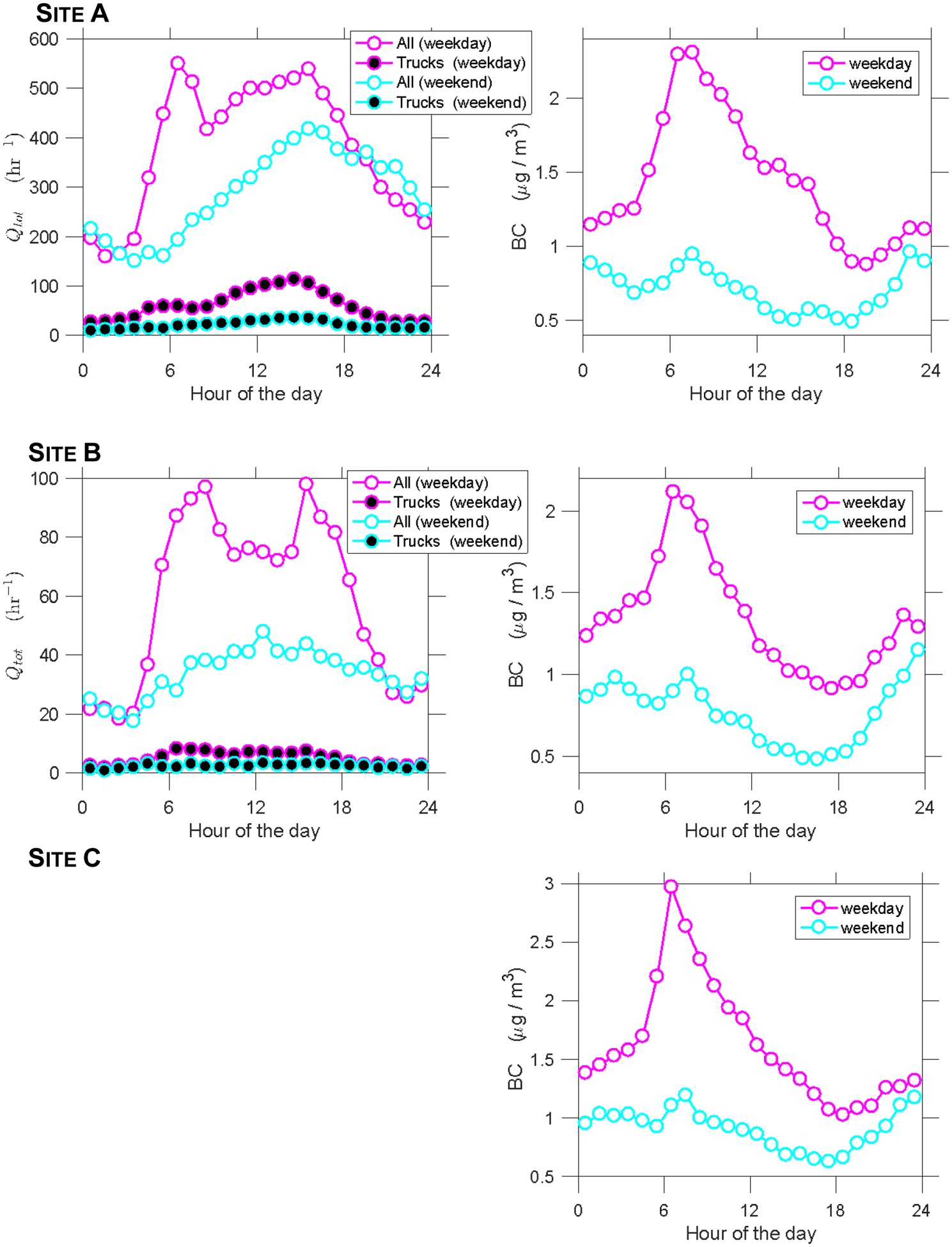
Hourly averages of radar-derived traffic flow and BC levels across the entire sampling period at the three sites. Lines connect the 1-hour averages (symbols) and do not have a physical meaning.

BC levels did not entirely follow traffic flow. At all three sites, BC levels peaked in the morning between 6–8 am, the time window in which total vehicle and truck flows peaked at Sites A and B. However, BC levels did not peak during the afternoon rush hour. Instead, BC levels decreased almost monotonically after 8 am, even though traffic picked up at 9 am at Sites A and B. Only after 6 pm did BC levels increase again.

To examine potential correlations between BC peaks and short-term traffic increases, we show in Figure A.3 sample BC levels and vehicle flows versus time. The plots reflect features of the average diurnal data from Figure 2. BC levels rose in the early morning when traffic picked up and then decreased until 6 pm, even though traffic remained about constant until 6 pm. BC peaks were not always accompanied by peaks in traffic flow. For instance at Site A, the maximum BC level was observed at 10 am. At Site B, BC levels rose in the early morning when traffic picked up and then decreased until about 4 pm. At that point in time, BC levels increased about 1.5-fold, and total traffic flow peaked at the same time. However, BC peaks are again not always associated with traffic flow peaks, e.g., at 7 am.

The lag between congestion color code CCC and radar speed RS was t_lag = 4 minutes at Site A and t_lag = 2 minutes at Site B.

3.3. Relationships between traffic variables

• Site A: Figure 3a shows the four box plots for the four distributions of radar speed RS for all those 15-min observational windows when the rounded color code CCC was 1, 2, 3 and 4. Color code CCC = 5 was not observed. The median vehicle speed is a strictly monotonically increasing function of CCC and the IQRs almost non-overlap. Figure 3c illustrates the distributions of vehicle flow for the four rounded congestion color codes CCC. Median traffic flow was maximum for CCC = 3. Traffic flow decreased monotonically when CCC decreased from 3 to 2 and then to 1. Figure 3e shows the distribution of vehicle flow when the radar-derived vehicle speed RS fell into the five equal-width bins between the minimum and maximum observed radar speed. The relationship resembles the one between vehicle flow and CCC (Figure 3c), because RS is a proxy for CCC.

• Site B: For the most part, the median radar speed RS increases monotonically with CCC, except from CCC = 1 to 2 (Figure 3b); however, the overlapping notches indicate that the observed decrease is statistically not significant. Moving from CCC = 2 to 4, the rate of increase is quite small. The relationships between measured vehicle speeds, i.e., either radar speed RS or color code CCC, and vehicle flow (Figures 3d and 3f) resemble those of Site A. Traffic flow is highest for intermediate vehicle speeds. However, median vehicles speeds for the five CCC values were much lower than at Site A.

Figure 3:

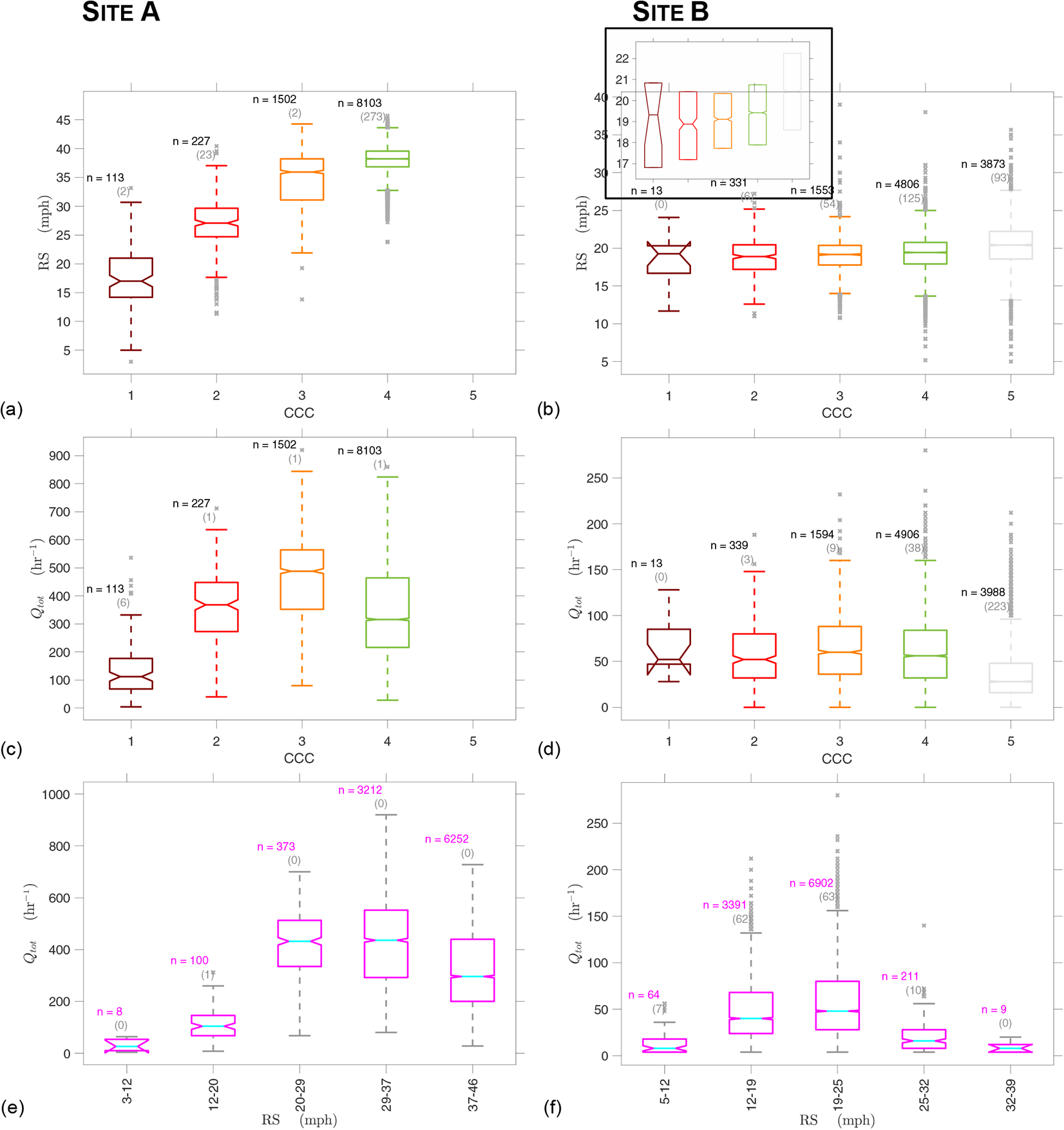
Relationships among various measures of traffic conditions at Sites A and B. All variable represent 15-minute averages. n-Values above upper whiskers indicate the number of data points used to calculate the boxplot. The parenthesized number underneath indicates the number of outliers. To illustrate better trends in median RS levels in subfigure b, we show boxplots both with and without outliers (in a smaller boxplot within the one with outliers).

3.4. Relationships between black carbon and single traffic variables

• Site A: Figure 4a shows the five boxplots for the distribution of BC levels observed when total vehicle flows Q_tot fell into the five vehicle flow bins between the minimum and maximum of Q_tot. Median BC levels increase monotonically with traffic flow, i.e., on average more traffic as quantified by traffic flow results in higher TRAP. Figure 4c shows five boxplots for the distribution of BC levels observed when radar speed was divided into five equal-width bins between the minimum and maximum observed speed. Median BC levels decrease monotonically as radar speed RS increases. Figure 4e reflects the findings from Figure 4c if one replaces in the discussion RS by its proxy CCC.

• Site B: BC levels tended to increase monotonically with total vehicle flow Q_tot, except for the 4^th Q_tot bin, for which BC levels are smaller than for the 3^rd and 5^th bin (Figure 4b). Due to the small sample size (n=3), it is not clear whether the 5^th bin has higher BC levels than the third bin. Median BC levels tend to increase with radar-derived vehicle speed, even though overlapping notches indicate that the increase may not be statistically significant for the first four radar speed bins (Figures 4d). And BC levels appear to be highest for the highest radar-speed bin (the notches of the 4^th and 5^th bins almost overlap reducing the statistical significance of the difference). Similarly, BC levels are higher for CCC = 5 than for 3 and 4 (Figures 4f). Interestingly, BC levels are highest for CCC=1 but lowest for the 1^st radar-speed bin.

• Site C: BC levels reflect features from Site A in that median levels decrease with CCC and that CCC = 5 was not observed (Figure 4g).

Figure 4:

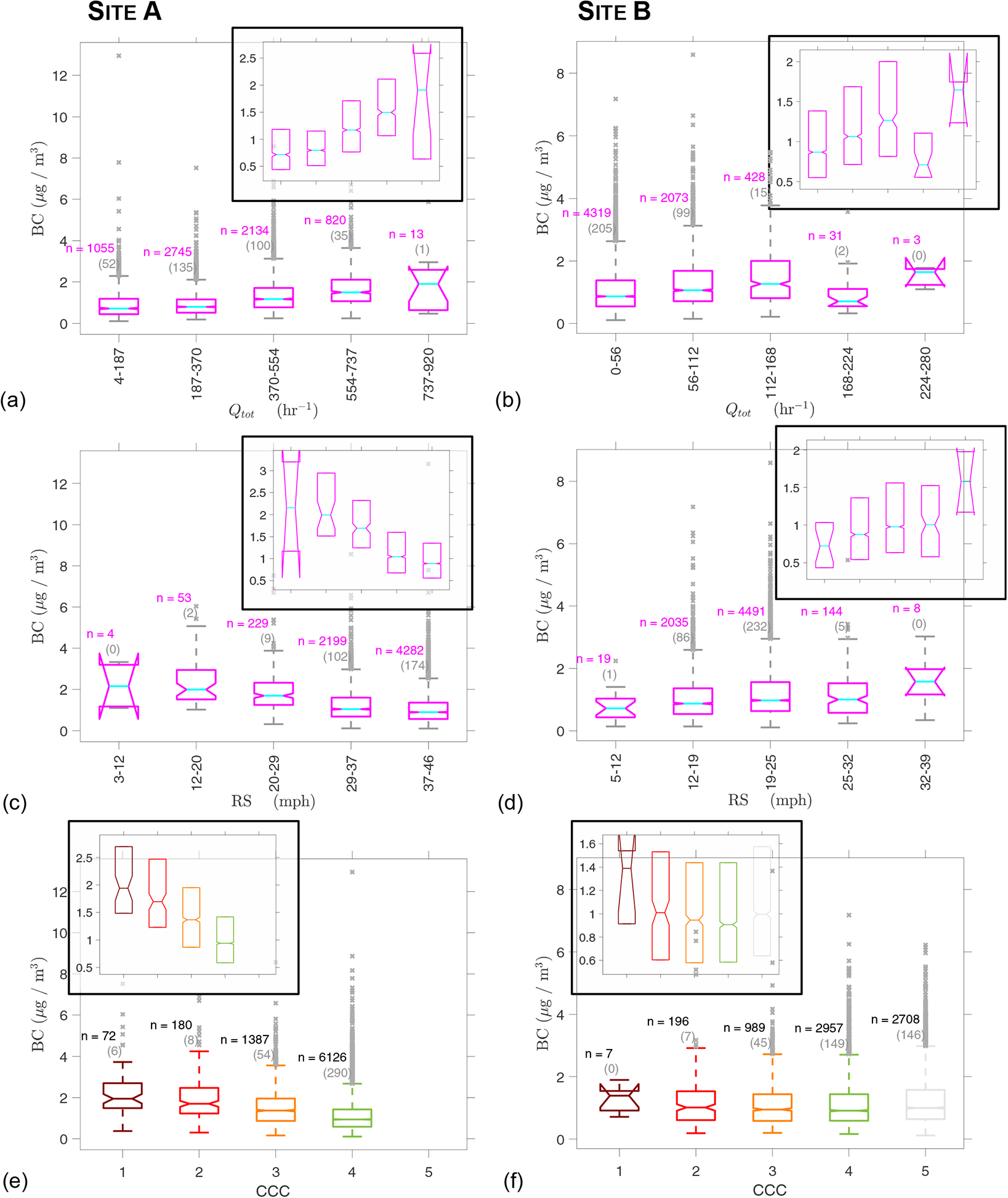
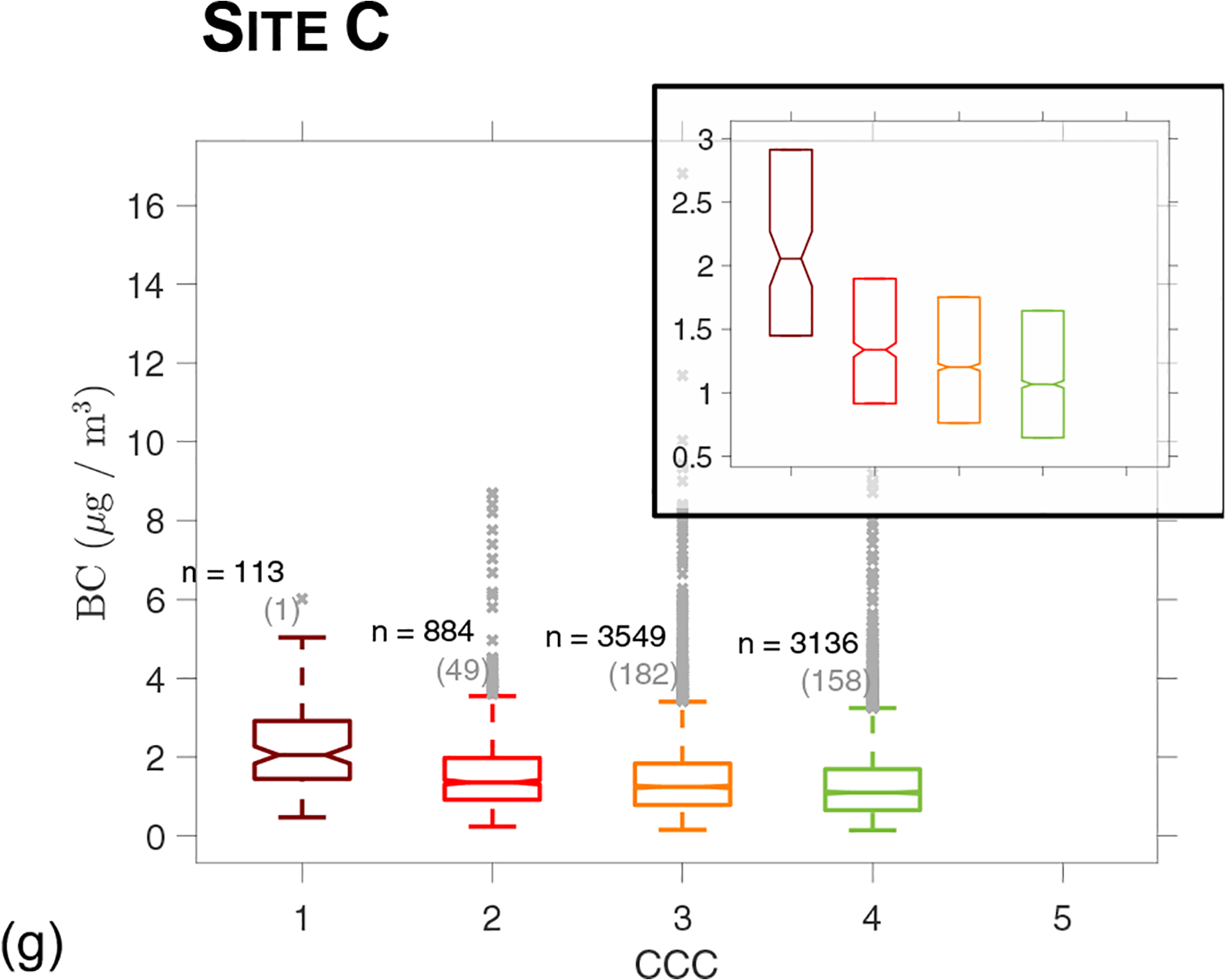
Dependencies of BC levels on various measures of traffic (traffic flow Q_tot, radar-derived vehicle speed RS, congestion color code CCC) at Sites A and B. To illustrate better trends in median BC levels, we show boxplots both with and without outliers (in a smaller boxplot within the one with outliers). Figure to be continued on next page to report results for Site C.

3.5. Regression analyses for black carbon

The regressions for Sites A and B that accounted for temporally resolved radar-derived traffic flows (Models 1 to 4) yielded similar results. The regression coefficients for the flows are all highly significant (p < 0.001) and positive, i.e., additional traffic flow causes BC levels to increase. Moreover, for each site the α_tot coefficients fitted for Models 2 to 4 are similar in that their confidence intervals overlap. Furthermore, for each model (1 to 4), regression coefficients obtained for each of the two sites are similar as their confidence intervals overlap. At both sites, emission factors are about 3 to 4 times higher for trucks than for cars. For Site A, accounting for segregated traffic flow yields an R² value that is 0.8% higher as a comparison of Models 1 and 2 shows. For Site B, accounting for segregated flows did not result in an improved model fit. Another important difference between Sites A and B is that for Site A regression coefficients for vehicle speed as quantified either by RS or CCC are all highly significant and negative; i.e., an increase in vehicle speed (with traffic flow being held constant) causes BC levels to drop. For Site B, however, only for Model 3 BC levels depend moderately (p < 0.1) on CCC.

For the regression that used ${\overline{Q}}_{tot}$CCC as the sole traffic-related predictor variable (Model 5), the β_CCC coefficient for Site A was highly significant (p < 0.001). For Site C, β_CCC was marginally significant (p < 0.1), whereas for Site B; β_CCC was not significant (p = 0.14). The confidence intervals of the β_CCC of Sites A and B overlap. The absolute value of the predicted β_CCC coefficient for Site C is about 10 times lower than absolute values for Sites A and B.

The R² values as well as the variation explained by traffic predictor variables, R_tr², were generally higher for the regressions that accounted for time-dependent traffic flows (Model 1 to 4) than for those that accounted only for a speed variable (Model 5 and 6). For any regression, only 3 out of the 6 meteorological variables were significant predictor variables (Table A.1). At all sites, relative humidity RH and wind direction WD were significant predictors. The fact that WD is a significant predictor variable is supported by the BC roses for the three sites, as the roses show an uneven distribution of the highest BC levels among the eight wind directions (Figure A.5). At Sites A and C, wind speed WS was the third predictor, while at Site B it was mixing height H. Use of either WS or H can be attributed to co-linearity between the two variables that we observed for the three sites during the measurement campaign. We note that regression coefficients including confidence intervals of the traffic predictor variables changed only marginally when regressions for Site B were ran using WS instead of H as a predictor variable. However, since then R_tr² decreased, we preferred to determine the meteorological predictor variables by iteratively removing the most insignificant ones.

Background BC levels were similar for the three sites as illustrated for Model 6 (Figure 5). Pearson correlation coefficients between background BC levels for different sites are r = 0.88 between Sites A and B, 0.94 between Sites A and C, 0.91 between Sites B and C.

Figure 5:

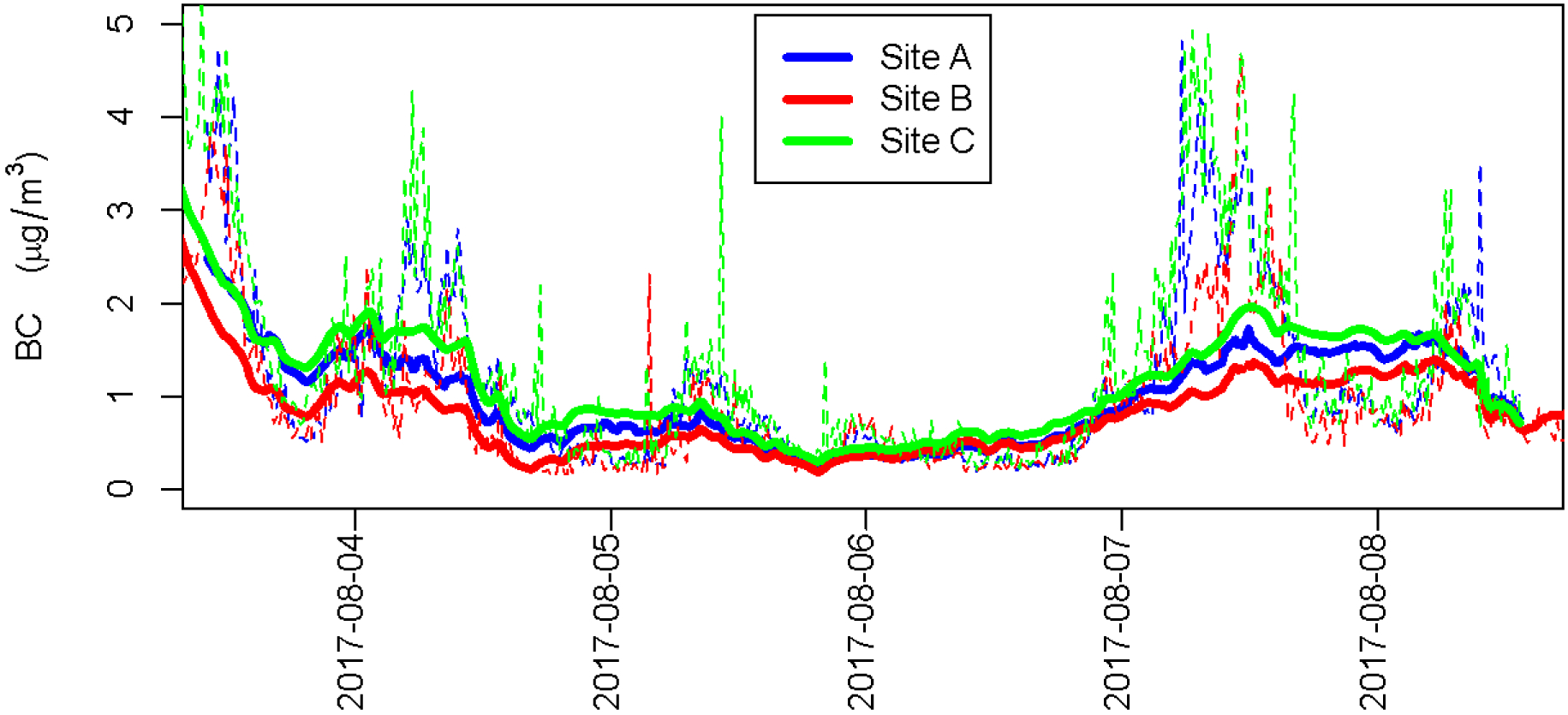
Illustration of modeled background BC levels (thick solid lines) for the traffic model according to Eq. 6 for a 6-day long subset of the data. Thin dashed lines represent measured BC data (15-minute averages).

To better characterize the BC – CCC relationship and assess potential deviations from linearity, we also ran regressions that allowed BC levels to depend on CCC through a smooth function s. To support the choice of model, we compared AIC scores⁵⁹ of the linear and nonlinear regressions. For all three sites, AIC scores of the linear and nonlinear regressions were almost the same. We therefore found no evidence that these nonlinear terms, the parameters of which are also harder to interpret than the speed slope factor β_CCC we suggest, improve the fit of our models.

We also performed sensitivity analyses to assess the usefulness of accounting for meteorological co-variates. For regressions that did not account for meteorological variables, absolute values of traffic-related regression coefficients were in most cases slightly smaller suggesting bias due to confounding. Moreover both R² and R_tr² decreased significantly. Thus we only present results of regressions that account for meteorological variables.

4. DISCUSSION

4.1. Associations between two traffic variables

Congestion color code CCC was found to increase with radar-derived vehicle speed RS. For Site A, the IQRs of the four box plots are almost non-overlapping, strongly suggesting that CCC is a proxy for vehicle speed. Complete non-overlap between the IQRs cannot be expected, because the traffic maps use smartphone data along the entire road segment, while the radar device provides more of a point measurement of vehicle speed RS. At Site B, the IQRs of RS overlap significantly for adjacent CCC values; however, a multi-comparison test of radar speeds measured for the different CCC values showed that there significant differences in radar speed between different CCC values (with 4 out of the 10 possible comparisons at significance levels p < 0.05). One possible explanation is again related to the fact that radar speed is measured at only one location contrary to CCC. The road segment at Site B lends itself to particularly non-uniform vehicle speed, because it ends at a “T” intersection, where vehicles need to decelerate to make either a left or right turn.

At Sites A and B, traffic flow Q_tot was on average highest for intermediate vehicle speeds, either quantified by RS or CCC. Flow decreased when the highest observed CCC value was approached, likely because smaller flow (indicating a lower traffic density) allows for higher vehicle speed. Maximum flow for intermediate vehicle speeds has also been observed in a study of freeway traffic⁶⁰ and is consistent with speed-flow curves known from traffic engineering.⁶¹ Moreover, the observation that traffic flow decreases monotonically as CCC approaches 1 is consistent with the theoretical argument that in the limit where the vehicle speed is zero, flow is zero. Contrary to Site B, CCC = 5 was not observed for Site A, likely because the ramp feeds vehicles from an interstate carrying traffic around the clock into a highly populated residential area and a large industrial complex at the South Bronx waterfront.

At Site B, most of the lowest radar speeds (defined here as < 10 mph) were measured when CCC = 4 and 5 (and not when CCC = 1 to 3) and are in the box plots represented by outliers. The transition from CCC = 4 to 5 (green to gray) appears to be associated with an apparently discontinuous jump in vehicle velocity. This jump might be due to the absence of crowd-sourced traffic data when CCC = 5.

While general trends in the relationships between CCC, RS and Q_tot are similar for Sites A and B, the relationships vary dramatically in magnitude indicating local calibration of crowd-sourced traffic data is needed. At Site B, CCC values are associated with smaller vehicle speeds when compared to Site A, likely because at Site B vehicles slowed down when they approached the T-intersection (Figure A.1). Mapping of vehicle speed on CCC is likely related to the maximum achievable speed.

4.2. Temporal BC variations

Diurnal variations in BC are similar for the three sites, with BC levels being high in morning rush hour and much lower in the afternoon rush hour, even though traffic counts are similar in both rush hours (Figure 2). Therefore, traffic conditions do not explain all the variation in BC levels. Likely, temporal variations in BC levels are affected by diurnal variations in meteorological conditions, e.g., increased wind speed peaking in the late afternoon (Figure A.4a).

BC spikes observed for a 5-min observational window were not always associated with increases in flow (Figure A.3). This could potentially be due to emission-rich vehicles or unresolved changes in meteorological conditions (at time scales < 1 hr), e.g., sudden periods of low wind speed and sudden changes in wind direction.

At the two sites, changes in CCC lagged 2 and 4 minutes behind changes in radar speed RS suggesting that traffic provider’s maps are broadcasted with some delay, perhaps because it takes some time to process the collected GPS data or because their algorithms are based on temporal averages of GPS data. This finding also suggests that associations between CCC and other variables should be examined for observational windows greater than the lag, e.g., 15 min, unless the CCC data is shifted in time.

4.3. Associations between BC levels and single traffic variables

Examination of associations between BC levels and one traffic variable suggests that more traffic as quantified by flow tended to cause an increase in BC levels (Figures 4a/b) and that vehicle speed might have also affected BC levels. BC levels do not approach a value of zero as Q_tot approaches zero due to BC background levels, e.g., from adjacent roads and wider urban sources, which can be expected to be confounding factors.

At Site A, median BC levels decreased as radar speed RS increased (Figure 4c) and also as CCC increased (Figure 4e). Based on field observations, we believe that vehicles were most of the time slow not because drivers elected to drive slow but because there was a lot of traffic and/or congestion. This could suggest that small vehicle speeds, being a proxy for congestion, caused higher BC levels due to repeated acceleration-related emissions.

At Site B, BC levels were higher for CCC = 5 than for 3 and 4 (Figure 4f). This seems counterintuitive, because CCC = 5 indicates that not many vehicles were present, which should result in only little BC emissions. One potential explanation is related to the fact that CCC = 5 was typically observed at night (Figure 1b) when the atmosphere tended to be stable causing air pollution to be higher, which is also seen in the diurnal variations in BC levels (Figure 2). I.e., the relationship between BC and vehicle speed is confounded by meteorological conditions. This illustrates the utility of crowd-sourced traffic data in the interpretation of air pollution data. However, other factors could have contributed to the higher night-time BC levels, potentially related to non-traffic BC sources.

At Site B, an apparent inconsistency occurs as BC levels are highest for CCC=1 but lowest for the 1^st radar-speed bin. This could be attributed to the small sample sizes (n=7 for CCC and n=19 for RS), which do not support the conclusion that BC was higher for CCC=1 than for CCC=2. Moreover, the entire range of radar speeds associated with CCC=1 (12–24 mph according to Figure 3b) does not correspond to the range of the lowest RS bin (5–12 mph according to Figure 4d). In fact, most of these small vehicle speeds were measured when CCC=4 and 5, represented by the outliers in Figure 3b, i.e., when traffic was flowing freely according to the traffic maps. The smallest vehicle speeds could therefore potentially be attributed to drivers who elected to drive slow, perhaps drivers of very large, emission-rich trucks who needed to slow down before approaching the T-intersection.

4.4. Regression analyses

To explore associations between measured BC levels and combinations of traffic variables, we fitted regression models to the measured BC-traffic data that contrary to the associations discussed above addressed confounding by modeling directly potentially confounding meteorological predictor variables and by including a slowly varying spline to represent vehicle emissions from roads surrounding our sites as well as wider urban BC levels. We note that not accounting for a confounding variable can result in biased estimates of regression coefficients.

The similarity of background BC levels at the three sites (Figure 5) as well as the high correlation coefficients between background levels of different sites provides confidence in our modeling approach of confounding background BC levels. Note that perfect agreement of background BC levels cannot be expected because of the nonuniform distribution of the other BC sources. The impact of immediately adjacent traffic is seen in the spiky measured BC data as also seen in a study of BC emissions from aircraft traffic.⁵⁵

For both Sites A and B, the regression coefficients for traffic flow predictor variables (α_car, α_tr, and α_tot) are positive, i.e., traffic flow causes BC levels to rise. Moreover, the values of α_car, α_tr, and α_tot were similar between the two sites. Note, however, that such agreement cannot be expected, because our statistical model does not account for important site characteristics. E.g., the air pollution monitor at Site B was mounted on a rooftop, while it was mounted through a third-floor double hung window at Site A.

At Site A, the association for BC-levels becomes stronger if segregated traffic counts are accounted for, with the variation explained by traffic predictor variables, R_tr², being 0.8% higher for Model 1 than Model 2 (Table 1). At Site B, R_tr² is about the same for Models 1 and 2. This can be explained by the hourly ratio of truck counts vs. total vehicle counts (Q_tr / Q_tot) which is relatively constant for Site B but not so for Site A (data not shown). In any instance, regression analysis of segregated traffic flows yields the mobile-source contributions for cars and trucks, α_car and α_tr, respectively. This information allows policy makers and communities to assess impacts of changes in truck or car traffic on air pollution and community health.

Table 1:

Summary of regression analyses for ln(BC) levels at the three sites (meteorological parameters are shown in Table A.1). Confidence intervals are given in parentheses. The highlighted cells emphasize the major findings that BC levels can be predicted from CCC and average traffic flow.

ln(BC)-traffic model	αtot [μg/m3 per 100 vehic/hr]	αtr [μg/m3 per 100 trucks/hr]	αcar [μg/m3 per 100 cars/hr]	βrad [μg/m3 per 10 mph & 100 veh/hr]	βCCC [μg/m3 per CCC &100 veh/hr]	R2 [%]	Rtr2 [%]
Site A
$Q_{tr}+Q_{car}+{\overline{Q}}_{tot}\text{RS}$	–	0.15*** (0.13, 0.18)	0. 04*** (0.03, 0.05)	−0.05*** (−0.06, −0.04)	–	66.0	9.2
$Q_{tot}+{\overline{Q}}_{tot}\text{RS}$	0.05*** (0.04, 0.06)	–	–	−0.05*** (−0.05, −0.04)	–	65.2	8.4
$Q_{tot}+{\overline{Q}}_{tot}\text{CCC}$	0.06*** (0.05, 0.07)	–	–	–	−0.031*** (−0.036, −0.025)	65.5	8.7
$Q_{tot}$	0.05*** (0.05, 0.06)	–	–	–	–	62.7	5.9
${\overline{Q}}_{tot}\text{RS}$	–	–	–	−0.05*** (−0.05, −0.04)	–	60.1	3.3
${\overline{Q}}_{tot}\text{CCC}$	–	–	–	–	−0.023*** (−0.028, −0.018)	59.3	2.5
Site B
$Q_{tr}+Q_{car}+{\overline{Q}}_{tot}\text{RS}$	–	0.21*** (0.10, 0.31)	0.06*** (0.03, 0.08)	0.00 (−0.04, 0.04)	–	65.3	1.1
$Q_{tot}+{\overline{Q}}_{tot}\text{RS}$	0.07*** (0.04, 0.09)	–	–	0.01 (−0.03, 0.05)	–	65.3	1.1
$Q_{tot}+{\overline{Q}}_{tot}\text{CCC}$	0.07*** (0.04, 0.09)	–	–	–	−0.025. (−0.052, 0.003)	65.4	1.2
$Q_{tot}$	0.07*** (0.04, 0.09)	–	–	–	–	65.3	1.1
${\overline{Q}}_{tot}\text{RS}$	–	–	–	0.01 (−0.03, 0.05)	–	64.2	0.0
${\overline{Q}}_{tot}\text{CCC}$	–	–	–	–	−0.022 (−0.051, 0.006)	64.1	0.2
Site C
${\overline{Q}}_{tot}\text{CCC}$	–	–	–	–	−0.004. (−0.008, 0.000)	58.6	0.8

Significance codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Only at Site A, regression coefficients for vehicle speed (β’s) are highly significant. Moreover, they are negative, i.e., a decrease in vehicle speed causes BC levels to increase if traffic flow is kept constant, presumably due to congestion (higher vehicle density). Site C shows similar trends as Site A, however, with a much lower p-value (< 0.1). Moreover, the absolute value of β_CCC is about a factor of 5 smaller at Site C than at Site A. This is potentially caused by the greater distance between the air pollution monitor and the road at Site C, thereby also weakening the correlation between traffic and BC levels.

At Site B, vehicle speed is a much less significant predictor variable. Only for Model 3, which also uses transient traffic flow Q_tot as a predictor variable, CCC is of moderate significance (p < 0.1). The other four vehicle-speed dependent regression models do not show a significant dependence of BC levels on vehicle speed (at p < 0.1 level). This may be due to the fact that BC levels at Site B did indeed not depend on vehicle speed. This conjecture is supported by the fact that traffic flow depends much more on radar speed at Site A than at Site B as a comparison between Figures 3c and 3d shows. Thus vehicle speed and CCC were not affected much by congestion but rather by the fact that vehicles needed to decelerate as they approached a T-intersection at the end of the block to then make a left or right turn. It is interesting to note, however, that predicted values for β_CCC are very similar for Sites A and B: −0.023 and −0.022 μg/m³ per 100 veh/hr. This is consistent with similar values for α_tot for the two sites.

The variations explained by traffic, R_tr², might have been higher for Models 1 to 4 than those for Models 5 and 6, because time-dependent traffic flows provide a more direct measure for the actual number of emission-emitting vehicles present than a vehicle speed variable, from which one can infer flow only indirectly. The R_tr² for Model 5 relative to those for Models 1 to 4 was smaller for Site B than for Site A, perhaps because of the larger fraction of time during which no crowd-sourced traffic data was available (CCC = 5) for Site B.

In summary, only at Site A, BC levels can be inferred from the product CCC(t)${\overline{Q}}_{tot}$ at a significance level p < 0.05. At Site C, BC levels were moderately correlated with CCC(t)${\overline{Q}}_{tot}$, at a much lower significance level though (p < 0.1), potentially because the air pollution monitor at Site C was much further from the road than at Site A. At Site B, BC levels did not depend significantly on CCC(t)${\overline{Q}}_{tot}$, but it is interesting that the corresponding regression coefficient β_CCC is very similar to the one for Site A, as could be expected because regression coefficients for traffic flows are similar for the two sites. Finally, the negative speed slope factors (β’s) we found appear to consistent with results shown by Ntziachristos et al.⁶² who found NO_x emissions from passenger cars to increase when the mean vehicle speed decreased from about 47 to 6 mph (our vehicle speed regime), even though the comparison is slightly hampered by the fact that their mean vehicle speed differs from ours in that it is defined as the average vehicle speed measured during different driving cycles. We note that our models do not predict an increase of emissions with vehicle speed, which has been observed under free-flow traffic conditions;⁶³ however, these conditions were not prevalent at our monitoring sites.

4.5. Comparison to mobile-source contributions to BC levels from other studies

In 1999, Lena et al.¹⁹ performed measurements to examine the impacts of truck traffic on sidewalk level elemental carbon (EC) levels in a transportation hub in New York City. They found 1.69±0.37 μg/m³ elemental carbon (EC) per 100 large trucks/hr, which is larger than our values but measured 18 years earlier when there was a larger fraction of older and emission-richer diesel vehicles within the commercial fleet.. We found α_tr = 0.15±0.01 μg/m³ per 100 trucks/hr for Site A and α_tr = 0.21±0.05 μg/m³ per 100 trucks/hr for Site B. Furthermore, the difference may be attributed to the fact that measurements by Lena et al. were taken at the elevation of the traffic emissions, whereas ours were taken in the third floor or higher where TRAP levels can be expected to be lower to do dispersion.

Between 2002 and 2003, deCastro et al.²² performed measurements to examine the impacts of traffic on 2^nd-floor BC levels along a traffic artery in Baltimore. They found a mobile-source contribution of 66 ng/m³ of BC per 100 vehicles every 5 min (based on the traffic-air pollution model according to Eq. 4), which using our notation and units becomes α_tot = 0.006 μg/m³ per 100 vehicles/hr. The deCastro values are an order of magnitude smaller than ours, α_tot = 0.05 μg/m³ per 100 vehicles/hr for Site A and α_tot = 0.07 μg/m³ per 100 vehicles/hr for Site B. We are not certain why they observed smaller values, even though they sampled outdoor air closer to street level (2^nd-floor window) where TRAP should be higher. Seasonal effects (their study ran for one year) could potentially explain the difference.

In 2003 and 2004, Patel et al.³⁷ performed measurements to study the impacts of truck traffic on BC levels at a suburban and an urban school within the NYC metropolitan area, respectively. They found 0.62 μg/m³ per 443 trucks/hr (α_tr = 0.14 μg/m³ per 100 trucks/hr) at the urban school and 0.20 μg/m³ per 70.5 trucks/hr (α_tr = 0.28 μg/m³ per 100 trucks/hr) at the suburban school. Their values are very similar to ours.

It is encouraging that we obtained order-of-magnitude or better agreement with other studies that also quantified the mobile-source contributions to BC levels. Observed differences can be attributed to factors the regression models do not account for such as distance to roadways and elevation of the BC monitors.

4.6. Limitations

From an air pollution perspective, the study area is complex as road traffic at the three sites is not the only contribution to atmospheric BC at a site. Additional BC sources existed which did not only include traffic at surrounding roads but also domestic and industrial sources, and maritime traffic. However, an advantage of the timing of this study was that it was not performed during the heating season. Hence, little BC emissions occurred due to heating-related combustion of oil and natural gas. We represented the additional BC sources by a site-specific slowly varying function, also to reduce confounding effects of these sources on traffic-related regression coefficients. The background BC levels (predicted by assuming traffic to be constant at a site) for the three sites were similar to each other as could be expected for the relative small study area.

Ideally one would construct a mechanistic model that explicitly accounts for all pollutant (BC in our study) sources, the dispersion of air pollutants, pollutant transformation, atmospheric and pollution level boundary conditions, and topographic features causing, e.g., street canyon effects.^64,65 Due to the expense of such modeling approaches and their required inputs, we used a relatively simplistic modeling approach that is based on linear regression. However, concepts introduced in this study can potentially be incorporated into more mechanistic air pollution models based on, e.g., air dispersion modeling^66–70 or computational fluid dynamics.^71–76 For instance, CCC data that is potentially calibrated to account for road-specific traffic flows could be incorporated into traffic emissions estimation models such as HBEFA.⁷⁷ Alternatively, one could generalize the statistical model we proposed to account for distance to roadways and elevations of receptors.

5. CONCLUSIONS

Our study suggests that levels of primary air pollutants (BC in our study) can depending on traffic flow patterns and site characteristics be estimated from a model that uses radar-calibrated CCC data, i.e., the product CCC${\overline{Q}}_{tot}$ as an input. For Sites A and B, we measured the mean flows ${\overline{Q}}_{tot}$ with our own radar devices, while for Site C we estimated ${\overline{Q}}_{tot}$ from published DOT data. Indeed, for many streets ${\overline{Q}}_{tot}$ can be obtained from departments of transportation, which in the US publish Annual Average Daily Traffic (AADT) data. This opens up the possibility that BC levels can be inferred from time-dependent crowd-sourced traffic data and average vehicle flow data ${\overline{Q}}_{tot}$, which in big cities are often available.

We tested our approach at three sites, at all of which free-flow traffic conditions were typically not present due to the nearby presence of traffic lights or forced turns. This explains why the dependence of BC on vehicle speed (and CCC) could be described by a speed slope factor, i.e., a linear model. Future studies should therefore address free-flow traffic conditions, and it appears entirely possible that then the concept of speed slope factor needs to be generalized, because of the non-monotonicity of observed relationships.

Interpretation of our study is hampered by the fact that the strength of the correlation between BC levels and CCC is low for two out of the three sites. This could be due to the higher elevation of the air pollution monitors at these two sites. Future studies should therefore examine better the effects of elevation of the BC measurements. Statistical models for the mobile-source contributions to BC levels could potentially become generalizable if they accounted explicitly for site characteristics such as elevation of BC exposure. Alternatively CCC data could be used as an input into air dispersion and CFD models, which can more directly account for site characteristics and the transformation of different air pollutants.

Use of crowd-sourced traffic data offers great promise in air pollution modeling as it is inexpensive. While we only analyzed air pollution at three road segments, crowd-sourced traffic data together with AADT data yield information about traffic in entire street networks, allowing potential prediction of TRAP at the neighborhood and city scales and perhaps interpretation of air quality indices.

Appendix

A. Observational Windows

Different types of data were collected at different temporal resolution. Radar events were logged at discrete points in time when vehicles were detected, at a 1-second resolution. Data gaps of several minutes occurred when data were downloaded from the radar devices; however, these data gaps typically lasted only about 5 minutes and occurred about every 4 weeks. There were also two occasions were radar data was missing for longer periods of time, presumably because the internal memory of the radar devices overflew. Congestion color code CCC was obtained every minute. BC aethalometer data were logged every minute, except when the internal filter tape used for BC quantification advanced.

15-minute observational windows were used to examine associations between different time-dependent variables and to perform regression analyses. This period of time was deemed long enough to reduce the role of a possible time lag of the crowd-sourced traffic data and to avoid too many data points, for which no average radar speed data can be determined because of no observed traffic counts. At the same time, a 15-minute window is short enough to capture temporal variations in the data. Data acquired at a less than 15-min resolution (BC, CCC) was averaged while data acquired at a larger resolution (meteorological data) was linearly interpolated. The event-based radar data were integrated over the observational windows in order to determine traffic flows and mean vehicle speed for each window.

Figure A.1:

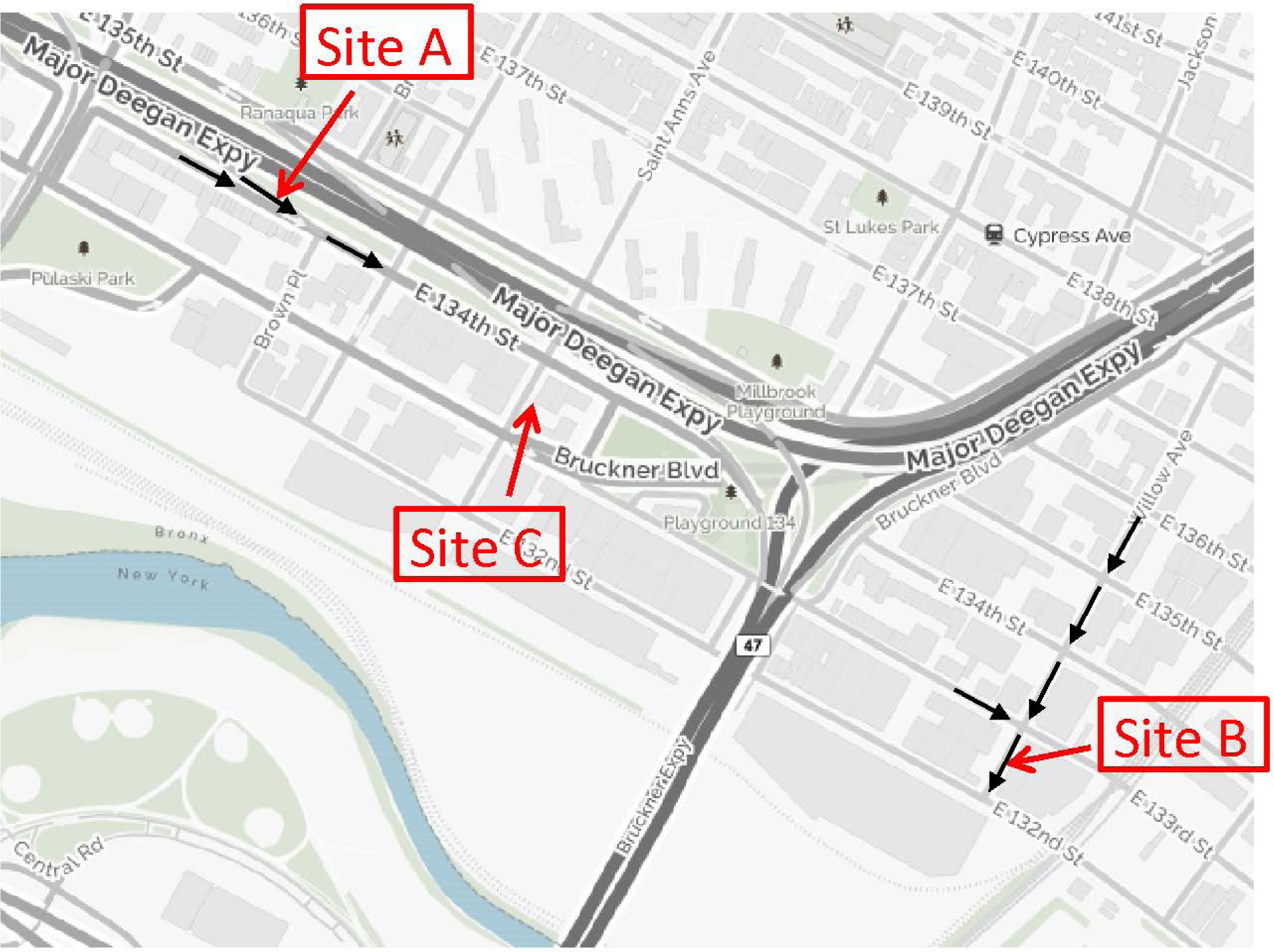
Maps of the study area. Site A is located at an (one-way) exit ramp from interstate I-87 that carries truck traffic toward the Harlem River Yard and Hunt’s point (to the East, not shown). Site B is located at a one-way street that carries truck and other vehicle traffic toward the Harlem River Yard. Site C is located at a two-way street that carries truck and other vehicle traffic toward the Harlem River Yard. Black arrows indicate the direction of traffic (shown only for selected roads).

Figure A.2:

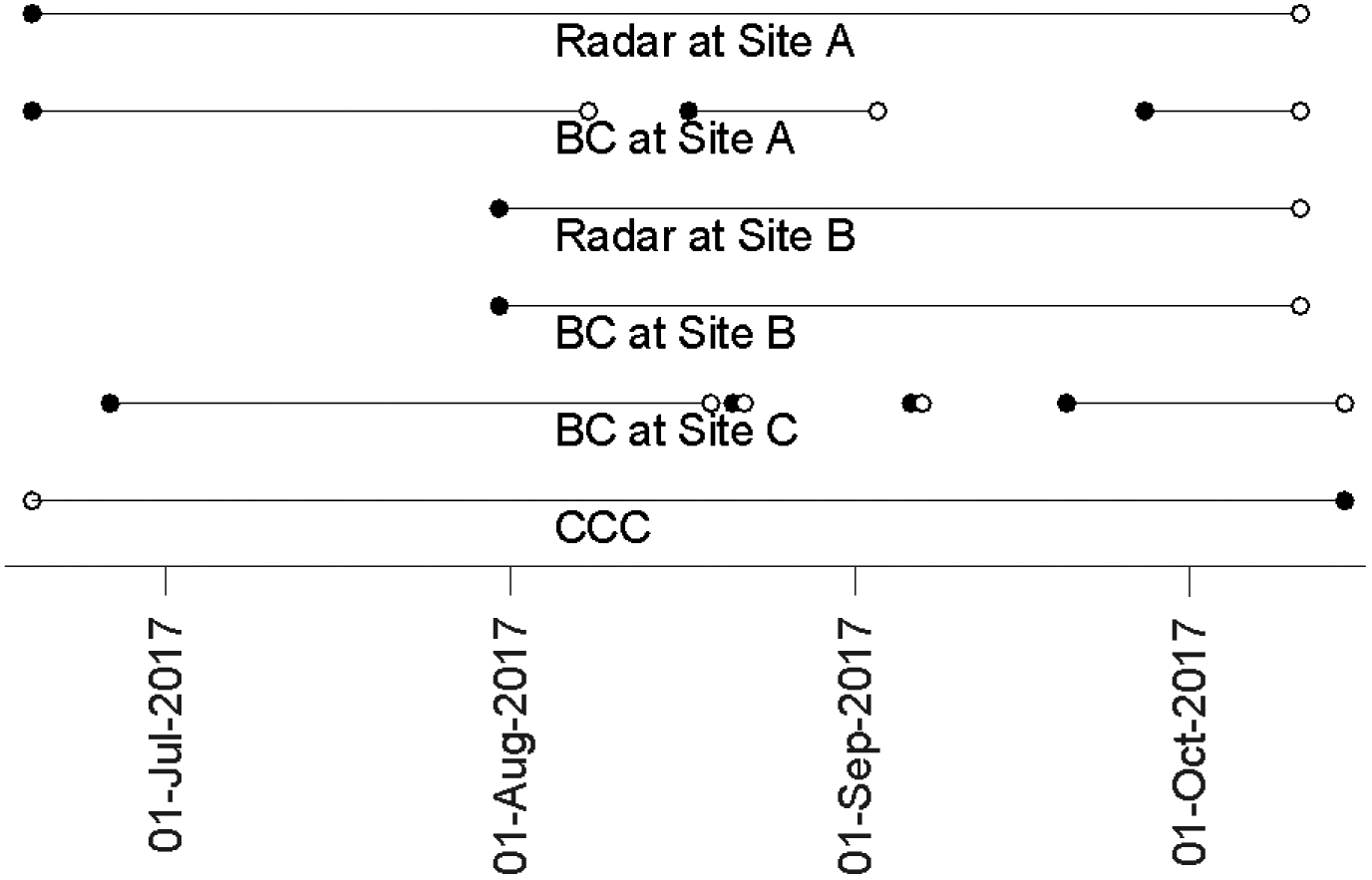
Summary of data collection. Filled and open circles indicate the beginning and end of a period of uninterrupted data collection, respectively.

Figure A.3:

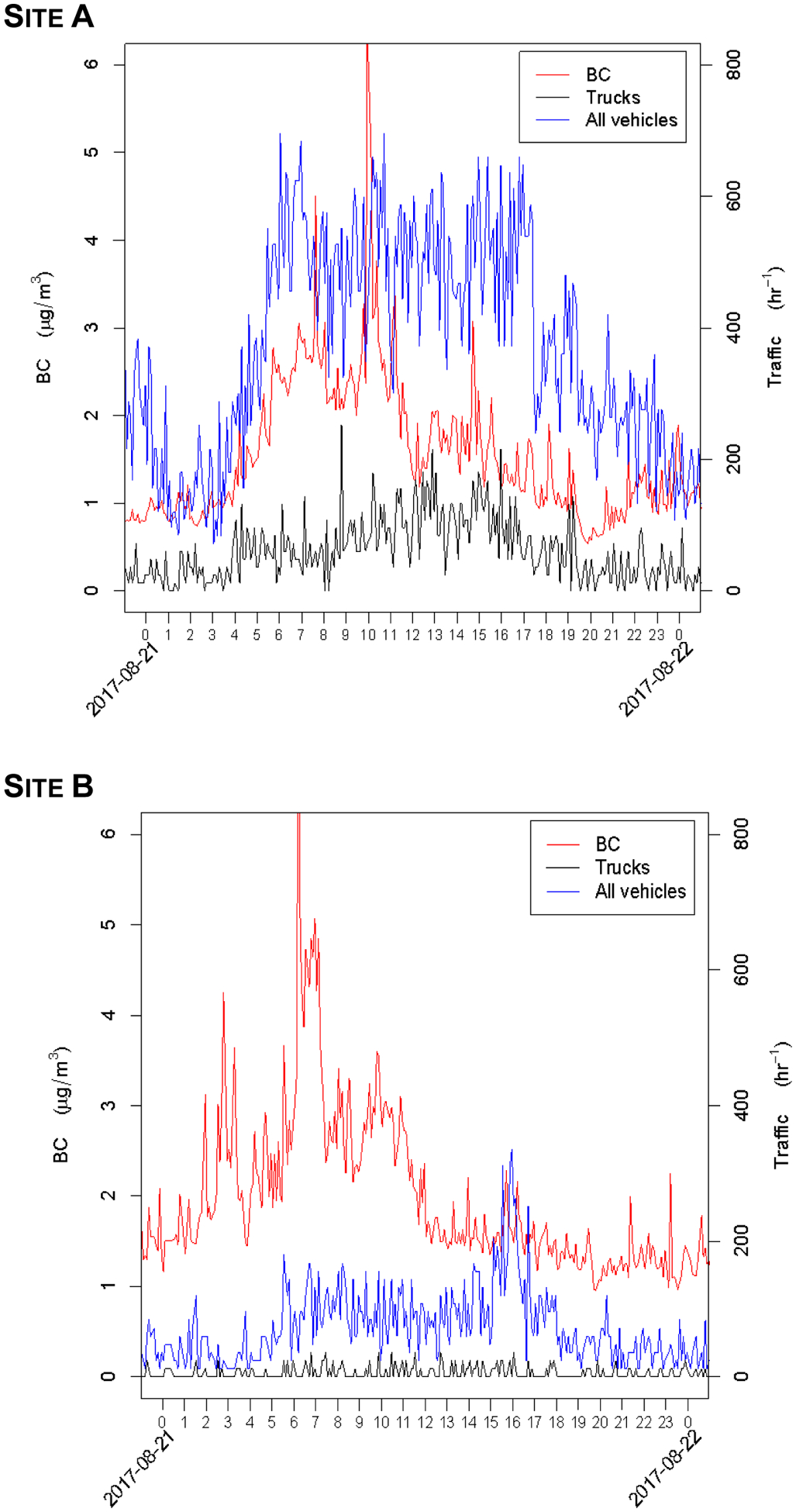
High temporal resolution times series of BC levels as well as total traffic and truck flow on August 24, 2017. A 5-min instead of a 1-min observational window was used, because for the latter, the higher variability of the flow data would conceal correlations between the different time series.

Figure A.4:

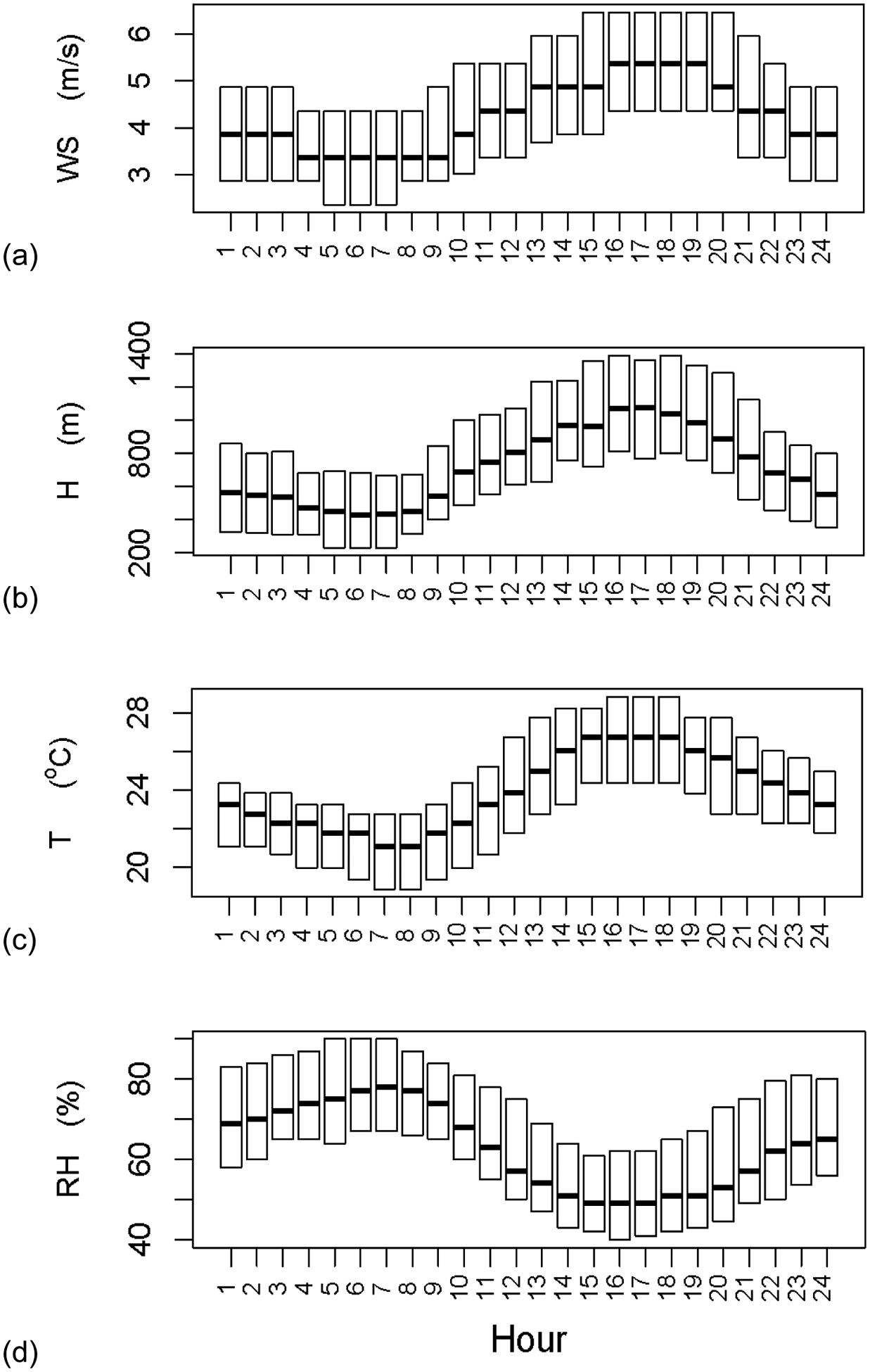
Diurnal variations of the meteorological variables, which were used in the final regressions for BC levels. WS: wind speed. H: height of mixing layer. T: temperature. RH: relative humidity.

Figure A.5:

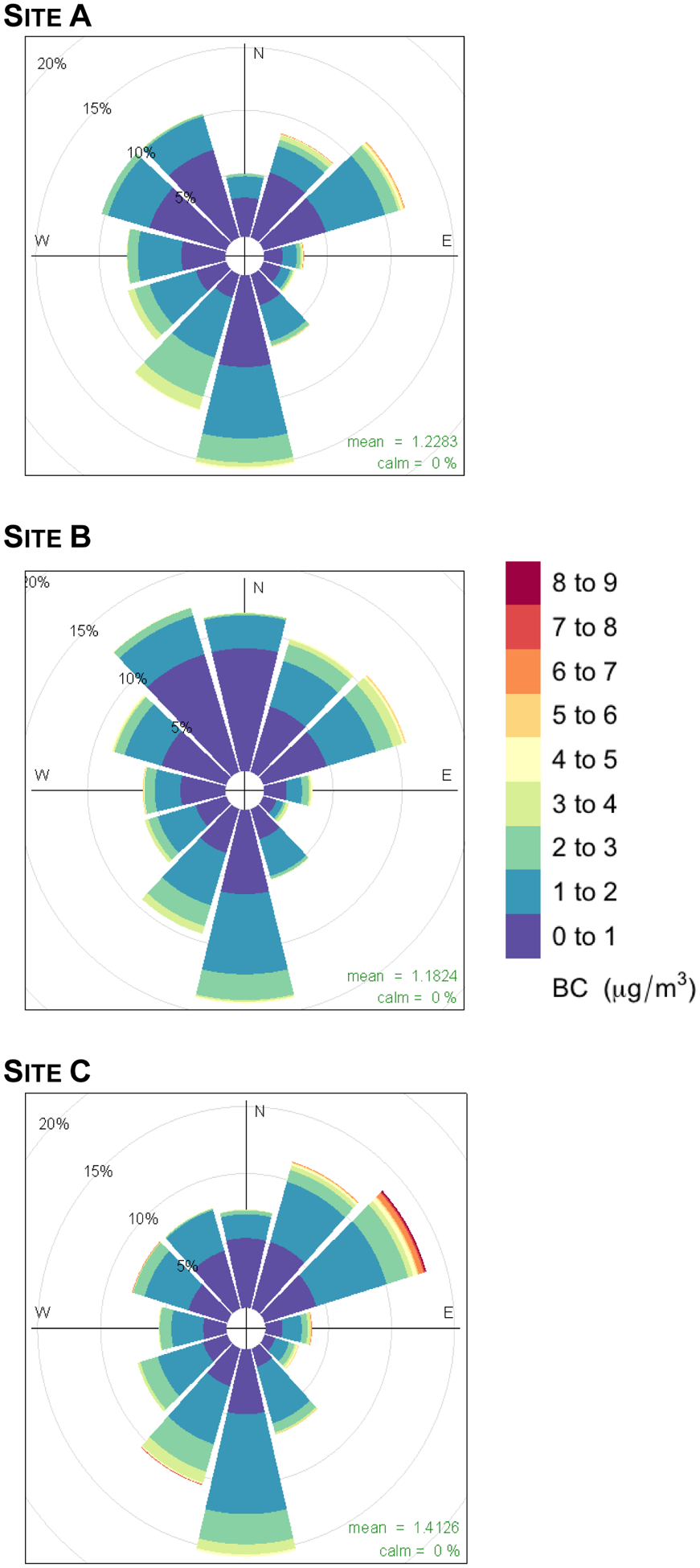
Black carbon (BC) roses for the three sites. The charts illustrate the frequency distribution of BC levels along twelve wind directions.

Table A.1:

Summary of results for meteorological predictor variables of the regression analyses for ln(BC) levels.

ln(BC)-traffic model	γH	γWS	γT	γRH	γPD	γWD
Site A
$Q_{tr}+Q_{car}+{\overline{Q}}_{tot}\text{RS}$	-	−9.5*** (−10.8, −8.3)	-	0.71*** (0.45, 0.87)	-	***
$Q_{tot}+{\overline{Q}}_{tot}\text{RS}$	-	−9.3*** (−10.6, −8.0)	-	0.67*** (0.50, 0.84)	-	***
$Q_{tot}+{\overline{Q}}_{tot}\text{GCC}$	-	−9.2*** (−10.5, −7.9)	-	0.69 *** (0.53, 0.86)	-	***
$Q_{tot}$	-	−8.9*** (−10.2, −7.5)	-	0.66*** (0.48, 0.84)	-	***
${\overline{Q}}_{tot}\text{RS}$	-	−8.1*** (−9.6, −6.6)	-	0.56*** (0.36, 0.76)	-	***
${\overline{Q}}_{tot}\text{GCC}$	-	−8.1*** (−9.5, −6.6)	-	0.54*** (0.35, 0.74)	-	***
Site B
$Q_{tr}+Q_{car}+{\overline{Q}}_{tot}\text{RS}$	−0.4*** (−0.4, −0.3)	-	-	0.99*** (0.79, 1.20)	-	***
$Q_{tot}+{\overline{Q}}_{tot}\text{RS}$	−0.4*** (−0.4, −0.3)	-	-	0.99*** (0.79, 1.20)	-	***
$Q_{tot}+{\overline{Q}}_{tot}\text{GCC}$	−0.4*** (−0.4, −0.3)	-	-	1.01*** (0.80, 1.22)	-	***
$Q_{tot}$	−0.4*** (−0.4, −0.3)	-	-	0.99*** (0.79, 1.20)	-	***
${\overline{Q}}_{tot}\text{RS}$	−0.3*** (−0.4, −0.3)	-	-	0.97*** (0.75, 1.19)	-	***
${\overline{Q}}_{tot}\text{GCC}$	−0.3*** (−0.4, −0.3)	-	-	1.00*** (0.78, 1.23)	-	***
Site C
${\overline{Q}}_{tot}\text{GCC}$	-	−6.9*** (−8.4, −5.3)	-	0.98*** (0.77, 1.18)	-	**

Significance codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1