Assessing the predictability of nonlinear dynamics under smooth parameter changes

Abstract

Short-term forecasts of nonlinear dynamics are important for risk-assessment studies and to inform sustainable decision-making for physical, biological and financial problems, among others. Generally, the accuracy of short-term forecasts depends upon two main factors: the capacity of learning algorithms to generalize well on unseen data and the intrinsic predictability of the dynamics. While generalization skills of learning algorithms can be assessed with well-established methods, estimating the predictability of the underlying nonlinear generating process from empirical time series remains a big challenge. Here, we show that, in changing environments, the predictability of nonlinear dynamics can be associated with the time-varying stability of the system with respect to smooth changes in model parameters, i.e. its local structural stability. Using synthetic data, we demonstrate that forecasts from locally structurally unstable states in smoothly changing environments can produce significantly large prediction errors, and we provide a systematic methodology to identify these states from data. Finally, we illustrate the practical applicability of our results using an empirical dataset. Overall, this study provides a framework to associate an uncertainty level with short-term forecasts made in smoothly changing environments.

1. Introduction

Predicting the behaviour of natural and physical systems has been one of the great challenges of scientific inquiry [1–3]. In the past, the main limitation for the short-term predictability of most natural systems was the lack of an exact knowledge of their governing equations and the uncertainty associated with their parameters [1,4]. Then, in the late 1970s and early 1980s, the pioneering work of Takens [5] showed that important properties of nonlinear systems could be reconstructed solely based on empirical observations, allowing subsequent development of novel non-parametric methods for time-series forecasting [2,6,7]. Indeed, our capacity to build predictive non-parametric models has advanced substantially thanks to a combination of multivariate generalizations of Takens’s embedding theorem [8,9] and deep-learning algorithms [4,10,11]. However, the possibility to predict nonlinear dynamics in empirical settings has remained fundamentally limited by the fact that, in changing environments, model parameters are in constant change (e.g. species competition within biological communities increases in periods of food scarcity [12], interest rates are affected by bank policies [13,14], among others) and these changes can have significant effects on the system’s dynamics [15].

Unfortunately, the effects of environmental variability on a system’s trajectory cannot be easily predicted solely based on past observations. This is simply because predictive models built on properties learned from already observed data cannot generalize well on new data generated by unseen processes. Put differently, minimizing a cost function over training data generated by a given model does not ensure that the cost is also minimized over data generated by a different model [16]. This is a fundamental limitation arising in the applicability of modern statistical learning theories for the predictability of nonlinear dynamics in changing environments—where model parameters are changing frequently.

A possible way to estimate the effects of environmental variability on a system’s dynamics is to use non-parametric scenario exploration [17]: an approach developed to assess the effect of a small change in a physical driver on empirically reconstructed dynamical systems. However, in this approach, the environmental drivers need to be explicitly included in the reconstructed dynamics and, therefore, its applicability may be limited when the drivers of the dynamics are only partially or not at all observed.

To overcome these limitations and to better address the real-world challenge of characterizing predictability in changing environments here we propose a non-parametric approach that focuses on estimating the local structural stability of the underlying data-generating process. This estimate is then used as an indicator of its predictability at any given point in time—the predictability associated with a particular location or ‘state’ in phase space. The local structural stability of a given dynamical system can be defined as the time-varying stability of the phase portrait under smooth changes of the vector field [18]. That is, the local structural stability of a dynamical system can be interpreted as the resistance to change its trajectory after a smooth change in model parameters. To test these ideas, we combine non-parametric methods and machine learning algorithms to detect time points where a system is more predictable. The remainder of this work is organized as follows. We first present the theoretical background; next we test our theoretical framework on synthetic time-series data; and then we validate our theory on an empirical biological time series.

2. Background

To illustrate our approach, we consider nonlinear time series generated by some unknown dynamical system

$$\dot{\mathit{x}}=\mathcal{F}(\mathit{x},\mathit{\omega }),$$ 2.1

where $\mathcal{F}\in C^1$ is a nonlinear vector field (i.e. nonlinear dynamical model), $\mathit{x}\in {\mathbb{R}}^d$ is the state vector and ω is a vector of environment-dependent parameters (e.g. interaction strength between species in population dynamics models, interest rates in financial models). We assumed that environmental changes affect the model dynamics through smooth perturbations of the components of ω, but we did not choose a particular parametric form for $\mathcal{F}$. In this work, our goal is to estimate the predictability of equation (2.1) from empirical observations and without information on environmental variability, given that in many empirical cases we cannot control or measure all environmental parameters.

In nonlinear systems under changing environments, the accuracy of a forecast of the state variable x depends both on the power of the learning algorithm (e.g. artificial neural network, local regression) used for prediction and on how predictable the system is. If a perfect learning algorithm were available, the predictability of equation (2.1) would only depend on how changes in $\mathcal{F}$ or its parameters ω (due to environmental changes) affect the value of the future state variables x. In this case, the predictability of equation (2.1) would depend on the structural stability of $\mathcal{F}$, that is, the stability of this dynamical system against perturbations of its vector field or its parameters. Note that we are extending the classic definition of structural stability [19] (which looks at the capacity to remain in a given global qualitative state) to a local quantitative property [18,20]. Moreover, because we assumed $\mathcal{F}$ to be nonlinear, the extent to which perturbations to $\mathcal{F}$ result in changes of x also depends upon the state of the system (figure 1a). That is, the resistance of a nonlinear dynamical system to changes in its trajectory is state dependent. In the remainder of this work, we use the term local structural stability [18] to refer to structural stability that is state dependent—that can vary with the specific location in phase space.

Figure 1.

Volume contraction rate (VCR) and local structural stability in changing environments. The time series in (a) and (c) are generated from a numerical integration of a five-dimensional chaotic dynamical system (figure S1). The panels show that the same parameter perturbation occurring at two different points along the model’s trajectories (i.e. t = 2000 and t = 3400) can have completely different effects on the dynamics. This effect can be measured as the deviation $ϵ$ between perturbed (red dotted line) and unperturbed (green dotted line) trajectories. This result is analysed further in (b). The two figures show the PDF and CDF for the percentage difference in the deviation of trajectories (after perturbing the dynamics) at points with small (${ϵ}_{\hspace{0.17em}\mathrm{small}}$) and large (${ϵ}_{\hspace{0.17em}\mathrm{large}}$) VCRs (the perturbation is the same at the two points). The red line in the left panel indicates the median of the distribution. The blue line in the right panel corresponds to the probability below which ${ϵ}_{\hspace{0.17em}\mathrm{small}}<{ϵ}_{\hspace{0.17em}\mathrm{large}}$. In (d), we analyse the tail of the distribution. The y-axis is the complement of the cumulative distribution function of the ratio between the two deviations. The panel shows that the probability that a small perturbation leads to a large effect (i.e. large deviation between perturbed and unperturbed trajectories) is much larger at points with large VCRs (top black line) than at points with small VCRs (bottom blue line). This result is validated on other chaotic dynamical systems (see electronic supplementary material, figure S1). Overall, the figure shows that a system’s response to a perturbation to the parameters depends on the value of the VCR at the time at which the perturbation occurs. (Online version in colour.)

Following the argument above, we investigate the association between local structural stability and the predictability of nonlinear time series in smoothly changing environments.¹ Estimating the local structural stability of nonlinear systems is in general extremely challenging. Importantly, previous work has found that the inverse of the volume contraction rate (VCR) of the vector field at a given point in the state space is a proxy for its local structural stability [18]. Here, we go a step further and propose that the VCR is also an inverse measure of local predictability in changing environments. The VCR ($\mathcal{V}$) of a continuous dynamical system is the divergence of the vector field $\mathcal{F}$ [19],

$$\mathcal{V}\equiv \mathrm{\nabla }\cdot \mathcal{F}=\text{Tr}(\mathcal{J}),$$ 2.2

where $\mathcal{J}$ is the Jacobian matrix of $\mathcal{F}$ and $\text{Tr}(\mathcal{J})$ is the trace of this matrix. For example, in a system with three state variables x = [x, y, z] and a vector field with three components (i.e. three differential equations) we have

$$\mathcal{V}=\frac{\mathrm{\partial }{\mathcal{F}}_x}{\mathrm{\partial }x}+\frac{\mathrm{\partial }{\mathcal{F}}_y}{\mathrm{\partial }y}+\frac{\mathrm{\partial }{\mathcal{F}}_z}{\mathrm{\partial }z}.$$ 2.3

Note that, generally, in nonlinear systems with interacting terms $\mathcal{V}:\mathcal{V}(\mathit{x})$ (i.e. the VCR is state dependent). Therefore, unless the equilibrium dynamics is a stable fixed point, the structural stability of the system changes in time.² Below, we provide a heuristic argument for using the VCR as an inverse measure of local predictability of nonlinear time series under changing environments.

Let $\mathcal{S}$ be the state space of equation (2.1), whereas we call ω and $\hat{\mathit{\omega }}$ the unperturbed and perturbed parameters of equation (2.1), respectively. For the purposes of working with empirical data, we can assume that, for any $\mathit{x}\in \mathcal{S}$ and small perturbations to the parameters (i.e. for $d(\mathit{\omega },\hat{\mathit{\omega }})\sim 0$ under some metric d such as Euclidean distance), $\text{Tr}(\mathcal{J}(\mathit{x},\mathit{\omega }))\sim \text{Tr}(\hat{\mathcal{J}}(\mathit{x},\hat{\mathit{\omega }}))$. That is, for small parameter perturbations, the perturbed and unperturbed dynamics have similar VCRs. Note that this is a very reasonable assumption for continuous and differentiable functions, and it is applicable to many scenarios of environmental change in empirical data [19]. Yet, it is important to recall that this argument is only valid under the assumption of smooth parameter perturbations (i.e. smooth changes in the environmental conditions) and does not apply to strong qualitative changes in the dynamics (e.g. invasion or extinction of a species in an ecosystem).

In a nonlinear dynamical system, the VCR provides a measure of how the volume of the state space changes under the flow of the vector field. Regions in the state space with small VCR correspond to regions under which volumes in the state space do not increase and, therefore, trajectories do not diverge. Within these regions of the state space, two nearby models (i.e. the model with original parameters and the model with perturbed parameters) have, by the assumption above, similarly low VCRs. Therefore, going from one model (unperturbed) to the other (perturbed), their respective trajectories do not diverge. By contrast, the effects of perturbations occurring at states with a large VCR are, on average, magnified by the flow. This observation allows us to link the VCR to the predictability of the dynamics. That is, because, without prior information on perturbations, a learning algorithm can only predict the unperturbed trajectory, prediction errors will be small when perturbed and unperturbed trajectories do not diverge (i.e. at states with small VCR). On the other hand, when the divergence of the trajectories is magnified by the flow (i.e. when the VCR is large) prediction errors will be larger. As such, this suggests that the VCR can be used to estimate the local predictability of nonlinear time series under changing environments.

Note that the VCR at a given state of a nonlinear dynamical system is the sum of the local Lyapunov exponents (i.e. finite-time Lyapunov exponents computed with the given state as initial condition) [21,22]. Thus, differently from the largest Lyapunov exponent, the VCR contains information about the stretching of nearby trajectories along all the stable and unstable directions. That is to say, the VCR is a linear function of the whole Lyapunov spectrum that captures how volumes in a d-dimensional space expand or contract. This implies that, for each point in time, the VCR provides an average rate of divergence or convergence of nearby trajectories, providing a robust estimation of local structural stability and, therefore, of predictability in smoothly changing environments. It is important to note that, because there is always uncertainty associated with the magnitude and direction of perturbations, any predictability metric such as the VCR can only measure the probability of committing small or large prediction errors. Because the ultimate goal of our approach is to analyse empirical data, we would like to highlight that the estimation of the VCR only requires knowing the diagonal elements of the Jacobian matrix of the dynamics—a quantity that can be efficiently estimated from multivariate time series with available non-parametric methods (see discussion below and electronic supplementary material, figure S5, for examples of the inference of the VCR from noisy nonlinear time series [12,23]).

3. Prediction of synthetic data

To validate our approach, we provide a numerical illustration using synthetic data. Specifically, we show that the VCR can be used to estimate the local structural stability of the dynamics. Then, we show that structural stability implies predictability. First, to show that the VCR is a valid estimator of local structural stability (i.e. the stability of a system’s trajectory in response to smooth parameter perturbations), we compare the effect of the same parameter perturbation at points on the attractor with a small VCR versus points with a large VCR. For this purpose, we integrate the dynamics of a five-dimensional chaotic dynamical system (see electronic supplementary material, figure S1) and compute the VCR along the trajectory using the analytical Jacobian matrix $\mathcal{J}$. Then, we sample one random point with a large VCR and one random point with a small VCR from the system’s trajectory. We took the small VCR within the lower 15th percentile of the VCR distribution, whereas the large VCR is within the upper 15th percentile of the same distribution. Then, we perturb a random number of parameters and integrate the dynamics again with the new perturbed parameters using the two sampled points on the attractor as initial conditions.

Parameter perturbations are of the form

$${\hat{\omega }}_i={\omega }_i+\mathcal{N}(0,\frac{{\omega }_i}{\mathcal{U}(1,\eta )}),$$ 3.1

where ω_i ∈ ω, $\mathcal{N}$ and $\mathcal{U}$ are the normal and uniform distributions, respectively. That is, the perturbation to the parameter is a random number sampled from a Gaussian distribution with zero mean and standard deviation proportional to the value of the parameter itself. By changing the standard deviation of the perturbation (i.e. by changing the value of η), we can change the overall level of perturbation to the system. In order to preserve the spirit of a non-parametric framework (where in principle there is no knowledge about the governing equations and their parameters), at every realization we also randomly sample which and how many parameters to perturb. Yet, understanding the effects of individual parameters can be a fruitful research area that future work can explore.

After the integration of the new dynamics, we measured the root mean square distance (RMSD) between perturbed and unperturbed trajectories at the small VCR state (${ϵ}_{{\mathrm{small}}_{\mathcal{V}}}$) and at the large VCR state (${ϵ}_{{\mathrm{large}}_{\mathcal{V}}}$; see figure 1a,c for an illustrative example). We repeat this same numerical experiment 10⁵ times. In order to estimate the effect of the same parameter perturbation on two different system states we analyse the distribution of two statistics. First, we compute the percentage difference between RMSD after perturbations at points with small and large VCR, i.e. $X=({ϵ}_{{\mathrm{small}}_{\mathcal{V}}}-{ϵ}_{{\mathrm{large}}_{\mathcal{V}}})/({ϵ}_{{\mathrm{small}}_{\mathcal{V}}}+{ϵ}_{{\mathrm{large}}_{\mathcal{V}}})$. We show in figure 1b the kernel density estimation of the probability density function (PDF) and cumulative distribution function (CDF) of this statistic. The PDF shows that the mass of the distribution is skewed towards negative values (〈X〉 ∼ −0.12), indicating that, on average, ${ϵ}_{{\mathrm{small}}_{\mathcal{V}}}<{ϵ}_{{\mathrm{large}}_{\mathcal{V}}}$. Similarly, the CDF shows that the probability that this inequality holds is clearly greater than 50% (i.e. $\mathcal{P}({ϵ}_{{\mathrm{small}}_{\mathcal{V}}}<{ϵ}_{{\mathrm{large}}_{\mathcal{V}}})\sim 60\text{\%}$).

Because mean values can be misleading, we also analyse the severity of the extreme events (i.e. the tail risk) and compute the statistics $Y=({ϵ}_{{\mathrm{small}}_{\mathcal{V}}})/({ϵ}_{{\mathrm{large}}_{\mathcal{V}}})$ and $Z=({ϵ}_{{\mathrm{large}}_{\mathcal{V}}})/({ϵ}_{{\mathrm{small}}_{\mathcal{V}}})$. We then plot the complement of the empirical cumulative distribution function for the random variables Y and Z. For a given ratio r of RMSDs, the condition Pr(Z > r) > Pr(Y > r) implies that points on the attractor with small VCR are more structurally stable than points with large VCR under the exact same parameter perturbation. Figure 1c shows that the complements of the two cumulative distribution functions, i.e. Pr(Z > r) and Pr(Y > r), are substantially different, with the former being much larger than the latter. This reveals that the impact of smooth perturbations occurring at points with large VCR is much larger than the impact of perturbations taking place at states with low VCR. To further validate this result, we repeat the same numerical experiment with three additional chaotic dynamical systems (see electronic supplementary material, figure S1). The results are shown in electronic supplementary material, figure S1, and are consistent with our theoretical expectations. These examples provide support to the hypothesis that the VCR is a good estimator of local structural stability in nonlinear dynamical systems [18].

It is worth noting that similar results can be obtained using the largest local Lyapunov exponent as a measure of local structural stability (electronic supplementary material, figure S5 and figure S2). However, as shown in electronic supplementary material, figure S2, which was generated mirroring the simulation done to generate figure 1b, the shift of the mass of the PDF and CDF towards negative values is more significant when predictability is estimated using the VCR. While Lyapunov exponents are not considered a measure of predictability [24], this result is not surprising as a local perturbation in the parameters should induce changes in the trajectories, which will then diverge at a rate measured by the Lyapunov exponents. Yet, as discussed above, the VCR provides a more grounded measure of this divergence because it is a metric constructed by weighting stable and unstable manifolds equally. Moreover, from a practical and computational point of view, the VCR is a more reliable metric to estimate from empirical data than the largest Lyapunov exponent. That is, the computation of the VCR only requires the estimation of the diagonal elements of the Jacobian matrix (d parameters), while the Lyapunov exponents require the whole matrix (d² parameters), making the latter more prone to errors [7,25].

Having corroborated the validity of the VCR as a measure of local structural stability, we now show that, in changing environments, predictions from structurally stable states are less error prone. To illustrate the relationship between local structural stability and predictability, we repeat the same numerical experiment outlined above. However, differently from above, rather than integrating the dynamics, here we forecast the trajectories after each perturbation using a long short-term memory (LSTM) artificial neural network [26,27]. Then, we compute the root mean square error (RMSE), which is widely adopted as a measure of forecasting skill [10,28], between the perturbed and predicted trajectories. Note that the RMSD and the RMSE are mathematically the same, but conceptually different. We used this terminology to distinguish the two types of experiments: divergence (RMSD) and forecasting (RMSE). We focus on short-term predictions (i.e. small forecast horizon) because long-term predictions of nonlinear systems are known to be very unreliable in empirical data even in the absence of parameter perturbations. This analysis is repeated for different levels of perturbations in model parameters (see appendix A for details).

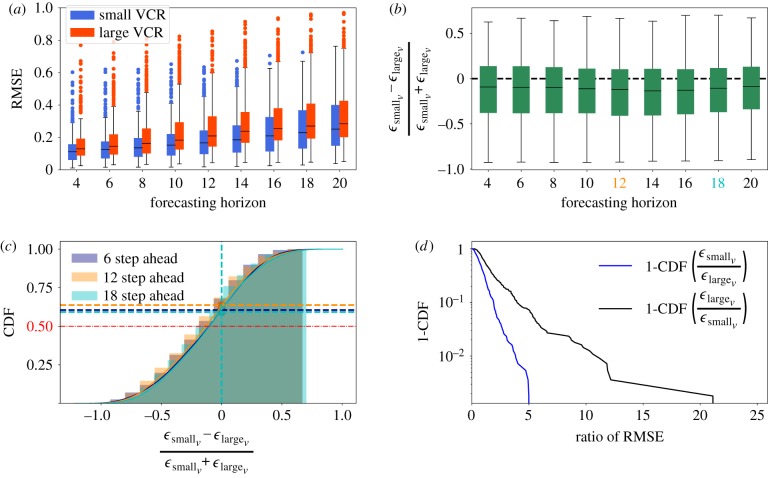
Figure 2a shows the distribution of RMSE of predictions at small and large VCRs as a function of the forecast horizon with a given level of perturbation (i.e. η = 6 in equation (3.1); results for a larger level of perturbation are reported in electronic supplementary material, figure S3). This figure illustrates that predictions at states with a small VCR are more accurate than predictions at states with a large VCR, confirming that the VCR is an effective estimator of the uncertainty in short-term predictions of a dynamical system. These results further confirm the link between local structural stability and local predictability. The difference in mean RMSE between small and large VCR is statistically significant for all forecast horizons, and this result is robust to the choice of the sample size (see electronic supplementary material, figures S2 and S4). Figure 2b,c is equivalent to figure 1b. The two panels show that, in line with our theoretical expectation, the mass of the distribution is moved towards negative values, i.e. prediction errors after perturbations at small VCR are on average smaller than prediction errors after perturbations at large VCR.

Figure 2.

Theoretical validation of the volume contraction rate (VCR) as an estimator of predictability in changing environments. (a) The distribution (boxplots) of RMSE in the test set at different forecasting horizons. Predictions are made with a long short-term memory (LSTM) artificial neural network after perturbations at points with small and large VCRs (left and right boxplots, respectively). Perturbations are performed as in the analysis presented in figure 1b, but here we measure the deviations between perturbed and predicted trajectories (i.e. RMSE) instead of deviations between perturbed and unperturbed trajectories (i.e. RMSD). Points at small (large) VCR are sampled from the lower (upper) 15th percentile of the trace of the Jacobian matrix, which is computed numerically at each point on the attractor. The means of the two distributions (i.e. small and large VCRs) are different and the robustness of this result to various sample sizes is discussed in electronic supplementary material, figures S2 and S4. (b) The same distribution shown in figure 1b but as boxplots, which are a function of the forecasting horizon. This panel, together with the CDF in (c), shows that the mass of the distribution is moved towards negative values, i.e. prediction errors after perturbations at small VCRs are on average smaller than prediction errors after perturbation at large VCRs. The blue, orange and cyan lines show the probability mass corresponding to negative values in the percentage difference as a function of forecasting horizon. (d) As expected from figure 1d, the same parameter perturbation has a much greater impact on the predictability of points with large VCRs (top black line) than points with small VCRs (bottom blue line). Overall, the figure shows that the VCR is a consistent measure of predictability in smoothly changing environments. (Online version in colour.)

Similarly to the analysis shown in figure 1c, we also estimate the effect on predictability of the same parameter perturbation at different VCR states. Figure 2d shows that the complement of the cumulative distribution function of the ratio of the RMSEs follows our theoretical expectations (figure 1c). That is, in the presence of smooth perturbations to the model parameters (i.e. in smoothly changing environments), the probability of large prediction errors is much larger when predictions are made from states with a large VCR.

4. Prediction of empirical data

The theoretical framework and results above support the hypothesis that the VCR can be used to estimate the predictability of nonlinear time series in smoothly changing environments. We now turn to demonstrate the practical applicability of our approach on empirical data. Specifically, we analyse a biological time series of a rocky intertidal community that exhibits dynamics at the edge of chaos [29]. The community consists of three species (mussels, algae and barnacles) that compete for space on bare rock. Data were collected daily for over 20 years in New Zealand [29].

Following the analysis carried out on synthetic data, we compare the RMSEs after predictions at points with small and large VCRs (see appendix A for further details). Differently from the numerical simulations, the Jacobian matrices at each time step are not available when dealing with empirical data. Therefore, to compute the empirical VCRs non-parametrically, we reconstruct the Jacobian coefficients from the observed time series using the regularized S-map [23], which we also use for forecasting. The regularized S-map is a locally weighted regularized state-space regression model that has been shown to be a robust estimator of Jacobian coefficients from noisy time-series data [7,12,23,25]. See electronic supplementary material, figure S3 for further details on the S-map. Electronic supplementary material, figure S5 shows an illustrative example of inference of VCR from synthetic data and electronic supplementary material, figure S6 shows a comparison of the forecasting skill of the regularized S-map and LSTM. To avoid any cross-contamination between training and test data, rather than computing the VCR over the whole time series and then sampling points beyond which to forecast (as in the synthetic data analysis section), we compute the VCR sequentially using only past data and then we perform out-of-sample forecasts (see appendix A for further details).

Figure 3a confirms the theoretical results shown in figure 2. In particular, the figure shows that predictions at states (i.e. time points) with a small VCR have, on average, a smaller RMSE than predictions at states with a large VCR. This difference between small and large VCR is statistically significant for all forecast horizons (see electronic supplementary material, table S7). Hence, in line with the results found using synthetic data, the VCR computed empirically from the time series can be used to estimate the local predictability of the data. Note that predictions were made up to five months ahead with a threshold in the VCR set at the 15th percentile. The robustness of the results at different percentiles is shown in electronic supplementary material, figure S9.

Figure 3.

Empirical validation of the volume contraction rate as an estimator of predictability in changing environments: NZ rocky intertidal example [30]. (a) The distribution (boxplots) of the root mean square error (RMSE) of the predictions as a function of the forecast horizon (months) for the empirical time series. In line with theoretical expectations (figure 2), the VCR is a good measure of predictability. (b) The results of the significance test described in appendix A; the figure illustrates that the results in (a) are statistically significant. The vertical blue line corresponds to the mean RSME of all predictions made using points with small VCRs (lower 15th percentile of the trace of the inferred Jacobian matrix and predictions are one step ahead), whereas the grey distribution corresponds to the ensemble of mean RMSEs calculated from random samples of the (one step ahead) predictions. The blue curve and red curve in (c) show the kernel density estimation of the distribution of RMSEs in the test set at points with small and large VCRs, respectively. The panel illustrates that very large errors are significantly more likely after predictions at states with large VCRs. Electronic supplementary material, figure S9 shows the robustness of the results to the choice of percentile and prediction horizons. (d) The results of the causality test (y-axis is the correlation between predicted and estimated) of VCR with temperature (top brown line) and mean wave height (bottom green line). The shaded regions correspond to the expected cross-mapping skills from randomized time series (see appendix A). The panel illustrates that sea temperature has a much greater causal effect on the VCR than mean wave height. (Online version in colour.)

To further test the validity of our analysis, we also test for the statistical significance of our results by comparing the observed RMSEs in the lower percentile of the VCR with the distribution of possible mean RMSEs that one would have obtained by using random criteria of predictability. This distribution is computed by randomly sampling multiple subsets of RMSEs, regardless of the VCR at the time of prediction, and then computing the mean of each subset (see appendix A for a more detailed explanation of the test). We found that the VCR is a statistically significant measure of predictability (figure 3b) as long as the separation criterion between small and large VCR is within the 35% of the inferred trace of the Jacobian matrix (see electronic supplementary material, figure S8). Figure 3c shows the kernel density estimation of the distribution of the RMSE in the test set in the lower and upper percentiles of the VCR. The figure clearly illustrates that the two distributions have not only different means but also different shapes. Specifically, even though the distribution of errors at large VCRs (red region) has a peak at low RMSE, it is clearly more skewed towards larger errors than the distribution of errors at small VCRs (cyan region). This result implies that the probability of large prediction errors is substantially higher when predictions are made at states (i.e. time points) with large VCR. The overlap of the two distributions also implies that other factors, such as noise in the empirical data, most likely affect the local predictability of a time series. Our results are consistent with theoretical expectations (figures 1, 2 and electronic supplementary material, figure S1) and are robust to the choice of the threshold in the VCR (see the distributions in electronic supplementary material, figure S9)

It is important to notice that, unlike the synthetic example, the biological example is not a closed system but is part of a broader environmental context. Thus, an interesting question to ask is how the predictability of this community might be related to relevant environmental variables that are exogenous to the system. To answer this question, we investigate the causal relationship between the VCR with temperature and mean wave height using a non-parametric causality test known as convergent cross mapping [31] (CCM; see appendix A for further details on CCM). It is known that temperature and mean wave height are two key environmental drivers of rocky intertidal communities [18,29,32,33]. Figure 3d reveals that sea temperature has a causal influence on the VCR and, therefore, on predictability. However, there is no significant causal relationship between mean wave height and VCR. This result is interesting because it illustrates that environmental variables (e.g. mean wave height) can play a crucial role in the dynamics (e.g. regulate the mortality rate [32]) but have no effect on the predictability of the community dynamics. The statistical significance of the causal links is assessed using surrogate time series (shaded area in figure 3d; see appendix A).

5. Discussion

Forecasting with nonlinear time series is a central challenge in science and engineering [1–3]. The issue is particularly hard to address when true dynamics are unknown and parameters are likely to change in response to environmental variations. In this context, it is of practical relevance to know when predictions can be trusted the most. To address this issue, here we have provided theoretical arguments, as well as synthetic and empirical evidence in support of the hypothesis that the VCR, a local property of the deterministic skeleton of the dynamics, provides reliable information about the local predictability of nonlinear dynamical systems in smoothly changing environments. Interestingly, analysing synthetic and empirical data, we have found that the distributions of prediction errors at states (i.e. time points) with small and large VCR differ considerably. In particular, the probability of very large prediction errors with respect to the mean is significantly higher when predictions are made at states with a large VCR. We believe that this is an important finding that can have practical implications and that requires further theoretical investigation. For example, with sufficient empirical data, it is in principle possible to compare the current VCR with historical values in order to check if the current VCR is large compared with past values. If this is true, there is a greater risk of making inaccurate forecasts at the current system state.

Despite the potential applicability of the VCR, it is also important to discuss the limitations of this approach. One evident pitfall is that, theoretically, there could be cases in which the VCR stays constant throughout the time. A clear example is the Lorenz system: a chaotic dynamical system whose predictability is notoriously state dependent [34] but, at the same time, has a constant VCR. Yet, while theoretically possible, empirical systems with nonlinear dynamics but constant VCR are probably the exception rather than the rule. For example, a simple process noise (i.e. a noise typically proportional to the square root of the state variable) would generate state-dependent VCRs. A second limitation is the (in)accuracy of the reconstruction of the VCR from empirical data. In the example provided in this article, we have detailed information about the system under investigation. Specifically, all the relevant variables were observed, allowing us to use a fully multivariate embedding from which we know we can reconstruct the VCR accurately using the regularized S-map [12,23]. In cases where not all variables are collected from experiments or observational studies, the dynamics can still be reconstructed from the available observations using Takens's embedding theorem [5]. However, the results will be sensitive to the details of the attractor reconstruction (e.g. the selection of the optimal time lag and embedding dimension). Because the trace of the Jacobian matrix cannot be associated with the VCR if the reconstructed attractor is not embedded in the correct dimensional space, particular care needs to be placed on the application of the methods from reconstructed dynamics. Overall, we have provided a framework to estimate, non-parametrically, the local predictability of empirical nonlinear time series under smooth parameter changes. We believe that this approach and its potential extensions can have important practical applications in management and risk-assessment studies.

Appendix A

A.1. Analysis of synthetic data

To show that the VCR is a valid measure of predictability in smoothly changing environments, we ran the following analysis. We considered a five-species chaotic population dynamics model as in figure 1a (see electronic supplementary material, figure S1 for details on the model). We integrated the dynamics over 10⁵ time points and sampled equally spaced points along the trajectories (one every 150 points). Then, we numerically computed the VCR along the attractor using equation (2.2), and we sampled a pair of points in the lower and upper 15th percentiles of this measure.³ Using these points, we perturbed a random number of parameters with Gaussian random variables at zero mean and with standard deviation proportional to the value of the parameters themselves (see electronic supplementary material, figure S1). Then, we integrated again the dynamics with the new parameters, taking as the initial condition the two perturbed points (i.e. lower and upper percentiles). Note that we applied the very same perturbation to each pair of points. This provided two unperturbed trajectories (i.e. before the two perturbation points) over which we trained an LSTM artificial neural network [26,27] and we then made forecasts over the two perturbed trajectories. Training was performed over the 500 data points preceding the perturbation time, i.e. t_training ∈ [t_p−500, …, t_p], where t_p is the time of perturbation. Forecasts were performed up to 20 time steps in the future (i.e. we were interested in short-term forecasts given that long-term predictability of chaotic systems in changing environments is practically unfeasible). Finally, we computed the RMSE at different forecast horizons in the two test sets, i.e. one after the perturbation at the structurally stable points and the second one after the perturbation at the structurally unstable points. We repeated these numerical experiments 500 times at different levels of perturbations. Results of this analysis are shown in figure 2.

A.2. Analysis of empirical data

We used a multivariate time series of species abundances collected from a 22-year-long observational study of a marine intertidal community from New Zealand. The data can be downloaded from [30]. The community is composed of three species (mussels, algae and barnacles) competing for space on bare rock. Because the three species compete for space, the overall system has four dimensions. It has already been shown that the time series exhibits dynamics at the edge of chaos [30], making it a perfect candidate for our analysis. The time series, as downloaded from [30], is already pre-processed (see [29] for further details on the system).

To test the validity of the VCR as an inverse measure of predictability we run the following analysis: first, we trained the S-map on 150 data points. Then, we computed the VCR from the estimated Jacobians (coefficients of the S-map; see electronic supplementary material and [12]). At this point, we made predictions up to five months ahead and we saved (i) the VCR before the prediction and (ii) the RMSE of the forecast. Then, we took a new point from the data, fitted the new Jacobian coefficients, computed the new VCR, predicted again and computed the new RMSE. We repeated this numerical experiment up to the final point of the time series. Finally, we plotted the RMSEs as a function of the forecasting horizon for all those points below and above a certain threshold of the VCR. All the forecasts are completely out-of-sample and the VCR is always computed using training data only. The threshold was fixed at the first 15th percentile in the figure shown in the main text. The results at different thresholds are shown in electronic supplementary material, figure S9.

A.3. Causality test

To test for the existence of a causal link between variables in nonlinear dynamical systems, we used CCM [31], a non-parametric test for causality developed within an empirical dynamic modelling (EDM) framework. Given two variables X and Y, CCM uses the results from Takens's theorem to reconstruct two versions of the same manifold, one with embedding of X and one with embedding of Y. Then, variable X is said to be a causal driver of variable Y if information of X is contained in the manifold of Y, i.e. Y cross maps X. See [31] for a more detailed presentation of the causality test. To ensure the statistical significance of the causal links with CCM, two conditions need to be satisfied: (i) convergence towards higher cross-mapping skills as the number of data points increases and (ii) CCM skills need to be higher than the one we would obtain with a surrogate version of the time series. Because temperature has a strong seasonal pattern, we used a null model that takes into account seasonality in the data. Specifically, we used the function make_surrogate_season in the rEDM package in R. Note that before performing the causality test, for an accurate reconstruction of the VCR, we have used an ensemble method to compute the Jacobian coefficients [25]; see electronic supplementary material. In electronic supplementary material, figure S10, we show that CCM provides results that meet biological expectations, i.e. the VCR has no causal effect on environmental variables in the biological time series. That is, the VCR does not influence either sea temperature or mean wave height, confirming what would be naturally expected.

A.4. Statistical tests

As a first test for the validity of the VCR as a measure of predictability, we performed a t-test on the two distributions (i.e. errors at small and large VCR). Results are shown in electronic supplementary material, table S7. The p-value of the test is significantly smaller than 5% for all cases. Because the sample size of the predictions in the empirical dataset is relatively small, we ran a second analysis to test if results are statistically significant. First, we set a threshold on the VCR (e.g. 15th percentile as in the main text). Then, we computed the mean RMSE in the test set for all the predictions made at points below this threshold (cyan line in figure 3b). Then, we randomly sampled a subset of the predictions in the test set regardless of the value of the VCR at the time of prediction, and we also computed the mean RMSE in this subset. We chose as sample size the same size as the one in the lower 15th percentile of the VCR. This is effectively a null model that assumes that VCR is not an estimator of predictability. In other words, the null hypothesis establishes that the mean RMSE observed in low VCR states is expected to happen from any randomly chosen VCR state. Note that our test statistic is the mean RMSE. Hence, the null distribution is not the RMSE distribution, but the mean RMSEs sampled from different VCR states. We repeated this sampling process 10⁴ times and we calculated their distribution (grey curve in figure 3b) and a p-value as area under the curve below the true RMSE (cyan line). The results of the significance test at different thresholds of the VCR and at different forecasting horizons are shown in electronic supplementary material, figure S8.

Code availability

The code to reproduce the figures is available on GitHub at https://github.com/MITEcology/JRSI-Cenci-Medeiros-Sugihara-Saavedra-2019.git. The folder also includes a code to estimate the VCR from a multivariate time series.

Data accessibility

The data used in the manuscript can be downloaded from www.pnas.org/content/112/20/6389/tab-figures-data.

Authors' contributions

S.C., G.S. and S.S. designed the study, S.C. and L.P.M. performed the study, S.S. supervised the study. S.C., G.S., L.P.M. and S.S. wrote the manuscript.

Competing interests

We declare we have no competing interests.

Funding

Funding was provided by DoD-Strategic Environmental Research and Development Program 15 RC-2509, Lenfest Ocean Program 200028335, NSF 3DEB-1655203, NSF ABI-1667584, the McQuown Fund and the McQuown Chair in Natural Sciences, University of California, San Diego (G.S.), MIT Research Committee funds and the Mitsui Chair (S.S).