The mechanics of nectar offloading in the bumblebee Bombus terrestris and implications for optimal concentrations during nectar foraging

Abstract

Nectar is a common reward provided by plants for pollinators. More concentrated nectar is more rewarding, but also more viscous, and hence more time-consuming to drink. Consequently, theory predicts an optimum concentration for maximizing energy uptake rate, dependent on the mechanics of feeding. For social pollinators such as bumblebees, another important but little-studied aspect of foraging is nectar offloading upon return to the nest. Studying the bumblebee Bombus terrestris, we found that the relationship between viscosity (µ) and volumetric transfer rates (Q) of sucrose solutions differed between drinking and offloading. For drinking, Q ∝ µ^−0.180, in good agreement with previous work. Although offloading was quicker than drinking, offloading rate decreased faster with viscosity, with Q ∝ µ^−0.502, consistent with constraints imposed by fluid flow through a tube. The difference in mechanics between drinking and offloading nectar leads to a conflict in the optimum concentration for maximizing energy transfer rates. Building a model of foraging energetics, we show that including offloading lowers the maximum rate of energy return to the nest and reduces the concentration which maximizes this rate by around 3%. Using our model, we show that published values of preferred nectar sugar concentrations suggest that bumblebees maximize the overall energy return rather than the instantaneous energy uptake during drinking.

1. Introduction

For many floral visitors, including numerous species of insects, birds and mammals, nectar is one of the main sources of food [1]. Nectar is a solution of varying concentrations of the sugars sucrose, glucose and fructose, though further sugars and a variety of other compounds may also be present [2–5]. The composition of nectar will influence its value and attractiveness to different animals [6–9], structuring the assemblage of species which visit the plant in question.

The sugar concentration of nectar is a key trait influencing attractiveness, as it directly determines how energetically rewarding the nectar is. Nectar energy density rises linearly with increasing sugar concentration. However, nectar viscosity increases exponentially with increasing nectar concentration; therefore, more viscous nectar requires more energy or time to drink [9–12]. Thus, an animal aiming to maximize instantaneous energy intake rates should not necessarily seek to drink the most concentrated nectar, but rather choose the concentration which optimizes the balance between the opposing factors of energy density and drinking speed. If the nectar concentration is too low, energy intake rates are limited by the low sugar content, whereas if concentration is too high, rates are limited by the slow drinking speed [9,13,14].

The nectar sugar concentration for maximizing energy intake rates depends on the mechanics of feeding of the species in question. For bumblebees and honeybees, which feed on nectar by lapping, dipping their feathery glossa (tongue) into the nectar [9,15,16], models of drinking rates predict that this optimum concentration is around 50–60% w/w [9–11], depending on nectar chemical composition and temperature. By contrast, for species such as Euglossine bees, which drink nectar through suction, the optimum concentration is lower [8,14,17]. Therefore, nectar feeding mechanics should directly influence nectar preference and the plant species visited.

For social insects such as bumblebees, which store collected nectar in ‘honeypots' in the nest [18], a second key aspect of nectar foraging is offloading the honeycrop (also known as the honey stomach) upon return from a foraging trip. Bumblebee foragers do this by regurgitating the collected nectar directly into the honeypots. In contrast to the substantial body of work on nectar drinking, nectar offloading is poorly explored. Offloading has received some attention in the honeybee Apis mellifera, where viscosity does affect flow rates [19]. In A. mellifera, however, initial offloading occurs via trophallaxis (transfer between individuals), in contrast to the direct offloading of bumblebees. If nectar offloading rates in bumblebees are also affected by nectar viscosity, then this may be a previously unrecognized factor influencing their foraging behaviour. In particular, this could alter predictions of the optimum nectar concentration for maximizing energy return to the nest. This rate of energy return will be influenced by the duration of all the different activities (including drinking and offloading) that make up a foraging trip. The relative importance of each activity will depend on the proportion of the overall time spent on it and whether this proportion varies with nectar concentration. In some preliminary work, we noted that worker B. terrestris (n = 4) appeared to take much longer in the nest when foraging on 70% w/w sucrose solution versus 55%, suggesting that offloading rates may indeed be affected by viscosity.

Here, to explore the mechanics of nectar offloading and its influence on foraging preferences in more detail, we investigated both nectar drinking and nectar offloading in the bumblebee Bombus terrestris. We measured the relationship between volumetric transfer rates and viscosity by observing feeding and offloading behaviour of B. terrestris workers when foraging on sucrose solutions of three different concentrations. We also explored whether sucrose concentration affected other behaviours during foraging bouts, such as the time spent on activities other than foraging or offloading.

2. Methods and materials

2.1. Experimental set-up and protocol

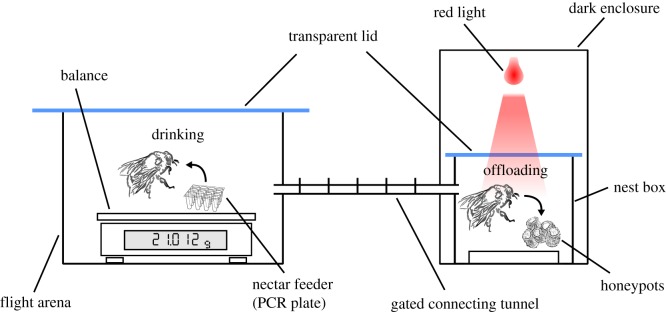
We measured drinking and offloading rates using the bumblebee Bombus terrestris audax. Bees were housed in a plastic nestbox, connected to a flight arena by a gated connecting tube (figure 1; see also electronic supplementary material). During experiments, the nestbox was covered by an enclosure approximately 0.5 × 0.5 × 1.0 m, which stopped light from reaching the colony. An opaque black cloth was fitted to the front of the enclosure so that an observer could stand with their head and torso inside the enclosure without letting outside light in. A red light-emitting diode placed above the nest allowed the offloading behaviour of returning foragers to be viewed with minimal disturbance (figure 1). Although bees can see red light to a limited extent, their sensitivity at these wavelengths is comparatively poor [20].

Figure 1.

The experimental set-up for recording drinking and offloading rates. (Online version in colour.)

Rates of sucrose solution transfer during drinking and offloading were recorded for 30 workers, from three colonies, foraging on one of three sucrose solution concentrations: 35, 50 and 65% w/w $((\text{mass\hspace{0.17em}of\hspace{0.17em}solute}÷\mathrm{mass}\hspace{0.17em}\mathrm{of}\hspace{0.17em}\mathrm{solution})\times 100)$, made up of table sugar (sucrose) (Tate and Lyle, London, UK) dissolved in deionized water. Previous work has shown that the optimum concentration for maximizing energy uptake rates during drinking is around 50–60% for bumblebees [9]. The three concentrations chosen here include this range and also avoid issues with insufficient foraging motivation which can occur at concentrations below 35% [9,10]. Ten bees were measured for each sucrose concentration, with each bee tested individually on a single concentration only. Each bee was observed for 10 foraging bouts, giving 300 bouts in total. For each foraging bout, the bee was allowed into the flight arena and presented with sucrose solution in a 48-well PCR plate. The PCR plate was positioned on a balance (Mettler Toledo PG503-S) accurate to 1 mg (figure 1), such that the mass of the bee and the mass of sucrose solution consumed could be recorded for each bout. In addition to drinking time, offloading time, bee mass and solution mass, several further parameters were recorded for each bout: the time spent in the flight arena not drinking, the time spent in the nestbox not offloading and the number of offloading events (electronic supplementary material).

2.2. Statistical analysis

The volume of sucrose solution and mass of sucrose collected were calculated for each foraging bout (electronic supplementary material). ANOVAs were used to test for any effect of sucrose concentration on the volume carried by bees, using the mean volumes of solution from the 10 foraging bouts for each bee and standardizing for bee size using the minimum recorded bee mass (i.e. unladen mass) from the 10 bouts. ANOVA and Levene's test were used to check for significant differences in the mean and variance of the mass of bees between treatments.

As the relationship between sucrose concentration and rate of transfer is nonlinear and may be influenced by several factors, we initially explored the differences between concentrations by considering concentration as a three-level factorial variable. From the 10 foraging bouts for each bee, we calculated means for each of volumetric (µl solution s⁻¹) and energy (mg sucrose s⁻¹) drinking and offloading rates, time in the flight arena not spent feeding, and time in the nest not spent offloading. The differences between concentrations were tested for each parameter using an ANOVA with Tukey HSD post hoc tests. Data were log₁₀-transformed to better meet model assumptions for all parameters. Bees always had at least one offloading event per foraging bout, so a difference in the number of additional offloading events between concentrations was tested using a likelihood ratio test of nested generalized linear mixed models with and without concentration as a predictor, with a Poisson error structure and bee identity as random effect.

Previous work found that the drinking rate in bumblebees decreases with viscosity [9]. Assuming that the power for drinking is constant, a power-law relationship between drinking rate and viscosity was derived [9,21]. Following these studies, we modelled volumetric flow rate of sucrose solution Q (in μl s⁻¹) and viscosity µ (in mPa s) using Q = X μ^k, where X is an individual-specific constant taking account of factors not affected by viscosity such as bee size and proboscis length [9,21]. Consequently, the viscosity dependence of flow rate can be represented by the general relationship Q ∝ μ^k. Viscosity was calculated from concentration in % w/w and temperature in °C using the Génotelle equation [22] (and see electronic supplementary material). For drinking rate, we calculated viscosity assuming that the sucrose solution was at an air temperature of 23°C (average laboratory temperature to the nearest degree); for offloading, we assumed that the sucrose solution was at abdominal temperature, calculated as 27°C [23] (and see electronic supplementary material).

For both drinking and offloading rates, we fitted ordinary least-squares linear models to log₁₀ transformed data for Q and μ, giving the slope k and intercept log₁₀X. The slope from these models is the key parameter describing how flow rate changes with viscosity. Using the fitted models, the relationship between concentration and energy transfer rate (mg sucrose transferred s⁻¹; electronic supplementary material, equation (7)) was estimated for sucrose uptake and offloading, which in turn allowed prediction of an optimum concentration for maximizing energy transfer rates for uptake (drinking) and offloading of sucrose solutions. Finally, we built an overall model incorporating the viscosity dependence of drinking and offloading with the times spent on other activities during a foraging trip and the metabolic rate during these activities to calculate a combined rate of energy return to the nest, and to predict the respective concentration which maximizes this rate for foraging trips of different lengths (electronic supplementary material). All statistics were carried out in R v. 3.4.1 [24]; Tukey HSD and Levene's test used the car package [25]; the generalized linear mixed model was carried out using the lme4 package [26].

3. Results

Bees on average drank 105 ± 17 µl (mean ± s.d., n = 30) on a foraging bout, with this value ranging from 52 µl to 163 µl across all 300 bouts. The bees carried on average 79.7 ± 10% (mean ± s.d., n = 30) of their unladen body mass in sucrose solution, though a few bees occasionally managed to carry more than their body mass, with a maximum of 109% of body mass. Once standardized for bee size, there was no evidence that concentration affected the volume of solution carried (ANOVA, F_2,27 = 0.848, p = 0.44). There was no difference between the mean or variance in body mass of bees from the different sucrose concentration treatments (ANOVA, F_2,27 = 1.05, p = 0.36, Levene's test, F_2,27 = 0.45, p = 0.64).

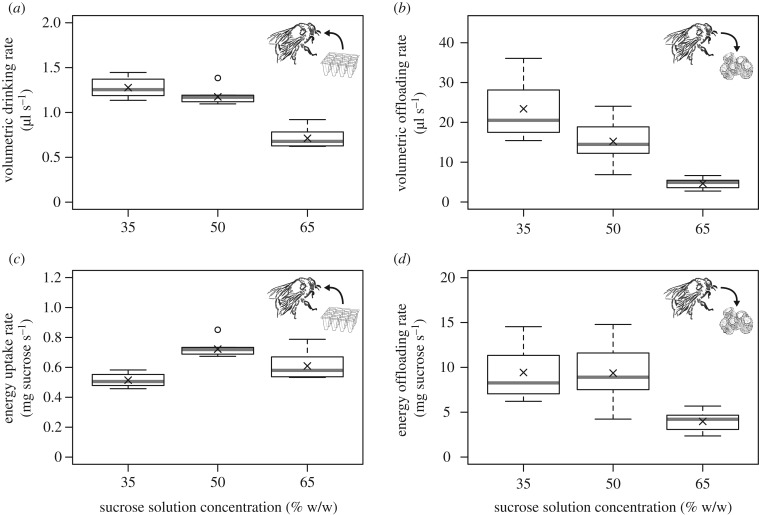
Both the volumetric drinking rate and the volumetric offloading rate varied significantly between sucrose concentrations (ANOVA, F_2,27 = 99.9, F_2,27 = 68.6, respectively, both p < 0.0001). Offloading was much faster than drinking (figure 2a,b). For both drinking and offloading, the volumetric rate was lowest at the highest concentration. For drinking, there was a small, but non-significant, decrease in volumetric rate from 35% to 50% sucrose solution (Tukey HSD, q_3,27 = 2.58, p = 0.182), and a larger decrease from 50% to 65% (Tukey HSD, q_3,27 = 15.88, p < 0.0001, figure 2a). For offloading, the decreases in rate from 35% to 50% and from 50% to 65% were both significant (Tukey HSD, q_3,27 = 4.42, p = 0.011 and q_3,27 = 11.61, p < 0.0001, respectively, figure 2b).

Figure 2.

Boxplots of mean sucrose transfer rates for B. terrestris bumblebees during drinking and offloading of sucrose solution of 35%, 50% and 65% w/w, expressed as volumetric and energy transfer rates. n = 10 bees per concentration; each observation (bee) is the mean of 10 foraging bouts. Boxes are interquartile ranges, thick lines are medians and crosses indicate overall means. The open circles are outliers. (a) Volumetric drinking rate, (b) volumetric offloading rate, (c) energy uptake rate, (d) energy offloading rate.

When considering uptake rate in terms of energy transfer, the increased energetic content of higher sucrose concentrations results in different dynamics between concentrations from that observed for volumetric transfer rates (figure 2). For both drinking and offloading, there were significant differences in energy transfer rate between concentrations (ANOVA, F_2,27 = 28.53, F_2,27 = 23.82, respectively, both p < 0.0001). Energy uptake rate during drinking was highest at 50% and lowest at 35%, with significant differences between all three concentrations (Tukey's HSD, all q_3,27 > 5.1, p < 0.005, figure 2c). Contrastingly, for energy offloading rate, there was no significant difference in rate between 35% and 50% sucrose solution (Tukey's HSD, q_3,27 = 0.23, p = 0.99), whereas offloading rate at 65% was significantly lower than both 35% and 50% (Tukey's HSD, both q_3,27 > 8.3, p < 0.0001, figure 2d).

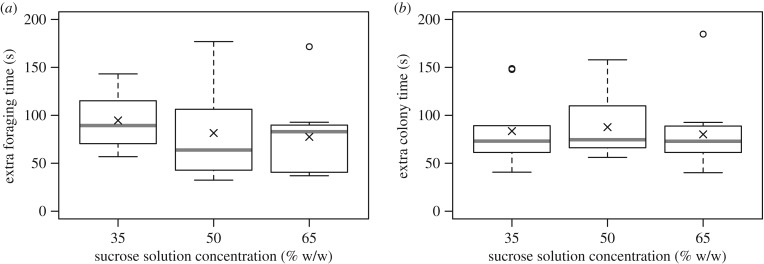
None of the other parameters recorded showed any significant differences between concentrations. There was no difference between sucrose concentrations in ‘extra foraging time', the time in the arena not spent drinking (ANOVA, F_2,27 = 1.03, p = 0.37, figure 3a) or ‘extra colony time', the time in the nest once offloading times were excluded (ANOVA, F_2,27 = 0.26, p = 0.77, figure 3b). When in the nest, the number of offloading events did not vary between concentrations (likelihood ratio test, ${\chi }_2^2=3.29,$ p = 0.19). The relationship between sucrose concentration and foraging speed was, therefore, further explored by focusing on uptake and offloading rates.

Figure 3.

Boxplots of the time spent on activities other than drinking or offloading sucrose solution during foraging behaviour. (a) Extra foraging time, i.e. the time in the flight arena not directly spent drinking. (b) Extra colony time, i.e. the time in the nest not spent offloading. n = 10 bees per concentration; each observation is the mean of 10 foraging bouts per bee. Boxplots as in figure 2.

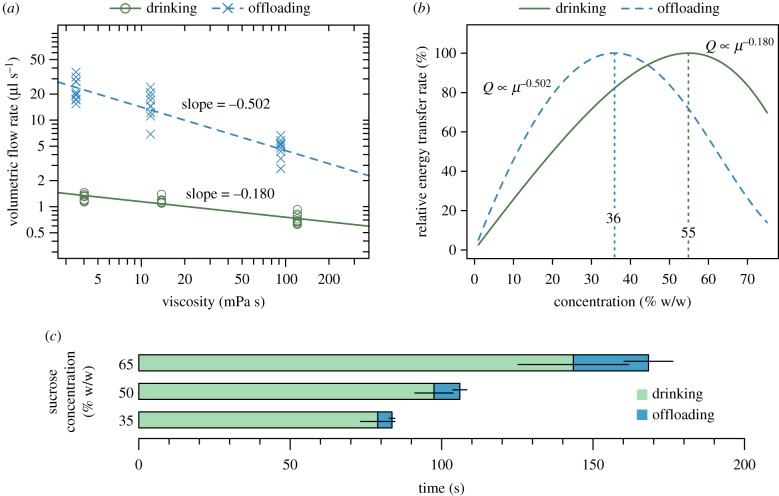
Modelling the relationship between volumetric flow rate and viscosity assuming a power-law scaling relationship resulted in a good fit to the data for offloading, although the fit for drinking was poorer (figure 4a). For sucrose solution uptake, the slope is −0.180 [95% CI: −0.211, −0.148] whereas for offloading, the slope is −0.502 [95% CI: −0.590, −0.413], hence the rates of solution transfer (Q) for these two aspects of foraging behaviour in bumblebees have different relationships with viscosity (µ) (figure 4a). For drinking, Q ∝ µ^−0.180; for offloading, Q ∝ µ^−0.502 (see electronic supplementary material for full equations). Representing these modelled relationships as the relative rate of energy transfer as a function of sucrose concentration allows prediction of the respective optimum sucrose concentrations for maximizing energy transfer for each aspect of foraging (figure 4b). For drinking, the predicted optimum sucrose concentration is 55%, whereas for offloading, the optimum is 36% (figure 4b). A consequence of the differing viscosity dependence of drinking and offloading is that the ratio of the time spent drinking to offloading decreases with increasing concentration (figure 4c).

Figure 4.

The relationship between sucrose concentration and foraging efficiency. (a) Data (circles: drinking, and crosses: offloading) and fitted models (lines) of volumetric flow rate versus viscosity for drinking and offloading of sucrose solutions. The slope for drinking, −0.180 [95% CI: −0.211, −0.148], was less steep than that for offloading, −0.502 [−0.590, −0.413]. (b) Modelled relationships for relative instantaneous energy transfer versus concentration for drinking and offloading, using the fitted (slope) parameters from (a), and assuming an air temperature of 23°C for drinking, and abdominal temperature of 27°C for offloading. These relationships give optimum concentrations for maximizing energy transfer rates of 55% for drinking and 36% for offloading. (c) The mean (±95% CI) time spent transferring 35, 50 and 65% w/w sucrose solution. The ratio of time spent drinking to offloading is approximately 17 : 1, 11 : 1 and 6 : 1 for 35, 50 and 65% sucrose solution, respectively. n = 10 bees per concentration, each observation is the mean of 10 foraging bouts per bee. (Online version in colour.)

A complete foraging bout includes time spent on activities other than drinking and offloading nectar, such as flight time to and from patches of flowers; this additional time strongly affects the overall rate of energy return (figure 5). As flight time increases, the optimum concentration at which the rate of energy return to the nest is maximized also increases, rising from 65% at a flight time (total roundtrip) of 100 s to 74% at a flight time of 900 s. Increasing flight time also lowers the overall rate of energy return at any given concentration (figure 5). The influence of the viscosity dependence of offloading behaviour in this model is illustrated by comparing our full model with a model where offloading time is fixed at the mean value of 7.3 s (electronic supplementary material) for all concentrations. At a flight time of 100 s, when the viscosity dependence of offloading is removed the optimum concentration increases from 65% to 68% and the maximum rate of energy return increases from 3.93 to 4.14 J s⁻¹ (figure 5). This effect of including the viscosity dependence of offloading results in similar changes for other flight times.

Figure 5.

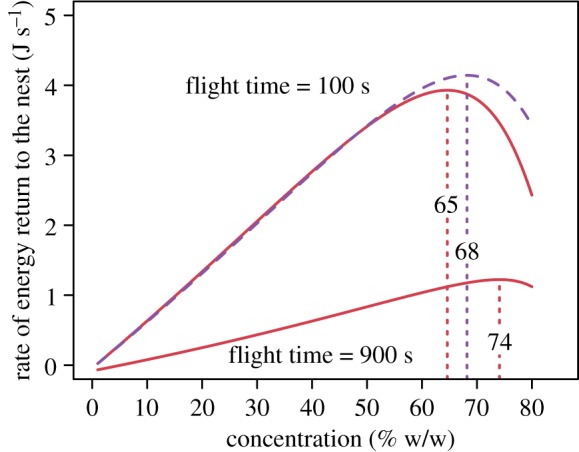
Overall energetic models for a complete foraging bout, calculated for total flight times of 100 s and 900 s and assuming a nectar (sucrose solution) load of 105 µl and bee mass of 163 mg. The rate of energy return to the nest is maximized at a sucrose concentration of 65% for a foraging bout with a flight time of 100 s and 74% for a flight time of 900 s (solid lines). The effect of excluding the viscosity dependence of sucrose offloading is illustrated by the dashed line; this is also for a flight time of 100 s but with a fixed offloading time across all concentrations and raises the concentration at which the rate of energy return is maximized to 68%. (Online version in colour.)

4. Discussion

Nectar and other sugar solutions are one of the main food sources for many animals, including numerous pollinator species [1,27–29]. The foraging preferences and behaviour of such nectar feeders will be shaped by the energetic gains and costs of foraging on particular nectars. Two key factors influencing nectar energetic value are the sugar content and drinking speed, both related to nectar sugar concentration. Although energetic value increases linearly with nectar sugar concentration, nectar viscosity increases exponentially, reducing drinking speed. At a certain sugar concentration, the costs and benefits of these two opposing factors lead to a maximal energy uptake rate for nectar feeders [9–11,14]. This value is dependent on the morphological and physiological characters of the species concerned [8,9] and is likely to be an important factor in driving foraging behaviour.

For social bees that transport resources back to a communal nest, it is not necessarily the energy uptake rate per se that is of greatest importance, but rather the rate of energy return to the nest. For these species, nectar offloading is another key component of foraging behaviour. Here, we show that in the social bumblebee B. terrestris foraging on sucrose solutions, the rate of offloading also depends on viscosity, and that, intriguingly, offloading rate is much more sensitive to viscosity than drinking rate. Consequently, there is a conflict between the nectar concentration for maximizing the rate of energy transfer between nectar drinking and offloading (figure 4).

To predict how these factors affect the rate of energy return to the nest, we developed an overall foraging model (figure 5) which combines the influence of the viscosity dependence of drinking and offloading and takes account of the time (and energy) spent on other activities during a foraging bout. This model highlights the importance of including the time spent on these additional activities. The model also illustrates that in B. terrestris, including the viscosity dependence of offloading influences both the rate of energy return to the nest and, to a lesser extent, the concentration which maximizes this rate.

4.1. Viscosity dependence, and the mechanics of nectar transport

Bumblebees drink nectar by lapping, extending and retracting their feathery glossa (tongue) in the fluid. Nectar is absorbed onto the glossa when it is extended and removed while retracted [9,16]. The volumetric drinking rate of nectar will depend on two parameters: the rate of lapping, and the volume ingested per lap [9]. On measuring these parameters in experiments with three bumblebee species, Harder [9] found that the lapping rate is independent of sucrose concentration, thus for bumblebees it is likely to be solely the volume ingested per lap that determines drinking rate.

We use the general power law Q ∝ μ^k to describe the relationship between flow rate (Q) and viscosity (µ). Here, we found that in B. terrestris, for drinking sucrose solutions, k = −0.180 [95% CI: −0.211, −0.148] such that this relationship is Q ∝ μ^−0.180. This is in good agreement with a model developed by Kim et al. [21], which predicts $k=-0.167$, and a little higher than that measured by Harder [9] who recorded $k=-0.205$ and $k=-0.225$. Discrepancy between these two previous studies may be explained by two factors: 1. Kim et al. [21] assumed that tongue retraction speed decreases with increasing concentration; this would lead to a decreased rate of lapping, something which, at least for bumblebees, appears not to be correct [9]; 2. Harder observed that bumblebee drinking rate (n = 22 across 9 species) is constant at low concentrations and only decreases with increasing concentration above 40%. Interestingly, if we calculate the decrease in mean drinking rate with our data just between 50 and 65%, we instead obtain $k=-0.230$, in agreement with Harder. We only recorded rates at three concentrations; therefore, we cannot detect whether drinking rate was constant below 40%. However, this, combined with our drinking rate model residuals (figure 4), suggests some caution should be applied to the interpretation of our drinking rate data.

This phenomenon of a threshold concentration, below which drinking rate is relatively constant, has also been observed in other species which feed by lapping, including honeybees and meliponine bees [11] and the bat Glossophaga soricina [12]. By contrast, with Bombus impatiens, Nardone et al. [10] found an increase in drinking rate with increasing sugar concentration from 10 to 27% w/w, before a subsequent decrease at higher concentrations. However, Nardone et al. only used one trial per bee and note that this positive correlation between drinking rate and concentration up to 27% w/w may reflect increased motivation of the bees as concentration increases. By comparison, Harder [9] selected the fastest drinking rate from several trials. Here, we used the mean rate over 10 trials, though there is no evidence that motivation influenced our measured drinking (or offloading) rates. Refitting our models using the maximum rate for each bee gives very similar coefficients (electronic supplementary material).

For offloading of sucrose solution, we observed a completely different relationship of flow rate with viscosity, of Q ∝ µ^−0.502. Although we are unaware of the exact mechanism of offloading, a reasonable hypothesis is that offloading occurs through muscular contraction of the honeycrop, driving the fluid back through the oesophagus so that it can be offloaded into a honeypot in the nest. Our observations suggest that the proboscis remains folded during this process. The flow rate is, therefore, likely limited by the speed at which fluid can pass through the oesophagus. This mechanism is somewhat analogous to the reverse of nectar feeders that drink using suction, such as butterflies [13,30] and Euglossine (orchid) bees [17]. Although observations and models of this process imply a more complicated relationship with viscosity than a simple power law, also influenced by feeding structure morphology [8,30], they all show a relationship where flow rate decreases with increasing viscosity more strongly than nectar feeding through lapping. A simplified model of the viscosity dependence of suction feeding by Kim et al. [21], which does not include some of these effects of feeding structure morphology, gives a relationship of Q ∝ µ^−0.5, in excellent agreement with our model of offloading (for which k = −0.502 [95% CI, −0.590, −0.413]). We therefore suggest that the relationship between viscosity and the rate of nectar offloading in bumblebees may be subject to similar constraints as nectar drinking in suction feeders and is limited by the rate of fluid flow through a tube.

In bumblebees, body size [9,10,31], glossa (tongue) length and flower depth [9] also affect drinking speed, and will contribute to species-specific differences in drinking rate [9]. However, in bumblebees, these factors do not interact with viscosity [9] (and see electronic supplementary material) and so will not affect the optimum concentration for maximizing instantaneous energy uptake rates. Indeed, the inclusion of body mass has a negligible effect on our models of viscosity versus flow rate (electronic supplementary material).

4.2. Optimal sugar concentrations for maximizing energy transfer rates

Our models of the viscosity dependence of volumetric flow and energy transfer rates indicate a conflict between drinking and offloading in the sucrose concentration which maximizes energy transfer rate, with an optimum of 55% w/w for drinking and 36% w/w for offloading. Previous models exploring optimal sugar concentrations for maximizing energy gain have not considered nectar offloading (e.g. [9]). To explore the conflict between drinking and offloading, we combined the time spent on these two behaviours into an overall model of energy return to the nest by also including the duration of other activities on a foraging trip and the energy used (i.e. the metabolic rate) throughout the trip. This shows that offloading only has a small effect on the optimum concentration, of around 3% w/w (figure 5). This relatively small effect is explained by the fact that offloading is much quicker than drinking (figure 4c).

The inclusion of offloading also lowers the estimate of the maximum rate of energy return and changes the shape of the relationship between concentration and energy transfer rates above the optimum concentration (figure 5). Although energy return rate changes relatively slowly around the optimum concentration, the rapid decrease in energy return rates above the optimum concentration in the model with offloading included could affect bee behaviour. For example, in the combined model and with a flight time of 100 s, at 75% w/w the energy return rate is around 15% lower than the maximum rate if offloading is included, but only 5% lower than the maximum if offloading is excluded. This effect is only present at very high concentrations, and involves extrapolation of our data, so it is unclear whether this will have actual effects in the field.

The models of instantaneous energy transfer rate (figure 4b) and energy return to the nest (figure 5) are based on a drinking temperature of 23°C and abdominal (offloading) temperature of 27°C. Viscosity is inversely related to temperature, and although the rate of energy return will decrease as it gets colder, changes in temperature do not have a large effect on the optimum concentration. Bumblebees are distributed from polar regions to the tropics and considering the likely temperature extremes experienced by foraging bees [23], at a flight time of 100 s, the optimum concentration in our model would vary from 67% at 35°C to 61% at 2°C.

In bumblebees, some heat is transferred between the thorax and abdomen, in contrast to honeybees [32]. This means that at low ambient temperatures, abdominal temperatures of foraging bumblebees are higher than ambient [23]. This will act to warm the carried nectar and speed up offloading, especially at higher sugar concentrations. For example, at an ambient temperature of 2°C, if abdominal temperature was only 2°C then, using our model of the viscosity dependence of offloading (figure 4a), we can predict a bee carrying 105 µl of 65% sucrose solution would offload in 63 s. However, at 2°C, abdominal temperature will actually be 18°C [23] and so offloading will only take 31 s. This effect will be enhanced if the abdomen is further warmed by being in the nest.

Although the relationship between concentration and energy return rate is structured by the viscosity dependence of both drinking and offloading, this relationship is strongly affected by the time spent on other activities during a foraging trip (figure 5). Factors such as the location of floral resources in relation to the nest, nectar volume per flower, the number of flowers per inflorescence, search for and handling of flowers will all influence this time [9]. We illustrate the general effect of changing foraging trip duration in our model by calculating energy return rates for two different flight times. By increasing flight time from 100 s to 900 s, the concentration which optimizes energy return rates increases considerably from 65% to 74%. This increase in the optimum concentration occurs because, as flight time lengthens, the proportion of the foraging trip spent drinking and offloading nectar (and thus relative importance of these behaviours in the model) decreases.

In contrast to the large effect of foraging time, our model prediction of the concentration which maximizes energy return rate is largely insensitive to variations in metabolic rate (electronic supplementary material). It should also be noted that we use a fixed nectar volume and bee mass in our model (the mean values from our data) and so the predictions quoted are for these mean parameters. Although not the focus of our study, we briefly discuss the influence of varying these parameters in the electronic supplementary material.

4.3. Foraging preferences of bumblebees

The actual nectar concentration preferences of foraging bumblebees will depend on what exactly the bees are aiming to maximize. If making the best use of time on flowers is important, for example, to reduce the risk of predation, then maximizing the energy gain during drinking may be of key importance. In this case, we would expect bees to preferentially visit concentrations of around 55% (figure 4b). By contrast, if maximizing the energy return rate to the nest is more important, then the optimum concentration will depend on the total foraging trip duration. In our model, assuming a flight time of 100 s, we would expect the bees' preference to be for sucrose concentrations of around 65% (figure 5).

The two situations described above assume that bees are trying to maximize rates of energy transfer. Schmid-Hempel and colleagues [33–36] showed in a series of papers that, at least for honeybees, this hypothesis of rate maximization may be wrong. Instead, honeybee foraging behaviour is more consistent with maximization of the energetic efficiency of foraging, i.e. the ratio of energy gained to energy used. They suggest that this is because all energetic expenditure has a cost in terms of reducing a bee's lifespan. By foraging in a way that optimizes the ratio of energy gained to energy used, the bee may prolong its lifespan and thus transport more nectar over its lifetime [33,35,36]. Using our data to calculate the ratio of energy gained to energy used (electronic supplementary material) gives, for a flight time of 100 s, an optimum concentration for maximizing energy ratio of 75% w/w, much higher than the estimates from the other models. It should be noted, however, that the optimum concentration for maximizing energy ratio is sensitive to the values chosen for the metabolic rates for drinking and offloading. Given that we did not include thermoregulatory costs (e.g. [37]) in our estimates for these, caution should be applied to this prediction. Understanding the energy currency of the species concerned is thus crucial for understanding floral reward preference.

How do the predicted optimum concentrations compare with actual concentration preferences for foraging bumblebees? The majority of studies exploring nectar concentration preferences have focused on less concentrated solutions, typically lower than around 50% w/w. At this concentration range, there is considerable evidence that bumblebees generally prefer more concentrated nectar [38–42], but preferences at concentrations higher than this are less-well understood.

One of the few studies investigating higher concentrations in bumblebees gives intriguing results. Bailes et al. [43] showed in a laboratory-based experiment that although Bombus terrestris workers preferred 55% over 40% w/w sucrose solution, they made equal numbers of visits to feeders with 55% and 68% sucrose solution. This result is in much better agreement with bees trying to maximize the rate of energy return to the nest (expected optimum of 65% w/w) rather than maximizing the rate of energy uptake while drinking (expected optimum of 55%). Indeed, in our overall model for energy return to the nest, lowering the sucrose concentration from 55 to 40% w/w results in relative energy return rates decreasing by 25%, whereas raising the concentration from 55 to 68% results in an increase in relative energy return rates of just 6%. This agrees well with the seeming ambivalence of the bees to a choice between 55% and 68% w/w sucrose observed by Bailes et al. [43].

Nachev & Winter [39] conducted an extensive concentration preference experiment with Bombus impatiens. Although they only looked at concentrations varying from 15 to 50% w/w, they showed that preference for the higher concentration is larger not only when the concentration difference is large but also when the absolute levels of the concentration are lower. That is, a 15% w/w concentration difference is more highly valued between 20% and 35% than between 35% and 50%. Although they discuss this result in terms of limits of perceptual discrimination between concentrations, this is indistinguishable from foraging preference and their data are consistent with that expected if there was an optimum concentration preference.

So far, we have only considered sucrose solutions. The relationship between sugar concentration, viscosity and energy content differs between sucrose, fructose and glucose [10] and thus optimum concentrations will vary with nectar sugar composition. Bee preference and taste perception vary between these three sugars [41,44] and so this is an additional factor to consider. Secondary nectar compounds such as feeding deterrents and amino acids can also affect preference [45,46] as well as altering viscosity [47]. Honeybees prefer lower-viscosity nectar if the sugar concentration is held constant [48], and it is likely that the same is true for bumblebees.

4.4. Wider implications and conclusions

Many animals drink sugar solutions other than nectar, such as fruit juices [28] or hemipteran honeydew [27,29], and the concepts explored here will apply more widely in these situations as well. Not all species foraging for sugar solutions need to offload—for example, butterflies drink sugar solutions for their own nutrition—and the extent to which offloading influences foraging decisions will strongly depend on how offloading is incorporated into a foraging trip.

The direct offloading shown by bumblebees also occurs in many species of solitary bees, which offload into nest cells they are currently provisioning [49]. Multiple trips are often necessary to provision a cell; however, nectar is typically just one (often minor) component of total provisions [49]. The importance of nectar offloading in this situation will depend on the proportion of time spent on provisioning the cell with nectar versus other resources. It is also likely that the nutritional requirements of the larvae, and potentially factors affecting longevity of stored nectar, will be more important than (or at least interact with) the optimization of energy return rates in driving nectar concentration preferences. This point may apply to many species which offload nectar.

Very commonly, offloading occurs via trophallaxis to another individual. For example, this happens in workers of ants [50], honeybees [15], meliponine bees [51] and in females of the nectivorous bat Glossophaga soricina when feeding their young [52]. As regurgitation is much quicker than drinking, the overall rate of offloading will be limited by the drinking rate of the receiving individual. This has several interesting consequences. Drinking and offloading will show similar overall viscosity dependence, but offloading will take much longer than if it was direct (as in bumblebees). Consequently, both the overall rate of energy return and the concentration that maximizes that rate will be lower than if that species offloaded directly. The drinking rate of the receiving individual may, therefore, play a part in influencing the nectar preferences of the forager, particularly when the drinking speed of the receiver is comparatively slow, which may be the case, for instance, for a juvenile bat.

Direct offloading is not an option for G. soricina but, given the energetic costs, why might honeybee foragers engage in time-consuming trophallaxis rather than offloading directly into the nest? Although the speed of trophallaxis is affected by viscosity [19], the timing is also modified by the bees involved, with the suggestion that this plays a role in information transfer, informing other bees about profitable nectar sources [19,53]. Furthermore, honeybee colonies are much larger than those of bumblebees, and it may be that although trophallaxis is comparatively slow, overall it is more efficient to partition tasks and let a nest bee spend time searching for a location to store collected nectar.

In summary, by exploring the mechanics of nectar offloading behaviour, this study has addressed a little-explored aspect of optimal concentrations in nectar feeding. In bumblebees, nectar offloading shows very different mechanics from nectar drinking and influences the rates of energy return to the nest. Despite the now considerable body of research on optimal nectar concentrations, there is still little work on how these predicted concentrations agree with actual foraging preferences, especially at higher concentrations, and this would be a valuable avenue for further investigation. Plants may be unlikely to offer nectar of optimal composition, instead seeking to manipulate visitor behaviour to maximize pollination efficiency [54,55]. Resolving how pollinator preference and floral nectar composition interact is a key aspect to understanding plant–pollinator coevolution.

Data accessibility

The data supporting this paper are available as electronic supplementary material.

Authors' contributions

J.G.P. conceived the ideas. J.G.P., H.A.S. and B.J.G. designed the methodology. H.A.S. collected the data. J.G.P. and W.F. analysed the data. J.G.P. led the writing of the manuscript. All authors contributed critically to the final draft.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by a Biotechnology and Biological Sciences Research Council PhD Studentship under grant no. BB/J014540/1 to J.G.P.