Machine-learned patterns suggest that diversification drives economic development

Abstract

We combine a sequence of machine-learning techniques, together called Principal Smooth-Dynamics Analysis (PriSDA), to identify patterns in the dynamics of complex systems. Here, we deploy this method on the task of automating the development of new theory of economic growth. Traditionally, economic growth is modelled with a few aggregate quantities derived from simplified theoretical models. PriSDA, by contrast, identifies important quantities. Applied to 55 years of data on countries’ exports, PriSDA finds that what most distinguishes countries’ export baskets is their diversity, with extra weight assigned to more sophisticated products. The weights are consistent with previous measures of product complexity. The second dimension of variation is proficiency in machinery relative to agriculture. PriSDA then infers the dynamics of these two quantities and of per capita income. The inferred model predicts that diversification drives growth in income, that diversified middle-income countries will grow the fastest, and that countries will converge onto intermediate levels of income and specialization. PriSDA is generalizable and may illuminate dynamics of elusive quantities such as diversity and complexity in other natural and social systems.

Computers can learn to predict the future using vast datasets too large for humans to grasp. The logic behind a machine’s prediction, however, is often inscrutable [1], and accuracy, not insight, is often the goal. Scientists, meanwhile, generate new theories using intuition or derive them incrementally from existing models. Recent advances in interpretable machine learning are enabling the generation of theories to be automated: machines have identified mathematical laws in physical and biological systems that took many years for scientists to solve manually [2–6]. But while pendulums and fluid dynamics may follow elegant governing equations, systems comprising capricious humans may not. Thus, in social sciences, it is challenging for machines to teach humans better theories.

We introduce a method for identifying interpretable patterns in high-dimensional time series called Principal Smooth-Dynamics Analysis (PriSDA), and apply it to a unifying question within the social sciences: why some countries are rich and others are poor. PriSDA ingests time-series data from a system characterized by potentially many dimensions, and it identifies a small number of dynamical equations involving smoothing splines that model how the system changes over time. The resulting model is optimized for accuracy yet is readily interpretable.

Traditionally, one builds an economic theory by manually choosing a dimension-reduced representation of a complex process, such as ‘utility’ or an aggregated value such as gross domestic product. Then one constructs models of how those few quantities change over time, and finally one estimates the derived model with data. These models often neglect important patterns, such as the emergence of the tremendous diversity of goods or why rich countries trade with other rich countries [7]. Agnostic of explicit traditions of economics, what theory of economic growth would an automated economist find?

Here, we analyse machine-reduced dimensions of countries’ export baskets (corrected for population size) using principal components analysis (PCA) [8], and then we train generalized additive models (GAMs) [9] to predict yearly changes in export baskets and in per capita income. The results indicate the fundamental importance of an economy’s (complexity-weighted) diversity, both as a summary statistic—diversity captures more variance of export baskets across time than any other direction—and as a predictor of growth. The method, PriSDA, is generally applicable and may illuminate the emergence of diversity and complexity in other biological, physical and social systems.

1. Methods

The PriSDA method identifies equations that predict changes over time (using non-parametric regression, here GAMs) in a complex system described using dimension reduction and potentially other aggregate quantities. Crucial to its success is providing it data that allows large and small units (here, national economies) to be comparable yet allow for absolute growth.

1.1. Multidimensional characterization of the productive capabilities of economies

There is growing interest in multi-dimensional metrics of economic development and poverty [10,11]. We track macro-level multidimensional economic development based on annual exports, for which there are high-quality data for all countries over the past half-century. A country’s exports indicate its international competitive advantages, and unlike domestic production, exports share a common classification system. Indices of the complexity or competitive fitness of economies have been constructed using exports data [12–14], a literature summarized in electronic supplementary material, SM-1 and discussed more below.

Instructions for accessing the data and details on its preprocessing are in electronic supplementary material, SM-2 and SM-3. Because data on exports are noisy, products are aggregated into 59 categories (electronic supplementary material, SM-3.1). The value of a country c’s exports of a product p in year t, denoted X_cpt, tends to correlate positively with the size of the country’s population, P_ct. To account for that relationship, X_cpt is divided by an expectation according to a null model of a country’s expected value of an export given that country’s population. To remove the effects of global price shocks, this quantity is divided by the total value of the world’s exports of that product, which is also normalized by a null model that predicts global export value using global population. We call the resulting quantity the absolute advantage of a country c in a certain product p in year t, denoted ${\mathcal{R}}_{cpt}$:

$${\mathcal{R}}_{cpt}=\frac{X_{cpt}/\mathbb{E}\hspace{0.17em}[X_{cpt}|P_{ct}]}{\sum _c{X}_{cpt}/\mathbb{E}\hspace{0.17em}[\sum _c{X}_{cpt}|\sum _c{P}_{ct}]}.$$ 1.1

Details are in electronic supplementary material, SM-3.2. We consider countries as length-59 vectors of ${\mathcal{R}}_{cpt}$ across all products; a two-dimensional projection of two trajectories of ${\mathcal{R}}_{cpt}$ is shown in figure 1a. Unlike relative quantities such as revealed comparative advantage [15], a country can grow its absolute advantage arbitrarily. For example, in 2016, Belgium and The Netherlands were the only countries that ‘punched above their weight’ (i.e. had ${\mathcal{R}}_{cpt}>1$) for all 59 products p.

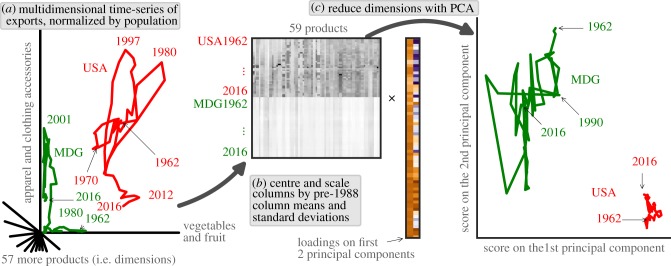
Figure 1.

Preprocessing and reducing dimensions of export baskets. (a) Begin with time series of export values of 59 product categories, normalized by population (electronic supplementary material, Eq. (SM-1)) and logarithmically transformed (electronic supplementary material, Eq. (SM-5)) to make large and small countries comparable. For illustration, we show the trajectories of the United States (USA) and Madagascar (MDG). We are illustrating two dimensions here, but in reality the red and green curves live in 59 dimensions. (b) Centre and scale columns by their pre-1988 means and standard deviations. (c) Reduce dimensions with principal components analysis (PCA). Each country’s score in a given principal component represents a certain linear combination of its export basket. Together, the scores on the first few principal components summarize the country’s export basket with just a few numbers. (Online version in colour.)

To put products on equal footing with each other, we centre and scale ${\mathcal{R}}_{cpt}$ by the mean and standard deviation of ${\mathcal{R}}_{cpt}$ across all countries and across all years t ≤ 1988 (figure 1b). We call the resulting quantity scaled absolute advantage and denote it by R_cpt. Scaled absolute advantage is the number of standard deviations above the pre-1988 mean of all countries’ absolute advantage in that product. R_cpt > 0 means that country c excels at producing and exporting product p in year t. Making products comparable—by dividing by the product’s global export market in ${\mathcal{R}}_{cpt}$ and by centring and scaling each product in R_cpt—enables detecting how expertise in one product enables developing expertise in another, regardless of the sizes of the markets of those products.

1.2. Reducing dimensions of export baskets

We reduce dimensions using PCA [8] because the resulting dimensions are interpretable and because summing exports reduces the noise in export data. Other methods are discussed in electronic supplementary material, SM-1.

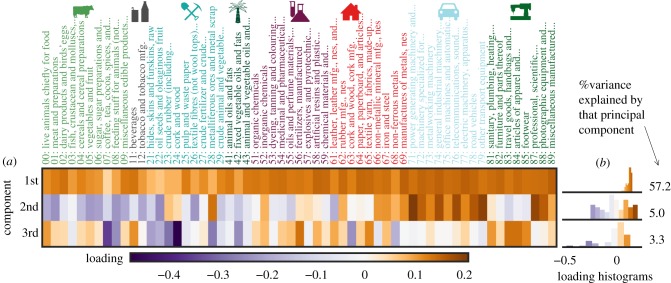
Figure 2 shows the loadings (weights) of the first three principal components on the 59 products. The score of a country’s export basket on the kth principal component—denoted ϕ_k—is the dot product (illustrated in figure 1c) of the country’s export basket, ${(R_{cpt})}_{\hspace{0.17em}p\in \mathcal{P}}$, with that principal component’s loading vector, drawn as a row of rectangles in figure 2a. We interpret this PCA in the Results section below.

Figure 2.

The first three principal components are approximately (1) total absolute advantage summed across all products (with more weight on product codes above 50), (2) machinery minus agriculture, and (3) textiles and fertilizer minus coffee and cork. In plot (a), the rows are principal components, the columns are products, and the rectangles’ colours represent the loading (or ‘weight’) of that principal component on that product. The first component loads positively on all products. Thus, what distinguishes countries, above all, is their ‘diversification’ across products. The second component loads highly on machinery (product codes beginning with 7) and other manufactured goods, and it loads negatively on agricultural products. Thus, the direction in 59-dimensional product space orthogonal to the first component that most spreads out observations points towards machinery and away from agriculture. The third component loads positively on clothing and textile products and negatively on cork and wood (24) and coffee, tea and spices (07). The plots labelled (b) are histograms of loadings, across all 59 products, in the corresponding rows. (Online version in colour.)

1.3. Inferring dynamics of export baskets

To understand patterns in economic development, next we examine how two summary measures of an export basket, ϕ₀ and ϕ₁, interact with per capita income [16] (transformed logarithmically): $\mathtt{G}\mathtt{D}\mathtt{P}\mathtt{p}\mathtt{c}\equiv {\log }_{10}(\text{GDP}\hspace{0.17em}\hspace{0.17em}per\hspace{0.17em}capita)$. Because excelling at exports reflects the capabilities and know-how within a country [12,17,18], by inferring a model of how the triple $({\varphi }_0,{\varphi }_1,\mathtt{G}\mathtt{D}\mathtt{P}\mathtt{p}\mathtt{c})$ changes over time, we aim to shed light on fundamental economic patterns.

The three variables $({\varphi }_0,{\varphi }_1,\mathtt{G}\mathtt{D}\mathtt{P}\mathtt{p}\mathtt{c})$ are aggregate descriptions of an economy, so we expect them to change smoothly over time. A natural choice for a smooth model are cubic smoothing splines [9, ch. 3 and 4]. We chose this class of GAMs because they are interpretable yet predict as well as other general-purpose learning methods like gradient boosting (electronic supplementary material, table SM-4). This method provides us with the following system of dynamical equations:

$$g(\mathrm{\Delta }{\varphi }_0(t))=c_0+s_{00}({\varphi }_0(t))+s_{01}({\varphi }_1(t))+s_{02}(\mathtt{G}\mathtt{D}\mathtt{P}\mathtt{p}\mathtt{c}(t))$$ 1.2a

$$g(\mathrm{\Delta }{\varphi }_1(t))=c_1+s_{10}({\varphi }_0(t))+s_{11}({\varphi }_1(t))+s_{12}(\mathtt{G}\mathtt{D}\mathtt{P}\mathtt{p}\mathtt{c}(t))$$ 1.2b

$$\begin{array}{r}\mathrm{and}g(\mathrm{\Delta }\mathtt{G}\mathtt{D}\mathtt{P}\mathtt{p}\mathtt{c}(t))=c_2+s_{20}({\varphi }_0(t))+s_{21}({\varphi }_1(t))+s_{22}(\mathtt{G}\mathtt{D}\mathtt{P}\mathtt{p}\mathtt{c}(t))\end{array},$$ 1.2c

where Δ takes the expected difference in time, $\mathrm{\Delta }f(t)\equiv$ $\mathbb{E}[f(t+1)-f(t)]$; the c_i are intercept terms; the s_i,j are cubic smoothing splines with smoothing strength chosen using nested-in-time cross validation (electronic supplementary material, SM-5.1.1); and the link function g(x) ≡ sign(x)|x|^1/2 is applied to make the residuals’ distributions closer to a normal (electronic supplementary material, SM-5.2). The goodness of fit (R² ≈ 0.04) and the GAM’s competitiveness with other statistical learning methods are discussed in electronic supplementary material, SM-5.1.2.

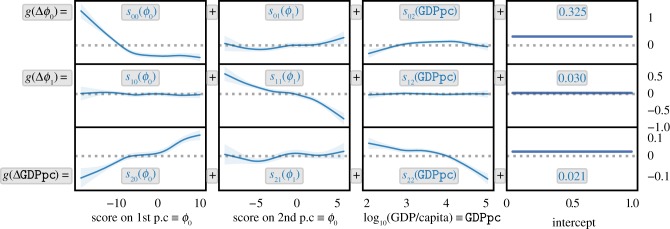
The terms of (1.2) are plotted in figure 3, where one can compare not only the shapes but also the magnitudes. The GAM (1.2) can be understood as a dynamical model inferred from the data, with which we can attempt to predict the future; it can also be understood as a histogram smoother that helps us see signal amid the noise.

Figure 3.

Export baskets tend to diversify and converge to a balance of agriculture and manufactured goods. Shown are partial dependence plots of the three equations in (1.2). Each blue (solid) curve is an additive contribution to the quantity written in black on the left-hand side of this figure, which is a link function g applied to the expected yearly change in one of the three variables ϕ₀, ϕ₁, $\mathtt{G}\mathtt{D}\mathtt{P}\mathtt{p}\mathtt{c}$. (See the text after (1.2) for the definition of g.) In each plot, the quantity being plotted is written in blue within the plot. Adding the blue expressions across a row gives the right-hand sides of (1.2). The shaded regions show the 95% CI. Each equation has an intercept, c_i, shown in the right column. The plots on the diagonal have negative trends, suggesting convergence. Interestingly, income is not associated with changes in export baskets, but ϕ₀ appears to drive $\mathtt{G}\mathtt{D}\mathtt{P}\mathtt{p}\mathtt{c}$: diversifying precedes income growth. (Replacing ϕ₀ with diversification preserves the positive trend in the bottom-left plot, but replacing it with per capita exports greatly weakens that relationship; see electronic supplementary material, Figs. SM-13 and SM-14.) (Online version in colour.)

2. Results

2.1. How a machine summarizes an economy

The first principal component is the direction in product space along which countries are most spread out in terms of variance [8]. We find this direction to be associated with total per capita exports and the diversification across products. This first component explains more than half of the variation in export baskets (57.2%) across countries and years.

Mathematically, a country’s score ϕ₀ on the first principal component is a weighted sum of R_cpt (scaled absolute advantage) across all products. The weights are fixed once PCA has been fitted, but since export baskets change in time, scores ϕ₀ change from year to year (and from country to country). The weights of this principal component are all positive and are depicted in the top row of figure 2a. The score ϕ₀ is highly correlated with per capita exports summed across products, $\sum _p{X}_{cpt}/P_{ct}$ (Pearson ρ = 0.82; electronic supplementary material, Fig. SM-6). This correlation, however, is trivial and unsurprising given that ϕ₀ is a positively weighted sum across products. However, the finding that the weights are all positive, together with the fact that this principal component explains almost 60% of the variation, is not trivial and is of economic significance.

More surprising is the association between the score on the first component, ϕ₀, and diversity, the number of distinct product categories exported in large numbers (see electronic supplementary material, SM-4.2.2). Diversity is more correlated with ϕ₀ than per capita exports are (Pearson ρ = 0.67 versus ρ = 0.46). The values of ϕ₀ remain highly correlated with per capita exports and diversity even after controlling for other covariates (namely, Worldwide Governance Indicators and measures of educational attainment; see electronic supplementary material, Fig. SM-6–SM-10). Thus, in the dimension defined by the first principal component, countries are separated by not just how much they export in total but how diversified those exports are.

The score ϕ₀ on the first principal component also emphasizes the complexity of products: notice in the top row of figure 2a that the loadings are not uniform: they are about twice as large on the more complex products. These variations in the loadings, in fact, are highly correlated with the Product Complexity Index [12] (Pearson ρ = 0.81; electronic supplementary material, Fig. SM-5). Thus, the score ϕ₀ captures the diversification [12] of an economy, with an emphasis on more complex goods. Relationships between ϕ₀ and other quantities are characterized in electronic supplementary material, SM-4.

The next direction that most spreads out export baskets across countries and across time—conditional on being orthogonal to the first component—loads highly on machinery and negatively on agricultural products (figure 2a, middle row). Thus, after knowing a country’s complexity-weighted diversity ϕ₀, the next characteristic that most spreads out countries is how much more they export in machinery relative to agricultural goods. This second principal component explains 5% of the variance, 11 times less than that explained by ϕ₀.

Garments have long been considered to be the first sector to industrialize in a country, including in England during the industrial revolution and in many East Asian countries since the 1960s [19]. However, these products are not an important direction of variation of export baskets between 1962 and 1988 in the first and second principal components. Only in the third principal component are textile products substantially loaded (figure 2a, bottom row). Because this component only explains 3.3% of the variance of export baskets, hereafter, we focus on the first two principal components.

2.2. Complexity-weighted diversity predicts growth

The partial dependence plots in figure 3 show how yearly changes in ϕ₀, ϕ₁, and $\mathtt{G}\mathtt{D}\mathtt{P}\mathtt{p}\mathtt{c}$ are predicted by sums of one-dimensional functions of those same variables. The rows of figure 3 depict the three equations (1.2a)–(1.2c). Note that per capita income is not a strong predictor of changes in export baskets as measured by ϕ₀ and ϕ₁ (see the top and middle plots in the third column of figure 3). By contrast, the score ϕ₀ on the first principal component is associated with significant growth in income, even though ϕ₀ and ϕ₁ were defined independently of income. The fact that ϕ₀, the complexity-weighted diversity of an economy, seems to drive income, and not the reverse, is consistent with the hypothesis that income is the outcome: income emerges from the productive capabilities of an economy, captured here by ϕ₀ and ϕ₁.

If the ‘off-diagonal’ terms $s_{01}({\varphi }_1)+s_{02}(\mathtt{G}\mathtt{D}\mathtt{P}\mathtt{p}\mathtt{c})$ in (1.2a) were absent, then ϕ₀ would settle onto a value near − 10. This amount is approximately the value of ϕ₀ of the poorest countries in 2016, such as Liberia, Angola and the Democratic Republic of the Congo. However, the large intercept in (1.2a) (the top-right plot in figure 3) suggests a general positive tendency to diversify, regardless of the country’s absolute advantage in machinery relative to agriculture (ϕ₁).

Exporting more agricultural than machinery products (i.e. ϕ₁ < 0) is typically associated with a slight drag on ϕ₀ (second column, top plot in figure 3); once machinery and agriculture balance (ϕ₁ ≈ 0), that drag on ϕ₀ vanishes.

Once a country has complexity-weighted diversification ϕ₀ > 0, it can expect significant growth in income (first column, left plot of figure 3). Interestingly, simply exporting more per capita, regardless of the allocation across products, is not associated with growth: when ϕ₀ is substituted with total per capita exports, the relationship with income growth flattens (electronic supplementary material, Fig. SM-13). Exporting more kinds of goods matters: replacing ϕ₀ with another notion of diversity [12] preserves the positive relationship with income growth (electronic supplementary material, Fig. SM-14).

We note, in addition, that the lack of clear association between s₂₁ (ϕ₁) and growth of $\mathtt{G}\mathtt{D}\mathtt{P}\mathtt{p}\mathtt{c}$ implies that there are weak returns to specialization. In fact, ϕ₁ tends towards zero, regardless of the other two variables, meaning that countries tend towards a diversified export basket that balances agriculture with machinery. These results suggest that export baskets tend to increasingly resemble one another. Next, we examine this convergence in more detail.

2.3. Two-dimensional projections of the data and of the learned dynamics

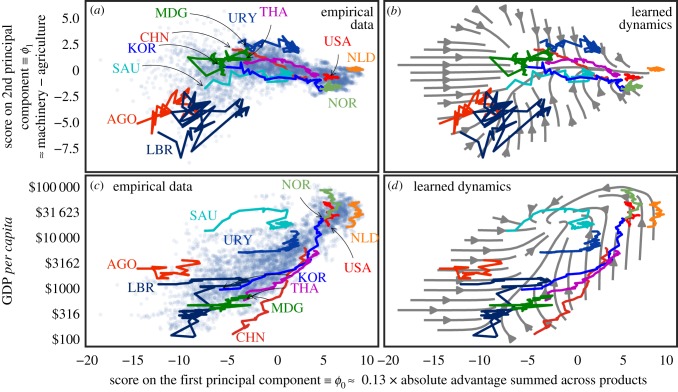
In figure 4, we compare the model (1.2) with the empirical data. This figure projects the data onto (ϕ₀, ϕ₁) (top row) and onto $({\varphi }_0,\mathtt{G}\mathtt{D}\mathtt{P}\mathtt{p}\mathtt{c})$ (bottom row). The left-hand column shows empirical data, with some countries’ trajectories highlighted. The right-hand column visualizes the vector field of (1.2) as a ‘stream plot’, with the third variable not plotted taken to be the pre-1988 mean. That is, the arrows are the expected movement for countries whose third variable (the one not plotted) equals the pre-1988 mean; for other countries, the arrows approximate their expected movement.

Figure 4.

The learned dynamics (1.2) predict that countries are converging. The left column shows empirical data with blue dots; the right column shows predictions of the model (1.2) as stream plots. The empirical trajectories of eight countries over years 1962–2016 are superimposed on all four plots. Trajectories are labelled at the first available sample (year 1985 for Angola, 1962 for the rest). A country is represented by a triple $({\varphi }_0,{\varphi }_1,\mathtt{G}\mathtt{D}\mathtt{P}\mathtt{p}\mathtt{c})$, and the model (1.2) has been trained on this three-dimensional space, but here we show projections onto (ϕ₀, ϕ₁) in the top row and onto $({\varphi }_0,\mathtt{G}\mathtt{D}\mathtt{P}\mathtt{p}\mathtt{c})$ in the bottom row. (a) Countries tend to diversify (increase ϕ₀) and strike a balance between machinery and agriculture (ϕ₁ ≈ 0). (c) Development success stories (e.g. THA, KOR, CHN) share a common trajectory of increasing ϕ₀ and income. (d) Poor countries may follow in their footsteps, but income in the richest countries may stagnate or even fall. Countries are labelled with United Nations ISO-alpha3 codes. (Online version in colour.)

The data in figure 4a show that countries tend to move from left to right (they export more and diversify) and towards the middle of the vertical axis (they move towards ϕ₁ ≈ 0, a balance between agriculture and machinery). The grey streamlines of the inferred model in figure 4b confirm this pattern, suggesting that countries converge towards the trajectory like that of Thailand’s (purple, labelled THA). In the bottom row, the data in figure 4c show that development success stories like South Korea (KOR), Thailand and China (CHN) share a common trajectory of increasing ϕ₀ and income. The inferred model’s streamlines in figure 4d suggest that poor countries will follow in their footsteps, but also that income in the richest countries may fall. The ‘J’ shape in figure 4c,d suggests that growth only takes over after diversification reaches a critical value.

It is interesting to compare the bottom row of figure 4 with the analogous plots in figs 1 and 2 of Cristelli et al. [20], who constructed a ‘fitness’ index of a country’s intangible capabilities using an iterative calculation involving export baskets. (A summary of this index and of others like it is in electronic supplementary material, SM-1.) Here, ϕ₀ plays a role analogous to the fitness index. Our method automatically recovered the behaviour found in [20] that countries tend to diversify before their per capita income grows. Whereas the coarse-grained dynamics of Cristelli et al. [20] indicate that chaos and turbulence characterize poorer countries, the splines (1.2) chose more smoothness in that region.

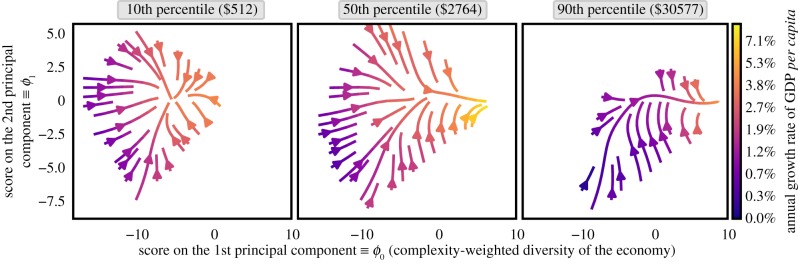
2.4. Stream plots of export baskets at different levels of income

In figure 5, we vary $\mathtt{G}\mathtt{D}\mathtt{P}\mathtt{p}\mathtt{c}$ across three values, the 10th, 50th and 90th percentiles of per capita income in year 1988. As a country’s per capita income rises, the map of how its export basket moves through the space of products (as described by ϕ₀, ϕ₁) morphs from the plot on the left to the plot on the right. The colours denote the model’s predicted change in per capita income (equation (1.2c)). In the plot on the left, we see that the poorest countries tend towards a fixed point: what little they export (ϕ₀ ≈ −8) tends towards a balance between agriculture and machinery (ϕ₁ tends to zero). Countries with per capita income near the median ($2764 per year) tend to grow their complexity-weighted diversification ϕ₀ (note the trend to the right in the middle plot of figure 5), a pattern that continues for the richest countries (right-hand plot of figure 5). It appears that one need not be very rich to begin to diversify.

Figure 5.

Inferred dynamics of export baskets, at three levels of per capita income, predict convergence in the long run. The streamlines show how a country’s export basket, described by its scores (ϕ₀, ϕ₁) on the first two principal components, changes over time according to the GAM (1.2). From left to right, the plots correspond to GDP per capita at the 10th, 50th and 90th percentiles of per capita income among countries in the year 1988. Those percentiles are the value inserted into (1.2); we show streamlines at (ϕ₀, ϕ₁) pairs in the convex hull of all empirical samples $({\varphi }_0,{\varphi }_1,\mathtt{G}\mathtt{D}\mathtt{P}\mathtt{p}\mathtt{c})$ with $\mathtt{G}\mathtt{D}\mathtt{P}\mathtt{p}\mathtt{c}$ within 15% of the value shown at the top of the plot. The predicted yearly change in per capita income is plotted in colour. The model predicts that poor countries move towards a balance of agriculture and machinery before increasing their total exports. (Said formally, ϕ₁ → 0 in the left plot, and ϕ₀ increases substantially in the middle and right plots.) Eventually, all countries are predicted to become rich and to have diverse export baskets (high ϕ₀) that balance between agriculture and machinery (ϕ₁ ≈ 0). (Online version in colour.)

This movement in product space (ϕ₀, ϕ₁) appears to maximize expected short-run increases in income, according to (1.2) (electronic supplementary material, Fig. SM-18). High-income countries tend to be best at moving towards higher income (except for brief periods), and China has been exceptional at it since 1990.

2.5. Long-run predictions of per capita income

Research on economic complexity has focused on growth predictions as validation [12,20] and, recently, research [21] has benchmarked these predictions against those of the International Monetary Fund. We found that predicting the change of export baskets simultaneously with the change of per capita income was inherently a hard problem across different statistical learning methods (electronic supplementary material, SM-5.1.2). Instead, we found our low-dimensional model to be better suited for generating interpretable, qualitative insights rather than making competitive predictions. With this caveat in mind, we investigate the model’s long-run predictions by iterating 1-year predictions starting from 2016 data.

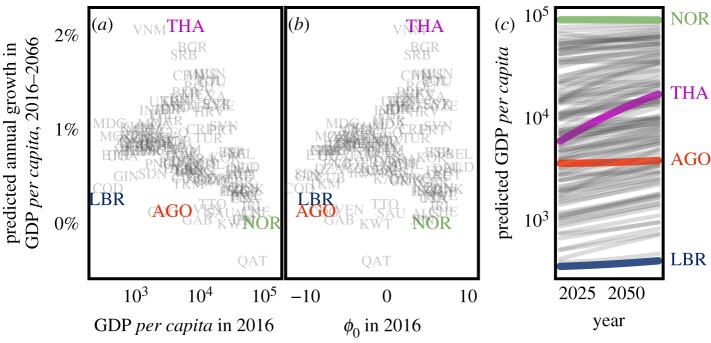
Figure 6 shows the model’s long-run predictions of growth in per capita income as a function of (A) per capita income and (B) ϕ₀ in 2016. The model predicts that the diverse, middle-income countries today will significantly catch up to the richest ones, growing at an annual rate of 2%. Meanwhile, it predicts that poor countries (such as Liberia) and middle-income countries with low diversity ϕ₀ (such as Angola) are predicted to grow between 0 and 1% annually. Rich countries like Norway are predicted to barely grow at all. The next economic success stories, according to this model, are those with intermediate income and diversification today. These results are consistent with one of the ‘New Kaldor facts’ [22] that rich countries grow more slowly than middle-income countries.

Figure 6.

Catch-up of the diverse, middle-income countries. Shown are predicted annual growth rates of per capita income (in constant 2010 USD per person per year) over the next 50 years as a function of (a) current per capita income and (b) current score ϕ₀ on the first principal component. (c) Predicted trajectories of per capita income. Highlighted are four countries representative of four groups: low-income countries predicted to grow little (Liberia, LBR); middle-income countries with high diversity (high ϕ₀) today predicted to grow a lot (Thailand, THA); middle-income countries with low diversity (low ϕ₀) predicted to grow little (Angola, AGO); and high-income countries predicted to grow little (Norway, NOR). The GAM (1.2) predicts the highest growth in income for economies that currently have intermediate income (annual growth $\approx 1.5\text{\%}$ to 2% for countries with yearly per capita income between $1000 and $20 000) and lower growth rates for poorest countries (0 to 1% growth) and the richest countries (0 to 0.5% growth). (Online version in colour.)

3. Discussion

This investigation sits at the intersection of three recent developments in the quantitative social, natural, and physical sciences: (1) the roles of complexity and diversity as drivers of economic growth [12,23]; (2) identifying universal, low-dimensional patterns of complex human systems over time [24]; and (3) using machine learning to uncover governing laws of biological and physical systems [4–6].

We accordingly developed a new method, PriSDA, by applying tools from statistical learning—namely, dimension reduction and GAMs—to identify stylized patterns in economic development. Our measure of countries’ proficiencies in exporting 59 product categories allows for small and large countries to be comparable, adjusts for global shocks, and can account for absolute economic growth. Given these data, PriSDA found a complexity-weighted measure of diversity, and it approximately recovered the product complexity index [12].

Our analysis generated two core insights. First, diversity appears to drive per capita income; merely exporting a lot per capita has a weaker association with income growth. Second, countries are not predicted to split into rich and poor clubs, nor into manufacturing hubs and agricultural hubs, but instead to converge on the same increasingly diverse basket of goods (and capabilities). We hope that future research reconciles these patterns of diversification with the specialization predicted by Ricardian theories of comparative advantage [25,26]. The most dynamic economies of the twenty-first century are predicted to be middle-income economies that are somewhat diversified across products. The least diversified countries have dismal prospects for economic growth, consistent with previous findings [23].

The importance of this approach rests on its applicability beyond the specific case studied here. In general, systems whose evolution is described by a multiplicity of properties are amenable to analysis such as the one we propose here. For example, it is known that wildfires typically reduce the number of species that inhabit an ecosystem, but then species recolonize over time as diversity rises in a process called ecological succession [27]. The composition of species in a system can also converge due to migration [28]. PriSDA could reveal other patterns, still unknown, in such ecological systems. These commonalities suggest the possibility of general theories of complex systems, uncovered by machines less tied to disciplinary paradigms.

Rapidly advancing ways for machines to learn interpretable models bode well for followup studies. Because the model (1.2) is additive, it does not capture interactions, so the effect of ϕ₁ on ϕ₀, for example, is assumed to be independent of ϕ₀. Future work could relax that assumption, using methods like GA²M [29]. High-dimensional data could be fitted with GAMs that both smooth the data and select terms, such as GAMSEL [30] or SPLAM [31]. PriSDA takes a step towards this broader goal of using machines to generate fundamental theories of complex natural and social systems.

Data accessibility

The data, available at Dataverse, were analysed using open-source software, including NumPy, pandas, SciPy and pyGAM [32]. Code to reproduce this work is available at GitHub. Details on the standardization and preprocessing of this dataset are in electronic supplementary material, SM-2 and SM-3.

Authors' contributions

C.D.B. and A.G.L. performed research. C.D.B. wrote programming and statistical code. All authors designed research, wrote the paper and gave final approval for publication.

Competing interests

The authors declare that they have no competing interests.

Funding

C.D.B. and M.H.B. acknowledge funding from the James S. McDonnell Foundation for the Postdoctoral Award and the Scholar Award (respectively) in Complex Systems.