Revisiting double diffusion encoding MRS in the mouse brain at 11.7T: Which microstructural features are we sensitive to?

Abstract

Brain metabolites, such as N-acetylaspartate or myo-inositol, are constantly probing their local cellular environment under the effect of diffusion. Diffusion-weighted NMR spectroscopy therefore presents unparalleled potential to yield cell-type specific microstructural information. Double diffusion encoding (DDE) consists in applying two diffusion blocks, where gradient’s direction in the second block is varied during the course of the experiment. Unlike single diffusion encoding, DDE measurements at long mixing time display some angular modulation of the signal amplitude which reflects microscopic anisotropy (μA), while requiring relatively low gradient strength. This angular dependence has been formerly used to quantify cell fiber diameter using a model of isotropically oriented infinite cylinders. However, how additional features of the cell microstructure (such as cell body diameter, fiber length and branching) may also influence the DDE signal has been little explored. Here, we used a cryoprobe as well as state-of-the-art post-processing to perform DDE acquisitions with high accuracy and precision in the mouse brain at 11.7 ​T. We then compared our results to simulated DDE datasets obtained in various 3D cell models in order to pinpoint which features of cell morphology may influence the most the angular dependence of the DDE signal. While the infinite cylinder model poorly fits our experimental data, we show that incorporating branched fiber structure in our model allows more realistic interpretation of the DDE signal. Lastly, data acquired in the short mixing time regime suggest that some sensitivity to cell body diameter might be retrieved, although additional experiments would be required to further support this statement.

1. Introduction

Elucidating brain cells’ structural complexity is a formidable task that has been driving decades of intense methodological development in the field of nuclear magnetic resonance (NMR) in vivo. Magnetic resonance imaging (MRI) is based on the detection of the abundant pool of water molecules in biological tissues and offers a variety of contrasts such as diffusion MRI, which has led to invaluable insights into brain microstructure (Alexander et al., 2019; Novikov et al., 2019). Improvements in scanner hardware has allowed the implementation of magnetic resonance spectroscopy (MRS) at very high field in vivo, yielding highly-resolved spectra for the accurate quantification of brain metabolites (Tkac et al., 2009). MRS therefore opens up a direct and specific access to brain biochemistry to non-invasively assess and monitor pathologies affecting the central nervous system (CNS) (Gill et al., 1989). It is furthermore possible to be sensitive to metabolite diffusion, e.g. using a pair of diffusion gradients as proposed by Stejskal-Tanner (Stejskal and Tanner, 1965). This is of particular interest because intracellular metabolites are constantly exploring their local environment under the effect of diffusion, thus potentially reporting precious information on several features of cell microstructure such as cell fiber length or diameter (Palombo et al., 2018c). Moreover, unlike water, some metabolites are known to be confined in specific cell compartments, as in the case of N-acetylaspartate (NAA) and glutamate (Glu), which are neuronal markers, or myo-inositol (Ins) and choline compounds (tCho), which are associated with glial cells (Choi et al., 2007). This enables probing the microstructure of specific cell types, which might be highly relevant in a neuropathological context where severe morphological alterations of specific cells can occur, for instance neuronal atrophy or neuroinflammation (Ercan et al., 2016).

Different diffusion-weighted MRS (DW-MRS) approaches have been proposed to quantify cell microstructure, such as high-b value experiments (mainly to probe fiber diameter but also presumably yielding some sensitivity to cell body diameter (Ligneul et al., 2019; Palombo et al., 2017b; Palombo et al., 2019b; Palombo et al., 2018a, b)), or measurements of the apparent diffusion coefficient (ADC) up to very long diffusion times (td) to probe long-range cell structure (potentially enabling quantification of cell fiber branching and length (Ligneul et al., 2019; Palombo et al., 2016)). Such approaches were recently used to quantitatively estimate alterations of astrocytic morphology in a mouse model of reactive astrocytes, where the diffusion of Ins was significantly different compared to the control group, while the diffusion of other metabolites remained unchanged (Ligneul et al., 2019). In that work, modeling of Ins data resulted in higher values for fiber diameter and length in the case of activated astrocytes, which was confirmed by quantitative morphological analysis of astrocytes using confocal microscopy ex vivo, thus demonstrating the potential of the technique for microstructure quantification. Unfortunately, going to very long diffusion times or high b-values leads to low signal-to-noise ratio, and high b-values require very high gradient strength, making the implementation of such measurements on clinical scanners highly challenging.

One approach circumventing these issues is double diffusion encoding (DDE) (Shemesh et al., 2010). In DDE, two diffusion blocks are successively applied while the relative directions of the corresponding diffusion-sensitizing gradients are varied by an angle ϕ during the course of the experiment. Unlike the more conventional Single Diffusion Encoding (SDE), DDE has been shown to display sensitivity to microscopic anisotropy (μA) that arises from the presence of anisotropic restricting boundaries at the scale of the diffusion distance (Mitra, 1995; Ozarslan, 2009; Ozarslan and Basser, 2008). Theoretical analysis of DDE was proposed by Mitra who examined two regimes based on null/short vs. long mixing time (TM) between the two diffusion blocks (Mitra, 1995). The long TM case is particularly interesting to disentangle between compartments without compartment shape anisotropy (e.g. spheres, or a tortuous medium with typical pore size much below the diffusion distance) and with compartment shape anisotropy (e.g. ellipsoidal pores or fibers). Indeed, Mitra demonstrated that at long TM, there is some angular dependence of the NMR signal magnitude for ellipsoidal pores but not for spherical ones. In this regime, in the case of ellipsoidal pores, a signal maximum is consequently expected in the parallel/antiparallel cases (ϕ ​= ​0 and 180°) whereas a signal minimum is predicted for the perpendicular case (ϕ ​= ​90 and 270°).

DDE-MRS was successfully pioneered by Shemesh et al. to non-invasively follow microstructural alterations of ischemic tissues in a stroke model (Shemesh et al., 2014). Signal modulation as a function of ϕ unambiguously demonstrated that metabolites diffuse in elongated compartments. Moreover, the authors reported a dramatic increase of the amplitude of the NMR signal angular dependence 24 ​h after the onset of ischemia for NAA, tCho and total creatine (tCr) suggesting that μA is increasing. Shemesh et al. further investigated the potential of DDE-MRS to quantitatively extract cell fiber diameter d_fiber from DDE signal modulation, which allowed distinguishing neuronal and astrocytic compartments (Shemesh et al., 2017): estimated cell-fiber diameter was smaller for NAA (d_fiber ​= ​0.04 ​μm) than for Ins (d_fiber ​= ​3.1 ​μm), which was well in line with d values inferred from high-b measurements in the study by Palombo et al. (2017b).

In this study, we revisit the works of Shemesh et al. with two main methodological differences: i) conventional radio frequency (RF) pulses are used (instead of polychromatic RF pulses targeting a few resonances of interest) to detect more metabolites, and ii) state-of-the-art post-processing pipeline is applied for accurate diffusion-weighted signal quantification, similarly to all our previous works on DW-MRS, including scan-to-scan phase correction, LCModel analysis and macromolecule (MM) signal quantification. In the end, signal modulation can be reliably quantified for six metabolites. Analysis of the experimental data with a model of isotropically oriented cylinders of infinite length, similarly as in (Shemesh et al., 2017), strongly suggests that this model does not satisfactorily account for our data. We propose that additional structural features are required to better describe DDE-MRS data.

2. Methods

2.1. DW-MRS experiments

All experimental protocols were reviewed and approved by the local ethics committee (CETEA N°44) and submitted to the French Ministry of Education and Research (approval: APAFIS#795-2015060914444077 v1). They were performed in a facility authorized by local authorities (authorization #B92-032-02), in strict accordance with recommendations of the European Union (2010-63/EEC). All efforts were made to minimize animal suffering and animal care was supervised by veterinarians and animal technicians. Mice were housed under standard environmental conditions (12-h light-dark cycle, temperature: 22 ​± ​1 ​°C and humidity: 50%) with ad libitum access to food and water.

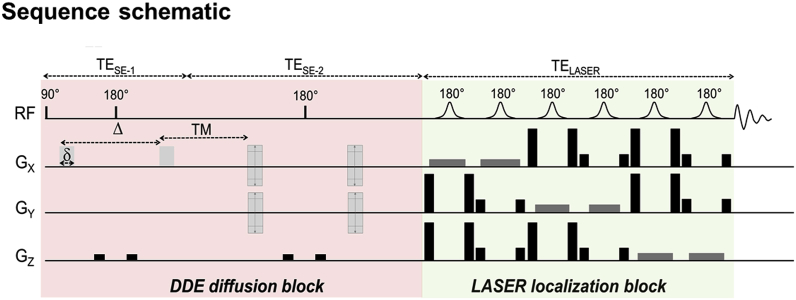
Four C57BL/6J wild type mice were anesthetized with 1.5% isoflurane in air/O2 mixture and scanned on an 11.7 ​T scanner (Bruker, Ettlingen, Germany) with maximal gradient strength on each axis G_max ​= ​752 ​mT/m, using a cryoprobe. DDE-MRS was performed in a 63 ​μL voxel positioned around the hippocampus, using a sequence comprising a double spin-echo module with two diffusion blocks followed by a LASER localization module (TE_SE/TE_LASER ​= ​119/25 ​ms, Δ/δ/TM ​= ​30/4.5/29.5 ​ms) similarly to (Shemesh et al., 2014). An illustration of the sequence implementation is proposed in Fig. 1. A total diffusion-weighting of 20 ​ms/μm² was applied, i.e. b ​= ​10 ​ms/μm² per diffusion block. Water signal was suppressed using a VAPOR module. MM acquisition was performed using a double inversion recovery (TI1/TI2 ​= ​2200/730 ​ms) and a diffusion weighting of b ​= ​10 ​ms/μm² on each block.

Fig. 1.

Schematic of the DDE-LASER sequence. DDE encoding is performed thanks to two pairs of diffusion gradients of duration δ and separated by a mixing time TM. The diffusion time within each block is defined by Δ- $\frac{\delta }{3}$. The first diffusion block is applied along the X direction whilst the direction of the second diffusion sensitizing gradient pair is varied in the XY plane at a ϕ angle ranging from 0° to 360° with respect to the x axis. A LASER localization block is then applied, thus avoiding any cross-term between the diffusion and selection gradients. Here TE-SE1 is different from TE-SE2 because of the need to add an extra delay during the second diffusion period to account for the TM duration.

The first pair of diffusion gradients was applied along X whilst gradient orientation for the second diffusion block was incremented from ϕ ​= ​0 to ϕ ​= ​360° in the XY plane by 45° steps (ϕ being defined following the convention proposed by Shemesh et al. (2016)). For each ϕ value, a total of 128 repetitions (split in four blocks of 32 repetitions interleaved with other ϕ values) were acquired.

Signal post-processing was performed as described in Ligneul et al. (2017), including individual scan phasing and inclusion of an experimental MMspectrum in the LCModel basis set (sum of two experimentally measured spectra). Signal attenuation reported in this paper corresponds to the ratio S(ϕ,b ​= ​20 ​ms/μm²)/S(b ​= ​0.04 ​ms/μm²).

We are providing Matlab codes to open Bruker data and perform post-processing at the following address: https://github.com/Meli64/DDE-data-processing. We are also providing adequate LCModel’s basis-set, as well as the CONTROL file to perform the analysis, and an example DDE dataset.

2.2. DDE data modeling

Experimental data for each animal and each metabolite was first fitted to the phenomenological equation A ​+ ​B ​× ​cos(2ϕ) as in Shemesh et al. (2014) using a Monte Carlo approach. The residual sum of squares corresponding to the best initial fit was used as standard deviation to randomly induce artificial Gaussian noise in our experimental data before repeating the fitting operation. This process was performed 10,000 times. The resulting A and B coefficients therefore correspond to the mean values obtained over the generated dataset. The ratio $\frac{B}{A}$ was then used to quantify the amplitude of the signal angular modulation with respect to the global MR signal attenuation.

Furthermore, simulations based on analytical computation of DDE-MRS signals in infinite, isotropically oriented cylinders were performed using the MISST toolbox (Drobnjak et al., 2010, 2011; Ianus et al., 2013) for D_free ranging from 0.1 to 0.5 ​μm²/ms and d_fiber from 0.1 up to 5 ​μm, and compared to experimental data to estimate the parameter values that best explain the data, as performed by Shemesh et al. (2017). Calculation of least square residuals was used as the fitting cost function. Errors on estimated parameters were calculated using a Monte Carlo procedure, as described above.

3. Results

3.1. DDE signal modulation for brain metabolites

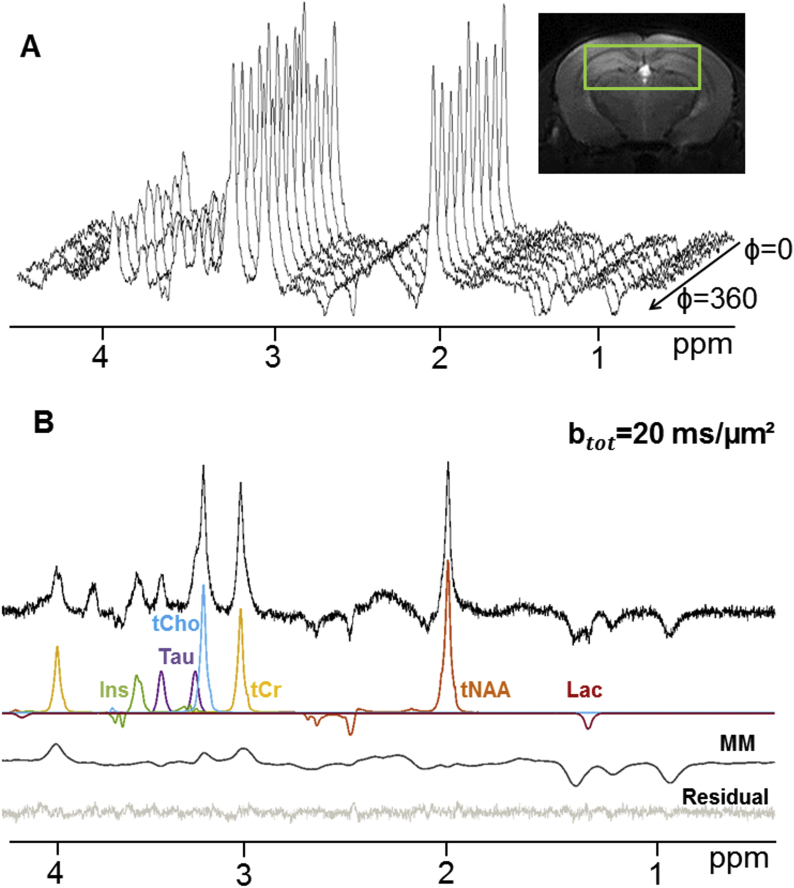
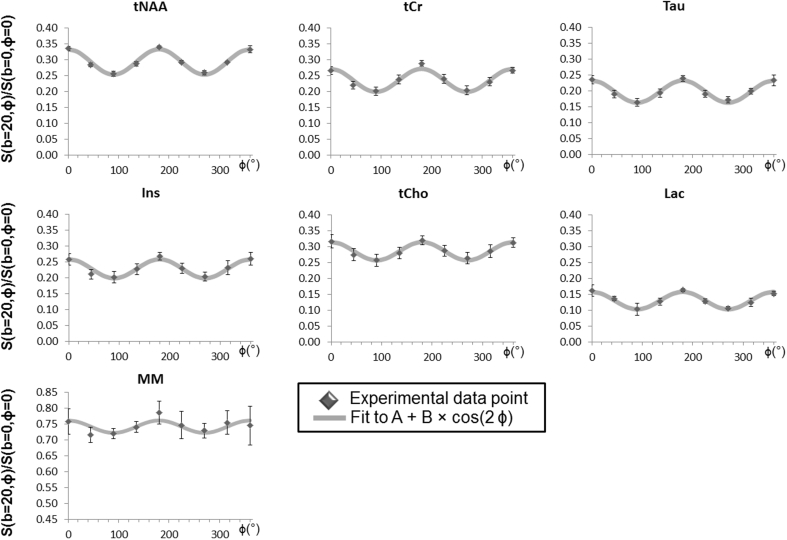
Fig. 2A shows a series of DDE-MRS spectra acquired in one mouse whereas Fig. 2B shows LCModel spectral decomposition for ϕ ​= ​0 in this experiment. Signal attenuation could be reliably quantified for total NAA (tNAA), tCr, Ins, tCho and taurine (Tau) with Cramer-Rao lower bounds CRLB<3% for all ϕ values. Total NAA accounts for both NAA and NAAG (N-acetylaspartylglutamate), however, it is reasonable to consider that tNAA diffusion predominantly reflects NAA compartmentation as NAAG signal represents 8–11% of the tNAA signal. Lactate resonance was quantified with slightly poorer precision (CRLB values of ~10%). Fig. 3 displays the signal angular dependence at TM ​= ​29.5 ​ms for six metabolites as well as for MM. In this figure, the experimental data points are fitted to the function A ​+ ​B*cos(2ϕ) appearing in light grey. The very low standard deviations that were achieved for all experiments can be appreciated. These results are coherent with Özarslan’s work that confirmed Mitra’s findings and proposed a Taylor expansion of the MR signal attenuation up to the fourth-order term, showing that the angular dependence of the diffusion signal in finite cylinders can be characterized by the function A ​+ ​B*cos(2ϕ) whose coefficients can be related to L and d (Ozarslan, 2009) (see Fig. 3).

Fig. 2.

Examples of experimental data. (A) One dataset acquired using DDE-MRS (Δ/δ/TM ​= ​30/4.5/29.5 ​ms, b ​= ​10 ​ms/μm² per diffusion block), displaying the angular dependence of peak amplitudes. The top-right inset shows the voxel positioned in the mouse hippocampus. (B) Spectral decomposition of one diffusion-weighted spectrum using LCModel, only showing the 6 metabolites presented in the paper together with macromolecules. The overall LCModel fit is also displayed. It was obtained with a basis set comprising an experimental MM spectrum as well as 18 metabolites generated using home-made simulation routines based on the density matrix formalism.

Fig. 3.

Signal modulation as a function of angular values for all 6 metabolites as well as macromolecules. Each experimental point corresponds to the ratio of the signal intensity obtained for b ​= ​20 ​ms/μm² and ϕ ​= ​0–360° to the signal intensity obtained for b ​= ​0.02 ​ms/μm². The grey line corresponds to the function A ​+ ​B ​× ​cos(2ϕ) fitted to the experimental data. Data was acquired in four mice. Error bars stand for the standard deviation.

Coefficients A and B are reported in the top part of Table 1. It can be seen that the amplitude modulation of the DDE-MRS signal - reflected here by B - is larger for tNAA (neuronal metabolite) than for non-specific (tCr and Tau) or glial markers (tCho and Ins), which might at first glance be intuitively interpreted as neurons exhibiting narrower fibers, i.e. larger μA than glia (Palombo et al., 2017b; Shemesh et al., 2017), although this simple picture will be challenged later in the following sections. Interestingly, lactate exhibits stronger signal attenuation, which could be explained by the intrinsically fast diffusion of lactate (which is a small metabolite), but also by the contribution of a significant extracellular lactate pool with a rather faster, “free-like” diffusion (Pfeuffer et al., 2000). In line with this idea, lactate exhibits less pronounced angular amplitude modulation than intracellular metabolites, consistent with the notion that, unlike within cellular fibers, which is in the extracellular space correlation between subsequent diffusion directions is rapidly lost. Lastly, it can be observed that MM signal is only slightly attenuated and displays moderate angular dependence. This is consistent with the fact that MM signal arises from a pool of slowly diffusing molecules. The normalized modulation $\frac{B}{A}$ is also reported for each metabolite in Table 1, and will be used later for comparison with simulations.

Table 1.

Top part: A and B coefficients obtained for each metabolite when fitting the function A ​+ ​B ​× ​cos(2ϕ). The B coefficient is higher for neuronal than glial marker. The cost function was calculated for each subject using $c=\sqrt{\sum _{\text{ϕ}}(x_{\varphi }-y_{\varphi })²}$, $x_{\varphi }$ and $y_{\varphi }$ being the fitted and experimental data respectively. Here, the mean and standard deviation for c clearly increase in the case of MM, underlining the poor quality of the fit due to lower signal modulation as well as more pronounced inter-individual variations. Error corresponds to the standard deviation calculated over four animals. Bottom part: D_free and d_fiber values corresponding to the best fit for each metabolite to a basis of simulated signals using the infinite cylinder model. Error on D_free and d_fiber was estimated using Monte Carlo simulations. D_free appears underestimated whereas d_fiber is overestimated.

	METABOLITES
	tNAA (neuronal marker)	tCr	Tau	Ins (glial marker)	tCho (glial marker)	Lac	MM
Fitting to A ​+ ​B ​× ​cos(2ϕ)
Offset (A)	0.293 ​± ​0.004	0.235 ​± ​0.012	0.197 ​± ​0.011	0.228 ​± ​0.016	0.286 ​± ​0.018	0.130 ​± ​0.004	0.742 ​± ​0.030
Amplitude Modulation (B)	0.040 ​± ​0.004	0.036 ​± ​0.004	0.035 ​± ​0.005	0.030 ​± ​0.003	0.029 ​± ​0.003	0.028 ​± ​0.006	0.020 ​± ​0.012
B/A ratio	0.137 ​± ​0.014	0.155 ​± ​0.020	0.177 ​± ​0.024	0.132 ​± ​0.015	0.101 ​± ​0.014	0.212 ​± ​0.051	0.026 ​± ​0.016
Cost function	0.018 ​± ​0.006	0.027 ​± ​0.004	0.020 ​± ​0.004	0.024 ​± ​0.006	0.017 ​± ​0.006	0.029 ​± ​0.002	0.055 ​± ​0.019
Fitting to the infinite cylinders model
Dfree (μm2/ms)	0.20 ​± ​0.02	0.22 ​± ​0.04	0.25 ​± ​0.03	0.21 ​± ​0.03	0.17 ​± ​0.02	0.34 ​± ​0.06	/
dfiber (μm)	3.22 ​± ​0.29	3.89 ​± ​0.43	4.20 ​± ​0.26	4.14 ​± ​0.0.15	3.76 ​± ​0.30	4.80 ​± ​0.27	/

3.2. Estimating fiber diameter: simulations in infinite cylinders using MISST

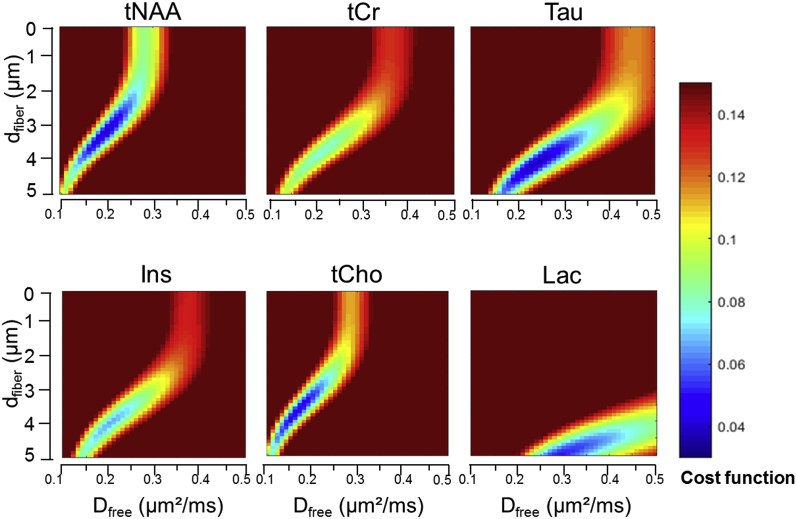
Heatmaps based on least square residuals for each metabolite as compared to DDE simulations performed with MISST, as a function of D_free and d_fiber, are presented in Fig. 4. They show similar aspect for all metabolites except lactate. Diameters and D_free values corresponding to the best fits for each metabolite are reported in the bottom part of Table 1. Values for d_fiber are in the 3–5 ​μm range, while D_free is found to be ~0.2 ​μm²/ms. These values are not in good agreement with previously published values. DW-MRS works performed at high b or short t_d rather reported diameters below 3 ​μm (Kroenke et al., 2004; Ligneul et al., 2017; Marchadour et al., 2012; Palombo et al., 2017b) which better agrees with histological estimates for axons and dendrites as well as for astrocytic processes (Ligneul et al., 2019). While it is more difficult to compare D_free to ground truth value, past DW-MRS works consistently estimated D_free to be larger than 0.3 ​μm²/ms (and up to ~0.6 ​μm²/ms for certain works) (Kroenke et al., 2004; Ligneul et al., 2017; Marchadour et al., 2012; Palombo et al., 2016, 2017b; Ronen et al., 2013).

Fig. 4.

Heatmaps of the cost function estimated for all Dfree (0.1–0.5 ​μm²/ms) and d_fiber (0.1–5 ​μm) values for each metabolite, when using a model of isotropically oriented cylinders simulated by MISST. The cost function is defined by $c=\sqrt{\sum _{\text{ϕ}}(x_{\varphi }-y_{\varphi })²}$, $x_{\varphi }$ being the simulated diffusion signal attenuation and $y_{\varphi }$ the experimentally measured signal attenuation for the angle ϕ.

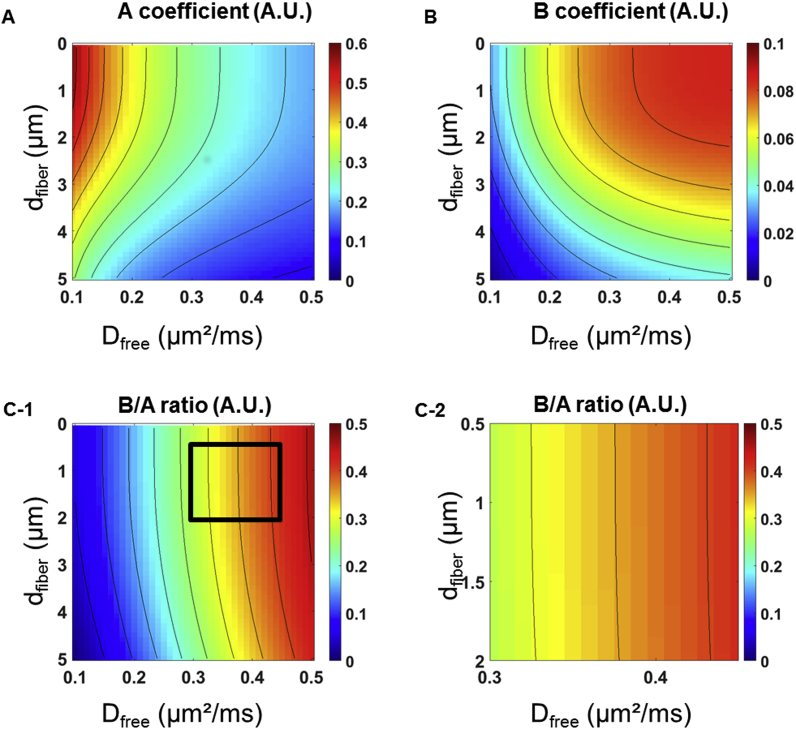
These unexpected results led us to further investigate the effect of d_fiber on the amplitude of the signal angular dependence. We therefore carefully examined MISST simulations, in particular for D_free ranging from 0.3 to 0.45 ​μm²/ms and d_fiber from 0.5 to 2 ​μm and subsequently fitted each of the basis signals to $A+B\times \text{cos}(2\varphi )$, as performed for the metabolites. Fig. 5 displays the A, B and $\frac{B}{A}$ for each combination of d_fiber/D_free values, revealing that no variation of the ratio values was obtained when varying d_fiber whereas D_free seemed to have a greater effect on the signal angular modulation, therefore illustrating the lack of sensitivity to fiber diameter for d_fiber<2 ​μm.

Fig. 5.

A and B coefficients obtained after fitting the simulated dataset in MISST to the A ​+ ​B ​× ​cos(2ϕ) function. (A) Variations of the A coefficient with respect to D_free and d_fiber. As expected, the overall signal attenuation increases with D_free as well as in wider fibers. (B) Variations of the B coefficient with respect to D_free and d_fiber. The amplitude of the signal angular modulation is impacted by both D_free and d_fiber, making it challenging to use this parameter to accurately estimate d_fiber. The sensitivity to d_fiber values below 3 ​μm appears limited, even for a fixed D_free. (C-1)$\frac{B}{A}$ ratios for all D_free and d_fiber values. (C-2) Zoom-in on a realistic range of D_free (0.3–0.45 ​μm²/ms) and d_fiber (0.5–2 ​μm) values, as delineated by the square shown in C-1. The $\frac{B}{A}$ ratios do not vary according to d_fiber, further confirming the poor sensitivity of DDE-MRS experiments to this structural parameter.

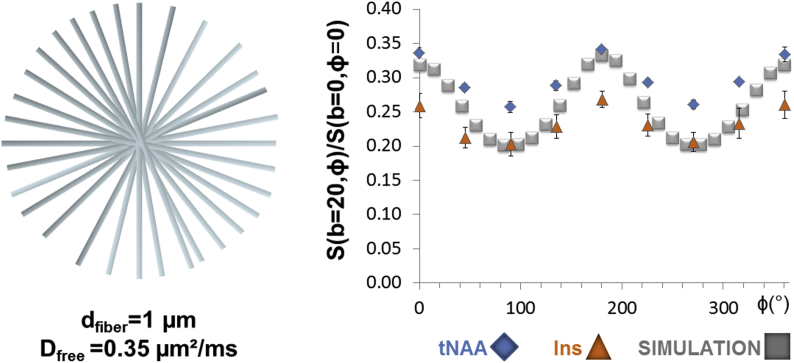
Quite strikingly, $\frac{B}{A}$ values were much higher in the case of the simulated signals (0.26–0.42) than for the metabolites (0.101–0.212). This is well in agreement with the results displayed in Fig. 6, showing the superposition of tNAA and Ins experimental data to a simulated signal obtained from a model of 1-μm diameter infinite cylinders (D_free ​= ​0.35 ​μm²/ms). Hence, a striking result is that the signal angular dependence of our experimental data (quantified by the ratio $\frac{B}{A}$) is much less pronounced than expected from analytical simulations using realistic parameter values, as least when considering diffusion in randomly oriented infinite cylinders.

Fig. 6.

Representation of the isotropically oriented infinite cylinders in MISST together with a superposition of a simulated signal obtained for d_fiber ​= ​1 ​μm and D_free ​= ​0.35 ​μm²/ms (grey square) to tNAA (blue diamonds) and Ins (orange triangle) experimental data. The amplitude of signal modulation obtained in the simulated case is markedly higher than for our experimental data.

4. Discussion

4.1. Limited sensitivity to cell fiber diameter

Heatmaps of the cost function presented in Fig. 4 exhibit a global minimum for unrealistic d_fiber and D_free values for all metabolites. In their former study, Shemesh et al. were able to infer realistic d_fiber and D_free values, but we were unable to reproduce those results. It should be noted that there were some notable methodological differences between the two experiments, as Shemesh et al. used longer epochs of 60 ​ms for each diffusion block, together with lower b-values that were about half of the ones used in this study. Moreover, Shemesh et al. performed acquisitions at ultrahigh field (21.1 ​T), which caused significant T2 weighting, especially considering the longer TE needed to account for longer diffusion time. Additionally, they used judiciously designed radiofrequency selective pulses which eliminated the need for water suppression module and simplified spectra, so that signal was quantified by peak integration. Here we worked at lower field strength, but still benefited from exquisite sensitivity thanks to a cryoprobe. We used broadband radiofrequency pulses exciting the whole ppm range to detect more metabolites, and we minimized potential bias in metabolite signal quantification by performing scan-to-scan phase correction, accounting for the contribution of MM signal and using LCModel. As a result, standard deviations achieved in the present study are very low, which might help better identify discrepancies between data and models. It shall be acknowledged here that we did not perform averaging over different planes and therefore did not assess how signal modulation depended on plane’s orientation. However, it was evaluated in a previous work (Ligneul et al., 2017) that the large spectroscopic voxel used here exhibited no macroscopic anisotropy in SDE-MRS experiments. It is reasonable to assume that this would still be valid for the DDE-MRS experiments (which was actually directly verified in rats in Shemesh et al. (2017)).

The results shown in Fig. 5 strongly suggest that DDE-MRS offers limited sensitivity to cell fiber diameter, despite the use of a relatively high b-value of 20 ​ms/μm². One could argue that diffusion-weighted signal is less sensitive to fibers of smaller diameter, as previously pointed out by Burcaw et al. (2015). However, this holds true for SDE-MRS experiments which were previously performed in our team and for which we did not extract such unrealistically large fiber diameter (Palombo et al., 2017b). It is therefore unlikely that potential bias towards larger fiber diameter may explain present data. Improved sensitivity to d_fiber may be achievable by optimizing the gradient waveform, as proposed by Drobnjak et al. who were able to distinguish smaller axon radii below 5 ​μm when using gradients of increasing frequency (Drobnjak et al., 2010). Shemesh later on investigated the DDE and the double oscillating diffusion encoding (DODE) schemes in fixed spinal cords at 16.4 ​T. He showed superior sensitivity to axon diameter when performing DODE measurements, which is line with the idea that oscillating gradients can probe smaller spin displacements occurring perpendicularly to the main diffusion axis (Shemesh, 2018).

A study performed by Ianus et al. on DDE and DODE imaging implied that simple geometric models such as infinite cylinders may be insufficient when trying to accurately quantify microscopic diffusion anisotropy and the need of considering structures along the fiber axis was underlined (Ianus et al., 2018). Experimental parameters such as the b-value and sequence timing parameters, in particular t_d and TM, were also pointed out as potential sources of bias when trying to accurately estimate the cell μA.

The unrealistic parameter values extracted from data fitting, as well as the large discrepancy between experimental and simulated data shown in Fig. 6, clearly suggest that the infinite cylinders model seems to fail to satisfactorily describe our experimental data when using realistic parameter values: in particular, experimentally measured amplitude modulation (and normalized amplitude) appears too low. This suggests that metabolite DDE signature may contain more complex and intricate information reflecting various microstructural features beyond fiber diameter.

4.2. Which feature of cell microstructure could the DDE signal be sensitive to?

In an attempt to better understand what morphological features may explain the observed DDE signal modulation, we considered 3D cell-substrates with additional degrees of complexity. Our driving hypothesis is that the lower signal amplitude modulation observed in the experimental data is due to loss of correlation between subsequent diffusion directions that may be induced by a) non-negligible fraction of diffusing metabolites restricted in isotropic (i.e. spherical) soma compartment and/or b) branching of cellular fibers, leading to hopping of diffusing metabolites from one fiber branch oriented in one direction to another branch oriented in a different direction.

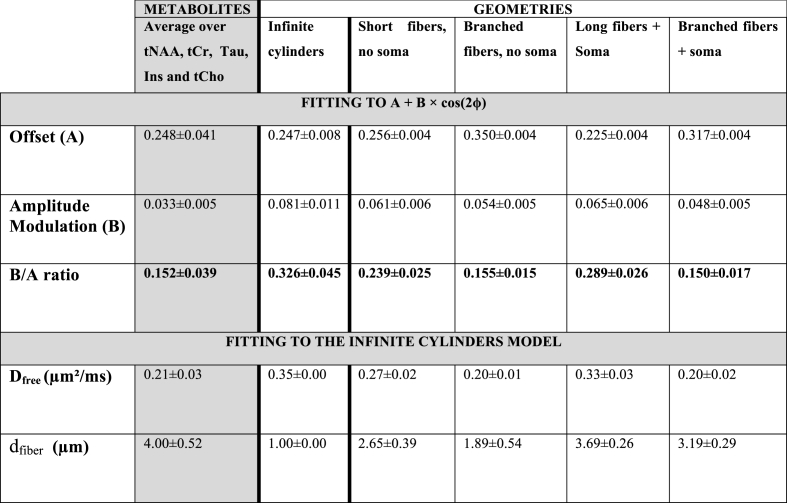
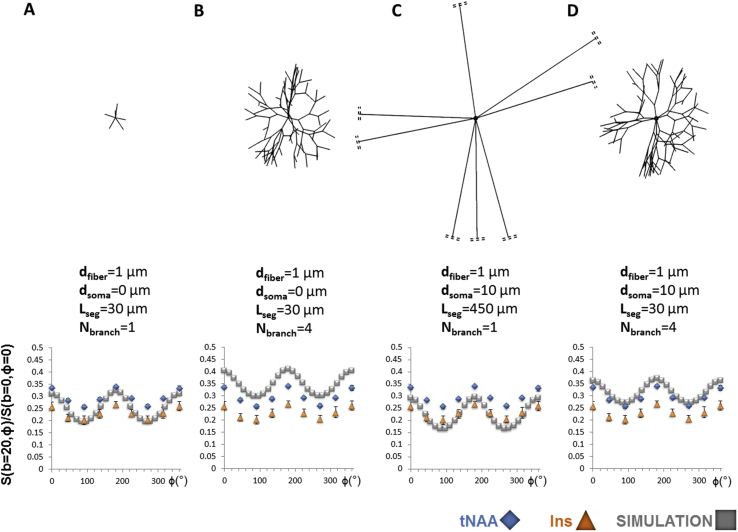
To investigate the validity of these hypotheses, Monte Carlo simulations of diffusion NMR signal were carried out in realistic brain cell morphologies obtained by using the generative model recently introduced by Palombo et al. (2019a). In brief, using 12 selected features like soma radius, branch radius, branch order, branching angle etc., the model generates realistic 3D computational models of any brain cell in a controlled and flexible fashion. Then, the diffusion of 3000 particles within 50 different instances of such realistic cell-substrates (resulting in a total of 1.5 ​× ​10⁵ diffusing particles) was simulated using Camino (Cook et al., 2006) with diffusion coefficient D_free and time step of 20 ​μs From the resulting spin trajectories, the DDE signal was computed by phase accumulation approach, using exactly the same sequence parameters of the experiments (see Methods section). In all simulations described below, eight fibers of finite length were connected to a central “soma”. Fiber diameter was fixed to a realistic value (d_fiber ​= ​1 ​μm), but anyway this has little impact on DDE modulation with the current acquisition parameters, as already explained earlier. The free diffusion coefficient was also set to a realistic value of D_free ​= ​0.35 ​μm²/ms (Kroenke et al., 2004; Palombo et al., 2017b). Starting from that, we investigated the effect of fiber structure (number of successive branches N_branch and length of segments between embranchment L_seg, e.g. as defined in Palombo et al. (2016) as well as soma size (d_soma) on DDE behavior. Instead of a systematic study, here we decided to focus on four cases, already spanning a broad range of conditions. To facilitate comparison with intracellular metabolite DDE data, simulation results were also fitted with to $A+B\times \text{cos}(2\varphi )$ to derive A, B and $\frac{B}{A}$ (reported in the top part of Table 2).

• Case 1: Short fiber segments, no embranchement and no soma. The first case aimed at assessing DDE behavior for short segments (L_seg ​= ​30 ​μm), without successive embranchment (N_branch ​= ​1), and with a soma being reduced to a simple point (d_soma ​= ​0) (Fig. 7A). This case is used as benchmark for the simple case of connected randomly oriented thin fibers. A slight decrease of B and $\frac{B}{A}$ can be observed as compared to unconnected infinite cylinders as simulated with MISST, for the same fiber diameter and D_free.

• Case 2: Short fiber segments, some embranchments and no soma. The second case aimed at evaluating if introducing some branching had a strong effect. Hence we set N_branch ​= ​4, while keeping L_seg ​= ​30 ​μm and d_soma ​= ​0 (Fig. 7B). We found that the effect is quite strong, with a large increase in A (becoming actually slightly larger than for experimental data) while B keeps decreasing, resulting in a quite low $\frac{B}{A}$ of ~0.16, i.e. twice as low as the reference case of unconnected infinite cylinders, and much closer to experimentally measured behavior.

• Case 3: Long fiber segments, no embranchement and a large soma. We then wondered if a realistic soma, rather than a branched fiber structure, was also able to better account for DDE behavior. Hence we set d_soma ​= ​10 ​μm, while imposing a very simple fiber structure, so we set N_branch ​= ​1 and L_seg ​= ​450 ​μm, so that fibers can be considered “almost” infinite and simultaneously ensures that the soma occupies ~16% of the total cellular volume, which is a realistic volume fraction for both neurons and astrocytes (Chklovskii et al., 2002; Chvatal et al., 2007; Ligneul et al., 2019; Sherwood et al., 2004) (Fig. 7C). A very strong drop of A is observed, while B is slightly higher than in case 1. As a result $\frac{B}{A}$ is very high, almost as high as for unconnected infinite cylinders. Overall this is not consistent with experimental data.

• Case 4: Short fiber segments, some embranchements and a large soma. The last case we studied was the most realistic (Fig. 7D), i.e. with the branched fiber structure of case 2 (N_branch ​= ​4, L_seg ​= ​30 ​μm), and the realistic soma of case 3 (d_soma ​= ​10 ​μm). With such parameters the soma still occupies ~16% of the total cellular volume. The resulting behavior is just slightly different from the case with d_soma ​= ​0 (case 2), and is now even closer to experimental data (differences between simulated data and values averaged over intracellular metabolites for A, B and $\frac{B}{A}$ are less than ~25%).

Table 2.

Top part: A, B and $\frac{B}{A}$ values obtained for each model (infinite cylinder model and 3D-cell simulations) when fitting the function A ​+ ​B ​× ​cos (2ϕ). These values can be compared to the grey column on the left-hand side that indicates the average A, B and $\frac{B}{A}$ calculated over five metabolites (mean ​± ​s.d.). Error on parameters extracted from geometric models (D_free, d_fiber) was estimated using Monte Carlo simulations. Models exhibiting embranchments exhibit lower $\frac{B}{A}$ values that better match our experimental data. Bottom part: Fitting to the infinite cylinders model for each 3D-cell simulation. This model fails to yield the expected ground truth values for D_free and d_fiber (i.e. 0.35 ​μm²/ms and 1 ​μm) for all simulations. Most strikingly, the obtained values are close to that of the average D_free and d_fiber obtained for our experimental data (mean ​± ​s.d. over five metabolites), further illustrating the fact that the infinite cylinders model does not satisfactorily describe the experimental data.

Fig. 7.

Four simulated datasets superposed to tNAA and Ins experimental data. (A) DDE signal and $\frac{B}{A}$ ratio for a model of short connected fibers. (B) DDE signal and $\frac{B}{A}$ ratio for a model of connected fibers exhibiting short segments and branching (N_branch ​= ​4). (C) DDE signal and $\frac{B}{A}$ ratio for a model of a 10-μm diameter soma connected to long fibers. The soma volume fraction is ~16%. Note that fibers are cut on the figure (double dash lines). (D) DDE signal and $\frac{B}{A}$ ratio for a 10-μm diameter soma connected to fibers with short segments and branching (N_branch ​= ​4). The succession of short segments across successive embranchments appears to best explain our experimental data when comparing $\frac{B}{A}$ ratios. Adding a cell body has little impact on B/A, although it shifts overall signal attenuation (~A) towards lower value (as increased D_free would do).

Conversely, we wondered how DDE signals in these various cases would translate into fiber diameter d_fiber and D_free, if “naively” analyzed using the infinite cylinder model as initially done. These results are reported at the bottom of Table 2. It clearly appears that branching results in strong underestimation of D_free and moderate overestimation of d_fiber, while the presence of soma has little effect on D_free but results in strong overestimation of d_fiber. In the end, data simulated with the full model (case 4) and fitted with the infinite cylinder model yields D_free~0.20 ​μm²/ms and d_fiber~3.2 ​μm, which is in surprisingly good agreement with values obtained for intracellular metabolites (average over intracellular metabolites: D_free~0.20 ​μm²/ms and d_fiber~3.8 ​μm).

Overall these simulations strongly suggest that a branched fiber structure is paramount to get a more sensible interpretation of our DDE-MRS data. A likely explanation for this could be that, in such structure, and considering that segment length is commensurable with the distance potentially traveled under the effect of diffusion during TM, the main diffusion direction may change between the two successive diffusion blocks for a significant fraction of molecules, resulting in correlation loss and ultimately reduced amplitude modulation. Adding a non-zero cell diameter seems to better account for experimental data, but considering the sequence parameters used here, the main effect arises from the fiber structure. It is important to note that the branched fiber structure proposed here may not be the sole possible feature explaining experimental data. Although we did not investigate that in the current work, fiber undulations or beads (Brabec et al., 2019; Ozarslan et al., 2018) might possibly result in a similar effect to that of fiber branching, as they would also result in loss of correlation between diffusion directions during the two diffusion blocks (Jespersen et al., 2019). Similarly, secondary structures such as dendritic spines or astrocytic leaflets may also strongly influence the modulation of signal intensity. This would be in line with the previous findings of Palombo et al., where experimental SDE-MRS measurements were compared to Monte Carlo simulations performed in various cell models that included spines and leaflets, showing that these finer structures may have a non-negligible effect on the intracellular diffusion of metabolites (Palombo et al., 2017a).

4.3. Can we glean additional information by performing measurements at short TM?

Both our simulations and experimental data at long TM imply that sensitivity to the microstructure of cell bodies is relatively limited. This is coherent with Mitra’s theory that indicates that DDE experiments are only sensitive to the μA arising from the delineations of spherical compartments when the null/short TM condition is met (Mitra, 1995). This was also experimentally confirmed in vivo by Koch and Finsterbusch who achieved DDE experiments on a 3T clinical scanner to assess cell size in the human brain (Koch and Finsterbusch, 2008). In this case, the expected signal angular modulation describes a bell-shaped function and the difference measured between the maximum and minimum signal intensities respectively obtained in the anti-parallel (ϕ ​= ​180°) and parallel cases (ϕ ​= ​0/360°) can be analytically related to the apparent compartment size (Finsterbusch, 2011; Mitra, 1995).

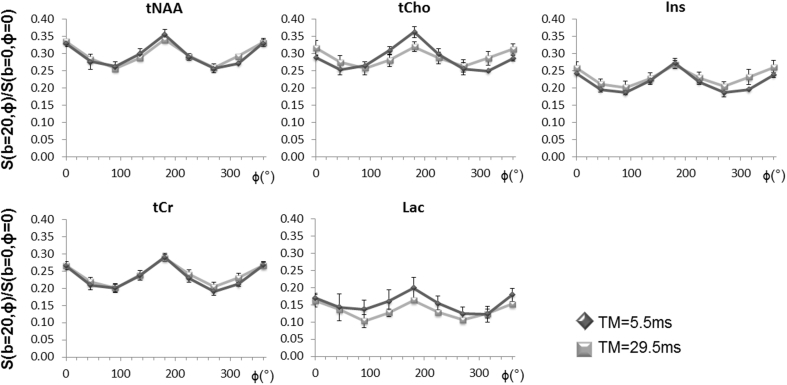
We therefore postulated that some sensitivity to soma size could be retrieved when acquiring DDE-MRS signatures at shorter TM, and we performed another series of acquisitions for TM ​= ​5.5 ​ms, keeping other parameters unchanged (Δ/δ ​= ​30/4.5 ​ms, b ​= ​10 ​μm²/ms on each block). In this case, five metabolites could be reliably quantified (tNAA, tCr, Ins, tCho and Lac) with CRLB values of 1% for tNAA, tCr and tCho, 3% for Ins and 10% for Lac. Fig. 8 displays the angular modulation obtained for these metabolites at TM ​= ​5.5 ​ms (as compared to TM ​= ​29.5 ​ms for reminder). At shorter TM, sinusoidal signal angular modulation could still be observed. More interestingly, a maximum MR signal intensity was reached for ϕ ​= ​180° while slightly stronger signal attenuation was obtained for the ϕ ​= ​0/360° data points as compared to ϕ ​= ​180°. This trend was particularly remarkable for tCho but could also be observed for tNAA, Ins and Lac.

Fig. 8.

Comparison of experimental signal attenuation (mean ​± ​s.d. over 4 animals in each group) measured for TM ​= ​5.5 and 29.5 ​ms for 5 metabolites (taurine could not be measured at TM ​= ​5.5 ​ms). For most metabolites it is clear that a peak appears at ϕ ​= ​180° when shortening TM.

This may indicate an intermediary state between the long and null TM regimes predicted by Mitra, and we thus hypothesized that increasing $\frac{S_{\varphi =180}}{S_{\varphi =0}}$ ratio could possibly reflect increasing sensitivity to cell bodies when shortening TM. This ratio is reported for the five metabolites at both TM in Table 3, consistently reporting higher values in the case of TM ​= ​5.5 ​ms as compared to TM ​= ​29.5 ​ms. These results shall however be interpreted cautiously, as we were able to report a statistically significant difference in the case of tCho only, according to a Kruskal-Wallis test. We further investigated this intuition by performing simulations at TM ​= ​5.5 ​ms in the four models discussed in Section 4.2 and presented in Fig. 7. This enabled us to compare the evolution of the $\frac{S_{\varphi =180}}{S_{\varphi =0}}$ ratio when shortening TM for different features of the cell morphology. Results are presented in Table 3 and revealed that the highest increase in the $\frac{S_{\varphi =180}}{S_{\varphi =0}}$ ratio was obtained when incorporating a spherical compartment in our model. In contrast, branching seemed to have a negligible effect on the TM dependence of this ratio. These findings therefore support the hypothesis that sensitivity to cell body diameter is maximized and might be experimentally accessible at shorter TM.

Table 3.

Left-hand side:$\frac{S_{\varphi =180}}{S_{\varphi =0}}$ ratio obtained for five metabolites at TM ​= ​5.5/29.5 ​ms. This ratio tends to increase for all metabolites except tCr at shorter TM, however this increase is statistically significant in the case of tCho only. Error corresponds to the standard deviation calculated over four animals. **p ​< ​0.05 according to Kruskal-Wallis test. Right-hand side:$\frac{S_{\varphi =180}}{S_{\varphi =0}}$ calculated on simulated signals for the four models presented in Fig. 7. This ratio greatly increases when including a soma in our simulation model, suggesting an increased sensitivity to cell bodies when shortening TM.

$\frac{\mathbf{S}(\mathbf{\varphi }=180°)}{\mathbf{S}(\mathbf{\varphi }=0°)}$	METABOLITES					GEOMETRIES
	tNAA (neuronal marker)	tCr	Ins (glial marker)	tCho (glial marker) **	Lac	Short Fibers	Branching	Soma	All features
TM ​= ​5.5 ​ms	1.08 ​± ​0.04	1.09 ​± ​0.06	1.14 ​± ​0.07	1.26 ​± ​0.05	1.14 ​± ​0.12	1.07	1.03	1.10	1.10
TM ​= ​29.5 ​ms	1.02 ​± ​0.01	1.08 ​± ​0.01	1.03 ​± ​0.02	1.02 ​± ​0.01	1.04 ​± ​0.07	1.04	1.02	1.01	1.03

5. Conclusion

DDE measurements of brain metabolites offer an unprecedented and specific access to the μA of neural and glial cells while requiring relatively low diffusion-weighting. The measured signal carries complex information encompassing several aspects of the cell microstructure such as fiber segment lengths, branching and soma size, at least in the rodent brain, which mainly consists of grey matter. Mathematical models based on simple geometries for which an analytical solution can be derived, such as the infinite cylinder model, appear insufficient to fully describe experimental data. Our work strongly suggests that an accurate and reliable interpretation of DDE-MRS signature may instead necessitate simulations in complex, realistic 3D cell-substrates. Besides the structural features investigated in the present study, i.e. soma and branching, it would be utterly relevant to consider alternative structures at the subcellular level such as axonal beadings, dendritic spines or astrocytic leaflets, and undulations of cell branches, to which DDE-MRS experiments may be sensitive (Jespersen et al., 2019; Palombo et al., 2017a). Consequently, a heavy fitting pipeline may be needed to analyze experimental data, for instance involving a dictionary approach based on Monte Carlo simulations (Ligneul et al., 2019; Palombo et al., 2016; Rensonnet et al., 2019). The sensitivity to a specific feature of the cell microstructure, i.e. fiber processes or cell bodies, can be modulated by tuning the DDE sequence timing parameters such as TM. The relationship between sensitivity to a desired microstructural parameter, for instance the fiber diameter, and experimental parameters such as b-value, gradient waveform and diffusion time should be further explored.