Intelligent Inverse Treatment Planning via Deep Reinforcement Learning, a Proof-of-Principle Study in High Dose-rate Brachytherapy for Cervical Cancer

Abstract

Inverse treatment planning in radiation therapy is formulated as solving optimization problems. The objective function and constraints consist of multiple terms designed for different clinical and practical considerations. Weighting factors of these terms are needed to define the optimization problem. While a treatment planning optimization engine can solve the optimization problem with given weights, adjusting the weights to yield a high-quality plan is typically performed by a human planner. Yet the weight-tuning task is labor intensive, time consuming, and it critically affects the final plan quality. An automatic weight-tuning approach is strongly desired. The procedure of weight adjustment to improve the plan quality is essentially a decision-making problem. Motivated by the tremendous success in deep learning for decision making with human-level intelligence, we propose a novel framework to adjust the weights in a human-like manner. This study used inverse treatment planning in high-dose-rate brachytherapy (HDRBT) for cervical cancer as an example. We developed a weight-tuning policy network (WTPN) that observes dose volume histograms of a plan and outputs an action to adjust organ weighting factors, similar to the behaviors of a human planner. We trained the WTPN via end-to-end deep reinforcement learning. Experience replay was performed with the epsilon greedy algorithm. After training was completed, we applied the trained WTPN to guide treatment planning of five testing patient cases. It was found that the trained WTPN successfully learnt the treatment planning goals and was able to guide the weight tuning process. On average, the quality score of plans generated under the WTPN’s guidance was improved by ~8.5% compared to the initial plan with arbitrarily set weights, and by 10.7% compared to the plans generated by human planners. To our knowledge, this was the first time that a tool was developed to adjust organ weights for the treatment planning optimization problem in a human-like fashion based on intelligence learnt from a training process, which was different from existing strategies based on pre-defined rules. The study demonstrated potential feasibility to develop intelligent treatment planning approaches via deep reinforcement learning.

1. INTRODUCTION

Inverse treatment planning is a critical component of radiation therapy (Oelfke and Bortfeld, 2001; Webb, 2003). It is typically formulated as an optimization problem, in which the objective function and constraints contain several terms designed for various clinical or practical considerations, such as dose volume criteria and plan deliverability. The optimization problem is solved mathematically to determine values of the set of variables defining a treatment plan, e.g. fluence map in external-beam radiation therapy (EBRT) and dwell time in high-dose-rate brachytherapy (HDRBT). These optimized values are further converted into control parameters of a treatment machine, namely a medical linear accelerator in EBRT and a remote afterloader in HDRBT, based on which the optimized treatment plan is delivered.

Mathematical formulation of the optimization problem in treatment planning typically contains a set of parameters to define different objectives. Examples of these parameters include, but are not limited to, positions and relative importance of different dose volume criteria. When adjusting these parameters, although the general formalism of the optimization problem remains unchanged, the resulting plan quality is affected. A modern treatment planning system can effectively solve the optimization problem with given parameters using a certain mathematical algorithm (Bazaraa et al., 2013), such as simulated annealing (Morrill et al., 1991; Webb, 1991) and BFGS (Lahanas et al., 2003). Nonetheless, tuning these parameters for a clinically satisfactory plan quality is typically beyond the capability of the algorithm. In a typical clinical setup, a human planner adjusts these parameters in a manual fashion. Not only does this prolong the treatment planning process, the final plan quality is affected by numerous factors, such as the experience of the planner and the available time on planning. Hence, there is a strong desire to develop automatic approaches to determine these parameters.

Over the years, extensive studies have been conducted to solve this parameter tuning problem (Xing et al., 1999; Wu and Zhu, 2001; Yang and Xing, 2004; Lu et al., 2007; Wahl et al., 2016; Chan et al., 2014; Boutilier et al., 2015; Tol et al., 2015; Lee et al., 2013; Wang et al., 2017). The most common approach is to add an additional iteration loop of parameter adjustment on top of the iteration used to solve the plan optimization problem with a fixed set of parameters. In a seminal study, Xing et. al. (Xing et al., 1999) proposed to evaluate the plan quality in the outer loop and determine parameter adjustment using Powell’s method towards optimizing the plan quality score. Similar approaches were taken by Lu et. al. using a recursive random search algorithm in intensity modulated radiation therapy (Lu et al., 2007) and by Wu et. al using the genetic algorithm in 3D conformal therapy (Wu and Zhu, 2001). This two-loop approach was recently generalized by Wang et. al. to include guidance from prior plans designed for patients of similar anatomy. They also implemented the method in a treatment planning system to allow an automated planning process (Wang et al., 2017). In the case with a large number of parameters in the optimization problem, e.g. one parameter per voxel, a heuristic approach was developed to adjust voxel-dependent parameters based on dose values of the intermediate solution (Yang and Xing, 2004; Wahl et al., 2016) or based on the geometric information of the voxel (Yan and Yin, 2008). Other methods were also introduced to solve this problem. Yan et. al. employed a fuzzy inference technique to adjust the parameters (Yan et al., 2003a; Yan et al., 2003b). A statistical method was used by Lee et. al. (Lee et al., 2013), which built the relationship between the parameters and the patient anatomy. Chan et. al. analyzed previously treated plans and developed a knowledge-based methods to derive the parameters needed to recreate these plans (Boutilier et al., 2015; Chan et al., 2014; Babier et al., 2018).

Parameter tuning in the plan optimization is essentially a decision making problem. Although it is difficult for a computer to automate this process, the task seems less of a problem for humans, as evidenced by the common clinical practice of manual parameter adjustment: a planner can adjust the parameters in a trial-and-error fashion based on human intuition. It is of interest and importance to model this remarkable intuition in an intelligence system, which can then be used to solve the parameter-tuning problem from a new angle. Recently, the tremendous success in deep-learning regime demonstrated that human-level intelligence can be spontaneously generated via deep-learning techniques. Pioneer work in this direction showed that a system built as such is able to perform certain tasks in a human-like fashion, or even better than humans. For instance, employing a deep Q-network approach, a system can be built to learn to play Atari games with a remarkable performance (Mnih et al., 2015).

In fact, a human planner using a treatment planning system to design a plan is conceptually similar to a human playing computer games. Motivated by this similarity and the tremendous achievement in the deep learning area across many different problems (Mnih et al., 2015; Silver et al., 2016; Silver et al., 2017), we propose in this paper to develop an artificial intelligence system to accomplish the parameter-tuning task in an inverse treatment planning problem. Instead of tackling the problem in the EBRT context, we focus our initial study on an example problem of inverse planning in HDRBT with a tandem-and-ovoid (T/O) applicator for the purpose of proof of principles. This choice is made because of the relatively small problem size and therefore low computational burden. More specifically, based on an in-house optimization engine for HDRBT, we will build an intelligent system called Weight Tuning Policy Network to adjust organ weights in the optimization problem in a human-like fashion. The validity and generalization of this approach to the EBRT context will be discussed at the end of the paper.

2. METHODS AND MATERIALS

2.1. Optimization model for T/O HDRBT

Before presenting the system for organ weight tuning, we will first briefly define the optimization problem for T/O HDRBT. In this study, we considered an in-house developed optimization model:

$${\text{min}}_{\mathit{t}}{\sum }_i\frac{{\lambda }_i}{2}{\Vert D_{OAR}^{i}t\Vert }_2^2+\frac{1}{2}{\Vert \nabla t\Vert }_2^2,$$ (1)

$$\text{s}.\text{t}.d^{CTV}=D_{CTV}t,$$

$$d^{CST}=D_{CST}t,$$

$$d^{CTV}(90\%)=d_p,$$

$$d^{CST}\in [0.8d_p,1.4d_p],$$

$$t_j\in \left[0,t_{max}\right],j=1,2,\dots ,n.$$

In this model, $D_{OAR}^i\in R^{m_i\times n}$ and $D_{CTV}\in R^{m_{CTV}\times n}$ are dose deposition matrices for the i-th organs at risk (OARs) and the clinical target volume (CTV). They characterized the dose to voxels in corresponding volumes of interest contributed from each dwell position at a unit dwell time. m_i, m_CTV, and n are number of voxels in the OAR, that of the CTV, and the number of dwell positions, respectively. t ∈ R^n×1 is a vector of dwell time. The first term of the objective function was formulated to minimize the dose to OARs. ${\Vert \nabla t\Vert }_2^2$ is the regularization term with ∇ being the differential operator, evaluating the dwell time difference between adjacent dwell positions. The regularization term enforced smoothness of the dwell time to ensure robustness of the resulting plan with respect to geometrical uncertainty of source positions. In addition, we imposed the constraint to CTV, such that 90% of CTV volume should receive dose not lower than the prescription dose d_p. Moreover, according to the treatment planning guideline at our institution, a control structure (CST) was defined as two line segments that are parallel to the ovoid central axes and are on the outer surface of the ovoids. Dose in CST d^CST should be within [0.8d_p, 1.4d_p]. The last constraint of the problem ensured that dwell time should be non-negative and less than a pre-defined maximum value. In this study, four OARs were considered, namely bladder, rectum, sigmoid and small bowel. λ_is are the weights controlling trade-offs among them. These organ weights determined the quality of the optimized plan, turning which is the interest of this paper.

For a given set of weights, we solved the optimization problem using the alternating direction method of multiplier (ADMM)(Boyd et al., 2011; Liu et al., 2016; Gao, 2016). The main idea was to split the original optimization problem into multiple easy sub-problems. The ADMM tackled the optimization problem via its augmented Lagrangian:

$$L\left(t,x,\Gamma \right)={\sum }_i\frac{{\lambda }_i}{2}{\Vert D_{OAR}^{i}t\Vert }_2^2+\frac{1}{2}{\Vert \nabla t\Vert }_2^2+\frac{\beta }{2}{\Vert \widehat{D}t-x\Vert }_2^2+\langle \Gamma ,\widehat{D}t-x\rangle +{\delta }_1\left(x\right)+{\delta }_{box}\left(t\right),$$ (2)

where $\widehat{D}=\left(\begin{array}{c}{D}_{CTV}\\ D_{CST}\end{array}\right)$ and $x=\left(\begin{array}{c}{d}^{CTV}\\ d^{CST}\end{array}\right)$. Γ indicates the Lagrangian multiplier and β is the algorithm parameter to control the convergence. δ₁(x) and δ_box(t) are index functions that give 0 if constraints on x and t are satisfied, or +∞ otherwise. The iterative process of the algorithm is summarized in Algorithm 1.

Algorithm 1.

ADMM algorithm solving the problem in Eq. (1) with a given set of organ weights.

Input: $D_{OAR}^i$, $\widehat{D}$, x(0), Γ(0), λi, β and tolerance σ

Output: t*

Procedure:

1. Set k = 0;

2. $\text{Compute }{t}^{\left(k+\frac{1}{2}\right)}={\left({{\sum }_i{\lambda }_i{D}_{OAR}^i}^T{D}_{OAR}^i+{\nabla }^T\nabla +\beta {\widehat{D}}^T\widehat{D}\right)}^{-1}\left(\beta {\widehat{D}}^T{x}^{\left(k\right)}-{\widehat{D}}^T{\Gamma }^{\left(k\right)}\right)$

3. $\text{Compute }{t}_j^{\left(k+\frac{1}{2}\right)}=\{\begin{array}{l}0,if{t}_i^{\left(k+\frac{1}{2}\right)}<0\hfill \\ t_{max},if{t}_i^{\left(k+\frac{1}{2}\right)}>t_{max}\\ t_i^{\left(k+\frac{1}{2}\right)},\text{ otherwise}\end{array};$

4. $\text{Compute }{x}^{\left(k+\frac{1}{2}\right)}=\widehat{D}{t}^{\left(k+1\right)}+\frac{{\Gamma }^{\left(x\right)}}{\beta },\left(\begin{array}{c}{d}^{CTV}\\ d^{CST}\end{array}\right)=x^{\left(k+\frac{1}{2}\right)};$

5. $\text{Compute }s=d^{CTV}(90\%),d_j^{CTV}=\{\begin{array}{l}{d}_p,d_j^{CTV}\ge sand{d}_j^{CTV}<d_p\hfill \\ d_j^{CTV},\text{ otherwise}\end{array},$

$\text{Compute }{d}_j^{CST}=\{\begin{array}{l}0.8d_p,\text{ if }{d}_j^{CST}<0.8d_p\hfill \\ 1.4d_p,\text{ if }{d}_j^{CST}>1.4d_p\\ d_j^{CST},\text{ otherwise}\end{array},$

$\text{Compute }{x}^{\left(k+1\right)}=\left(\begin{array}{c}{d}^{CTV}\\ d^{CST}\end{array}\right);$

6. $\text{Compute }{\Gamma }^{\left(k+1\right)}={\Gamma }^{\left(k\right)}+\beta \left(\widehat{D}{t}^{\left(k+1\right)}-x^{\left(k+1\right)}\right)$

7. If $\frac{{\Vert t^{\left(k+1\right)}-t^{\left(k\right)}\Vert }_2}{{\Vert t^{\left(k+1\right)}\Vert }_2}<\sigma$, set t* = t(k+1);

Otherwise, set k = k + 1, go to Step 2.

2.2. Weight tuning methodology

We proposed an automatic weight adjustment method for the aforementioned optimization engine by an artificial intelligence system that sequentially selected a weight and adjusts it. The system operated in a way analogous to the human-based treatment planning workflow: a planner repeatedly observes the plan obtained under a set of weights and makes a decision about weight adjustment, until a satisfactory plan quality is achieved (Fig. 1(a)). We aimed at developing a Weight-Tuning Policy Network (WTPN) that serves the same purpose as a human planner in this workflow (Fig. 1(b)).

Figure 1.

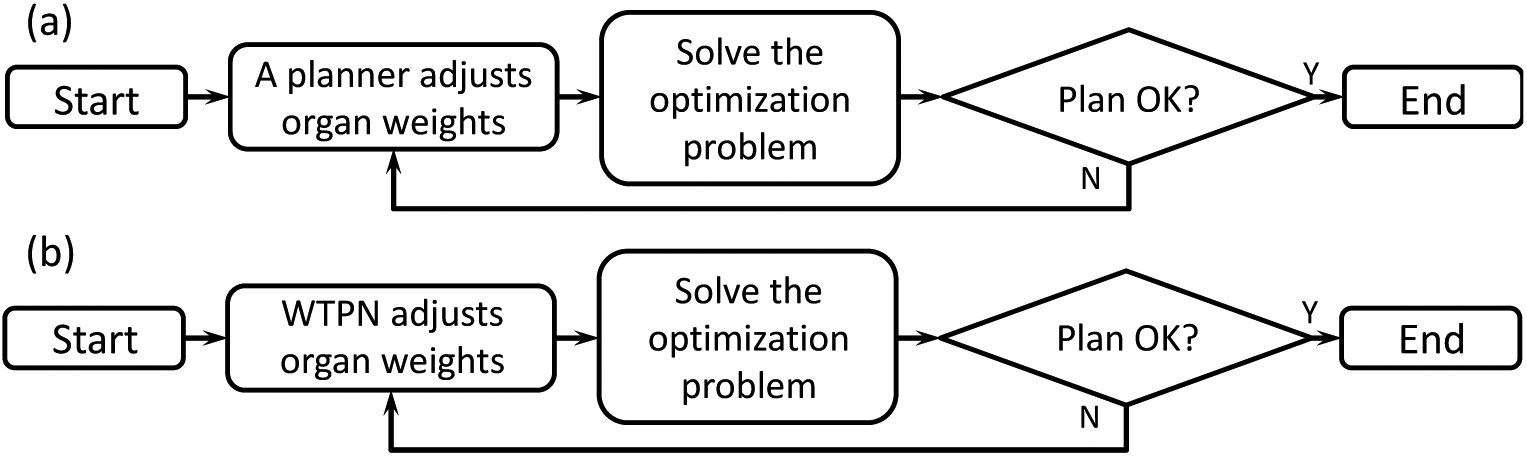
Illustration of weight tuning workflow (a) by a human planner and (b) by the WTPN.

More specifically, WTPN adjusted the organ weighting factors in an iterative fashion (the loop in Fig. 1(b)) to improve the plan quality. Let us use l to index the weight-tuning steps. At the step l, WTPN took the dose-volume histograms (DVHs) of the plan as inputs and output a decision of weight adjustment: the organ weight to tune, and the direction and amplitude of the adjustment. Then, we updated the weight and solved the optimization problem with the Algorithm 1. This process repeated, until plan quality cannot be further improved.

To realize the proposed WTPN, we incorporated the Q-learning framework (Watkins and Dayan, 1992) that tried to build the optimal action-value function defined as:

$$Q^{*}\left(s,a\right)=\underset{\pi }{\text{max}}[r^l+\gamma r^{l+1}+{\gamma }^2{r}^{l+2}+\cdots |s^l=s,a^l=a,\pi ].$$ (3)

s is the current state, i.e. plan DVHs, and s^l stands for the state at the l-th weight tuning step. a is the action, i.e. which weight to adjust and how to adjust, and a^l indicates the selected action. r^l is the reward obtained at step l. In this study, the reward was calculated based on a pre-defined reward function related to clinical objectives. A positive reward was given, if the clinical objectives were better met by applying the action a^l on the state s^l, and negative otherwise. γ ∈ [0, 1] is a discount factor. π = P(a|s) denotes the weight tuning policy: taking an action a based on the observed state s. The goal of automatic weight tuning was to build the Q* function. Once this was achieved, the policy was determined as choosing the action that maximizes the Q* function value under the observed state s, i.e. $a=\text{arg }\underset{a^{\prime }}{\text{max}}{Q}^{*}\left(s,a^{\prime }\right)$.

The form of the Q* function is generally unknown. In this paper, we proposed to parametrize Q* via a deep convolutional neural network (CNN), denoted as Q(s, a; W). W = {W₁, W₂,…, W_N} indicates the network parameters. The network consists of N independent subnetworks (see Fig. 2(a)), each for an OAR weight. The subnetworks shared the same structure as displayed in Fig. 2(b). We defined five possible tuning actions for each weight: increase or decrease the weight by 50%, increase or decrease the weight by 10%, and keep the weight unchanged. The values 50% and 10% were arbitrary chosen, as we expected they would not critically affect the capability of weight tuning but only the speed to reach convergence. Each subnetwork had five outputs. The network took observed state s, i.e. DVHs as inputs, and output values of the Q function at each output node, corresponding to an action. The parameters W_i of each network will be determined via the reinforcement learning strategy presented in the next section.

Figure 2.

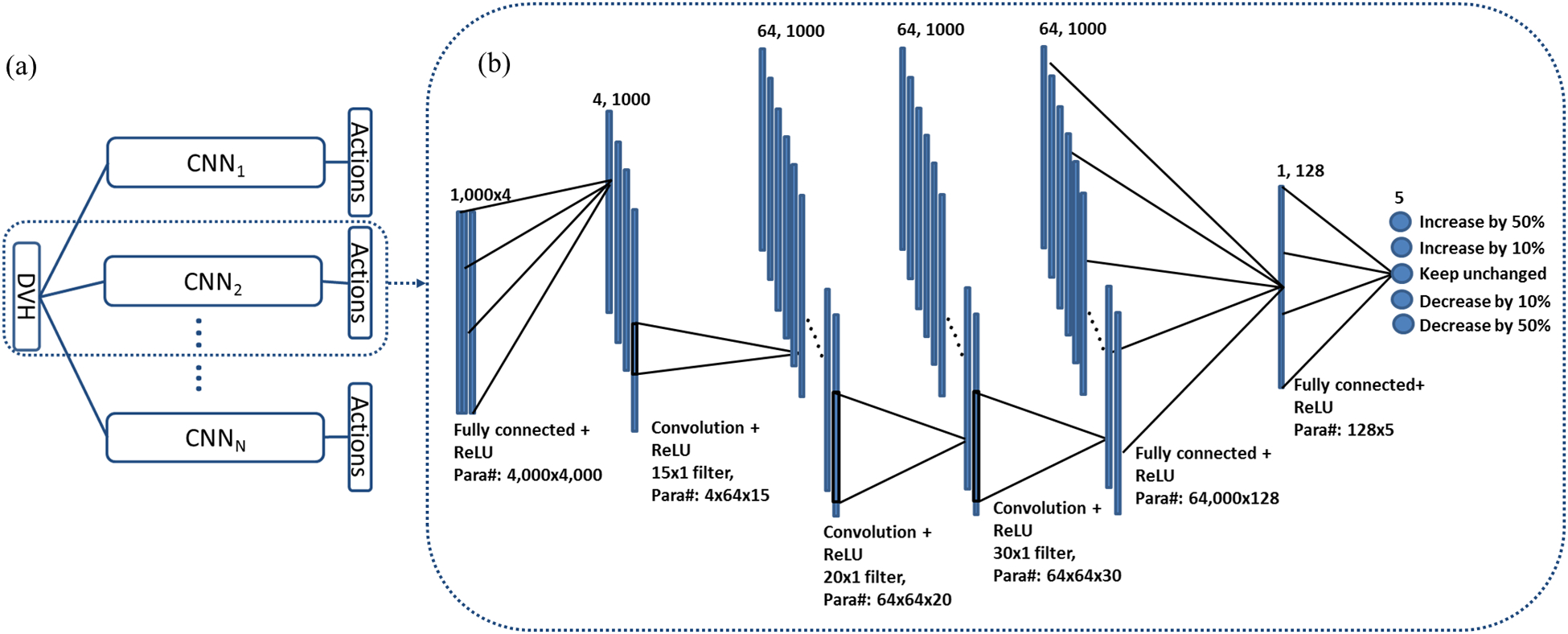
Network structure of the WTPN. (a) gives the overall structure of WTPN. The complete network consists of N subnetworks with identical structures. Each subnetwork corresponds to one OAR. The input is DVHs of a treatment plan. (b) Detailed structure of the subnetwork. Numbers and sizes of different layers are specified at the top of the layer. Connections between layers and number of parameters are presented at the bottom. Output value of each network node is the corresponding Q function value of defined action.

2.3. Deep reinforcement learning

2.3.1. General idea of network training

The main idea of the training process was to seek for a solution satisfying Bellman equation (Bellman and Karush, 1964), a general property of the optimal action-value function Q*(s, a):

$$Q^{*}\left(s,a\right)=r+\gamma \underset{a^{\prime }}{\text{max}}{Q}^{*}\left(s^{\prime },a^{\prime }\right),$$ (4)

where r is the reward after applying action a to the current state s and s′ is the state after taking the action a. Using a CNN Q(s, a; W) as an approximation of the Q function, we defined a quadratic loss function with respect to the network parameter W:

$$H(W)={\left[r+\gamma {\text{max}}_{a^{\prime }}Q\left(s^{\prime },a^{\prime };W\right)-Q\left(s,a;W\right)\right]}^2.$$ (5)

Our goal was to determine W through a reinforcement learning strategy to minimize this loss function, which hence ensured Eq. (4) and therefore Q(s, a; W) would approach Q*(s, a; W). It was difficult to minimize the loss function in Eq. (5) due to the term max_a′ Q(s′, a′; W), e.g. to compute its gradient with respect to W. To avoid this problem, we employed a process consisting of a sequence of stages. Within each training stage, we fixed the CNN parameters in max_a′ Q(s′, a′; W) as $\widehat{W}$. Then the loss function with respect to W became:

$$L\left(W\right)={\left[r+\gamma {\text{max}}_{a\prime }Q(s\prime ,a\prime ;\widehat{W})-Q\left(s,a;W\right)\right]}^2.$$ (6)

At each stage, W was calculated to minimize L(W) with the stochastic gradient descent method. The gradient of the loss function L(W) can be simply derived as

$$\frac{\partial L\left(W\right)}{\partial W}=\left[Q\left(s,a;W\right)-r-\gamma \underset{a^{\prime }}{\text{max}}Q\left(s^{\prime },a^{\prime };\widehat{W}\right)\right]\frac{\partial Q\left(s,a;W\right)}{\partial W},$$ (7)

where the last term $\partial Q\left(s,a;W\right)/\partial W$ was computed via the standard back-propagation strategy (LeCun et al., 1998). With the gradient of loss function ready, W at each step was updated by a gradient descent form:

$$W^{j+1}=W^j-\delta \frac{\partial L\left(\text{W}\right)}{\partial \text{W}}{|}_{W^j},$$ (8)

where δ is the step size and j is the index of gradient descent steps. We used stochastic gradient descent that computed the gradient and updated W with a subset of the training data randomly selected from the training data set. After finishing each stage of training, $\widehat{W}$ was updated by setting $\widehat{W}\text{ =}W$ and was then fixed for the next stage of training. Eventually, $\widehat{W}$ and W were expected to converge at the end of the learning process.

2.3.2. Reward function

One important issue is to quantitatively evaluate the plan quality. In general, this is still an open problem and different evaluation metrics can be proposed depending on the clinical objectives. In our case, since the plan was always normalized to d^CTV (90%) = d_p in the optimization algorithm (Algorithm 1), we considered OAR sparing to assess the plan quality, as quantified by d_2cc in the HDRBT context (Viswanathan et al., 2012). For simplicity, we measured the plan quality as $\psi =\sum _i{\omega }_i{d}_{2cc}^i$ where ω_i are the preference factors indicating the radiation sensitivity of the i-th OAR. the lower ψ was, the better plan quality was. In principal, a larger ω_i should be assigned to a more radiation sensitive OAR. We then formulated the following reward function regarding the change of from state s to s′:

$$\Phi \left(s,s^{\prime }\right)=\psi \left(s\right)-\psi \left(s\text{'}\right)=\sum _i{\omega }_i\left(d_{2cc}^i\left(s\right)-d_{2cc}^i\left(s\text{'}\right)\right).$$ (9)

s indicates the state (DVHs) prior to weight adjustment, while s′ is that after. The reward Φ(s, s′) explicitly measured the difference in plan quality between the two states. Φ(s, s′) was positive if plan quality was improved, and negative otherwise.

2.3.3. Training strategy

The training process was performed in a number of N_episode epochs. Each epoch contained a sequence of N_train steps indexed by l. At each step, we selected an action to adjust an OAR’s weight using the ∈-greedy algorithm. Specifically, with a probability of ∈, we randomly selected one of the OARs and one action to adjust its weight. Otherwise, the action a that attained the highest output value of the network Q(s, a; W) was selected, i.e. $a^l=\text{arg }{\text{max}}_{a}Q\left(s^l,a;W\right)$. After that, we applied the selected action to the corresponding OAR’s weight and solved the plan optimization problem of Eq. (1) using the Algorithm 1, yielding a new plan with DVHs denoted as s^l+1. s^l and s^l+1 were then fed into the reward function Φ defined in Eq. (9) to calculate r^l.

At this point, we collected {s^l, a^l, r^l, s^l+1} into the pool of training data set for the network Q. W was then updated by the experience replay strategy. Specifically, we used a number of N_batch training samples randomly selected from the training data pool at each training step to update W via Eq. (8). During DRL, the state-action pairs sequentially generated are highly correlated. The main purpose of the experience replay strategy was to overcome the strong correlation (Mnih et al., 2015). Once the maximum number of training step N_train was reached, we moved to the next patient and applied the above training process again. Within this process, $\widehat{W}$ was updated by letting $\widehat{W}\text{ =}W$ at every N_update steps. The complete structure of the training framework is outlined in Algorithm 2.

Algorithm 2.

Overall algorithm to train the WTPN.

Initialize network coefficients W;

for epoch = 1, 2, …, Nepoch

for k = 1, 2, …, Npatient do

Initialize λ1, λ2, …, λN;

Run Algorithm 1 with {λ1, λ2, …, λN} for s1;

for l = 1, 2, …, Ntrain do

Select an action al:

Case 1: with probability ∈, select al randomly;

Case 2: otherwise $a^l=\text{arg }{\text{max}}_{a}Q\left(s^l,a;W\right)$;

Based on selected al, adjust corresponding organ’s weight;

Run Algorithm 1 updated weights for sl+1;

Compute reward rl = Φ(s, sl+1);

Store reward {sl, al, rl, sl+1} in training data pool;

Train W:

Randomly select Nbatch training data from training data pool;

Compute gradient using Eq. (7);

Update W using Eq. (8);

Set $\widehat{W}\text{ =}W$ every Nupdate steps;

end for

end for

end for

Output W

The WTPN framework was implemented using Python with TensorFlow (Abadi et al., 2016) on a desktop workstation equipped with eight Intel Xeon 3.5 GHz CPU processors, 32 GB memory and two Nvidia Quadro M4000 GPU cards. We used five patient cases in training and another five patient cases as testing. All patients had cervical cancer and were previously treated at our institution with external beam radiotherapy followed by HDRBT with a T/O applicator. HDRBT plans of these cases produced by clinical physicists were collected for comparison purpose. Note that the data to train the WTPN were in fact {s^l, a^l, r^l, s^l+1} generated in the process outlined above. With five patient cases, we generated a large number of training samples. The initial weights for all OARs were set to unity. Other major hyperparameters to configure our system are summarized in Table 1.

Table 1.

Hyperparameters to train the WTPN.

Hyperparameter	Value	Description
σ	5×10−4	Stopping criteria in Algorithm 1
β	5	Penalty parameter in Algorithm 1
n	4	Number of weights (OARs) to be tuned
γ	0.5	Discount factor
∈	0.99 ~ 0.1	Probability of ∈-greedy approach
Npatient	5	Number of training patient cases
Nepoch	100	Number of training epoch
Ntrain	25	Number of training steps in each epoch
Nupdate	10	Number of steps to update $\widehat{W}\text{ =}W$
δ	1×10−4	Learning rate (step size of gradient descent for W)

2.4. Validation studies

The WTPN was developed to adjust organ weights to gain a high reward Φ, which would improve the plan quality, as quantified by reduction of $\psi ={\sum }_i{\omega }_i{d}_{2cc}^i$. To validate the WTPN, we used the trained WTPN to adjust OAR weights in those five cases used in training and five additional independent testing cases. Without loss of generality, we set ω_bladder = 0.2 while ω_rectum = ω_sigmoid = ω_sma = 1 in ψ, as bladder is more radiation resistant compared to the other OARs. In each case, we performed the weighting adjustment process using the trained WTPN as shown in Fig. 1(b). Evolution of the plan quality in this process was examined in detail.

In addition, it is mathematically possible to directly solve an optimization problem to minimize ψ, although the highly non-convex nature of this problem would make it hard to ensure optimality of the result. We minimized ψ using an algorithm in the Appendix and compared the resulting ψ values with those obtained by the proposed approach.

The proposed framework does not have any restrictions on the plan quality metrics and is applicable to any metrics. To demonstrate this fact, we also trained and tested another WTPN using the preference factors ω_i = 1, for i = 1, …, 4. The plan quality metric in this case was denoted as $\widehat{\psi }$. Clinically, different plan quality metrics can be interpreted as different preference of organ trade-offs, probably among different physicians. Being able to accommodate different plan quality metrics is an important aspect to ensure practicality of WTPN. Additionally, we compared the performances of the two WPTNs trained with ψ and $\widehat{\psi }$ functions.

3. RESULTS

3.1. Training process

It took around four days to complete the training of WTPN. The recorded reward and Q-values along training epochs are displayed in Fig. 3. Note that reward reflects the plan score obtained via automatic weight tuning using WTPN, while the Q-value indicates output of WPTN approximating future rewards to be gained via weight adjustment. It can be observed in Fig. 3 that the reward and Q-value both showed increasing trends, indicating that the WTPN gradually learnt a policy of weight tuning that can improve the plan quality.

Figure 3.

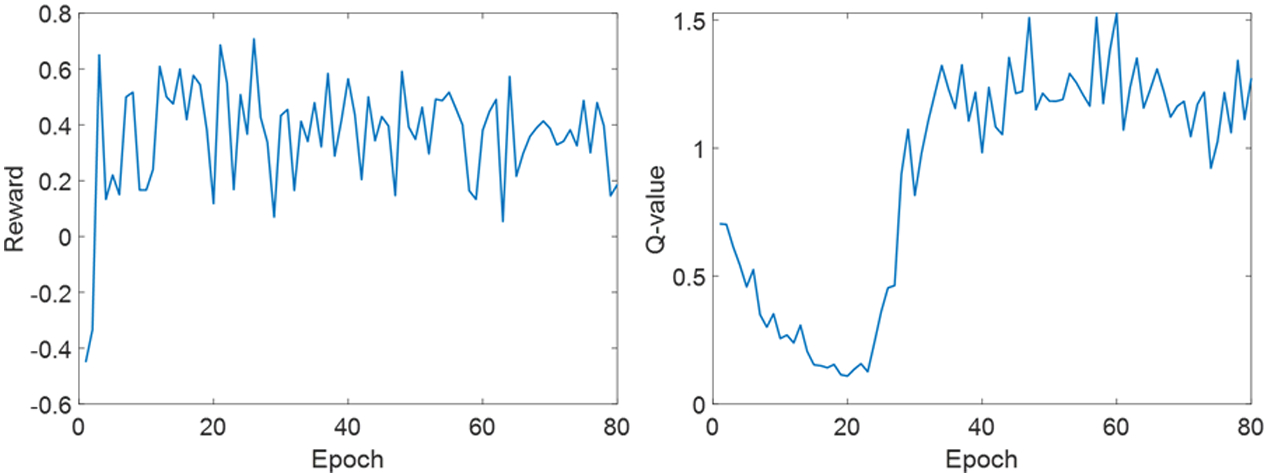
Reward (left) and Q-values (right) obtained along training epochs.

3.2. Weight tuning process

In Fig. 4, we present how the trained WTPN performed weight adjustment in an example case 3 that was used in training. Fig. 4(a) shows evolution of the weights. Corresponding d_2cc values of different OARs are displayed in Fig. 4(b), which provide insights of how the proposed WTPN decided weight adjustment. In the initial eight steps, WTPN first increased the rectum weight, resulting in a successful reduction of $d_{2cc}^{\mathit{\text{rectum}}}$ at the expense of increasing $d_{2cc}^{\mathit{\text{sigmoid}}}$ and $d_{2cc}^{\mathit{\text{small bowel}}}$. $d_{2cc}^{\mathit{\text{bladder}}}$ was first reduced and later increased. The ψ function value was greatly reduced. From step 8 to 12, the bladder weight was reduced, allowing reduction of other organ doses and slightly reduction of ψ. Starting from step 12, WPTN decided to increase the small bowel weight probably due to the observed large $d_{2cc}^{\mathit{\text{smallbowel}}}$. Overall, the ψ function value showed an decreasing trend, indicating that the plan quality was improved under the guidance of WTPN. The final ψ value was lower than that of the clinical plan that was used in our clinic to treat this patient. In addition, we plot the DVHs at tuning steps 0 (initial), 5, and 25 in Fig. 4(d), while DVHs plotted with absolute volume around 2cc are shown in 4(e).

Figure 4.

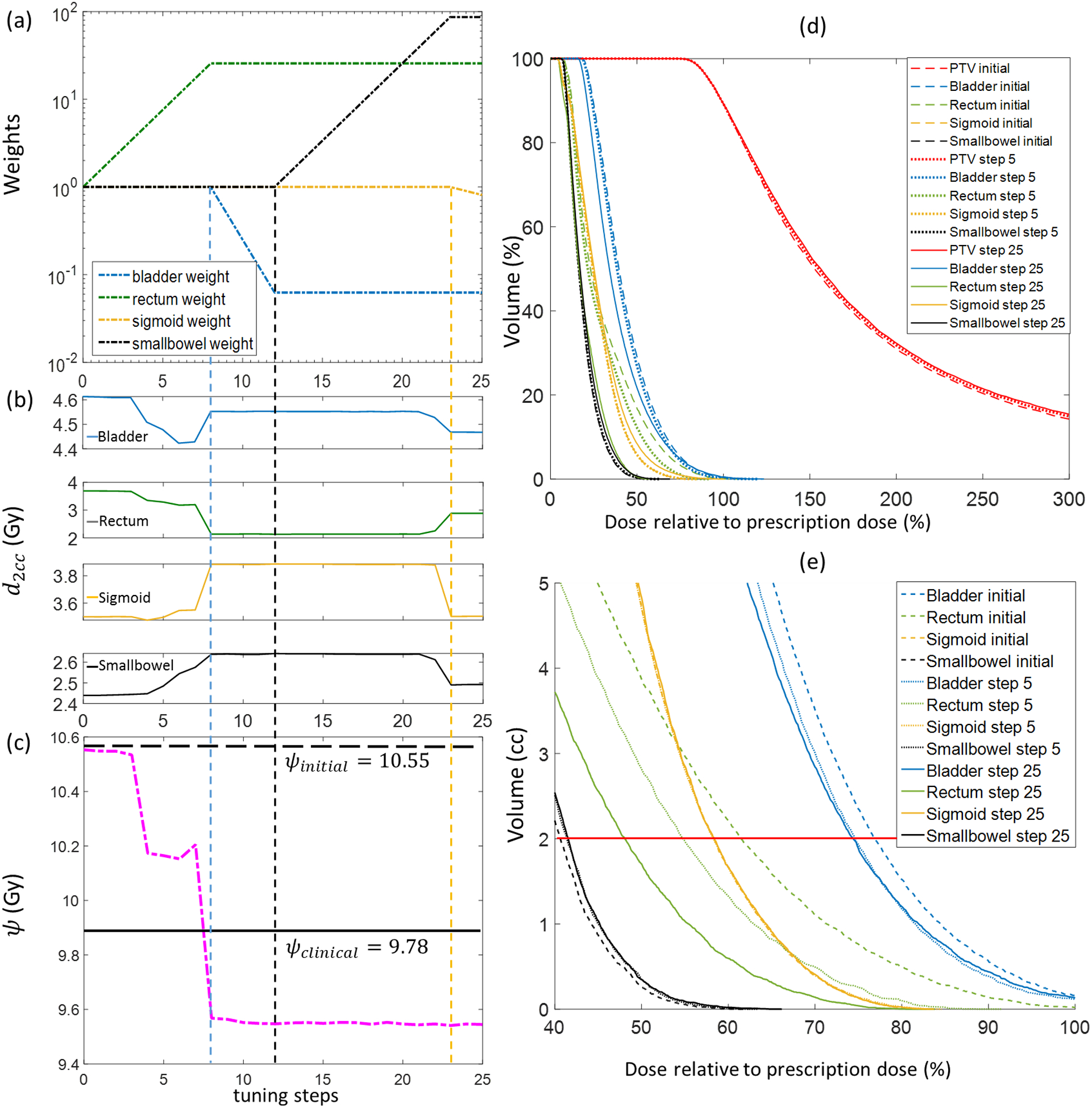
Weight-tuning process using the WTPN for a training case (training case 3). (a) Evolution of organ weights; (b) Corresponding d_2cc of different OARs; (c) ψ function values; (d) DVHs of plans at weight tuning steps 0 (initial weights), 5 and 25; (e) DVHs plotted with absolute volume. Horizontal line shows 2cc volume.

Similarly, we show in Fig. 5 the weight-tuning process for the testing case 3 that was not included in the training of the WTPN. For this case, WTPN decided to first increase rectum weights, causing reduced d_2ccs for bladder, rectum, and sigmoid. Starting from step 15, WTPN increased small bowel weight. Dose to small bowel was successfully reduced without affecting too much dose to rectum and sigmoid. $d_{2cc}^{\mathit{\text{bladder}}}$ increased a little, which was reasonable, as it is our assumption that bladder is more radiation resistant (with a lower preference factor of 0.2). In general, the ψ function value, as well as dose to OARs for this testing case were successfully reduced in this process.

Figure 5.

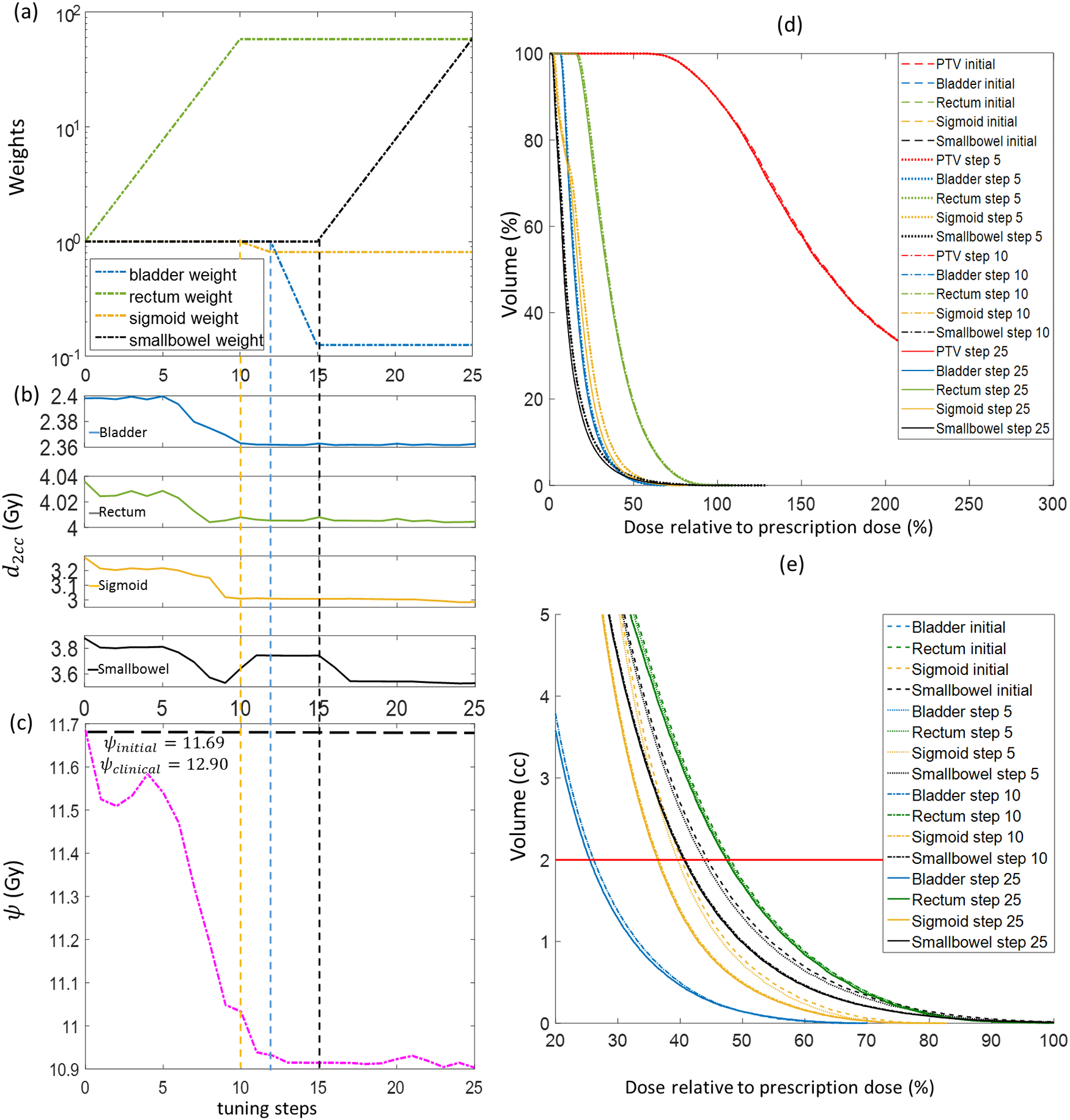
Weight-tuning process using the WTPN for a testing case (testing case 3). (a) Evolution of organ weights; (b) Corresponding d_2cc of different OARs; (c) ψ function values; (d) DVHs of plans at weight tuning steps 0 (initial weights), 5 and 25; (e) DVHs plotted with absolute volume. Horizontal line shows 2cc volume.

Given input DVHs, WTPN was able to predict the weigh-tuning action very efficiently (within 1 second). The major computational burden along the weight-tuning process was to solve the inverse optimization problem repeatedly. On average, it took ~10 seconds to complete the optimization process once. In this study, we performed 25 steps of weight adjustment for each patient case and the total time was 4–5 minutes.

3.3. All training and testing cases

We report the performance of WTPN on the five training and five testing cases in Table 2. Consistent improvements were observed for all the cases compared to those plans generated with initial weights. The plans after weight tuning were also better than those manually generated by the planners in our clinic. For all the training cases, on average the ψ function values after automatic weight tuning were reduced by 0.63 Gy (~7.5%) compared to the initial plans, and 0.50 Gy (~6%) compared to clinical plans. In the testing cases, average ψ values under WPTN guidance were 0.76 Gy (~8.5%) and 0.97 Gy (~10.7%) lower than those of the initial plans and those of the clinical plans, respectively. Comparing with plans obtained by directly optimizing the ψ function, the plans after weight tuning achieved lower ψ values in most cases. These numbers clearly demonstrate the effectiveness of the developed WTPN.

Table 2.

ψ function value of plans obtained by using an initial weights ψ_initial, adjusted weights by our method ψ_tuned, plans used in our clinic ψ_clinical, and those obtained by directly optimizing the ψ function. Numbers in bold face are the smallest values in each case.

Cases	ψinitial (Gy)	ψtuned (Gy)	ψclinical (Gy)	ψopt (Gy)
Training patient 1	6.53	6.17	6.62	6.23
Training patient 2	8.37	7.31	8.28	8.05
Training patient 3	10.55	9.35	9.78	9.48
Training patient 4	10.72	10.54	10.79	10.63
Training patient 5	6.18	5.82	6.19	5.51
Testing patient 1	6.81	6.48	6.61	6.56
Testing patient 2	5.95	5.07	6.13	5.57
Testing patient 3	11.69	10.90	12.90	11.21
Testing patient 4	9.74	8.94	10.02	9.30
Testing patient 5	10.18	9.19	9.78	9.53

To get a better understanding on the plan quality, we use the testing patient 5 as an example and show its DVH curves of the initial plan, clinical plan and automatically tuned plan in Fig. 6. It is clear that doses to rectum, sigmoid and small bowel were effectively reduced by the WTPN. Among them, the DVH curves for sigmoid and small bowel obviously outperformed those of the clinical plan. The dose to bladder was higher than that under the initial organ weight setup. Due to the assumption that bladder is more radiation resistant compared to the other OARs (ω_bladder = 0.2), WTPN decided to sacrifice bladder to reduce ψ and hence increase plan quality.

Figure 6.

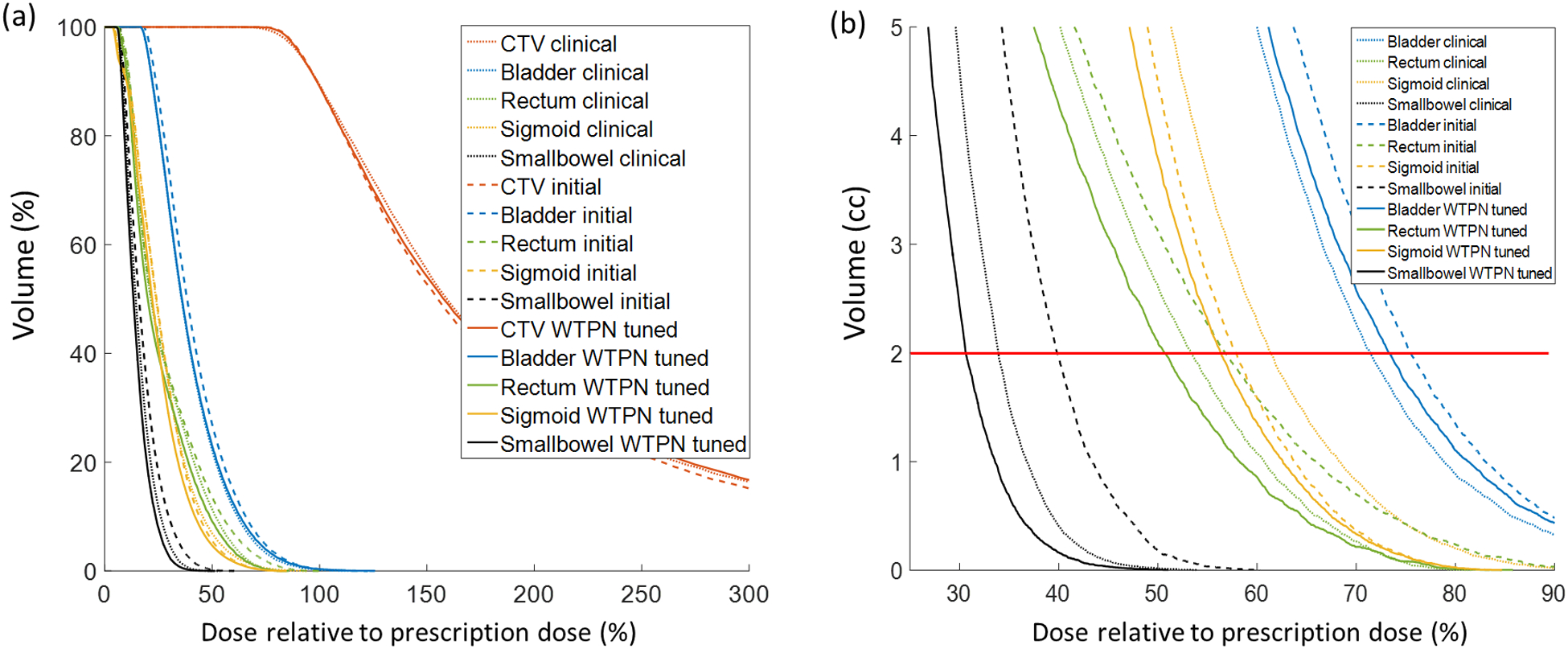
DVH comparison curves for testing patient case 5.

The advantage of WTPN can be also observed directly on isodose lines. Using the testing patient 2 as an example, the OARs were spared successfully, especially in the highlighted areas indicated by pink circles in Fig. 7. More specifically, it is shown in coronal view that the dosages to small bowel, sigmoid and rectum using WTPN were apparently the lowest among the three plans. Similarly, in sagittal view, sigmoid and small bowel received lower dose in the weight-adjusted plan than the other two plans. Note that all these cases had the same CTV coverage of d^CTV (90%) = dp because of the constraint in the optimization problem.

Figure 7.

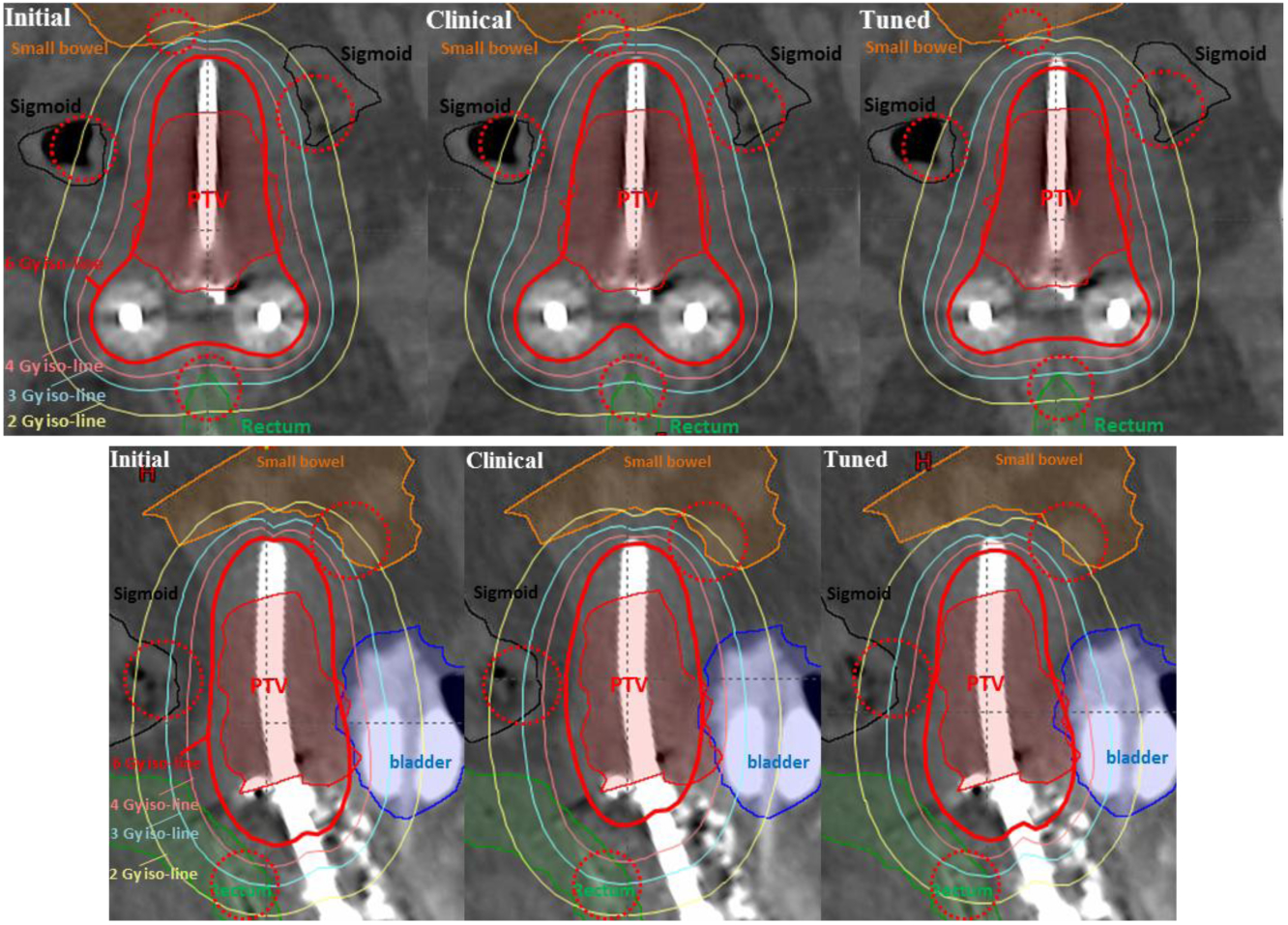
Dose map comparison in coronal (top) and sagittal (bottom) view for patient case 2.

3.4. Impact of preference factors in reward function

Table 3 reports weight tuning results using $\widehat{\psi }$ in the reward function, in which the preference factors for all the OARs are set to unity. After training the WTPN with the new reward function, WPTN was again able to successfully adjust OAR weights of the objective function, so that the values $\widehat{\psi }$ were reduced through the planning process. The resulting $\widehat{\psi }$ at the end were lower than those in the clinical plan, indicating better plan quality.

Table 3.

Weight tuning results for testing cases. Numbers in bold face are the smallest values in each case.

Cases	${\widehat{\psi }}_{\mathit{\text{initial}}}$ (Gy)	${\widehat{\psi }}_{\mathit{\text{tuned}}}$ (Gy)	${\widehat{\psi }}_{\mathit{\text{clinical}}}$ (Gy)
Testing patient 1	10.03	9.40	9.75
Testing patient 2	6.85	6.45	7.17
Testing patient 3	13.60	13.31	15.47
Testing patient 4	13.39	12.79	13.94
Testing patient 5	13.80	12.75	13.21

Table 4 compares plan results generated by WTPN with two different reward functions using ψ and $\widehat{\psi }$. Note that the difference between the two setups was that bladder was considered to be more important in $\widehat{\psi }\left({\omega }_{\mathit{\text{bladder}}}=1\right)$. In response to the increased preference factor for bladder, the resulting plan had a lower bladder d_2cc. At the same time, other OARs were affected to different degrees. d_2cc of them were mostly increased when $\widehat{\psi }$ was used because of the consideration of bladder sparing.

Table 4.

Effect of different reward functions on testing cases.

Cases	Reward	${\text{d}}_{2\text{cc}}^{\mathit{\text{bladder}}}$ (Gy)	$d_{2cc}^{\mathit{\text{rectum}}}$ (Gy)	$d_{2cc}^{\mathit{\text{sigmoid}}}$ (Gy)	$d_{2cc}^{\mathit{\text{smallbowel}}}$ (Gy)
Testing patient 1	ψ	3.89	2.55	2.09	1.06
	$\widehat{\psi }$	3.76	2.56	2.08	1.00
Testing patient 2	ψ	1.18	1.35	2.89	0.59
	$\widehat{\psi }$	0.97	1.70	3.12	0.66
Testing patient 3	ψ	2.51	3.96	2.95	3.49
	$\widehat{\psi }$	2.38	4.01	3.18	3.74
Testing patient 4	ψ	4.56	3.29	2.13	2.60
	$\widehat{\psi }$	4.45	3.41	2.19	2.74
Testing patient 5	ψ	4.47	3.06	3.37	1.87
	$\widehat{\psi }$	4.41	3.09	3.39	1.86

4. DISCUSSIONS

4.1. Motivations and study focus

The proposed study was motivated by the tremendous success achieved by deep learning across a wide range of applications (LeCun et al., 2015; Mnih et al., 2015; Silver et al., 2016; Wang, 2016; Shen et al., 2018; Ma et al., 2018; Iqbal et al., 2017). In particular, deep learning techniques have recently been incorporated to tackle many important tasks for radiation therapy, such as image quality enhancement (Brosch and Tam, 2013; Chen et al., 2017; Iqbal et al., 2018; Liang et al., 2018), target/organ segmentation (Chen et al., 2018; Ibragimov and Xing, 2017; Balagopal et al., 2018; Chen et al., 2019), dose prediction/calculation (Landry et al., 2019; Nguyen et al., 2017; Nguyen et al., 2018), treatment planning (Kim et al., 2009), adaptive therapy (Tseng et al., 2017), and outcome prediction (Nie et al., 2016; Zhen et al., 2017). To the best of our knowledge, our study is the first time to autonomously encode intelligent treatment planning behaviors in an artificial intelligence system. The WTPN system was developed under the motivation to represent the clinical workflow, in which a planner repeatedly tunes the organ weights based on human intuition to improve the clinical objective. The WTPN, once trained, could assume the planner’s role in this workflow (Fig. 1). We would also like to emphasize that the focus of this study was not to propose a new method specifically for inverse treatment planning of T/O HDRBT of cervical cancer. In fact, manual forward planning is still used widely in current clinical practice of T/O HDRBT. We chose the this problem as a proof-of-principle study for the consideration of using a relatively small-size problem to reduce the computational burden.

4.2. Relationships with existing works and alternative approaches

As mentioned in the introduction section, a representative approach in existing efforts to adjust weighting factors in the treatment planning optimization problem is to add a second loop on top of the iteration of solving the plan optimization problem. In each step, the weights are adjusted based on certain mathematical rules aiming at improving the plan quality, as quantified by a certain metric (Xing et al., 1999; Wu and Zhu, 2001; Lu et al., 2007; Wang et al., 2017). Compare to these approaches, our method attained a similar structure, in the sense that the OAR weights were adjusted in an iterative fashion in the outer loop. Nonetheless, a notable difference is that, in contrast to previous approaches adjusting weights by a certain rigorous or heuristic mathematical algorithms, our system was designed and trained to develop a policy that can intelligently tune the weights, akin to the behavior of a human planner. The reward function involving the plan quality metric was only used in the training stage to guide the system to generate the intelligence. When WTPN was trained, the goal of treatment planning, i.e. to improve plan quality metric, was understood and memorized by the system. The subsequent applications of the WTPN to new cases did not explicitly operate in a way aiming at mathematically improving the plan quality metric. Instead, WTPN behaved with the learnt intention to improve the plan.

Another, but more straightforward way to determine the weights using a deep learning method is to use a large number of optimized cases to build a connection between patient anatomy and the weights. This is in fact the mainstream of current applications of deep learning techniques in medicine. Yet one drawback is the requirement on the number of training cases. The number necessary to build a reliable connection is typically very large, posing a practical challenge. In contrast, our study was motivated by mimicking human behaviors. In fact, the key behind the reinforcement learning process was to let the WTPN to try different parameter tuning strategies in the ∈-greedy algorithm, differentiate between proper and improper ways of adjustment, and memorize those proper ones. This was similar to teaching a human planner to learn how to develop a high-quality plan. As demonstrated in our studies, one apparent advantage is that, with a relatively low number of patient cases, successful training can be accomplished. We emphasize that the actual data to train WTPN were not the patient cases, but the state-action pair {s^l, a^l, r^l, s^l+1} generated in the reinforcement learning process from these patient cases. If we count the paired state-action data, the number of training data was in fact large: N_train(25) × N_patient(5) × N_episode(100) = 12500. Of course, given the small number of patients involved in training, generality of the trained WTPN to different patient cases needs to be further investigated by testing it in more patient cases.

4.3. Potential advantages

One advantage of the proposed method is that it naturally works on top of any existing optimization systems. Similar to the study by Wang et. al. (Wang et al., 2017), the developed system can be partnered with an existing treatment planning system (TPS). The only requirement is that the TPS has an interface to allow querying a treatment plan and inputting updated weights to launch an optimization, which is already feasible in many modern TPSs, for instance Varian Eclipse API (Varian Medical Systems, Palo Alto, CA). In addition, one notable fact in the proposed approach is it takes a plan that is generated by an optimization engine as input. This could be the plan after all required processing steps by the TPS, for instance after leaf sequencing operations in an EBRT problem. This fact is has practical benefits, as it can address the subtle quality difference in a plan caused by the leaf sequencing operations. In contrast, if we were to directly add a layer of weight optimization to the plan optimization by solving the problem from a mathematically rigorous way, it would be difficult to derive operations to account for this difference. Heuristic approach would likely have to be used.

In principle, once a planning objective is defined, e.g. the ψ function in this study, it can be directly optimized, e.g. using the algorithm in the Appendix. Nonetheless, the optimization problem is often complicated and the non-convex nature makes it difficult to justify the solution optimality. On the other hand, the proposed method was trained to learn to manipulate the optimization process and derive a high-quality plan. Although it is not possible to rigorously prove the advantages of this method over the direct optimization approach, at least in the cases studied in this paper, effectiveness of the proposed method has been observed.

4.4. Limitations of this study and future directions

The current study is for the purpose of proof of principle and has the following limitations. First, the reward function may not be clinically realistic. The choice of Eq. (8) was a simple one that reflects physician’s idea to a certain extent in HDRBT. By no means it should be interpreted as the one used in a real clinical situation. However, we also point out that the reward function in our system can be changed to any quantities based on clinical or practical considerations. In essence, the system was developed to mimic the human planner’s behavior in the clinical treatment planning workflow. Hence, the reward function here is akin to a metric to quantify the physician’s judgement of a plan. In the past, there have been several studies aiming at developing such a metric (Moore et al., 2012; Zhu et al., 2011). In principle, these metrics can be used in our system. In addition, recent advancements in imitation learning and inverse deep reinforcement learning (Wulfmeier et al., 2015) allow learning the reward function based on human behavior. In the treatment planning context, it may be possible to learn the physician’s preference as represented by the reward function. It is our ongoing work to perform studies as such.

The weight adjustment steps of 50% and 10% in WTPN were arbitrary chosen, as we expect they would not critically affect the capability of weight tuning but only the speed to reach a good plan. For instance, a proper action of increasing a weight by 21% can be achieved by two steps with each one increasing by 10% (1.1²=1.21). In general, we can set a larger number of possible actions in WTPN for finer adjustments each time. If trained successfully, this setup would likely increase the efficiency of the weight tuning process. However, this would make the training of the network more challenging (Dulac-Arnold et al., 2015). In the future, we would like to tackle this problem by employing the continuous actions (Lillicrap et al., 2015).

Another limitation is that WTPN only takes DVH as input, which hence neglects other aspects of a plan. For instance, in an EBRT problem, DVH cannot capture position-specific information such as locations of hot/cold spots, which a physician often pays attention to. Again, at this early stage of developing an human-like intelligence system for weight tuning, we made the decision to start with a relatively simple setup to illustrate our idea. Further extending the system to include more realistic and clinically important features will be down the road.

One apparent issue is that the developed WTPN is a black box. It is difficult to interpret the reasons for weight adjustments and to justify the rigor of the approach. All that can be shown is that the trained WTPN appeared to work in a human-like manner. In fact, it is a central topic in the deep learning area to decipher the underlying intelligence in a trained system (Zhang et al., 2016; Zhang et al., 2018; Che et al., 2016; Sturm et al., 2016). It will be our ongoing work to pursue this direction, which is essential for a better understanding of the developed system, for further improving its performance, and for its safe clinical implementation.

Despite these limitations, it is conceivable that the proposed approach is generalizable to the optimization problem in EBRT. In fact, the method described in Section 2 has a rather generic structure that takes an intermediate plan as input and outputs the way to change parameters in the optimization problem. It does not depend on the specific optimization problem of interest. Nevertheless, we admit that generalization of the proposed method to the EBRT regime will encounter certain difficulties. Not only will the optimization problem itself be substantially larger in size, which will inevitably prolongs computation time each time solving the optimization problem, the number of parameters to tune will also be much larger in an EBRT problem. The latter issue will lead to a much larger WTPN to train, which will hence cause a larger computational burden to train the network. We also envision that, in the EBRT regime, justifying a plan quality is a much complex problem than in that of HDRBT. This will yield the challenge of properly defining the reward function, i.e. a counterpart of Eq. (8) in EBRT. It will be our future study to extend the proposed approach to EBRT, as well as to overcome the aforementioned challenges.

5. CONCLUSION

In this paper, we have proposed a deep reinforcement learning-based weight tuning network WTPN for inverse planning of radiotherapy. We chose the relatively simple context of T/O HDRBT to demonstrate the principles. The WTPN was constructed to decide organ weight adjustments based on observed DVHs, similar to the behaviors of a human planner. The WTPN was trained via an end-to-end reinforcement learning procedure. When applying the trained WTPN, the resulting plans outperformed those plans optimized with initial weights significantly. Compared to the clinically accepted plans made by human planers, WTPN generated better plans with same CTV coverage in all the testing cases. To our knowledge, this was the first time that an intelligent tool is developed to adjust organ weights in a treatment planning optimization problem in a human-like fashion based on intelligence learnt from a training process, which is fundamentally different from existing strategies based on pre-defined rules. Our study demonstrated potential feasibility to develop intelligent treatment planning approaches via deep reinforcement learning.

APPENDIX

Algorithm to directly optimize planning objective Ψ

We consider the following optimization problem to directly minimize the planning objective $\psi ={\sum }_i{\omega }_i{d}_{2cc}^i$:

$${\text{min}}_{\mathit{t}}\psi +\frac{\lambda }{2}{\Vert \nabla t\Vert }_2^2,$$ (A.1)

$$\text{s}.\text{t}.d_{2cc}^i={D_{OAR}^i|}_{2cc}t,$$

$$d^{CTV}=D_{CTV}t,$$

$$d^{CST}=D_{CST}t,$$

$$d^{CTV}\left(90\%\right)=d_p,$$

$$d^{CST}\in \left[0.8d_p,1.4d_p\right],$$

$$t_j\in \left[0,t_{max}\right],j=1,2,\dots ,n.$$

Again we employ ADMM to solve the optimization problem. The augmented Lagrangian function of the optimization problem is given as

$$L\left(t,x,\Gamma \right)={\sum }_i{w}_i{\left\{D_{OAR}^{i}t\right\}}_{2cc}+\frac{\lambda }{2}{\Vert \nabla t\Vert }_2^2+\frac{\beta }{2}{\Vert \widehat{D}t-x\Vert }_2^2+\langle \Gamma ,\widehat{D}t-x\rangle +{\delta }_1\left(x\right)+{\delta }_{box}\left(t\right),$$ (A.2)

where $\widehat{D}=\left(\begin{array}{c}{D}_{CTV}\\ D_{CST}\end{array}\right)$ and $x=\left(\begin{array}{c}{d}^{CTV}\\ d^{CST}\end{array}\right)$. The optimization scheme to tackle this problem is similar to that of optimization problem in Eq. (1) and we summarize it in Algorithm 3.

Algorithm 3.

ADMM algorithm solving the problem in Eq. (A.1)

Input: $D_{OAR}^i$, $\widehat{D}$, x(0), Γ(0), λi, β, t(0) and tolerance σ

Output: t*

Procedure:

1. Set k = 0;

2. Compute $d_{OAR}^i=D_{OAR}^i{t}^{\left(k\right)}$, compute $d_{2cc}^i$ according to $d_{OAR}^i$;

3. Identify ${D_{OAR}^i|}_{2cc}$ according to $d_{2cc}^i$;

4. $\text{Compute }{t}^{\left(k+\frac{1}{2}\right)}={\left(\lambda {\nabla }^T\nabla +\beta {\widehat{D}}^T\widehat{D}\right)}^{-1}\left(\beta {\widehat{D}}^T{x}^{\left(k\right)}-{\widehat{D}}^T{\Gamma }^{\left(k\right)}-\sum _i{w}_i{D_{OAR}^i|}_{2cc}^T\right);$

5. $\text{Compute }{t}_j^{\left(k+\frac{1}{2}\right)}==\{\begin{array}{l}0,if{t}_i^{\left(k+\frac{1}{2}\right)}<0\hfill \\ t_{max},if{t}_i^{\left(k+\frac{1}{2}\right)}>t_{max}\\ t_i^{\left(k+\frac{1}{2}\right)},\text{ otherwise}\end{array};$

6. $\text{Compute }{x}^{\left(k+\frac{1}{2}\right)}=\widehat{D}{t}^{\left(k+1\right)}+\frac{{\Gamma }^{\left(k\right)}}{\beta },\left(\begin{array}{c}{d}^{CTV}\\ d^{CST}\end{array}\right)=x^{\left(k+\frac{1}{2}\right)};$

7. $\text{Compute }s=d^{CTV}\left(90\%\right),d_j^{CTV}=\{\begin{array}{l}{d}_p,d_j^{CTV}\ge sand{d}_j^{CTV}<d_p\hfill \\ d_j^{CTV},\text{ otherwise}\end{array};$

$\text{Compute }{d}_j^{CST}=\{\begin{array}{l}0.8d_p,if{d}_j^{CST}<0.8d_p\hfill \\ 1.4d_p,if{d}_j^{CST}>1.4d_p\\ d_j^{CST},\text{ otherwise}\end{array};$

$\text{Compute }{x}^{\left(k+1\right)}=\left(\begin{array}{c}{d}^{CTV}\\ d^{CST}\end{array}\right);$

8. $\text{Compute }{\Gamma }^{\left(k+1\right)}={\Gamma }^{\left(k\right)}+\beta \left(\widehat{D}{t}^{\left(k+1\right)}-x^{\left(k+1\right)}\right);$

9. If $\frac{{\Vert t^{\left(k+1\right)}-t^{\left(k\right)}\Vert }_2}{{\Vert t^{\left(k+1\right)}\Vert }_2}<\sigma$, set t* = t(k+1);

Otherwise, set k = k + 1, go to Step 2.