Diverse mechanisms of sound frequency discrimination in the vertebrate cochlea

Abstract

Discrimination of different sound frequencies is pivotal to recognizing and localizing friend and foe. Here, I review the various hair-cell tuning mechanisms employed among vertebrates. Electrical resonance, filtering of the receptor potential by voltage-dependent ion channels, is ubiquitous in all non-mammals, but has an upper limit of about 1 kHz. The frequency range is extended by mechanical resonance of the hair bundles in frogs and lizards, but may need active hair-bundle motion to achieve sharp tuning up to 5 kHz. Tuning in mammals employs somatic motility of outer hair cells, underpinned by the membrane protein prestin, to expand the frequency range. The bird cochlea may also employ prestin at high frequencies, but hair cells below 1 kHz show electrical resonance.

Hair cell tuning mechanisms and cochlear structure

Hair cells, the sensory receptors of the vertebrate inner ear, convert sound stimuli into electrical signals, and also separate the frequency constituents of the sound, enabling different subsets of hair cells to encode different frequencies. To ensure survival, an animal employs its auditory apparatus both to identify the sound source, whether friend, food or foe, and to spatially localize it. Are the cries within the forest at night those of an offspring or a predator? Crucially, from which direction do they originate? Can you recognize the voice of a friend across a dark room at a crowded party? Accurate classification and localization of sounds depend on their frequency make-up [1, 2]. The mechanisms involved in frequency discrimination differ between the vertebrate classes, reptile, bird or mammal, and importantly depend on the tonal range to be detected. In the evolution of the land vertebrates, there has been a drive to extend the upper frequency limit of hearing from a few hundred Hz in the simplest amphibians or reptiles up to about 100 kHz in small mammals. To this end, changes have occurred in sound transmission through the middle ear, in the structure of the cochlea, and in the roles of the hair cells. The reasons for the frequency extension are not known for certain. They may partly derive from selective pressure for localizing sounds in animals with small heads like the first mammals, or in finding tiny offspring from their high-frequency cries. Another factor driving frequency extension is communication between species members, exemplified by the croaks of frogs, the chirps of geckos and bird songs, which are all composed of kilohertz sound frequencies.

This review describes the evidence for the different cochlear mechanisms, all of which depend upon resonant behavior. A simple illustration of resonance is that generated by a mass, M, suspended on the end of a spring of stiffness K: when the mass is displaced, it oscillates with a resonant frequency, F_O, equal to 1//2π.(K/M)^1/2, F_O increasing with larger stiffness and smaller mass. Resonance refers to the increase in the oscillation’s amplitude if an external force is applied at the resonant frequency (but not if the external force is applied at frequencies far from it). In practice, the oscillations will be damped if the mass is immersed in fluid rather than air. In the cochlea, the resonance can be mechanical or electrical and, to generate a range of resonant frequencies, one or both parameters are graded systematically with position along the cochlea. Thus, each subset of hair cells is associated with a limited tonal set the bounds of which vary according to hair cell location in an arrangement known as the tonotopic map (Figure 1A). The cochlea therefore performs the equivalent of a Fourier analysis on the incoming sound, so that the amplitudes of the component frequencies can be signaled to the brain enabling central categorization of the sound. At least three well-defined frequency selective processes operate in vertebrates: electrical resonance of the hair cell, mechanical amplification by voltage-dependent hair cell contractions, and passive mechanical resonances possibly reinforced by active force generation by the hair bundle. These disparate processes are manifested in different cochlear organization.

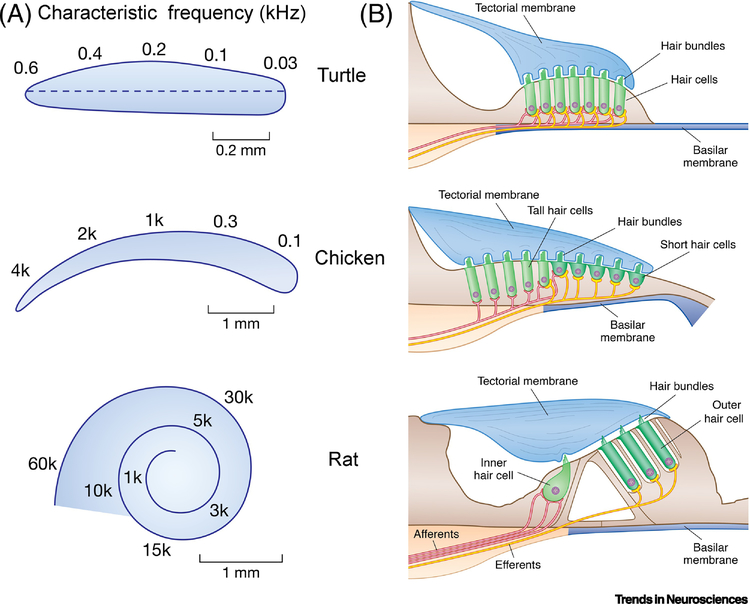
Figure 1.

Structure of three vertebrate cochleas. (A) Top view of the basilar membrane in turtle, chicken and rat showing the tonotopic characteristic frequency mapping form base (left) to apex (right). CFs in kHz. (B) Transverse sections through the cochlear duct showing the hair cells, afferent (red) and efferent (yellow) innervation patterns. In the chicken and rat, there are two hair cell types with different patterns of innervation. For turtle and chicken, each auditory nerve fiber contact a single hair cell, whereas in mammals up to 20 nerve fibers innervate each inner hair cell. For scale, hair cells are 25 μm long in turtle, and hair cells of similar length are tall hair cells in chicken and mid-cochlear OHCs in rat.

In all amniotes, comprising reptiles, birds, and mammals, the cochlea is a blind-ending tube projecting from the saccular division of the inner ear; it varies in length from under 1 mm in turtles to 4 mm in chickens, and in mammals 10 mm in rats, 34 mm in humans and 60 mm in elephants [3]. The cochlear tube is partitioned longitudinally by an elastic basilar membrane surmounted by an epithelium containing the sensory hair cells (Figure 1B). From the top of each hair cell projects a staircase of stereocilia termed the hair bundle, which inserts into an overlying acellular tectorial membrane. Sound-induced motions of the basilar membrane elicit deflections of the hair bundle which are the ultimate stimulus to the hair cell, acting to tension tip links between neighboring stereocilia to apply force on the mechanotransduction channel [4]. Because all tip links course parallel to the hair bundle’s axis of symmetry, the bundles are functionally polarized in that rotations towards the taller edge tension the links and are excitatory, whereas those in the opposite direction relax the links and are inhibitory. In most vertebrate cochleas (apart from some lizards), the bundles all point in one direction, away from the neural limb.

The simplest cochlear structure, epitomized by that of the turtle, is a short epithelium of hair cells of relatively uniform appearance and innervation; in these cells, the receptor potential is tuned by an electrical resonance [5, 6] resulting from activation of voltage-dependent ion channels. The electrical resonance has a limited frequency range extending only to about 1 kHz, and is not employed in mammals [7] needing to hear to much higher frequencies. In contrast, the cochleas of mammals (and birds) possess two types of hair cell with distinct morphology and innervation known as inner (short) hair cells and outer (tall) hair cells (OHCs) [8, 9]; inner hair cells receive the major glutamatergic afferent innervation, whereas outer hair cells are contacted by cholinergic efferents. In mammals, the hair cell epithelium supports a broad mechanical resonance [10] augmented by the contractions of OHCs [11], that perhaps with other unknown processes generates sharp mechanical tuning of the basilar membrane [12, 13]. These two mechanisms, electrical resonance and hair cell somatic motility, represent the extremes, and intermediate processes exist in other vertebrates. For example, both frogs and lizards display electrical resonance at low frequencies supplemented by other mechanical resonances at high frequencies.

Electrical resonance

Ion channels in electrical tuning

During acoustic stimulation, vibrations of the hair bundle modulate the hair cell membrane potential in an analog fashion. Action potentials are not generated until the spiral ganglion cells, the axons of which relay the auditory message to the brainstem cochlear nucleus. At frequencies less than 1 kHz, the waveform of the hair-cell receptor potential resembles that of the sound stimulus and is graded in amplitude with stimulus intensity. In electrical tuning, the receptor potential is shaped and filtered by voltage-dependent ion channels in the hair cell membrane [5]; in the turtle cochlea, this electrical resonance accounts for almost all of the frequency tuning to sound stimuli [5]. The mechanism can be revealed by injecting extrinsic current pulses into a hair cell through a recording electrode, thus circumventing the transduction apparatus. Extrinsic current pulses elicit damped oscillations in membrane potential at the onset and termination of the step, reminiscent of the ringing of a struck bell (Figure 2). The frequency of the damped oscillation, the resonant frequency, F_O, changes systematically with hair cell location along the cochlea to encompass the auditory range of the turtle extending from 30 Hz to 600 Hz at 25°C [14]. However, as discussed below, this range is temperature sensitive.

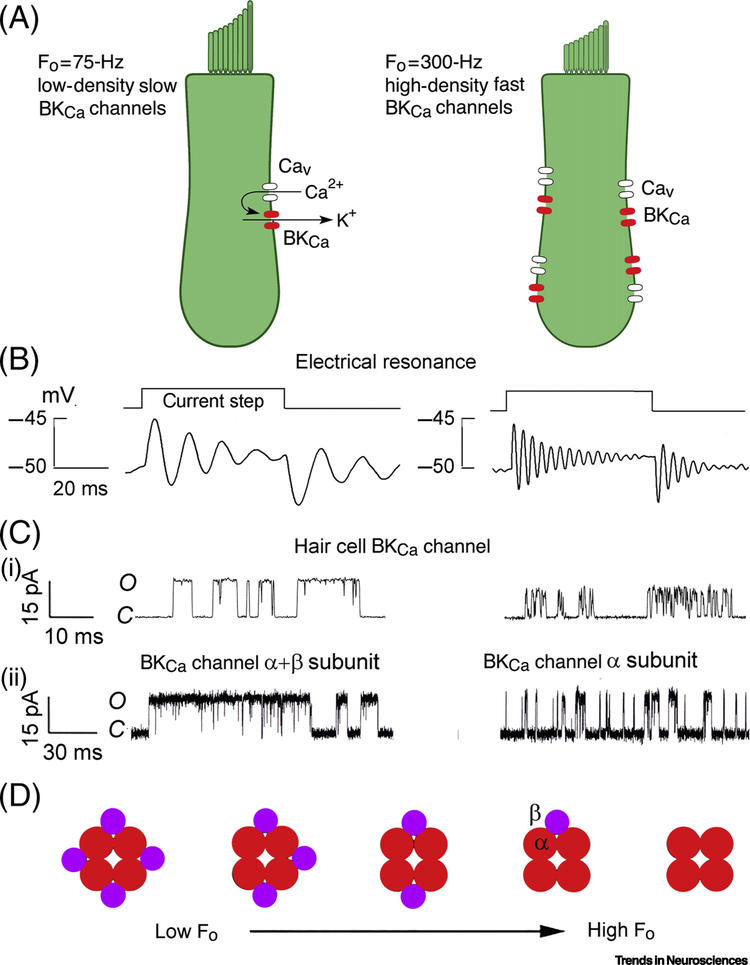
Figure 2.

Mechanisms of electrical tuning in low- frequency and high-frequency turtle hair cells. (A) Resonance arises from voltage-dependent Ca²⁺ channel (Ca_v) and Ca²⁺-activated K⁺ (K_Ca) channels. An increase in resonant frequency from 75Hz (left) to 300Hz (right) requires four-fold increase in channel numbers. (B) Examples of voltage ringing induced by current steps. (C) Cell-attached patch recordings from K_Ca channels in isolated hair cells tuned to 75 and 300 Hz (top); and K_Ca channels expressed in Xenopus oocytes, for α+β and α subunits (see references 20, 23). (D) Scheme for tonotopy: four K_Ca channel α subunits associated with one to four β subunits.

Electrical tuning stems from negative feedback between the membrane potential and the current through voltage-dependent K⁺ channels. In all hair cells, the resting potential is approximately −50 mV, positive to the K⁺ equilibrium potential (−75 mV), so that the depolarization induced by the current step activates the K⁺ channels through which an outward repolarizing current flows. Since the K⁺ channels activate with a delay, the feedback produces several oscillatory cycles. For most of the frequency range, the effective voltage-dependent K⁺ channel is fashioned [15, 16] from the combined action of voltage-dependent Ca²⁺ channels (Cav1.3) and large-conductance Ca²⁺ activated K⁺ (BK_Ca) channels (gene KCNMA1). Thus, depolarization opens Ca²⁺ channels and the Ca²⁺ influx and depolarization collude to activate nearby BK_Ca channels; this channel arrangement augments the voltage-sensitivity of the BK_Ca channels and sharpens the frequency tuning. Other types of voltage-dependent K⁺ channels, including A-currents (Kv4.2) and inward rectifiers (Kir), may also contribute at low frequencies [17–19], but the principle of their action is similar. At the resonant frequency, F_O, the current flowing through the BK_Ca channels is approximately equal and opposite to the capacitive current, so at F_O the membrane impedance is large, maximizing the receptor potential amplitude. F_O can be changed by altering the electrical properties of the resonator. On the idea of a negative feedback between membrane potential and current through the BK_Ca channels, the larger and faster the K⁺ current, the more rapidly it counters the voltage change to elicit higher-frequency oscillations: a higher density of faster BK_Ca channels causes an increase in F_O [20] (Figure 2A, B). Quantitatively, F_O is proportional to the BK_Ca channel density and to the inverse square of the BK_Ca channel activation time constant [20], but what mechanisms might govern these channel parameters? One factor that modulates the speed of the BK_Ca channels is their association with an accessory β-subunit (gene KCNMB1) [21–23] (Figure 2C). The association between the pore-forming and auxiliary subunits can have variable stoichiometry [24], between one and four β-subunits being associated with four pore-forming α-subunits: more β subunits produce incrementally slower BK_Ca channels (Figure 2D). There is also evidence that the BK_Ca channel clusters can be regulated by β subunits, in particular β1 and β4, which are preferentially expressed towards the low frequency region of the chick cochlea [25]. However, control of BK_Ca channel density and kinetics is still not fully understood, and factors other than β-subunits may be involved [26, 27]. There is some evidence in the chicken cochlea (which also employs electrical tuning) that the tonotopic gradient is established in early embryogenesis by gradients in the secreted morphogens Bmp7 and retinoic acid [28, 29].

The frequency limits of electrical tuning

In the auditory organs of all non-mammalian vertebrates, electrical tuning probably acts as the hair-cell tuning mechanism at frequencies below 1 kHz. The mechanism has been shown to occur in the frog amphibian papilla [19, 30], the chicken basilar papilla [31, 32] (Figure 3A, 3B), the alligator basilar papilla [33] and probably in the gecko [34]. It has also been reported in the saccule of the bullfrog [15] and the goldfish [35]. The electrical resonance exhibits distinctive traits, including amplification (due to increased membrane impedance), broadening of the tuning at higher sound levels (due to progressive activation of the BK_Ca channels) and spontaneous oscillatory activity, in which the hair cell membrane potential displays noisy oscillations around the resonant frequency [14]. One consequence of the spontaneous fluctuations in hair cell membrane potential is a sinusoidal discharge of action potentials in the auditory nerve fibers, with an inter-spike interval approximately equal to the inverse of the fiber’s acoustic characteristic frequency (CF). This auditory nerve phenomenon has been reported in the turtle [14], the pigeon [36] and the gecko [34], but contrasts with the bimodal spontaneous discharge of mammalian auditory nerve fibers [37]. Periodicity in spontaneous auditory nerve firing in the tokay gecko, and temperature dependent CFs (see below), are indirect evidence for electrical tuning in this lizard up to 500 Hz [34, 38].

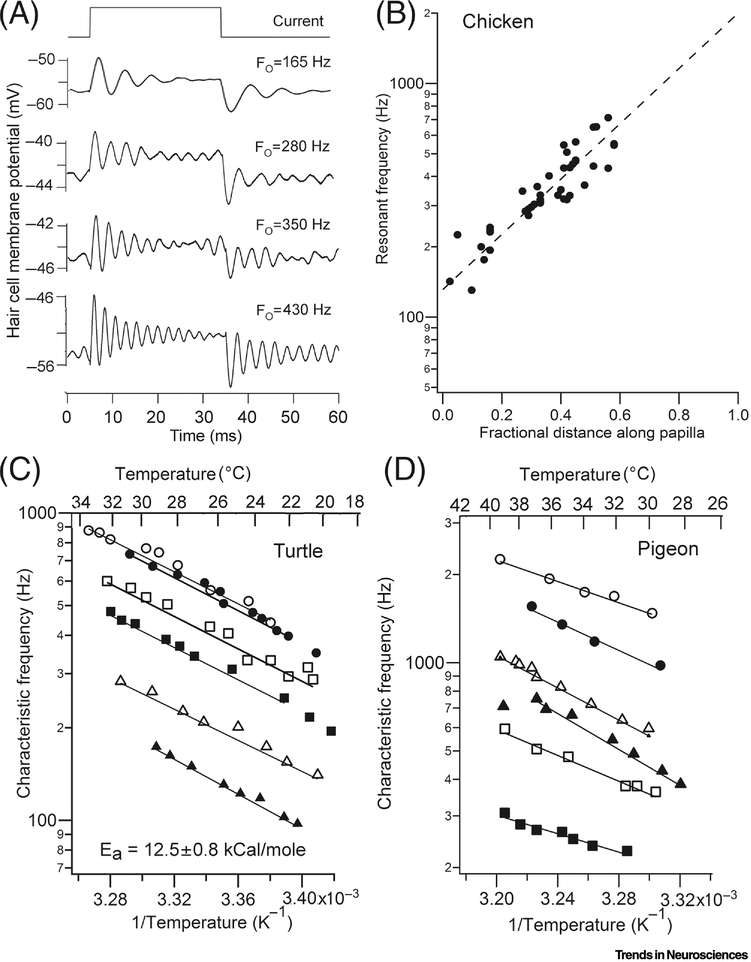
Figure 3.

Electrical tuning in reptile and bird. (A). Example of voltage ringing in four tall hair cells of chicken. (B) Tonotopic map of resonant frequencies in chicken cochlea (T = 33°C); the fit to the resonant frequency measurements is extrapolated to base giving predicted FO of 2 kHz. (C) Arrhenius plots of temperature dependence of characteristic frequencies for sound stimuli in six auditory nerve fibers of turtle. (D) Arrhenius plots of temperature dependence of characteristic frequencies for sound stimuli in six auditory nerve fibers of pigeon; results replotted from reference [40]. Fits giving activation energies Ea have similar slopes in turtle and bird.

The resonant frequencies are also temperature dependent, as might be expected for a mechanism that is limited by ion channel gating kinetics that can have a Q₁₀ of 4.0. For the basilar papilla of the turtle [39] and the pigeon [40], F_O roughly doubles for a 10°C rise in temperature. The slopes of Arrhenius equation plots, in which the logarithm of the CF is plotted against the inverse of the absolute temperature (T) can be used to determine the activation energy (E_a) for a reaction. The Arrhenius equation is: log (CF) = A – E_a/RT, where A is a constant and R is the gas constant. These plots (Figure 3C, 3D) yield activation energies for the tuning mechanism of 12.5 ± 0.8 kcal/mole (n=6) for the turtle, 10.3 ± 2.1 kcal/mole (n=6) for the pigeon. For comparison, the activation energy for diffusion, with a Q₁₀ of 1.4, is about 6 kcal/mol. In contrast with the turtle and chicken, there is no evidence for a strong temperature effect on nerve fiber CFs in the mammalian cochlea, which does not employ electrical tuning [41, 42]. Electrical tuning of tall hair cells in the chicken basilar papilla can be recorded up to 700 Hz [32], and extrapolation of the results to the most basal hair cells predicts a resonant frequency of 2 kHz (Figure 3D). If the frequency limit in turtle auditory nerve fibers, 600 Hz at 22°C, is extrapolated to 40°C, this gives an upper limit of 2 kHz for the mechanism. Recordings in vivo give the auditory range in the chicken as 5 kHz [43], suggesting another tuning process may contribute in the kilohertz range.

The hair cell electrical resonance has been well simulated using gating schemes for the underlying ion channels, the voltage-dependent Ca²⁺ channel and the Ca²⁺ activated K⁺ channel [39, 44]. The computed resonant frequency increases with K_Ca channel density and speed as found experimentally. This approach also enabled prediction, based on simulation of turtle hair cells, of an upper limit which at 40°C would be 2.6 kHz with no other assumptions. A constraint is imposed by shortening of the kinetics of the BK_Ca channel, which cannot get faster than the activation rate of voltage-dependent Ca²⁺ channels. To cover the audible range of the chicken, up to 5 kHz, required assuming a kinetic limit for the BK_Ca channels coupled with an unrealistically large channel density [39]. It therefore seems unlikely that electrical tuning could operate at frequencies above 5 kHz detected by mammals.

Frequency tuning in the mammalian cochlea

The contribution of outer hair cells

The tuning mechanism in the mammalian cochlea has been extensively studied and reviewed [4, 11, 13]. The frequency-tuning curves of the auditory nerve fibers are narrow V-shaped functions of sound frequency, having maximal sensitivity at the CF of the fiber (Figure 4A). Tuning curves are depicted for the gerbil [45] with a frequency range of 0.3–30 kHz [46]. The nerve fiber tuning curves are similar in shape to the vibration patterns of the basilar membrane embodying the mechanical filter ( [13, 47] (Fig. 4C), and differ from the turtle, where basilar membrane vibration contributes no significant frequency selectivity [48]. Mammalian frequency tuning stems from multiple processes in the cochlea. Each sound frequency generates a traveling wave along the basilar membrane, propagating longitudinally from base to apex and growing in magnitude until it attains a peak amplitude at the place specific for frequency of stimulation [10]. Gradations of stiffness and mass along the basilar membrane [10, 49, 50] are thought to create a bank of filters, decreasing in resonant frequency from base to apex. For example, the point stiffness of the gerbil basilar membrane increases 330-fold from apex to base [49]. These gradients generate damped mechanical resonances that are amplified and sharpened by extra force supplied by OHCs which counteracts fluid damping and boosts the motion of the basilar membrane. At low sound levels, the amplification confers a 40 to 60 dB (100- to 1000-fold) increase in sensitivity at frequencies around the CF, but at higher sound levels, the OHC contribution saturates, sensitivity diminishes, and tuning broadens.

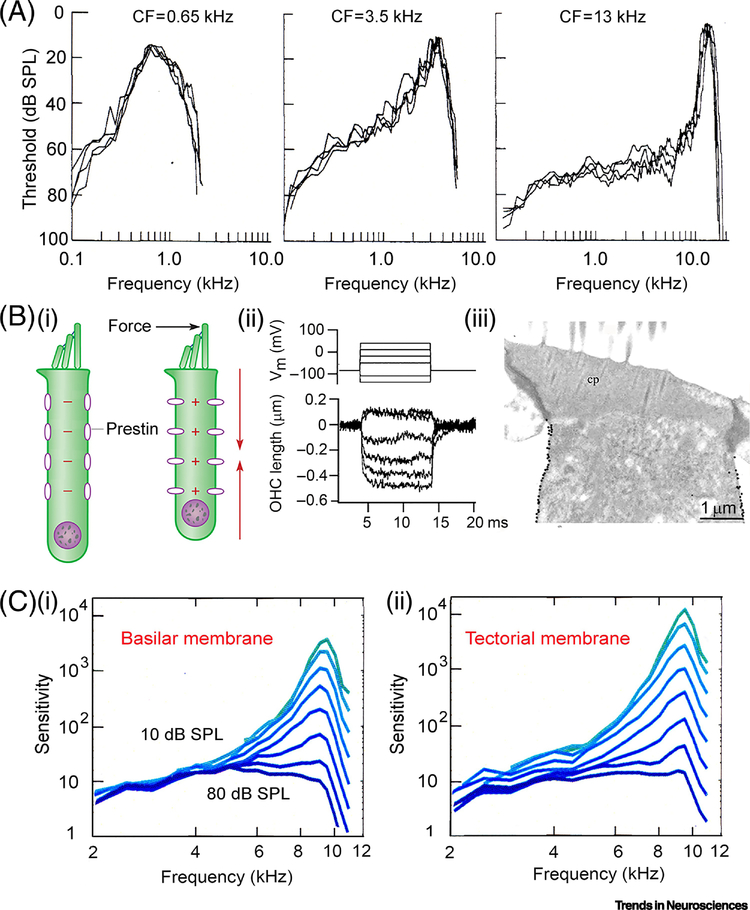
Figure 4.

Frequency selectivity in the mammalian cochlea. (A) Three auditory nerve fiber tuning curves for in gerbil cochlea, threshold plotted against sound frequency, from reference [45]. (B) Somatic motility in OHCs: hair bundle stimulation elicits cell contraction (left); voltage-clamped rat OHC, decreases in length on depolarization (middle); immunogold labeling for prestin of OHC lateral wall in rat (right). (C) Frequency tuning curves measured using OCT for basilar and tectorial membrane of mouse cochlear apex, in eight 10 dB increments. Tuning is sharpest at lowest sound level. Reproduced with permission from reference [47].

This mechanism was initially deduced from experiments demonstrating the crucial requirement of OHCs for cochlear sensitivity, which was diminished when they were preferentially destroyed by gentamicin [51]. The mechanism was bolstered by the unexpected finding that OHCs, when isolated in a dish and electrically stimulated, changed their length by up to 4 percent of their length, 1.0 μm for a 25 μm cell [52–54] (Figure 4B). The contractions and elongations of the cylindrical OHC body are thought to be driven by voltage-dependent conformational changes in prestin, an 80 kDa piezoelectric protein [55] packed at high density in the OHC membrane [56]. Prestin is a modified anion transporter, SLC26A5, requiring chloride ions to support or modulate its voltage-sensitivity [57, 58], and blocked by millimolar concentrations of the anion salicylate extracellularly [59, 60]. Since salicylate is amphiphilic, the binding site may be cytoplasmic, where the blocking concentration is lower [57, 60]. Strong evidence on the importance of prestin for cochlear amplification was obtained using a mouse harboring a mutant prestin that was nonfunctional but still targeted to the OHC lateral membrane. Isolated OHCs from this mutant had much reduced electromotility and 60 dB loss of acoustic sensitivity in vivo [61]. The genetic manipulation argues that OHC electromotility based on prestin is important for cochlear amplification and frequency selectivity. In accord with this conclusion, when the tuning curves of auditory nerve fibers were characterized in gerbils, administration of salicylate caused an elevation of the sound threshold at CF and a reduced sharpness of tuning over the entire frequency range [62]. Moreover, basilar membrane mechanical tuning curves were reversibly abolished by 5 mM salicylate, and by reducing perilymph [Cl⁻] [63], which underscores prestin’s importance.

Uncertainties regarding prestin

Despite the discovery of prestin and the productive outcomes of the subsequent studies, several areas of contention persist. A key problem is the speed with which the prestin protein can operate as a quasi-piezoelectric element. It was originally argued that OHCs contract and elongate on each cycle of the sound stimulus in order to provide cycle-by-cycle feedback. However, this assumes an ultrafast feedback process in which the membrane time constant is brief and prestin, as a voltage-dependent protein, activates on a microsecond timescale. Original claims that OHCs can undergo cyclical length changes at frequencies of tens of kilohertz [64, 65] have been challenged by recent experiments [66, 67]. Furthermore, measurements of the OHC time constant (which will filter the receptor potential), have yielded variable values [54], the smallest being 25 μs [68], equivalent to a corner frequency of 6 kHz. It has been argued that OHC membrane corner frequencies may be higher when these cells are embedded in the organ of Corti compared to isolated hair cells [69] [70]. A recent in vivo assay of OHC vibrations, applying optical coherence tomography, indicated that motility showed low-pass performance with corner frequencies around 3 kHz [71]. In spite of these apparent kinetic limitations, finite element modeling of the guinea pig cochlea, using existing time constants for OHC electromotility, predicted sharp tuning up to 18 kHz [72, 73]. It has also been shown experimentally that a salicylate-sensitive electromotile process can operate up to 100 kHz at the base of the intact guinea-pig cochlea [74]. There is therefore no general agreement on whether prestin-mediated OHC contractions can underlie cochlear tuning at frequencies of 50–100 kHz used in the ultrasonic hearing of mice and bats [75].

Another area of uncertainty is the origin of tuning at the cochlear apex, at frequencies below a 1 kHz, where auditory nerve fiber tuning curves have a different, more symmetrical, shape (Figure 4A) [37]. These and other observations have led to the proposal that an alternate tuning mechanism may operate at the cochlear apex [76] [73]. It is conceivable that the mass and stiffness of the tectorial membrane, together with the OHC hair bundle stiffness, generate an auxiliary resonance that modifies the mechanical stimuli relayed to the IHC [77] [78]. The stiffness of the tectorial membrane [79] and of the OHC hair bundles [80] both increase progressively towards the base of the cochlea, and together could theoretically generate gradations in the mechanical resonant frequency. The tuning may be enabled by the complex cellular anatomy, notably the pillar and Deiters’ cells, of the organ of Corti [81]. But the difficulty of accessing the organ of Corti and vulnerability of frequency tuning in vivo has hampered systematic investigation of the micromechanics along the cochlea.

Extension of the frequency range in non-mammals

Frogs

A number of non-mammalian species, including frogs, birds and lizards, show extensions of the frequency range above that provided by electrical tuning, which we shall assume operates up to about 1 kHz. The frog inner ear contains two main sound-sensitive end organs, the amphibian papilla and the basilar papilla [82]. Much of the amphibian papilla employs electrical tuning with acoustic CFs ranging from 100 to approximately 1000 Hz at room temperature [83]. Although electrical resonance was not recorded at the highest frequencies (probably due to experimental limitations whereby slight damage to hair cells introducing leak conductance can annihilate the resonance), hair cells across the whole range possessed Ca²⁺-activated K⁺ channel currents [19]. However, the other organ, basilar papilla, functions as a single auditory filter, with all auditory nerve fibers having nearly identical shapes and CFs [84]. The spheroidal basilar papilla lacks a basilar membrane but possesses a tectorial membrane over the hair bundles of the sensory hair cells. Sound-induced vibrations of the tectorial membrane were measured in Rana pipiens and found to be tuned to 2 kHz [85], similar to the CFs of the basilar papilla nerve fibers. This observation suggests that the frequency selectivity of the organ is largely attributable to a resonance of basilar end organ [85]. The mechanical coupling between the tectorial membrane and hair bundles may behave as a mechanical resonator, with a resonance frequency dependent on the vibrating mass and the hair bundle stiffness. When compared across species, the anuran basilar papilla is tuned to the principle frequency of the call [86]. More recently, a number of frog species with hearing above 10 kHz have been studied [87]. Recalling that resonant frequency is proportional to the square root of the stiffness divided by the mass, the ultrasonic range can be accounted for by its correlation with modifications of the frog basilar papilla, which will filter the mechanical input to the hair cells [87]. These modifications include a smaller tectorial membrane (reducing the vibrating mass) and shorter hair bundles (increasing their stiffness), which combine to elevate the resonant frequency.

Chickens

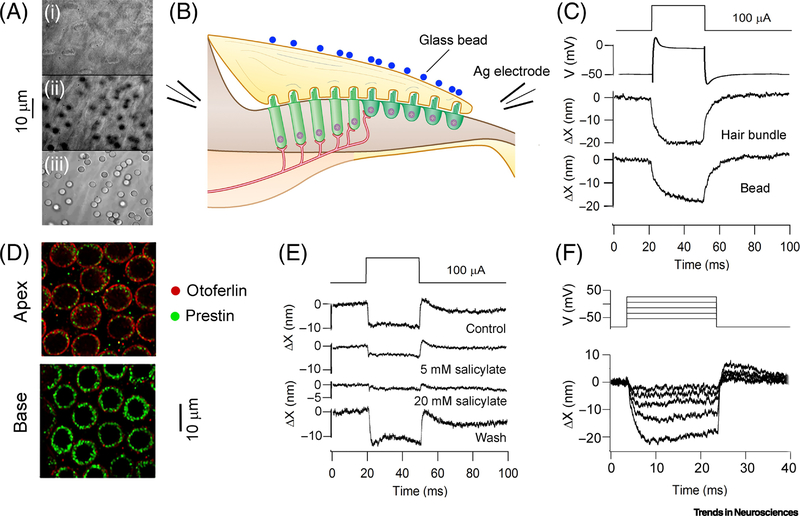
Birds such as chickens and pigeons have an audible range extending to 5 kHz [43, 88]. Auditory hair cells that are electrically tuned will have acoustic CFs higher than the turtle due to the increased body temperature of 40°C. The avian basilar papilla, like the mammalian organ of Corti, contains two types of hair cell with different innervation (Figure 1), suggesting that other processes operate. Tall hair cells overlying the cartilaginous limbus contact afferents, whereas short hair cells surmounting the basilar membrane have little or no afferent innervation. Another mammalian similarity is the presence of a traveling wave on the pigeon basilar membrane propagating from base to apex, but with broad frequency tuning up to a cut-off at about 6 kHz [89]. Furthermore, auditory nerve fiber tuning is susceptible to intra-cochlear perfusion of up to 20 mM Na salicylate. The agent causes threshold elevation, particularly in mid to high frequencies (0.8 – 4 kHz), which, similar to mammals, suggest that prestin may be involved in amplification and tuning [90]. Although there is no direct evidence for electromotility of chicken prestin [91], the protein is present in the chicken basilar papilla [92]. In addition, electrical stimulation when applied across the papilla, or to individual hair cells, evokes significant motion of the hair bundles and tectorial membrane [92]. Hair cell depolarization produces bundle deflections towards the neural limbus (Figure 5), which can be abolished with extracellular salicylate at millimolar concentrations (Figure 5E), similar to those that block prestin [59]; salicylate at these concentrations has no effect on mechanotransduction [92]. Taken together, the results argue that receptor potentials in the short hair cells are amplified and mechanically relayed via the tectorial membrane to the tall hair cells on the neural limbus. Antibody labeling demonstrates that prestin is more heavily concentrated in high-frequency hair cells compared to low frequency cells (Figure 5D). Such a gradient in prestin concentration accords with the frequency dependent effects of salicylate in the pigeon, the drug preferentially elevating thresholds above 1 kHz [90]. It seems that prestin may confer amplification and frequency tuning in the bird basilar papilla too. It is possible that residual (low quality factor) electrical tuning in the short hair cells augments the mechanical amplification [93]. Despite the presence of prestin, and the high body temperature, most bird species have experienced no selective pressure to extend the upper limit of hearing beyond 5 kHz. An exception is the owl, for which CFs exceed 9 kHz [94], though it is unclear how this is accomplished. The frequency range of song-birds may be matched to the composition of their song, which is usually restricted to the low kilohertz range [95]. An example is the white-crowned sparrow, whose song comprises an initial 4 kHz whistle followed by a 3 to 5 kHz trill [95, 96].

Figure 5.

Prestin in the chicken cochlea. (A) Images of hair bundles (top), middle of tectorial membrane (middle) and top of tectorial membrane showing 3μm glass beads (bottom). (B). Schematic of experiment to polarize hair cells with electrodes on either side of chicken basilar papilla. (C). Displacements evoked by 100 μA extracellular current pulse: intracellular voltage record from tall hair cell, deflections of hair bundle and of bead, both towards neural limb. (D). Labeling of short hair cells with prestin antibody shows more at the basal than apical regions of papilla. (E) Na salicylate inhibits hair bundle motion to 100 μA current pulse across papilla. (F) Motion of hair bundle is graded with depolarization of voltage-clamped short hair cell.

Lizard

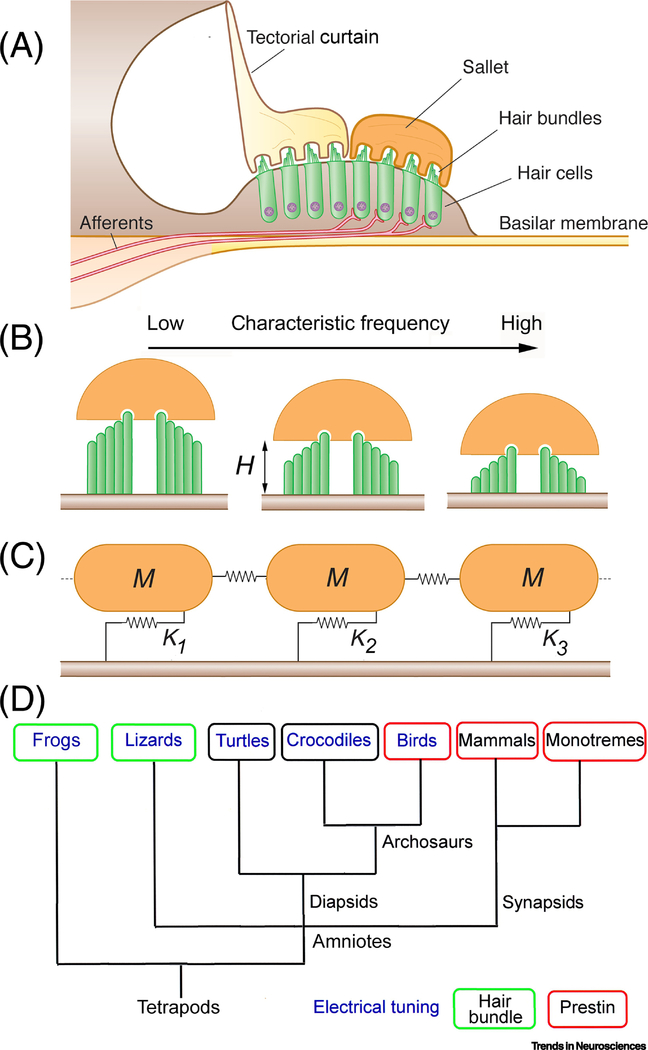
Frequency tuning in the lizard auditory periphery shows principles similar to that of the frog, but differs in that the low- and high-frequency mechanisms are united in a single papilla. The frequency range extends from about 150 Hz to 5 kHz (e.g., tokay gecko, Gekko gecko [34]; bobtail skink, Tiliqua rugosa [97]). The gecko papilla consists of two parts. One third of the papilla resembles that of the turtle, encodes frequencies below 1 kHz, and is most likely served by an electrical resonance (see above). The other two thirds cover frequencies above 1 kHz [98], and this part is demarcated by a change in the organization of the papilla, which is split longitudinally into two parallel sections with distinct tectorial coats. Hair cells located near the neural limb are overlain with a continuous tectorial curtain, whereas abneural hair cells are topped by discrete tectorial domes known as sallets [99–101] (Figure 6A). The two parallel strips also differ in their innervation. All afferent fibers project solely to the abneural salletal hair cells, and neural hair cells surprisingly appear to lack innervation, based upon antibody labeling for neurofilament-associated protein 200 [102], casting their role into doubt. In the gecko, there are 170 sallets, each covering a single transverse row of between four and eight hair cells. Auditory nerve tuning due to tectorial sallets has been proposed to stem from a mechanical resonance created by the mass of the sallet, M, and the stiffness of the attached hair bundles [101] [103, 104]. Morphology suggests a low to high frequency gradient in stiffness because of a decrease in hair bundle height (H = 16 – 4.6 μm) (Figure 6B), and increases in stereociliary complement (N_S = 32–48) and in numbers of bundles devoted to each sallet (N_HB = 4 to 8) [99, 100, 103]. Thus high frequency sallets are predicted to have a higher resonant frequency because they envelope more bundles that are shorter and contain more stereocilia. The relationship can be quantified as F_O = 1/2π (α. N_S.N_HB/ H².M)^1/2, where α is the rotational stiffness of a single stereocilium, 0.026 × 10⁻¹⁴ N.m/rad [105]. This analysis predicts passive resonant frequencies from 1.2 to 7.4 kHz, having similar range and extent to those observed experimentally (1 to 5 kHz).In practice, the sharpness of tuning and the resonant frequencies will be reduced by damping from the fluid endolymph [103], and by the fibrous connections between neighboring sallets [99], which are represented as weak springs in Figure 6C [106].

Figure 6.

Lizard basilar papilla. (A) Transverse section of gecko papilla in high frequency region shows two types of tectorial structure. Hair bundles of non-innervated neural hair cells covered with a tectorial membrane that forms ‘curtain’ above papilla, whereas hair bundles of innervated abneural hair cells are surmounted by a tectorial ‘sallet’. (B). Schematic of hair bundles inserted into sallets for progressive distance from low- to high-frequency positions. Note the hair bundles are bidirectional and their height, H, decreases (16 μm to 4.6 μm; [100]) with increase in frequency. (C) Model of longitudinal section through salletal region depicting three sallets of mass M attached to hair bundles represented by springs of stiffness K₁, K₂, and K_3, decreasing with increase in ‘H’. M was calculated by taking each sallet as a semicircular slice, 40 μm diameter, 3 μm thick and density 1000 kg/m³, giving a total mass, M = 1.9 × 10⁻¹² kg. (D) Evolutionary tree indicating tuning mechanisms shown to operate in auditory hair cells of different vertebrate classes. Tree based on reference [112].

Evidence also exists for an amplification mechanism attributable to active force generation by the hair bundle, albeit much weaker than prestin [105] [107]. An active force generator may, depending on its phase, counteract the viscous damping imposed by the surrounding fluid, and hence increase the sharpness of tuning. The mechanoelectrical transducer channels in the hair bundle are activated by force delivered via tip-links connecting adjacent stereocilia [4]. Active hair bundle motility is proposed to reflect a bidirectional coupling between tip-link tension and transducer channel gating: increased tension opens the channels, but conversely, channel closure, as occurs during transducer adaptation, exerts a force that moves the bundle [93]. This mechanism has been extensively characterized in frog saccular hair cells, where it can drive spontaneous oscillations at a specific frequency [107, 108]. It may also operate in the salletal hair cells of the gecko papilla, where each hair bundle has been hypothesized to be mechanically active and generate sustained oscillations that might drive spontaneous otoacoustic emissions [109, 110]. Such emissions are faint tones continuously radiated from the external ear in the absence of a stimulus, and occur in many vertebrates, but those in the tokay gecko are evident as a dozen or more equally spaced peaks between 1 and 4 kHz [106, 110]. However, hair cells covered by a single sallet possess hair bundles pointing in both neural and abneural directions (Figure 6A). Since active force production will be unidirectional, the bidirectional hair bundles linked to one sallet will not cooperate as an efficient force generator. Further experiments are required to clarify how active bundle motility might function in these cells.

Concluding remarks

At least three distinct mechanisms are employed to produce frequency-selective tuning in the vertebrate inner ear (Figure 6D). A fairly ubiquitous electrical resonance, filtering of the receptor potential by voltage-dependent ion channels, has an upper limit of about 1 kHz. A selective drive to extend the frequency range in all vertebrate classes employs a mechanical resonance stemming from stiffness of the hair bundles coupled with the mass of attached tectorial covering. The sharpness of tuning, the quality factor of the resonance, may in such cases be amplified by force generation from the hair bundle motion linked to transducer channel gating. To widen the frequency range, an unusual mechanism operates in mammals. Here, one class of hair cell, the OHC, generates amplification by somatic contractions mediated by a biologically-piezoelectric protein prestin, though whether it underlies frequency tuning at the mouse upper limit of 70 kHz [111] is unclear. The basilar papilla in birds also comprises two classes of hair cell and may also employ prestin over a limited frequency band. It has become clear that there are multiple designs for achieving frequency tuning in the vertebrate ear, each having particular limitations on the operating range of frequencies, and each appropriate to the animal’s behaviour.

Outstanding questions.

• Can the upper frequency limit of electrical resonance in the inner ear be precisely defined, what determines that limit, and how are the resonant properties set up developmentally?

• What underlies frequency-tuning in the salletal hair cells of the gecko lizards, and is the tuning reinforced by active hair bundle motility?

• Can prestin be gated on a cycle-by-cycle basis to provide amplification up to 100 kHz, and if not, how does prestin produce amplification at the highest frequencies?

• What are the voltage-dependent changes in the tertiary structure of prestin that underlie OHC electromotility?

• A different mechanism is employed for frequency tuning in the apical low-frequency region of the mammalian cochlea compared to the high-frequency region. What is the mechanism operating in the low-frequency region?

Highlights.

• The vertebrate cochlea contains a bank of filters to separate the sound frequency components in the sensory hair cells. This computation enables auditory nerve fibers to relay spectral information to the brain, which aids with communication and sound localization.

• In non-mammals, the hair cell receptor potential is electrically tuned by Ca²⁺-activated K⁺ channels, generating band-pass filters with center frequencies less than 1 kHz. This mechanism is limited by the intrinsic kinetics of the K⁺ channel.

• Evolutionary pressure for higher frequency hearing has recruited two other processes. One, a mechanical resonance of the sensory hair bundles, encompasses frequencies up to 10 kHz, and is employed in frogs and lizards. In mammals, a separate mechanism creates narrow-band filters extending up to 100 kHz. For all or part of the range, this involves contractions of the outer hair cell body, produced by the voltage-sensitive membrane protein prestin.

• The cochlea of the bird, similar to the mammal, contains two types of hair cell probably due to convergent evolution. Bird cochlear outer hair cells may also employ prestin over a limited high frequency range, but auditory hair cells are electrically tuned below 1 kHz.