How noise contributes to time-scale invariance of interval timing?

Abstract

Time perception in the supra-second range is crucial for fundamental cognitive processes like decision making, rate calculation, and planning. In the vast majority of species, behavioral and neurophysiological manipulations, interval timing is scale invariant: the time-estimation errors are proportional to the estimated duration. The origin and mechanisms of this fundamental property are unknown. We discuss the computational properties of a circuit consisting of a large number of (input) neural oscillators projecting on a small number of (output) coincidence detector neurons, which allows time to be coded by the pattern of coincidental activation of its inputs. We showed that time-scale invariance emerges from the neural noise, such as small fluctuations in the firing patterns of its input neurons and in the errors with which information is encoded and retrieved by its output neurons. In this architecture, time-scale invariance is resistant to manipulations as it depends neither on the details of the input population, nor on the distribution probability of noise.

I. INTRODUCTION

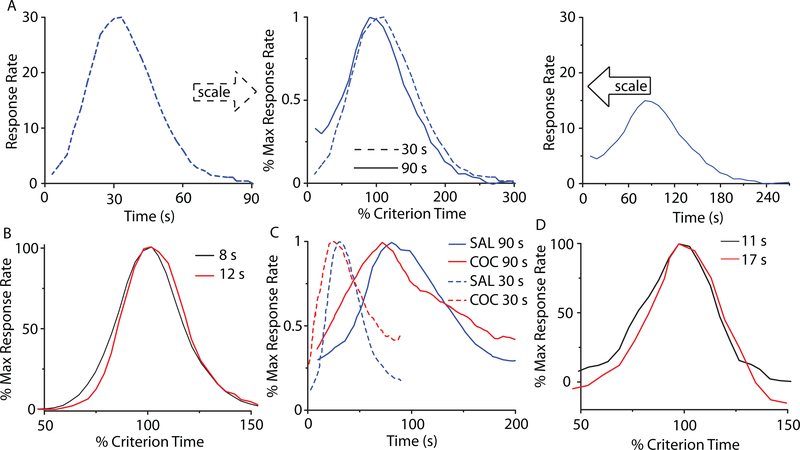
The perception and use of durations in the seconds-to-hours range (interval timing) is essential for survival and adaptation, and is critical for fundamental cognitive processes like decision making, rate calculation, and planning of action [1]. The fixed-interval (FI) procedure is the classic interval timing experiment in which a subject’s behavior is reinforced for the first response (e.g., lever press) made after a pre-programmed interval has elapsed since the previous reinforcement. Although no external time cues is provided, the subjects trained on a FI procedure typically pause after the delivery of reinforcement and start responding after a fixed proportion of the interval has elapsed. A widely-used discrete-trial variant of FI procedure is the peak-interval (PI) procedure [2, 3]. In a PI procedure, a stimulus such as a tone or light is turned on to signal the beginning of the to-be-timed interval and in a proportion of trials the subjects first response after the criterion time is reinforced. In the remainder of the trials, known as probe trials, no reinforcement is given and the stimulus remains on for about three-four times the criterion time. The mean response rate over a very large number of trials has a Gaussian shape whose peak measures the accuracy of criterion time estimation and the spread of the timing function measures its precision. In the vast majority of species, protocols, and manipulations to date, interval timing is both accurate and time-scale invariant, i.e., time-estimation errors increase linearly with the estimated duration [4–7] (Fig. 1). Accurate and time-scale invariant interval timing was observed in many species [1, 4] from invertebrates to fish, birds, and mammals, such as rats [8] (Fig. 1A), mice [9] and humans [10] (Fig. 1B). Time-scale invariance is stable over behavioral (Fig. 1B), lesion [11], pharmacological [12, 13] (Fig. 1C), and neurophysiological manipulations [14] (Fig. 1D).

FIG. 1. (Color online) Accurate and time-scale invariant interval timing.

(A) The response rate of rats timing a 30s interval (left) or 90s interval (right) overlap (center) when normalized by the maximum response rate (vertical axis), respectively, the criterion time (horizontal axis); redrawn from [8]. (B) Time-scale invariance in human subjects for 8s and 21s criteria; redrawn from [10]. (C) Systemic cocaine (COC) administration speeds-up timing proportional (scalar) to the original criteria 30s and 90s; redrawn from [8]. (D) The hemodynamic response associated with a subject’s active time reproduction scales with the timed criterion, 11s v. 17s; redrawn from [14].

In 1963, Treisman introduced the elements of one of the most influential interval timing paradigms - the pacemaker-accumulator clock (pacemaker-counter). According to Treisman (1963), the interval timing mechanism that links internal clock to external behavior also requires some kind of store of reference times and a comparison mechanism for time judgement. Treisman’s pacemaker-counter mode was rediscovered two decades later and became the Scalar Expectancy Theory (SET) [6, 15]. According to SET, the interval timing emerges from the interaction of three abstract blocks: a clock, an accumulator (working or short-term memory), and a comparator. The internal pacemaker generates pulses that accumulate in the working memory until the occurrence of an important event, such as reinforcement. At the time of the reinforcement, the number of clock pulses accumulated is transferred from the working (short-term) memory to the reference (or long-term) memory. A response (output) is produced by computing the ratio between the value stored in the reference memory and the current accumulator total. When the ratio falls below a threshold, responding begins. One of the major shortcomings of SET is that it predicts greater relative accuracy at longer time intervals: “If there is no error in the accumulator, or if the error is independent of accumulator value, and if there is pulse-by-pulse variability in the pacemaker rate, then by the law of large numbers, relative error (standard deviation divided by mean, coefficient of variation) must be less at longer time intervals.” (see Staddon and Higa [16] for details). This theoretical prediction of SET contradicts the time-scale invariance observed in experiments.

Another influential interval timing paradigm is the Behavioral Timing (BeT) theory [17, 18]. BeT assumes a “clock” consisting of a fixed sequence of states with the transition from one state to the next driven by a Poisson pacemaker. Each state is associated with different classes of behavior, and, the theory claims, these behaviors serve as discriminative stimuli that set the occasion for appropriate operant responses (although there is not a 1:1 correspondence between a state and a class of behavior). The added assumption that pacemaker rate varies directly with reinforcement rate allows the model to handle some experimental results not covered by SET, although it has failed some specific tests (see [16] for a review).

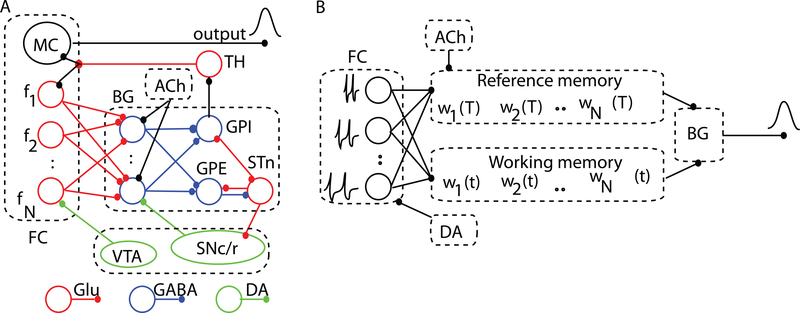
A handful of neurobiologically-inspired models explain accurate timing and time-scale invariance as a property of the information flow in the neural circuits [19, 20]. Shadlen was the first to suggest that timing of sub-second intervals may be addressed at the level of single neurons [21], though how such a mechanism accounts for timing of supra-second durations is unclear. Killeen and Taylor [22] attempted solving this issue by explaining timing in terms of information transfer between noisy counters, although the biological mechanisms were not addressed. Meck and associates [4, 23] (Fig. 2A) proposed a different approach called the Striatal Beat Frequency (SBF) model in which timing is coded by the coincidental activation of neurons, which produces firing beats with periods spanning a much wider range of durations than single neurons [24]. As Matell and Meck (2004) suggested, the interval timing could be the product of multiple and complimentary mechanisms. They suggested that the same neuroanatomical structure could use different mechanisms for interval timing. A possible common ground for all interval timing models could be the threshold accommodation phenomenon that allows stimulus selectivity [25, 26] and promote coincidence detection [9]. Farries (2010) showed that dynamic threshold change in subthalamic nucleus that projects to the output nuclei of the basal ganglia (BG) allows subthalamic nucleus (STn) to act either as an integrator for rate code inputs or a coincidence detector [27] (see Fig. 2).

FIG. 2. (Color online) The neurobiological structures involved in interval timing and the corresponding simplified SBF architecture.

(A) Schematic representation of some neurobiological structures involved in interval timing. The color-coded connectivities among different areas emphasize appropriate neuromodulatory pathways. The two main areas involved in interval timing are frontal cortex (FC) and basal ganglia (BG). (B) In our implementation of the SBF model, the states of the N cortical oscillators (input neurons) at reinforcement time T are stored in the reference memory as a set of weights w_i(T). During test trials, the working memory stores the current weights w_i(t) and, together with the reference memory, projects its content onto spiny (output) neurons of the BG. FC: frontal cortex; MC: motor cortex; BG: basal ganglia; TH: thalamus. GPE: globus pallidus external; GPI: globus pallidus internal; STn: subthalamic nucleus; SNc/r: substantia nigra pars compacta/reticulata; VTA: ventral tegmental area; Glu: glutamate; DA: dopamine; GABA: gamma-aminobutyric acid; ACh: acetylcholine.

Here we showed analytically that in the context of the proposed SBF neural circuitry, time-scale invariance emerges naturally from variability (noise) in models’ parameters. We also showed that time-scale invariance is independent of both the type of the input neuron, and the probability distribution or the sources of the noise.

This paper is organized as follows. The SBF model is described in Sec. II. A brief neurobiological justification is provided for each major functional block of the SBF model. The analytical and numerical results are described in Sec. III. In the absence of noise, the SBF network produces accurate interval timing but violates time-scale invariance. At least one source of noise added to the SBF model produces both accurate and time-scale invariant interval timing. We conclude in Sec. IV with a discussion of our results. Detailed analytical derivations of time-scale invariance in the presence of noise are summarized in the Appendices.

II. THE STRIATAL BEAT FREQUENCY MODEL

Our paradigm for interval timing is inspired by the SBF model [4, 23], which assumes that durations are coded by the coincidental activation of a large number, N, of cortical (input) neurons projecting onto N_o spiny (output) neurons in the striatum that selectively respond to particular reinforced patterns [28–30] (Fig. 2A).

A. The cortical oscillators

Neurobiological justification

There is strong experimental evidence that oscillatory activity is a hallmark of neuronal activity in various brain regions, including the olfactory bulb [31–33], thalamus [34, 35], hippocampus [36, 37] and neocortex [38]. Cortical oscillators in the alpha band ([8, 13] Hz) were previously considered as pacemakers for temporal accumulation [39], as they reset upon occurrence of the to-be-remembered stimuli [40].

Numerical implementation

Neurons that produce stable membrane potential oscillations are mathematically described as limit cycle oscillators, i.e., they pose a closed and stable phase space trajectory [41]. Since the oscillations repeat identically, it is often convenient to map the high-dimensional space of periodic oscillators using a phase variable that continuously covers the interval (0, 2π). Phase oscillator models have a series of advantages: (1) provide analytical insights into the response of complex networks, (2) any neural oscillator can be reduced to a phase oscillator near a bifurcation point [42], and (3) allow numerical checks in a reasonable time. All neurons operate near a bifurcation, i.e., a point past which the neuron produces large membrane potential excursions - called action potentials [41].

In this SBF-sin implementation, the cortical neurons are represented by N (input) phase oscillators with intrinsic frequencies f_i (i = 1,…, N) uniformly distributed over the interval (f_min, f_max), projecting onto N_o (output) spiny neurons [23] (Fig. 2B). A sine wave is the simplest possible phase oscillator that mimics periodic transitions between hyperpolarized and depolarized states observed in single cell recordings. For analytical purposes, the membrane potential of i^th cortical neuron was approximated by a sine wave v_i(t) = a cos(2πf_it), where a is the amplitude of oscillations. We also implemented an SBF-ML network in which the input neurons are conductance-based Morris-Lecar (ML) model neuron with two state variables: membrane potential and a slowly varying potassium conductance [43, 44] (see Appendix C for detailed model equations).

B. The memory of criterion time

Neurobiological justification

Among the potential areas involved in storing brain states related to salient features of stimuli in interval timing trials are the hippocampus (see [45] and references therein) and the striatum, which we mimic in our simplified neural circuitry (see Fig. 2A).

Numerical implementation

The memory of the criterion time T is modeled by the set of state parameters (or weights) w_ij that characterize the state of cortical oscillator i during the FI trial j. In our implementation of the noiseless SBF-sin model, the weights w_ij ∝ v_i(T_j), where T_j is the stored value of the criterion time T in the FI trial j. The state of PFC oscillators i at the reinforcement time T_j is the normalized average over all memorized values T_j of the criterion time: $w_i(T)=\frac{1}{S}\sum _{j=1}^{N_m}{v}_i\left(T_j\right)$, where we used $S=Max\left(\sum _{j=1}^{N_m}{v}_i\left(T_j\right)\right)\le N_m$ such that the normalized weight is bounded |w_i(T)| ≤ 1 (see Fig. 2B). We found no difference between the response of the SBF model with the above weights or the positively-defined weight $w_i(T)=\frac{1}{2S}\sum _{j=1}^{N_m}\left(1+v_i\left(T_j\right)\right)$.

C. Coincidence detection with spiny neurons

Neurobiological justification

Support for the involvement of the striato-frontal dopaminergic system in timing comes from imaging studies in humans [46–49], lesion studies in humans and rodents [50, 51], and drug studies in rodents [52, 53] all pointing towards the basal ganglia as having a central role in interval timing (see also [54] and references therein). Striatal firing patterns are peak-shaped around a trained criterion time, a pattern consistent with substantial striatal involvement in interval timing processes [55]. Lesions of striatum result in deficiencies in both temporal-production and temporal-discrimination procedures [56]. There are also neurophysiological evidences that striatum can engage reinforcement learning to perform pattern comparisons (see [57]). Another reason we ascribed the coincidence detection to medium spiny neurons is due to their bistable property that permits selective filtering of incoming information [58, 59]. Each striatal spiny neuron integrates a very large number of afferents (between 10,000 and 30,000) [28, 29, 59], of which a vast majority (≈ 72%) are cortical [60, 61]. The comparison between a stored representation of an event, e.g., the set of the states of cortical oscillators at the reinforcement (criterion) time w_i(T), and the current state of the same cortical oscillators during the ongoing test trial w_i(t) is believed to be distributed over many areas of the brain [62] (Fig. 2A).

Numerical implementation

Based on neurobiological data, in our implementation of the striato-cortical interval timing network we have a ratio of 1000:1 between the input (cortical) oscillators and output (spiny) neurons in the BG (Fig. 2B). The output neurons, which mimic the spiny neurons in the BG, act as coincidence detectors: They fire when the pattern of activity (or the state of cortical oscillators) w_i(t) at the current time t matches the memorized reference weights w_i(T). Numerically, the coincidence detection was modeled using the product of the two sets of weights:

$$O(t)=\sum _{i=1}^N{w}_i(T)w_i(t).$$ (1)

The purpose of the coincidence detection given by Eq. (1) is to implement a rule that produces a strong output when the two vectors w_i(T) and w_i(t) coincide and a weaker responses when they are dissimilar. Although there are many choices, such as sigmoidal functions (which involve numerically expensive calculations due to exponential functions involved), we opted for implementing the simplest possible rule that would fulfill the above requirement, i.e., the dot product of the vectors w_i(T) and w_i(t). Without reducing the generality of our approach, and in agreement with experimental findings [61], for analytical analyses we only considered one output neuron in Eq. (1).

D. Noise in the SBF model

Neurobiological justification

Variability in the SBF model could be ascribed to channel gating fluctuations [63, 64], noisy synaptic transmission [65], and background network activity [66–68]. Single-cell recordings support the hypothesis that irregular firing in cortical interneurons is determined by the intrinsic stochastic properties (channel noise) of individual neurons [69, 70]. At the same time, fluctuations in the presynaptic currents that drive cortical spiking neurons have a significant contribution to the large variability of the interspike intervals [71, 72]. For example, in spinal neurons, synaptic noise alone fully accounts for output variability [71]. Additional variability affects either the storage (writing) or retrieval (reading) of criterion time to or from the memory [73, 74]. Another source of criterion time variability comes from considerations of how animals are trained [75, 76]. In this paper, we were not concerned with the biophysical mechanisms that generated irregular firing of cortical oscillators nor we investigated how reading / writing errors of criterion time happened. We rather investigated if the above assumed variabilities in the SBF model’s parameters can produce accurate and time-scale invariant interval timing.

Numerical implementation

Two sources of variability (noise) were considered in this SBF implementation: 1) Frequency variability, which was modeled by allowing the intrinsic frequencies f_i to fluctuate according to a specified probability density function pdf_f, e.g., Gaussian, Poisson, etc. Computationally, the noise in the firing frequency of the respective neurons was introduced by varying either the frequency, f_i (in the SBF-sin implementation), or the bias current I_bias required to bring the ML neuron to the excitability threshold (in the SBF-ML implementation). 2) Memory variability was modeled by allowing the criterion time T to be randomly distributed according to a probability density function pdf_T.

III. RESULTS

A. No time-scale invariance in a noiseless SBF model

In the absence of noise (variability) in the SBF-sin model, the output given by Eq. (1) for one spiny (output) neuron (N_o = 1) becomes:

$$\begin{gathered} O(t)=\sum _{i=1}^N{w}_i(T)w_i(t)=\sum _{i=1}^N\cos \left(2\pi f_{i}T\right)\cos \left(2\pi f_{i}t\right) \\ =\frac{\sin \left(N\pi \left(f_{max}-f_{min}\right)(t-T)\right)\cos \left(N\pi \left(f_{max}+f_{min}\right)(t-T)\right)}{2\sin \left(\pi \left(f_{max}-f_{min}\right)(t-T)\right)} \\ +\frac{\sin \left(N\pi \left(f_{max}-f_{min}\right)(t+T)\right)\cos \left(N\pi \left(f_{max}+f_{min}\right)(t+T)\right)}{2\sin \left(\pi \left(f_{max}-f_{min}\right)(t+T)\right)}. \end{gathered}$$ (2)

The first term determines a sharp output when the current time t approaches the criterion time T and we dropped the second symmetrical term that peaks at t = −T. The cos(Nπ(f_max + f_min)(t − T)) factor is a very fast oscillating function that fills out the envelope of the output function, i.e., sin(Nπ(f_max −f_min)(t−T))/(2sin(π(f_max −f_min)(t−T))). Based on Eq. (2), we found that O(t = T) = N and the width of the output function σ_o in the absence of noise can be determined from O(T + σ_o/2) = O(t = T)/2, i.e.,

$$\frac{\sin \left(N\pi \left(f_{max}-f_{min}\right){\sigma }_o/2\right)\cos \left(N\pi \left(f_{max}+f_{min}\right){\sigma }_o/2\right)}{\left(2\sin \left(\pi \left(f_{max}-f_{min}\right){\sigma }_o/2\right)\right)}=\frac{N}{2}.$$ (3)

The equation (3) that determines the width of the output function in the absence of noise contains only the number of cortical oscillators N and the values of the frequency range f_min and f_max, respectively. Therefore, σ_o is independent of the criterion time and violates time-scale invariance.

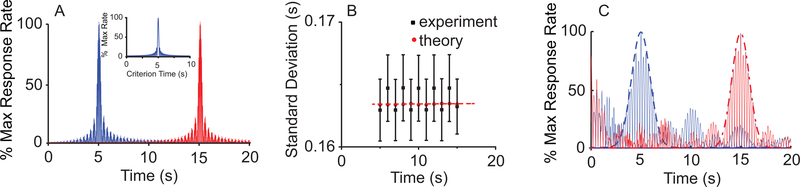
To numerically verify the above predictions, the envelope of the output function of a noise-free SBF-sin model (Fig. 3A) was fitted with a Gaussian whose mean and standard deviations were contrasted against the theoretically-predicted values (Fig. 3B). Although the standard deviations obtained from the fitting of the envelope (Fig. 3A) were not strictly constant (Fig. 3B, filled rectangles), they were close to the theoretically predicted values (Fig. 3B, filled circles) in the limit of fitting errors.

FIG. 3. (Color online) A noise-free SBF model does not produce time-scale invariance.

(A) Analytically predicted (inset) and numerically generated output of a noise-free SBF-sin model with N = 100 for T = 5s and T = 15s. (B) As predicted analytically (theoretical), the width the output function of a noise free SBF-sin model is independent of the criterion time. (C) A noise-free SBF-ML model does not produce time-scale invariance either. The width of the Gaussian envelopes (dashed line for T = 5s and dashed-dotted line for t = 15s) remains constant.

The above result regarding the emergence of time-scale property from noise in SBF-sin model can extend to any type of input neuron. Indeed, according to Fourier’s theory, any periodic train of action potentials can be decomposed into discrete sine-wave components. It results that irrespective of the type of input neuron, a noise-free SBF model cannot produce time-scale invariant outputs. We verified this prediction by replacing the sine-wave oscillator inputs with biophysically-realistic noise-free ML neurons. Numerical simulations confirmed that the envelope of the output function can be reasonably fitted by a Gaussian, but the width of the Gaussian output does not increase with the timed interval (see Fig. 3C), thus violating the time-scale invariance (scalar property).

B. Time-scale invariance emerges from noise in the SBF model

Many sources of noise (variability) may affect the functioning of an interval timing network, such as small fluctuations in the intrinsic frequencies of the inputs, and in the encoding and retrieving the weights w_i(T) by the output neuron(s) [23, 24, 77, 78]. Here we showed analytically that one noise source is sufficient to produce time-scale invariance [23]. Without compromising generality, in the following we examined the role of the variability in encoding and retrieval of the criterion time by the output neuron(s). The cumulative effect of all noise sources (trial-to-trial variability, neuromodulatory inputs, etc.) on the memorized weights w_i(T) was modeled by the stochastic variable T_j distributed around T according to a given pdf_T. For only one spiny (output) neuron (N_o = 1), the output function given by Eq. (1) becomes:

$$\begin{gathered} O(t)=\sum _{i=1}^N\sum _{j=1}^{Trials}\left(\cos \left(2\pi f_{i}t\right)\cos \left(2\pi f_i{T}_j\right)\right) \\ =\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^{Trials}\left(\cos \left(2\pi f_i\left(t-T_j\right)\right)+\cos \left(2\pi f_i\left(t+T_j\right)\right)\right), \end{gathered}$$ (4)

which has the first term centered at t = +T_j and the second symmetrical at the unphysical value of t = −T_j. Based on the central limit theorem, the output function given by Eq. (4), which is a sum of a (very) large number Trials of stochastic variables T_j, is always a Gaussian regardless the pdf_T of the criterion time.

To examine time-scale invariance, we estimate again the relationship between the width of the output function σ_o and the criterion time T. Briefly, using trigonometric identities we rewrote the output function with respect to the stochastic displacement x of a particular realization T_j with respect to T in terms of the new variable θ(x) = π(t − T − Tx)df (see Appendix A). The function θ(x) is a phase difference between the current (running) time t and the memorized criterion time T_j.

To investigate time-scale invariance of the results given in Eq. (4), the physically realizable term centered around t = +T_j was transformed to:

$$z=O(x)=\frac{\sin (N\theta (x))\cos \left(\left(2f_{min}/df+N\right)\theta (x)\right)}{\sin (\theta (x))},$$ (5)

where θ(x) = π(t−T−Tx)df, and df = (f_max−f_min)/N. The pdf_z of the new stochastic variable z(x) is related to the pdf_x of the criterion time p_X(x) through p_Z(z) = p_X(h⁻¹(z))|dx/dz| (see [79]). For a very large number of cortical (input) oscillators and irrespective of the noise distribution pdf_T of the criterion time, the expected value of the output function given by Eq. (5) becomes:

$$\overline{z}=\underset{x_{min}}{\overset{x_{max}}{\int }}\frac{\sin (N\theta (x))\cos \left(\left(2f_{min}/df+N\right)\theta (x)\right)}{\sin (\theta (x))}{p}_X(x)dx,$$ (6)

where the range (x_min, x_max) depends on the specific type of pdf_X(x) considered. To estimate the expression in Eq. (6), we used the mean value theorem for integrals which states that there always exists a number x_min < γ < x_max such that the integral in Eq. (6) is approximated by:

$$\overline{z}=\frac{\sin (N\theta (\gamma ))\cos \left(\left(2f_{min}/df+N\right)\theta (\gamma )\right)}{\sin (\theta (\gamma ))}{p}_X(\gamma ).$$ (7)

To find the width of the time-dependent expected value of the output function in Eq. (7), we require that $\overline{z\left(t=T+{\sigma }_o/2\right)}=\overline{z(t=T)}/2$, i.e., the expected value at the time t = T + σ_o/2 that corresponds to the half-width of the output function must be 1/2 of the expected value at criterion time t = T. By solving Eq. (7) (see Appendix A), we found that σ_o/(2Tγ) = const., i.e., σ_o ∝ T. Therefore, in the presence of at least one source of noise (variability in the encoding / decoding of criterion time T) the SBF-sin has: (1) a Gaussian output function centers at T (accurate interval timing) that (2) obeys the scalar property.

1. Particular case: Time-scale invariance in the presence of Gaussian noise

Although we already showed that the output function for the SBF-sin model and arbitrary pdf_T for the criterion time noise is always Gaussian and produces accurate interval timing that also obeys scalar property, it is illuminating to grasp the meaning of the theoretical coefficients in our general result by investigating a biologically relevant particular case. If the criterion time is affected by a Gaussian noise with zero mean and standard deviation σ_T, one can show that, in the limit of a large pool of inputs, the standard deviation of the output function becomes:

$${\sigma }_o=T{\sigma }_T.$$ (8)

Briefly (see Appendix B for details), in this particular case, the reference weights are normalized sums of the stochastic variable y = cos(2πf_iT(1 + G(0, σ_T))) ∈ [−1, 1], where G(0, σ_T) is a Gaussian stochastic variable with zero mean and σ_T standard deviation. By replacing the stochastic vector of reference weights w_i(T) in Eq. (1) with its expected value the output function is given by:

$$O(t)=\frac{1}{4T{\sigma }_T\sqrt{2\pi }}\left(e^{-\frac{{(t+T)}^2}{2T^2{\sigma }_T^2}}+e^{-\frac{{(t-T)}^2}{2T^2{\sigma }_T^2}}\right),$$ (9)

which has two Gaussian terms centered at t = ±T with a standard deviation given by Eq. (8). The Eq. (9) shows that the SBF-sin model produces accurate interval timing with a Gaussian shape that has a with given by the scaling Eq. (8), i.e., obeys time-scale invariance property.

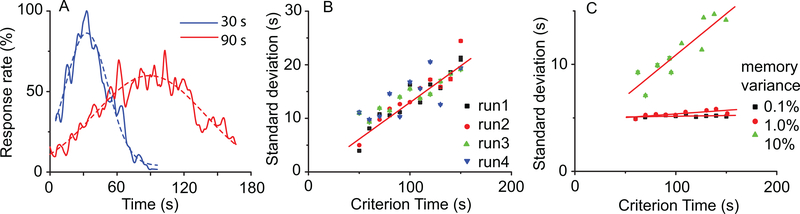
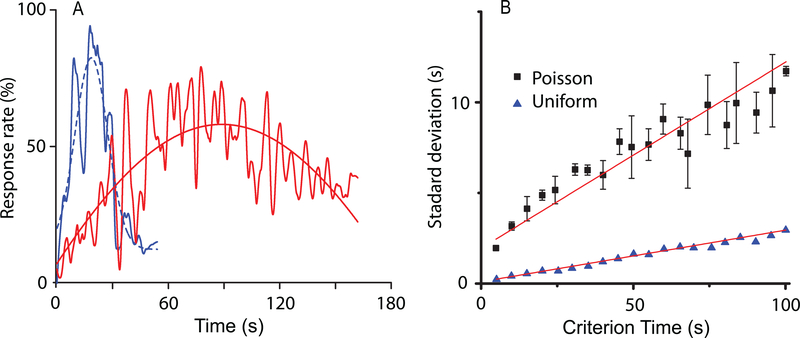
We used the SBF-sin implementation to numerically verify our prediction given by Eq. (8) over multiple trials (runs) of this type of stochastic process and for different values of T. The output functions (see continuous lines in Fig. 4A) for T = 30s and T = 90s are reasonably fitted by Gaussian curves (see dashed lines in Fig. 4A). Our numerical results show a linear relationship between σ_o of the Gaussian fit of the output and T (Fig. 4B). We found that the resultant slope of this linear relationship matched the theoretical prediction given by Eq. (8): For example, for σ_T = 10% the average slope was 11.3% ± 4.5% with a coefficient of determination of R² = 0.93, p < 10⁻⁴.

FIG. 4. (Color online) Time-scale invariance emerges from criterion time noise in the SBF model.

(A) Time-scale invariance emerges spontaneously in a nosy SBF-sin model; here the two criteria are T = 30s and T = 90s. The output functions (continuous lines) were fitted with Gaussian curves (dashed lines) in order to estimate the position of the peak and the width of the output function. (B) In an SBF-sin model, the standard deviation increases linearly with the criterion time in all four trials shown with different symbols. (C) In an SBF-ML implementation, low levels of Gaussian noise (solid rectangles represent σ_T = .1% and circles σ_T = 1%) produce an almost constant standard deviation of the output function similar to noise free case. At high enough levels of noise (solid triangles represent σ_T = 10%), the SBF-ML model with criterion time variance produces a standard deviation σ_o that increases linearly with the criterion time T, which is the hallmark of time-scale invariance.

We noticed that the SBF-ML neurons is less sensitive to the level of criterion time noise. For example, a noise level of 0.1% that would lead to a linear dependence of standard deviation on criterion time in the case of the SBF-sin implementation, rendered no significant change in standard deviation with the SBF-ML implementation (Fig. 4C). The scalar property is indeed valid (Fig. 4C), but it emerges only at such levels of (memory) variance that were not even accessible to SBF-sin implementation. The slope of the standard deviation was insignificant 0.001±0.001 (R² = 0.342) for %0.1 memory variance, 0.007±0.002(R² = 0.789) for %1 variance, respectively, 0.07 ± 0.01(R² = 0.898) for 10% memory variance. The fact that the slope of standard deviation versus criterion time increases ten times (from 0.007 to 0.07) while the memory variance increases ten times (from 1% to 10%) suggests that σ_o ∝ σ_TT for SBF-ML as we predicted and already checked for the SBF-sin model.

We also checked numerically that time-scale invariance is preserved by adding other sources of noise, e.g., small fluctuations in f_i, beside the noise in encoding the criterion time pdf_T (Fig. 5A). Not only time-scale invariance was preserved, but the output function became slightly skewed (longer tail), as often described in the literature (see Fig. 1), suggesting that other properties of the output function may also derive from noise. These results further suggest that the more sources of noise are considered, the more stable the scalar property is, thus explaining its ubiquity [1, 4, 12]. Only when all the noise sources are eliminated, the output ceases to be time-scale invariant, as shown by Eq. (2).

FIG. 5. (Color online) Time-scale invariance is robust to noise manipulation in the SBF model.

(A) In the presence of both criterion time and frequency variance, the SBF-ML produces accurate and time-scale invariant output. At the same time, multiple sources of noise determine a long tail in the output function, which is similar with experimental findings. (B) The scalar property is also preserved regardless the type of criterion time variability (uniform noise - solid triangles, Poisson noise - solid squares).

IV. DISCUSSION

Computational models of interval timing vary largely with respect to the hypothesized mechanisms and the assumptions by which temporal processing is explained, and by which time-scale invariance, or drug effects are explained. The putative mechanisms of timing rely on pacemaker/accumulator processes [6, 7, 80, 81], sequences of behaviors [18], pure sine oscillators [8, 23, 82–84], memory traces [16, 85–89], or cell and network-level models [21, 90]. For example, both neurometric functions from single neurons and ensemble of neurons successfully paralleled the psychometric functions for the to-be-timed intervals shorter than one second [21]. Reutimann et al. (2004) also considered interacting populations that are subject to neuronal adaptation and synaptic plasticity based on the general principle of firing rate modulation in single-cell. Balancing LTP and LTD mechanisms are thought to modulate the firing rate of neural populations with the net effect that the adaptation leads to a linear decay of the firing rate over time. Therefore, the linear relationship between time and the number of clock ticks of the pacemaker-accumulator model in the SET of interval timing [6] was translated into a linearly decaying firing rate model that maps time and variable firing rate.

By and large, to address time-scale invariance current behavioral theories assume convenient computations, rules, or coding schemes. Scalar timing is explained as either deriving from computation of ratios of durations [6, 7, 91], adaptation of the speed at which perceived time flows [18], or from processes and distributions that conveniently scale-up in time [16, 82, 85, 87, 88]. Some neurobiological models share computational assumptions with behavioral models and continue to address time-scale invariance by specific computations or embedded linear relationships [92]. Some assume that timing involves neural integrators capable of linearly ramping up their firing rate in time [90], while others assume LTP/LTD processes whose balance leads to a linear decay of the firing rate in time [93]. It is unclear whether such models can account for time-scale invariance in a large range of behavioral or neurophysiological manipulations.

Neurons are often viewed as communications channels which respond even to the precisely delivered stimuli sequence in a random manner consistent with Gaussian noise [94]. Biological noise was shown to play important functional roles, e.g., enhance signal detection through stochastic resonance [95, 96] and stabilize synchrony [97, 98]. Firing rate variability in neural oscillators also results from ongoing cortical activity (see [98, 99] and references therein), which may appear noisy simply because it is not synchronized with obvious stimuli. Our theoretical predictions based on an SBF model show that time-scale invariance emerges as the property of a (very) large and noisy network. Furthermore, we showed that the output function of an SBF mode always resembles the Gaussian shape found in behavioral experiments regardless the type of noise affecting the timing network. Our results regarding the effect of noise on interval timing support and extend the speculation [23] by which an SBF model requires at least one source of variance (noise) to address time-scale invariance. Rather than being a signature of higher-order cognitive processes or specific neural computations related to timing, time-scale invariance naturally emerges in a massively-connected brain from the intrinsic noise of neurons and circuits [4, 21]. This provides the simplest explanation for the ubiquity of scale invariance of interval timing in a large range of behavioral, lesion, and pharmacological manipulations.

Appendix A: General case: Time-scale invariance from noise with arbitrary distribution

To estimate the width of the output function using Eq. (7), we notice that at t = T the function θ(γ) = −πTγdf which leads to:

$$\begin{gathered} O\left(t=\overline{T}\right)=\frac{\sin (N\pi T\gamma df)\cos \left(\left(2f_{min}/df+N\right)\pi T\gamma df\right)}{\sin (\pi T\gamma df)}{p}_X(\gamma ) \\ =\frac{\sin (a)\cos (b)}{\sin (a/N)}{p}_X(\gamma ), \end{gathered}$$ (A1)

where we used the notation a = πTγ(f_max − f_min), b = πTγ(f_max + f_min). Similarly, the estimated value of the output function at t = T + σ_o/2, i.e., the half width of the output function, is

$$O\left(t=\overline{T}+{\sigma }_o/2\right)=\frac{\sin (a(1-x))\cos (b(1-x))}{\sin (a(1-x)/N)}{p}_X(\gamma ),$$ (A2)

where x = σ_o/(2Tγ) is proportional to the coefficient of variation of the criterion time. By solving $O\left(t=\overline{T}+{\sigma }_o/2\right)=O(t=\overline{T})/2$, we find that:

$$\frac{\sin (a)\cos (b)}{\sin (a/N)}{p}_X(\gamma )=\frac{1}{2}\frac{\sin (a(1-x))\cos (b(1-x))}{\sin (a(1-x)/N)}{p}_X(\gamma ).$$ (A3)

Using a Taylor series approximation for the right hand side of Eq. (A3), we obtain:

$$\frac{1}{2}\frac{\sin (a)\cos (b)}{\sin (a/N)}=a_{1}x+O\left(x^2\right),$$ (A4)

where the constant $a_1=\frac{\sin (a/N)(a\cos (a)\cos (b)-b\sin (a)\sin (b))-a/N\sin (a)\cos (b)\cos (a/N)}{{\sin }^2(a/N)}$, and O(x²) includes second order terms and higher. From Eq. (A4), the first order approximation of the expected width of the output function is:

$$x=\frac{\sin (a)\cos (b)}{2\sin (a/N)a_1}=Const.,$$ (A5)

which proves that x = σ_o/(2Tγ) = Const., i.e., σ_o ∝ T. This proves that the scalar-time property is fulfilled regardless the pdf_T.

Appendix B: Particular case: Time-scale invariance from Gaussian noise

When the criterion time is affected by a Gaussian noise, the reference weights w_i(T) become:

$$\begin{gathered} w_i(T)=\sum _{j=1}^{N_o}\frac{\cos (2\pi f_i{T}_j)}{S} \\ =\sum _{j=1}^{N_o}\frac{\cos (2\pi f_{i}T(1+G{(0,{\sigma }_T)}_j))}{S}. \end{gathered}$$ (B1)

The stochastic variables y = cos(2πf_iT(1 + G(0, σ_T))) ∈ [−1, 1] under summation in Eq. (B1) has the pdf [100]:

$$p_Y(y)=\frac{1}{\sqrt{2\pi }2\pi {\sigma }_T{f}_{i}T}{e}^{\frac{-{\left(\frac{\arccos (y)}{2\pi f_{i}T}-1\right)}^2}{2{\sigma }_T^2}}.$$

The mean of pdf_y is ${\mu }_y=\underset{-1}{\overset{1}{\int }}y{p}_Y(y)dy$, which rewrites as:

$$\begin{gathered} {\mu }_y=\frac{1}{\sqrt{2\pi }{\sigma }_T}\underset{-\infty }{\overset{\infty }{\int }}\cos \left(2\pi f_{i}T(1+x)\right)e^{-\frac{x^2}{2{\sigma }_T^2}}dx \\ =e^{\frac{-{\left(2\pi f_{i}T{\sigma }_T\right)}^2}{2}}\cos \left(2\pi f_{i}T\right). \end{gathered}$$ (B2)

By replacing the stochastic vector of reference weights w_i(T) in Eq. (1) with the expected value from Eq. (B2) one obtains:

$$O(t)=\sum _{i=1}^N\cos \left(2\pi f_{i}T\right)\cos \left(2\pi f_{i}t\right)e^{\frac{-{\left(2\pi f_{i}T{\sigma }_T\right)}^2}{2}},$$ (B3)

which, for a very broad spectrum of frequencies (theoretically 0 < f < ∞) and a very large pool of neural oscillators (theoretically N → ∞), becomes:

$$\begin{gathered} O{\left(t\right)}_{N\to \infty }=\underset{0}{\overset{\infty }{\int }}\cos (2\pi fT)\cos (2\pi ft)e^{-\frac{{(2\pi fT{\sigma }_T)}^2}{2}}df \\ =\frac{1}{4T{\sigma }_T\sqrt{2\pi }}\left(e^{-\frac{{(t+T)}^2}{2T^2{\sigma }_T^2}}+e^{-\frac{{(t-T)}^2}{2T^2{\sigma }_T^2}}\right). \end{gathered}$$ (B4)

which is equivalent to Eq. (8).

Appendix C: Morris-Lecar model equations

We used a dimensionless Morris-Lecar model [43, 101] described by the following equations

$$\begin{gathered} x_1^{\prime }=f_1\left(x_1,x_2\right)=-I_{Ca}-I_K-I_L+I_0, \\ {x}_2^{\prime }=f_2\left(x_1,x_2\right)=\xi {\lambda }_0\left(x_1\right)\left(w_{\infty }\left(x_1\right)-x_2\right), \end{gathered}$$ (C1)

where x₁ is the membrane potential, x₂ is the slow potassium activation and all ionic currents are described by I_x = g_x(x₁ −E_x), where g_x is the conductance of the voltage gated channel x and E_x is the corresponding reversal potential. In particular, the calcium current is I_Ca = g_Cam_∞(x₁)(x₁ − E_Ca), the potassium current is I_K = g_Kx₂(x₁ − E_K), and the leak current is I_L = g_L(x₁−V_L). The reversal potentials for calcium, potassium and leak currents are E_Ca = 1.0,E_K = −0.7,E_L = −0.5, respectively. The steady state activation function for calcium channels is m_∞(x₁) = 1 + tanh((x₁ − V₁)/V₂))/2, where V₁ = −0.01, V₂ = 0.15, the steady state activation function for potassium channels is w_∞(x₁) = (1 + tanh((x₁ − V₃)/V₄])/2 where V₃ = 0.1, V₄ = 0.145, the inverse time constant of potassium channels is λ₀(x₁) = cosh((x₁ −V₃)/V₄/2), the potassium and leak conductances are g_K = 2.0, g_L = 0.5, respectively, and the ξ = 1.0/3.0.

The two control parameters that can switch the ML model from a Class I excitable cell [102] to a Class II are the calcium conductance g_Ca and the bias current I₀. For example, if g_Ca = 1.0 and 0.083 < I₀ < 0.242 the equations (C1) describe what was classified by A.L. Hodgkin as Class I excitable cells. For example, if g_Ca = 0.5 and 0.303 < I₀ < 0.138 the equations (C1) describe what was classified by A.L. Hodgkin as Class II excitable cells. In our simulations, we used a Class II ML model neuron that has a membrane potential shape very close to a sine-wave.