A Mesh-Free Approach to Incorporate Complex Anisotropic and Heterogeneous Material Properties into Eye-Specific Finite Element Models

Abstract

Commercial finite element modeling packages do not have the tools necessary to effectively incorporate the complex anisotropic and heterogeneous material properties typical of the biological tissues of the eye. We propose a mesh-free approach to incorporate realistic material properties into finite element models of individual human eyes. The method is based on the idea that material parameters can be estimated or measured at so called control points, which are arbitrary and independent of the finite element mesh. The mesh-free approach approximates the heterogeneous material parameters at the Gauss points of each finite element while the boundary value problem is solved using the standard finite element method. The proposed method was applied to an eye-specific model a human posterior pole and optic nerve head. We demonstrate that the method can be used to effectively incorporate experimental measurements of the lamina cribrosa micro-structure into the eye-specific model. It was convenient to define characteristic material orientations at the anterior and posterior scleral surface based on the eye-specific geometry of each sclera. The mesh-free approach was effective in approximating these characteristic material directions with smooth transitions across the sclera. For the first time, the method enabled the incorporation of the complex collagen architecture of the peripapillary sclera into an eye-specific model including the recently discovered meridional fibers at the anterior surface and the depth dependent width of circumferential fibers around the scleral canal. The model results suggest that disregarding the meridional fiber region may lead to an underestimation of local strain concentrations in the retina. The proposed approach should simplify future studies that aim to investigate collagen remodeling in the sclera and optic nerve head or in other biological tissues with similar challenges.

1. Introduction

The biomechanics of the human eye play an important role in the functionality of the organ. The development of realistic and patient-specific multi-scale models of the eye can provide new insight into the role of ocular biomechanics in physiological and pathophysiological conditions. The Finite Element Method (FEM) is a powerful commonly used numerical approach to solve biomechanical boundary value problems of the eye [1–8]. However, it is a major challenge to first obtain and translate the geometry of the organ’s macro-structure into eye-specific FEM models, and then to incorporate realistic material and eye-specific micro-structural properties into such models. The main load bearing constituent of the ocular coats is fibrillar collagen (Type I). The collagen fibrils together with other constituents are responsible for the highly nonlinear, anisotropic, and heterogeneous material properties of the ocular tissues. Similar observation can be made for most other organs of the human body including the heart, skin, tendons, and muscles. Effectively incorporating such complex material properties into FEM models of the eye remains an open challenge.

Because of its great importance in ocular biomechanics, and therefore in physiology and pathophysiology, many imaging modalities have been utilized to measure the anisotropy of the collagen fibers in the eye. These include small-angle light scattering [9, 10], X-ray scattering [11–14], second harmonic imaging [15, 16], scanning electron [17–19], transmission electron microscopy [20], and magnetic resonance imaging [21, 22]. Recently, Jan et al. [23, 24] and Gogola et al. [25] demonstrated a technique based on polarized light microscopy that allows visualization and quantification, with micrometer-scale resolution, of the distribution and orientation of collagen in the posterior sclera and lamina cribrosa of sheep, human, monkey, pig, cow and goat eyes.

Incorporating the large amount of eye-specific data that these techniques produce into numerical models has been a long-standing challenge in ocular biomechanics. Bellezza et al. [26] incorporated some rough aspects of scleral canal geometry and a highly simplified, but not uniform, lamina cribrosa. Sigal et al. [27, 28, 29] developed models of human posterior poles with eye-specific geometries to explore the IOP-induced deformation of the ONH, and their sensitivity to tissue geometry and mechanical properties. Later, Sigal et al. [30, 31] introduced a morphing technique that allows smooth variations in the model geometry to parametrically explore the sensitivity to changes in geometry. Their models, however, incorporated only highly simplified linear, isotropic, homogeneous material properties. Roberts et al. [32, 33] created models of monkey eyes with a eye-specific lamina cribrosa embedded in realistic, but not eye-specific, scleral shells. The lamina cribrosa was modeled as anisotropic and inhomogeneous, but the models were still linear and highly simplified. Norman et al. [34] developed human globe models that combining the eye-specific corneo-scleral shells and generic ONHs to study the effects of globe shape and size on ONH biomechanics. All of the models, consistently support the conclusion that the sclera properties are a major determinant on ONH biomechanics, and therefore that accurately predicting sensitivity to IOP will require accurately capturing sclera properties.

Models incorporating inhomogeneous, anisotropic and nonlinear tissue mechanical properties have also been developed. Zhang et al. [35] created planar models of the human ONH and peripapillary sclera, incorporating collagen anisotropy from small-angle light scattering. Campbell et al. [36] created a model of the posterior porcine eye with a generic geometry but anisotropic mechanical properties of the lamina cribrosa based on eye-specific measurements of connective tissue volume fraction and collagen beam orientation obtained from micro-computed tomography imaging. Voorhees et al. [37, 38] developed eye-specific anisotropic models of the lamina microstructure based on polarized light microscopy.

Despite their complexity, previous anisotropic models still had major simplifications. For example, they typically assumed a circumferential ring of collagen fibers around the ONH that had a constant width across the scleral thickness [3, 39–44]. The exception being the model by Pijanka et al. which incorporated depth-dependent collagen fiber anisotropy. Other models incorporated experimental measurements of the collagen fiber distribution [12, 45], but they were based on average measurements of the collagen fiber distribution across the scleral thickness.

Recently, Gogola et al. [25] showed that the anisotropic architecture of the peripapillary sclera varies significantly though the scleral thickness and is more complex than previously assumed. It was reported that the peripapillary sclera is composed of regions with circumferential, meridional, and isotropic collagen fiber distributions (Figure 1). In particular, two features were previously unknown or underappreciated: (i) the existence of meridional fibers at the anterior surface of the sclera and (ii) the thickness-dependent width of the ring of circumferential collagen fibers around the scleral canal. Both features add significant complexity to models that aim to investigate these complex architectures. Note that Gogola et al. [25] refer to what we call meridional fibers as radial fibers in that they radiate from the scleral canal. To our knowledge, the meridional or thickness-dependent width of circumferential fibers of the peripapillary sclera have never been incorporated into a biomechanical model of the eye.

Figure 1:

Virtual longitudinal cross section of a human ONH from a stack of images acquired using polarized light microscopy as described in Jan et al. [23], Gogola et al. [25]. Colors represent local fiber orientation in polar coordinates relative to the scleral canal axis as per the legend on the bottom right (C: Circumferential; R: Radial). Regions of circumferential or radial fibers are indicated by the ovals and arrows, respectively.

Most commercially available FEM software packages are now equipped with micro-structurally motivated constitutive models for the realistic simulation of collagenous soft tissues as found in the eye. However, software tools to easily incorporate highly heterogeneous and anisotropic properties into FEM models are typically not provided as only a limited set of analytical coordinate systems (Cartesian, cylindrical, and spherical coordinate systems) are commonly available in commercial FEM packages to define anisotropic material orientations [46]. Finite elements can be grouped into element sets to define heterogeneous material parameters across the model. These strategies seem to provide sufficient options to the user to effectively generate generic models of the eye but are insufficient to incorporate highly heterogeneous material properties into eye-specific multi-scale models. As new nondestructive techniques are being developed to measure material properties at arbitrary points in ocular tissues in vivo [47, 48], effective methods to incorporate these heterogeneous material properties into patient-specific models are needed. In this paper, we propose a mesh-free approach to effectively incorporate heterogeneous and anisotropic material properties into eye-specific FEM models. While we use eye-specific models of the optic nerve head to illustrate the strengths of our methodology, it can be applied to any tissue, organ, or other mechanical problem with similar challenges.

2. Mesh-free approach to define heterogeneous materials

The basic idea of mesh-free methods is the approximation of scattered data [49]. We take advantage of this idea assuming that material parameters can be measured or approximated at discrete locations, which are arbitrary and independent of the finite element mesh. To solve a boundary value problem using FEM, knowledge of the material parameters is needed at the Gauss points of each finite element. We propose to approximate the material parameters at the Gauss points using a mesh-free approach.

Let m be a heterogeneous material parameter that is defined at N control points c_I with I = 1, …, N. The approximated value of the material parameter $\tilde{m}\left(\mathbf{\text{x}}\right)$ is computed at a point x (e.g. at a Gauss point) as

$$\tilde{m}\left(x\right)=C_w\sum _{I=1}^{N}w\left(\frac{\Vert x-c_I\Vert }{d_{\text{ref}}\varrho }\right)m\left(c_I\right),$$ (1)

where C_w is a normalization constant, d_ref is a reference distance, ϱ is a dilation parameter, and w is the window function. The approximation (1) remains valid if m is a vector or second order tensor. We use the common cubic spline function [50] to define the window function

$$w\left(y\right)=\{\begin{array}{ll}8\left(|y|-1\right)y^2+4/3\hfill & |y|\le 0.5\hfill \\ 8{\left(1-|y|\right)}^3/3\hfill & 0.5<|y|1\hfill \\ 0\hfill & 1\le |y|.\hfill \end{array}$$ (2)

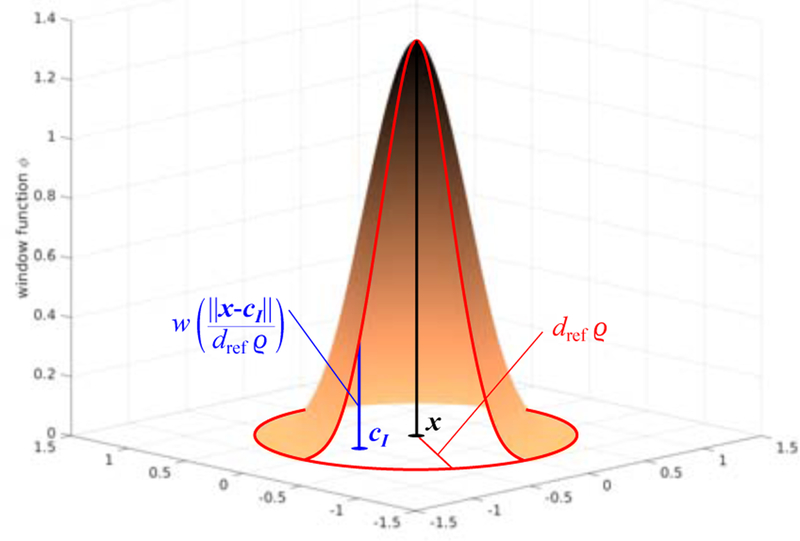
Figure 2 illustrates the shape of the window function (2). The normalization constant is computed as

$$C_w={\left[\sum _{I=1}^{N}w\left(\frac{\Vert x-c_I\Vert }{d_{\text{ref}}\varrho }\right)\right]}^{-1}.$$ (3)

The reference distance d_ref represents a characteristic length such as the thickness of the sclera. The dilation parameter ϱ controls the degree of smoothing. Note that the dilation parameter must be large enough to avoid aliasing, while excessively large value for ϱ will lead to excessive smoothing.

Figure 2:

Illustration of the window function $\left(\frac{\Vert x-c_I\Vert }{d_{\text{ref}}\varrho }\right)$ assuming that the points x and c_I lie on a plane and d_ref ϱ = 1. Control points that are close to x influence the approximation of the material parameter more than points that are further away. Control points that lie at a distance larger than d_ref ϱ do not influence the approximation at x.

The approximated material parameters can be directly computed at the Gauss points of each finite element. Alternatively, the material parameters can be approximated and stored at the nodal locations of the mesh. In the latter case, the standard shape functions can be used to interpolate the nodal values to obtain the material parameters at the Gauss points. We implemented the mesh-free approach into the free and open-source FEM package CaluliX [51]. While the calculation of (1) will add computational cost to the FEM solution, the approximation of the material parameters has to be computed only once as long as the materials dont change. The method may also be helpful in simplifying defining material evolution or remodeling. Furthermore, the calculation of (1) can be easily parallelized.

To incorporate realistic anisotropic material properties into realistic, patient-specific finite element models of a human organ is not a trivial task and can be approached in different ways. Many anisotropic constitutive models use a local orthonormal basis to define local material orientations. We propose to use the above mesh-free approach to approximate a local basis used to define anisotropic material properties. Let e_i be an orthonormal basis that represents the characteristic material directions. We assume that this basis can be experimentally measured or estimated at the control points c_I (I = 1, …, N). Applying the mesh-free approximation (1) to the local basis will not ensure that the resulting basis is orthonormal at x

$${\tilde{e}}_i\left(x\right)=C_w\sum _{I=1}^{N}w\left(\frac{\Vert x-c_I\Vert }{d_{\text{ref}}\varrho }\right)e_i\left(c_I\right).$$ (4)

However, one can easily enforce orthonormality by using the following modified basis

$$\begin{gathered} {\widehat{e}}_1={\tilde{e}}_1/\Vert {\tilde{e}}_1\Vert \\ {\widehat{e}}_2={\tilde{e}}_3\times {\widehat{e}}_1/\Vert {\tilde{e}}_3\times {\widehat{e}}_1\Vert \\ {\widehat{e}}_3={\widehat{e}}_1\times {\widehat{e}}_2. \end{gathered}$$ (5)

We and others have used second-order tensors such as a generalized structure tensors or fabric tensor to define anisotropic constitutive models [52–54]. The material approximation presented here can be easily extended to constitutive models that use second-order tensors H to define anisotropy. Typically, generalized structure tensors or fabric tensors are designed to satisfy the condition $\text{tr}\left(H\right)={\sum }_{i=1}^3{H}_{ii}=1.$ To ensure that this condition is satisfied at the Gauss point, we propose to normalize the tensor that results form the mesh-free approximation (1)

$$\widehat{H}=\tilde{H}/\text{tr}\left(\tilde{H}\right)\text{with}\tilde{H}=C_w\sum _{I=1}^{N}w\left(\frac{\Vert x-c_I\Vert }{d_{\text{ref}}\varrho }\right)H\left(c_I\right).$$ (6)

Note that the normalization (6) and the modification of the material basis (5) are important to ensure that the unloaded configuration remains stress free.

3. Application of the mesh-free approach to an eye-specific model

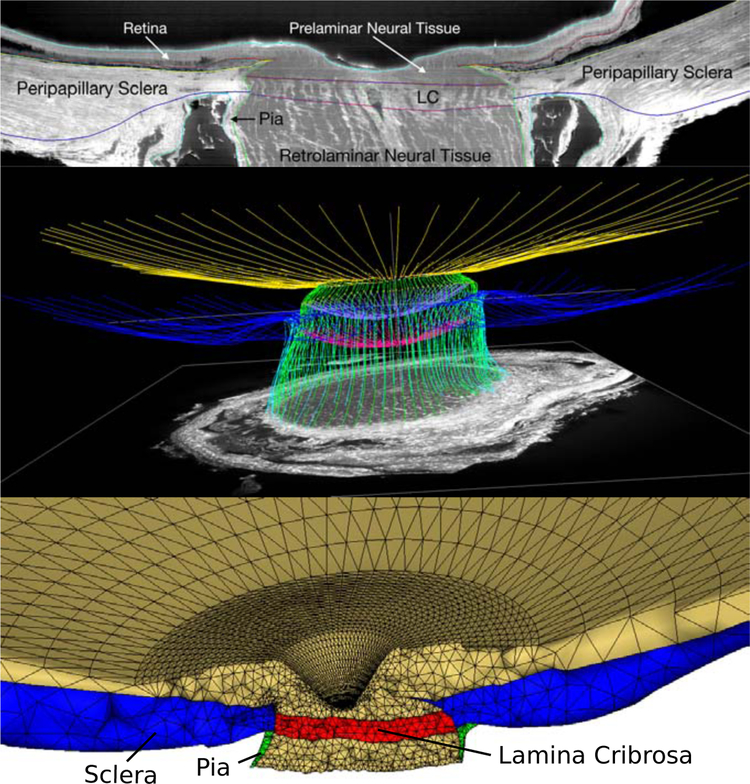
An eye-specific finite element mesh of a human optic nerve head (ONH) was created from a three-dimensional reconstruction of the ONH connective tissues acquired using a microtome-based serial sectioning and block face imaging device [32, 55–57]. The tissues of the ONH were manually delineated using radial sections through the reconstructed ONH volume. The eye-specific finite element mesh was generated based on the point cloud that was obtained from the manual segmentation. The model includes the sclera, lamina cribrosa, pre- and retro-laminar tissues, retina, and pia (Figure 3). In the following subsections, we present three specific applications of our mesh-free approach to illustrate the versatility of the approach in incorporating complex anisotropic and heterogeneous material properties into eye-specific models.

Figure 3:

Eye-specific finite element modeling of the human posterior eye. A: The macro-architecture of the model is first defined by 3D delineation of anatomic surfaces in a 3D fluorescent reconstruction of a human posterior eye, based on serially imaging the block face of a paraffin-embedded ONH specimen at 1.5 × 1.5 μm/pixel resolution using an episcopic fluorescent microscope fitted with a 16-megapixel, monochrome CCD camera after each 1.5-μm-thickness microtome section is cut. Approximately 1200 images are precisely aligned to build a 3D reconstruction of an ONH using a laser displacement sensor that records the specimen position for each image. Once the autofluorescent images are aligned and stacked to create a volume, custom delineation software was used to slice the volume on 40 radial sagittal planes centered on the optic nerve head. Within each radial section, the anatomic surfaces were delineated using Bezier curves to define the morphology of the lamina cribrosa (LC), peripapillary sclera, and pia as shown [57]. B: 3D view of the Bezier curve delineations for the full set of 40 radial marking planes for a human eye, showing the anterior and posterior scleral surfaces (yellow and blue), scleral canal surface (green), exterior pial boundaries (light blue) and the anterior and posterior lamina cribrosa surfaces (lavender and magenta). C: 3D surfaces are then fit to the families of Bezier curves seen in (B) and the resulting eye-specific geometries of the optic nerve head and peripapillary sclera are then fit into a larger generic posterior scleral shell with anatomic shape and thickness. Finally, a parameterized, anatomic surface defining the prelaminar neural tissues, retina and choroid (gold, top) is added. These surfaces are then used to build the eye-specific, high-fidelity finite element mesh of the human posterior eye using quadratic tetrahedral elements with ten nodes.

3.1. Incorporating discrete measurements of the lamina cribrosa micro-structure

The 3D reconstructed volume of the ONH has a isotropic voxel size of 1.5 μm providing sufficient resolution to extract anisotropic features of the collagenous micro-structure of the lamina cribrosa. We extracted a binary representation of the collagenous micro-structure and used the mean-intercept-length (MIL) algorithm to compute the connective tissue volume fraction n_LC and fabric tensor H_LC at discrete locations throughout the lamina cribrosa. A detailed description of the methodology can be found in Roberts et al. [56]. We used the mesh-free approach (1) and (6) to approximate the connective tissue volume fraction and fabric tensor at the Gauss points of the finite element mesh, respectively. The reference distance was set to the average thickness of the lamina cribrosa (d_ref = 180μm) while the dilation parameter was varied (ϱ = 0.5,2.0,10.0) to illustrate its effect. The fabric tensor represents the anisotropy of the lamina beam structure. We propose the following strain energy density function to model the constitutive response of the lamina cribrosa

$$\begin{gathered} W_{\text{LC}}=n_{\text{LC}}\left(W_{\text{ISO}}+W_{\text{beams}}\right)+U \\ {W}_{\text{ISO}}=\frac{1}{2}\mu \left(J^{-2/3}\text{tr}C-3\right) \\ {W}_{\text{beams}}=W_{\text{fib}}\left({\lambda }_{\text{fib}}=\sqrt{H_{\text{LC}}:C}\right) \\ U=\frac{1}{2}k{\left(\text{ln}J\right)}^2 \end{gathered}$$ (7)

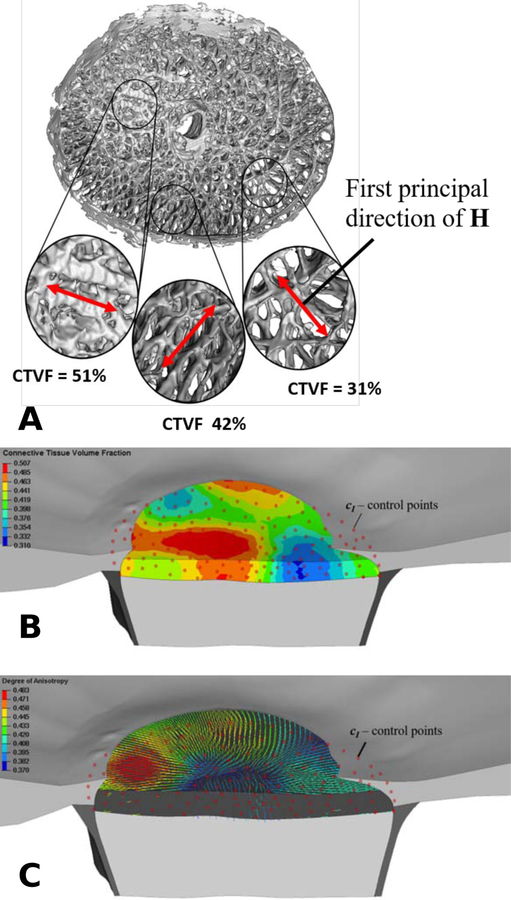
An isochoric Neo-Hookean material model [58] is used to model the constitutive response of the ground substance, where μ represents the shear modulus, C is the right Cauchy-Green tensor and $J=\sqrt{\det C.}$. We use our microstructural-motivated material model W_fib [59] to define the strain energy density function of the lamina cribrosa beams W_beams as a function of the fabric tensor H_LC. The microstructural-motivated model W_fib consists of three parameters that define the collagen fiber crimp and stiffness. The pure hydrostatic part U controls the compressibility of the of the material, where κ represents the bulk modulus. We have previously used a similar constitutive model to simulate the biomechanical response of the lamina cribrosa by using fabric tensors that were derived for individual elements [52]. Note that scaling the strain energy parts W_iso + W_beams with the connective tissue volume fraction n_LC in (7) is identical to scaling the shear modulus μ and the elastic modulus of collagen fibers E_fib as proposed in our previous work [52]. Using the mesh-free approach proposed herein decouples the material definition from the mesh definition and provides smooth transitions of n_LC and the fabric tensor H_LC across the elements of the lamina cribrosa as seen in Figure 4. In this plot, the degree of anisotropy is defined as (H₁ − H₂)/(H₁ + H₂), where H₁ and H₂ are the first and second eigenvalues of the fabric tensor. The first eigenvector of H_LC is used to illustrate the predominant local orientation of the lamina cribrosa beams.

Figure 4:

A: A 3D, segmented lamina cribrosa reconstruction of a human eye, showing large variation in local connective tissue volume fraction (CTVF) and predominant laminar beam orientations; local CTVF and the fabric tensor H_LC were calculated from overlapping conical volumes with discrete center locations, which serve as control points for the mesh-free approach. B: Contour plot of the connective tissue volume fraction in the finite element model of the lamina cribrosa. Red dots represent the control points at which the micro-structure was evaluated. C: First principal directions of the fabric tenor H_LC. The color of the principal directions represents the degree of anisotropy. The mesh-free approach leads to a smooth approximation of both, the material parameter n_LC and the fabric tensor H_LC, across the lamina cribrosa model. The dilation parameter was set to ϱ = 2.0.

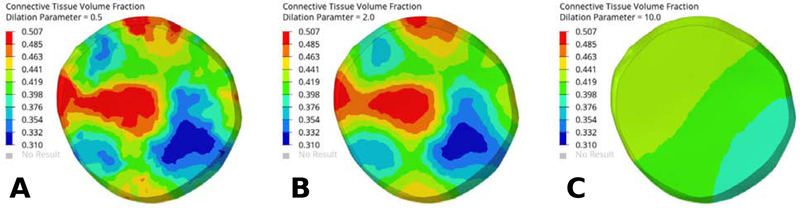
Figure 5 illustrates the smoothing effect of the dilation parameter ϱ on the approximation the connective tissue volume fraction in the lamina cribrosa model. Increasing ϱ from 0.5 to 2.0 led to a smoother approximation of the heterogeneous material parameter, while ϱ = 10.0 led to excessive smoothing. A similar evaluation of the effect of ϱ should be performed when replicating our method. We found that $\varrho =2.0\cdot {\overline{d}}_w/d_{\text{ref}}$ is good starting value with moderate smoothing of the control point values, where ${\overline{d}}_w$ represents the average of the shortest distance between two control points

$${\overline{d}}_w=\sum _{I-1}^N\underset{J\ne I}{\underset{J=1\dots N}{\min }}\left(\Vert c_J-c_I\Vert \right).$$ (8)

Figure 5:

The smoothing effect of varying the dilation parameter ϱ on the approximation of the connective tissue volume fraction of the lamina cribrosa model. Contour plots of the connective tissue volume fraction for dilation parameter values ϱ = 0.5 (A), ϱ = 2.0 (B), and ϱ = 10.0 (C). The same control point locations and values were used for all three models as shown in Figure 4. The degree of smoothing increased with larger values for ϱ.

3.2. Approximating scleral material orientation from macro-structure

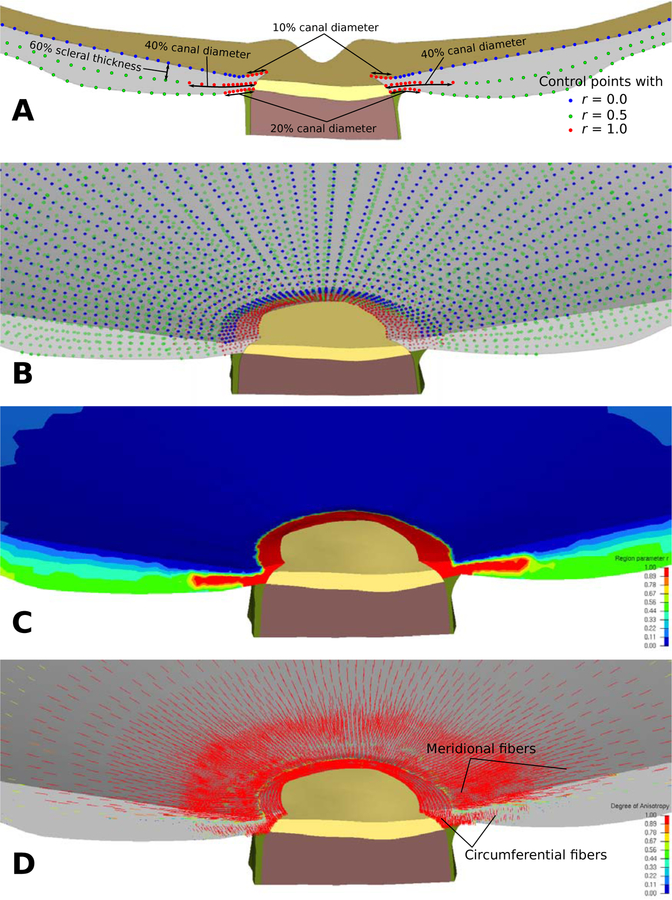
Previous finite element models of the ONH often used a spherical coordinate system to define circumferential, meridional, and normal directions in the sclera [40, 44, 54, 60]. These directions were used to model the anisotropic constitutive response of the sclera. Defining similar characteristic directions in an eye-specific geometry can be a very difficult task as typically no analytical coordinate system can be identified that can approximate the actual eye-specific geometry of the peripapillary sclera surfaces and scleral canal boundary, which are a natural basis of the collagen fiber orientation in those tissues. We propose to define characteristic material directions at convenient locations of the scleral model: the anterior and posterior scleral surfaces. While the scleral canal geometry is complex with a more elliptical than circular cross section, traverses the sclera at an oblique angle, and is generally much larger at the posterior scleral boundary compared to the anterior scleral boundary, the circumferential direction can be defined as the tangential direction at scleral canal. Similarly, the normal direction can be easily computed at the anterior and posterior scleral surface. Based on this idea, control points were seeded on the anterior and posterior scleral surface. We used the local surface geometry to calculate a normal orientation at each control point. The circumferential orientation was obtained at the scleral canal by fitting an ellipse to the anterior insertion points of the lamina cribrosa into the sclera. The tangential direction of this ellipse was projected to each control point on the sclera surface and used to define the circumferential orientation. The meridional direction was obtained from the orthonormality condition. The mesh-free approach (4) with (5) was used to approximate these orientations across the scleral thickness with d_ref = 300μm and ϱ = 2. The approximated material directions are plotted in Figure 6 showing the smooth transition of the material direction between the top and bottom surfaces of the sclera.

Figure 6:

The (A) circumferential, (B) meridional, and (C) normal material directions (black lines) of the scleral model. The material directions were defined at the control points (red dots) and approximated across the scleral model using the mesh-free approach.

3.3. Approximating the complex material anisotropy of the peripapillary sclera

As mentioned in the introduction, incorporating the complex structure and mechanical behavior of the lamina cribrosa and sclera into numerical models has remained a major challenge for ocular biomechanics. Models have either lacked the detailed eye-specific geometry, the eye-specific complex properties, or, in most cases, both. To the best of our knowledge, there have been no reports describing eye-specific ONH models with realistic nonlinear, anisotropic mechanical properties of the sclera including the meridional or thickness-dependent width of circumferential fibers that were recently identified by Gogola et al. [25]. We use our mesh-free approach to approximate the complex collagen fiber architecture reported by Gogola et al. [25] into our eye-specific model.

In the previous subsection, we defined local material direction that are used here to define the local circumferential and meridional directions. We introduce the region parameter r, which is used to distinguish the three regions identified by Gogola et al. [25]:

1. r = 0 represents the meridional fiber region

2. r = 0.5 represents the isotropic distributed fiber region

3. r = 1 represents the circumferential fiber region

We use three layers of control points to define the region parameter across the peripapillary sclera (Figure 7A, B). The first and third layers are defined at the anterior and posterior scleral surfaces. The second layer is defined at 60% depth through the scleral thickness, where the circumferential fiber region was found to extend furthest into the human peripapillary sclera [25]. For each layer of control points, we defined r = 1 at the scleral canal and up to a width that approximated the depth-dependent width of the circumferential region identified by Gogola et al. [25, (see Fig. 15)]. Peripheral to the circumferential ring region, the region parameter was set to r = 0, r = 0.5, and r = 0.5 at the anterior, middle, and posterior layer of control points, respectively. The mesh-free approach (1) was used to approximate the region parameter throughout the sclera with d_ref = 100μm and ϱ = 2 (Figure 7C).

Figure 7:

A: Illustration of three layers of control points and with r = 0, 0.5, and 1 representing the meridional, isotropic, and circumferential region in the model, respectively. B: The three layers of control points were seeded across the scleral portions of the model. C: Contour plot showing the distribution of the region parameter r across the sclera. The mesh-free approach was used to approximate r across the scleral mesh. D: The first principal direction of the structure tensor (15) representing predominant fiber orientations. The mesh-free approach effectively approximated the circumferential and meridional fiber regions.

For the constitutive response of the sclera, we propose a model with two fiber families, where each family has distributed fiber orientations that follow a normalized von Mises distribution. The strain energy function is composed of three parts

$$W_{\mathrm{sclera}}=W_{\text{iso}}+W_{\text{col}}+U$$ (9)

where only the part W_col differs from the lamina cribrosa model (7). Let e₁ and e₂ be the local circumferential and meridional directions, respectively. e₀ represents a unit vector defined in the e₁-e₂ plane by means of an Eulerian angle ϕ ∈ [π/2;π/2] as

$$e_0=\cos \left(\varphi \right)e_1+\sin \left(\varphi \right)e_2$$ (10)

The axial stretch in the direction ϕ can be computed as

$$\lambda =\sqrt{e_{0}C{e}_0}$$ (11)

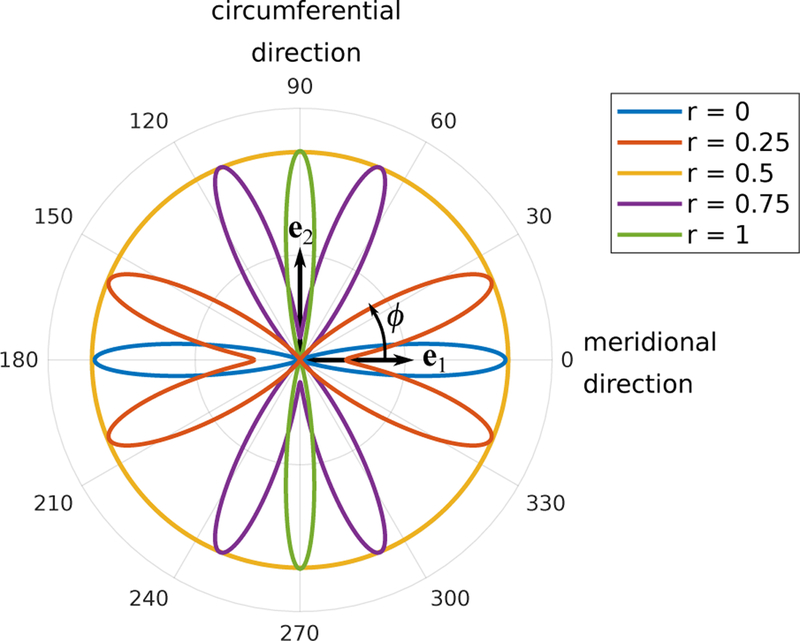
We define the fiber orientation distribution function ρ as

$$\rho =\frac{\exp \left(b_{\text{fib}}\cos \left(2\left(\varphi +\alpha \right)\right)\right)+\exp \left(b_{\text{fib}}\cos \left(2\left(\varphi -\alpha \right)\right)\right)}{2\pi I_0},$$ (12)

where b is the concentration parameter, I₀ is the modified Bessel function of the first kind and order zero, and α modulates the angular distance between the preferred orientations of the two fiber families. To simulated the different fiber regions of the peripapillary sclera, we define the b and α as functions of the region parameter r

$$\begin{gathered} \text{meridional}\text{region,}\text{r}\text{=}\text{0}\text{:}b=15\text{and}\alpha \text{= 0} \\ \text{isotropic region,}\text{r}\text{=}0.5:b=0\text{and}\alpha \text{=}\pi /4 \\ \text{circumferential}\text{region,}\text{r}\text{=}\text{1}:b=20\text{and}\alpha \text{=}\pi /2 \end{gathered}$$ (13)

For all other values of r, the parameters were linearly interpolated between the above defined values. We estimated the values of b in (13) such that the degree of anisotropy of our density function ρ matched the measured fiber distributions at the meridional, isotropic, and circumferential fiber regions [25]. Figure 8 illustrates the fiber distributions at the different regions including two intermediate regions. Note that by using the region parameter and two fiber families, the fiber orientation distribution can be smoothly transitioned between the different regions.

Figure 8:

Polar plot of the fiber orientation distribution (12) for variable region parameters r. For illustration purposes, the distributions were scaled to have matching maximum radial value.

The strain energy function of the scleral collagen network is represented by the integral over our microstructural-motivated strain energy function [59] weighted by the density function ρ

$$W_{\text{col}}=\underset{-\pi /2}{\overset{\pi /2}{\int }}\rho \left(\varphi \right)W_{\text{fib}}\left(\lambda \left(\varphi \right)\right)\text{d}\varphi .$$ (14)

Lastly, we introduce the following structure tensor to plot the preferred fiber orientation in our model

$$H_{\text{col}}=\underset{-\pi /2}{\overset{\pi /2}{\int }}\rho \left(\varphi \right)e_0\left(\varphi \right)\otimes e_0\left(\varphi \right)\text{d}\varphi \text{.}$$ (15)

The mesh-free method effectively incorporated the meridional and circumferential fiber regions into the model. Figure 7D shows the 1^st principal direction of the structure tensor (8) representing the preferred fiber orientation across the scleral portions of the model. The color of the plotted directions represents the degree of anisotropy.

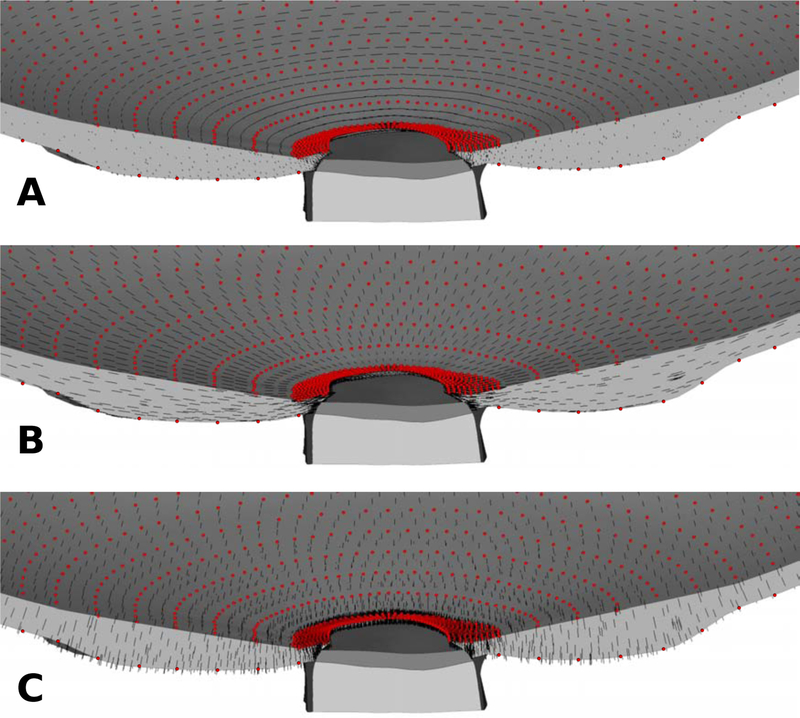
Note, that the material definition using our mesh-free approach is independent of the definition of the finite element mesh. The same control points can be used for different mesh densities. This makes the method very convenient when studying the effect of mesh density on the model results, or optimizing mesh densities in areas of large stress/strain gradients and/or material or geometric discontinuities. Figure 9 shows the approximated region parameter r for three different mesh densities but using the same control points.

Figure 9:

Contour plot of the region parameter r for models with a coarse (A), medium (B), and fine mesh density (C) in the ONH and peripapillary sclera. The same control points as illustrated in Figure 7 were used for all three models to approximate the region parameter.

3.4. Investigating the effect of the meridional fiber region of the peripapillary sclera

Lastly, we present one example, where we investigate the effect of the meridional fiber region of the peripapillary sclera using the proposed eye-specific model. We compare the maximum principal strain in the lamina cribrosa between two models. Model I represents the above derived eye-specific model including the complex collagen architecture of the peripapillary sclera and the eye-specific, heterogeneous, anisotropic micro-structure of the lamina cribrosa. Model II is identical to model I except that the meridional fiber region (r = 0) of the peripapillary sclera was replaced by isotropically distributed fibers (r = 0.5). Table 1 summarizes the material parameters that were used for the simulations. The constitutive model of the sclera was also used to model the pia assuming an isotropic distribution of collagen fibers (r = 0.5) in the plane of the pia and otherwise identical material parameters. While the scleral material parameters were also applied to the lamina cribrosa model, its constitutive response was more compliant compared to the sclera due to the scaling of the strain energy function with the local connective tissue volume fraction n_LC (7). The isotropic Neo-Hookean model W_iso was used to model the retina, and pre- and -retro laminar neural tissues. The geometry of the model was obtained from a 71 year old donor eye, which was fixed at 10 mmHg of intraocular pressure (IOP). We used our prestressing method [52] to account for the pre-existing stresses and strains at the (loaded) reference configuration at which the geometry was obtained. After prestressing at 10 mmHg, IOP was elevated to 45 mmHg.

Table 1:

Material parameters used for the eye-specific model. The scleral properties were estimated based on the age (71 years) and ethnicity (European decent) of the donor [44]. The bulk modulus was set to κ = 100μ for all tissues.

Tissue	Parameter	Value	Description
Sclera, lamina cribrosa, pia
	μ	0.282 MPa	shear modulus
	Efib	38.950 MPa	elastic modulus of collagen fibers
	θ0	5.515°	crimp angle of collagen fibers
	R0/r0	5.3	crimp parameter
Retina, pre- and retro-laminar tissues
	μ	0.01 MPa	shear modulus

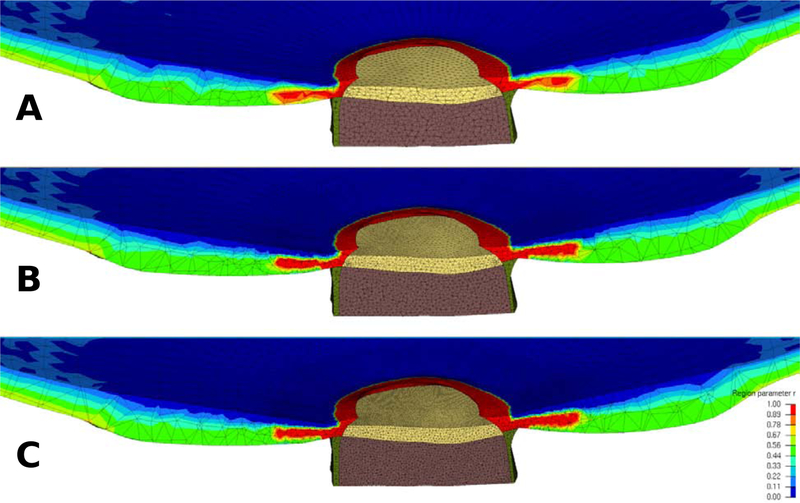
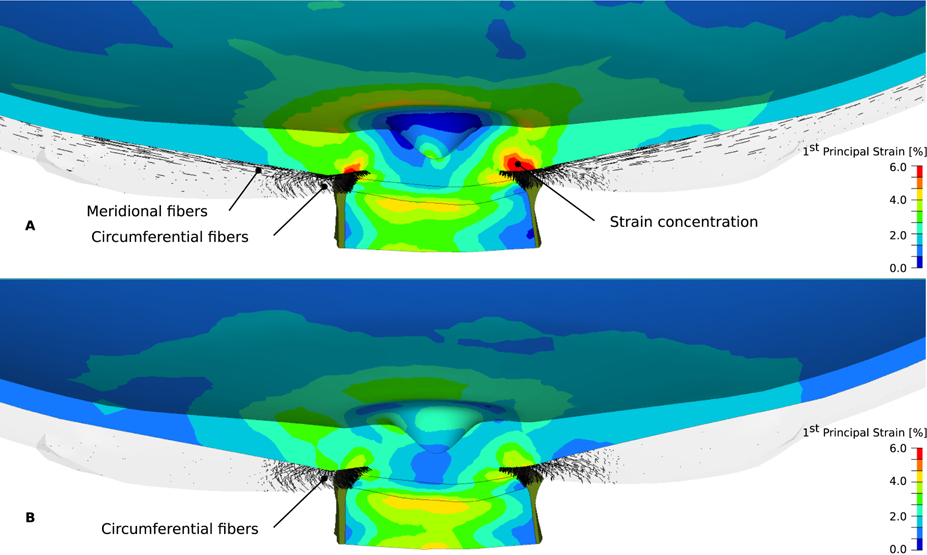
Figure 10 shows the maximum principal strain distribution in the lamina cribrosa, pre- and retro-laminar neural tissues, and retina for both models at 45 mmHg IOP. In contrast to model II, model I shows a strain concentration in the retina anterior to the circumferential ring region of the peripapillary sclera. This examples illustrates the important role of the peripapillary collagen architecture on ONH biomechanics. Disregarding the meridional collagen fiber region in the peripapillary sclera may lead to underestimations of the local strains in the retina.

Figure 10:

The maximum principal strain (contour plot) in the retina, pre- and retro lamina, and lamina cribrosa for model I (A) and II (B) subjected to 45 mmHg IOP. The predominant fiber orientations of the peripapillary sclera are shown as black lines.

4. Conclusions

A mesh-free approach was presented, which simplifies the incorporation of complex, anisotropic and heterogeneous material properties into FEM models. The method is based on the idea that material parameters and orientations can be obtained or estimated at particular points. We used an eye-specific model of a human ONH and posterior pole to illustrate the method. The proposed method effectively incorporated direct measurements of the lamina cribrosa micro-structure into the model by applying the mesh-free approach to a fabric tensor. The method was, in particular, useful to approximate material directions, which could be estimated at convenient locations (scleral surfaces) and approximated throughout the model using the mesh-free approach. This effective approximation of material directions is a critical advantage when modeling eye-specific geometries, where commonly used analytical coordinate systems (e.g. a spherical coordinate system) are inconsistent with the model geometry. Using a coordinate system that is inconsistent with the model geometry may lead to a non-physiological approximation of the fiber architecture, where fibers could transverse out of the surface of the sclera. Our method allowed for a smooth transition of martial directions that were defined at the scleral surfaces ensuring that the fiber directions were tangential at the anterior and exterior scleral surfaces. Furthermore, we were able to use our method to easily incorporate the complex collagen architecture of the peripapillary sclera that was recently reported by Gogola et al. [25].

A major advantage of our approach is that the material definition is independent of the mesh definition (i.e. the control points can be defined independent of the mesh). In contrast to previous approaches, where material properties are defined for individual elements or element sets, the material definition using the mesh-free approach does not change if the mesh is altered (e.g when investigating the effect of mesh density). At the tissue-level, most biological tissues exhibit smooth transitions between heterogeneous material and micro-structural properties. The mesh-free approach allows for a smooth transition of the material properties across the FEM model and the degree of smoothing can be controlled by the dilation parameter. Existing methods used interpolation functions to model complex heterogeneous material parameters with smooth transitions across FE models of the sclera or mitral valves [43, 61]. In contrast to interpolation-based approaches, the mesh-free approach does not require the definition of a connectivity between control points making adjustments of an existing approximation a trivial task that is independent of the complexity of the approximated parameter. Control points can be simply moved, added or deleted without the need to establish a new connectivity between them making the method easily adoptable to even the most complex material heterogeneity. The resolution of approximated material heterogeneity can be increased by placing more control points at locations with insufficient resolution.

Mesh-free methods can be directly used to solve a boundary value problem but are typically associated with higher computational cost compared to mesh-based methods like FEM. We propose to use a mesh-free approach to solely approximate the material definition of the model and solve the boundary value problem using FEM. In this sense, we combine the benefits of both approaches into one simulation strategy.

We have used an eye-specific model to investigate the role of the recently reported meridional fiber region at the anterior surface of the peripapillary sclera [25]. Our results suggest that disregarding the meridional fiber region may lead to underestimations of the local retinal strains. Further studies are needed to fully explore the role of the meridional fiber region on ONH biomechanics.

The application of the proposed methods is not limited to the effective approximation of heterogeneous material parameters alone, but could be extended to benefit computationally intensive multi-scale simulations [42, 62–66]. In two-scale FE simulations, representative FE models of the micro-structure are typically solved at the Gauss points of the macro-scale model making these simulations computationally expensive. Instead of solving the micro-scale problem at every Gauss point of the macro-mesh, the micro-scale problem could be evaluated at distinct control points and the mesh-free approach could be used to approximate the homogenized micro-scale solutions across the macro-scale model. This approach has the potential to significantly decrease the computational cost of multi-scale simulations, but consistent scale transitions still need to be defined.

In summary, we have proposed a strategy to effectively incorporate complex anisotropic and heterogeneous material properties that are either estimated at convenient locations or directly obtained from the tissue micro-structure into eye-specific finite element models. The approach should simplify future studies to investigate ONH remodeling in eye-specific models and to elucidate the role of biomechanical factors in glaucoma. The proposed method may also be useful to study the biomechanical response of other biological tissues with similar challenging material properties.

Highlights.

• Combining advantages of mesh-free and mesh-based computational methods

• Effective approximation of complex anisotropic and heterogeneous material properties

• Eye-specific finite element modeling of the human eye