Preparing sparse solvers for exascale computing

Abstract

Sparse solvers provide essential functionality for a wide variety of scientific applications. Highly parallel sparse solvers are essential for continuing advances in high-fidelity, multi-physics and multi-scale simulations, especially as we target exascale platforms. This paper describes the challenges, strategies and progress of the US Department of Energy Exascale Computing project towards providing sparse solvers for exascale computing platforms. We address the demands of systems with thousands of high-performance node devices where exposing concurrency, hiding latency and creating alternative algorithms become essential. The efforts described here are works in progress, highlighting current success and upcoming challenges.

This article is part of a discussion meeting issue ‘Numerical algorithms for high-performance computational science’.

1. Introduction

Sparse solver libraries represent some of the most successful efforts to provide reusable, high-performance software capabilities to scientific applications. These libraries provide efficient implementations of widely used solver algorithms on a variety of architectures and, at the same time, expose adaptable interfaces that enable integration into multiple application codes.

The solution of large, sparse linear systems is fundamental to many areas of computational science and engineering, and other technical fields. Sparse problems are typically formulated as the equation Ax = b, where A is a large matrix, usually non-singular and square, whose terms are known and mostly zero, b is a vector with known values, and x is a vector whose values the solver must determine in order to satisfy the equation, up to a certain tolerance. Sometimes, A may not be explicitly constructed, but only defined as function that computes the values of a vector z given a vector y: z = Ay. Rapid solution of these problems on parallel computers represents a core enabling capability for multi-physics, multi-scale and high-fidelity simulations. From the solution of a single nonlinear simulation problem to the optimal solution of a simulation problem with quantified uncertainty, the performance of sparse linear solvers often determines the size, fidelity and quality of the computational results.

Within the United States (US) Department of Energy (DOE) Exascale Computing Project (ECP), we are placing particular emphasis on adaptation of our software capabilities, including sparse solvers, to highly concurrent node architectures such as GPUs. Owing to practical limitations on processor clock speeds, increased concurrency is the primary path to realizing improved computational performance. GPUs and similar devices are viable platforms because they can execute scientific computations fairly well and have markets in other areas such as visualization and data sciences to help amortize development costs.

Regardless of the specific device, all paths to building a computer capable of an Exaflop (a billion-billion floating-point operations per second) require very high on-node concurrency, as represented by today’s GPU platforms such as Summit at Oak Ridge National Laboratory [1].

(a). Exascale architectures and challenges

The United States exascale computing systems are expected to be available in the early 2020s. These systems will have thousands of nodes where the node architectures are designed to deliver very high computational rates. The pre-exascale systems Summit [1] and Sierra [2] provide a reasonable approximation to exascale systems in that successful use of these systems requires very large amounts of on-node concurrency in order to achieve scalable performance. Other node architectures, for example many-core processors with vectorization capabilities, may be significantly different in design details but still require the same qualitative level of concurrency. Exposing concurrency in algorithms and implementation represents one of the most important challenges facing all scientific software developers, including sparse solvers.

Another important design trend is the availability of memory systems that support increasing concurrency to assist the programmer in reading and writing data. These memory systems promise to provide significant bandwidth improvements, but do not substantially improve latency. In other words, we can access large amounts of data from memory with lower average access times but the amount of time required to receive the first data element has not improved. Hiding memory latency by better algorithmic design and implementation is another important challenge faced by scientific software developers.

Other challenges include exploring and enabling better coordination between inter-node and intra-node computation and communication tasks. The message passing interface (MPI) [3] is the preferred interface for most parallel scientific applications. Many options exist for encoding on-node parallel computations. An evolving standard is OpenMP, which has targeted efficient execution on accelerated devices since v. 4.5. OpenMP is anticipated to be one of the dominant on-node parallel programming environments for ECP, either by programmers using it explicitly or through an abstraction layer such as RAJA [4] or Kokkos [5]. Regardless of the specific on-node programming environment, interleaving MPI communications with on-node parallel execution will be challenging.

One last challenge, which seems to be a lesser concern at this time, is frequent system failure due to software or hardware faults. Early in the ECP, efforts in application-level resilience were considered as a way to address system failure. However, pre-exascale systems have been extremely reliable. Furthermore, the availability of non-volatile memory components woven into the network fabric of high-end machines has dramatically improved the effective latency of classic checkpoint-restart as the primary means for application codes to recover from system failure. At this point, we do not foresee that novel resilience strategies are needed.

(b). Key sparse solver design and implementation challenges

Addressing the above exascale challenges, sparse solver developers must provide algorithms and implementations that expose very high levels of concurrency, especially for on-node execution. In addition, memory references for matrices and vectors, both sparse and dense must be tuned for concurrency, and safe concurrent writes. Classic algorithms for recursive sparse computations, such as incomplete factorizations and corresponding solve operations, must be revised for better concurrency or replaced by other approaches.

Another challenge that has emerged gradually with increasing concurrency requirements is the problem set-up. Traditional use of sparse solvers requires assembling matrix and vector objects that define the linear system. In most instances, the sparse matrix is assembled by providing a portion of matrix coefficients at a time, as would happen when constructing a global stiffness matrix from local element stiffness matrices in a finite-element formulation. While there is ample available parallelism in the set-up phase to enable highly concurrent execution, expressing it in a way that is convenient for library users has been historically challenging. The convenience of constructing a single local matrix is attractive. Transforming the construction process to perform well on GPU and vectorizing architectures is hard. A related issue for sparse solvers, especially those for unstructured patterns, is data-dependent communication patterns. On exascale systems, we anticipate needing better latency hiding and more interleaving of communication and computation for distributed matrix and vector operations. We expect asymptotic performance of sparse computations to remain about the same, achieving only small percentages of peak rates for most sparse kernels. Therefore, even if we are successful in improving latency hiding, we will always have bandwidth limitations on the performance of our computations.

One way to address assembly and sparse data structure challenges is the ever-attractive approach of avoiding explicit formation of sparse matrix representations and instead use matrix-free formulations where only the action of the linear operator is provided. Matrix-free techniques can bypass many of the scaling challenges traditional approaches face.

(c). Libraries overview

In this paper, we present the efforts of five solver development teams to provide capabilities needed by the high-performance computing (HPC) community, especially the ECP. Two of the teams, PETSc (led from Argonne National Laboratory) and Trilinos (led from Sandia National Laboratories), provide specific solver components and infrastructure for coordinating component use. Ginkgo (led from the University of Tennessee), hypre (led from Lawrence Livermore National Laboratory) and SuperLU/STRUMPACK (led from Lawrence Berkeley National Laboratory) provide key solver capabilities that can be used independently or as part of the PETSc and Trilinos infrastructures.

The hypre package (§3) provides distributed memory parallel sparse iterative solvers and is particularly well known for its multigrid preconditioners. PETSc (§4) and Trilinos (§6) provide comprehensive solver capabilities widely used in the community. SuperLU (§5) provides sparse parallel direct solvers. All of these projects have been available to the HPC community for many years and have evolved over time to support a variety of computing platforms. Ginkgo (§2), STRUMPACK (also in §5) and KokkosKernels (also in §6) are newer efforts that have emerged to address the particular challenges that modern node architectures present. Their details are discussed below.

In the remainder of this paper, we discuss how each of our library development efforts is addressing the challenges we have described above. All of the solvers discussed in this paper are freely available as open-source software.

2. Ginkgo

Ginkgo [6] is a relatively new software effort that provides solvers, preconditioners and central basic building blocks for the iterative solution of sparse linear systems. Ginkgo benefits significantly from leveraging the expertise and experience of other math library projects. Notable lessons learned from other libraries include software design in terms of expressing all functionality as linear operators, which enables leveraging class inheritance of modern C++, and software interoperability in terms of adopting community policies from the community solver interoperability project, xSDK [7]. A strong asset of Ginkgo is its focus on software sustainability, correctness, reproducibility and productivity. Ginkgo is designed as an open-source C++ linear algebra library under BSD 3-clause license following the SOLID software design principles [8]: single responsibility; open/closed; Liskov substitution; interface segregation; and the dependency principle.

With the goal of maximizing compatibility and extensibility, Ginkgo separates algorithms from architecture-specific kernel implementations. Using an architecture-specific ‘Executor’ allows adding, removing or modifying backends according to future changes in hardware architectures and parallelization strategies. Currently, Ginkgo is designed for node parallelism, featuring backends for NVIDIA GPUs and OpenMP-supporting platforms. Additionally, it features a sequential reference executor that is used in unit tests to ensure the correctness of hardware-specific parallel kernels, via the Google Test [9] framework.

A central Git repository, requiring two reviews on every merge, is automatically mirrored into a private repository to allow for the development of novel algorithms and implementations without exposing new ideas to the community prior to academic publication. Public and private feature developments are automated with the help of a continuous integration (CI) framework that checks the compilation process for a large number of hardware architectures and compiler/library environments (cross-platform portability), the successful completion of the unit tests, and code quality in terms of design, memory leaks, etc. [10].

In terms of technical functionality, Ginkgo focuses on novel algorithms and component design strategies that enable efficient utilization of the large degree of parallelism provided by many-core and accelerator processors under the challenges of increasing arithmetic performance via concurrency and growing memory system complexity [11].

As with a distributed computing system, growing parallelism makes synchronizing communication increasingly expensive. As sparse iterative problems typically prohibit the use of dense matrix–matrix mathematical routines with high computational intensity, the use of algorithms like Gaussian elimination with strong sparse data dependencies often leverage only a small fraction of the available compute power. However, algorithms that relax or remove conventional synchronization-enforcing paradigms can achieve higher performance on many-core and accelerator architectures. An example is incomplete factorization (ILU) preconditioners where the synchronizations of a truncated Gaussian elimination process allows for only limited parallelization via level scheduling, notoriously resulting in low performance. Based on the observation that incomplete factorizations as used for preconditioning are typically only a rough approximation of the exact factorization and the fact that for a given sparsity pattern S of the ILU, the incomplete factorization is exact in the locations of S [12], it is possible to formulate the search for values in the incomplete factors as an iterative process [13]. In an element-wise parallel fixed-point iteration of the form (L, U) = F(A, L, U), the unknowns l_ij in L and u_ij in U can be approximated via

$$\begin{array}{rl}& l_{ij}=\frac{1}{u_{jj}}(a_{ij}-\sum _{k=1}^{j-1}{l}_{ik}{u}_{kj}),i>j,\end{array}$$ 2.1

$$\begin{array}{rl}& u_{ij}=a_{ij}-\sum _{k=1}^{i-1}{l}_{ik}{u}_{kj},i\le j\end{array}$$ 2.2

$$\begin{array}{rl}\text{and}& l_{ij}=1,i=j.\end{array}$$ 2.3

Aside from the theoretical proof that the fixed-point iteration updating all values in the incomplete factors converges (for a suitable initial guess) in the asymptotic sense [13], experiments using this ParILU algorithm in highly parallel environments reveal that a few sweeps are often sufficient to generate preconditioners competitive in terms of quality to those generated via the (sequential) truncated Gaussian elimination process [13–15]. As a result, the ParILU algorithm has been established as an attractive alternative to the traditionally employed Gaussian elimination process for generating level-ILU preconditioners on many-core and accelerator architectures, typically outperforming the classical approach by a significant margin [14].

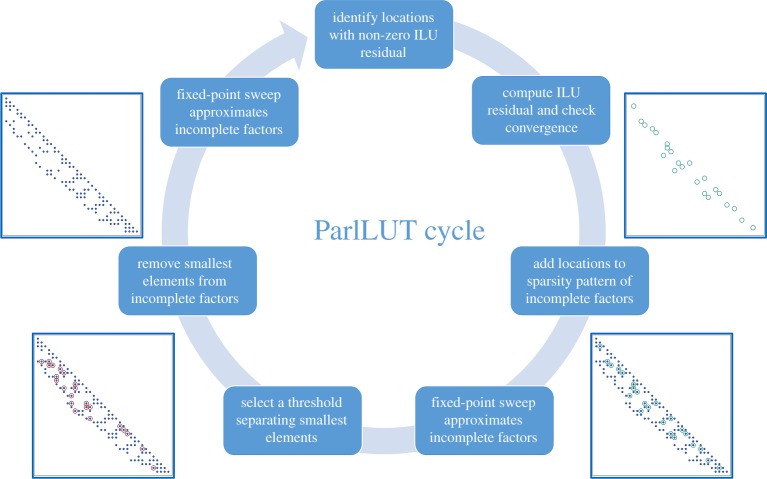
To enhance the quality of incomplete factorization preconditioners, it is possible to interleave the fixed point iterations approximating the values in the incomplete factors with a strategy that dynamically adapts the sparsity pattern to the problem characteristics [16] (figure 1). In an iterative process based on highly parallel building blocks, this strategy not only allows us, for the first time, to generate threshold-based ILU factorizations on parallel shared-memory architectures, but also enables us to efficiently leverage streaming-based architectures like GPUs [17].

Figure 1.

Iterative ParILUT algorithm for computing incomplete factorizations based on thresholding via a parallel process. (Online version in colour.)

Based on our understanding of future node architectures and their projected computational and bandwidth rates, we estimate that the asymptotic performance of unstructured sparse matrix computations, assuming eight bytes (double precision) for the non-zero entries of the matrix and vectors, and four bytes for the integer indexing values, will continue to be 1–2% of peak performance. Latency in real-time will stay roughly the same, so that internode communication latencies, measured in microseconds, will require 2–10 million operations in order to cover the latency cost of communicating the first bytes of data. In other words, both latency and bandwidth will continue to limit the performance of sparse computations.

Therefore, because sparse algorithms are memory-bound on virtually all modern architectures, a variety of strategies have been explored to mitigate pressure on memory bandwidth, ranging from sparse data formats over hierarchical structures to compression techniques and mixed precision algorithms. Ginkgo addresses the memory bottleneck by moving towards a modular precision ecosystem that decouples memory precision from the arithmetic precision format, preserving full precision only for the arithmetic operations and dynamically adapting memory precision to algorithmic requirements. For example, with block-Jacobi preconditioners typically only providing a few digits of accuracy, it is possible to reduce the precision format in which the distinct inverted diagonal blocks are stored without impacting the preconditioner accuracy [18]. Maintaining full precision in all arithmetic operations by converting between the formats in the processor’s registers, the preconditioner remains a constant operator–thereby removing the need for a flexible solver variant [18]. With the format being optimized for each Jacobi block individually (carefully protecting against under/overflow and preserving regularity), memory access reduction directly translates into runtime and energy savings [18].

3. hypre

The hypre software library provides high-performance preconditioners and solvers for the solution of large sparse linear systems on massively parallel computers. One of its attractive features is the provision of conceptual linear system interfaces, which include a structured, semi-structured and traditional linear algebra-based interface. The (semi-)structured interfaces are an alternative to the standard matrix-based interface that describes rows, columns and coefficients of a matrix. Here, instead, matrices are described primarily in terms of stencils and logically structured grids. These interfaces give application users a more natural means for describing their linear systems and provide access to methods such as structured multigrid solvers, which can take advantage of the additional information beyond just the matrix. Since current architecture trends are favouring regular compute patterns to achieve high performance, the ability to express structure has become much more important.

The hypre library historically uses an MPI/OpenMP model and was not GPU-enabled. However, the team has recently begun to investigate various ways of enabling hypre to take advantage of GPUs. The library provides both structured and unstructured algebraic multigrid solvers, which use completely different data structures, as well as Krylov solvers.

The data structures in the structured interface are based on structured grids and stencils. Loops within the structured solvers that use these data structures are generally abstracted with macros called BoxLoops. These macros were completely restructured to allow the incorporation of CUDA, OpenMP 4.X, RAJA [4] and Kokkos (§6) into the isolated BoxLoops. Since hypre is written in C, but RAJA and Kokkos are written in C++11, it was necessary to enable hypre to be compiled with the C++ compiler, particularly nvcc, requiring many changes to the library. With these changes it is now possible to run the structured solvers completely on the GPU using CUDA, OpenMP 4.X, RAJA or Kokkos.

On the unstructured side, focus has been on the algebraic multigrid solver BoomerAMG. BoomerAMG consists of a set-up and a solve phase. The solve phase consists mainly of matrix-vector multiplications and the smoother. While the default smoother is based on Gauss-Seidel requiring triangular solves, one can also use matvec-based smoothers, such as Jacobi or polynomial smoothers. CUDA implementations of the basic kernels were added. Since the matrix data structures are based on the compressed sparse row (CSR) storage format, it was possible to use the CuSPARSE matrix-vector multiplication routine. When suitable smoothers are used, the solve phase can be performed on the GPU. The current version requires unified memory; however, this requirement will be removed in the future. The set-up phase, which consists of coarsening algorithms and the generation of interpolation and coarse grid operators, is highly complex and not well suited for efficient implementation on the GPU. Therefore, it currently remains on the CPU; however, efforts are underway to implement some of the more suitable components as well as to design new algorithms that are suitable for GPU performance while still delivering good multigrid convergence.

There are also several special multigrid solvers, such as the auxiliary-space Maxwell solver (AMS) for H(curl) problems and the auxiliary-space divergence solver (ADS) for H(div) problems. Since they are built on top of BoomerAMG, any GPU advances in BoomerAMG will carry over to AMS and ADS.

Because of the growing disparity between communication and computation costs on computer architectures, it is important to develop algorithms that attempt to minimize communication-to-computation ratios. This is especially difficult to do for methods like multigrid that have optimal O(N) computational complexity. Eliminating communication often has the side effect of degrading convergence and hence may not speed up overall solve times (or reduce power usage). However, the hypre team has already had some success with a number of approaches, including sparse interpolation techniques [19], highly concurrent additive multigrid approaches that converge with multiplicative multigrid rates [20] and non-Galerkin methods for reducing coupling and communication on coarse grids [21–23]. These breakthroughs have led to speed-ups of more than 10× for three-dimensional variable-coefficient diffusion problems (fig. 9.2 in [19]), up to 2.5× for various three-dimensional unstructured Laplace problems (Section 5 in [20]), and between 15% and 400% for constant-coefficient three-dimensional Laplace problems (Section 5.3 in [22]).

Another way to minimize communication-to-computation ratios is to increase local computation on each processor, the idea being that this increase in computation will improve convergence. However, it is a basic multigrid principle that local computations have little effect on global convergence. To overcome this problem, the team developed the AMG domain decomposition algorithm (AMG-DD) [24]. The algorithm is based on a number of earlier methods [25–29] that share the idea to assign a discretization of the global problem to each processor, but on a mesh with fine resolution in one region of the domain and successively coarser resolution away from that region. The AMG-DD algorithm constructs the graded meshes and corresponding composite operators algebraically from an existing multigrid hierarchy. These graded meshes keep the computational cost and memory use per processor down to a reasonable size, and provide a way of doing extra computations locally on a processor that are not strictly local with respect to the grid. As a result, the potential to accelerate convergence is greatly increased. A crucial contribution of the research in [24] is that both the set-up phase and solve phase of the parallel AMG-DD solver have the same log (N) communication overhead as the underlying multigrid algorithm on which it is based. The addition of AMG-DD to hypre is underway and initial experiments show promise. The team is also seeking to improve the convergence of the algorithm when solving only to discretization accuracy, motivated by a related non-algebraic algorithm in [30] that was shown to be significantly faster than multigrid in parallel.

Computations that exhibit structure are ideal for GPU-based architectures. Although the hypre library supports a semi-structured system interface and corresponding underlying data structure, efforts to develop a multigrid solver that can exploit the local structure have only recently begun. Semi-structured matrices in hypre are defined as the sum of two matrices, A = A_s + A_u, where A_s is structured and A_u is unstructured. If interpolation is similarly defined as P = P_s + P_u, it is easy to see that a semi-structured multigrid method would be composed of semi-structured matrix-vector operations, which would, in turn, build on structured and unstructured matrix-vector operations. One complication is that P_s is a rectangular (non-square) matrix, which is not a straightforward concept to implement (see [31] for more details). The hypre team has recently added a rectangular matrix to the structured component of the library (this is not yet released) and has begun to implement a semi-structured multigrid method that uses it.

The use of high-order discretization methods is also gaining popularity due to their demonstrated performance potential on GPU-based architectures. This performance is again realized by exploiting structure in the system matrix, but in this case the structure is present in the finite-element stiffness matrices instead of the grid. For these problems, matrix-free operations are required, because it is not practical to fully assemble the matrix. As a result, existing algebraic multigrid methods are not suitable. To address this, the hypre team is developing a variety of matrix-free multigrid approaches.

4. PETSc

The portable extensible toolbox for scientific computing (PETSc) provides a large collection of composable, hierarchical and nested solvers [32,33]. As such, PETSc addresses two needs: the first need consists of more complex physical models, the coupling of diverse models, and work towards predictive science needed by scientific applications. The second need is to run efficiently on high-performance computing systems, where algorithms and implementations need to map well onto many-core node architectures, hybrid combinations of accelerators and conventional processors. This section provides a sketch of how PETSc addresses these two needs.

PETSc currently handles GPUs through dedicated subclasses of existing CPU-based classes [34]. For example, the main compressed sparse row matrix class MATAIJ is CPU-based. The subclasses with GPU support are MATAIJCUSPARSE (for CUDA) and MATAIJVIENNACL (for CUDA, OpenCL, or OpenMP). These subclasses internally manage the data on the GPU. Operations for which GPU-optimized routines are available—provided by the cuSPARSE or ViennaCL libraries—are executed on the GPU, and routines for which no GPU-optimized routines are available will be executed via a fallback implementation on the CPU. (Libraries such as Intel MKL that provide vendor-optimized CPU kernels are leveraged in a similar fashion.) Such a fallback mechanism has been shown to be superior over an approach where only GPU-accelerated functionality is provided. First, one can always access the full set of operations and incrementally remove bottlenecks. Second, there are operations for which no efficient GPU implementation is possible; however, an inefficient, yet functional fallback implementation may still suffice for a particular use case.

Currently in PETSc only a single (virtual) GPU can be associated with an MPI process and needed communication between GPUs takes place through the associated MPI process and its CPU memory. A challenge with this model is optimizing direct GPU to GPU memory transfers (within a single compute node where direct communication paths exist between the GPUs). MPI extensions that allow MPI message passing directly between different GPU’s memory (thus preserving the clean separation of concerns between MPI code and the GPU details) are one possible path, for which it is not yet clear whether broad support will be available. The alternative is to introduce another level of complexity of the programming model that handles in-node inter-GPU communication.

(a). The many-core composability challenge

As a platform for algorithmic experimentation, PETSc offers interfaces to many other solver libraries, for example to the multigrid package hypre. Library users can thus quickly combine and compare specialized solvers from different packages through a unified and mature PETSc interface that facilitates runtime composability. As new libraries (for example, Ginkgo) addressing the low-level needs of many-core architectures become available, PETSc can quickly adopt these and leverage the new capabilities for more efficient high-level solvers.

The third-party packages interfaced by PETSc provide different approaches for many-core architectures: CPU-centric packages may use—among others—OpenMP, pthreads, or C++11 threads for threading. GPU-accelerated libraries typically use CUDA, but may use OpenCL, OpenACC, OpenMP or other approaches instead. This lack of a unified approach poses a considerable challenge on the software stack in general. In order to combine functionality from, for example, a CUDA-based library with an OpenCL-based library, memory handles need to be converted between CUDA and OpenCL. Compiler-based approaches such as OpenMP or unified memory (CUDA) complicate the issue further, since the actual placement of the data is now implicit within a translation unit rather than explicitly encoded in the memory buffer.

PETSc addresses the challenge of different many-core approaches used by third-party libraries through internal conversion routines, cf. figure 2. Where possible, any data movement (for example between host and GPU) is avoided; otherwise, an explicit (and potentially costly) conversion is carried out. This enables users to experiment with the full range of solver building blocks and use a mixture of different low-level approaches. If the conversion cost turns out to be significant for an otherwise robust and algorithmically efficient solver, the conversion overhead can still be addressed by the user in a second step.

Figure 2.

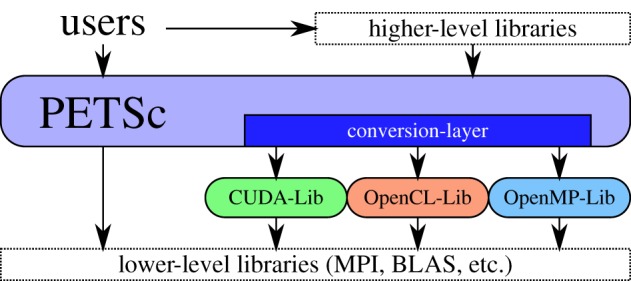
PETSc provides a unified interface for seamless composition of different GPU-accelerated libraries. (Online version in colour.)

The composability challenge not only affects the interoperability of different third-party libraries used by PETSc, but also user callback routines. For example, a user may decide to write matrix-free implementation of a sparse matrix-vector product with a particular programming model. Callback interfaces in PETSc do not restrict the user in the use of a particular programming model; thus, users can directly retrieve and operate with, for example, CUDA-based data. The user’s choice may have an impact on performance due to internally required conversion: In such case, PETSc’s integrated performance logging will allow the user to quickly identify this bottleneck.

(b). Hybrid execution on hybrid hardware

PETSc already offers the ability to use different programming approaches concurrently using ViennaCL [35]. In particular, a user may switch between CUDA, OpenCL, OpenMP or conventional single-threaded execution individually on each MPI rank. In principle, such an approach enables fully saturating all the available execution units on a hybrid architecture, thus maximizing performance by splitting up the workload relative to the respective execution speed.

For more complex operations, a suitable workload decomposition becomes challenging. A good example is sparse matrix–matrix products, which are encountered during the set-up phase of algebraic multigrid methods: the many indirect memory accesses favour CPUs with large caches, so most of the workload should be directed towards CPUs. The multigrid solver cycle phase, however, consists of sparse matrix–vector products that can be efficiently executed on GPUs, so the workload should be directed to GPUs. An on-the-fly redistribution of the workload is typically too expensive, so the user is left with the choice of either a non-optimal solver set-up phase (when executed on the GPU) or a non-optimal solver cycle phase (when executed on the CPU). The answer is more complex code that allows for the different phases to be performed on different hardware and manages the data transfers.

Similarly, the best architecture for a particular operation also depends on the size of the workload. For example, it has been observed that multigrid methods can benefit from GPU acceleration on the finest levels, but CPUs are more efficient on the coarser levels [36]. Current activities in PETSc focus on providing maximum flexibility for the user to fine-tune the execution units used for the different stages of a full solver hierarchy.

5. SuperLU/STRUMPACK

Sparse factorizations and the accompanying solution algorithms (e.g. triangular solution associated with the LU factorization) are often the most robust algorithmic choices for linear systems from multi-physics and multi-scale simulations. They can be used as direct solvers, as coarse-grid solvers in multigrid (e.g. hypre), or as preconditioners for iterative solvers. The two solver libraries we have been developing encompass the two widely used sparse LU algorithm variants: supernodal (SuperLU library [37]) and multifrontal (STRUMPACK library [38]). Both solvers are purely algebraic, applicable to a wide variety of application domains.

SuperLU has over 20 years of development history, evolving from multicore, distributed memory, to recent many-core GPU clusters. SuperLU is used by numerous applications in DOE, industry and academia (38 000+ downloads in FY15). Despite their wide usability, a fundamental scaling impediment of traditional factorization algorithms is that the required flops and memory are more than linear in problem size, hence non-optimal. By contrast, STRUMPACK is a relatively new software effort, motivated by the need for optimal factorization-based solvers and preconditioners. It was first released in 2015 and currently has a number of DOE users. The baseline algorithm in STRUMPACK is a multifrontal sparse LU solver. On top of this, we introduce data-sparseness in the dense blocks (frontal matrices) in the sparse factors using several hierarchical matrix low-rank compression formats, including hierarchically semi-separable (HSS) [39], hierarchically off-diagonal low rank (HODLR) [40] and a non-hierarchical format called block low rank (BLR) [41]. The resulting factorizations have nearly optimal complexity in flops and memory. STRUMPACK approaches are based on a large body of literature on hierarchical matrix algebra. The most general rank structured matrix format is the class of $\mathcal{H}$ matrices, where the matrix is recursively divided in 2 × 2 blocks and each block can be dense, low rank or $\mathcal{H}$. In the ${\mathcal{H}}^2$ format, low-rank factors are nested, with the low-rank bases from one level given as a linear combination of those on a finer level. These hierarchical matrix formats are shown to be usable as direct solvers for integral equations and PDEs with smooth kernels, or as low-accuracy direct solvers for broader problems, or, more generally, as powerful preconditioners.

In addition to reducing arithmetic complexity, we are redesigning parallel algorithms to reduce communication complexity, in particular to reduce the number of messages, hence to mitigate latency cost. For SuperLU, we developed a novel communication-avoiding factorization and triangular solve method where MPI processes are arranged as a three-dimensional process grid, with selective data replication along the third dimension of the process grid, trading off small amount of increased memory for much reduced per-process communication. Theoretically, we proved that the communication complexity, in both message count and volume, is asymptotically lower than the widely used two-dimensional process configuration. In practice, we observed runtime speed-ups up to 27× on 32 k cores for sparse LU factorization [42] (Section V.F., p. 917), and up to 7× on 12 k cores for sparse triangular solve [43] (Section 5.3, p. 135).

The solve phase is more challenging to scale up than factorization because of lower arithmetic intensity and higher task dependency. Recently, we introduced two main techniques to reduce amount of synchronization. The first technique uses an asynchronous binary-tree-based communication scheme implemented via non-blocking MPI functions, leading to 4× improvement on 4000+ cores [44]. The second technique leverages the one-sided MPI communication functions to implement a synchronization-free task queue, allowing more overlap of communication and computation, leading to additional 2× improvement on 4000+ cores [45].

For the factorization function in SuperLU, we have done extensive work to improve on-node efficiency for many-core and accelerator machines: aggregating small GEMMs into larger GEMM, use OpenMP ‘task parallel’ to reduce load imbalance and ‘nested parallel’ to increase parallelism, and vectorizing Gather/Scatter operations. We designed an asynchronous, pipelined CPU-GPU algorithm to off-load part of Schur-complement update to GPU. For the GPU accelerated three-dimensional sparse factorization algorithm, we have obtained up to 3.5× runtime improvement on Titan’s 4096 GPU-nodes over the CPU-only code [[46], fig. 15(b)]. A recent port of this code to one-node Summit machine achieved 5× speed-up over the CPU-only code.

STRUMPACK provides a sparse direct solver and approximate factorization-based preconditioners. It uses the multifrontal formulation of sparse LU. The multifrontal version simplifies the communication pattern along the elimination tree, since Schur complement updates from supernodes are accumulated and only passed to the next supernode to be eliminated, instead of scattered throughout the sparse triangular factors. Although it results in a more synchronized execution, it leads to larger dense matrix operations, for which STRUMPACK can exploit the use of BLAS 3 and LAPACK routines and ScaLAPACK in distributed memory. After the triangular factorization is performed, linear systems can be solved very efficiently. STRUMPACK relies on BLAS, LAPACK, ScaLAPACK, Metis, and optionally ParMetis and PT-Scotch libraries.

The preconditioners available in STRUMPACK are also based on the multifrontal LU factorization algorithm. In the triangular factors, the fill occurs in large dense blocks, called fronts or frontal matrices, which correspond to supernodes or the separators from a nested dissection fill reducing ordering. STRUMPACK uses rank structured, also called data sparse, matrix approximation on these frontal matrices. STRUMPACK uses the HSS format, which is a subclass of ${\mathcal{H}}^2$, where all off-diagonal blocks are assumed to be of low rank, a property called weak admissibility. It is shown in the literature that for many PDE based problems, this is indeed the case. For low-rank compression, STRUMPACK heavily relies on random projection, which provides accurate results with very high probability, and with lower asymptotic cost than standard techniques, while also lending itself well to execution on current architectures such as GPUs. We have developed an efficient and robust blocked version of adaptive randomized low rank approximation for use in HSS matrix construction [47].

Exploiting both the typical sparsity as well as data sparsity leads to optimal-complexity solvers for specific model problems, such as elliptic partial differential equations in two spatial dimensions. However, for numerically more challenging systems, such as those arising from high-frequency Helmholtz problems, the numerical ranks in the hierarchical matrix approximations, or the pre-factors in the complexity analysis, become too large, as illustrated in a recent report [48]. As a remedy, we are incorporating other rank-structured matrix representations into the STRUMPACK sparse preconditioner. For instance, the Hierarchically Off-Diagonal Low Rank (HODLR) and BLR formats will lead to lower pre-factors and ranks, respectively. For very high-frequency problems like Maxwell and acoustic scattering, we are developing Butterfly-based matrix compression. The Butterfly format [49] is a multilevel low-rank scheme based on ideas from the FFT. These different new formats are all being incorporated into the sparse solver using randomized projection for the low-rank constructions.

These rank-structured matrix representations are also applicable to many dense linear systems, such as those arising from integral equations through the boundary element method, to kernel methods as used in machine learning, etc. Through the use of random projection, which only requires matrix times (multiple) vector multiplication, we are developing matrix-free or partially matrix-free solvers for these type of systems [50,51].

STRUMPACK uses hybrid MPI + OpenMP parallelism. The STRUMPACK solver and preconditioners exploit multiple levels of parallelism: concurrency from the sparse elimination tree, concurrency from the HSS hierarchy and from BLAS/(Sca)LAPACK routines. In distributed memory, independent sub-trees are mapped to distinct MPI sub-communicators, using ScaLAPACK for the linear algebra. Within a node, the code heavily relies on OpenMP task parallelism. Dynamic scheduling of fine-grained tasks can handle the irregular workloads in STRUMPACK that arise from different sparsity patterns and numerical rank distributions.

The multiple levels of parallelism in STRUMPACK make porting of the code to GPU architectures very challenging. Work has started on adding GPU support to STRUMPACK, initially relying on the SLATE (Software for Linear Algebra Targeting Exascale) framework as a ScaLAPACK replacement with GPU off-loading capabilities. A further design study is required to define an efficient strategy to fully exploit the computational power of GPUs. We expect to rely on batched BLAS operations, grouping many smaller matrix operations, to achieve high performance.

6. Trilinos and Kokkos Kernels

Trilinos [52] is a large collection of software packages for scientific computing. The Trilinos project is an effort to facilitate the design, development, integration, and support of mathematical software libraries. The main focus is on scalable solvers within an object-oriented framework to support complex multi-physics and multi-scale engineering applications on parallel computers. Over time, Trilinos has grown to include many other capabilities such as partitioning and load-balancing, discretizations, and algorithmic differentiation.

Trilinos was originally designed for ‘flat MPI’ but as node concurrency has grown in recent years with the widespread adoption of first multicore then many-core architectures (e.g., GPU), Trilinos has adopted a two-level parallel model. At the top level, objects (matrices, vectors) are distributed across MPI ranks. The distribution is given by a map, a first-order object in the Petra object model (as implemented in the Epetra [53] and Tpetra [54] packages).

One of the significant problems in designing solvers for exascale architectures is to plan for an architecture that is yet to be designed. The complexity of this problem increases as we consider that the new solvers have to work on multiple existing architectures. Our solution to this problem focuses on designing solvers based on abstractions that are representative of current architectural features and expected features in future architectures. With these abstractions in place, one can implement the solvers in a number of different ways to handle different architectures such as using a directive-based approach or library-based approach. Within Trilinos we rely on a library-based approach for portability and our abstractions are provided by the Kokkos ecosystem [5].

The core programming model in Kokkos allows users to choose memory layouts for data structures that are suitable for different architectures. It also allows users to express the parallelism in the code with data-parallel, task-parallel or hierarchical-parallel constructs. Kokkos Kernels is a library in the Kokkos ecosystem that provides optimized and portable implementations of performance-critical sparse/dense linear algebra and graph kernels. Solvers in Trilinos use these kernels for achieving portable performance. This library-based approach in Trilinos defines clear responsibilities where Kokkos has to maintain/modify its abstractions as the architectures evolve and Kokkos Kernels has to deliver high-performance kernels in different architectures. This insulates the solvers from architecture changes. The key kernels that currently exist in Kokkos Kernels include sparse matrix–vector multiplication, sparse matrix-matrix multiplication [55], preconditioners such as symmetric Gauss-Seidel. In terms of graph algorithms, Kokkos Kernels features include distance-1 colouring [56] to enable parallel assembly in finite element codes, distance-2 colouring to support aggregation in multigrid methods, triangle counting [57,58] to enable social network analysis. One of the key developments in the move towards exascale computing is the new requirement from applications for batched linear algebra and BLAS/LAPACK routines at different levels of hierarchical parallelism (e.g. a GEMM call that can use an entire accelerator, or a team of threads in the accelerator or a single thread). Kokkos Kernels provides a subset of the BLAS implementation that can be called at the device-level, team-level or in serial [59]. This has been successfully used to enable portable CFD simulations [60].

With the core programming model as MPI+X, and Kokkos ecosystem providing the flexibility to select different choices for the on-node programming (the ‘X’), Trilinos users will simply choose an appropriate execution space for the target architecture. This hybrid MPI+X parallel model is supported via the Tpetra linear algebra package and compatible solver packages. Tpetra replaces Epetra and has several advantages: (a) support for multi- and many-core architectures via Kokkos, (b) templated scalar types to allow easy switch (mixing) of precision and (c) 64-bit integers and pointers to support very large problem sizes. The solver stack has been rewritten using Kokkos from the ground up to support exascale architectures. This redesigned solver stack has been used effectively in several scientific simulations [60,61].

In Trilinos, there is a distinction between solvers and preconditioners. Solvers include direct sparse methods such as sparse LU/Cholesky in Amesos2, and iterative methods (mostly Krylov methods) in Belos [62]. Preconditioners include stationary methods and incomplete factorizations (Ifpack2 [63]), domain decomposition methods and (in)complete factorizations (ShyLU [64]), and algebraic multigrid (MueLu [65]). There is some overlap among these packages in terms of functionality. In particular, the preconditioners in Ifpack2 are mostly serial and/or MPI parallel, while ShyLU was designed to take advantage of on-node (shared memory) parallelism. The primary focus on exascale readiness has been on developing accelerator focused iterative solvers in Belos, multithreaded and GPU-ready multigrid methods in MueLu, Kokkos-based direct factorizations such as Basker [66] and Tacho [67] in ShyLU, GPU-ready domain decomposition methods in Ifpack2 and ShyLU.

A recent algorithmic focus supported by the ECP PEEKS and Clover projects, is communication-avoiding (CA) methods. The Belos package now supports single-reduce, pipelined, and s-step (CA) solvers. These are three different ways to reduce communication and synchronization, which is increasingly becoming an issue on extreme-scale systems. While Krylov methods have good convergence properties, they typically rely on global inner products (or orthogonalization), which can be expensive at large scale. Single-reduce methods reduce the number of global (all-) reduce calls to one per iteration, by combining two or more all-reduce operations into one. Pipelined methods overlap global communication, local communication, and computation. S-step methods only communicate every s steps, where is s is a small integer. In CA-GMRES, the orthogonalization step is replaced by more efficient block orthogonalization. The trade-off is that more memory is needed to ‘ghost’ data. A potential future improvement is adoption of the ‘matrix powers kernel’ to compute the Krylov basis {x, Ax, A² x, …}. This is fairly straightforward without a preconditioner, but very challenging if a preconditioner is embedded into the kernel (as the preconditioner itself requires communication). It appears most current preconditioners cannot be used in this setting, and special ‘communication-avoiding’ preconditioners have been proposed for this case [68,69].

7. Conclusion

The U.S. Exascale Computing Project invests in sparse solver libraries in order to provide a resource to application developers who want robust and scalable capabilities on a broad set of platforms. The solver libraries discussed in this paper represent both new and established efforts to provide these capabilities. New projects (Ginkgo, STRUMPACK and KokkosKernels) are expressly focused on algorithms and implementations targeting emerging node architectures. Established libraries (hypre, PETSc, SuperLU and Trilinos), by virtue of a modular design, are integrating these and other new libraries, and adapting implementations of their own capabilities with little or moderate interface changes, to the benefit of their large user bases. Our efforts to prepare for accelerated architectures—represented most concretely by today’s GPU platforms such as Summit [1] and Sierra [2]—challenge us to design algorithms and software that expose very high levels of concurrency underneath each MPI process and to further enable efficient scaling to thousands of nodes containing multiple accelerated devices.

We are confident that our efforts will lead to successful use of Exascale systems and simultaneously help us prepare for post-Exascale parallel computing systems, even those with significantly different designs. High levels of concurrency will be necessary for all foreseeable future system. In addition, nodes with more heterogeneous devices are very likely [70]. Our Exascale systems preparations will provide the foundation for algorithms and software that will be needed for future target devices. These new devices will operate at clock speeds similar to today, but will have favourable designs for higher bandwidth and better latency hiding, leading to improved sparse solver performance on systems developed beyond the exascale time frame.

Data accessibility

Each of the solver libraries discussed in this paper provides detailed information available from the respective project website, cited in the bibliography.

Authors' contributions

H.A. is the primary author of §2 on Ginkgo. R.F. and U.M.Y. are the primary authors of §3 on hypre. K.R., L.C.M., R.T.M. and B.S. are the primary authors of §4. P.G. and X.L. (Sherry) are the primary authors of §5. E.B., S.R., M.H. and I.Y. are the primary authors of §6. Finally, M.H. is the primary author of the document overview and context, §1 and 7.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by the Exascale Computing Project (17-SC-20-SC), a collaborative effort of the US Department of Energy Officeof Science and the National Nuclear Security Administration.