Abstract
Resource availability can powerfully influence host–parasite interactions. However, we currently lack a mechanistic framework to predict how resource fluctuations alter individual infection dynamics. We address this gap with experiments manipulating resource supply and starvation for a human parasite, Schistosoma mansoni, and its snail intermediate host to test a hypothesis derived from mechanistic energy budget theory: resource fluctuations should reduce schistosome reproduction and virulence by inhibiting parasite ingestion of host biomass. Low resource supply caused hosts to remain small, reproduce less and produce fewer human-infectious cercariae. Periodic starvation also inhibited cercarial production and prevented infection-induced castration. The periodic starvation experiment also revealed substantial differences in fit between two bioenergetic model variants, which differ in their representation of host starvation. Simulations using the best-fit parameters of the winning model suggest that schistosome performance substantially declines with resource fluctuations with periods greater than 7 days. These experiments strengthen mechanistic theory, which can be readily scaled up to the population level to understand key feedbacks between resources, host population dynamics, parasitism and control interventions. Integrating resources with other environmental drivers of disease in an explicit bioenergetic framework could ultimately yield mechanistic predictions for many disease systems.
Keywords: parasitism, energy budget, resources, fluctuation, parasite production, reproduction
1. Introduction
Parasites can harm individual hosts, regulate populations and communities, alter ecosystem structure and function and harm human health [1–4]. Epidemics often vary in size and severity along ecological gradients because variation in factors such as resource availability, temperature and pollution can shape the individual-level demographic and epidemiological traits of hosts, vectors and parasites [5–8]. Thus, a mechanistic understanding of the environmental drivers of infection dynamics could improve spatio-temporal disease mapping and prediction as well as identify novel control strategies.
Resources are a powerful environmental driver of disease [9–11]. Parasites steal resources from their hosts to enable their own growth and reproduction. Therefore, starving hosts could cause resource limitation in their parasites [12]. However, immune defences are energetically costly, and poorly fed hosts could exhibit weak immune defences [13]. These mechanisms can operate simultaneously, leading to positive, negative or unimodal relationships between resource acquisition by hosts and infection severity or parasite production [14]. These individual-level effects scale up to population and evolutionary dynamics [15,16]. For example, in systems with positive relationships between resources and parasite production, larger epidemics occur in habitats with greater resource availability [10], resistant organisms that compete for resources reduce epidemics in focal hosts [17] and nutrient enrichment increases infection intensity or the density of infected hosts [18,19].
Despite these strong effects, we currently lack a mechanistic framework to quantitatively predict the effects of resource variability, i.e. fluctuations, pulses or shifts, on the multivariate dynamics of infection for individuals. This knowledge gap exists, in part, because infection experiments often use gradients of constant food supply [14] and the vast majority of susceptible--infected--recovered (SIR)-type models ignore resource availability entirely [20]. These approaches may be problematic because resource acquisition rates of hosts in natural populations vary widely depending on resource density and quality, interference and exploitative competition, food web structure, abiotic factors and anthropogenic influences [21–23]. Additionally, parasites themselves can alter per capita access to resources for hosts by regulating host populations and changing the flow of resources through ecosystems [24,25].
We address this gap by using mechanistic bioenergetic theory to explain infection dynamics across scenarios of constant and periodic resource supply using the human parasite Schistosoma mansoni and its snail intermediate host Biomphalaria glabrata. More than 250 million people are infected with schistosomes, which disproportionately harm women and children [26]. Humans become infected following dermal contact with cercariae, which are released by snails in freshwater environments. Cercarial production by individual snails depends on diet quantity and quality, and we previously built a bioenergetic model based on dynamic energy budget (DEB) theory that quantitatively explains infection dynamics (the time-specific trajectories of growth, reproduction, parasite production and death of infected and uninfected snails) across gradients of resource supply and competition [27,28]. The model assumes that hosts build up or catabolize energy reserves according to their feeding history and that parasites consume host reserves to fuel their own growth and reproduction. It predicts that low resource supply reduces host reserves, which then limits parasite ingestion, growth, reproduction and virulence, explaining the positive resource supply parasite production link commonly seen in invertebrate disease systems [14].
Here, we challenge our bioenergetic theory to explain infection dynamics across constant and periodic resource supply scenarios. We test a specific prediction that resource fluctuations can reduce the growth, reproduction and virulence of S. mansoni in B. glabrata snails by limiting energy acquisition by parasites. In doing so, we parameterize a resource-explicit model of infection that can generate quantitative predictions for any resource scenario (e.g. constant, step up/down, periodic or unpredictable). The prediction regarding fluctuations arises for two reasons (figure 1). First, host ingestion rate follows a saturating (type II) functional response to resource density, so variance in resource supply reduces the average rate of energy acquisition, a consequence of Jensen's inequality [29]. This reduces the mean reserve density of hosts. Second, resource fluctuations can cause fluctuations in host reserve density because hosts build reserves when resources are abundant, but must catabolize reserves during periods of scarcity [28]. Parasite ingestion similarly follows a type II functional response to reserve density in hosts, so both of these factors reduce the average ingestion rate of parasites. Saturating functional responses are theoretically supported and ubiquitous among consumers [28,29]; therefore, resource fluctuations could predictably alter infection dynamics across many host–parasite systems by systematically changing resource acquisition rates of hosts and parasites.
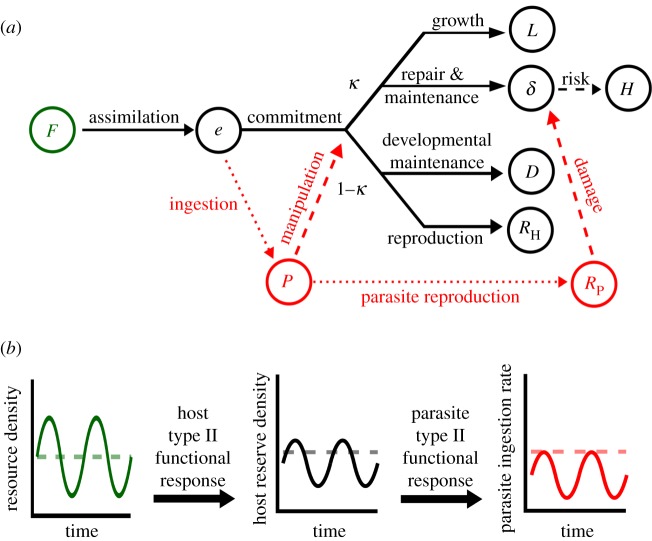
Figure 1.
Schematic of (a) the dynamic energy budget (DEB) model for a free-living host (black) infected with a population of parasites (red). DEB theory tracks assimilation of food resources (F, green) into energy reserves, e. Reserve energy is then committed to somatic or reproductive processes with a fixed allocation fraction, κ. Reserve allocated to soma pays for maintenance and repair, which decreases damage, δ, and surplus is used for structural growth, which increases length, L. Allocation to reproduction similarly pays developmental maintenance, and surplus fuels additional development, D, or reproduction, RH. Here, a population of parasites, P, exerts four potential effects (red dotted and dashed lines). Trophically, parasites consume host reserves, increasing their own biomass and ultimately producing new propagules, RP (dotted lines). Physiologically, parasites can also manipulate the host's allocation rule and induce tissue damage upon emergence (dashed lines). (b) Visual illustration of the hypothesis that resource fluctuations inhibit parasite ingestion. Compared with constant resource density (dashed lines), resource fluctuations (solid lines) and the host's type II functional response combine to induce fluctuations and lower the mean density of host energy reserves. In turn, these effects combine with the parasite's type II functional response to cause fluctuations and lower the average per parasite ingestion rate, limiting parasite growth, reproduction and virulence. (Online version in colour.)
2. Material and methods
(a). Experiments
(i). Periodic starvation experiment
We manipulated the starvation period while holding the average supply rate constant and tracked the growth, reproduction, parasite production and survival of infected and uninfected snail hosts. We fed snails a homogenized blend of 4 g organic chicken feed (Naturewise Meatbird Crumbles; Nutrena Animal Feeds, Minneapolis, MN, USA) and 2 g fish flakes (Omega One Freshwater Flakes; OmegaSea, Painsville, OH, USA) in 1 g agar dissolved in 90 ml deionized water. We factorially crossed exposure of randomly selected 14-day-old B. glabrata snails (NMRI strain, length = 2.48 ± 0.06 s.e. mm) to parasites (0 or 8 freshly hatched miracidia of NMRI strain S. mansoni) for 24 h in 5 ml of HHCOMBO lake water medium with four feeding regimes. Following exposure, we maintained snails individually in 160 ml of medium in lidded plastic containers at 26°C with a 12 : 12 h light:dark regime. We fed all snails ad libitum food on days 15 and 18, and then initiated weekly measurement, water change and feeding regimes from day 21 to day 140. In each feeding regime, snails received an average supply of 8.07 mg C dry weight food per week, divided equally among Monday, Wednesday and Friday feedings. The feeding regimes varied in the duration of periodic starvation (constant supply: 8.07 mg each week, one-week period: 16.14 mg and 0 mg on alternating weeks, two-week period: 24.21 mg for one week followed by 0 mg for two weeks and three-week period: 32.28 mg followed by 0 mg for three weeks). On each feeding date, we removed any uneaten food prior to supplying new food.
Each week, we measured the shell diameter of each host, transferred them to new containers with fresh medium and food (if applicable) and counted the number of eggs laid in the old container on a dissecting microscope (at 10–25×). Starting on day 42 (week 6; 28 days post exposure), we placed each snail individually in 30 ml beakers with 10 ml fresh medium for 2 h under otherwise identical conditions and then returned them to their containers. We then stained the 10 ml samples with Lugol's iodine solution and counted the number of cercariae released on a dissecting scope (at 10–25×). We repeated this process for all surviving snails for 13 additional weeks. Unexposed snails never released cercariae. The initial number of replicates differed for exposed (n = 15) and unexposed (n = 5) treatments. We excluded exposed hosts from the analysis if they died without releasing cercariae (67% of exposed hosts) because we could not definitely determine infection status. In most cases, visual inspection of exposed hosts prior to death and observed reproductive activity suggested that these hosts were probably uninfected. Therefore, these exclusions are unlikely to strongly bias our analyses of infection dynamics. These exclusions resulted in sample sizes of n = 3–8 infected hosts per treatment.
(ii). Resource supply experiment
In a separate experiment, we manipulated constant resource supply rates and tracked the growth, reproduction and parasite production of snails with identical methods, except for the following changes (full details are presented in [27]). We exposed 28-day-old hosts (length: 4.66 ± 0.05 s.e. mm) and provided 0.6875, 1.375, 2.75, 5.5, 11 or 16.5 mg C dry weight per twice-weekly feeding of food containing 6 g dry powdered Spirulina algae and 6 g fish flakes in 1 g agar. We tracked these hosts as above for 32 weeks following exposure. After excluding exposed snails that did not become infected, we obtained sample sizes of n = 10–12 infected hosts and n = 5 uninfected hosts per resource supply treatment.
(b). Bioenergetic model
We fit two variants of a bioenergetic model simultaneously to the infection dynamics of both experiments. The model builds on the ‘standard' model of DEB theory for a free-living organism [28]. It tracks changes in the abundance of food in the environment, F, and several traits of an individual host using coupled differential equations: physical length, L (defined here as maximum shell diameter and proportional to the cube root of structural biomass); the scaled density of energy reserves, e; and resources invested in maturity/development, D, and in reproduction, RH. Previously, we added two modules to this standard DEB model. The first tracks the change in parasite biomass, P, and the resources invested in parasite reproduction, RP. The second module tracks the accumulation of (scaled) damage density, δ, which in turn influences host survival through the instantaneous hazard rate, H [27]. The model is presented in equations (2.1)–(2.10), and the state variables, parameters and some equalities that simplify the presentation of the model are listed in electronic supplementary material, table S1. Subscripts H and P distinguish host and parasite variables and parameters.
| 2.1 |
| 2.2 |
| 2.3 |
| 2.4 |
| 2.5 |
| 2.6 |
| 2.7 |
| 2.8 |
| 2.9 |
| 2.10 |
Hosts consume food, F, with a surface area (L2)-dependent maximum ingestion rate, iM; and a type II scaled functional response, fH, with half-saturation constant, Fh (equation (2.1); electronic supplementary material, table S1). Hosts assimilate food into an energy reserve, with yield YEF. The maximum assimilation rate, aM, is the product of the maximum ingestion rate and the yield of reserves on food. Hosts use reserve energy to build two types of biomass: structure (which performs vital functions and requires maintenance at rate mV) and reproductive matter (reserve permanently committed to gametes). Reserve dynamics without infection derive from the ‘weak homeostasis' assumption [28]. Hosts allocate a constant portion, κ, of mobilized reserves, C, to somatic (versus reproductive) processes. Hosts grow in length based on the yield of structure on reserves, YVE, and the difference between energy mobilized for somatic processes and the costs of somatic maintenance and repair (equation (2.2)). Energy allocated to ‘reproduction' is used by juveniles for development, D (equation (2.4)). Reproduction begins after reaching the developmental threshold for reproduction, DR, and developmental status is maintained at the specific rate mD.
A population of parasites consumes host reserves to build its own biomass and offspring (if hosts are infected; equation (2.3)). Parasite biomass (equation (2.6)) increases via the ingestion and assimilation of host reserves, following a type II scaled functional response, fP, with a half-saturation coefficient, eh, maximum mass-specific ingestion rate, iPM, and yield of parasite biomass on host reserve, YPE. Parasite biomass decreases because of maintenance at the mass-specific rate, mP. A proportion, rp, of the assimilated reserve is allocated to parasite reproduction, while the rest is allocated to parasite biomass growth. The allocation proportion, rp, itself increases as a sigmoid function of parasite density within the physical volume of the snail host's shell, with an inflection point at ph (electronic supplementary material, table S1), reflecting within-host density dependence in parasite growth. The magnitude of ph influences the timing of parasite reproduction and the maximum density of parasite biomass within host tissue. The biomass of parasite offspring (cercariae) increases from parasite allocation to reproduction, with the relative yield of parasite reproduction biomass on assimilated reserve, γRP. Infection can also alter the host's realized allocation between soma and reproduction, κ*, with parasite density-dependent manipulation rate, α, yielding an effective allocation rule, κ* = min(κ + αP). If infection increases κ, it can cause parasitic castration, the rapid cessation of reproduction by infected hosts and host gigantism, as well as increased growth of infected hosts relative to uninfected hosts—phenomena that are seen across a variety of host–parasite systems [30,31]. This parasite module provides a parsimonious description of snail–schistosome physiology, e.g. potential for reproductive manipulation, castration and gigantism, while also generically representing the consumption of host energy for growth and the production and release of infectious propagules (reviewed in [27]).
If growth is non-negative, the standard model applies to many species [28]. However, species can idiosyncratically respond to starvation, when energy allocation to somatic or reproductive processes falls short of covering maintenance costs [21]. Given our focus on starvation, we examined two host response rules. First, we examined a ‘shifting-κ' rule [27,32], which includes two thresholds: mild and severe starvation. Under mild starvation, host allocation to soma is insufficient to cover somatic maintenance, and so allocation is diverted from reproduction to cover this shortfall. Under severe starvation, total host allocation is insufficient to cover somatic maintenance, and so total allocation is increased to cover somatic maintenance. In this model, which we previously applied to this system, host structure cannot shrink, but mild starvation reduces reproduction and severe starvation eliminates reproduction and causes developmental regression (loss of reproductive capability) and a rapid decrease in reserve density [27]. Second, we examined a ‘shrinking and regression' rule [15]. Under this model, hosts do not alter their allocation rules. If allocation is insufficient to cover maintenance costs, then the host loses structure (shrinks in soft tissue, i.e. structural mass or length within the model; however, shell size (observable length) does not shrink [33]) or developmentally regresses, according to the deficit in energy ([28]; see electronic supplementary material for additional details of both variants).
The survival module assumes that hosts die from damage caused by low energy reserve density or emerging parasite offspring. Scaled damage density, δ, increases because of the release of parasite offspring with damage intensity, Θ. The damage repair rate, kR, determines the rate of damage caused by reserve depletion and damage repair. Damage density also decreases through dilution by growth (equation (2.8)) and may be concentrated by shrinkage, in the ‘shrinking and regression model'. Damage repair by hosts requires energy, and we assume that these costs, mR, are an explicit portion of somatic maintenance. Cumulative hazard, H, increases with the background hazard rate, hb, and a linear function of damage density above a threshold, δ0, with hazard coefficient hδ (equation (2.9)). Host survival probability, Prob(Survival[t]) is a negative exponential function of cumulative hazard, H (equation (2.10)). We define several derived parameters and functions to simplify the presentation of the model and the statistical analysis (electronic supplementary material, table S1). When we fitted these models to the data (see the electronic supplementary material for additional details), we assumed that biomass invested in host or parasite reproduction is immediately released as eggs or parasite cercariae, with carbon content per host egg, εH, or parasite propagule, εP.
(c). Analysis
We parameterized the model by simulating infections under the defined resource supply dynamics and infection status of each treatment ([27]; see electronic supplementary material for additional details). Briefly, we numerically integrated the model for individuals from birth (initial values: L = 0.7, e = 0.9, D = 0, RH = 0, P = 0, RP = 0, δ = 0, H = 0) through the end of each experiment, 140 and 245 days, respectively. We explicitly incorporated ‘events' into the simulations to reflect feeding and infection events on identical days as in the experiments. Food additions matched the feeding treatments in both experiments, and we drew parameter values randomly to generate model predictions. We then compared predictions and observations for host length, cumulative host and parasite reproduction, and host survival simultaneously for each infected and uninfected host in the periodic starvation and resource supply experiments in a Bayesian framework (see electronic supplementary material for additional details on priors, likelihood model and Markov chain Monte Carlo (MCMC) sampling). We conducted analyses with three replicate MCMC chains (1.5 × 105 iterations) after a 5 × 104 iteration burn-in. We compared the relative performance of the two starvation models using the deviance information criterion, DIC, based on the total likelihoods summed across each time series for both experiments [34]. Following Johnson et al. [35], we applied diagnostic tests of global convergence to the chains of log-posterior probabilities. We assessed absolute model fit of the highest posterior density parameter estimates (i.e. the best fits for each model) with the concordance correlation coefficient, rc (for length, reproduction and parasite production), and the area under the receiver operating characteristic, AUC (for survival), calculated separately for each time series from all observations and each individual trajectory for both experiments [36,37]. Lastly, we calculated 99% credible prediction intervals for the mean dynamics of each observed variable for both experiments by drawing parameter sets from the posterior distributions and simulating the predicted dynamics for each treatment.
(i). Model simulations
We simulated infection dynamics using the highest posterior density parameter estimates of the ‘shrinking and regression' model under fluctuating resource conditions to explore the general consequences of resource variability on schistosome infections in snails. We specified the scaled host functional response, fH, as a sine wave centred on f = 0.5 and varied the amplitude (from 0 to 0.5) and period (1, 7, 28 or 56 days) of oscillations (initial conditions: L = 8 mm, e = 0.5, D = 0.617 mg C, RH = 0, P = 2.85 × 10−5 mg C, RP = 0 mg C, δ = 0, H = 0). For each simulation, we calculated the expected daily cercarial production rate, time until full castration of the host and median host survival time.
3. Results
(a). Periodic starvation experiment
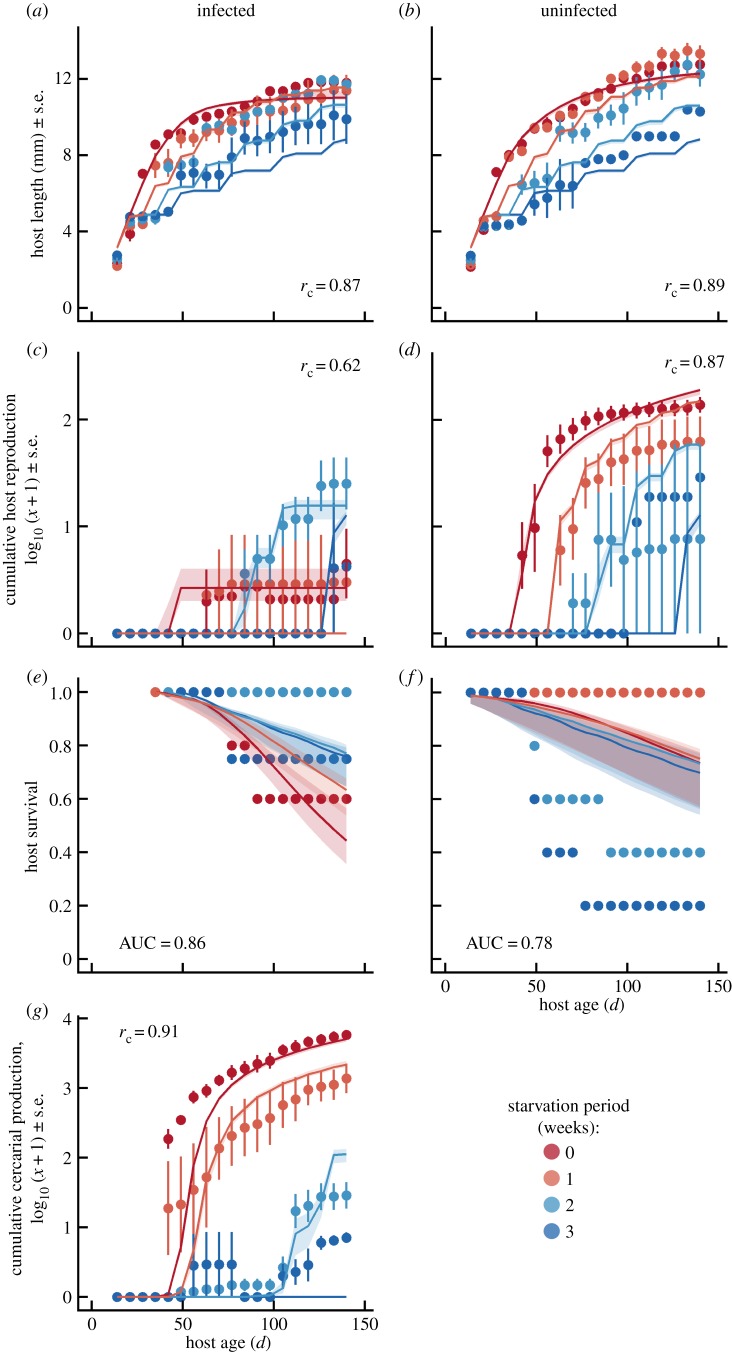
Periodic starvation reduced the growth and reproduction of uninfected hosts (figure 1). Uninfected snails fed constantly were 24% larger and produced 4.8-fold more offspring than snails facing three-week starvation periods by the end of the experiment. Infected snails fed consistently were 19% larger and produced approximately 820-fold more cercariae than snails undergoing the three-week starvation treatment. Infected snails fed weekly or every other week reproduced earlier than snails experiencing longer starvation periods, but they ceased reproduction earlier. Ultimately, infected snails experiencing two- or three-week starvation periods produced more offspring, despite their slightly smaller size. Infected snails fed consistently died slightly faster than snails in the starvation treatments. However, uninfected snails in this experiment survived poorly, especially in the two- and three-week starvation treatments.
(b). Resource supply experiment
Greater resource supply caused the final length and reproductive output of uninfected snails to increase by 2.7- and approximately 6000-fold, respectively (figure 2). Similarly, infected hosts were 2.4 times larger and produced 60 times more cercariae across the supply gradient. Reproduction by infected hosts increased from 0 to approximately 120 eggs over the gradient. Uninfected host survival increased with resource supply, but infected host survival was lower and more consistent across treatments.
Figure 2.
Life history and infection dynamics in the experiment manipulating starvation period (colours) and infection (columns). Points represent treatment means ± s.e. Prediction lines and shaded envelopes represent the median and 99% posterior credible interval of the mean dynamics of the ‘shrinking and regression' model. Growth of infected (a) and uninfected (b) snails was substantially reduced with increasing starvation period. Infected snail reproduction (c) was ultimately highest in the longest starvation treatments. However, uninfected snail reproduction (d) was reduced approximately 10-fold in the longest starvation treatments. Infected host survival (e) was higher in the longer starvation treatments, whereas uninfected hosts survived best with consistent feeding (f). Hosts fed consistently produced approximately 1000-fold more parasite cercariae than those in the longest starvation treatments (g). The ‘shrinking and regression' model explains these dynamics extremely well, with concordance correlation coefficients rc = 0.62–0.91 and AUC = 0.78–0.86. In particular, this model slightly underpredicted snail growth in the two- and three-week starvation period treatments, but it captures snail and parasite reproduction extremely well. (Online version in colour.)
(c). Model parameterization and competition
Overall, the ‘shrinking and regression’ starvation model vastly outperformed the ‘shifting-κ' model, ΔDIC = 885.5, model weight ≈ 0 (see electronic supplementary material, table S2 for fit statistics and parameter estimates). Substantial differences emerged between the two models in their ability to explain the dynamics of the periodic starvation experiment. The ‘shrinking and regression’ model provided a strong fit to these data. This model captured growth (concordance correlation coefficient, rc = 0.95 (infected), 0.97 (uninfected)), reproduction (rc = 0.71 (infected), 0.93 (uninfected)) and parasite production (rc = 0.97) extremely well, and it explained survival moderately well (AUC = 0.87 (infected), 0.77 (uninfected)). By contrast, the ‘shifting-κ' model fitted substantially worse, particularly by underpredicting snail growth (rc = 0.56 (infected), 0.89 (uninfected)), infected snail reproduction (rc = 0.01) and parasite production (rc = 0.86). Generally, these failures were worse for the longer starvation treatments (electronic supplementary material, figure S1). By contrast, both models explained a large majority of the variation in infection dynamics in the resource supply experiment. For both models, rc was high for growth (rc ≥ 0.94), moderate to high for reproduction (rc ≥ 0.73 (infected), ≥ 0.93 (uninfected)) and high for parasite production (rc = 0.97) through time (figure 2; electronic supplementary material, figure S2). Both models performed moderately well for host survival in this experiment as well (AUC = 0.87 (infected), ≥ 0.73 (uninfected)).
(d). Model simulations
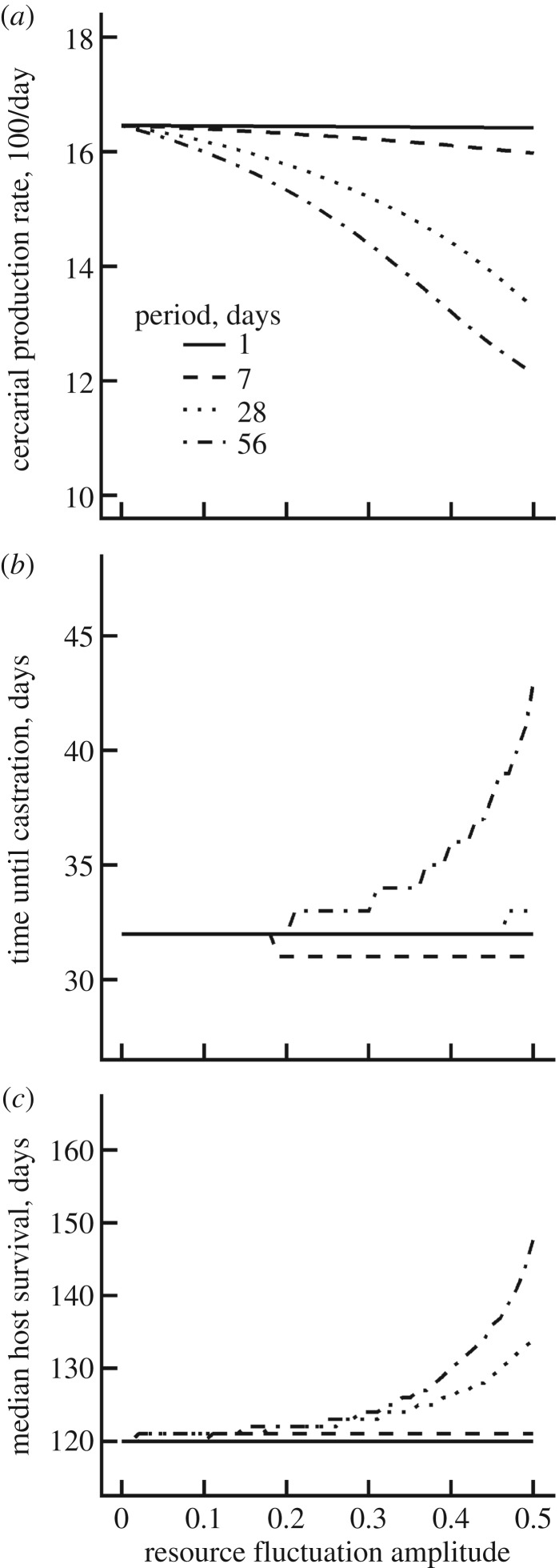
Fluctuations in resource supply inhibit parasite performance, as indexed by the productivity and virulence of the infection (figure 3). Larger and longer oscillations in the scaled host feeding rate decrease the production rate of schistosome cercariae (figure 3a) and also increase the time until complete parasitic castration (figure 3b) and host mortality (figure 3c). The highest posterior density parameter estimates of the ‘shrinking and regression' model indicate that fluctuations on daily or weekly scales have little effect, while fluctuations at longer time scales can substantially harm parasite performance.
Figure 3.
Life history and infection dynamics in the experiment manipulating resource supply rate (colours) and infection (columns). Points represent treatment means ± s.e. Prediction lines and shaded envelopes represent the median and 99% posterior credible interval of the mean dynamics of the ‘shrinking and regression' model. (a–d) Growth and reproduction of infected and uninfected snails increased substantially over the supply gradient. Survival decreased with food supply for infected individuals (e), but increased with food supply for uninfected individuals (f). Parasite production increased approximately 60-fold over the supply gradient (g). The ‘shrinking and regression’ model explains these dynamics extremely well, with concordance correlation coefficients rc = 0.71–0.97 and AUC = 0.78–0.86. (Online version in colour.)
4. Discussion
Resource availability has profound effects on infection dynamics. Greater and more consistent resource supply caused snail hosts of the human parasite S. mansoni to grow larger, reproduce more and produce more human-infectious cercariae. Our bioenergetic model successfully predicted that low resource supply and long periods of starvation, which deplete host energy reserves, would reduce parasite performance (cercarial production and host castration) by reducing the rate at which parasites ingest host resources. It also captured the high sensitivity of parasite reproduction to adverse food conditions relative to other traits. For example, infected host length varied by 19% and 2.4-fold in the two experiments, whereas cercarial production varied by 820- and 60-fold. The positive resource supply parasite performance patterns predicted and seen here for B. glabrata and S. mansoni are common among many snail–trematode combinations, and a variety of host–parasite systems more broadly [14,18,38]. These predictions follow from the saturating functional responses of hosts and parasites assumed in our bioenergetics models, which are theoretically supported and found ubiquitously among consumers [28,29]. Thus, resource fluctuations could predictably influence infection dynamics in many host–parasite systems by systematically reducing resource acquisition rates of hosts and parasites. Infection experiments with resource fluctuations are rare, but there may be scenarios where parasites may be insensitive or even benefit from variable resource supply. First, parasites with the ability to store reserves should be less sensitive to fluctuations. However, given that parasites are typically much smaller than their hosts, parasites are predicted to have much smaller reserve capacities [28]. Alternatively, parasites might benefit from resource fluctuations when host immune defences are disproportionately harmed by fluctuations or immune responses respond slowly to increases in resource availability [39].
The periodic starvation experiment revealed large differences between the two models for host starvation (figure 1; electronic supplementary material, figure S1). Both models could successfully explain infection dynamics under constant resource supplies (figure 2; electronic supplementary material, figure S2). However, when we manipulated the starvation period and generated extremely adverse food conditions, the two models diverged. As seen elsewhere for free-living organisms [40], the ‘shifting-κ' rule predicted starvation to death much more rapidly than we observed. This model also underpredicted the performance of snails and schistosomes under the worst conditions (i.e. the longest starvation periods). By contrast, the ‘shrinking and regression' model provided much better predictions of snail and schistosome performance under poor resource conditions (see electronic supplementary material for additional discussion of parameter estimates for both models). This reinforces the value of resource fluctuation and starvation experiments for parameterizing and competing bioenergetic models [41].
We then evaluated the general consequences of resource oscillations on schistosome infections in snails by simulating infections for hosts experiencing sinusoidal fluctuations in their scaled functional response. Resource fluctuations with larger amplitudes and longer periods reduce the rate of cercarial production and prolong the time until host castration and death (figure 4). Our best parameter estimates suggest that these effects emerge for schistosome-infected snails facing resource fluctuations on time scales greater than one week (figure 4). Resource availability can vary for snails in natural populations owing to resource competition as well as seasonal changes in rainfall, temperature or other factors. However, resource dynamics are generally not considered in epidemiological studies of human schistosomes. A deeper understanding of the variability or periodicity in per capita resource acquisition rates of snails in nature could, therefore, improve predictions of transmission potential for humans.
Figure 4.
Resource fluctuations generally decrease schistosome performance in intermediate host snails. Simulation results using the highest posterior density parameter estimates of the better performing ‘shrinking and regression' model coupled with the scaled functional response of snail hosts is represented with a sine wave. In simulations that varied the amplitude (x-axis) and period (line type), resource fluctuations reduced cercarial production (a) and the time required to castrate (b) or kill (c) the snail host. These effects increased with the amplitude and period of the simulated resource fluctuations. The best-fit parameter estimates suggest that snail–schistosome infection dynamics are sensitive to resource fluctuations with periods greater than one week.
Models of host and parasite performance that perform well across diverse resource scenarios are critical for ecological and epidemiological modelling because resource availability can vary dramatically within and across populations at time scales relevant to disease outbreaks [10,42]. Thus, the ‘shrinking and regression' model serves as a strong foundation for an individual-based model (IBM) for snail–schistosome dynamics. We recently built an IBM [15] by combining this model with a mechanistic transmission function [43] and functions describing the production of resources (algae or detritus). The IBM illustrates the key role that resource competition among snails has in the total production of schistosome cercariae by populations. It also predicts that cercarial production can be concentrated in intense peaks when snail populations grow from low densities, and that there can be overcompensatory dynamics—total cercarial production can increase with increasing snail mortality rate because of a weakening of resource competition. These novel, testable predictions contradict predictions from widely used schistosome models that ignore resources [44].
While bioenergetic models may provide novel epidemiological predictions, they are considerably more complex than SIR-type compartment models. Thus, parametrization can require a greater amount of data that are more labour-intensive and different from data required for SIR-type models. Here, we demonstrate the potential to parameterize and select between two bioenergetics models using life table experiments. However, the construction of the parasitism module itself benefitted greatly from substantial previous research on snail–schistosome physiology. Such detailed data may only be available for model organisms or those of elevated interest, such as vectors or intermediate hosts of human parasites. Key challenges for applying bioenergetics models more widely will be to understand the resource sensitivity and dynamics of host immune defences or more complex patterns of parasite development. Customizable and more complex bioenergetic models can be built for non-model organisms that exhibit complex immune interactions with their parasites [39]. However, selecting among such models solely using life table data may be infeasible. Ultimately, the ability of bioenergetic models to make quantitative, multivariate predictions across many contexts might facilitate reanalysis of existing data or suggest novel experiments to yield physiological and epidemiological insights despite their complexity. The advantages of bioenergetics models will be greatest for systems where parasite growth or host defence are strongly sensitive to resources, when resources naturally fluctuate, when resource competition among hosts is strong or when parasite-induced mortality can trigger trophic cascades [15,25].
Despite the strong performance of the ‘shrinking and regression' model, there are still areas for improvement. In general, the model predictions for host survival are the weakest. The current survival module parsimoniously accounts for damage caused by starvation [45] and damage caused by emerging parasites, which can burrow through host tissues. This simple representation may be missing underlying nonlinearities or additional processes relating to damage, repair and death. More detailed survival experiments focusing on starvation, feeding history, body size and infection status are needed to explore more detailed or system-specific hazard models. Alternatively, the poor fit of the model to survival data may simply reflect the stochastic nature of mortality or trade-offs in the process of fitting the model simultaneously to many endpoints (host size, reproduction, parasite production and survival) across two experiments.
Energetically explicit theory for infectious disease can yield novel insights for epidemics and the consequences of control interventions. We encourage the development of bioenergetics theory for other host–parasite systems, and we call for field surveys of snail population density, size structure, resource availability and cercarial production to assess the relevance of these predictions for natural dynamics. These models lay the groundwork for the explicit incorporation of other environmental factors that modulate traits of hosts and parasites, especially temperature and pollutants [46,47]. Integrating resources with other environmental drivers of disease in an explicit bioenergetic framework could ultimately yield mechanistic predictions for a variety of disease systems across an enormous range of environmental contexts.
Supplementary Material
Acknowledgements
Roger Nisbet provided advice on starvation modelling. The NIAID, NIH Schistosomiasis Resource Center provided parasite eggs and snails.
Data accessibility
Data and analysis code are publicly available on GitHub (https://github.com/DaveCivitello/Periodic_starvation).
Authors' contribution
D.J.C. and R.B.H. conceived the experiments. All authors conducted the experiments. D.J.C. conducted the analysis. D.J.C. wrote the first draft and all authors edited and approved the manuscript.
Competing interests
We declare we have no competing interests.
Funding
D.J.C. was supported by NSF IOS-1755002.
References
- 1.Bekerman E, Einav S. 2015. Combating emerging viral threats. Science 348, 282–283. ( 10.1126/science.aaa3778) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Morens DM, Folkers GK, Fauci AS. 2004. The challenge of emerging and re-emerging infectious diseases. Nature 430, 242–249. ( 10.1038/nature02759) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Duffy MA, Ochs JH, Penczykowski RM, Civitello DJ, Klausmeier CA, Hall SR. 2012. Ecological context influences epidemic size and parasite-driven evolution. Science 335, 1636–1638. ( 10.1126/science.1215429) [DOI] [PubMed] [Google Scholar]
- 4.Hudson PJ, Dobson AP, Newborn D. 1998. Prevention of population cycles by parasite removal. Science 282, 2256–2258. ( 10.1126/science.282.5397.2256) [DOI] [PubMed] [Google Scholar]
- 5.Anderson RM, May RM. 1986. The invasion, persistence and spread of infectious disease within animal and plant communities. Phil. Trans. R. Soc. Lond. B 314, 533–570. ( 10.1098/rstb.1986.0072) [DOI] [PubMed] [Google Scholar]
- 6.Civitello DJ, Penczykowski RM, Hite JL, Duffy MA, Hall SR. 2013. Potassium stimulates fungal epidemics in Daphnia by increasing host and parasite reproduction. Ecology 94, 380–388. ( 10.1890/12-0883.1) [DOI] [PubMed] [Google Scholar]
- 7.Mordecai EA, et al. 2013. Optimal temperature for malaria transmission is dramatically lower than previously predicted. Ecol. Lett. 16, 22–30. ( 10.1111/ele.12015) [DOI] [PubMed] [Google Scholar]
- 8.Rohr JR, et al. 2008. Agrochemicals increase trematode infections in a declining amphibian species. Nature 455, 1235–1239. ( 10.1038/nature07281) [DOI] [PubMed] [Google Scholar]
- 9.Becker DJ, Streicker DG, Altizer S. 2015. Linking anthropogenic resources to wildlife–pathogen dynamics: a review and meta-analysis. Ecol. Lett. 18, 483–495. ( 10.1111/ele.12428) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Civitello DJ, Penczykowski RM, Smith AN, Shocket MS, Duffy MA, Hall SR. 2015. Resources, key traits and the size of fungal epidemics in Daphnia populations. J. Anim. Ecol. 84, 1010–1017. ( 10.1111/1365-2656.12363) [DOI] [PubMed] [Google Scholar]
- 11.Pedersen AB, Greives TJ. 2008. The interaction of parasites and resources cause crashes in a wild mouse population. J. Anim. Ecol. 77, 370–377. ( 10.1111/j.1365-2656.2007.01321.x) [DOI] [PubMed] [Google Scholar]
- 12.Seppälä O, Liljeroos K, Karvonen A, Jokela J. 2008. Host condition as a constraint for parasite reproduction. Oikos 117, 749–753. ( 10.1111/j.0030-1299.2008.16396.x) [DOI] [Google Scholar]
- 13.Sheldon BC, Verhulst S. 1996. Ecological immunology: costly parasite defences and trade-offs in evolutionary ecology. Trends Ecol. Evol. 11, 317–321. ( 10.1016/0169-5347(96)10039-2) [DOI] [PubMed] [Google Scholar]
- 14.Cressler CE, Nelson WA, Day T, McCauley E. 2014. Disentangling the interaction among host resources, the immune system and pathogens. Ecol. Lett. 17, 284–293. ( 10.1111/ele.12229) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Malishev M, Civitello DJ. 2019. Linking bioenergetics and parasite transmission models suggests mismatch between snail host density and production of human schistosomes. Integr. Comp. Biol. 59, 1243–1252. ( 10.1093/icb/icz058) [DOI] [PubMed] [Google Scholar]
- 16.Hite JL, Cressler CE. 2018. Resource-driven changes to host population stability alter the evolution of virulence and transmission. Phil. Trans. R. Soc. B. 373, 20170087 ( 10.1098/rstb.2017.0087) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Strauss AT, Civitello DJ, Caceres CE, Hall SR. 2015. Success, failure and ambiguity of the dilution effect among competitors. Ecol. Lett. 18, 916–926. ( 10.1111/ele.12468) [DOI] [PubMed] [Google Scholar]
- 18.Johnson PTJ, Chase JM, Dosch KL, Hartson RB, Gross JA, Larson DJ, Sutherland DR, Carpenter SR. 2007. Aquatic eutrophication promotes pathogenic infection in amphibians. Proc. Natl Acad. Sci. USA 104, 15 781–15 786. ( 10.1073/pnas.0707763104) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Halstead NT, et al. 2018. Agrochemicals increase risk of human schistosomiasis by supporting higher densities of intermediate hosts. Nat. Commun. 9, 837 ( 10.1038/s41467-018-03189-w) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Keeling MJ, Rohani P. 2011. Modeling infectious diseases in humans and animals. Princeton, NJ: Princeton University Press. [Google Scholar]
- 21.Hargrave CW, Hambright KD, Weider LJ. 2011. Variation in resource consumption across a gradient of increasing intra- and interspecific richness. Ecology 92, 1226–1235. ( 10.1890/09-1948.1) [DOI] [PubMed] [Google Scholar]
- 22.Müller-Navarra D, Lampert W. 1996. Seasonal patterns of food limitation in Daphnia galeata: separating food quantity and food quality effects. J. Plankton Res. 18, 1137–1157. ( 10.1093/plankt/18.7.1137) [DOI] [Google Scholar]
- 23.Shurin JB, Borer ET, Seabloom EW, Anderson K, Blanchette CA, Broitman B, Cooper SD, Halpern BS. 2002. A cross-ecosystem comparison of the strength of trophic cascades. Ecol. Lett. 5, 785–791. ( 10.1046/j.1461-0248.2002.00381.x) [DOI] [Google Scholar]
- 24.Sato T, Watanabe K, Kanaiwa M, Niizuma Y, Harada Y, Lafferty KD. 2011. Nematomorph parasites drive energy flow through a riparian ecosystem. Ecology 92, 201–207. ( 10.1890/09-1565.1) [DOI] [PubMed] [Google Scholar]
- 25.Buck JC, Ripple WJ. 2017. Infectious agents trigger trophic cascades. Trends Ecol. Evol. 32, 681–694. ( 10.1016/j.tree.2017.06.009) [DOI] [PubMed] [Google Scholar]
- 26.Hotez PJ, et al. 2014. The global burden of disease study 2010: interpretation and implications for the neglected tropical diseases. PLOS Neglected Trop. Dis. 8, e2865 ( 10.1371/journal.pntd.0002865) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Civitello DJ, Fatima H, Johnson LR, Nisbet RM, Rohr JR. 2018. Bioenergetic theory predicts infection dynamics of human schistosomes in intermediate host snails across ecological gradients. Ecol. Lett. 21, 692–701. ( 10.1111/ele.12937) [DOI] [PubMed] [Google Scholar]
- 28.Kooijman SALM. 2010. Dynamic energy budget theory for metabolic organisation. Cambridge, UK: Cambridge University Press. [Google Scholar]
- 29.Ruel JJ, Ayres MP. 1999. Jensen's inequality predicts effects of environmental variation. Trends Ecol. Evol. 14, 361–366. ( 10.1016/S0169-5347(99)01664-X) [DOI] [PubMed] [Google Scholar]
- 30.Hall SR, Becker C, Cáceres CE. 2007. Parasitic castration: a perspective from a model of dynamic energy budgets. Integr. Comp. Biol. 47, 295–309. ( 10.1093/icb/icm057) [DOI] [PubMed] [Google Scholar]
- 31.Lafferty KD, Kuris AM. 2009. Parasitic castration: the evolution and ecology of body snatchers. Trends Parasitol. 25, 564–572. ( 10.1016/j.pt.2009.09.003) [DOI] [PubMed] [Google Scholar]
- 32.Hall SR, Simonis JL, Nisbet RM, Tessier AJ, Caceres CE. 2009. Resource ecology of virulence in a planktonic host-parasite system: an explanation using dynamic energy budgets. Am. Nat. 174, 149–162. ( 10.1086/600086) [DOI] [PubMed] [Google Scholar]
- 33.de Jong-Brink M. 1973. The effects of desiccation and starvation upon the weight, histology and ultrastructure of the reproductive tract of Biomphalaria glabrata, host of Schistosoma mansoni. Zeitschrift für Zellforschung und Mikroskopische Anatomie 136, 229–262. ( 10.1007/BF00307443) [DOI] [PubMed] [Google Scholar]
- 34.Link WA, Barker RJ. 2009. Bayesian inference: with ecological applications. New York, NY: Academic Press. [Google Scholar]
- 35.Johnson LR, Pecquerie L, Nisbet RM. 2013. Bayesian inference for bioenergetic models. Ecology 94, 882–894. ( 10.1890/12-0650.1) [DOI] [Google Scholar]
- 36.Lin LI. 1989. A concordance correlation coefficient to evaluate reproducibility. Biometrics 45, 255–268. ( 10.2307/2532051) [DOI] [PubMed] [Google Scholar]
- 37.Hanley JA, McNeil BJ. 1982. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 143, 29–36. ( 10.1148/radiology.143.1.7063747) [DOI] [PubMed] [Google Scholar]
- 38.Sandland GJ, Minchella DJ. 2003. Effects of diet and Echinostoma revolutum infection on energy allocation patterns in juvenile Lymnaea elodes snails. Oecologia 134, 479–486. ( 10.1007/s00442-002-1127-x) [DOI] [PubMed] [Google Scholar]
- 39.Leeuwen A, Budischak SA, Graham AL, Cressler CE. 2019. Parasite resource manipulation drives bimodal variation in infection duration. Proc. R. Soc. B 286, 20190456 ( 10.1098/rspb.2019.0456) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Martin BT, Jager T, Nisbet RM, Preuss TG, Grimm V. 2013. Predicting population dynamics from the properties of individuals: a cross-level test of dynamic energy budget theory. Am. Nat. 181, 506–519. ( 10.1086/669904) [DOI] [PubMed] [Google Scholar]
- 41.Tolla C, Kooijman S, Poggiale JC. 2007. A kinetic inhibition mechanism for maintenance. J. Theor. Biol. 244, 576–587. ( 10.1016/j.jtbi.2006.09.001) [DOI] [PubMed] [Google Scholar]
- 42.Hall SR, Knight CJ, Becker CR, Duffy MA, Tessier AJ, Caceres CE. 2009. Quality matters: resource quality for hosts and the timing of epidemics. Ecol. Lett. 12, 118–128. ( 10.1111/j.1461-0248.2008.01264.x) [DOI] [PubMed] [Google Scholar]
- 43.Civitello DJ, Rohr JR. 2014. Disentangling the effects of exposure and susceptibility on transmission of the zoonotic parasite Schistosoma mansoni. J. Anim. Ecol. 83, 1379–1386. ( 10.1111/1365-2656.12222) [DOI] [PubMed] [Google Scholar]
- 44.Lo NC, Gurarie D, Yoon N, Coulibaly JT, Bendavid E, Andrews JR, King CH. 2018. Impact and cost-effectiveness of snail control to achieve disease control targets for schistosomiasis. Proc. Natl Acad. Sci. USA 115, E584–E591. ( 10.1073/pnas.1708729114) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Gergs A, Jager T. 2014. Body size-mediated starvation resistance in an insect predator. J. Anim. Ecol. 83, 758–768. ( 10.1111/1365-2656.12195) [DOI] [PubMed] [Google Scholar]
- 46.Civitello DJ, Forys P, Johnson AP, Hall SR. 2012. Chronic contamination decreases disease spread: a Daphnia-fungus-copper case study. Proc. R. Soc. B 279, 3146–3153. ( 10.1098/rspb.2012.0684) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Mordecai EA, et al. 2019. Thermal biology of mosquito-borne disease. Ecol. Lett. 22, 1690–1708. ( 10.1111/ele.13335) [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data and analysis code are publicly available on GitHub (https://github.com/DaveCivitello/Periodic_starvation).