Overcoming Challenging Substituent Perturbations with Multisite λ-Dynamics: A Case Study Targeting β-Secretase 1

Abstract

Alchemical free energy calculations have made a dramatic impact upon the field of structure-based drug design by allowing functional group modifications to be explored computationally prior to experimental synthesis and assay evaluation, thereby informing and directing synthetic strategies. In furthering the advancement of this area, a series of 21 β-secretase 1 (BACE1) inhibitors developed by Janssen Pharmaceuticals was examined to evaluate the ability to explore large substituent perturbations, some of which contain scaffold modifications, with multisite λ-dynamics (MSλD), an innovative alchemical free energy framework. Our findings indicate that MSλD is able to efficiently explore all structurally diverse ligand end-states simultaneously within a single MD simulation with a high degree of precision and with reduced computational costs compared to the widely used approach TI/MBAR. Furthermore, computational predictions were shown to be accurate to within 0.5–0.8 kcal/mol when CM1A partial atomic charges were combined with CHARMM or OPLS-AA-based force fields, demonstrating that MSλD is force field independent and a viable alternative to FEP or TI approaches for drug design.

Graphical Abstract

Rigorous physics-based alchemical free energy calculations are powerful techniques to calculate free energy differences for a variety of biological processes, including solvation, association, protonation, and conformational equilibria.^1,2 As a result, these methods have dramatically impacted the field of structure-based drug design (SBDD). For example, the ability to calculate binding affinity changes associated with functional group modifications can focus experimental design efforts by highlighting the most promising chemical spaces to explore when optimizing the binding affinity or inhibitory activity of a lead compound.^3–5 Moreover, current approaches suggest that computed free energies of binding (ΔΔG_bind) are generally accurate to within 0.5–1.5 kcal/mol of experimental inhibitory activities, which is in many instances sufficient to facilitate the refinement process in silico.^3–12

A majority of studies that have employed alchemical free energy methods for SBDD and lead optimization have used traditional methods, such as free energy perturbation theory (FEP) or thermodynamic integration (TI).^3–12 However, the scope of FEP or TI methods is limited by two main factors. First, these approaches require a full alchemical transformation to be broken up into many steps, usually 10–20 along the alchemical coupling parameter λ, to ensure sufficient phase space overlap between adjacent steps and to obtain statistically precise free energy results.¹³ This makes these conventional methods expensive, although calculations may be accelerated using enhanced sampling approaches or sped-up by exploiting graphic processing units (GPUs).^14,15 Second, these methods are inherently limited to the determination of free energy differences between two ligand end-states. Thus, the cost of scanning through a large set of ligand perturbations grows linearly with the number of perturbations. Methods that reduce the costs associated with a single perturbation or improve scaling to multiple perturbations can improve the efficiency of free energy calculations.

λ-dynamics is an innovative solution that achieves both of these goals.^16,17 Rather than using a set of discrete states, λ-dynamics allows the alchemical coupling parameter to fluctuate continuously between ligand end-states in conjunction with the coordinates of a system using an extended Lagrangian approach. From a single molecular dynamics (MD) simulation, free energy differences can be calculated as the ratio of the amount of time one ligand is sampled compared to a reference ligand (eq 1).^16,17 Furthermore, additional λ parameters can be introduced to explore multiple functional groups of interest simultaneously.¹⁷ Multisite λ-dynamics (MSλD) further extends this ability to examine multiple perturbations to different sites around a common ligand core, leading to a combinatorial space of chemical endpoints.¹⁸ Thus, λ-dynamics can improve upon the scalability limitations encountered with FEP or TI methods. Recent work has shown that tens to hundreds of relative free energies can be computed simultaneously within a single MSλD simulation.^19,20

$$\mathrm{\Delta }\mathrm{\Delta }{G}_{i\to j}=-k_{B}Tln\frac{P_j}{P_i}$$ (1)

In lead optimization, both small and large functional group modifications to a lead compound may be important to investigate. This work evaluates MSλD’s precision, efficiency, and accuracy when applied to larger and more challenging substituent modifications. An inhibitor series developed by Janssen Pharmaceutical (JP) to target β-secretase 1 (BACE1) was chosen for investigation (Figure 1A),¹¹ and MSλD is found to be aptly suited for pharmaceutics design involving these modifications.

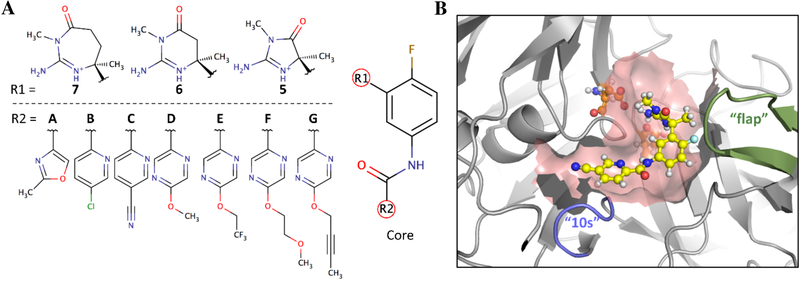
Figure 1.

(A) The JP N-(4-fluorophenyl)-acetamide core with R1 and R2 substituents. (B) The BACE1 binding pocket: BACE1 is represented in grey, with flexible “flap” and “10s” loops colored green and purple, respectively. The catalytic aspartic acids are shown in orange, and the 5C ligand is shown in yellow. The surface of the binding pocket is colored pink.

Two decades ago, BACE1 was shown to cleave amyloid precursor proteins and contribute to an increase in the amount of cellular beta-amyloid peptides,²¹ a major component of amyloid plaques observed in Alzheimer’s disease (AD) brains.²² As a result, BACE1 has been a prominent AD target for both academic and industrial researchers.^23,24 As an aspartic acid protease, most inhibitors designed to target BACE1 feature amidine or guanidine-like cationic moieties that bind to the catalytic Asp32 and Asp228 residues in the enzyme’s active site (Figure 1B) as well as fill adjacent P2’, P1, and P3 pockets.²⁵ The JP ligands follow this trend and explore substituent modifications at two sites (Figure 1A). Specifically, acylguanidinium heterocyclic rings of different sizes, 5-, 6-, and 7-membered rings, are investigated at one site on the ligand core, R1, and three different heteroaromatic rings featuring long and flexible groups are investigated at a second site, R2.¹¹ The acylguanidinium heterocyclic rings bind to the catalytic Asp32 and Asp228 residues and fill the P1 pocket, while the R2 substituents extend below the 10s loop of BACE1 to fill the P3 pocket (Figure 1B). Advantageously, experimental activity measurements were reported for all 21 R1×R2 combinatorial states of the JP inhibitor, and surrogate ΔG_expt can be estimated from the IC₅₀s using equation 2.¹¹

$$\mathrm{\Delta }{G}_{\text{exp}t}\approx -RTln\left(I{C}_{50}\right)$$ (2)

The JP substituents vary in size, flexibility, and polarity, which add to the difficulty of sampling between them in a combinatorial fashion with MSλD. Scaffold modifications, exemplified by changing the R1 acylguanidine ring size, have traditionally been very difficult to explore with alchemical free energy methodologies. Only recently has the “Core Hopping FEP+” algorithm offered an attractive solution to efficiently explore ring size modifications via a “soft bond” stretch potential without considering the entire ring as a separate substituent.²⁶ In the original JP publication, Tresadern and co-workers evaluated both approaches and found improved stability, reproducibility, and accuracy with the “Core Hopping FEP+” algorithm.¹¹ However, the “soft bond” stretch potential used in the “Core Hopping FEP+” algorithm is not obviously necessary with MSλD, so we employed the later approach of considering the entire ring as a separate substituent and investigate MSλD’s potential to explore such difficult modifications.

To evaluate the reproducibility of MSλD computed binding free energies, ΔG_bind, additional free energy calculations were performed using a community accepted standard, TI calculations coupled with the multistate Bennett acceptance ratio free energy estimator (TI/MBAR).^27,28 The details for both approaches are discussed in the Supporting Information (SI). In brief, simulations were performed on GPUs using the CHARMM molecular software package^29,30 with CHARMM based force fields: CHARMM36 and CGenFF for protein and ligand components, respectively.^31–35 MSλD explored all R1 and R2 substituents collectively within a single simulation using adaptive landscape flattening (ALF) and biasing potential replica exchange (BP-REX) to enhance end-state sampling.^36,37 Five independent trials were carried out for the bound and unbound sides of the thermodynamic cycle (Figure S1) for a total of 1.84 μs of sampling. In contrast, the TI/MBAR calculations explored perturbations one at a time, in a pairwise manner. In keeping with recommended protocols,³⁸ redundant calculations were performed within closed perturbation cycles (Figure S2) to eliminate the hysteresis around each cycle and reduce error propagation along chains of subsequent perturbations.³⁹ Each calculation was performed in triplicate and consisted of 11 λ-states, with 5 ns of sampling per state. A total of 21 R1 and 24 R2 perturbations were performed in bound and unbound states for 14.85 μs of sampling. Computed ΔΔG_comp were then converted to absolute values using equation 3.^7,11

$$\mathrm{\Delta }{G}_{comp}=\mathrm{\Delta }\mathrm{\Delta }{G}_{comp}-\left(\frac{\mathrm{\Sigma }\mathrm{\Delta }\mathrm{\Delta }{G}_{comp}}{n}-\frac{\mathrm{\Sigma }\mathrm{\Delta }{G}_{\text{exp}t}}{n}\right)$$ (3)

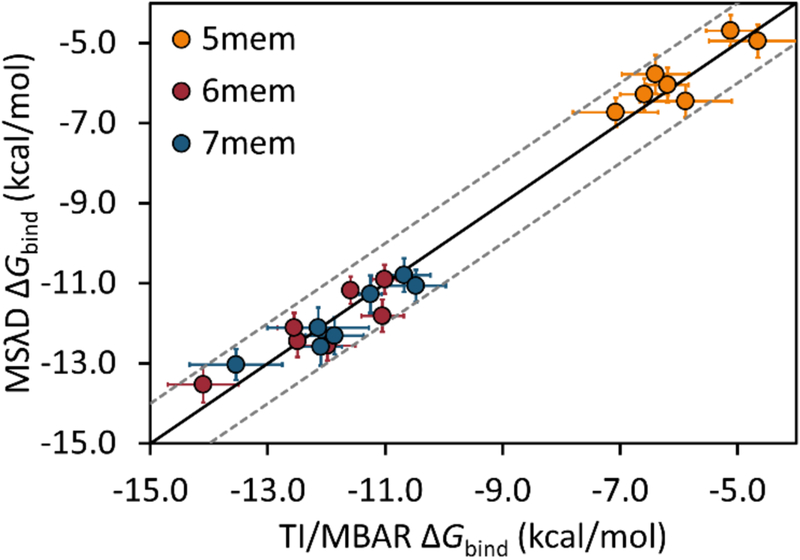
When comparing methods and assessing precision, agreement to within statistical noise is desirable. Standard deviations for computed protein-ligand ΔG_bind are typically 0.3–0.5 kcal/mol.⁷ As shown in Figure 2, excellent agreement is observed between MSλD and TI/MBAR results. The standard error estimates of the mean are less than 0.5 for all MSλD and many TI/MBAR data points, although some TI/MBAR uncertainties are as large as 0.86 kcal/mol (Table S1). A mean unsigned error of 0.37 kcal/mol and a Pearson correlation of 0.99 thus suggest that the MSλD results are precise and reproducible compared to TI/MBAR. A Welch’s t-test with a 99% confidence level confirms that all data points originate from the same distribution (Table S2). From this analysis, a comparison of efficiency can also be made. Timing benchmarks suggest no apparent overhead difference for running MD with MSλD vs TI in CHARMM; thus, simulation time lengths can be used directly for an efficiency comparison. With 1.84 μs of sampling, MSλD required 8 times fewer resources than TI/MBAR to compute all 21 ΔΔG_bind. However, differences in the uncertainties between methods should also be accounted for, e.g. some TI/MBAR uncertainties are nearly twice as large as MSλD uncertainties (Table S1). Reducing the amount of MSλD sampling to 10 and 15 ns for unbound and bound states of the ligand, respectively, retains consistent sampling of all 21 ligands, but increases the MSλD uncertainties by 25%. The MUE between TI/MBAR and MSλD is still small, 0.42 kcal/mol, but MSλD is now 20 times more efficient. Thus, even when more difficult transformations are performed, including large substituent perturbations and scaffold modifications, MSλD yields precise, reproducible free energy predictions and is ~8–20 times more efficient than traditional free energy approaches.

Figure 2.

Correlation between MSλD and TI/MBAR computed ΔG_bind with CHARMM36 and CGenFF force fields. R1 substituents are colored according to the ring size: orange (5-membered), red (6-membered), and blue (7-membered). The solid black line represents y=x, and grey dashed lines represent y = x ± 1.

Accuracy is also an important consideration and computed binding affinities must correlate with experimental activity measurements to be useful. For alchemical free energy methods, it is well understood that accuracy is dictated by the quality of sampling, i.e. the proficiency of the method, and the correctness of the force field for a given biochemical system.⁴⁰ The best agreement with experiment that has been observed using current molecular mechanics force fields is typically within 0.5–1.0 kcal/mol.^{3–12,18–20,26,37,39} The above analysis demonstrates that free energy results from MSλD are precise compared to TI/MBAR; thus, sampling with MSλD is expected to be well converged in this work. Any measure of accuracy in the following discussion thus reflects the quality of the force field employed with MSλD. Fortunately, MSλD is force field independent, meaning it can be used with any force field, and force field adjustment can be performed to improve accuracy for a given system, if necessary.

Using CHARMM-based force fields, initial agreement with experiment was unsatisfactory for this system, with a MUE of 1.83 kcal/mol (Figure S3 and Table S1). Experimentally, the most favorable inhibitors feature the 6-membered R1 substituent and the least favorable inhibitors have the 5-membered R1 substituent. The 7-membered ring is ~1.9 kcal/mol less favorable than the 6-membered ring, but ~1.3 kcal/mol more favorable than the 5-membered ring.¹¹ Using CGenFF ligand parameters, however, the 6-membered and 7-membered rings were predicted to bind equally well, differing by only ~0.2 kcal/mol. The 5-membered ring was less favorable than the 6-membered ring by ~6.0 kcal/mol, much larger than the experimental difference of ~3.2 kcal/mol (Table S1). We note that high penalty scores of greater than 100 provided by the CGenFF program suggested some parameter inconsistencies may be present. The original authors of the JP ligands saw relatively good agreement when they employed Schrödinger’s OPLSv3 force field with CM1A-BCC partial atomic charges, achieving a MUE of ~1.2 kcal/mol.^11,41 To test if an error in the CGenFF ligand parameterization was the source of our lower accuracy, new ligand parameters were obtained from the publicly available LigParGen server.⁴² This provides OPLS-AA force field parameters coupled with CM1A partial atomic charges for small molecules.^43,44 Two tests were performed. First, the CM1A charges were substituted for the original CGenFF charges, while all other CHARMM-based force field parameters remained unchanged. Second, all protein and ligand parameters were changed to the OPLS-AA/M and OPLS-AA/CM1A force fields, respectively.^43–45 For each test case, new MSλD calculations were performed and the free energy results were compared to experiment.

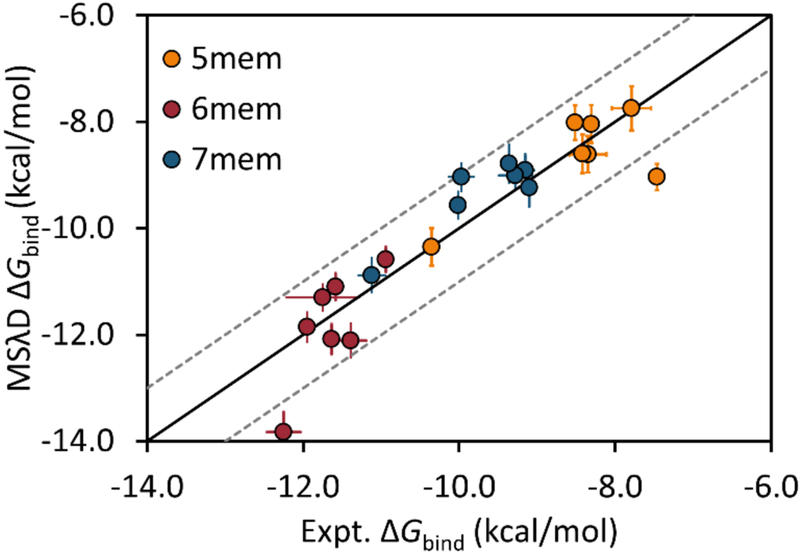
When CM1A charges were used in conjunction with CHARMM36 and CGenFF force field parameters (CGenFF/CM1A), the agreement with experiment was excellent (Figure 3, Table S2). The observed MUE was 0.47 kcal/mol and the Pearson R was 0.92. In addition, correct ranking is now observed between R1 substituents: 6-membered < 7-membered < 5-membered rings, matching experimental trends.¹¹ As shown in Figure S4, excellent agreement and correct ranking is also observed when OPLS-AA-based force fields were used with MSλD (see also Table S2). Importantly, this represents an important demonstration that MSλD is force field independent. The excellent agreement using CGenFF/CM1A parameters suggests that the partial charges in our original CGenFF ligand parameters were problematic. An in-depth analysis provided in the SI identified charge mismatching on the 5-membered ring to be the key culprit. This caused inhibitors featuring the 5-membered R1 ring to be over-solvated, introducing a large energetic penalty for pulling these ligands out of solution to bind to BACE1. Hence, large ΔΔG_bind errors were observed in the initial MSλD calculations. In contrast, hydration free energies were comparable for all JP ligands with CM1A charges and excellent ΔΔG_bind were computed. With correct force field representation, MSλD can provide very accurate free energy predictions.

Figure 3.

Correlation between MSλD computed and experimental free energies of binding (kcal/mol) for the JP ligands. These results were obtained with CHARMM36 and CGenFF/CM1A force field parameters. R1 substituents are colored according to the ring size: orange (5-membered), red (6-membered), and blue (7-membered). The solid black line represents y=x, and grey dashed lines represent y = x ± 1.

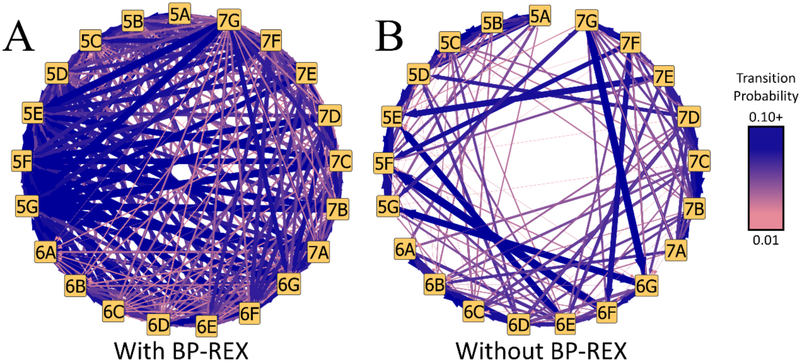
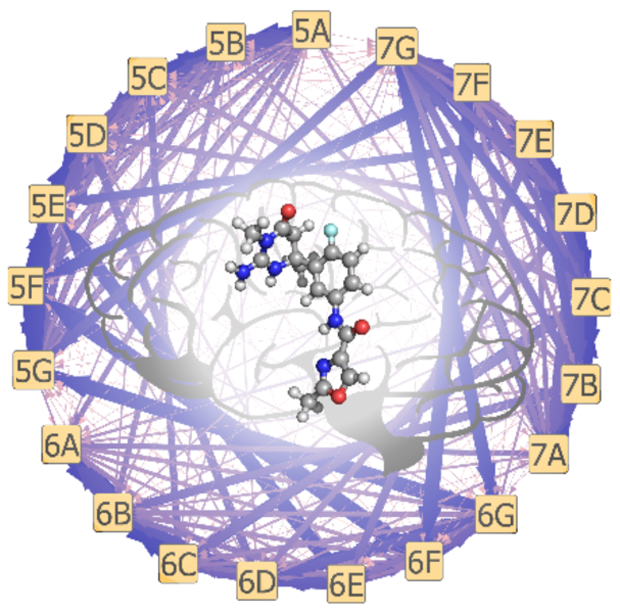
To combinatorially sample challenging substituent modifications with MSλD, and obtain accurate and precise ΔG_bind, enhanced sampling with BP-REX was beneficial. Equivalent simulations without BP-REX were performed, but not all 21 ligand end-states were consistently sampled over the course of a single MSλD calculation. Free energy convergence with MSλD is dependent upon visiting and transitioning between end-states many times.^{17–20,36,37} In Figure 4 we illustrate the protein-ligand transition probabilities that were observed with and without BPREX, averaged over 5 independent trials of 40 ns each. Without BP-REX (Figure 4B), 90% of all transitions occurred via an independent R1 or R2 change, e.g. 5E→{5A, 5B, 5C, 5D, 5F, 5G} or 5E→{6E, 7E}. However, with BP-REX, multiple dual site transitions were observed, e.g. 5E→{6G, 7C, 7G, …}, with probabilities greater than 5% per transition (Figure 4A), and dual site transitions now account for ~50% of all transitions. A similar trend is observed for unbound ligand simulations in water (Figure S5). This suggests that enhanced sampling algorithms are helpful for exploring these large substituent perturbations with MSλD and accelerating ΔG_bind convergence over shorter timescales. For example, our MSλD vs. TI/MBAR MUE was only 0.42 kcal/mol when MSλD simulations were shortened to 15 ns or less.

Figure 4.

Transition probability pathways for alchemically perturbing between ligand end-states with MSλD in the protein-ligand complex. (A) Significantly more transitions are observed when the BP-REX algorithm is employed. (B) Few transitions are observed without replica exchange. Arrow thickness and color correlate to high (blue, thick) to low (pink, thin) transition probabilities.

Lastly, there was substantial conformational flexibility observed for the flap and 10s loops of BACE1. Tresadern and co-workers found that inconsistent sampling of these motions introduced large variance between FEP+ ΔΔG_bind results and experiment. In their work, consistent sampling of these movements generally required 20 ns or longer per λ-window to reduce these artifacts.¹¹ Fortuitously, MSλD naturally uses longer timescales to sample all combinatorial ligand states within a single MD simulation. In this work, insufficient sampling of the loop motions is again observed for our 5 ns long TI calculations (Figure S6A), likely contributing to the larger TI/MBAR uncertainties (Table S1). MSλD, however, shows consistent sampling of open and closed loop conformations over the course of each simulation (Figure S6B) facilitating precise and accurate ΔG_bind predictions to be computed.

In conclusion, this work has investigated the applicability of MSλD to the exploration of large and challenging substituent modifications within the context of a pharmaceutical design problem addressing β-secretase 1 (BACE1), a prominent Alzheimer’s disease target. At two sites off a common ligand core, whole aromatic rings featuring long, flexible moieties at their para-position and scaffold modifications associated with a change in ring size were sampled in a combinatorial fashion with MSλD. All 3×7 perturbations were considered simultaneously within a single simulation. Accurate and reproducible modeling of terminal scaffold modifications did not require a “soft-bond” potential with MSλD.²⁶ Computed free energies of binding were demonstrated to be as accurate as a community accepted standard, TI/MBAR, to within 0.4 kcal/mol, yet MSλD was an order of magnitude more efficient. Though initial CGenFF force field parameters were unreliable for the 5-membered acylguanidinium heterocyclic ring, when MSλD calculations were performed with CM1A charges, the ΔΔG_bind results were accurate to within 0.5 kcal/mol of experimental IC₅₀s. Furthermore, performance of MSλD calculations with OPLS-AA based force fields is demonstrative proof that MSλD is force field independent, though polarizable force fields remain to be tested. Furthermore, this work demonstrates that MSλD is a viable alternative to FEP or TI methods for use in SBDD and lead optimization. MSλD can explore very large chemical spaces in a combinatorial manner, enabling the rapid identification of new inhibitor designs, and can illustrate structural insights into ligand bindings that can guide synergistic experimental discoveries.