Skip to main content
PMC home page
The Saudi Dental Journal logoLink to The Saudi Dental Journal
. 2019 Jun 17;32(2):101–107. doi: 10.1016/j.sdentj.2019.06.001

Dental implant primary stability in different regions of the Jawbone: CBCT-based 3D finite element analysis

Razan Alaqeely 1,⁎, Nadir Babay 1, Montaser AlQutub 1
PMCID: PMC7016247  PMID: 32071539

Abstract

Aim

This study aimed to analyze the primary stability of dental implant in maxillary and mandibular anterior and posterior regions using a finite element analysis.

Materials and methods

CBCT images of maxillary and mandibular regions were collected from patients’ radiographic data and transformed to 3D models. A Straumann Dental implant was inserted in each bone model and then pulled-out, where amount von-Mises stress was obtained and analyzed for each. A comparison between the insertion and the pull-out was evaluated.

Results

Twenty-four images were randomly selected for analysis from 122 scans. In both the insertion and the pull-out of the dental implant, von-Mises stress was high in cortical as compared to the cancellous bone (p < 0.0001). Maxillary posterior region had a low von-Mises stress (p < 0.001). Bone plastic deformation was higher in cancellous than the cortical bone in all bone regions and was the lowest in maxillary posterior region (p < 0.001). Bone displacement decreased from Type I to type IV bone.

Conclusion

Evaluation of von-Mises stress showed different measurements in maxillary and mandibular regions. Bone deformation was low in the maxillary posterior region.

1. Introduction

Dental implants are considered the gold standard in the restoration of missing teeth with a high rate of clinical success (Al-Nawas et al., 2012, Kammerer et al., 2014, Shatkin and Petrotto, 2012).

Factors such as implant geometry, design, the surgical technique and the quality as well as the quantity of jawbone are directly related to the osseointegration of dental implant (Mavrogenis et al., 2009). Bone quality and quantity of jawbone can directly influence the primary stability of dental implants (Alghamdi et al., 2011, Elias et al., 2012). Bone quality is affected by its mineral density, trabecular size, architecture, and matrix properties (Unnanuntana et al., 2011). These criteria are different between the jawbone regions which might explain the variation in clinical success rate of dental implant therapy.

Determining the primary stability prior to dental implant placement will provide a more accurate treatment planning and optimized treatment time (Dorogoy et al., 2017).

Several invasive and non-invasive methods were used for the measurement of the primary stability (Swami et al., 2016). The insertion torque of dental implant gives information about the condition of bone characteristics and stability at the time of insertion (Aparicio et al., 2006, Molly, 2006). However, its clinical use is limited since it is destructive and can only be used once (Ahn et al., 2012). Dental implant pull-out can give a clearer picture of primary stability and how the dental implant will initially engage the bone (Ahn et al., 2012).

To perform a nondestructive assessment of the implant primary stability, computed-simulation models to study the biomechanical behaviors of dental implants in the jawbone were developed (Martini et al., 2013). Finite element analysis (FEA) is a non-clinical non-invasive method, which provide a productive evaluation of the distribution of peri-implant bone strain and stability of the bone-implant contact (BIC) (Sugiura et al., 2015).

As the bone differences will influence the bone to implant contact, Lekhom and Zarb classified the jawbone into four different groups (Type I, II, III, IV) according to its quality (Lekhom and Zarb, 1985). This classification lacked the precise description of the bone trabeculation. A new revised classification was established to capture the bone differences based on CT scans such as: Type 1: entirely homogenous compact bone, Type 2a: thick layer of compact bone surrounding a core of dense trabecular bone, Type 2b: thick layer of compact bone surrounding a core of medium-density trabecular bone, Type 2c: thick layer of compact bone surrounding a core of low-density trabecular bone, Type 3a: thin layer of compact bone surrounding a core of dense trabecular bone, Type 3b: thin layer of compact bone surrounding a core of medium-density trabecular bone, and Type 4: thin layer of compact bone surrounding a core of low-density trabecular bone (Al-Ekrish et al., 2018). Such specific details aided in efficiently distinguishing between the various combinations of the compact and the trabecular bone.

The prediction of implant stability and evaluation of biomechanical contact between the dental implant and the bone are helpful in studying dental implants design and geometry in different anatomical regions of the jawbone (Cook et al., 1882, Tang et al., 2012, Inglam et al., 2013). Finite element analysis (FEA) is a non-clinical non-invasive method which provide a productive evaluation of the stresses and strains for a given geometry.

The present study aimed to evaluate the von-Mises stress and peri-implant bone stability of a Straumann standard-plus dental implant placed in different anatomical jawbone regions and analyzing it with a computed tomography-based 3D finite element analysis model.

2. Materials and methods

After the approval by the College of Dentistry Research Centre (CDRC) (PR 0056j), the study was conducted in the college of dentistry at King Saud University as well as using the facility and the support of the advanced manufacturing institute (AMI) of the College of Engineering.

Cone-beam CT (CBCT) images of maxillary and mandibular anterior and posterior regions obtained from October 2016 to May 2017 were collected (ProMax 3D Mid, Planmeca, USA).

Inclusion criteria for the selected images were as follow: Healthy Saudi male or female patients aged 25–55 years, CBCT scans for the purpose of dental implant site assessment, sites assessed by CBCT are resting areas; Bucco-lingual bone width of at least 7–8 mm and bone height of at least 10 mm (avoiding the maxillary sinuses and the inferior alveolar nerve canals).

Images were excluded if they contained any metallic restorations to minimize the scattering. Sites with recent dental extraction sockets (3–6 months after extraction) or sites with previous bone grafting procedures were also excluded.

Cone-beam CT (CBCT) set of images of edentulous areas were randomly-obtained and grouped according to the area of missing teeth:

Region 1: anterior maxilla. Region 2: posterior maxilla. Region 3: anterior mandible. Region 4: posterior mandible.

The selected CBCT images were classified according to the revised classification of Lekhom and Zarb and exported as DICOM (digital imaging and communication in medicine) files.

Using the medical modeling software (Materialise Mimics, Leuven, Belgium), the DICOM files were transformed from a 2D image to a full 3D solid model (Table 1).

Table1.

Three-dimensional models of different bone type according to Al-Ekrish et al. (2018).

graphic file with name fx1.gif
Open in a new tab

The cortical and cancellous bone were identified according to a gray-scale value predefined in the program (cancellous = 148–661, cortical = 662–1988). A 3D graphic model was generated for the cortical and cancellous bony and saved in STereoLithography (STL) format (Fig. 1a). A solid three-dimensional model was created using CATIA (Catia v5.20. © Dassault Systems) (Fig. 1b).

Fig. 1.

Fig. 1

Open in a new tab

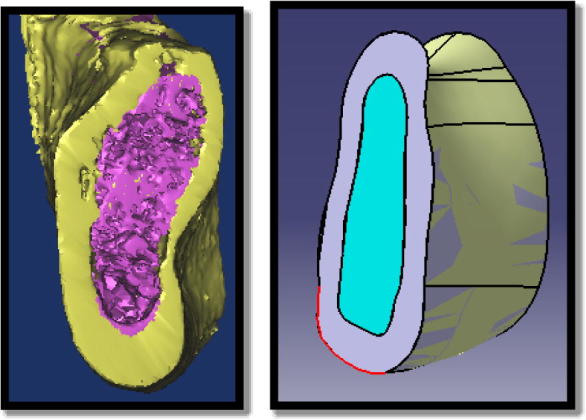
Cross section of the three- bone model (a) and solid 3D bone model (b).

A Straumann® standard plus dental implant with a length of 10 mm, ∅4.1 mm, and a platform of ∅4.8 mm was the experimental design chosen for the study (Institute Straumann AG, Waldenburg, Switzerland). One design of dental implant is used in this study to study the effect of different bone type only without other variable.

The detailed geometric information (e.g., length, diameter, macro-micro thread configuration) in millimeters were used to create a CAD model of the dental implant using 3-matic software (Materialise 3-matic, Leuven, Belgium).

A dental implant bed was prepared by creating a cylindrical hole at the middle of each experimental model with a width of 3.5 mm and a length of 10 mm according to the manufacturer’s recommendations. The coronal aspect of the simulated bone was widened to 4.1 mm resembling the effect of a profile drill as per the manufacturer’s instructions. A cylindrical hole was made in the middle of the bone model in a buccolingual and mesiodistal direction simulating the position of a clinical dental implant. The prepared experimental bone models were imported in ANSYS Workbench 17 (Swanson Analysis Inc., Houston, PA, U.S.A.) with the dental implant being placed inside the bone prior to the analysis.

2.1. Setting of materials properties

Material properties of cortical and cancellous bone were assumed to be transversely isotropic and linearly elastic whereas the dental implant was isotropic, homogeneous, and linearly elastic (Table 2).

Table 2.

Material properties used in FE model (Geng et al., 2001).

Material Young’s modulus [MPa] Poisson’s ratio Yield strength [MPa]
Cancellous bone 700 0.35 4.7
Cortical bone 18,000 0.35 107
Titanium implant 117,000 0.36 480
Open in a new tab

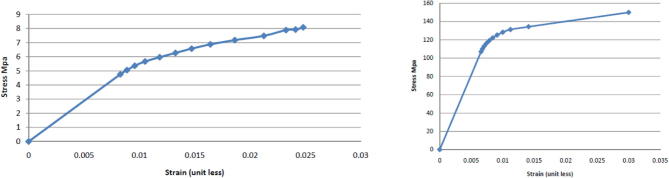
The stress-strain curve of both cortical and cancellous bone (Fig. 2a and b) were used to resemble the elastic and plastic deformation that can occur in bone with the application of forces (Rho et al., 1993).

Fig. 2.

Fig. 2

Open in a new tab

a: (left) Cancellous bone true tensile stress-strain curve. b: (right) Cortical bone plastic strain hardening curve.

2.2. Meshing and contact characteristics

The bone geometry underwent meshing into tetrahedral parabolic solid elements of up to 0.3 mm in the bone area corresponding to the dental implant hole to have an efficient analysis (Fig. 3). The nature of the contact between the bone and the dental implant was set as contact interfaces (non-osseointegration) with the friction coefficient set to 0.3 (12, 13).

Fig. 3.

Fig. 3

Open in a new tab

Meshing of bone model.

2.3. Load and constraints

In each experimental bone model, the boundary conditions were set as fixed at the most mesial, distal and apical nodes of the model in all directions. Analysis of insertion was simulated using an equal average insertion torque provided by the manufacturer (25 N cm) at the top of the dental implant.

Measurements were taken during the dental implant insertion into the bone followed by a pull-out force with a constant speed of 1 mm per minute and a load cell of 1 kN (Nonhoff et al., 2015). The measurements were made at 1.5 s after starting the removal of the dental implant from its bed. The maximum stress concentration in the cortical and cancellous bone was expressed as von Mises equivalent stress in MegaPascal (MPa).

2.4. Statistical analysis

SPSS® software version 21 (IBM Corporation, Armonk, NY, USA) was used.

The study sample number was calculated based on a power-analysis using the following formula: n = 1 + 2C(s/d)2 assuming a standard deviation (s) of 12 and an effect size (d) of 15 based on previous FEA studies tested the correlation between bone density and implant stability. C-value was fixed at 7.85 (resulting from 1 − β = 0.8 and α = 0.05).

Significant differences between the models was determined using one-way analysis of variance (ANOVA) and Tukey-Kramer Multiple comparison test with significance level at (p < 0.05).

3. Results

A total of one-hundred twenty-two CBCT images were obtained for the purpose of implant site assessment from October 2016 to May 2017. These CBCT images were analyzed according to the inclusion and exclusion criteria and randomly selected (Fig. 4).

Fig. 4.

Fig. 4

Open in a new tab

CBCT images obtained and evaluated.

The constructed finite element model of the dental implant and bone models’ elements and nodes were of a range of 29,365 elements and 51,476 nodes for the bone models and 3082 elements and 8829 nodes for the dental implant model. The bone type was classified according to the jawbone region where three bone models were selected for each bone type.

3.1. Biomechanical analysis of insertion force

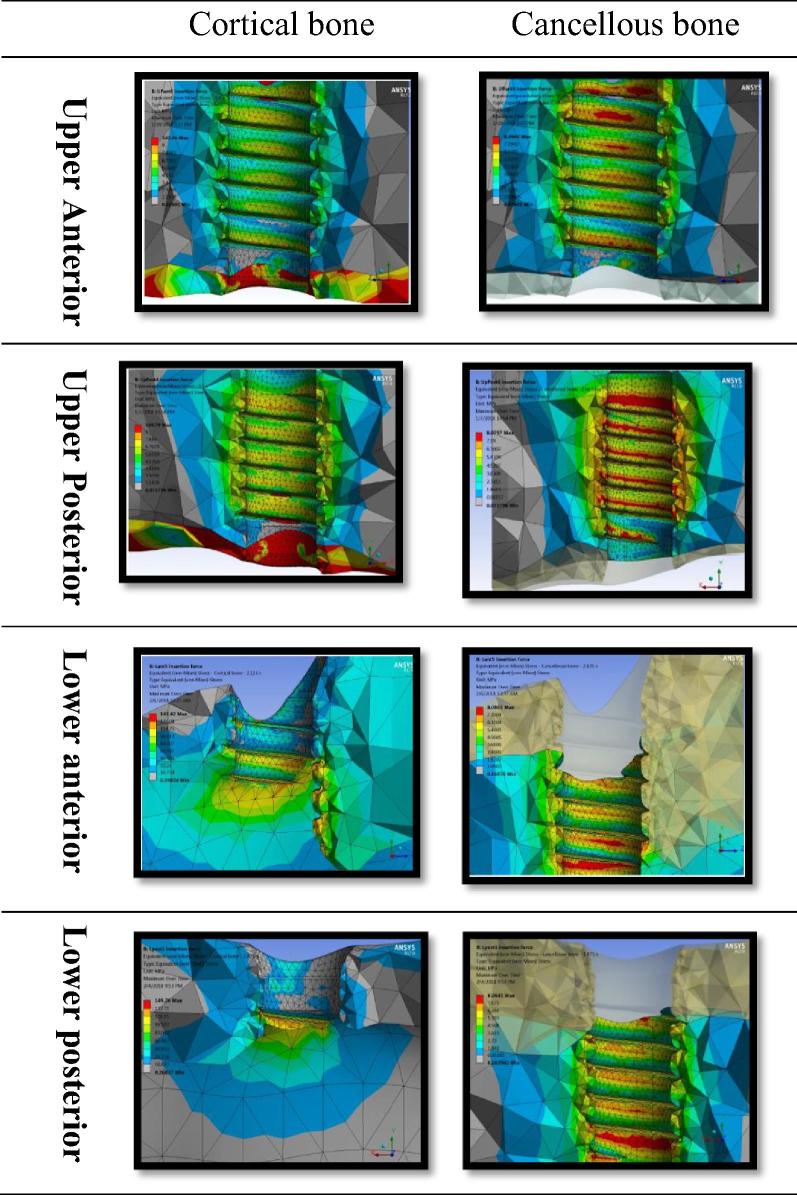
Mean stresses generated in bone models during dental implant insertion according to jawbone region are shown in Table 3.

  • a.

    Bone von-Mises stress (Fig. 5): The von-Mises stress values for the maxillary anterior, mandibular anterior and posterior cortical bone were similar and respectively 145.50 ± 3.261 MPa, 142.16 ± 6.804 MPa, and 146.46 ± 4.337 MPa. The difference between the anatomical regions was not statistically significant difference between them (p < 0.52).

  • The maxillary posterior region had significantly low von-Mises stress in the cortical bone (58.325 ± 10.105 MPa). The difference was statistically significant when compared to the maxillary anterior and mandibular anterior (P < 0.001). Considering bone type, Type I bone had the highest value (147.8 MPa ± 2.2) while type IV bone had the lowest value (73.8 ± 1.5 MPa).

  • Von-Mises stress in type III b (119.2 MPa ± 5.6) was low in comparison to type I, II, IIIa bone(p < 0.05) and higher when compared to type IV bone (P < 0.05).

  • b.

    Bone plastic strain: The maxillary and the mandibular cancellous bone had significant higher plastic deformation as compared to the cortical bone. The mean plastic strain for the cancellous bone was 0.52 and 0.03 for the cortical bone in all bony regions with statistically significant difference (p < 0.001). The cortical bone plastic deformation decreased from Type I bone (0.074) to type IV bone (0.034) with no statistically significant difference between them (p < 0.4).

  • c.

    Bone displacement: The maxillary posterior region had the lowest bone displacement value of 309.23 N when compared to the maxillary anterior and the mandibular anterior and posterior regions (P < 0.001).

  • The bone displacement decreased from type I bone (1205.5 N) to type IV bone (310.1 N) with type IIa bone having the maximum displacement (1400 N).

Table 3.

Mean equivalent von-Mises stress and plastic deformation in bone models during implant insertion.

Anatomical region Cortical bone
 Cancellous bone
Von Mises stress (MPa) Plastic strain (deformation) Von Mises stress (MPa) Plastic strain (deformation)
Maxillary posterior 58.325 ± 10.105 0.02 8.03 ± 0.03 0.38
Maxillary anterior 145.50 ± 3.261 0.03 8.06 ± 0.03 0.74
Mandibular posterior 142.16 ± 6.804 0.04 8.04 ± 0.05 0.34
Mandibular anterior 146.46 ± 4.337 0.06 8.07 ± 0.02 0.62
Open in a new tab

Fig. 5.

Fig. 5

Open in a new tab

Von-Mises stress from dental implant insertion in maxillary and mandibular anterior and posterior regions in cortical and cancellous bone.

3.2. Biomechanical analysis of pull-out force

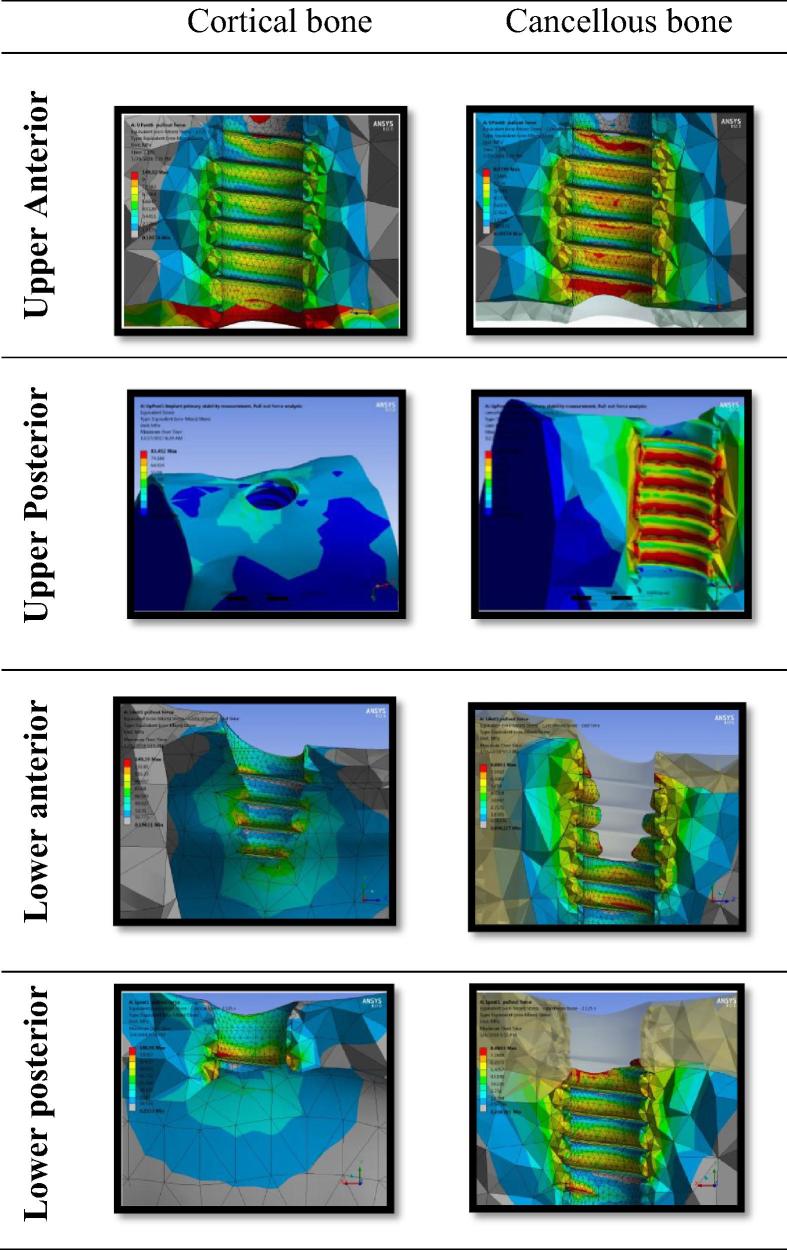
The Von-Mises stresses and the plastic strain during dental implant pull out according to jawbone region are represented in Table 4.

  • a.

    Bone von-Mises stress (Fig. 6): The Mean von-Mises stress values for the maxillary anterior, mandibular anterior and the posterior cortical bone were similar and respectively 142.4 ± 3.9 MPa, 147 ± 1.6 MPa, and 127.8 ± 15.1 MPa. The difference between the anatomical regions was not statistically significant (p < 0.2). The von-Mises stress value of the maxillary posterior cortical bone was significant low (54.13 ± 19 MPa) when compared to the maxillary anterior, mandibular anterior and the posterior regions with the difference statistically significant (P < 0.001).

  • The von-Mises stress value of the maxillary and mandibular cancellous bone was similar and the difference not statistically significant (p < 0.5).

  • Von-Mises stress decreased from type I bone (147.1 ± 2.3) to type IVbone (69.5 ± 10.6 MPa). Type I and II (a,b,c) bone values were not statistically significant (P < 0.05). A statistically significant difference was found between Type IIIa (688.6 ± 3.5 MPa) and Type IIIb (399 ± 4.2 MPa) (p < 0.05).

  • b.

    Bone plastic strain: The maxillary and mandibular cancellous bone had significant higher plastic strain (deformation) as compared to the cortical bone. The mean plastic deformation in cancellous bone maxillary and mandibular bone regions was 0.95 and 0.034 in cortical bone and the difference was statistically significant (p < 0.001). The values of the maxillary anterior, mandibular anterior and the posterior cortical bone deformation were similar and respectively of 0.05 ± 0.03, 0.016 ± 0.016, and 0.07 ± 0.02, The difference between the anatomical regions was not statistically significant (P < 0.5). The highest amount of bone strain was found in type IIIa cancellous bone with a value of 4.8 ± 1.8.

  • c.

    Bone displacement: The bone displacement value of the maxillary anterior, mandibular anterior and the posterior regions were similar and respectively 810.14 N, 969.31 N, and 712.78 N. The difference between the anatomical regions was not statistically significant (p < 0.74). The maxillary posterior region had a lower bone displacement (302.85 N) when compared to the maxillary anterior, anterior and the posterior mandibular with the difference not statistically significant (p < 0.008). The mandibular anterior region had the highest bone displacement with a value reaching 969.31 N. The comparison to other anatomical regions was not statistically significant (p < 0.46). The bone displacement decreased from type I bone (1020.3 ± 12.5 MPa) to type IV bone (315 ± 5.8 MPa). There was no significant difference between type I and type II a and b bone (P < 0.1).

Table 4.

Mean equivalent von Mises stress and plastic deformation in bone models during implant pull-out.

Anatomical region Cortical bone
 Cancellous bone
Von Mises stress (MPa) Plastic strain (deformation) Von Mises stress (MPa) Plastic strain (deformation)
Maxillary posterior 54.13 ± 19 0.0008 ± 0.002 8.05 ± 0.01 0.4 ± 0.3
Maxillary anterior 142.4 ± 3.9 0.05 ± 0.03 8.06 ± 0.03 1.2 ± 0.9
Mandibular posterior 127.8 ± 15.1 0.016 ± 0.016 8.07 ± 0.02 1.6 ± 0.4
Mandibular anterior 147 ± 1.6 0.07 ± 0.02 8.07 ± 0.03 0.6 ± 0.2
Open in a new tab

Fig. 6.

Fig. 6

Open in a new tab

Von-Mises stress from dental implant pull-out in maxillary and mandibular anterior and posterior regions in cortical and cancellous bone.

4. Discussion

This study represented a thorough investigation of the dental implant insertion and the pullout in different anatomical areas of the jawbone. Multiple bone samples for each anatomical region aided in better understanding the variations due to the bone thickness natural differences (Faber and Fonseca, 2014).

During the dental implant insertion, the significant difference of von-Mises stress found in the maxillary posterior region might be explained by the difference in bone density (Lin et al., 2005).

Initially elevated von-Mises stress in the cortical-cancellous interface was observed, thus increasing the insertion depth resulted in increased stress in the cancellous bone. This observation is in agreement with a stepwise analysis of dental implant insertion which concluded that the cortical bone around the implant neck represented the area of the maximum stress (Van Staden et al., 2006, Guan et al., 2011).

The bone displacement evaluation was in accordance to the quality of bone. The more cortical bone available, the more stress was generated, and the bone displacement occurred. This finding is in agreement with a finite element analysis study on the maxillary posterior area which concluded that the bone density is directly related to the stress.

A lower density resulted in lower von-Mises stress (Lin et al., 2008). This finding was explained by Hao et al. (2014) results in a cone beam computed tomography evaluation. The bone density increased as cortical bone thickness increased and the cortical bone was more prevalent in the anterior rather than the posterior and in mandibular rather than the maxillary regions (Hao et al., 2014).

In the pull-out force, the maximum von-Mises stress distribution was recorded in the cortical-cancellous interface and around the dental implant most apical thread. This could be explained by the high elastic modulus and the shear strength of the cortical bone (Chapman et al., 1996).

Adding to that, the cortical bone exhibited a strengthening effect to the underlying cancellous bone (Lin et al., 2008).

In the area of dental implant most apical thread, the increase in the von-Mises stress could be related to the change in dental implant width by the thread geometry. According to the mechanical tests, the pull-out force response depended on the change in width, length, or the shear strength of the material (Chapman et al., 1996). This observation is in disagreement with the dental implant pull-out which had no effect on cortical bone (Rittel et al., 2017). The difference can be a result of model simulation difference as they assumed a uniform cortical bone thickness of ∼2 mm which was completely damaged in dental implant insertion (Dorogoy et al., 2017).

This study in contrast used more accurate measurements of bone thickness and morphology simulation resulting in a precise analysis for the stress distribution in different jawbone types (Alper et al., 2012).

5. Conclusion

In conclusion, von-Mises stress was found to be proportional to the presence of bone quality.

Lower bone quality manifests a lower bone displacement values explaining the dental implant decreased primary stability.

Precise surgical bone preparation technique to have a primarily stable dental implant in low-dense bone area i.e (type IV and type IIIb) is recommended.

The study focused on single implant design. A variation in implant geometry might affect the von-Mises stress values.

Declaration of Competing Interest

The authors declare that there is no conflict of interest

Footnotes

Peer review under responsibility of King Saud University.

References

  1. Ahn S.-J., Leesungbok R., Lee S.-W., Heo Y.-K., Kang K.L. Differences in implant stability associated with various methods of preparation of the implant bed: an in vitro study. J. Prosthet. Dent. 2012;107:366–372. doi: 10.1016/S0022-3913(12)60092-4. [DOI] [PubMed] [Google Scholar]
  2. Al-Ekrish A.A., Widmann G., Alfadda S.A. Revised, computed tomography-based Lekholm and Zarb Jawbone quality classification. Int. J. Prosthodont. 2018;31:342–345. doi: 10.11607/ijp.5714. [DOI] [PubMed] [Google Scholar]
  3. Alghamdi H., Anand P.S., Anil S. Undersized implant site preparation to enhance primary implant stability in poor bone density: a prospective clinical study. J. Oral Maxillofac. Surg. 2011;96:e506–e512. doi: 10.1016/j.joms.2011.08.007. [DOI] [PubMed] [Google Scholar]
  4. Al-Nawas B., Bragger U., Meijer H.J.A., Naert I., Persson R., Perucchi A., Muller F. A double-blind randomized controlled trial (RCT) of titanium-13zirconium versus titanium grade IV small-diameter bone level implants in edentulous mandibles–results from a 1-year observation period. Clin. Implant Dent. Relat. Res. 2012;14:896–904. doi: 10.1111/j.1708-8208.2010.00324.x. [DOI] [PubMed] [Google Scholar]
  5. Alper B., Gultekin P., Yalci S. Application of finite element analysis in implant dentistry. Finite Elem. Anal. – New Trends Dev. 2012 [Google Scholar]
  6. Aparicio C., Lang N.P., Rangert B. Validity and clinical significance of biomechanical testing of implant/bone interface. Clin. Oral. Implants Res. 2006;17:2–7. doi: 10.1111/j.1600-0501.2006.01365.x. [DOI] [PubMed] [Google Scholar]
  7. Chapman J.R., Harrington R.M., Lee K.M., Anderson P.A., Tencer A.F., Kowalski D. Factors affecting the pullout strength of cancellous bone screws. J. Biomech. Eng. 1996;118:391–398. doi: 10.1115/1.2796022. [DOI] [PubMed] [Google Scholar]
  8. Cook S.D., Weinstein A.M., Klawitter J.J. A three-dimensional finite element analysis of a porous rooted Co-Cr-Mo alloy dental implant. J. Dent. Res. 1882;61:25–29. doi: 10.1177/00220345820610010501. [DOI] [PubMed] [Google Scholar]
  9. Dorogoy A., Rittel D., Shemtov-Yona K., Korabi R. Modeling dental implant insertion. J. Mech. Behav. Biomed. Mater. 2017;68:42–50. doi: 10.1016/j.jmbbm.2017.01.021. [DOI] [PubMed] [Google Scholar]
  10. Elias C.N., Rocha F.A., Nascimento A.L., Coelho P.G. Influence of implant shape, surface morphology, surgical technique and bone quality on the primary stability of dental implants. J. Mech. Behav. Biomed. Mater. 2012;16:169–180. doi: 10.1016/j.jmbbm.2012.10.010. [DOI] [PubMed] [Google Scholar]
  11. Faber J., Fonseca L.M. ow sample size influences research outcomes. Dent. Press. J. Orthod. 2014;19:27–29. doi: 10.1590/2176-9451.19.4.027-029.ebo. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Geng J., Tan K., Liu G. Application of finite element analysis in implant dentistry a review of the literature. J. Prosthet. Dent. 2001;85:585–598. doi: 10.1067/mpr.2001.115251. [DOI] [PubMed] [Google Scholar]
  13. Guan H., VAN Staden R.C., Johnson N.W., Loo Y. Dynamic modelling and simulation of dental implant insertion process—a finite element study. Finite Elem. Anal. Des. 2011;47:886–897. [Google Scholar]
  14. Hao Y., Zhao W., Wang Y., Yu J., Zou D. Assessments of jaw bone density at implant sites using 3D cone-beam computed tomography. Eur. Rev. Med. Pharmacol. Sci. 2014;18:1398–1403. [PubMed] [Google Scholar]
  15. Inglam S., Chantarapanich N., Suebnukarn S., Vatanapatimakul N., Sucharitpwatskul S., Sitthiseripratip K. Biomechanical evaluation of a novel porous-structure implant: finite element study. Int. J. Oral Maxillofac. Implants. 2013;28:e48–e56. doi: 10.11607/jomi.1666. [DOI] [PubMed] [Google Scholar]
  16. Kammerer P.W., Palarie V., Schiegnitz E., Hagmann S., Alshihri A., Al-Nawas B. Vertical osteoconductivity and early bone formation of titanium-zirconium and titanium implants in a subperiosteal rabbit animal model. Clin. Oral. Implants Res. 2014;25:774–780. doi: 10.1111/clr.12175. [DOI] [PubMed] [Google Scholar]
  17. Lekhom U., Zarb G. Patient selection and preparation. Tissue-Integr. Prosthesis: Osseointegr. Clin. Dent. 1985:199–209. [Google Scholar]
  18. Lin Chun-Li, Kuo Yu-Chan, Lin Ting-Sheng. Effects of dental implant length and bone quality on biomechanical responses in bone around implants: a 3-D non-linear finite element analysis. Biomed. Eng.Appl Basis Comm. 2005;17:44–49. [Google Scholar]
  19. Lin C., Wang J., Ramp M.S.L.C., Liu P. Biomechanical response of implant systems placed in the maxillary posterior region under various conditions of angulation, bone density, and loading. Int. J. Oral Maxillofac. Implants. 2008;23:57–64. [PubMed] [Google Scholar]
  20. Martini A.P., Barros R.M., Junior A.C., Rocha E.P., de Almeida E.O., Ferraz C.C., Pellegrin M.C., Anchieta R.B. Influence of platform and abutment angulation on peri-implant bone. A three-dimensional finite element stress analysis. J. Oral. Implantol. 2013;39:663–669. doi: 10.1563/AAID-JOI-D-11-00029. [DOI] [PubMed] [Google Scholar]
  21. Mavrogenis A.F., Dimitriou R., Parvizi J., Babis G. Biology of implant osseointegration. J. Musculoskel. Neuron. Interact. 2009;9:61–71. [PubMed] [Google Scholar]
  22. Molly L. Bone density and primary stability in implant therapy. Clin. Oral. Implants Res. 2006;17:124–135. doi: 10.1111/j.1600-0501.2006.01356.x. [DOI] [PubMed] [Google Scholar]
  23. Nonhoff J., Moest T., Schmitt C.M., Weisel T., Bauer S., Schlegel K.A. Establishment of a new pull-out strength testing method to quantify early osseointegration – an experimental pilot study. J. Craniomaxillofac. Surg. 2015;43:1966–1973. doi: 10.1016/j.jcms.2015.10.005. [DOI] [PubMed] [Google Scholar]
  24. Rho J.Y., Ashman R.B., Turner C.H. Young's modulus of trabecular and cortical bone material: ultrasonic and microtensile measurements. J. Biomech. 1993;26:111–119. doi: 10.1016/0021-9290(93)90042-d. [DOI] [PubMed] [Google Scholar]
  25. Rittel D., Dorogoy A., Shemtov-Yona K. Modelling dental implant extraction by pullout and torque procedures. J. Mech. Behav. Biomed. Mater. 2017;71:416–427. doi: 10.1016/j.jmbbm.2017.04.010. [DOI] [PubMed] [Google Scholar]
  26. Shatkin T.E., Petrotto C.A. Mini dental implants: a retrospective analysis of 5640 implants placed over a 12-year period. Compen. Cont. Edu. Dent. 2012;33:2–9. [PubMed] [Google Scholar]
  27. Sugiura T., Yamamoto K., Kawakami M., Horita S., Murakami K., Kirita T. Influence of bone parameters on peri-implant bone strain distribution in the posterior mandible. Medicina Oral Patología Oral y Cirugia Bucal. 2015:e66–e73. doi: 10.4317/medoral.19878. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Swami V., Vijayaraghavan V., Swami V. Current trends to measure implant stability. J. Indian Prosthodont. Soc. 2016;16:124–130. doi: 10.4103/0972-4052.176539. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Tang C.B., Liul S.Y., Zhou G.X., Yu J.H., Zhang G.D., Bao Y.D., Wang Q.J. Nonlinear finite element analysis of three implant-abutment interface designs. Int. J. Oral Sci. 2012;4:101–108. doi: 10.1038/ijos.2012.35. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Unnanuntana A., Rebolledo B.J., Khair M.M., Dicarlo E.F., Lane J. Diseases affecting bone quality: beyond osteoporosis. Clin. Orthopaed. Relat. Res. 2011;469:2194–2206. doi: 10.1007/s11999-010-1694-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Van Staden R.C., Guan H., Loo Y.C. Griffith University; 2006. Application of Finite Element Method in Dental Implant Research. PhD. [DOI] [PubMed] [Google Scholar]

Articles from The Saudi Dental Journal are provided here courtesy of Elsevier

RESOURCES