Abstract
The precise determination of the dead time is essential in a chromatography system as it is a primary parameter for the determination of other secondary parameters such as the adjusted retention time, relative retention time, retention factor and retention index. Several of the indirect methods used for the determination of the dead time in this study were iteration, nonlinear, spreadsheet and statistics methods, which were implemented using the ANSI C programming language. The calculation of each method was tested with temperature and column variations for measuring the retention time of a n-alkane homologous series and accuracy analysis of each mathematical method (indirect method) to the marker substance (direct method). Changes in the temperature and column variations (type, polarity and column length) affected the calculation of the dead time values but did not affect its accuracy. The value of the dead time generated by the non-linear method was relatively high, with errors above 10%, while the other methods utilized are quite good with errors below 8% regardless of the column and temperature variations.
Keywords: Analytical chemistry, Chemical engineering, Gas chromatography, Alkanes, Dead time, Column and temperature effect, Mathematical methods
Analytical chemistry; Chemical engineering; Gas chromatography; Alkanes; Dead time; Column and temperature effect; Mathematical methods
1. Introduction
The accurate determination of the dead time is a crucial factor in chromatographic analysis (Watanachaiyong et al., 2000; Peng, 2010). The accuracy of the dead time determines the accuracy of other retention parameters (Didaoui et al., 1999) such as the adjusted retention time, capacity factor, retention index (Kováts, 1958), selectivity, separation efficiency, plate theory, resolution and so on (Grob and Barry, 2004). The dead time can be calculated by two methods, direct and indirect methods. The direct method was carried out through the injection of unretained compounds in a chromatography column, while the indirect method was performed using mathematical algorithmic approaches (Quintanilla-López et al., 1997).
The determination of the dead time by a direct method on a gas chromatography system, as measured by the inert gas retention time (García Domínguez and Diez-Masa, 2001), still faced problems such as the mismatch in the use of an inert gas with certain types of detectors. The inert gas showed good unretained character in the GC column (Dallos et al., 2003; Arey et al., 2005; McGinitie and Harynuk, 2012), but it could not be detected using the FID detector (Cramers et al., 1970). In addition, other problems were also found such as noise interference and difficulty in identifying the peak (Von Mühlen and Marriott, 2011) at certain gas concentrations at the beginning of chromatographic elution.
To resolve the problems with the direct method, indirect methods began to be studied through the use of mathematical algorithms. Several different algorithmic approaches have been developed for the calculation of the dead time by indirect methods (García Domínguez and Diez-Masa, 2001). These approaches were non-linear algorithms (Wätzig and Ebel, 1991; Wätzig et al., 1992), iterations (Guardino et al., 1976), spreadsheets (Braithwaite and Cooper, 1993), statistics (Grobler and Balizs, 1974) and so on. Calculations were performed by utilizing the retention times and carbon number of a homologous series (Suliman, 2002; Pang et al., 2007; Zhang et al., 2001). This procedure is more accessible and more practical than the direct method procedure because the problems that occurred in the direct method could be avoided. The n-alkane homologous series is also used to determine the Kovats retention index in gas chromatography systems (Idroes, 2011; Bieri and Marriott, 2008). This method is also suitable to be implemented in (Idroes, 2005; Pratiwi et al., 2015) liquid chromatography systems.
In many indirect method studies, researchers' reviews still often question the logic and capability of algorithms to calculate the dead time. The accuracy and robustness of the method towards experimental condition changes is a critical aspect that is rarely discussed (Quintanilla-López et al., 1997). This increases doubt and lacks justification for the calculated results of each method. Method comparison studies are also rarely carried out, and each method is examined separately so that it is difficult to determine the best approach to use. Only a few researchers were found to have compared several indirect methods (Didaoui et al., 1999; Quintanilla-López et al., 1997; Wu et al., 2006). The recent study reported that the statistical analysis by using Randomized Block Design method to dead times by several methods showed that there are a significant effect of the temperature and column variation to the dead time determination (Idroes et al., 2019a) except Parcher's method (Parcher and Johnson, 1980). But the research only focus on the effect of the temperature and column variation to dead time determination without considering the accuracy of the methods.
The indirect methods are still not practical to be widely applied. Some methods such as non-linear and spreadsheet methods are still presented in the algorithmic form (Wätzig and Ebel, 1991; Braithwaite and Cooper, 1993), and there are no software or flowchart products to facilitate use by other researchers or the general public. The statistical method is more straightforward to implement because its flowchart is available in the published literature (Grobler and Balizs, 1974). However, software is still needed to facilitate the application of the method to be applied. Only the iteration method has complete information, including algorithms, flowcharts (Guardino et al., 1976) and source code by Furr, (1989). Unfortunately, the programming language used by Furr is not compatible with current compilers.
In this study, the development of flowcharts and calculation software was carried out for the non-linear and spreadsheet methods. For the iteration and statistics methods, the flowcharts are available in the literature (Guardino et al., 1976; Grobler and Balizs, 1974), and the researcher only developed the calculation software. The calculation of each method was tested against temperature and column variation for measuring n-alkane homologous series retention data, and the accuracy of each indirect method was analyzed by comparing it to a substance marker (direct method).
2. Experimental
2.1. Material and methods
The determination of the dead time can be performed by two methods: direct and indirect. The direct method is a direct measurement by measuring the dead time of an unretained gas on the chromatography column, while the indirect method is an indirect determination by calculating the dead time through an algorithmic approach from retention times and carbon number data of a homologous series (García Domínguez and Diez-Masa, 2001). In this study, indirect methods were carried out through algorithmic calculations using the retention times and carbon number data of a n-alkane homologous series. The results from indirect methods were calibrated to the direct method results that were obtained from the measurement of the argon dead time using a gas chromatography column.
The software development of indirect methods was based on non-linear, iteration, spreadsheet and statistical algorithms. The mathematical calculations and approach were implemented using the ANSI C programing language by utilizing some of its library. The software for each method was made in several separate files.
2.2. Non-linear method
Waetzig et al. introduced the non-linear algorithm for a liquid chromatography system (Wätzig and Ebel, 1991). The algorithm was used to create software. Based on the algorithm, the determination of the dead time was performed through non-linear regression based on the linear relationship between the carbon number and logarithm of adjusted retention times. Differentiations of Deadtime (tM), slope (a0) and intercept (a1) from the exponential of the linear relationship were used as the dead time and determined parameters. Furthermore, some vectorial equations were used that involve matrix multiplication, matrix inverse and iteration processes until the accurate dead time and determined parameters were obtained. The non-linear algorithms were then also applied by Waetzig to a gas chromatography system with several changes (Wätzig et al., 1992).
In the implementation of the non-linear algorithm, some additions and changes were made. These were necessary because the original non-linear algorithms lacked the information and provisions to produce a credible calculation. Additions were made to two algorithms: the inverse algorithm of the DTD matrix and multiplication matrix. In the inverse algorithm of the DTD matrix, the result of the matrix calculation was close to zero. A number digit behind the comma must be added to 300 digits so that the calculation could be defined. In the multiplication matrix, the function must be changed to an absolute function. Direct matrix multiplication in the non-linear algorithm allowed a minus value that could produce an infinity (Anton, 2000). In an unpublished thesis by Zamzami (Zamzami, 2014), a matrix multiplication function has been changed to the absolute function ‘abs()’. However, this function wasn't fitted because the data type in the matrix was the double data type (Anton, 2000). The calculation of a double negative value with the integer function would be converted to zero. In this research, the function ‘abs()’ must be changed to the function ‘fabs()’ so that the value could be calculated. The application development from the non-linear algorithm was performed by a flowchart established by a software manufacturer [Figure 1a].
Figure 1.
The flowcharts of software: non-linear method (a) and spreadsheet method (b).
2.3. Iteration method
The iteration method was developed by Guardino et al., (1976). The determination of the dead time began with an initial dead time estimation, calculation of the adjusted retention time, and determination of the slope and intercept from the linearity of the plot of the semi-logarithm using a least-squares fit. The determination of the dead time was continued with iterations until the best values of the dead time, slope and intercept were determined by minimizing the sum of squares of the difference between the known and estimated index retention values. Guardino et al. have provided the flowchart for this approach (Guardino et al., 1976), and a source code has also been written by Furr et al. (Furr, 1989) in visual basic. These three bases were used as the basis to create software. However, the source code that was written by Furr et al. (Furr, 1989) wasn't compatible with the current visual basic compiler. The source code must be rewritten in the method development in this study. The iteration method has been extensively tested in some literature and showed several advantages such as being the most accurate (Idroes, 2011, 2005; Idroes et al., 2019b; Quintanilla-López et al., 1997), quickest (Braithwaite and Cooper, 1993) and most easily reproduced (Furr, 1989). These advantages made the iteration method an often used reference method for other indirect methods.
2.4. Spreadsheet method
The spreadsheet method was based on the logarithmic relationship between the adjusted retention time and the carbon number. The calculation process was carried out automatically based on the graphical method, which has been developed using the statistical method. This procedure produced a linear graph for any homologous series of any carbon numbers that was used for the determination of the dead time. The dead time calculation was performed by running a spreadsheet macro initiated with a keystroke that has been determined and operated as an iterative process. The initial arbitrary dead time (tR1) was used to determine the adjusted retention times and correlation coefficients of the plots of the logarithm of the adjusted retention times versus the carbon numbers. The iterative process with a decrease of the dead time (dtM) was carried out until it reached the optimal correlation coefficient to produce the most accurate dead time. The complete spreadsheet algorithm can be seen in the literature of Braithwaite (Braithwaite and Cooper, 1993). The application development from the spreadsheet algorithm was performed by a flowchart established by a software manufacturer (Figure 1B).
2.5. Statistical method
The statistical algorithm was introduced by Grobler et al. (Grobler and Balizs, 1974) to calculate a retention index using the antilog of the slope (q) and dead time. The slope (b) was calculated with a linear regression using the retention times of four or more successive homologous series from the logarithm of the differences between the retention times of adjacent n-alkanes. The algorithm of anti-log b (q) was formed from the slope (b). The antilog of the slope (q) and the retention time were used to determine the dead time with the non-linear regression. This algorithm and flowchart of the statistical method were then used as a basis to create software.
2.6. Direct method
The direct method in this study was carried out by measuring the dead time of argon under the same experimental conditions as for the measurement of the retention times of the homologous series. This procedure has been carried out in the literature of Lopez et al. (Quintanilla-López et al., 1997), and the data was taken as the dead time of the direct method. This data was then used for comparison of the dead time with the indirect method.
2.7. Data collection
The data that were used for the dead time calculation were the secondary retention times and carbon numbers of a n-alkane homologous series that was obtained from the literature of Lopez et al. (Quintanilla-López et al., 1997). The data were measured in different columns and at different column temperatures. The columns that were used were a PS-255 (column 1) with a length of 4 m and a % stationary phase of 19.4%; an OV-11 (column 2) with a length of 2 m and a % stationary phase of 16.3%; a CPSIL-5CB (column 3) with a length of 50 m; a HP-5 (column 4) with a length of 60 m; and HP-INNOWAX (column 5) with a length of 60 m. The column temperatures were set at 60 °C, 90 °C, 120 °C and 150 °C. At 150 °C, columns 2 and 5 weren't used. The collected data were presented in two types of series: successive and spaced homologous series. The successive homologous series are regular series types (nC5 up to nC17), while the spaced homologous series are regular series types plus methane (nC1, nC5 up to nC17) (Quintanilla-López et al., 1997).
3. Results and discussion
3.1. Software development for the indirect method
The non-linear method software was built based on the flowcharts (Figure 1a). The initial stage of the software is the process of inputting tR and nC data from the secondary data and storing it into an array. Then, the initialization process of the variables i, tM, a0 and a1 as well as the limit of accuracy were carried out. The first loop was performed to calculate the t’R value, Δt and matrix D (d1, d2, d3) based on the equation of Waetzig13,14. The next loop is the calculation of (DT D)-1, Δx and new values of tM, a0 and a1. The looping is performed until the values of ΔtM, Δa0 and Δa1 are smaller than the specified limit of accuracy ε so that the last tM value is the tM value generated by the software (Figure 1a).
The spreadsheet method software uses the maximum correlation coefficient as the reference calculation. The flowchart software can be seen in (Figure 1B), starting with the input process for tR and nC data as well as initializing the variables kv1, kv2, I, dtM, tM and prec. kv1 and kv2 are the first and second correlation coefficients, respectively, based on the equation in the Braithwaite literature (Braithwaite and Cooper, 1993), and the kv2 value is calculated by tM diminished to dtM. The loop starts by giving the initial value of tM (tM = tR [0]). Then, the value of tM is diminished dtM to recalculate kv1. The value of tM is updated with the same process and then used to calculate kv2. If (1-kv1) < (1-kv2), the tM value will be updated again, and the same checking process will be carried out. The loop is performed until the value of dtM = prec, and then, the final value of tM is obtained (Figure 1b).
The statistical method software was developed based on the tR and nC successive logarithms with the utilization of several statistical equations. The software was written based on the statistical equations and flowchart to calculate dead time in the Grobler literature (Grobler and Balizs, 1974). The last software is the iteration method software that was developed based on Guardino's algorithm and flowchart (Guardino et al., 1976) as well as Furr's source code (Furr, 1989). The iteration software was built using programming languages that are easy to reproduce.
3.2. Method comparison
The dead time calculation by indirect methods has been performed using four different methods: non-linear, iteration, spreadsheet and statistical methods. The calculation results were tabulated and are presented in Table 1. The dead times calculated by indirect methods, both on successive and spaced homologous series, were compared with the argon dead time (direct method). In general terminology, one of the related parameters to determine the dead time accuracy of the indirect methods, besides the retention time of the lowest carbon number and the retention index, is the marker dead time (the dead time of the direct method). A good dead time by an indirect method has the same or a smaller value than the marker dead time. The smaller the dead time value found by an indirect method, the more accurate that dead time (Idroes, 2011). A dead time from indirect methods that is greater than the marker dead time is considered less reliable and allows overlapping values with the retention time of the lowest carbon number as well as highly eluted compounds (error dead time).
Table 1.
Dead time calculation results from indirect methods.
| nC |
Successive Homologous Series (min) |
Spaced Homologous Series (min) |
Marker (min) | |||||
|---|---|---|---|---|---|---|---|---|
| Method | IT | NL | SS | ST | IT | NL | SS | |
| Column 1 | ||||||||
| 60 °C | 1.868 | 2.440 | 1.868 | 1.868 | 2.007 | 2.174 | 2.077 | 2.280 |
| 90 °C | 2.146 | 3.397 | 2.147 | 2.150 | 2.231 | 2.709 | 2.231 | 2.420 |
| 120 °C | 2.320 | 4.030 | 2.320 | 2.330 | 2.350 | 3.320 | 2.350 | 2.540 |
| 150 °C | 2.450 | 5.190 | 2.460 | 2.470 | 2.480 | 4.540 | 2.480 | 2.690 |
| Column 2 | ||||||||
| 60 °C | 1.892 | 2.147 | 1.892 | 1.891 | 1.988 | 2.052 | 1.979 | 2.040 |
| 90 °C | 2.155 | 2.777 | 2.156 | 2.159 | 2.217 | 2.532 | 2.209 | 2.270 |
| 120 °C | 2.280 | 3.950 | 2.280 | 2.290 | 2.280 | 3.420 | 2.280 | 2.440 |
| Column 3 | ||||||||
| 60 °C | 2.610 | 4.092 | 2.611 | 3.765 | 3.225 | 3.795 | 3.159 | 3.250 |
| 90 °C | 3.486 | 4.074 | 3.487 | 3.520 | 3.497 | 3.956 | 3.419 | 3.520 |
| 120 °C | 3.700 | 4.330 | 3.710 | 3.720 | 3.710 | 4.220 | 3.630 | 3.740 |
| 150 °C | 3.900 | 4.710 | 3.910 | 3.920 | 3.910 | 4.610 | 3.820 | 3.930 |
| Column 4 | ||||||||
| 60 °C | 5.331 | 5.438 | 5.332 | 5.333 | 5.357 | 5.403 | 5.279 | 5.370 |
| 90 °C | 5.689 | 6.053 | 5.689 | 5.696 | 5.708 | 5.965 | 5.629 | 5.730 |
| 120 °C | 6.010 | 12.300 | 6.020 | 9.370 | 5.910 | 10.620 | 5.920 | 6.020 |
| 150 °C | 6.250 | 7.190 | 6.260 | 6.290 | 6.260 | 7.060 | 6.180 | 6.290 |
| Column 5 | ||||||||
| 60 °C | 5.310 | 5.496 | 5.314 | 5.313 | 5.315 | 5.537 | 5.219 | 5.320 |
| 90 °C | 5.667 | 6.230 | 5.668 | 5.659 | 5.674 | 6.140 | 5.579 | 5.680 |
| 120 °C | 5.960 | 6.150 | 5.960 | 5.670 | 5.960 | 6.090 | 5.860 | 5.970 |
| εtM | 6% | 18% | 6% | 7% | 3% | 14% | 4% | |
(IT): Iteration Method15; (NL) Non-linear Method13; (SS): Spreadsheet Method16; Statistics Method17; nC: Carbon number.
The calculated dead times from indirect methods, both on successive and spaced homologous series, indicated that the dead times of the iteration and spreadsheet methods always showed smaller values than the marker dead time. The dead time of the statistical method that is only able to calculate the successive homologous series was a smaller value than the marker dead time except in column 3 (CPSIL-5CB) at 60 °C and column 4 (HP-5) at 150 °C. Under both conditions, the dead time of the statistical method is higher than the marker dead time. Using non-linear methods, both for successive and spaced homologous series, the calculated dead times were almost always greater than the marker dead time. The calculated dead times that were less than the marker dead time were only obtained in spaced homologous series at 60 °C, whereas in successive homologous series, the widening of the dead time of the non-linear method was greater than in spaced homologous series. Based on the differences between the relative dead times of indirect methods and the marker dead time, the % error values of the dead time for successive homologous series were 6% for iteration and spreadsheet, 7% for statistical, and 18% for non-linear methods.
Meanwhile, the % error values of the dead time in spaced homologous series were 3% for iteration, 4% for spreadsheet, and 14% for non-linear methods. This result showed that the iteration, spreadsheet (both on successive and spaced homologous series) and statistical (only on spaced homologous series) methods gave relatively small errors (<10%). The non-linear method (both on successive and spaced homologous series) showed relatively large errors (>10%). In the spaced homologous series, we always found a smaller error than for the successive homologous series for all indirect methods with column and temperature variations (see Table 1).
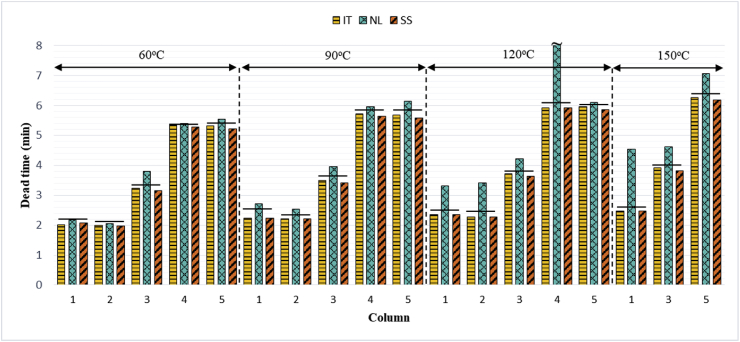
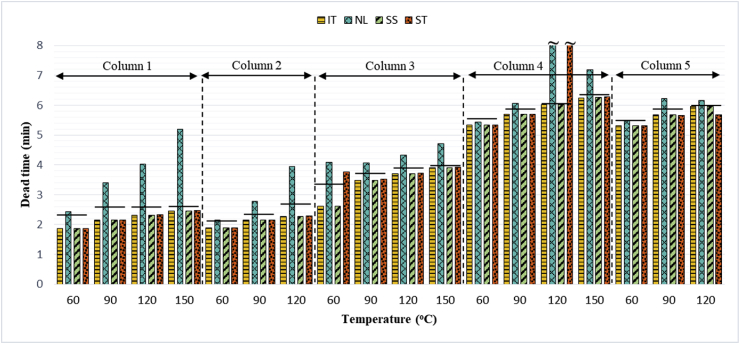
From this analysis, it has been confirmed that the iteration method has the best accuracy and is robust for both successive and spaced homologous series. These results were in accordance with the report of previous studies that suggested that this method could be used as the reference method for the indirect methods (Furr, 1989; Idroes, 2005; Quintanilla-López et al., 1997; Braithwaite and Cooper, 1993). In harmony with the iteration method, the spreadsheet method also showed good accuracy. Therefore, it could be stated that the iteration and spreadsheet methods had the best accuracy (minimal error). Both methods were also robust because they were able to be applied to both successive and spaced homologous series. The statistical method also provided excellent results with not much different error from the iteration and spreadsheet methods. However, this method is limited to use on successive homologous series only. The non-linear method still provided the most inaccurate calculation compared to the three other methods, with a relatively large error. However, in some conditions the non-linear method could still be applied well, i.e., at low column temperatures (60 °C) for all column types [Figures 4 and 5], whereas at higher temperatures, it could only be used in polar capillary columns [Figures 2 and 3].
Figure 4.
The overview of the trend of the column effect (successive homologous series).  Marker dead time as a reference.
Marker dead time as a reference.
Figure 5.
The overview of the trend of the column effect (spaced homologous series).  Marker dead time as a reference.
Marker dead time as a reference.
Figure 2.
The overview of the trend of the temperature effect (successive homologous series).  Marker dead time as a reference.
Marker dead time as a reference.
Figure 3.
The overview of the trend of the temperature effect (spaced homologous series).  Marker dead time as a reference.
Marker dead time as a reference.
3.3. Temperature effect
The temperature of the column is one of the variables that is most often varied in analysis using gas chromatography. The column temperature is always adjusted to the character of the component that is analyzed. Changes in the column temperature will cause changes in the retention times of the separated compounds (Héberger and Kowalska, 1999). In the study of the dead time by indirect methods, the calculation of its value was carried out using the retention times of a homologous series, and in this study, a n-alkane homologous series was used. A change in the column temperature for the separation of n-alkanes will cause a shift in the retention time of each n-alkane compound. Therefore, analysis was necessary to observe the effect of the retention time shift caused by the column temperature change on the calculation and accuracy of the dead time by indirect methods.
Based on the observation of the dead time for the successive homologous series, the dead time of all indirect and direct methods increased with the increase of the column temperature [Figure 2]. However, the dead time increases of the iteration and spreadsheet methods still fitted with the marker dead time (reference) increase. The dead time increase of the statistical method also relatively fitted with the marker dead time increase except in column 3 at 60 °C and column 4 at 120 °C. Under these conditions, the dead time of the statistical method was greater than the marker dead time. The dead time increase of the non-linear method showed different behavior. In the packed column, the dead time increase of the non-linear method was very significant for the temperature increase compared to the capillary column. However, the dead time increase of the non-linear method couldn't be fitted to that of the direct method because almost all of its values were greater than the dead time of the direct method.
According to the observation of the dead time for the spaced homologous series, the dead times of all indirect and direct methods increased with increases in the column temperature [Figure 3]. However, the dead time increases of the iteration and spreadsheet methods still corresponded with the marker dead time (reference) increase. In this homologous series, the dead time of the statistical method couldn't be calculated due to the method mismatch with the data type (Grobler and Balizs, 1974). In the non-linear method, the dead time increase showed different behavior. In the packed column, the increase was very significant with the increase of the column temperature compared to the capillary column. However, the dead time increase of the non-linear method was almost always greater than that of the direct method (reference).
Based on the analysis of the temperature effects on the dead times calculated by indirect methods, there were dead time increases in the four indirect methods with column temperature increases for both the successive and spaced homologous series [Figures 2 and 3]. However, the dead times of the indirect methods in the iteration, spreadsheet and statistical methods were still fitted with the dead time of the direct method and directly proportional to the column temperature increase. Generally, the column temperature increase will cause the retention times of the compounds that are separated to decrease. This is due to the inlet pressure increase that accelerated the elution of compounds because of a large pressure gradient between the column inlet and column outlet. In contrast to the marker dead time (direct method), the temperature increase caused the viscosity of gas inside the column to increase, which leads to the slowing of the flow toward the column outlet (Nahir and Morales, 2000). Although the temperature increase caused the retention times of n-alkanes to decrease (Quintanilla-López et al., 1997), the dead time of the indirect method based on n-alkanes didn't follow the behavior of n-alkanes themselves, but it still fit with the dead time of the direct method (reference).
In the packed column, column temperature changes affected the dead time values of the non-linear method. The higher the column temperature, the higher the differences between the dead time of the non-linear method and the marker dead time [Figures 2 and 3]. In the successive homologous series, the dead time differences were greater than in the homologous spaced series. However, the change trends didn't occur in the capillary column. These results showed that the calculation of the dead time of the non-linear method in the packed column could only be performed under the low-temperature conditions with the spaced homologous series.
3.4. Column effect
Three variables are used as the fundamentals for column selection in chromatographic analysis: type (packed or capillary), polarity (polar, semi-polar or nonpolar) and length of the column. The variables determine the separation resolution between components. Ideally, the dead time isn't affected by variable condition changes.
Based on the observations of the dead times of the indirect methods for the successive homologous series, the dead time accuracies of the iteration, spreadsheet and statistical methods weren't affected by the column variations [Figure 4]. The same result has also been observed in the homologous spaced series. The dead time accuracy of the iteration and spreadsheet methods wasn't influenced by column variations [Figure 5]. In the non-linear method, the effect of the column variation couldn't be observed in the dead time. This was caused by that the non-linear method was only accurate on packed columns at low temperature and polar capillary columns. In other columns, the non-linear method wasn't accurate.
The calculated dead time, both by indirect and direct methods, indicated that differences in the length of the column with the same type and polarity resulted in different dead times. However, these differences didn't affect the dead time accuracy of the iteration, spreadsheet and statistical methods compared to the marker dead time [Figures 4 and 5]. In the non-linear method, the length of the column also affected the dead time, but differences in the trend of the column length influence on the dead time accuracy compared to the marker dead time couldn't be observed. The effect of the length of the column on the dead times of indirect and direct methods could be seen in columns 3 and 4 in all successive and spaced homologous series and with temperature variations. The marker dead time was assumed to not be influenced by chemical factors, but it was influenced by physical factors due to differences in gas mileage in the column (García Domínguez and Diez-Masa, 2001).
In the same type and the length of column, the different column polarities didn't affect the values and accuracy of the dead times for the iteration, spreadsheet and statistical methods for both successive and spaced homologous series [Figures 4 and 5]. In the non-linear method, the trend of the influence of the polarity on the dead time couldn't be observed. The effect of the column polarity on the dead time by either an indirect method or direct method could be observed in columns 4 and 5 at all temperatures for successive and spaced homologous series. The same result was also showed by the calculated dead times of the indirect methods that were fitted with the dead time of the direct method. This phenomenon indicated that the assumption of the dead time as the holding time of a substance that is considered unretained in a column held up, which could be proved experimentally (García Domínguez and Diez-Masa, 2001).
The differences in column types, both for successive and spaced homologous series, also didn't affect the dead time accuracy in the iteration, spreadsheet and statistical methods. Both the packed (1 & 2) and capillary columns (3, 4, 5) showed calculated dead times for indirect methods that were appropriate with the marker dead time. Even in the polar capillary column (column 5), the non-linear method showed a value that wasn't significantly different from that of the direct method. These results showed that the dead times of indirect methods could be applied to both types of columns as well.
4. Conclusion
The analysis results of the dead time calculations using the indirect methods showed that the iteration and spreadsheet methods could be used correctly and accurately both for the successive and spaced homologous series, while the statistical method could only be applied for a successive homologous series. Under certain conditions, the non-linear method could also be applied to calculate the dead time, especially at relatively low column temperatures (60 °C) for all columns. For relatively high column temperatures, it was only suitable for polar capillary columns. These results indicated that the spreadsheet method had almost the same reliability as the iteration method, and thus, it was recommended to be used as a reference in the determination of the dead time that could be used for the calculation of the Kovats retention index.
Overall, temperature changes and column differences (type, polarity and length) could affect the dead time calculations. However, the value changes didn't show a significant effect on the dead time accuracy of the indirect methods compared to the dead time of the direct method (substance marker). Not all of the methods produced the same tM value for a given chromatography phase system. Therefore, to define other retention parameters such as the retention index, the method that was used to estimate the dead time must be defined. Therefore, we propose the use of the iteration and spreadsheet methods as the best ways thus far to estimate the dead time by using n-alkane homologues series, regardless of column and temperature variations.
Declarations
Author contribution statement
R. Idroes: Conceived and designed the experiments; Wrote the paper.
Saiful, Muslem. Mahmudi: Performed the experiments; Analyzed and interpreted the data.
Irvanizam, R. Suhendra, G. M. Idroes: Contributed reagents, materials, analysis tools or data.
Funding statement
This research was funded by Universitas Syiah Kuala through “Penelitian Dasar” scheme, grant number: 215/SP2H/LT/DPRM/2019.
Competing interest statement
The authors declare no conflict of interest.
Additional information
No additional information is available for this paper.
References
- Anton Howard. eighth ed. John Wiley; 2000. Elementary Linear Algebra.https://www.amazon.co.uk/Elementary-Linear-Algebra-8th-Eighth/dp/B002T9O34Y [Google Scholar]
- Arey J. Samuel, Nelson Robert K., Xu Li, Reddy Christopher M. Using comprehensive two-dimensional gas chromatography retention indices to estimate environmental partitioning properties for a complete set of diesel fuel hydrocarbons. Anal. Chem. 2005;77(22):7172–7182. doi: 10.1021/ac051051n. [DOI] [PubMed] [Google Scholar]
- Bieri Stefan, Marriott Philip J. Dual-injection system with multiple injections for determining bidimensional retention indexes in comprehensive two-dimensional gas chromatography. Anal. Chem. 2008;80(3):760–768. doi: 10.1021/ac071367q. [DOI] [PubMed] [Google Scholar]
- Braithwaite A., Cooper M. A rapid spreadsheet method for the estimation of dead time. Chromatographia. 1993;37(1–2):86–92. [Google Scholar]
- Cramers C.A., Luyten J.A., Rijks J.A. “Direct measurement of the ‘dead time’ in gas chromatography with a flame-lonisation detector. Chromatographia. 1970;3(9):441–442. [Google Scholar]
- Dallos András, Kresz Richárd, Kováts Ervin Sz. Solvation properties and limiting activity coefficients of halogenated hydrocarbons in C78H158branched saturated alkane solvent. Fluid Phase Equil. 2003;210(1):57–67. [Google Scholar]
- Didaoui Linda, Touabet A., Badjah Hadj Ahmed A.Y., Meklati B.Y., Engewald Werner. Evaluation of dead time calculation in reversed-phase liquid chromatography using a multiparametric mathematical method. HRC J. High Resolut. Chromatogr. 1999;22(10):559–564. [Google Scholar]
- Furr Harold C. Calculation of chromatographic dead times and retention indices with the aid of a computer program in BASIC. J. Chromatogr. Sci. 1989;27(5):216–220. doi: 10.1093/chromsci/27.5.216. http://www.ncbi.nlm.nih.gov/pubmed/2745662 [DOI] [PubMed] [Google Scholar]
- García Domínguez J.A., Diez-Masa J.C. Retention parameters in chromatography (IUPAC recommendations 2001) Pure Appl. Chem. 2001;73(6):969–992. http://www.iupac.org/publications/pac/pdf/2001/pdf/7306x0969.pdf#page=14%5Cnhttp://digital.csic.es/handle/10261/42959 [Google Scholar]
- Grob Robert L., Barry Eugene F. 2004. Modern Pratice of Gas Chomatography. [Google Scholar]
- Grobler A., Balizs G. Computer program for a statistical calculation of retention indices. J. Chromatogr. Sci. 1974;12(2):57–58. [Google Scholar]
- Guardino X., Albaigés J., Firpo G., Rodríguez-Vinãls R., Gassiot M. Accuracy in the determination of the Kováts retention index. J. Chromatogr. A. 1976;118(1):13–22. [Google Scholar]
- Héberger Károly, Kowalska Teresa. Quantitative structure-retention relationships VI. Thermodynamics of Kovats retention index-boiling point correlations for alkylbenzenes in gas chromatography. Chemometr. Intell. Lab. Syst. 1999;47(2):205–217. [Google Scholar]
- Idroes Rinaldi. Determination of absolute retention index system in high performance liquid chromatography (RP-HPLC) Malaysian Journal of Analytical Science. 2005;9(3):224–232. [Google Scholar]
- Idroes Rinaldi. Dead time determination and its influence to retention index in GC system using polar capillary column. Majalah Farmasi Indonesia. 2011;(3):257–264. [Google Scholar]
- Idroes R., Husna I., Muslem Mahmudi, Rusyana A., Helwani Z., Idroes G.M., Suhendra R., Yandri E., Rahimah S., Sasmita N.R. Vol. 364. IOP Publishing; 2019. Analysis of temperature and column variation in gas chromatography to dead time of inert gas and n-alkane homologous series using randomized block design. (IOP Conference Series: Earth and Environmental Science). No. 1. [Google Scholar]
- Idroes R., Idroes G.M., Suhendra R., Paristiowati M., Muslem, Mahmudi, Saiful, Irvanizam, Zamzami . Vol. 364. IOP Publishing; 2019. Dead time determination of 2-alkanone homologues series using methanol/water eluent in high performance liquid chromatography system by indirect method. (IOP Conference Series: Earth and Environmental Science). No. 1. [Google Scholar]
- Kováts E. Gas-chromatographische charakterisierung organischer verbindungen. Teil 1: retentionsindices aliphatischer halogenide, alkohole, aldehyde Und Ketone. Helv. Chim. Acta. 1958;41(7):1915–1932. [Google Scholar]
- McGinitie Teague M., Harynuk James J. Considerations for the automated collection of thermodynamic data in gas chromatography. J. Separ. Sci. 2012;35(17):2228–2232. doi: 10.1002/jssc.201200192. [DOI] [PubMed] [Google Scholar]
- Nahir Tal M., Morales Kathryn M. Constant holdup times in gas chromatography by programming of column temperature and inlet pressure. Anal. Chem. 2000;72(19):4667–4670. doi: 10.1021/ac0004153. [DOI] [PubMed] [Google Scholar]
- Pang Tao, Zhu Shukui, Lu Xin, Xu Guowang. Identification of unknown compounds on the basis of retention index data in comprehensive two-dimensional gas chromatography. J. Separ. Sci. 2007;30(6):868–874. doi: 10.1002/jssc.200600471. [DOI] [PubMed] [Google Scholar]
- Parcher J.F., Johnson D.M. Methane retention time versus mathematical dead time. J. Chromatogr. Sci. 1980;18(6):267–272. [Google Scholar]
- Peng C.T. Prediction of retention indices. VI: isothermal and temperature-programmed retention indices, methylene value, functionality constant, electronic and steric effects. J. Chromatogr. A. 2010;1217(23):3683–3694. doi: 10.1016/j.chroma.2010.02.005. Elsevier B.V. [DOI] [PubMed] [Google Scholar]
- Pratiwi Sylvia Utami Tunjung, Lagendijk Ellen Louise, de Weert Sandra, Idroes Rinaldi, Hertiani Triana, Van den Hondel Cees. Effect of cinnamomum Burmannii nees Ex Bl. and Massoia Aromatica Becc. Essential oils on planktonic growth and biofilm formation of Pseudomonas Aeruginosa and Staphylococcus Aureus in vitro. Int. J. Appl. Res. Nat. Prod. 2015;8(2):1–13. [Google Scholar]
- Quintanilla-López, Eduardo Jesús, Lebrón-Aguilar Rosa, García-Domínguez JoséAntonio. The hold-up time in gas chromatography II. Validation of the estimation based on the concept of a zero carbon Atoms alkane. J. Chromatogr. A. 1997;767(1–2):127–136. [Google Scholar]
- Suliman Fakhr Eldin O. Off-line optimization of the separation of 2,4-dinitrophenylhydrazones by gas chromatography using chemometric techniques. Talanta. 2002;56(1):175–183. doi: 10.1016/s0039-9140(01)00554-9. [DOI] [PubMed] [Google Scholar]
- Von Mühlen Carin, Marriott Philip J. Retention indices in comprehensive two-dimensional gas chromatography. Anal. Bioanal. Chem. 2011;401(8):2351–2360. doi: 10.1007/s00216-011-5247-1. [DOI] [PubMed] [Google Scholar]
- Watanachaiyong T., Jeyashoke N., Krisnangkura K. A convenient method for routine estimation of dead time in gas chromatography. J. Chromatogr. Sci. 2000;38(2):67–71. doi: 10.1093/chromsci/38.2.67. http://www.scopus.com/inward/record.url?eid=2-s2.0-0037332509&partnerID=40&md5=aa0098613c345982a3c3b2a2301603d9 [DOI] [PubMed] [Google Scholar]
- Wätzig H., Ebel S. Estimation of dead-time in liquid chromatography from retention behaviour of homologous series by non-linear regression. Chromatographia. 1991;31(11–12):544–548. [Google Scholar]
- Wätzig H., Ebel S., Holley A. A straightforward algorithm to estimate the dead time in GC from the retention behavior of homologous series. Fresenius’ J. Anal. Chem. 1992;344(7–8):354–356. [Google Scholar]
- Wu N.S., Wu G.S., Wu M.Y. A comparative study of methods for determining gas hold-up time. J. Chromatogr. Sci. 2006;44(5):244–246. doi: 10.1093/chromsci/44.5.244. [DOI] [PubMed] [Google Scholar]
- Zamzami . Syiah Kuala University; 2014. Perhitungan Waktu Mati Pada Kromatografi Gas Metode Non Linier Dengan Banhasa Pemrograman ANSII-C. [Google Scholar]
- Zhang Xiaoyun, Qi Jianhua, Zhang Ruisheng, Liu Mancang, Hu Zhide, Xue Huifeng, Fan Botao. Prediction of programmed-temperature retention values of naphthas by wavelet neural networks. Comput. Chem. 2001;25(2):125–133. doi: 10.1016/s0097-8485(00)00074-7. [DOI] [PubMed] [Google Scholar]