Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2020 Jan 10;16(2):1007–1017. doi: 10.1021/acs.jctc.9b01064

Time-Dependent Magnons from First Principles

N Tancogne-Dejean †, F G Eich †,*, A Rubio †,‡,§,∥
PMCID: PMC7017386  PMID: 31922758

Abstract

graphic file with name ct9b01064_0001.jpg

We propose an efficient and non-perturbative scheme to compute magnetic excitations for extended systems employing the framework of time-dependent density functional theory. Within our approach, we drive the system out of equilibrium using an ultrashort magnetic kick perpendicular to the ground-state magnetization of the material. The dynamical properties of the system are obtained by propagating the time-dependent Kohn–Sham equations in real time, and the analysis of the time-dependent magnetization reveals the transverse magnetic excitation spectrum of the magnet. We illustrate the performance of the method by computing the magnetization dynamics, obtained from a real-time propagation, for iron, cobalt, and nickel and compare them to known results obtained using the linear-response formulation of time-dependent density functional theory. Moreover, we point out that our time-dependent approach is not limited to the linear-response regime, and we present the first results for nonlinear magnetic excitations from first principles in iron.

1. Introduction

Collective magnetic excitations play a central role in our understanding of the stability of magnetic materials; for example, they determine the Curie (Néel) temperature of (anti-) ferromagnets.1 In recent years, the experimental confirmation of intrinsic two-dimensional magnets2−7 has attracted a lot of attention, since it adds magnetism to the toolbox of van der Waals heterostructures, which bears the promise for creating efficient novel devices with tailored electronic, optical, and magnetic properties.8 To understand the coupled spin and charge dynamics of extended electronic systems, numerical simulations can provide insight into the involved physical processes and complement experimental investigation. Broadly speaking, there are two approaches to study the spin magnetization dynamics: (1) A phenomenological approach, where the spin degrees of freedom are encoded in a model Hamiltonian, such as the Heisenberg model, and the magnetization dynamics is computed, for example, by solving the classical Landau–Lifshitz–Gilbert equation.9 (2) The first-principles approach, based on the solution of the microscopic Pauli–Schrödinger equation for the electrons, where magnetism emerges due to the intrinsic magnetic moment of the interacting electrons. In our work, we follow the latter route; however, the direct solution of the (time-dependent) Schrödinger equation for interacting electrons is not possible in practice, at least for extended systems. We employ instead the exact reformulation of quantum mechanics based on density functional theory (DFT).10−12 Since its inception, DFT has evolved into the most widespread approach to numerically study extended systems from first principles. Its generalization to time-dependent or out-of-equilibrium phenomena, the so-called time-dependent DFT (TD-DFT),13−15 is currently the only viable and reliable route to study the dynamics of large-scale quantum mechanical systems from first principles despite the intrinsic limitations introduced by approximating interaction effects beyond the classical Hartree interaction. Specifically, the linear-response formulation of TD-DFT has been used to study not only optical properties but also magnetic excitations such as magnons, which are collective fluctuations of the spin magnetization.16−23

Over the last couple of years, first studies investigating magnetization dynamics from first principles in real time have emerged. For example, the ultrafast demagnetization due to intense laser pulses24 has been successfully investigated using TD-DFT approaches.25−29 In the present work, we are interested in modeling transverse magnetic excitations, specifically magnons, which are long-wavelength collective excitations of magnetic materials with a typical energy of tens to hundreds of milli-electronvolts. We propose a time-dependent alternative to the widely used linear-response formulation, in spirit closely related to the work of Bertsch et al. for optical excitations,30 which allows us to go beyond the linear regime and address the response of the system to arbitrary spatially and time-dependent electromagnetic fields. To induce magnetization dynamics in the system, we employ a “transverse magnetic kick”. The subsequent time evolution of the spin magnetization, governed by the time-dependent Schrödinger equation, is then analyzed to obtain the density of states (DOS) of transverse magnetic excitations. We show that for small magnetic kicks we recover the results from the linear-response theory. However, our approach does not rely on the assumption of small perturbations and we can analyze magnetic excitations beyond the linear response. Surprisingly, we find that the frequency of magnons in the ferromagnetic metal iron gets detuned to higher energies, in contrast to the prediction of simple models for the magnons based on the Heisenberg model.

The outline of the paper is as follows: In Section 2, we introduce our prescription to induce transverse magnetic excitations in a real-time TD-DFT framework. Results for the simple transition metals iron, cobalt, and nickel are presented in Section 3, and we provide our conclusions and outlook in Section 4. Furthermore, there are two appendices detailing more technical aspects of our approach. In Appendix A, we provide a more in-depth discussion of the TD-DFT linear-response formalism, and in Appendix B, we discuss the so-called generalized Bloch theorem, which allows for the efficient simulation of long-wavelength magnons using the chemical unit cell.

2. Real-Time Magnons within TD-DFT

We consider a Hamiltonian of the form

2. 1

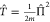where Inline graphic is the kinetic energy operator and n̂(r) and σ̂(r) are the local operators yielding the electronic density, n(r, t) = ⟨Φ(t)|n̂(r)|Φ(t)⟩, and the spin magnetization, m(r, t) = ⟨Φ(t)|σ^(r)|Φ(t)⟩, which couple to the scalar potential v(r, t) and the magnetic field B(r, t), respectively. The momentum operator Π̂ contains the vector potential and spin–orbit coupling,31−34 but in the absence of an external laser pulse and ignoring the spin–orbit coupling, it is simply given by Π̂ = −iℏ∇. Finally, Ŵ represents the interaction between the electrons, a Coulombic density–density interaction. Within TD-DFT, the time-dependent densities, here the electronic density n(r, t) and the spin magnetization m(r, t), are determined by solving a time-dependent Schrödinger equation for effectively noninteracting electrons, the so-called Kohn–Sham (KS) equation

2. 2a
2. 2b
2. 2c

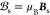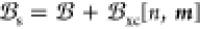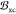Here, Φs,n represents the KS Pauli spinors labeled by a generic index n and fn is the corresponding occupation number specifying the initial state. The effective potentials vs and Inline graphic are related to the external potential, v, and magnetic field, Inline graphic, of the interacting Hamiltonian (1) by vs = v + vH[n] + vxc[n, m] and Inline graphic, respectively. The Hartree potential vH is the classical potential due to the electronic density n. 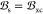The so-called exchange-correlation (xc) potential and magnetic field, vxc and Inline graphic, are functionals of the density and spin magnetization and need to be approximated in practice. The xc terms take electron–electron interactions beyond the classical Hartree interaction into account. Within DFT, a magnetic material is characterized by an effective field, Inline graphic, that is, the effective magnetic field is purely internal (due to electron–electron scattering). Put differently, the xc magnetic field is crucial to stabilize the magnetic order.

A common approach to study transverse magnetic excitations is to employ the linear-response formulation of TD-DFT. In a nutshell, one computes the transverse magnetic susceptibility χ+–, which determines the transverse spin magnetization response induced by a weak transverse magnetic field, that is

2. 3

In eq 3, we introduced m± = mx ± imy and Inline graphic, which diagonalizes the transverse magnetic response for systems with a collinear ground-state magnetization.35 The transverse magnetic excitation spectrum is encoded in the susceptibility χ+–. It is worth noting that the transverse magnetic excitation provides complementary information to the longitudinal magnetic response.36 The longitudinal magnetic response of finite systems has been studied, for example, using a dipolar kick in refs (37, 38). We provide a more detailed discussion of the linear response within TD-DFT in Appendix A.

Next, we describe an alternative approach for the investigation of transverse magnetic excitation based on the time propagation of the KS equations of TD-DFT (2). We can rewrite the time-dependent Schrödinger equation for the KS electrons as

2. 4

In the previous equation, we denote all explicitly time-independent contributions to the Hamiltonian by Ĥs. To induce transverse magnetic excitations in the system, we add an explicit time-dependent contribution, Δ̂(t), to the Hamiltonian based on the building block

2. 5

which corresponds to a time-dependent Zeeman coupling due to a magnetic field characterized by the wave vector q and frequency ω, that is

2. 6

The operators σ̂±(r) = σ̂x(r) ± iσ̂y(r) are the local spin-raising and -lowering operators, respectively. Taking a superposition of the building blocks (5) over all frequencies, we arrive at

2. 7

where we damped high frequencies with a characteristic time τ > 0. Averaging over the frequencies leads to the Poisson kernel representation of the delta function in time, δτ(t) = τ/π(t2 + τ2), with a pulse width ∝ τ. In the limit of vanishing pulse width (τ → 0) and infinite field strength Inline graphic, we arrive at

2. 8

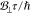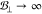The angle θ is defined as the finite limit of Inline graphic when τ →0 and Inline graphic. One can interpret this somewhat artificial “transverse magnetic kick” as exciting all transverse magnetic modes with a wave vector q and an arbitrary frequency. Working in the limit of an infinitesimally sharp kick also allows us to compute the effect of this transverse magnetic kick on the KS states analytically. The propagator from the initial time t0 = 0 to the time just after the transverse magnetic kick, t0+ = 0+, is simply given by

2. 9a
2. 9b

where we have used the integral only over an infinitesimal time interval and therefore only the contribution proportional to the δ-function survives. In eq 9a, we give the definition of the infinitesimal propagator representing the transverse magnetic kick, and in eq 9b, we show its explicit form acting on two-component spinor wave functions in real space. It is instructive to look at the spin magnetization just after the kick

2. 10

where m0(r) = ⟨Ψ(t = 0)|σ^|Ψ(t = 0)⟩, the ground-state spin magnetization (oriented here along the z-axis), and Rq(r) is a spatially varying rotation matrix characterized by the wave vector q

2. 11

Equation 11 corresponds to a rotation around a spatially dependent rotation axis u = [cos(q·r),sin(q·r), 0]T by a constant angle θ. A pictorial presentation of the effect of the transverse magnetic kick on the spin magnetization is given in Figure 1.

Figure 1.

Figure 1

Open in a new tab

Schematic representation of the effect of the initial transverse magnetic kick on the ground-state spin magnetization of a solid. The initial spin magnetization is shown as hollow black arrows (ferromagnetic “atomic” moments). The transverse magnetic kick rotates the spin by an angle θ around a rotation axis in the x–y plane. The rotation axis itself (represented by green, dashed lines with black arrowheads) is rotating in the plane perpendicular to the ground-state spin magnetization with the wavelength given by 2π/|q|. The resulting spins, depicted as filled red arrows, form a spin wave.

After the transverse magnetic kick, the system is no longer in an eigenstate of Ĥs, and a subsequent propagation with a field-free Hamiltonian, that is, a Hamiltonian with no additional (explicitly) time-dependent external field or potential, leads to nontrivial dynamics of the observables. In this work, we are explicitly interested in the dynamics of the transverse spin magnetization encoded in m±(r). For a small opening angle θ, we expect to recover the linear-response features contained in χ± ∓.

The main numerical challenge for such a calculation is that typical magnon frequencies are in the range of tens to hundreds of milli-electronvolts while we are interested in wave vectors within the first Brillouin zone. To resolve frequencies on the order of milli-electronvolts, we need to propagate the system up to a picosecond. Moreover, if we are interested in a wave vector, which is a fraction 1/m of the reciprocal lattice vector for the ground-state magnetic unit cell of the magnetic material,a we have to construct an m × 1 × 1 supercell (m repetitions along the wave vector q), which can host the magnetic structure with a periodicity given by q. However, there is a way to circumvent the construction of supercells, which goes by the name of the generalized Bloch theorem (GBT). The GBT has been introduced first by Sandradskii for the calculation of ground-state spin waves.39 In Appendix B, we show that the GBT can also be used for the time propagation of the states induced by the magnetic kick given in eqs 9a and 9b.

3. Results for Simple Magnetic Transition Metals

We have implemented the transverse magnetic kick, described in Section 2, and the GBT, detailed in Appendix B, in Octopus,40 which is a real-time, real-space implementation of TD-DFT. The initial kick, defined in eq 9b, is straightforward to implement in a real-space code because it is simply a local rotation of two-component Pauli spinors. The GBT is more involved since it corresponds to modified boundary conditions on the spinors (cf. Figure 7 in Appendix B). In principle, the GBT allows for arbitrary wave vectors q for the initial kick or, equivalently, the induced magnetic excitation. In practice, however, we found that the propagation turns out to be unstable if q is not commensurate with the k-point grid. A transverse magnetic kick with the wave vector q mixes spin-up and spin-down components of a spinor, which differ by a wave vector of q. Only if the wave vectors differing by q are representable by the k-point grid, this mixing of the spin-up and spin-down components is numerically accurate. This means that small wave vectors require a very dense k-point grid. A way around this numerical challenge could be to use two k-point meshes, one for spin-up components and the other for spin-down components, which are shifted by q.

Figure 7.

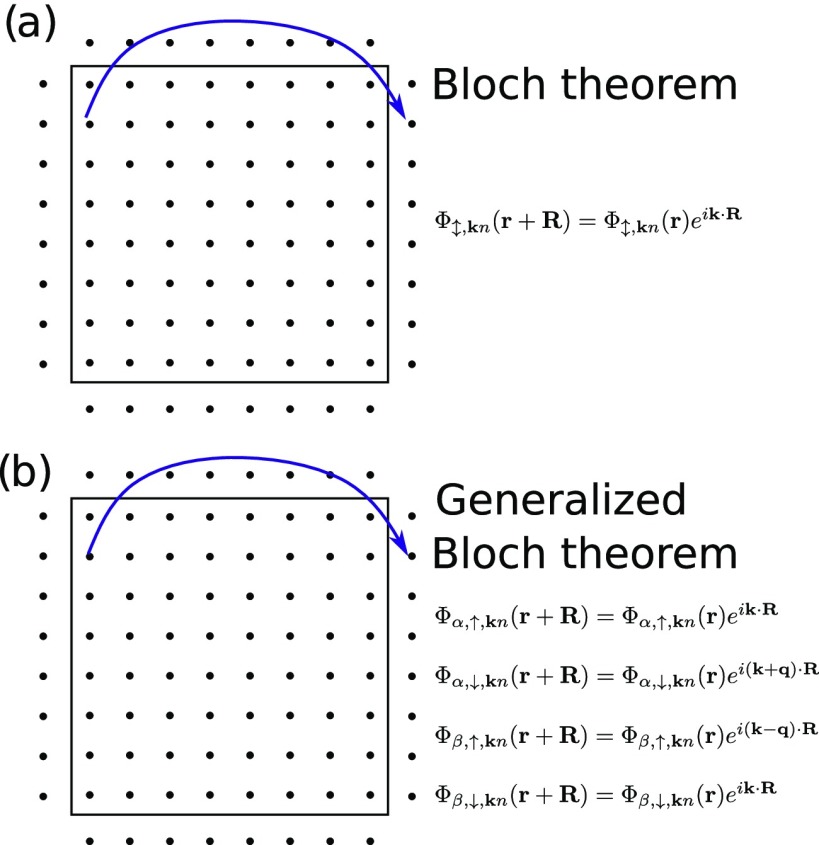
Figure 7

Open in a new tab

Schematic representation of the boundary conditions used for the (a) Bloch theorem and (b) generalized Bloch theorem. We implemented these “twisted” boundary conditions for which an extra phase factor is added to the boundary points. This extra phase depends on the label (α or β) and the component of the Pauli spinor, as explained in the main text.

Subsequently, we show results for the well-studied reference magnetic transition metals iron (Fe), cobalt (Co), and nickel (Ni), frequently used benchmarks for experimental and theoretical approaches to investigate magnetic excitations. In all of the reported results, we employed the “twisted” boundary conditions to benefit from the GBT, and the calculations are performed in primitive cells of the materials unless stated differently. For each transition metal, we induce transverse magnetic excitations at a fixed wave vector q applying the kick described above with an opening angle of θ = 2 × 10–2. This value of the opening angle was determined by decreasing θ until a clear spectral feature, such as a magnon peak at small wave vectors, did not change its position further, indicating that the linear-response regime is reached. We record the time evolution of the spin magnetization, specifically

3. 12

where the spin magnetization is computed from the KS states [cf. eq 2c]. Next, we compute the Fourier transform of m±(q, t), that is

3. 13

where the time signal is artificially damped, described by a rate Inline graphic, such that it decays to a numerically small value at the final time T of the propagation interval. Hence, we can formally take T → ∞ for the upper integration limit in eq 13. Note that a finite value of α fixes the value of the broadening, which in our studies was chosen to be α = 5. The m±(q, ω) values are then proportional to the transverse spin susceptibilities χ±∓(q, ω; G = G′ = 0), provided the initial kick is not too strong. Below, we show heat maps of the imaginary part of m+(q, ω) as a function of the wave vector q along high-symmetry lines (x-axis) and the energy (y-axis), which correspond to the density of states (DOS) of magnetic excitations. All results are obtained using the adiabatic local-density approximation (LDA) for the effective potentials, allowing us to compare our results to prior studies. Unless specified otherwise, we propagated the system after the initial magnetic kick for T = 18 000 au ≈ 435 fs. The spectral resolution, Δω, can be estimated by requiring that half a period is resolved within the propagation time, T, which yields Δω = ℏπ/T ≈ 5 meV.

3.1. Nickel

We compute Ni using an FCC unit cell with a theoretical lattice constant of a = 3.436 Å,23 a 16 × 16 × 16 k-point mesh with four shifts, and a norm-conserving Hamann–Schlüter–Chiang–Vanderbilt (HSCV) pseudopotential.45,46 The real-space grid is sampled along the primitive lattice vectors of the cell using a grid spacing of 0.27 Bohr. This specific k-point grid allows us to compute 16 distinct wave vectors along Inline graphic. In Figure 2, we show a heat map of the imaginary part of (the negative of) eq 13. For small wave vectors, x < 0.25, we find a pronounced peak in the DOS at low energies, which corresponds to the collective magnon mode. At larger wave vectors, this peak gets broadened due to the vicinity of the Stoner continuum, that is, the continuum of single spin-flip excitations (cf. right panel of Figure 2). From the lowest three wave vectors, we can fit a quadratic dispersion relation, ω(q) = Dq2, shown as the black parabola. Toward the Brillouin zone boundary, the strength of the mode decreases and its energy settles around 400 meV. The value for the fitted spin stiffness47 (D = 890 meV Å2) and the energy toward the Brillouin zone boundary is in good agreement with the available linear-response studies using the adiabatic LDA.18,19,21−23,48

Figure 2.

Figure 2

Open in a new tab

Left panel: density of states of magnetic excitations for nickel. Green stars represent experimental results from inelastic neutron scattering (INS).41 The discrepancy between the INS results and the TD-DFT results within the adiabatic LDA is sometimes attributed to the overestimated spin gap within LDA.42,43 Yellow stars are results obtained from inelastic scanning tunneling spectroscopy (ISTS).44 Right panel: Density of states for several fixed wave vectors in arbitrary units.

3.2. Cobalt

For simulating the magnetization dynamics of Co, we employed an FCC unit cell with a theoretical lattice constant of a = 3.429 Å23 and, similar to the calculations for Ni, a 16 × 16 × 16 k-point mesh with four shifts, a grid spacing of 0.27 Bohr, and an HSCV pseudopotential. Figure 3 depicts the DOS of transverse magnetic excitations for Co. At small wave vectors, we find a clear magnon peak, which fades out around halfway through the Brillouin zone along Inline graphic. The value of the spin stiffness estimated from the lowest three wave vectors (D = 325 meV Å2) is in good agreement with linear-response studies using the adiabatic LDA18,23,48 and, in contrast to Ni, close to experimental values obtained from inelastic neutron scattering.49

Figure 3.

Figure 3

Open in a new tab

Density of states of magnetic excitations for cobalt. The black line depicts a quadratic fit, ω(q) = Dq2, of the first three magnon peaks. Yellow stars are results estimated from inelastic scanning tunneling spectroscopy (ISTS) measurements.44

3.3. Iron

In contrast to our study on Ni and Co, we did not use the elementary (chemical) unit cell for Fe but instead used a cubic supercell containing two Fe atoms. This allowed us to compute the transverse magnetic response at Inline graphic without using the GBT, hence numerically verifying the validity of the GBT. We found no sizable difference between the supercell calculation and the GBT, thus validating our implementation of the GBT. For our simulation, we used the experimental lattice constant of a = 2.867 Å, a 16 × 16 × 16 k-point grid, a grid spacing of 0.27 Bohr, and a PseudoDojo51 pseudopotential Fe, which we found to be softer for Fe than the HSCV pseudopotential, used for Ni and Co. The use of the specified k-point mesh enabled the computation of 16 wave vectors along Inline graphic and eight wave vectors along Inline graphic. No shifts are applied to the k-point mesh, which yields the same density of wave vectors as in our studies of Ni and Co. We find that only for small wave vectors around Γ, that is, roughly up to Inline graphic and Inline graphic, respectively, we get a clear peak corresponding to the collective magnon mode. For larger wave vectors, the magnon peak gets broadened by the Stoner continuum (see Figure 4). Again, as for Ni and Co, our results for Fe are in good agreement with the available linear-response calculations using the adiabatic LDA within TD-DFT.18,19,21−23,48

Figure 4.

Figure 4

Open in a new tab

Density of states of magnetic excitations for iron. We show the DOS along two high-symmetry lines, that is, along Inline graphic and Inline graphic. Experimental results (isotropic) from inelastic neutron scattering are shown as green stars.50 For each high-symmetry line, we fitted a quadratic magnon dispersion relation. The anisotropy is slightly reduced compared to the linear-response TD-DFT presented in ref (48).

The main advantage of our approach to compute transverse magnetic excitations is that we are not limited to the linear-response regime. A simple way to go beyond the linear regime is to increase the opening angle of the magnetization spiral formed due to the initial kick (cf. Figure 1). Since we found that the positions of relevant spectral features are already converged for a propagation time of T = 9000 au ≈ 220 fs in the linear regime, all following results are obtained with this shorter propagation time. 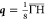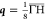In Figure 5, we show the DOS for the fixed wave vectors Inline graphic and Inline graphic, for various opening angles θ. For a wave vector of Inline graphic, where we have a clear magnon peak in the linear regime, we find that the magnon becomes stiffer for wider opening angles (stronger perturbations). This is quite interesting because a simple, classical Heisenberg model with nearest-neighbor (ferromagnetic) couplings between the spins predicts a softening of the magnon frequency for wider opening angles. Even more surprising is the behavior of the DOS at Inline graphic, where we do not have a clear magnon peak in the linear regime due to the damping by the single spin-flip excitations (Stoner continuum). We find that the spectral signal sharpens as we increase the opening angle such that around θ = 0.1, we find a clear single peak, similar to the magnon peaks at smaller wave vectors in the linear regime. This suggests that the Stoner continuum can no longer efficiently damp the collective magnon modes. Increasing the opening angle further, we observe a stiffening of the peak similar to the behavior of the magnon peak at smaller wave vectors.

Figure 5.

Figure 5

Open in a new tab

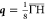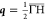Left panel: dependence of the DOS on the opening angle for a wave vector Inline graphic for iron. Right panel: density of states at wave vector Inline graphic for various opening angles θ.

4. Conclusions and Outlook

In our work, we proposed a novel approach to study magnetic excitations from first principles. The basic idea is to induce magnetization dynamics by an ultrashort kick with a transverse magnetic field. We implemented two approaches in the real-space real-time TD-DFT code Octopus: One is based on the use of supercells that are big enough to contain the wave vector of interest. The other uses the flexibility of the real-space grid to implement the “twisted” boundary conditions of the GBT, which allows for the computation of magnetic excitation of any fixed wave vector using the primitive cell. For the second approach, we found the sampling of the Brillouin zone to be important.

As a consistency check, we performed calculations in the linear-response regime, where we can compare against known results and found an excellent agreement with previously published results. In the linear-response regime, our approach has several features that render it different from the usual way of computing the linear response.b First of all, it scales linearly with the number of occupied states and does not require unoccupied states, in contrast to the construction of the linear-response function, which usually requires a summation over unoccupied (virtual) states. This becomes increasingly important for simulating large-scale systems and is therefore extremely relevant in case the GBT cannot be applied, for example, when spin–orbit interactions are included. Second, since we are solving the Schrödinger equation, and not the Dyson equation, for the linear-response function, we only need an approximation for the exchange-correlation potentials and not for the exchange-correlation kernel. Formally, the exchange-correlation kernel is given by the functional derivative of the exchange-correlation potentials with respect to the densities, but in practice, it might be rather cumbersome to implement the required kernel. For example, this plays a role when using orbital functionals, for example, meta- or hyper-GGAs,53 or mixed approaches like hybrid functionals and LDA+U54 because for these approaches, which may be referred to as generalized KS schemes,55,56 it is not obvious how to construct the proper kernel for the linear-response Dyson equation. Finally, even if the exchange-correlation potentials and the corresponding exchange-correlation kernels are available, the ground-state KS equation, which yields the KS response function, and the Dyson equation from which the interacting response function emerges are usually represented in different numerical basis sets. This can lead to a (numerical) violation of the Goldstone theorem, which states that the magnon frequency vanishes for q → 0 in the absence of spin–orbit coupling, while it is by construction satisfied in our approach.

Most importantly, our approach is not limited to the linear-response regime. Already, our proof-of-principles studies for iron revealed interesting trends as transverse magnetic modes are excited more violently. In the region of the energy–momentum space, where a clear magnon peak is present already in the linear regime, we found a stiffening of the magnon frequency. While general nonlinearities can either soften or stiffen the frequency of a harmonic oscillator, the classical Heisenberg model with the nearest-neighbor (ferromagnetic) coupling, for example, predicts a softening of the magnon frequency when the magnon is excited more strongly in contrast to our results. Similarly, magnon–magnon interactions tend to soften the magnon frequency. However, our study on iron, a prototypical ferromagnetic metal, shows the opposite behavior. Even more striking are our findings in the region of the energy–momentum space where collective magnetic excitations are strongly damped by single-electron spin-flip excitations in the linear regime: A stronger excitation seems to “un-burrow” the collective mode, since a clear peak emerges in the density of states. This will be further analyzed in future works.

We stress that our approach is not limited to (anti-) ferromagnetic materials. For example, the machinery can readily be applied to systems exhibiting a nontrivial magnetic order in the ground state, such as spin spirals or skyrmions. However, starting from an already noncollinear ground state implies that transverse and longitudinal magnetic excitations are mixed and so the interpretation of the results might be more difficult.

Finally, using our approach, it is straightforward to include spin–orbit coupling or to combine the magnetic kick with other external drivers, such as periodic lasers (Floquet engineering57) or ultrashort intense laser pulses (e.g., pump-probe spectroscopy). This opens up exciting possibilities to study the interplay of electronic and magnetic excitations in and out of equilibrium within the first-principles framework.

Acknowledgments

N.T.-D. and F.G.E. thank Martin Lüders for stimulating discussions. A.R. acknowledges financial support from the European Research Council (ERC-2015-AdG-694097) and Grupos Consolidados (IT578-13).

Appendix A: Linear-Response TD-DFT for Magnons

In this appendix, we provide a concise summary of the linear-response formulation of TD-DFT. We emphasize that all new results presented in this work are obtained from the time propagation presented in the main body of this paper and not within the linear-response approach discussed in this appendix. The motivation for this appendix is twofold: First of all, we would like to give a short recap of the linear-response formulation of magnetic excitations to provide the minimal background for readers not deeply familiar with magnetic excitations, for example, the definition of magnons within the linear response formalism. Second, we provide the linear-response formulas using our “notational” conventions to allow for a direct comparison to other approaches formulated in the linear response regime.

In the linear regime, the response of the density and the spin magnetization to a perturbation by a scalar potential and magnetic field is given by

graphic file with name ct9b01064_m039.jpg 14

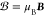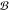In eq 14, we have employed a compressed notation where we omit the dependence on (r, t) of the induced density and spin magnetization and the dependence on (r′, t′) of the perturbing scalar potential and magnetic field. Note that we have included the coupling constant μB in the definition of the perturbing magnetic field, Inline graphic, which means that the “magnetic field” Inline graphic has the same units as the scalar potential v, that is, both have the units of energy. The response matrix χ̲ depends on, both, (r, t) and (r′,t′), and the * denotes a contraction (integral) over (r′,t′). Within TD-DFT, the response function of the interacting system χ̲ is computed from the response function of the effective KS electrons χ̲s and the so-called (Hartree-)exchange-correlation kernel f̲Hxc by solving the following equation

graphic file with name ct9b01064_m042.jpg 15

The KS response is determined from the eigenstates and eigenvalues of the static KS equation. A common reformulation of the linear response eq 14 is to introduce the following linear combination of the densities and potentials

graphic file with name ct9b01064_m043.jpg 16a
graphic file with name ct9b01064_m044.jpg 16b
graphic file with name ct9b01064_m045.jpg 16c
graphic file with name ct9b01064_m046.jpg 16d

In terms of these densities and potentials, the KS Hamiltonian takes the form

graphic file with name ct9b01064_m047.jpg 17

and the KS response χ̲s is diagonal for magnetic systems with a negligible spin–orbit coupling and a collinear ground-state magnetizationc, that is

graphic file with name ct9b01064_m048.jpg 18

The Hartree-exchange-correlation kernel can couple the different channels. In fact, already the Hartree contribution leads to a coupling between the ↑↑ and ↓↓ channels, but it vanishes for the +– and −+ channels, since it stems from a density–density interaction. In this work, we focus on the adiabatic local-density approximation (ALDA) for the exchange-correlation contribution to the effective potentials. In the linear-response formulation of TD-DFT, this leads to an exchange-correlation kernel f̲xc, which is local in space and time, that is

graphic file with name ct9b01064_m049.jpg 19

where f̲xcunif is the static (ω → 0) long-wavelength (q → 0) limit of the exchange-correlation kernel for a uniform electron gas with the density n and spin magnetization m evaluated at the local ground-state density and spin magnetization, n0(r) and m0(r), respectively, of the system. Like the Hartree contribution, it is block-diagonal in the “up”–“down” sector, but, in contrast to the Hartree contribution, it has a nonvanishing diagonal in the +– and −+ channels. This contribution is crucial for the description of magnons, which are collective excitations of the transverse spin magnetization: without fxc, there would be no magnons, much like there would be no plasmons without the Hartree contribution. In Figure 6, we show a sketch of the imaginary part of χ+–, which represents the density of states of magnetic excitations perpendicular to the ground-state magnetization.

Figure 6.

Figure 6

Open in a new tab

Sketch of Im[χ+–] (DOS of magnetic excitations) for a typical ferromagnet. The so-called Stoner continuum is contained in the KS response χs,+– (blue-shaded area). The Stoner continuum is composed of single-electron excitations involving a spin flip. The red curve depicts the dispersion relation for magnons, collective modes induced by the interaction effects described by fxc,+– within TD-DFT.

Appendix B: Time-Dependent Generalized Bloch Theorem

The generalized Bloch theorem (GBT) has been introduced already some time ago by Sandratskii39 to study magnetic systems exhibiting a spin spiral configuration in the ground state. Moreover, this approach can also be used to compute a constrained ground state, that is, the minimal energy state compatible with a magnetization forming a spin spiral, which can be used to compute adiabatic or frozen magnons. To the best of our knowledge, the GBT has not been applied within a time-dependent framework. Hence, within this appendix, we answer the question regarding the conditions under which the application of the GBT is possible within a time-dependent approach.

Let us start by recalling why the Bloch theorem is applicable for the propagation of solids: If the KS Hamiltonian for all times commutes with translations by crystal lattice vectors, the propagator commutes itself with these translations. Hence, if the propagation is started in an eigenstate of the translation operator, for example, a Bloch state, it remains an eigenstate of the translation operator. Now, let us look at how the states after the transverse magnetic kick, defined in eq 9a and 9b, behave under translations by a lattice vector. We assume that the system is collinear in the ground state, which means that we ignore the spin–orbit coupling or a noncollinear spin magnetization due to frustration (for example, in a two-dimensional hexagonal lattice with anti-ferromagnetic nearest-neighbor coupling). This implies that the states before the magnetic kick are Bloch states, which are either pure “spin-up” or pure “spin-down”. After the initial kick, the states are given as follows

graphic file with name ct9b01064_m050.jpg 20a
graphic file with name ct9b01064_m051.jpg 20b

uInline graphic,kn is invariant under transformations by lattice vectors, which means that the new states Φ̃ transform under shifts by lattice vectors as follows

graphic file with name ct9b01064_m052.jpg 21a
graphic file with name ct9b01064_m053.jpg 21b

From eqs 21a and 21b, it is evident that the states after the kick are no longer eigenstates of the translation operator. The transformation law is spoiled by an additional local phase shift between the spin-up and spin-down components. However, we can introduce a new symmetry operator

graphic file with name ct9b01064_m054.jpg 22

which corresponds to a translation in space by a lattice vector and a simultaneous rotation in the spin space around the z-axis by an angle q·Rd. The states Φ̃ are eigenstates of this new symmetry operation that is

graphic file with name ct9b01064_m055.jpg 23a
graphic file with name ct9b01064_m056.jpg 23b

We can define two generic time-dependent states, labeled as α and β, that is

graphic file with name ct9b01064_m057.jpg 24a
graphic file with name ct9b01064_m058.jpg 24b

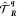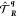which are eigenstates of Inline graphic, provided the uInline graphicαβ, kn are periodic under lattice translations. It is straightforward to see that the states Φ̃ can be written in this way. To compute finite differences (derivatives) on the real-space grid, the implementation of specific boundary conditions is required for the generalized Bloch theorem, as illustrated in Figure 7. Now, to show that eqs 24a and 24b are solutions of the time-dependent KS equation, we need to establish that the Hamiltonian at all times commutes with Inline graphic. For a truly noninteracting system, this can be explicitly checked because the Hamiltonian is determined for all times. However, the KS Hamiltonian depends on time-propagated states themselves and therefore we need to verify that the employed approximation for the self-consistent potentials vxc and Inline graphic leads to an effective KS Hamiltonian, which still commutes with symmetry operation 22. The density associated with the orbitals (24a and 24b) is given in terms of Inline graphic and is therefore periodic under lattice translations. The expectation value of the spin magnetization for the orbitals (24a and 24b) is given by

graphic file with name ct9b01064_m062.jpg 25a
graphic file with name ct9b01064_m063.jpg 25b

where Inline graphic is a rotation matrix describing rotations of the spin magnetization around the z-axis by an angle q × r

graphic file with name ct9b01064_m065.jpg 26

The “partial” spin magnetizations mα/β0 are determined exclusively by Inline graphic and therefore are lattice periodic

graphic file with name ct9b01064_m066.jpg 27

where we introduced φα/β(r, t) = arg[(uα/β↑)†uα/β] and the longitudinal and transverse spin magnetizations, mα/β,∥ = |uα/β↑|2 – |uα/β|2 and mα/β,⊥ = 2 |(uα/β↑)†uα/β|, respectively. Accordingly, the full spin magnetization is given by

graphic file with name ct9b01064_m067.jpg 28

The condition that the KS Hamiltonian commutes with the symmetry 22 is equivalent to the requirement

graphic file with name ct9b01064_m068.jpg 29

in the absence of spin–orbit coupling and without an external magnetic field. Within the ALDA, the exchange-correlation magnetic field is given by

graphic file with name ct9b01064_m069.jpg 30

where F(m) is a scalar function depending only on the magnitude of the spin magnetization m(r, t). Using (25), we find immediately

graphic file with name ct9b01064_m070.jpg 31

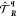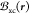which means that, within the ALDA, the KS Hamiltonian commutes for all times with Inline graphic and the generalized Bloch theorem applies. In fact, any approximation for Inline graphic, which is derived from an approximation to the exchange-correlation energy Exc[n,m], for example, adiabatic GGAs, which only depend on properly contracted scalars of the density and spin magnetization and their respective gradients, will fulfill condition 29.34,36,58,59 For an approximation based on ground-state orbital functionals for the exchange-correlation energy, which have to be considered within a generalized KS scheme, one should check whether the generalized KS Hamiltonian, which may contain nonlocal couplings, commutes with the symmetry 22. Finally, let us briefly comment on how we determine the labels α or β from the initial (ground-state) KS states in practice. Using the fact that the states before the magnetic kick are either pure “spin-up” or pure “spin-down” states, we compute for each KS state the expectation of Ŝz. Depending on its sign, a state is labeled as α or β. This information is written such that it can be read in the case of a restart of the time-dependent calculation.

Author Contributions

⊥ N.T.-D. and F.G.E. contributed equally to this work.

The authors declare no competing financial interest.

Footnotes

a

Here, we take the magnetic unit cell to be identical to the chemical unit cell, since we are interested in simple ferromagnetic materials.

b

The Sternheimer approach52 adopted for magnetic excitations17,21,22 shares these features.

c

This implies that the spin magnetization is aligned along the same axis, defined as the z-axis, everywhere in space.

d

We refer to the rotation angle of the spin magnetization, which is twice the corresponding rotation angle for the spinor (cf. eqs 9 and 11).

References

  1. Moriya T.Spin Fluctuations in Itinerant Electron Magnetism; Springer Series in Solid-State Sciences; Springer: Berlin, Heidelberg, 2012. [Google Scholar]
  2. Lee J.-U.; Lee S.; Ryoo J. H.; Kang S.; Kim T. Y.; Kim P.; Park C.-H.; Park J.-G.; Cheong H. Ising-Type Magnetic Ordering in Atomically Thin FePS3. Nano Lett. 2016, 16, 7433–7438. 10.1021/acs.nanolett.6b03052. [DOI] [PubMed] [Google Scholar]
  3. Huang B.; Clark G.; Navarro-Moratalla E.; Klein D. R.; Cheng R.; Seyler K. L.; Zhong D.; Schmidgall E.; McGuire M. A.; Cobden D. H.; Yao W.; Xiao D.; Jarillo-Herrero P.; Xu X. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit. Nature 2017, 546, 270. 10.1038/nature22391. [DOI] [PubMed] [Google Scholar]
  4. Bonilla M.; Kolekar S.; Ma Y.; Diaz H. C.; Kalappattil V.; Das R.; Eggers T.; Gutierrez H. R.; Phan M.-H.; Batzill M. Strong room-temperature ferromagnetism in VSe2 monolayers on van der Waals substrates. Nat. Nanotechnol. 2018, 13, 289–293. 10.1038/s41565-018-0063-9. [DOI] [PubMed] [Google Scholar]
  5. O’Hara D. J.; Zhu T.; Trout A. H.; Ahmed A. S.; Luo Y. K.; Lee C. H.; Brenner M. R.; Rajan S.; Gupta J. A.; McComb D. W.; Kawakami R. K. Room Temperature Intrinsic Ferromagnetism in Epitaxial Manganese Selenide Films in the Monolayer Limit. Nano Lett. 2018, 18, 3125–3131. 10.1021/acs.nanolett.8b00683. [DOI] [PubMed] [Google Scholar]
  6. Sun Y.-J.; Tan Q.-H.; Liu X.-L.; Gao Y.-F.; Zhang J. Probing the Magnetic Ordering of Antiferromagnetic MnPS3 by Raman Spectroscopy. J. Phys. Chem. Lett. 2019, 10, 3087–3093. 10.1021/acs.jpclett.9b00758. [DOI] [PubMed] [Google Scholar]; PMID: 31088058.
  7. Kim K.; Lim S. Y.; Kim J.; Lee J.-U.; Lee S.; Kim P.; Park K.; Son S.; Park C.-H.; Park J.-G.; Cheong H. Antiferromagnetic ordering in van der Waals 2D magnetic material MnPS3 probed by Raman spectroscopy. 2D Mater. 2019, 6, 041001 10.1088/2053-1583/ab27d5. [DOI] [Google Scholar]
  8. Basov D. N.; Averitt R. D.; Hsieh D. Towards properties on demand in quantum materials. Nat. Mater. 2017, 16, 1077. 10.1038/nmat5017. [DOI] [PubMed] [Google Scholar]; Review Article.
  9. Gilbert T. L. A phenomenological theory of damping in ferromagnetic materials. IEEE Trans. Magn. 2004, 40, 3443–3449. 10.1109/TMAG.2004.836740. [DOI] [Google Scholar]
  10. Hohenberg P.; Kohn W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. 10.1103/PhysRev.136.B864. [DOI] [Google Scholar]
  11. Kohn W.; Sham L. J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
  12. Dreizler R. M.; Gross E. K. U.. Density Functional Theory; Springer-Verlag: Berlin, Heidelberg, 1990. [Google Scholar]
  13. Runge E.; Gross E. K. U. Density-Functional Theory for Time-Dependent Systems. Phys. Rev. Lett. 1984, 52, 997. 10.1103/PhysRevLett.52.997. [DOI] [Google Scholar]
  14. Fundamentals of Time-Dependent Density Functional Theory; Marques M. A. L.; Marques M. A. L.; Maitra N. T.; Nogueira F. M. S.; Gross E. K. U.; Rubio A., Eds.; Lecture Notes in Physics; Springer: Berlin, Heidelberg, 2012; Vol. 837. [Google Scholar]
  15. Ullrich C. A.Time-Dependent Density-Functional Theory: Concepts and Applications; Oxford Graduate Texts - Oxford University Press: Oxford, 2012. [Google Scholar]
  16. Halilov S. V.; Eschrig H.; Perlov A. Y.; Oppeneer P. M. Adiabatic spin dynamics from spin-density-functional theory: Application to Fe, Co, and Ni. Phys. Rev. B 1998, 58, 293–302. 10.1103/PhysRevB.58.293. [DOI] [Google Scholar]
  17. Savrasov S. Y. Linear Response Calculations of Spin Fluctuations. Phys. Rev. Lett. 1998, 81, 2570–2573. 10.1103/PhysRevLett.81.2570. [DOI] [Google Scholar]
  18. Buczek P.; Ernst A.; Sandratskii L. M. Different dimensionality trends in the Landau damping of magnons in iron, cobalt, and nickel: Time-dependent density functional study. Phys. Rev. B 2011, 84, 174418 10.1103/PhysRevB.84.174418. [DOI] [Google Scholar]
  19. Rousseau B.; Eiguren A.; Bergara A. Efficient computation of magnon dispersions within time-dependent density functional theory using maximally localized Wannier functions. Phys. Rev. B 2012, 85, 054305 10.1103/PhysRevB.85.054305. [DOI] [Google Scholar]
  20. Wysocki A. L.; Valmispild V. N.; Kutepov A.; Sharma S.; Dewhurst J. K.; Gross E. K. U.; Lichtenstein A. I.; Antropov V. P. Spin-density fluctuations and the fluctuation-dissipation theorem in 3d ferromagnetic metals. Phys. Rev. B 2017, 96, 184418 10.1103/PhysRevB.96.184418. [DOI] [Google Scholar]
  21. Gorni T.; Timrov I.; Baroni S. Spin dynamics from time-dependent density functional perturbation theory. Eur. Phys. J. B 2018, 91, 249 10.1140/epjb/e2018-90247-9. [DOI] [Google Scholar]
  22. Cao K.; Lambert H.; Radaelli P. G.; Giustino F. Ab initio calculation of spin fluctuation spectra using time-dependent density functional perturbation theory, plane waves, and pseudopotentials. Phys. Rev. B 2018, 97, 024420 10.1103/PhysRevB.97.024420. [DOI] [Google Scholar]
  23. Singh N.; Elliott P.; Nautiyal T.; Dewhurst J. K.; Sharma S. Adiabatic generalized gradient approximation kernel in time-dependent density functional theory. Phys. Rev. B 2019, 99, 035151 10.1103/PhysRevB.99.035151. [DOI] [Google Scholar]
  24. Bigot J.-Y.; Vomir M.; Beaurepaire E. Coherent ultrafast magnetism induced by femtosecond laser pulses. Nat. Phys. 2009, 5, 515. 10.1038/nphys1285. [DOI] [Google Scholar]
  25. Krieger K.; Dewhurst J. K.; Elliott P.; Sharma S.; Gross E. K. U. Laser-Induced Demagnetization at Ultrashort Time Scales: Predictions of TDDFT. J. Chem. Theory Comput. 2015, 11, 4870–4874. 10.1021/acs.jctc.5b00621. [DOI] [PubMed] [Google Scholar]
  26. Elliott P.; Müller T.; Dewhurst J. K.; Sharma S.; Gross E. K. U. Ultrafast laser induced local magnetization dynamics in Heusler compounds. Sci. Rep. 2016, 6, 38911 10.1038/srep38911. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Simoni J.; Stamenova M.; Sanvito S. Ultrafast demagnetizing fields from first principles. Phys. Rev. B 2017, 95, 024412 10.1103/PhysRevB.95.024412. [DOI] [Google Scholar]
  28. Shokeen V.; Sanchez Piaia M.; Bigot J.-Y.; Müller T.; Elliott P.; Dewhurst J. K.; Sharma S.; Gross E. K. U. Spin Flips versus Spin Transport in Nonthermal Electrons Excited by Ultrashort Optical Pulses in Transition Metals. Phys. Rev. Lett. 2017, 119, 107203 10.1103/PhysRevLett.119.107203. [DOI] [PubMed] [Google Scholar]
  29. Krieger K.; Elliott P.; Müller T.; Singh N.; Dewhurst J. K.; Gross E. K. U.; Sharma S. Ultrafast demagnetization in bulk versus thin films: an ab initio study. J. Phys. Condens. Matter 2017, 29, 224001 10.1088/1361-648X/aa66f2. [DOI] [PubMed] [Google Scholar]
  30. Bertsch G. F.; Iwata J.-I.; Rubio A.; Yabana K. Real-space, real-time method for the dielectric function. Phys. Rev. B 2000, 62, 7998–8002. 10.1103/PhysRevB.62.7998. [DOI] [Google Scholar]
  31. Fröhlich J.; Studer U. M. Gauge invariance and current algebra in nonrelativistic many-body theory. Rev. Mod. Phys. 1993, 65, 733–802. 10.1103/RevModPhys.65.733. [DOI] [Google Scholar]
  32. Bencheikh K. Spin-orbit coupling in the spin-current-density-functional theory. J. Phys. A: Math. Gen. 2003, 36, 11929. 10.1088/0305-4470/36/48/002. [DOI] [Google Scholar]
  33. Abedinpour S. H.; Vignale G.; Tokatly I. V. Gauge-invariant formulation of spin-current density-functional theory. Phys. Rev. B 2010, 81, 125123 10.1103/PhysRevB.81.125123. [DOI] [Google Scholar]
  34. Pittalis S.; Vignale G.; Eich F. G. U(1)×SU(2) gauge invariance made simple for density functional approximations. Phys. Rev. B 2017, 96, 035141 10.1103/PhysRevB.96.035141. [DOI] [Google Scholar]
  35. Giuliani G. F.; Vignale G.. Quantum Theory of the Electron Liquid; Cambridge University Press: Cambridge, 2005; Chapter 3, pp 111–156. [Google Scholar]
  36. Eich F. G.; Pittalis S.; Vignale G. Transverse and longitudinal gradients of the spin magnetization in spin-density-functional theory. Phys. Rev. B 2013, 88, 245102 10.1103/PhysRevB.88.245102. [DOI] [Google Scholar]
  37. Oliveira M. J. T.; Castro A.; Marques M. A. L.; Rubio A. On the Use of Neumann’s Principle for the Calculation of the Polarizability Tensor of Nanostructures. J. Nanosci. Nanotechnol. 2008, 8, 3392–3398. 10.1166/jnn.2008.142. [DOI] [PubMed] [Google Scholar]
  38. Oliveira M. J. T.; Medeiros P. V. C.; Sousa J. R. F.; Nogueira F.; Gueorguiev G. K. Optical and Magnetic Excitations of Metal-Encapsulating Si Cages: A Systematic Study by Time-Dependent Density Functional Theory. J. Phys. Chem. C 2014, 118, 11377–11384. 10.1021/jp4096562. [DOI] [Google Scholar]
  39. Sandratskii L. M. Energy Band Structure Calculations for Crystals with Spiral Magnetic Structure. Phys. Status Solidi B 1986, 136, 167–180. 10.1002/pssb.2221360119. [DOI] [Google Scholar]
  40. Andrade X.; Strubbe D.; De Giovannini U.; Larsen A. H.; Oliveira M. J. T.; Alberdi-Rodriguez J.; Varas A.; Theophilou I.; Helbig N.; Verstraete M. J.; Stella L.; Nogueira F.; Aspuru-Guzik A.; Castro A.; Marques M. A. L.; Rubio A.. Real-space grids and the Octopus code as tools for the development of new simulation approaches for electronic systems. Phys. Chem. Chem. Phys. 2015. 10.1039/C5CP00351B [DOI] [PubMed] [Google Scholar]
  41. Mook H. A.; Paul D. M. Neutron-Scattering Measurement of the Spin-Wave Spectra for Nickel. Phys. Rev. Lett. 1985, 54, 227–229. 10.1103/PhysRevLett.54.227. [DOI] [PubMed] [Google Scholar]
  42. Karlsson K.; Aryasetiawan F. Spin-wave excitation spectra of nickel and iron. Phys. Rev. B 2000, 62, 3006–3009. 10.1103/PhysRevB.62.3006. [DOI] [Google Scholar]
  43. Capelle K.; Vignale G.; Ullrich C. A. Spin gaps and spin-flip energies in density-functional theory. Phys. Rev. B 2010, 81, 125114 10.1103/PhysRevB.81.125114. [DOI] [Google Scholar]
  44. Balashov T.Inelastic Scanning Tunneling Spectroscopy: Magnetic Excitations on the Nanoscale. Ph.D. Thesis, Karlsruhe Institute of Technology, 2009. [Google Scholar]
  45. Hamann D. R.; Schlüter M.; Chiang C. Norm-Conserving Pseudopotentials. Phys. Rev. Lett. 1979, 43, 1494–1497. 10.1103/PhysRevLett.43.1494. [DOI] [Google Scholar]
  46. Vanderbilt D. Optimally smooth norm-conserving pseudopotentials. Phys. Rev. B 1985, 32, 8412–8415. 10.1103/PhysRevB.32.8412. [DOI] [PubMed] [Google Scholar]
  47. Eich F. G.; Pittalis S.; Vignale G. A shortcut to gradient-corrected magnon dispersion: exchange-only case. Eur. Phys. J. B 2018, 91, 173 10.1140/epjb/e2018-90253-y. [DOI] [Google Scholar]
  48. Niesert M.Ab initio Calculations of Spin-Wave Excitation Spectra from Time-Dependent Density-Functional Theory 2011. Record converted from VDB: 12.11.2012.
  49. Pickart S. J.; Alperin H. A.; Minkiewicz V. J.; Nathans R.; Shirane G.; Steinsvoll O. Spin-Wave Dispersion in Ferromagnetic Ni and fcc Co. Phys. Rev. 1967, 156, 623–626. 10.1103/PhysRev.156.623. [DOI] [Google Scholar]
  50. Lynn J. W. Temperature dependence of the magnetic excitations in iron. Phys. Rev. B 1975, 11, 2624–2637. 10.1103/PhysRevB.11.2624. [DOI] [Google Scholar]
  51. van Setten M.; Giantomassi M.; Bousquet E.; Verstraete M.; Hamann D.; Gonze X.; Rignanese G.-M. The PseudoDojo: Training and grading a 85 element optimized norm-conserving pseudopotential table. Comput. Phys. Commun. 2018, 226, 39–54. 10.1016/j.cpc.2018.01.012. [DOI] [Google Scholar]
  52. Sternheimer R. M. Electronic Polarizabilities of Ions from the Hartree-Fock Wave Functions. Phys. Rev. 1954, 96, 951–968. 10.1103/PhysRev.96.951. [DOI] [Google Scholar]
  53. Rappoport D.; Crawford N. R. M.; Furche F.; Burke K. In Computational Inorganic and Bioinorganic Chemistry, Solomon E. I.; King R. B.; Scott R. A., Eds.; John Wiley & Sons, Inc.: Chichester. Hoboken, 2009. [Google Scholar]
  54. Anisimov V. I.; Zaanen J.; Andersen O. K. Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B 1991, 44, 943–954. 10.1103/PhysRevB.44.943. [DOI] [PubMed] [Google Scholar]
  55. Seidl A.; Görling A.; Vogl P.; Majewski J. A.; Levy M. Generalized Kohn-Sham schemes and the band-gap problem. Phys. Rev. B 1996, 53, 3764–3774. 10.1103/PhysRevB.53.3764. [DOI] [PubMed] [Google Scholar]
  56. Baer R.; Kronik L. Time-dependent generalized Kohn-Sham theory. Eur. Phys. J. B 2018, 91, 170 10.1140/epjb/e2018-90103-0. [DOI] [Google Scholar]
  57. Oka T.; Kitamura S. Floquet Engineering of Quantum Materials. Annu. Rev. Condens. Matter Phys. 2019, 10, 387–408. 10.1146/annurev-conmatphys-031218-013423. [DOI] [Google Scholar]
  58. Eich F. G.Non-Collinear Magnetism in Density-functional Theories. Ph.D. Thesis, Freie Universität: Berlin, 2012. [Google Scholar]
  59. Eich F. G.; Gross E. K. U. Transverse Spin-Gradient Functional for Noncollinear Spin-Density-Functional Theory. Phys. Rev. Lett. 2013, 111, 156401 10.1103/PhysRevLett.111.156401. [DOI] [PubMed] [Google Scholar]

Articles from Journal of Chemical Theory and Computation are provided here courtesy of American Chemical Society

RESOURCES