Super-Resolution PET Imaging Using Convolutional Neural Networks

Abstract

Positron emission tomography (PET) suffers from severe resolution limitations which reduce its quantitative accuracy. In this paper, we present a super-resolution (SR) imaging technique for PET based on convolutional neural networks (CNNs). To facilitate the resolution recovery process, we incorporate high-resolution (HR) anatomical information based on magnetic resonance (MR) imaging. We introduce the spatial location information of the input image patches as additional CNN inputs to accommodate the spatially-variant nature of the blur kernels in PET. We compared the performance of shallow (3-layer) and very deep (20-layer) CNNs with various combinations of the following inputs: low-resolution (LR) PET, radial locations, axial locations, and HR MR. To validate the CNN architectures, we performed both realistic simulation studies using the BrainWeb digital phantom and clinical studies using neuroimaging datasets. For both simulation and clinical studies, the LR PET images were based on the Siemens HR+ scanner. Two different scenarios were examined in simulation: one where the target HR image is the ground-truth phantom image and another where the target HR image is based on the Siemens HRRT scanner — a high-resolution dedicated brain PET scanner. The latter scenario was also examined using clinical neuroimaging datasets. A number of factors affected relative performance of the different CNN designs examined, including network depth, target image quality, and the resemblance between the target and anatomical images. In general, however, all deep CNNs outperformed classical penalized deconvolution and partial volume correction techniques by large margins both qualitatively (e.g., edge and contrast recovery) and quantitatively (as indicated by three metrics: peak signal-to-noise-ratio, structural similarity index, and contrast-to-noise ratio).

I. Introduction

POsitron emission tomography (PET) is a 3D medical imaging modality that allows in vivo quantitation of molecular targets. While oncology [1], [2] and neurology [3], [4] are perhaps the fields where PET is of the greatest relevance, its applications are expanding to many other clinical domains [5], [6]. The quantitative capabilities of PET are confounded by a number of degrading factors, the most prominent of which are low signal-to-noise ratio (SNR) and intrinsically limited spatial resolution. While the former is largely driven by tracer dose and detector sensitivity, the latter is driven by a number of factors, including both physical and hardware-limited constraints and software issues. On the software front, resolution reductions are largely a product of smoothing regularizes and filters commonly used within or post-reconstruction for lowering the noise levels in the final images [7]. Together image blurring and tissue fractioning (due to spatial sampling for image digitization) lead to the so-called partial volume effect that is embodied by the spillover of estimated activity across different regions-of-interest (ROIs) [8].

Broadly, the existing computational approaches to address the resolution challenge encompass both within-reconstruction and post-reconstruction corrections. The former family includes methods that incorporate image-domain or sinogram-domain point spread functions (PSFs) in the PET image reconstruction framework [9]–[11] and/or smoothing penalties that preserve edges by incorporating anatomical information [12]–[19] or other transform-domain information [20]–[22]. The latter family of post-reconstruction filtering techniques includes both non-iterative partial volume correction methods [8], [23]–[27] and techniques that rely on an iterative deconvolution backbone [28]–[30] which is stabilized by different edge-guided or anatomically-guided penalty or prior functions [31], [32].

Unlike partial volume correction, strategies for which are often modality-specific, super-resolution (SR) imaging is a more general problem in image processing and computer vision. SR imaging refers to the task of converting a low-resolution (LR) image to a high-resolution (HR) one. The problem is inherently ill-posed as there are multiple HR images that may correspond to any given LR image. Classical approaches for SR imaging involve collating multiple LR images with subpixel shifts and applying motion-estimation techniques for combining them into an HR image frame [33]–[35]. More recently, many single-image SR (SISR) techniques have been proposed. Some SISR methods exploit self-similarities or recurring redundancies within the same image by searching for similar “patches” or sub-images within a given image [36]–[39]. Other SISR methods (the so-called “example-based” techniques) learn mapping functions from external LR and HR image pairs [40]–[44]. With the proliferation of deep learning techniques, LR-to-HR mapping functions based on deep neural networks have been demonstrated to yield state-of-the-art performance at SR tasks. One of the earliest deep SR approaches uses a 3-layer CNN architecture (commonly referred to in the literature as the SRCNN) [45]. Subsequently, a very deep SR (VDSR) CNN architecture [46] that had 20 layers and used residual learning [47] was shown to yield much-improved performance over the shallower SRCNN approach. Even more recently, SR performance has been further boosted by leveraging generative adversarial networks (GANs) [48], although these methods are somewhat limited by the challenges of GAN training, which remains notoriously difficult. While many recent papers have successfully utilized deep neural networks for PET image denoising and radiation dose reduction [49]–[51], the application of deep learning for SR PET imaging is a less-explored research territory [52], [53]. Unlike the denoising problem which aims to create a smoother image from a noisy one while ideally preserving edges, the SR problem aims to create a sharper image from a blurry one. Accordingly, SR requires distinct network design strategies and data preparation than denoising. Our previous work on SR PET spans a wide gamut, including both (classical) penalized deconvolution based on joint entropy [32], [54] and deep learning approach based on the VDSR CNN [53]. This work is an extension of the latter effort.

In this paper, we design, implement, and validate several CNN architectures for SR PET imaging, including both shallow and very deep varieties. As a key adaptation of these models to PET imaging, we supplement the LR PET input image with its HR anatomical counterpart, e.g. a T1-weighted MR image. Unlike uniformly-blurred natural images, PET images are blurred in a spatially-variant manner [10], [55]. We, therefore, further adjust the network to accommodate spatial location details as inputs to assist the SR process. “Ground-truth” HR images are required for the training phase of all supervised learning methods. Though simulation studies are not constrained by this demand, it is a challenge for clinical studies where it is usually infeasible to obtain the “ground-truth” HR counterparts for LR PET scans of human subjects. To ensure clinical utility of this method, we extend it to training based on imperfect target images derived from a higher-resolution clinical scanner, thereby exploiting the SR framework to establish a mapping from an LR scanner’s image domain to an HR scanner’s image domain. In section II, we describe the underlying network architecture, the simulation data generation steps and the network training and validation procedures. In section III, we present simulation results comparing the performance of CNN-based SR with three well-studied reference approaches. A discussion of this method and our overall conclusions are presented in sections IV and V respectively.

II. Methods

A. Network Design

1). Network Inputs:

One key contribution of this paper is the tailoring of the CNN inputs to address the needs of SR PET imaging. All CNNs implemented here have the LR PET as the main input. To further assist the resolution recovery process, additional inputs are incorporated as described below:

a). Anatomical Inputs:

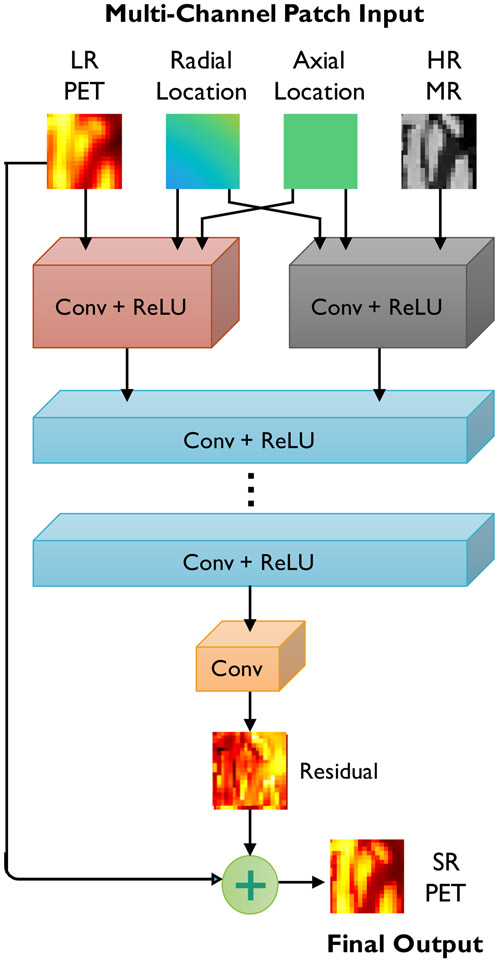
In generating the SR PET images, we seek to exploit the similarities between the PET and its high-resolution anatomical counterpart. Most clinical and preclinical PET scanners come equipped with anatomical imaging capabilities in the form of computed tomography (CT) or MR imaging to complement the functional information in PET with structural information. As illustrated in the schematic in Fig. 1, we employ CNNs with multi-channel inputs, that include LR PET and HR MR input channels.

Fig. 1.

CNN architecture for SR PET. The network uses up to 4 inputs: (i) LR PET (the main input), (ii) HR MR, (iii) radial locations, and (iv) axial locations. The network consists of alternating convolutional (Conv) layers and rectified linear units (ReLUs) for nonlinear activation. It predicts the residual PET image which is later added to the input LR PET to generate the SR PET.

b). Spatial Inputs:

The spatial inputs are two 3D matrices of the same size as the image. One matrix stores the axial coordinates of each voxel, while the other stores the radial coordinates. In light of the cylindrical symmetry of PET scanners, these radial and axial inputs are sufficient for learning the spatially-variant structure of the blurring operator directly from the training data.

c). Fusion:

For natural RGB images, where the three input channels typically have a high degree of structural similarity, usually the same set of kernels is effective for feature extraction. In contrast, our CNN architecture exhibits a higher degree of input heterogeneity. Our initial experiments indicated the need for greater network width to accommodate a diverse set of features based on the very different input channels. We found an efficient solution to this by using separate kernels at the lower levels and fusing this information at higher levels as demonstrated in Fig. 1.

2). Network Depth and Width:

A key finding of the VDSR paper was that the deeper the network, the better its performance. The paper showed that VDSR outperforms SRCNN by a great margin in terms of PSNR [46]. Here, we implement networks with different depths:

a). Shallow CNN:

We designed and implemented a set of “shallow” networks loosely inspired by the 3-layer SRCNN [45]. This network only has three convolutional layers, each followed by a rectified linear unit (ReLU), except for the last output layer. Two key modifications were made to the 3-layer SRCNN to adapt it for SR PET imaging: 1) residual learning and 2) modified inputs as described in section II-A1. While, as a rule of thumb, the qualifier “deep” is applied to networks with three or more layers, we use the word “shallow” in this paper in a relative way.

b). Very Deep CNN:

We designed and implemented a series of “very deep” CNNs based on the VDSR architecture in [46], but with a different input design and a fusion layer described in section II-A1. The very deep SR networks all have 20 convolutional layers, each followed by a ReLU, except for the last output layer.

For all the CNNs, the stride and padding for the convolution kernels were both set to 1. A 3 × 3 kernel was adopted. All the convolutional layers had 64 filters except for the last layer, which had only 1 filter.

We implemented, validated, and compared both shallow (3-layer) and very deep (20-layer) CNN architectures with varying numbers of inputs. For the rest of the paper, we refer to these configurations as S1, S2, S3, S4, V1, V2, V3, and V4 as summarized in Table I.

TABLE I.

CNN architectures

Network properties	S1	V1	S2	V2	S3	V3	S4	V4
Number of layers	3	20	3	20	3	20	3	20
Input types	LR PET	LR PET	LR PET HR MR	LR PET HR MR	LR PET Radial locations Axial locations	LR PET Radial locations Axial locations	LR PET HR MR Radial locations Axial locations	LR PET HR MR Radial locations Axial locations

3). Network Implementation and Optimization:

All networks were trained using an L₁ loss function. For an unknown SR PET image vectorized as $\mathit{x}\in {\mathbb{R}}^N$ and a target HR PET image ${\mathit{x}}_{\mathrm{HR}}\in {\mathbb{R}}^N$, where N is the number of voxels in the HR image domain, the L₁ loss function is computed as:

$${\Phi }_{\text{training}}(\mathit{x}\mid {\mathit{x}}_{\text{HR}})=\Vert \mathit{x}-{\mathit{x}}_{\text{HR}}{\Vert }_1.$$ (1)

Although the L₂ loss is the more frequently used variety of loss functions, recent literature [56] shows that the L₁ loss achieves improved performance with respect to most image quality metrics such as the peak signal-to-noise ratio and the structural similarity index.

All networks were implemented on the PyTorch platform. Training was performed using GPU-based acceleration achieved by using an NVIDIA GTX 1080 Ti graphics card. Minimization of the L₁ loss function was performed using Adam, an algorithm for optimizing stochastic objective functions via adaptive estimates of lower-order moments [57].

B. Simulation and Experimental Details

In the following, we describe two simulation studies using the BrainWeb digital phantom and the ¹⁸F-fluorodeoxyglucose (¹⁸F-FDG) radiotracer and a clinical patient study also based on ¹⁸F-FDG. The inputs and targets for the studies are summarized in Table II. All LR PET images were based on the Siemens ECAT EXACT HR+ scanner. For the first simulation study, the HR PET images were the “ground-ruth” images generated from segmented anatomical templates. For the second simulation study and the clinical study, the HR PET images were based on the Siemens HRRT scanner. Bicubic interpolation was used to resample all input and target images to the same voxel size of 1 mm × 1 mm × 1 mm with a 256×256×207 grid size. The LR and HR scanner properties are summarized in Table III [58].

TABLE II.

Simulation and experimental studies

Study index	Study type	LR image (input)	HR image (target)
1	Simulation	HR+ PET	True PET
2	Simulation	HR+ PET	HRRT PET
3	Clinical	HR+ PET	HRRT PET

TABLE III.

LR and HR image sources

Image Image	Scanner	Spatial resolution	Bore diameter	Axial length
LR	HR+	4.3 - 8.3 mm	562 mm	155 mm
HR	HRRT	2.3 - 3.4 mm	312 mm	250 mm

1). Simulation Setup:

a). HR+ PSF Measurement:

An experimental measurement of the true PSF was made by placing 0.5 mm diameter sources filled with ¹⁸F-FDG inside the HR+ scanner bore, which is 56.2 cm in diameter and 15.5 cm in length. The PSF images were reconstructed using ordered subsets expectation maximization (OSEM) with post-smoothing using a Gaussian filter. The PSFs were fitted with Gaussian kernels. We assumed radial and axial symmetry and calculated the PSFs at all other in-between locations as linear combinations of the PSFs measured at the nearest measurement locations. Interpolation weights for the experimental datasets were determined by means of bilinear interpolation over an irregular grid consisting of the quadrilaterals formed by the nearest radial and axial PSF sampling locations from a given point.

b). Target Image Generation for Study 1:

Realistic simulations were performed using the 3D BrainWeb digital phantom (http://brainweb.bic.mni.mcgill.ca/brainweb/). 20 distinct atlases with 1 mm isotropic resolution were used to generate a set of “ground-truth” PET images. The atlases contained the following region labels: gray matter, white matter, blood pool, and cerebrospinal fluid. Static PET images were generated based on a ~ 1 hour-long ¹⁸F-FDG scan as described in our earlier paper [32]. This “ground-truth” static PET is referred to as “true PET” for the rest of the paper. In Study 1, our purpose was to train the networks using the perfect “ground-truth” (clean target images). The target HR PET images are, therefore, the true PET images.

c). Target Image Generation for Study 2:

In Study 2, we trained the networks using simulated HRRT PET images as our target HR images. The geometric model of the HRRT scanner was used to generate sinogram data. Poisson noise realizations were generated for the projected sinograms with a mean of 10⁸ counts for a scan duration of 3640 s. The images were then reconstructed using the OSEM algorithm (6 iterations, 16 subsets). OSEM reconstruction results typically appear grainy due to noise. We, therefore, perform post-filtering with a 2.4 mm full width at half maximum (FWHM) 3D Gaussian filter. Since the intrinsic resolution of the HRRT scanner is in the 2.3-3.4 mm range, this step improves image quality without any appreciable reduction in the resolution.

d). Input Image Generation for Studies 1 and 2:

The geometric model of the HR+ scanner was used to generate sinogram data. Noisy data was generated using Poisson deviates of the projected sinograms, a noise model widely accepted in the PET imaging community [59]. The Poisson deviates were generated with a mean of 10⁸ counts for the full scan duration of 3640 s. The data were then reconstructed using the OSEM algorithm (6 iterations, 16 subsets). The images were subsequently blurred using the measured, spatially-variant PSF to generate the LR PET images. In order to match HR PET image grid size, the LR PET images were interpolated into 256 × 256 × 207 from the HR+ output size of 128 × 128 × 64 using bicubic interpolation. T1-weighted MR images with 1 mm isotropic resolution derived directly from the BrainWeb database were used as HR MR inputs.

2). Experimental Setup:

a). Clinical Data Source:

Clinical neuroimaging datasets for this paper were obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI, http://adni.loni.usc.edu/) database, a public repository containing images and clinical data from 2000+ human datasets. We selected 30 HRRT PET scans and the anatomical T1-weighted MPRAGE MR scans for clinical validation of our method. For consistency, all datasets were based on the ADNI1 protocol. 10 of the 30 subjects were from the cognitively normal (CN) category. The remaining 20 subjects had mild cognitive impairment (MCI). The full scan duration was 30 minutes (6 × 5-minute frames). The OSEM algorithm (6 iterations, 16 subsets) was used for reconstruction.

b). Target Image Generation for Study 3:

The OSEM-reconstructed HRRT PET images were post-filtered using a 2.4 mm FWHM 3D Gaussian filter to generate target HR PET images for the clinical study. This post-filtering step, as previously explained in the context of Study 2, reduces the noise without substantially reducing the image resolution of the HRRT images.

c). Input Image Generation for Study 3:

The LR counterparts of the HRRT images were generated by applying the measured spatially-variant PSF of the HR+ scanner to the OSEM-reconstructed HRRT images. While not directly derived from the HR+ scanner, the use of a measured image-domain PSF ensures parity in terms of spatial resolution with true HR+ images. Rigidly co-registered T1-weighted MR images with 1 × 1 × 1 voxels were used as HR MR inputs. Cross-modality registration was performed using FSL (https://fsl.fmrib.ox.ac.uk) [60], [61].

3). Training and Validation:

a). Cohort Sizes:

A cohort size of 20 human subjects was used for Studies 1 and 2. The size was dictated by the number of subjects in the BrainWeb database. For Study 3, the cohort comprised a total of 30 human subjects. The training and validation subsets each included a mix of MCI and CN subjects. For all the studies, training was performed using 15 subjects to predict a residual image that is an estimated difference between the input LR PET and the ground truth HR PET. For Studies 1 and 2, the validation dataset consisted of 5 simulation subjects, while for Study 3, the validation dataset consisted of 15 clinical subjects.

b). Input Dimensions:

We trained all the networks using multi-channel 2D transverse patches. For instance, when training S4 and V4, we sliced the four 3D input channels with combined dimensions of 256 × 256 × 207 × 4 into 207 samples of size 256 × 256 × 4 (2D slices + 4 channels). The input intensities were normalized into the range [0, 1]. Data augmentation was achieved by randomly rotating the inputs by 1 to 360° and randomly cropping them to the size of 96 × 96 × 4.

c). Training Parameters:

Consistent selections of training parameters were used for all the CNN types and for all the studies. The learning rate was initially set to 0.0003 and decreased by 5 × 10⁻⁷ at every epoch. The batch size was 10. The networks were trained for 400 epochs.

C. Reference Approaches

We compared the SR images generated by the networks S1, V1, S2, V2, S3, V3, S4, and V4 with the following approaches: deconvolution stabilized by a joint entropy (JE) penalty based on an anatomical MR image, deconvolution stabilized by the total variation (TV) penalty, and region-based voxel-wise (RBV) correction (a partial volume correction technique).

For an unknown SR PET image vectorized as $\mathit{x}\in {\mathbb{R}}^N$ and a scanner-reconstructed LR PET image $\mathit{b}\in {\mathbb{R}}^n$, the least squares cost function for data fidelity is:

$${\Phi }_{\text{PSF}}(\mathit{x}\mid \mathit{b})=\frac{1}{2}(\mathit{A}\mathit{x}-\mathit{b}{)}^T(\mathit{A}\mathit{x}-\mathit{b}).$$ (2)

Here N and n are the respective numbers of voxels in the SR/HR and LR images and $\mathit{A}\in {\mathbb{R}}^{n\times N}$ represents a blurring and downsampling operation based on the measured spatially-variant PSF of the scanner [32]. The two deconvolution techniques used as reference in this paper seek to minimize a composite cost function, Φ_PSF + βΦ_reg, where β is a regularization parameter and Φ_reg is a regularization penalty function. Given an HR MR image, denoted by a vector $\mathit{y}\in {\mathbb{R}}^N$, the JE penalty is defined as [32]:

$${\Phi }_{\text{reg-JE}}(\mathit{x}\mid \mathit{y})=-\sum _{i=1}^M\sum _{j=1}^M\delta u\delta vp(u_i,v_j)\log p(u_i,v_j).$$ (3)

Here $\mathit{u}\in {\mathbb{R}}^M$ and $\mathit{v}\in {\mathbb{R}}^M$ are intensity histogram vectors based on the PET and MR images respectively and M is the number of intensity bins [32]. The TV penalty is defined as:

$${\Phi }_{\text{reg-TV}}(\mathit{x})=(\Vert {\Delta }_1\mathit{x}{\Vert }_1+\Vert {\Delta }_2\mathit{x}{\Vert }_1+\Vert {\Delta }_3\mathit{x}{\Vert }_1),$$ (4)

where Δ_k (k = 1, 2, or 3) are finite difference operators along the three cartesian coordinate directions [32].

The RBV technique [26] is a voxel-based extension of the popular geometric transfer matrix (GTM) method [8], a popular partial volume correction technique used in PET. It computes the corrected image $\mathit{x}\in {\mathbb{R}}^N$ from an upsampled blurry image of the same size, $\tilde{\mathit{b}}\in {\mathbb{R}}^N$ as follows:

$$\begin{gathered} \mathit{x}=\tilde{\mathit{b}}\odot [\mathit{s}\oslash (\mathit{s}\otimes \mathit{h})], \\ \mathit{s}=\sum _{i=1}^{N_{ROI}}{g}_i{\mathit{p}}_i. \end{gathered}$$ (5)

Here $\mathit{h}\in {\mathbb{R}}^N$ is the approximate, spatially-invariant PSF, ⊙ and ⊘ represent Hadamard (entrywise) multiplication and division respectively, ⊗ represents 3D convolution, N_ROI = 2 represents the two gray and white matter anatomical ROIs, p_i is a binary mask for the ith ROI (p_ij = 1 if voxel j belongs to ROI i, 0 otherwise), and g_i is the GTM-corrected intensity for the ith ROI [8].

D. Evaluation Metrics

The evaluation metrics used in this paper are defined below. In the following, the true and estimated images are denoted x and $\widehat{x}$ respectively. We use the notation μ_x and σ_x respectively for the mean and standard deviation of x.

1). Peak Signal-to-Noise Ratio (PSNR):

The PSNR is the ratio of the maximum signal power to noise power and is defined as:

$$\text{PSNR}(\widehat{\mathit{x}},\mathit{x})=20{\log }_{10}\left(\frac{\max (\widehat{\mathit{x}})}{\text{RMSE}(\widehat{\mathit{x}},\mathit{x})}\right),$$ (6)

where the root-mean-square error (RMSE) is defined as:

$$\text{RMSE}(\widehat{\mathit{x}},\mathit{x})=\sqrt{\frac{1}{N}\sum _k({\widehat{\mathit{x}}}_k-{\mathit{x}}_k{)}^2}.$$ (7)

2). Structural Similarity Index (SSIM):

The SSIM [62] is a well-accepted measure of perceived image quality and is defined as:

$$\text{SSIM}(\widehat{\mathit{x}},\mathit{x})=\frac{(2{\mu }_x{\mu }_{\widehat{x}}+c_1)(2{\sigma }_{x\widehat{x}}+c_2)}{({\mu }_x^2+{\mu }_{\widehat{x}}^2+c_1)({\sigma }_x^2+{\sigma }_{\widehat{x}}^2+c_2)}.$$ (8)

Here c₁ and c₂ are parameters stabilizing the division and ${\sigma }_{x\widehat{x}}$ is the covariance of x and $\widehat{x}$.

3). Contrast-to-Noise Ratio (CNR):

The CNR for a target ROI $\mathcal{R}$ and a reference ROI ${\mathcal{R}}_{\text{ref}}$ is defined as:

$$\text{CNR}=\frac{\mid {\mu }_{\widehat{x}}^{\mathcal{R}}-{\mu }_{\widehat{x}}^{{\mathcal{R}}_{\text{ref}}}\mid }{\sqrt{[({\sigma }_{\widehat{x}}^{\mathcal{R}}{)}^2+({\sigma }_{\widehat{x}}^{{\mathcal{R}}_{\text{ref}}}{)}^2]}}.$$ (9)

In this work, the gray matter ROI is treated as the target and the white matter ROI as the reference.

III. Results

A. Study 1: Simulation Results

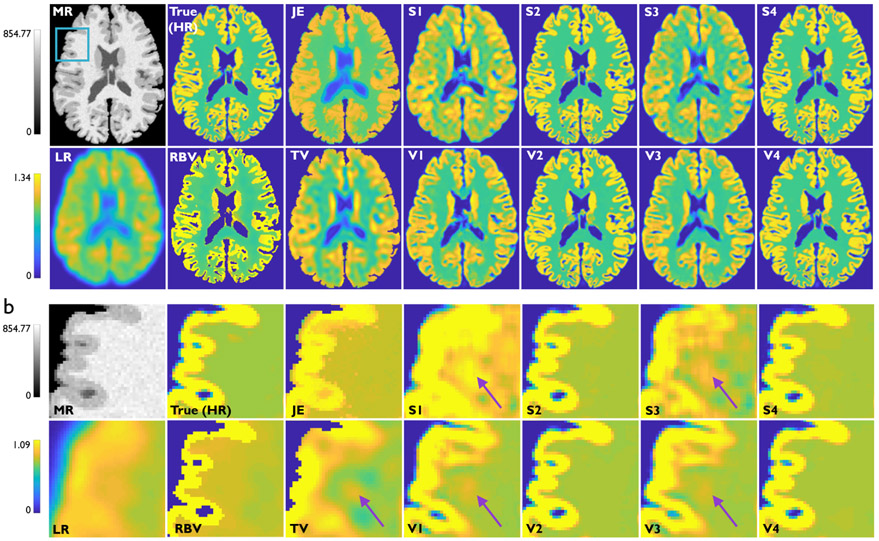
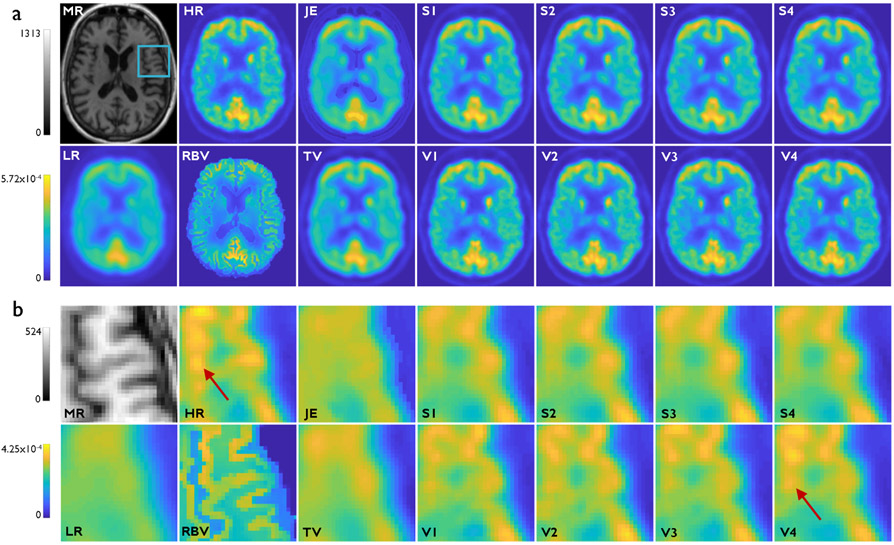
Fig. 2a showcases results from Study 1 — transverse slices from the HR MR, HR PET (same as the true PET in this case), LR PET, RBV PET, and the SR imaging results from the two deconvolution methods and eight CNNs described in Table I. The image frames are from one subject from the validation dataset. Magnified subimages in Fig. 2b highlight artifacts/inaccuracies indicated by purple arrows that are observed in all the techniques that lack anatomical guidance, namely TV, S1, V1, S3, and V3. Comparison of the subimage pairs (S1, S3) and (V1, V3) illustrates that, in the absence of anatomical information, spatial information greatly enhanced image quality. Comparison of the subimage pairs (S1, V1) and (S3, V3) also shows that the addition of more convolutional layers (increased network depth) is also very effective in the absence of anatomical information. Among the non-deep-learning methods, JE and RBV, which incorporate anatomical information, show better edge recovery than TV. The performance metrics (PSNR, SSIM, and gray-to-white CNR) for the different methods are tabulated in Table IV. The values of these metrics computed for the HR images (true PET images for Study 1) are also included in this table for reference. This table indicates that methods with anatomical information perform better than methods without this information. CNN-based approaches that incorporate anatomical information vastly exceed the performance of classical methods.

Fig. 2.

Study 1: Simulation results from one subject belonging to the validation dataset. (a) Transverse slices from the T1-weighted HR MR image, true PET image (also the HR image for this case), LR PET image (HR+ scanner), RBV-corrected PET image, JE-penalized deconvolution result, TV-penalized deconvolution result, and the Sr outputs from the following CNNs: S1, V1, S2, V2, S3, V3, S4, and V4. The blue box on the MR image indicates the region that is magnified for closer inspection. (b) The corresponding magnified subimages. Purple arrows indicate areas in the white-matter background region where prominent noise-induced artifacts arise for TV and for the CNNs without anatomical inputs, namely S1, V1, S3, and V3.

TABLE IV.

Study 1: Performance comparison

Metric	Reference	HR	LR	RBV	TV	JE	S1	V1	S2	V2	S3	V3	S4	V4
PSNR	True	∞	21.47	23.68	22.35	22.37	26.86	27.71	37.17	37.61	27.17	27.98	37.27	37.93
PSNR s.d.		0.00	0.41	0.45	0.66	0.68	0.71	0.72	0.77	0.56	0.74	0.76	0.73	0.61
SSIM	True	1.00	0.74	0.74	0.85	0.86	0.82	0.86	0.9 t7	0.97	0.84	0.87	0.97	0.98
SSIM s.d.		0.000	0.007	0.013	0.012	0.006	0.005	0.003	0.002	0.0008	0.005	0.004	0.001	0.001
CNR	-	0.95	0.09	0.59	0.52	0.53	0.50	0.56	0.89	0.85	0.53	0.57	0.88	0.91
CNR s.d.		0.09	0.04	0.06	0.08	0.08	0.08	0.08	0.09	0.09	0.09	0.08	0.09	0.09

In terms of PSNR, the supervised CNNs outperform the classical approaches by a wide margin. S2, S4, V2, and V4, the networks that have anatomical guidance, show stronger performance in terms of PSNR, SSIM and CNR than S1, V1, S3, and V3, the networks which lack anatomical guidance. The PSNR, SSIM, and CNR values for S1 vs. S3 show that these metrics increase noticeably with the addition of spatial information for the shallow case.

B. Study 2: Simulation Results

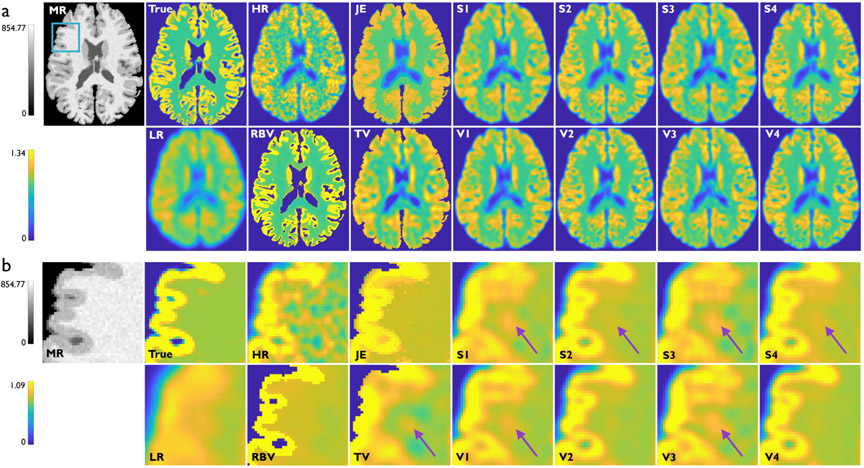
Fig. 3a showcases results from Study 2 — transverse slices from the HR MR, true PET, HR PET, LR PET, RBV PET, and the SR imaging results from the two deconvolution methods and eight CNNs described in Table I. The displayed images are all from the same subject from the validation dataset. As with Study 1, the CNNs with MR-based anatomical inputs (S2, V2, S4, and V4) continue to produce the best results. However, since the target image is now a corrupt image with diminished structural similarity with the MR image, the margin of gain from using anatomical information is now reduced. Magnified subimages in Fig. 3b highlight artifacts/inaccuracies indicated by purple arrows that are more preponderant in this study compared to Study 1. Interestingly, for this more challenging problem, the deeper networks (V2 and V4) have reduced background noise variations than their shallower counterparts (S2 and S4), as indicated by purple arrows in the latter. It should be noted that the JE, TV, and RBV images, which are unsupervised, are the same as those showcased in Fig. 2.

Fig. 3.

Study 2: Simulation results from one subject belonging to the validation dataset. (a) Transverse slices from the T1-weighted HR MR image, true PET image, HR PET image (HRRT scanner), LR PET image (HR+ scanner), RBV-corrected PET image, JE-penalized deconvolution result, TV-penalized deconvolution result, and the SR outputs from the following CNNs: S1, V1, S2, V2, S3, V3, S4, and V4. The blue box on the MR image indicates the region that is magnified for closer inspection. (b) The corresponding magnified subimages. Purple arrows indicate areas in the white-matter background region where prominent noise-induced artifacts arise. These artifacts are the least prominent for V2 and V4 — very deep CNNs with anatomical inputs.

The PSNR, SSIM, and gray-to-white CNR of the different methods are tabulated in Table V. The values of these metrics computed for the HR images (HRRT PET images for Study 2) are also included in this table for reference. An additional goal for this study was to understand the variability in results that could be anticipated when imperfect HR images were used for training. We, therefore, computed two sets of PSNR, SSIM, and CNR measures: one with respect to the target HR PET and another with respect to the true PET. Our results show that there is an overall reduction in performance when the true PET is used as the reference. This is expected with the HR PET used for training deviates substantially from the true PET. But a key observation here is that the CNNs exhibit consistent relative levels of accuracy for the two reference images. As with Study 1, anatomically-guided networks showed better performance than the non-anatomically guided networks and the three classical methods. Also, interestingly, when the true PET is used as the reference, all CNN-based SR images show lower PSNR values than the HR image (HRRT in this case). This can be attributed to the denoising properties of CNNs that lead to SR results that are smoother than the noisy and imperfect target images used for training.

TABLE V.

Study 2: Performance comparison

Metric	Reference	HR	LR	RBV	TV	JE	S1	V1	S2	V2	S3	V3	S4	V4
PSNR	HRRT	∞	27.83	26.55	26.68	27.48	35.11	35.69	38.37	38.48	35.48	35.92	38.44	38.69
PSNR s.d.		0.00	0.17	0.45	0.55	0.50	0.36	0.33	0.24	0.26	0.33	0.29	0.28	0.27
PSNR	True	22.15	21.47	21.84	22.35	22.37	22.69	23.06	22.46	23.92	23.07	23.48	23.78	24.29
PSNR s.d.		0.52	0.41	0.70	0.66	0.68	0.070	0.70	0.072	0.70	0.71	0.61	0.71	0.70
SSIM	HRRT	1.00	0.76	0.81	0.83	0.83	0.82	0.80	0.88	0.88	0.85	0.82	0.89	0.90
SSIM s.d.		0.000	0.033	0.012	0.006	0.005	0.050	0.001	0.062	0.0028	0.024	0.002	0.014	0.003
SSIM	True	0.84	0.74	0.74	0.85	0.86	0.77	0.75	0.86	0.86	0.79	0.77	0.86	0.87
SSIM s.d.		0.003	0 .007	0.013	0.012	0.006	0.022	0.008	0.020	0.006	0.021	0.007	0.021	0.006
CNR	-	0.67	0.09	0.59	0.52	0.53	0.48	0.50	0.58	0.63	0.46	0.49	0.61	0.64
CNR s.d.		0.06	0.04	0.06	0.08	0.08	0.03	0.03	0.12	0.01	0.04	0.04	0.01	0.04

C. Study 2: Network Depth and Width

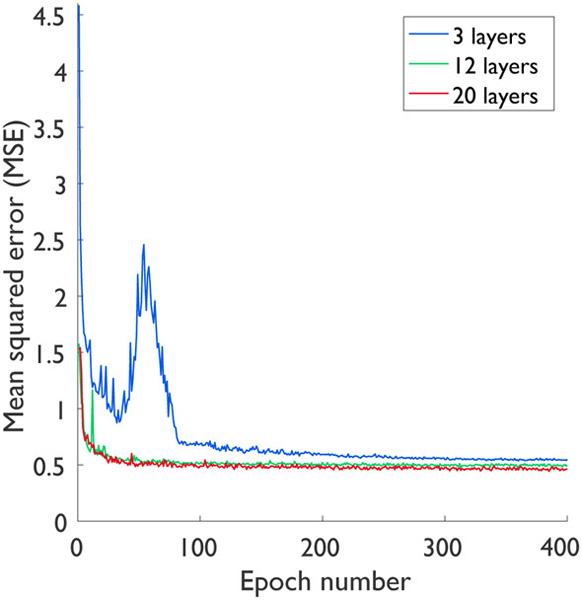
To examine the impact of CNN depth and width, we extended Study 2 to compare three different network depths (3, 12 and 20 layers) and two different network widths (32 and 64 filters). More specifically, all the networks compared had either 32 or 64 filters in each layer, except for their output layers which had only 1 filter. For this study, all networks were trained using the 4-channel inputs (LR PET, HR MR, radial coordinates, and axial coordinates) to ensure a fair comparison. As shown in Table VI, the 20-layer network yielded the best performance in terms of PSNR and SSIM, while the 12-layer network outperformed the 3-layer network. Also, as expected, the networks with 64 filters led to consistently higher PSNR and SSIM than those with 32 filters. Fig. 4 shows the plots of mean squared error (MSE) against the epoch numbers. As demonstrated in this figure, the 20-layer network leads to the fastest convergence rate, followed the 12-layer and 3-layer networks respectively.

TABLE VI.

Depth and width comparison

Metric	# of Filters╲# of Layers	3	12	20
PSNR	32	37.72	38.48	38.60
SSIM	32	0.882	0.905	0.907
PSNR	64	38.46	38.55	38.69
SSIM	64	0.905	0.907	0.908

Fig. 4.

Convergence curves for different depths: 3, 12, and 20 layers.

D. Study 3: Experimental Results

Fig. 5a showcases results from Study 3 — the HR MR, HR PET, LR PET, RBV PET, and the SR imaging results from the two deconvolution methods and eight CNNs described in Table I. For this study, the deeper networks (V1, V2, V3, and V4) produced visually sharper images than their shallower counterparts (S1, S2, S3, and S4). This is clearly evident from the magnified subimages in Fig. 5b. This is consistent with our previous observation that, in the absence of a strong contribution of the anatomical inputs, the extra layers lead to a stronger margin of improvement. That said, V4, which is deeper and uses anatomical information, led to the highest levels of gray matter contrast as highlighted by red arrows.

Fig. 5.

Study 3: Clinical results from one subject belonging to the validation dataset. (a) Transverse slices from the T1-weighted HR MR image, HR PET image (HRRT scanner), LR PET image (HR+ scanner), RBV-corrected PET image, JE-penalized deconvolution result, TV-penalized deconvolution result, and the Sr outputs from the following CNNs: S1, V1, S2, V2, S3, V3, S4, and V4. The blue box on the MR image indicates the region that is magnified for closer inspection. (b) The corresponding magnified subimages. The very deep CNNs (V1, V2, V3, and V4) yield sharper images than their shallow counterparts (S1, S2, S3, and S4). The red arrows points to bright gray matter areas in the HR image that are recovered with the highest contrast in V4.

The PSNR, SSIM, and gray-to-white CNR of the different methods are tabulated in Table VII. The values of these metrics computed for the HR images (HRRT PET images for Study 3) are also included in this table for reference. As displayed in the table, V4 continues to exhibit the best performance in terms of PSNR, SSIM, and CNR. As in Studies 1 and 2, all CNN-based methods outperformed RBV, JE, and TV.

TABLE VII.

Study 3: Performance comparison

Metric	Reference	HR	LR	RBV	TV	JE	S1	V1	S2	V2	S3	V3	S4	V4
PSNR	HRRT	∞	27.24	28.33	29.65	30.13	33.46	35.83	34.28	36.38	34.50	36.23	34.52	37.02
PSNR s.d.		0.00	0.59	0.38	0.48	0.45	0.58	0.14	0.78	0.19	0.70	0.17	0.83	0.22
SSIM	HRRT	1.00	0.86	0.70	0.93	0.89	0.95	0.97	0.95	0.97	0.95	0.97	0.95	0.98
SSIM s.d.		0.000	0.017	0.02	0.007	0.011	0.008	0.002	0.010	0.002	0.009	0.002	0.009	0.002
CNR	-	0.46	0.19	0.23	0.26	0.23	0.34	0.35	0.39	0.41	0.35	0.39	0.40	0.41
CNR s.d.		0.11	0.15	0.03	0.09	0.09	0.11	0.13	0.13	0.12	0.12	0.12	0.12	0.12

IV. Discussion

Overall, our results indicate that CNNs vastly outperform penalized deconvolution and partial volume correction at the SR imaging task. Among different CNN architectures, relative performance depends on the problem at hand. Our simulation and clinical studies all agree that deep CNNs outperform shallow CNNs and that the additional channels contribute to the improvement of overall performance. Like network depth, network width also helped improve performance. These improvements, however, come at the expense of added computational cost. With 4-channel inputs, for example, the training times for 3-, 12-, and 20-layer networks based on 64 filters were 4.7, 7.8, and 12.2 hours respectively. Furthermore, based on our experiments, we concluded that the relative importance of anatomical and spatial input channels depends on the underlying structural similarity between the HR MR and the true PET.

One limitation of our simulation study is the limited size of the validation dataset, which consisted of only 5 subjects. This limitation was overcome in the clinical datasets, where the validation cohort size was increased to 15 subjects. We observed that the performance trends of the compared methods are similar for the experimental and simulation studies. This observation enhances the credibility of our simulation results, despite the small cohort size.

Another limitation of the presented SR approach is the lack of portability of the trained models to inputs with image characteristics (e.g., noise, blur, contrast) substantially different from those used for training. This is a shortcoming that is shared by most supervised learning models. The results presented here correspond to the HRRT-HR+ scanner pair and the ¹⁸F-FDG radiotracer. Additionally, our experimental study relied on data based on a single acquisition protocol. While the network can be easily retrained for alternative scanner pairs, tracer types, and acquisition protocols, the performance characterization may need to be repeated for these specific scenarios. The SR performance is expected to drop when the LR inputs are based on a much lower or higher tracer dose than the datasets used for training. Our future work will characterize the performance of these networks when input noise levels are varied. One remedial approach to address noise sensitivity is the use of transfer learning for easy retraining of the networks with a much smaller training dataset containing LR inputs with altered SNR. Another more sophisticated strategy is to use the CNN output as a prior in reconstruction. We have previously used this approach and produced promising results for denoising [63] and anticipate that it will work for deblurring and SR by extension.

The presence of axial and radial inputs makes the overall network well-equipped to handle 3D inputs as well as 2D slice stacks from all three coordinate directions in a given training dataset. In the current analysis, we used 2D transverse slices alone for training and validation. In this setting, the axial inputs are particularly critical for modeling axial variation of resolution. The radial slices offer some redundancy as the radial location information for each voxel could be derived from the PET or MR image slices directly. However, based on our experience, explicitly providing this information serves as additional feature guidance and is helpful in tackling spatially-variant blurring. Due to the computational cost, we resorted to 2D convolutions instead of 3D. 3D kernels are expected to perform better than 2D ones. However, with 3D kernels, the computational cost is expected to skyrocket. This could prove to be a major bottleneck toward implementing a very deep network (a key contribution of this paper).

In this paper, we exclusively focused on neuroimaging applications. However, the methodology is well generalizable to other parts of the body subject to the availability of appropriate training data. It should be noted that the utilization of anatomical images in conjunction with functional images required co-registration. To ensure robustness, a well-tested standardized registration tool was used for the task. Since the registration is intra-subject, rigid registration based on mutual information suffices for this application.

Another limitation of CNN-based SR (and perhaps the most significant one) is that it relies on supervised learning and, therefore, requires paired LR PET and HR PET images for training. This requirement is easy to address while training using simulated datasets. But paired LR and HR clinical scans are rare. To address this limitation, we are currently exploring self-supervised learning strategies based on adversarial training of generative adversarial networks, that circumvent the need for paired training inputs.

V. Conclusion

We have designed, implemented, and validated a family of CNN-based SR PET imaging techniques. To facilitate the resolution recovery process, we incorporated both anatomical and spatial information. In the studies presented here, the anatomical information was provided as an HR MR image. So as to easily provide spatial information, we supplied patches containing the radial and axial coordinates of each voxel as additional input channels. This strategy is well-consistent with standard CNN multi-channel input formats and, therefore, convenient to implement. Both simulation and clinical studies showed that the CNNs greatly outperform penalized deconvolution both qualitatively (e.g., edge and contrast recovery) and quantitatively (as indicated by PSNR, SSIM, and CNR).

While PSNR and SSIM are metrics that are well-trusted in the image processing and computer vision communities, CNR is probably is a more clinically-meaningful performance metric. Our results confirm that the PSNR and SSIM improvements are also accompanied by improvements in CNR. We, therefore, conclude that SR PET imaging using very deep CNNs is clinically promising. As future work, we will develop new networks based on self-supervised learning that will enable us to circumvent the need for paired training datasets. We will also explore avenues to ensure the applicability of this method to super-resolve inputs with noise levels different from those in the training data. Furthermore, as a strategy for ensuring more robust performance with clinical data, we plan to use a hybrid (simulation + clinical) dataset for CNN training and validation. From an applications perspective, we are interested in using this technique to super-resolve PET images of tau tangles, a neuropathological hallmark of Alzheimer’s disease, with the goal of developing sensitive image-based biomarkers for tau [38].