Research Pearls: The Significance of Statistics and Perils of Pooling. Part 2: Predictive Modeling

Abstract

The focus of predictive modeling or predictive analytics is to use statistical techniques to predict outcomes and/or the results of an intervention or observation for patients that are conditional on a specific set of measurements taken on the patients prior to the outcomes occurring. Statistical methods to estimate these models include using such techniques as Bayesian methods; data mining methods, such as machine learning; and classical statistical models of regression such as logistic (for binary outcomes), linear (for continuous outcomes), and survival (Cox proportional hazards) for time-to event outcomes. A Bayesian approach incorporates a prior estimate that the outcome of interest is true, which is made prior to data collection, and then this prior probability is updated to reflect the information provided by the data. In principle, data mining uses specific algorithms to identify patterns in data sets and allows a researcher to make predictions about outcomes. Regression models describe the relations between 2 or more variables where the primary difference among methods concerns the form of the outcome variable, whether it is measured as a binary variable (i.e., success/ failure), continuous measure (i.e., pain score at 6 months postop), or time to event (i.e., time to surgical revision). The outcome variable is the variable of interest, and the predictor variable(s) are used to predict outcomes. The predictor variable is also referred to as the independent variable and is assumed to be something the researcher can modify in order to see its impact on the outcome (i.e., using one of several possible surgical approaches). Survival analysis investigates the time until an event occurs. This can be an event such as failure of a medical device or death. It allows the inclusion of censored data, meaning that not all patients need to have the event (i.e., die) prior to the study’s completion.

Statistical methods are important tools to determine whether results from a research study are significant and can be applied to the general population. Statistical models can be used to describe data, explain the significance of data or predict outcomes, and establish, or at least suggest, causality. The statistical methods used are an important part of any research study and are essential for the correct design of a research project.¹ However, many authors have only a rudimentary understanding of statistical concepts, especially when more complex analysis is required.¹

With descriptive statistics, data are summarized in a more compact manner. The focus is to describe measured outcome variables and/or demographic characteristics of the study population quantitatively.^2,3 In general, measures of central tendency describe the data “average” (mean, median, mode) and measures of dispersion that spread around the “average” (range, interquartile range, variance, standard deviation). The primary difference between the types of measures of central tendency and their corresponding measures of dispersion has to do with whether the data are symmetrically distributed or not. The purpose of descriptive analysis or modeling is not to establish causal relationships between variables or predict outcome but rather to allow a researcher to have a general sense of what the data are showing, on a variable by variable basis.

An explanatory model describes the effect of an intervention on outcome.⁴ In this model one or more variables can be controlled by the researcher to a certain extent.⁴ For example, a study design investigating the effect of anterior cruciate ligament reconstruction (ACLR) on the incidence of meniscus injuries compared to a control group that received conservative treatment investigates the effect of surgery on a specific condition. This would be an example of a comparative study. Let us assume that meniscal injuries are significantly lower in the ACLR group. The intervention (ACLR) therefore explains the lower incidence of meniscal injuries in the intervention group. A causal relationship between surgery and meniscus injury could be suggested if this study were designed properly, meaning if the patients were randomized to receive either treatment being examined and if the patients included in the study represented a random sample of all possible patients who could receive a meniscus injuryd–in other words, if the intervention has had an effect on the measured outcome variable. Explanatory statistics can be used for both experimental studies or observational data.⁴ In general, it is more challenging to make causal inferences in observational studies since patients are not randomized to receive a treatment, and thus it is difficult to determine whether a difference between treatments is due to the treatment itself or the difference in patients who nonrandomly received one treatment or another.

In predictive modeling, observations are used to predict outcome and/or the results of an intervention or observation.⁵ This model investigates associations between one or more (dependent) variables of interest and the independent predictor variables.

In a basic scientific experiment, the independent variables can be controlled to investigate their effect on the dependent variable. For example, in a cadaver model, the effect of varying the femoral and tibial tunnel position with or without anterolateral ligament reconstruction (independent variables) on rotational knee stability (dependent variable) is investigated. By changing the 2 independent variables (predictors), the outcome will change. In clinical studies, these predictors may not be controlled. A study investigating the effect of ACLR on functional outcome (dependent variable) with a validated scoring system (Lysholm, International Knee Documentation Committee, or similar) that intends to assess the influence of gender, body mass index (BMI), age, mechanism of injury, time to surgery, chondral and meniscal injuries, previous ACLR, and other associated injuries (independent variables) on outcome would be an example of a clinical study. Here it is not possible to easily vary or change the independent variables. When applying a predictive model to this study, predictions about the “future” are possible. The results of the analysis can help the researcher understand which of the independent variables influences (or predicts) the outcome.

Predictive Modeling

Prediction research aims to predict outcomes based on a set of independent variables and can provide information about the risk of developing a certain disease or predict the course of a disease based on the analysis of these predictor variables.^6,7

Predictive modelling uses statistical techniques to predict outcomes, and several statistical models can be used.^5,7 Prediction research is any model that produces predictions⁵ and includes such approaches as Bayesian techniques, data mining techniques such as machine learning, and classical statistical models of regression, logistic, linear, and Cox proportional hazards models, depending on the number and character of outcome variable(s).⁸

Bayesian Statistics

To describe all the differences between a classical frequentist approach to statistical inference and a Bayesian approach to statistical inference goes beyond the scope of this paper. Therefore we now give a brief overview of the differences in the approaches, recognizing that we are oversimplifying many of the details.

The main difference between classical hypothesis testing and Bayesian statistics is that in classical (frequentist) methods, a null hypothesis is constructed about a specific parameter (i.e., the mean value of a distribution) and then data are collected to estimate this parameter (i.e., data are collected and an estimate of population mean is made by calculating a sample mean from the data). The frequentist approach will then examine the data collected and the hypothesis made and determine whether (1) the data appear to contradict the null hypothesis, leading to rejecting the null hypothesis, or (2) the data seem consistent with the null hypothesis, leading to not rejecting the null hypothesis. In this framework of statistical modeling, the assumption is that what is observed during a particular experiment is only one plausible set of outcomes from a possibly much larger set of all possible outcomes. The frequentist tries to determine the likelihood that this one set of outcomes observed is consistent with a hypothesis that was previously stated (the null hypothesis), recognizing that when making inferences one can always make an error, that is, rejecting a null hypothesis when it was true (type 1 error) or failing to reject a null hypothesis when it is false (type 2 error). Prior to the data being collected, a researcher using this approach should specify the criteria for rejecting or not rejecting the null hypothesis. In general, researchers often use a 0.05 (5%) threshold to determine whether to reject the null hypothesis or not–meaning that if the data suggest that there is less than a 5% chance that the null hypothesis is true given the data observed (i.e., P <.05), one should reject the null hypothesis. There are several drawbacks to using this method, in particular 2 of them are the following: (1) if the P value is .049 there is still a 4.9% chance that the null hypothesis is true and a type 1 error could be made and (2) statistical significance does not always directly link to clinical significance–meaning a P <.05 does not imply that the actual difference between groups is at all meaningful in real clinical practice.

In Bayesian statistics the researcher begins with a prior distribution that describes his current hypotheses concerning the question to be studied. If, for instance, previous studies had already taken place looking at this question, then the previous results of those studies could be used to generate a prior distribution or estimate for plausible outcome of the new study. This generation of a prior distribution to be used in the research occurs prior to collection of the data.⁹ These prior probabilities allow researchers to make estimates about the efficiency of a particular treatment and allow the researcher to incorporate all information of both the treatment arm and control group prior to data collection. If there is only anecdotal evidence about a particular treatment effect, these uncertainties can also be incorporated into the analysis.⁹ In principle, analysis entails 4 steps. In step 1, prior evidence is collected from the existing literature. In step 2, data are collected. In contrast to the classical hypothesis testing, an a priori sample size calculation is not necessarily needed, although there are methods for determining an appropriate sample size to be collected. In step 3, the collected data are used to revise the preestimates (“priors”) using Bayes’s theorem, and in a final step the posterior or poststudy estimates are used to interpret the collected data.⁹ In contrast to the classical hypothesis testing, there is no arbitrary cutoff of probabilities to call something statistically significant (i.e., no focus on whether P <.05). Bayesian analysis rather describes probabilities that a certain treatment has an effect on outcome. For example, “there is a 95% probability that arthroscopic assisted ACLR with hamstring grafts results in a stable knee.”

Here is another example to make it easier to understand the Bayesian approach. Let’s say that we have a simple blood test to determine whether a patient will develop rheumatoid arthritis (RA) in her lifetime. Let’s also say that the known prevalence is 1/1,000; this is the prior distribution or probability. The known false-positive rate of this test is 10%. When we apply this test in a study including 1,000 patents we will therefore find that 101 patients test positive. In classical statistics our results would therefore indicate that the chance of RA in our population group is 10.1% with a clinician raising fear in these 101 patients. With Bayesian statistics, the prior distribution would be included and now we would conclude that only 1/101 will be positive, allowing us to make better sense of the collected data.

Data Mining–Machine Learning

Simply speaking, machine learning uses algorithms to identify specific patterns in data sets to make predictions about outcomes. The variables (predictors) of interest and outcomes are identified; the software then applies these variables to make predictions about outcome. This approach often makes no assumptions about the underlying distributions of the data being examined, whereas both classical and Bayesian models do make assumptions about the data (i.e., they usually assume that continuous data follow a normal distribution). The major advantage of this technique is that no specific hypothesis, in contrast to conventional regression analysis, is needed to predict that predictor A is associated with outcome variable B.¹⁰ One of the major disadvantages of this technique is that generally large data sets are needed to allow useful conclusions. This is because machine-learning approaches often involve fitting relatively complex models from the data that would involve multiple interaction terms in a traditional modeling framework. In general, these techniques have arisen out of the field of computer science and not statistical science and therefore implement optimization algorithms found often in that field, without specific connections to modeling assumptions that are prevalent in statistical models. One criticism of this method is that often the optimal algorithm may appear to be “overfitting” the data, meaning that more parameters are included in these models than would be considered appropriate for the sample size used, and this limitation can only be addressed with large sample sizes. Furthermore, and similar to regression analysis, the principle of Occam’s razor is followed, with many algorithms assuming that predictor variables are independent of one another.¹⁰ However, with machine learning, nonlinear relationships and interdependent variables can be examined in a more unstructured approach, which may lead to innovative predictive models that may have been difficult to identify using more conventional approaches.¹¹ A simple example of machine learning are algorithms that allow a system to find patterns and correlations within a set of large data, that is, identifying groups of friends in social network data.

Classical Hypothesis Testing–Regression Models

A more conventional approach to predictive modeling includes classic regression models.⁸ It is important to understand that there are 2 fundamental differences in interpretation between the more conventional explanatory theory in regression and predictive modeling using regression. Fundamentally, a difference between these 2 approaches is the underlying goal of the research being performed. In explanatory models, the goal of the research is often to understand specifically the relationship of a particular independent variable to a particular dependent (outcome) variable. Thus, the goal is to understand, for example, what the effect of BMI is on functional outcomes following ACLR. The reason to do this type of research is to determine (or recommend) what kind of modification of BMI may lead to what level of improvement (or worsening) of functional outcomes following ACLR. The specific relationship of BMI and functional outcomes is of interest. In predictive modeling one is not specifically interested in the relationship of any individual predictor (independent) variable and the dependent (outcome) variable; rather one is interested in finding a group of predictor variables that best allow one to predict what the outcome will be in the future. Thus, explanatory models focus on a particular relationship between the predictor and outcome, where it is assumed that there is a cause-effect relationship where Y is caused by X. It is retrospective testing of an already existing hypothesis.⁴ Predictive models focus on understanding the predicted value of the outcome conditional on a set of predictor variables.

In both types of models, when the outcome of interest is measured on a continuous scale, the statistic R² can be used to measure the “goodness of fit” of a particular model. This statistic represents the proportion of the variability in the outcome measure that is explained by the predictor variable(s). In explanatory models, the focus often is on whether there exists a high R² when one looks at the relationship between the independent variable of interest (i.e., BMI) and the outcome of interest (functional outcomes following ACLR). If, for instance, we observed a direct and statistically significant relationship between these 2 variables, with an R² of 0.32 (meaning that 32% of the variability in functional outcomes following ACLR is explained by a patient’s BMI), we may not believe that there is a fully causal relationship between BMI and the outcome, since 68% of the variability would not be explained by BMI. However, if the calculated R² were 0.94, then the results would have a different meaning.

In predictive modeling, the relationship between X and Y is examined in a prospective fashion, establishing the relationship between 2 variables.⁴ Often the goal of predictive modeling is to determine the best set of variables to make an accurate prediction of an outcome of interest, where the goal is not to understand any particular variable’s role in the model, but rather the overall impact of the variables included. Therefore, the inclusion of many variables, even some not thought to be statistically significant, is often thought to be appropriate in predictive modeling since the goal is to get the best predictive value of the outcome. Thus a high R² is more critical in predictive modeling than examining the specific impact of any particular variable in the model. The challenge faced in these models is that it can be shown mathematically that R² must increase as more variables are included in the model; however, the inclusion of variables with little relationship with the outcome can also lead to overfitting problems, similar to those mentioned above in machine-learning algorithms. In theory, the lack of association cannot be compensated with a larger sample size as these predictions should be independent of the sample size. In contrast, the lack of a strong relationship in explanatory models may be due to a type 2 error and an increase in the sample may change the associations significantly.¹

For simplification we will only outline the more classical regression model with explanatory modeling. As practicing clinicians we are far more familiar with these techniques. In principle, regression analysis examines the relationship or correlation between variables.

Simple Linear Regression

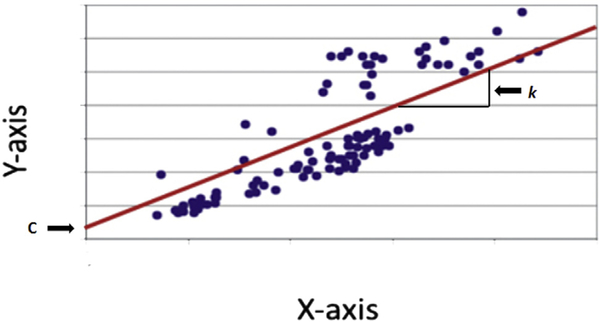
Simple linear or univariable regression is a mathematical technique that describes the relationship between 2 variables.^1,12 The relationship between the outcome variable y and the predictor variable x can be plotted on a scatter diagram (Fig 1).¹² When looking at the scatterplot, it is often possible to visualize a line that passes through the middle of all points.¹ The regression line can be calculated by using a simple mathematical formula:

$$y\text{=}kx\text{+}c,$$

where k is the coefficient that describes the slope or gradient of the linear relationship and c is a constant that describes where x crosses the y-axis.¹² For inference or significance testing, 4 assumptions about the relationship must be met¹²:

Fig 1.

Scatter plot. The scatter plot is also called the x-y graph. Each observation has 2 coordinates. The x-coordinate is the predictor variable and defines the distance from the y-axis. Vice versa, the y-coordinate is the outcome variable and defines the distance from the x-axis. The regression line can often be visualized and should pass through the middle; alternatively a statistical software program can be used to draw the regression line. The regression line quantifies an inexact relationship meaning that the 2 variable are related to each other. The correlation coefficient measures the strength of the relationship between the 2 variables and falls between (−)1 and (+)1. A correlation coefficient of 0 means that there is no relationship at all and the observations scatter all over the graph. If the correlation coefficient is 1, all observations are perfectly linear and located directly on the regression line. With correlation coefficients between 0 and 1, the regression line represents the best fit. The variable k is the gradient and simply describes the steepness of the regression line; c describes where the regression line crosses the y–axis, which is not always at 0.

1. A linear relationship between the 2 variables exists. If the points scatter randomly and do not center around a straight line, a relationship does not exist.

2. The variation around the regression line must be constant. In other words, the distance from the regression line for all points should be similar.

3. The data follow a normal distribution.

4. The deviation from the regression line for each datapoint is independent of other data points.

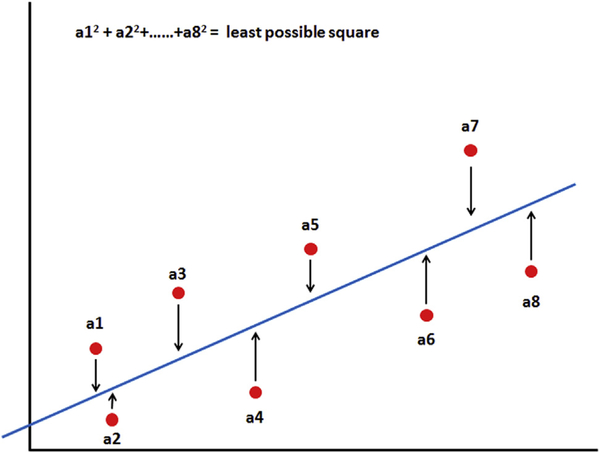
If these 4 assumptions are met, the model is valid. To establish the best fit of these regression lines, a visual approach may help to get an idea where the line should be drawn, but it is more accurate to use a more scientific mathematical approach for best fit. Several estimation methods have been described, but the most commonly used technique to find the best fit in linear regression is called the method of least squares.¹³ This technique is based on the following 2 formulas and calculates the least square estimates for the constant c and the coefficient k:

$$c^{\prime }=M_y-k{M}_x,$$

$$k^{\prime }=\frac{\sum \left(Y_i-M_y\right)\left(X_i-M_x\right)}{\sum {\left(X_i-M_x\right)}^2}.$$

The variables M_y and M_x are the mean values of both variables, and Y_i and X_i are pairs of observations. What does this all mean? The least squares model establishes the smallest vertical distance between data points (Fig 2) and the regression line, reducing error and creating the best fit for the regression line for all data points in the scatterplot.

Fig 2.

Best fit: method of least squares. The method of least square measures the distance of all data points from the regression line, and the smallest vertical distance from the regression line is established by calculating the sum of the squares of the vertical distances.

A classical measure for linear relationships between 2 variables is Pearson’s moment correlation. The correlation coefficient r ranges between −1 and +1. A positive relationship indicates an upward slope, whereas a negative relationship indicates a downward slope on the scatterplot. A value of 1 means that the relationship between the 2 variables is perfect (and linear) and the regression line moves through every data point. In contrast, if the relationship is 0, there is no linear relationship between the 2 variables. An example of a simple regression would be a study design that wants to establish whether posterior tibial slope is related to the amount of knee flexion. If the assumed relationship between the 2 variables is r = +0.95, the results would suggest that an increased posterior slope is associated with more knee flexion. In contrast, if the relationship is r = −0.95, an increased posterior slope is related to less knee flexion. With Pearson’s moment correlations, the variables must be normally distributed and the relationship must be linear. The square of the correlation coefficient is R², the measure of goodness of fit described above, which represents the proportion of the variability in the outcome variable in the simple linear regression model that is explained by the predictor variable. An intuitive understanding of R² is the following: if one has a single continuous outcome variable measured that has a normal distribution, the best guess for any future measure of that outcome is the average (mean) value of the data already observed. However, if a predictor variable can be used in a regression model to predict the outcome, R² represents how much better the prediction is than just guessing the mean value.

If the variables in a regression model are not normally distributed or the relationship is not linear, then linear regression or Pearson correlations may be inappropriate to use. A nonparametric approach to examining correlation is to use Spearman’s rank correlation, which essentially estimates the correlation between the ranks of the data (rather than actual observed values in the data set). However, since the actual values of the data are transformed into their ranks, the Spearman correlation coefficient provides an assessment of association rather than a linear association.¹

For simple linear regression it is advisable to produce graphs to inspect data visually to ensure that the assumptions are met and outliers are checked.¹² For significance testing, a parametric test such as a t-test can be used to determine whether the slope of the regression line is equal to 0 or not.

Multiple Linear Regression

In orthopaedic surgery as in most other fields of medicine, it is unlikely that one variable determines the outcome of a particular disease or intervention. When there is more than one predictor, different tests must be employed. Multiple linear regression or multivariable linear regression is a mathematical technique that allows us to investigate the relationship between multiple independent predictor variables and a single dependent outcome variable.¹² It is an extension of the simple linear regression, and the same 4 assumptions must be met. The predictor variables can range from 2 to a large number depending on how many patients are included in the research study. Similar to simple linear regression, the regression line can be calculated by using a simple mathematical formula:

$$y\text{=}{k}_{\text{1}}{x}_{\text{1}}\text{+}{k}_{\text{2}}{x}_{\text{2}}\text{+}{k}_n{x}_n\text{+}c.$$

To establish the best fit for a multiple linear regression, the method of least squares can also be used. If there are many predictor variables or covariates, it is absolutely critical to have a large sample size. As a general rule there should be at least 10 times as many observations or patients per predictor variable.¹ For example, if we would like to determine whether age, gender, BMI, sporting code, and weekly exercise hours (5 predictor variables) influence the functional outcome of ACLR, a minimum of 50 patients are needed to make useful predictions. However, it must be remembered that sample size has a distinct effect on what R² can be detected with statistical significance. Subsequently, an increase in observations (patients) may change the associations significantly, a fact that needs to be considered when designing these type of studies and also when interpreting the results. Another important consideration is collinearity between predictor variables. It is not uncommon that predictor variables are related (correlated) to each other. In the above example it may be that the higher BMI is highly correlated to the weekly exercise hours. This phenomenon is called collinearity and means that one predictor also predicts another predictor. Collinearity can have a significant effect on the outcome of the analysis and complicates the interpretation of the results. An obvious warning sign would be a substantial increase or decrease of R² when either removing or adding a predictor variable. In addition, when counterintuitive regression coefficients appear in the same model (i.e., a predictor variable that alone should have a positive correlation with the outcome, but in a multiple linear regression model it has a negative slope in the model), this is often a signal that collinearity may exist in the model. Possible solutions are to remove highly correlated predictors or possibly perform a stepwise regression procedure, which allows variables to enter one at a time into the model, and therefore highly correlated variables will likely not enter into the same model. Another approach is use the partial least squares regression method. In principle, partial least squares regression reduces predictors to the uncorrelated variables and then performs least squares regression on the remaining predictors.¹⁴

Logistic Regression

If the outcomes (dependent variables) are ordinal or categorical, simple linear and multiple regression should not be applied. For example, if the dependent variable is a “yes” or “no”, a logistic regression model is more suitable. Logistic regression describes the relationships between one or multiple numerical independent variables and one dependent categorical (yes/ no) variable. There are several assumptions in such models. These include the following:

1. The outcome is measured on a binary (2-level) or ordinal scale.

2. The units (patients) included in the model are independent of each other.

3. The independent variables and the outcomes are linearly related on the log odds scale.

This last assumption, of the linearity on the log odds scale, is more technical to explain than is needed in this paper; however, in most cases with continuous predictors that have a somewhat symmetric distribution (i.e., approximately normal), the linearity assumption will be met. This method uses logistic transformations to establish the probability of outcomes in a binary fashion. The outcome is then expressed as the odds ratio as a “yes” or “no” response. For example, if the risk of ACL injury in males soccer player is 1 (control) and the odds ratio for females performing the same sports is 5, the results would indicate that females have a 5 times higher risk of ACL injury when playing soccer. If one would assess specific risk factors in the female cohort like coronal and sagittal knee flexion angles during a landing task, phases of the menstrual cycle, quadriceps strength, or radiological alignment of the lower extremity, logistic regression can estimate the odds, confidence intervals, and significance (P value) of each variable.

As with any analysis, the findings and conclusions drawn from the analysis depend on whether an appropriate model has been used and whether the assumptions of the model have been satisfied. A critical step is to assess how well the model describes the observed data.¹⁵ One of the traditional approaches to assess good ness of fit in logistic regression is to use Pearson’s chi-squared test to examine the sum of the squared differences between the expected and observed number of cases divided by the standard error. One of the major problems with this test is its dependence on sample size. A smaller sample size may lead to the wrong conclusion of non-significance, and increasing the sample size of ten leads to significance.¹⁶ In addition, a C-statistic is often calculated from a logistic regression model, and this measures the predictive accuracy of the logistic regression model. A C-statistic of 1.0 would suggest that the model used perfectly predicts the outcome of interest, whereas a C-statistic of 0 would suggest that the model could not predict the outcome of interest.

Survival Analysis

Survival analysis investigates the time until an event occurs.¹⁷ This outcome can be described as failure or survival time (i.e., time to reoperation) or death. Failure or survival time is also called event time, and the data examined are always positively valued. A typical example in orthopaedic surgery is the survival of total joint arthroplasty in joint registries around the world.^18,19 For patients who survive their arthroplasty and require revision surgery for septic or aseptic loosening, the event time is known exactly and the observation is complete. If patients cannot be followed up until failure occurs (i.e., death, loss to follow-up, or withdrawal), survival or event time is not fully observed. These incomplete observations are defined as censored data.¹⁷ Censored data also occur if a study ends and some of the included patients did not have an event during the study period. This type of censoring is called right censoring and occurs when a participant does not have an event during the study period or drops out before the study ends.^20,21 Left censoring occurs when the event has already occurred before the study period.²² This is very rarely encountered in orthopaedic studies. For example, a cross-linked polyethyelene insert is tested in the laboratory with cyclic loading and checked every 2 hours for failure. The first checkpoint occurs at 2 hours, but the insert fails at 20 minutes, long before the first check occurs. If the insert fails between 2 checkpoints, that is, at 4.5 hours, this is defined as interval censored and means that there is uncertainty as to when the insert fails as the status is only checked every 2 hours. For this particular example, the insert then fails between 2 and 4 hours.

In contrast to standard regression models, survival analysis allows inclusion of both censored and uncensored data. In some ways, survival analysis is the combination of the linear and logistic regression in one technique. This is because it accounts for the outcome using a continuous and binary form–specifically, the “time” until the event occurs is a continuous measure and whether the event occurs (yes/no) is a binary measure. The challenging part of this model is that when an event is censored, the time variable is a lower estimate of the time to event and this must be accounted for in the model. The most commonly used approach for analyzing survival data in orthopaedic surgery is the Kaplan-Meier approach, which is a nonparametric statistical approach.²³ The Kaplan-Meier test uses lifetime data to estimate the probability of survival. Basic assumptions are used in this analysis: censored patients have the same prognosis as those who continue to be followed up or are uncensored, and survival probabilities are the same for all patients irrespective of whether they were included early or late.

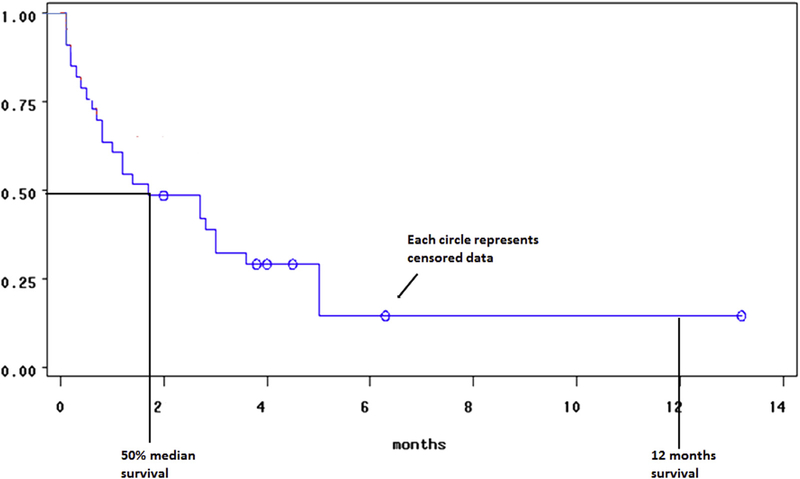
The Kaplan-Meier survival approach allows one to construct a curve that is a graphical tool demonstrating the results of the analysis (Fig 3).²³ The horizontal axis measures time, and the vertical axis measures the proportion of patients free of the event. Thus, using the graph, one can estimate the time it takes for a certain proportion of events to occur.²⁴ When interpreting the survival curves it is important to identify the units of measurement along the x-axis. Small steps with shorter intervals in general means larger patient cohorts, whereas large steps have limited patient numbers.²⁴ This can typically be seen at the right aspect of the graph if either a large group had their event or data were censored during earlier study intervals. Large steps should be interpreted with caution and are not very accurate. Poor study design or ineffective treatment may result in large numbers of censored events and may also result in large steps and again requires caution with analysis. It should be noted that in these analyses, the only data that contribute to the actual statistical modeling is when events occur; thus censored data do not directly contribute to the estimates of the statistics needed to estimate the survival curves.

Fig 3.

Kaplan-Meier survival curve represents survival times. The x-axis denotes time and the y-axis denotes the percentage of a particular subject or object of interest has survived. Drops only occur at event times, and the curve does not go to 0 if there is no event at the last checkpoint or when the study has finished. The circle or dot points along the curve represent censored data. The curve allows us to plot the 50% median survival time and check survival at specific time points. In medical research, especially in cancer research, 1 and 5 year survival rates are used to establish the effect of treatment on survival.

The Kaplan-Meier approach is a useful approach to examine survival curves and compare these curves among groups. If the main interest is to investigate the influence of risk factors on survival, a Cox proportional hazards regression (often referred to as Cox regression) allows analysis for the relationship between time-to-event outcomes and one or more predictors.^23,24 For example, Cox regression could investigate the influence of age, gender, and radiological malalignment of a total joint arthroplasty on survival of the implant. Cox regression uses a nonparametric approach to fit the model.²³ The basic assumption that must be met is that the hazard or risk must be proportional. For example, if women have twice the risk of ACL injury compared with men at age 20, they also must have twice the risk at age 30. In addition, the risk of an event occurring over time must be comparable between groups, so if women had twice the probability of an event occurring after 12 months of follow-up postsurgery when compared to men, then women should also have twice the probability of an event occurring after 24 months of follow-up postsurgery when compared to men. Generally speaking, Cox regression allows one to estimate the risk for a particular individual to have an event considering all potential variables that can result in the event. The hazard function is a way to express the probability of an event occurring for a predetermined time interval.²⁵ The hazard function can be expressed as

$$h(t)=\frac{\text{Number}\text{of}\text{individuals}\text{with}\text{an}\text{event}\text{occurring}\text{during}\text{the}\text{time}\text{interval}}{\text{Number}\text{of}\text{individuals}\text{without}\text{an}\text{event}\text{during}\text{the}\text{time}\text{interval}}.$$

The hazard ratio is an expression of the chance of an event occurringduringaspecifictimeinterval.^23,25 For example, if 1,000 patients are surveyed during the month of September and October for ACL injury and 50 patients sustain an injury in both September and October, the hazard ratio is 0.05 (50/1000) for September and 0.053 (50/950) for October. The hazard ratio can also be used to assess risk in more than one group. For example, survival rates for ACLR over a specific time interval or 2 different surgical techniques could be evaluated.

Discussion

We have presented a brief overview of several possible statistical techniques that can be used in predictive modeling research. Table 1 summarizes the most commonly used terms and definitions with regards to these statistical tests, and Table 2 summarizes the statistical tests typically used for classical predictive modeling. Each method has potential strengths and limitations, and researchers should be aware of these prior to initiating such a project. Among the methods described above, the ones that are most often used in current research are those that focus on either binary outcomes (i.e., 2-year revision rates) or time-to-event outcomes (i.e., median time to joint failure after surgery). When examining these types of outcomes, Bayesian methods can be used in conjunction with classical regression techniques (logistic regression or Cox regression). In addition, machine-learning approaches can also be used to examine these types of outcome models. Finally, the classical (frequentist) approaches of logistic and Cox regression models can be used without a Bayesian framework.

Table 1.

Terms and Definitions

Dependent variable	Also called the outcome variable. The variable responds to the independent variable(s) and changes if the independent variable(s) are manipulated.
Independent variable	Also called the experimental or predictor variable. It can be manipulated and represents input and directly affects the dependent variable.
Parametric data	Follow a normal Gauss distribution and display homogeneous variance.
Nonparametric data	The distribution follows any pattern and variance.
Variance	A measure of how the data are spread, defined as the average of the squared differences from the mean.
Standard deviation	A measure of how the data are spread, defined as the square root of the variance.
Z-score	A measure of how many standard deviations below or above a raw score is. The raw score is the original score from one test/individual.
Sample size calculation	If a sample size calculation is done before data collection, it is called a priori and is used to establish that the sample is sufficiently powered. Post hoc power or the observed power of the sample is performed once the data have been collected and is based on the effect size estimate.
Type 1 error	Occurs when the null hypothesis is rejected when the null hypothesis is true. It is also referred to as “false positive.” Alpha levels (P values) are the probabilities of a type 1 error occurring. For example a P = .05 means that there is a 5% chance that a true null hypothesis will be rejected.
Type 2 error	Occurs when the null hypothesis is false but accepted. This is also referred to as “false negative.” This error most often occurs when there is no difference in outcome because the sample is too small.
Type 3 error	Occurs when the right answer to the wrong question is provided. For example, it is correctly concluded that the 2 groups are different but sampling results in a variable to be lower in one group. With more samples the variable then increases and results in no differences between the 2 groups.
Occam’s razor	Derived from the philosophical principle by William of Occam stating that entities should not be multiplied without necessity. In data mining it means that when there are 2 models with the same error, the simpler should be preferred because it has possibly a lower generalization error.
Correlation coefficient r	Measures the strength and direction of a linear relationship between 2 variables. A value of +1 is perfect positive relationship and a value of −1 is a perfect negative relationship. Values can range between +1 and −1.
Coefficient of determination R-squared	R-squared is a measure of how close the data are to the regression line and explains the variability of data around the mean; 100% indicates that the model explains all the variability and 0% means that the model does not explain the variability. In other words, it is the percentage of variability that is explained by the model.

Table 2.

Which Statistical Tests to Use for Classical Predictive Modeling

	Parametric Data (Normal Gauss Distribution)	Nonparametric Data (Non-Gauss Distribution)	Two Possible Outcomes (Binominal)	Survival Analysis
Descriptive	Mean, standard deviation	Median, interquartile range, range	Proportions	Kaplan-Meier estimate and survival curve
Relationship between 2 variables	Pearson moment correlations	Spearman rank correlation	Contingency tables and coefficients
Predict outcome from one measured variable	Simple linear regression	Nonparametric regression	Logistic regression	Cox proportional hazards regression
Predict outcome from multiple measured variables	Multiple linear regression		Multiple logistic regression	Cox proportional hazards regression

Regardless of which method is used, one should focus on the primary goal in such analyses, which is to best predict the likelihood of the event of interest (i.e., the occurrence of a revision surgery within 2 years or joint failure after surgery). Therefore, it is imperative that all pertinent predictor variables are measured during the study. These include patient-level characteristics such as age, gender, race, BMI, and smoking status, as well as other risk factors and comorbid conditions that could influence the outcome such as diabetes, hypertension, number of previous surgeries, and so on.

Ultimately, one goal of developing predictive models is to be able provide to clinicians decision support systems that can eventually provide real-time pertinent information concerning their patients and recommendations on treatment decisions that should be made in order to optimize long-term results on procedures to be performed.

Conclusions

Predictive modeling is a technique that can use several different statistical techniques to predict future outcomes. There are 2 principal approaches. When the relationship is examined in a prospective fashion, the relationship between 2 or more variables is established to predict future outcomes. With classical hypothesis testing, regression models are applied to retrospectively test an already existing hypothesis. Simple and multiple or multivariable regression models are used for continuous data and logistic regression for categorical data.

For all regression analysis it is worthwhile creating scatterplots and visually inspect for goodness to fit and outliers. Goodness-of-fit tests should be used to create the best fit for the regression line representing all data points in the plot and reducing error.

Survival analysis uses censored and noncensored data and is a useful statistic to analyze survival. If the main interest is how risk factors influence survival, the Cox proportional hazards regression can be used to investigate the effect of predictor variables on survival.

As quality metrics are becoming part of the evaluation of performance for surgeons and will likely be linked to reimbursement rates, it will be more important to have accurate predictive models available to assist with evaluating performance and also guide decisions to be made in the clinical setting. To do this accurately, one needs to use valid statistical methods, and understanding these methods will provide a higher probability of success in these endeavors.