Geometric Control of Frequency Modulation of cAMP Oscillations due to Calcium in Dendritic Spines

Abstract

The spatiotemporal regulation of cyclic adenosine monophosphate (cAMP) and its dynamic interactions with other second messengers such as calcium are critical features of signaling specificity required for neuronal development and connectivity. cAMP is known to contribute to long-term potentiation and memory formation by controlling the formation and regulation of dendritic spines. Despite the recent advances in biosensing techniques for monitoring spatiotemporal cAMP dynamics, the underlying molecular mechanisms that attribute to the subcellular modulation of cAMP remain unknown. In this work, we model the spatiotemporal dynamics of calcium-induced cAMP signaling pathway in dendritic spines. Using a three-dimensional reaction-diffusion model, we investigate the effect of different spatial characteristics of cAMP dynamics that may be responsible for subcellular regulation of cAMP concentrations. Our model predicts that the volume/surface ratio of the spine, regulated through the spine head size, spine neck size, and the presence of physical barriers (spine apparatus), is an important regulator of cAMP dynamics. Furthermore, localization of the enzymes responsible for the synthesis and degradation of cAMP in different compartments also modulates the oscillatory patterns of cAMP through exponential relationships. Our findings shed light on the significance of complex geometric and localization relationships for cAMP dynamics in dendritic spines.

Significance

Dendritic spines are small signaling subcompartments along dendrites in neurons. They are the primary sites of postsynaptic activity. Here, we investigate how spine size and spatial organization of enzymes can change the dynamics of cyclic adenosine monophosphate, a second messenger interacting with calcium. The findings from our study have implications for structural plasticity, learning, and memory formation.

Introduction

Dendritic spines, small bulbous protrusions from the dendrites of neurons, are the main excitatory synaptic sites that compartmentalize postsynaptic responses. Spine dynamics are intimately associated with long-term potentiation (LTP), long-term depression, and synaptic plasticity (1,2). The influx of calcium due to neurotransmitter release and the associated gating of ion channels is universally accepted as the first step toward these processes (3,4). However, spines are more than hotbeds of electrical activity; recent studies have shown that dendritic spines are subcompartments of signaling and biochemical activity downstream of calcium influx (5,6), and there is a tight coupling between electrical and chemical activity in spines (7). In particular, the connection between calcium dynamics and cyclic adenosine monophosphate (cAMP)/protein kinase A (PKA) activation is one of the key elements for connecting the short-timescale events associated with calcium influx to the longer timescale of structural plasticity (8, 9, 10). In response to calcium influx, cAMP transients have been reported in neurons (11), and cAMP/PKA dynamics are tightly coupled to that of calcium (12, 13, 14). In a companion study, we developed a computational model for calcium-induced cAMP/PKA activity in neurons (15) and predicted that the cAMP/PKA pathway acts as a leaky integrator of calcium signals. We also experimentally showed that calcium spontaneously oscillates in dendritic spines of hippocampal subregional volumes, Cornu Ammonis 1 (CA1) neurons (15).

One of the interesting features of cAMP signaling is its spatial localization. It is well documented that the spatial localization of cAMP-regulating molecules and spatial aspects of signaling can govern its dynamics (16, 17, 18). Ca²⁺/calmodulin-stimulated adenylyl cyclase 1 (AC1), an enzyme that catalyzes the synthesis of cAMP from ATP, is highly expressed in the postsynaptic density (PSD) and extrasynaptic regions (19,20), and its activity is required for both pre- and postsynaptic LTP (21,22). Adenylyl cyclases (ACs) can also be colocalized with other components of the pathway and synthesize cAMP locally (12,23, 24, 25, 26). Phosphodiesterases (PDEs), which catalyze the hydrolysis of cAMP to AMP, are another group of enzymes that are believed to be responsible for cAMP subcellular compartmentalization. They act as sinks and diffusion barriers that enable the formation of cAMP microdomains (27, 28, 29). A-kinase anchoring proteins (AKAPs) are capable of directly and/or indirectly interacting with proteins that either regulate the cellular content of cAMP, such as ACs and PDEs, or are regulated by cAMP such as PKA (30). All of the different AC isoforms bind some selection of AKAPs, allowing colocalization of the source and the target of cAMP (31). PDE4 isoforms can also form a complex with PKA and AKAPs and generate negative feedback for cAMP (32, 33, 34). Experimental observations demonstrate the localization of these key proteins in dendritic spines of neurons. Paspalas et al. (35) have shown the localization of PDE4 in the spine neck and spine head, Di Biase et al. (36) have shown the localization of AKAP 79/150 in spine heads, and Sanderson et al. (37) have shown the colocalization of PKA and AKAP 79/150 in dendritic spines (Fig. 1 A). These data suggest that localization of different cAMP-regulating proteins is an important aspect of signaling in dendritic spines.

Figure 1.

cAMP pathway modeled in dendritic spines. (A) A schematic of the spatially organized reaction network for the cAMP-PKA pathway in dendritic spines inspired by experimental observations showing (AI) the liberation of PKA-C (PKA catalytic subunit) from the regulatory subunit upon activation and its association with the membrane via myristoylation in dendritic spines of rat hippocampal CA1 neurons (reproduced with permission from Fig. 2 A of (103)), (AII) colocalization of PKA-RII in spines with the AKAP 79 in rat hippocampal neurons (reproduced with permission from Fig. 6 of (37)), (AIII) PDE4 subtypes localization in the spine neck and spine head of monkey prefrontal cortex (reproduced with permission from Fig. 4 of (35)), (AIV) overlapping peaks of AKAP 79/150 and PSD-95 labeling intensity in the spine head of mouse hippocampal neuron (reproduced with permission from Fig. 1 of (36)). (B) In this study, we consider different geometric and spatial aspects that affect cAMP dynamics in dendritic spines. (C) 3D geometries of the spines used in this model to study cAMP dynamics; these geometries are designed to study the role of different spine head size, neck sizes, and the presence and absence of the spine apparatus. To see this figure in color, go online.

Another key factor that regulates LTP is the geometry of dendritic spines (38, 39, 40). Spine morphology can affect synaptic potential integration in dendrites (41), and their variety of shapes and sizes provide high functional diversity (42). The head shape, neck length, and neck diameter in spines can change during the synaptic plasticity (43); changes in spine morphology and spine density are associated with learning and memory (43). Because spatial organization and cAMP signaling are tightly coupled, many computational models have been developed to explain cAMP compartmentation mechanisms. The most studied effects on cAMP compartmentalization are localized cAMP synthesis (44,45), localized cAMP degradation (27,46, 47, 48), cell shape (49,50), restricted diffusion (46,48,51), and cAMP buffering (46,51). Iancu et al. (44) have developed a model that shows that in comparison to bulk cytosolic cAMP concentration, cAMP concentration in submembrane domains provides better regulation of PKA in cardiac ventricular myocytes. On the other hand, Chen et al. (47) have mathematically shown that phosphodiesterases need to be localized in the vicinity of the cAMP sources to ensure tight control of the spatial regulation of the cAMP. Furthermore, using analytical and numerical techniques, studies have shown that cAMP microdomains in hippocampal neurons can form for small width of the dendrite/soma radius ratio (50), and surface/volume ratio effect can change the dynamics of cAMP microdomains substantially (49). However, to date, how the spatial organization of the key signaling molecules in dendritic spines along with spine geometry, may affect the temporal behavior of calcium-induced cAMP oscillations, particularly the frequency response, has not been investigated.

These observations led us to the following questions: can geometric and spatial features of spines regulate the periodically forced cAMP/PKA oscillations due to oscillating calcium dynamics? If so, how? To answer these questions, we developed a three-dimensional (3D) reaction-diffusion model of calcium-induced cAMP/PKA dynamics in dendritic spines and focused on how two critical spatial aspects—spine geometry and enzyme localization—change cAMP/PKA dynamics. We studied the effect of features that regulate volume/surface ratio and spine head size and neck size along with the presence or absence of the spine apparatus as a physical barrier for molecular diffusion. Because we know that many of these enzymes are not uniformly distributed, we also investigated the role of localization of AC1 and PDE4 based on experimental observations of (Fig. 1 A; (19,35)). Our results show that spatial localization of enzymes on the spine membrane and in the cytoplasm can alter the temporal response of cAMP to induced calcium transients. Thus, in addition to kinetic properties as shown previously (15), we predict that the spatial organization of molecules in the dendritic spine can affect how cAMP/PKA dynamics respond to calcium input.

Model Development

Model assumptions

To simulate the spatiotemporal dynamics of cAMP dendritic spines, we developed a reaction-diffusion model that accounts for the different biochemical species (see Tables S1 and S2 for the list of reactions and the list of parameters) and their localization on the plasma membrane or in the cytosol and boundary fluxes (Fig. 1). We briefly discuss the assumptions made in developing this model and outline the key equations below.

Timescales

We focus on cAMP/PKA dynamics at timescales of tens of minutes. Calcium dynamics are modeled as sinusoidal oscillations with exponential decays based on the experimental observations on the second and minute timescales. The second-scale oscillations (0.5 Hz) were set up based on experimental observations in our companion study (15), and minute-scale oscillations (0.003 Hz) were inspired by Gorbunova and Spitzer’s (11) observations.

Spine head

Spine volumes range from 0.003 to 0.55 μm³, spine neck diameters are within a range of 0.04 to 0.5 μm, and the total length of spines are between 0.2 and 2 μm (52) in the hippocampal CA1 region. Based on the head and neck shape, spines are classified as stubby, thin (<0.6 μm in diameter), and mushroom spines (>0.6 μm in diameter) (52). Here, we study two spherical heads with two different spine head volumes (0.065 and 0.268 μm³), which are within the range of experimentally measured spine head volumes (Fig. 1 C).

Spine neck

The spine neck is modeled as a cylinder with a diameter of 0.1, 0.2, and 0.4 μm and a length of 1.32, 0.66, and 0.33 μm representing a thin, an average, and a thick neck, respectively. Thin spines are known as small head spines with a thin and long neck. Mushroom spines are spines with a large mushroom-shaped head with a thick and short neck. The geometric specifications of the studied spine geometries are shown in Table 1 and in Fig. 1 C.

Table 1.

Geometric Specifications of the Different Spines Considered in This Study

Spine Name	Head Diameter (μm)	Neck Diameter (μm)	Neck Length (μm)	Spine Surface (μm2)	Spine Volume (μm3)	Volume/Surface (μm)
1a: Spines with Different Head Sizes
Control	0.5	0.2	0.66	1.174	0.086	0.073
L.Avg.Avga	0.8	0.2	0.66	2.400	0.288	0.120
1b: Spines with Different Neck Sizes
S.Tn.Ln	0.5	0.1	1.32	1.194	0.076	0.064
S.Tn.Avg	0.5	0.1	0.66	0.986	0.070	0.071
Control	0.5	0.2	0.66	1.174	0.086	0.073
L.Avg.Avg	0.8	0.2	0.66	2.400	0.288	0.120
L.Tc.Avg	0.8	0.4	0.66	2.732	0.347	0.127
L.Tc.Sh	0.8	0.4	0.33	2.317	0.305	0.132
1c: Spines with or without Spine Apparatus
L.Avg.Avg	0.8	0.2	0.66	2.400	0.288	0.120
L.Avg.Avg.Sa	0.8	0.2	0.66	2.400	0.244	0.102
					VSA = 0.044
	SA Head Shape	SA Head Size (μm)	SA Neck Diameter (μm)	SA Neck Length (μm)	SA Volume (μm3)	SA Surface (μm2)
1d: Spine Apparatus Geometry
	spheroid	a = 0.225	0.05	0.823	0.044	0.719
		b = 0.225
		c = 0.200

^aThe first letter in the spine name represents the size of the spine head (S: small; L: large). The second part of the spine name represents its neck diameter (Tn: thin; Avg: average; Tc: thick). The third part of the spine name represents its neck length (L: long; Avg: average; Sh: short). The fourth part of the spine name represents the spine apparatus (Sa: with spine apparatus). Spine names without the fourth part do not have a spine apparatus.

Postsynaptic density

The PSD area in hippocampal CA1 region ranges from 0.008 to 0.54 μm² (52). We chose the size of the PSD based on the correlation between the head volume and PSD area reported by Allerano et al. (53) to localize cAMP synthesis on the spine head surface. Calcium enters the spine through N-methyl-D-aspartate glutamate receptors (NMDAR) influx. Postsynaptic calcium is released by presynaptic glutamate binding to NMDAR and removal of Mg²⁺ block as a result of postsynaptic depolarization (54). The input calcium function (see Fig. S1 and corresponding details in Supporting Materials and Methods) enters the spine head from the PSD area (Fig. 1 A). The resting cytosolic calcium is 0.1 μM, and it can rise up to 1 μM (55). Calcium oscillations for the model have been designed based on the concentration range and timescale of calcium oscillations in neurons (11,15).

Spine apparatus

To investigate the effect of physical barriers such as spine apparatus, we modeled large spines with spine apparatus. The size of the spine apparatus is a spheroid head with a = 0.225, b = 0.225, c = 0.200 μm and a cylindrical neck with D = 0.05 μm and L = 0.823 μm ($V_{SA}=$0.044 μm³) (Table 1). The size of the spine apparatus is taken from image constructions of the spines by Wu et al. (56) (Table 1). In this model, the membrane of the spine apparatus acts as a reflective barrier for cAMP/PKA without any sink or source terms.

Plasma membrane fluxes

In our model, AC1, AC1 ⋅ Ca₂ ⋅ CaM, and AC1 ⋅ Ca₄ ⋅ CaM are localized on the plasma membrane, whereas all other species are in the spine volume. We do not explicitly include the various calcium channels and pumps on the PSD but rather prescribe the calcium profile in the spine.

Ca²⁺ buffers

We include two types of calcium buffers in this model: mobile buffers and immobile buffers (57). In the spines of hippocampal neurons, calbindin is known as the major mobile buffer (58). The reported concentration of calbindin in the CA1 region of pyramidal neurons is 45 μM (59) with a diffusion constant of 9.3 μm²/s (60) and K_D of 0.7 μM (k_f = 28 μM/s, k_b = 19.6 1/s) (60). A single immobile buffer has also been considered in this model at a concentration of 78.7 μM (58), with a diffusion constant of zero and K_D of 2.1 μM ($k_f^{\prime }$ = 247 μM/s, $k_b^{\prime }$ = 524 1/s) (58). We used the reactions from (58,60) to simulate the action of calcium buffers, and they are reproduced in Table S1.

Deterministic approach

We assume that all molecules in the model have large molecular concentration and model the reaction-diffusion equations using deterministic approaches.

Based on these assumptions, we constructed a 3D spatial model of calcium-induced cAMP/PKA pathway in dendritic spines. Our control geometry is a small-sized spine with an average neck and a total volume of ∼0.086 μm³ without a spine apparatus. Although all the simulations are conducted in 3D (Fig. 1 C), results from the simulations are shown for a two-dimensional cross-section for simplicity and ease of interpretation.

Governing equations

The spatiotemporal dynamics of each species, c, in the volume is given by a reaction-diffusion equation as follows:

$$\frac{\partial c_i}{\partial t}=D_i{\mathit{\nabla }}^2{c}_i+R_i,$$ (1)

where $c_i$, $i\in$ $\left\{\mathrm{1,2},\dots ,21\right\}$, represents the concentration of the i^th species as a function of time and space, D_i is the diffusion coefficient, ${\mathit{\nabla }}^2$ represents the Laplacian operator in 3D, and R_i is the net reaction flux for the i^th species. The diffusion coefficients of different species and the initial concentration of the different species are shown in Table S3. For membrane-bound species, the volume concentrations are converted to surface concentrations by multiplying them by the volume/surface ratio.

Boundary condition at the Plasma Membrane (PM)

Flux boundary conditions that balance diffusive flux with reaction rate are used to represent reactions that take place at the plasma membrane between molecules on the membrane and in the volume. There are four species for which these boundary conditions apply. Specifically, in this case, Ca²⁺ and Ca₂ ⋅ CaM binding with AC1 and the enzymatic conversion of ATP to cAMP due to the action of PM-bound AC1 becomes a time-dependent flux boundary condition for both cAMP and ATP, which can be written as follows:

$$\begin{array}{c}{-D_{C{a}_2\cdot CaM}\left(\mathbf{n}\cdot \mathit{\nabla }C{a}_2\cdot CaM\right)|}_{PM}=-R_3,\\ {-D_{C{a}^{2+}}\left(\mathbf{n}\cdot \mathit{\nabla }C{a}^{2+}\right)|}_{PM}=-2R_4,\\ {-D_{cAMP}\left(\mathbf{n}\cdot \mathit{\nabla }cAMP\right)|}_{PM}=R_9,\\ {-D_{ATP}\left(\mathbf{n}\cdot \mathit{\nabla }ATP\right)|}_{PM}=-R_9.\end{array}$$ (2)

Here, n represents the normal to the surface. These time-dependent fluxes in the boundary conditions closely couple the temporal responses encoded in the reaction terms, and the curvature response encoded in the normal vector in the diffusive flux term (61).

Boundary condition at the spine apparatus membrane

We assume that the spine apparatus is purely a diffusive barrier and does not play an active role in modulating any of the biochemical dynamics. Therefore, for all the species, the boundary condition at the spine apparatus, SA, is a Neumann boundary condition, given as follows:

$${-D\left(\mathbf{n}\cdot \mathit{\nabla }{c}_i\right)|}_{SA}=0.$$ (3)

Geometries used in the model

We modeled the dendritic spines using simplified geometries of spheres. Dendritic spines consist of a spine head attached to a neck, with a similarly structured spine apparatus within the spine (Fig. 1 C). The different geometries used in the model are shown in Table 1, Table 2.

Table 2.

Parameters for Fractional Area Localization of AC1

	Head Size (μm)	Neck Diameter (μm)	Neck Length (μm)	Spine Surface (μm2)	Localization Surface (μm2)	Fractional Surface
2a: Spine with Localized AC1
L.Avg.Avg	0.8	0.2	0.66	2.400	0.268	0.112
	Head Diameter (μm)	Neck Diameter (μm)	Neck Length (μm)	Spine Volume (μm3)	Localization Volume (μm3)	Fractional Volume
2b: Spine with Localized PDE4
L.Avg.Avg	0.8	0.2	0.66	0.288	0.011	0.038
	Head Diameter (μm)	Neck Diameter (μm)	Neck Length (μm)	Spine Surface (μm2)	Localization Surface (μm2)	Fractional Surface
2c: Spines with Different AC1 Localization Surface
L.Avg.Avg	0.8	0.2	0.66	2.400	0.134	0.056
L.Avg.Avg	0.8	0.2	0.66	2.400	0.268	0.112
L.Avg.Avg	0.8	0.2	0.66	2.400	0.540	0.225
L.Avg.Avg	0.8	0.2	0.66	2.400	1.005	0.419

Avg, average; L, long.

Numerical methods

Simulations were conducted using the commercially available finite-element software COMSOL Multiphysics 5.3 (62). To solve our system of partial differential equations, we used time-dependent general partial differential equations and general boundary partial differential equations modules (62). Starting with a coarse and unstructured mesh, we decreased the mesh size until we obtained the same results when using the maximum mesh size. COMSOL was allowed to optimize the element sizes through the “physics-controlled mesh” option. The linear system was solved directly by using the MUMPS solver. Newton’s method (nonlinear method) was used to linearize the system. Time integration was performed using a backward differentiation formula with both adaptive order and adaptive step sizes. The mesh statistics are shown in Table 3. The link to the model is available on https://github.com/donya26/cAMP-PKA-spatial.

Table 3.

Mesh Statistics for the Control Spine (Spherical Spine with Small Head and Average Neck)

Element Type	Number of Elements	Min Element Quality	Avg Element Quality	Element Volume Ratio	Mesh Volume (m3)
Tetrahedron	6006	0.2229	0.6423	4.921E−4	8.32E−20
Element type	Number of Elements	Min Element Quality	Avg Element Quality	Element Area Ratio	Mesh Face Area (m2)
Triangle	1638	0.3982	0.8263	0.004638	1.177E−12
Element type	Number of Elements	Element Length Ratio	Mesh Edge Length (m)
Edge element	278	0.1238	9.944E−6
Element type	Number of Elements
Vertex element	31

Avg, average; Min, minimal.

Metrics for cAMP/PKA dynamics

To compare cAMP concentration across different spine geometries shown in Table 1, we normalized the cAMP concentrations in each case with respect to the cAMP concentration in the control spine to compare across different geometries. We multiplied cAMP concentration by $\left(S/S_{Ctrl}\right)/\left(V/V_{Ctrl}\right)$, in which $S_{Ctrl}$ and $V_{Ctrl}$ are total surface area and total volume of the control geometry, and S and V are the total surface area and the total volume of the geometry under consideration. In addition to studying the spatiotemporal dynamics of cAMP in spines of different geometries, we also compare the peak time for each period, the peak concentration, and the area under the curve (AUC) for each period. These metrics allow us to compare the oscillatory behaviors of cAMP in dendritic spines (63,64).

Results

Spatiotemporal dynamics of cAMP/PKA in dendritic spines

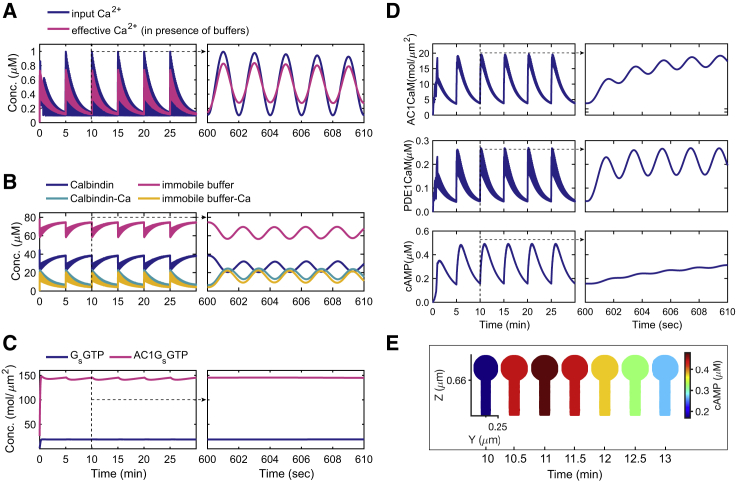
We studied the spatiotemporal dynamics of cAMP and PKA in response to Ca²⁺ influx in a dendritic spine. The Ca²⁺ input, effective Ca²⁺ after the action of buffers, and the resulting cAMP dynamics in the control spine are shown in Fig. 2. The calcium stimulation patterns are based on a sinusoidal function with 0.5-Hz pulses and 5-min separation between bursts and an exponential decay along each burst (15). In-phase oscillations of calcium and cAMP have been reported in neurons (11) and other cell types (32), and the oscillation timescales are based on the suggested oscillation period for cAMP and Ca²⁺ in the literature (11,65). Ca²⁺ buffers limit Ca²⁺ availability; however, they do not change the oscillation patterns of Ca²⁺ (Fig. 2 A) or cAMP (Fig. S2). Both mobile and immobile buffers oscillate in sync with ${\text{Ca}}^{2+}$ (Fig. 2 B). Activation of G-protein subtype (G_s) does not show oscillations because it is not activated by Ca²⁺ (Fig. 2 C). AC1 is stimulated by G_s-coupled receptors when it is activated by intracellular Ca²⁺ (66). Therefore, AC1 that has been activated by Ca²⁺/calmodulin complex (AC1 ⋅ CaM) binds to G_sGTP and forms AC1 ⋅ G_sGTP that oscillates with Ca²⁺ (Fig. 2 C). Both AC1 and PDE1 enzymes that are activated by Ca²⁺/calmodulin complex oscillate with Ca²⁺ (Fig. 2 D). Finally, cAMP also oscillates with Ca²⁺; however, unlike AC1 ⋅ CaM and PDE1 ⋅ CaM, cAMP barely shows oscillations on the shorter timescale (seconds) and only oscillates with Ca²⁺ spikes every 5 min (Fig. 2 D). It should be pointed out that there is no discernible gradient of cAMP in these spines (Fig. 2 E).

Figure 2.

Oscillatory dynamics of Ca²⁺, Ca²⁺ buffers, AC1 ⋅ G-protein subtype (G_s), AC1 ⋅ CaM, PDE1 ⋅ CaM, and cAMP in the spatial model. (A) Input Ca²⁺ and effective Ca²⁺ dynamics in the 3D control spine. The stimulus is a Ca²⁺ input with a frequency of 0.5-Hz and 5-min bursts, oscillating between 0.1 μM (Ca²⁺ at rest) and 1 μM (stimulated Ca²⁺). The effective Ca²⁺ is Ca²⁺ dynamics after binding to mobile and immobile buffers. The figure insets show that the concentration profiles on the second-scale (in the range of 600–610 s). (B) Mobile (calbindin) and immobile buffers of Ca²⁺ simulated in the cytoplasm of the control spine. (C) Activation of G_s by binding of isoproterenol to β-adrenergic receptor and eventually activation of AC1 by G_s. (D) AC1 ⋅ CaM, PDE1 ⋅ CaM, and cAMP dynamics in a 3D control spine. (E) cAMP spatial maps during one burst of Ca²⁺ (one oscillation) show a variation in concentration corresponding to the amplitude in (D) but no spatial gradients. To see this figure in color, go online.

cAMP dynamics are affected by modulating spine volume/surface ratio

The volume/surface area ratio is an important characteristic of spine geometry and organization because it accounts for the effect of both volume and membrane reaction fluxes. Volume/surface ratio can be modified in multiple ways by changing the spine head size, spine neck size, and by the presence or absence of a spine apparatus. We investigated the effect of volume/surface ratio on cAMP dynamics in our model by systematically varying these geometric features (Table 1).

Effect of spine head size

To study the effect of the spine head size, we considered two spherical heads with different sizes (D₁ = 0.5 μm and D₂ = 0.8 μm), while maintaining the same neck diameter and neck length (Table 1) resulting in different volume/surface ratios. We observed that for the same calcium input, the head size plays a significant role in defining the oscillatory pattern of cAMP dynamics (Fig. 3 A). These temporal patterns map to the spatial patterns shown in Fig. 3 B. As the volume/surface area ratio of the spine decreases, cAMP concentration increases, as expected. A spine with a smaller head, which has lower volume/surface ratio shows not just a higher but also a broader range of concentrations from the peak to the base (from t = 11 to 15 min). The cAMP concentration in all different cases in this study is normalized with respect to the control spine. No discernible difference was observed between cAMP concentrations at different points inside a given geometry. Furthermore, we noticed that the change in spine head size not just changed the concentration of cAMP but also altered the oscillatory dynamics as characterized by the peak time, AUC, and the peak amplitude (Fig. 3 C). Increasing the volume/surface ratio of the spine by modulating the spine head size results in lower peak amplitude of cAMP concentration, lower area under the curve, and a delay in the peak time. This is because the change in the volume/surface area ratio affects the time-dependent flux boundary conditions shown in Eq. 2.

Figure 3.

The effect of the spine head size on the cAMP dynamics. (A) The effect of spine head size on the cAMP concentration profile. (B) Spatial maps of cAMP concentration profile in spines with different head sizes shown in (A) during one oscillation of cAMP show that decreasing the volume/surface area can increase the cAMP concentration substantially. (C) The effect of spine head size on the peak time (second peak shown in A), peak amplitude, and area under the curve (AUC) (during one oscillation period). The spine with a larger head shows a lower peak amplitude, a lower AUC, and a (16-s) delay in the peak time compared to that of the smaller spine, reflecting the coupling between boundary conditions due to membrane-bound species. To see this figure in color, go online.

Effect of spine neck size

Small, thin spines (D < 0.6 μm) are usually associated with a thin and long neck, and mushroom spines (D > 0.6 μm) usually have a thicker and shorter neck in comparison to thin spines (67). We investigated how changes to spine neck size, which affect the volume/surface ratio of spines affect cAMP dynamics (Fig. 4). We constructed geometries that reflect different combinations of spine head and neck sizes (Table 1). These neck sizes are in the range of experimentally measured spines for each of these two thin and mushroom categories (53,67). Decreasing the neck diameter from 0.2 to 0.1 μm and increasing the neck length from 0.66 to 1.32 μm increases the cAMP concentration (Fig. 4 A). In other words, by decreasing the volume/surface area ratio of the spines, the cAMP concentration increases (Fig. 4 B), and the spine with small neck diameter and long neck length shows the highest peak amplitude, the highest area under the curve, and earliest peak time (Fig. 4 E). For mushroom-like spines, by increasing the neck length from 0.33 to 0.66 μm and decreasing the neck diameter from 0.4 to 0.2 μm, the cAMP concentration in spines with large heads increases (Fig. 4 C). Similar to small head spines, in spines with large heads, by decreasing the volume/surface ratio, cAMP concentration increases (Fig. 4 D), and the thinnest and the longest neck shows the highest peak amplitude and area under the curve with earliest peak time (Fig. 4 E).

Figure 4.

The effect of neck size on cAMP dynamics in spines with different spherical head sizes. (A) A comparison of cAMP concentration in three spines with the same head size (D = 0.5 μm) but different neck diameters (0.1 and 0.2 μm) and different neck lengths (0.66 and 1.32 μm). (B) Spatial maps of cAMP concentration in spines with a small head (D = 0.5 μm) and different neck sizes during a 5-min oscillation period. (C) cAMP concentration in three spines with larger heads in comparison to those shown in (A) (D = 0.8 μm) with different neck lengths (0.66 and 0.33 μm) and different neck diameters (0.2 and 0.4 μm). (D) Spatial maps of cAMP in spines with large heads (D = 0.8 μm) during one oscillation period. (E) The spine with the highest volume/surface area ratio has the lowest peak amplitude, the lowest AUC, and the highest delay in the peak time. To see this figure in color, go online.

Effect of spine apparatus

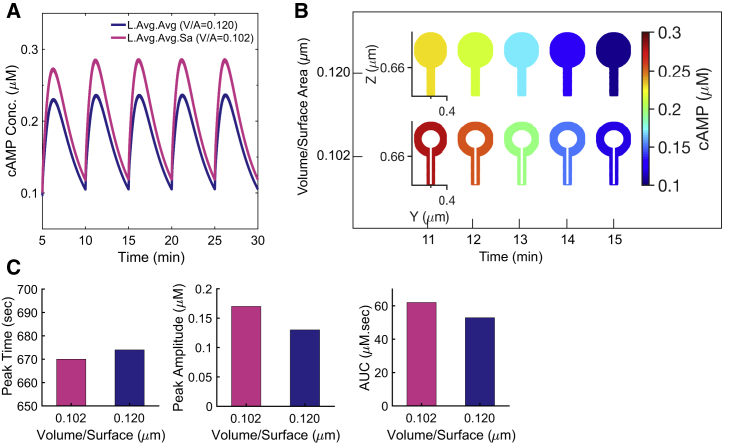
An additional geometric feature of dendritic spines is their internal organization; roughly more than 80% of the large mushroom spines in hippocampal CA1 dendrites of adult rats have a specialized endoplasmic reticulum called the spine apparatus (68). To understand the role of internal organelles such as spine apparatus that can act as a physical barrier, especially in spines with larger heads (D > 0.6 μm), we modeled the cAMP pathway in a spine with a large head (D = 0.8 μm) and a spine apparatus. The spine apparatus was modeled as a spheroid with a = 0.225, b = 0.225, c = 0.200 μm and a cylindrical neck with D = 0.05 μm and L = 0.823 μm (Table 1). Presence of the spine apparatus decreases the volume/surface ratio and thereby increases cAMP concentrations (Fig. 5, A and B). As a result, we predict that the presence of the spine apparatus as a physical barrier to diffusion decreases the volume/surface area and increases the peak amplitude and the area under the curve and expedites the peak time (Fig. 5 C).

Figure 5.

The effect of spine apparatus (SA) as a diffusion physical barrier on cAMP concentration in spines with large heads. (A) The effect of SA on cAMP concentration in large heads (D = 0.8 μm). (B) cAMP concentration maps of the spine with a large head with and without SA during one oscillation period. (C) The effect of SA on peak time, peak amplitude, and AUC. The spine with SA shows a higher peak amplitude and a higher AUC, and its peak time precedes the spine without the SA. To see this figure in color, go online.

cAMP dynamics are modulated by localized synthesis and degradation through enzyme localization

One of the key features of cAMP dynamics is the localization of the cyclase and PDEs (17,28,69). The coupling between enzyme localization and cAMP microdomains has been hinted at in the literature but has not been explicitly considered in our model so far. To investigate how localization of these molecules affects cAMP dynamics, we considered the following scenarios: localization of membrane-bound molecules (AC1 ⋅ Ca₂ ⋅ CaM and AC1 ⋅ CaM) to the head surface, localization of PDE4 in the spine head, and localization of both AC1 and PDE4 (Fig. 6 A; Table 2). We set the size of the AC1 localization area to be 0.268 μm² based on the head volume/PSD area correlation reported by (53). Interestingly, we observed that by localizing AC1 on the head surface in a large head, the oscillation amplitude of cAMP increases by almost 10-fold (Fig. 6 B). Localization of PDE inside of the head volume, on the other hand, only has a negligible effect on cAMP concentration. However, localization of both AC1 and PDE further increases the cAMP concentration relative to the nonlocalized case (Fig. 6 B). Fig. 6 C shows the cAMP concentration profile characteristics for nonlocalized, localized AC1, localized PDE4, and localized AC1 and PDE4. AC1 localization seems to increase the peak amplitude and the area under the curve substantially and cause a significant delay relative to the nonlocalized case (almost 40 s). The spatial maps of AC1 localization show a delay in the peak time occurrence (Fig. 6 D). However, PDE4 localization with much lower cAMP concentration does not show this delay (Fig. 6 E).

Figure 6.

The effect of enzyme localization on cAMP dynamics in dendritic spines with a large head (D = 0.8 μm) and average neck size (D = 0.2 μm, L = 0.66 μm). (A) A schematic of AC1 localization on the spine head surface and PDE4 localization in the spine head volume in the large head. (B) The effect of AC1 and PDE4 localization in the large head on cAMP dynamics. (C) The effect of enzyme localization on the peak time, peak amplitude, and AUC for one oscillation period. AC1 localization increases the peak amplitude and AUC substantially and causes a delay in the peak time, whereas PDE4 localization shifts the peak time backward and expedites the peak time. (D) A comparison of spatial maps of AC1 localization and both AC1 and PDE4 localization in the large head. (E) The effect of PDE4 localization on spatial maps of cAMP in the large head. To see this figure in color, go online.

Because localization of AC1 seems to affect the temporal response of cAMP through membrane fluxes (boundary conditions), we next asked if the fractional area of localization could tune the temporal dynamics in a deterministic matter. To investigate how the area of AC1 localization on the spine head can shift the cAMP concentration peak time, peak amplitude, and area under the curve, we studied the AC1 localization effect in four different localization surface areas (Table 2). We found that decreasing the localization area size shifts the peak time further forward relative to the nonlocalized case and increases the peak amplitude and the area under the curve (Fig. 7 A). We observed that the shift in peak time, peak amplitude increase, and area under the curve increase showed an exponential relationship with the fractional area of localization (Fig. 7 B). These exponential relationships hint at well-defined size-shape relationships between spine size and function.

Figure 7.

The effect of AC1 localization area on cAMP oscillation pattern. (A) The effect of AC1 localization area on the cAMP peak time for four different AC1 localization areas: 0.134, 0.268, 0.540, and 1.005 μm². The fractional area of localization is calculated by dividing the localization area by the total surface area (2.4 μm²) of a spine with a large head (D = 0.8 μm) and an average neck (D = 0.2 μm, L = 0.66 μm). Decreasing the localization area to 0.134 μm² (fractional area = 0.056) causes a delay of almost 40 s in the peak time. (B) The effect of AC1 localization area on the peak amplitude. Decreasing the localization area to 0.134 μm² (fractional area = 0.056) shows an almost 10-fold increase in the peak amplitude. (C) The effect of AC1 localization area on the AUC during one oscillation period. The AUC increases substantially (almost 17-fold) by decreasing the AC1 localization fraction to 0.056. (D) Decreasing the AC1 localization area with respect to the total spine surface area shifts the cAMP oscillation peak time forward, and in comparison to the uniform AC1 case, the shift in peak time increases exponentially. (E) The cAMP oscillation peak amplitude changes exponentially by changing the AC1 localization area. (C) The AUC is another cAMP oscillation property that changes exponentially by changing the AC1 localization area. To see this figure in color, go online.

Discussion

In neurons, cAMP oscillations are thought to have an important role in regulating the pulsatile release of hormones, such as gonadotropin-releasing hormone (70,71), and axon guidance (72,73). It is also well known that calcium spikes are necessary for changes in cAMP concentrations, but only certain bursts of calcium spikes increase cAMP levels in neurons (11). The dynamics of calcium-induced cAMP has been modeled by us and others (15,27,48,74) with a focus on identifying the mechanisms underlying interdependent oscillations. We showed that cAMP is primarily sensitive to the longer timescale effects of calcium rather than the shorter timescales (15). Here, we investigated how spatial features of dendritic spines such as spine size and ultrastructure and localization of enzymes can impact the dynamics of cAMP. We expected that spatial aspects of cAMP dynamics would simply reflect the temporal behavior of cAMP as observed in a well-mixed model (15). However, we found that geometric factors can have unexpected effects on the temporal dynamics of cAMP. Our findings and model predictions can be summarized as follows: first, spine volume/surface ratio, which can be modulated through spine head size, spine neck geometry, and by the presence or absence of the spine apparatus, affects the temporal dynamics of cAMP. Furthermore, we found that increasing volume/surface ratio increases the peak time, decreases the peak amplitude, and decreases the AUC of cAMP exponentially (Figs. 3, 4, and 5). Second, spatial localization of cAMP-producing enzymes (AC1) and cAMP-degrading enzymes (PDE1) also impacts the temporal response of cAMP in response to calcium oscillations (Fig. 6). The temporal dynamics of cAMP oscillations depend then not only on the calcium influx but also on the fractional area of localization of these enzymes (Fig. 7).

The first prediction is particularly relevant in the context of spine size and shape variation during development and disease (75, 76, 77). In the adult human hippocampus, almost 65% of spines are thin spines (small bulbous-shaped head with a diameter smaller than 0.6 μm), 25% are mushroom spines (mushroom-shaped head with a diameter larger than 0.6 μm), and the rest are stubby, multisynaptic, filopodial, or branched (67,78). Furthermore, spine geometry is thought to restrict the diffusion of both cytosolic and membrane-bound molecules (79). In general, a low volume/surface ratio in different parts of a cell has been suggested to be responsible for generating cAMP gradients in finer structures (49,50,80,81). We have found that different ways of modulating the volume/surface area ratio alter cAMP response predictably and point to the role of both spine membrane surface area and spine volume. These geometric characteristics are important in considering how the complex geometry of a spine can affect the dynamics of these different molecules.

The second prediction on how protein localization can impact the temporal dynamics of cAMP is based on some classical partial differential equation analysis. Indeed, the representation of all the surface reactions on the boundaries of the geometry results in a system of partial differential equations spanning two compartments (the membrane and the cytosol) coupled with time-dependent Robin boundary conditions (82). Recently, in a theoretical study, we conducted extensive analyses for such equations and showed that indeed boundary conditions by themselves can alter the spatiotemporal profiles of second messengers (61). Here, we apply a similar mathematical construction, informed by experimental observations of protein localization, and show that localization of different molecules can alter the temporal response of cAMP oscillations. We found that localization of AC1 and PDE1 can substantially change the cAMP concentration level, oscillation amplitude, and peak time (Fig. 6), and these features depend on the fractional area of localization (Fig. 7). Other important factors responsible for compartmentalization of cAMP include colocalization of key components of the pathway by scaffold proteins, such as AKAP 79 (83,84). AKAPs are known to tether PKAs to specific sites to phosphorylate Glutamate Receptor 1 (GluR1) receptors or facilitate AC action specificity (45,85, 86, 87).

Our model predictions on geometric regulation of cAMP dynamics in dendritic spines have implications for spatial control of information processing in spines and size-function relationships in structural plasticity (88, 89, 90). We predict that frequency control of cAMP dynamics in response to calcium influx occurs not only through kinetic mechanisms (15) but also through spatial regulation of volume/surface area globally and locally. These results also point toward the need to study the role of local volume/surface ratios in realistic geometries such as those developed by Wu et al. (56). There may also be extensive spatial feedback mechanisms that can further affect the dynamics of calcium and cAMP in the long timescale. For example, it is well known that insertion of channels on the spine head, such as NMDAR and the α-amino-3-hydroxy-5-methyl-4-isoxazoleproprioninc acid receptor (AMPAR) (91, 92, 93), and their activity (94,95) are functions of downstream effects of calcium and its effectors (91,93,96). Although this area of research is still under active investigation, it is likely that these studies will shed light into localized feedback loops between protein or channel localization (97) and second messenger concentration in spines. Such feedback loops likely enhance compartmentalization and spatial effects and provide further means to tune the frequency effects we predict here.

Despite our model predictions, there are a few limitations of our work that must be acknowledged. Our model assumes a uniform diffusion coefficient of cAMP, which may not be the case in the crowded environment of the spine head (38,98,99) (see Fig. S3 for the effect of diffusion coefficient of cAMP and Ca²⁺). We further assume that ATP is available in large quantities and is not rate limiting (see Fig. S4 for ATP dynamics). However, we know that mitochondria are positioned at the base of the dendrite, and their size can scale with synaptic plasticity (100, 101, 102). Therefore, the role of ATP availability in the spine head and diffusion of ATP through the neck and the crowded head remains to be explored. Furthermore, in this model, we have assumed that the spine apparatus is simply acting as a diffusion barrier for cAMP and have ignored stochastic effects. However, in longer timescales, both mitochondria and spine apparatus couple cAMP, calcium, and ATP dynamics, and these effects will need to be included. These and other effects are the focus of current and future studies in our group.

Author Contributions

D.O. and P.R. conceived the study, analyzed the data, and wrote the manuscript. D.O. performed the simulations.

Editor: Eric Sobie.