Measurement of Residual Dipolar Couplings in Methyl Groups via Carbon Detection

Abstract

Residual dipolar couplings (RDCs) provide both structural and dynamical information useful in the characterization of biological macromolecules. While most data come from the interaction of simple pairs of directly bonded spin-1/2 nuclei (¹H-¹⁵N, ¹H-¹³C, ¹H-¹H), it is possible to acquire data from interactions among the multiple spins of ¹³C-labeled methyl groups (¹H₃-¹³C). This is especially important because of the advantages that observation of ¹³C-labled methyl groups offers in working with very large molecules. Here we consider some of the options for measurement of methyl RDCs in large and often fully protonated proteins and arrive at a pulse sequence that exploits both J-modulation and direct detection of ¹³C. Its utility is illustrated by application to a fully protonated two domain fragment from the mammalian glycoprotein, Robo1, ¹³C-methyl-labeled in all valines.

Introduction

Isotope labeling of methyl groups simultaneously in all or a subset of isoleucine, leucine, and valine residues ^1–3, or selectively in alanine^4,5 or methionine⁶ residues, has emerged as a powerful method for studying large protein systems.^7,8 The improved sensitivity and resolution has been an important driver for this type of isotope labeling. Methyl proton observation is inherently more sensitive because of three equivalent protons contributing to a single signal; in addition, spin relaxation interference (methyl-TROSY effects) narrows lines, especially carbon lines in heteronuclear multiple quantum coherence (HMQC) spectra. This further improves sensitivity. However, when labeling only methyl groups, the reduced number of observable sites in a typical protein has made the collection of a more diverse set of structural data types important. Among the data that can be collected are residual dipolar couplings (RDCs). RDCs provide information on bond vector orientation relative to the alignment frame of partially oriented molecules.⁹ These can in turn be used to refine the global structure of a protein, facilitate resonance assignment, and probe domain orientation and dynamics. Interactions leading to methyl RDCs are potentially a little more complicated than those leading to the more commonly observed ¹H-¹⁵N RDCs. Rapid methyl rotation leads to projection onto the axis of methyl rotation rather than a C-H bond and the C-H bond is slightly longer than the N-H bond, leading to a reduction by a factor of 0.27. However, this is compensated by the larger ¹³C moment, resulting in RDCs that are about 70% the size of ¹H-¹⁵N RDCs. Measurement is also a little more complex because of the increased multiplicity of coupled methyl systems. Here we introduce a method that avoids some of the complexities of dealing with methyl multiplets and yields methyl RDCs with reliable error estimates.

Measurement techniques for methyl RDCs have been developed in the past. Most rely on indirect detection in heteronuclear multiple quantum coherence (HMQC) or heteronuclear single quantum coherence (HSQC) style experiments and measurement of RDCs in a frequency domain.^10–12 Kontaxis and Bax ¹⁰ introduced a method based on a constant time (CT)-HSQC pulse sequence with spectral editing in the indirect dimension to produce 4 sub-spectra that could be combined to produce spectra containing a single component of the multiplet. More recent methods have taken advantage of the Methyl-TROSY effect in HMQC type experiments that dramatically improves resolution for large, perdeuterated proteins and protein complexes.^7,8 And, Sprangers and Kay¹¹ implemented an HMQC-IPAP experiment that allowed measurement of the coupling constant from the direct ¹H frequency dimension. Recently, our lab has utilized an HMQC pulse sequence that introduced J-modulation (actually J+D, where D is the RDC contribution) in the first polarization transfer element in order to extract an RDC by fitting time domain data.¹² While J-Modulation experiments require collection of multiple points in a third time domain, the number of points can be small in number and selected to optimize sensitivity to the J-modulation frequency. Also, programs used to fit the data usually provide a direct estimate of error, something that is important in using RDCs for either resonance assignment or structure refinement.

Indirect detection of a heteronucleus through attached protons, as is done in an HMQC experiment, is not always optimal. These experiments include significant periods of time where proton magnetization is transverse. For large molecules proton transverse relaxation becomes very efficient and significant intensity is lost during these periods. In these cases, the loss may actually outweigh the sensitivity advantages of proton detection. This has been nicely illustrated by the Wagner group where direct detection of ¹⁵N in large proteins using an ¹⁵N-optimized NMR probe out performs more conventional experiments using a proton optimized probe.^13,14 This is especially the case with proteins that are not perdeuterated, as transverse proton spin relaxation becomes even more efficient and interference effects leading to TROSY enhancements are outweighed by other relaxation pathways. A similar situation occurs with ¹³C-methyl detection. Many of the proteins we study are glycosylated proteins that are best expressed in mammalian cell culture where perdeuteration is not an option. Hence, proton relaxation is efficient. Moreover, we frequently use the anisotropic magnetic susceptibility of paramagnetic tags to induce the partial alignment needed for RDC measurement. This adds additional relaxation mechanisms that further enhance proton relaxation in comparison to ¹³C relaxation.

Here, we propose an experiment for measuring RDCs that combines the inherent sensitivity of methyl groups with the favorable relaxation properties of carbon observation. We retain a J-modulation element due to the convenience of fitting data in the time domain and eliminate multiplet complexities from this element by making it constant time for evolution of all proton magnetization except that involving carbon. Application is to a ¹³C-valine-methyl labeled construct containing the two N-terminal Ig-like domains of a fully protonated glycoprotein, Robo1. The N-terminal domain has a lanthanide-binding peptide replacing a short loop between two beta strands.¹⁵ Comparison of paramagnetic (Dy³⁺ or Tb³⁺) and diamagnetic (Lu³⁺) complexes, as well as field dependence of the Dy³⁺ complex, is used to extract RDCs. The data are expected to elucidate the inter-domain geometry of this molecule and contribute an understanding of how it may transmit signals that govern axon guidance in developing nerve cells.

Experimental

Isotopic Enrichment, Protein Expression and Purification.

Design, expression, and purification of the two-domain construct of Robo1 containing a lanthanide binding loop has been described elsewhere.¹⁵ Briefly, Robo1 was expressed in lec⁻ HEK297 cells grown in FreeStyle medium deficient in valine and supplemented with [¹³C,¹³C]-methyl-valine. Purified protein was treated with endoglycosidase F, leaving a single N-acetylglucosamine residue at the one glycosylation site (confirmed by mass spectrometry).

Sample Preparation.

Solutions of the Robo1-Ig1–2-loop construct, ¹³C labeled in all valine methyls, were prepared in 100% D₂O, 25 mM tris buffer, 100 mM KCl, 4 uM DSS, 3 uM NaN₃, pH 7.4 (uncorrected) at a final concentration of 300 uM. For the diamagnetic sample, an equimolar amount of lutetium chloride (LuCl₃) was added, while the paramagnetic samples were prepared using an equimolar amount of dysprosium chloride (DyCl₃) or terbium chloride (TbCl₃).

NMR Spectroscopy.

Spectra were recorded on a 600 MHz magnet with a Bruker DCH probe optimized for ¹³C detection and an Avance III Console or on a 900 MHz magnet with a Bruker TCO probe optimized for ¹⁵N/¹³C detection and an Avance III Console. J-Modulated HETCOR data were collected with 2048 x 32 points and spectral widths of 6 and 3 ppm in the direct and indirect dimensions, respectively. All spectra were processed identically using nmrPipe.¹⁶ In the direct dimension, data were zero-filled and apodized with a cosine-bell, while in the indirect dimension the number of points was increased to 64 using linear prediction, zero-filled and apodized with a cosine-squared-bell. Peak picking was performed in Sparky,¹⁷ and integrals were taken using nmrPipe with a footprint fixed in size and position that captured about 80% of modulated crosspeak intensity.

Data Analysis.

J-modulation curves were extracted from the processed data and converted to text format using nmrPipe.¹⁶ Coupling constants were extracted by curve fitting implemented in MATLAB. The curve was assumed to be of the form: $e^{\left(-R\tau \right)}\sin \left(\pi \left(J+D\right)2\tau -c\right)$, where (J+D) is the extracted coupling, τ is the variable modulation delay, R is a decay factor, and c is a phase offset associated with imperfections in the experimental setup; R, (J+D) and c are the fitting parameters.

Results

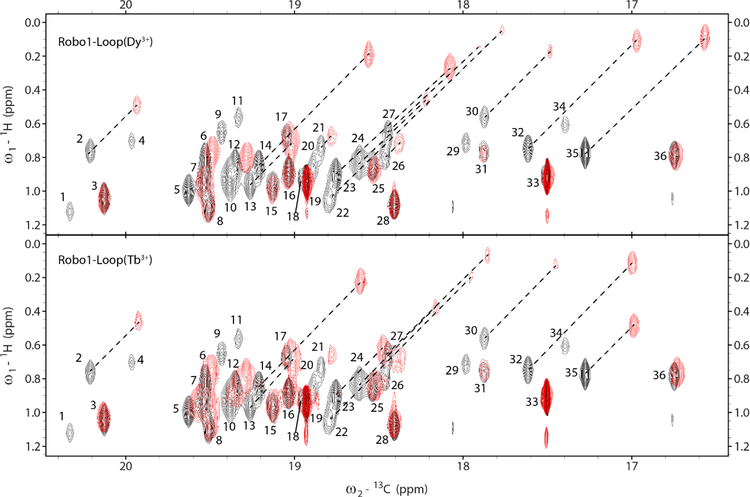
¹³C-detected two dimensional ¹H-¹³C spectra of our Robo1 construct (a HETCOR spectrum) are shown in Figure 1. Black crosspeaks are from a 300 µM sample with a diamagnetic ion (Lu³⁺) in its lanthanide-binding loop; this spectrum was collected in approximately 3 hrs at 600 MHz for protons on a 300 µL sample. The resolution, particularly in the ¹³C dimension, is excellent for a fully protonated 25 kDa protein. There are 19 valines in the construct; 36 of the 38 expected peaks are observable. The sensitivity is also excellent and is very comparable to that of a spectrum collected at 600MHz with a proton optimized cryoprobe (manuscript in preparation). The red crosspeaks are from samples with a paramagnetic lanthanide ion in the binding loop (Dy³⁺ in the upper panel and Tb³⁺ in the lower panel). There are notable pseudo contact shifts (PCSs) in both cases. As shifts are approximately the same in both ¹H and ¹³C dimensions, peaks in the presence of diamagnetic and paramagnetic ions can be connected by diagonal lines in most cases. The shifts are slightly different for Dy³⁺ and Tb³⁺ due to the different magnetic susceptibility anisotropy tensors for the two paramagnetic complexes.¹⁸ Also, the paramagnetically shifted peaks are missing in several cases due to the enhanced relaxation. However, the loss of peaks is significantly less than in corresponding HSQC or HMQC spectra, because of the absence of an additional ¹H observation period where paramagnetic contributions to transverse relaxation are larger than for ¹³C.

Figure 1.

HETCOR spectra of [¹³CH₃,¹³CH₃]-Valine-Robo1-Ig1–2-Loop showing overlays of the diamagnetic (black) Lu³⁺ complex with the paramagnetic (red) Dy³⁺ and Tb³⁺ complexes. Spectra were acquired on 300 µM samples in approximately 3 hrs at 600 MHz for protons. Resonance assignments have not been completed and peaks in the diamagnetic spectra are labeled with arbitrary numbers. Several peaks experience large pseudocontact shifts in the paramagnetic spectra and are connected to their diamagnetic counterparts with dashed lines.

There are some subtilties to collection of the spectra in Figure 1. Transfer of proton magnetization at the end of the t₁ period results in antiphase components for the four proton-coupled ¹³C lines. A simulation in the absence of paramagnetic relaxation contributions for the spectrum at this point using MATLAB scripts that calls functions from the SPINACH package¹⁹ is shown in Figure 2. The behavior of an isolated ¹³C¹H₃ methyl group with rapid rotation about its symmetry axis and tumbling with the correlation time of a protein was simulated by giving it an on-axis rotational correlation time of 10 ps and an off-axis correlation time of 10 ns. Note that the inner multiplet components are sharper because of the partial interference of α and β spins in the mixed proton states for these lines. The relative integrals are actually 1:1:1:1 because the experiment begins with proton magnetization and there is three times the magnetization transferred to the outer lines, compensating for the three-fold degeneracy of the inner lines. Immediate decoupling of protons would result in zero signal. Full refocusing of the ¹³C magnetization before decoupling is not possible but decoupling after a total refocusing delay of 1/3J results in a single line of nearly twice the intensity of the two sharper central lines with no contribution from the outer lines. A slightly shorter delay results in maximum refocusing of intensity in the limit where all lines have equal widths.²⁰ Note that RDCs can in principle be measured by acquiring a coupled spectrum immediately after transfer of proton magnetization. However, turning each crosspeak of Figure 1 into the four crosspeaks of Figure 2 with a mix of positive and negative intensities would be very hard to deconvolute.

Figure 2.

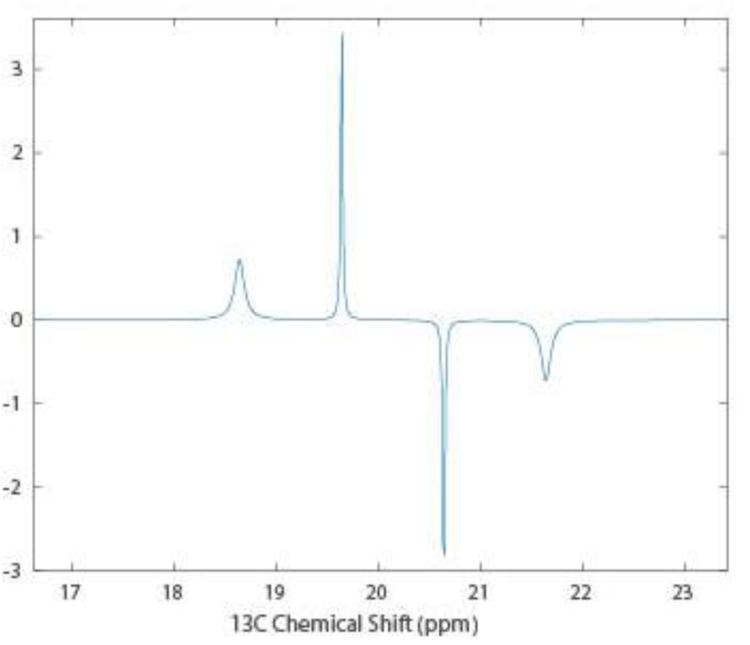
SPINACH simulation of ¹³C magnetization for a proton coupled methyl group in a HETCOR experiment before the final refocusing period.

There have also been some attempts to measure RDCs directly in the proton dimension.¹¹ To illustrate the complexities of this approach we have simulated a ¹³C-coupled proton spectrum using SPINACH functions (see Figure 3). As for Figure 2, rapid methyl rotation was simulated using anisotropic diffusion. The effects of partial orientation were introduced by defining an order tensor with principal values of 2e-4, 2e-4 and −4e-4 and the z-axis parallel to the methyl rotation axis. Note that, unlike a system with just scalar coupling, which would have two single lines, the presence of proton-proton dipolar couplings produces a ¹H proton spectrum with two triplets. Inner lines of the triplets are sharp due to the interference of relaxation contributions from pairs of α and β ¹H spins. The outer lines of the triplet are of unequal widths due to interference with relaxation contributions from the ¹³C spin. Again, measurement of RDCs from the positions of six superimposed crosspeaks for each crosspeak shown in Figure 1 would be difficult. Hence, we have chosen to design a pulse sequence that yields a simple time modulation of the intensity of each crosspeak seen in Figure 1.

Figure 3.

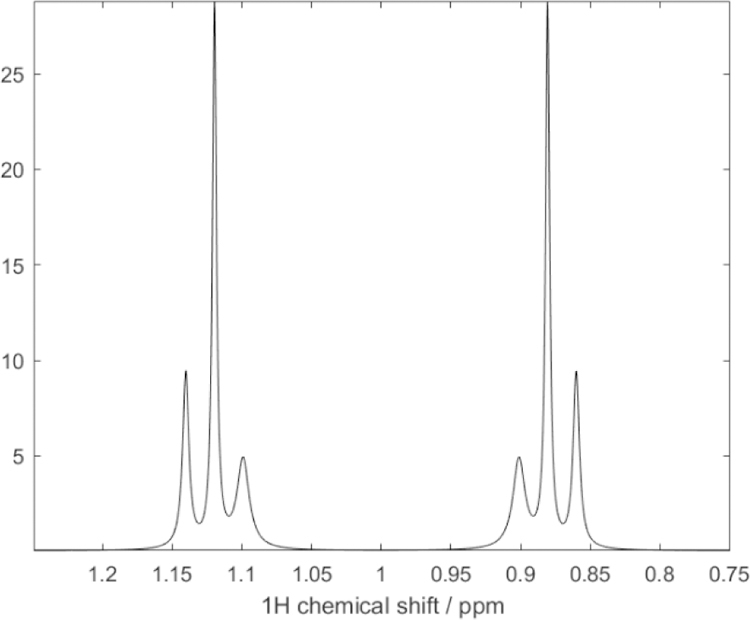
SPINACH simulation of a 1D 600 MHz ¹H spectrum of an isolated (¹³C¹H₃) spin system under conditions of partial alignment. The large splitting is due to ¹J_CH. The proton lines are also split into triplets due to the a ¹H⁻¹H RDC of approximately 12 Hz. Cross-correlation effects between ¹³C-¹H and ¹H-¹H dipole-dipole relaxation cause the differential linewidths for the inner and outer lines of each triplet.

Sequence design.

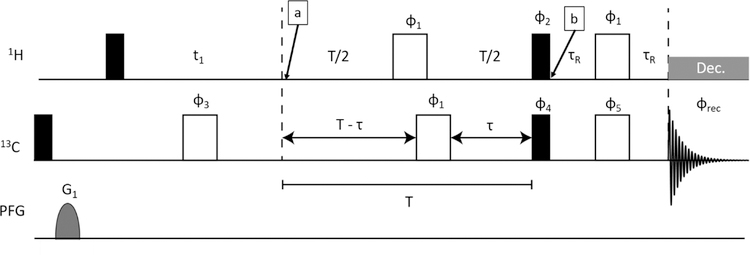
The sequence we generated is shown in Figure 4. It is a modification of a standard HETCOR sequence in which a constant time J-modulation period has been inserted between the end of the ¹H t₁ evolution period and transfer to ¹³C by a pair of ¹H and ¹³C 90° pulses. Making the J-modulation period, T, constant time removes modulation due to proton-proton couplings. Insertion of a 180° carbon pulse at a time τ before the end of the modulation period allows modulation due to carbon-proton couplings for times that vary from 0 to T as τ is incremented from 0 to T/2. Ideally, the value of T should be long enough to allow at least two zero crossings of the coupling evolution as points near these crossings are most sensitive to the modulation frequency (¹J_CH+¹D_CH in the presence of an RDC). However, measured intensities, and signal to noise ratios, decay as exp(−R₂T) as T is increased, limiting the number of zero crossings that can be accessed. In our application the constant time period, T, was set to 32 ms (4/J for J = 125 Hz) and τ was incremented from 2 to 16 ms in steps of 0.93 ms. The refocusing delays at the end of the sequence allow the antiphase lines of the ¹³C multiplet to come partially in phase so protons can be decoupled during observation. τ_R was set to 0.8 ms to optimize signal intensity with some sacrifice in resolution over collection of just the inner lines of the ¹³C multiplet.

Figure 4.

J modulated HETCOR pulse sequence. Filled pulses are 90° and unfilled are 180°. Pulse phases are as follows: ϕ₁ = [x, x,−x,−x], ϕ2 = [y,−y], ϕ₃ = [y, y, −y, −y], ϕ4 = [4x,4y,4(−x),4(−y)], ϕ_rec = [2(x, −x), 2(y, −y), 2(−x, x), 2(−y, y)]. All other pulses have x-phase. All gradients were 1 ms duration and strength of 52 G/cm.

A methyl group is an IS₃ spin system and is not rigorously described by the common product operator treatment used to describe experiments on ¹⁵N¹H spin pairs; however, it has been shown elsewhere⁷ that the eigen basis contains a spin-1/2 manifold, and for the purposes of describing the expected J-modulation a spin pair product operator treatment is adequate. For this description we will only consider magnetization that is ultimately converted to an observable form. During the indirect evolution period the C-H coupling is refocused and ¹H chemical shift evolution gives $-\cos \left({\omega }_1{t}_1\right){\widehat{I}}_y$ at time point (a) in Figure. 4. At the end of the constant-time INEPT period this magnetization becomes $-\cos \left({\omega }_1{t}_1\right)\sin \left(\pi \left(J+D\right)2\tau \right){\widehat{I}}_z{\widehat{S}}_x$ (Figure. 4 - point b). The final refocusing period converts most of the I_zS_x coherence to S_y for observation. One thing that is not included in this treatment is spin relaxation. Proton transverse relaxation effects are largely eliminated by using a constant time. However, ¹³C T₁ relaxation dephases modulation and results in a slow exponential decay. Also, the 180° ¹³C pulse that interconverts α and β states interchanges the broad and narrow components of the proton triplets seen in Figure 3, potentially resulting in a small rise of intensities at longer τ values. Both of these effects are well modeled in SPINACH simulations which do show a slight decay of the sinusoidal modulation. We model this by including an exponential term exp(−Rτ) in our fitting function. One possible effect not included in the simulation is that of a small three bond ¹H-¹³C coupling to the second valine methyl group (~4 Hz). In the interest of generality, we have not explicitly included this in our derivation. However, its small effects are likely absorbed in the exponential fitting constant, R and phase correction, c. Hence, after Fourier transform and measurements of crosspeak integrals as a function τ, intensities, I, are fit to equation 1.

$$\sin \left(\pi \left(J+D\right)2\tau +c\right)\exp \left(-R\tau \right)$$ Eq. 1.

RDC Measurement.

The above discussion applies to data acquired with any means of alignment. However, our Robo1 construct contains a lanthanide ion binding loop. When paramagnetic ions like Dy³⁺ and Tb³⁺ are present, field induced alignment can be utilized. Valine ¹³C^γ−¹H RDCs were measured on a fully protonated sample of our 25 kDa Robo1 construct using alignment by Dy³⁺ and Tb³⁺ at two magnetic field strengths, 21T for 900 MHz data and 14T for 600 MHz. Fitting of modulation data in the presence of these ions gave values for (J+D). A third measurement with the diamagnetic ion (Lu³⁺) provided a measurement of J. Since we do not expect J to vary significantly from site to site or with magnetic field, the average taken from the most precise measurements (those from peaks 19 and 33) was used to evaluate J (125.8 Hz) and extract RDCs from (J+D) measurements. In the diamagnetic sample, 36 peaks were observed (Figure 1); Enhanced relaxation in the samples containing paramagnetic ions caused several peaks to become greatly attenuated or disappear entirely. Also, pseudocontact shifts caused additional overlap of peaks, preventing some measurements. Of the original 36 peaks, only 10 allowed extraction of RDCs from the Dy³⁺ sample and only 13 allowed extraction of RDCs from the Tb³⁺ sample. The extracted RDCs are reported in Table 1; for the Dy³⁺ complex at 21T they range from approximately −3 to +6 Hz, and for the Tb³⁺ complex they range from approximately 0 to 7 Hz. Figure 5 shows the modulation curves of peak 16 in the diamagnetic and paramagnetic Dy³⁺ samples at 21T (900 MHz). This clearly shows the difference in modulation frequency that we attribute to an RDC.

Table 1.

Field-induced RDCs measured for the Robo1 Dy³⁺ and Tb³⁺ complexes at 900 MHz and 600 MHz. RDCs were measured as the difference in J+D in the paramagnetic complex and an average value of J from the diamagnetic complex

	Dy3+ Complex			Tb3+ Complex
Peak Label	900DCH	600DCH	Scaled	900DCH	600DCH	Scaled
3	−1.8 ± 1.3	1.4 ± 1.8	3.1 ± 3.6	1.4 ± 1.3	0.2± 1.9	0.4 ± 2.8
5	N/Aa	N/Aa	N/Aa	1.8 ± 1.8	0.8 ± 2.3	1.8 ± 3.4
6	0.1 ± 1.6	1.1 ± 1.5	2.5 ± 2.3	−0.3 ± 1.6	3.5 ± 2.3	7.9 ± 3.4
8	2.1 ± 1.8	1.1 ± 1.9	2.5 ± 2.3	5.4 ± 1.3	3.9 ± 0.9	8.8 ± 1.4
10	N/Ab	N/Ab	N/Ab	6.4 ± 1.7	N/Ab	N/Ab
12	6.2 ± 3.4	0.8 ± 2.5	1.8 ± 3.8	2.6 ± 1.8	N/Ab	N/Ab
15	N/Aa	N/Aa	N/Aa	4.1 ± 2.3	3.5 ± 1.6	7.9 ± 2.4
16	6.4 ± 1.6	3.5 ± 1.4	7.9 ± 2.0	7.1 ± 2.4	6.1 ± 1.6	13.7 ± 2.5
19	0.0 ± 0.1	−0.1 ± 0.2	−0.2 ± 0.3	−0.2 ± 0.2	0.2 ± 0.6	0.4 ± 0.8
25	−2.7 ± 1.8	2.2 ± 1.4	4.9 ± 2.0	2.0 ± 3.2	0.6 ± 2.6	1.3 ± 3.7
28	3.9 ± 1.1	2.5 ± 1.5	5.6 ± 2.3	4.4 ± 0.8	2.9 ± 1.6	6.5 ± 2.3
33	0.0 ± 0.1	0.0 ± 0.3	0.0 ± 0.4	−0.2 ± 0.1	−0.3 ± 0.2	−0.7 ± 0.3
36	2.7 ± 2.3	1.7 ± 2.5	3.8 ± 3.7	1.4 ± 2.1	−1.2 ± 2.4	−2.7 ± 3.5

^aPeaks were greatly attenuated and reliable measurements could not be made.

^bPeaks 10and 12 show significant overlap and could not be fit well in all spectra.. Errors are standard deviations propagated from curve fitting estimates.

Figure 5.

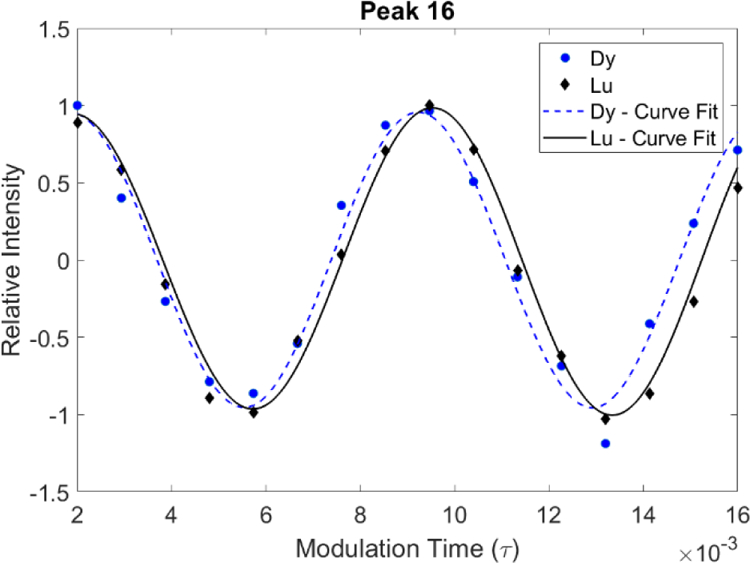
Overlay of measured J-modulation curves as a function of τ for peak 16 in paramagnetic Robo1+Dy sample and diamagnetic Robo1+Lu sample recorded using the pulse sequence in Figure 4. Both samples were measured at 900 MHz at concentrations of 300µM in approximately 24 hrs.

Collection of RDCs at more than one field strength can be useful. There can be field dependent broadening of resonances due to modulation of PCSs by internal motion, making some crosspeaks broader and less intense at higher fields; the known field dependence can also be used to extract an RDC in the absence of a separate measurement of scalar couplings or, when scalar couplings are known, compare results as an additional check on data quality. Both the induced magnetic moments and the interaction energies depend linearly on magnetic field, so RDCs depend on field squared.²¹ RDCs are therefore expected to be 2.25 times as large at 21 T as 14 T. In Table 1 we have scaled up the 600 MHz RDC values and their estimated errors by this factor and entered this in columns 4 and 7 so that direct comparisons of data collected at the two field strengths can be made. Three of the 21 possible comparisons lie more than 1 Hz outside the sum of our estimated errors (peak 25 for Dy³⁺and 8 and 16 for Tb³⁺). All three peaks are in crowded regions of the spectrum and the curve fitting procedure may be negatively impacted by signal overlap. A more sophisticated peak fitting approach that simultaneously fits multiple peaks could improve the quality of extracted intensities in these instances. The estimated errors in many cases seem large compared to the RDCs. However, it is important to point out that in applications such as crosspeak assignment or protein domain orientation, it is the error relative to the range of RDC measurements that counts. The ratio of the average error relative to the range for Dy³⁺ and Tb³⁺ are 0.16 and 0.22 respectively. This precision proves to be useful for many applications.

Discussion

The above data demonstrate J-modulation combined with ¹³C detection to be a viable method of measuring ¹³C-methyl RDCs. These RDCs are useful both for assignment of resonances and monitoring of structural changes. For proteins such as Robo1, which is natively glycosylated and best expressed in mammalian cell culture, assignment procedures based on uniform isotopic labeling are often not an option. We have recently introduced a procedure for assignment that uses comparison of easily acquired data, such as NOEs, chemical shifts and RDCs, to predictions based on known domain structures.^12,15,22 Utilization of the RDCs collected with our ¹³C-detected J-modulation experiment in assignment of the valine methyl resonances of our Robo1 construct is a high priority moving forward. Once assigned, there are emerging questions about the inter-domain orientation in our two-domain construct of Robo1. The RDCs we have measured, as well as the PCSs, will be useful in assessing inter-domain geometry.

Our Robo1 construct is not a particularly large protein, but even here ¹³C-observe methods appear competitive with ¹H-observe methods. This is in part a consequence of an inability to perdeuterate natively glycosylated systems. We anticipate that the advantages of ¹³C-detection methods will only increase as protein targets become larger and the number of glycosylated systems under investigation increases.

The pulse sequence and data fitting protocols presented here are likely to be refined in the future. We have already mentioned the possibility of explicitly including the effects of long-range couplings, such as that from protons of the methyl group observed to the ¹³C of the second intra-residue valine methyl group, in our fitting function. For methyl labeling, this is a unique problem arising from ¹³C-enrichment in both the methyls of the valine we used. However, similar problems can arise with leucine, and if uniform labeling of other methyl-containing amino acids is used (uniformly labeled alanine, for example), it will arise there as well. In the latter case, substitution of a selective pulse for the hard 180° pulse in our modulation period may eliminate the problem with long-range couplings.

We have also not collected modulation data in the most time-efficient way. First, we have picked a rather long modulation period for the purpose of showing a more complete modulation curve. In principle, two zero crossings are likely to be adequate; this corresponds to T= 2/J = 16 ms, a factor of 2 shorter than that used in our illustration. While the shorter modulation time would sacrifice some precision, we would expect a substantial increase in signal to noise of each point measured. Proton transverse relaxation is occurring during our modulation period, and based on proton line widths from HSQC spectra (not shown), we estimate T2 to be roughly 11 ms. Assuming mono-exponential decay during the J-modulation element, the signal intensity would be approximately 4 times greater with a 16 ms delay than with 32 ms delay used in our data.

Also, there is no need to collect equally incremented modulation points. Assuming that noise is constant as a function of τ, the contribution a measurement at a particular τ value can make to the accuracy of J (or J+D) should be proportional to the variation of intensity with J. This variation is given in equation 2, Where the effect on intensity as a function of transverse relaxation (R₂) during the total modulation period, T, is also included.

$$\frac{\partial I}{\partial J}=\pi 2\tau e^{-R_{2}T}\cos \left[\pi J2\tau \right]$$ Eq. 2

It is clear from equation 2 that contributions would have local maxima (or minima) at 2τ = n/J (zero crossings of Figure 5, where J = 125 Hz). It is also clear that values at these points would rise linearly with τ, but decrease exponentially as T was made longer to accommodate additional zero crossings. For our estimate of R₂ contributions would drop off rapidly after the first two zero crossings. To account for other factors, including phase offsets and decay as τ is incremented, it would be advisable to also place a few of the observation points near the first maximum and minimum of the curve and clustering the rest near the first two zero-crossings. With these improvements in mind, we expect that applications to protein systems significantly larger than our Robo1 construct should be possible.

Conclusion

We have designed a carbon detected pulse sequence for measurement of methyl ¹H-¹³C RDCs, which uses an intensity modulation scheme, and we have demonstrated this pulse sequence on a fully protonated, two-domain construct from the glycoprotein, Robo1. Our proposed design allows the efficient collection of RDCs and is broadly applicable to any system containing isotopically labeled methyl groups.