Indistinguishable photons from deterministically integrated single quantum dots in heterogeneous GaAs/Si₃N₄ quantum photonic circuits

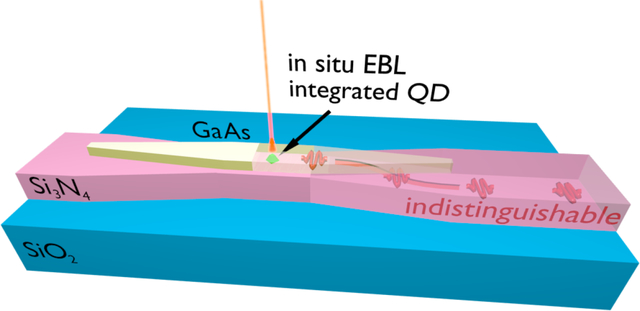
Abstract

Silicon photonics enables scaling of quantum photonic systems by allowing the creation of extensive, low-loss, reconfigurable networks linking various functional on-chip elements. Inclusion of single quantum emitters onto photonic circuits, acting as on-demand sources of indistinguishable photons or single-photon nonlinearities, may enable large-scale chip-based quantum photonic circuits and networks. Towards this, we use low-temperature in situ electron-beam lithography to deterministically produce hybrid GaAs/Si₃N₄ photonic devices containing single InAs quantum dots precisely located inside nanophotonic structures, which act as efficient, Si₃N₄ waveguide-coupled on-chip, on-demand single-photon sources. The precise positioning afforded by our scalable fabrication method furthermore allows observation of post-selected indistinguishable photons. This indicates a promising path towards significant scaling of chip-based quantum photonics, enabled by large fluxes of indistinguishable single-photons produced on-demand, directly on-chip.

Graphical Abstract

Main

In the development of advanced photonic quantum information systems, exemplified by various devised schemes for quantum simulation¹ and communication,² the ability to produce, manipulate and detect multiple identical photons in multiple spatial modes is a necessity. Integrated photonics has a great potential to fulfill such tasks, by allowing the creation of compact, complex, chip-scale photonic circuits that can implement phase-stable, reconfigurable, and integratable interferometric networks for linear optical operation at the single-photon level.^3,4

Silicon-based photonic integrated circuits are most promising for large system scaling, as foundry services offer the fabrication of user-designed, high quality integrated circuits comprising thousands of elements on shared wafer projects.⁵ Importantly, photonic losses in on-chip waveguides and related linear elements - e.g., beam splitters and combiners, phase delay paths and linear filters - can be reduced sufficiently through design and process control, to enable significant scaling of integrated quantum photonic systems. Adding to a favorable set of characteristics, the introduction of solid-state quantum emitters⁶ into silicon-based integrated quantum photonic circuits may yield unprecedented system scalability and functionality. Quantum emitters can e.g. act as high-rate, on-demand sources of indistinguishable single photons,^7–9 providing the large on-chip photon fluxes necessary for linear optical quantum systems such as boson sampling simulators.^10,11 Emitters with optically addressable spins may furthermore act as stationary qubits in photonic networks, and, along similar lines, single-photon nonlinearities in single-emitter quantum cavity-electrodynamic systems^12,13 may allow networks of deterministic quantum logic gates to be implemented.

In terms of silicon-compatible quantum light emitters, color centers in SiC have been shown to display promising optical and spin properties in a silicon-based material that is amenable to photonic integration.^14,15 Equally attractive emitters have not yet been identified in silicon or Si₃N₄. As a result, efforts to incorporate quantum emitters into photonic circuit platforms based on such materials have relied on hybrid integration with guest/host material systems that provide the desired optical properties. For instance, nitrogen-vacancy (NV) centers in diamond,¹⁶ epitaxially grown InAs quantum dots (QDs) in GaAs,¹⁷ and InAsP QDs in InP¹⁸ have been integrated with Si₃N₄ waveguides. In addition, InAs QDs in InP ¹⁹ on silicon-on-insulator, InAs QDs on GaAs-on-insulator, ²⁰ as well as carbon nanotubes ²¹ and 2D materials²² on silicon have also been shown. To date, however, Stranski-Krastanov (SK) self-assembled QDs have generally demonstrated superior optical coherence,^7,8,23 commonly evidenced by high degrees of two-photon interference, which is a pre-requisite to enable photon-photon interactions, e.g. in quantum gates. Thus, SK QDs currently offer the most favorable prospects for integrated quantum photonics.

One important drawback of the SK growth mode is the QDs’ random spatial distribution across the growth surface. This imposes considerable challenges for maximizing light-matter interactions through nanophotonic geometries,²⁴ which must be leveraged to create an efficient optical interface between the QD and the photonic circuit.¹⁷ In such geometries, QDs must be positioned with high precision within the nanophotonic geometry, to maximize coupling to specific spatial modes, and at the same time the QD must be sufficiently far away from etched surfaces, to minimize effects detrimental to the QD coherence.²⁵ A number of methods have been developed for precisely locating individual SK QDs on a wafer surface, allowing subsequent fabrication of nanophotonic devices precisely located around selected dots.^26–30 However, no hybrid devices have so far been demonstrated through such techniques.^17–20

Here, we employ cryogenic cathodoluminescence (CL) spectroscopy and in situ electron beam lithography (EBL)^31,32 to deterministically create hybrid integrated quantum photonic devices containing precisely positioned, preselected, individual InAs SK quantum dots. Our devices are based on a heterogeneous photonic integrated circuit platform, where GaAs devices containing positioned QDs are produced on top of Si₃N₄ waveguides.¹⁷ We demonstrate triggered emission of single photons from a single QD in a hybrid nanowaveguide, coupled directly into a Si₃N₄ waveguide. In addition, we report the observation of two-photon interference, which indicates generation of post-selected indistinguishable photons from a single device. This is achieved through precise positioning of the single emitter at maximum distance from etched surfaces through our deterministic approach. Single-photon indistinguishability is essential for quantum photonic systems based on linear optical operations, and yet has never been reported in hybrid QD-silicon platforms. Our unprecedented results indicate good prospects for generation of on-demand indistinguishable photons in a scalable hybrid silicon photonic platform.

Efficiently interfacing individual QDs embedded in a III-V host with Si₃N₄ photonic waveguides has two requirements. First, the III-V host must be carefully shaped to support spatial modes into which emission from the individual QD can be efficiently funneled, and these modes must be simultaneously and efficiently coupled to Si₃N₄ WG modes.¹⁷ Second, the QD must be located with high precision within the III-V host for optimal coupling to the desired spatial mode.²⁴ In the hybrid devices of ref.,¹⁸ individual InAsP QDs were grown with high spatial precision within InP nanowires. Because such nanowires are generated through self-assembled growth, geometrical control of the QD-hosting InP is limited, which results in less efficient QD-waveguide interfaces - for instance, limiting the ability to create small mode-volume cavity modes for Purcell enhancement.²⁴ Other groups^19,20 have relied on lithography and etching to produce high-resolution, geometrically complex nanophotonic hosting geometries for embedded, randomly positioned SK QDs. No attempt has been made to position individual QDs precisely within the hosting geometries, however. In addition, in both demonstrations,^19,20 QD-containing III-V devices were produced separately from the silicon photonic chip, then transferred onto the latter via pick-and-place processes, which offer limited scalability. The heterogeneous integration technique used in ref.¹⁷ and this work, which starts from the wafer bonded stack in Fig. 1 a), allows for the creation of InAs SK QD-containing, complex GaAs nanophotonic devices directly integrated with Si₃N₄ waveguides. Here, this technique is combined with the cathodoluminescence spectroscopy and in situ electron-beam lithography of refs.,^31,32 which has been shown to provide QD positioning accuracies of 34 nm.³³ To realize tapered GaAs nanowaveguides for mode transformers, it is crucial to achieve device features sizes in the 50 nm to 100 nm range. Using the high patterning resolution of the in situ EBL along with proximity-correction grey-scale writing,³⁴ feature sizes down to 50 nm³³ can be reliably achieved. The combination of heterogeneous integration¹⁷ with in situ EBL³² therefore offers a deterministic, high resolution and scalable, purely top-down fabrication scheme. A comparison to other deterministic manufacturing approaches can be found in ref.³²

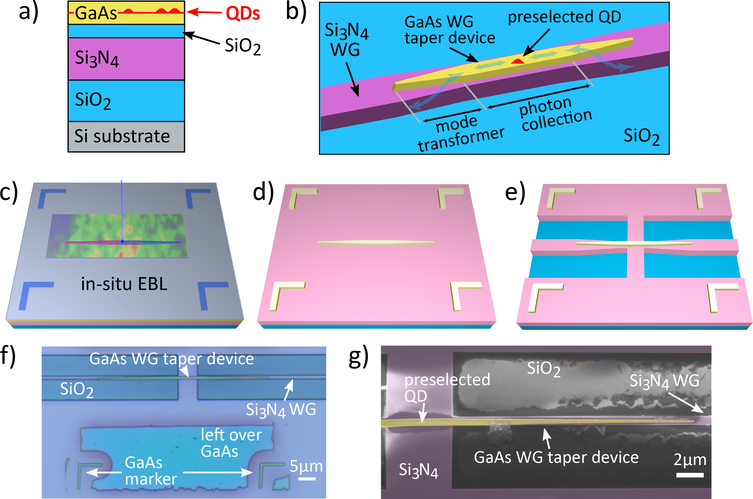
Figure 1:

a) Schematic layout of the wafer-bonded sample stack. b) Schematic GaAs-Si₃N₄ device design: The preselected InAs QD is hosted in a GaAs nanowaveguide that collects the QD’s emission. The emission is then coupled into the Si₃N₄-SiO₂ WG using mode transformers. c) - e): Visualization of key sample fabrication steps: c) in situ EBL of a GaAs nanowaveguide pattern and markers aligned to a QD which was preselected using low temperature CL spectroscopy. d) GaAs nanowaveguide and markers on Si₃N₄ after etching the GaAs patterns and removing excess GaAs. e) fully-fabricated GaAs-Si₃N₄-SiO₂ WG device. f) false-color optical micrograph of fully-fabricated device QD 1. g) false-color SEM image of device QD 1, showing the GaAs WG taper (yellow) and the Si₃N₄ WG (pink).

The in situ EBL technique has been used to produce a variety of photonic devices with deterministically positioned QDs, all on semiconducting (GaAs)^31,32,34,35 or conducting (gold) substrates.^36,37 For samples containing insulating layers like Si₃N₄ and SiO₂, as in this work, charging poses a major challenge. When the electron beam irradiates an insulating sample, the induced charge is not drained to the scanning electron microscope (SEM) ground and charges accumulate. This can already be a problem in standard EBL with positive tone resist doses on the order of $50\frac{\mu C}{{\text{cm}}^2}$, which require conductive polymers or thin metal films to be deposited onto the EBL resist. It becomes more severe for the in situ EBL which operates at electron doses in the $5000–50000\frac{\mu \mathrm{C}}{{\text{cm}}^2}$ range. Small amounts of charging lead to electron beam deviations, and the fast build-up of large charge numbers leads to unstable beam jumps, which inhibit CL mapping or EBL patterning. High acceleration voltages reduce the amount of charge deposited in thin insulating layers,³⁸ but likewise the number of electron-hole-pairs created in the GaAs layer decreases and QD excitation becomes inefficient. The present work demonstrates that a sufficient balance can be achieved, allowing for high resolution QD positioning and pattern definition on heterogeneous substrates with thin insulating layers.

Using in situ EBL^31,32 as well as aligned standard EBL,¹⁷ we deterministically fabricated a sample containing hybrid on-chip single-photon sources depicted schematically in Fig. 1 b). Such sources are composed by a straight GaAs nanowaveguide section (labeled “photon collection”) which hosts the preselected SK InAs QD and captures its emission into guided modes that are strongly confined in the GaAs ridge. Such GaAs-confined modes are subsequently converted into Si₃N₄ modes by mode transformers implemented at the two ends of the photon capture section. As discussed in ref.,¹⁷ such a geometry may offer QD-Si₃N₄ coupling efficiencies in excess of 90 %, through a combination of high photon capture probabilities and modal transformer efficiencies. Optimal collection efficiency was shown, through simulations, to be achieved for GaAs ridges of width ≈ 250 nm, which support only a single TE mode. On the other hand, significant linewidth broadening has recently been reported for QDs located at distances < 300 nm from etched GaAs surfaces.²⁵ In an attempt to minimize linewidth broadening, in the present work we have produced GaAs ridges with widths ranging from 400 nm to 800 nm. In the mode transformer sections, the GaAs ridges were tapered from such widths down to 100 nm at the tip along a 20 μm length, while the underlying Si₃N₄ waveguide maintained a width of ≈ 650 nm. The substrate cladding was thermal SiO₂ and a 100 nm thick spacer of SiO₂ was featured between the GaAs and Si₃N₄, see Fig. 1 a). As predicted by Finite Difference Time Domain (FDTD) simulations, such geometries offer maximum QD coupling efficiencies ranging from 26 % (400 nm width) to 8 % (800 nm width) in one direction. Such lower efficiencies, as compared to the optimized device of ref.,¹⁷ are due to two factors. Firstly, for widths > 300 nm, the GaAs ridge becomes multimode and non-negligible QD coupling to high-order guided modes, as well as radiative modes, leads to a reduced overall QD coupling efficiency into the Si₃N₄ waveguide. Secondly, the mode transformers were not optimized for the individual central waveguide widths and were therefore less efficient than those for the single-mode design of ref.¹⁷ A detailed account of all such inefficiencies for a 620 nm wide GaAs waveguide is given in the Supporting Information. We note that deposition of Al₂O₃ by Atomic Layer Deposition was shown to reduce QD linewidths that had been broadened by proximity to nearby etched GaAs surfaces²⁵ and could be a viable strategy for producing higher-efficiency, single-mode (< 300 nm wide) waveguide devices with narrow QD linewidths.

In the in situ EBL sample fabrication process, spatially resolved CL maps yield positions and spectra of suitable, individual QDs. Immediately after localization, proximity-corrected grey-scale in situ EBL,³⁴ as illustrated in Fig. 1 c), was performed at 7 K to define the GaAs waveguide taper patterns and markers, both aligned to the identified QDs. The intermediate sample layout after cleanroom processing is illustrated in Fig. 1 d). The Si₃N₄ waveguide patterns were defined as in ref.,¹⁷ resulting in the final device shown in Fig. 1 e). The sample was cleaved to allow endfire coupling to optical fibers inside of a cryostat.

Figure 1 f) shows a false-color optical micrograph of a finalized device. The positioned QD is located at the center of the 5 μm long, 620 nm wide straight portion of the GaAs nanowaveguide. Figure 1 g) shows a false-color SEM image of the same device, in which an unintended, vertical displacement of ≈ 60 nm between the fabricated GaAs and Si₃N₄ waveguides is apparent. We note the GaAs marker dimensions and positions relative to the QD were manually calibrated in the in situ EBL system, which likely led to write field distortion and scaling errors. As a result, the markers featured imperfections that disallowed nanometer precision automatic alignment in the 100 kV EBL system. Vertical displacements were systematically observed in all devices, and are likely due to the manual alignment procedure used for the fabrication of the Si₃N₄ layer, based on visual information from SEM scans and interferometric stage position readout.

Notably, some of the GaAs WG tapers that were fabricated with in situ EBL showed a bending at their left-hand side as shown in Fig. 2 b) and c), while their right-hand side and the overall WG position remained unaffected. This bending stems from minor charging which occurs in parts of the sample and is explained in more detail in the Supplementary Material.

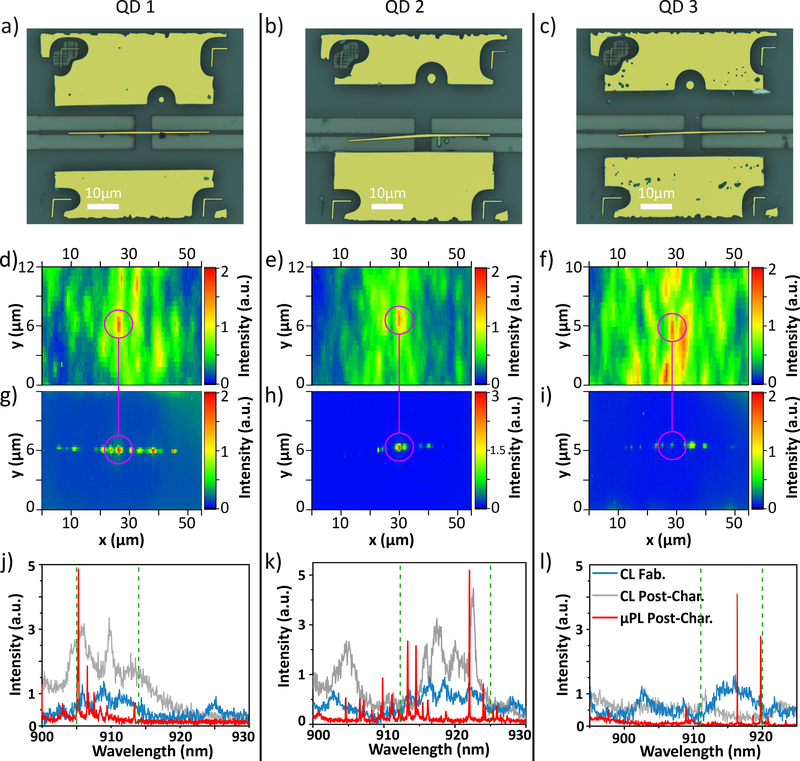
Figure 2:

a) - c): False-color optical micrographs showing devices QD 1–3, with GaAs colored in yellow for better contrast. The left-hand side of the GaAs WGs in b) and c) is bent downwards due to charging. d) - f): CL maps taken during in situ EBL to locate QDs 1–3. The pink circles mark the QD emission patterns that were used for QD localization. g) - i): CL maps taken on the fully-fabricated devices. Here, pink circles mark the GaAs WG center. The CL intensity in all maps d) - i) is integrated over those spectral regions, that were used to localize the QDs during the in situ EBL. These spectral regions are highlighted in j) - l) by green dashed lines. j - l): CL spectra taken during (after) fabrication in blue (grey) along with μPL spectra after fabrication in red.

The successful fabrication of heterogeneous waveguide devices and the integration of preselected QDs was checked through conventional microscopy, scanning electron microscopy as well as micro-photoluminescence (μPL) and CL spectroscopy on the fully fabricated sample. Figure 2 a) – c) show microscope images of three example WG devices QD 1, QD 2 and QD 3 with a GaAs nanowaveguide width of ≈ 620 nm that have been successfully positioned on preselected QDs. CL intensity maps of each QD taken during fabrication are visible in Fig. 2 d) – f) and after fabrication in Fig. 2 g) – i). The maps show the CL intensity integrated over those spectral regions that were used to determine the QD positions during fabrication, marked by green dashed lines in Fig. 2 j) – l). The pre- and post-fabrication CL maps for QD 1, QD 2 and QD 3 (Figs. 2 d) – i)) display spatially matching, localized high intensity spots, marked by red pixels within the pink guide to the eye, that indicate successful, deterministic waveguide placement around the preselected individual QDs. Figure 2 j) – l) show CL spectra with an exposure time of 50 ms during (blue) and after (grey) fabrication from representative pixels at the positioned QD location, as indicated by each intensity maximum inside the pink guide to the eye in Fig. 2 d) – i). μPL spectra were obtained with an exposure of 1 s after fabrication, but before the post-fabrication CL mapping, and are displayed in red. These spectra, which display broad CL, as well as sharp μPL emission from individual QDs within the same spectral ranges, further support successful deterministic integration. The apparent discrepancy between the CL and μPL spectra are due to differences in QD excitation conditions, where the various QD excitonic complexes are populated with different efficiencies. Also, in CL, the large injected charge density necessary for sufficient luminescence to be produced leads to spectrally broad QD lines. While QD 3 produced spectrally aligned pre-fabricated CL and μPL emission, the post-fabrication CL emission displays considerably less intensity within the same spectral range. We believe that the repeated thermal cycles to which the sample was subjected, between the μPL characterization and subsequent post-fabrication CL mapping, caused such degradation. Nonetheless, the pre-and post-fabrication CL maps still display the same localized intensity spots at the selected QD location. We note that all μPL measurements were obtained by pumping the center region of the QD devices. Moving the pumping spot to other locations caused the emission spectra to vary considerably, as expected.

The finalized sample was tested inside of a closed-cycle cryostat at 7 K. The sample was excited from the top using CW or pulsed tunable lasers through an NA=0.28 microscope objective, and the emission was captured from the Si₃N₄ WGs at the sample facet using aligned lensed single mode fibers inside the cryostat.¹⁷ Figure 3 a) shows a μPL spectrum from the fabricated device housing QD 3, illuminated by a CW free-space laser beam tuned to ≈ 904 nm, exciting the p-shell of the positioned QD 3 and giving rise to a narrow emission line at ≈ 916.3 nm. The intensity of this PL line as a function of pump power is shown in Fig. 3 b), showing saturation at a power of 155μW. The PL intensity was obtained as the peak area of a Gaussian model fit to each spectrum of the power series. Interestingly, a red-shift of the emission line is observed for increasing pump powers, see Fig. 3 c). This shift is likely due to a local increase in temperature in the GaAs WG, which lies on top of thermally insulating Si₃N₄-SiO₂. To investigate this hypothesis, we assume a linear temperature increase with excitation power due to linear absorption in the GaAs. With this model, we are able to faithfully fit the power-dependent spectral position of the QD line with a Bose-Einstein phonon law that describes the temperature dependence of the semiconductor bandgap,³⁹ confirming a temperature-related effect. Moving towards strictly resonant excitation in the future, sample heating can be neglected, as the necessary pump powers are orders of magnitude lower than in p-shell excitation. More details and a comparison to temperature series measurements are given in the Supplementary Material.

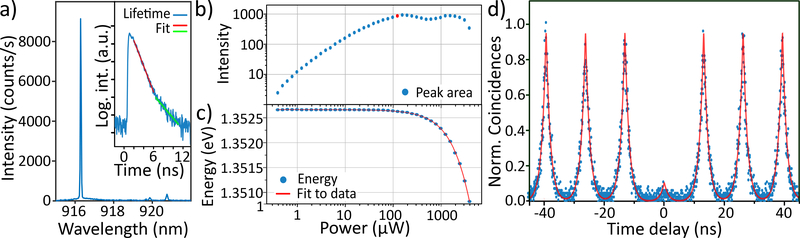
Figure 3:

a) PL spectrum of QD 3 in CW p-shell excitation. Inset: Natural logarithm of the excited state lifetime trace with two linear fits returning τ_r = 1.39 ns and τ_r,2 = 3.15 ns. b) PL intensity of the 916.3nm line over excitation power, in 1 dB steps. c) Peak energy over excitation power (blue) and fit to data (red), showing a redshift with increasing excitation power. d) Pulsed excitation autocorrelation curve (blue) with fit to data (red) yielding g⁽²⁾(0) = 0.11.

We next measured the lifetime of the ≈ 916.3 nm state by exciting QD 3 with a pulsed laser with a 76 MHz picosecond pulse train at ≈ 904 nm. The excitation laser was suppressed with a ≈ 500 pm free spectral range fiber-coupled grating filter with a transmission of ≈ 60% in addition to an edge pass filter. The filtered PL was detected on a superconducting nanowire single-photon detector (SNSPD) with a timing resolution of ≈ 90 ps. The natural logarithm of the data is plotted in the inset of Fig. 3 a) and shows a double exponential decay. By fitting two linear curves to the natural logarithm of the data, we extract two decay constants of τ_r = (1.39±0.04) ns and τ_r,2 = (3.15±0.29) ns (uncertainties are standard errors). The slower decay hints at a recapture process often seen in QDs.⁴⁰ To evaluate the single-photon emission purity of QD 3, pulsed excitation close to saturation was used, as indicated by the red dot in Fig. 3 b). The collected PL was split in a 50/50 fiber beam splitter and then detected by two SNSPDs with an overall timing resolution of ≈ 130 ps in a Hanbury-Brown and Twiss (HBT) type configuration. Detection coincidences with time delay τ were tracked with a 64 ps bin size. The normalized autocorrelation curve g⁽²⁾(τ) is depicted in Fig. 3 d). The data was fitted with a two-sided exponential decay function convolved with a Gaussian that represented the experimental timing resolution. We used a Poissonian statistics maximum likelihood estimator for fitting.⁴¹ Without any corrections, we obtain a conservative estimate of g⁽²⁾(0) = 0.11 ± 0.04 (uncertainty marks the 95 % confidence interval), clearly showing that the positioned QD 3 emits triggered single photons into the Si₃N₄ WG. Details on the fit functions and the Poissonian estimator can be found in the Supporting Information.

Next, we estimate the emission efficiency of our hybrid single photon source from the QD into the lensed fiber. During the HBT measurement, a combined photon stream of ≈ 50 kHz is measured on the detectors. Taking into account the grating filter and fiber transmission as well as the detector efficiency, we estimate a setup efficiency from collection fiber to detector of η_Setup ≈ 0.09. Assuming 100 % quantum efficiency, the QD-to-fiber efficiency is η_Source ≈ 50 kHz/(76 MHz·η_Setup) ≈ 0.7% without further corrections. Considering the Si₃N₄to-fiber coupling of efficiency of ≈ 23% obtained from FDTD simulations (see Supporting Information), we estimate a QD coupling efficiency of ≈ 3% into the Si₃N₄ waveguide. We compare the measured QD-to- fiber efficiency with Finite Difference Time Domain simulations of a dipole radiating inside a geometry that closely approximates that of the real device, including fabrication imperfections. The simulations include the emission coupling from a dipole source into the 620 nm wide GaAs WG, power transfer between the GaAs and Si₃N₄ guides, and coupling between the Si₃N₄ WG and collection lensed fiber (details in the Supporting Information). Modelling the QD as linear dipole, we obtain η_Source,1 ≈ 3% and modelling the QD as rotating dipole resembling a trion state we find η_Source,2 ≈ 1%. The linear dipole result gives a conservative upper bound for the optimum source efficiency η_Source achievable with the WG examined here. We note that the simulated QD to GaAs WG coupling efficiency is ≈ 42% for one propagation direction, and the overall coupling efficiency can potentially be significantly increased, by improving the fiber-to-Si₃N₄ waveguide coupling, the mode transformer design, and introduction of a high reflectivity mirror on the back port of the GaAs waveguide.¹⁷

While the transfer of single-photon emission from QDs into silicon photonic circuits has been shown before using various sample preparation methods,^17–20 the degree of indistinguishability of the emitted photons has never been evaluated in such hybrid systems. In fact, the close presence of dissimilar material interfaces to the QD introduces defect-rich regions that can reduce the QD coherence through electronic interaction with surface or defect states,²⁵ inhibiting emission of indistinguishable photons. A high degree of single-photon indistinguishability, however, is necessary for quantum photonic systems based on linear optical operations, and can serve as a baseline criterion for evaluating the quality of the fabrication process, regarding preservation of the QD coherence. In the following, we evaluate the coherence of photons emitted by the fully-fabricated device QD 3, pumped by CW laser light at ≈ 904 nm, close to saturation with an excitation power of 123 μW, marked by the red dot in Fig. 3 b).

As a first indicator of photon coherence, we measured the linewidth of the ≈ 916.3 nm emission line by passing it through a high resolution scanning Fabry-Perot interferometer (FPI) with a finesse of ≈ 200 and free-spectral range of 40 GHz, and detecting the filtered signal with an SNSPD. The recorded spectrum is shown in Fig. 4 a), where it is apparent that QD 3 has a linewidth of ≈ 2 GHz. Since there is no fine structure splitting the emission line stems most probably from a charged excitonic complex. Considering the GaAs nanowaveguide width of 620 nm, the narrow linewidth suggests that severe degradation of the QD coherence through etched surfaces in the QD’s vicinity²⁵ is avoided due to precise deterministic positioning. Fitting the FPI spectrum with a Voigt line function returns a more faithful result than Lorentzian or Gaussian shapes (see Supporting Information) and we obtain a Voigt linewidth of ΔΓ_V = (2.20±0.19) GHz full-width at half-maximum (FWHM). A Lorentzian component of ΔΓ_L = (1.07±0.27) GHz FWHM suggests homogeneous broadening beyond the Fourier limit of ≈ 0.1 GHz, likely due to dephasing from phonon interactions. The Gaussian component of ΔΓ_G = (1.54±0.26) GHz FWHM suggests inhomogeneous linewidth broadening due to spectral diffusion.⁴² All uncertainties mark the 95 % confidence interval. In our hybrid device both homogeneous and inhomogeneous broadening values are comparable to those observed under p-shell excitation in refs.^41,42 and resonant excitation in ref.⁴³ in purely GaAs-AlGaAs-InAs-based samples. From the Lorentz linewidth we can extract an upper bound for the photon coherence time, yielding τ_c,FPI = 1/πΔΓ_L = (0.30 ± 0.03) ns.⁴⁴

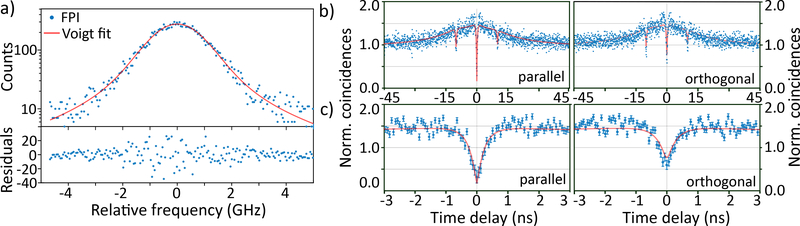
Figure 4:

a) top: FPI spectrum of QD 3 (blue) with a fitted Voigt profile (red). Bottom: Voigt fit residuals. b) TPI coincidence curve (blue) and fitted model (red) for parallel (orthogonal) configuration is shown in the left (right) hand side panel. c) Same as b), including error bars and magnified around zero time delay for clarity.

Next, we measured the two-photon interference (TPI) contrast of subsequently emitted photons of the same ≈ 916.3 nm line from QD 3, under the same CW excitation conditions, in a Hong-Ou-Mandel (HOM) type experiment. Details on the setup are given in the Supporting Information. The raw HOM autocorrelation traces for parallel and orthogonal photons are depicted in blue in Fig. 4 b) and magnified around τ = 0 in Fig. 4 c). The error bars in Fig. 4 c) are the $1/\sqrt{N}$ Poissonian uncertainty for each time bin with N counts. At τ = 0, the trace for parallel-polarized photons is clearly below 0.5 and below the orthogonal trace, marking the emission of indistinguishable photons. The bunching around τ = 0 hints blinking due to coupling of the QD to a dark state.^43,45

To extract an estimate for the coherence time τ_c,HOM and the two-photon interference visibility V we follow Ref.⁴⁶ and model the parallel and orthogonal coincidence traces with autocorrelation functions $g_{\text{HOM},\parallel }^{(2)}(\tau )$ and $g_{\text{HOM},\perp }^{(2)}(\tau )$, respectively. Their fits to the coincidence data are plotted in Fig. 4 b) and c). We obtain τ_c,HOM = (0.33 ± 0.12) ns and $V={0.89}_{-0.29}^{+0.11}$, where the uncertainty states the 95 % confidence interval. τ_c,HOM indicates a post-selection time window where indistinguishable photons are available. Since we are pumping close to saturation, our estimate for the coherence time τ_c,HOM represents a lower bound of what can be achieved in our system.⁴⁷ Within the uncertainty range, τ_c,HOM lies below the upper bound τ_c,FPI deduced from the FPI measurement.

Both the FPI spectrum analysis and the observation of two-photon interference indicate that our heterogeneous photonic integration platform can produce waveguide-coupled single-photon sources emitting light with a reasonable level of coherence. Both experiments were performed in quasi-resonant, and not strictly resonant excitation (a QD signal-to-pump laser noise ratio of about 1:2 was estimated for resonant excitation, which prevented observation of resonance fluorescence - see Supporting Information for details). Since the QD was not excited resonantly - with which the highest optical coherence level can be achieved^23,48 - a clear-cut evaluation of the adversity imposed by our fabrication process upon QD coherence is not possible. In particular, QD 3 was not evaluated pre-fabrication, or even pre-wafer bonding, so its starting optical properties are unknown. Nonetheless, the QD linewidths and coherence times reported here are comparable with those observed from QDs in purely GaAs-based devices^41–43 with which high degrees of two-photon interference were demonstrated, indicating good prospects for our technique.

Precise alignment of the EBL patterns with respect to the QDs is essential to avoid excessive proximity to etched sidewalls, which may lead to degradation of quantum efficiency and, especially, coherence.²⁵ Our observation of a 2.2 GHz linewidth from a positioned QD emission line, and subsequent demonstration of two-photon interference, indicate that the required precision can be met in our platform, and suggests that our fabrication method has minimal adverse effects on QD coherence. In order to increase the source efficiency η_Source while preserving such high levels of photon coherence, photonic designs that avoid GaAs etched surfaces closer than 300 nm to the QD⁴⁹ while improving the emitter-WG-coupling are required. Creating sophisticated cavity-based devices⁵⁰ for such a goal can be envisioned with our deterministic proximity-corrected grey-scale EBL process.

Even though CL excitation is restricted to conditions that avoid charging, which may be problematic for positioning precision and pattern resolution, we have been able to produce structures with widths ≤ 620 nm with high precision around single, preselected QDs. We are able to consistently achieve 100 nm thin waveguide taper tips through proximity-corrected grey-scale lithography in the in situ EBL step. In our samples, some level of charge draining is achieved through the GaAs top layer and Si substrate, so that, at a 20 kV electron-beam acceleration voltage, charging due to the Si₃N₄-SiO₂ layers is avoided, allowing sufficiently clear CL signals for QD positioning. Charging can nonetheless be further reduced through various measures: lower QD densities in the GaAs would require lower beam currents for efficient excitation and precise localization; a thinner bottom SiO₂ layer would absorb less energy without reducing optical confinement; electrically conductive polymers deposited on the resist would reduce charging in the latter and connect the GaAs to the silicon and the ground via the sample edge.

The devices presented in this work show imperfections in the alignment between the GaAs and the Si₃N₄ waveguides, which stem from the manual alignment of the Si₃N₄ waveguide layer. Incorporating the CL mapping system into state-of-the-art EBL equipment promises nanometer precision automatic alignment throughout the whole process in the future. Also, lower QD densities in the range of ≤ 10⁸ cm⁻² are crucial to enable higher positioning accuracies and higher device yield.

While in the current work high excitation beam currents led to broad CL preselection spectra, in general, CL allows the preselection of multiple QDs with sharp, closely spectrally matching emission lines with a < 1 nm accuracy.⁵¹ This way, multi-emitter experiments can be envisioned with our platform as well, with QDs that produce indistinguishable photons at identical wavelengths. Still, spectral fine-tuning mechanisms are likely necessary. Local electrical control over the emission wavelength in GaAs p-i-n-doped layers through the quantum Stark effect is a promising approach, that is fully compatible with both the in situ EBL and heterogeneous sample stacks. Reduced diffusion lenghts of hot electrons in p- and n-doped layers even improve the CL positioning accuracy through a more localized excitation as compared to the undoped sample used here. Electrical contacting also allows control of the QD charge environment, which has proven helpful in increasing the coherence of emitted photons.⁷

By applying in situ EBL to a heterogeneous GaAs / Si₃N₄ bonded wafer, we demonstrate the ability to deterministically produce GaAs nanophotonic devices with preselected and precisely located InAs QDs, which can be efficiently accessed by Si₃N₄ waveguides in an on-chip network. Our unprecedented demonstration of both triggered single-photon emission and post-selected indistinguishable photons produced by a single QD in a hybrid photonic circuit indicate a clear path towards highly scalable, chip-based quantum photonics. This can enable experiments such as Shor’s algorithm ⁵² to be performed on-chip with triggered photons at rates substantially higher than currently available.

METHODS

Deterministic device fabrication

Fabrication started with a low-temperature plasma-bonded wafer stack consisting of a Si substrate, 3 μm thermal SiO₂, 250 nm low-pressure chemical vapor deposition (LPCVD) Si₃N₄, 100 nm plasma-enhanced chemical vapor deposition (PECVD) SiO₂ and 190 nm of GaAs containing SK InAs QDs at its center,¹⁷ as shown in Fig. 1 a). The plasma-bonded GaAs forms a uniform layer that spans over areas of several tens of square millimeters. GaAs nanowaveguides were deterministically patterned at the position of single preselected InAs QDs through in situ EBL^31,32 as follows: The sample was coated with a dual-tone EBL resist which exhibits high contrast and high resolution at cryogenic temperatures,⁵³ mounted onto a custom-made liquid helium flow cryostat inside an SEM, and cooled to 7 K. In the chamber, the sample was excited by an electron beam, and emitted light was collected through an NA = 0.8 elliptical mirror, then dispersed in a grating spectrometer. Through this process, spatially resolved CL spectrum maps over regions of hundreds square microns with 500 nm steps were taken, while the electron dose remained well below the negative-tone onset-dose. Applying an acceleration voltage of 20 kV and a beam current of 0.5 nA, sample and resist charging was minimized while still operating at a high QD excitation. Comparing the CL imaging of sample regions with bonded GaAs to those without, we find that less charge accumulates in regions with GaAs, indicating beneficial charge carrier diffusion in the GaAs. On-the-fly spectral analysis of the CL maps yielded positions and spectra of suitable, individual QDs within a few minutes. Immediately after localization, proximity-corrected grey-scale in situ EBL,³⁴ as illustrated in Fig. 1 c), was performed at 7 K to define 45 μm long symmetrical GaAs waveguide taper patterns (see Supporting Information) aligned to the identified QDs. The QD positioning uncertainty is about 55 nm (68 % confidence interval; convolution of a 54 nm CL mapping accuracy obtained from CL maps of 28 devices and a 12 nm positioning accuracy³³). The uncertainty is slightly higher than the previously achieved 34 nm³³ due to a high QD density in the sample, which reduces the dynamic range of the 2D Gaussian fits used for QD localization if other emitters are spectrally and spatially within the fitting range. In addition, four L-shaped marker patterns, also aligned to the QD positions, were written outside the CL mapping area. The sample was then brought to room temperature, developed, and the resist pattern was transferred into the GaAs with an inductively coupled plasma reactive ion etch. Unpatterned GaAs was subsequently removed in a nitric acid/ceric ammonium nitrate aqueous solution, using a resist mask to protect the etched device and alignment mark areas, resulting in the intermediate sample layout shown in Fig. 1 d). The GaAs alignment marks (visible in the micrograph in Fig. 1 f)) were included for aligned EBL to be performed in a commercial 100 kV system. The Si₃N₄ waveguide patterns were defined as in ref.¹⁷ and transferred via reactive-ion etching into the Si₃N₄ (Fig. 1 e)).

Postcharacterization of deterministically integrated QDs

For μPL, the sample was mounted inside a closed-cycle cryostat and cooled down to 7 K. An off-resonant continuous wave (CW) laser at 821 nm was focussed through an NA=0.28 microscope objective onto the designated QD position inside the GaAs WG. QD emission was collected from the Si₃N₄ WG endface through a lensed single mode fiber. CL maps and spectra are taken at a temperature of 7 K, an electron beam current of 4 nA and an acceleration voltage of 20 kV.

Hanbury-Brown and Twiss evaluation

The HBT data shown in Fig 3 d) of the main text is modeled with a two-sided exponential decay function, taking into account only the faster QD decay rate τ_r for a conservative estimate of g⁽²⁾(0):

$$g^{(2)}(\tau )=A_0\exp \left(-\left|\tau \right|/{\tau }_{\text{r}}\right)+A_{\text{Side}}\sum _{k\ne 0}\exp \left(-\left|\tau -{\tau }_{\text{k}}\right|/{\tau }_{\text{r}}\right)$$ (1)

Here, A₀ is the central peak area, A_Side the side peak area, τ_r the QD radiative lifetime and τ_k the side peak position. This model is convolved with the detector time response of 129 ps to obtain $g_{\text{Conv}}^{(2)}(\tau )$ for the fit. Since the coincidence data around τ = 0 is close to 0, we fit our model using a logarithmic Poissonian noise distribution⁴¹ ln(Poiss(μ, K)) = −μ + K ln(μ) − ln(K!) and a maximum likelihood routine that minimizes

$$-\sum _i\ln \left[\mathrm{Poiss}\left(g_{\text{Conv}}^{(2)}\left({\tau }_i\right),N_i\right)\right].$$ (2)

Here, i enumerates the time bins, τ_i is the time delay in bin i and N_i is the number of coincidences in bin i. The peak areas A₀ and A_Side are the only free parameters in the t, yielding g⁽²⁾(0) = A₀/A_Side = 0.11 ± 0.04, where the uncertainty gives the propagated 95 % confidence interval.

Two-photon interference evaluation

We follow Ref.⁴⁶ to model the two HOM coincidence traces with the functions $g_{\text{HOM},\parallel }^{(2)}(\tau )$ and $g_{\text{HOM},\perp }^{(2)}(\tau )$, where g⁽²⁾(τ) accounts for the bunching around zero time delay:

$$g^{(2)}(\tau )=1-A_1\exp \left(-\left|\tau \right|/{\tau }_1\right)+\left(A_1-1\right)\exp \left(-\left|\tau \right|/{\tau }_2\right)$$ (3)

$$g_{\text{HOM},\perp }^{(2)}(\tau )=\underset{G_1(\tau )}{\underbrace{4\left(T_1^2+R_1^2\right)R_2{T}_2{g}^{(2)}(\tau )}}+\underset{G_2(\tau )}{\underbrace{4R_1{T}_1\left[T_2^2{g}^{(2)}(\tau -\delta \tau )+R_2^2{g}^{(2)}(\tau +\delta \tau )\right]}}$$ (4)

$$g_{\text{HOM},\parallel }^{(2)}(\tau )=G_1(\tau )+G_2(\tau )\left[1-V\exp \left(-2\left|\tau \right|/{\tau }_{c,\text{HOM}}\right)\right]$$ (5)

Here, A₁, τ₁ and τ₂ describe the bunching around τ = 0 in the CW autocorrelation curve g⁽²⁾(τ). R₁ = 0.50 and T₁ = 0.50 as well as R₂ = 0.54 and T₂ = 0.46 are the reflection and transmission coefficients of the first and second beam splitter in the Mach-Zehnder interferometer. Fitting $g_{\text{HOM},\perp }^{(2)}(\tau )$ to the orthogonal case of Fig. 4 b), we can extract g⁽²⁾(τ). We obtain A₁ = 1.64 ± 0.01, τ₁ = (0.30 ± 0.02) ns and τ₂ = (14.61 ± 0.32) ns, where the uncertainties are standard errors. We use this to fit $g_{\text{HOM},\parallel }^{(2)}(\tau )$ to the parallel case of Fig. 4 b), with τ_c,HOM and V as the only free parameters.