We have clarified a physical guideline for controlling thermoelectric properties of conducting polymers by continuous doping.
Abstract
Conducting polymer thin films containing inherent structural disorder exhibit complicated electronic, transport, and thermoelectric properties. The unconventional power-law relation between the Seebeck coefficient (S) and the electrical conductivity (σ) is one of the typical consequences of this disorder, where no maximum of the thermoelectric power factor (P = S2σ) has been observed upon doping, unlike conventional systems. Here, it is demonstrated that a thiophene-based semicrystalline polymer exhibits a clear maximum of P through wide-range carrier doping by the electrolyte gating technique. The maximum value appears around the macroscopic insulator-to-metal transition upon doping, which is firmly confirmed by the temperature dependence of σ and magnetoresistance measurements. The effect of disorder on charge transport is suppressed in the metallic state, resulting in the conventional S-σ relation described by the Mott equation. The present results provide a physical background for controlling the performance of conducting polymers toward the application to thermoelectric devices.
INTRODUCTION
Thermal energy harvesting from low-temperature heat sources, such as the human body, is a promising method to feed energy to a vast number of microdevices and sensors in Internet of Things technologies. In particular, thermoelectric generators using conducting polymers are highly suitable for this purpose owing to their inherent lightweight, flexible, and low-toxic nature and their easy fabrication method based on solution processes (1–3). However, the thermoelectric performance of conducting polymers is still much lower than that of commercial products, and therefore, guiding principles for optimization are required to design high-performance thermoelectric materials and devices.
One of the key performance parameters in thermoelectric devices is the power factor, P = S2σ, where S is the Seebeck coefficient and σ is the electrical conductivity. It has been suggested that most conducting polymers, except for poly(3,4-ethylenedioxythiophene)–based materials, exhibit no maxima of P upon carrier doping, i.e., P continuously increases with increasing σ for higher doping levels (4–11). The origin of this unconventional behavior lies in the empirically known power-law relation of S ∝ σ−1/s, where s is equal 3 or 4 in most cases. It has been widely accepted that this unconventional relationship appears due to the disordered nature of the polymer films, where the charge transport is affected by structural/energetic disorders within the film. The S-σ relationship in many doped polymers has recently been phenomenologically reproduced by a model considering an energy-dependent transport function (7). On the basis of the concept above, active control of the disorder effects on the charge transport process is a fundamental approach to control P through the modification of the empirical S-σ relationship.
Here, we demonstrate that the empirical S-σ relationship of conducting polymer can indeed be modified through the controlled carrier doping. We focus on poly[2,5-bis(3-alkylthiophen-2-yl)thieno(3,2-b)thiophene] (PBTTT) as a target polymer since it exhibits the highest conductivity of 1300 S/cm among solution-processable semicrystalline polymers via chemical carrier doping with 4-ethylbenzenesulfonic acid (11), indicating that the doped PBTTT is one of the key materials which are minimally affected by disorders. Actually, we have previously demonstrated that the macroscopic insulator-to-metal transition is induced in the PBTTT thin film by increasing the doping level using the electrolyte gating technique (12). Unlike the conventional transistors using the solid gate insulator (13, 14), the present technique can continuously control the doping level of conducting polymers up to very high concentrations through an electrochemical process (12, 15–20). Thus, the electrolyte-gated PBTTT provides a suitable platform to completely understand the thermoelectric properties of PBTTT including the metallic state.
In the present study, we observed the maximum P in PBTTT around the insulator-to-metal transition upon carrier doping. In addition, we carefully examined the structural/energetic disorder induced by electrochemical doping by using x-ray diffraction and electron spin resonance (ESR) measurements. A disorder-free film enables the metallic charge transport process in a highly doped state, where the S-σ relation is well described by the Mott equation, providing the maximum P at the boundary with the nonmetallic region exhibiting the empirical S ∝ σ−1/s relation.
RESULTS
Thermoelectric properties of PBTTT thin films doped by electrolyte gating
Figure 1 (A and B) shows a schematic illustration of the experimental setup, which enables simultaneous measurements of S and σ upon carrier doping (18), and a photograph of the thin-film transistor (TFT) structure of PBTTT, respectively. The TFT device was formed on top of a glass substrate with an ionic-liquid gate insulator as described in Materials and Methods. The carrier concentration can be continuously controlled by applying the gate voltage (Vg) throughout the electrochemical doping process, where the dopant ions infiltrate the bulk film. σ is determined from the current-voltage characteristics obtained under the application of Vg, as shown in Fig. 1C. S is determined from the slope of the thermoelectromotive force (ΔV) versus the temperature difference (ΔT) between the electrodes (S = ΔV/ΔT) for each Vg, as shown in Fig. 1D.
Fig. 1. Simultaneous measurements of S and σ by using the ionic-liquid–gated TFT structure.
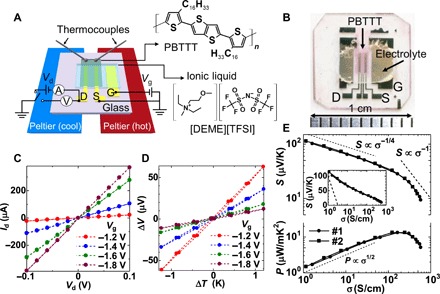
(A) Schematic illustration of the measurement system for the thermoelectric properties under electrolyte gating together with the chemical structures of PBTTT and the ionic liquid [DEME][TFSI]. The ionic-liquid–gated TFT is mounted between two Peltier devices, and the induced temperature difference (ΔT) between the S/D electrodes is monitored by two thermocouples. (B) A photograph of the ionic-liquid–gated TFT. (C) An example of the drain current (Id)–drain voltage (Vd) characteristics. (D) An example of the thermoelectromotive force (ΔV) measurement with respect to ΔT under the application of the gate voltage (Vg). (E) Electrical conductivity (σ) dependence of the Seebeck coefficient (S) and the thermoelectric power factor (P) obtained with the electrolyte gating technique. The dashed lines represent the S ∝ σ−1/4 relation and P ∝ σ1/2 relation expected from the empirical relation, as well as the S ∝ σ−1 relation expected from the Mott equation. The inset shows the S-log σ (Jonker) plot with a dashed line corresponding to the case of the conventional thermally activated process. Photo credit: K. Kanahashi, Waseda University.
Figure 1E shows the σ dependence of S (top) and P (bottom) obtained for two independent devices at room temperature. We obtained highly reproducible data between the two devices with rather small data dispersion due to the continuous carrier doping by the electrolyte gating technique. The observed shape of the S-σ relation is reversible unless Vg exceeds the degradation threshold of device operation (fig. S1). We immediately notice that P exhibits a clear maximum above approximately 100 S/cm. Although there have been a few reports on doped PBTTT showing an indistinct signature of a maximum P value, no physical background of this behavior has yet been clarified (19, 20). In general, the formation of a maximum P is expected in the following two cases: The first case is the conventional nondegenerate semiconductors, where the S-σ relation is described by the logarithmic relation of S ∝ ln σ (see section S1) (21, 22). In this case, the S-σ relation becomes linear in the S versus log σ plot (Jonker plot) with an absolute slope of 198 μV/K, which is shown by the dashed line in the inset of Fig. 1E. However, the observed slope of the Jonker plot is much smaller than the expected value, as previously reported for doped polyaniline and polypyrrole (23). Furthermore, we observe that the slope of the Jonker plot exhibits gradual changes around σ ~ 10 and 100 S/cm, indicating that the conventional thermally activated process cannot simply explain our experimental data. In the second case, it has been pointed out that a maximum P tends to be observed if the electronic state changes from nondegenerate to degenerate states upon carrier doping (24, 25). In this case, the S-σ relation (or P-σ relation) can be divided into two regions at the doping level giving the maximum P, reflecting the fundamental change in the electronic properties of the doped materials. The S-σ relation observed in Fig. 1E follows the empirical trend of S ∝ σ−1/4 (or P ∝ σ1/2) in the low-conductivity region (σ < 100 S/cm), whereas it deviates from this relation as σ increases, approaching the S ∝ σ−1 relation, as shown by the dashed lines in Fig. 1E. The inverse relation of S ∝ σ−1 is, in fact, expected from the Mott equation derived for the degenerate (or metallic) states (see section S1) (22, 26).
In the following, we consider the feasibility of the above scenario from the viewpoints of the structure, microscopic electronic states, and macroscopic transport properties of the doped PBTTT films. Since the electrochemical doping process involves the infiltration of dopant ions into the film, we first examine the possibility of structural modification of the molecular arrangement during the doping process, which can affect the thermoelectric properties. For this purpose, we carried out grazing incidence x-ray diffraction (GIXD) experiments on the doped polymer film as described below.
X-ray structural analyses of doped PBTTT thin films
Figure 2 summarizes the results of GIXD experiments obtained from ex situ measurements (see Materials and Methods). Similar results obtained from in situ measurements are also shown in fig. S2. In the pristine film (Vg = 0 V), we observed clear out-of-plane (h00) scattering peaks corresponding to the lamellar structure up to the fourth order, as well as an in-plane (010) peak corresponding to π-π stacking, indicating the highly crystalline nature of the PBTTT thin film (27). Atomic force microscopy (AFM) imaging of the film surface also supports the high crystallinity (fig. S3). Upon carrier doping, the peak profiles exhibit clear changes, which are shown in Fig. 2 (B and D) for the (100) peak and Fig. 2 (C and E) for the (010) peak. The scattering vector qz of the (100) peak shifts to lower values continuously as |Vg| increases due to the expansion of the interlamellar distance from 23.3 Å at Vg = 0 V to 29.4 Å at Vg = −1.6 V, as shown in Fig. 2D. This expansion is caused by the intercalation of the bis(trifluoromethanesulfonyl)imide (TFSI) anions within the film, which has also been reported for 2,3,5,6-tetrafluoro-7,7,8,8-tetracyanoquinodimethane (F4-TCNQ)–doped PBTTT (28) or TFSI-doped poly(3-hexylthiophene) (P3HT) (29, 30). Compared to those in previous studies, however, the increase in the lattice spacing in the present case is much larger (~6 Å), which is close to the length of the TFSI anion of ~8.0 Å (long axis) (31). This result implies that the TFSI molecules are located in the interlamellar position to form an end-to-end configuration with alkyl side chains, as schematically illustrated in Fig. 2F. Note that even with such a large lattice expansion, we observe no line broadening of the diffraction peaks, as shown in Fig. 2D, indicating that the crystallinity of the lamellar structure is not degraded by anion intercalation. Furthermore, the anion intercalation takes place reversibly as evidenced by the fact that the lattice spacing recovers close to the initial value when we apply a positive voltage after the doping, which is confirmed by the in situ measurements shown in fig. S2B. The time scale of the doping/dedoping process is more than 20 min, judging from the reversibility of the GIXD data. This slow process causes a large hysteresis of σ with respect to the upward and downward Vg scans as shown in the insets of fig. S1. However, if we focus on the S-σ relation in fig. S1B, then no hysteresis is observed, indicating that the ion infiltration does not cause any irreversible damage to the film.
Fig. 2. GIXD measurements of the PBTTT thin film under electrolyte gating.
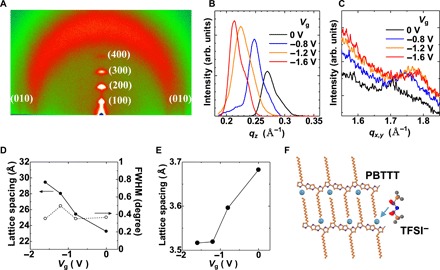
(A) GIXD patterns obtained from the pristine PBTTT film on a glass substrate. (B) Vg dependence of the (100) peak and (C) (010) peak obtained by ex situ measurements, where the ionic-liquid film is removed before the measurements after the application of Vg. (D) The Vg dependence of the interlamellar distance obtained from the (100) peak position and the full width at half maximum (FWHM) of the corresponding peaks. (E) π-π stacking distance obtained from the (010) peak position. (F) Schematic illustration of the molecular arrangements in the doped film, where the TFSI anions are located in the alkyl chain regions.
In addition, we also observe a clear shift in the scattering vector qxy of the (010) peak to higher values upon doping, indicating the contraction of the π-π stacking distance, as shown in Fig. 2 (C and E). Similar contraction has also been reported in electrolyte-gated P3HT thin films (29, 30). A recent density functional theory (DFT) calculation suggests that interchain polaron delocalization through π-π stacking can be a possible origin of such contraction in doped P3HT (32). The present GIXD measurements strongly suggest that the system exhibits no structural degradation upon doping, indicating that the deviation of the S-σ relation from the empirical trend in Fig. 1E does not originate from the modification of the crystallinity by doping. Then, we consider the change in the electronic state or charge transport properties induced by doping. First, we discuss below the change in the electronic state within the crystalline domains observed by ESR spectroscopy.
ESR measurements of doped thin films
Figure 3A shows a schematic illustration of the ionic-liquid–gated TFT device, which enables simultaneous ESR and conductivity measurements under the application of Vg (33). By applying a negative Vg to the device, we observe a clear ESR signal of positive carriers (polarons) on the PBTTT chain, as shown in Fig. 3B. The ESR signal is observed with a g value of 2.003 independent of the Vg value when we apply an external magnetic field (H) perpendicular to the substrate. This result indicates that the carriers reside in the edge-on oriented region, as shown in Fig. 3C, consistent with the GIXD results showing no crystalline degradation in the doped film (see also section S5).
Fig. 3. ESR measurements of the PBTTT thin film under electrolyte gating.
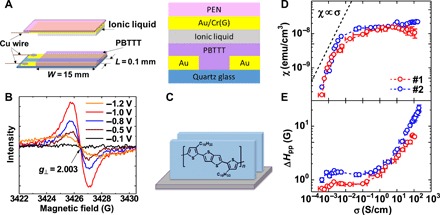
(A) Schematic illustration of the top-gate bottom contact TFT structure adopted for the ESR measurements under electrolyte gating. Two substrates with a polymer film and an ionic-liquid film on each of them are laminated to form a staggered TFT structure. (B) ESR signal obtained under the application of Vg with a magnetic field (H) perpendicular to the substrate. The background signal at Vg = +1 V was subtracted from all the data. (C) Schematic illustration of the edge-on oriented molecules. (D) σ dependence of the spin susceptibility χ obtained from the integrated ESR intensity. (E) Peak-to-peak ESR linewidth (ΔHpp). The dashed line in (D) shows a guide to the χ ∝ σ relation.
From the integrated intensity of the ESR signal, we determined the spin susceptibility χ of the doped film. Figure 3D shows the plot of χ with respect to σ obtained simultaneously with the ESR measurements. In the low-conductivity region, we observe a steep increase in χ as σ increases. In the lightly doped regions, where polarons are magnetically isolated, the spin susceptibility follows the Curie law of χ = Ng2μB2S(S + 1)/3kBT, where N is the total spin number. In this case, the spin susceptibility is proportional to the carrier concentration n, and then, the relation χ ∝ σ is expected under the assumption of constant mobility. This relation is indeed observed in the very low-conductivity region of σ < 0.01 S/cm in Fig. 3D, indicating that the isolated polarons dominate the charge transport through the hopping process. In this case, it is well documented that the ESR linewidth is governed by the hyperfine interaction with neighboring proton nuclei (see also fig. S4A), which is independent of n (33, 34). This phenomenon is consistent with the fact that the peak-to-peak ESR linewidth (ΔHpp) exhibits almost no σ dependence in the low-conductivity region, as shown in Fig. 3E.
Above σ ~ 1 S/cm, on the other hand, we observe clear line broadening, as shown in Fig. 3E, indicating qualitatively different spin dynamics in this region. Similar line broadening has also been observed in our previous ESR measurements of doped PBTTT (33, 35), and the origin of this behavior is reasonably ascribed to the Elliott mechanism of conduction electrons (36). In this case, the spin-flip scattering of the conduction electrons by phonons determines the spin relaxation time, causing the broadening of the linewidth. Since the spin-phonon interaction is mediated by spin-orbit coupling, similar to the g-shift (Δg) from the free electron g value (2.0023), the linewidth in this process strongly correlates with the g value according to the relation of ΔHpp ∝ (Δg)2/τ, where τ denotes the spin-flip scattering time (37). A positive correlation between the g value and linewidth is observed in the angular dependence of the g value and linewidth, as shown in fig. S4, in the region of σ > 1 S/cm, strongly supporting that the carriers start to delocalize. This fact indicates that the energetic disorder, which tends to result in trap-limited charge transport, does not dominate the transport process within the crystalline domain above 1 S/cm.
When the delocalized carriers form the degenerate (or metallic) state upon doping, the Curie law no longer holds, and Pauli spin susceptibility is expected. In this case, χ is proportional to the density of states at the Fermi energy level, not to n (38). We have previously confirmed that temperature-independent Pauli spin susceptibility is indeed observed in highly doped PBTTT using the electrolyte gating technique, although the σ dependence of χ was absent (33). In the present study, we observe that the increase in χ almost saturates as σ increases above 1 S/cm, which involves line broadening due to carrier delocalization. This observation is the microscopic signature of the formation of the degenerate (or metallic) electronic state within the edge-on oriented domains. The present ESR parameters exhibit no prominent anomalies around σ ~ 100 S/cm, where the S-σ relation shows deviation from the S ∝ σ−1/4 relation in Fig. 1E, although the line broadening causes relatively large errors in estimating χ in this region. This finding indicates that the thermoelectric property changes independently of the microscopic electronic state within the domains. We then examine the change in macroscopic charge transport processes upon carrier doping, as discussed below.
Macroscopic charge transport properties of doped films
Figure 4A shows the temperature dependence of σ obtained at various Vg values. We observe a clear increase in the room temperature conductivity (σRT) as |Vg| increases. A region exhibiting a negative temperature gradient (dσ/dT < 0), indicating the metallic state, appears in the high |Vg| region. Metallic behavior is observed even below 200 K at |Vg| > 1.7 V, which is lower than the freezing temperature of the electrolyte, indicating that the appearance of metallic behavior is not an artificial effect due to the mobile ions. Although the conductivity exhibits nonmetallic behavior at low temperatures, the crossover temperature shifts toward lower temperature sides as |Vg| increases, indicating that the metallic state becomes more stabilized as the doping level increases. We further confirm the formation of the metallic state from the magnetoresistance measurements at Vg = −2.2 V and 150 K. The result is shown in Fig. 4B with H perpendicular to the substrate. We observe a small but finite positive magnetoresistance (Δρ = ρ(H) − ρ (0)) following the simple quadratic relation of Δρ ∝ H2, characteristic of the metallic state. No signatures of weak localization or variable-range hopping mechanisms are observed in Fig. 4B, in contrast to the case of doped PBTTT exhibiting nonmetallic conductivities (dσ/dT > 0) (28). These findings strongly indicate that the present PBTTT undergoes a macroscopic metallic transition through the electrolyte gating technique at high temperatures. Further details of the macroscopic charge transport processes, especially for low-temperature insulating state, will be published elsewhere.
Fig. 4. Macroscopic charge transport measurements of doped PBTTT thin films.
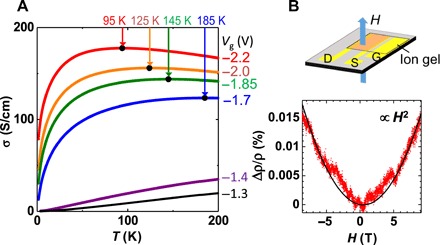
(A) Temperature dependence of σ obtained under the application of Vg. The arrows and filled data points indicate the position of the conductivity maximum. (B) Magnetic field dependence of the magnetoresistance ratio (Δρ/ρ) obtained under Vg = −2.2 V at 150 K. The magnetic field is applied perpendicular to the film plane, as illustrated in the figure. The solid curve shows the fitting of the experimental data by the quadratic relation of H.
Relation between the charge transport and thermoelectric properties
Figure 5A summarizes the room temperature S-σ relations obtained in the present study together with those reported by other groups with different doping methods and dopants (5, 8, 9, 19, 20). The information about the electronic state and the charge transport process, found as described above, is also included in the figure. We immediately notice that the conductivity at which the S-σ relation deviates from the empirical trend agrees fairly well with the conductivity at which metallic transport properties are observed, i.e., σRT ~ 100 S/cm. This finding strongly supports that the S ∝ σ −1 relation observed in the high-conductivity region indeed follows the Mott equation, reflecting the metallic nature of the system. In contrast, σ exhibits a nonmetallic temperature dependence in the region of σRT < 100 S/cm, although the microscopic electronic state within the crystalline domain is metallic above 1 S/cm. This result indicates that the macroscopic charge transport process is mainly limited by structural inhomogeneity, such as domain boundaries, not by the charge trapping within the crystallites. The empirical relation of S ∝ σ−1/4 seems to be observed in this case independent of the microscopic electronic states, such as the degenerate state, nondegenerate state, or isolated polarons. We stress here that the maximum power factor appears at the boundary of the macroscopically metallic state and the nonmetallic state in the doped PBTTT film.
Fig. 5. Relation of thermoelectric properties and charge transport processes.
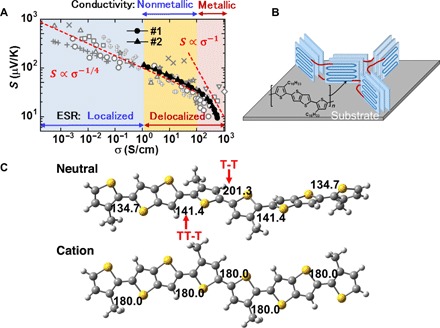
(A) S-σ relations obtained in the present study together with data reported by other groups using different doping methods and dopants (5, 8, 9, 19, 20). The information about the microscopic electronic state obtained from the ESR measurements, as well as the macroscopic transport properties obtained by the temperature dependence of σ, is also shown. The dashed lines represent the same information as in Fig. 1E. (B) Schematic illustration of the ordered (or crystalline) domains and the domain boundaries in the PBTTT thin film. Adjacent domains are connected by tie molecules, shown in red, which enable macroscopic charge transport. (C) Structural optimization of the dimer unit in a single PBTTT chain in the neutral (top) and cationic (bottom) states. The numbers are dihedral angles between the adjacent subunits of thiophene (T) and thienothiophene (TT).
Here, we discuss how macroscopic metallic transport becomes possible by electrolyte gating of the present polycrystalline PBTTT film. It is widely accepted that the macroscopic charge transport process in polycrystalline polymer films is mediated by tie molecules between the crystalline domains, as schematically illustrated in Fig. 5B (39, 40). In this case, the local structure of the tie molecules crucially affects the transport process. We then carried out the structural optimization of the neutral and cationic states of an isolated PBTTT molecule by DFT calculation considering the dimer units. As in the case of a similar optimization reported previously (41), the PBTTT backbone in the neutral state tends to show a large torsion at the thiophene-thienothiophene bonds, as shown in Fig. 5C (top), which should limit the on-chain charge transport of the tie molecule and thus the interdomain transport. However, the optimized structure in the cationic state shown in Fig. 5C (bottom) exhibits perfect planarity with C2h symmetry. In addition, the structure becomes more resilient to conformational disorder than the structure in the neutral state as demonstrated in fig. S5. The planar molecules enable highly efficient interdomain connection (40–44), which may explain the metallic transition observed in the present study. However, the domain connection by tie molecules should be quite sensitive to the doping condition, presumably due to the structural/energetic disorder of the isolated tie molecules induced by the dopant. The metallic behavior in the present study using a thin ion gel insulator is observed down to much lower temperatures than those in our previous report using a thick and viscous ionic-liquid insulator (12). This finding is also consistent with the fact that the metallic temperature dependence of σ is not commonly observed in the PBTTT thin films, although highly sophisticated doping methods are adopted (28, 45). We conclude that moderate doping by the present electrolyte gating technique enables efficient interconnection of the crystalline domains, resulting in the macroscopic metallic transition to give the maximum P in the PBTTT thin film.
DISCUSSION
The present results demonstrate that the thermoelectric power factor in conducting polymers can be maximized by careful doping; the electrolyte gating technique enables moderate control of the carrier concentration without inducing structural/energetic disorder, resulting in modification of the macroscopic transport properties from inhomogeneous nonmetallic transport limited by domain boundaries to homogeneous metallic transport mediated by the rigid tie molecules connecting the adjacent domains. The maximum power factor is observed at the boundary of these transport processes.
The above scenario will be further supported if we obtain the temperature dependence of the Seebeck coefficient at various doping concentrations, which provides detailed information of the charge transport mechanism (1, 14, 41). These measurements are now under preparation. Furthermore, evaluation of the thermal conductivity is essential to determine the thermoelectric figure of merit ZT (46, 47). The combined research using this information provides further physical background for designing high-performance polymer-based thermoelectric devices for future energy harvesting technologies.
MATERIALS AND METHODS
Sample preparation
Samples of PBTTT with hexadecyl side chains (Mw = 73,700 to 82,800) were purchased from Merck Co. Ltd. The electrolyte-gated TFT structure for the measurements of thermoelectric properties was fabricated on a glass substrate (Corning XG) with typical dimensions of 1 mm by 1 mm by 0.5 mm cleaned by sonicating in deionized water, acetone, and 2-propernol for 5 min each. The substrate was then treated with octyltrichlorosilane vapor to form a hydrophobic surface. The polymer layer was then fabricated by spin-coating o-dichlorobenzene solution (7.5 mg/ml; 2000 rpm for 120 s), followed by annealing (180°C, 30 min) on the substrate patterned with Cr (3 nm)/Au (30 nm) gate/source/drain electrodes. Last, the ionic-liquid film was fabricated by drop-casting [N,N-diethyl-N-methyl-N-(2-methoxymethyl)ammonium][bis(trifluoromethanesulfonyl)imide] [(DEME)(TFSI)] (Nisshinbo Holdings Inc.) on the device to form the side-gate TFT structure, as illustrated in Fig. 1A. The typical channel length (L) and channel width (W) were 400 μm and 2 mm, respectively.
For the ex situ GIXD measurements, we fabricated the side-gate device structure as described above, except that the spin-coating condition of the PBTTT solution is slightly different (4000 rpm for 90 s). For the in situ GIXD measurements, we also adopted the side-gate device structure as mentioned above, except that we adopted an ion gel insulator. The acetone solution of [DEME][TFSI] and poly(vinylidene fluoride-co-hexafluoropropylene) with a 1:1 weight ratio was spin-coated (6000 rpm, 120 s) on a glass substrate. Upon evaporation of the solvent, a thin ion gel film with a typical thickness of ~1 μm was obtained. The ion gel film was delaminated from the substrate and then laminated on the polymer film formed on the electrode-patterned substrate instead of the drop of ionic liquid in the case of ex situ GIXD measurements.
For ESR measurements, we adopted a top-gate bottom contact (or staggered) device structure, as illustrated in Fig. 3A and reported previously (33). The polymer film was fabricated on a 3-mm by 30-mm quartz substrate patterned by Cr (5 nm)/Au (30 nm) source/drain electrodes. L and W are 100 μm and 15 mm, respectively. The ionic-liquid film was separately formed on a polyethylene naphthalate substrate patterned with a Cr (3 nm)/Au (30 nm) gate electrode by drop-casting an ethyl acetate solution of [DEME][TFSI] and poly(methyl methacrylate) (Mw = 120,000; Aldrich Co. Ltd.) with a weight ratio of 9:1. Last, these two substrates were laminated with each other and sealed into an ESR sample tube.
For determination of the temperature dependence of the conductivity and magnetoresistance measurements, we fabricated side-gate TFTs with a thin ion gel insulator as described above. The polymer film was fabricated by spin-coating (4000 rpm for 90 s), followed by annealing at 215°C for 20 min and subsequent slow cooling. L and W were 40 μm and 2 mm, respectively. By using a thin ion gel insulator with a typical thickness of 1 μm, the surface tension at the polymer/ion gel interface produced by different thermal expansion coefficients is minimized, which is necessary to avoid sample cracking during low-temperature measurements.
Device characterization
Thermoelectric properties were measured at room temperature as follows. The electrolyte-gated TFT was mounted between two Peltier elements to give a temperature gradient. The electrical conductivity was determined from the current-voltage characteristics obtained by the two-probe method under the application of Vg. The Seebeck coefficient was determined from the linear slope of the thermoelectromotive force (ΔV) versus the temperature difference (ΔT) induced between the source and drain electrodes for each Vg value. The ΔT was measured by two thermocouples (K type, ϕ = 100 μm). Note that the linearity of the ΔV-ΔT slope was degraded when the channel resistance was high in the low |Vg| region, possibly due to the voltage drop caused by the small leakage current. Thus, the Seebeck coefficient in the low-conductivity region of σ < 1 S/cm was not measured in the present study.
GIXD measurements were performed using a Rigaku FR-E Micro-focus High Intensity X-ray generator system with a CuKa x-ray source (λ = 1.5418 Å) at the High Intensity X-ray Diffraction Laboratory at Nagoya University. The in-plane and out-of-plane diffractions were detected by an imaging plate. Ex situ measurements were carried out by removing the ionic liquid before the GIXD measurements after the application of each Vg for ~15 min. After the GIXD measurements, the ionic liquid was dropped again, and the next Vg was applied. The in situ measurements were carried out with the ion gel film formed on top of the polymer film during the application of Vg. The incident x-ray was irradiated on the polymer film surface through the ionic-liquid layer.
ESR measurements were performed using a Bruker E-500 spectrometer. A TE011 cylindrical cavity with a high-quality factor was adopted for highly sensitive measurements. The magnetic field was determined with an accuracy of ±0.01 G using a nuclear magnetic resonance teslameter. The spin susceptibility was determined by twice integration of the first-derivative ESR signal calibrated according to that of CuSO4·5H2O.
The temperature dependence of the conductivity and the magnetoresistance measurements were performed by using a physical property measurement system (PPMS) (model 6000, Quantum Design). The gate voltage was applied at room temperature. After waiting until the gate current falls to a stationary value (typically 20 min), the sample was cooled at a rate of 5 K/min down to 180 K. The conductivity above 180 K was measured by the pseudo-four-probe method under the application of Vg. The current-voltage characteristics were measured by using an Agilent B1500A semiconductor parametric analyzer, whereas the voltage drop between the source-drain electrodes was monitored by a nanovoltmeter (Hewlett-Packard 34420A). Below 180 K, where the ion gel is frozen, the cooling rate was reduced to 0.3 to 0.5 K/min, and the conductivity was directly measured by the PPMS system without applying Vg because the doping level is maintained in this case. The magnetoresistance was measured under a magnetic field applied perpendicular to the film.
DFT calculation
DFT calculations of the optimized structures of the dimer units were performed with the B3LYP functional and 6-311G(d, p) basis set. The alkyl side chains were replaced by methyl units. The calculations were carried out using the Gaussian 16 software package (48).
Supplementary Material
Acknowledgments
We thank T. Hikage for support with the x-ray diffraction experiments. Funding: This work was financially supported by Grant-in-Aid for Scientific Research (JP17H01069 and 19K22127) and a Grant-in-Aid for Scientific Research on Innovative Areas (JP26102012) from the Japan Society for the Promotion of Science (JSPS) and by JST CREST (JPMJCR17I5). This work was performed under the Cooperative Research Program of “Network Joint Research Center for Materials and Devices” from MEXT. Author contributions: H.O. designed the experimental setup of the Seebeck measurements. K.K. and N.T. measured the Seebeck coefficient and the electrical conductivity under electrolyte gating at room temperature. N.T. carried out the ESR and AFM measurements. H.M. performed GIXD, determined the temperature dependence of the conductivity, and carried out the magnetoresistance measurements. Y.S. carried out the DFT calculations. H.I. and H.T. designed the total experiments. H.T. wrote the manuscript with input from all co-authors. T.T. supervised the project. All authors discussed the results and approved the manuscript draft. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the corresponding authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/7/eaay8065/DC1
Section S1. S-σ relations expected for conventional semiconductors and metals
Section S2. Effects of high Vg on the transport and thermoelectric properties
Section S3. In situ GIXD measurements during the application of Vg
Section S4. AFM imaging of the PBTTT thin film
Section S5. Anisotropy of the ESR parameters
Section S6. DFT calculation of backbone rigidity in the neutral and cationic states
Fig. S1. Thermoelectric properties of the electrolyte-gated PBTTT thin films.
Fig. S2. In situ GIXD measurements of electrolyte-gated PBTTT thin films.
Fig. S3. AFM imaging of the PBTTT thin film.
Fig. S4. Angular dependence of the ESR parameters at various doping levels.
Fig. S5. DFT calculation of the torsion potential.
REFERENCES AND NOTES
- 1.Bubnova O., Crispin X., Towards polymer-based organic thermoelectric generators. Energ. Environ. Sci. 5, 9345–9362 (2012). [Google Scholar]
- 2.Bahk J.-H., Fang H., Tazawa K., Shakouri A., Flexible thermoelectric materials and device optimization for wearable energy harvesting. J. Mater. Chem. C 3, 10362–10374 (2015). [Google Scholar]
- 3.Bharti M., Singh A., Samanta S., Aswal D. K., Conductive polymers for thermoelectric power generation. Prog. Mater. Sci. 93, 270–310 (2018). [Google Scholar]
- 4.Kaiser A. B., Thermoelectric power and conductivity of heterogeneous conducting polymers. Phys. Rev. B 40, 2806–2813 (1989). [DOI] [PubMed] [Google Scholar]
- 5.Glaudell A. M., Cochran J. E., Patel S. N., Chabinyc M. L., Impact of the doping method on conductivity and thermopower in semiconducting polythiophenes. Adv. Energy Mater. 5, 1401072 (2015). [Google Scholar]
- 6.Abdalla H., Zuo G., Kemerink M., Range and energetics of charge hopping in organic semiconductors. Phys. Rev. B 96, 241202(R) (2017). [Google Scholar]
- 7.Kang S. D., Snyder G. J., Charge-transport model for conducting polymers. Nat. Mater. 16, 252–257 (2017). [DOI] [PubMed] [Google Scholar]
- 8.Patel S. N., Glaudell A. M., Peterson K. A., Thomas E. M., O’Hara K. A., Lim E., Chabinyc M. L., Morphology controls the thermoelectric power factor of a doped semiconducting polymer. Sci. Adv. 3, e1700434 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Thomas E. M., Popere B. C., Fang H., Chabinyc M. L., Segalman R. A., Role of disorder induced by doping on the thermoelectric properties of semiconducting polymers. Chem. Mater. 30, 2965–2972 (2018). [Google Scholar]
- 10.Gregory S. A., Menon A. K., Ye S., Seferos D. S., Reynolds J. R., Yee S. K., Effect of heteroatom and doping on the thermoelectric properties of poly(3-alkylchalcogenophenes). Adv. Energy Mater. 8, 1802419 (2018). [Google Scholar]
- 11.Kang K., Schott S., Venkateshvaran D., Broch K., Schweicher G., Harkin D., Jellett C., Nielsen C. B., McCulloch I., Sirringhaus H., Investigation of the thermoelectric response in conducting polymers doped by solid-state diffusion. Mater. Today Phys. 8, 112–122 (2019). [Google Scholar]
- 12.Harada T., Ito H., Ando Y., Watanabe S., Tanaka H., Kuroda S.-i., Signature of the insulator–metal transition of a semicrystalline conjugated polymer in ionic-liquid-gated transistors. Appl. Phys. Express 8, 021601 (2015). [Google Scholar]
- 13.Pernstich K. P., Rössener B., Batlogg B., Field-effect-modulated Seebeck coefficient in organic semiconductors. Nat. Mater. 7, 321–325 (2008). [DOI] [PubMed] [Google Scholar]
- 14.Venkateshvaran D., Kronemeijer A. J., Moriarty J., Emin D., Sirringhaus H., Field-effect modulated Seebeck coefficient measurements in an organic polymer using a microfabricated on-chip architecture. APL Mater. 2, 032102 (2014). [Google Scholar]
- 15.Panzer M. J., Frisbie C. D., High carrier density and metallic conductivity in poly(3-hexylthiophene) achieved by electrostatic charge injection. Adv. Funct. Mater. 16, 1051–1056 (2006). [Google Scholar]
- 16.Dhoot A. S., Yuen J. D., Heeney M., McCulloch I., Moses D., Heege A. J., Beyond the metal-insulator transition in polymer electrolyte gated polymer field-effect transistors. Proc. Natl. Acad. Sci. U.S.A. 103, 11834–11837 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kim S. H., Hong K., Xie W., Lee K. H., Zhang S., Lodge T. P., Frisbie C. D., Electrolyte-gated transistors for organic and printed electronics. Adv. Mater. 25, 1822–1846 (2013). [DOI] [PubMed] [Google Scholar]
- 18.Pu J., Kanahashi K., Cuong N. T., Chen C.-H., Li L.-J., Okada S., Ohta H., Takenobu T., Enhanced thermoelectric power in two-dimensional transition metal dichalcogenide monolayers. Phys. Rev. B 94, 014312 (2016). [Google Scholar]
- 19.Zhang Q., Sun Y., Xu W., Zhu D., What to expect from conducting polymers on the playground of thermoelectricity: Lessons learned from four high-mobility polymeric semiconductors. Macromolecules 47, 609–615 (2014). [Google Scholar]
- 20.Zhang F., Zang Y., Huang D., Di C.-a., Gao X., Sirringhaus H., Zhu D., Modulated thermoelectric properties of organic semiconductors using field-effect transistors. Adv. Funct. Mater. 25, 3004–3012 (2015). [Google Scholar]
- 21.G. D. Mahan, Good thermoelectrics, in Solid State Physics (Academic Press, 1998), vol. 51, chap. 2, pp. 81–157. [Google Scholar]
- 22.N. F. Mott, E. A. Davis, Electronic Processes in Non-Crystalline Materials (Clarendon, 1971). [Google Scholar]
- 23.Mateeva N., Niculescu H., Schlenoff J., Testardi L. R., Correlation of Seebeck coefficient and electric conductivity in polyaniline and polypyrrole. J. Appl. Phys. 83, 3111–3117 (1998). [Google Scholar]
- 24.Snyder G. J., Toberer E. S., Complex thermoelectric materials. Nat. Mater. 7, 105–114 (2008). [DOI] [PubMed] [Google Scholar]
- 25.Pei Y., Wang H., Snyder G. J., Band engineering of thermoelectric materials. Adv. Mater. 24, 6125–6135 (2012). [DOI] [PubMed] [Google Scholar]
- 26.Cutler M., Mott N. F., Observation of Anderson localization in an electron gas. Phys. Rev. 181, 1336–1340 (1969). [Google Scholar]
- 27.McCulloch I., Heeney M., Bailey C., Genevicius K., MacDonald I., Shkunov M., Sparrowe D., Tierney S., Wagner R., Zhang W., Chabinyc M. L., Kline R. J., McGehee M. D., Toney M. F., Liquid-crystalline semiconducting polymers with high charge-carrier mobility. Nat. Mater. 5, 328–333 (2006). [DOI] [PubMed] [Google Scholar]
- 28.Kang K., Watanabe S., Broch K., Sepe A., Brown A., Nasrallah I., Nikolka M., Fei Z., Heeney M., Matsumoto D., Marumoto K., Tanaka H., Kuroda S.-i., Sirringhaus H., 2D coherent charge transport in highly ordered conducting polymers doped by solid state diffusion. Nat. Mater. 15, 896–902 (2016). [DOI] [PubMed] [Google Scholar]
- 29.Guardado J. O., Salleo A., Structural effects of gating poly(3-hexylthiophene) through an ionic liquid. Adv. Funct. Mater. 27, 1701791 (2017). [Google Scholar]
- 30.Thomas E. M., Brady M. A., Nakayama H., Popere B. C., Segalman R. A., Chabinyc M. L., X-ray scattering reveals ion-induced microstructural changes during electrochemical gating of poly(3-hexylthiophene). Adv. Funct. Mater. 28, 1803687 (2018). [Google Scholar]
- 31.Beltrop K., Meister P., Klein S., Heckmann A., Grünebaum M., Wiemhöfer H.-D., Winter M., Placke T., Does size really matter? New insights into the intercalation behavior of anions into a graphite-based positive electrode for dual-ion batteries. Electrochim. Acta 209, 44–55 (2016). [Google Scholar]
- 32.Liu W., Müller L., Ma S., Barlow S., Marder S. R., Kowalsky W., Köhn A., Lovrincic R., Origin of the π−π spacing change upon doping of semiconducting polymer. J. Phys. Chem. C 122, 27983–27990 (2018). [Google Scholar]
- 33.Tanaka H., Nishio S., Ito H., Kuroda S.-i., Microscopic signature of insulator-to-metal transition in highly doped semicrystalline conducting polymers in ionic-liquid-gated transistors. Appl. Phys. Lett. 107, 243302 (2015). [Google Scholar]
- 34.Matsui H., Kumaki D., Takahashi E., Takimiya K., Tokito S., Hasegawa T., Correlation between interdomain carrier hopping and apparent mobility in polycrystalline organic transistors as investigated by electron spin resonance. Phys. Rev. B 85, 035308 (2012). [Google Scholar]
- 35.Tanaka H., Hirate M., Watanabe S., Kuroda S.-i., Microscopic signature of metallic state in semicrystalline conjugated polymers doped with fluoroalkylsilane molecules. Adv. Mater. 26, 2376–2383 (2014). [DOI] [PubMed] [Google Scholar]
- 36.Elliott R. J., Theory of the effect of spin-orbit coupling on magnetic resonance in some semiconductors. Phys. Rev. 96, 266–279 (1954). [Google Scholar]
- 37.Beuneu F., Monod P., The Elliott relation in pure metals. Phys. Rev. B 18, 2422–2425 (1978). [Google Scholar]
- 38.H. G. Kiess, Conjugated Conducting Polymers (Springer-Verlag, 1992). [Google Scholar]
- 39.Noriega R., Rivnay J., Vandewal K., Koch F. P. V., Stingelin N., Smith P., Toney M. F., Salleo A., A general relationship between disorder, aggregation and charge transport in conjugated polymers. Nat. Mater. 12, 1038–1044 (2013). [DOI] [PubMed] [Google Scholar]
- 40.Son S. Y., Kim Y., Lee J., Lee G.-Y., Park W.-T., Noh Y.-Y., Park C. E., Park T., High-field-effect mobility of low-crystallinity conjugated polymers with localized aggregates. J. Am. Chem. Soc. 138, 8096–8103 (2016). [DOI] [PubMed] [Google Scholar]
- 41.Venkateshvaran D., Nikolka M., Sadhanala A., Lemaur V., Zelazny M., Kepa M., Hurhangee M., Kronemeijer A. J., Pecunia V., Nasrallah I., Romanov I., Broch K., McCulloch I., Emin D., Olivier Y., Cornil J., Beljonne D., Sirringhaus H., Approaching disorder-free transport in high-mobility conjugated polymers. Nature 515, 384–388 (2014). [DOI] [PubMed] [Google Scholar]
- 42.Sirringhaus H., 25th Anniversary Article: Organic field-effect transistors: The path beyond amorphous silicon. Adv. Mater. 26, 1319–1335 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Himmelberger S., Salleo A., Engineering semiconducting polymers for efficient charge transport. MRS Commun. 5, 383–395 (2015). [Google Scholar]
- 44.Tanaka H., Wakamatsu A., Kondo M., Kawamura S., Kuroda S.-i., Shimoi Y., Park W.-T., Noh Y.-Y., Takenobu T., Microscopic observation of efficient charge transport processes across domain boundaries in donor-acceptor-type conjugated polymers. Commun. Phys. 2, 96 (2019). [Google Scholar]
- 45.Shi W., Ye J., Checkelsky J. G., Terakura C., Iwasa Y., Transport properties of polymer semiconductor controlled by ionic liquid as a gate dielectric and a pressure medium. Adv. Funct. Mater. 24, 2005–2012 (2014). [Google Scholar]
- 46.Wu J., Sun Y., Pei W.-B., Huang L., Xu W., Zhang Q., Polypyrrole nanotube film for flexible thermoelectric application. Synth. Met. 196, 173–177 (2014). [Google Scholar]
- 47.Yao C.-J., Zhang H.-L., Zhang Q., Recent progress in thermoelectric materials based on conjugated polymers. Polymers 11, e107 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, D. J. Fox, Gaussian16, Rev A.03 (Gaussian Inc., 2016).
- 49.Fritzsche H., A general expression for the thermoelectric power. Solid State Commun. 9, 1813–1815 (1971). [Google Scholar]
- 50.Paulsen B. D., Frisbie C. D., Dependence of conductivity on charge density and electrochemical potential in polymer semiconductors gated with ionic liquids. J. Phys. Chem. C 116, 3132–3141 (2012). [Google Scholar]
- 51.Yamamoto J., Furukawa Y., Raman characterization and electrical properties of poly(3-hexylthiophene) doped electrochemically in an ionic liquid-gated transistor geometry. Org. Electron. 28, 82–87 (2016). [Google Scholar]
- 52.Furukawa Y., Akiyama K., Enokida I., Yamamoto J., Raman spectra of carriers in ionic-liquid-gated transistors fabricated with poly(2,5-bis(3-tetradecylthiophen-2-yl)thieno[3,2-b]thiophene). Vib. Spectrosc. 85, 29–34 (2016). [Google Scholar]
- 53.DeLongchamp D. M., Kline R. J., Jung Y., Germack D. S., Lin E. K., Moad A. J., Richter L. J., Toney M. F., Heeney M., McCulloch I., Controlling the orientation of terraced nanoscale "ribbons" of a poly(thiophene) semiconductor. ACS Nano 3, 780–787 (2009). [DOI] [PubMed] [Google Scholar]
- 54.Umeda T., Tokito S., Kumaki D., High-mobility and air-stable organic thin-film transistors with highly ordered semiconducting polymer films. J. Appl. Phys. 101, 054517 (2007). [Google Scholar]
- 55.Marumoto K., Muramatsu Y., Nagano Y., Iwata T., Ukai S., Ito H., Kuroda S.-i., Shimoi Y., Abe S., Electron spin resonance of field-induced polarons in regioregular poly(3-alkylthiophene) using metal-insulator-semiconductor diode structures. J. Phys. Soc. Jpn. 74, 3066–3076 (2005). [Google Scholar]
- 56.Watanabe S.-i., Tanaka H., Kuroda S.-i., Toda A., Nagano S., Seki T., Kimoto A., Abe J., Electron spin resonance observation of field-induced charge carriers in ultrathin-film transistors of regioregular poly(3-hexylthiophene) with controlled in-plane chain orientation. Appl. Phys. Lett. 96, 173302 (2010). [Google Scholar]
- 57.Tanaka H., Hirate M., Watanabe S.-i., Kaneko K., Marumoto K., Takenobu T., Iwasa Y., Kuroda S.-i., Electron spin resonance observation of charge carrier concentration in organic field-effect transistors during device operation. Phys. Rev. B 87, 045309 (2013). [Google Scholar]
- 58.Pedersen H. J., Scott J. C., Bechgaard K., Electron-spin-resonance studies of a family of organic conductors. Phys. Rev. B 24, 5014–5025 (1981). [Google Scholar]
- 59.Enoki T., Imaeda K., Kobayashi M., Inokuchi H., Saito G., ESR studies of organic conductors with bis(ethylenedithio)tetrathiafulvalene (BEDT-TTF), (BEDT-TTF)2ClO4(C2H3C13)0.5, and (BEDT-TTF)3(ClO4)2, and their two-dimensionality. Phys. Rev. B 33, 1553–1558 (1986). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/7/eaay8065/DC1
Section S1. S-σ relations expected for conventional semiconductors and metals
Section S2. Effects of high Vg on the transport and thermoelectric properties
Section S3. In situ GIXD measurements during the application of Vg
Section S4. AFM imaging of the PBTTT thin film
Section S5. Anisotropy of the ESR parameters
Section S6. DFT calculation of backbone rigidity in the neutral and cationic states
Fig. S1. Thermoelectric properties of the electrolyte-gated PBTTT thin films.
Fig. S2. In situ GIXD measurements of electrolyte-gated PBTTT thin films.
Fig. S3. AFM imaging of the PBTTT thin film.
Fig. S4. Angular dependence of the ESR parameters at various doping levels.
Fig. S5. DFT calculation of the torsion potential.


