The Nernst effect in Corbino geometry

Significance

The Nernst effect consists in the induction of an electric current by a combined effect of the external magnetic field and the temperature gradient. We consider a Corbino disk geometry, where the temperature difference is applied between the outer and inner edges of the disk, while the magnetic field is perpendicular to the plane of the disk. We show that the circular diamagnetic currents flowing along the edges of the disk are the oscillatory functions of the filling factor of Landau levels of the electron gas in the disk. The Corbino geometry offers a unique opportunity for observation of the magnetization currents that have a purely thermodynamic nature, e.g., are independent of the conductivity of the sample.

Abstract

We study the manifestation of the Nernst effect in the Corbino disk subjected to the normal external magnetic field and to the radial temperature gradient. The Corbino geometry offers a precious opportunity for the direct measurement of the magnetization currents that are masked by kinetic contributions to the Nernst current in the conventional geometry. The magnetization currents, also referred to as the edge currents, are independent on the conductivity of the sample which is why they can be conveniently described within the thermodynamic approach. They can be related to the Landau thermodynamic potential for an infinite system. We demonstrate that the observable manifestation of this, purely thermodynamic, Nernst effect consists in the strong oscillations of the magnetic field measured in the center of the disk as a function of the external field. The oscillations depend on the temperature difference at the edges of the disk. Dirac fermions and 2D electrons with a parabolic spectrum are characterized by oscillations of different phase and frequency. We predict qualitatively different power dependencies of the magnitude of the Nernst signal on the chemical potential for normal and Dirac carriers.

A Corbino disk represents one of the most important experimental designs for studies of transport effects in solids (1). In contrast to the Hall bar geometry (2), in a Corbino disk the Lorentz force induced by a magnetic field normal to the plane of the structure is not compensated by the induced electrostatic force. The Lorentz force gives rise to circular edge currents that can be studied through the magnetization generated by them (3). These currents are usually referred to as magnetization or diamagnetic currents (4). They are governed by the gradient of the magnetization in a sample and are formally independent of the electric conductivity henceforth. In classical language they arise because of the reflection of carriers circulating on their cyclotron orbits from the inner and the outer edges of the disk (5–7). In the range of classically strong magnetic fields, the magnetization currents exhibit oscillations with a periodicity governed by the resonances between Fermi and Landau energy levels (8). These oscillations can be studied, e.g., by measuring the magnetic field induced by edge currents in the center of the disk.

The Hall effect in the Corbino geometry has been studied in both classical (9) and quantum (10) limits. In contrast, the most important thermomagnetic effect, namely the Nernst effect, remains poorly explored in the disk geometry. The Nernst effect (11) consists in the induction of an electric current by a combined action of the crossed external magnetic field and the temperature gradient. It may be considered as a heat counterpart of the Hall effect. Recently, the giant Nernst or Nernst–Ettingshausen effects have been observed in graphene (12, 13), in pseudogap phase of quasi–two-dimensional high-temperature superconductors (14–17), in conventional superconducting films being in the fluctuation regime (18, 19).

Generally speaking, the Nernst signal consists of two contributions: the kinetic one and the thermodynamic one. The former is governed by the conductivity of the sample and the derivative of chemical potential of the carriers over temperature. The latter is related to the stationary magnetization currents induced by the temperature gradient: $I_N^{th}=c\left(\frac{\partial m_z}{\partial \mathbf{T}}\right)\Delta T$ (where $m_z\left(T\right)$ is the magnetization per square of the disk). This relation was initially obtained by Obraztsov for the Hall bar geometry more than 50 y ago (4). It is worthwhile to mention that this problem has been readdressed in almost every decade (20–25) due to its importance for the quantum Hall effect, the Nernst–Ettinghausen effect in fluctuating superconductors, and the anomalous thermospin effect in the low-buckled Dirac materials, etc. The existence of magnetization currents is crucial for the validity of such fundamental properties of thermomagnetic coefficients as the Onsager relations as well as the third law of thermodynamics (4, 25, 26). Yet, their existence and importance for the Nernst effect often have been neglected (for instance ref. 27 and discussion in ref. 28) or even denied (29–31).

The Corbino geometry offers a unique opportunity for the observation of the purely thermodynamic contribution to the Nernst effect generated exclusively by magnetization currents. Indeed, in the regime of classically strong magnetic fields, if the chemical potential of the electron gas in the disk lies between the Landau quantization levels, the electric current does not propagate between the inner and outer edges of the disk, and one can safely neglect the kinetic part of the Nernst response. In the same regime, in the presence of the magnetic field and temperature gradient, the contribution of the edge currents remains significant, so that the total circular current in the sample is dominated by magnetization currents.

Below we calculate the magnetization currents of carriers characterized by parabolic or Dirac energy dispersion relations (32) in a Corbino disk subjected to a radial temperature gradient and a strong magnetic field $B$ applied normally to the plane. Specifically, we analyze the magnetic field $B_{\mathrm{i}\mathrm{n}\mathrm{d}}$ induced by these currents in the center of the disk that can be experimentally measured, e.g., by a SQUID magnetometer (33, 34). For the recent experimental work on the measurement of the Hall conductivity in Corbino geometry by a sensible magnetometer we refer the reader to ref. 35. We show that this field experiences pronounced unharmonic oscillations as a function of the external field $B$. These oscillations are dominated by an interplay of two competing factors. The background contribution to the induced magnetic field that exists at zero temperature gradient is proportional to the second (for normal carriers) or third (for Dirac fermions) power of the chemical potential. At low temperatures, the chemical potential exhibits a characteristic saw-tooth oscillatory dependence on the magnetic field that is well known (36, 37). The second contribution to the magnetization, proportional to the difference of temperatures at the inner and the outer edges of the disk, is governed by the differential entropy per particle dependence on the external magnetic field (38). It can be calculated knowing the density of electronic states in the system for given temperature and magnetic field (39, 40). The difference of the values of the induced magnetic field $B_{\mathrm{i}\mathrm{n}\mathrm{d}}$ measured for the opposite signs of the temperature variation between inner and outer edges of the disk is no more sensitive to the background effect and allows for extracting the contribution induced by the temperature gradient, i.e., the Nernst effect. The shape and the period of Nernst current oscillations in the Corbino geometry carry precious information on the type of carriers and on the trajectories of topologically protected edge currents. The universal link between the Nernst current and the induced magnetization established in this work offers a powerful tool for the experimental studies of transport phenomena in 2D crystals.

The Relation between the Edge Current and Thermodynamic Potential in the Corbino Geometry

The edge currents in Corbino geometry can be related to the thermodynamic potential of the system based on very generic thermodynamic consideration. Indeed, let us start from consideration of a homogeneous metallic disk of the radius $R$, placed in a thermal reservoir of temperature $T$ and subjected to the magnetic field $H$ normal to the plane of the disk. The contribution to the thermodynamic potential dependent on the induced current can be written as

$${\mathrm{\Omega }}_H=\frac{1}{c}\int \mathbf{j}\left(\mathbf{r}\right)\hspace{0.17em}\mathbf{A}\left(r\right)\hspace{0.17em}dV,$$ [1]

where $\mathbf{A}$ is the vector potential. Consequently, the current can be expressed as

$$\mathbf{j}\left(\mathbf{r}\right)=\frac{c}{hS}\left(\frac{\partial {\mathrm{\Omega }}_H}{\partial \mathbf{A}}\right),$$ [2]

with $S=\pi R^2$ being the area of the disk and $h$ its height. Assuming that the radius of the disk is much larger than the magnetic length, one can choose the vector potential in the Landau gauge, $\mathbf{A}\hspace{0.17em}=\hspace{0.17em}\left(0,Hx\right)$ that yields for total current flowing through the disk

$$J=\frac{c}{SH}{\int }_0^R\frac{\partial {\mathrm{\Omega }}_H}{\partial x}dx=\frac{c}{SH}{\mathrm{\Omega }}_H\left(T\right).$$ [3]

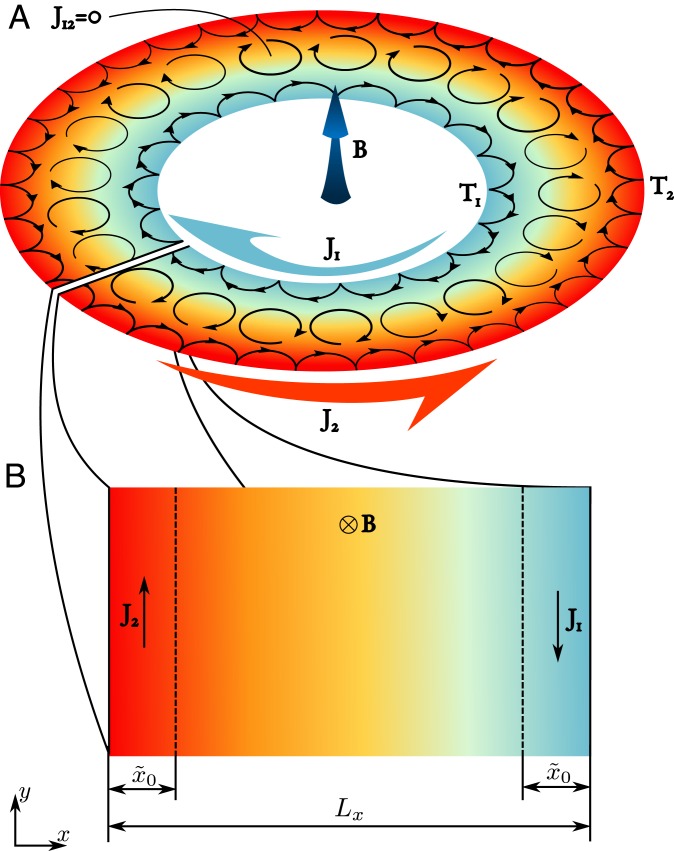
From Fig. 1A one can see that the current is concentrated only in the vicinity of the edge of the disk.

Fig. 1.

(A) The schematic showing the edge currents flowing in a Corbino disk subjected to an external magnetic field normal to its plane and to a radial temperature gradient. (B) The schematic showing the edge currents flowing in a conducting strip subjected to an external magnetic field normal to its plane.

Now one can represent the Corbino disk (ring) as the large disk of the radius $R_2$ from which a smaller disk of the radius $R_1$ is cut out. As a result, the total current flowing along the edges is given by the difference between the outer and internal edge currents. Both currents are defined by the same Eq. 3, taken with different areas of the disk. Accounting for the temperature difference between the edges, one can finally obtain

$$J_{\mathrm{t}\mathrm{o}\mathrm{t}}=\frac{c}{H}\left[\frac{\Omega \left(T_2\right)}{S_2}-\frac{\Omega \left(T_1\right)}{S_1}\right].$$ [4]

The derivation above is based on classical arguments that may seem contradictory to the quantum nature of Landau diamagnetism. This is why in the following section we reproduce the final expression for the current (Eq. 3) in the framework of a quantum mechanical approach.

The Microscopic Approach to Calculation of Edge Currents

The Eigenvalue Problem.

Let us consider now the Corbino disk with the inner edge radius $R_1$ and the outer edge radius $R_2$ subjected to the magnetic field $H$ applied normally to the disk plane in a microscopic approach. We are interested here in the regime of classically strong magnetic fields, where the energy separation between the neighboring Landau levels exceeds their broadening, yet remains small with respect to the Fermi energy, $max\left\{T,\mathrm{\Gamma }\right\}\ll \hslash {\omega }_c\ll E_F$, where $T$ is temperature, $\mathrm{\Gamma }$ is the Dingle temperature, ${\omega }_c$ is the cyclotron frequency, and $E_F$ is the Fermi energy. In what concerns the requirements for the disk geometry, we assume that $R_1,R_2,R_2-R_1\gg l_B$, where the magnetic length is $l_B=\sqrt{\hslash c/\left|e\right|H}$.

We use here the thermodynamic approach to the Nernst effect developed in refs. 4 and 8. Namely, we describe the system by the Gibbs thermodynamic potential

$$\mathrm{\Omega }=-2kT\sum _{\alpha }\ln \left[1+e^{\frac{\mu -{\epsilon }_{\alpha }}{kT}}\right],$$ [5]

where ${\epsilon }_{\alpha }$ are the eigenvalues, and the summation is performed over the complete set of the quantum numbers $\left\{\alpha \right\}$, and $\mu \left(T\right)$ is the chemical potential of the electron gas, coinciding with the Fermi energy at zero temperature. The spin degeneracy of the electron gas under study is postulated, which results in the appearance of the factor 2 in Eq. 5. In the case corresponding to the 2D gas of free electrons (2DEG) subjected to a magnetic field, the electronic Hamiltonian has the familiar Landau form (the specifics of carriers having a Dirac dispersion are discussed later)

$$Ĥ=-\frac{{\hslash }^2}{2m}\frac{d^2}{d{x}^2}+\frac{m{\omega }_c^2}{2}{\left(x-x_0\right)}^2,$$ [6]

with ${\omega }_c=\left|e\right|H/\left(mc\right)$. The set of quantum numbers is $\alpha =\left\{x_0,n\right\}$, where $x_0=l_B^2{k}_y$ is the $x$ coordinate of the center of the electron cyclotron orbit, $k_y$ is the tangential component of the electron momentum (schematic in Fig. 1A), and $n$ is the index of the energy quantization level in the potential induced by the magnetic field (with the minimum at the point $x_0$).

The rule for summation over eigenvalues in Eq. 5 takes a form

$$\sum _{\alpha }\dots =\frac{\left|e\right|H}{c}\frac{L_y}{2\pi \hslash }{\int }_{-\infty }^{\infty }d{x}_0\sum _{n=0}^{\infty }\dots ,$$ [7]

where $L_y$ is the linear dimension of the system along the edge.

The Shrödinger equation with the Hamiltonian 6 and the specific boundary conditions $W_{\alpha }\left(0\right)=W_{\alpha }\left(L_x\right)=0$ [Teller’s model (5)] determine the spectrum ${\epsilon }_{\alpha }$ and the set of eigenfunctions:

$$Ĥ\hspace{0.17em}{W}_{\alpha }\left(x\right)={\epsilon }_{\alpha }{W}_{\alpha }\left(x\right).$$ [8]

The latter turn out to be the Weber functions $W_{\alpha }\left(x\right)$ (41), while the electron eigenenergies in the vicinity of the edge $x=0$ can be approximated by

$${\epsilon }_{\alpha }=\hslash {\omega }_c\left\{\begin{array}{c}\hspace{0.17em}\hspace{0.17em}\begin{array}{cc}\hfill \left(n+\frac{1}{2}\right)+\frac{2^n}{\sqrt{\pi }n!}{\left(\frac{x_0}{l_B}\right)}^{2n+1}\hspace{0.17em}\exp \hspace{0.17em}\left[-\frac{x_0^2}{l_B^2}\right],\hfill & \hfill \hspace{0.17em}{x}_0\gg l_B\hfill \\ \hfill \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}2\left(n+\frac{3}{4}\right)-2\frac{\left(2n+1\right)\mathrm{\Gamma }\left(n+1/2\right)}{\pi n!}\left(\frac{x_0}{l_B}\right),\hfill & \hfill \hspace{0.17em}{x}_0\lesssim l_B\hfill \end{array},\hspace{1em}\hfill \end{array}\right.$$ [9]

(we note that similar expressions were obtained in ref. 6, while some errors in the coefficients and the erroneous factor of “2” in the exponential function are present in that work). The upper line in [9] corresponds to the cyclotron orbits centered far from the edges ($x_0\gg l_B$). The energy spectrum for these states coincides with the Landau one with an exponential accuracy. The lower line in [9] describes the energy spectrum for the states whose orbits are centered close to the border ($x_0\lesssim l_B$). The doubling of the cyclotron frequency that appears in the first term is due to the supplementary quantum confinement of carriers in a half-parabolic potential that appears due to their reflection from the boundary.

The Edge Currents Calculated from the First Principles.

We consider a macroscopic Corbino disk and assume that the curvature of the edges can be safely neglected on the length scale of the cyclotron orbits (Fig. 1B). In this case, one can calculate the edge currents starting from the exact quantum mechanical expression for the charge flow in a pure quantum state $\alpha$ (6, 42):

$$j_{y\alpha }\left(x,x_0\right)=-\frac{\left|e\right|{\omega }_c}{L_y}\left(x-x_0\right)W_{\alpha }^2\left(x\right).$$ [10]

The full current $J_{\mathrm{t}\mathrm{o}\mathrm{t}}$ is obtained by summing $j_{y\alpha }$ over all eigenstates $\left\{\alpha \right\}$ of the problem, accounting for the occupation numbers $f\left({\epsilon }_{\alpha }\right)={\left[\exp \left(\left({\epsilon }_{\alpha }-\mu \right)/kT\right)+1\right]}^{-1}$ and integrating over the width of the disk:

$$\begin{array}{cc}\hfill J_{\mathrm{t}\mathrm{o}\mathrm{t}}& ={\int }_0^{L_x}\sum _{\alpha }{j}_{y\alpha }\left(x,x_0\right)f\left({\epsilon }_{\alpha }\right)dx\hfill \\ \hfill & =-m\frac{\left|e\right|{\omega }_c^2}{\pi \hslash }\sum _{n=0}^{\infty }\underset{-\infty }{\overset{\infty }{\int }}d{x}_{0}f\left[{\epsilon }_n\left(x_0\right),T\right]\underset{0}{\overset{L_x}{\int }}dx\left(x-x_0\right)W_{\alpha }^2\left(x\right).\hfill \end{array}$$ [11]

One can relate the integral over $x$ in Eq. 11 to the derivative of the eigenenergy over $x_0$, employing the Feynman theorem (42),

$${\int }_0^{L_x}dx\left(x-x_0\right)W_{\alpha }^2\left(x-x_0\right)=\frac{1}{m{\omega }_c^2}\frac{\partial {\epsilon }_{\alpha }}{\partial x_0},$$ [12]

that results in

$$J_{\mathrm{t}\mathrm{o}\mathrm{t}}=-\frac{\left|e\right|}{\pi \hslash }\sum _{n=0}^{\infty }\underset{-\infty }{\overset{\infty }{\int }}\hspace{0.17em}\hspace{0.17em}\frac{d}{d{x}_0}\ln \hspace{0.17em}\hspace{0.17em}\left[1+\exp \left(\frac{\mu \left(T\right)-{\epsilon }_n\left(x_0\right)}{kT}\right)\right]d{x}_0.$$ [13]

We underline that far from the edges of the disk the electron energy levels (9) coincide with the Landau levels with an exponential accuracy; i.e., in this domain ${\stackrel{\sim }{x}}_0\lesssim x\lesssim L_x-{\stackrel{\sim }{x}}_0$ the derivative $\partial {\epsilon }_{\alpha }/\partial x_0$ = 0. The value ${\stackrel{\sim }{x}}_0$ can be estimated by imposing the phenomenological requirement (6):

$${\left(\frac{\partial {\epsilon }_{\alpha }}{\partial x_0}\right)}_{x_0={\stackrel{\sim }{x}}_0}=0.$$

One can see from Eq. 9 that ${\stackrel{\sim }{x}}_0\sim l_B\sqrt{2n+1}$, which is nothing but the radius of the cyclotron orbit at the $n$th Landau level. Having this in mind, the integration in [13] can be restricted to the vicinity of the edges of the sample: ]$-\infty ,{\stackrel{\sim }{x}}_0$], [$L_x-{\stackrel{\sim }{x}}_0,\infty$ [. The contribution to the current from the bulk region tends to zero (Fig. 1).

The Corbino Disk with Differently Heated Edges.

To study the Nernst effect we assume that the inner (outer) edge of the disk is kept at equilibrium with the thermal bath of the temperature $T_1\left(T_2\right)$. We assume that the temperature gradient is small enough, so that on the scale of the order of ${\stackrel{\sim }{x}}_0$ it can be neglected. In this case the full circular current is determined by the difference of two edge currents,

$$J_{\mathrm{t}\mathrm{o}\mathrm{t}}=J\left(T_1\right)-J\left(T_2\right),$$ [14]

where

$$J\left(T\right)=-\frac{\left|e\right|kT}{\pi \hslash }\sum _{n=0}^{\infty }\ln \left[1+\exp \left(\frac{\mu \left(T\right)-{\epsilon }_n\left(\stackrel{\sim }{x_0}\left(n\right)\right)}{kT}\right)\right].$$ [15]

Since the sum in [15] is determined by its upper limit, one can use the expression for ${\epsilon }_n\left(\stackrel{\sim }{x_0}\left(n\right)\right)$ from the upper line of Eq. 9. Neglecting the exponentially small second term, we reproduce the result discussed in [7]:

$$J\hspace{0.17em}\left(T\right)\approx -\frac{\left|e\right|kT}{\pi \hslash }\sum _{n=0}^{\infty }\ln \left[1+\exp \left(\frac{\mu \left(T\right)-\hslash {\omega }_c\left(n+1/2\right)}{kT}\right)\right].$$ [16]

Eqs. 14–16 describe the total current induced by the external magnetic field in the Corbino geometry. The chemical potential $\mu \left(B,T,\rho \right)$ depends on the magnetic field, temperature, and the carrier concentration $\rho$. Comparing Eq. 16 with the thermodynamic potential calculated for the Landau energy spectrum (Eqs. 5–7)

$$\begin{array}{cc}\hfill {\mathrm{\Omega }}_L\left(T\right)& =-2kT\frac{\left|e\right|H}{c}\frac{S}{2\pi \hslash }\hfill \\ \hfill & \hspace{1em}\times \sum _{n=0}^{\infty }\ln \left[1+\exp \left(\frac{\mu \left(T\right)-\hslash {\omega }_c\left(n+1/2\right)}{kT}\right)\right],\hfill \end{array}$$ [17]

one finds the universal relation which was first derived by Obraztsov in ref. 4:

$$J\left(T,H,\mu \right)=\frac{c}{HS}{\mathrm{\Omega }}_L\left(T,H,\mu \right).$$ [18]

Let us stress that the sign in Eq. 18 is a matter of convention: In the chosen form it corresponds to the direction of the current flowing along the internal edge of the ring.

The problem of calculation of the Gibbs potential in the presence of a homogeneous magnetic field was considered long ago in relation to the de Haas–van Alphen oscillations. The corresponding expression can be easily obtained from [17]. In the limit of low temperatures $kT\ll \mu \left(T\right)$, the exponential term in the argument of the logarithmic function strongly exceeds unity. The expression for the current thus reduces to

$$J^{\mathrm{2}\mathrm{D}\mathrm{E}\mathrm{G}}\left(T,\mu \right)=-\frac{\left|e\right|}{\pi {\hslash }^2}\frac{{\mu }^2\left(T\right)}{2{\omega }_c}.$$ [19]

In the case of graphene characterized by the linear dispersion of Dirac carriers, the Landau quantization leads to the appearance of a nonequidistant energy spectrum ($E_n=\pm \sqrt{2n\hslash \left|e\right|B{v}_F^2/c}$), in which case the summation in Eq. 15 results in

$$J^{\mathrm{g}\mathrm{r}}\left(T,\mu \right)=-\frac{c}{H}\frac{|\mu \left(T\right){|}^3}{3\pi {\hslash }^2{v}_F^2},$$ [20]

where $v_F$ is the Fermi velocity.

The Nernst Oscillations in 2DEG and Graphene

Oscillations of the Edge Currents.

The local chemical potential $\mu \left(T_{\mathrm{1,2}},H\right)$ at the edge of the disk as a function of the temperature and magnetic field is defined by the equation

$$\frac{1}{S}{\left.\frac{\partial {\mathrm{\Omega }}_L\left(T,H,\mu \right)}{\partial \mu }\right|}_{H,T_{\mathrm{1,2}}}=-\rho .$$ [21]

Here $\rho$ is the concentration of carriers.

At low temperatures, in a system with a fixed carrier density the chemical potential can be presented as $\mu \left(T,H\right)=E_F+\stackrel{\sim }{\mu }\left(T,H\right)$, where the oscillating part of the chemical potential $\stackrel{\sim }{\mu }$ is given by Eq. 21 (8, 32, 37). This equation that is implicit for $\stackrel{\sim }{\mu }$ can be solved analytically only at $T=0$ (43), while at finite temperatures one needs to resort to the numerical analysis. In the case of weak smearing of the Landau levels $\stackrel{\sim }{\mu }$ turns out to be of the order of $\hslash {\omega }_c$. However, if $\mathrm{\Gamma }$ approaches $\hslash {\omega }_c/\left(2\pi \right)$, the value of $\stackrel{\sim }{\mu }$ exponentially decays (37). In this case the approximate expression for $\stackrel{\sim }{\mu }$ both for a 2DEG of carriers having a parabolic dispersion and for Dirac fermions in graphene can be written as

$$\begin{array}{cc}\hfill & \stackrel{\sim }{\mu }\hspace{0.17em}=\hfill \\ \hfill & -\frac{\hslash {\omega }_c}{\pi }\hspace{0.17em}\sum _{l=1}^{\infty }\hspace{0.17em}\frac{\psi \left(l\lambda \right)}{l}\sin \left[2\pi l\left(\frac{c\mathcal{S}\left(E_F\right)}{2\pi e\hslash B}+\frac{1}{2}+\beta \right)\right]\exp \left(-\frac{2\pi l\mathrm{\Gamma }}{\hslash {\omega }_c}\right),\hfill \end{array}$$ [22]

where

$$\psi \left(z\right)=\frac{z}{\sinh z},\hspace{1em}\hspace{1em}\lambda =\frac{2{\pi }^{2}kT}{\hslash {\omega }_c},$$ [23]

is the temperature factor, $\mathcal{S}\left(E_F\right)$ is the electron cyclotron orbit area in the momentum space, and $\beta$ is the topological part of the Berry phase. In the case of a 2DEG characterized by a parabolic dispersion of charge carriers, $ϵ=p^2/\left(2\hspace{0.17em}m\right)$, the electron orbit area is $\mathcal{S}\left(E_F\right)=2\pi m{E}_F$, and the trivial phase, $\beta =0$. In its turn, for the massless Dirac fermions, $ϵ=\pm v_{F}p$, the area is $\mathcal{S}\left(E_F\right)=\pi E_F^2/v_F^2$, while the cyclotron frequency depends on the Fermi energy ${\omega }_c=v_F^2\left|e\right|H/\left(c\left|E_F\right|\right)$. In contrast to the case of a 2DEG with a parabolic dispersion, for Dirac fermions the phase becomes nontrivial, $\beta =1/2$. All of the above is valid for the range of classically strong magnetic fields, $\hslash {\omega }_c\ll E_F$ (we assume that $E_F>0$).

Substituting Eq. 22 into Eqs. 19 and 20 one can find explicitly the magnetic-field dependence of the edge currents

$$J\left(T,H\right)=-\frac{\left|e\right|}{\pi {\hslash }^2}\frac{E_F^2}{{\omega }_c}\left[\eta +\frac{\stackrel{\sim }{\mu }}{E_F}\right],$$ [24]

with $\eta =1/2$ for 2DEG and $\eta =1/3$ for the Dirac electrons in graphene, respectively.

Applying the above expression for the edge currents flowing in the Corbino disk with differently heated inner and outer edges one can find the sum of two edge currents as

$$J_{\mathrm{t}\mathrm{o}\mathrm{t}}\left(T_1,T_2\right)=\frac{\left|e\right|}{\pi {\hslash }^2}\frac{E_F}{{\omega }_c}\left[\stackrel{\sim }{\mu }\left(T_2,H\right)-\stackrel{\sim }{\mu }\left(T_1,H\right)\right].$$ [25]

In the case of a relatively small temperature difference $\mathrm{\Delta }T=T_1-T_2\ll T_1$ one can expand $\stackrel{\sim }{\mu }$ and obtain the explicit dependence of the oscillating total current on the magnetic field:

$$\begin{array}{ccc}\hfill \begin{array}{cc}\hfill J_{\mathrm{t}\mathrm{o}\mathrm{t}}\left(T,\mathrm{\Delta }T\right)& =\frac{\left|e\right|E_F}{{\pi }^2\hslash }\left(\frac{\mathrm{\Delta }T}{T}\right)\sum _{l=1}^{\infty }\frac{{\psi }^{\prime }\left(l\lambda \right)}{l}\hfill \\ \hfill & \hspace{1em}\times \sin \left[2\pi l\left(\frac{c\mathcal{S}\left(E_F\right)}{2\pi e\hslash B}+\frac{1}{2}+\beta \right)\right]\exp \left(-\frac{2\pi l\mathrm{\Gamma }}{\hslash {\omega }_c}\right).\hfill \end{array}& \hfill & \hfill \\ \hfill & \hfill & \hfill \end{array}$$ [26]

The amplitude factor

$${\psi }^{\prime }\left(l\lambda \right)=\frac{\lambda l\left[\lambda l\coth \left(\lambda l\right)-1\right]}{\sinh \left(\lambda l\right)}=\left\{\begin{array}{cc}\frac{\lambda l}{3}\left[1-\frac{7}{30}{\left(\lambda l\right)}^2\right],\hspace{1em}\hfill & \lambda l\ll 1\hfill \\ 2\lambda l\exp \left(-\lambda l\right),\hspace{1em}\hfill & \lambda l\gg 1\hfill \end{array}\right.\hspace{0.17em},$$ [27]

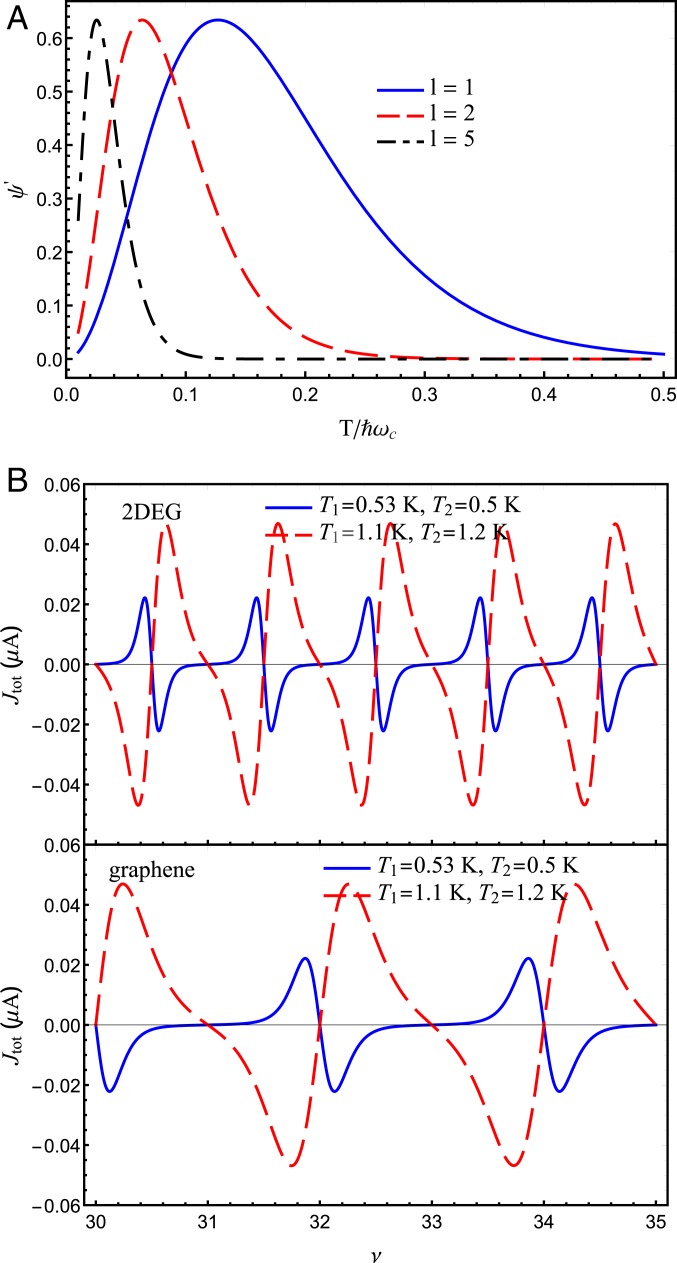
is presented in Fig. 2A. In contrast to the conventional factor $\psi \left(l\lambda \right)$, it is a nonmonotonic function of temperature.

Fig. 2.

(A) The dimensionless amplitude factor 27 plotted as a function of temperature $T$ measured in the units of $\hslash {\omega }_c$ for three different values of $l$. (B) The sum of two edge currents $J_{\text{tot}}$ in $\mu A$ as a function the Landau filling factor $\nu$ that is introduced for the cases of 2DEG and graphene in main text. The Fermi energy is assumed to be $E_F=500\hspace{0.17em}\text{K}$ and the level broadening $\mathrm{\Gamma }=0.5\hspace{0.17em}\text{K}$. The cyclotron energy $\hslash {\omega }_c=E_f/\nu$. Note that $T_1>T_2$ for the blue curves and $T_1<T_2$ for the red ones. The direction of the temperature gradient strongly affects the shape of the oscillations.

Note that the same function ${\psi }^{\prime }\left(l\lambda \right)$ appears in the expression for the oscillating part of the Seebeck coefficient in an electron gas subjected to a strong magnetic field (44).

The total edge current $J_{\mathrm{t}\mathrm{o}\mathrm{t}}\left(T_1,T_2,\nu \right)$ as a function of the filling factor of a Landau level

$$\nu =\frac{\pi \hslash c\rho }{eB}=\left\{\begin{array}{cc}\frac{E_F}{\hslash {\omega }_c},\hspace{1em}\hfill & 2\text{DEG}\hfill \\ \frac{c{E}_F^2}{\hslash eH{v}_F^2},\hspace{1em}\hfill & \text{graphene}\hfill \end{array}\right.$$ [28]

is plotted in Fig. 2B. One can see that the period of oscillations for graphene is two times larger due to the valley degeneracy. The phase of oscillations for graphene is shifted with respect to 2DEG. The sharp features correspond to the Fermi level crossing by the Landau levels. Note that the shape of obtained current oscillations shown in Fig. 2B resembles that of the thermoelectric power coefficient for the 2DEG calculated in ref. 44.

We recall that all our calculations are performed within the assumption of the smallness of the magnitude of the $\stackrel{\sim }{\mu }\ll \hslash {\omega }_c$ that implies a noticeable smearing of Landau levels ($\mathrm{\Gamma }/k+T\sim 1.5\hspace{0.17em}\text{K}\sim \hslash {\omega }_c/\left(2\pi k\right)\sim 2\hspace{0.17em}\text{K}$). It is important to note that this experimentally relevant limit allows us to demonstrate the existence of unusual Nernst oscillations which appear due to the imbalance of magnetization currents in the Corbino geometry.

The Induced Magnetic Field and Its Oscillations in the Corbino Geometry.

The circular electric currents $J\left(T_{\mathrm{1,2}}\right)$ along the edges of the disk lead to the induction of the magnetic field in the center of the disk $B_{ind}\left(T_1,T_2\right)=B_1+B_2$ with $B_{\mathrm{1,2}}=\pm 2\pi J\left(T_{\mathrm{1,2}}\right)/c{R}_{\mathrm{1,2}}$. This field constitutes a diamagnetic response of the ring generated by the persistent currents that have a purely thermodynamic nature

$$B_{ind}\left(T_1,T_2\right)=\eta \frac{\left|e\right|E_F}{\hslash c}\left(\frac{E_F}{\hslash {\omega }_c}\right)\left(\frac{1}{R_1}-\frac{1}{R_2}\right)+B_{osc}.$$ [29]

The first term in Eq. 29 monotonously decreases with the increase of the external magnetic field as a result of the reduction of the magnitude of the edge currents. The oscillating part $B_{osc}$ of the induced magnetic field for the specific cases of carriers with parabolic and linear dispersions is given by

$$\begin{array}{cc}\hfill B_{osc}& =\frac{\left|e\right|E_F}{2\pi \hslash c}\sum _{l=1}^{\infty }\frac{1}{l}\left[\frac{\psi \left[l\lambda \left(T_1\right)\right]}{R_1}-\frac{\psi \left[l\lambda \left(T_2\right)\right]}{R_2}\right]\hfill \\ \hfill & \hspace{1em}\times \sin \left[2\pi l\left(\frac{c\mathcal{S}\left(E_F\right)}{2\pi e\hslash B}+\frac{1}{2}+\beta \right)\right]\exp \left(-\frac{2\pi l\mathrm{\Gamma }}{\hslash {\omega }_c}\right).\hfill \end{array}$$

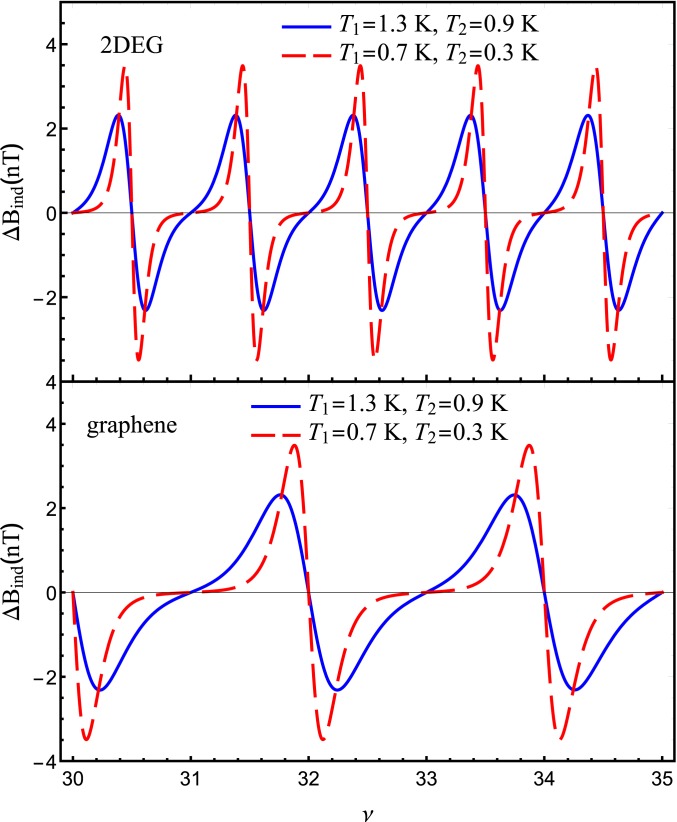
To exclude the background part of $B_{ind}$ that is independent of the temperature gradient one can study the difference of the induced fields $\mathrm{\Delta }{B}_{ind}\left(T_1,T_2\right)=B_{ind}\left(T_1,T_2\right)-B_{ind}\left(T_2,T_1\right)$. The dependence of $\mathrm{\Delta }{B}_{ind}\left(T_1,T_2\right)$ on the filling factor is shown in Fig. 3. The phase and magnitude of the oscillatory features corresponding to the resonances of Landau and Fermi levels are strongly dependent on the temperature gradient in the studied sample. The oscillations depend on the temperature difference at the edges of the disk. Dirac fermions and 2D electrons with a parabolic spectrum are characterized by oscillations of different phase and frequency. We predict qualitatively different power dependencies of the magnitude of Nernst signal on the chemical potential for normal and Dirac carriers.

Fig. 3.

The contribution to the induced magnetic field $\mathrm{\Delta }{B}_{ind}$ at the center of the Corbino disk that is induced by a temperature gradient in $nT$ plotted as a function of the filling factor $\nu$. Upper panel describes the 2DEG characterized by a parabolic dispersion of charge carriers. Lower panel corresponds to the case of graphene characterized by the linear dispersion of charge carriers. The blue curves are calculated with $T_1=1.3$ K, $T_2=0.9$ K and the red curves correspond to $T_1=0.7$ K, $T_2=0.3\hspace{0.17em}K$. The other parameters used in this calculation are $R_1=100\hspace{0.17em}\mathrm{\mu }\text{m}$, $R_2=110\hspace{0.17em}\mathrm{\mu }\text{m}$, $E_F=500\hspace{0.17em}\text{K}$, $\mathrm{\Gamma }=0.5\hspace{0.17em}\text{K}$.

Conclusions

We have demonstrated that the Corbino geometry offers a precious opportunity for the observation of the specific Nernst effect having a purely thermodynamic nature. The effect is caused by the imbalance of magnetization currents flowing along the inner and outer edges of the Corbino disk maintained at different temperatures. We demonstrate that the experimentally observable manifestation of this thermodynamic Nernst effect consists in the appearance of the specific oscillations of the magnetic field measured in the center of the disk as a function of the external field. The measurement should be done in the presence of a temperature gradient between the inner and outer edges of the disk. Subtracting the values of the magnetic field measured in the center of the disk for opposite signs of the temperature gradient, one should be able to extract the specific contribution of the magnetization currents to the Nernst signal.

We have developed the microscopic model describing such an oscillatory diamagnetic response of the Corbino disk made of a normal metal and of graphene in the presence of the radial temperature gradient. The total current exhibits oscillations corresponding to the resonances of Fermi and Landau levels in the disk. The value and the direction of the radial temperature gradient in the sample strongly affect the magnitude and the shape of the oscillations in the dependence of the induced magnetic field on the Landau filling factor. An experimental study of such diamagnetic oscillations in the center of the Corbino disk would allow for the high-precision measurement of the Nernst effect that is expected to be of strongly different magnitude in graphene and in normal metals. Such a study would also shed light on the contribution of the diamagnetic currents to the Nernst effect that has been a subject of debate for many years.

Materials and Methods

All data relevant to this work are contained in the text.