Significance
Humans cannot help but turn their gaze to objects that catch their attention. Our knowledge of the factors that govern this seizure, or of its effects in the context of learned decision making, is currently rather incomplete. We therefore monitored the gaze of human subjects as they learned to choose between multiple options whose value was initially unknown. We found evidence that attention was influenced by uncertainty and that the use of, and reduction in, uncertainty were, in turn, influenced by attention. Our findings provide evidence for approximately optimal models of learning and choice and uncover an intricate interplay between learning, choice, and attentional processes.
Keywords: reinforcement learning, decision making, uncertainty, visual fixation, exploration–exploitation
Abstract
Uncertainty plays a critical role in reinforcement learning and decision making. However, exactly how it influences behavior remains unclear. Multiarmed-bandit tasks offer an ideal test bed, since computational tools such as approximate Kalman filters can closely characterize the interplay between trial-by-trial values, uncertainty, learning, and choice. To gain additional insight into learning and choice processes, we obtained data from subjects’ overt allocation of gaze. The estimated value and estimation uncertainty of options influenced what subjects looked at before choosing; these same quantities also influenced choice, as additionally did fixation itself. A momentary measure of uncertainty in the form of absolute prediction errors determined how long participants looked at the obtained outcomes. These findings affirm the importance of uncertainty in multiple facets of behavior and help delineate its effects on decision making.
We often need to decide between alternative courses of action about whose outcome we are uncertain. Common examples include choosing a dish in a restaurant, a holiday trip, or a financial investment. Uncertainty, which derives from initial ignorance and sometimes ongoing change, has two characteristic statistical and computational facets. One is straightforward: If we try an option, then the amount of learning—i.e., the extent to which we should update our beliefs—depends on our current uncertainty relative to the noise in the observation (1). The greater our uncertainty, the greater the impact an observation inconsistent with our current beliefs should have on our subsequent beliefs. There is good evidence that humans and other animals adapt their rate of learning to various factors in the environment which increase, or reduce, uncertainty (2–6).
The second facet concerns choice. Here, it is the options that we are uncertain about and that we need to learn about through sampling. This is more complicated, as our ignorance about their beneficial or malign consequences implies that we need to take a sampling risk. This is the notorious exploration/exploitation dilemma. Although there are elegant computational solutions for important special cases (Gittins indices; ref. 7), a general solution is intractable. There is evidence that when choosing options, people explore in a directed manner, by integrating values with uncertainty about these values (8–12), particularly when these are carefully dissociated (9, 10). However, there is also evidence for a simpler form of random, undirected exploration, which is sensitive to value but not to its uncertainty (5, 13). Integration of value and the uncertainty in its estimation is sensible. Estimation uncertainty serves as a proxy for how informative a choice is or what the potential for improvement in value is (14, 15). The distinction from irreducible uncertainty is important. Irreducible uncertainty stems from the inherent stochastic nature of the environment that generates rewards and cannot be reduced through learning.
Most studies only admit indirect inferences about the processes of learning and decision making, exploiting the trajectory of choices alone. However, when options are presented visually and are spatially distinct, we have an opportunity to gain a window into these processes by examining what people choose to look at—that is, their visual fixations (16–25). In typical tasks, including the one we employ in our experiment, we can expect two sorts of revealing fixation behavior—namely, the relative time spent on each option when deciding (which bears on choice) and the absolute fixation time when receiving feedback about the consequences of choices (which bears on learning).
Fixation time might be correlated not only with subjects’ internal states relevant to learning and choice, but might actually affect those states directly (18, 21). This also allows factors other than value and estimation uncertainty, including stimulus salience, momentary lapses of attention, or unrelated cognitive processes, to influence fixation (26–28) and exert statistically untoward effects on behavior.
In the case of choice, a prominent view is that the process leading up to a decision involves accumulating information about the options until one is judged to be sufficiently good or sufficiently better than the alternatives (29, 30). Under this framework, looking at an option facilitates accumulating information specifically about that option (18, 21). This would provide a mechanism through which relative fixation time before making a choice can have a direct influence on the decision itself. In this case, for choices to be approximately optimal (7, 8, 10, 11), the relative fixation time before a choice would have to reflect the learning history, with respect to both the value and estimation uncertainty. Our focus on directed exploration and estimation uncertainty distinguishes the present study from previous ones on reinforcement learning and attention, which focused on effects of value (22) and irreducible uncertainty (24), or did not in any case involve exploration (25).
In the case of learning, absolute fixation time might have a direct influence on the magnitude of belief change in response to a prediction error, which amounts to the learning rate. For instance, visual fixations facilitate working-memory and memory-retrieval operations (31–35). Based on this evidence, fixation time might influence how well a newly observed outcome is integrated with an old value retrieved from memory. Thus, to follow the precepts of Bayesian statistical learning, fixation should be related to an option’s estimation uncertainty (3), allowing the latter to be observable from the former. While this prediction was made almost two decades ago, empirical evidence has been lacking (16).
To examine the role of estimation uncertainty and complex interactions between visual fixation, learning, and choice, we administered a multiarmed bandit (MAB) task in which we also tracked subjects’ gaze as they chose repeatedly between six, initially unknown, options. We varied the mean and variance of options’ outcomes to motivate exploration and to ensure ample variability in value and estimation uncertainty. When ignoring fixation behavior, we found that both value and estimation uncertainty play a role in learning and choice. As predicted, we found that, over the course of decision making, estimation uncertainty and value jointly influenced relative fixation times. During feedback, when subjects could update their beliefs, uncertainty, in the form of the unsigned reward-prediction error, guided the total fixation time on the chosen option. Even though relative fixation time during choice carried information about value and estimation uncertainty, fixation exerted a much stronger independent influence on choices than was warranted by that information. This indicates that an important fixation-specific component influenced choice. Finally, we show that a model including value, estimation uncertainty, and relative fixation time before choice best explained actual choices. This suggests that the influence of the first two of these quantities is not completely mediated by their effect on the third and that capturing an internal valuation process is therefore still important.
Results
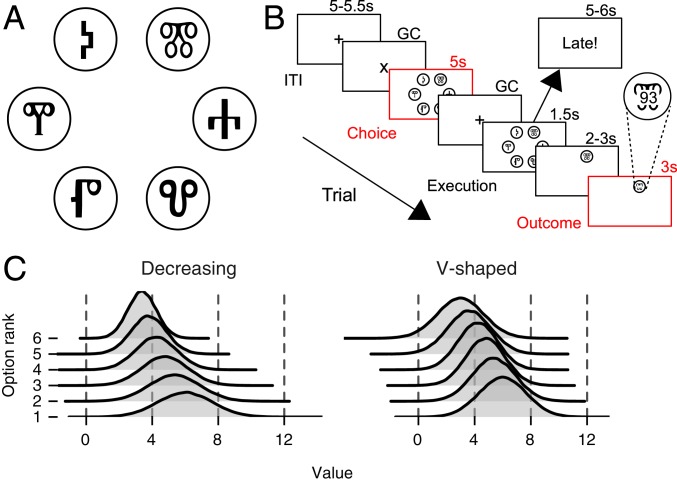
Participants completed two games. In each game, they repeatedly chose between six options, for a total of 60 trials (Fig. 1A, Materials and Methods, and SI Appendix, SI Methods). Each game was an MAB task in which rewards for each option were drawn from different Gaussian distributions (Fig. 1C). Participants were instructed to maximize the cumulative sum of rewards in each game. To attain this goal, they needed to explore the options in the choice set in order to learn which option had the highest average reward and subsequently exploit this knowledge.
Fig. 1.
Illustration of the six-armed bandit task. (A) Participants chose between six options on each of 60 trials. Each option was represented by a letter from the Glagoljica alphabet. Options were displayed in a circle around the center of the screen, always at the same location. (B) Time course of a single trial. Each box denotes a stage in a trial, with duration displayed above the boxes. For visual-fixation analyses, the main stages of interest were choice stage, where participants considered which option to choose, and outcome stage, where they observed a choice outcome (B, Inset displays reward outcome overlaid over the option). Two stages were gaze contingent (GC), where participants triggered an onset by fixating on a fixation cross. ITI, intertrial interval. (C) To facilitate detecting whether estimation uncertainty guided participants’ exploration, the variances of the reward distributions differed between each of the options. In the decreasing variances game, distributions get narrower (more certain and easier to learn) going from the best (rank 1) to the worst (rank 6) option, while for the V-shaped variances game, they are the narrowest for the middle ranking and broader (more uncertain and taking more trials to learn) for the better and worse ranking options, respectively.
To facilitate detecting whether estimation uncertainty guided participants’ exploration, the variances of the reward distributions differed between each of the options. The rationale behind this manipulation was that choices that are guided by value alone would be less directly affected by such differences in variances. In a decreasing variances game, variance decreased as the mean reward of the option decreased, so that, for instance, the option with the highest mean had the highest variance (Fig. 1 C, Left). In a V-shaped variances game, the variance was largest for the options with the highest and smallest means and smaller for the middle options (Fig. 1 C, Right). Different games allow for better generalization of results and can serve as a further check for directed exploration, as, again, choices guided by value alone would be less sensitive to such differences.
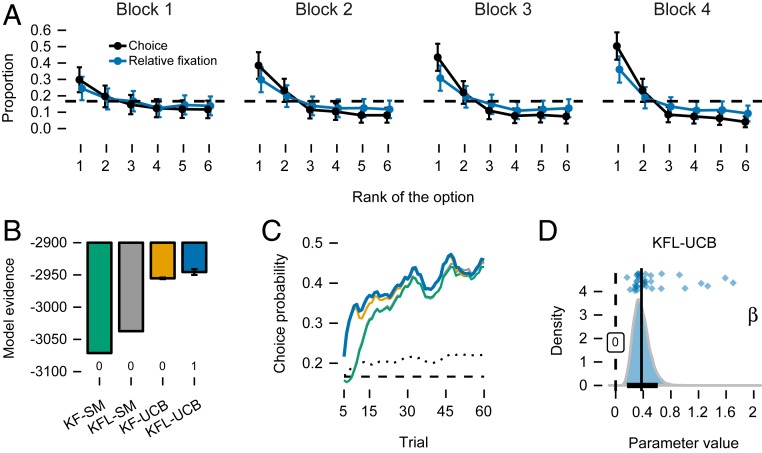
Options’ expected rewards were constant throughout the bandit task. In such a task, any reasonable reinforcement learning agent that maximizes cumulative rewards would gradually allocate more and more choices to high-value options as its estimates of options’ rewards improve with experience. Indeed, choices improved from the first to the last block of 15 trials (Fig. 2A), as indicated by a clear negative block effect (mixed-effects regression estimates: intercept = 2.50, credible interval [CI] ; block = , CI ; game = 0.06, CI ; blockgame = 0, CI ; Mixed-Effect Regressions). There was no strong difference in choice performance between the games, indicating that low-ranking options did not attract more choices in the V-shaped game. While this could be due to choices not being guided by estimation uncertainty, an alternative explanation is that participants learned to ignore the low-ranking options very quickly. This would result in weak difference between the games, since it was mainly these that distinguished the distributions between games. In most cases, choice performance did not reach ceiling by the last block of 15 trials (mean of 2.08, ), suggesting that the games were not trivial, and participants were still exploring by the end of the task.
Fig. 2.
(A) Proportion of choices allocated to options with higher expected values (i.e., rank closer to 1) increased from the first to the fourth block. Relative fixation in the choice stage shows similar learning effect. Error bars are SEM. (B) Model evidence (bars) and model comparison (numbers below bars) show that KFL-UCB captures choices best. Error bars are interquartile ranges of bridge-sampling repetitions (for some models too small to be visible; SI Appendix, SI Methods). (C) Mean probability with which models predict participants’ choices are above chance level (dashed black line) and above a nonlearning model with fixed choice probabilities (dotted black line). The probability is highest for the KFL-UCB model (blue line). Means are computed over a rolling window of five trials. (D) Posterior of the group-level parameter for the KFL-UCB model that acts as a weight on uncertainty in the UCB choice rule (). The posterior mean (vertical line) and 95% CI (black bar on the x axis) show the magnitude of uncertainty influence. Dots are posterior means of individual game-level parameters.
In the following section, we outline a computational model built to determine the extent to which estimation uncertainty influenced choice. We then use this model to examine the multiway relationships between the visual fixation during the period preceding each choice, the values and uncertainties of all of the options estimated by the model, and the actual decision made by participants. We repeat this analysis for the relationships among fixation statistics at the time of reward feedback, the prediction error and estimation uncertainty that the model estimated participants entertain about the chosen option, and the ensuing learning.
Estimation Uncertainty and Choice.
To identify learning and choice processes underlying participants’ behavior, we fitted computational models to their decisions. These models consisted of a learning component, in which participants learn or estimate properties of each option, and a choice component, where they rely on these estimates to decide between the options.
Along with four control models often used to capture learning and choice in these types of tasks (SI Appendix, Modeling Learning and Choices—Control Models), we considered two more sophisticated learning models, each coupled with two forms of choice. The learning models were either a Kalman filter (KF) (8, 13, 36) or a “lazy” KF (KFL), both of which use a variant of the delta rule to update estimated values from a reward-prediction error (Materials and Methods and Eqs. 1 and 2). The KF is a Bayesian model that tracks the expected values of options, as well as the uncertainties in those expectations (i.e., estimation uncertainty). Moreover, it dynamically adjusts the learning rate according to its current estimation uncertainty and the relative noise in the observed rewards. At each point in time, the KF provides an estimate of the value of an option as a normal distribution, whose mean reflects the expected value, and whose variance reflects estimation uncertainty (in the remainder of the text, we will use the term “uncertainty” to refer to estimation uncertainty). These means and variances are the key quantities we subsequently used to examine the role of value and uncertainty in visual fixations. The KFL is similar to the regular KF, but with one crucial difference: It uses a learning rate which is a fraction of that of the regular KF (hence its moniker). Both models take into account differences in variances of options’ rewards in each game (i.e., irreducible uncertainty), leading to different learning rates for each option.
The choice component in the models consisted of either a softmax (SM; Eq. 3; ref. 37) or an upper confidence bound (UCB; Eq. 4; ref. 14) rule. The SM choice rule only uses estimated value to determine choice. As such, exploration is not guided by uncertainty. By contrast, the UCB choice rule implements a form of directed exploration. It uses the uncertainty to approximate the information gained by choosing an option and adds this as an “uncertainty bonus” to the estimated value (38), implying that exploration is driven by a form of expected information gain.
We used a Bayesian hierarchical approach to estimate the parameters of the models. This assumes the parameters at the individual participant level are drawn from common group-level distributions (39). Model evidence shows that models with the UCB choice rule fit the data better than models using the SM choice rule that ignores uncertainty (Fig. 2B). The KFL model with a UCB choice rule described participants’ choices best (KFL-UCB), with a posterior probability of ∼0.99. Lazy versions of KF learning also outperformed the standard ones for the SM choice rule. The KF models with the UCB choice rule convincingly outperformed all four control models (SI Appendix, SI Results). The probability of accurately predicting participants’ choices with the KFL-UCB model increased steadily over the course of a game, reaching a mean of 0.46 () by trial 60 (Fig. 2C), well above the chance level () and above a simple nonlearning model in which we estimate fixed probabilities of choosing each option (mean choice probability of 0.21). The overwhelming evidence in favor of the UCB choice rule shows that estimation uncertainty plays a clear role in choice. This shows that our model-based analysis is more sensitive than the model-free analysis predicated on the different variance patterns. The lack of a between-game effect in performance was likely due to participants quickly learning to ignore the low-value options.
Since the only difference between the best-fitting KFL-UCB model and its SM counterpart (KFL-SM) is the parameter that acts as a weight on uncertainty in the UCB choice rule, the strong evidence favoring the KFL-UCB model over the KFL-SM model indicates that the parameter is reliably positive. Indeed, the posterior distribution of the parameter of the KFL-UCB model has a mean of 0.37, and the CI is (Eq. 4; Fig. 2D). This “inflation of value” is a sizable uncertainty bonus, given that the expected values of options ranged between 2.5 and 6 and their variances between 0.75 and 2.75. As a final check, we also fitted a variant of the KFL-UCB model where the parameter was not constrained to be nonnegative. The KFL-UCB model with the nonnegative parameter outperformed the unconstrained KFL-UCB model with a posterior probability of ∼0.99 (SI Appendix, KFL-UCB Model with Unconstrained β Parameter). This result further affirmed that the parameter is positive and that uncertainty guides choice together with value.
We can also examine the usefulness of the “laziness” parameter () that biases the learning rate in the KFL-UCB model. A value of would make the KFL equivalent to the regular KF. The bias seems to be rather small, as evidenced by the group-level posterior mean (0.93, CI ; Eq. 1). However, the individual variability is substantial: For a sizable number of games (and individuals), parameter values were much lower and closer to 0 (SI Appendix, Fig. S5C). This suggests that the laziness parameter captures significant variation in behavior. Values of the remaining parameters are depicted in SI Appendix, Fig. S5.
Interactions Between Choice and Fixation Process.
We next sought to assess three-way interactions between fixation during the choice epoch, the choice itself, and the combination of value and uncertainty. We first report basic properties of fixation during the choice epoch. We then look at how value and uncertainty influence fixation. Finally, we ask whether and how fixation influences choice.
Properties of the Fixation Process in the Choice Stage.
To analyze interactions between choice and fixation, we focused on the choice stage of a trial (Fig. 1B). Here, participants had 5 s to consider which option to choose, before continuing to the next stage, where they had to execute their choice quickly. The fixation measure of interest in this section is the proportion of time spent fixating on each of the options. We computed the sum of the fixation durations received by each option and divided this quantity by the sum total of fixation durations over all options. We refer to this measure of visual fixation as relative fixation.
Relative fixation resembled the allocation of choice, with increased allocation to high-ranking options as learning progressed (Fig. 2A). This close correspondence to the choice distribution, including the gradual shift of fixation distribution toward high-value options over time, was a first indication that relative fixation might be affected by the same learning process that is guiding choices, as we originally hypothesized. Importantly, relative fixation followed the expected value of each option (i.e., option rank) to a lesser extent than choice proportions (Fig. 2A). This could be due to a greater role of uncertainty in the trial-by-trial fixation dynamics, but could also be attributable to external, potentially independent, factors. Also as expected, and consistent with a reduction in uncertainty, the total time spent fixating on any of the options decreased over the course of learning (mixed-effects regression estimates: intercept = 3.82, CI ; block = , CI ; game = , CI ; block game = 0, CI ; Fig. 3A). As for choice performance, there was no clear difference between the games. For analysis of other measures of the depth and breadth of the visual search process in the choice stage, see SI Appendix, Additional Properties of Visual Fixation.
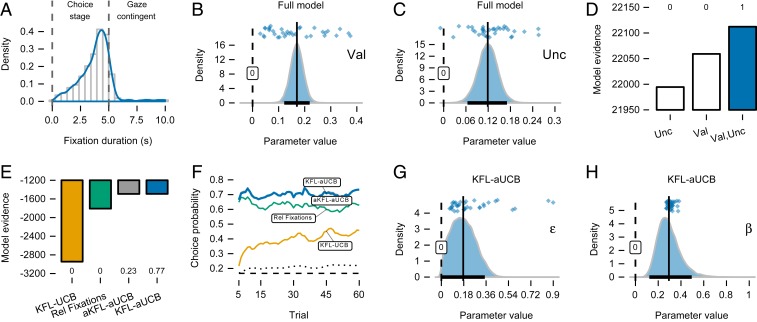
Fig. 3.
Interactions between choice and relative fixation in the choice stage. (A) Density of total fixation duration for all games. Options disappeared after 5 s, but participants sometimes kept fixating on the same location before triggering the execution stage. (B and C) Posteriors of the group-level value (Val; B) and uncertainty parameter (Unc; C) in the full model regressing value and uncertainty on relative fixation. Both parameters are clearly positive, as evident from the mean (vertical line) and 95% CIs entirely above zero (black bar on the x axis). Dots are posterior means of individual game-level parameters. (D) Model evidence (bars) and model comparison (numbers above bars) for the full model and simpler models that regressed either value or uncertainty alone. The full model fits the data best. Error bars are interquartile ranges of bridge-sampling repetitions (too small to be fully visible; SI Appendix, SI Methods). (E) Choice model modulated by relative (Rel) fixation (KFL-aUCB) outperforms the model that regressed relative fixation directly on choices. This indicates that modeling learning and the choice process is important, even when relative fixation is taken into account. The KFL-aUCB model also outperforms the model where learning process is modulated as well (aKFL-aUCB); the KFL-UCB model was included for comparison. (F) The KFL-aUCB model predicts participants’ choices with the highest mean probability. All three are well above the chance level (dashed line) and a nonlearning model that estimates fixed probabilities of choosing options (dotted line). Means are computed in a rolling window of five trials. (G) The group-level parameter in the KFL-aUCB, which determines a pseudo relative fixation for options that were not fixated, is small and closer to zero, indicating that relative fixation was useful as is. (H) The group-level parameter from the UCB choice rule in the KFL-aUCB model shows a decrease in the magnitude of the weight placed on uncertainty after accounting for relative fixation, but the weight is still substantial.
Visual Fixations in the Choice Stage Are Guided by Both Value and Uncertainty.
Given these suggestive results, we considered the conjoint influence of value and uncertainty on fixation in more detail. Previous studies that examined the relationship between choice and fixation (18, 21, 40) could not do this, since they used one-shot choices which precluded modeling of learning and thereby examining the role of uncertainty. To examine such influences, we regressed estimates of value and uncertainty from the KFL-UCB model-fitting choices best on relative fixation in each trial (Modeling Relative Fixation in the Choice Stage). Importantly, it was beliefs about values and uncertainty that were established at the end of the one trial that were used to explain variation in relative fixation in the next trial. We assumed that relative fixation followed a Dirichlet distribution whose shape was influenced by value, uncertainty, and a game-type indicator as a control variable and whose scale was set by a separate parameter (Eq. 6 and 7).
As predicted, the results of Bayesian hierarchical estimation showed a clear positive contribution of both value and uncertainty in explaining variability in relative fixation. The whole of the measurable posterior distribution of the value parameter (Val; Eq. 7) was on the positive side of zero (mean of 0.17, CI ; Fig. 3B), and the same held for the uncertainty parameter (Unc; Eq. 7; mean of 0.12, CI ; Fig. 3C). Estimated game-type effects were negligible (mean of , CI ; Eq. 7), while the estimated scale parameter mostly acted to flatten the predicted relative fixation further (mean parameter was 0.60, CI ; Eq. 6). We verified these results by additionally comparing the full model to two simpler models, where we either regressed uncertainty alone or value alone on relative fixation, keeping the game-type indicator as a control variable (Fig. 3D). The results of model comparison show that the model with both value and uncertainty clearly explained the relative fixation best (posterior probability of ∼1), with simpler models lagging far behind. Hence, options with larger value and estimation uncertainty learned from previous trials attracted more relative fixation in the current trial. Thus, the same value and estimation uncertainty quantities that underlie block-wise changes in choice underlie block-wise changes in fixation allocation.
Visual Fixations in the Choice Stage Influence Choice.
Having established that value and uncertainty affect the fixation process in the choice stage, we next examined whether visual fixation influenced choices. Such an influence has been shown in one-shot value-based choices (18, 40), but not yet for choices in a learning setting.
We first examined the effect of visual fixations on choices by regressing relative fixations in the choice stage directly on choices, using a simple multinomial logistic regression model (Modeling Choices with Visual Fixations Alone). The results of Bayesian hierarchical estimation showed that this simple model had a posterior probability of ∼1 in comparison to the KFL-UCB model that fit choices best previously. What was surprising is the margin by which this simple model outperformed the KFL-UCB model, as shown clearly when examining the probability of accurately predicting participants’ choices (Fig. 3F). Here, it is evident that the ability of the simple regression model to predict choice is almost twice that of KFL-UCB, reaching a mean of 0.63 () by trial 60. This result establishes a strong effect of visual fixation on choice, suggesting the presence of a large choice-related, but value- and uncertainty-independent, component in visual fixations, which was not captured in our KFL-UCB model.
Values and Uncertainty Are Not Completely Reflected in Visual Fixations.
The excellent fit of choice using purely visual fixations prompted the question as to whether the effect of value and uncertainty on choice (KFL-UCB model; Fig. 2B) is mediated by their modest effect on fixation (Fig. 3D), or whether a part of the valuation process that enters choice is not reflected in visual fixation. To test this, we incorporated relative fixation into the best-fitting KFL-UCB model (KFL-aUCB model—“a” prefix marks “attention-modulated”; Modeling Learning and Choices Modulated by Visual Fixations) and examined whether this variant describes choice better than a simple model regressing relative fixation on choice. There are various ways in which relative fixation might be included; here, we assumed that values and uncertainty of options were warped in proportion to the relative fixation that options captured (Eq. 12).
Bayesian hierarchical estimation showed that the KFL-aUCB model outperformed the simple regression model, describing participants’ choices best with a posterior probability of ∼0.77 (Fig. 3E; we included the KFL-UCB base model as well for comparison). The aKFL-aUCB model, in which learning process was modulated as well, followed suit with a posterior probability of ∼0.23. Examining the models’ probability of accurately predicting participants’ choices again, we saw a clear improvement over the simple regression model, with a constant advantage for the KFL-aUCB model throughout the game, reaching a mean of 0.73 () by trial 60 (Fig. 3F). This provides evidence that value and uncertainty are not completely reflected in visual fixation and that explicitly modeling learning and choice processes provides additional predictive power. As a robustness check, we fitted additional attention-modulated models with an SM choice rule instead of UCB and a KF lacking the “laziness” parameter (SI Appendix, Comparison of Learning and Choice Models Modulated by Visual Fixation and Fig. S6). The results showed that the UCB component is important, as all models with it substantially outperformed SM-based models. The laziness parameter is important as well, but it has comparatively smaller impact.
We can compare the parameter governing the strength of uncertainty guidance in the UCB choice rule between the KFL-aUCB and -UCB models. The posterior of in KFL-aUCB was still clearly positive, but its magnitude was less once relative fixation was taken into account (posterior mean of 0.29, CI ; Eq. 4; Fig. 3H)—about of the value for in the KFL-UCB model without fixation modulation (Fig. 2D). Thus, some of the effect through which more uncertain options are more likely to be selected was sublimated when relative fixation was also taken into account.
In the KFL-aUCB model, the attention distribution over options was generated by squashing the relative fixation statistics according to a parameter (Eq. 11). The inferred value of this parameter can inform us about the importance of relative fixation. If is near 1, the distribution would be near uniform, independent of the relative fixation. If is near 0, then the distribution is dominated by the allocation of looking time. Consistent with the other analyses, the posterior distribution of the parameter was small, with a mean value of 0.18 and CI (Fig. 3G).
Interactions Between Learning and Fixation Process.
For analyzing interactions between the learning and fixation process, we focused on the outcome stage of a trial (Fig. 1B), the 3-s period during which participants could observe the reward outcome of their choice. The fixation measure of interest in this section was the total time fixating on the reward feedback in each trial. We will refer to this measure as absolute fixation. As for choice, we first examined the statistics of this measure and then considered successively the effect of value and uncertainty on it and, finally, its potentially additional effect on learning.
Properties of the Fixation Process in the Outcome Stage.
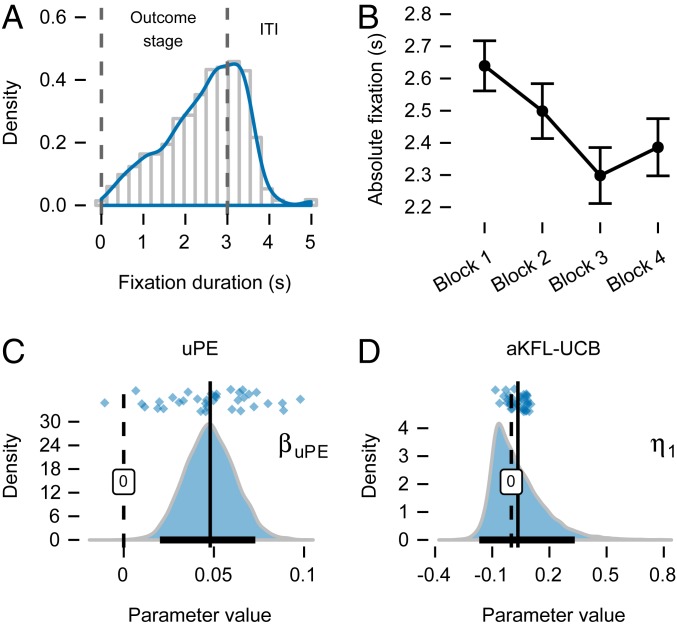
We first considered trial-by-trial variability in absolute fixation. Mean absolute fixation decreased over the course of learning, and there are some, albeit weak, differences between the games (mixed-effects regression estimates: intercept = 2.36, CI ; block = , CI ; game = , CI ; block game = 0.06, CI ). The negative effect of the block is circumstantial evidence that uncertainty, which also decreased over the course of learning, is related to absolute fixation (Fig. 4B). There was a ceiling effect due to the 3-s outcome presentation time, and this led to a left-skewed distribution of absolute fixation (Fig. 4A), but a mean of 2.36 s indicated that the effect was not particularly strong. Participants often continued looking at the feedback location for a few seconds more during the intertrial interval (Fig. 4A). We assumed that these fixations were also associated with processing the reward feedback and included last fixations that ended within 2 s of the intertrial interval. Most importantly for our subsequent considerations, when we repeated the same analysis on the SDs of absolute fixation, we observed considerable variability in absolute fixation (mixed-effects regression estimates: intercept = 0.85, CI ; block = 0.07, CI ; game = 0.03, CI ; block game = , CI ), as evidenced by the intercept estimate. For analysis of other measures of the visual search process, see SI Appendix, Additional Properties of Visual Fixation.
Fig. 4.
Interactions between learning and fixation processes at the outcome stage. (A) Density of absolute fixation in the outcome stage. Even though the option and feedback disappeared after 3 s, participants often kept fixating on the same location during the intertrial interval (ITI). Fixations that extended 2 s into the ITI (i.e., 5 s in total) were also used in the analysis. (B) Like uncertainty and unsigned reward-prediction errors, absolute fixation decreased over the course of learning. (C) Posterior of the group-level slope parameter in the model regressing unsigned reward-prediction error () on absolute fixations in the outcome stage. Almost complete posterior is positive, including the 95% CI (black bar on the x axis), indicating a clearly positive relationship. (D) The group-level slope parameter () that biases the learning rate in the aKFL-UCB model has a positive mean, suggesting a reduced bias for longer fixation on the feedback; however, the CI includes zero.
Unsigned Reward-Prediction Error Guides Fixation in the Outcome Stage.
We next examined interactions between learning and fixation, focusing first on the theory-driven expectation that time spent looking at the reward feedback is guided by uncertainty, as is the case for the learning rate (3). There are two measures of uncertainty of interest here. One is the estimation uncertainty derived from the KF learning model ( variable, Eq. 2), the same quantity used in the UCB choice rule. The other is based on the prediction error and reflects both estimation and irreducible uncertainty (41). As predictions improve and estimation uncertainty decreases, unsigned (i.e., absolute) prediction error should generally decrease as well. However, because unsigned prediction error (uPE) contains irreducible uncertainty (i.e., the variance of options’ reward distributions), it will have continuing fluctuations as well, giving it a momentary character. Prediction errors play no role in uncertainty computations in the KF (Eq. 2), so these two measures should be largely decoupled. Indeed, the correlation between the two measures is negligible, with an average correlation across participants of 0.02 ().
We regressed trial-by-trial uncertainty, prediction error, uPE, and value obtained from the KFL-UCB model on absolute fixation (Modeling Absolute Fixation in the Outcome Stage and Eqs. 8 and 9). We assumed that absolute fixation follows a skew normal distribution constrained to the interval (Fig. 4A), and we included a game-type indicator as a control variable (Eq. 9). We compared the full model with all four predictors to simpler models that excluded particular predictors (Materials and Methods). The results of these model comparisons (SI Appendix, Fig. S7), which naturally take into account model complexity, show that a model including only uPE explained absolute fixation best (), with a model including uPE and value (uPE, Unc model) following suit (). In the uPE model, the effect of a uPE was clearly positive (Fig. 4C), with almost the entire posterior distribution on the positive side (mean of 0.05; CI ). This means that reward outcomes accompanied with large uPE tended to attract longer absolute fixation.
These results suggest that uPE could, in principle, be a more important form of uncertainty than estimation uncertainty for guiding choice. On this basis, we reexamined whether a class of models that uses uPE, instead of estimation uncertainty, in the UCB choice rule might explain choices better than the KFL-UCB model. We implemented two models. The KFL-UPE model used a simple delta rule to learn slow-moving estimates of uPEs coming from the KFL learning model. These estimates were then used in the UCB rule. The K2-UPE model used instead the K2 learning model, which computes estimates of uPEs in a more principled manner, following ref. 41. However, the KFL-UCB model outperformed both models with a posterior probability of ∼1 (SI Appendix, Choice Models with Unsigned Prediction Errors and Fig. S4). Evidently, estimation uncertainty is more relevant for guiding choice than uPEs.
Fixation in the Outcome Stage Influences the Learning Rate.
Given our finding that learning influences visual fixations in the outcome stage, we next considered whether there was a relation in the other direction, i.e., whether fixations affected the course of learning. As for choice, we tested this by comparing the KFL-UCB model that fitted choices best to a similar model in which we allowed absolute fixation at the outcome stage to modulate the learning rate, now referred to as aKFL-UCB (Materials and Methods and Eqs. 2, 4, and 13). We decomposed the laziness parameter of the KFL into an intercept and a slope that multiplied the absolute fixation in the outcome stage.
The slope is the main parameter of interest in the aKFL-UCB model. While the larger portion of its posterior was positive, with a mean of 0.03, the CI included zero, suggesting that the overall effect was weak (Eq. 13; Fig. 4E). To further assess its significance, we compared the aKFL-UCB model to the KFL-UCB model, where learning is not modulated by absolute fixation. The KFL-UCB model outperformed the aKFL-UCB model, with a posterior probability of ∼0.98, suggesting that absolute fixation does not modulate the learning rate.
Discussion
This study enriches our understanding of human reinforcement learning behavior by looking at the four-way interaction between uncertainty, choice, learning, and visual fixation. Our results offer evidence that people learn and choose in partial accordance with normative models, leveraging estimation uncertainty for both choice and learning. We show influences of fixation in reinforcement learning. Signatures of directed exploration can be seen in relative fixation at choice, which goes beyond previous findings on the effects of value and irreducible uncertainty on fixation at choice. Lastly, we provide evidence for the theoretical prediction that fixation at outcome is modulated by estimation uncertainty.
Examining choices alone supports a model where exploration is guided by both value and estimation uncertainty. The winning KFL-UCB model adds an “exploration bonus” to options’ expected rewards (14, 38). This model can be viewed as an approximation to the optimal solution for MAB problems (7, 42) and adds to a growing body of evidence that people use uncertainty-guided choice strategies (8–12). The KFL-UCB also includes a Bayesian learning component (KF) which adapts its learning rate according to uncertainty. This dovetails with previous studies demonstrating a dynamic modulation of learning rate by uncertainty (4, 6). Our results imply that people track uncertainty about estimated value and incorporate it in their choices. This aligns with evidence from perceptual decision making that people have well-calibrated confidence in their choices (43) and from bandit tasks that they have accurate sense of confidence in their value estimates (10, 44). Indeed, neuroimaging studies show that the brain tracks both mean and variance (45, 46), while studies of neuronal population activity support a coding scheme where both mean and variance are represented (47, 48).
Our analyses of visual fixation during choice provide evidence on the role of estimation uncertainty in choice. During the choice stage, where participants considered which option to choose, we found that both value and estimation uncertainty, derived from estimation based on all previous trials, guided visual fixation in the current trial. Hence, directed exploration principles guide both choice and fixation. Examining choices alone does not always reveal the role of estimation uncertainty in exploration (5, 13), but including fixation may provide a more reliable method to decode its role. Previous studies (18, 21, 40) mostly focused on one-shot choices and, hence, could not examine whether and how visual fixation during choice is influenced by learning history, neither value nor estimation uncertainty. There are several exceptions. Perhaps the closest to the present study is recent work by Leong et al. (22), who show that fixation during choice is influenced by value learned from previous trials. However, the authors did not consider models that track uncertainty about value. Another recent study by Walker et al. (24) showed that irreducible uncertainty increases exploration in both choice and attention, i.e., less focus on best options. However, their study used a between-subjects design and cannot explain what components of learning drive fixation on a trial-by-trial basis. Consequently, their results are inconclusive about the role of estimation uncertainty. Several other studies that examined the relation between choice and attention in reinforcement learning eliminated the exploration aspect of the task and, hence, did not examine the role of estimation uncertainty (25, 49).
We found that uPEs guide visual fixation on the reward feedback during learning. Because estimation uncertainty modulates the learning rate, we expected that it would guide fixation (3). Our additional prediction was that reward-prediction errors might also influence fixation, as these indirectly incorporate both estimation and irreducible uncertainty. As learning progresses, estimated value becomes more accurate, and prediction errors correspondingly decrease, thus mimicking the decrease in estimation uncertainty over time. Because prediction errors are influenced by irreducible uncertainty, they track both fast-moving momentary uncertainty and slow-moving estimation uncertainty. Looking at relative fixations to aversive stimuli in a conditioning task, ref. 16 also found evidence for the influence of momentary uncertainty during the outcome stage. Results of both studies jointly provide supportive evidence for a prediction based on ref. 3 that fixation should be related to option uncertainty, following the precepts of Bayesian statistical learning. Interestingly, we did not find that performance of a model where we allowed absolute fixation at the outcome stage to modulate the learning process (aKFL-UCB) improved over a model without fixation modulation (KFL-UCB). This result suggests that fixation reflects the update process rather than having an influence on it. By contrast, refs. 16 and 22 found evidence for such modulation. In ref. 16, learning process was directly observed, and in ref. 22, fixation measure was more detailed, tracking various features of options. These differences likely resulted in a greater sensitivity for detecting the fixation modulation in these studies.
Relative fixation in the choice stage exerted a stronger influence on choice than warranted by the information about value and estimation uncertainty contained in it. In fact, choices were better predicted from relative fixation alone than by the KFL-UCB model. This suggests that fixation carries additional choice-relevant factors which are potentially unrelated to value and estimation uncertainty. For example, low-level features of the symbols denoting individual options may have attracted gaze and biased choice toward those options (28). Such effects are anticipated by an attention-modulated sequential sampling model (18). Here, we identify the magnitude of this modulation in a learning setting: Our ability to predict choice nearly doubled, even for early trials that are usually difficult to predict by reinforcement learning models (Fig. 3F). This indicates that much can be gained by taking into account the visual search process in modeling learning and choices. The KFL-aUCB model, an example of how fixations can be incorporated into reinforcement learning models, explained choice better than relative fixation alone. This suggests that value and estimation uncertainty influenced choices both directly, through an internal valuation process, and indirectly, via fixation. This result invites an interesting conjecture about directed and random exploration (9). The source of directed exploration might be an internal choice process, while that of random exploration might lie in fixation-specific factors unrelated to decision variables.
In tasks where people learn about options’ values from reward feedback, looking at the options in the choice stage does not convey new information per se. In learning tasks, quantities such as estimated value and associated uncertainty must be represented in memory rather than externally. This raises the question of why participants’ fixations in the choice stage were informative of their choices. To make an informed choice between the options, participants will likely retrieve experienced rewards or other indicators of options’ value from memory. Looking at the stimuli, even though not informative per se, can facilitate memory-retrieval and working-memory operations (31, 32, 50, 51). This is akin to the rationale behind sequential sampling mechanisms in one-shot value-based decision making. Ref. 18 hypothesized that the brain accumulates evidence by extracting the features of choice options, retrieving their learned values from the memory, and integrating these for each option. Similar assumptions underlie integrated reinforcement learning and sequential sampling models (20, 52–54). A negative side effect is that fixations can introduce bias, as suggested by ref. 18. Our findings provide insight into the nature of this bias. Being shaped by the learning history, the bias is partly adaptive, as a subset of fixations reflect cognitive processes behind directed exploration.
The attentional drift diffusion model by Krajbich et al. (18) is an appealing account of the within-trial choice process and how this may be influenced by fixation. Recent models combining reinforcement learning and sequential sampling have added across-trial learning dynamics (52–54). These models are not applicable in our task, as the choice stage was fixed to 5 s and separated from the execution (Fig. 1B). Therefore, response times are not informative about the evidence-accumulation process. When we allowed for self-selected choice times in pilot experiments, we discovered that participants plan their next choice immediately after the feedback and during the intertrial interval, making the collection of useful eye-movement data difficult. While such separation seems artificial in a laboratory task, it arguably brings the task closer to real-world situations. For instance, purchasing a certain type of product in a supermarket might happen every few days, effectively separating the choice opportunities and forcing the consumer to make a final choice once they are in front of the shelf. Applying sequential sampling models would require experimental designs that solve the issue of deciding in nonchoice time in a different way. One potential solution would be to use several bandit problems simultaneously and on each trial randomly assign one of these, thereby reducing the usefulness of planning a choice before choice options are presented. Another is to use a contextual bandit problem, where new options can be presented on every trial, while learning would allow making useful predictions about the value of these new options (10, 22, 55).
One pertinent question is how our results regarding visual fixations relate to the role of attention in reinforcement learning. In theoretical work on associative learning in nonhuman animals, the Mackintosh model (56) predicts that stimuli with high predictive value should attract attention, while the Pearce–Hall model (2) predicts that uncertainty has a primary role. These seemingly contradictory accounts of attention have both received empirical support (57). Ref. 3 reconciled the two accounts, proposing that both are correct, but at different stages: During choice, attention is guided by predictive value, while during learning, it is guided by uncertainty. Our results are consistent with this latter account. Fixations during the outcome stage were mainly driven by uPEs, the measure of surprise in the Pearce–Hall model (2). Our results for relative fixations in the choice stage support an extension of the ref. 56 account based on approximately optimal solutions to the exploration–exploitation trade-off (14, 38). In this extension, both value and estimation uncertainty play a role in the choice stage.
Although imperfect, eye movements provide trial-by-trial empirical measures of attention. By recording fixations, attention need not be inferred solely from a computational model (58–60). But there is scope for further integrating measured attention into our models. Rather than using fixations as exogenous modulators of learning and choice, as we have done here (see also ref. 22), a more satisfying treatment would endogenize fixations in a model that learns to direct attention and choose both within and across trials. Research in vision science has suggested that, in tasks such as scene viewing (61) and visual search (62), eye movements are guided by visual information gain. Sprague and Ballard (63) proposed a reinforcement learning model of eye movements where uncertainty guides eye movements. In their model, eye movements to visually uncertain stimuli are reinforced because learning about the identity or state of the stimuli results in decisions that maximize the amount of reward. Previous studies have provided qualitative support for the model, albeit not in a reinforcement learning context (64). Manohar and Husain (65) modeled fixations in one-shot choices between monetary gambles, where the authors argued that visual attention aims to minimize uncertainty about the expected value of gambles. In the latter study, as well as those concerning visual scene detection, fixation directly provides novel information. This contrasts with our study, where fixating on an option can benefit memory retrieval, which, in turn, may serve a similar aim of information gain. This then paves the way to extending previous efforts to endogenize fixations to the current setting, a focus of future research that we plan.
In summary, we provide a detailed window on the interplay between learning, choice, and visual fixation that allows us to trace the path through which uncertainty affects behavior. Our study has theoretical and practical implications. First, it shows that attention and reinforcement learning processes might be more intertwined than previously thought, prompting a need for closer integration of the two in the future studies. It also raises questions, such as whether the source of random exploration can be traced to the learning-independent properties of the fixation process. Second, it illustrates the utility of monitoring eye movements during learning and choice. The ability of reinforcement learning models to predict individual choice substantially improves when fixations are taken into account. Third, since fixations are shaped by learned values and associated uncertainties, the potential for fixation to bias choice is smaller. Finally, the same result could explain everyday phenomena, such as what shelf space in supermarkets people pay attention to and how companies can leverage this to induce exploration of new products.
Materials and Methods
Participants.
We recruited 34 participants (18 female, and ) from the Aarhus University subject pool. After applying a priori exclusion criteria separately to each game played by each participant, 23 participants remained (12 female, and ) and 36 games in total, with 19 decreasing variances and 17 V-shaped variances games (see SI Appendix, SI Methods for details). The experimental sessions were conducted individually in the Cognition and Behavior Lab at Aarhus University and lasted for 75 min on average. Participants had normal or corrected-to-normal vision. The study was approved by the Aarhus University Research Ethics Committee, and all participants provided written informed consent. Participants received a show-up fee of 100 Danish krone and an additional performance-contingent bonus (100 Danish krone on average).
Task.
The experiment comprised two separate MAB tasks (games) with 60 trials each. In each task, participants made repeated choices between the same six options, represented by different symbols (Fig. 1A) and shown in the same location on each trial. Key stages of a trial were the choice stage and outcome stage. In the choice stage, options were presented for a fixed duration of 5 s, during which participants considered which option to choose. They registered their choice in the execution stage that followed the choice stage. In the outcome stage, participants were shown reward feedback overlaid over the chosen option for 3 s. Participants were instructed to maximize the cumulative sum of the rewards during each task.
The main difference between the games was in the variance of the rewards. In the decreasing variances game, the variance of each option decreased from the best option to the worst (according to expected reward). In the V-shaped variances game, the variance decreased from the best option to the third best and then increased again from the fourth best to the worst option. To minimize carryover effects between the games, we used a different set of letters from the Glagoljica alphabet (Fig. 1A) and rescaled rewards differently for each game. The alphabet letters, the options’ locations, the order of the games, and the currencies and scaling factors associated with each game were randomized. At the end of each game, participants received feedback about the experimental points they accumulated and corresponding earnings. After participants finished both games, we informed them which game was randomly selected for the payout, debriefed them, and paid their earnings. A detailed description of the time course of each trial, stimuli construction in each game, and procedure is provided in SI Appendix, SI Methods.
Eye Tracking.
Participants sat in front of a screen with resolution of 1,650 × 1,050 pixels and physical size of mm (widths and heights, respectively). They used a chinrest at ∼60-cm distance from the screen. We recorded eye movements and pupillary responses using a desk-mounted EyeLink 1000 eye tracker (SR Research) with a monocular sampling rate of 500 Hz. We performed a 13-point calibration with the dominant eye, followed by a 13-point drift validation test. We accepted calibrations with offset less than 1 of visual angle. In gaze-contingent stages of the trial—triggering the onset of the choice and execution stage— of gaze locations within a 1-s window needed to be in a circular area with a 3-cm radius around the fixation cross. To make a response in the execution stage, participants had to press a key, and an eye data sample had to be recorded at the same time within a circle representing an option. We used the default algorithm provided by SR Research to detect fixations. In data analysis, we drew an area of interest (AOI) with radius of 3 cm around the center of every option and assigned all fixations falling into these AOIs to the corresponding options. See SI Appendix, SI Methods for further details on the eye-tracking setup.
Data Analysis.
We present here an abbreviated overview of analyses and models. More detailed descriptions, together with model-fitting and comparison procedures, are given in SI Appendix, SI Methods.
Mixed-Effect Regressions.
We examined learning effects in games and differences between game types using Bayesian mixed-effect regressions. We computed averages across blocks and regressed an intercept, a block indicator (coded as for blocks one to four) and a game-type indicator (coded as for decreasing variances and 1 for V-shaped variances game), as well as their interaction on choice performance (chosen option rank) and fixation measures in the choice and outcome stages (total fixation duration, number fixations, and number of options fixated). Intercept and blocks were entered as game-specific random effects, while game type was entered as a fixed effect. CIs were computed as highest posterior density intervals.
Modeling Learning and Choices.
We fitted four main computational models to participants’ choices. Each model consisted of a learning and a choice component. The learning component was either a KF (8, 13, 36) or a KFL model. For the choice component, the models used either an SM (37) or a UCB choice rule (14).
The KF model assumed that participants updated their estimates of the expected reward of choosing option on trial from the observed reward on trial as
| [1] |
where the so-called “Kalman gain” term acts as a learning rate. Term is a simple indicator variable, with a value of 1 if option is chosen on trial and 0 otherwise. The Kalman gain was updated on every trial and depended on the current level of uncertainty
| [2] |
where is the variance of the posterior distribution of the mean reward, updated in every trial as ; is the innovation variance and the reward variance parameter which modulate the learning rate. Parameter determines a bias in the Kalman gain, allowing the filter to learn at slower pace (hence the term “lazy”). In the standard KF, we fixed this parameter to , while in lazy versions, it was an estimated parameter. In both variants, we initialized the estimate of the expected value to . Initial variance was a free parameter such that . We took into account differences between variances of options by setting the parameter to option’s objective variance that we used to draw rewards from: in decreasing variances and in the V-shaped variances game.
In the SM choice rule, participants chose probabilistically according to relative estimated value
| [3] |
where is probability of choosing option at trial , and the inverse temperature parameter determines the sensitivity to differences in estimated values, and with it the amount of exploration.
The UCB choice rule combines estimated value and estimation uncertainty
| [4] |
where is the weight a participant places on estimation uncertainty. While the original UCB rule chooses the option with the highest resulting value deterministically, we implemented a stochastic version by using an SM transformation.
Modeling Relative Fixation in the Choice Stage.
We used trial-by-trial subjective estimates of value and uncertainty from the KFL-UCB model fitting choices best and regressed them on relative fixations in the choice stage. We controlled for potential differences between games by including a game-type indicator. Relative fixations were operationalized as the summed duration of fixations on each of the options divided by the sum of these quantities across all options.
We assumed that relative fixations in the choice stage () follow a Dirichlet distribution
| [5] |
with the probability density function defined as
| [6] |
where is a multinomial beta function that acts as a normalizing constant. The vector of concentration parameters for each trial is obtained by passing values () and estimation uncertainty () of each option obtained from the KFL-UCB model, as well as a game-type indicator as a control variable (), through an SM function
| [7] |
where and are weights on value and uncertainty, while is the effect of game type. We log-transformed estimation uncertainty to linearize it. Games were coded as for the decreasing variances and for the V-shaped variances game, and this effect was included at a group level only. We assumed an additional precision parameter that multiplies the concentration parameters, governing how much probability mass is near the expected value.
Modeling Absolute Fixation in the Outcome Stage.
We used trial-by-trial uncertainty, reward-prediction errors, and value from the KFL-UCB model that fit the choices the best and regressed them on absolute fixations in the outcome stage. We controlled for potential differences between games by including a game-type variable. Absolute fixation measure was operationalized as a sum of durations of all fixations on the reward feedback.
We assumed that fixation durations during the outcome stage () follow a skew normal distribution
| [8] |
truncated to interval . In the full model, the location parameter for each trial is a linear combination of intercept, uncertainty (), prediction error (), uPE (), and value () of chosen option obtained from the KFL-UCB model and game-type indicator variable ()
| [9] |
where , , , and are weights on uncertainty, signed prediction errors, uPEs, and value; is the intercept; and is the effect of game type. We computed uPEs as absolute value of the prediction error, and we log-transformed estimation uncertainty to linearize it. Games were coded as for decreasing variances and for V-shaped variances game, and this effect was included at a group level only. We assumed an additional scale parameter and shape parameter , modeled at an individual game level, without a group-wise parameter.
Modeling Choices with Visual Fixations Alone.
We also regressed relative fixation in the choice stage alone on choices, without explicitly modeling the learning and choice process. We used a simple multinomial logistic regression model, where relative fixation for option in trial , , was passed through an SM function to obtain the probability of choosing option at trial
| [10] |
where the inverse temperature parameter determines the sensitivity to differences in relative fixations.
To avoid the measure of relative fixation taking the value of zero for options that were not fixated on at all in certain trials, we assigned each option a minimum value of which was treated as a free parameter:
| [11] |
Modeling Learning and Choices Modulated by Visual Fixations.
We assumed that visual fixations can modulate the choice or learning component of the KFL-UCB model. We marked the learning and choice component with an “a” prefix to indicate which aspect was modulated by fixations. For example, in the aKFL-UCB model, visual fixations modulated the learning process, while in the KFL-aUCB, they modulated the choice process.
We assumed that visual fixations in the choice stage entered the choice process by reweighting the choice probabilities produced by the models based on options’ estimated values and estimation uncertainty (Eq. 4). The relative fixation measure defined in Eq. 11 enters the UCB rule in an additive way:
| [12] |
We assumed that visual fixations in the outcome stage influence the learning process by making the bias in the Kalman gain update dependent on how long the reward feedback was fixated on in total in the outcome stage of the trial. We implemented this by replacing the parameter in Eq. 2 with a baseline parameter and a slope parameter that depends on , the absolute fixation duration in outcome stage:
| [13] |
where is the standard normal cumulative distribution function, used to constrain the resulting parameter to the range.
Data and Code Availability.
The data, code used for our analyses, and other project-related files are publicly available at the Open Science Framework website: https://osf.io/539ps/ (66).
Supplementary Material
Acknowledgments
We thank Toby Wise, Eran Eldar, Nitzan Shahar, and Rani Moran for their feedback on the project; and Anna Nason for help with collecting the data. H.S., J.L.O., and R.J.D. were supported by Lundbeckfonden Grant R281-2018-27. H.S. and R.J.D. were supported by Max Planck Society Grant 647070403019. R.J.D. was also supported by Wellcome Trust 098362/Z/12/Z. P.D. was supported by the Gatsby Charitable Foundation and the Max Planck Society. This work was carried out while R.J.D. was in receipt of a Lundbeck Visiting Professorship (R290-2018-2804) to Danish Research Centre for Magnetic Resonance, Copenhagen.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
Data deposition: The data, code used for our analyses, and other project-related files are publicly available at the Open Science Framework website: https://osf.io/539ps/.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1911348117/-/DCSupplemental.
References
- 1.Anderson B. D., Moore J. B., Optimal Filtering (Courier Corporation, North Chelmsford, MA, 2012). [Google Scholar]
- 2.Pearce J. M., Hall G., A model for Pavlovian learning: Variations in the effectiveness of conditioned but not of unconditioned stimuli. Psychol. Rev. 87, 532–552 (1980). [PubMed] [Google Scholar]
- 3.Dayan P., Kakade S., Montague P. R., Learning and selective attention. Nat. Neurosci. 3, 1218–1223 (2000). [DOI] [PubMed] [Google Scholar]
- 4.Behrens T. E., Woolrich M. W., Walton M. E., Rushworth M. F., Learning the value of information in an uncertain world. Nat. Neurosci. 10, 1214–1221 (2007). [DOI] [PubMed] [Google Scholar]
- 5.Payzan-LeNestour E., Bossaerts P., Risk, unexpected uncertainty, and estimation uncertainty: Bayesian learning in unstable settings. PLoS Comput. Biol. 7, e1001048 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Nassar M. R., Wilson R. C., Heasly B., Gold J. I., An approximately Bayesian delta-rule model explains the dynamics of belief updating in a changing environment. J. Neurosci. 30, 12366–12378 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gittins J., Glazebrook K., Weber R., Multi-armed Bandit Allocation Indices (John Wiley & Sons, New York, NY, 2011). [Google Scholar]
- 8.Speekenbrink M., Konstantinidis E., Uncertainty and exploration in a restless bandit problem. Top. Cogn. Sci. 7, 351–367 (2015). [DOI] [PubMed] [Google Scholar]
- 9.Wilson R. C., Geana A., White J. M., Ludvig E. A., Cohen J. D., Humans use directed and random exploration to solve the explore–exploit dilemma. J. Exp. Psychol. Gen. 143, 2074–2081 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Stojic H., Schulz E., Analytis P. P., Speekenbrink M., It’s new, but is it good? How generalization and uncertainty guide the exploration of novel options. https://psyarxiv.com/p6zev/ (23 October 2019). [DOI] [PubMed]
- 11.Gershman S. J., Deconstructing the human algorithms for exploration. Cognition 173, 34–42 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Knox W. B., Otto A. R., Stone P., Love B., The nature of belief-directed exploratory choice in human decision-making. Front. Psychol. 2, 398 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Daw N. D., O’Doherty J. P., Dayan P., Seymour B., Dolan R. J., Cortical substrates for exploratory decisions in humans. Nature 441, 876–879 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Auer P., Cesa-Bianchi N., Fischer P., Finite-time analysis of the multiarmed bandit problem. Mach. Learn. 47, 235–256 (2002). [Google Scholar]
- 15.Thompson W. R., On the likelihood that one unknown probability exceeds another in view of the evidence of two samples. Biometrika 25, 285–294 (1933). [Google Scholar]
- 16.Wise T., Michely J., Dayan P., Dolan R. J., A computational account of threat-related attentional bias. PLoS Comput. Biol. 15, e1007341 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ashby N. J., Rakow T., Eyes on the prize? Evidence of diminishing attention to experienced and foregone outcomes in repeated experiential choice. J. Behav. Decis. Mak. 29, 183–193 (2016). [Google Scholar]
- 18.Krajbich I., Armel C., Rangel A., Visual fixations and the computation and comparison of value in simple choice. Nat. Neurosci. 13, 1292–1298 (2010). [DOI] [PubMed] [Google Scholar]
- 19.Konovalov A., Krajbich I., Gaze data reveal distinct choice processes underlying model-based and model-free reinforcement learning. Nat. Commun. 7, 12438 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cavanagh J. F., Wiecki T. V., Kochar A., Frank M. J., Eye tracking and pupillometry are indicators of dissociable latent decision processes. J. Exp. Psychol. Gen. 143, 1476–1488 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Shimojo S., Simion C., Shimojo E., Scheier C., Gaze bias both reflects and influences preference. Nat. Neurosci. 6, 1317–1322 (2003). [DOI] [PubMed] [Google Scholar]
- 22.Leong Y. C., Radulescu A., Daniel R., DeWoskin V., Niv Y., Dynamic interaction between reinforcement learning and attention in multidimensional environments. Neuron 93, 451–463 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Schoemann M., Schulte-Mecklenbeck M., Renkewitz F., Scherbaum S., Forward inference in risky choice: Mapping gaze and decision processes. J. Behav. Decis. Mak. 32, 521–535 (2019). [Google Scholar]
- 24.Walker A. R., Luque D., Le Pelley M. E., Beesley T., The role of uncertainty in attentional and choice exploration. Psychon. Bull. Rev. 26, 1–6 (2019). [DOI] [PubMed] [Google Scholar]
- 25.Hu Y., Kayaba Y., Shum M., Nonparametric learning rules from bandit experiments: The eyes have it! Games Econ. Behav. 81, 215–231 (2013). [Google Scholar]
- 26.Zhaoping L., Understanding Vision: Theory, Models, and Data (Oxford University Press, Oxford, UK, 2014). [Google Scholar]
- 27.Orquin J. L., Lagerkvist C. J., Effects of salience are both short-and long-lived. Acta Psychol. 160, 69–76 (2015). [DOI] [PubMed] [Google Scholar]
- 28.Orquin J. L., Loose S. M., Attention and choice: A review on eye movements in decision making. Acta Psychol. 144, 190–206 (2013). [DOI] [PubMed] [Google Scholar]
- 29.Usher M., McClelland J. L., The time course of perceptual choice: The leaky, competing accumulator model. Psychol. Rev. 108, 550–592 (2001). [DOI] [PubMed] [Google Scholar]
- 30.Ratcliff R., McKoon G., The diffusion decision model: Theory and data for two-choice decision tasks. Neural Comput. 20, 873–922 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Awh E., Jonides J., Overlapping mechanisms of attention and spatial working memory. Trends Cognit. Sci. 5, 119–126 (2001). [DOI] [PubMed] [Google Scholar]
- 32.Awh E., Vogel E. K., Oh S. H., Interactions between attention and working memory. Neuroscience 139, 201–208 (2006). [DOI] [PubMed] [Google Scholar]
- 33.Johansson R., Johansson M., Look here, eye movements play a functional role in memory retrieval. Psychol. Sci. 25, 236–242 (2014). [DOI] [PubMed] [Google Scholar]
- 34.Holm L., Mäntylä T., Memory for scenes: Refixations reflect retrieval. Mem. Cogn. 35, 1664–1674 (2007). [DOI] [PubMed] [Google Scholar]
- 35.Usher M., Cohen J. D., Servan-Schreiber D., Rajkowski J., Aston-Jones G., The role of locus coeruleus in the regulation of cognitive performance. Science 283, 549–554 (1999). [DOI] [PubMed] [Google Scholar]
- 36.Zajkowski W. K., Kossut M., Wilson R. C., A causal role for right frontopolar cortex in directed, but not random, exploration. eLife 6, e27430 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Sutton R. S., Barto A. G., Reinforcement Learning: An Introduction (MIT Press, Cambridge, MA, 1998). [Google Scholar]
- 38.Kakade S., Dayan P., Dopamine: Generalization and bonuses. Neural Netw. 15, 549–559 (2002). [DOI] [PubMed] [Google Scholar]
- 39.Kruschke J. K., Doing Bayesian Data Analysis: A Tutorial with R, JAGS, and Stan (Academic Press, New York, NY, 2014). [Google Scholar]
- 40.Armel K. C., Beaumel A., Rangel A., Biasing simple choices by manipulating relative visual attention. Judgment Decis. Making 3, 396–403 (2008). [Google Scholar]
- 41.Sutton R. S., “Gain adaptation beats least squares” in Proceedings of the 7th Yale Workshop on Adaptive and Learning Systems (Yale University, New Haven, CT, 1992), pp. 161–166. [Google Scholar]
- 42.Whittle P., Multi-armed bandits and the Gittins index. J. R. Stat. Soc. Ser. B 42, 143–149 (1980). [Google Scholar]
- 43.Moran R., Teodorescu A. R., Usher M., Post choice information integration as a causal determinant of confidence: Novel data and a computational account. Cogn. Psychol. 78, 99–147 (2015). [DOI] [PubMed] [Google Scholar]
- 44.Boldt A., Blundell C., De Martino B., Confidence modulates exploration and exploitation in value-based learning. Neurosci. Conscious. 2019, niz004 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Symmonds M., Wright N. D., Bach D. R., Dolan R. J., Deconstructing risk: Separable encoding of variance and skewness in the brain. Neuroimage 58, 1139–1149 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Critchley H. D., Mathias C. J., Dolan R. J., Neural activity in the human brain relating to uncertainty and arousal during anticipation. Neuron 29, 537–545 (2001). [DOI] [PubMed] [Google Scholar]
- 47.Ma W. J., Jazayeri M., Neural coding of uncertainty and probability. Annu. Rev. Neurosci. 37, 205–220 (2014). [DOI] [PubMed] [Google Scholar]
- 48.Ma W. J., Beck J. M., Latham P. E., Pouget A., Bayesian inference with probabilistic population codes. Nat. Neurosci. 9, 1432–1438 (2006). [DOI] [PubMed] [Google Scholar]
- 49.Beesley T., Nguyen K. P., Pearson D., Le Pelley M. E., Uncertainty and predictiveness determine attention to cues during human associative learning. Q. J. Exp. Psychol. 68, 2175–2199 (2015). [DOI] [PubMed] [Google Scholar]
- 50.Theeuwes J., Belopolsky A., Olivers C. N., Interactions between working memory, attention and eye movements. Acta Psychol. 132, 106–114 (2009). [DOI] [PubMed] [Google Scholar]
- 51.Kiyonaga A., Egner T., Working memory as internal attention: Toward an integrative account of internal and external selection processes. Psychon. Bull. Rev. 20, 228–242 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Ratcliff R., Frank M. J., Reinforcement-based decision making in corticostriatal circuits: Mutual constraints by neurocomputational and diffusion models. Neural Comput. 24, 1186–1229 (2012). [DOI] [PubMed] [Google Scholar]
- 53.Pedersen M. L., Frank M. J., Biele G., The drift diffusion model as the choice rule in reinforcement learning. Psychon. Bull. Rev. 24, 1234–1251 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Frank M. J., et al. , fMRI and EEG predictors of dynamic decision parameters during human reinforcement learning. J. Neurosci. 35, 485–494 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Schulz E., Konstantinidis E., Speekenbrink M., Putting bandits into context: How function learning supports decision making. J. Exp. Psychol. Learn. Mem. Cogn. 44, 927–943 (2018). [DOI] [PubMed] [Google Scholar]
- 56.Mackintosh N. J., A theory of attention: Variations in the associability of stimuli with reinforcement. Psychol. Rev. 82, 276–298 (1975). [Google Scholar]
- 57.Pearce J. M., Mackintosh N. J., “Two theories of attention: A review and a possible integration” in Attention and Associative Learning: From Brain to Behaviour, Mitchell C., LePelley M., Eds. (Oxford University Press, Oxford, UK, 2010), pp. 11–39. [Google Scholar]
- 58.Yu A. J., Dayan P., Uncertainty, neuromodulation, and attention. Neuron 46, 681–692 (2005). [DOI] [PubMed] [Google Scholar]
- 59.Niv Y., et al. , Reinforcement learning in multidimensional environments relies on attention mechanisms. J. Neurosci. 35, 8145–8157 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Marković D., Gläscher J., Bossaerts P., O’Doherty J., Kiebel S. J., Modeling the evolution of beliefs using an attentional focus mechanism. PLoS Comput. Biol. 11, e1004558 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Bruce N. D. B., Tsotsos J. K., Saliency, attention, and visual search: An information theoretic approach. J. Vis. 9, 1–24 (2009). [DOI] [PubMed] [Google Scholar]
- 62.Wolfe J. M., Visual search. Curr. Biol. 20, R346–R349 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Sprague N., Ballard D., “Eye movements for reward maximization” in Proceedings of the 16th International Conference on Neural Information Processing Systems, Thrun S., Saul L. K., Schölkopf B., eds. (MIT Press, Cambridge, MA, 2004), pp. 1467–1474. [Google Scholar]
- 64.Sullivan B. T., Johnson L., Rothkopf C. A., Ballard D., Hayhoe M., The role of uncertainty and reward on eye movements in a virtual driving task. J. Vis. 12, 1–17 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Manohar S., Husain M., Attention as foraging for information and value. Front. Hum. Neurosci. 7, 711 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Stojic H., Orquin J. L., Dayan P., Dolan R., Speekenbrink M., Project files for “Uncertainty in learning, choice, and visual fixation.” Open Science Framework, https://osf.io/539ps. Deposited 10 December 2019. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data, code used for our analyses, and other project-related files are publicly available at the Open Science Framework website: https://osf.io/539ps/ (66).