Privacy-preserving model learning on a blockchain network-of-networks

Abstract

Objective

To facilitate clinical/genomic/biomedical research, constructing generalizable predictive models using cross-institutional methods while protecting privacy is imperative. However, state-of-the-art methods assume a “flattened” topology, while real-world research networks may consist of “network-of-networks” which can imply practical issues including training on small data for rare diseases/conditions, prioritizing locally trained models, and maintaining models for each level of the hierarchy. In this study, we focus on developing a hierarchical approach to inherit the benefits of the privacy-preserving methods, retain the advantages of adopting blockchain, and address practical concerns on a research network-of-networks.

Materials and Methods

We propose a framework to combine level-wise model learning, blockchain-based model dissemination, and a novel hierarchical consensus algorithm for model ensemble. We developed an example implementation HierarchicalChain (hierarchical privacy-preserving modeling on blockchain), evaluated it on 3 healthcare/genomic datasets, as well as compared its predictive correctness, learning iteration, and execution time with a state-of-the-art method designed for flattened network topology.

Results

HierarchicalChain improves the predictive correctness for small training datasets and provides comparable correctness results with the competing method with higher learning iteration and similar per-iteration execution time, inherits the benefits of the privacy-preserving learning and advantages of blockchain technology, and immutable records models for each level.

Discussion

HierarchicalChain is independent of the core privacy-preserving learning method, as well as of the underlying blockchain platform. Further studies are warranted for various types of network topology, complex data, and privacy concerns.

Conclusion

We demonstrated the potential of utilizing the information from the hierarchical network-of-networks topology to improve prediction.

INTRODUCTION

Background and significance

Cross-institutional predictive modeling can accelerate clinical, genomic, and biomedical research^1–5 by learning more generalizable models from the increased number of patient records (Figure 1A). Aiming at protecting privacy of the patients, several centralized privacy-preserving algorithms^6–9 were developed based on the principle of exchanging the models instead of disseminating Protected Health Information (PHI) data directly (Figure 1B). Although these approaches ensured prediction correctness while honoring patients’ privacy, the fact that only a central server manages the entire model training process creates problems yet to be solved: (1) imbalance in the compute resource allocation can occur, where the central server can potentially assign work to a participating healthcare institution unfairly while letting the other institutions remain idle most of time; (2) model parameters in the central server can be modified obliviously during model training; (3) the provenance (ie, source institution) of models may be changed by the central server in an undetectable way by local sites; and (4) information gaps about disseminated models occur between the central servers with full visibility about generated models and non-central-servers with only partial visibility.¹⁰ These potential concerns can become hurdles when adopting privacy-preserving learning algorithms among multiple institutions.

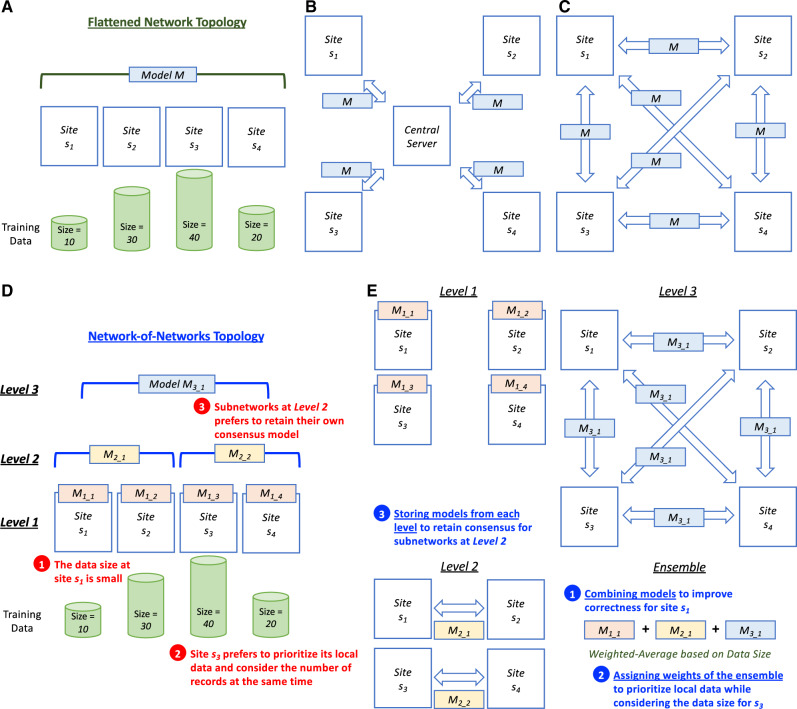
Figure 1.

Comparison of privacy-preserving learning methods on different network topologies. A. The participating sites in a flattened network topology, which is a fully-connected network. The number indicates the size of the records in the database at each site. For a smaller site (eg, s₃), the number of records may not be enough to train a generalizable predictive model, however the direct exchange of data is not preferred due to privacy considerations. B. The centralized learning methods can build a global model by exchanging the models instead of the data on a flattened network. However, they may have risk concerns such as single point of control, mutable data/records, change provenance, and partial visibility.¹⁰C. The decentralized methods on a flattened network can address the abovementioned privacy risks by having no single point of control, immutable data/records, data provenance, and complete visibility.¹⁰D. The real-world network-of-networks topology which may contain practical issues such as (1) data size may be small for rare diseases/conditions, (2) each site may prefer to prioritize their local data while considering the data size, and (3) each subnetwork may prefer to retain their own models. E. The proposed hierarchical learning method exploiting the network-of-networks information, which is not fully utilized by the decentralized learning methods designed for a flattened network, to address the practical issues. Specifically, by computing, recording, and combining the models from each level with different weights based on data size, the hierarchical method aims at (1) improving predictive correctness with small data (eg, s₁), (2) prioritizing local data for each site (eg, s₃), and (3) retaining consensus for each subnetwork (eg, Level 2). It also inherits the advantages of the decentralized method designed for a flattened network.

To mitigate these risks, a plausible solution is to adopt blockchain,¹¹ the underlying technology of modern fully decentralized crypto-currencies (Figure 1C). (1) As a peer-to-peer architecture,¹² blockchain can serve as a distributed ledger for the institutions to exchange machine learning models without a central server thus removing the concern of a single-point-of-control and potential computational unfairness. (2) The design of the consensus protocols in blockchain makes the change of the ledger extremely difficult and therefore ensures the immutability of the models stored on the blockchain.¹² (3) Blockchain also preserves provenance of the ledger, which makes the source of the models verifiable.¹³ (4) Blockchain is transparent (ie, “everyone can see everything”),¹³ and therefore all models are visible to every participating healthcare institution. It should be noted that although there are many other existing decentralized architecture (eg, gossiping algorithms^14–16) blockchain contains the above-mentioned technical features (ie, immutability, provenance, and transparency) and has been adopted for critical financial applications for an extended period of time.¹¹ Therefore, we utilize blockchain as the decentralized architecture to alleviate the concerns of centralization.

However, the state-of-the-art blockchain-based learning methods^10,17,18 assume that the network has a “flattened” topology, as shown in Figure 1A. In the real world, the structure of research networks can be more complicated than a simple topology. For example, PCORnet,¹⁹ a major initiative to support an effective, sustainable national research infrastructure, includes 13 clinical data research networks (CDRNs). Specifically, pSCANNER,²⁰ one of the CDRN subnetworks in PCORnet led by University of California San Diego (UCSD), includes subnetworks with data from diverse sites, and is part of this multi-level “network-of-networks” (ie, pSCANNER includes SCANNER²¹ and UCReX²² subnetworks, with each containing multiple sites).

As shown in Figure 1D, such a real-world network-of-networks topology can imply practical issues such as (1) small data size for rare diseases/conditions (eg, Kawasaki Disease^23,24), (2) each site may prefer to prioritize their own model (eg, UCSD may tend to put more weight on the model learned from local data, while still including models from other institutions to increase model generalizability) while still considering its data size; and (3) subnetwork model maintenance (eg, the pSCANNER network may prefer to retain the aggregated model from its own participating networks in parallel with the model learned from the whole network such as PCORnet). Without utilizing the information of the hierarchical topology, the learning method designed for a flattened topology^10,17,18 could not address these practical issues effectively. As a result, the attempt to improve the correctness of the cross-institutional predictive modeling while preserving patient privacy may not be feasible due to the insufficiency of the existing methods regarding small data size, model prioritization, and model maintenance for subnetworks.

Therefore, a hierarchical approach (Figure 1E) that considers the network-of-networks information is critical to address these issues. By computing, recording, and combining the models from each level with different weights based on data size, we anticipate the hierarchical method to (1) improve predictive correctness with small data, (2) prioritize local data for each site while considering the number of records, and (3) retain consensus for each subnetwork. Also, the benefits of the methods designed for flattened network (eg, the property of fair compute loads for every site of GloreChain¹⁰) and the advantages of adopting a decentralized architecture (ie, no single point of control, immutable data/records, data provenance, and complete visibility¹⁰) should be inherited.

Objective

We aim at developing a hierarchical modeling framework with 3 goals: (a) inherit the benefits of the privacy-preserving learning methods designed for flattened network, (b) retain the advantages of adopting a decentralized architecture, and (c) address practical data size, local model, and subnetwork consensus issues on a real-world clinical, genomics and biomedical research network-of-networks.

MATERIALS AND METHODS

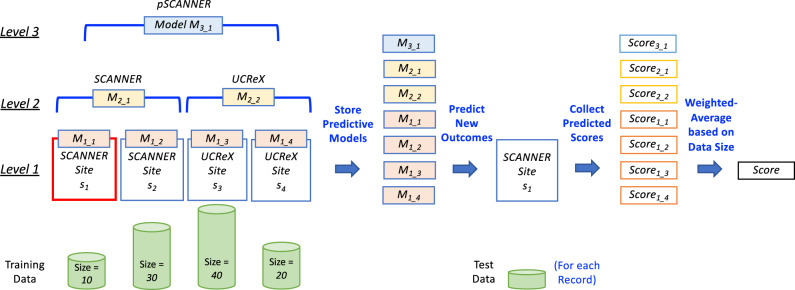
To achieve the first goal of inheriting the benefits of the state-of-the-art learning method at every level of the hierarchical network-of-network topology (Figure 1E), we adopt the learning methods designed for a flattened network. With this design, we ensure that at each level the predictive correctness and fair compute loads properties are preserved. Next, to retain the advantages of a decentralized architecture, we utilized peer-to-peer blockchain technology^{11,13,25–35} to disseminate models and therefore avoid concerns such as single point of control. Finally, to tackle the practical issues on a real-world research network-of-networks, we propose to leverage the hierarchical topology information to store and combine the models from each level. Figure 2 demonstrates the concept of the proposed hierarchical consensus learning using an example of pSCANNER, which consists of 2 subnetworks (SCANNER and UCReX).

Figure 2.

Hierarchical consensus learning. Suppose this 3-level hierarchical network-of-networks consists of 4 sites (Level 1) from 2 subnetworks (SCANNER²¹ and UCReX²² at Level 2) of an overarching network (pSCANNER²⁰ at Level 3), and we would like to predict a new outcome for site s₁. After the consensus models are learned at each level, we first stored all models (7 in this example), used each of the models to predict the score for the new record (in the test data on site s₁), collected the prediction scores for the new record, and then combined the scores using weighted-average method based on the size of the training data.

We developed HierarchicalChain to evaluate our proposed framework. HierarchicalChain contains the following 3 main components: 1) a level-wise learning method which is originally designed for a flattened network, 2) a blockchain network and its on-chain data structure, and 3) a hierarchical consensus learning algorithm. These components are introduced in the next 3 subsections, followed by the implementation details, datasets, and experiment settings.

Level-wise GloreChain decentralized model learning

Our proposed general framework can adopt both online and batch decentralized learning algorithms. Online methods, such as ModelChain¹⁷ and ExplorerChain,¹⁸ focus on efficient retraining (ie, updated model for new data without a complete retrain of the model). In contrast, batch methods, such as GloreChain,¹⁰ emphasize effective prediction results (ie, learn mode using all data at once to achieve higher correctness).

For HierarchicalChain, we selected the batch method GloreChain, because we aim at achieving high predictive correctness. GloreChain also provides an additional advantage of having fair compute loads for each participating site.¹⁰ GloreChain is based on GLORE,⁷ a centralized privacy-preserving learning method. We adapted GloreChain to a level-wise method, such that the consensus models can be trained at each level of the hierarchical topology (eg, a total of 7 models learned from 3 levels as shown in Figure 2). We denote the adapted method as GloreChain-LevelWise.

The blockchain network and on-chain data structure

HierarchicalChain utilized a permissioned blockchain network, in which only authorized sites (eg, member institutions of consortia like PCORnet¹⁹) can participate. Such a permissioned network improves privacy protection by prefiltering participants. The incentives for each site and each subnetwork are the improved model generalizability and thus predictive correctness, as well as the immutably recorded models for each level of the network-of-networks. Although the network structure is hierarchical, we use only one blockchain network to disseminate all models. This simple design can reduce the maintenance cost.

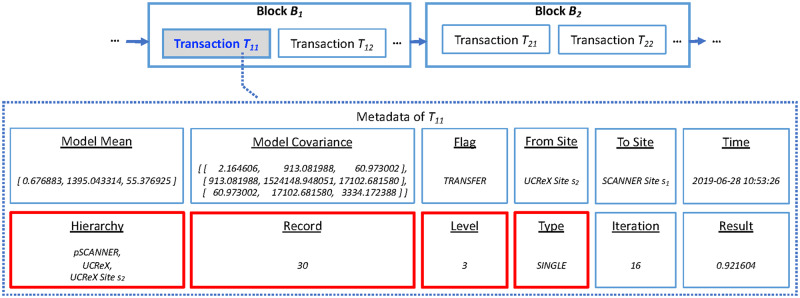
The transaction metadata of blockchain was exploited to store the models and related information, as shown in Figure 3. The transaction amount are all zeroes because we adopt blockchain as a pure ledger for data dissemination instead of coin transferring. The details of the data stored on-chain are explained in Table 1. Compared to GloreChain,¹⁰ we added 4 new fields (ie, “Hierarchy,” “Record,” “Level,” and “Type”) in HierarchicalChain to incorporate information from the hierarchical topology. The space complexity of the on-chain transaction metadata is O (M² + H), where M is the number of covariates and H is the number of the level of the hierarchy. By only disseminating partially learned models (ie, aggregated parameters) on-chain and keeping all observation-level PHI data off-chain, the privacy of the patient can be preserved.

Figure 3.

Example of block, transaction, and transaction metadata of HierarchicalChain. The predictive model and related information are stored in the transaction metadata (eg, Metadata of Transaction T₁₁). The 4 red fields (“Hierarchy,” “Record,” “Level,” and “Type”) incorporate the newly added hierarchical information for HierarchicalChain compared to GloreChain.¹⁰ The details of the data fields are described in Table 1.

Table 1.

An example of on-chain data of HierarchicalChain. In this example, M = 2 is the number of the covariates in the dataset and H = 3 is the number of levels of the hierarchy. The partial model of GloreChain-LevelWise contains both “Model Mean” and “Model Covariance,” while the final model is the consensus mean vector.^7,10 The “Flag” is TRANSFER, representing the submission of a model from 1 site to another via the blockchain. In this round, the model is transferred from the UCReX Site s₂ (“From Site”) to the SCANNER Site s1 (“To Site”) at “2019-06-28 10: 53: 26” (“Time”). The “Hierarchy” of “pSCANNER, UCReX, and UCReX Site s₂” represents the subnetworks of the local site (“UCReX Site s₂”), and the number of records on the local site is 30 (“Record”). The “Level” of 3 shows the current learning process happening on Level 3, and the “Type” of the model is single-level (“SINGLE”). The “Iteration” of 16 is the number of learning iterations at current level, and the “Result” indicates the value of the evaluation metric for correctness (eg, the full area under the receiver operating characteristic curve [AUC]).^36–38 The 4 newly added fields, compared to GloreChain,¹⁰ are marked with an asterisk.

Field	Description	Possible Values	Example
Model Mean	The mean vector of the GloreChain-LevelWise partial model7,10	A numerical vector with its length equals M+1	[ 0.676883, 1395.043314, 55.376925 ]
Model Covariance	The variance-covariance matrix of the GloreChain-LevelWise partial model7,10	A numerical (M+1) x (M+1) square symmetric matrix	[ [ 2.164606, 913.081988, 60.973002 ], [ 913.081988, 1524148.948051, 17102.681580 ], [ 60.973002, 17102.681580, 3334.172388 ] ]
Flag	The type of action a site has taken to the model	UNKNOWN, HIERARCHY, INITIALIZE, UPDATE, EVALUATE, TRANSFER, CONSENSUS, COMPLETE, TEST, CLEAR	TRANSFER
From Site	The site that has submitted the model	A unique name or identifier representing the site	UCReX Site s2
To Site	The site which will receive the model	A unique name or identifier representing the site	SCANNER Site s1
Time	The time that the site submitted the model	A timestamp	2019-06-28 10: 53: 26
Hierarchy *	The subnetworks that the local site belong to	A string vector with its length equals H and contains unique names or identifiers of each level of the hierarchy	pSCANNER, UCReX, UCReX Site s2
Record *	The number of the records of the local site	A non-negative integer	30
Level *	The current level of hierarchy for learning (“1” for ensemble models)	A non-negative integer	3
Type *	The type of the model, either single-level (“SINGLE”) or ensemble (“HORIZONTAL” or “VERTICAL”)	UNKNOWN, SINGLE, HORIZONTAL, VERTICAL	SINGLE
Iteration	The current iteration of the learning process at current level	A non-negative integer	16
Result	The value of the evaluation metric when the learning process completes	A numerical value between 0 and 1	0.921604

The Proof-of-Hierarchy consensus learning algorithm

We developed Proof-of-Hierarchy (PoH), a new algorithm to learn the consensus predictive model on a hierarchical network-of-networks. First, the consensus models of each level are learned using GloreChain-LevelWise method. These models are stored on the single shared blockchain network and thus can be accessed by every site freely. Finally, to predict the outcome of a new patient data record, a site computes the prediction scores using all models and combines the scores to generate the final prediction result.

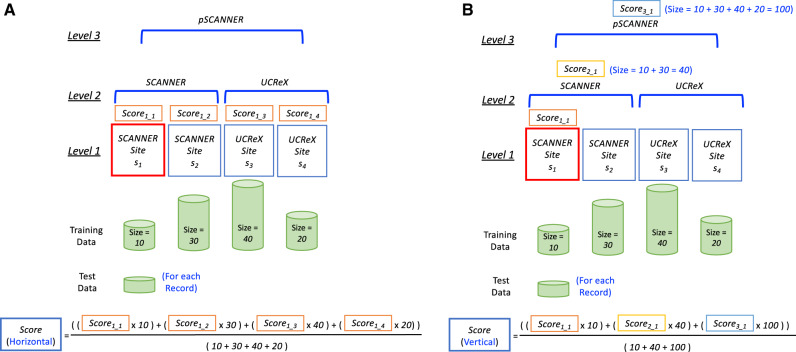
To combine the scores, we adopted an ensemble approach, which has been utilized often in biomedical informatics research, such as in medical information extraction on clinical notes^23,39 and early detection of breast cancer using X-ray images.⁴⁰ In the PoH algorithm, we exploited 2 simple weighted-average ensemble methods⁴⁰: horizontal ensemble and vertical ensemble. The horizontal ensemble (Figure 4A) combines Level 1 models, weighted by their training data size, with the intuition that a large institution may prefer to emphasize their own model for the prediction. The vertical ensemble (Figure 4B) combines all levels of models related to the local site weighted by the size of each level of network. The intuition of this method is to consider both the specificity from the small/local data and the generalizability from the remote/subnetwork data. Note that although these 2 ensemble methods combine the results from the models of each level of the hierarchical topology, those models are stored immutably on the blockchain and can be retrieved at any time as needed.

Figure 4.

Examples of the ensemble methods adopted in the Proof-of-Hierarchy (PoH) algorithm. A. Horizontal ensemble. For each of the new patient records at SCANNER Site s₁, we first identify all Level 1 sites (ie, SCANNER Site s₁, SCANNER Site s₂, UCReX Site s₃, and UCReX Site s₄). The prediction scores from each Level 1 models (ie, Score_{1_1}, Score_{1_2}, Score_{1_3}, and Score_{1_4}) are then combined using weighted-average with the training data sizes of each site (ie, 10, 30, 40, and 20 for SCANNER Site s₁, SCANNER Site s₂, UCReX Site s₃, and UCReX Site s₄, respectively) as the weights. B. Vertical ensemble. For each of the new patient records at SCANNER Site s₁, we first identify the levels related to SCANNER Site s₁, including SCANNER Site s₁ itself (Level 1), SCANNER (Level 2), and pSCANNER (Level 3). Then, the prediction scores from the models of each level (ie, Score_{1_1}, Score_{2_1}, and Score_{3_1}) are then combined using weighted-average with the training data sizes of each level of the hierarchy (ie, 10, 40, and 100, for SCANNER Site s₁, SCANNER, and pSCANNER, respectively) as the weights.

The details of the PoH algorithm are described in Supplementary Algorithms A.1, A.2, and A.3 in Appendix A. The main PoH (Supplementary Algorithm A.1) contains both level-wise model learning (Supplementary Algorithm A.2) and horizontal/vertical ensemble (Supplementary Algorithm A.3). We assume the topology of the network-of-network is a perfect tree (eg, the network-of-networks contains 2 sub-networks and each sub-network contains 2 sites; that is, the number of levels is 3, and the total number of participating sites is 4). The 5 hyperparameters of PoH includes the polling time period Δ, the waiting time period Θ, the maximum per-level iteration Ω, the total number of participating sites N, and the number of levels H.

The implementation of HierarchicalChain

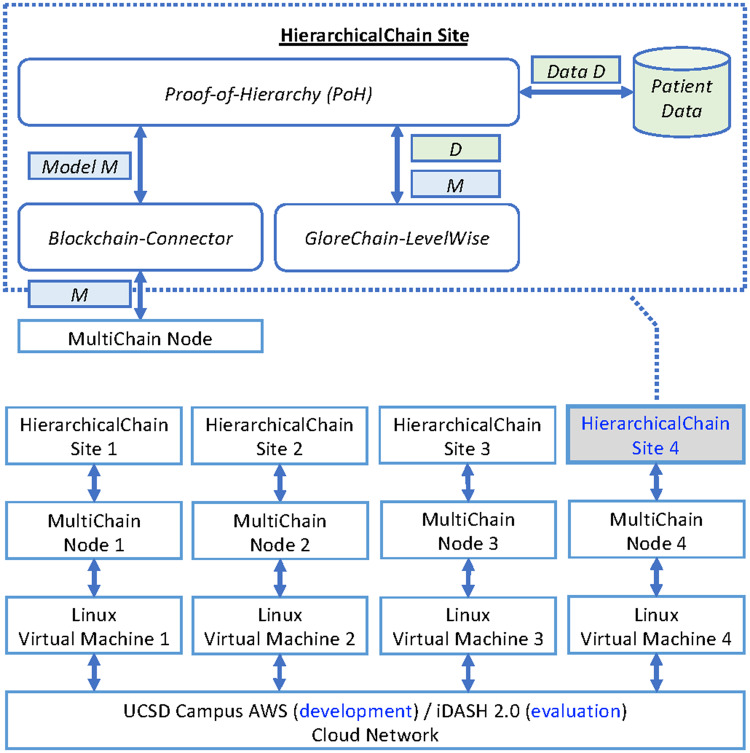
The system architecture of HierarchicalChain is shown in Figure 5. We implemented PoH, Blockchain-Connector, and GloreChain-LevelWise in Java. HierarchicalChain only uses the patient data to compute the models (in the GloreChain-LevelWise component) without disseminating the data to the blockchain network. We adopted MultiChain^27,41 as our blockchain platform, because it is both a system built on top of the well-known Bitcoin Blockchain^11,42 and a permissioned blockchain network for general-purpose ledgering.^10,12,18 The default consensus protocol, Mining Diversity,^27,41 is adopted with default parameters for MultiChain. The system was developed in the UCSD campus Amazon Web Services (AWS)^43,44 and evaluated on the integrating Data for Analysis, Anonymization, and SHaring (iDASH) 2.0 cloud network,^45,46 a private cloud network also based on AWS⁴⁴ and compliant with the Health Insurance Portability and Accountability Act (HIPAA) requirements. In both cloud networks, we used Linux-based Virtual Machines (VMs) to simulate 4-site scenario, and the type of each VM is Amazon EC2 T2 Large (ie, 2 virtual CPUs and 8GB of RAM) with 100GB of storage.⁴⁷

Figure 5.

System architecture of HierarchicalChain which contains 4 participating sites. The Blockchain-Connector component connects the main HierarchicalChain software to the underlying blockchain platform (MultiChain^27,41 in our implementation). Abbreviations: AWS, Amazon Web Services;^43,44 iDASH, integrating Data for Analysis, Anonymization, and Sharing.^45,46

Datasets

To evaluate the algorithms and models of HierarchicalChain, we adopted the following 3 datasets, each with one binary outcome: (1) Edinburg Myocardial Infarction (Edin):⁴⁸ this dataset includes 9 covariates and 1253 observations with the purpose of predicting the presence of disease (class distribution: 0.219 positive and 0.781 negative); (2) Cancer Biomarkers (CA):⁴⁹ there are 2 covariates and 141 observations to predict the presence of cancer (class distribution: 0.638 positive and 0.362 negative); and (3) Total Hip Arthroplasty (THA):^10,50 the data contains 34 covariates and 960 observations aiming at predicting extended hospital stay (ie, hospital length of stay for total hip arthroplasty surgery > 3 days). For the THA dataset, an IRB Exemption Category 4 (Project Number 190385XX) was certified by the UCSD Human Research Protections Program (HRPP) on March 20, 2019.

Experiment settings

Our goal of experiment is to evaluate whether HierarchicalChain can improve the prediction correctness for practical issues—especially for small training data—by using the hierarchical topology information, prioritizing local data, and retaining consensus models from each level in the hierarchy. We compare the horizontal and vertical ensemble methods of HierarchicalChain (ie, HierarchicalChain-Horizontal and HierarchicalChain-Vertical) with GloreChain,¹⁰ the state-of-the-art blockchain-based decentralized learning method designed for flattened network topology.

For both HierarchicalChain and GloreChain methods, the precision of the convergence criterion was 10⁻⁶,^7,10 with the following same hyperparameters based on previous studies,^10,18 the network latency of the cloud networks, and the various sizes and splitting methods of the data: the polling time period Δ = 1 (second), the waiting time period Θ = 5 (seconds), the maximum per-level iteration Ω = 100. The latest 4 transactions with the size of the transaction metadata > 20 were checked to identify new transactions on the blockchain network.

We used the abovementioned 3 datasets (ie, Edin, CA, and THA) to evaluate the methods. For the hierarchical topology, we set the total number of participating sites to N = 4, and the total level of hierarchy to H = 3 (ie, the same topology as shown in Figure 2). That is, we simulated the network-of-networks by splitting each of the 3 datasets into 4 sites in a hierarchical topology.

To simulate the real-world scenario, we tested 2 different ways to split the training data among sites: balanced (ie, the number of records on each site is even) and imbalanced (ie, the number of records on each site is uneven). Therefore, we split each dataset randomly with (1) balanced ratio of 25% for each site, and (2) imbalanced ratios of 10%, 20%, 30%, and 40% for each of the 4 sites, respectively. For each site, the data was randomly divided into 50% training and 50% test records. To further evaluate the effect of the small training data size, we randomly sampled the training data from 0.1 to 1.0 (using the full training data), in increments of 0.1, for the Edin and THA datasets. Since the original size of the CA dataset is already small (141 records), we randomly sampled the training data from only 0.5 to 1.0, in increments of 0.1. For each training and test dataset, including the sampled training data, we preserved a class distribution similar to the original dataset, and kept at least 1 positive and 1 negative record. Our evaluation metric is the full area under the receiver operating characteristic curve (AUC).^36–38 We calculated weighted-average AUC on the test data with the data ratio as the weights (eg, 10%, 20%, 30%, and 40% for imbalanced data splitting) accounting for both balanced and imbalanced data-splitting scenarios. We measured consensus iterations and execution times as well.

The abovementioned process (ie, data splitting, predictive modeling, and weighted-average test AUC computing) was repeated 30 times to collect the results. For the configuration with the smallest training sizes, we further conducted a Wilcoxon signed-rank test^51,52 to examine whether the 2 ensemble methods (ie, horizontal and vertical) of HierarchicalChain perform with statistical significant difference when compared with GloreChain in terms of predictive correctness. We reset the blockchain network for each trial to collect a more accurate execution time.

RESULTS

Predictive correctness

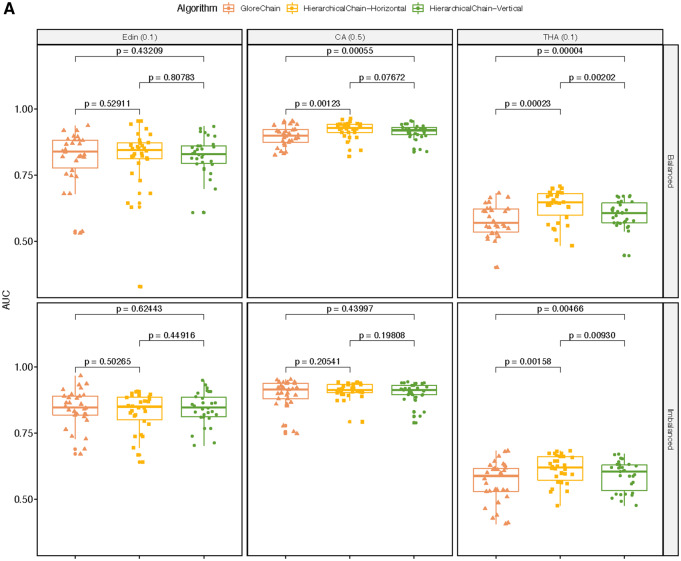
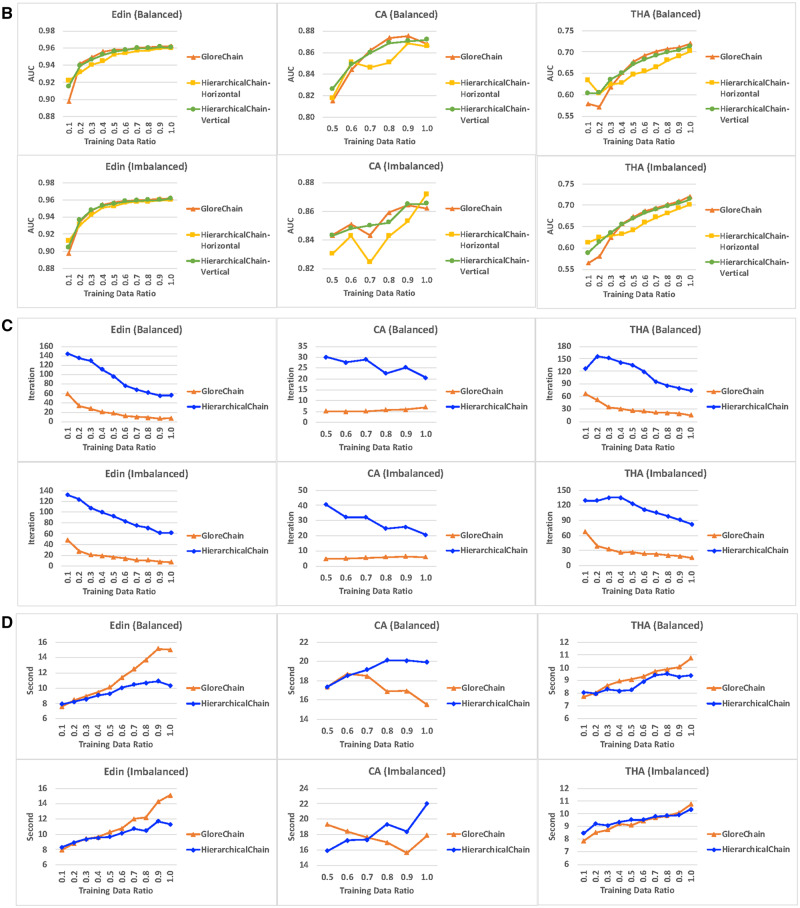
The predictive correctness results on the small training datasets are shown in Figure 6A. In general, both ensemble methods of HierarchicalChain outperformed GloreChain. Especially for the balanced split Edin and THA datasets and the imbalanced split THA datasets, the differences in AUC were statistically significant (with P value < .05). For the CA dataset, vertical ensemble performed better on data with both types of splitting methods, and horizontal ensemble performed better for the balanced split data; however, all of the results have P value ≥ .05. Also, in almost all cases (except the horizontal ensemble on CA dataset), HierarchicalChain showed smaller standard deviation when compared with GloreChain. The results for different training data ratio are depicted in Figure 6B. In general, HierarchicalChain-Vertical performed similar to GloreChain with a larger training data size, while HierarchicalChain-Horizontal provided worse correctness results and was less stable. The lower performance of HierarchicalChain-Horizontal may be due not using high-level models (ie, models from Level 2 and Level 3).

Figure 6.

The results on data with different training data ratio, including 3 datasets (Edin, CA, and THA) as well as 2 data-splitting methods (balanced and imbalanced). We compared 2 ensemble methods (horizontal and ensemble) of HierarchicalChain with the state-of-the-art GloreChain.¹⁰ The data are split to balanced or imbalanced ratios among the sites. A. The predictive correctness results on small training data. The top header represents dataset name (data split ratio). The models are trained using only small portions of the training data. The evaluation metrics is the weighted-average AUC and the P values are computed using the Wilcoxon signed-rank test. B. Prediction correctness, measured in weighted-average test AUC for different training data ratio. C. Learning iterations for different training data ratios. D. Per-iteration execution time measured in seconds for different training data ratios.

Learning iteration

The results of learning iteration on the small training data are shown in Table 2. In general, HierarchicalChain required 2–10 times of iterations when compared with GloreChain. The results for different size of training data are illustrated in Figure 6C. Note that the iterations for HierarchicalChain (computing Level 1, Level 2, and Level 3) were expected to be around 3 times the iterations of GloreChain (computing only Level 3). While this was true for the full-sized training data, on smaller training data the variation became larger.

Table 2.

Learning iteration results on small training data, including both mean and standard deviation (SD). Note that the learning iteration of HierarchicalChain were the sum of the iterations for learning models on Level 1, Level 2, and Level 3, and the computation of vertical and horizontal ensemble did not contribute to the number of iterations. Therefore, only one result per data/split combination was reported for HierarchicalChain. It should also be noted that the maximum per-level iteration Ω in our experiments is set to 100, and therefore the upper limit of the iterations for GloreChain is 100, while the limit for HierarchicalChain is 100 (iterations) x 3 (levels) = 300

Dataset(Training Data Ratio)		Edin(0.1)	CA(0.5)	THA(0.1)
Iterations		Mean (SD)	Mean (SD)	Mean (SD)
Balanced Data Splitting	GloreChain	59.300 (22.968)	5.133 ( 2.871)	66.567 (23.636)
	HierarchicalChain	143.983 (28.953)	30.042 (19.370)	126.575 (28.100)
Imbalanced Data Splitting	GloreChain	47.967 (20.388)	4.800 ( 3.818)	66.900 (22.716)
	HierarchicalChain	131.842 (27.006)	40.608 (25.022)	129.183 (25.776)

Abbreviations: CA, cancer biomarkers; Edin, Edinburg myocardial infarction; THA, total hip arthroplasty.

Execution time

The execution time results for the small training data are shown in Tables 3 and 4. While the total execution times (Table 3) are roughly in proportion to the learning iterations (Table 2), the per-iteration execution times (Table 4) demonstrate similar results for HierarchicalChain and GloreChain. The per-iteration execution time results for different sizes of training data are depicted in Figure 6D. In general, the per-iteration time on smaller training data was also shorter, because the same overhead (eg, initialization time) was shared by a larger number of learning iterations. Also, HierarchicalChain had lower per-iteration time, because the same overhead was shared by 3 levels of computation (GloreChain only computed for 1 level). According to a previous study,¹⁰ most of the execution time was used for waiting/synchronization, and only a small portion of the time (eg, < 0.2 second¹⁰) was used for actual computation of the models.

Table 3.

Total execution time results on small training data, including both mean and standard deviation (SD). The measurements are in seconds and are averaged over 4 sites. The time for HierarchicalChain includes the computation of the model on Level 1, Level 2, and Level 3, as well as the calculation of the horizontal and vertical ensembles

Dataset(Training Data Ratio)		Edin(0.1)	CA(0.5)	THA(0.1)
Execution Time (Second)		Mean (SD)	Mean (SD)	Mean (SD)
Balanced Data Splitting	GloreChain	451.292 (152.107)	89.200 ( 29.019)	515.275 (160.332)
	HierarchicalChain	1142.308 (227.684)	522.142 (213.102)	1023.15 (199.914)
Imbalanced Data Splitting	GloreChain	382.483 (140.145)	92.733 ( 26.047)	526.033 (159.897)
	HierarchicalChain	1094.283 (228.273)	645.392 (284.194)	1095.542 (197.014)

Abbreviations: CA, cancer biomarkers; Edin, Edinburg myocardial infarction; THA, total hip arthroplasty.

Table 4.

Per-iteration execution time results (total execution time in Table 3 divided by the average iterations, which are shown in Table 2)

Dataset(Training Data Ratio)		Edin(0.1)	CA(0.5)	THA(0.1)
Execution Time (Second)		Mean (SD)	Mean (SD)	Mean (SD)
Balanced Data Splitting	GloreChain	7.610 (2.565)	17.377 (5.653)	7.741 (2.409)
	HierarchicalChain	7.934 (1.581)	17.381 (7.094)	8.083 (1.579)
Imbalanced Data Splitting	GloreChain	7.974 (2.922)	19.319 (5.426)	7.863 (2.390)
	HierarchicalChain	8.300 (1.731)	15.893 (6.998)	8.481 (1.525)

Abbreviations: CA, cancer biomarkers; Edin, Edinburg myocardial infarction; THA, total hip arthroplasty.

DISCUSSION

Findings

According to the results, HierarchicalChain, using vertical ensemble to combine the models and prioritize the local ones, outperforms GloreChain for small training data—especially for the THA dataset collected from UCSD Health. Also, in general, the prediction correctness of HierarchicalChain is comparable to GloreChain. Despite the increased learning iterations, the per-iteration execution time of HierarchicalChain remains at the same level as the one for GloreChain. Additionally, HierarchicalChain inherits the benefits of GloreChain (eg, fair compute loads) and advantages of blockchain (eg, no single point of control), and can record models for each level on chain immutably. Finally, HierarchicalChain is more generalizable than GloreChain. That is, HierarchicalChain can be deployed on a flattened network, and, in this case, it becomes exactly the same as GloreChain.

HierarchicalChain, based on GloreChain, can adopt any privacy-preserving learning algorithms, including both batch and online methods.¹⁰ HierarchicalChain overcomes blockchain confidentiality issues by exchanging models from each level without transferring patient-level data; avoids the blockchain scalability issue, because the per-iteration learning time (5–30 seconds per iteration) is way longer than the average transaction time of a blockchain (< 1 second); and mitigates the blockchain 51% attack issue because of the permissioned network nature.

HierarchicalChain can also adopt different underlying blockchain platforms. That is, in our experiment, we adopted MultiChain with its low energy-consuming Mining Diversity consensus protocol; however, any other blockchain platform can also serve as the peer-to-peer infrastructure. The size of the model in our experiments is about 5 KB, which is smaller than the default size limit (2 MB) of MultiChain or other mainstream blockchain platforms.⁵³ Also, the iDASH 2.0 cloud network provides an additional layer of security protection beyond the permissioned blockchain network.

Limitations

The limitations for this work include: (1) Topology. HierarchicalChain was not tested on nonperfect tree topologies, which can contain different site numbers in various levels and may impact the performance of the correctness, iterations, and execution time; (2) Data. We did not evaluate on data with a large number of covariates, missing/nonrepresentative data, and highly different data distribution among the sites or the levels; (3) Advanced privacy concerns. Although this study focused on protecting patient privacy by having healthcare institutions exchange aggregated machine learning model without disseminating patient-level data, more advanced privacy concerns, such as institutional privacy⁵⁴ (ie, the model may still reveal some information for the institution) and differential privacy⁵⁵ (ie, the patient-level data may be inferred under certain circumstances), were not covered. Also, our method assumed that each participating institution is “honest but curious,”⁵⁶ and therefore did not deal with the situation where an institution may submit a malicious model in an attempt to jeopardize the learning process or to inspect information from other institutions. (4) Ethical, Legal, and Social Implications (ELSI). We focused on providing a technical solution and have yet to investigate the ELSI considerations regarding the tradeoff of privacy risks versus patient benefits, which can depend on the purposes of the analysis (eg, London cholera outbreak,^57–60 bioterrorism attack,^61,62 or Ebola outbreak^63–65).

CONCLUSION

By training the predictive models using level-wise methods, disseminating the models using a blockchain network, and combining models using a novel hierarchical consensus learning algorithm, our privacy-preserving learning framework: 1) improves prediction correctness especially for the use case of having a small training dataset for rare diseases/conditions; 2) keeps similar per-iteration execution time; 3) inherits benefits from decentralized learning and blockchain technology; and 4) records models of each level, immutably. Although such an improvement may not have clinical significance and more learning iterations are needed, we demonstrated the potential of utilizing the information from the hierarchical network-of-networks topology to improve the prediction. With further evaluations and enhancements, our proposed framework can create more generalizable predictive models to support clinical/genomic/biomedical studies within real-world research networks.

FUNDING

T-TK is funded by the U.S. National Institutes of Health (NIH) (R00HG009680, R01HL136835, R01GM118609, and U01EB02385) and UCSD Academic Senate Research Grant (RG084150). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. The use of the integrating Data for Analysis, Anonymization, and SHaring (iDASH) 2.0 and the UCSD Campus Amazon Web Services (AWS) cloud network is supported by Michael Hogarth, MD and Andrew Greaves.

AUTHOR CONTRIBUTIONS

T-TK contributed in conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, validation, visualization, supervision, and writing (original draft). JK contributed in validation, visualization, and writing (review and editing). RAG contributed in data curation and writing (review and editing).